The First Step to Learning Place Value: A Role for Physical Models?

Very few questions have cast such an enduring effect in cognitive science as the question of “symbol-grounding”: Do human-invented symbol systems have to be grounded to physical objects to gain meanings? This question has strongly influenced research and practice in education involving the use of physical models and manipulatives. However, the evidence on the effectiveness of physical models is mixed. We suggest that rethinking physical models in terms of analogies, rather than groundings, offers useful insights. Three experiments with 4- to 6-year-old children showed that they can learn about how written multi-digit numbers are named and how they are used to represent relative magnitudes based on exposure to either a few pairs of written multi-digit numbers and their corresponding names, or exposure to multi-digit number names and their corresponding physical models made up by simple shapes (e.g., big-medium-small discs); but they failed to learn with traditional mathematical manipulatives (i.e., base-10 blocks, abacus) that provide a more complete grounding of the base-10 principles. These findings have implications for place value instruction in schools and for the determination of principles to guide the use of physical models.

Introduction

Do symbols need to be grounded to their physical referents to have meanings? Thirty years ago, Harnad (1990) posed this question motivating empirical studies and theoretical debates across many subfields of cognitive science (Taddeo and Floridi, 2005; Steels, 2008; De Vega et al., 2008; Dove, 2016). The issues are still theoretically (Socher et al., 2013; Wang et al., 2019) and practically relevant, especially within the field of education (Alibali and Nathan, 2012; Pouw et al., 2014; Stolz, 2015). How do symbols—the letters of the alphabet, the digits of Arabic numbers—become able to convey meaning? A grounded symbol is one that gains meaning directly through the perception of that meaning, as the symbol “7” may gain meaning through the direct perception of seven discrete entities. In mathematics education, theoretical ideas about symbol grounding influenced and encouraged the use of physical models and manipulatives as a way to make abstract concepts directly perceivable (Sowell, 1989; Sarama and Clements, 2009; Carbonneau et al., 2013). Efficacy studies, however, yielded mixed results (Son et al., 2008; McNeil et al., 2009; Carbonneau et al., 2013; Mix et al., 2014; Mix et al., 2017) and no clear principles as to when physical models are helpful. Here, we propose a rethinking of physical models in education—not as a path to grounding, but as analogies that help learners discover inherently abstract relations. We consider these ideas with respect to children’s early learning about multi-digit notation.

Multi-digit Arabic numbers represent magnitudes through a base-10 system: 232 is named as “two hundred thirty-two”, and is composed of 2 sets of 100 s, 3 sets of 10 s, and 2 sets of 1 s. 232 is less than 322, because the former indicates 2 rather than 3 sets of hundreds—even though these two numbers are composed of the exact same set of individual digits. Understanding this hierarchical structure and the algebraic relations within multi-digit numbers is the goal of formal place value instruction and the foundation for developing advanced calculation skills. Both research and educational practice (Montessori, 1917; Bruner, 1966; Fuson, 1986; Fuson and Briars, 1990; Geary, 2007; Bussi, 2011) have focused on how to ground base-10 relations (e.g., 100 is 10 sets of 10, and 10 is 10 sets of 1) in physical models, sometimes also known as mathematical manipulatives. For example, base-10 blocks ground the meanings of the counts of each place, the multiplicative relations among the places, and the exact represented discrete quantities using blocks composed of small cubes such that each cube represents one, bars (called “longs” in math education) contain 10 ones, and large blocks (called “flats” in math education) contain 100 ones. These blocks are then used to physically instantiate specific amounts such that “232” is represented as 2 big blocks, 3 bars, and 2 cubes. Despite widespread use, early learners can have difficulties in understanding just what this is all about: some when shown a display such as that for “232” count the total number of blocks (seven blocks), some try to count all the cubes (Chan et al., 2014), and some studies show little benefit of the addition of these physical models (Ball, 1992). We believe that the problem may be that these blocks try to provide a full grounding of the unit size of places, their counts, and the exact quantity, and in doing so, base-10 blocks—just like the base-10 system itself—are too much for a naïve learner to grasp all at once. A complete grounding of the base-10 hierarchy may benefit later learning, but it may not be the best way to introduce the multi-digit number system.

Recent studies suggest that children’s learning about place value starts early and proceeds incrementally (Byrge et al., 2014; Mix et al., 2014; Mix et al., Under review; Yuan et al., 2019). Children first learn about the place relations that structure multi-digit numbers before formal school instruction on place value. This early understanding does not include precise knowledge of the different quantities represented by the places nor their multiplicative relations to each other (Byrge et al., 2014; Mix et al., 2014; Yuan et al., 2019; Yuan et al., 2020). Instead, it is an “approximate” understanding that multi-digit numbers are made up of places that represent different relative magnitudes ordered from left to right. Critically, this early approximate knowledge strongly predicts later success in learning and using base-10 principles (Mix et al., Under review), suggesting that approximate understanding is a useful step to more explicit correct understanding. Current evidence suggests further that young children acquire this approximate understanding through experience with the correspondences between spoken and written number names, e.g., learning that the “hundred” and the “-ty” in “two hundred thirty two” mark the places in the string “232” as signifying different amounts (Mix et al., Under review; Yuan et al., 2020). Multiple experiments (Byrge et al., 2014; Mix et al., 2014; Mix et al., 2017; Yuan et al., 2019) have shown that this partial knowledge enables preschool and kindergarten children to map unfamiliar number names to written forms for 3- and 4-digit numbers, to judge the relative magnitudes of 3- and 4-digit numbers, and to write multi-digit numbers given the spoken name (albeit sometimes with meaningful and interesting errors) (Mix et al., 2014). The three experiments reported here focus on this first step in learning about place value: that there are different places that signify different amounts. We ask whether and how physical models might benefit this learning.

In science, physical models are often used not to ground meaning but as analogies to distill the skeleton of an idea: for example, an atom is like the Solar System in that each has smaller elements rotating around a larger one (Gentner, 1983). These simple analogies are helpful to initialize learning and can support higher conceptual inferences, but they are not fully correct (Gentner and Stevens, 1983; Mix, 2010; Mix et al., 2019; Richland et al., 2017; Richland and Simms, 2015). Gentner’s Structure Mapping theory (Gentner, 1983; Gentner, 2010) proposes that analogies work because they support the alignment of two relational systems that enable the relations—independent of the elements in those relations—to be extracted. The key to extracting the common relational structure is the alignment and mapping of corresponding elements—e.g., the nucleus to the Sun, the planets to electrons. Experiments with many kinds of materials and different aged participants show that relational structures can be discovered and broadly generalized in very few trials if the learner properly aligns the elements across examples (Loewenstein and Gentner, 2001; Namy and Gentner, 2002; Rattermann and Gentner, 1998; Yuan et al., 2017). Figure 1 provides an illustration of the relevant findings. Given an array such as that in Figure 1A, 4-year-olds do not immediately see the big-medium-small structure and have considerable difficulty at picking out another configuration that exemplifies the same relational structure (Kotovsky and Gentner, 1996). But adding another configuration as shown in Figure 1B and inviting children to compare the two significantly increases the likelihood that they can find the relational pattern and apply it to a new configuration. The dotted lines in Figure 1B denote the one-to-one alignment between elements in the two examples; through these alignments, children may start to “see”, for example, that although the biggest square of the left configuration is perceptually different from the biggest circle in the right configuration, they both stand in the same relation to the other members of the array. Perceptual properties or added components that disrupt the alignment of elements disrupt the discovery and generalization of the relational pattern (Kaminski and Sloutsky, 2013; McNeil et al., 2009; Paik and Mix, 2008; Uttal et al., 2008; Rattermann and Gentner, 1998; Son et al., 2012a; Yuan et al., 2017). For example, as shown in Figure 1C, the medium square of the left configuration can be mapped either to the largest square of the right configuration (because they are perceptually identical: Object match) or to the medium square of the right configuration (because they are both the medium one within each triplet: Relational match). Likewise, finding the common relational structure is also more difficult when the component elements are heavily detailed and perceptually rich. As shown in Figure 1D, the perceptual richness of the Mickey mouses and the keys with all of their vivid color and interesting shapes can make the individual categories so salient that children represent the left configuration as “They are Mickeys!” rather than “These Mickeys are ordered from largest to smallest”. Consistent with this view, past research (McNeil et al., 2009) showed that teaching children calculation with mathematical manipulatives that resembled real money with many details was significantly less effective than using white paper money with only written numbers on them without other extraneous perceptual features.

FIGURE 1

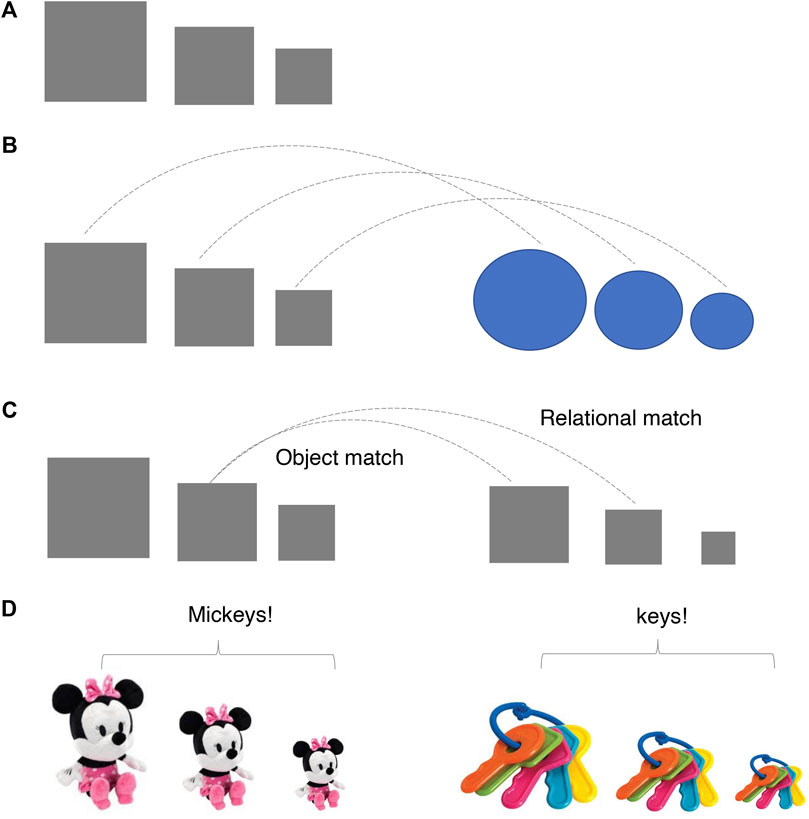
FIGURE 1. The challenges and ways to extract relational structures: (A) Extracting relational patterns from a single exemplar is difficult for young children. (B) Aligning and comparing two analogs that share the same relational pattern can help. (C) Alignment based on relational match is difficult to establish with the presence of object match. (D) Richly detailed components often draw learners’ attention to object identities rather than relational patterns.

From the perspective of the Structure Mapping Theory and as illustrated in Figure 2, base-10 blocks present a web of mappings at multiple levels all at once, an approach that is contrary to the existing evidence that too many mappings may obscure the discovery of relational structure. The demand of multiple levels of mappings in visual illustrations—meant to clarify text—has been shown to be unhelpful even for college students’ learning (Wills et al., 2008; Okeefe et al., 2014; Rau, 2017). This problem of “coordinating multiple representations” is well recognized in the learning science literature on teaching and learning in higher education (Rau, 2017), but it is rarely discussed for children’s early learning. This problem is also compounded—for example, in the case of base-10 blocks—when there are features that draw learners’ attention to the properties of individual elements at the expense of highlighting the relations among the elements. For example, marking the individual 100 small cube units in a large block (or the “flats”) focuses too much on faithfully grounding the “hundred” unit to 100 discrete entities rather than highlighting the relation that the “hundred” place is larger than the “decade” place (which is further larger than the “unit” place). Past research has shown that perceptual properties that contain too many details about individuals often result in learners’ failures in recognizing and learning about the relations among individuals and that subtle changes in the direction of presenting the “skeleton” of the relational structure can benefit learning (Rattermann and Gentner, 1998; Paik and Mix, 2008; Kaminski and Sloutsky, 2013; Yuan et al., 2017).

FIGURE 2

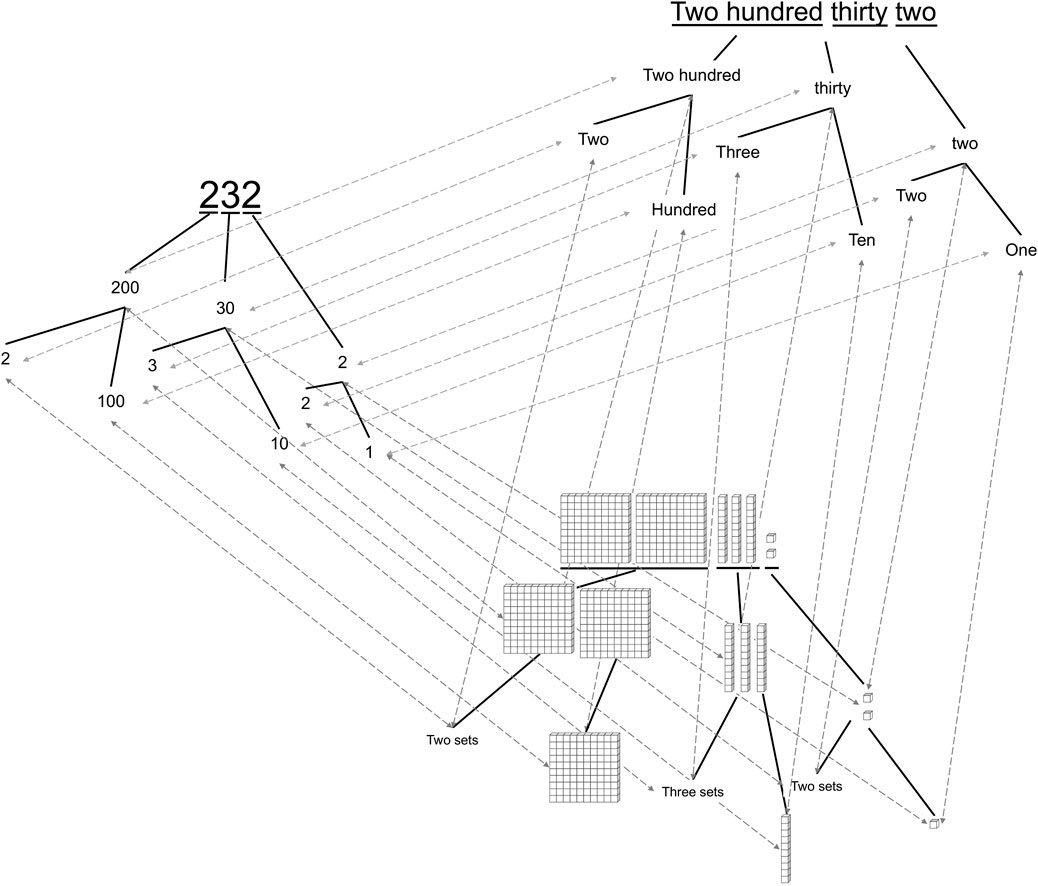
FIGURE 2. Systems of relational mappings among a written multi-digit number, its corresponding number name, and the base-10 blocks representation of its numerical quantity. The solid lines highlight the structure within each representation, while the dotted lines denote the myriad relational mappings between corresponding components.

From the perspective of the Structure Mapping Theory, relations are found through aligning arrays with the same relational structure and do not necessarily require that the aligned arrays include physical models. Thus, the alignment of number names (one symbolic form) to written forms (another symbolic form)—with no physical model—could be sufficient for an early learner (Mix et al., 2019; Yuan et al., 2020). Multi-digit number names and the written forms have distinct surface forms, but the same underlying relational structure as shown in Figure 2. Thus, mapping multi-digit number names to their written forms could yield the discovery of the relational structure—that there are places ordered by relative magnitudes from left to right. This could work because multi-digit number names likely have intuitive meanings that young children partially know—e.g., that “hundred” means “a whole lot” and “-ty” signals a pretty big number as well. These intuitive meanings do not have to be exact to help children find the relational structures. For example, given the big-medium-small relational pattern in Figure 1A, children are helped in finding and generalizing that pattern when the elements are aligned with the words “daddy-mommy-baby” (Kotovsky and Gentner, 1996), which only roughly imply size. These arguments, however, do not mean that physical analogies cannot help, they should if they help children align the elements in spoken and written number names.

Rationale for the Three Experiments

The three experiments examine the role of relational mapping and physical models in children’s discovery of place value through the alignment of multi-digit number names, written notation, or physical models. Across all three experiments, there are pretests and posttests, as well as mapping experiences in between those tests. The mapping experiences merely coach the alignment of elements across examples (spoken number names, written numbers, and physical models) with the same relational structures. Because alignment has been shown to support the extraction of the relational structure in a few trials (Son et al., 2012a; Son et al., 2012b), there were not many mapping trials. In addition, explanations are minimal—typical in relational learning experiences—since aligning elements is the hypothesized key factor to discovering relations. The participants were 4- to 6-year-olds, who were in preschool or kindergarten classes and who had not been formally introduced to the place value system in school.

Experiment 1

Experiment 1 was designed to test whether the discovery of the common relational structure of multi-digit number names, their written forms, and their magnitudes is better achieved—through the use of physical models (base-10 blocks and abacus) which provide groundings of the base-10 hierarchies (e.g., 100 is 10 sets of 10), or merely by mapping the two symbolic forms (written and spoken) of multi-digit numbers. In the experiment, the Symbols-to-Symbols condition involves only number names and their corresponding digits with the mapping goal consisting of a direct alignment between corresponding elements of the two symbol systems. Next in complexity is the Symbols-to-Abacus condition; in addition to number names and written forms, the columns of the abacus align spatially with the places and the numbers of discs at each column align with the digit in each place, providing the common meaning that links the written symbols and their spoken names. The Symbols-to-Blocks condition is the most complex; the symbols align with the number of whole blocks, the cells within the blocks align with the actual amount represented, and the spatial arrangement of the blocks aligns with different places. If the number of correlated features supports finding the aligned relation, one might expect the Symbols-to-Blocks condition to best support the relational structure underlying number names, their written forms, and their relative magnitudes. If simplicity and alignment of common elements is the key, then the Symbols-to-Symbols condition may lead to better discovery of places and their relative magnitudes.

In all conditions, we used a coached imitation task to foster alignment of heard number names, written digits, and physical models (in the physical model conditions). The experimenter said the number name, created the written number with digit cards, and then in the model conditions, made a model of the number with the manipulatives, repeating the number name, and aligning the model and the written number in space. The child was then asked to copy these constructions with the experimenter’s model and digit cards in view, and if the child made a mistake, he or she was coached to make the correct constructions by the experimenter. We measured and used the number of errors in the mapping task as an indicator of the perceptual transparency of the alignments to the children. We also measured children’s pre- and post-test performance using numbers that were not trained during mapping. There were two pre- and posttest tasks: mapping number names to written digits and magnitude comparison of written numbers.

Participants

Seventy-five children (37 females and 38 males, age range: 4.03–6.88 years) participated in the study. As noted above, the participating children in this and all following studies were enrolled in preschool or kindergarten; none had entered first grade. The age of the sample was sensibly and positively skewed (median: 5.33 years, mean: 5.44 years), reflecting a range of 4 to early 6 years, with very few older 6-year-olds who had not yet started first grade at the time of the study due to various reasons (e.g., their birthday fell after the school district’s fall cut-off for 6-year-olds to enter first grade). This age range was appropriate, given that we were broadly interested in children’s early learning of multi-digit numbers before formal education. Participants were recruited through community organizations (e.g., farmers’ markets, child outreach events, boys’ and girls’ clubs) and local preschool and daycare centers. The sample of children was broadly representative of the local population (84% European American, 5% African American, 5% Asian American, 2% Latino, 4% Others) and consisted of predominantly working- and middle-class families. The study was approved by the Human Subjects and Institutional Review Boards at Indiana University. In this and all following studies, informed consents were obtained from the legal guardian and assents were obtained from the children prior to the experiment. Children were randomly assigned to one of three conditions: Symbols-to-Symbols mapping (n = 27), Symbols-to-Abacus mapping (n = 23), and Symbols-to-Blocks mapping (n = 25).

Materials and Procedure

This experiment had three phases: pretest, relational mapping trials, and posttest.

Pre- and Posttest

The pre- and posttests consisted of two established tasks: the which-N and which-More tasks (Mix et al., 2014; Yuan et al., 2019). On each trial, children were presented with a pair of written multi-digit numbers. In the Which-N task, children were told a spoken number name and then asked to select the written form that matched the name; in the which-More task, they were asked to select the one that was more. There were 16 trials for each of the tasks with a total of 32 trials (Table 1). Accordingly, 32 cards were made with two multi-digit numbers (roughly 17.78 cm wide and 12.7 cm tall) printed at the center of the card. The particular numbers used in the tasks were randomly sampled from 1- to 4-digit numbers. The pair of target and foil numbers were chosen from a variety of different types to avoid the possibility that knowing any single strategy or heuristic would allow the participant to solve all (or majority) of the trials. For example, simply knowing that numbers with more digits signify larger values is not enough to successfully choose the larger value between 223 v 220. Similarly, knowing that “three hundred and five” should start with “3” alone is not enough to choose the correct written form of “three hundred and five” given 350 v 305. These different types have been used in previous research (Yuan et al., 2019) and include single digits numbers (e.g., 2 v 8), numbers with different numbers of places (e.g., 36 v 306), transpositions (e.g., 350 v 305), numbers that differed in only one digit (e.g., 105 v 125), and numbers with no digit overlapping (e.g., 11 v 24). Items in the which-More task were sampled using the same method as those used in the which-N task, but the two tasks involved different numbers to avoid the possibility that exposure to items in one task would influence participants’ responses to the same items in the other task. Because during the which-More task children were expected to always choose the numerically larger number, consistent with established procedures and to counterbalance the response demand across the two tasks, the experimenter always asked the numerically smaller number of the two in the which-N task.

TABLE 1

TABLE 1. All tasks and items used in the three experiments.

For each of the test tasks, the same items were used at both pretest and posttest, which allowed us to measure the effectiveness of relational mapping on children’s discovery of the relational structure. Two versions were created that counterbalanced the order of the individual items. If a child received version A at pretest, she/he would receive version B at posttest; we did this to minimize the test-retest effect. No feedback was given at pretest or posttest.

Mapping

As shown in Figure 3 top, during the mapping trials, participants imitated the experimenter to make multi-digit numbers using three different sets of materials (i.e., number cards only, number cards with abacus, number cards with base-10 blocks). The base-10 blocks included three types that each represents one place value unit. The small squares were 1.016 cm wide and 1.016 cm tall and were used to represent the unit of one. The bars were composed of ten small squares attached together to form a bar shape (1.016 cm wide and 10.16 cm long), and they represented the unit of ten. The big squares were composed of ten bars attached together to form a big square (10.16 cm by 10.16 cm), and they represented the unit of hundred. The abacus was 28 cm wide and 25 cm tall, composed of two horizontal bars at the top and bottom and three vertical bars for holding the discs at each place value unit (e.g., left bar: the hundred place, middle bar: the decade place, right bar: the unit place). Nine discs were attached to each of the vertical bars and different colors were used to help participants differentiate the places: discs in the hundred place were blue, those in the decade place were yellow, and those in the unit place were red. All of the discs were of the same size (with a diameter of 3 cm). The number cards (4 cm wide and 7 ¼ cm tall) were composed of individual cards with single digits (i.e., 0–9) printed at the center of each card in Times font. There were 15 mapping trials during which children from all three conditions were first presented with a target card (12 cm wide and 7 ¼ cm tall) with the target multi-digit number printed at the center in Times font. The 15 target numbers were: 14, 163, 187, 65, 4, 23, 451, 52, 6, 673, 72, 8, 901, 838, 94. The multi-digit numbers that participants received during mapping and those used for pre- and post-tests were different. In other words, if participants’ performances in the testing tasks have improved from pre- to post-test, then it would suggest that they have learned from the mapping experience and generalized that learning to different items used in the testing tasks.

FIGURE 3

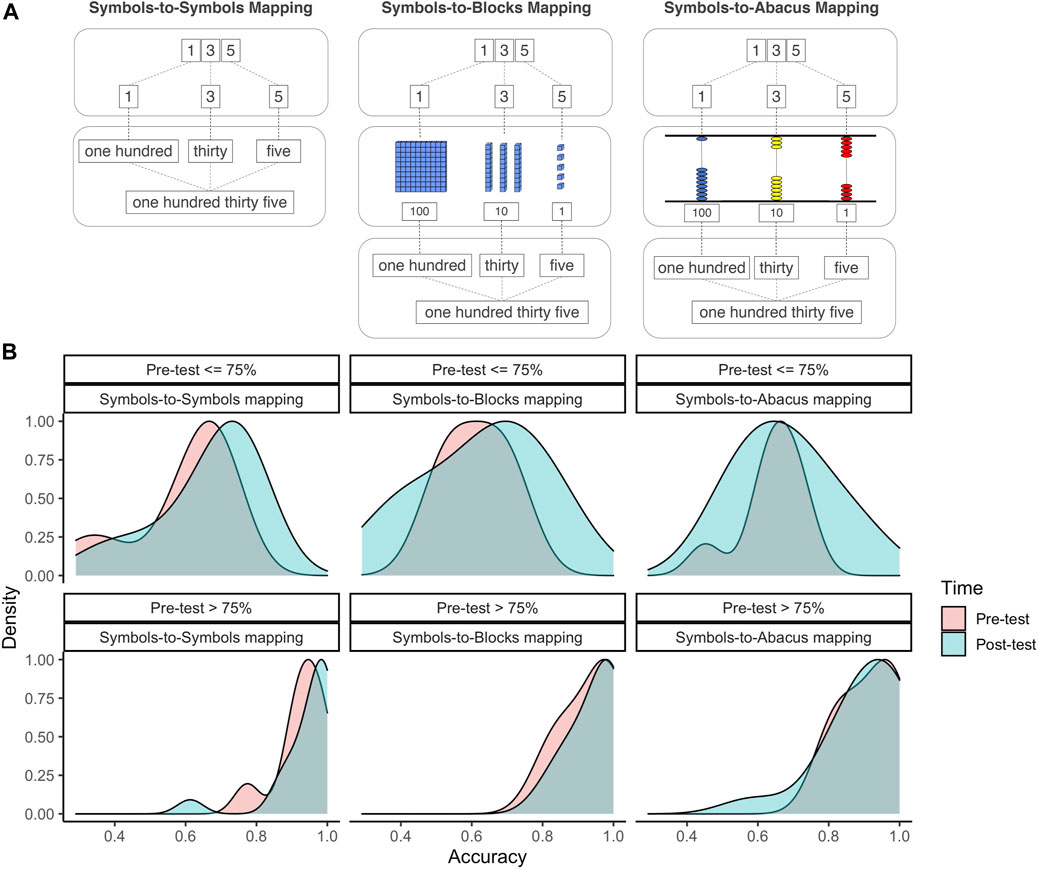
FIGURE 3. (A): Illustrations for the three mapping conditions in Experiment 1. (B): Density graphs of participants’ accuracy in Experiment 1 by condition, test time (pre- and post-test), and pre-test familiarity with multi-digit number symbols. In (B)top row: children who scored less than or equal to 75% at pre-test. In (B)bottom row: children who scored above 75% at pre-test. Pink indicates pre-test performance and turquoise indicates post-test performance.

For all three conditions, 10 piles of individual digits cards from “0” to “9” were laid out in sequence on the left side of a table. During the mapping trials, both the experimenter and the child took individual cards from these piles to make multi-digit numbers. In each condition, there were 15 mapping trials; this small number is consistent with prior work which has shown that a relatively few such mapping experiences can yield generalizable discovery of relations in preschoolers (Rattermann and Gentner, 1998; Son et al., 2012a; Yuan et al., 2017).

Symbols-to-Symbols mapping. The experimenter first introduced the individual number cards to the participant, “We have some number cards here.” She then pointed to each pile from “0” to “9” and named the digit for the child from “zero” to “nine”. She told the child that they were going to make some numbers using these cards. She gave one example by picking up a card with “1” and a card with “3”, laying them down on the table side-by-side while saying, “I have made thirteen. Can you make thirteen using these cards?” There were 15 such mapping trials. Children only had to copy the same actions as the experimenter, so potentially performance could be errorless. The ability to make correct copies—trial by trial—provides a measure of the obviousness of the alignment between different components (e.g., number names to written forms). In all conditions, initial copy attempts by the child were scored as correct or incorrect (e.g., if the to be copied item was “13” and the child took a 7 instead of a 1, or made 31 instead of 13, it would be scored as incorrect). On all incorrect trials, the experimenter coached the child into making a final correct copy and repeated the name (e.g., “See you made 13”) to the correct version of the written form.

Symbols-to-Abacus mapping. The experimenter introduced and named the digits cards from “0” to “9” similar to the Symbols-to-Symbols condition. She then familiarized the participant to the abacus, telling the children the name of the abacus and showing them how the discs could be moved and allowing them to do so. The experimenter then gave an example by laying down the cards “1” and “3” while saying “Here is thirteen. Now watch, I am going to make thirteen using the abacus.” She then put the correct abacus configuration down underneath the cards while saying, “I’m making thirteen,” or “Here is thirteen.” She then asked the child, “Can you make thirteen using your cards and then with the abacus?” The participant then made the corresponding number first with their own cards and then with the abacus and the experimenter repeated the spoken name when the written number was correctly formed and when the abacus model was correctly formed. On all incorrect trials, the experimenter coached the child into making the final correct copy and repeated the correct number name.

Symbols-to-Blocks mapping. The experimenter first introduced and named the digits cards from “0” to “9” in the same way as the Symbols-to-Symbols condition and introduced the different sized blocks. During the mapping trials, the experimenter first picked out individual cards and laid them down on the table to make a target number. For example, she might pick out cards “1” and “3”, laying them down side-by-side on the table while telling the participant that “I have made thirteen using our cards. Next, I am going to make thirteen using our blocks.” She then put the correct number of blocks down underneath the cards (a tens block under the card “1” and three ones blocks under the card “3”) while saying, “I’m making thirteen,” or “Here is thirteen.” She then asked the child, “Can you make thirteen using your cards and blocks?” The participant then made the corresponding number first with their own cards and then with their own blocks. The experimenter repeated the number name when the written form was correctly formed and also when the block model was correctly formed. On all incorrect trials, the experimenter coached the child into making the final correct copy and repeated the correct number name.

Results

To determine the possibility of pre-existing group differences, we compared children’s performance at pre-test across the three conditions. In this and all following analyses, logistic mixed effect models were used to evaluate children’s performance under different training conditions. Such models allowed us to utilize item-level data from each participant (rather than computing a summary score—e.g., mean, median—for each participant) and to take into consideration the multi-level hierarchical structure of experimental studies, in which multiple trials are nested within corresponding participants and multiple participants are nested within corresponding experimental conditions (Singmann and Kellen, 2019). A logistic mixed effect model was conducted in the R environment (R Core Team, 2020) using the Afex package (Singmann et al., 2015). Condition was entered as a fixed variable, participant and test item were entered as random variables; the dependent variable was the accuracy of the individual trials (i.e., 0 or 1) in the which-N and which-More tasks at pre-test. There was no significant main effect of condition, χ² (2) = 0.71, p = 0.70, suggesting that children assigned to the three mapping conditions started out at comparable levels of competencies. As evident in Figure 3, there were, however, considerable individual differences with some children performing at levels above 75% at pretest but other children performing much more poorly. These individual differences in early informal knowledge have been reported previously (Byrge et al., 2014; Yuan et al., 2019). Although continuous age (in month) was correlated with individual children’s performance at pretest (r² = 0.42, p < 0.001) and post-test (r² = 0.38, p < 0.001), there was no evidence that age was related to how much children had improved after the training (overall: r² = 0.0005, p = 0.85; Symbols-to-Symbols condition: r² = 0.04, p = 0.29; Symbols-to-Blocks condition: r² = 0.02, p = 0.54; Symbols-to-Abacus condition: r² = 0.007, p = 0.69). As stated above, none of the participants had yet attended first grade at the time of the study. Given that we were broadly interested in how children can learn from symbolic and physical representations of multi-digit numbers before receiving formal place value instructions at schools and the large individual differences in early knowledge beyond the factor of age, we collapsed children across the different age groups in all following analyses.

Children’s ability to copy the experimenter’s models (and the need of direct coaching) during the mapping trials provides a measure of the obviousness of the alignment of elements across arrays. Children were reasonably successful in the copying task across the three conditions but were better able to correctly copy the arrays in the Symbols-to-Symbols conditions than in the two physical models conditions. A logistic mixed effect model, in which condition was entered as the fixed variable, participant and test item were entered as random variables, revealed a significant main effect of condition, χ² (2) = 33.46, p < 0.001. Children were significantly more accurate during mapping trials in the Symbols-to-Symbols condition (Mean = 0.98, SE = 0.008) than in the Symbols-to-Blocks condition (Mean = 0.78, SE = 0.039), t (26) = 4.77, p < 0.001, and the Symbols-to-Abacus condition (Mean = 0.87, SE = 0.036), t (24) = 3.16, p = 0.004. There was no significant difference between the Symbols-to-Blocks and Symbols-to-Abacus conditions, t (46) = 1.38, p = 0.17.

The key test of the discovery of the relational pattern is whether children can apply the pattern to arrays that were not experienced during training (measured in the Which-N task) and whether they can make inferences from the relational patterns as to the indicated magnitude (measured in the Which-More task). Children’s performances relative to pretest increased in the Symbols-to-Symbols condition but not in the Symbols-to-Blocks or the Symbols-to-Abacus conditions. Logistic mixed effect models on the pre- and post-test performances were conducted for each condition with test time (pre-test vs. post-test) and test task (which-N vs. which-More) entered as fixed variables and participant and test item entered as random variables, and accuracy on individual items as the dependent variable. For the Symbols-to-Symbols condition, there was a significant main effect of test time, χ² (1) = 4.24, p = 0.039, with performance improving from pre-test (Mean = 0.80, SE = 0.04) to post-test (Mean = 0.84, SE = 0.03). There was no reliable main effect of test task, χ² (1) = 1.72, p = 0.19, nor interaction between the two fixed effects, χ² (1) = 0.13, p = 0.72. For both the Symbols-to-Blocks condition and the Symbols-to-Abacus condition, the models failed to detect any significant main effect of test time (ps > 0.43), task (ps > 0.14), nor an interaction between them (ps > 0.71).

Figure 3 bottom shows density plots of children’s performance at pre-test and post-test for the three conditions and separated by children with high and low prior knowledge (defined by 75%¹ accuracy in the composite score of the which-N and which-More task at pre-test). In the Symbols-to-Symbols condition, the performance distributions for both children with high and low prior knowledge have shifted to the right from pre- to post-test. Interestingly, for both the Symbols-to-Abacus condition and the Symbols-to-Blocks condition, the distribution of children with low prior knowledge widened after the mapping experience, suggesting that the use of physical models helped some children but hurt others. Past work has shown that relational structures become easier to perceive with expertise and exposure to the content domain (Chi, 1978; Chi et al., 1981). Thus, one possible explanation for the ineffectiveness of traditional manipulatives in the current experiment is that most children were not ready for and could not yet utilize the information in these more complex (albeit more accurate) models of the notational system. We return to these issues in Experiment 3 and in the General Discussion.

Discussion

Experiment 1 shows that 1) the alignment of number names and written forms is sufficient for children to discover the relational patterns that map number names to written forms and to judge the relative magnitudes of multidigit numbers, and 2) it illustrates how adding additional information—even though relevant and even though redundant—can make the initial discovery of the relational patterns through structure mapping less likely.

Experiment 2

The finding that a few Symbols-to-Symbols mapping experiences supported the discovery and generalization of the relational pattern underlying number names and their written forms is surprising in the context of a body of literature that has generally concluded that the mapping between number names and written forms is hard to learn (Baroody, 1990; Fuson, 1990). Accordingly, the explicit goal of Experiment 2 was to replicate with a larger sample the finding that relatively few mapping trials enabled learners to find and generalize the pattern. To this end, we realized the mapping trials in two different ways: using the approach of Experiment 1 and also a slightly different approach that has been commonly used in Montessori schools. In the Digits mapping condition as in Experiment 1, children created multi-digit numbers by using individual digit cards (e.g., “2”, “3”, “2”) mapped to their spoken name “two hundred”, “thirty”, “two”). In the Expanded mapping condition, they mapped expanded cards (e.g., “200”, “30”, “2”—“two hundred”, “thirty”, “two”) to the name by stacking them on top of each other to form a visual array showing the place value notation (“232”).

Participants

Ninety-three children (50 females) recruited from the same general population as Experiment 1 participated in this study (age range 4.03–6.82 years, median: 5.26, mean: 5.39). Children were randomly assigned to the Digits mapping condition (n = 42) or the Expanded mapping condition (n = 51). The study was approved by the Human Subjects and Institutional Review Boards at Indiana University. Informed consents were obtained from the guardian and assents were obtained from the children prior to the study.

Materials and Procedures

The which-N and which-More tasks were used as Pre- and Post-tests like Experiment 1. There were 20 trials for each of the tasks (shown in Table 1) with 10 easier trials that involved mostly 2- and 3-digits numbers and 10 harder trials that involved 3- and 4-digit numbers. Children were first given the 10 easy trials; if they got 7 out of 10 of those trials correct, we proceeded onto the next set of 10 trials. We used this approach to maintain the participation of children who found the tasks (particularly at pre-test) too difficult to continue through all 20 trials. Two orders were created that counterbalanced the order of the individual items across pre- and post-tests. No feedback was given at pre- and post-tests.

Mapping

There were 20 mapping trials and correspondingly 20 cards with the numbers 163, 51, 846, 47, 271, 94, 18, 36, 328, 451, 62, 65, 719, 653, 594, 587, 23, 89, 72, 972. The mapping experiences immediately followed the pre-test for all participants. In both conditions, the procedures were structured similarly as in Experiment 1 except for two differences. First, we followed a “progressive alignment” approach (Thompson and Opfer, 2010; Gentner et al., 2011) often used in relational mapping studies that began with 10 mapping trials involving two-digit numbers and followed by 10 mapping trials with three-digit numbers. Second, because the Expanded mapping condition involved all possible numbers from single to three-digit numbers (i.e., 1–900), laying out all of these components (as in Experiment 1) in front of the child was not feasible. Instead, on each mapping trial, the experimenter had a set of individual cards needed for assembling the target number. She also gave the child an identical set of cards. For example, as shown in Figure 4, if the target mapping number was 135 and the child was in the Expanded mapping condition, both the experimenter and child would have cards 135, 100, 30, and 5. The 3-digit number cards were 12 cm wide and 7 ¼ cm tall; the 2-digit number cards were 8 cm wide and 7 ¼ cm tall; the 1-digt number cards were 4 cm wide and 7 ¼ cm tall. If the child was in the Digits mapping condition, they would both have the cards 135, 1, 3, and 5. Since all of the cards were single digit in this condition, they all have the dimension of 4 cm wide and 7 ¼ cm tall. The experimenter always handed the child his or her set of cards at the beginning of each trial. She then demonstrated how to make the number, had the child copy her action after each step, and scaffolded if needed.

FIGURE 4

FIGURE 4. (A): Illustrations for the two mapping conditions in Experiment 2. (B): Density graphs of participants’ accuracy in Experiment 2 by condition and test time (Pre- and Post-test). Pink indicates pre-test performance and turquoise indicates post-test performance.

Results

Pre-test performance in the Digits and Expanded mapping conditions did not differ as indicated by a logistic mixed effect model—in which condition was entered as a fixed variable, participant and test item were entered as random variables, and the dependent variable was the accuracy of the individual trials (i.e., 0 or 1), χ² (1) = 0.12, p = 0.73. Again, as shown in Figure 4, there were considerable individual differences in pre-test performance as some children performed very well and others quite poorly at pre-test. During the mapping task when children were asked to imitate the experimenter in making the written forms in response to hearing the name, children readily imitated the experimenter with very few errors (overall 99% correct in both conditions), thus readily discovering the relations between number names and written digits. Children in both conditions also performed better at post-test than pre-test on untrained digits indicating generalization of the learning. To ask whether the advantage of one mapping condition was higher than the other, we entered both conditions in one logistic mixed effect model. Condition and test time were entered as fixed variables, participant and test item were entered as random variables. The model detected a significant main effect of test time, performance improved from pre-test to post-test, χ² (1) = 11.27, p < 0.001, while there was no significant main effect of condition, χ² (1) = 0.06, p = 0.81, nor condition and test time interaction, χ² (1) = 0.08, p = 0.77. Both of the Expanded mapping condition (pre-test Mean = 0.76, SE = 0.02, post-test Mean = 0.79, SE = 0.02) and the Digits mapping condition (pre-test Mean = 0.75, SE = 0.02, post-test Mean = 0.78, SE = 0.03) improved from pre- to post-test. As shown in Figure 4, children improved from pre- (Mean = 0.75, SE = 0.005) to post-test (Mean = 0.78, SE = 0.004) after the mapping experience, regardless of their conditions.

Because of the large individual differences and strong performance of some children at pre-test, we also repeated the analyses using only the data from children (N = 50) who were correct less than or equal to 75% of the trials on the combined which-N and which-More tasks at pre-test. Condition and test time were entered as fixed variables, participant and test item were entered as random variables. The model detected a significant main effect of test time, performance improved from pre-test to post-test, χ² (1) = 5.69, p = 0.017, while there was no significant main effect of condition, χ² (1) = 0.39, p = 0.53, nor condition and test time interaction, χ² (1) = 0.01, p = 0.92.

Discussion

The post-test required children both to generalize the relational structure to new number names and written forms and generalize their learning about the relational mappings to judgements of magnitude—a task on which they were given no experience during the relational mapping experiences and so children had to use the discovered relational structure in a new way. The effects of the brief mapping experience were small and were not proposed as a sufficient training procedure in and of themselves. However, they indicated the potential value of reconceptualizing the initial learning problem as one of discovering relational patterns, and the results showed that relational mapping from Symbols (heard names)-to-Symbols (written forms) is useful in this domain just as in other cognitive domains (McNeil et al., 2009; Kaminski and Sloutsky, 2013).

Experiment 3

Although the results from Experiment 1 did not seem to support the idea that early knowledge about multi-digit number symbols can be learned via grounding to physical objects, it is important to further determine why and how before making a sweeping generalization. If analogical mapping is the core mechanism that drives the positive results of the Symbols-to-Symbols mapping in Experiment 1 and 2, then mapping symbols to physical models should be helpful if they direct the learners’ attention to the relevant relations (Gentner and Toupin, 1986; Goldstone, 1998; Jee et al., 2010; Jee et al., 2013). The two physical model conditions in Experiment 1 may have failed to do so. For instance, as shown in Figure 2, the number of mappings between base-10 blocks and number symbols may be too much, too distracting, and not focused on the critical early knowledge—e.g., there are different places representing different relative magnitudes—that children need to know when first learning the multi-digit system.

To test the above hypothesis, in Experiment 3, we chose to focus on the abacus as a physical model. We chose the abacus because the relational structure of the abacus is analogy-like in that it does not represent the exact magnitudes (as in Base-10 Blocks) but instead represents the system as the counts of units (the discs) in the different places. To directly test the role of physical models and to reduce the complexity of the alignments (a potential problem for the physical models conditions in Experiment 1), the mapping experiences were from the spoken names to the physical models. The written forms were not used in the mapping experiences but were included in the pre- and post-tests. Success at post-test thus required generalization of experienced mapping (heard name to physical model) to a new mapping between spoken number names to the written forms (the which-N task used in Experiments 1 and 2).

We constructed three “abacus” conditions as shown in Figure 5: 1) Standard abacus: the original abacus as in Experiment 1, 2) Sized abacus: the original abacus to which we added a redundant place cue in which the discs varied in size so that the relative magnitude (not exact) was modeled by the relative sizes of the counters; and 3) Discs only: a deconstructed “abacus” that used only discs varying in size and set on the table in separate groups.

FIGURE 5

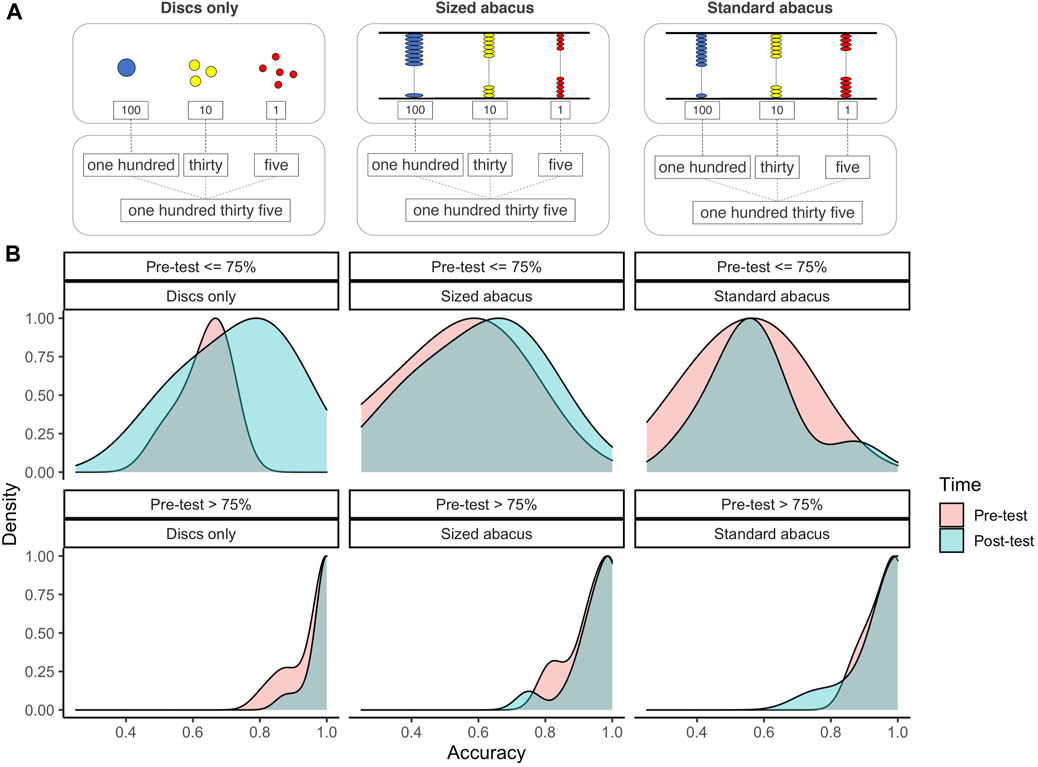
FIGURE 5. (A): Illustrations for the three mapping conditions in Experiment 3. (B): Density graphs of participants’ accuracy in Experiment 3 by condition, test time (pre- and post-test), and pre-test familiarity with multi-digit number symbols. In (B) top row: children who scored less than or equal 75% at pre-test. In (B) bottom row: children who scored above 75% at pre-test. Pink indicates pre-test performance and turquoise indicates post-test performance.

The Sized abacus condition is just as complex as the Standard abacus condition, but the different sizes may make the relative magnitudes of the places more mappable by highlighting that property. The Discs only condition takes this potentially greater mappability—bigger discs indicate places that stand for bigger quantity—and simplifies the context of the presentation. The Discs only condition is like the Symbols-to-Symbols conditions of Experiments 1 and 2 in that heard number named were mapped to visual patterns; only here the visual patterns are not written multi-digit numbers but discs that vary in size—representing the relative magnitudes of the quantities represented in each place.

The Discs only condition was also motivated by prior findings on children’s proportional reasoning Boyer et al. (2008) As shown in Figure 6, one study presented 4- to 6- year-old children with an exemplar (showing a particular proportion) together with two choices and asked the children to find the one that showed the same proportion as the exemplar. Children were more successful with continuous length than with discrete length (Figure 6A) in which each individual unit was clearly and perceptually defined. Given discrete representations, the children attended to the individual units, prompting strategies such as counting units, rather than attending to the part-and-whole relation that defines the concept of proportion. Likewise, early “approximate” learning about base-10 concept may benefit more from seeing different sized discs that mark only the main idea—relative magnitudes of different places—compared to base-10 blocks that convey not only the relative magnitudes but also the precise place value principles (e.g., 100 is 100 sets of 1s). As illustrated in Figure 6B), the presence of the individual units on a base-10 block may prompt children to count, rather than attending to the relative magnitude of the places (hundred > decade > unit) and the mapping between places to their number names. In contrast, as shown in Figure 6C), the use of three simple discs allows for more efficient mapping because the only difference among the discs is their relative size—there is no other feature that would allow an alternative mapping.

FIGURE 6

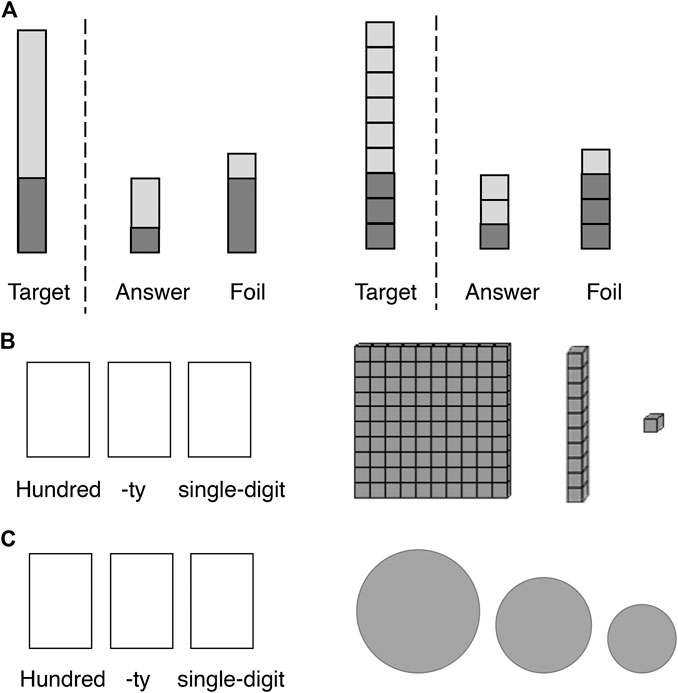
FIGURE 6. How discrete presentation draws attention to individual units rather than relational patterns and how to better highlight the relational structure of place value. (A) Left: the continuous presentation format, Right: the discrete presentation format used in a proportional reasoning task (Boyer et al., 2008). (B) How base-10 blocks represent the relational structure of place value. (C) How simple shapes (e.g., big, medium, and small discs) represent the relational structure of place value.

In sum, the mapping experiences in Experiment 3 were between multi-digit number names (with place value terms) to a physical representation of the numerical magnitude: the Discs only condition used relative size (big, medium, small) and the number of discs to represent quantity; the Standard abacus uses spatial arrangement (left, middle, right) and the number of discs; the Sized abacus uses both size and spatial arrangement of discs to represent quantity. The abacus—both standard and sized—also have other details that could be distracting (the top and bottom, the metal poles, etc.). Given the result from Experiment 1, we expect that the Standard abacus condition will not lead to significant learning. The interesting question here is whether the Discs only condition and/or the Sized abacus condition would be more helpful. On the one hand, the redundant cues (size and spatial arrangement) presented in the Sized abacus condition might be beneficial, because it allows for multiple strategies (if one way fails, there is a backup). In contrast, a “less is more” principle to relational discovery suggests that only having one cue—one way to establish the mapping—might be better because it will draw the learner’s attention directly to the to-be-discovered relation.

Participants

Fifty-nine children (29 females and 30 males, age range: 4.00–7.04 years, median: 5.39, mean: 5.50) from the same general population as Experiments 1 and 2 participated in this study. They were randomly assigned to three conditions: Standard abacus (n = 19), Sized abacus (n = 19), and Discs only (n = 21). The study was approved by the Human Subjects and Institutional Review Boards at Indiana University. Informed consents were obtained from the legal guardian and assents were obtained from the children prior to the experiment.

Materials and Procedure

The experiment has 4 phases: 1) A pre-test that consisted solely of the which-N task with the choices being written digits (as in Experiments 1 and 2), 2) mapping trials in which children imitated the experimenters in making of the number in one of the three “abacus” conditions, 3) a post-test using physical models as described below, and 4) a which-N post-test using the written symbols.

Which-N Pre- and Post-test

These tests are similar to those used in Experiments 1 and 2. There were 16 trials (Table 1) that sampled from one to three digit numbers to form a variety of different comparisons (e.g., transpositions, 2- vs. 3-digit numbers). All other aspects were identical to experiments 1 and 2.

Models Post-tests

The Models post-tests consisted of two tasks. The Make-a-model task presented children with a spoken number name and asked them to make that number using the corresponding models that they were trained with during the mapping task. In other words, this was the same task as the mapping task; only the experimenter did not make a representation of the number using the model for children to copy. There were 6 trials using numbers not used in the mapping task (Table 1). The second task, Choose-a-model, was structured just like the Which-N task—in which children were given a spoken number name and asked to choose the named number between two written numbers—only in the Choose-a-model task, they chose between two already constructed models of the number. That is, children chose between two photographs (28 cm by 30 cm) of already constructed abacus or loose discs (corresponding to the model that they used during the mapping experience) on the table—one correct and one incorrect. This task included 16 trials using numbers not used in the mapping task (Table 1).

Mapping Tasks

The Standard abacus condition (same-sized discs) was the same as the one used in Experiment 1; the diameter of the discs was 3 cm. The Sized Abacus condition with different-sized discs had the same overall dimension as the typical abacus, except that the discs were of different sizes: the hundred place discs had a diameter of 4 cm, the decade place discs had a diameter of 3 cm, and the unit place discs had a diameter of 2 cm. For the Discs only condition, discs were the same as the Sized Abacus condition but were presented loose. The set of mapping numbers for the 15 mapping trials were: 15, 186, 2, 24, 309, 38, 4, 7, 74, 851, 9, 6, 662, 50, 941. There were two orders of the mapping number sequence to which the different conditions were counterbalanced.

The procedure with the Standard abacus was the same as in Experiment 1 with two exceptions: First, there were no written numbers displayed during the mapping trials. Instead, the child was presented with the heard name, the experimenter made a model and repeated the name, and the child was encouraged to make the model. Second, in the traditional use of the abacus, discs are pushed from the bottom to the top to represent a number. Some children in Experiment 1 wanted to push the discs down not up. So, in this experiment, the represented counts were made by pushing the discs down. The discs for each count were counted by the experimenter and named as they were moved. The procedure for the Sized abacus condition was identical to the Standard abacus condition. The Discs only condition was also the same except that the number of different discs were counted and laid on the table from left to right for the hundreds, tens, and ones. As shown in Figure 5, within each count unit, individual discs were laid out separately (as opposed to being piled on top of each other) but spatially organized within its unit group. This spatial layout was—by design—different from how discs are organized on an abacus and was hypothesized to be more intuitive for children (e.g., without the remaining, potentially distracting discs on the vertical frame of an abacus).

Results

Children in all three conditions were successful in copying the experimenter’s physical model of a spoken number, performing at 94% overall (SE = 0.9%) with no significant difference among conditions. A logistic mixed effect model, in which condition was entered as a fixed effect, participants and test items were entered as random effects, failed to detect a significant main effect of condition, χ² (2) = 0.64, p = 0.73. Children in the three mapping conditions also did not differ in pre-test performance on the which-N task as revealed by a logistic mixed effect model in which condition was entered as a fixed variable, participant and test item were entered as random variables, χ² (2) = 0.45, p = 0.80 (Standard abacus: Mean = 79%, SE = 5%, Sized abacus: Mean = 83%, SE = 5%, Discs only: Mean = 86%, SE = 4%). Again, as shown in Figure 5, there were considerable individual differences in children’s performances at pre-test with some children performing quite poorly but others near perfectly. We will return to this fact, evident, in all three experiments in the General Discussion.

Model Post-tests

Did the mapping experience, making model representations of the spoken numbers, enable children to make those representations on their own with new numbers? In the Make-a-model post-test, children were most successful in the Discs only condition which involved choosing the right number of different sized discs and laying them on the table. A logistic mixed effect model, in which condition was entered as a fixed effect, participants and items were entered as random effects, detected a significant main effect of condition, χ² (2) = 5.97, p = 0.05. The mean proportion correct in the Standard abacus condition was 0.42 (SE = 0.08) and was significantly worse than those in the Discs only condition (Mean = 0.67, SE = 0.07), t (36) = 2.37, p = 0.02, or the Sized abacus condition (Mean = 0.65, SE = 0.08) with a trending significant difference, t (36) = 2.05, p = 0.047. This result suggests that one source of challenge in the use of traditional abacus is that using places on the abacus to indicate relative magnitudes (e.g., hundred, decade, unit) is not intuitive for young children. Notice, according to the Structure Mapping theory (Gentner, 1983; Gentner, 2010), there is little to help children align the components of the heard number name to the places on the traditional abacus. Using discs of different sizes at the different positions may help children align the components and thus discover the relational pattern.

The Choose-a-model post-test only required children to recognize the correct model representation of named numbers from the corresponding abacus or loose discs that children received during mapping. A logistic mixed effect model was performed in which condition was entered as a fixed effect, participants and items were entered as random effects. The model failed to detect any significant main effect of condition, χ² (2) = 0.79, p = 0.67 (Standard abacus: Mean = 0.68, SE = 0.05, Sized abacus: Mean = 0.71, SE = 0.04, Discs only: Mean = 0.74, SE = 0.04). In brief, children in each condition apparently learned enough to recognize (above chance) the correct model representation.

Which-N Task: Mapping Names to Written Symbols

In this study, children were never exposed to written multi-digit numbers but instead mapped number names to physical models of those quantities. Does this experience bolster children’s understanding of how spoken number names map to the places of written notation? In all three logistic models, one for each condition, test time (pre, post) was entered as the fixed variable, participant and test item were entered as random variables, while the dependent variable was the accuracy of the individual test trials (i.e., 0 or 1). The Discs only condition, but not the other two conditions, led to improved performance in mapping heard number names to their written form. For the Discs only condition, there was a significant main effect of test time, χ² (1) = 5.02, p = 0.025; children performed significantly better at post-test (Mean = 0.89, SE = 0.03) compared to how they performed at pre-test (Mean = 0.84, SE = 0.04), indicating that mapping names to counts of different sized discs generalized to mapping novel multidigit numbers names to their written forms. For both the Standard abacus and Sized abacus, the models failed to detect any significant main effect of time (ps > 0.21). Figure 5 shows the density plots of children’s performance from pre- to post-test in the three conditions, separated by those with high and low prior knowledge. As can be seen, only the Discs only condition showed systematic improvement.

Discussion

These findings make two contributions: First, physical models for discovering how number names map to the places of written multi-digit notation do not work if the relations to be discovered are not sufficiently obvious in the model. If the models are too complex and intricate, their value as a revealing analogy—that simplifies and brings to front a main idea—is lost. The complexity of the Abacus models, and the non-obviousness of the relational structure, was clearly evident in children’s difficulties in correctly creating model representations in the Models Post-test measures. Second, experiences in directly mapping number names to written notation (symbols-to-symbols mapping) are not the sole route to helping children find the relational structure; mappings to a physical model can lead to generalization and better insights about written notation if—as the Discs only condition—the analogy foregrounds the single concept to be discovered. All in all, the results of the three experiments suggest an incremental approach that does not try to do too much all at once. Within such an approach, physical models might better be used as analogies that distill a complex idea into an immediately understandable concept rather than a physical grounding of the meaning. Physical models that are not readily understandable in and of themselves cannot do that.

General Discussion

Like many other domains of knowledge, place value principles of multi-digit numbers are acquired incrementally. Studies of children’s informal learning about multi-digit numbers before school indicate a potentially key starting point: On their own, many children start by learning that there are different places in written multi-digit numbers and that these places signify different relative magnitudes (Byrge et al., 2014; Mix et al., 2014; Mix et al., 2017; Yuan et al., 2019). Although this entry learning does not include the multiplicative hierarchy of base-10 system, it contains the core idea of places that represent different magnitudes and strongly predicts later learning of the precise algebraic relations of multi-digit numbers (Mix et al., Under review). These previous findings—as well as the large individual differences observed in pre-test performance in the present study—indicate that children differ substantially in whether they formed this entry knowledge prior to formal schooling about place value. Given this predictive relation between this early knowledge and later learning, the implicated developmental pathway, and the individual differences, we believe that the introduction to multi-digit numbers and place value should be focused on building this early knowledge. The present findings provide useable information as to how this might be accomplished.

Our central hypothesis was that mathematical manipulatives work by serving as analogical bases—much like metaphors and analogies—to highlight the relational structure within a symbol system (Mix, 2010; Mix et al., 2019). If this is correct, then the effectiveness of symbolic or physical representations in teaching symbols does not lie on whether it accurately grounds the symbols to their complete perceivable meaning, but it is determined by whether the perceptual features of the teaching materials highlight the relational structure of the symbol system that the learner needs to learn at that point in the developmental pathway. Previous work on analogical mapping has repeatedly shown that learning is often better achieved when the component elements in the analogical base and to-be-learned system are alignable and highlight the underlying relational structures, and that aligning corresponding elements is disrupted by complicated and overly-rich stimuli that distract learners’ attention away from relational patterns and to object-level details (Kotovsky and Gentner, 1996; Loewenstein and Gentner, 2001; Rattermann and Gentner, 1998; Uttal et al., 2008; Yuan et al., 2017). Under this “symbol-grounding as analogy” framework, the use of base-10 blocks in the context of first-grade place value teaching presents many challenges that may significantly limit how much students can learn. These challenges—visualized in Figure 2—include the large number of mappings among the different representations of written numbers, spoken number names, and base-10 blocks; the not-so-obvious perceptual structure among units of base-10 blocks (e.g., big squares, bars, small cues); and the inclusion of individual units (e.g., the 100 small squares within one big square) that may draw learners’ attention to the counts of units rather than the initial understanding of the relative magnitudes of different places (e.g., hundred > decade > unit). Consistent with these considerations, neither of the two traditional mathematical manipulatives—base-10 blocks or abacus—was very effective in initially introducing students to the multi-digit number symbol system. In contrast, and as predicted by the Structure Mapping theory (Gentner, 1983; Gentner, 2010), shapes with simple but easily understood structure—big, medium, small discs—may be a more effective analogical basis for students to acquire the initial learning about places and their relative magnitudes. Base-10 blocks or abacuses may be useful tools for later learning of the precise multiplicative hierarchy of base-10 symbols—learning that goes beyond the early multi-digit number knowledge examined and measured (with the which-N and which-More tasks) in the current study—and may require substantial initial learning about the physical representations in and of themselves (e.g., their physical attributes, correspondences to symbols, and their meanings).

In contrast to the differential learning outcomes following physical models in the current studies, experience based on mapping the two symbolic forms—multi-digit number names and their corresponding written forms—have consistently produced significant improvement in children’s early familiarity with multi-digit number names and their relative magnitudes. Under the “symbol-grounding as analogy” framework, there is no fundamental difference between physical models or symbolic representations in teaching symbol systems: The format of teaching materials may be different, but the key is still in aligning the elements that are in the same relation to other elements in the pattern. From a straight-up information processing perspective, heard number names and written symbols might even be better than physical representations, because the former is often more perceptually sparse and devoid of the many rich details that often characterize physical representations—and thus more “relational-orientated”. It is also likely that most children already learned names for digits from 1 to 9. Their knowledge of the relative magnitudes indicated by these written symbols, their names and perhaps some knowledge of the relative magnitudes of “thousand”, “hundred”, and names with “-ty” (Lyons et al., 2018; Litkowski et al., 2020) enable them to align the corresponding elements in number names and written forms. This familiarity with number names may be a critical pre-requisite to generalizable learning from mappings of number names to written forms and another indicator of the importance of early parents’ talks about numbers during the preschool years (Levine et al., 2010).

In the present study, both forms of symbolic representations used here—expanded cards (e.g., making 325 with 300, 20, and 5) and digits cards (e.g., making 325 with 3, 2, 5)—turned out to be effective. At first glance, mapping “three hundred” to “300” rather than to “3” seems to be a more transparent mapping. But two factors may explain the lack of difference between the two presentation formats. First, in the case of the digits card condition, one does not just map “three hundred” to “3”, but to “3XX”; in other words, the spatial information—the location of each place value unit—is already baked into the mapping, and the ambiguity with respect to “where does the word hundred go with” is greatly reduced. Second, even if a learner is initially unsure about the mapping between “hundred” and “3”, such mappings may become clear with repeated exposures via cross-situational statistical learning (Yu and Smith, 2007; Lany and Saffran, 2013; Rebuschat et al., 2021). For example, by encountering a series of pairs, such as “325”—“three hundred twenty five”, “35”—“thirty five”, “105”—“one hundred and five”, the learner may accumulate enough co-occurrence information—e.g., “hundred” is often co-occur with three-digit numbers, and in such cases often occur right after the name of the leftmost digit—to arrive at the correct mapping. Examining how relational mappings are established in the midst of the ambiguity, that often characterize real-world learning data, constitutes an open and exciting future direction for building entry-level knowledge and skills about place value.

Implications for Education and Teaching

The current finding has several implications for introducing children to the symbolic number system and its place value principles. Foremost, children’s later success in mastering place value may benefit from exposure to multi-digit numbers during the preschool and kindergarten years. Accumulating evidence with large and nationally representative samples (Byrge et al., 2014; Mix et al., 2014; Yuan et al., 2019; Yuan et al., 2020) indicates that many young children, before formal schooling, are building partial (not perfect but often correct) knowledge about how relative magnitudes are represented by place and the naming conventions for 3- and 4-digit numbers, and that this early knowledge is a strong predictor to later school learning of mathematics (Mix et al., Under review). The present result further suggests that early familiarity with these structures is learnable by preschool children with just a few trials—through mapping number names to their written forms, and/or to simple physical analogies about relative magnitudes—embedded in a game-like context without explicit teaching of the precise base-10 principles (Yuan et al., 2020).

This result may seem surprising to many researchers and educators given the well-documented difficulties that school-age children have (Baroody, 1990; Fuson et al., 1997). But these findings also make sense given what is known about young children’s prodigious ability to extract, learn, and use syntactical structures by engaging in mechanisms of relational and statistical learning (Smith and Yu, 2008; Gentner, 2010). There are existing curricula (e.g., Montessori, 1917; Parrish, 2014; Mix et al., 2019) focused on teaching the relational structure of the symbolic number system, but these usually focus on older children (e.g., 5-year-old and beyond). As a result, children’s early approximate knowledge about multi-digit numbers often remains a hidden competency to parents and teachers. Those children whose early experiences did not include exposure to multi-digit numbers have a hidden deficit relative to what might be critical entry knowledge. This fact—that early familiarity with written and spoken multi-digit number symbols is not only learnable, but individual differences in that understanding is highly correlated with later math learning—strongly suggests the benefit of early exposure for all children. The tasks used here—brief and easy (coached imitation)—appear suitable for early exposure.

Many researchers and educators have suggested that multi-digit number words are initial barriers to understanding because of inconsistencies (e.g., the teens numbers in English or the not initially obvious mappings of “twenty” to “two”) (Miura and Okamoto, 1989; Fuson and Kwon, 1991). The present findings suggest that multi-digit number words are useful tools for entry to the symbolic number system despite the inconsistencies. The relation between language and thought is a complex one with a long history of back-and-forth debates among different theorists (Gentner and Goldin-Meadow, 2003). In the context of multi-digit number words and number learning, one often cited and emphasized result is that different language systems have different structures with some more consistent than others. One notable example is the claim that Chinese children’s accelerated number learning ability—compared to English speaking children—results from the transparency of the Chinese multi-digit number words (e.g., twenty is named as two tens); in comparison, the English number words filled with inconsistencies, such as numbers in the teens range, can lead to many difficulties and represent a barrier to English speaking children’s numerical development (Fuson and Kwon, 1991; Miller et al., 2000). Perhaps, because of this perception, multi-digit number words are often not the focus of formal teaching. The current study, together with a large literature from cognitive psychology (Chang et al., 2006; Lupyan, 2012), suggests that the syntactic structures of natural languages play a vital role in organizing perceptual input—including written number symbols—yielding deep latent knowledge about more abstract ideas despite the exceptions and idiosyncrasies (Yuan et al., 2020). Without experiences with number words and their inherent regularities, a child may represent a written number such as “123” as a compilation of three digits— “1”, “2”, and “3”. But by mapping the corresponding number name “one hundred twenty-three” to the written form “123”, the child may start to learn about important structural regularities, such as number words name written digits from left to right, that 3-digit numbers all have the word “hundred” in them and often appear early in the number word—regularities that are part of the place value system. This symbols-to-symbols mapping merits renewed interest by researchers as a potential critical early pathway into place value notation.

The present findings also indicate that the use of traditional manipulatives may sometimes be more of a problem than a benefit, and this may be especially the case for entry-level learning. The ultimate goal of education is for students to successfully interpret and manipulate symbols (e.g., numbers, words, equations) on the basis of their relations. In this sense, mathematical manipulatives are training wheels for learning mathematical symbols and concepts, and—like training wheels—need at some point to be abandoned. While most current educational practices in introducing students to the multi-digit number system and place value focus on “grounding” symbols into mathematical manipulatives such as base-10 blocks, studies have questioned the effectiveness of math manipulatives due to extraneous features—features that are not critical to the to-be-learned relational structure—that may be distracting to learning (McNeil et al., 2009; Kaminski and Sloutsky, 2013). But the 100 small cubes within a big base-10 block are not extraneous features; they represent the critical multiplicative relation that 100 is 100 sets of 1. Instead, manipulatives such as base-10 blocks may be ineffective in first introducing children to the multi-digit number system but might be useful later. Perhaps base-10 blocks should be simplified at first—that is, presented as different sized but same shaped blocks with no markings to indicate internal units—and then add the details relevant to the multiplicative relations between places. Traditional manipulatives have been shown useful for teaching of the precise base-10 relations in older children (Carbonneau et al., 2013). Another approach might be to incorporate both number symbol mappings and manipulatives and introduce the mappings in a balanced way (Mix et al., 2017). If learning the place value system is incremental, then the use of physical analogies to highlight its learning may need to be incrementally organized as well.

Implications for the “Symbol-Grounding” Problem

The idea of “symbol-grounding” has many different and nuanced interpretations (see De Vega et al. (2008) for a comprehensive review). Nonetheless, much of the theoretical discussion divides into two broad camps: symbols alone are sufficient (Pylyshyn, 1980; Fodor, 1983; Landauer and Dumais, 1997), or that perceptual and sensorimotor experiences support symbol acquisition (Barsalou, 1999, Barsalou, 2008). This dichotomy is likely to be too simple to be useful in education. At some points in learning, physical models and manipulatives—if they fit the needs of the specific task—can support learning. Physical symbols—letters and numbers—can also be used as models and with active engagement. The key question in education is when, in what way, and for what specific incremental bit of learning. Here we believe that the broad contributions of research on analogy and Structure Mapping Theory (Gentner, 2010) may help the field find useable principles.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Indiana University. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

LS, KM, and RP contributed to the conception and design of the study. LY performed the statistical analyses. LY wrote the first draft of the manuscript. LS and KM contributed to the revision.

Funding

This research was supported by IES R305A080287 grant to LS and KM, and NIH F32 HD090827-02 grant to LY. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Institute of Education Sciences or the National Institutes of Health.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Cody Stitzel for assisting with data collection.

Footnotes

¹Using median-split as a grouping method does not change the pattern of results

²This item was originally added as a catch on for the strategy of just counting the number of digits. Many children indeed utilized this strategy. Since this trial contained a non-existing number, it was not included in the reported analysis. Additional analysis including this trial did not change the pattern of results

References

Alibali, M. W., and Nathan, M. J. (2012). Embodiment in Mathematics Teaching and Learning: Evidence from Learners' and Teachers' Gestures. J. Learn. Sci. 21 (2), 247–286. doi:10.1080/10508406.2011.611446

CrossRef Full Text | Google Scholar

Ball, D. L. (1992). Magical Hopes: Manipulatives and the Reform of Math Education. Am. Educator 16, 14–20.

Google Scholar

Baroody, A. J. (1990). How and When Should Place-Value Concepts and Skills Be Taught? J. Res. Maths. Educ. 21 (4), 281–286. doi:10.2307/749526

CrossRef Full Text | Google Scholar

Barsalou, L. W. (2008). Grounded Cognition. Annu. Rev. Psychol. 59, 617–645. doi:10.1146/annurev.psych.59.103006.093639

PubMed Abstract | CrossRef Full Text | Google Scholar

Barsalou, L. W. (1999). Perceptual Symbol Systems. Behav. Brain Sci. 22 (4), 577–660. doi:10.1017/S0140525X99002149

PubMed Abstract | CrossRef Full Text | Google Scholar

Bartolini Bussi, M. G. (2011). Artefacts and Utilization Schemes in Mathematics Teacher Education: Place Value in Early Childhood Education. J. Math. Teach. Educ 14 (2), 93–112. doi:10.1007/s10857-011-9171-2

CrossRef Full Text | Google Scholar

Boyer, T. W., Levine, S. C., and Huttenlocher, J. (2008). Development of Proportional Reasoning: where Young Children Go Wrong. Dev. Psychol. 44 (5), 1478–1490. doi:10.1037/a0013110

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruner, J. S. (1966). Toward a Theory of Instruction. Harvard University Press.

Byrge, L., Smith, L. B., and Mix, K. S. (2014). Beginnings of Place Value: How Preschoolers Write Three-Digit Numbers. Child. Dev. 85 (2), 437–443. doi:10.1111/cdev.12162

PubMed Abstract | CrossRef Full Text | Google Scholar

Carbonneau, K. J., Marley, S. C., and Selig, J. P. (2013). A Meta-Analysis of the Efficacy of Teaching Mathematics with concrete Manipulatives. J. Educ. Psychol. 105 (2), 380–400. doi:10.1037/a0031084

CrossRef Full Text | Google Scholar

Chan, W. W. L., Au, T. K., and Tang, J. (2014). Strategic Counting: A Novel Assessment of Place-Value Understanding. Learn. Instruction 29, 78–94. doi:10.1016/j.learninstruc.2013.09.001

CrossRef Full Text | Google Scholar

Chang, F., Dell, G. S., and Bock, K. (2006). Becoming syntactic. Psychol. Rev. 113, 234–272. doi:10.1037/0033-295X.113.2.234

PubMed Abstract | CrossRef Full Text | Google Scholar

Chi, M. T. H., Feltovich, P. J., and Glaser, R. (1981). Categorization and Representation of Physics Problems by Experts and Novices. Cogn. Sci. 5 (2), 121–152. doi:10.1207/s15516709cog0502_2

CrossRef Full Text | Google Scholar

Chi, M. T. H. (1978). “Knowledge Structures and Memory Development,” in Children’s Thinking: What Develops?. Editor R. S. Siegler (Psychology press), 73–96.

Google Scholar

De Vega, M., Graesser, A. C., and Glenberg, A. M. (2008). “Reflecting on the Debate,” in Symbols and Embodiment: Debates on Meaning and Cognition, 397–440. doi:10.1093/acprof:oso/9780199217274.003.0019

CrossRef Full Text | Google Scholar

Dove, G. (2016). Three Symbol Ungrounding Problems: Abstract Concepts and the Future of Embodied Cognition. Psychon. Bull. Rev. 23 (4), 1109–1121. doi:10.3758/s13423-015-0825-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Fodor, J. A. (1983). The Modularity of Mind. Cambridge: The MLT.

Fuson, K. C., and Briars, D. J. (1990). Using a Base-Ten Blocks Learning/Teaching Approach for First- and Second-Grade Place-Value and Multidigit Addition and Subtraction. JRME 21 (3), 180–206. doi:10.5951/jresematheduc.21.3.0180

CrossRef Full Text | Google Scholar

Fuson, K. C. (1990). Conceptual Structures for Multiunit Numbers: Implications for Learning and Teaching Multidigit Addition, Subtraction, and Place Value. Cogn. Instruction 7 (4), 343–403. doi:10.1207/s1532690xci0704_4

CrossRef Full Text | Google Scholar

Fuson, K. C., and Kwon, Y. (1991). Chinese-based Regular and European Irregular Systems of Number Words: The Disadvantages for English-speaking Children. Lang. Math. Educ. Res. Pract., 211–226.

Google Scholar

Fuson, K. C., Wearne, D., Hiebert, J. C., Murray, H. G., Human, P. G., Olivier, A. I., et al. (1997). Children's Conceptual Structures for Multidigit Numbers and Methods of Multidigit Addition and Subtraction. JRME 28 (2), 130–162. doi:10.5951/jresematheduc.28.2.0130

CrossRef Full Text | Google Scholar

Fuson, K. (1986). Roles of Representation and Verbalization in the Teaching of Multi-Digit Addition and Subtraction. Eur. J. Psychol. Educ. 1 (2), 35–56. doi:10.1007/BF03172568

CrossRef Full Text | Google Scholar

Geary, D. C. (2007). “Development of Mathematical Understanding,” in Handbook of Child Psychology, 777–810. doi:10.1002/9780470147658.chpsy0218

CrossRef Full Text | Google Scholar

Gentner, D., Anggoro, F. K., and Klibanoff, R. S. (2011). Structure Mapping and Relational Language Support Children's Learning of Relational Categories. Child. Dev. 82 (4), 1173–1188. doi:10.1111/j.1467-8624.2011.01599.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Gentner, D. (2010). Bootstrapping the Mind: Analogical Processes and Symbol Systems. Cogn. Sci. 34 (5), 752–775. doi:10.1111/j.1551-6709.2010.01114.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Gentner, D., and Goldin-Meadow, S. (2003). “Whither Whorf,” in Language in Mind. Editors D. Gentner, and S. Goldin-Meadow (The MIT Press). doi:10.7551/mitpress/4117.003.0004

CrossRef Full Text | Google Scholar

Gentner, D., and Stevens, A. L. (1983). Mental Models. Psychology Press. doi:10.4324/9781315802725

CrossRef Full Text

Gentner, D. (1983). Structure-Mapping: A Theoretical Framework for Analogy. Cogn. Sci. 7 (2), 155–170. doi:10.1207/s15516709cog0702_3

CrossRef Full Text | Google Scholar

Gentner, D., and Toupin, C. (1986). Systematicity and Surface Similarity in the Development of Analogy. Cogn. Sci. 10 (3), 277–300. doi:10.1207/s15516709cog1003_2

CrossRef Full Text | Google Scholar

Goldstone, R. L. (1998). Perceptual Learning. Annu. Rev. Psychol. 49, 585–612. doi:10.1146/annurev.psych.49.1.585

PubMed Abstract | CrossRef Full Text | Google Scholar

Harnad, S. (1990). The Symbol Grounding Problem. Physica D 42, 335–346.

CrossRef Full Text | Google Scholar

Jee, B. D., Uttal, D. H., Gentner, D., Manduca, C., Shipley, T. F., and Sageman, B. (2013). Finding Faults: Analogical Comparison Supports Spatial Concept Learning in Geoscience. Cogn. Process. 14 (2), 175–187. doi:10.1007/s10339-013-0551-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Jee, B. D., Uttal, D. H., Gentner, D., Manduca, C., Shipley, T. F., Tikoff, B., et al. (2010). Commentary: Analogical Thinking in Geoscience Education. J. Geosci. Educ. 58 (1), 2–13. doi:10.5408/1.3544291

CrossRef Full Text | Google Scholar

Kaminski, J. A., and Sloutsky, V. M. (2013). Extraneous Perceptual Information Interferes with Children's Acquisition of Mathematical Knowledge. J. Educ. Psychol. 105 (2), 351–363. doi:10.1037/a0031040

CrossRef Full Text | Google Scholar

Kotovsky, L., and Gentner, D. (1996). Comparison and Categorization in the Development of Relational Similarity. Child. Develop. 67 (6), 2797–2822. doi:10.1111/j.1467-8624.1996.tb01889.x

CrossRef Full Text | Google Scholar

Landauer, T. K., and Dumais, S. T. (1997). A Solution to Plato's Problem: The Latent Semantic Analysis Theory of Acquisition, Induction, and Representation of Knowledge. Psychol. Rev. 104 (2), 211–240. doi:10.1037/0033-295X.104.2.211

CrossRef Full Text | Google Scholar

Lany, J., and Saffran, J. R. (2013). Statistical Learning Mechanisms in Infancy. Neural Circuit Development and Function in the Heathy and Diseased Brain 3, 231–248. doi:10.1016/B978-0-12-397267-5.00034-0

CrossRef Full Text | Google Scholar

Levine, S. C., Suriyakham, L. W., Rowe, M. L., Huttenlocher, J., and Gunderson, E. A. (2010). What Counts in the Development of Young Children's Number Knowledge? Dev. Psychol. 46 (5), 1309–1319. doi:10.1037/a0019671

PubMed Abstract | CrossRef Full Text | Google Scholar

Litkowski, E. C., Duncan, R. J., Logan, J. A. R., Purpura, D. J., and Litkowski, E. C. (2020). When Do Preschoolers Learn Specific Mathematics Skills? Mapping the Development of Early Numeracy Knowledge. J. Exp. Child. Psychol. 195, 104846. doi:10.1016/j.jecp.2020.104846

CrossRef Full Text | Google Scholar

Loewenstein, J., and Gentner, D. (2001). Spatial Mapping in Preschoolers: Close Comparisons Facilitate Far Mappings. J. Cogn. Develop. 2 (2), 189–219. doi:10.1207/S15327647JCD0202_4

CrossRef Full Text | Google Scholar

Lupyan, G. (2012). Linguistically modulated perception and cognition: the label-feedback hypothesis. Front. Psychol. 3, 54. doi:10.3389/fpsyg.2012.00054

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyons, I. M., Bugden, S., Zheng, S., De Jesus, S., and Ansari, D. (2018). Symbolic Number Skills Predict Growth in Nonsymbolic Number Skills in Kindergarteners. Dev. Psychol. 54 (3), 440–457. doi:10.1037/dev0000445

PubMed Abstract | CrossRef Full Text | Google Scholar

McNeil, N. M., Uttal, D. H., Jarvin, L., and Sternberg, R. J. (2009). Should You Show Me the Money? Concrete Objects Both Hurt and Help Performance on Mathematics Problems. Learn. Instruction 19 (2), 171–184. doi:10.1016/j.learninstruc.2008.03.005

CrossRef Full Text | Google Scholar

Miller, K., Major, S. M., Shu, H., and Zhang, H. (2000). Ordinal knowledge: number names and number concepts in Chinese and English. Can. J. Exp. Psychol. 54 (2), 129–140. doi:10.1037/h0087335

PubMed Abstract | CrossRef Full Text | Google Scholar

Miura, I. T., and Okamoto, Y. (1989). Comparisons of U.S. And Japanese First Graders' Cognitive Representation of Number and Understanding of Place Value. J. Educ. Psychol. 81 (1), 109–114. doi:10.1037/0022-0663.81.1.109

CrossRef Full Text | Google Scholar

Mix, K. S., Prather, R. W., Smith, L. B., and Stockton, J. D. (2014). Young Children's Interpretation of Multidigit Number Names: from Emerging Competence to Mastery. Child. Dev. 85 (3), 1306–1319. doi:10.1111/cdev.12197

PubMed Abstract | CrossRef Full Text | Google Scholar

Mix, K. S., Bower, C. A., Hancock, G., Yuan, L., and Smith, L. B (Under review). The Development of Place Value Concepts: Principles after Approximation.

Google Scholar

Mix, K. S., Smith, L. B., and Crespo, S. (2019). “Leveraging Relational Learning Mechanisms to Improve Place Value Instruction,” in Constructing Number - Merging Perspectives from Psychology and Mathematics Education (Cham: Springer Publishing), 87–121. doi:10.1007/978-3-030-00491-0_5

CrossRef Full Text | Google Scholar

Mix, K. S., Smith, L. B., Stockton, J. D., Cheng, Y.-L., and Barterian, J. A. (2017). Grounding the Symbols for Place Value: Evidence from Training and Long-Term Exposure to Base-10 Models. J. Cogn. Develop. 18 (1), 129–151. doi:10.1080/15248372.2016.1180296

CrossRef Full Text | Google Scholar

Mix, K. S. (2009). “Spatial Tools for Mathematical Thought,” in The Spatial Foundations of Language and Cognition. Editors K. S. Mix, L. B. Smith, and M. Gasser (Oxford University Press), 41–66. doi:10.1093/acprof:oso/9780199553242.003.0003

CrossRef Full Text | Google Scholar

Montessori, M. (1917). The Advanced Montessori Method A0. New York: Frederick A. Stokes.

Namy, L. L., and Gentner, D. (2002). Making a Silk Purse Out of Two Sow's Ears: Young Children's Use of Comparison in Category Learning. J. Exp. Psychol. Gen. 131 (1), 5–15. doi:10.1037/0096-3445.131.1.5

CrossRef Full Text | Google Scholar

O’Keefe, P. A., Letourneau, S. M., Homer, B. D., Schwartz, R. N., and Plass, J. L. (2014). Learning from Multiple Representations: An Examination of Fixation Patterns in a Science Simulation. Comput. Hum. Behav. 35, 234–242. doi:10.1016/j.chb.2014.02.040

CrossRef Full Text | Google Scholar

Paik, J. H., and Mix, K. S. (2008). It's All Relative: Different Levels of Relational Similarity Used in Children's Comparisons. Br. J. Develop. Psychol. 26 (4), 499–505. doi:10.1348/026151007X260163

CrossRef Full Text | Google Scholar

Parrish, S. (2014). Number Talks: Helping Children Build Mental Math and Computation Strategies, Grades K-5. Sausalito, CA: Math Solutions.

Pouw, W. T. J. L., van Gog, T., and Paas, F. (2014). An Embedded and Embodied Cognition Review of Instructional Manipulatives. Educ. Psychol. Rev. 26 (Issue 1), 51–72. doi:10.1007/s10648-014-9255-5

CrossRef Full Text | Google Scholar

Pylyshyn, Z. W. (1980). Computation and Cognition: Issues in the Foundations of Cognitive Science. Behav. Brain Sci. 3 (1), 111–132. doi:10.1017/S0140525X00002053

CrossRef Full Text | Google Scholar

R Core Team (2020). R: The R Project for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. Available at: https://www.r-project.org/.

Google Scholar

Rattermann, M. J., and Gentner, D. (1998). More Evidence for a Relational Shift in the Development of Analogy: Children's Performance on a Causal-Mapping Task. Cogn. Develop. 13 (4), 453–478. doi:10.1016/S0885-2014(98)90003-X

CrossRef Full Text | Google Scholar

Rau, M. A. (2017). Conditions for the Effectiveness of Multiple Visual Representations in Enhancing STEM Learning. Educ. Psychol. Rev. 29 (Issue 4), 717–761. doi:10.1007/s10648-016-9365-3

CrossRef Full Text | Google Scholar

Rebuschat, P., Monaghan, P., and Schoetensack, C. (2021). Learning Vocabulary and Grammar from Cross-Situational Statistics. Cognition 206, 104475. doi:10.1016/j.cognition.2020.104475

PubMed Abstract | CrossRef Full Text | Google Scholar

Richland, L. E., and Simms, N. (2015). Analogy, Higher Order Thinking, and Education. Wiley Interdiscip. Rev. Cogn. Sci. 6 (2), 177–192. doi:10.1002/wcs.1336

PubMed Abstract | CrossRef Full Text | Google Scholar

Richland, L. E., Begolli, K. N., Simms, N., Frausel, R. R., and Lyons, E. A. (2017). Supporting Mathematical Discussions: the Roles of Comparison and Cognitive Load. Educ. Psychol. Rev. 29 (1), 41–53. doi:10.1007/s10648-016-9382-2

CrossRef Full Text | Google Scholar

Sarama, J., and Clements, D. H. (2009). “Concrete” Computer Manipulatives in Mathematics Education. Child. Develop. Perspect. 3 (3), 145–150. doi:10.1111/j.1750-8606.2009.00095.x

CrossRef Full Text | Google Scholar

Singmann, H., Bolker, B., Westfall, J., and Aust, F. (2015). Afex: Analysis of Factorial Experiments. R package version 0.13–145.

Google Scholar

Singmann, H., and Kellen, D. (2019). “An Introduction to Mixed Models for Experimental Psychology,” in New Methods in Cognitive Psychology (Routledge), 4–31. doi:10.4324/9780429318405-2

CrossRef Full Text | Google Scholar

Smith, L. B., and Yu, C. (2008). Infants rapidly learn word-referent mappings via cross-situational statistics. Cognition 106 (3), 1558–1568. doi:10.1016/j.cognition.2007.06.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Socher, R., Ganjoo, M., Manning, C. D., and Ng, A. Y. (2013). Zero-Shot Learning Through Cross-Modal Transfer. Advances in Neural Information Processing Systems, 935–943.

Google Scholar

Son, J. Y., Smith, L. B., and Goldstone, R. L. (2012b). Connecting Instances to Promote Children's Relational Reasoning. J. Exp. Child. Psychol. 108 (2), 260–277. doi:10.1016/j.jecp.2010.08.011.Connecting

CrossRef Full Text | Google Scholar

Son, J. Y., Smith, L. B., Goldstone, R. L., and Leslie, M. (2012a). The Importance of Being Interpreted: Grounded Words and Children's Relational Reasoning. Front. Psychol. 3, 45. doi:10.3389/fpsyg.2012.00045

PubMed Abstract | CrossRef Full Text | Google Scholar

Son, J. Y., Smith, L. B., and Goldstone, R. L. (2008). Simplicity and Generalization: Short-Cutting Abstraction in Children's Object Categorizations. Cognition 108 (3), 626–638. doi:10.1016/j.cognition.2008.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Sowell, E. J. (1989). Effects of Manipulative Materials in Mathematics Instruction. J. Res. Maths. Educ. 20 (5), 498. doi:10.2307/749423

CrossRef Full Text | Google Scholar

Steels, L. (2008). “The Symbol Grounding Problem Has Been Solved, So What’s Next?,” in Symbols and Embodiment: Debates on Meaning and Cognition (Oxford University Press), 223–244. doi:10.1093/acprof:oso/9780199217274.003.0012

CrossRef Full Text | Google Scholar

Stolz, S. A. (2015). Embodied Learning. Educ. Philos. Theor. 47 (5), 474–487. doi:10.1080/00131857.2013.879694

CrossRef Full Text | Google Scholar

Taddeo, M., and Floridi, L. (2005). Solving the Symbol Grounding Problem: A Critical Review of Fifteen Years of Research. J. Exp. Theor. Artif. Intell. 17 (4), 419–445. doi:10.1080/09528130500284053

CrossRef Full Text | Google Scholar

Thompson, C. A., and Opfer, J. E. (2010). How 15 Hundred Is like 15 Cherries: Effect of Progressive Alignment on Representational Changes in Numerical Cognition. Child. Dev. 81 (6), 1768–1786. doi:10.1111/j.1467-8624.2010.01509.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Uttal, D. H., Gentner, D., Liu, L. L., and Lewis, A. R. (2008). Developmental Changes in Children's Understanding of the Similarity between Photographs and Their Referents. Dev. Sci. 11 (1), 156–170. doi:10.1111/j.1467-7687.2007.00660.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., Zheng, V. W., Yu, H., and Miao, C. (2019). A Survey of Zero-Shot Learning, ACM Trans. Intell. Syst. Technol. 10 (Issue 2), 1–37. doi:10.1145/3293318

CrossRef Full Text | Google Scholar

Wills, T., Shipley, T. F., Chang, B. L., Cromley, J. G., and Booth, J. L. (2008). “What Gaze Data Reveal about Coordinating Multiple Mathematical Representations,” in Proceedings of the Annual Meeting of the Cognitive Science Society, 3113–3118.

Google Scholar

Yu, C., and Smith, L. B. (2007). Rapid Word Learning under Uncertainty via Cross-Situational Statistics. Psychol. Sci. 18 (5), 414–420. doi:10.1111/j.1467-9280.2007.01915.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, L., Prather, R. W., Mix, K. S., and Smith, L. B. (2019). Preschoolers and Multi-Digit Numbers: A Path to Mathematics through the Symbols Themselves. Cognition 189, 89–104. doi:10.1016/j.cognition.2019.03.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, L., Uttal, D., and Gentner, D. (2017). Analogical Processes in Children's Understanding of Spatial Representations. Dev. Psychol. 53 (6), 1098–1114. doi:10.1037/dev0000302

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, L., Xiang, V., Crandall, D., and Smith, L. (2020). Learning the Generative Principles of a Symbol System from Limited Examples. Cognition 200, 104243. doi:10.1016/j.cognition.2020.104243

PubMed Abstract | CrossRef Full Text | Google Scholar