The Complexity of Comparative Judgments in Assessing Argumentative Writing: An Eye Tracking Study

Comparative judgment (CJ) has been recently introduced in the educational field as a means of assessing competences. In this judgement process, assessors are presented with two pieces of student work and are asked to choose which one is better in relation to the competencies being assessed. However, since student work is heterogeneous and highly information loaded, it raises the question as to whether this type of assessment is too complex for assessors to use. Previous research on the topic has operationalized experienced complexity by employing self-report measures, which have been criticized for common problems associated with their use. In our study, we used eye tracking to study 23 high school teachers when they made 10 comparative judgments, and their pupil diameter was used as an indicator of the experienced complexity. This study builds on previous research that integrated Campbell’s theory on task complexity (1988) into CJ. Based on this framework, three hypotheses regarding the role of decision accuracy were formulated and empirically tested. Hypothesis one assumes that the distance between two pieces of student work on the rank-order (rank-order distance) is negatively related to experienced complexity, irrespective of decision accuracy. Hypothesis two assumes that decision accuracy moderates the relationship between rank-order distance and experienced complexity. Hypothesis three builds on hypothesis two by adding a negative relationship between experience and experienced complexity. In all three hypotheses, the average experienced complexity is assumed to vary between assessors, as is the strength of the expected relationships. An information-theoretic approach was used to test the holding of all three hypotheses. All hypotheses were translated into statistical models, and their relative and absolute fit were assessed. Results provided strong evidence for hypothesis three: both the moderating role of decision accuracy on the relationship between rank-order distance and experienced complexity, and the relationship between experience and experienced complexity, were confirmed.

Introduction

Comparative judgment (CJ) has been introduced in the educational field as a means of assessing competences in various subjects such as writing (Pollitt, 2012a; van Daal, et al., 2019). In this discernment process, assessors are presented with two texts and are asked to determine which one is of higher quality. After making their choice, the assessor then receives a new pair of texts to compare. Based on all comparative judgments, a ranking scale is generated, which orders the pieces of student work from lowest to highest quality (Pollitt, 2012a; Pollit, 2012b). This scale is assumed to reflect the consensus among the assessors regarding the quality of these texts (Jones and Alcock, 2014; Lesterhuis, 2018; Pollitt, 2012a; van Daal et al., 2019). Although research has demonstrated the reliability and validity of this method (e.g., Pollitt, 2012a; Pollit, 2012b; Jones and Inglis, 2015; Lesterhuis, 2018), it is questionable whether assessors can easily discriminate, decide which one is better, between all pairs of texts. Not only do these texts contain information related to various aspects of textual quality (Sadler, 1989), such information can be heterogeneous in nature (e.g., a well-structured text that is poor in argumentation). Consequently, the assessor must engage in an increased amount of information processing, thereby adding to the complexity of the judgment task (Campbell, 1988; Sadler, 1989; Bramley, 2007; Liu and Li, 2012). Thus, we raise the question as to whether this type of CJ is too complex for assessors to use.

Two perspectives on the complexity of CJ can be found in the literature: experienced complexity and objective complexity. The former concentrates on the complexity that assessors experience while making comparative judgments. The experienced complexity of CJ is underpinned mainly by the qualitative evidence of assessors who report that some comparisons are too difficult to make (e.g., Pollitt, 2012a; Whitehouse, 2012; Jones, et al., 2015). With regard to the latter, the objective perspective considers complexity as an objective characteristic of the pair of texts to compare. Related research evidences that a bigger discrepancy in quality between two pieces of work is related to a higher degree of decision accuracy (Gill and Bramley, 2013). This finding supports the statement by Pollitt (2012b) that comparing two texts of similar quality is more difficult, which means that both experienced and objective complexity have to be considered when studying the merits and drawbacks of the comparative judgment method.

Van Daal et al. (2017) contributed to the scarce empirical research in this area by integrating both perspectives on the complexity of CJ. They showed that assessors experience CJ as more complex if comparisons concern two texts of similar quality. This finding only applies to comparisons that are accurately judged, as inaccurate decisions are associated with a higher degree of experienced complexity, no matter their difference in quality. Two limitations of this study can be found. First, van Daal et al. (2017) did not take into account any of the background characteristics of the assessors. We can, however, assume that experienced assessors interact differently with the texts they have to compare and are better equipped to tackle more complex comparisons (Guo et al., 2012). Secondly, a self-report measure was used to operationalize experienced complexity. However, previous research showed that self-report measures are not the most valid method to capture concepts such as complexity (e.g., Martin, 2014).

This study will conceptually replicate the findings of van Daal et al. (2017), meaning that the findings of the 2017 will be re-examined using a different set-up (Schmidt, 2009), and address both limitations. First, the methodological limitation of the 2017 study will be tackled by using an objective measure, namely eye tracking (pupil diameter), to operationalize experienced complexity. Furthermore, because previous research assumes that assessors need experience in assessment in order to be a credible assessor (Bisson et al., 2016; Jones et al., 2015; Pollitt, 2012a; Pollit, 2012b), this assessor characteristic will be integrated into the theoretical framework on the complexity of CJ. In sum, this study examines the complexity of assessing writing using comparative judgment by relating an objective characteristic of comparative judgments on two texts (the quality difference between two texts) and characteristics of the assessor (experience) to experienced complexity.

Theoretical Framework

First, we describe the theoretical model of CJ task complexity outlined by van Daal et al. (2017), and provide support for the use of rank-order distance as the operationalization of objective complexity in CJ. Second, we examine the role of decision accuracy in the complexity of comparative judgment. Third, we elaborate on the role of expertise in the experienced complexity concept of CJ. Last, we explain the use of eye tracking for pupil diameter as the operationalization of experienced complexity.

Complexity of CJ

The theoretical model of CJ complexity outlined by van Daal et al. (2017) builds on the task complexity framework of Campbell (1988). This model distinguishes between two types of task complexity—objective and experienced complexity. The former refers to characteristics of the judgment task that enhance its complexity, while the latter concerns the complexity as experienced by the assessors.

As stated earlier, the comparison of two randomly selected pairs of student work represents the core process of CJ. Thurstone (1927a,b) states that the valid application of CJ requires assessors to correctly discriminate between any pair of texts with which they are presented. Assessors’ discrimination abilities can, however, be put to the test when they must evaluate two texts of similar quality. The degree of similarity between two texts is reflected by their rank-order distance; to enable correct judgment, the distance on the rank-order between two pieces of student work must be large enough to enable a correct judgment (Thurstone, 1927a). Building on this, we can conceptualize rank-order distance as an objective comparison characteristic that defines a comparison’s objective complexity. When a comparison consists of two pieces of student work far apart on the rank-order, it will be easier to discriminate between them, that is, decide which one is better. As a result, in this scenario, decision uncertainty and objective complexity are low. In contrast, when assessors need to distinguish between two pieces of student work of similar quality, the decision uncertainty—as well as its objective complexity—will be higher (van Daal et al., 2017). Findings by van Daal et al. (2017) confirm the negative relation of rank-order distance with experienced complexity.

The objective complexity of a comparison is linked to its experienced complexity, which refers to the complexity as experienced by the assessor. Since experienced complexity is conceptualized as the result of the interaction between the comparative judgment task and the assessor, it is expected to vary between assessors (Campbell, 1988). Indeed, van Daal et al. (2017) found that assessors differed in mean experienced complexity, as some assessors experienced CJ as more complex than others. Furthermore, the strength of the negative relation between experienced complexity and rank-order distance varied across assessors. This means that the same decrease in rank-order distance is associated with a different increase in experienced complexity across assessors (van Daal et al., 2017).

The Role of Decision Accuracy

Considering the fact that rank-order distance is theoretically related to decision accuracy, the latter needs to be taken into account. Van Daal et al. (2017) suggest two ways in which decision accuracy can interfere in the relation between rank-order distance and experienced complexity. The first possibility builds upon the fact that whether or not a decision is accurate can only be identified after the final rank-order is established. This implies that while making comparative judgments, assessors are unaware of the accuracy of their decision. If so, only rank-order distance specifies assessors’ experienced complexity, and the same negative relationship between experienced complexity and rank-order distance can be expected for accurate and inaccurate decisions. However, inaccurate assessors are found to be more uncertain about the holistic scores they assigned to essays (Zhang, 2016). Furthermore, Gill and Bramley (2013) established that more inaccurate decisions were made if assessors felt less confident about CJ. These findings suggest that experienced complexity might be higher for inaccurate decisions. Van Daal et al. (2017) tested both hypotheses and found compelling evidence for the moderating role of decision accuracy: rank-order distance negatively related to experienced complexity, but this only applied to accurate decisions. For inaccurate decisions, experienced complexity was high, irrespective of the quality difference between the pieces of work that were compared.

The Role of Assessors’ Expertise

The study by van Daal et al. (2017) supports the notion that comparative judgment is more complex for some assessors than for others. To explain these differences, they point to the background characteristics of assessors in general, the most promising of which seems to be the assessor’s expertise. Several scholars assume that assessors should have enough experience to be able to engage in the comparative judgment process (Bisson et al., 2016; Jones et al., 2015; Pollitt, 2012a; Pollit, 2012b). Experienced assessors are assumed to have a rich knowledge base relevant for the judgment task at hand—for example, how to recognize writing quality (e.g., Sadler, 1989). This knowledge is stored in the assessor’s long-term memory as mental schema, which can then be called upon and used effortlessly while making comparative judgments (Sweller, 1994; Sweller et al., 1998). In other words, experts need to exert less mental effort than novice assessors in processing the information required to make a comparative judgment. We can assume, therefore, that assessors with more expertise experience the same comparison as less complex than do novice assessors.

Using Eye Tracking to Monitor Mental Effort

Linking expertise to mental effort also offers new possibilities to measure experienced complexity. Mental effort reflects differences in the amount of information processing that is required of assessors to make a certain comparative judgment (Sweller, 1994; Sweller et al., 1998). Consequently, mental effort can also be used as an indicator of experienced complexity because it results from the interaction between the assessor and the comparative judgment task. Several approaches can be used to operationalize mental effort (see Wierwille and Eggemeier, 1993). According to Sweller et al. (1998), changes in cognitive functioning can be reflected in physiological measures. Techniques included in these kinds of measurements are measures of heart rate and heart rate variability, eye activity, and brain activity. This study will make use of eye tracking and, more specifically, the measure of pupil dilation.

A large number of studies indicate that the pupils of an observer dilate when cognitive demand increases (Kahneman, 1973). This effect was found for tasks such as mental arithmetic (Hess, 1965), sentence comprehension (Just and Carpenter, 1993), letter combination (Beatty and Wagoner, 1978), and visual searching (Porter et al., 2007). The correlation between pupil size and mental workload has been argued in a number of investigations (Juris and Velden, 1977; Beatty, 1982; Hoeks and Levelt, 1993). Researchers have stated that pupil dilation takes place in short latencies following the beginning of a task and fades away rather quickly after the completion of a task. More importantly, the size of the pupil diameter appears to be a function of the mental effort necessary to complete a cognitive task. Beatty (1982) states that pupil dilation, triggered by a task, indicates the mental effort necessary at that moment. Triggered pupil dilation is frequently used as a tool to examine and measure the different aspects of human information processing, such as perception, memory, reasoning, and learning. Moreover, in order to examine mental workload and cognitive processing, pupil dilation has been identified as a reputable measure to use (Holmqvist, 2011). Our investigation will therefore use the measure of pupil diameter to operationalize mental effort.

This Study

This study focuses on the complexity of comparative judgment to assess argumentative writing, and its goal is twofold. First, it aims to conceptually replicate the findings of van Daal et al. (2017). Accordingly, the current study re-investigates the two hypotheses tested by the authors and uses a different measure to operationalize experienced complexity (pupil diameter). Second, the study of van Daal et al. (2017) did not include the relation of assessors’ expertise with experienced complexity. As expertise is assumed to ease the comparative judgment task by lowering the mental effort required of assessors (Sweller, 1994; Sweller et al., 1998), the expected negative relation of expertise with experienced complexity is tested in this study as well.

Hypothesis 1 assumes that if two texts are more similar in quality, this is related to higher experienced complexity. Hence, a negative relation between rank-order distance and experienced complexity is expected, irrespective of whether an accurate or inaccurate decision was made. In contrast, hypothesis 2 expects that decision accuracy moderates the relation of rank-order distance with experienced complexity. More specifically, rank-order distance is expected to be negatively related to experienced complexity for accurate decisions, while inaccurate decisions are assumed to yield higher experienced complexity regardless of the rank-order difference between both texts. In both hypotheses, it is posited that assessors differ in average experienced complexity as well as in the strength of the negative relationship of experienced complexity with rank-order distance.

The results provided by van Daal et al. (2017) indicate that the same rise in rank-order distance is associated with a different decrease in experienced complexity across assessors. Van Daal et al. (2017) explain these differences by referring to the differences between assessors in terms of background characteristics such as experience. More experienced assessors are expected to be better in handling larger amounts of information than novices (Campbell, 1988; Sweller, 1994; Sweller et al., 1998; Liu and Li, 2012). Hence, experienced assessors need to exert less mental effort to process a certain comparative judgment. Therefore, hypothesis 3 builds on hypothesis 2 by adding the assumption that an assessor’s experience is negatively correlated to experienced complexity. In other words, an assessor who has more experience will find the comparison of two texts of similar quality to be less complex than an assessor who does not.

Methodology

This study is a conceptual replication of the study by van Daal et al. (2017). To qualify as a conceptual replication, the findings of the 2017 study should be re-examined using a different set-up (Schmidt, 2009). Therefore, the current study manipulated the pairs of texts with which the assessors were presented and operationalized experienced complexity using an eye tracking measure. Other differences between the design of this study and the 2017 study will be described whenever applicable. To examine the hypotheses, comparative judgments on the assessment of argumentative writing were gathered. In line with the study by van Daal et al. (2017), an information-theoretic approach is used to provide evidence for the holding of the three hypotheses. This approach comprises two important steps. First, each hypothesis is translated into a statistical model. Subsequently, the three models are ranked based on Akaike Information Criterion corrected for sample size (AICc; Burnham and Anderson, 2002; Anderson, 2008), which gives an indication of how plausible each model is in representing full reality. After describing the context of this assessment, an outline of the measures used is given. Then, the procedures used for AIC model selection are described.

Context of This Study

Assessors

Twenty-three high school teachers participated as assessors in our study on a voluntary basis and gave their informed consent. Teachers were contacted via the university network, personal networks, and websites for job searchers. The criterion for participant inclusion was work experience in secondary education, since knowledge of the Flemish attainment goals was mandatory for the study. Their average age was 37.22 years (SD = 9.86). Ten of the participants held a master’s degree, while 13 held a bachelor’s degree. Unfortunately, the data of seven participants could not be used due to common problems associated with eye tracking data quality, calibration, and equipment failure (Holmqvist et al., 2011). Therefore, the data of sixteen (n = 16) assessors were available for analysis.

This sample substantially differs from the sample used in the study by van Daal et al. (2017) with regard to participants’ teaching position, as their study also included student teachers and participants who were, at that moment, teaching in primary education. Furthermore, in our sample, the distribution of participants’ degrees is roughly equal, with 10 being a master’s and 13 a bachelor’s, whereas the 2017 study had 91.84% master’s degrees.

Texts

Three different batches were created, each containing 10 comparisons. All batches contained the same composition of comparisons regarding the characteristics of the pairs; the pairs, however, were not the same. Each comparison has its own unique characteristics. These can be defined by the quality of the argumentative texts (below average, average, and above average) they contain, the rank-order distance that exists between these two texts, and the combined quality of each pair.

Sixty texts that were, among others, also included in the study of van Daal et al. (2017) were selected for this study. Text selection was based on the following criteria: 1) matched the competence description, 2) had been successfully used in earlier scientific studies, 3) was suitable for Flemish students in the fifth year of general secondary education, 4) could be written in a short time frame, and 5) would result in a short text. The maximum length for the texts was one A4 page. The texts discussed the topic of “having children” and were written by 135 students of the fifth year of the “Economics and Modern Languages” track in general secondary education in Flanders, Belgium. The task was adapted to the Flemish context and was successfully piloted previously in van Weijen (2009) and Tillema (2012). (For more information on the original assessment, see Lesterhuis et al., 2018; van Daal et al., 2017).

The texts used in this study differ from the texts used in the study by van Daal et al. (2017) with regard to the topics discussed in the texts. While the study of van Daal et al. (2017) used two different topics, this study used only one. Furthermore, the manner in which the texts were combined into pairs also differs. Van Daal et al. (2017) completely randomized the pairing, whereas this study created three different batches, each containing 10 comparisons. Based on these batches, pairs were made considering the characteristics of the pairs and the rank-order distance between them.

Judgment Procedures

Assessors were asked to read and assess argumentative texts using CJ. The assessors were first provided with information about the assignment that was given to the students and with a general description of the competence to be assessed (i.e., the final attainment goals regarding argumentative writing of the Flemish government). Each assessor made 10 comparisons, and the order of these comparisons was randomized using the Tobii randomizer tool.

The assessments took place in a laboratory setting. Assessors were invited individually to the laboratory and were seated behind a computer screen equipped with an integrated eye tracker. After being randomly assigned to one of the batches, a calibration procedure for the eye tracker was carried out.

Measures

Rank-order Distance and Decision Accuracy

Since the texts were previously assessed (see van Daal et al., 2017; Lesterhuis et al., 2018), a quality score expressed in logits was already available for each text. To calculate the rank-order distance, the logit score of the lower-ranked text was subtracted from that of the higher-ranked text. The resulting difference expresses the quality difference between both texts in logits. Rank-order distance ranged between 0.16 and 1.39 (mean = 0.73, SD = 0.33), and was standardized before analysis.

A decision is classified as accurate if an assessor picks the text with a higher quality score (based on the scores established in the studies of Lesterhuis et al., 2018; van Daal et al., 2017), while for an inaccurate decision, the opposite is true. The variable decision accuracy was dummy coded and indicates whether a decision is in line with the shared consensus (coded as 1) or not (coded as 0). Overall, assessors took 120 accurate decisions (63.16%).

The descriptive measures for both variables were in line with those of the variables used in the study by van Daal et al. (2017).

Teaching Experience

As stated earlier, expertise refers to the subject-specific knowledge stored in the assessor’s long-term memory, which they can call upon and use in an effortless manner (Sweller, 1994; Sweller et al., 1998). This facility frees assessor’s working memory capacity to process information that is unfamiliar to them (Sweller, 1994; Sweller et al., 1998). Because it can be assumed that teachers with more years of teaching experience have more subject-specific knowledge concerning the assessment of writing, years of teaching experience is used as a proxy for expertise. On average, assessors had 10.77 years teaching experience (SD = 9.57, range = 0.5–33 years), and experience was standardized before analysis.

Experienced Complexity

Experienced complexity is operationalized using the eye tracking measure of pupil dilation, which reflects the amount of mental effort necessary to complete a cognitive task (Beatty, 1982). To capture pupil dilation, the Tobii TX300 dark pupil eye tracker and 23-inch TFT monitor, with a maximum resolution of 1920 × 1080 pixels, were used. Data were sampled binocularly at the rate of 300 Hz. A head stabilization system was not required because head movement was allowed (37 × 17 cm). A gaze accuracy of 0.4° and gaze precision of 0.15° were reported by Tobii Technology (Stockholm, Sweden). The latency of the eye tracker was between 1.0 and 3.3 mls. The Tobii-Studio (3.2) software was used to record the eye tracking measures. A calibration process, in which assessors were seated about 60 cm from the screen, took place before starting the experiment. A five-point calibration procedure that required assessors to track five calibration dots on a gray, plain background was used. The eye tracking procedure was started once the calibration was successful.

First, in order to increase the validity of the data, pupil diameter measures with a validity rating of 0 were filtered from the data. Validity ratings of 0 indicate that the system is certain that it has recorded all relevant data for a particular eye, and that the data recorded belongs to that particular eye. In a second step, the distribution of pupil diameter was analyzed using the fitdistrplus package version 1.0–14 (Delignette-Muller and Dutang, 2015). To begin, a Cullen and Frey graph was plotted, which identified a normal distribution to be the most appropriate. Next, normal distribution was fitted to the empirical data; corresponding graphical assessment indicates that the distribution of pupil diameter approximates a normal distribution.

Analysis

An information-theoretic approach was used to test the holding of all three hypotheses. Anderson (2008) states that this approach requires a one-on-one translation of each hypothesis into a statistical model, while assuming that models can only be approximations of full reality (Burnham and Anderson, 2002). Then, model selection is done using Akaike’s Information Criterion (Burnham and Anderson, 2002; Anderson, 2008).

Modeling the Hypotheses

Pupil diameter is collected at the level of fixations; thus, every fixation is a data point. Given that each assessor completed 10 comparisons and that multiple fixations are registered during each comparison, a total of 62,119 data points for pupil diameter were collected. These data points are nested in assessors and comparisons. Hence, to adequately model the hypotheses, the hierarchical structure of the CJ data needs to be taken into account. Therefore, the hypotheses were modeled using mixed-effects models with cross-classification (Snijders and Bosker, 1999; Baayen, 2008; Baayen et al., 2008). Analyses were conducted using the lme4 package (Bates et al., 2015) in R (R Core Team, 2017).

Hypothesis 1 assumes that if two texts are more similar in quality, this is related to higher experienced complexity. Consequently, a negative relationship between rank-order distance (ROD) and experienced complexity (EC) is expected. It is supposed that decision accuracy is unrelated to experienced complexity. Therefore, it is not included in the equation of model 1. To model the experienced complexity EC_f(ar) for fixation f of comparison c by assessor a, the following formula is used:

$E{C}_{f\left(ca\right)}= {\beta }_0+ {\beta }_1\ast {\text{ROD}}_{ca}+\left({\mu }_{0a}+ {\mu }_{1a}\ast {\text{ROD}}_{ca}+ {\mu }_{0c}\right)+ {\epsilon }_{0f\left(ca\right)}$

Looking at this formula, ${\beta }_0$ indicates the complexity as experienced by a random assessor for a random comparison with average rank-order distance, and ${\beta }_1$ accounts for the relationship between rank-order distance and experienced complexity. This model allows experienced complexity to vary between assessors (μ_0a), comparisons (μ_0c), and fixations (ε_0f(ar)). The latter is the residual variance which also incorporates variation in experienced complexity due to, for example, interactions between assessors and comparisons. Ultimately, a random slope is added for rank-order distance, since its effect is expected to vary between assessors (μ_1a). It denotes the residual for the slope of rank-order distance for assessor r.

Hypothesis 2 builds on hypothesis 1 by adding the moderating role of decision accuracy (AccuD). More specifically, it assumes that experienced complexity (EC) is high for inaccurate decisions, irrespective of the rank-order distance (ROD). For accurate decisions, the same negative relation of rank-order distance with experienced complexity-as in hypothesis 1-is expected. Then, the experienced complexity EC_f(ca) for fixation f of comparison c by assessor a is modeled as:

$E{C}_{f\left(ca\right)}= {\beta }_0+ {\beta }_1\ast {\text{ROD}}_{ca}+ {\beta }_2\ast \text{AccuD}+ {\beta }_3\ast \left(\text{ROD}\ast \text{AccuD}\right)+\left({\mu }_{0a}+ {\mu }_{1a}\ast {\text{ROD}}_{ca}+ {\mu }_{0c}\right)+{\epsilon }_{0f\left(ca\right)}$

Model two adds the dummy variable AccuD to the fixed part of model 1. ${\beta }_2$ represents the difference in experienced complexity for accurate decisions (AccuD is coded as zero for inaccurate decisions). ${\beta }_1$ still accounts for the relation of rank-order distance with experienced complexity, but only for inaccurate decisions, while the interaction term between decision accuracy and rank-order distance (${\beta }_3$) represents the relation of rank-order distance with experienced complexity for accurate decisions.

Finally, hypothesis 3 adds the additional assumption to hypothesis 2 that a more experienced assessor will experience the comparison of two texts of similar quality as less complex than an assessor with less experience. This results in the following formula that represents the experienced complexity EC_f(ca) for fixation f of comparison c by assessor a:

$E{C}_{f\left(ca\right)}= {\beta }_0+ {\beta }_1\ast {\text{ROD}}_{ca}+{\beta }_2\ast \text{AccuD}+{\beta }_3\ast \left(\text{ROD}\ast \text{AccuD}\right)+{\beta }_4\ast \text{Exp}+\left({\mu }_{0a}+ {\mu }_{1a}\ast {\text{ROD}}_{ca}+ {\mu }_{0c}\right)+ {\epsilon }_{0f\left(ca\right)}$

Model 3 further expands upon model 2 by adding the relation between assessor’s experience (Exp) and experienced complexity. ${\beta }_4$ accounts for the expected negative relationship between experience and experienced complexity.

AIC Model Selection

Akaike’s Information Criterion corrected for sample size (AICc) is used to rank all models according to their plausibility. The corrected version is used rather than AIC since AICc converges to AIC as the sample size gets large; therefore, Burnham and Anderson (2004), Anderson (2008) recommend using AICc. Using their AICc values, all models are ranked according to their relative fit. Relative fit refers to each model’s ability to represent full reality: the lower AICc, the better the model is in doing so. To evaluate the plausibility of all competing models, two effect sizes will be used: evidence ratio (E) and weight of evidence (w). Calculations of these models are done using the R-package AICcmodavg version 2.2–2 (Mazerolle, 2019).

The evidence ratio (E) expresses how much more likely the top-ranked model is. The likelihood of model i is calculated by dividing its model likelihood with that of the best fitting model as a reference point (for formula, see Anderson, 2008; Burnham and Anderson, 2002). Hence, E_i represents the likelihood of model i being the best model in approximating full reality. The evidence ratio of the best model always equals 1, while the evidence ratio of model i, indicates how many times less likely (than the top-ranked model) model i is. In the literature on the information-theoretic approach, no clear cutoffs can be found concerning the evidence ratio.

However, Anderson (2008) states that models with evidence ratios up to eight provide reasonable support for the model being investigated, while models with evidence ratios up to about 20 (Richards et al., 2011) or 400 (Anderson, 2008) can be judged as plausible. The 2017 study stated that the guidelines of Anderson (2008) would be applied, but it is unclear which evidence ratios were judged as implausible. Therefore, this study judges all models with evidence ratios of up to 10 as plausible. However, these guidelines are used cautiously in line with the 2017 study of van Daal and colleagues.

Besides the evidence ratio, the weight of evidence for each model is also presented. The weight of evidence for a model i (w_i) can be interpreted as the probability that model i is the best model in approximating full reality, given the set of candidate models and the data (e.g., Burnham an Anderson, 2002). It can be calculated by dividing its likelihood by the sum of all model likelihoods (for formula, see Anderson, 2008; Burnham an Anderson, 2002). Moreover, it also expresses model selection uncertainty, which arises from the fact that model evaluation is based on a single sample (Burnham and Anderson, 2002; Anderson, 2008). In other words, if the researcher would gather another sample and fit the same models to this new sample, the model ranked as the most plausible could be different. Model selection uncertainty is low when the weight of the highest-ranked model is higher than 90%. This indicates that if another sample was used, the probability that the same model would be ranked as most plausible is very high (i.e., 90%). However, when the weight of evidence of the top-ranked model is below 90%, the same approach as in the study of van Daal et al. (2017) is used. Model selection uncertainty is taken into account by selecting all plausible models with a cumulative weight of 90% (Burnham and Anderson, 2011).

Finally, Anderson (2008) states that evaluation of the absolute model fit is also required, since AICc only provides evidence regarding relative fit. Therefore, the approach of Vonesh and Chinchilli (1997) is used to estimate the marginal R². This measure estimates the variance in experienced complexity accounted for by only the fixed effects in the model. It can be calculated using the following formula:

$R^2={\left[\text{cor}\left(E{C}_{ca},{\widehat{EC}}_{ca}\right)\right]}^2$

In this formula, EC_ca refers to the observed experienced complexity, and ${\widehat{EC}}_{ca}$ refers to the corresponding expected values based on the fixed effects in the model.

Reporting the Results

Depending on which model(s) is selected, evidence for or against each of the hypothesis is provided. An overview is presented in Table 1.

TABLE 1

TABLE 1. Overview of expected relations in each model.

If only model 1 is selected, this provides evidence for the plausibility of the role of rank-order distance in explaining experienced complexity. At the same time, this also implies that it is implausible that decision accuracy or teaching experience are related to experienced complexity (hypotheses 2 and 3). Similarly, the selection of model 2 refutes hypothesis 3 (role of teaching experience), but underpins the plausibility of the role of rank-order distance and decision accuracy (hypotheses 2 and 3). The selection of model 3 implies that rank-order distance, decision accuracy, and the experience of the assessors play a role in experienced complexity and provides evidence for all hypotheses. However, to verify this, the parameters and 85% confidence intervals that represent these expectations should be examined as well (e.g., direction of the slope of ROD to check its expected negative relation with experienced complexity) (Burnham and Anderson, 2002; Anderson, 2008). Irrespective of which model is selected, the random intercept of assessors and the random slope of rank-order distance will also be discussed because differences between assessors in average experienced complexity and in the relation of rank-order distance are assumed in all models.

Results

Model Selection

All fitted models are ranked by their plausibility to be the best approximating model, given the data and the three candidate models (see Table 2).

TABLE 2

TABLE 2. AICc, weight of evidence (w), and evidence ratio (E).

Model 3 is the most plausible model (AICc = 29,228.6, K = 10). Evidence ratios of model 1 and model 2 indicate that these models are at least 23 times less likely than model 3. Consequently, they can be judged as implausible (E > 10). Furthermore, the weight of evidence of model 3 approaches 1 (w = 0.959). Thus, model selection uncertainty is low. Therefore, only model 3 is judged as plausible. Model 3 represents hypothesis 3 and incorporates the role of rank-order distance, decision accuracy, and assessors’ experience with experienced complexity. Moreover, it expects mean experienced complexity and the strength of the relationship between rank-order distance and experienced complexity to differ between assessors.

The marginal R² of model 3 indicates that the fixed effects explain about 44.6% of the variance in experienced complexity. Hence, this indicates a good absolute fit of model 3. Furthermore, the assumptions regarding linear models (linearity, homoscedasticity, normality of residuals, and the absence of influential data points) were checked and met for this model. Next, the parameter estimates and 85% confidence intervals of model 3 will be used to further examine the expectations that were formulated in hypothesis 3.

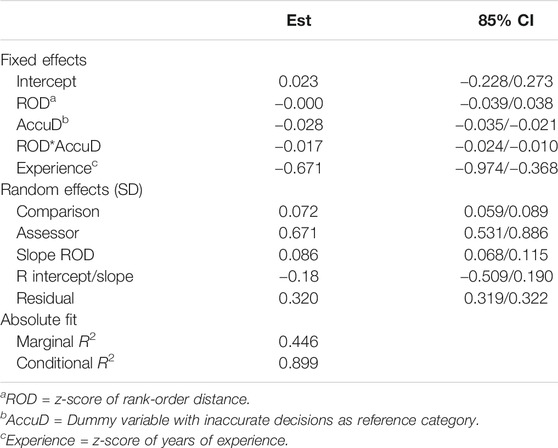
Parameter Estimates and 85% Confidence Intervals

As can be seen in Table 3, assessors experience a comparison as 0.028 SD less complex if they make an accurate decision (β_AccuD = −0.028). In other words, in line with expectations, an inaccurate decision is experienced as more complex irrespective of the rank-order distance. The absence of a main effect of rank-order distance (β_ROD = −0.000, 85% CI: −0.039|0.038) on experienced complexity indicates that this effect cannot be generalized beyond the sample. The main effect of rank-order distance, however, only accounts for inaccurate decisions. Hence, if an assessor makes an inaccurate decision, it is experienced as more complex, no matter how different in quality both texts are. As expected, this is different for accurate decisions.

TABLE 3

TABLE 3. Parameter estimates (Est.), 85% confidence intervals (85% ci), and R² for Model 3.

The interaction effect between rank-order distance and decision accuracy (β_ROD*AccuD = −0.017) confirms the expected negative relationship between rank-order distance and experienced complexity for accurate decisions. More specifically, an increase of 1 SD in rank-order distance decreases the average experienced complexity by 0.017 SD. In other words, assessors experience an accurate judgment as less complex if the two texts are farther apart on the rank-order. However, assessors differ in average experienced complexity (SD_assessor = 0.671) and in the strength of the relationship of rank-order distance with experienced complexity, as indicated in the random part of the model (SD_ROD = 0.086 SD). In other words, an increase of 1 SD in rank-order distance is, for some assessors, associated with a larger decrease in experienced complexity, while for others, this decrease is smaller. The negative correlation between the random intercept for assessors and the random slope of rank-order distance (r = −0.18) indicates that for assessors who experience comparative judgment as more complex than average, the negative relation of rank-order distance is less strong (and vice versa).

The main effect of experience confirms the expected negative relationship between teachers’ experience and experienced complexity (β_Experience = −0.671). More specifically, an increase of 1 SD in years of teaching experience decreases experienced complexity by 0.671 SD. We thus conclude that assessors experience comparative judgment on two texts as less complex if they have more teaching experience.

Conclusion and Discussion

In recent times, comparative judgment (CJ) has been introduced to assess competences, such as for example writing (e.g., Pollitt, 2012a; Pollit, 2012b; Verhavert, Bouwer, Donche, & De Maeyer, 2019). Assessors compare two texts and make relative, holistic judgments. The resulting pairwise comparison data are used to create a scale that orders the texts from worst to best. Despite the evidence that underpins the reliability and validity of CJ (eg, Lesterhuis, 2018; Jones and Inglis, 2015; Pollitt, 2012a,b), critical concerns are raised about the complexity of comparing pieces of student work. However, studies examining the complexity of CJ are scarce, with the work of van Daal et al. (2017) being one of the exceptions. As evidenced by their study, the complexity of CJ originates from the interaction between comparison characteristics and the assessor. More specifically, van Daal et al. (2017) established that CJ is experienced as more complex if the pieces of work to be compared differ less in quality. Furthermore, assessors were also found to differ in the complexity they experienced. It is worth noting that the 2017 study of van Daal and colleagues has two important limitations. First, it used a self-report measure to operationalize experienced complexity. Second, it did not include the impact of assessors’ background characteristics to explain the differences found across assessors. Therefore, the current study conceptually replicated the study of van Daal et al. (2017) using another sample, while also addressing the two shortcomings of the 2017 study.

This study examined the complexity of CJ to assess students’ argumentative writing. Sixteen assessors made comparative judgments on 10 pairs of texts. These pairs of texts consisted of 60 texts that were, among others, used in the study by van Daal et al. (2017). These texts were combined into 10 pairs in such a way that all batches contained the same composition of comparisons regarding the characteristics of the pairs. Data was gathered individually in a laboratory setting using eye tracking. The latter allowed us to operationalize experienced complexity using an objective measure-pupil dilation-instead of self-reports. In our investigation, we tested three hypotheses. The first and second hypotheses were already tested by the study of van Daal et al. (2017). Both hypotheses assume a negative relation between quality difference and experienced complexity that varies across assessors, but differ in the role of decision accuracy (whether or not decision accuracy acts as a moderator). To take assessors’ background characteristics into account, a third hypothesis has been examined that builds upon hypothesis 2 and adds the expectation that for assessors with more expertise, CJ is less complex. To gather evidence for the plausibility of these hypotheses, an information-theoretic approach to model selection is employed (Anderson, 2008), as in van Daal et al. (2017).

This study provides compelling evidence for the hypothesized negative relationship between rank-order distance and experienced complexity for accurate decisions. In other words, when the rank-order distance between two texts increases, the experienced complexity decreases accordingly. This replicates the findings from the study by van Daal et al. (2017) and supports the suggestion made by Pollitt (2012b), Gill and Bramley (2013). This negative relationship is theoretically sound: if two pieces of student work differ more in quality, the decision uncertainty of the comparison decreases accordingly. Consequently, such comparisons are experienced as less complex.

Convincing evidence was found for the hypothesis that assumes inaccurate decisions to be associated with higher experienced complexity than accurate decisions. This finding is in line with the evidence provided by Zhang (2016), which states that assessors experience inaccurate decisions as more difficult. The results replicate those of the study by van Daal et al. (2017). Also, in line with van Daal et al. (2017), it remains unclear whether the relationship of experienced complexity with rank-order distance is positive or absent for inaccurate decisions. This study found a negative relationship between experienced complexity and rank-order distance for inaccurate decisions, but was not able to generalize this relationship beyond the sample of this study. The nature of the relationship between experienced complexity and rank-order distance for inaccurate decisions should be elaborated on in future studies.

Our results indicate that the same increase in rank-order distance between two pieces of student work is associated with a different decrease in experienced complexity across assessors. This finding underpins the assumed differences in experienced complexity between assessors and confirms the results of van Daal et al. (2017). It also supports the theoretical framework on task complexity by Campbell (1988), which assumes that experienced complexity is the result of the interaction between the objective complexity of the judgment task and each individual assessor. In other words, experienced complexity is assumed to vary according to the experience and information handling capacity possessed by the assessors. These insights have implications regarding the practical use of CJ. Since assessors vary in average experienced complexity as a result of how they interact with the objective characteristics of each comparison, it is important to take the differences in discriminating ability between assessors into account when setting up CJ assessments. More concretely, algorithms that take into account the differences in discriminating ability across assessors to distribute pairs of student work should be developed (van Daal et al., 2017).

Hypothesis 3 operationalized expertise by teaching experience. It is assumed that teachers with more teaching experience have more mental schemas relevant for the judgment task at hand (Sweller, 1994; Sweller et al., 1998). Looking at hypothesis 3, this study provides compelling evidence for the negative relationship between experience and experienced complexity for an average assessor, as an assessor with more experience will experience less complexity in CJ. This is in line with the suggestion made by van Daal et al. (2017), that assessors’ background characteristics could offer an explanation for variation in experienced complexity across assessors. Although assessors’ background characteristics have, in the past, been integrated into the theoretical framework on CJ, these studies provided mixed findings and did not incorporate experienced complexity (e.g., Jones et al., 2015). Furthermore, the theoretical advancements on CJ concerning the impact of expertise suggested in this study also provide us with implications regarding the practical use of CJ. Since experienced complexity lowers drastically as experience increases, this suggests that assessors should reach a certain degree of experience with the competences being assessed in order to participate in CJ. However, to gain insight into which level of expertise is optimal, further research into the link between experienced complexity and the quality of the decisions that assessors make is needed. The importance for research regarding expertise in the context of comparative judgment is underlined by the differences in conceptualizations that are being employed in research, and the fact that none of those are grounded in a clear, theoretical framework. For example, some studies operationalize expertise as assessment skills (Whitehouse and Pollitt, 2012; Jones et al., 2015), while others refer to it as having subject-specific knowledge (Jones and Alcock, 2012; Jones and Alcock, 2014; van Daal et al., 2019) or as having experience with the educational level on which the respective assessment takes place (Heldsinger and Humphry, 2010; Whitehouse and Pollitt, 2012). Future studies should investigate the effects of the above described operationalizations of expertise and their relationship with experienced complexity. In doing so, a clear framework on the influence of expertise and its implications for experienced complexity in comparative judgment can be built and linked to what it takes to validly choose between two texts.

Our results clearly support the framework on comparative judgment task complexity, as laid out in the study by van Daal et al. (2017). However, some critical assumptions can be made about our research findings. As stated previously, this study operationalized experienced complexity by pupil dilation (diameter), and previous research considers a smaller pupil to be an indication of less experienced complexity (Holmqvist et al., 2011). This study found that an increase in experience results in a decrease in pupil diameter and thus a decrease in experienced complexity. However, it is important that we look at the effect of age on our operationalization of experienced complexity. Many studies have linked age to a decline in pupillary reaction times after the onset of a stimulus (Sharpe and Sylvester, 1978; Bitsios et al., 1996). Therefore, this relationship should be further investigated in future studies using other eye tracking measures (e.g., fixation duration, transition) or other psycho-physiological measures, such as heart rate or galvanic skin response. A second approach to further test the hypothesis regarding the negative relationship between experience and experienced complexity in CJ is keeping the operationalization of experienced complexity by pupil diameter, but controlling for the impact of age by selecting participants of the same age group. Additionally, more fine-grained conceptualizations and operationalizations of objective complexity in CJ should be developed and used. This study used the relative difference in quality (ROD) to operationalize objective complexity, and in the context of CJ, is a commonly used operationalization; however, it can be seen as a disadvantage since it is directly grounded in the assessors’ holistic perceptions of quality. Because it is a reflection of quality based on the perception of a group of assessors (e.g., Pollitt, 2012a; Pollitt, 2012b), it thus fails to capture the true degree of difference in quality between two texts. An interesting avenue for further research is the inclusion of expert ratings on sub-aspects of the quality of texts (e.g., language use, layout). As a result, the extent to which two texts differ in quality regarding different dimensions can be identified and used to further operationalize objective complexity in a more fine-grained manner.

Apart from the limitations mentioned above, this study is the first to conceptually replicate the findings by van Daal et al. (2017) regarding the role of quality difference and decision accuracy in the experienced complexity of CJ. Results show that the conclusions of the replicated study also apply when using another sample and another measure to operationalize experienced complexity. In this way, our study shows that findings can be generalized across dependent measures and samples. Although additional (conceptual) replications are needed to examine whether this also applies to CJ in the assessment of other competences or types of student work (e.g., portfolios), this conceptual replication study clearly validates the hypotheses of the original study. Finally, the theoretical advancements suggested by this study show that the information-theoretic approach by Chamberlin (1890) holds promise in further accelerating theory development within CJ and, more broadly, the educational sciences as a whole.

Data Availability Statement

The datasets presented in this article are not readily available, the datasets generated for this study are available on request to the corresponding author. Requests to access the datasets should be directed to MG, marijn.gijsen@uantwerpen.be.

Ethics Statement

Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author Contributions

MG, SM, and ML contributed to the conception and the design of this study. ML was responsible for the data collection. Data analyses and interpretation of the data were conducted by MG and TD, who also drafted the manuscript. All other authors critically revised this manuscript and made suggestions for its improvement. All authors approved the final version of the manuscript for publication and are accountable for all aspects of the work.

Funding

This work was supported by the Flanders Innovation and Entrepreneurship and the Research Foundation (grant number 130043).

Conflict of Interest

ML and SM are both co-founders of the spin-off company, Comproved, which is a tool that makes use of the principles of comparative judgment. However, this association was not in place during the data collection and analysis conducted for this study.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank Irina Rets, PhD for her assistance in improving the manuscript stylistically. In addition, the final version of this paper benefited greatly from the constructive comments of the reviewers and the editor.

References

Anderson, D. R. (2008). Model based inference in the life sciences: a primer on evidence, NewYork, NY, Springer.

CrossRef Full Text | Google Scholar

Baayen, H. (2008). Analyzing linguistic data: a practical introduction to statistics using R, Cambridge, United Kingdom, Cambridge University Press.

CrossRef Full Text | Google Scholar

Baayen, H., Davidson, D., and Bates, D. (2008). Mixed-effects modeling with crossed random effects for subjects and items. J. Mem. Lang. 59, 390–412. doi:10.1016/j.jml.2007.12.005

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Software 67 (1), 1–48. doi:10.18637/jss.v067.i01

CrossRef Full Text | Google Scholar

Beatty, J. (1982). Task-evoked pupillary responses, processing load, and the structure of processing resources. Psychol. Bull. 91(2), 276–292. doi:10.1037/0033-2909.91.2.276

PubMed Abstract | CrossRef Full Text | Google Scholar

Beatty, J., and Wagoner, B. L. (1978). Pupillometric signs of brain activation vary with level of Cognitive processing. Science 199 (4334), 1216–1218. doi:10.1126/science.628837

PubMed Abstract | CrossRef Full Text | Google Scholar

Bisson, M., Gilmore, C., Inglis, M., and Jones, I. (2016). Measuring conceptual understanding using comparative judgement. Int. J. Res. Undergrad. Mathemat. Educ., 2 (2), 141–164. doi:10.1007/s40753-016-0024-3

CrossRef Full Text | Google Scholar

Bitsios, P., Prettyman, R., and Szabadi, E. (1996). Changes in autonomic function with age: a study of pupillary kinetics in healthy young and old people. Age Ageing 25 (6), 432–438. doi:10.1093/ageing/25.6.432

PubMed Abstract | CrossRef Full Text | Google Scholar

Bramley, T. (2007). “Paired comparison methods,” in Techniques for monitoring the comparability of examination standards, Editors P. Newton, J.-A. Baird, H. Goldstein, H. Patrick, and P. Tymms. London, United Kingdom, Qualifications and Curriculum Authority, 246–300.

Google Scholar

Burnham, K. P., Anderson, D. R., and Huyvaert, K. P. (2011). AIC model selection and multimodel inference in behavioral ecology: some background, observations, and comparisons. Behav. Ecol. Sociobiol. 65 (1), 23–35. doi:10.1007/s00265-010-1029-6

CrossRef Full Text | Google Scholar

Burnham, K. P., and Anderson, D. R. (2002). Model selection and inference: a practical information-theoretic approach, 2nd Edn. New York, NY: Springer-Verlag. doi:10.1007/b97636

CrossRef Full Text | Google Scholar

Burnham, K. P., and Anderson, D. R. (2004). Multimodel inference: understanding AIC and BIC in model selection. Socio. Methods Res. 33, 261–304. doi:10.1177/0049124104268644

CrossRef Full Text | Google Scholar

Campbell, D. J. (1988). Task complexity: a review and analysis. Acad. Manag. Rev. 13 (1), 40–52. doi:10.5465/AMR.1988.4306775

CrossRef Full Text | Google Scholar

Chamberlin, T. C. (1890). The method of multiple working hypotheses. Science 15 (92), 92–96. doi:10.1126/science.148.3671.754

PubMed Abstract | CrossRef Full Text | Google Scholar

Delignette-Muller, M., and Dutang, C. (2015). Fitdistrplus: an R package for fitting distributions. J. Stat. Software, 64 (4), 1–34. doi:10.18637/jss.v064.i04

CrossRef Full Text | Google Scholar

Gill, T., and Bramley, T. (2013). How accurate are examiners’ holistic judgments of script quality? Assessment in education: principles, Policy Pract. 20 (3), 308–324. doi:10.1080/0969594X.2013.779229

CrossRef Full Text | Google Scholar

Guo, J.-P., Pang, M. F., Yang, L.-Y., and Ding, Y. (2012). Learning from comparing multiple examples: on the dilemma of “similar” or “different”. Educ. Psychol. Rev. 24 (2), 251–269. doi:10.1007/s10648-012-9192-0

CrossRef Full Text | Google Scholar

Heldsinger, S., and Humphry, S. (2010). Using the method of pairwise comparison to obtain reliable teacher assessments. Aust. Educ. Res. 37 (2), 1–19. doi:10.1007/BF03216919

CrossRef Full Text | Google Scholar

Hess, E. H. (1965). Attitude and pupil size. Sci. Am. 212, 46–54. doi:10.1038/scientificamerican0465-46

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoeks, B., and Levelt, W. J. M. (1993). Pupillary dilation as a measure of attention: a quantitative system analysis. Behav. Res. Methods Instrum. Comput. 25 (1), 16–26. doi:10.3758/BF03204445

CrossRef Full Text | Google Scholar

Holmqvist, K., Nyström, M., Andersson, R., Dewhurst, R., Jarodzka, H., and Van de Weijer, J. (2011). Eye tracking: a comprehensive guide to methods and measures. Oxford, United Kingdom, Oxford University Press.

Google Scholar

Jones, I., and Alcock, L. (2012). “Summative peer assessment of undergraduate calculus using adaptive comparative judgement,” in Mapping university mathematics assessment practices. Editors P. Iannone and A. Simpson (Norwich: University of East Anglia), 63–74.

Jones, I., and Alcock, L. (2014). Peer assessment without assessment criteria. Stud. High Educ. 39 (10), 1774–1787. doi:10.1080/03075079.2013.821974

CrossRef Full Text | Google Scholar

Jones, I., and Inglis, M. (2015). The problem of assessing problem solving: can comparative judgement help? Educ. Stud. Math. 89 (3), 337–355. doi:10.1007/s10649-015-9607-1

Jones, I., Swan, M., and Pollitt, A. (2015). Assessing mathematical problem solving using comparative judgment. Int. J. Sci. Math. Educ. 13 (1), 151–177. doi:10.1007/s10763-013-9497-6

CrossRef Full Text | Google Scholar

Juris, M., and Velden, M. (1977). The pupillary response to mental overload. Psychobiology 5 (4), 421–424. doi:10.3758/BF03337847

CrossRef Full Text | Google Scholar

Just, M. A., and Carpenter, P. A. (1993). The intensity dimension of thought: pupillometric indices of sentence processing. Can. J. Exp. Psychol. 47 (2), 310–339. doi:10.1037/h0078820

PubMed Abstract | CrossRef Full Text | Google Scholar

Kahneman, D. (1973). Attention and effort, Upper Saddle River, NY, Prentice Hall.

Google Scholar

Lesterhuis, M. (2018). The validity of comparative judgement for assessing text quality: an assessor’s perspective (Unpublished doctoral dissertation). Antwerp, Belgium: University of Antwerp.

Google Scholar

Lesterhuis, M., van Daal, T., Van Gasse, R., Coertjens, L., Donche, V., and De Maeyer, S. (2018). When teachers compare argumentative texts: decisions informed by multiple complex aspects of text quality. L1 Educ. Stud. Lang. Lit. 18, 1–22. doi:10.17239/L1ESLL-2018.18.01.02

CrossRef Full Text | Google Scholar

Liu, P., and Li, Z. (2012). Task complexity: a review and conceptualization framework. Int. J. Ind. Ergon., 42, 553–568. doi:10.1016/j.ergon.2012.09.001

CrossRef Full Text | Google Scholar

Mazerolle, M. J. (2019). Model selection and multimodel inference based on (Q)AIC(c) v. 2.2–2. Available at: https://cran.r-project.org/web/packages/AICcmodavg/AICcmodavg.pdf (Accessed July 12, 2020).

Google Scholar

Martin, S. (2014). Measuring cognitive load and cognition: metrics for technology-enhanced learning. Educ. Res. Eval. 20 (7-8), 592–621. doi:10.1080/13803611.2014.997140

CrossRef Full Text | Google Scholar

Pollitt, A. (2012b). Comparative judgment for assessment. Int. J. Technol. Des. Educ. 22 (2), 157–170. doi:10.1007/s10798-011-9189-x

CrossRef Full Text | Google Scholar

Pollitt, A. (2012a). The method of adaptive comparative judgement. Assessment in Education 19 (3), 281–300. doi:10.1080/0969594X.2012.665354

CrossRef Full Text | Google Scholar

Porter, G., Troscianko, T., and Gilchrist, I. D. (2007). Effort during visual search and counting: insights from pupillometry. Q. J. Exp. Psychol. (Hove) 60 (2), 211–229. doi:10.1080/17470210600673818

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team (2017). R: a language and environment for statistical computing. Available at: https://www.R-project.org/

Richards, S. A., Whittingham, M. J., and Stephens, P. A. (2011). Model selection and model averaging in behavioural ecology: the utility of the IT-AIC framework. Behav. Ecol. Sociobiol. 65 (1), 77–89. doi:10.1007/s00265-010-1035-8

CrossRef Full Text | Google Scholar

Sadler, D. R. (1989). Formative assessment and the design of instructional systems. Instr. Sci. 18 (2), 119–144. doi:10.1007/BF00117714

CrossRef Full Text | Google Scholar

Schmidt, S. (2009). Shall we really do it again? The powerful concept of replication is neglected in the social sciences. Rev. Gen. Psychol. 13 (2), 90–100. doi:10.1037/a0015108

CrossRef Full Text | Google Scholar

Sharpe, JA, and Sylvester, TO (1978). Effect of aging on horizontal smooth pursuit. Invest. Ophthalmol. Vis. Sci. 17 (5), 465–468.

PubMed AbstractGoogle Scholar

Snijders, T., and Bosker, R. (1999). Multilevel analysis: an introduction to basic and advanced multilevel modeling, Thousand Oaks, CA, SAGE Publications.

Google Scholar

Sweller, J. (1994). Cognitive load theory, learning difficulty and instructional design. Learn. InStruct. 4, 295–312. doi:10.1016/0959-4752(94)90003-5

CrossRef Full Text | Google Scholar

Sweller, J., van Merrienboer, J. J. G., and Paas, F. G. W. C. (1998). Cognitive architecture and instructional design. Educ. Psychol. Rev. 10 (3), 251–296. doi:10.1023/A:1022193728205

CrossRef Full Text | Google Scholar

Thurstone, L. L. (1927a). A law of comparative judgment. Am. J. Psychol. 34 (4), 273–286. doi:10.1037/h0070288

CrossRef Full Text | Google Scholar

Thurstone, L. L. (1927b). Psychophysical analysis. Am. J. Psychol. 38 (3), 368–389. doi:10.2307/1415006

CrossRef Full Text | Google Scholar

Tillema, M. (2012). Writing in first and second language: empirical studies on text quality and writing processes. Utrecht, Netherlands: The Netherlands Graduate School of Linguistics.

Google Scholar

Van Weijen, D. (2009). Writing processes, text quality, and task effects: empirical studies in first and second language writing. Utrecht, Netherlands: The Netherlands Graduate School of Linguistics.

Google Scholar

Van Daal, T., Lesterhuis, M., Coertjens, L., Donche, V., and De Maeyer, S. (2017). The complexity of assessing student work using comparative judgment: the moderating role of decision accuracy. Front. Educ. 2 (44), 1–13. doi:10.3389/feduc.2017.00044

CrossRef Full Text | Google Scholar

Van Daal, T., Lesterhuis, M., Coertjens, L., Donche, V., and De Maeyer, S. (2019). Validity of comparative judgement to assess academic writing: examining implications of its holistic character and building on a shared consensus. Assess Educ. Princ. Pol. Pract. 26 (1), 59–74. doi:10.1080/0969594X.2016.1253542

CrossRef Full Text | Google Scholar

Verhavert, S., Bouwer, R., Donche, V., and De Maeyer, S. (2019). A meta-analysis on the reliability of comparative judgement. Assess Educ. Princ. Pol. Pract. 2 (5), 1–22. doi:10.1080/0969594X.2019.1602027

CrossRef Full Text | Google Scholar

Vonesh, E. F., and Chinchilli, V. M. (1997). Linear and nonlinear models for the analysis of repeated measurement, New York, NY, Marcel Dekker.

Google Scholar

Whitehouse, C. (2012). Testing the validity of judgements about geography essays using the adaptive comparative judgement method, Manchester, United Kingdom, AQA Centre for Education Research and Policy.

Google Scholar

Whitehouse, C., and Pollitt, A. (2012). Using adaptive comparative judgement to obtain a highly reliable rank order in summative assessment, Manchester, United Kingdom, AQA Centre for Education Research and Policy.

Google Scholar

Wierwille, W. W., and Eggemeier, F. L. (1993). Recommendations for mental workload measurement in a test and evaluation environment. Hum. Factors 35 (2), 263–281. doi:10.1177/001872089303500205

CrossRef Full Text | Google Scholar

Zhang, J. (2016). Same text different processing? Exploring how raters’ cognitive and meta-cognitive strategies influence rating accuracy in essay scoring. Assess. Writ. 27, 37–53. doi:10.1016/j.asw.2015.11.001

CrossRef Full Text | Google Scholar