Investigating a Singapore-Based Mathematics Textbook and Teaching Approach in Classrooms in England

The high mathematics performance of pupils in Singapore on international assessments has prompted educational initiatives in other countries—such as the UK and the USA—to adopt Singapore-based approaches in an attempt to raise mathematics achievement. Empirical evidence to support the transferability of such approaches beyond the Singaporean context, however, is limited. This article reports findings from a mixed methods Cluster Randomized Controlled Trial (mmCRCT) evaluating the use of a primary mathematics textbook series and teaching approach in England based on a textbook and teaching approach from Singapore. Main features of the intervention included textbook use, mixed-ability groups, use of manipulatives, and emphasis on mastery (i.e., ensuring all pupils grasp core concepts before proceeding to new topics). A delayed treatment experimental design was used within the mmCRCT, with 12 schools randomly allocated into two groups. The experimental group used the textbooks and teaching approach from September 2015. The delayed treatment control group proceeded with “business as usual” until January 2016, then started using the textbooks and teaching approach. Data were collected (in the first, second and third terms of one school year) on pupils' mathematics knowledge and skills, pupils' attitudes toward mathematics, classroom practice (based on structured observation schedules and qualitative field notes), teacher perspectives (from semi-structured interviews), and intervention-specific professional development (in July 2015 for the experimental group, December 2015 for the delayed treatment control group, observed by researchers and followed by focus-group interviews). Results showed a small but significant positive effect by Term 3 of using the mastery-oriented materials and approach from September on pupils' subsequent mathematics knowledge and skills, but no persistent difference between groups across terms on their attitudes. Differences in classroom practice between the two groups were observed in the first term but insignificant by the third term. Qualitative findings elaborate on and illustrate these first-term differences, teachers' perspectives on their practice, variations in textbook use and teaching approach implementation, and considerations of fidelity to intervention. Implications are drawn for policy and practice in mathematics teaching and for research using mixed methods experimental designs to evaluate a combination of processes, perspectives and outcomes.

Introduction

High-profile international assessments such as PISA and TIMSS have drawn considerable attention from policymakers across the globe. The high mathematics performance of pupils in Singapore in particular (e.g., OECD, 2016) has prompted initiatives in other countries with comparatively lower performance on the same assessments—such as the UK and the USA—attempting to implement approaches to teaching mathematics that are based on those used in Singapore, with the hope that this will raise pupils' mathematics achievement. For example, in 2016 the UK Government made a £41M investment to support schools in adopting mastery approaches based on East Asian—Shanghai and Singapore—approaches to teaching by purchasing mastery-oriented textbooks (Department for Education, 2016) while in the USA, most states had adopted a set of standards that emphasize a mastery orientation (Common Core State Standards Initiative, 2016).

The approach to teaching primary mathematics in Singapore is characterized by textbook use and an emphasis on mastery-based instruction. “Mastery” here refers to a focus on making sure that every pupil secures understanding of a particular concept before moving on to the next, in contrast to placing the priority on content coverage (which has traditionally characterized curricula in the UK). Early mastery learning theory built on Carroll's (1963) “Model of School Learning,” which conceptualized aptitude in terms of time to learn and time needed, thus identifying learners as “fast” or “slow” rather than possessed of some absolute level of ability. Bloom (1968) built upon and applied this conceptualization to classroom instruction, focusing on “how individual differences in learners can be related to the learning and teaching process” (p.2) to provide the conditions for more pupils to master a subject, with the underlying principle that all or most pupils can achieve mastery given the right conditions to support their learning. Guskey (1980) extended the theoretical notion of mastery to consider practical implementation, attending to teacher development and pedagogy as well as curriculum and teaching materials, ultimately finding indications that mastery instruction (if properly implemented) could facilitate pupil progress as well as improve pupils' attitudes toward learning.

Variation theory also plays an important role in the teaching of mathematics in Singapore. The terminology used to describe variation theory has differed across theorists who have written on the topic. Bruner and Kenney (1965) conceived of variation in terms of the presentation of different “constructions and perceptual events” to facilitate children's abstraction and generalization of broader mathematical principles. Runesson (2005) focuses on perceptual variability and the centrality of how learners experience and interact with the object of learning. One of the most influential theorists with regard to the approach to teaching mathematics in Singapore, Dienes (1960), proposed that teaching should systematically incorporate mathematical variability and perceptual variability. The former involves presenting pupils with conceptually-related problems but different values or different irrelevant attributes that lead to deeper understanding (e.g., pupils might learn addition first without and then with regrouping, and progress within each of these strategies from adding 2- to 1-digit and 2- to 2-digit numbers, “varying” only one aspect—the size of the second number and use of regrouping or not — at a time). The latter involves presenting pupils with different physical representations of the same concept (e.g., pictures, concrete objects, and written sums), facilitating pupils' understanding of abstract mathematical concepts; this builds on the progression from concrete to abstract in Piaget's (1952) theory of children's learning and development. In the Singapore approach to teaching mathematics, variation theory is operationalized via the use of a Concrete-Pictorial-Abstract (CPA) scaffolding of representations (with a heavy weighting toward the former two types of representations in earlier years of schooling). That is, a concept is taught first by using manipulatives such as interlocking cubes, then by representing problems visually (e.g., using bar models), and finally by engaging with problems represented using mathematical symbols and numerals. The CPA approach draws on theory by Bruner (1966), in particular his conception of enactive (action-based), iconic (image-based) and symbolic (abstract) stages of representation and the proposition that “if it is true that intellectual development moves from enactive through iconic to symbolic representation of the world, it is likely that an optimum [teaching] sequence will progress in the same way” (p.49).

Despite policy emphasis on international comparisons and transfer or imitation of a Singapore approach to teaching mathematics in the UK and the USA, the evidence to support the use of these methods is relatively limited. Some previous research has demonstrated the educational effectiveness of Singapore-based approaches (e.g., Gross and Merchlinsky, 2002; Ginsburg et al., 2005; Hoven and Garelick, 2007; Goldman et al., 2009; Uribe-Zarain, 2010). However, studies involving an experimental design are relatively few and have found small-to-modest positive effects on pupils' mathematical knowledge and skills (Vignoles et al., 2015; Jaciw et al., 2016; Jerrim and Vignoles, 2016). Further, these experimental studies have not systematically studied teaching practice via direct lesson observations, or where such observations are mentioned they are not reported in detail. By contrast, qualitative studies have also been undertaken to explore teachers' perceptions and experiences of using Singapore-based approaches to teaching mathematics in other settings (e.g., Naroth and Luneta, 2015), and some studies have explored teaching practice specific to the implementation of such approaches (e.g., Boyd and Ash, 2018). However, these studies have not made direct links between teachers' perceptions, teachers' practices, and pupil attainment and progress.

This article reports results from a study that adds to this evidence base, using mixed methods within an experimental (Cluster Randomized Controlled Trial; CRCT) design to evaluate the use of a particular set of materials—including textbooks, pupil practice books, pupil assessment books, and teacher's guides — and teaching approach in England in Year 1 (age 5–6) classrooms, based on a textbook and pedagogical approach from Singapore. The focus on Year 1 is well-supported by previous research. For example, Sammons et al. (2013) showed that by the end of Year 1, attending a more academically effective primary school could narrow gaps in pupil achievement associated with early disadvantage.

The specific textbook and accompanying materials used in this study were the Inspire Maths series distributed by the Oxford University Press (OUP); this series was based on the textbook series My Pals are Here! (Marshall Cavendish Edition; Fong et al., 2015), used in many Singapore primary schools. While the results presented below are particular to this set of materials and the teaching approach used in classrooms alongside it, which heavily emphasized textbook use and mixed-ability grouping alongside the CPA approach, the findings contribute to the broader evidence base on the use of Singaporean (or Singapore-inspired) approaches to mathematics teaching in settings outside of Singapore. Further, this study illustrates the value added by using mixed methods within an experimental design, which is of methodological relevance beyond the study's specific substantive focus.

To the best of our knowledge, this study is the first to investigate the impact of introducing a Singapore-based approach to teaching mathematics to another country while accounting for pupil attainment and progress, pupil attitudes, teachers' practice, and teachers' perceptions and experiences, using a mixed method experimental design. The novel integrated findings that follow allow a more complete “story” to be told than in past research, connecting effects on pupil attainment and progress to possible reasons for those effects based on what took place in lessons, accounting for fidelity to the intervention, and lending insight into the benefits and challenges associated with implementation according to practitioners' perspectives.

With this purpose in mind, this paper addresses the following research questions:

• Is the use of the Inspire Maths materials and teaching approach in Year 1 classrooms associated with differences in Year 1 pupils' attainment and progress in mathematics?

• Is the use of the Inspire Maths materials and teaching approach associated with differences in Year 1 pupils' attitudes toward mathematics?

• Is the use of the Inspire Maths materials and teaching approach associated with differences in Year 1 teaching practice, and if so, how can these differences be characterized?

• How do Year 1 teachers' perspectives and qualitative lesson observation findings explain (in a non-statistical sense), elaborate upon, and/or illuminate links between any observed effects (or lack thereof) of the use of the Inspire Maths materials and teaching approach on pupils' attainment and progress, pupils' attitudes toward mathematics, and observed (measurable) differences in teaching practice?

Materials and Methods

Design

The overall design of the study consisted of a mixed method cluster Randomized Controlled Trial (mmCRCT) design with a delayed treatment control group. First, the research team drew a random sample of schools from a list of schools in England that had expressed an interest in using the Inspire Maths materials and approach¹. One group of schools (here referred to as the “experimental group”) were randomly chosen to begin using the Inspire Maths teaching approach and materials from the beginning of the UK school year in September 2015. The remaining schools (here referred to as the “delayed treatment group”) proceeded with math lessons as usual through the Autumn 2015 term and then began using the Inspire Maths materials and teaching approach in January 2016. Each group received professional development (in July 2015 for the experimental group, and in December 2015—during the term break—for the delayed treatment group) to prepare them and give them time to plan in order to begin using the Inspire Maths materials and teaching approach at the start of the relevant term (September 2015 and January 2016, respectively).

The rationale for a delayed treatment control group rather than a “pure” control group was primarily based on practical considerations. A control group without delayed treatment would have affected the feasibility of recruitment, as control group schools would have had less incentive to participate in the study. Furthermore, schools rather than teachers were randomly allocated into either the experimental or the delayed treatment group to avoid diffusion (i.e., interaction and discussion between two teachers in the same school allocated to different groups) and preserve internal validity (Raudenbush et al., 2007). The use of mixed methods was in keeping with a pragmatist epistemological stance, underpinned by the primacy of the research questions and the selection of methods to best answer these questions (Tashakkori and Teddlie, 2010). Further, mixed methods studies have been increasingly used as an appropriate approach to studying the complexities of classroom practice and teacher effectiveness (Sammons and Davis, 2017), aspects that are highly emphasized in this study.

Research visits to each participating teacher's classroom took place three times during the school year: once in September-October 2015 (during Term 1), once in January-February 2016 (during Term 2), and once in April-May 2016 (during Term 3). All fieldwork was undertaken by a single researcher who was trained and experienced in the use of the data collection methods, detailed below.

In addition to these research visits, the Continuing Professional Development (CPD) sessions offered alongside the Inspire Maths materials were observed, with notes taken to document the sessions. For the experimental group, 3 days of CPD took place in July 2015, followed by an additional 2 days of CPD in January. For the delayed treatment group, the same sequence of sessions took place in December (3 days) and March (2 days). A focus group interview was conducted with participating teachers following the first 3-day CPD sequence for each group to elicit their views and experiences of these training sessions, and teachers filled out a brief background questionnaire about their teaching experience (total years teaching, years teaching in Year 1, other year groups taught previously, past career break(s), years in present school) and confidence teaching mathematics (1 item on a scale from 1 = “Very low” to 5 = “Very high”).

Sample

The sample included 12 schools, 20 teachers, and 576 Year 1 pupils (aged rising 6 years). Nine teachers (in 6 schools) were assigned to the experimental group, and 11 teachers (in 6 schools) were assigned to the delayed treatment group. Four of the 12 schools (3 in the experimental group) were single-form entry, meaning they had one class of Year 1 pupils in the 2015-16 school year, 8 schools (3 in the experimental group) were two-form entry, and one school (in the experimental group) was three-form entry (with one class participating in the pilot but not in the main study). One classroom had a mix of Year 1 and Year 2 pupils; only Year 1 pupils were included in the analysis presented here for the sake of comparability.

Table 1 presents further information on the characteristics of the teachers in the experimental and delayed treatment groups. The delayed treatment group teachers had, on average, more years of total teaching experience and lower confidence in teaching mathematics at baseline, but the experimental and delayed treatment groups of teachers were similar on average in their experience teaching Year 1, years teaching in their current school, and gender distribution (only one teacher—in the delayed treatment group — was male). The pupil gender distributions in the experimental and delayed treatment groups were slightly different (51.29% male in the experimental group, 47.54% male in the delayed treatment group), but the groups were similar in terms of pupils' average age at baseline in years (M = 5.52, SD = 0.28 in the experimental group; M = 5.57, SD = 0.30 in the delayed treatment group).

TABLE 1

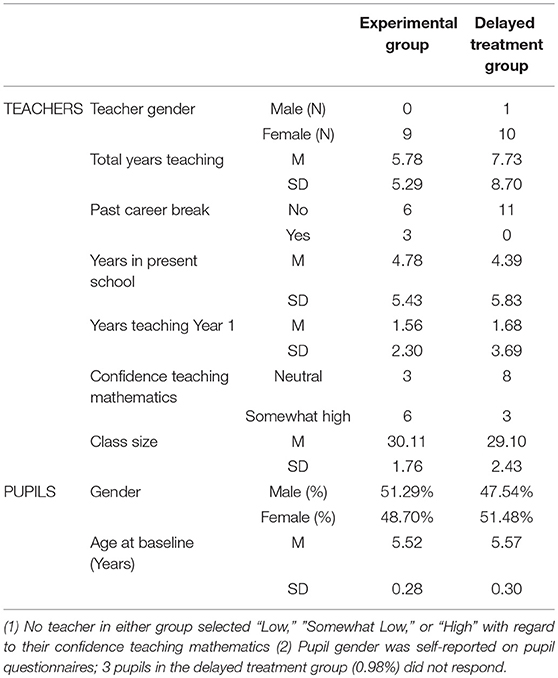
Table 1. Descriptive information about the sample of teachers and pupils by group (experimental/delayed treatment).

Data Sources and Measures

This research drew on multiple sources of qualitative and quantitative data including:

• Pupil assessments

• Pupil questionnaires

• Classroom observation ratings based on structured schedules

• Classroom and CPD observation field notes

• Semi-structured teacher interviews

Details of the measures (for quantitative data) and approaches (for qualitative data) are given in the subsections that follow.

Pupil Assessments

Pupils' mathematics knowledge and skills were measured using the Progress Test in Mathematics (PTM; GL Assessment 2015). The PTM series of mathematics assessments was selected because of its alignment to England's National Curriculum content, and the availability of different levels of the test according to pupil age groups (from the early years up to secondary school). PTM tests provide age-standardized measures of pupils' mathematical content knowledge and reasoning skills, and are vertically equated to allow for progress tracking over time; more information is available from the publisher (https://www.gl-assessment.co.uk/products/progress-test-in-maths-ptm/). The PTM tests were aligned to the National Curriculum, but they were not specifically aligned to the Inspire Maths series. An assessment specifically designed around the Inspire Maths sequence of concepts (which, in Year 1, include numbers to 100, addition, subtraction, multiplication, division, money, time, measurement, picture graphs, and shapes and patterns) would potentially have biased results in favor of the experimental group, especially at the first time point.

In PTM tests designed for the age group included in this study, items are generally presented in a pictorial format and questions/problems are read aloud to pupils during test administration. PTM 5 was used in the first and second terms of the 2015-16 school year, and PTM 6 was used in the third term. The higher-level PTM 6 test was used at the third time point in keeping with the publisher's protocol (i.e., as most pupils were age 6 by the third term, the level 6 test was most appropriate), taking into consideration the higher average age of Year 1 children by this time and their greater experience of formal schooling. Further, using the PTM 6 (rather than PTM 5) test at the third time point also reduced the risk of test familiarity that might otherwise have biased pupil outcomes.

Pupil Attitudes

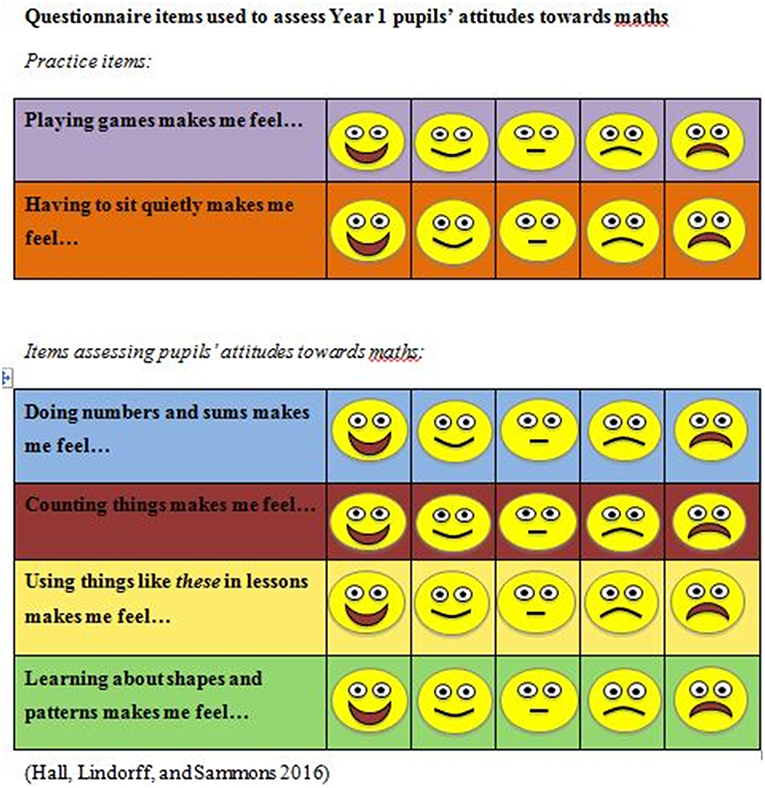
The research team designed a 4-item questionnaire to measure Year 1 pupils' attitudes toward and enjoyment of mathematics in their lessons. Items were rated by pupils on a 5-point Likert scale (0 = “Very unhappy” to 5 = “Very happy”), with each item asking how pupils felt about a type of activity. Types of activity included Doing numbers (or number sentences) and sums, Counting things, Using things like these in lessons (for age appropriateness, phrased as “things like these” with accompanying display of various manipulatives), and Learning about shapes and patterns. The format of the paper questionnaire distributed to pupils used a differently colored background for each item and faces showing the relevant emotions for each point on the Likert scale (from a very sad face to a very happy face image (see Figure 1; Hall et al., 2016). Two practice items were included to familiarize pupils with the questionnaire and response format; these were unrelated to mathematics and were not included in the analysis.

FIGURE 1

Figure 1. Pupil attitudes towards and enjoyment of mathematics questionnaire.

The questionnaire was administered by a researcher during normal class time directly after the mathematics assessment (except in a few instances where the schedule required administering the questionnaire slightly later in the school day). The questionnaire was administered last as it was less time-consuming; administering the questionnaire and assessment in the reverse order might have risked incomplete or incorrect responses on the assessment due to exhaustion rather than pupils' knowledge or skills. The researcher began by asking all pupils to sit on the carpet and discussing the happy to sad faces and what they meant as a whole class. Pupils were also instructed that there were no right or wrong answers, and told that the researcher wanted to learn about how they felt. Pupils then moved to tables answered items at the same pace while the researcher read out the items and circulated to tables to display manipulatives for the final item. Pupils were asked to draw a “tick” on the face that showed how they felt about each item (during the carpet session, the researcher also ensured that all pupils understood what a tick was and how to place a tick on a face using some example questions not related to mathematics and including at least one negative and one positive example).

The questionnaire was piloted in 1 Year 1 classroom that did not participate in the main study, with 1 teacher and 30 pupils. In the pilot, Cronbach's alpha (α = 0.58) indicated modest but sufficient internal consistency (Nunnally and Bernstein, 1994). Values were higher but still indicated modest internal consistency in the main study based on questionnaire responses from Terms 1, 2, and 3 (α = 0.64, α = 0.68, and α = 0.69, respectively).

Classroom Observation Schedules

Three structured observation schedules were used for each lesson, with items on each schedule filled out as soon after the observed lesson as possible. All observations took place in person, with the researcher in the classroom for the duration of the observed lesson. As noted above, the researcher who undertook all fieldwork for this study was trained and experienced in the use of each of these instruments and in lesson observation more generally. Key details about each instrument are given below, although finer-grained analyses of the strengths, weaknesses and specific features of these instruments have been discussed elsewhere (e.g., Lindorff and Sammons, 2018; Muijs et al., 2018).

Quality of Teaching (QoT) lesson observation form

The QoT instrument² (van de Grift et al., 2004) was based on consultation with inspectors and researchers as well as a review of the relevant literature on teacher effectiveness, and was validated in four European countries including the UK.

International System for Teacher Observation and Feedback (ISTOF)

The ISTOF instrument (Teddlie et al., 2006; Kyriakides et al., 2010) was designed as part of an international study across 19 countries including the UK. The instrument was developed using a modified Delphi technique drawing on expert opinion of what constitutes “effective teaching” across participating countries. This observation schedule includes 45 items, each rated on a 5-point scale (1 = “Strongly disagree” to 5 = “Strongly Agree”).

Mathematics Enhancement Classroom Observation Recording System (MECORS)

The MECORS instrument (Schaffer et al., 1998) was designed specifically for an evaluation of a primary mathematics program in England. It was selected for use in the present study because of its inclusion of mathematics-specific items.

The protocol for using the MECORS instrument includes the researcher taking notes during the lesson, including details of each activity that takes place and time-sampling the number of on- and off-task pupils every 5 min with time codes recorded in the notes. Following the lesson, the researcher then codes 57 items, each on a 5-point scale from 1 = “rarely observed” to 5 = “consistently observed,” with the additional option of “not applicable.”

Classroom and Continuing Professional Development (CPD) Observation Field Notes

In addition to the three structured observation schedules described above, detailed field notes were taken during each lesson observation and during CPD sessions (as described in Design). Lesson observations included the information required according to the MECORS protocol as described above, but extended to additional details about the physical setting in the classroom, illustrative quotes, descriptions of interactions between teachers, pupils, and additional adults in the classroom (e.g., Learning Support Assistants or LSAs and parent volunteers), and researcher memos. This approach has been used in combination with multiple observation schedules to provide robust and thorough integrated observation findings in previous research on classroom practice (Day et al., 2007; Sammons et al., 2014, 2016; Lindorff and Sammons, 2018). Observation of CPD sessions involved the collection of field notes, the contents of which were then followed up within focus group interviews with the CPD-participating teachers.

Teacher Interviews

Semi-structured interviews with each participating teacher were conducted during each research visit in order to elicit their perspectives and descriptions of their experiences using Inspire Maths. For the delayed treatment group, teachers were still interviewed at the first time point, but questions pertaining to the use of Inspire Maths and participation in CPD sessions were omitted. Interviews varied in length, but were on average approximately 30 min in duration.

The interview schedule covered topics including:

• Teachers' professional backgrounds (in the first round of interviews)

• Any context about the observed classes that teachers thought were important for the researcher to understand

• Teachers' confidence teaching mathematics

• Views on using the textbook and teaching approach

• Perceptions of using the textbook and teaching approach compared to how they were previously teaching mathematics (or, in the first round of interviews for the delayed treatment group, accounts and perceptions of their current approaches to teaching mathematics)

• Views on the CPD sessions in which teachers participated, support available from the distributor, and accompanying online materials

• Perceptions of challenges and benefits associated with using Inspire Maths in their classrooms and schools

• Perceptions of any changes in pupils' motivation, engagement, mathematics knowledge and skills

Approach(es) to Analysis

Data from pupil assessments and attitude questionnaires were analyzed using multilevel models in SPSS (IBM Corp, 2012). Examination of Intra-class Correlation Coefficients (ICC) supported the appropriateness of this approach to account for the nesting of pupils in class groups (ρ = 0.17, 0.13, and 0.13 for Term 1, Term 2, and Term 3 pupil assessment scores, respectively, indicating substantial variation at the teacher/classroom level).

Data from observation schedules was analyzed using general linear models to compare ratings of practice across the experimental and delayed treatment groups of teachers. As ratings of classroom practice were teacher-level measures, multilevel models were not required.

Qualitative data from interview transcripts and lesson observation field notes was analyzed thematically using NVivo (QSR International, 2012). An initial pass of coding was conducted based on themes defined by the interview questions in order to disentangle emergent themes from themes driven by the interview schedule. A second pass of coding was then undertaken using a more grounded approach (Glaser, 1992), followed by iterative passes of increasingly fine-grained coding. Initial results from this process are reported elsewhere (see Hall et al., 2016); however, substantial re-analysis was undertaken for the purpose of this paper, and the emphasis of the qualitative analysis presented below was to explore variations in teaching practice particular to the use of the materials and teaching approach, to elaborate upon and illustrate findings from the statistical analysis of observation data where significant differences were found, and to identify and describe cases in which there was a lack of fidelity to the intended implementation of textbook use and teaching approach. Additional analysis of the qualitative data was therefore undertaken, again using iterative passes of coding from broad to narrow, focusing particularly on variation in the use of the materials and teaching approach and areas of teaching practice that mapped to categories in which significant differences were found in the quantitative observation data. Second, a more fine-grained and grounded approach was used to code text that identified and described particular behaviors, practices and perceptions to illustrate themes identified in the previous pass of coding. Third, a process of pattern-matching was undertaken across teachers/lessons at each time point and then within each teacher/class across time points to explore differences and similarities between teachers and September/January start groups, and changes over time in perceptions and practices.

Ethical Considerations

This research was conducted with ethical approval from the Central University Research Ethics Committee (CUREC) of the University of Oxford. Research was undertaken in adherence to ethical guidelines in education research as outlined by the British Educational Research Association (British Educational Research Association, 2011), with attention to participant confidentiality and data protection.

Head teachers were approached for opt-in informed consent for schools to participate in the study, and teachers in schools where head teachers had given consent were then invited to participate with their individual opt-in informed and voluntary consent. Because research activities were focused on the teachers, lessons, and classes rather than on individual pupils, pupil participation was via opt-out consent; information letters about the project were sent home to parents with a form to fill out and sign if they wished for their children not to participate in the study. One parent returned the signed form but subsequently requested that the relevant child be re-included in the study due to a misunderstanding of the form. Transcripts and field notes were de-identified after each research visit; quotes and excerpts from field notes are reported using anonymized school and teacher identifiers (uniquely assigned letters for schools and numbers for teachers).

Results

Pupil Attainment and Progress in Mathematics

Table 2 provides basic descriptive statistics for pupil attainment at each time point and in each group as well as overall. The sample as a whole was performing somewhat below average based on their Standard Age Scores across all time points (SAS; M = 89.15, SD = 12.83 in Term 1; M = 95.08, SD = 12.46 in Term 2; M = 96.81, SD = 12.94 in Term 3; where 100 represents national average performance). Both groups showed upward trajectories in their mean attainment over time.

TABLE 2

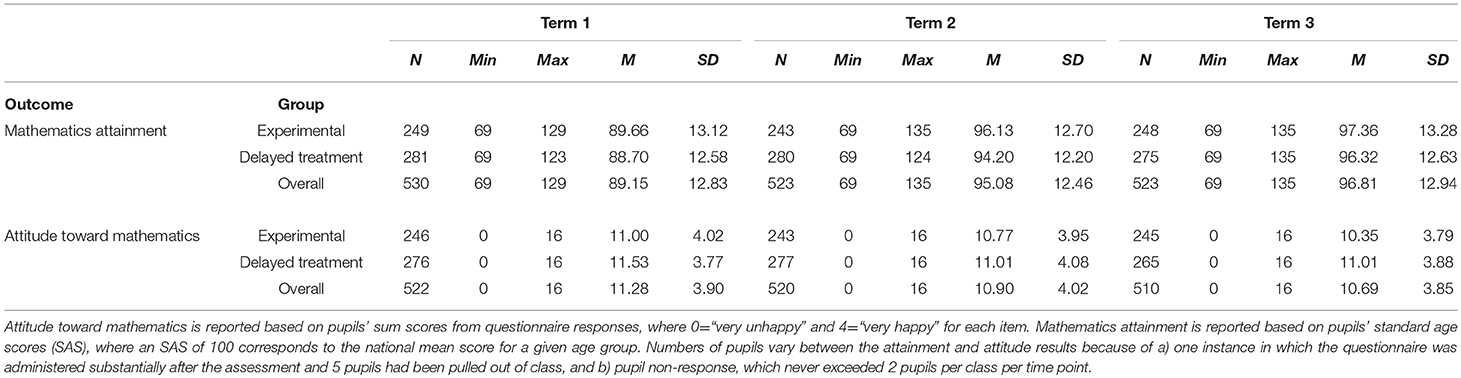
Table 2. Pupil descriptive statistics for mathematics attainment and attitudes toward mathematics by group (experimental/delayed treatment) and overall.

Table 3 shows the results from 2-level (pupils nested within teachers) models with overall mathematics knowledge and skills scores on the PTM 5/6 assessments at each time point as outcomes. Scores were age-standardized to account for developmental differences between pupils. Models further controlled for pupil gender as well as time (in days) since the first group was tested at a given time point and (for Term 2 and Term 3 results) time (in days) since the first class group was tested at the previous time point to account for any differences due to variations in test date. For Term 2 and Term 3 results, pupil scores at the previous time point were included as a control variable to provide a measure of value-added progress. At the teacher level, models also include controls for total years of teaching experience (in years) and proportion of total teaching experience spent teaching Year 1.

TABLE 3

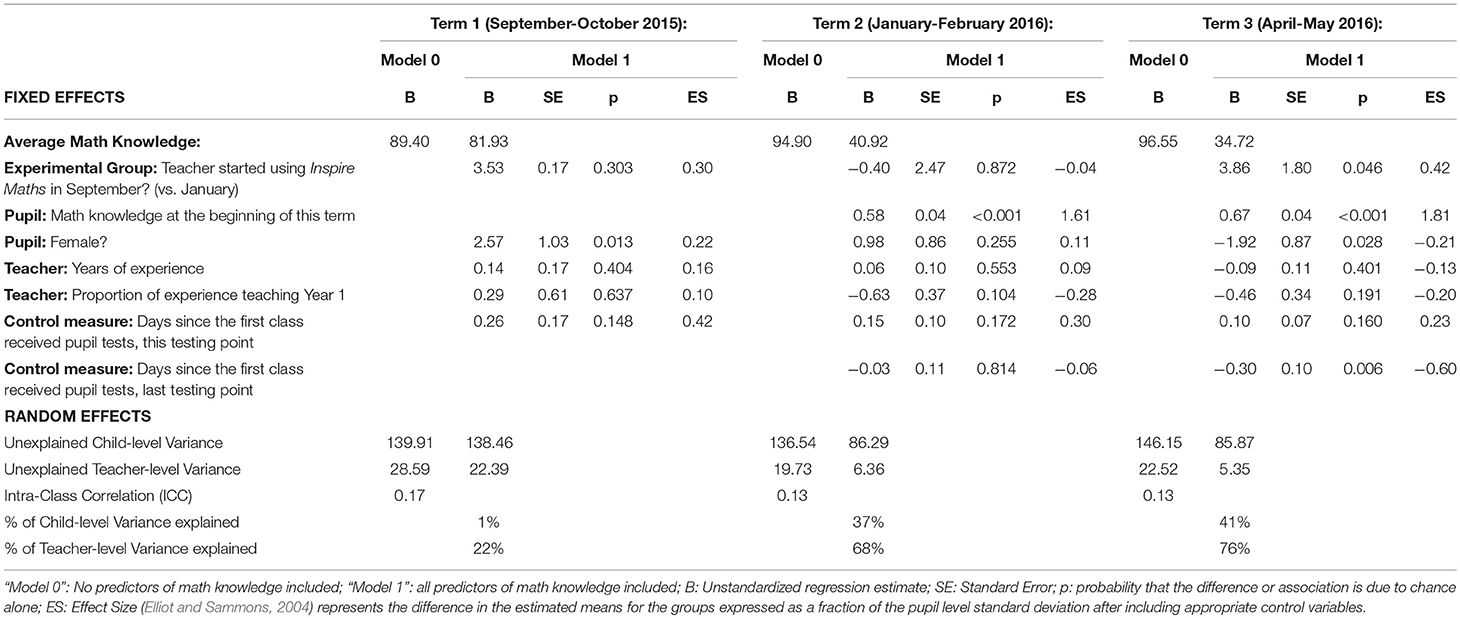
Table 3. Pupil mathematics knowledge and skills in experimental and delayed treatment groups – multilevel General Linear Model results.

Term 1 results showed no significant differences in mathematics attainment between the experimental and delayed treatment groups (B = 3.53, p = 0.303). Term 2 results again showed no significant differences in pupil progress in mathematics between the experimental and delayed treatment groups (B = −0.40, p = 0.872). Term 3 results, however, showed a significant difference in pupil progress in mathematics between the two groups since Term 2 (B = 3.86, p = 0.046). The multilevel effect size (SD = 0.42; Elliot and Sammons, 2004) classifies this as a small difference according to Cohen (1988).

Pupil Attitudes

Table 4 shows the results from 2-level (pupils nested within teachers) models with pupil attitudes in each term as outcomes. Controls in these models were equivalent to those noted above for pupil mathematics attainment and progress models.

TABLE 4

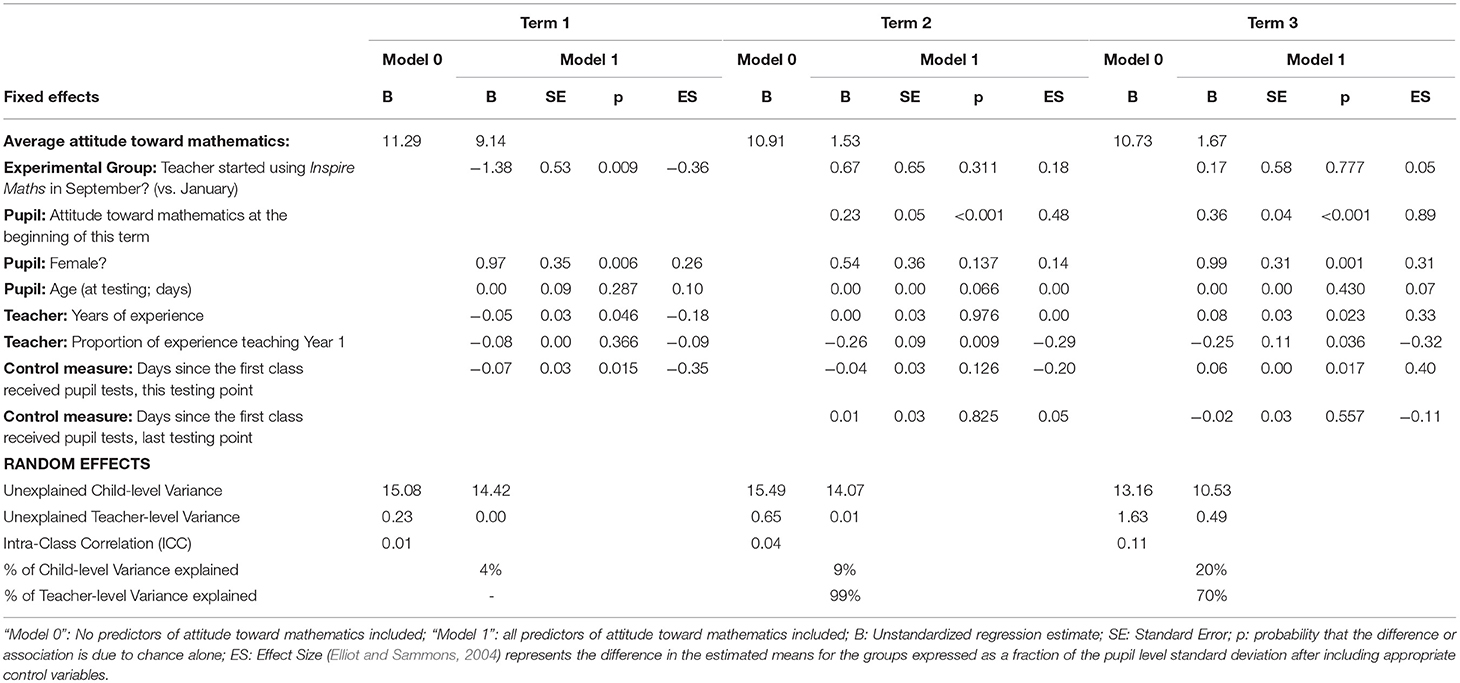
Table 4. Pupil attitudes toward mathematics in experimental and delayed treatment groups—multilevel General Linear Model results.

Patterns in average pupil attitudes overall showed a slight decline over time. A significant difference were found in Term 1 (September-October 2015) for pupil attitudes (B = −1.38, p = 0.009; controlling for pupil gender, age, teacher years of experience and proportion of experience spent teaching Year 1, and time since the first class was surveyed), with pupils in the experimental group classes having more negative attitudes toward mathematics on average. However, no significant differences were found in Term 2 (B = 0.67, p = 0.311) or Term 3 (B = 0.17, p = 0.777), each controlling for the prior term's pupil attitude scores and time since the first class was tested in the previous term to account for change in attitudes over time and for the surveying of different classes on different days, as well as controlling for the variables noted above for Term 1.

The more negative attitudes of pupils in the experimental group classes in Term 1 may reflect the more pronounced contrast between learning environments pupils had experienced prior to the beginning of Year 1; for many pupils, this may well have been their first experience of formal mathematics instruction and whole-day school attendance, and the use of the materials and teaching approach may have introduced additionally unfamiliar structure to pupils' experiences of mathematics lessons.

Teaching Practice

Quantitative Observation Findings

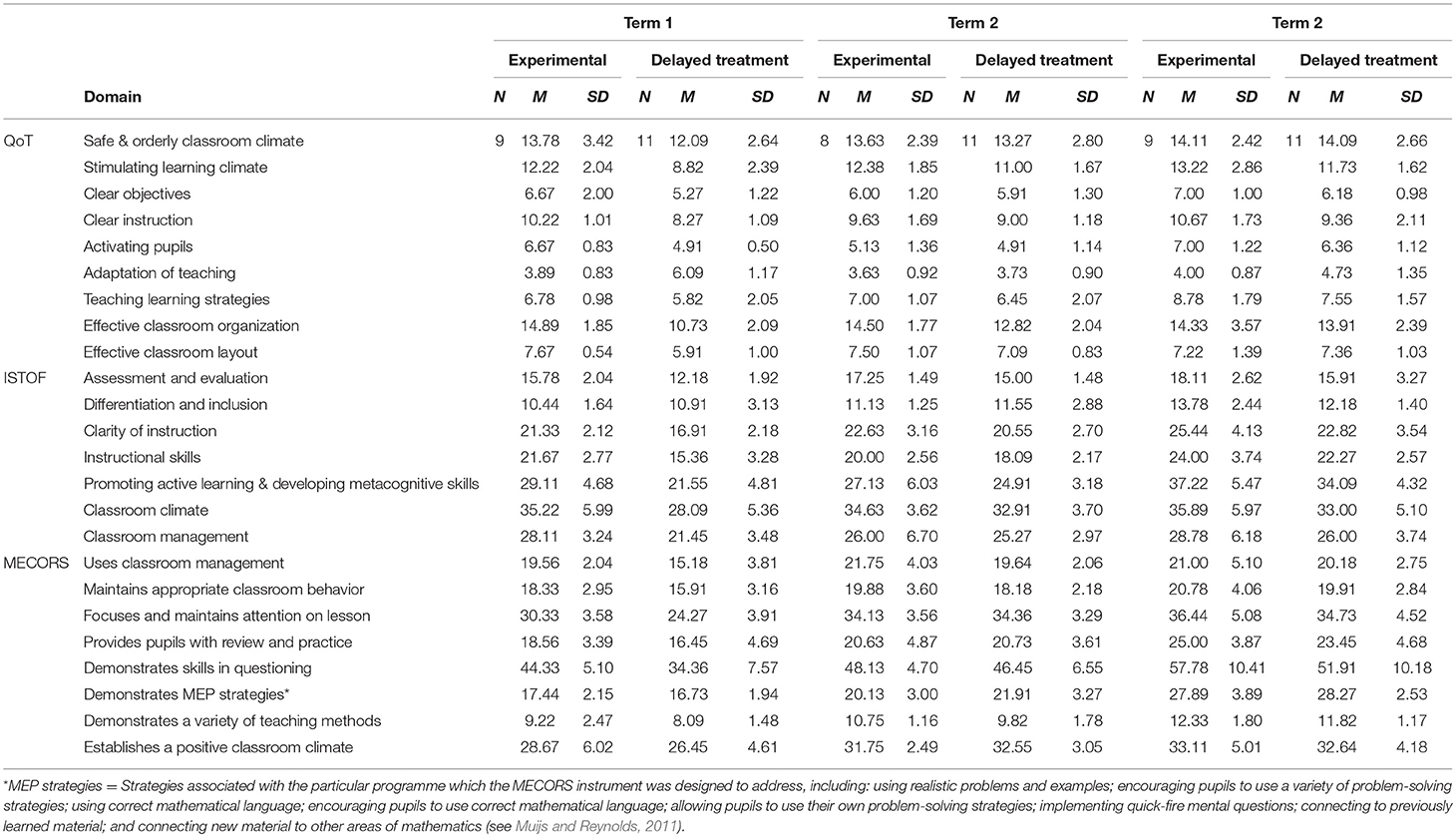
Table 5 displays descriptive statistics by group (experimental and delayed treatment) of teacher sum scores across each domain of the MECORS, QoT, and ISTOF instruments. These give an initial indication of patterns across groups based on the three different observation schedules.

TABLE 5

Table 5. Teacher sum scores on each domain of each observation instrument—Descriptive statistics.

In September-October 2015 (Term 1), large differences were found in teachers' observed practice according to most of the MECORS, QoT, and ISTOF domains. As the underlying meanings of the domains as given by the authors of the instruments are not always immediately obvious from their names, we include descriptions of the included items below when reporting our statistical results.

Table 6 shows results from “unadjusted” general linear models including only group allocation (experimental or delayed treatment), for each domain of each instrument in Term 1, Term 2, and Term 3, where coefficients represent the average difference in sum score on a given domain of a given instrument associated with being in the experimental group. General linear models were also run controlling for time since previous and first observations where appropriate, teacher experience, and score on each given domain in the previous term's observation, as well as the gender composition of the class, with full results from these models given elsewhere (see Hall et al., 2016), however, these are not easily mapped to qualitative observation data given the various controls and ensuing meaning of the adjusted coefficients as, essentially, measures of progress in teaching behaviors and practices accounting for differences in teacher experience, class gender composition and timing of observations. Here, we focus just on the unadjusted estimates as these are more easily interpretable as corresponding directly to mean differences across groups in scales measuring observed teaching behaviors and practices.

TABLE 6

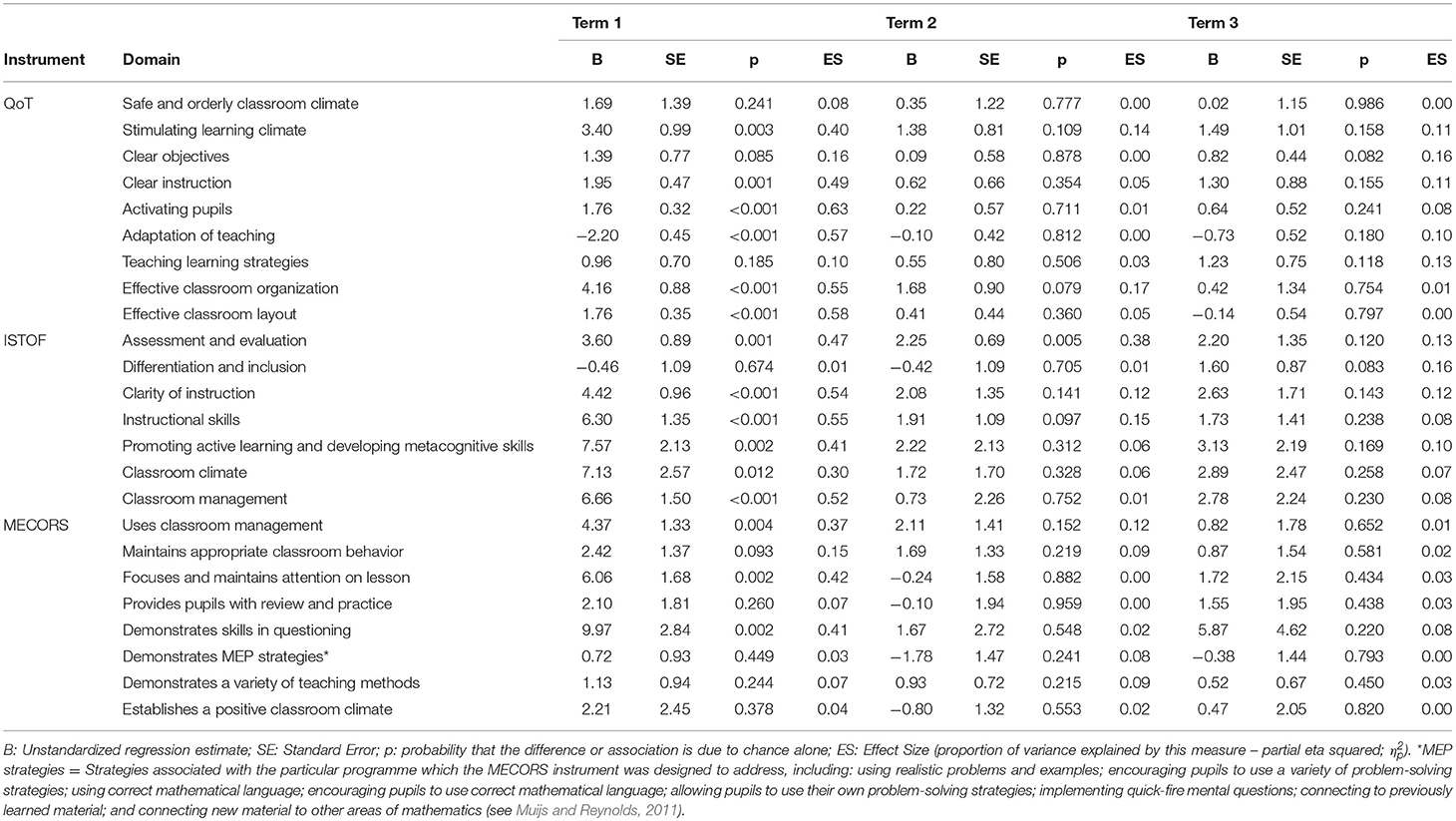
Table 6. Teacher sum scores in each domain of each observation instrument in experimental and delayed treatment groups—General Linear Model results.

For the QoT instrument, significant differences were found in Term 1 between groups on most domains. These differences can be considered large based on the Effect Size (ES) used here according to Cohen (1988; partial η² ≥ 0.14). Specifically, domains for which large differences were found included:

• “Stimulating learning climate” (B = 3.40, p < 0.001, ES = 0.40), the sum score for which was made up of 4 items related to ensuring cohesion, stimulating pupil independence, promoting cooperation between pupils, and facilitating good individual involvement from pupils.

• “Clear instruction” (B = 1.95, p = 0.001, ES = 0.49), the sum score for which was made up of 3 items related to giving clear instructions and explanations for lesson content, explaining learning materials and assignments clearly, and giving feedback to pupils.

• “Activating pupils” (B = 1.76, p < 0.001, ES = 0.63), the sum score for which was made up of 2 items related to involving all pupils in the lesson and using teaching methods that activate the pupils.

• “Adaptation of teaching” (B = −2.20, p < 0.001, ES = 0.57), the sum score for which was made up of 2 items related to adapting instruction to pupil differences and adapting assignments to pupil differences.

• “Effective classroom organization” (B = 4.16, p < 0.001, ES = 0.55), the sum score for which was made up of 4 items related to having a well-structured lesson, managing behavior and disruptions, using learning time efficiently, and ensuring that lesson materials are used and managed efficiently.

• “Effective classroom layout” (B = 1.76, p < 0.001, ES = 0.58), the sum score for which was made up of 2 items related to physical space and presentation of the classroom.

None of these differences in QoT domains persisted into Terms 2 and 3 after the delayed treatment group had begun to use the mastery-based materials and teaching approach.

For the ISTOF instrument, significant and large differences were also found in Term 1 on most domains, including:

• “Assessment and evaluation” (B = 3.60, p = 0.001, ES = 0.47), the sum score for which was made up of 4 items related to making clear why an answer is/is not correct, providing appropriate feedback, giving assignments that are closely related to what pupils are learning, and explaining how assignments align with learning goals.

• “Clarity of instruction” (B = 4.42, p < 0.001, ES = 0.54), the sum score for which was made up of 6 items related to checking for understanding regularly, communicating in a clear and understandable manner, clarifying the lesson objectives at the beginning of the lesson, asking pupils to explain why activities take place, presenting the lesson with a logical flow from simple to complex concepts, and implementing the lesson with smooth and well-managed transitions.

• “Instructional skills” (B = 6.30, p < 0.001, ES = 0.55), the sum score for which was made up of 6 items related to providing sufficient wait time and response strategies, giving assignments that stimulate all pupils to active involvement, posing questions that encourage thinking and elicit feedback, varying the pause after a question according to difficulty, using a variety of instructional strategies, and using different instructional strategies as appropriate for different groups of pupils.

• “Promoting active learning and developing metacognitive skills” (B = 7.57, p = 0.002, ES = 0.41), the sum score for which was made up of 10 items related to inviting pupils to use strategies to help them solve different types of problems, inviting pupils to explain the steps of the strategies they use, providing explicit problem-solving instruction, encouraging pupils to ask each other questions and explain to each other, giving pupils the opportunity to correct their own work, motivating pupils to think about advantages and disadvantages of approaches they use, asking pupils to reflect on their answers, inviting pupils to give their personal opinions, systematically using material and examples from pupils' daily life to illustrate content, and inviting pupils to give their own examples.

• “Classroom climate” (B = 7.13, p = 0.012, ES = 0.30), the sum score for which was made up of 8 items related to demonstrating warmth and empathy toward pupils, showing respect for pupils in behavior and language use, creating purposeful activities that engage every pupil in productive work, interactive instruction, involving pupils who do not volunteer, seeking to engage all pupils in classroom activities, praising pupils for efforts toward reaching their potential, and making clear that pupils are expected to make their best effort.

• “Classroom management” (B = 6.66, p < 0.001, ES = 0.52), the sum score for which was made up of 7 items related to starting the lesson on time, ensuring that pupils are involved in learning activities until the end of the lesson, taking action to minimize disruption, having clarity about when and how pupils can get help to do their work, providing clarity about what options are available when pupils finish their assignments, correcting misbehavior with measures that fit the seriousness of the misconduct, and dealing with disruptions and/or misbehavior by referring to the established rules of the classroom.

No significant difference was found for the one remaining domain, “Differentiation and Inclusion,” the sum score for which was made up of 4 items related to pupils communicating frequently with each other, all pupils being actively engaged in learning, distinction in the scope of the assignment for different groups of pupils, and giving additional opportunities for practice to pupils who need them. Of the differences found in ISTOF domain sum scores, only the difference between groups in “Assessment and evaluation” persisted into Term 2 (B = 2.25, p = 0.005, ES = 0.38), and there were no significant differences between groups by Term 3.

For the MECORS instrument, only 3 of the 8 domains showed significant (and large) differences between the experimental and delayed treatment groups in Term 1, including

• “Uses classroom management techniques” (B = 4.37, p = 0.004, ES = 0.37), with a sum score made up of 5 items related to clear understanding of rules and consequences, starting the lesson on time, using transition time efficiently in the lesson, having materials ready and distributing them effectively, and having limited disruptions in the lesson.

• “Focuses and maintains attention on the lesson” (B = 6.06, p = 0.002, ES = 0.42), with a sum score made up of 8 items related to clearly-stated lesson objectives, checking for prior knowledge, presenting content accurately, presenting content clearly, giving detailed directions, and explanations, emphasizing key points of the lesson, maintaining an academic focus, and using a brisk pace.

• “Demonstrates skills in questioning” (B = 9.97, p = 0.002, ES = 0.41), with a sum score made up of 14 items related to using a high frequency of questions, asking academic questions, asking open-ended questions, probing when a response is incorrect, elaborating on answers, asking pupils to explain how they reached solutions, asking for more than one solution, using appropriate wait time, noting pupils' mistakes, guiding pupils through errors, clearing up misconceptions, giving immediate feedback, giving accurate feedback, and giving positive feedback.

No significant or substantial differences based on the MECORS instrument persisted into Terms 2 and 3.

Insights From Qualitative Field Notes and Teacher Interviews

The qualitative analysis explored variation in implementation based on the observation field notes and interview transcripts. This allowed for more in-depth consideration of features of classroom practice particular to the use of the materials and teaching approach—as well as teachers' views — which the structured observation schedules were not designed to measure. Additionally, where large (and significant) differences were found between the experimental group and the delayed treatment group based on the Term 1 lesson observations, these were further explored via the observation field notes and teacher interviews in order to gain more detailed understanding of teachers' observed practices and behaviors and how teachers were thinking about their practice in relation to what was observed within each category below. This analysis considered practice across the three time points (Terms 1, 2, and 3) in order to offer qualitative insights into and potential explanations for the quantitative findings, supported by excerpts from the field notes and interview transcripts.

Classroom climate for learning

Teacher praise, warmth, and enthusiasm were observed to some degree in every classroom and lesson. More evidence of high expectations of all pupils, however, was more frequently directly observable in the classrooms of teachers who had started using the textbooks and teaching approach in September. Strategies for grouping pupils played a pivotal role in this aspect of classroom climate. For the most part, groups in “experimental group” classrooms were arranged according to a mix of perceived pupil ability or security with a given concept or topic, and high expectations were clearly communicated using phrases like “a new challenge for everyone…” (Teacher 20, School L, experimental group, Term 1 observation), “I think we have 29 people here with smart brains…” (Teacher 2, School E, experimental group, Term 1 observation), and positive climate for learning was also reflected through pupil excitement and eagerness to participate. The language used in professional development sessions focused on security of understanding with respect to a particular topic, rather than on perceptions of pupil ability in a more global sense. This may have contributed to the ways in which teachers who had already attended professional development sessions before the beginning of the school year were addressing and responding to pupils in their classrooms during mathematics lessons. Groups in the “delayed treatment group” classrooms, on the other hand, were more often defined by similar perceived pupil ability and were observed to be given explicitly different tasks (or difficulty levels of task) accordingly, sometimes accompanied by language that communicated lower expectations, e.g., “you may not be ready for that quite yet, why don't you try this instead…” (Teacher 15, School D, delayed treatment group, Term 1). This was not unilateral across the delayed treatment group; in 3 classrooms within this group, teachers assigned the same task to all pupils, and whether or not groups were defined in terms of homogeneous ability was not clearly observable.

By the end of the year, differences across the experimental and delayed treatment groups of teachers in terms of classroom climate were much less apparent. The textbook and teaching approach were being used in most classrooms (with the exception of those noted below in the section on fidelity to intervention), along with mixed-ability grouping strategies. There was still some variation, but this did not seem to represent a systematic pattern of differences across groups based on the analysis of field notes. Several delayed treatment group teachers expressed concerns in their interviews that the content they had started with in January was “too basic” or “too slow” for their pupils, but this was not directly observed in terms of the classroom climate of their lessons.

This theme linking classroom climate to grouping strategies and the use of a consistent activity across all groups of pupils converges with quantitative findings from the ISTOF and QoT instruments, specifically the Term 1 differences found in “Stimulating learning climate” on the QoT instrument and “Climate for learning” on the ISTOF instrument.

Clear teacher communication

In experimental group classrooms in Term 1 lesson observations, there were few instances observed in which whole groups of pupils were demonstrably misunderstanding procedures or activity instructions; pupils typically had activities explained verbally as well as represented in textbooks on their tables or projected on document projectors or smart boards. In about half of the delayed treatment group classrooms, there was some evidence of pupils misunderstanding directions or procedures communicated by the teacher, particularly in parts of lessons when pupils were expected to choose from a selection of different activities after some direct instruction, or engage in activities via different media. For example:

Task instructions were to build a tower and then add 1 more. Groups are building towers, one group building but without books to record what they are doing, one pupil working with one-to-one support, one group using white boards with TA [teaching assistant]. In three of the groups, pupils are not consistently adding 1 more after building; one of the groups with books is not recording. The teacher circulates to several but not all groups.

At the end of the lesson, the teacher says: “Some of you struggled with that, which is fine, we'll do it again tomorrow…” then goes through several more examples with the whole group responding in chorus. Some children are calling out incorrect answers but this does not stand out so is not always addressed but the correct answer is often repeated (Teacher 10, School H, delayed treatment group, Term 1 observation).

This is not a judgment of the skill of teachers in the delayed treatment group. Rather, as pervasive misunderstandings that reflected a lack of clear communication seemed to occur most when pupils were engaging in different activities at once, it seems possible that an aspect of practice used quite frequently with young children in England—giving them a choice of activity or assigning different tasks to different groups—has the potential to be detrimental to clear communication in the classroom.

By the Terms 2 and 3 lesson observations, teachers in both the experimental and delayed treatment groups were using textbooks and the Singapore-based Inspire Maths teaching approach in lessons. While there were some instances of task directions that were not clear in several classrooms, some delayed treatment group and some experimental group, no pervasive patterns were apparent from the analysis of the field notes.

The theme of clear communication linked to the use of textbooks and other printed materials as well as to the use of a consistent task for the whole class, which was also mentioned above for the theme related to climate for learning, converges with findings from the quantitative observation data. In particular, the specific aspects of lessons described in this section help to suggest possible reasons for the differences in “Clear instruction” on the QoT instrument and “Clarity of instruction” on the ISTOF instrument, as well as on “Focuses and maintains attention on lesson” on the MECORS instrument (which, as noted above, includes items relevant to clear communication, instructions and explanations).

Management of lesson resources and pupil task-oriented behavior

All teachers used strategies to get pupils to listen as a whole class. For example, over half of the teachers used either a clap-echo strategy (clapping a pattern for students to repeat as a signal to pay attention) or similar signal (e.g., ringing a bell; Teacher 2, School E, experimental group, Term 2 observation) to let students know that the teacher wanted them to be listening. Similarly, behavior management was largely similar across the experimental and delayed treatment groups, with most teachers frequently using positive approaches to ensure that students engaged in on-task behaviors (e.g., “I see [student name] ready, I see [student name] ready…”; Teacher 9, School J, delayed treatment group, Term 1 observation) and addressing disruptions in supportive ways (“Will you come to the table with me and show me how much you know?” in response to two pupils fighting over a toy in a corner of the room; Teacher 20, School L, experimental group, Term 2 observation).

Where different patterns were observed based on the field notes, however, was in the extent to which all pupils were kept on task. In 2 of the experimental group classrooms in term 1, vs. 5 of the delayed treatment group classrooms, situations were recorded in field notes in which one or more children were engaged in off-task (not actively disruptive) behaviors where teachers did not address this to re-engage pupils within a few minutes. This may have been related to relative heterogeneity of tasks and activities, as were clarity and climate; it is possible that off-task behaviors (particularly quiet off-task behaviors such as drawing and daydreaming) were more difficult to notice when different groups of pupils were engaged in different types of activity. For example, when a child in one delayed treatment classroom wandered to a corner to read rather than do one of the selection of mathematics activities at various tables from which pupils had been asked to choose, 6 min passed before the teacher asked the pupil to try the activity at a nearby table, and in the meantime the teacher had been working closely with a particular group of students in a different part of the classroom.

Similarly, efficient routines for organizing and distributing materials and resources were observed more frequently in Term 1 in experimental classrooms using the textbooks and teaching approach; 6 of these classrooms had either put caddies on tables with a selection of books and manipulatives to be used, or had packets of manipulatives and/or textbooks and practice books, while 3 had books on shelves and routines in place for pupils to get themselves (the latter typically took slightly more time away from learning activities). Teachers in 5 of the delayed treatment classrooms also had caddies with materials (e.g., markers, pencils, books, and glue sticks) on tables for pupils to access efficiently, and routines for getting pupils to record their work in books; 2 teachers in this group also had worksheets ready on tables at the beginning of the lesson. However, the majority of the delayed treatment group used some form of worksheet or manipulative during the lesson that took time to distribute, which took some time away from the learning activity at hand.

These findings from the field notes suggest that the differences found on the observation schedule domains (in “Effective classroom organization” and “Effective classroom layout” on the QoT instrument, “Classroom management” on the ISTOF instrument, and “Uses classroom management techniques” on the MECORS instrument”) were not related to relative differences in overall quality of classroom management or handling of disruptions and misbehavior. Instead, the more fine-grained detail available from the field notes illustrates the particular aspects where the use of the textbooks and teaching approach can make a difference, specifically with regard to facilitating the teacher's awareness of quiet off-task behaviors and efficient management of manipulatives, books and other classroom resources.

Attending to individual pupil needs and differences

The ways in which teachers spoke about pupils' abilities and needs shed light on how they were conceptualizing individual pupil needs and abilities. Notably, teachers in the experimental group were more commonly speaking about ability as a flexible and changeable concept, and about what pupils had and had not mastered in concrete and specific terms, by the first round of interviews in September-October:

“…There's one little boy in particular who's very, erm, hot, for want of a better word, on his maths concepts, he just seems to grasp and run with, so he's going to be one to keep an eye on to make sure we're extending. Erm, there's a little group, erm, that, erm, aren't as confident recognizing their numbers to 20. There's one little girl in particular who had one to one, erm, intervention last year, and she still can't write her name, and she still can't recognize all her sounds, erm, still can't count to ten and recognize all her numbers, so she will definitely be one to pinpoint in the followup…” (Teacher 8, School A, experimental group, Term 1 interview).

“…We've got a few girls, but again, quite normal, a few girls who actually, you would, by watching, possibly perceive them to be less able, but actually in talking to them they're just scared, and they just don't want to get anything wrong, so they're just reluctant to write something down in case it's not right.” (Teacher 20, School L, experimental group, Term 1 interview).

Meanwhile, in that first round of interviews, when teachers in the delayed treatment group discussed pupils' abilities, they more often used language such as “low” and “high” or “levels” to describe individuals and groups of pupils.

“…You have to keep pushing them to the point where you're teaching a completely different thing to those who are higher than to those who are lower.” (Teacher 11, School H, delayed treatment group, Term 1 interview)

“There's a child, [names the child], who, he, he's on the special needs registers, he's just very poor all round, and there's a speech and language issue as well, so he, he should come out as very low, unless he's sat next to somebody very able.” (Teacher 15, School D, delayed treatment group, Term 1 interview)

There were some exceptions to this general pattern. For example, one teacher in experimental group referring to pupils as “lows” and “highs,” and one teacher in the delayed treatment group spoke about using ability-based groups for some activities and not others to allow pupils to engage in activities and extend their learning based on interest rather than teacher-identified ability:

“They are my higher ability, erm, but I don't always have them working in that group all of the time, so that you could see there were lots of maths challenges out linked to our, erm, skill of addition, so, the way I try and do it is to let the children choose which activity they'd like to go to and take the learning to them…” (Teacher 14, School D, delayed treatment group, Term 1 interview)

While the above general patterns persisted somewhat through to Term 3, with several teachers in the delayed treatment group and one in the experimental group still referring to “low-” and “high-” ability pupils, most teachers were discussing pupils' specific grasping of a given concept rather than making global ability judgments. As one teacher described this shift in thinking explicitly:

“My TA said to me the other day, do you want me to sit with the lower ability, the lower, like, but for months now, the lower, like, we've been split into tables—and I've got one old lower here, one lower here, and I was like, no, no, no, we're not doing that. So, erm, yeah, it's just kind of changing that mindset, I think…” (Teacher 16, School F, delayed treatment group, Term 3 interview)

Strategies for grouping children during lessons were also indicative of the ways in which teachers conceptualized and addressed individual pupil needs and differences. The explicit advice given during professional development sessions provided before and during participating teachers' use of the textbook and teaching approach was that teachers should arrange pupils in mixed-ability groups outside of whole-class carpet work. While in most classes teachers adhered to a mixed-ability grouping strategy by the end of the year (only one September-start class was using observably ability-based grouping), the strategies that teachers used to arrange pupils in mixed-ability groups differed. For example, several teachers had relatively fixed groups over the course of a term, while others changed groupings according to how they found pupils coping with different topics; in some classes, pupils were paired or grouped who had differing but not widely differing levels of security in their understanding of the mathematics being taught, and in several other classes pairings or groupings were more extreme in heterogeneity (e.g., pupils with the most secure understanding of a given topic were paired with those who were struggling the most). The rationales behind these grouping strategies were not always immediately obvious through direct observation, but could be inferred to some degree from the ways in which teachers instructed and interacted with different pupils and groups during group-work and individual activities, such as time spent with particular groups or individuals while circulating, and the extent to which re-teaching vs. open-ended questioning took place during such interactions. By the end of the year, the lessons in some classrooms included established norms for immediate intervention that linked to the ways in which group-work was undertaken. In three classrooms, teachers or other adults in the classroom (e.g., Learning Assistants) pulled aside groups of pupils for additional support with group-work or individual activities, and in one of these classes the intervention group was observably lesson-specific as the teacher said explicitly, “The group that will be coming to the carpet to work with me today is…” (Teacher 4, School B, experimental group, Term 3 observation).

Although questioning techniques did not emerge as a major aspect of adapting teaching to individual needs as strongly as was found in Term 1, lesson observations and interviews in Term 3 reflected use and planning of questioning strategies as a particular feature of differentiation and inclusion. This was apparent across over half of the experimental group teachers' lessons, but also in several delayed treatment group lessons. One teacher's comments help to highlight this approach:

“Or trying to then make the links, if I change this, what happens. Or when we did the, erm, number trains with cubes, well could you then make three number trains that are less than seven, with twenty cubes, or can you make three trains that are greater than seven, they couldn't, well, brilliant, and some of them were just doing that, whereas others had finished and now, well how many more cubes would you need to make it possible. So I suppose it's having those other questions.” (Teacher 17, School F, delayed treatment group, Term 3 interview)

Taken together, these findings from interviews and field notes suggest that adopting a mastery-oriented teaching approach may shift conceptualizations of pupil ability and learning needs from global person-oriented to concept-specific and flexible judgments. This conceptualization led to more flexible ways of addressing individual needs lesson by lesson, which differs somewhat from the items included in relevant domains of the observation schedules used. The QoT sum score on “Adaptation of teaching,” for example, was influenced by items about adapting the scope of an assignment. Reflecting the whole class focus and emphasis on mastery and specific nature of the intervention related to not planning differently-pitched assignments for different pupils, experimental group teachers had lower ratings than the delayed treatment group in Term 1 on this domain. The ISTOF domain of “Differentiation and inclusion,” meanwhile, combined items related to involving all pupils with items related to adapting the scope of assignments and the amount of practice opportunities and showed no significant differences between groups in Term 1. The “Instructional skills” ISTOF domain, however, did show a significant difference in favor of the experimental group; this domain included one item on using different instructional strategies for different groups of pupils (which was overshadowed by a larger number of items not related to differentiation within that domain). The findings presented in this section demonstrate that the qualitative field notes and interviews were able to pick up on and illustrate aspects not covered in the observation instruments, presenting a much clearer narrative of the ways in which teachers were addressing and understanding individual needs and differences.

Questioning, feedback, and mathematical discourse around problem solving

In classrooms where the textbook and teaching approach were being used at the beginning of the year, teachers could be heard using more frequent “how” and “why” questions as part of their feedback in response to pupil contributions (e.g., Teacher says, “Brilliant, how do you know?” after a pupils says there are fewer of one object than another; Teacher 1, School K, experimental group, Term 1). By the third term, this was a feature in nearly all observed lessons. At the same time, there were also more rapid-fire questions requiring brief answers used in second- and third-term lessons in the classrooms where the textbooks and teaching approach had been used since September, though these forms of questioning were now being used in some delayed treatment classrooms as well. One teacher articulated that she saw a particular utility in using rapid-fire questioning to build fluency, and that she was using this more after implementing the teaching approach as part of the study:

“I wouldn't have used that approach before, but it gets the children involved, it turns on their thinking a bit [laughs] at the start…” (Teacher 12, School I, delayed treatment group, Term 3 interview)

Amongst the first-term lessons observed, an explicit focus on mathematical language was observed more frequently in classrooms in which the textbook and teaching approach were being used. For example, teachers in most of the experimental group classrooms explicitly guided pupils' use of language (e.g., around concepts of “more” and “fewer”) or prompted for complete answers (e.g., “Give me your full answer…”; Teacher 3, School B, experimental group, Term 1 observation) in lessons observed during the Term 1 school visits, while pupils were observed to give partial or vague answers that were accepted as correct in more than half of the delayed treatment group classrooms in Term 1. By Term 2, several experimental group teachers had routinized their focus on mathematical discourse. One teacher described a classroom routine as follows:

“We always start off our maths lesson with a bit of a conversation, or bit of a kind of a challenge thing, then they get to talk to their partners and discuss and give reasons as to how they came to the answer and why, rather than just, yeah, the answer's twelve, to explain it.” (Teacher 3, School B, experimental group, Term 2 interview)

In those first lesson observations, many teachers were necessarily prescriptive about procedures, because pupils were largely learning basic number concepts and comparisons. In later observations, there was some variety in the extent to which teachers co-constructed problem-solving approaches with children, mainly with regard to addition and subtraction. In the second term, most teachers were using a single approach with the whole class which pupils had the opportunity to practice in groups and individually using the scaffolding of concrete resources, then pictures to support problem-solving, then problems in a more abstract form (e.g., number bonds with a visual layout to support the part-part-whole approach). In a minority of 5 classrooms (2 experimental, 3 delayed treatment) teachers did not move beyond the stage of using manipulatives within the observed lessons, and in a few lessons there was less to no use of pictures (particularly when teaching structures of addition). The following except illustrates the typical flow of a problem solving conversation moving from concrete to abstract strategies:

Teacher: So you see that 3 and 1 make 4 [children nod]. How could we check?

Pupil: Because there's three, you can push in the extra one and then see it's four [referring to multi-link cubes.

Teacher: Yeah! We call this the part-part-whole [displaying image on board, one circle for each part linked to an additional circle for the whole]

[Pupil groups proceed with another example, and then the class comes back together to the carpet to debrief. After some [pupil] volunteers have demonstrated how to write what they have done with multi-link cubes in part-part-whole form, the teacher proceeds to ask…]

Teacher: Now if you're done it, is there another way? Show me another way in your books. (Teacher 18, School G, delayed treatment group, Term 2 observation)

These types of interactions were not entirely exclusive to the use of the textbook and teaching approach, as some delayed treatment teachers were prompting pupils in similar ways in Term 1 (e.g., “Can you think of another way to make 6?”; Teacher 14, School D, delayed treatment group, Term 1 observation). However, these types of conversations around solving in other ways and eliciting approaches and procedures from pupils happened more frequently in experimental group lessons in the first term, and subsequently more frequently over time within both groups in observed lessons in Terms 2 and 3.

Although for the most part solving procedures remained prescriptive across both experimental and delayed treatment groups through Term 3, there was evidence of increasing use of varying the ways of representing those procedures with increased use of the materials and teaching approach. This was observable in lessons, as most teachers represented problem-solving procedures in at least two ways in Term 2 and Term 3 observations across both experimental and delayed treatment groups. Some teachers also articulated this as a difference in their practice after implementing the materials and teaching approach. As one put it:

“We're trying to learn how to become masters and doing it in lots of different ways. And I think before when I thought I was doing that, probably now I can see the difference that actually I wasn't going into as much detail as I maybe should've been before, so I would say, no, that's definitely changed. And, you know, showing it in one way, and just because they can do it in one way doesn't mean they've got the understanding to show it in another, and I find that, that they can show me with the Numicon, but if I challenge them to show me in a different way, you know, they're kind of maybe thrown a little bit, so, working on that approach is really the main thing that has changed.” (Teacher 16, School F, delayed treatment group, Term 2 interview)

The findings from field notes suggest that the use of the textbook and teaching approach prompted different approaches to questioning and guiding conversations around problem-solving, supported by the use of multiple representations, which converges with the results from the observation schedules that showed differences in domains containing items relevant to questioning in Term 1 in favor of the experimental group (specifically, “Activating pupils” on the QoT instrument, “Promoting active learning and developing metacognitive skills” and “Instructional skills” on the ISTOF instrument, and “Demonstrates skills in questioning” on the MECORS instrument). The quotes and excerpts given above help to illustrate what questioning and feedback strategies and problem solving discourse looked and sounded like in lessons, as well as providing teachers' perspectives that illuminate some of the thinking that might have been driving these practices and how they changed across the three terms.

Variations in practice specific to the materials and teaching approach

The materials and teaching approach were designed to be comprehensive, with lessons taught in a particular sequence. This was discussed in the professional development sessions that teachers attended before they started to use the materials and teaching approach. There was, however, scope for teachers to use their professional judgment to guide the specific ways in which they used the textbook and printed materials, the way they structured their lessons, and the ways in which they used additional resources (e.g., manipulatives, additional warm-up activities). This section presents ways in which these aspects varied across teachers and classrooms based on qualitative field notes and interviews, including but not limited to cases in which variations in the use (or lack of use) of the textbooks and teaching approach constituted a lack of fidelity to the intervention within the context of this study.

Approaches to textbook use

There were a range of practices with regard to textbook use that shifted over the course of the year as teachers found what worked in their classrooms. Most were consistent about using textbooks and individual pupil practice books in lessons; there was little visible use of assessment books in the observed lessons but several teachers mentioned using or intending to use these in interviews, while two teachers (one in the experimental group, one in the delayed treatment group) said that they preferred to develop their own assessments and one further teacher in the delayed treatment group said that it was mandatory to use subject assessments developed in their schools. A few teachers had chosen, particularly by the third term, to project textbook pages (for example, using digitized versions or document cameras) and looking at these in a whole-class format only rather than having students use individual or pair textbooks at their tables.

Approaches to the use of manipulatives

In most classes, the range of concrete resources used was intentionally limited at the beginning of the year. This was true across both experimental and delayed treatment groups. In particular, many were using inter-locking cubes to represent mathematical problems in their lessons. Later in the year, about half of the participating classrooms had a variety of concrete resources available to pupils; some parceled these out in pre-prepared packs that pupils could fetch at the beginning of an activity to work individually or in pairs, and in one classroom these packs also included the individual practice books and other resources such as mini whiteboards. In several other classrooms, teachers had arranged a variety of resources in bins or caddies placed in the middle of each group's table so that pupils had easy access to a selection of different manipulatives that they were free to use during group and individual work.

Overall fidelity to the intervention

While not a feature picked up in the structured observation instruments, the extent to which teachers were actually using the mastery-based materials and teaching approach as suggested by the distributor was a critical consideration. Information about this was mainly available via field notes and teacher interviews.

In 10 of the 12 participating schools, no notable deviations from fidelity to the intervention were observed (across the three terms for the experimental group, and the two later terms for the delayed treatment group). There were 2 of the 12 schools in which substantial deviations from the intervention protocol – use of the textbooks and teaching approach—were noted. This included two teachers/classrooms from one two-form entry delayed treatment group school and one from a single-form entry experimental group school. In these cases, by the second or third term, it was apparent from lesson observations that while some of the printed materials and teaching approaches were being used, they were being interspersed with other content and materials, and the sequencing of topics and concepts had been rearranged. Interviews with these three teachers highlighted some of the reasons why they had not used the textbooks and teaching approaches as suggested in the professional development sessions and teacher's guides provided to accompany the textbooks. In both schools, teachers expressed that they were feeling pressure to “hit targets” and to cover content according to school pacing guides, which created a tension between using the mastery-oriented teaching approach and printed materials and complying with the expectations of school leadership teams. In the two-form entry school, both teachers also noted that they found the use of the textbooks and teaching approach to be out of keeping with a broader school ethos that emphasized child-led learning. In one of these two classrooms practice book pages were being used as one of many activities from which children could freely choose, and in the other classroom the teacher had the printed materials readily available but used them selectively and sometimes only with particular teacher-determined groups of pupils. In the teachers' own words:

“They [the pupils] didn't seem to mind doing it, but we found it quite dry, and not really, erm, enhancing what they knew, really…It just doesn't really fit in with how we teach.” (Teacher 15, School D, delayed treatment group, Term 2 interview)

“On account of what we, as a school, our kind of maths ethos… so in terms of having those resources out all the time and getting them to use them, that's kind of part and parcel of what we do anyway. I suppose it is nice having the teacher handbooks to refer to…but I can also see how it would be very easy to just teach from those handbooks and not necessarily think as a teacher, you would just say and do what was in those handbooks, and I don't want to do that.” (Teacher 14, School D, delayed treatment group, Term 3 interview)

“There's a lot more targets to hit, and we need to be doing this, need to be doing this…so although I've gotten more used to Inspire Maths, I've also got to fit it in with lots of other things, and so we have used it, more so for the place value and things, but yeah, we've kind of mixed it in with some other things still, to make sure I'm hitting all those other targets… I would like to just continue working on the basics and get them really strong, but we've got so many other bits to cover, and yeah, just the way that the Inspire Maths sets it out, and it covers a lot of things and then it moves up, but then there's also the way the school likes it to be set out, so you've got to do certain things each term, so to kind of put them together, I just want to get all the things ticked off in the computer program, really.” (Teacher 1, School K, experimental group, Term 3 interview)

Discussion

This study found a small but significant positive effect of using the materials and teaching approach on pupils' mathematics knowledge and skills after two terms, although no effect was found after using the materials and teaching approach for one term. Meanwhile, large differences in teaching practice were found near the beginning (September-October) and for one domain the middle (January-February) of the school year, with teachers who used the materials and teaching approach from September demonstrating more—or more consistent—features of effective practice (as defined by three different nationally and internationally established observation instruments) at the start of the year than those proceeding with business as usual through the first term. Such differences were much reduced (in effect size) by the third term (April-May), after teachers in the delayed treatment group had also been using the materials and teaching approach since January. Together, these findings suggest a tentative conceptual model for how the observed effect on pupil progress over the second term may have come about via observed changes in teaching practice which in turn may have shaped pupils' learning and shown up subsequently as a lagged effect on pupil progress.

The inclusion and analysis of qualitative data, including classroom observation field notes and semi-structured teacher interviews, was a particular strength of the mixed method study. The integration of quantitative and qualitative observation data provided a meaningful “point of interface” (Guest, 2012) after the data collection stage and with a well-defined purpose; that is, to allow for the exploration and illustration of the processes through which the textbook and teaching approach can have an effect, as well as highlighting aspects of practice particular to the intervention that were not picked up by observation schedules. Further, details from the qualitative observation and interview data provided information about fidelity (or lack of fidelity) to the intervention.

Strengths of the study included the use of rich qualitative data to explore processes and perspectives, with the potential to feed forward into future practice, integration of multiple perspectives (teacher/pupil/researcher) and findings from multiple data sources to inform a conceptual model linking processes to effects, and the use of a cluster randomized design with a delayed treatment control to balance feasibility with rigor. There were, of course, limitations of the study as well. The study was conceived as an evaluation of the materials and approach as they would normally be used in schools according to the guidelines of the distributor, meaning that the intervention itself was not researcher-designed (though the evaluation protocol was). There were further constraints due to having a small research team to conduct the study, meaning that school visits were spread out over approximately a month at each wave by necessity; while this was controlled for at the analysis stage, ideally this fieldwork would have taken place at as similar a time across all schools as possible if resources and staffing had allowed. Perhaps most importantly, the evaluation took place over the course of one school year, but materials are explicitly designed for Key Stage³ coverage rather than within-year coverage of mathematical content, and effects over a longer period of time may have been quite different had a longer-term study been possible.

Linking directly to the time limitation noted above, further research is needed to investigate how the Singapore-based, mastery-oriented textbook and teaching approach (or a similar set of materials and pedagogical approach) relates to pupils' attainment and progress over longer periods of time, including over a full Key Stage and over an entire phase of schooling (e.g., Primary, ages 5–11). Such studies would be able to make stronger claims about whether and to what extent using these Singapore-based materials in a different setting (here, England) have the potential to raise pupil attainment and progress. Moreover, analysis for different subgroups of pupils could investigate potential to narrow equity gaps in attainment. Further research is also needed to synthesize and compare findings across studies in which specific Singapore-based printed materials and teaching approaches were used in countries other than Singapore, perhaps via mixed method meta-analysis, to better inform general conclusions about the effects of transferring a Singapore-based approach to teaching mathematics to other settings and the processes and conditions promoting or hindering any such effects.

In this study, pupils' scores on mathematics assessments were used as measures of their mathematics knowledge and skills at each time-point, but the reasoning processes by which pupils arrived at each of their answers to assessment problems/questions were not accounted for. A third area for further research therefore relates to pupils' reasoning and problem-solving processes. That is, more research is needed to systematically investigate how pupils think through problems when taught using a mastery-oriented, Singapore-based approach in settings outside of Singapore, and how this differs from their reasoning and problem-solving processes when taught using traditional approaches in those other settings. The fact that a small positive effect was found in this study does not explain whether and in what ways pupils' mathematical reasoning and problem-solving skills may have changed with the use of the textbooks and teaching approach. Further research could investigate these aspects using different methods of data collection than those reported here (for example, having pupils explain what they were doing as they worked on the assessment problems, which would not have been feasible with whole classes of Year 1 children but could be done in small groups or individually for a smaller sample).

The results of this study have implications for researchers, policymakers, and practitioners alike. For researchers in the field of education, this study demonstrates the importance of using mixed methods within experimental designs in order to understand not only whether a particular intervention has an effect, but also the underlying processes and perspectives that may help to explain an effect (or lack thereof). For policymakers, findings indicate that the use of Singapore-based materials and approaches can have an effect, but that this effect may be modest when measured over short periods of time, and is unlikely to offer a quick fix for reducing attainment gaps or perceived low performance in mathematics. For practitioners, results from the study suggest that Singapore-based materials and approaches have the potential to be effective outside the Singaporean context, but for this to be the case, implementation must be supported by school leadership and broader school policy, alongside appropriately-aligned continuing professional development.

Ethics Statement

This study was carried out in accordance with the recommendations of the British Educational Research Association, Ethical Guidelines for Educational Research, with written informed consent from all subjects. All subjects (teachers and head teachers) gave written informed consent in accordance with the Declaration of Helsinki. Due to the young age of the children in participating classrooms, and due to the nature of research activities, parental opt-out consent was obtained for pupils in each participating class. The protocol was approved by the University of Oxford Central University Research Ethics Committee (CUREC).

Author Contributions

AL undertook data collection, contributed to instrument development (pupil questionnaires), conducted qualitative analysis, and made the majority contribution to the writing of this manuscript. JH designed the study, conducted quantitative analysis, and contributed to the writing and revision of the manuscript. PS designed the study, consulted with co-authors on data interpretation and analysis, and contributed to the writing and revision of this manuscript. All named authors provide their approval for the publication of this manuscript, and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Funding

The original study was funded by the Oxford University Press.

Conflict of Interest Statement

This research was funded by the Oxford University Press; the research team was (at the time at which the evaluation was conducted) employed by the Department of Education in the University of Oxford. To address any perceived conflict of interest, given the joint affiliation of the funder and the research team with a broader institution (the University of Oxford): The research team was explicitly independent from the funder, conducted random allocation and communicated with schools independently of the funder during data collection, and conducted the study under the explicit agreement that findings would be fed back to the funder and disseminated more broadly regardless of the results, and that the provision of the grant to fund the study did not constitute any guarantee that the study would show a positive effect of the intervention being evaluated.

Acknowledgments

The authors would like to acknowledge and thank the original creators of the MECORS (Schaffer et al., 1998), QoT (van de Grift et al., 2004), and ISTOF (Teddlie et al., 2006) instruments for their permission to use these in the study reported in this article.

Footnotes

1. ^This initial list was provided by the distributor, with recruitment and random allocation for the study undertaken independently by the research team.

2. ^Later developed into the International Comparative Analysis of Learning and Teaching (ICALT) observation instrument (van de Grift et al., 2017).

3. ^In England, Key Stages in primary school are defined according to the following age groups: Key Stage 1, 5–7 years; Key Stage 2, 7–11 years.

References

Bloom, B. S. (1968). Learning for Mastery. Eval. Comment 1, 1–12.

Boyd, P., and Ash, A. (2018). Teachers framing exploratory learning within a text-book based singapore maths mastery approach. Teacher Educ. Adv. Netw. J. 10, 62–73. Available online at: http://insight.cumbria.ac.uk/id/eprint/3587/

Google Scholar

British Educational Research Association (2011). Ethical Guidelines for Educational Research. Available online at: https://www.bera.ac.uk/wp-content/uploads/2014/02/BERA-Ethical-Guidelines-2011.pdf

Bruner, J. S. (1966). Toward a Theory of Instruction. Cambridge, MA: Belknap Press of Harvard University.

Bruner, J. S., and Kenney, H. J. (1965). Representation and mathematics learning. Monogr. Soc. Res. Child Dev. 30, 50–59. doi: 10.2307/1165708

CrossRef Full Text | Google Scholar

Carroll, J. B. (1963). A model of school learning. Teachers College Record 64, 723–733.

Google Scholar

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. Hillsdale, NJ: L. Erlbaum Associates.

Common Core State Standards Initiative (2016). About the Standards. Available online at: http://www.corestandards.org/about-the-standards/

Day, C., Sammons, P., Kington, A., Regan, E., Gunraj, J., and Towle, J. (2007). Effective Classroom Practice: A Mixed Methods Study of Influences and Outcomes: Interim Report Submitted to the ESRC. Swindon: Economic and Social Research Council.

Department for Education (2016). 8,000 Primary Schools in England Will Receive £41 Million over 4 Years to Support the ‘Maths Mastery’ Approach. School and Colllege Qualifications and Curriculum, July 12. Available online at: https://www.gov.uk/government/news/south-asian-method-of-teaching-maths-to-be-rolled-out-in-schools

Dienes, Z. P. (1960). Building up Mathematics. London: Hutchinson Educational.

Elliot, K., and Sammons, P. (2004). “Exploring the use of effect sizes to evaluate the impact of different influences on child outcomes: possibilities and limitations,” in But What Does It Mean? The Use of Effect Sizes in Educational Research, ed I. Schagen, K. Elliot (London: National Foundation for Educational Research), 6–24.

Google Scholar

Fong, H. K., Ramakrishnan, C., Pui Wah, B. L., Jalil, Z., and Choo, M. (2015). Inspire Maths. Oxford: Oxford University Press.

Ginsburg, A., Leinwand, S., Anstrom, T., and Pollock, E. (2005). What the United States Can Learn From Singapore's World-Class Mathematics System (and What Singapore Can Learn from the United States): An Exploratory Study. Washington, DC: American Institutes for Research.

Glaser, B. G. (1992). Basics of Grounded Theory Analysis: Emergence vs. Forcing. Mill Valley, CA: Sociology Press.

Google Scholar

Goldman, M. R., Retakh, V., Rubin, R. A., and Minnigh, H. A. (2009). The Effect of Singapore Mathematics on Student Proficiency in Massachusetts School District: A Longitudinal Statistical Examination. Bryn Mawr, PA: Gabriella and Paul Rosenbaum Foundation.

Gross, S., and Merchlinsky, S. (2002). Singapore Math Pilot Program: Year 1 Report. Rockville, MD: Montgomery County Public Schools Office of Shared Accountability.

Guest, G. (2012). Describing mixed methods research: an alternative to typologies. J Mixed Methods Res. 7, 141–151. doi: 10.1177/1558689812461179

CrossRef Full Text | Google Scholar

Guskey, T. R. (1980). Mastery learning: applying the theory. Theory Pract. 19, 104–11. doi: 10.1080/00405848009542882

CrossRef Full Text | Google Scholar

Hall, J., Lindorff, A., and Sammons, P. (2016). Evaluation of the Impact and Implementation of Inspire Maths in Year 1 Classrooms in England. Oxford: University of Oxford.

Hoven, J., and Garelick, B. (2007). Singapore math: simple or complex? Educ. Leadership 65, 28–31.

Google Scholar

IBM Corp (2012). IBM SPSS Statistics for Windows. Armonk, NY: IBM Corp.

PubMed Abstract | Google Scholar

Jaciw, A. P., Hegseth, W. M., Lin, L., Toby, M., Newman, D., Ma, B., et al. (2016). Assessing Impacts of Math in Focus, a ‘Singapore Math’ Program. J. Res. Educ. Effect. 9, 473–502. doi: 10.1080/19345747.2016.1164777

CrossRef Full Text | Google Scholar

Jerrim, J., and Vignoles, A. (2016). The link between east asian ‘mastery’ teaching methods and english children's mathematics skills. Econ. Educ. Rev. 50, 29–44. doi: 10.1016/j.econedurev.2015.11.003

CrossRef Full Text | Google Scholar

Kyriakides, L., Creemers, B. P. M., Teddlie, C., and Muijs, D. (2010). “The international system for teacher observation and feedback: a theoretical framework for developing international instruments,” in International Encyclopaedia of Education, eds P. Peterson, E. Baker, and B. McGaw, (Oxford: Elsevier), 726–734.

Lindorff, A., and Sammons, P. (2018). Going beyond structured observations: looking at classroom practice through a mixed method lens. ZDM 50, 521–534. doi: 10.1007/s11858-018-0915-7

CrossRef Full Text | Google Scholar

Muijs, D., and Reynolds, D. (2011). Effective Teaching : Evidence and Practice. 3rd ed. Thousand Oaks, CA: SAGE Publications.

Muijs, D., Reynolds, D., Sammons, P., Kyriakides, L., Creemers, B. P. M., and Teddlie, C. (2018). Assessing individual lessons using a generic teacher observation instrument: how useful is the International System for Teacher Observation and Feedback (ISTOF)? ZDM 50, 395–406. doi: 10.1007/s11858-018-0921-9

CrossRef Full Text | Google Scholar

Naroth, C., and Luneta, K. (2015). Implementing the singapore mathematics curriculum in south africa: experiences of foundation phase teachers. Afric. J. Res. Mathemat. Sci. Tech. Educ. 19, 267–277. doi: 10.1080/10288457.2015.1089675

CrossRef Full Text | Google Scholar

Nunnally, J. C., and Bernstein, I. H. (1994). Psychometric Theory. New York, NY: McGraw-Hill.

OECD (2016). PISA 2015 Results (Volume 1): Excellence and Equity in Education. Paris: OECD.

Piaget, J. (1952). The Origins of Intelligence in Children. Madison, WI: International Universities Press.

QSR International (2012). NVivo Qualitative Data Analysis Software. Available online at: http://www.qsrinternational.com

Raudenbush, S. W., Andres, M., and Spybrook, J. (2007). Strategies for improving precision in group-randomized experiments. Educ. Eval. Policy Analysis 29, 5–29. doi: 10.3102/0162373707299460

CrossRef Full Text | Google Scholar

Runesson, U. (2005). Beyond discourse and interaction. variation: a critical aspect for teaching and learning mathematics. Cambridge J. Educ. 35, 69–87. doi: 10.1080/0305764042000332506

CrossRef Full Text | Google Scholar

Sammons, P., and Davis, S. (2017). “Mixed methods approaches and their application in educational research,” in The BERA/SAGE Handbook of Educational Research, eds D. Wyse, N. Selwyn, and E. Smith, (SAGE Publications), 477–504.

Sammons, P., Hall, J., Sylva, K., Melhuish, E., Siraj-Blatchford, I., and Taggart, B. (2013). Protecting the development of 5–11-year-olds from the impacts of early disadvantage: the role of primary school academic effectiveness. School Effect. School Improve. 24, 251–268. doi: 10.1080/09243453.2012.749797

CrossRef Full Text | Google Scholar

Sammons, P., Kington, A., Lindorff-Vijayendran, A., and Ortega, L. (2014). Inspiring Teachers: Perspectives and Practices. Reading: CfBT Education Trust.

Sammons, P., Lindorff, A. M., Ortega, L., and Kington, A. (2016). Inspiring teaching: learning from exemplary practitioners. J. Professional Capital Community 1, 124–144. doi: 10.1108/JPCC-09-2015-0005

CrossRef Full Text | Google Scholar

Schaffer, E. C., Muijs, D., Kitson, C., and Reynolds, D. (1998). Mathematics Enhancement Classroom Observation Record. Newcastle upon Tyne: Educational Effectiveness and Improvement Centre.

Tashakkori, A., and Teddlie, C. (2010). SAGE Handbook of Mixed Methods in Social and Behavioral Research. Los Angeles, CA: SAGE Publications.

Google Scholar

Teddlie, C., Creemers, B., Kyriakides, L., Muijs, D., and Yu, F. (2006). The international system for teacher observation and feedback: evolution of an international study of teacher effectiveness constructs 1. Educ. Res. Eval. 12, 561–582. doi: 10.1080/13803610600874067

CrossRef Full Text | Google Scholar

Uribe-Zarain, X. (2010). Evaluation of the International Math Pilot: Exploring the Effectiveness of Singapore Math Year 2 [Report Number T.2010.13.5]. Newark, DE: Delaware Education Research and Development Center.

van de Grift, W., Matthews, P., Tabak, L., and de Rijcke, F. (2004). Preliminary Lesson Observation Form for Evaluating the Quality of Teaching. Utrecht; London: Inspectie van het Onderwijs; Office for Standards in Education.

Google Scholar

van de Grift, W. J. C M., Chun, S., Maulana, R., Lee, O., and Helms-Lorenz, M. (2017). Measuring teaching quality and student engagement in south korea and the Netherlands. School Effect. School Improve. 28, 337–349. doi: 10.1080/09243453.2016.1263215

CrossRef Full Text | Google Scholar

Vignoles, A., Jerrim, J., and Cowan, R. (2015). Mathematics Mastery: Primary Evaluation Report. London: Education Endowment Foundation.