- Centre for International Student Assessment, TUM School of Education, Technical University of Munich, Munich, Germany
Schools and teaching aim at fostering multidimensional learning goals. For attaining these goals, institutional effects such as school tracking as well as teaching quality play an important role and interact with each other. Using representative data from a class based German extension of the PISA 2012 study, the present study first investigated whether the factorial structure of three basic dimensions of teaching quality (cognitive activation, classroom management, and teacher support) in mathematics is comparable across high and low school tracks and tested whether tracks differed in students' perception of mathematics teaching quality. Second, differences between school tracks in the relationship between teaching quality and multidimensional learning goals, namely mathematics competence, interest, and self-efficacy were examined. Results indicated that students in both school tracks distinguish between three dimensions of teaching quality and that the factorial structure is comparable across tracks. Students at higher school tracks report higher levels of discipline but lower levels of teacher support. No difference has been found for cognitive activation. In association with different learning goals, tracks show individual profiles. Mathematics competence was related to classroom discipline on the student level in lower school tracks and on the class level at the Gymnasium. Mathematics interest was, on the student level, in both tracks associated with teacher support and discipline. In addition, in lower school tracks a cognitive activating learning environment was associated with more interest. High levels of mathematics self-efficacy were in both school tracks reported by students who perceived their lessons as cognitive activating. In addition, at the Gymnasium, students who felt more supported by their mathematics teachers reported higher levels of self-efficacy. The results speak clearly for the assumption of school tracks as differential learning environments. They ask for a differentiated view of teaching quality and its impact on reaching multidimensional learning goals in order to meet students' needs specifically and deal with increasing classroom heterogeneity.
Introduction
Schools and teaching do not only aim to foster knowledge, but also to develop students' specific interests and realistic self-views. Together with cognitive competencies, these outcomes not only form the foundation of lifelong learning processes but also influence career decisions, educational attainment, and labor market success (cf. Schiepe-Tiska et al., 2016b). Fostering different goals is particularly important for STEM fields (science, technology, engineering, and mathematics) as the shortage of skilled young people–especially among females–has become a concern in recent years (European Commission, 2007). For example, in mathematics, in particular girls who show high levels of competencies but only little interest in mathematics less frequently pursue careers that require a deeper mathematical understanding (Eccles, 2007).
However, learning mathematics rarely happens in informal contexts–the classroom provides the main learning opportunities not only for developing mathematics competence but also for fostering interest and self-efficacy. Models of teaching and learning postulate that the quality of learning opportunities depends on the quality of teachers' instruction (Hattie, 2009). Recent research has merged on three generic dimensions of teaching quality: Cognitive activation, classroom management, and teacher support (cf. Praetorius et al., 2018). However, institutional effects of schools such as tracking also influence the achievement of different learning goals (Dumont et al., 2013). Establishing different schools or classes that group students with regard to their abilities affects the provided learning opportunities, the actual work, and the learning conditions. Thus, tracking interacts with the dimensions of teaching quality. However, although this interplay is well-known, most studies on teaching quality use tracking rather as a control variable. The moderating effect of school tracks as differential learning environments on multidimensional goals has rarely been the focus of attention.
One commonly used approach for assessing teaching quality are student questionnaires as they provide an economic and easy way to gather information not on the offered but the perceived learning opportunities. Nevertheless, particularly when students are part of different groups such as school tracks, using student questionnaires raises critical questions about the validity of these ratings. Hence, testing the comparability of student ratings across groups needs to be an important first step before examining relationships with multidimensional learning goals. Although differences between school tracks in teaching quality are frequently reported on descriptive level, key aspects of construct validity are hardly tested.
Therefore, this paper used data from a class based German extension of the PISA 2012 study (Programme for International Student Assessment) and examined two questions: (1) is the factorial structure of basic dimensions of instructional quality comparable across high and low school tracks, and (2) are there differential profiles between school tracks in their mathematics teaching quality as well as their relationship with multidimensional learning goals.
School Tracks As Differential Learning Environments
Around the world, most educational systems eventually group students with regard to their abilities (OECD, 2013). The underlying idea for all of these attempts is to create homogenous learning environments that enable teachers to provide teaching instructions that meet students' needs specifically in order to better support all students (cf. Betts, 2011). However, educational systems differ in the age of separation and whether they group students into different schools or within a school into different tracks, separate classes, or within classes. For example, in Germany, students are distributed to different schools by the end of grade 4 or 6. In most of the German states, students change to an academic school track (“Gymnasium”) in order to achieve a general higher education entrance qualification or to a non-academic, more vocational oriented secondary school track with the aim of a general education school leaving certificate. The assignment of students to a school track is associated with their prior achievement and social background, which leads to a more heterogeneous student body at the non-academic school track (Dumont et al., 2013). However, school tracks do not only differ in the student body but most importantly in their curricula, work and learning conditions as well as their underlying pedagogical and didactical traditions. In Germany, this had historically led to two types of teacher education (cf. Baumert et al., 2010). While the teacher training for the Gymnasium focuses more on subject specific content knowledge and scientific propaedeutical procedures, the training for non-academic school tracks emphasizes a more practical oriented approach with a strong pedagogical orientation.
With regard to multidimensional learning goals, although the aim of ability grouping is to adapt teaching strategies to the specific needs of students more easily, the mere effect of ability grouping on achievement is low (cf. Hattie, 2009). Hattie concluded that tracking is less important but that good educational practices would benefit students in homogenous and heterogeneous classes. For motivational-affective learning goals, the effects of tracking are mostly examined in the framework of the Big-Fish-Little Ponds Effect showing that being placed in high-achievement groups can have negative effects for self-concept and interest because of unfavorable upward social comparisons (Marsh, 2007). However, a joint effect of tracking and teaching qualities has hardly been examined.
Basic Dimensions of Teaching Quality
Prominent models of teaching quality– although they use different terminologies –describe three generic dimensions of instruction in mathematics: Classroom management, teacher support, and cognitive activation (Pianta and Hamre, 2009; Walshaw and Anthony, 2017; Praetorius et al., 2018). Classroom management aims to use the provided learning time efficiently by establishing a clear structured and low-noise learning environment (Kounin, 1970). One key aspect is classroom discipline, which does not only aim to react to disturbances, but also focuses on using preventative strategies. Teacher support refers to how teachers align their teaching to the needs and goals of students (Pintrich et al., 1993). Their interest in students' learning progress as well as to registering and talking about problems sensitively, creates a positive learning climate. Cognitive activation refers to the degree of cognitive challenge in the lesson and the activation of higher order thinking (Klieme et al., 2001). While activating students' prior knowledge, they are encouraged to think more deeply about mathematical contents by exploring the results of tasks autonomously and monitoring their solving progress.
With regard to school track differences, descriptive results from the TIMSS-video study revealed that teachers most likely used elements of cognitive activation at the Gymnasium (Klieme et al., 2001). In the lowest school track (“Hauptschule”), teachers focused more on rehearsing procedures. However, when students were asked about their perception of cognitive activation in math classrooms, the results were mixed. In some studies, students at the lowest school track also reported lower levels of cognitive activation (Gruehn, 2000). Others revealed that students at the lowest school track even reported higher levels of cognitive activation (Kunter et al., 2005). At the Gymnasium, lessons were also more efficiently managed but teachers provided less learning support as compared to lower school tracks (Kunter et al., 2005; Schiepe-Tiska et al., 2013). Although all of these studies assumed that the assessed constructs showed the same measurement structure in both tracks and thus, teaching qualities could be compared, none of them had tested this assumption empirically.
Student Ratings of Teaching Quality
In order to assess teaching quality, different approaches exist; each has its advantages and disadvantages. Student ratings are one possible, economic way as they provide information not on the offered, but on the perceived learning opportunities, which have higher predictive power for students' learning outcomes as compared to teacher ratings (Wagner et al., 2016). These ratings represent an aggregated and thus more long-term view on teaching as compared to observations, which often refer to single or a few lessons (Praetorius et al., 2014). Student ratings can be aggregated on the class level in order to distinguish between the individual perception of students and the perception of the shared learning environment (Lüdtke et al., 2009). However, on the other hand, student ratings have also been suspected to be biased by individual idiosyncracies (Kunter and Baumert, 2006) and teacher popularity (Fauth et al., 2014).
Two of the most important concerns with regard to their construct validity are (a) whether students are able to discriminate between different components of teaching quality on the individual and class level (dimensionality) and, (b) whether the instruments assess the same constructs across different groups (generalizability) and thus, allow for meaningful mean comparisons. Previous studies confirmed the assumed three-dimensional structure of teaching quality on the class and individual level (e.g., Fauth et al., 2014; Schiepe-Tiska et al., 2016a), but they did not consider different groups of respondents. For generalizability, thus far, teaching quality has only been compared across subjects (Wagner et al., 2013). In English and German lessons teaching quality was only comparable for classroom organization but not for emotional support.
The Relationship Between Multidimensional Goals and Teaching Quality in Different School Tracks
Besides gaining knowledge, developing an interest and becoming confident in ones' own abilities are highly important learning goals in mathematics education for all students (NCTM, 2000). Although cognitive abilities provide a profound basis for dealing with daily challenges in mathematics, motivational-affective learning outcomes influence whether students will actively and of their own accord engage in situations where these competencies are necessary. The main learning opportunities for achieving these goals are provided in math classrooms and depend on the quality of teachers' instruction.
For math competence, a number of studies controlling for school track differences or focusing only on the Gymnasium documented the importance of students' shared perception of efficient classroom management as well as high levels of cognitive activation (e.g., Klieme et al., 2001; Klieme and Rakoczy, 2003; Lipowsky et al., 2009; Baumert et al., 2010; Kunter and Voss, 2013; see also Praetorius et al., 2018). Two studies that focused on differences between high and low school tracks assumed that teaching quality would mediate the effect of teacher knowledge and beliefs on math achievement but could not confirm this effect (Dubberke et al., 2008; Baumert et al., 2010). However, they did not report the results for track differences in the relationship between teaching quality and achievement. Hints for track differences come from research on aptitude-treatment-interaction by showing that low performing students profit more from a highly structured learning environment than high performing students (Snow and Lohman, 1984).
Interest is characterized by a cognitive, affective, and value related component (Krapp and Prenzel, 2011). It contributes to personality development and affects STEM-related career decisions (e.g., Pekrun et al., 2007). Math interest is positively related to students' individual perception of effective classroom management and their perceived teacher support (e.g., Klieme et al., 2001; Kunter et al., 2007; Kunter and Voss, 2013). Also at the Gymnasium, students experienced more math interest when they felt supported by their teachers (Klieme and Rakoczy, 2003). Whether cognitive activation affects interest is less clear. Most studies found no association (Klieme et al., 2001; Kunter and Voss, 2013), although one found a positive relation (Schiepe-Tiska et al., 2016a) that has also been shown in science education (Fauth et al., 2014). These varying results may stem from masked effects of different cognitive activating learning environments in school tracks.
Mathematics self-efficacy describes beliefs to master challenging actions and problems successfully (Bandura, 1977). When students think they have the necessary abilities to solve difficult math tasks, they show higher willingness to make an effort to work on the tasks and are more persevere (Klassen and Usher, 2010). In turn, the probability to solve these tasks rises, which affects future achievement expectations and predicts the enrollment of STEM-related university majors (Parker et al., 2014). Students who reported higher levels of math self-efficacy perceived their classrooms as more caring, challenging, and mastery oriented (Fast et al., 2010). For effects of ability grouping, a small Big-Fish-Little Ponds Effect has been found for science self-efficacy (Jansen et al., 2015). However, self-efficacy was more strongly related to inquiry-based learning opportunities that offer high levels of cognitive activation. A joint effect has not been tested.
Present Study
The present study examined the impact of school tracking on students' perception of teaching quality in mathematics and their joint effect on multidimensional learning goals. Representative data from a class based German extension of the PISA 2012 study was used and two central research questions were addressed using multilevel analyses.
First, previous studies reported school track differences in students' perception of teaching quality only on a descriptive level without testing the factorial structure within and across different groups (e.g., Kunter et al., 2005; Schiepe-Tiska et al., 2013). Therefore, I examined whether the factorial structure of student ratings of three basic dimensions of instructional quality (cognitive activation, classroom management, and teacher support) is comparable across high and low school tracks by analyzing the following questions. (a) Can students in different tracks distinguish between these dimensions of teaching quality (dimensionality), (b) are ratings of instructional quality generalizable across tracks (generalizability), and (c) do students in different tracks perceive instructional qualities differently (mean comparison)? I expected that in both groups a latent factor model with three dimensions at the class and student level would best fit the data and would be comparable across tracks. If so, students at the Gymnasium would report higher levels of classroom discipline but lower levels of teacher support. For cognitive activation, I assumed a difference, but because of controversial results of previous studies (Gruehn, 2000; Kunter et al., 2005; Schiepe-Tiska et al., 2013) no specific direction was formulated.
Second, because previous studies analyzing the relation between teaching quality in mathematics and different learning goals rather controlled for track differences, this study focused on the interaction of tracking and teaching quality on multidimensional goals, namely mathematics achievement and interest. Moreover, I extended previous research by examining self-efficacy as an important goal of mathematics learning (NCTM, 2000). I expected different profiles for school tracks in that classroom discipline is particularly important for math competence in lower school tracks (LST). For interest, I expected teacher support to be important in both tracks. However, as previous studies controlling for school track reported inconsistent results for cognitive activation, I assumed that there is a difference between tracks in its relation with math interest. For self-efficacy, I expected relations with students' perception of teacher support and cognitive activation. As students at the Gymnasium reported lower levels of teacher support in previous studies (Kunter et al., 2005; Schiepe-Tiska et al., 2013), it might positively affect particularly their level of self-efficacy. In line with prior studies, I expected relations with achievement to be found at the class level and relations with motivational outcomes on the individual level.
Methods
Participants and Procedure
The sample consisted of 211 schools with 412 classes and 9,845 ninth graders (Mage = 15.56; SDage = 0.62; nfemale = 4919; nmale = 4926). Students were sampled following a stratified sampling process. Schools were sampled first and in each school, two complete ninth grades were randomly selected in order to participate in PISA, which resulted in a nested data structure. At the Gymnasium, 3,825 students from 152 classes (average class size: M = 25.16, SD = 3.53) participated as compared to 6,020 students from 260 classes (average class size: M = 23.15, SD = 4.75) from LST. All students joint a two hour competency assessment. In addition, students answered a questionnaire covering contextual information including their perception of teaching quality (OECD, 2014). In PISA 2012, the questionnaire was distributed using a rotated design with three versions. Each version asked questions about the family background but only two-third of the students answered questions about the dimensions of instructional quality, mathematics interest, and self-efficacy.
Data was collected in the context of Germanys‘ participation in the PISA study, which is charged by the federal governments of the states. Students who were selected for participation as well as their parents were informed about the goals of the study and what would be assessed. By school law, participation in the test was mandatory for all selected students in order to ensure the internationally required representative sample. Whether participation in the questionnaire was mandatory too, depended on the state. In the states where participation was not mandatory, parents and students provided written informed consent, otherwise students only participated in the test. For the questionnaires, privacy officers of all states approved the internationally developed material. The study was conducted according to the Ethical Principles of Psychologists and Code of Conduct of the American Psychological Association from 2017. An ethics approval was not required by institutional guidelines or national regulations, in line with the guidelines of the “German Research Foundation” as the used data was anonymized and no disclosure outside the research is possible.
Measures
Cognitive Activation
Cognitive activation was assessed with nine items (OECD, 2014; α = 0.79). For example, students were asked how often their teacher presents mathematics problems for which there is no immediately obvious method of solution. Students answered items on a four-point Likert scale (always or almost always to never or rarely). One item was excluded because, with regard to its content and the results of statistical analyses, it could not be separated from the scale teacher support (“The teacher helps us to learn from mistakes we have made.”). A second item (“The teacher presents problems for which there is no immediately obvious method of solution.”) showed negative factor loadings in both groups but did also not load on another scale. Thus, is was also excluded from further analyses.
Classroom Discipline
Classroom discipline and teacher support were measured with five items (OECD, 2014; αdiscipline = 0.90; αteacher support = 0.85). Students answered items such as “the teacher has to wait a long time for students to quiet down” or “the teacher shows an interest in every student's learning” on a four-point Likert scale (every lesson to never or hardly ever).
The item specific Intra- class correlations (ICC1) for the dimensions of instructional quality (Lüdtke et al., 2009) were for the Gymnasium between 0.08 and 0.31, for LST between 0.05 and 0.23. The reliability of the class means was also satisfactory (ICC2 Gymnasium 0.88 to 0.99; ICC2LST 0.86 to 0.98).
Mathematics Competence
Mathematics competence was assessed with the PISA 2012 test (OECD, 2014). Four content categories were measured: Quantity, uncertainty and data, change and relationships, space and shape. Data were scaled with a one-dimensional Rasch model generating five plausible values. The reliability of the international test was 0.85. For the Gymnasium, 14.7% of the variance of mathematics competence was found between classes, for LST it had been 27.1%.
Mathematics Interest
Mathematics interest was assessed using four items such as “I am interested in the things I learn in mathematics” (OECD, 2014; α = 89; ICC1 Gymnasium 0.03 to 0.05, ICC1 LST 0.04 to 0.11). Students evaluated their agreement on a four-point Likert scale (strongly agree to strongly disagree).
Mathematics Self-Efficacy
Mathematics self-efficacy was assessed using eight items (OECD, 2014; α = 81; ICC1 Gymnasium 0.03 to 0.08, ICC1 LST 0.04 to 0.11). Students were asked about how confident they feel about having to do specific mathematics tasks (e.g., “Solving the equation 3x + 5 = 17,” “Calculating the petrol consumption rate of a car”). The items were evaluated on a four-point Likert scale (very confident to not at all confident).
Control Variables
As the assignment of students to school tracks is associated with prior achievement and the social background of students (Dumont et al., 2013), I controlled for general cognitive abilities (EAP estimator, scale figural analogies, Wilhelm et al., 2014) and the highest international socio-economic index of occupational status (HISEI; OECD, 2014). In addition, students also reported their gender.
Dealing With Missing Values
There were two types of missing data: missing answers due the rotated questionnaires (OECD, 2014) and missing answers of single items (instructional qualities 0.9–1.4 %; interest and self-efficacy 0.6–0.7 %, general cognitive abilities 7.1 %, HISEI 13.9 %). Recent literature suggests that using multiple imputation is more advantageous in dealing with missing data as compared to classical case deletion methods (Enders, 2010). With the help of an imputation model that included auxiliary variables from questions all students had answered (indicators of family background, see OECD, 2014), m = 20 datasets for each of the five plausible values of mathematics competence were created (in total 100 datasets). Taking the multilevel structure of the data into account, Mplus 7.3 (Muthén and Muthén, 1998–2011) was used for the imputation.
Statistical Analyses
Given the nested data structure of students in classrooms, for testing measurement invariance (dimensionality, generalizability, and mean comparison of teaching qualities), a series of multigroup multilevel confirmatory factor analyses was used with three factors at the between and the within level (Vandenberg and Lance, 2000). This procedure estimates separate models for each school track simultaneously, and introduces different equality constraints upon model parameters between the groups. The configural invariance model is the least restrictive model and imposes no equality constraints. The metric invariance model tests whether each item loads equivalently on the same factor in both groups by constraining the item factor loadings to be equal across the groups. The scalar invariance model as the most restrictive one constraints the factor loadings and intercepts to be equal across groups. In order to evaluate the model fits, suggestions of Iacobucci (2010) were followed. A model had a reasonable fit when (a) the robust comparative fit index (CFI) is close to 0.95, (b) the robust root mean square error of approximation (RMSEA) is <0.08, and (c) the standardized root-mean-square residuals (SRMR) are <0.09.
In order to test the moderating effect of school track, for each goal, a two-group-multilevel doubly latent model was specified. Studies testing the effects of teaching quality on learning outcomes often suffer from two problems: sampling bias and measurement errors in the data. Multilevel doubly latent models face these problems by integrating structural equation models and multilevel models in order to control simultaneously measurement error due to sampling of items and sampling error due to sampling of persons (Marsh et al., 2009). Therefore, this approach is modeling the measurement and structural model simultaneously at the individual and class level. The dimensions of instructional quality were assessed at the student level, and additionally aggregated at the class level in order to examine the perception of the shared learning environment (Lüdtke et al., 2009). The individual and aggregated scores have been used simultaneously at the individual and class level in all models. Mathematics interest and self-efficacy have also been modeled as latent factors. On the individual level, general cognitive abilities, socio-economic background (both grand mean centered), and gender were included. The moderator effect was tested by comparing changes in ΔCFI of a model with freely estimating the corresponding effect of teaching quality vs. assuming equality of the parameters (Cheung and Rensvold, 2002). Two models were assumed to be equivalent when ΔCFI ≤ −0.01. All models took students and class weights as well as the stratification of the sample into account. All analyses were calculated with each of the 100 datasets using Mplus 7.3. In order to get correct standard errors, the results were combined with the formula of Rubin (1987).
Results
Dimensionality, Generalizability, and Mean Comparison of Teaching Quality
Tables 1 and 2 show the latent intercorrelations between the dimensions of instructional quality for the Gymnasium and LST. On the class level, particularly cognitive activation and teacher support were highly correlated in both groups, which has also been found in other studies (Wagner et al., 2013; Fauth et al., 2014). For both tracks, the global model fit was good supporting the theoretically assumed three factor structure on both levels (Gymnasium: χ2 = 1218.00, df = 232, CFI = 0.94, RMSEA = 0.03, SRMRwithin = 0.04, SRMRbetween = 0.09; LST: χ2 = 1450.30, df = 232, CFI = 0.96, RMSEA = 0.03, SRMRwithin = 0.03, SRMRbetween = 0.08). However, because of the high correlations at the class level, I also compared the model fit with the fit of a model with only one factor at the between and three factors on the within level. For this model, the fit indices dropped and in particular the SRMRbetween, which specifically refers to the class level showed a poorer fit for both school tracks (Gymnasium: χ2 = 1864.75, df = 235, CFI = 0.91, RMSEA = 0.04, SRMRwithin = 0.04, SRMRbetween = 0.20; LST: χ2 = 2128.87, df = 235, CFI = 0.94, RMSEA = 0.04, SRMRwithin = 0.04, SRMRbetween = 0.23).
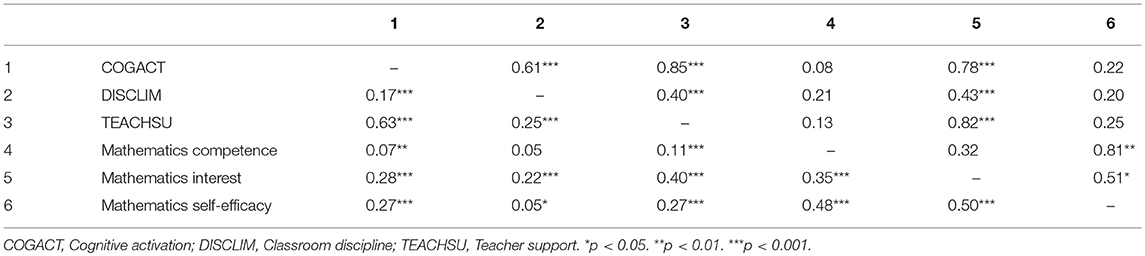
Table 1. Intercorrelations at the class level (above the diagonal) and at the individual level (below the diagonal) for the Gymnasium.
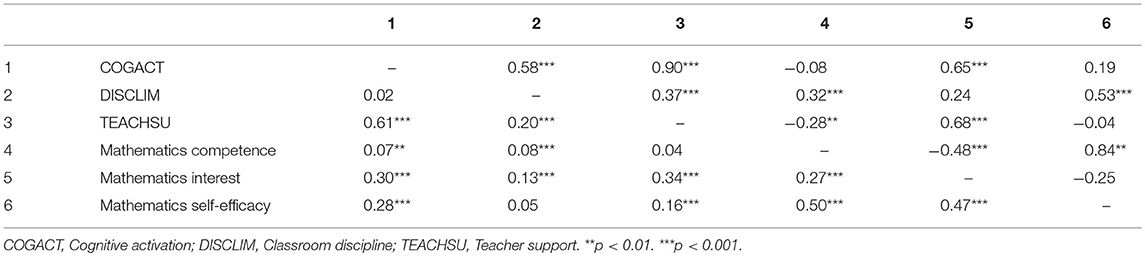
Table 2. Intercorrelations at the class level (above the diagonal) and at the individual level (below the diagonal) for the lower school tracks.
Table 3 presents in the first section (MCFA) the results for the test of invariance of factor loadings and intercepts across tracks. Scalar invariance was holding across tracks and thus, the factorial structure and intercepts were found to be equal in both tracks. Hence, the latent mean differences could be compared. At the Gymnasium, classroom discipline was perceived significantly higher (ΔMean = 0.13, SE = 0.04, p = 0.001), but teacher support significantly lower (ΔMean = 0.24, SE =.05, p = 0.000) as compared to LST. For cognitive activation, no difference occured (ΔMean = 0.04, SE = 0.06, p = 0.47).
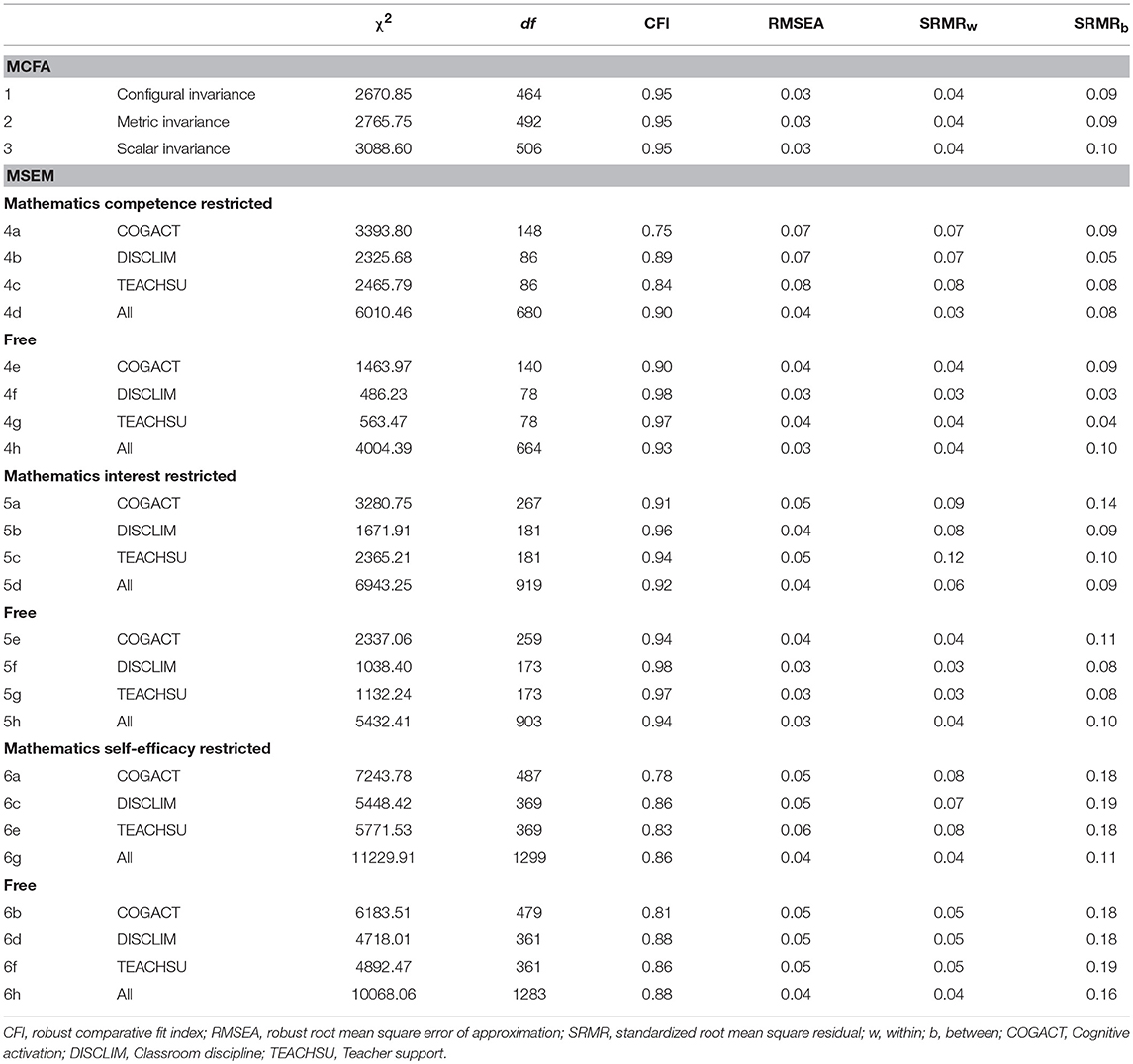
Table 3. Summary of fit indices of multilevel confirmatory factor analyses (MCFA) and multilevel structural equation modeling (MSEM).
School Tracks and the Relationship Between Multidimensional Goals and Teaching Quality
When testing the moderator effect of tracking by comparing ΔCFI of two-group-multilevel doubly latent models (Table 3, section MSEM), the model fits with restricted parameters were worse as compared to model fits with freely estimated parameters. Thus, tracks differed in all associations of teaching qualities and learning outcomes. The fit for the models with the freely estimated parameters represent the fit of the corresponding models in Tables 4–6, which show the results for the relationship between each educational goal and instructional qualities. With regard to the control variables at the individual level (not included in the tables), cognitive abilities were positively related to each goal in both groups. Girls always showed lower levels of competence, interest, and self-efficacy. Mathematics competence and self-efficacy were positively related with socio-economic background; no relation was found with mathematics interest.
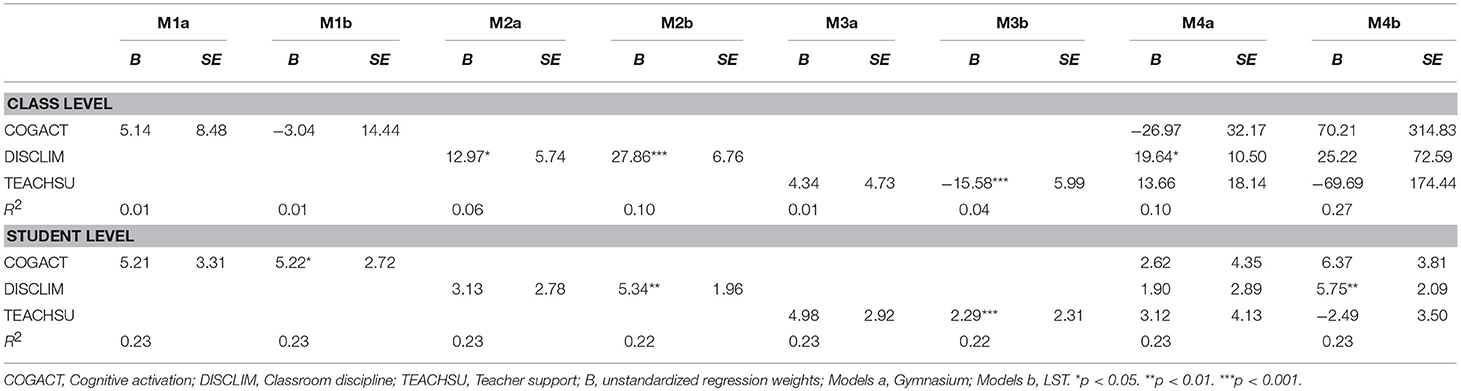
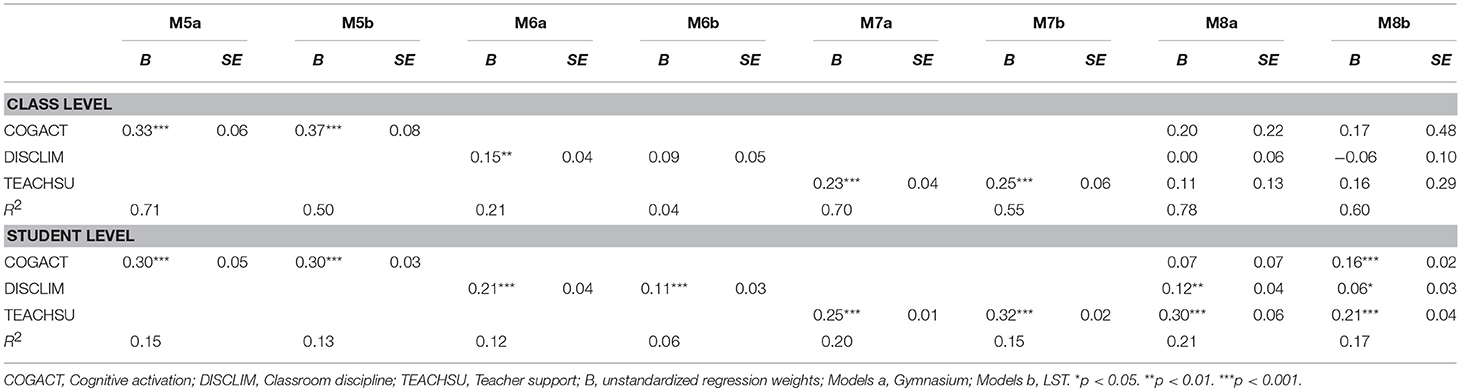
Table 4. Prediction of mathematics competence: Results of two-group-multilevel doubly latent models.
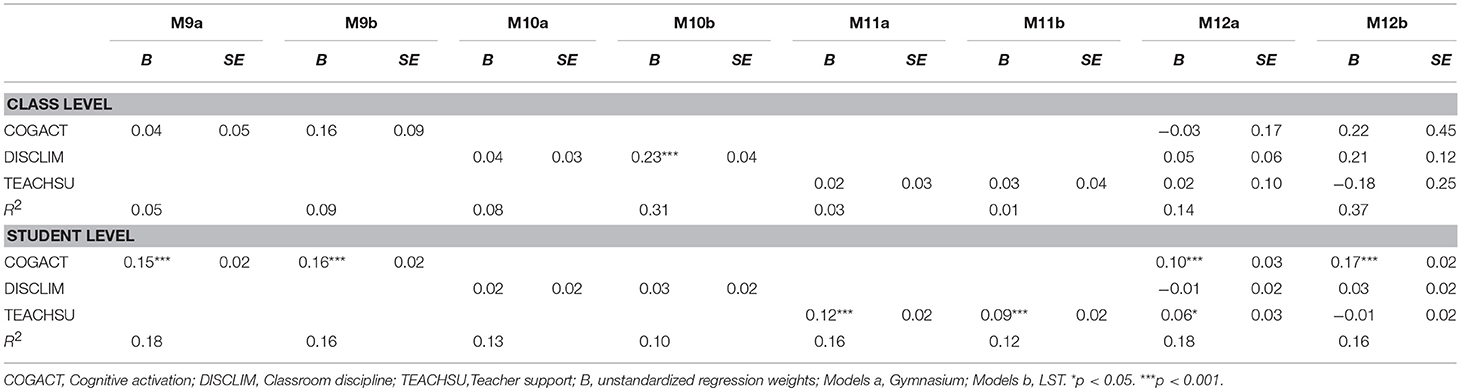
Table 6. Prediction of mathematics self-efficacy: Results of two-group-multilevel doubly latent models.
For mathematics competence (Table 4), considering each dimension of instructional quality separately, at the Gymnasium, a positive relation with discipline at the class level was found (Model 2a) that was still significant when all dimensions of instructional quality were considered simultaneously in the analyses (Model 4a). For LST, the perception of higher classroom discipline at the class level was also related to better competence (Model 2b). Moreover, classes reporting higher levels of teacher support showed lower levels of mathematics competence (Model 3b). At the student level, math competence was positively related to cognitive activation, discipline, and teacher support (Models 1b, 2b, 3b). However, when all dimensions of instructional quality were considered simultaneously in the analysis, only the relation with discipline at the individual level remained significant for LST (Model 4b).
For mathematics interest (Table 5), at the Gymnasium, all dimensions of teaching quality separately were positively related to interest at the class and individual level (Models 5a, 6a, 7a). However, when they were considered simultaneously in the analysis (Model 8a), only the relation with discipline and teacher support at the individual level remained significant. For LST, classes that reported high levels of cognitive activation and teacher support felt more interested in mathematics (Models 5b and 7b). The same results were found for the student level, additionally revealing that students who perceive higher levels of discipline also reported higher levels of interest. Considering all dimensions of teaching quality at the same time (Model 8b), only the results at the student level remained significant.
Mathematics self-efficacy, considering each dimension of instructional quality separately, was at the Gymnasium only at the student level positively related to cognitive activation and teacher support (Models 9a and 11a). This relation remained the same when all dimensions of teaching quality were considered at the same time in the analysis (Model 12a). For LST, considering each dimension of instructional quality separately, classes that reported a low-noise learning environment experienced higher levels of self-efficacy (Model 10b). At the student level, high levels of self-efficacy were related to perceived cognitive activation and teacher support (Models 9b and 11b). When taking all dimensions of teaching quality into account at the same time, only the positive relation between individual self-efficacy and cognitive activation remained significant (Model 12b).
Discussion
The present study investigated the factorial structure of teaching qualities across school tracks and examined whether tracks differed in students' perception of teaching quality. Following this, school track differences in the association between dimensions of teaching quality and multidimensional learning goals were tested. In support of my hypotheses, students in high and low school tracks distinguished between the dimensions of teaching quality cognitive activation, classroom discipline, and teacher support. Moreover, the factorial structure was comparable across tracks. Students at the Gymnasium reported higher levels of discipline but lower levels of teacher support. Unexpectedly, no difference occurred for cognitive activation.
In association with different learning goals, school track differences occurred for each learning goal. Math competence was related to classroom discipline on the student level in lower school tracks (LST) and on the class level at the Gymnasium. Math interest was, on the student level, in both tracks associated with teacher support and discipline. In addition, in LST a cognitive activating learning environment was associated with more interest. High levels of math self-efficacy were in both school tracks reported by students who perceived their lessons as cognitive activating. In addition, at the Gymnasium, students who felt more supported by their math teachers reported higher levels of self-efficacy. In the following, the findings are discussed in more detail.
Dimensionality, Generalizability, and Mean Comparison of Teaching Quality
Two key aspects of construct validity of student ratings are dimensionality within and generalizability across different groups of students. However, despite the fact that these are important preconditions for gathering valid results, it has rarely been studied whether the same factorial structure would emerge across different school tracks. The present results complement previous studies that found a three-dimensional structure (Dubberke et al., 2008; Wagner et al., 2013; Fauth et al., 2014) by showing that this structure is valid in different learning environments on the student and class level and that it can be compared across school tracks.
In line with other studies using student questionnaires and video ratings (Gruehn, 2000; Klieme et al., 2001; Kunter et al., 2005), students at the Gymnasium reported higher levels of classroom discipline but lower levels of teacher support and thus, supported the idea of school tracks as differential learning environments with regard to teaching qualities. As the student body at the Gymnasium is more homogenous and students have comparably more favorable preconditions in terms of prior achievement and social background (Dumont et al., 2013), it seems to be easier for teachers to establish a clear structured and low-noise learning environment. On the other hand, teachers in LST focused more on aligning their teaching to the needs and goals of their more heterogeneous student body. This may be due to the fact that the attitude of creating a supportive learning climate is also emphasized in their strong pedagogical orientation during teacher training. Moreover, teachers who decide to work in these schools might implicitly have comparatively higher commitment to supporting more disadvantaged students.
Contrary to previous studies, which found differences in the student perception of cognitive activation in one or the other direction (Gruehn, 2000; Kunter et al., 2005) students in the present study reported no differences. Previous studies found these differences particularly between the highest and the very lowest school track (“Hauptschule”). Kunter et al. (2005) had argued that students at the lowest school tracks might evaluate the task difficulty rather than the design of a task, and thus, reported higher levels of cognitive activation as compared to students at the Gymnasium. Video studies have revealed that using elements of cognitive activation most likely occurred at the Gymnasium as compared to the lowest school track (Klieme et al., 2001). However, in most German states, the lowest school track had merged with other non-academic school tracks to one type of school and the educational system is changing from a three- to a two-tier structure (KMK, 2017), creating a more heterogeneous student body in the non-academic track. Together with the rising awareness that students from disadvantageous background also profit from higher achievement expectations (Hutchings et al., 2012), teachers might not shy away from providing math tasks with multiple ways of solution and encouraging also lower performing students to deal with tasks more autonomously. Whether there is a true change in the math instruction in non-academic school tracks or whether the present results are based on the merge of tracks is a question for future studies. These should take the current two-tier structure of the educational system into account and additionally include external observations.
School Tracks as Differential Learning Environments and the Relationship Between Multidimensional Goals and Teaching Quality
The question whether school tracks differ in the association of multidimensional goals and teaching quality is important for designing lessons that adapt to different student bodies and meet different learning goals. This can be quite challenging for teachers. Depending on the goals and the target student group, they should accentuate their teaching in order to meet the needs of these students specifically. The results of the present study showed that some teaching strategies were beneficial for students' in all school tracks but they also revealed some important accentuations between tracks in their relationship with different learning goals.
In line with studies controlling for school track differences, in both school tracks, students who reported high levels of classroom management also showed higher levels of math achievement and math interest. In a low noise-learning environment without interruptions, learning time can be used efficiently and a clear structure can be established and followed which has also been found to be related to higher levels of flow experience (Schiepe-Tiska, 2013). However, contrary to my hypotheses, for achievement the effect occurred on different levels of analyses. For the Gymnasium, the assumption of previous studies that classroom management is in general a class level construct and students' individual perception of whether the classroom is more or less organized is less important for achievement (Aldrup et al., 2018) holds, but this does not hold for LST. It seems that because students in LST have a more heterogeneous background and classroom discipline is in general lower as compared to the Gymnasium, their individual perception of a low-noise learning environment in comparison to their classmates is more important for achieving higher levels of math competence.
In line with the idea that for motivational-affective outcomes students' individual perception of teaching quality is more important than the shared perception of the class, teacher support was in both school tracks related to higher math interest at the individual level. Although teacher support in general was perceived higher in LST, students at the Gymnasium also felt more interested in mathematics when teachers created a supportive learning environment. Moreover, only at the Gymnasium, perceived teacher support was additionally related to students' self-efficacy. Murdock and Miller (2003) proposed that students who perceived their teachers as supportive were more likely to view themselves as academically capable and set higher educational goals for themselves. This may be an important clue for teachers at the Gymnasium in order to improve their teaching as they often see themselves more as subject knowledge brokers and particularly math seem to be not a subject where teacher-student relations are as much a focus. Hence, from a practical perspective, particularly the awareness of mathematics teachers at the Gymnasium should be raised for the importance of positive student relationships for developing interest and positive self-views.
Contrary to studies controlling for school track (e.g., Klieme et al., 2001; Baumert et al., 2010; Kunter and Voss, 2013), there was no association between cognitive activation and math competence in both school tracks. This may be due to different assessments of cognitive activation as the present study used aggregated student ratings while others have used video ratings or task analyses (Kunter et al., 2007; Lipowsky et al., 2009). For the motivational-affective learning goals, in line with my hypotheses, higher levels of cognitive activation were in both school tracks related to more positive self-efficacy beliefs. Students who felt that their teachers think they are capable of solving math tasks with multiple ways of solution and encourage them to deal with these tasks more autonomously also believed in themselves, as social persuasion is one important source for developing self-efficacy (Bandura, 1977). This result is also in line with Jansen et al. (2015) who found that science inquiry-based learning opportunities that offer high levels of cognitive activation were related to higher levels of self-efficacy. For interest, however, as expected, a difference between school tracks occurred that might offer another possible explanation for the inconsistent results of previous studies besides different operationalization of cognitive activation (Klieme et al., 2001; Kunter and Voss, 2013; Fauth et al., 2014; Schiepe-Tiska et al., 2016a). Only in LST high levels of cognitive activation were related to higher math interest. Particularly, low performing students seem to profit from teachers who challenge them with tasks that require higher-order thinking and understanding. These students might sense that these teachers give them credit for being able to deal with this kind of tasks and together with a supportive learning environment, their interest in mathematics rises. From a theoretical perspective, stimulating deeper elaboration and engagement gives students learning opportunities to acquire mastery experiences (Bandura, 1977). These can foster their feelings of autonomy and competence, which in turn might affect their interest as well as their self-efficacy beliefs. Hence, teachers in LST might be encouraged to offer these kind of tasks to their students.
Limitations and Future Directions
Although the findings are based on a large representative class based dataset und multilevel modeling was applied, there are some limitations that come with using data from large-scale assessments for analyzing class level processes (cf. Müller et al., 2016). Here, I focus on two critical points: The use of student ratings and the cross-sectional nature of PISA. The question of what kind of insights about teaching processes can be gained from different perspective has often been asked. For the more cross-disciplinary dimensions classroom discipline and teacher support, student ratings have been found to provide valid information for predicting student outcomes (e.g. Gruehn, 2000; Kunter and Baumert, 2006; Aldrup et al., 2018; Praetorius et al., 2018). Still, they focus on the perceived rather than the intended or observable learning opportunities. As students mostly attend only one track through their school career, differences between tracks might be hard to depict. This is particularly important for the more subject-specific component of cognitive activation. Analyzing learning materials of teachers as well as external observations would provide valuable information to validate the present findings and gain insights into the interplay of different perspectives.
Moreover, the type of orchestration of teaching qualities for different learning goals have rarely been the focus of attention yet. For example, Dorfner et al. (2018) showed that for the development of interest in biology at the Gymnasium, cognitive activation mediated the effect of classroom management and supportive climate. However, other school tracks or learning outcomes were not included in the study. Another question would be whether higher levels of cognitive activation are always better for learning outcomes as students might be over challenged particularly in LST. For example, in science, the relationship between inquiry-based teaching that offers high levels of cognitive activation and achievement was found to be curvilinear (Teig et al., 2018).
Second, PISA is a cross-sectional study. Thus, only a teaching status description can be modeled, and inferences about the causality of teaching qualities and learning goals in different school tracks cannot be drawn. However, Kuger et al. (2017) analyzed the prognostic validity of mathematics teaching qualities on students' achievement 1 year later and concluded that, if carefully modeled, the inferences about structure and importance of teaching qualities for math competence based on cross-sectional data withstand longitudinally, although the absolute level of the relations might be overestimated. Future studies would benefit from a longitudinal design so that the impact of teaching qualities in different school tracks on multidimensional goals could be investigated.
Conclusion
The results speak clearly for the assumption of school tracks as differential learning environments. They ask for a more differentiated view of teaching quality and its impact on reaching multidimensional goals by explicitly examining these differences instead of controlling for them. In order to meet the underlying idea of ability grouping—answering students' needs specifically—these associations need to be understood more clearly in order to create matching learning environments. Only then can teachers be better prepared for the increasing challenges in dealing with classroom heterogeneity.
Ethics Statement
This study was carried out in accordance with the Ethical Principles of Psychologists and Code of Conduct of the American Psychological Association from 2017 and incorporated recommendations of data privacy officers from the German Federal states. By school law, participation in the test was mandatory for all selected students in order to ensure the internationally required representative sample. Whether participation in the questionnaire was mandatory too, depended on the state. In the states where participation was not mandatory, parents and students provided written informed consent, otherwise students only participated in the test. The protocol was approved by the data privacy officers from the German Federal states.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work was supported by the German Research Foundation (DFG) and the Technical University of Munich (TUM) in the framework of the Open Access Publishing Program.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Aldrup, K., Klusmann, U., Lüdtke, O., Göllner, R., and Trautwein, U. (2018). Social support and classroom management are related to secondary students' general school adjustment: a multilevel structural equation model using student and teacher ratings. J. Educ. Psychol. 110, 1066–1083. doi: 10.1037/edu0000256
Bandura, A. (1977). Self-efficacy: toward a unifying theory of behavioral change. Psychol. Rev. 84, 191–215. doi: 10.1037/0033-295X.84.2.191
Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., Jordan, A., et al. (2010). Teachers' mathematical knowledge, cognitive activation in the classroom, and student progress. Am. Educ. Res. J. 47, 133–180. doi: 10.3102/0002831209345157
Betts, J. R. (2011). “The economics of tracking in education,” in Handbook of The Economics of Education, eds. E. A. Hanushek, S. Machin, and L. Woessmann (Amsterdam: North Holland), 341–381.
Cheung, G. W., and Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Struct. Equat. Model. 9, 233–255. doi: 10.1207/S15328007SEM0902_5
Dorfner, T., Förtsch, C., and Neuhaus, B. J. (2018). Effects of three basic dimensions of instructional quality on students' situational interest in sixth-grade biology instruction. Learn. Instr. 56, 42–53. doi: 10.1016/j.learninstruc.2018.03.001
Dubberke, T., Kunter, M., McElvany, N., Brunner, M., and Baumert, J. (2008). Lerntheoretische Überzeugungen von Mathematiklehrkräften [Mathematics teachers' beliefs and their impact on instructional quality and student achievement]. Zeitschrift Pädagogische Psychol. 22, 193–206. doi: 10.1024/1010-0652.22.34.193
Dumont, H., Neumann, M., Maaz, K., and Trautwein, U. (2013). Die Zusammensetzung der Schülerschaft als Einflussfaktor für Schulleistungen. Internationale und nationale Befunde [The effect of student body composition on academic achievement: International and national evidence]. Psychol. Erziehung Unterricht 60, 163–183. doi: 10.2378/peu2013.art14d
Eccles, J. S. (2007). “Where are all the women? Gender differences in participation in physical science and engineering,” in Why aren't More Women in Science? Top Researchers Debate the Evidence, eds. S. J. Ceci and W. M. Williams (Washington, DC: American Psychological Association), 199–210. doi: 10.1037/11546-016
European Commission (2007). Labour Market Shortages in the European Union. Brussels: European Commission Directorate-General for Internal Policies. Available online at: http://www.europarl.europa.eu/RegData/etudes/STUD/2015/542202/IPOL_STU(2015)542202_EN.pdf
Fast, L. A., Lewis, J. L., Bryant, M. J., Bocian, K. A., Cardullo, R. A., Rettig, M., et al. (2010). Does math self-efficacy mediate the effect of the perceived classroom environment on standardized math test performance? J. Educ. Psychol. 102, 729–740. doi: 10.1037/a0018863
Fauth, B., Decristan, J., Rieser, S., Klieme, E., and Büttner, G. (2014). Student ratings of teaching quality in primary school: dimensions and prediction of student outcomes. Learn. Instr. 29, 1–9. doi: 10.1016/j.learninstruc.2013.07.001
Gruehn, S. (2000). Unterricht und schulisches Lernen: Schüler als Quellen der Unterrichtsbeschreibung [Teaching and learning: Students as raters of teaching quality]. Münster: Waxmann.
Hattie, J. (2009). Visible Learning: A Synthesis of Over 800 Meta-analyses Relating to Achievement. New York, NY: Routledge.
Hutchings, M., Greenwood, C., Hollingworth, S., Mansaray, A., Rose, A., Minty, S., et al. (2012). Evaluation of the City Challenge. London: Department for Education.
Iacobucci, D. (2010). Structural equations modeling: fit Indices, sample size, and advanced topics. J. Consum. Psychol. 20, 90–98. doi: 10.1016/j.jcps.2009.09.003
Jansen, M., Scherer, R., and Schroeders, U. (2015). Students' self-concept and self-efficacy in the sciences: differential relations to antecedents and educational outcomes. Contemp. Educ. Psychol. 41, 13–24. doi: 10.1016/j.cedpsych.2014.11.002
Klassen, R. M., and Usher, E. L. (2010). “Self-efficacy in educational settings: recent research and emerging direction,” in Advances in Motivation and Achievement, eds. T. C. Urdan and S. A. Karabenick (Bingley: Emerald), 1–33.
Klieme, E., and Rakoczy, K. (2003). “Unterrichtsqualität aus Schülerperspektive: Kulturspezifische Profile, regionale Unterschiede und Zusammenhänge mit Effekten von Unterricht [Teaching quality from students' perspective: Culture-specific profiles, regional differences, and relations with effects of teaching],” in PISA 2000: Ein Differenzierter Blick auf die Länder der Bundesrepublik Deutschland, eds. J. Baumert, C. Artelt, E. Klieme, M. Neubrand, M. Prenzel, U. Schiefele et al. (Opladen: Leske + Budrich), 333–359
Klieme, E., Schümer, G., and Knoll, S. (2001). “Mathematikunterricht in der Sekundarstufe I: Aufgabenkultur und Unterrichtsgestaltung [Mathematics teaching in secondary school: The culture of tasks and designing teaching],” in Bundesministerium für Bildung und Forschung (Hrsg.), TIMSS-Impulse für Schule und Unterricht. Forschungsbefunde, Reforminitiativen, Praxisberichte und Video-Dokumente [TIMSS impulses for school and teaching. Research results, reform initiatives, practice reports, and video documents] (S. 43–57). Berlin: BMBF.
KMK, Secretariat of the Standing Conference of the Ministers of Education, and Cultural Affairs of Germany. (2017). Basic Structure of the Education System in the Federal Republic of Germany. Available online at: https://www.kmk.org/fileadmin/Dateien/pdf/Dokumentation/en_2017.pdf (Accessed July 27, 2017).
Krapp, A., and Prenzel, M. (2011). Research on interest in science: theories, methods, and findings. Int. J. Sci. Educ. 33, 27–50. doi: 10.1080/09500693.2010.518645
Kuger, S., Klieme, E., Lüdtke, O., Schiepe-Tiska, A., and Reiss, K. (2017). Mathematikunterricht und Schülerleistung in der Sekundarstufe: Zur Validität von Schülerbefragungen in Schulleistungsstudien [Student learning in secondary school mathematics classrooms: on the validity of student reports in international large-scale studies]. Zeitschrift Erziehungswissenschaft 20, 61–98. doi: 10.1007/s11618-017-0750-6
Kunter, M., and Baumert, J. (2006). Who is the expert? Construct and criteria validity of student and teacher ratings of instruction. Learn. Environ. Res. 9, 231–251. doi: 10.1007/s10984-006-9015-7
Kunter, M., Baumert, J., and Köller, O. (2007). Effective classroom management and the development of subject-related interest. Learn. Instr. 17, 494–509. doi: 10.1016/j.learninstruc.2007.09.002
Kunter, M., Brunner, M., Baumert, J., Klusmann, U., Krauss, S., Blum, W., et al. (2005). Der Mathematikunterricht der PISA-Schülerinnen und -Schüler [Quality of mathematics instruction across school types: findings from PISA 2003]. Zeitschrift Erziehungswissenschaft 8, 502–520. doi: 10.1007/s11618-005-0156-8
Kunter, M., and Voss, T. (2013). “The model of instructional quality in COACTIV: A multicriteria analysis,” in Cognitive activation in the mathematics classroom and professional competence of teachers. Results from the COACTIV project, eds. M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss and M. Neubrand (New York, NY: Springer). 97–124. doi: 10.1007/978-1-4614-5149-5_6
Lipowsky, F., Rakoczy, K., Pauli, C., Drollinger-Vetter, B., Klieme, E., and Reusser, K. (2009). Quality of geometry instruction and its short-term impact on students' understanding of the Pythagorean Theorem. Learn. Instr. 19, 527–537. doi: 10.1016/j.learninstruc.2008.11.001
Lüdtke, O., Robitzsch, A., Trautwein, U., and Kunter, M. (2009). Assessing the impact of learning environments: how to use student ratings of classroom or school characteristics in multilevel modeling. Contemp. Educ. Psychol. 34, 120–131. doi: 10.1016/j.cedpsych.2008.12.001
Marsh, H. W. (2007). Self-Concept Theory, Measurement and Research into Practice: The Role of Self-Concept in Educational Psychology. Leicester: British Psychological Society.
Marsh, H. W., Lüdtke, O., Robitzsch, A., Trautwein, U., Asparouhov, T., Muthén, B., et al. (2009). Doubly-latent models of school contextual effects: integrating multilevel and structural equation approaches to control measurement and sampling error. Multivariate Behav. Res. 44, 764–802. doi: 10.1080/00273170903333665
Müller, K., Prenzel, M., Seidel, T., Schiepe-Tiska, A., and Kjaernsli, M. (2016). “Science teaching and learning in schools: theoretical and empirical foundations for investigating classroom-level processes,” in Assessing Context of Learning. An International Perspective, eds S. Kuger, E. Klieme, N. Jude, and D. Kaplan (New York, NY: Springer), 423–446.
Murdock, T. B., and Miller, A. (2003). Teachers as sources of middle school students' motivational identity: variable-centered and person-centered analytic approaches. Element. Sch. J. 103, 383–399. doi: 10.1086/499732
Muthén, L. K., and Muthén, B. O. (1998). Mplus User's Guide. Sixth Edition. Los Angeles, CA: Muthén & Muthén,. (1998-2011).
NCTM National Council of Teachers of Mathematics. (2000). Principles and Standards for School Mathematics: An Overview. Reston, VA: National Council of Teachers of Mathematics.
OECD Organisation for Economic Co-operation, and Development. (2013). PISA 2012 Results: What Makes Schools Successful? (Vol. IV). Paris: OECD Publishing.
OECD Organisation for Economic Co-operation and Development. (2014). PISA 2012 Technical Report. Paris: Organisation for Economic Co-operation and Development Publishing.
Parker, P. D., Marsh, H. W., Ciarrochi, J., Marshall, S., and Abduljabbar, A. S. (2014). Juxtaposing math self-efficacy and self-concept as predictors of long-term achievement outcomes. Educ. Psychol. 34, 29–48. doi: 10.1080/01443410.2013.797339
Pekrun, R., Vom Hofe, R., Blum, W., Frenzel, A. C., Goetz, T., and Wartha, S. (2007). “Development of mathematical competencies in adolescence: The PALMA longitudinal study,” in Studies on the Educational Quality of Schools: The Final Report on the DFG Priority Programme, ed. M. Prenzel (Münster: Waxmann), 17–38
Pianta, R. C., and Hamre, B. K. (2009). Conceptualization, measurement, and improvement of classroom processes: standardized bbservation can leverage capacity. Educ. Res. 38, 109–119. doi: 10.3102/0013189X09332374
Pintrich, P. R., Marx, R. W., and Boyle, R. A. (1993). Beyond cold conceptual change: the role of motivational beliefs and classroom contextual factors in the process of conceptual change. Rev. Educ. Res. 63, 167–199. doi: 10.3102/00346543063002167
Praetorius, A.-K., Klieme, E., Herbert, B., and Pinger, P. (2018). Generic dimensions of teaching quality: the German framework of Three Basic Dimensions. ZDM 50, 407–426. doi: 10.1007/s11858-018-0918-4
Praetorius, A.-K., Pauli, C., Reusser, K., Rakoczy, K., and Klieme, E. (2014). One lesson is all you need? Stability of instructional quality across lessons. Learn. Instr. 31, 2–12. doi: 10.1016/j.learninstruc.2013.12.002
Rubin, D. B. (1987). Multiple Imputation for Nonresponse in Surveys. New York, NY: J. Wiley & Sons. doi: 10.1002/9780470316696
Schiepe-Tiska, A. (2013). In the power of flow: The impact of implicit and explicit motives on flow experience with a special focus on the power domain (Dissertation). Technical University of Munich, Munich. Available online at https://mediatum.ub.tum.de/doc/1128674/1128674.pdf
Schiepe-Tiska, A., Heine, J.-H., Lüdtke, O., Seidel, T., and Prenzel, M. (2016a). Mehrdimensionale Bildungsziele im Mathematikunterricht und ihr Zusammenhang mit den Basisdimensionen der Unterrichtsqualität [Multi-dimensional educational goals in mathematics classrooms and their relationship with instructional quality]. Unterrichtswissenschaft 44, 211–225. doi: 10.3262/UW1603211
Schiepe-Tiska, A., Reiss, K., Obersteiner, A., Heine, J.-H., Seidel, T., and Prenzel, M. (2013). “Mathematikunterricht in Deutschland: Befunde aus PISA 2012 [Mathematics instruction in Germany: Results from PISA 2012],” in PISA 2012. Fortschritte und Herausforderungen in Deutschland [PISA 2012. Advances and challenges in Germany], eds. M. Prenzel, C. Sälzer, E. Klieme and O. Köller (Münster: Waxmann), 123–154.
Schiepe-Tiska, A., Roczen, N., Müller, K., Prenzel, M., and Osborne, J. (2016b). “Science-related outcomes: attitudes, motivation, value beliefs, strategies,” in Assessing Context Of Learning. An International Perspective, eds S. Kuger, E. Klieme, N. Jude, and D. Kaplan (New York, NY: Springer), 301–330.
Snow, R. E., and Lohman, D. F. (1984). Toward a theory of cognitive aptitude for learning from instruction. J. Educ. Psychol. 76, 347–376. doi: 10.1037/0022-0663.76.3.347
Teig, N., Scherer, R., and Nilsen, T. (2018). More isn't always better: the curvilinear relationship between inquiry-based teaching and student achievement in science. Learn. Instr. 56, 20–29. doi: 10.1016/j.learninstruc.2018.02.006
Vandenberg, R. J., and Lance, C. E. (2000). A review and synthesis of the measurement invariance literature: suggestions, practices, and recommendations for organizational research. Org. Res. Methods 3, 4–69. doi: 10.1177/109442810031002
Wagner, W., Göllner, R., Helmke, A., Trautwein, U., and Lüdtke, O. (2013). Construct validity of student perceptions of instructional quality is high, but not perfect: dimensionality and generalizability of domain-independent assessments. Learn. Instr. 28, 1–11. doi: 10.1016/j.learninstruc.2013.03.003
Wagner, W., Göllner, R., Werth, S., Voss, T., Schmitz, B., and Trautwein, U. (2016). Student and teacher ratings of instructional quality: consistency of ratings over time, agreement, and predictive power. J. Educ. Psychol. 108, 705–721. doi: 10.1037/edu0000075
Keywords: multidimensional goals, teaching quality, classroom management and discipline, teacher support, cognitive activation, mathematics, tracking, PISA 2012
Citation: Schiepe-Tiska A (2019) School Tracks as Differential Learning Environments Moderate the Relationship Between Teaching Quality and Multidimensional Learning Goals in Mathematics. Front. Educ. 4:4. doi: 10.3389/feduc.2019.00004
Received: 21 August 2018; Accepted: 15 January 2019;
Published: 31 January 2019.
Edited by:
Jesus de la Fuente, University of Navarra, SpainReviewed by:
Drew Gitomer, Rutgers University, The State University of New Jersey, United StatesBuket Akkoyunlu, Çankaya University, Turkey
Copyright © 2019 Schiepe-Tiska. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anja Schiepe-Tiska, c2NoaWVwZS10aXNrYUB0dW0uZGU=
 Anja Schiepe-Tiska
Anja Schiepe-Tiska