Individual Differences in Fourth-Grade Math Achievement in Chinese and English

Language has been widely acknowledged as a determining factor in mathematical achievement. Less understood, however, is the relationship between students' language and their performance on tests of mathematics when taking into consideration the presence of mathematical difficulties. We investigated the effects of two different language systems, Chinese and English, on the mathematical performance of fourth-grade (or age equivalent) students (N = 23,220) with varying levels of demonstrated mathematical and reading ability. For this investigation, we used a subset of the 2011 Progress in International Reading and Literacy Study (PIRLS) and Trends in International Mathematics and Science Study (TIMSS) from students who were tested in Chinese or English in nine countries. Findings from hierarchical linear modeling (HLM) analyses revealed that the main effect of language on mathematical performance remained significant once variables for mathematical ability were added to the model. Further, significant language-by-mathematical ability interactions were observed when controlling for country, gender, maternal education, and age. Thus, the effect of language on mathematical performance may be especially salient in the presence of mathematical difficulties. Implications of these findings include the need for further investigations of language and its effects on mathematical performance for Chinese- and English-speaking students in order to clarify how this relationship may vary within specific language populations.

Introduction

Despite the assumed relative universality of mathematical knowledge and algorithmic processes, the effectual relationship between math performance and numerical language has been well established (Miller et al., 2005). Many investigations into the cross-national/linguistic differences in math performance focus on Chinese and English speaking populations, and there is considerable evidence that children in China, Taiwan, Singapore, and Hong Kong, historically and currently outperform students in Australia, Ireland, Canada, England, Scotland, and the U.S.; these consistent, and even dramatic, differences in math achievement (Peak, 1996, 1997; Mullis et al., 2016) have been attributed to a number of child and contextual factors, including maturation, caregiver values and beliefs, instructional method, and the degree of transparency of the number naming system.

Cross-linguistic researchers have hypothesized that less transparent number naming systems (i.e., languages in which there are a larger number of unique, irregular, or opaque words for numbers and mathematical concepts) may be more difficult to learn than more obvious number naming systems (i.e., language systems in which number names are more logically ordered to include names of earlier numbers and mathematical concepts are more readily understood from numerical language), and such differences have been found to have an effect on the mathematical performance of children (e.g., Miller et al., 1995, 2004; Göbel et al., 2014) and number processing of adults (Moeller et al., 2015). However, what is less understood is whether the linguistic influences on mathematical learning play out equally for all speakers of a language, or if numerical language is particularly influential on subsets of learners—such as students who have difficulty in math.

Within the parallel field of reading development, it is well understood that the processes required for reading are language specific (e.g., Seymour et al., 2003; Frost, 2005). For example, learning to read in transparent (more consistently spelled according to distinct sounds represented; e.g., Spanish, Finnish, Welsh) alphabetic writing systems develops more quickly than in opaque (less transparent; English, French, Portuguese) alphabetic orthographies. Furthermore, learning to read in a logographic writing system, such as Chinese, may be uniquely demanding, as the learner acquires symbol/sound relationships as well as memorizes thousands of written characters that directly correspond to meaning (Perfetti et al., 2005; Tan et al., 2005).

However, the effect of orthographic depth (which characterizes alphabetic languages) on reading development has also been found to have the most powerful effect on students who have the most difficulty learning to read; specifically, higher rates of reading impairment have been observed in students who speak orthographically opaque languages such as English compared to students who speak more transparent languages such as Spanish (Caravolas, 2005). This unique effect of language on lower-performing students' reading development is evidenced in a study by Hanley et al. (2004): 6- and 7-year-old Welsh-speaking children, who were learning to read in the highly predictable Welsh orthography, performed significantly better on reading measures than Welsh English-speaking children learning to read in English. However, after these students had reached their sixth year of formal instruction, while the majority of the English-speaking children had caught up to their Welsh-speaking counterparts on word reading (and even had significantly greater reading comprehension skills), the lowest performing 25% of English readers continued to perform significantly below the lowest performing 25% of Welsh readers on all measures of reading achievement.

Similarly, researchers have investigated the cognitive underpinning of reading difficulty in Chinese and compared results to those in alphabetic languages (Bolger et al., 2005). For example, Siok et al. (2004) found that reading impairment in Chinese was specific to the logographic nature of the writing system—pointing to the possibility that it is possible to have reading difficulty in Chinese but not in English, or vice versa, depending on the individual's pattern of cognitive strengths and weaknesses that manifest according to the linguistic context.

Thus, while the association between domain-specific achievement and language has been observed for both math and reading, little is known about whether the challenges associated with learning math in the context of relatively opaque numerical language such as English (compared to Chinese) may be unique for the subset of students with the most difficulty learning math. Research in reading (e.g., Hanley et al., 2004) draws attention to the possibility that the linguistic influences on math competencies might be the most profound and long lasting for students with the lowest performance in math.

While we acknowledge the complex set of influences on math achievement, our focus here is on language. Specifically, we are interested in the possibility that Chinese and English numerical language may differentially affect students with the lowest demonstrated math ability. For this study, we aimed to further clarify differences in math performance that have been consistently observed across languages (e.g., Peak, 1996, 1997; Miller et al., 2005; Göbel et al., 2014). Specifically, we asked the following research questions:

(1) What is the relationship between math performance and language for children who demonstrate high vs. low levels of mathematical skill?

(2) What is the relationship between math performance and language for students who are dominant Chinese and English speakers?

We employed a subset of the 2011 Progress in International Reading and Literacy Study (PIRLS) and Trends in International Mathematics and Science Study (TIMSS) that included Chinese- or English-speaking students (N = 23,220) in order to investigate the relationships between language, math difficulty, and co-occurring reading and math difficulty at the fourth grade level. We posited that greater descriptive ambiguity in the relationship among mathematical concepts and the English words used to label them places additional demands on the learner and can therefore compromise or slow down fourth grade mathematical performance in English relative to Chinese. Furthermore, mathematical weaknesses, whether cognitive (Imbo et al., 2014) or due to environmental factors may be exacerbated when there is relatively less obviousness between mathematical concepts and the language used to represent them.

Learning to count base-10 Arabic numerals is a universal early math skill (Miller et al., 1995). However, the way in which labels or names map on to numerical items and the connotations implied to such items differ across languages (Hurford, 1975, 1987). For example, the word/character for “triangle” in Chinese is “三角,” which literally translates as “three cornered shape.” The first portion of this word (三) is the number 3, which is highly accessible to younger students due to the intuitive connections with the three lines represented. The English word “triangle” has a less transparent connection with the shape; one must understand that the morpheme “tri” indicates the meaning of three. Such linguistic differences may have a great impact on student learning of mathematical content like geometry (Miller et al., 2005).

Differences in Math Achievement in Chinese and English

Variation in Chinese and English Number Naming Systems

Although cross-linguistic differences in achievement have been attributed to differences in culture (Stevenson et al., 1986), curricula, and instruction (Stigler et al., 1982; Stevenson and Stigler, 1992) and language ideology (Arya et al., 2015), there is considerable evidence that variability in math performance in young children is, at least in part, associated with the variation in number naming systems. Such variation is thought to affect the relative ease and effectiveness with which children develop, access, store, and manipulate mathematical information (Miller et al., 1995; Imbo et al., 2014).

A comparison of the Chinese and English number naming systems highlights the characteristics of language that may affect the acquisition of math skills. Counting to 10 in both languages, for example, is similar in that the words used are unique to each number (Miller et al., 1995). However, after 10, the two languages differ in terms of the degree to which the names for larger numbers systematically include the same names used for the earlier numbers. Overall, the Chinese system is more morphographically obvious (as previously described) and involves less modification of the unit value number names (or fewer additional unique names) in larger numbers than the English system. For example, the Chinese names for numbers “11” and “12” are the equivalent to stating the name for “10” plus the name for the additional amount (ten-one; ten-two, etc.). This system is more obvious than the English system, which involves unique names (eleven, twelve, etc.). Thus, in Chinese, counting involves memorizing only the number names for 1 through 10 and then applying the base-10 rules to generate larger numbers (Okamoto, 2017). Furthermore, because counting and number representation are foundational to higher-level math skills, variability in the characteristics of number naming systems that affects these basic skills may have a long-term effect on achievement (Miller et al., 2004). In this study, we hypothesize that students with relatively weak or imprecise mathematical knowledge (compared to their peers who speak the same language) will face an additional challenge to mathematical learning when learning in the context of ambiguous or irregular numerical language (i.e., English compared to Chinese). Furthermore, we posit that specific weaknesses in mathematical understanding may be exacerbated by less obvious (i.e., less concretely descriptive) number naming systems within a given language context. As such, assessment items that feature words along with numbers to probe mathematical knowledge (including written directions and word problems) may present greater challenges when such inscriptions are less transparent.

Language Influences on Math Performance

Dramatic differences in math achievement in Chinese and English have been observed (e.g., Husen, 1967; Stevenson et al., 1986; Travers et al., 1987). For example, children in China have been shown to outperform U.S. children as early as preschool, which has been attributed in part to the relative transparency of the Chinese number naming system (Miller et al., 1995). Indeed, students from Chinese-speaking countries (e.g., China, Taiwan, Singapore, and Hong Kong) continue to score consistently higher than students from English-speaking countries (e.g., Australia, the U.S., Ireland, Scotland, and England) on international measures of fourth-grade mathematics achievement (Peak, 1996; TIMSS, 2011); and such differences have been found to increase as students advance throughout schooling (Stevenson et al., 1998; OECD, 2010). However, it is important to acknowledge the well-documented differences in curricula, instructional approaches, parental support, language ideologies, and educational systems between Asian and English-speaking countries, which undoubtedly contribute to observed differences in achievement (e.g., Stigler et al., 2000; Hiebert et al., 2003, 2005; Arya et al., 2015). Language is certainly only one of many contributors to cross-national and cross-linguistic differences in math achievement.

Findings from several cross-linguistic studies suggest an association between number names and math development when comparing Chinese and English. For example, Miller and Stigler (1987) found differences in math skill between the two languages emerged prior to any formal schooling, thus potentially ruling out the possibility that cross-national differences could be attributed to variation in instructional method. Moreover, Miller et al. (2004) found in their longitudinal study that differences in skill acquisition between Chinese and English could be observed precisely at the point in development when children are first learning numbers between 10 and 20, the point from which the consistency of the two number naming systems differ according to naming obviousness. Miller and colleagues conducted monthly “counting task” sessions with preschool-aged children in China and the United States. Beginning at age two, children from both countries demonstrated equally slow and error prone performance, and that there were no language differences in the ability to count to 10 for three or four year olds. However, by age three, the Chinese group made rapid progress in learning to count accurately between 10 and 20 compared with the American children. Furthermore, by age four, after the Chinese children had learned to count past 40, they were more readily able than the American children to generalize from the consistent Chinese number naming rules to count to 100. These researchers also concluded that the ability to accurately and rapidly name numbers and count may support higher-level math skills.

Differences in arithmetical skills (Miura et al., 1988; Fuson and Kwon, 1992), such as borrowing and carrying and math processing (Moeller et al., 2015) have been observed in Chinese/English comparisons as well as across other languages. Furthermore, there is some indication that individual differences demonstrated within a given linguistic context must be considered when investigating students' mathematical abilities. For example, Imbo et al. (2014) compared French and Dutch speaking children and found that both cognitive resources and language to played a role in number processing. Similarly, Miura (1987) and Miura and Okamoto (1989) showed that children who spoke relatively regular (e.g., Chinese and Japanese) vs. irregular (English and Swedish) number names developed different mental constructions of numbers, and argue that Chinese-based number systems uniquely influence how children mentally represent numbers.

However, while many researchers exploring cross-linguistic influences on arithmetic performance have controlled for general cognitive abilities (e.g., Helmreich et al., 2011), to our knowledge little is known about whether students with particular cognitive profiles are more or less sensitive to the relative ambiguity in the math language environment. Thus, what continues to be less clear from all the research presented thus far is whether this effect of numerical language (specifically, in this case, Chinese versus English) is the same for all students or whether the characteristics of numerical language may be particularly advantageous (Chinese) or detrimental (English) for students who already have difficulties in the domain of mathematical learning. That is, do students with weak, or imprecise representations of number and/or mathematical concepts (for any reason—e.g., lack of exposure or practice, instructional method, cognitive impairment) encounter an additional and/or ongoing obstacle to math fluency when learning in less obvious numerical language?

Mathematics Difficulty

A considerable number of children have been found to have difficulty with number representation (i.e., number symbols, number names, and their corresponding magnitudes; Geary et al., 1999, 2004; Passolunghi and Siegel, 2004; Rousselle and Noël, 2007), the conceptual understanding of counting (Geary et al., 1992), counting speed (Passolunghi and Siegel, 2004), counting strategies (Goldman et al., 1988), monitoring the counting process (Jordan and Montani, 1997), and storing and retrieving number problems and solutions during mental arithmetic (Geary, 1993).

This research has typically compared the cognitive profiles and mathematics performance of three groups: (1) children with math difficulty alone (math only), (2) children with co-occuring math and reading difficulty (math/reading), and (3) control children. The goal in studying these subgroups has been to identify and describe “pure” math impairment, and to acknowledge and elucidate the challenges faced by those children who have difficulty with both math and reading. For example, in a longitudinal study, Jordan et al. (2003) compared these three subsets of children. They found that the math-only group demonstrated significantly slower and less accurate calculation strategies with difficulty drawing on numerical information from memory. While the math/reading group was observed to have similar problems, their demonstrated weaknesses were even more severe compared with the math-only and control groups, suggesting that in addition to arithmetical challenges, phonological weaknesses may also contribute to mathematics performance; thus, linguistic ability (i.e., phonological processing) may also play a significant role in math ability, both of which in turn may play a role in learning new and higher-level math skills.

Thus, it stands to reason that English-speaking children who demonstrate math difficulty might encounter additional detrimental effects (relative to Chinese-speaking children) of learning math via language that less transparently corresponds to number names and symbols and the magnitudes and concepts they represent, which may lead to later weakness in engaging more complex calculations and problem-solving strategies.

The Current Study

We aimed to explore the relationship between math and reading ability and language by examining data at the fourth-grade level. Guided by previous research on math impairment (e.g., Swanson and Jerman, 2006) and cross-national (Peak, 1996, 1997) and cross-linguistic (Miller et al., 2005) differences in math performance, we selected variables from two large international databases, 2011 Progress in International Reading and Literacy Study (PIRLS) and Trends in International Mathematics and Science Study (TIMSS), to investigate our research questions about fourth-grade Chinese- and English-speaking children living in nine countries (N = 23,220). Specifically, we investigated the potential unique and lasting challenges of ambiguous numerical language on math learning for the lower performing students—by comparing Chinese and English results from the TIMSS Geometric Shapes and Measures and Data Display assessments.

Methods

Sample and Data

Sample

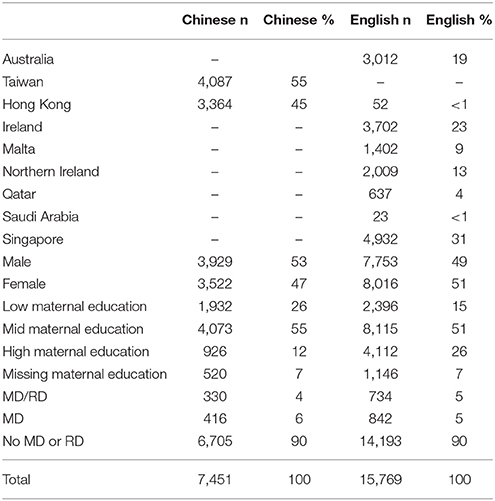
The sample includes 23,220 fourth-grade (or age equivalent 9.5–10.5) students from Australia, Taiwan, Hong Kong, Ireland, Malta, Northern Ireland, Qatar, Saudi Arabia, and Singapore who took part in 2011 PIRLS and TIMSS in Chinese or English. Students were included in this study if they took both assessments in either Chinese or English and spoke the language of the test at home (as indicated on a home survey). Thus, bilingual or multilingual students were dropped if they had a primary language other than the test language at home (Australia 6%, Taiwan 3%, Hong Kong 2%, Ireland 5%, Malta 5%, Northern Ireland, 1%, Qatar 44%, Saudi Arabia 65%, and Singapore 8%). Less than one percent of students who met our inclusion criteria were excluded because of missing data. To clarify, PIRLS, and TIMSS were not given in China, and students in the U.S. sat for either PIRLS or TIMSS, but not both assessments. As such these countries they were excluded from this study.

Data

The TIMSS and PIRLS assessments are conducted by the International Association for the Evaluation of Educational Achievement (IEA), and funded by the participating countries with support from the World Bank and the U.S. Department of Education's National Center for Educational Statistics (NCES; Martin and Mullis, 2012). Occurring every four (TIMSS) and five (PIRLS) years at the fourth-grade level (or its national equivalent), these assessment instruments are intended to provide internationally comparable information about mathematics, science, and reading literacy. In 2011, the TIMSS and PIRLS implementation came into alignment for the first time, and 34 countries took the opportunity to administer both TIMSS and PIRLS to the same students.

In using TIMSS and PIRLS datasets, our study involved only passive observation of publically available data, which did not contain identifying information, and thus ethics approval was not required per our institutional guidelines or national regulations.

Sampling Methodologies

All countries used a uniform sampling approach that followed international guidelines and specifications to ensure that differences in national achievement outcomes could not be attributed to the use of different sampling methodologies. Two-stage stratified sample designs were used, and probability samples were drawn from target populations (i.e., populations with the language as either English or Chinese) in each country (Mullis et al., 2009).

Participant Criteria

The TIMSS and PIRLS participants were representative samples of students in approximately their fourth year of formal schooling and who were between the ages of 9.5 and 10.5 who sat for both tests during the fall of 2011. Candidate participants for both studies are required to be able to follow basic instructions on the tests, and be able to read or speak the language of the test. Students with dyslexia and other learning disabilities were encouraged to participate in both PIRLS and TIMSS. The number of students excluded based on the above criteria did not exceed 5% in any country (Mullis et al., 2009).

Translation

In any cross-national study, it is critical that the measures are reliable and contain comparable information across languages. The development of TIMSS and PIRLS included exhaustive procedures to verify that the translation of the assessments corresponded to international standards, and to ensure equality across languages. Translation was provided for the test directions, passages, and items, student, home, and school questionnaires, directions for preparing and administering the assessment at schools, and scoring guides for students' open response questions (Mullis et al., 2009).

Math Achievement

In this study, math achievement was based on standardized performance (M = 0, SD = 1) on two of the three TIMSS content domains: Geometric Shapes and Measures (GSM) and Data Display (DD). In the GSM subsection, performance included the ability to measure and compare length, area, volume, and angle by drawing on knowledge about which units to use in each context. Students were required to approximate and estimate, and they used mathematical formulas to calculate the perimeter of rectangles and the volume of geometric figures. Data Display involved organizing, interpreting, and representing data. For example, students had to compare different types of data to make inferences, answer questions, and draw conclusions.

The development and validity check of the TIMSS achievement measures involved the use of item response theory (IRT), which enables the ability to analyze the relative level of difficulty of each individual item within a single measure and to use this information to determine the internal consistency of a given measure for the targeted domain of knowledge (e.g., Geometric Shapes). TIMSS measures were developed in workshops within the representative countries by respective researchers and educators who reviewed the items and passages extensively. The TIMSS assessment in this study was comprised of two domains: Geometric Shapes and Measures (GSM) and Data Display (DD). Each of these cognitive domains captured a range of processes involved in math problem solving: Knowing, Applying, and Reasoning. The format of the TIMSS items was multiple-choice and constructed-response. Overall reliability of all math items were estimated within the range of α = 0.80–0.89. Reliability estimates for specific math subtests were not available.

Comparison Groups

Drawing on previous research (e.g., Swanson and Jerman, 2006), we compared the math performance (i.e., GSM and DD) of three groups of students: (1) students with math difficulty (MM) only, (2) students with both math and reading difficulty (MD/RD), and (3) students with average or above average math performance (not MD or MD/RD) in Chinese and English. In each language, we included approximately the same percentage of children in these groups. The specific grouping criteria are described below.

Mathematics Difficulty (MD)

Having difficulty in math (only) was determined by student performance on the Number content domain of the TIMSS assessment. This subsection measured number representation, knowledge of place value, and the relationship between numbers. Students demonstrated an understanding of and computational fluency in addition, subtraction, multiplication, and division. This subsection of the TIMSS for fourth grade is considered to be the most basic and foundational of all the subsections (cf., TIMSS, 2011) and is thus a useful (albeit limited) proxy for potential math difficulty. Further, using the Number domain subsection as an indicator of math difficulty aligns with previously described studies that documented the long-term effects of basic computational ability on the performance of more complex tasks (cf., Miller et al., 2004). Math difficulty was operationalized as being above the 10th percentile in reading (see below) but below the 10th percentile on the Number subsection within his or her language group. These criteria were within the range of scores used to operationalize mathematics difficulty in previous research (below the 48–8th percentile on various math measures; Swanson and Jerman, 2006). (The development of TIMSS is described in the section above.).

Co-occurring Math and Reading Difficulty (MD/RD)

Students with co-occuring MD/RD performed below the 10th percentile on the Number subsection of TIMSS and below 10th percentile within his or her language group on a relatively simple measure of reading achievement: the PIRLS' “Straightforward Processing” subsection. This scale measured the reader's ability to answer questions about information explicitly stated in the text, a skill that largely relies on efficient word recognition, which, in turn, is supported by phonological processing (e.g., Vellutino, 1979). Specifically, students had to read the text, access meaning on a basic level, and retrieve information contained directly in the text (Mullis et al., 2009). The purpose of including this subgroup was for consistency with previous research that has examined the heterogeneous cognitive profiles associated with poor performance in math (e.g., Jordan et al., 2003; Swanson and Jerman, 2006).

The final version of the PIRLS reading assessment included texts that spanned many genres, including literary texts (e.g., short stories or episodes with illustrations), informational texts (e.g., biographies), and narratives and expositions (e.g., scientific, geographical, and procedural texts that included text boxes, photographs, maps, or diagrams; Mullis et al., 2009). Plausible values (i.e., estimates of student ability) were used to address issues of biased statistical inferencing and to allow the use of standard statistical tools to estimate population characteristics (Wu, 2005). Overall reliability of all reading comprehension items were estimated within the range of α = 0.86–0.91.

No MD or MD/RD

A final group of students were above the 10th percentile on the Number subsection of TIMSS—regardless of their reading ability.

Language

This variable denotes language of the test, the classroom instruction, and the student's home language, Chinese or English.

Student Background Characteristics

Drawing on previous research, we selected gender (e.g., Nosek et al., 2009; Pieng et al., 2016) and maternal education (Bradley and Corwyn, 2002) as control variables in this study. We also controlled for country because education systems and associated resources (e.g., sequence of, or approach to skills taught within a country's program or resources in school organizations within cities, districts, etc., and required or adopted school curricula) vary by country and age to ensure any cross-linguistic differences could not be explained by differences in maturation between language groups.

In the current study, students responded to the questions “when were you born” and “are you a boy or a girl,” and caregivers answered questions about maternal education. In order to simplify the analysis, the nine categories of mother's education in the TIMSS/PIRLS home survey were collapsed into low, middle, and high. The 7% of students with missing mother's education data were identified as their own category and were included in the analysis.

Analysis Approach

We employed chi-square tests of independence to determine if there were differences in the samples by language group (Chinese vs. English). Then, to investigate the main effect of language on math achievement (and corroborate previous research) standardized values of GSM and DD were regressed on control variables for country, age, sex, and maternal education, and a dummy variable for English (i.e., 1 = English, 0 = Chinese). An additional set of regression models addressed the purpose of our study by considering a set of dummy variables for math ability and language by math ability interactions in the analysis. We also compared ordinary regression models to hierarchical linear models (HLM) with likelihood ratio tests because students were nested in schools.

Results

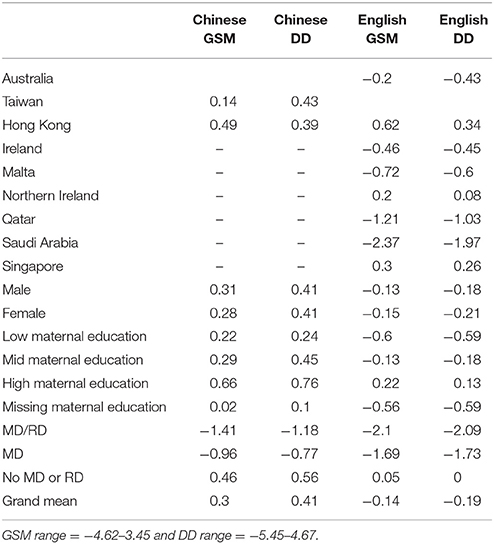
Results from initial chi-square tests showed that the Chinese- and English-speaking samples we roughly comparable in terms of student background characteristics. The only exception was that considerably more English-speaking students (26%) came from families in which the mother earned high degrees in education compared to their Chinese counterparts (12%; p < 0.001). As per the study design, the percentages of students with MD and MD/RD in both samples were consistent. The results from the descriptive statistics suggest that the language groups in each country performed consistently the same on GSM and DD in respect to whether or not they were above or below the grand mean. However, there was considerably more variability in the English scores across countries, than the Chinese scores, partly because there were simply more countries that that took the test in English (n = 8) compared to Chinese (n = 2). Table 1 provides descriptive statistics related to student demographics and Table 2 provides the mean scores on the GSM and DD subtests by subgroup.

TABLE 1

Table 1. Participants by Language.

TABLE 2

Table 2. Mean scores on geometric shapes and data display by language.

Based on the multilevel structure of TIMSS data (i.e., students nested within specific schools), likelihood-ratio tests were conducted, comparing ordinary regression to HLM models in order to investigate whether a random intercept for school was needed. Because all of the tests were significant, random intercepts for schools were included in all models. As a result, HLM models emerged as the best fitting to the data in all analyses, which we then presumed was the most appropriate analytic method to investigate cross-linguistic differences in math performance as a function of mathematical ability (Rabe-Hesketh and Skrondal, 2005). However, because the multilevel data structure was not the focus of this investigation, we do not discuss the multilevel aspects of our results further. Instead, we focus on interpreting the variables of interest in this study.

Table 3 provides the results from four models: Model (1) GSM was regressed on “English” (i.e., a dummy variable: English = 1, Chinese = 0) and the control variables, (2) GSM was regressed on English and the MD and MD/RD by English interactions and the control variables, (3) DD was regressed on “English” and the control variables, and (4) DD was regressed on English and the MD and MD/RD by English interactions and the control variables.

TABLE 3

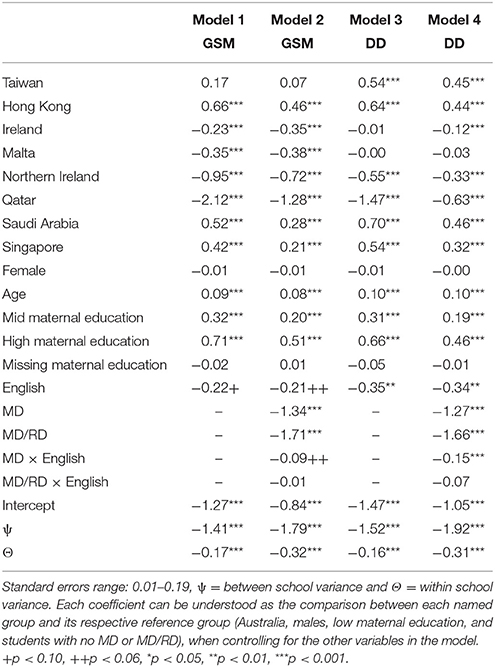
Table 3. Fixed effects estimates and variance-covariance estimates for models of the predictors of fourth-grade mathematics achievement (standardized geometric shapes and data display) on the TIMSS 2011 assessment.

Hierarchical linear modeling (HLM) analyses revealed a significant main effect of language on DD (p < 0.01; β = −0.34) and a borderline significant relationship between language and GSM (p < 0.06; β = −0.21) such that students who learned math in English were on average performing below students who learned in Chinese, (e.g., Peak, 1996, 1997). While there were no notable differences between Chinese- and English-speaking students with MD/RD, there were significant language by mathematics ability interaction effects, while controlling for country, gender, maternal education, and age. English-speaking students with only MD performed considerably below Chinese-speaking students with MD on DD (p < 0.001; β = 0.15) and GSM (p < 0.06; β = 0.09); while English-speaking students as a whole were, on average, 0.34 of a standard deviation below their Chinese-speaking counterparts on DD, there was an additional negative effect (−0.15 of a standard deviation) for English-speaking students with poor demonstrated math ability. Or, in other words, as students approached the tail end of the distribution, the gap between English and Chinese performance widened. This result is notable given that Singapore, in South East Asia, was the largest contributor to the English-speaking sample (31%).

Finally, results related to the control variables echoed findings from previous research in that students from families with relatively high maternal education outperformed lower maternal education students, and developmental maturity (age) was related to achievement such that older students had higher average scores than younger students. Gender was not related to achievement. Finally, the four top performing countries were Singapore and Saudi Arabia and Hong Kong and Taiwan. The lowest five countries were all English speaking (Malta, Qatar, Ireland, Northern Ireland, and Australia). Additionally, consistent with the descriptive statistics, even when accounting for the control variables, there were small differences in math performance in Hong Kong compared to Singapore (when students took the test in Chinese), and wide variability across the English students by country. However, even when taking into account the effects of country, age, and maternal education, and language, the additional joint effect of language and demonstrated math ability was consistently associated with math achievement.

Discussion

We aimed to investigate the potential impact of Chinese and English numerical language on fourth-grade mathematics learning, especially for students who were underperforming in math. Consistent with previous research, our findings suggested that, on average, Chinese-speaking students have stronger math performance compared with their English-speaking counterparts (Peak, 1996, 1997; Mullis et al., 2016). However, we also found preliminary evidence of an additional gap between Chinese and English math performance for students who were relatively proficient in reading but had the poorest math ability.

There are several limitations to this study. First, all findings are bound to the respective conceptual definitions and development of the PIRLS and TIMSS measures and procedures, which naturally constrains our approach for investigating explanatory variables (MD, MD/RD). Second, the TIMSS measures may lack the sensitivity needed to detect subtle differences between students with MD and those with co-occurring MD/RD. These weaknesses are balanced by the fact that large-scale datasets such as PIRLS and TIMSS provide the opportunity to investigate the relationship between math ability and language at a scale that is inaccessible to most individual researchers.

Third, as mentioned, it is not possible to account for the differences in instructional approaches and curricular sequences for math that may vary as a function of language and culture. This limitation is somewhat mitigated by the inclusion of control variables for country and random intercepts for schools, which controls for unobserved classroom-level variables (Rabe-Hesketh and Skrondal, 2005). Additionally, a significant weakness of our study is that only one country from the entire database administered the tests in both languages; as such, language may be confounded with country and/or culture for this particular investigation. However, notably, Singapore, in South East Asia, was the largest contributor to the English-speaking sample (31%), which supports the possibility that cross-language differences in our study are due to language differences rather than cultural differences.

Fourth, although both TIMSS and PIRLS made considerable efforts to make sure that the assessments were comparable across languages, it is quite possible that there were significant differences between the tests in the two languages (Flores, 2016), which is an especially important consideration given that the TIMSS math problems were given in a language context—most items included written directions and/or word problems. The fact that the tests were written in English and translated into Chinese could have considerable advantages/disadvantages for students, with the additional possibility that translation effects could uniquely influence students in the MD and MD/RD groups relative to the students without any MD. One additional point to consider, however, is that the fact that items originally constructed in English version would theoretically give students who took the assessment in English an advantage, which was not the case based on our findings. As such, we believe that the likelihood of problematic differences in test versions to have a minimal impact on performance.

Lastly, this study focused on cross-linguistic differences in math performance; however, it is quite possible that because the ability to solve a math problem is necessarily dependent on reading—e.g., comprehension of the directions or words in a word problem—there may be differences between Chinese and English math performance that are due to differences in orthographies (Perfetti et al., 1992) instead of, or in addition to, how numbers are represented and therefore processed in each language. However, the influence of orthographic differences on math performance was beyond the scope of this study. Yet, since we included an assessment of student reading skills, we were able to distinguish between students who seemed to have difficulty in math due to poor reading skills versus students who had domain-specific difficulties in math.

Despite all described limitations, several tentative conclusions can be drawn from this study. Our results corroborate previous research showing notable cross-linguistic differences in fourth-grade mathematics achievement between Chinese- and English-speaking students (e.g., Peak, 1996), The significant MD by language interaction (coupled with the non-significant MD/RD by language interaction) seen consistently across both the Geometric Shapes and Data Display domains does raise the possibility of a continuing negative effect of learning math in the English for students with the poorest demonstrated levels of math ability. Surprisingly, the interaction between ability and language was unique to the MD group (and not the MD/RD group). One explanation is that students with MD/RD struggle with math mainly because of their poor reading skills (e.g., they have trouble reading directions or understanding word problems). Thus, they are not slowed down or confused by the relative irregularity of the English number system, but are limited by their weaknesses that are relatively specific to reading. In contrast, students with MD alone, who demonstrate that they are more proficient in reading, presumably struggle with basic math skills such as retrieving, holding, and acquiring number information during simple arithmetic (Geary, 1993). One logical conclusion, therefore, is that students who demonstrate weaknesses specific to math would be negatively (English) or positively (Chinese) affected by the degree of obviousness of their numerical language, which places differential demands on the learner. However, reading difficulties, which presumably influence math difficulties in the context of reading word problems in both languages, might not interact with the numerical characteristics of language in the same way as domain specific difficulties in math.

However, our finding that the MD/RD group did not demonstrate equal or even lower math performance than the MD group may be a contrast to previous research that has honed in on math impairment (e.g., Jordan et al., 2003; Swanson and Jerman, 2006) and suggests demonstrated weaknesses in math and reading are tied to the same underlying cognitive mechanisms (e.g., phonological processing, working memory) and students with both MD and RD tend to have even more difficulty in math (due to more significant impairment) than students with MD alone. However, in our study, in which we focused on the tail end of distribution of math performance in Chinese and English (and not specific math impairment), the effect of relatively ambiguous numerical language on math performance seemed to be the most (negatively) pronounced for the English-speaking students whose learning differences are specific to domain of math (not reading).

The MD by language interaction may shed even more light on findings from other comparative studies on English- and Chinese-speaking students. For example, according to responses from the international assessment, Test for Schools, which is a part of the Program for International Student Assessment (PISA, OECD, 2013), even the most disadvantaged 15-year-old Chinese students in Shanghai are outperforming middle and higher socioeconomic students in the U.S. This disparity in academic performance had been generally described as the result of country-specific differences in the areas of teacher content knowledge, dedication, and support (Friedman, 2013; OECD, 2013). However, variation in language (i.e., the degree of transparency of number naming systems) may explain variation in math performance (Miller et al., 1995), and, according to findings from this present investigation, this effect of language on math performance may be conditional on math ability.

MD-Specific Interactions

In this study, we investigated the role of language on math performance for students of varying math abilities. This study contributes to these findings by examining the role of math ability in differing linguistic environments. Difficulty in the area of math is not entirely uncommon and has been associated with the difficulty to master number skills (e.g., representing the meaning of numbers; Geary et al., 1999; Landerl et al., 2004). Logically speaking, weaknesses in number representation may be exacerbated by number naming systems that less transparently correspond to numerical magnitudes. The results from this study provide cautious support for the hypothesis that cross-national differences (in both geometry and data analysis) in performance may be due in part to the obviousness (or lack thereof) of number naming systems that continues to be an obstacle for students with the poorest ability. This MD -specific interactions suggests that the students with the poorest ability, who might be on the tail end of the distribution in terms of their ability to represent numbers, counts, and manipulate mathematical information, may be uniquely challenged by languages that less transparently correspond to mathematical concepts (i.e., English). Thus, it may be informative for researchers and educators to look at particular subgroups of learners when considering cross-national and cross-linguistic differences in achievement, and that countries that lag behind Asian countries may consider specific changes in practice that target underperforming learners. For example, it may be particularly useful for students who are struggling in math in English to engage in on-going learning activities that strengthen knowledge of how (irregular) two-digit number names map on to numerical magnitudes according to the base-10 system (Zhang and Okamoto, 2017); and, teachers can be mindful of how early ease or difficulty with the acquisition of number names and their corresponding magnitudes in English, may continue to play a role in learning more advanced mathematical concepts in, such as in geometry or data analysis. For example, a solid understanding of the underlying base-10 structure of decimals such as (0.90) may be the necessary foundation for learning probability and statistical inference. Likewise, awareness of the underlying morphological structure of English words, such as “bi,” “tri,” and “quad,” may be a prerequisite that dispels confusion around basic concepts and supports understanding of more complex concepts in geometry.

The Obviousness of Number Naming Systems

Less transparent number naming systems have been shown to inhibit math skills in for broad populations of children. The findings from this study show that that such opaque number systems may be specifically more cognitively demanding for student with poor math ability compared to systems that are more straightforward. Such variability in number words appears to be related to number representation, counting, and the ability to manipulate numerical information—which support higher-level math skills (such as geometry and data analysis). The word “rectangle,” for example, is the proper English representation of a long square shape, while in Chinese, the word for this shape is also a clear description; its Chinese counterpart, 長方形 is literally translated as “long square shape.”

Previous research that has suggested that cross-national disparities in achievement outcomes cannot be completely attributed to differences in educational systems (e.g., U.S. versus China); and, and that instruction to address student weaknesses could focus on making the base-10 structure of number names more readily accessible to students (Miller et al., 1995). This study augments these findings by further specifying that efforts to support students should also target students with the poorest math ability. Future investigations on the effect of language on math performance should include the varying levels of math ability. Further explorations, perhaps more qualitative in nature, might be helpful in unpacking the observed differences in mathematical performance for Chinese speaking students in Taiwan and Hong Kong; country-level differences may have more to do with differences in educational standards and practices.

As educators, researchers and other scholars continue to investigate the differences in math performance across the world, the catalytic factors for varying levels of performance will undoubtedly be revealed. Demonstrating or using one's math knowledge is impossible without language and, as revealed in this study, specific difficulties in the domain of math may play a determining role in how much one's language becomes a hurdle (e.g., English) or springboard (e.g., Chinese) for demonstrating such knowledge. Understanding the potential roadblocks and supports for students as they continue to develop math knowledge and skills will ultimately benefit learning and instructional practice, regardless of how one counts out loud.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer BDF and handling Editor declared their shared affiliation.

References

Arya, D. J., McClung, N. A., Katznelson, N., and Scott, L. (2015). Language ideologies and literacy achievement: six multilingual countries and two international assessments. Int. J. Multilingual. 13, 40–60. doi: 10.1080/14790718.2015.1021352

CrossRef Full Text | Google Scholar

Bolger, D. J., Perfetti, C. A., and Schneider, W. (2005). Cross-cultural effect on the brain revisited: universal structures plus writing system variation. Hum. Brain Mapp. 25, 92–104. doi: 10.1002/hbm.20124

PubMed Abstract | CrossRef Full Text | Google Scholar

Bradley, R. H., and Corwyn, R. F. (2002). Socioeconomic status and child development. Annu. Rev. Psychol. 53, 371–399. doi: 10.1146/annurev.psych.53.100901.135233

PubMed Abstract | CrossRef Full Text | Google Scholar

Caravolas, M. (2005). “The nature and causes of dyslexia in different languages,” in The Science of Reading: A Handbook, eds M. J. Snowling and C. Hulme (Oxford: Blackwell), 336–355.

Google Scholar

Flores, G. S. (2016). Assessing English Language Learners: Theory and Practice. New York, NY: Routledge.

Google Scholar

Friedman, T. L. (2013). My Little (Global) School. Available online at: https://www.nytimes.com/2013/04/03/opinion/friedman-my-little-global-school.html

Frost, R. (2005). “Orthographic systems and skilled word recognition processes in reading,” in The Science of Reading: A Handbook, eds M. J. Snowling and C. Hulme (Oxford: Blackwell), 272–295.

Google Scholar

Fuson, K. C., and Kwon, Y. (1992). “Effects of the system of number words and other cultural tools on children's addition and substraction,” in Pathways to Number: Children's Developing Numerical Abilities, eds J. Bideaud and C. Maljac (Hillsdale, NJ: Erlbaum), 127–149.

Geary, D. C. (1993). Mathematical disabilities: cognitive, neuropsychological and genetic components. Psychol. Bull. 114, 345–362. doi: 10.1037/0033-2909.114.2.345

PubMed Abstract | CrossRef Full Text | Google Scholar

Geary, D. C., Bow-Thomas, C. C., and Yao, Y. (1992). Counting knowledge and skill in cognitive addition: a comparison of normal and mathematically disabled children. J. Exp. Child Psychol. 54, 372–391. doi: 10.1016/0022-0965(92)90026-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Geary, D. C., Hoard, M. K., Byrd-Craven, J., and DeSoto, M. C. (2004). Strategy choices in simple and complex addition: contributions of working memory and counting knowledge for children with math disability. J. Exp. Child Psychol. 80, 121–151. doi: 10.1016/j.jecp.2004.03.002

CrossRef Full Text | Google Scholar

Geary, D. C., Hoard, M. K., and Hamson, C. O. (1999). Numerical and arithmetical cognition: patterns of functions and deficits in children at risk for a mathematical disability. J. Exp. Child Psychol. 74, 213–239. doi: 10.1006/jecp.1999.2515

PubMed Abstract | CrossRef Full Text | Google Scholar

Göbel, S. M., Moeller, K., Pixner, S., Kaufmann, L., and Nuerk, H. C. (2014). Language affects symbolic arithmetic in children: The case of number word inversion. J. Exp. Child Psychol. 119,17–25. doi: 10.1016/j.jecp.2013.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldman, S. R., Pellegrino, J. W., and Mertz, D. L. (1988). Extended practice of basic addi- tion facts: strategy changes in learning disabled students. Cogn. Instr. 5, 223–265. doi: 10.1207/s1532690xci0503_2

CrossRef Full Text | Google Scholar

Hanley, R., Masterson, J., Spencer, L., and Evans, D. (2004). How long do the advantages of learning to read a transparent orthography last? An investigation of the reading skills and reading impairment of Welsh children at 10 years of age. Q. J. Exp. Psychol. 57, 1393–1410. doi: 10.1080/02724980343000819

PubMed Abstract | CrossRef Full Text | Google Scholar

Helmreich, I., Zuber, J., Pixner, S., Kaufmann, L., Nuerk, H.-C., and Moeller, K. (2011). Language effects on children's nonverbal number line estimations. J. Cross Cult. Psychol. 42, 598–613. doi: 10.1177/0022022111406026

CrossRef Full Text | Google Scholar

Hiebert, J., Gallimore, R., Garnier, H., Givvin, K., Hollingsworth, H., Jacobs, J., et al. (2003). Teaching Mathematics in Seven Countries: Results from the TIMSS 1999 Video Study. NCES 2003-013. Washington, DC: National Center for Education Statistics.

Google Scholar

Hiebert, J., Stigler, J. W., Jacobs, J. K., Givvin, K. B., Garnier, H., Smith, M., et al. (2005). Mathematics teaching in the United States today (and tomorrow): results from the TIMSS 1999 video study. Educ. Eval. Policy Anal. 27, 111–132. doi: 10.3102/01623737027002111

CrossRef Full Text | Google Scholar

Hurford, J. R. (1975). The Linguistic Theory of Numerals. Cambridge: Cambridge University Press.

Google Scholar

Hurford, J. R. (1987). Language and Number. Cambridge: Cambridge University Press.

Google Scholar

Husen, T. (1967). International Study of Achievement in Mathematics. New York, NY: Wiley.

Google Scholar

Imbo, I., Bulcke, C. V., De Brauwer, J., and Fias, W. (2014). Sixty-four or four-and-sixty? The influence of language and working memory on children's number transcoding. Front. Psychol. 5:313. doi: 10.3389/fpsyg.2014.00313

PubMed Abstract | CrossRef Full Text | Google Scholar

Jordan, N. C., Hanich, L. B., and Kaplan, D. (2003). A longitudinal study of mathematical competencies in children with specific mathematics difficulties versus children with co-morbid mathematics and reading difficulties. Child Dev. 74, 834–850. doi: 10.1111/1467-8624.00571

CrossRef Full Text | Google Scholar

Jordan, N., and Montani, T. (1997). Cognitive arithmetic and problem solving: a com- parison of children with specific and general mathematics difficulties. J. Learn. Disabil. 30, 624–634. doi: 10.1177/002221949703000606

PubMed Abstract | CrossRef Full Text | Google Scholar

Landerl, K., Bevan, A., and Butterworth, B. (2004). Developmental dyscalculia and basic numerical capacities: a study of 8–9 year old students. Cognition 93, 99–125. doi: 10.1016/j.cognition.2003.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, M. O., and Mullis, I. V. S. (2012). Methods and procedures in TIMSS and PIRLS 2011. Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Boston College.

Miller, K. F., Smith, C. M., and Zhang, H. (2004). Language and Number: A Longitudinal Study of Learning to Count in Chinese and English. Unpublished manuscript, University of Illinois at Urbana-Champaign.

Miller, K. F., Smith, C. M., Zhu, J., and Zhang, H. (1995). Preschool origins of cross-national differences in mathematical competence: The role of number-naming systems. Psychol. Sci. 6, 56–60.

Google Scholar

Miller, K. F., and Stigler, J. (1987). Counting in Chinese: cultural variation in basic cognitive skill. Cogn. Dev. 2, 279–305. doi: 10.1016/S0885-2014(87)90091-8

CrossRef Full Text | Google Scholar

Miller, K., Kelly, M., and Zhou, X. (2005). “Learning mathematics in China and the United States,” in Handbook of Mathematical Cognition, ed J. Campbell (New York, NY; Psychology Press), 163–178.

Google Scholar

Miura, I. T. (1987). Mathematics achievement as a function of language. J. Educ. Psychol. 79, 79–82. doi: 10.1037/0022-0663.79.1.79

CrossRef Full Text | Google Scholar

Miura, I. T., Kim, C. C., Chang, C., and Okamoto, Y. (1988). Effects of language characteristics on children's cognitive representation of number: cross-national comparisons. Child Dev. 59, 1445–1450. doi: 10.2307/1130659

CrossRef Full Text | Google Scholar

Miura, I. T., and Okamoto, Y. (1989). Comparisons of U.S. and Japanese first graders' cognitive representation of number and understanding of place value. J. Educ. Psychol. 81, 109–113. doi: 10.1037/0022-0663.81.1.109

CrossRef Full Text | Google Scholar

Moeller, K., Shaki, S., Göbel, S. M., and Nuerk, H. C. (2015). Language influences number processing–a quadrilingual study. Cognition 136, 150–155. doi: 10.1016/j.cognition.2014.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Mullis, I. V. S., Martin, M. O., Foy, P., and Hooper, M. (2016). TIMSS Advanced 2015 International Results in Advanced Mathematics and Physics. Boston College, TIMSS & PIRLS International Study Center. Available online at: http://timssandpirls.bc.edu/timss2015/international-results/advanced/

Mullis, I. V. S., Martin, M. O., Kennedy, A. M., Trong, K. L., and Sainsbury, M. (2009). PIRLS 2011 Assessment Framework. Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Lynch School of Education, Boston College.

Google Scholar

Nosek, B. A., Smyth, F. L., Sriram, N., Lindner, N. M., Devos, T., Ayala, A., et al. (2009). National differences in gender-science stereotypes predict national sex differences in science and math achievement. Proc. Natl. Acad. Sci. U.S.A. 106,10593–10597. doi: 10.1073/pnas.0809921106

PubMed Abstract | CrossRef Full Text | Google Scholar

OECD (2010). PISA 2009 Results: Executive Summary.

OECD (2013). PISA 2012 Assessment and Analytical Framework: Mathematics, Reading, Science, Problem Solving and Financial Literacy. OECDPublishing. doi: 10.1787/9789264190511-en

CrossRef Full Text

Okamoto, Y. (2017). “Effects of mathematics language on children's achievement and central conceptual knowledge,” in Language and Culture in Mathematical Cognition, ed D. Berch (San Diego, CA: Elsevier).

Passolunghi, M. C., and Siegel, L. S. (2004). Working memory and access to numerical information in children with disability in mathematics. J. Exp. Child Psychol. 88, 348–367. doi: 10.1016/j.jecp.2004.04.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Peak, L. (1996). Pursuing Excellence: A Study of U.S. Eighth-Grade Mathematics and Science Teaching, Learning, Curriculum, and Achievement in International Context: Initial Findings From The Third International Mathematics and Science Study (1995). Institute of Educational Sciences (IES). Available online at: http://nces.ed.gov/pubs97/timss/97198.asp

Peak, L. (1997). Pursuing Excellence. A Study of U.S. Eight-Grade Mathematics and Science Achievement in an International Context. Washington, DC: U.S. Government Printing Office.

Google Scholar

Perfetti, C. A., Liu, Y., and Tan, L. H. (2005). The lexical constituency model: some implications of research on Chinese for general theories of reading. Psychol. Rev. 112, 43–59 doi: 10.1037/0033-295X.112.1.43

PubMed Abstract | CrossRef Full Text | Google Scholar

Perfetti, C. A., Zhang, S., and Berent, I. (1992). “Reading in English and Chinese: evidence for a “universal” phonological principle,” in Advances in Psychology: Orthography, Phonology, Morphology, and Meaning, eds R. Frost and L. Katz (Oxford: NorthHolland), 227–248.

Google Scholar

Pieng, P., Okamoto, Y., and La Joy, J. (2016). “Exploring gender differences and developmental changes in Japanese adolescent and young adult self-concept,” in Handbook of Comparative and International Studies in Education, ed D. Sharps, A volume in the series: International Perspectives on Educational Policy, Research and Practice, ed G. E. Fischman (Charlotte, NC: Information Age Publishing), 495–514.

Rabe-Hesketh, S., and Skrondal, A. (2005). Multilevel and Longitudinal Modeling Using Stata, 3rd Edn. College Station, TX: Stata Press.

Google Scholar

Rousselle, L., and Noël, M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: a comparison of symbolic vs. non-symbolic number magnitude. Cognition 102, 361–395. doi: 10.1016/j.cognition.2006.01.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Seymour, P., Aro, M., and Erskine, J. (2003). Foundation literacy acquisition in European orthographies. Br. J. Psychol. 94, 143–174. doi: 10.1348/000712603321661859

PubMed Abstract | CrossRef Full Text | Google Scholar

Siok, W. T., Perfetti, C. A., Jin, Z., and Tan, L. H. (2004). Biological abnormality of impaired reading is constrained by culture. Nature 431, 71–76. doi: 10.1038/nature02865

PubMed Abstract | CrossRef Full Text | Google Scholar

Stevenson, H. W., Lee, S., and Rohlen, T. (1998). An examination of American student achievement from an international perspective. Brookings Pap. Educ. Policy 1, 7–52.

Google Scholar

Stevenson, H. W., Lee, S. Y., and Stigler, J. W. (1986). Mathematics achievement of Chinese, Japanese, and American children. Science 231, 693–699. doi: 10.1126/science.3945803

PubMed Abstract | CrossRef Full Text | Google Scholar

Stevenson, H. W., and Stigler, J. W. (1992). The Learning Gap. New York, NY: Summit Books.

Stigler, J. W., Gallimore, R., and Hiebert, J. (2000). Using video surveys to compare classrooms and teaching across cultures: examples and lessons from the TIMSS video studies. Educ. Psychol. 35, 87–100. doi: 10.1207/S15326985EP3502_3

CrossRef Full Text | Google Scholar

Stigler, J. W., Lee, S. Y., Lucker, G. W., and Stevenson, H. W. (1982). Curriculum and achievement in mathematics: a study of elementary school children in Japan, Taiwan and the United States. J. Educ. Psychol. 74, 315–322. doi: 10.1037/0022-0663.74.3.315

CrossRef Full Text | Google Scholar

Swanson, H. L., and Jerman, O. (2006). Math disabilities: a selective meta-analysis of the literature. Rev. Educ. Res. 76, 249–274. doi: 10.3102/00346543076002249

CrossRef Full Text | Google Scholar

Tan, L. H., Laird, A., Li, K., and Fox, P. T. (2005). Neuroanatomical correlates of phonological processing of Chinese characters and alphabetic words: a meta-analysis. Hum. Brain Mapp. 25, 83–91. doi: 10.1002/hbm.20134

PubMed Abstract | CrossRef Full Text | Google Scholar

TIMSS (2011). Assessment. Copyright © 2012 International Association for the Evaluation of Educational Achievement (IEA). Chestnut Hill, MA; Amsterdam: TIMSS& PIRLS International Study Center, Lynch School of Education, Boston College; International Association for the Evaluation of Educational Achievement (IEA), IEA Secretariat.

Travers, K. J., Crosswhite, F. J., Dossey, J. A., Swafford, J. O., McKnight, C. C., and Cooney, T. J. (1987). Second International Mathematics Study Summary Report for the United States. Champaign, IL: Stipes.

Vellutino, F. R. (1979). Dyslexia: Theory and Research. Cambridge, MA: MIT press.

Google Scholar

Wu, M. (2005). The role of plausible values in large-scale surveys. Stud. Educ. Eval. 31, 114–128. doi: 10.1016/j.stueduc.2005.05.005

CrossRef Full Text | Google Scholar

Zhang, Y., and Okamoto, Y. (2017). Encoding “10ness improves first graders” estimation of numerical magnitudes. J. Numerical Cogn. 2, 202–219. doi: 10.5964/jnc.v2i3.69

CrossRef Full Text | Google Scholar