- 1Department of Educational Psychology, University of Arizona, Tucson, AZ, USA
- 2Department of Psychological and Brain Sciences, Indiana University, Bloomington, IN, USA
Learners often struggle to grasp the important, central principles of complex systems, which describe how interactions between individual agents can produce complex, aggregate-level patterns. Learners have even more difficulty transferring their understanding of these principles across superficially dissimilar instantiations of the principles. Here, we provide evidence that teaching high school students an agent-based modeling language can enable students to apply complex system principles across superficially different domains. We measured student performance on a complex systems assessment before and after 1 week training in how to program models using NetLogo (Wilensky, 1999a). Instruction in NetLogo helped two classes of high school students apply complex systems principles to a broad array of phenomena not previously encountered. We argue that teaching an agent-based computational modeling language effectively combines the benefits of explicitly defining the abstract principles underlying agent-level interactions with the advantages of concretely grounding knowledge through interactions with agent-based models.
Providing learners with knowledge that they can apply in new situations and use to solve novel problems is a central goal of education. However, learners often fail to apply well-known knowledge to unfamiliar problems. Transfer of knowledge, whereby learners apply knowledge learned in one domain to a superficially different, novel domain, may be especially difficult for complex systems understanding because different instantiations of complex systems often share few, if any, superficial features. Here, we propose that instruction in an agent-based computer programming language can create complex systems knowledge that is transportable among superficially distant domains. First, we address why learning complex systems principles is both important and difficult. Then, we discuss why transferring learned complex systems knowledge is especially challenging. Finally, we outline eight pedagogical principles that should promote the far transfer of complex systems knowledge and discuss our implementation of these principles within a weeklong computer programming intervention in a local high school.
Complex Systems Principles are Important, but Difficult to Learn
Understanding complex systems has become increasingly important in many fields. Complex systems are systems made up of many independent units (aka “agents”) whose interaction produce higher order emergent behavior [for more details, see Goldstone and Wilensky (2008)]. Complex systems approaches, which enable researchers to study phenomena that have multiple causes and consequences and have structure at many different temporal, spatial, and organizational levels, have had a large impact on the fields of math and science (e.g., Deneubourg et al., 1986; Forrest, 1991; Dawkins, 1996; Epstein and Axtell, 1996) and are having an increasing impact on engineering, medicine, finance, law, and management (Jacobson and Wilensky, 2006). Despite the widespread influence of complex systems approaches in science and engineering, the tools and perspectives of complex systems have had significantly less influence in STEM curriculum (Jacobson and Wilensky, 2006).
Incorporating complex systems principles into the STEM curriculum is pedagogically promising for three major reasons: (1) the same complex systems principle frequently arises across superficially distant areas in different guises (e.g., positive feedback loops in microphone feedback and in the popularity of TV shows), (2) different instantiations of the same principle frequently behave very similarly [e.g., Navier–Stokes equations can be used to describe and predict wind flow patterns around an air foil, water in a damn, or crowds of people fleeing a burning building (Hughes, 2003)], and (3) complex systems principles are not obvious categories that students will usually learn on their own (e.g., positive feedback loops are not conspicuous). Students will learn the concepts of dogs, tables, and pencils on their own, but may not ever think about water flow in toilet tanks and thermoregulatory feathers on a bird as both being instantiations of negative feedback systems.
Successfully teaching complex systems has proven to be very difficult. Learners struggle to grasp complex systems ideas, such as those involved in equilibrium in chemistry and evolution in biology (Bishop and Anderson, 1990; Wilensky and Resnick, 1999; Penner, 2000, 2001; Charles, 2002, 2003; Stieff and Wilensky, 2003), because learners typically employ a centralized schema (i.e., a cognitive framework that helps to interpret, understand, and explain information). Learners with well-developed centralized and “clockwork” mindsets assume systematic control whenever they see patterns in the world and favor explanations that rely upon leaders, rules, and prearranged structures (Resnick, 1994; Resnick and Wilensky, 1998; Jacobson, 2001). Clockwork mindsets favor reductive understandings (e.g., stepwise sequences), centralized control, completely predictable agent actions, single causes, static ontologies, and small actions only causing small effects (Jacobson, 2001). Learners harbor resistance to the counterintuitive concepts of complex systems like emergence, self-organization, and probabilistic outcomes (Feltovich et al., 1989; Resnick, 1994, 1996; Wilensky, 1997; Wilensky and Resnick, 1999; Chi, 2005). Learners believe that a distinct leader must direct agents to create complex aggregate patterns (i.e., leader centralization) or that some outside event must start the events’ unfolding (i.e., seed centralization), rather than appreciate how complex patterns can arise from simple simultaneous interactions among agents (Resnick, 1996). For instance, flocking formations emerge from simple rules and interactions among birds (i.e., stay close to other birds, fly in the same direction as other birds, and stay a certain distance away from other birds), yet learners are likely to endorse the idea that an alpha goose must lead the rest. Further, learners resist seeing randomness as conducive to order and pattern (Goldstone and Wilensky, 2008). Learners may not fully endorse self-organization and decentralization because they cannot mentally model complex systems. Limited working memory spans may prohibit mental simulations involving hundreds of agent-level interactions simultaneously (Narayanan and Hegarty, 1998). Similarly, learners struggle to correctly connect the agent-level rules to the aggregate pattern (Wilensky and Resnick, 1999; Penner, 2000). Learners’ reasoning often “slips” between levels, as they simplify complex systems by viewing micro- and macrolevels as similar rather than distinct. Alternatively, learners may employ “mid-level constructions,” whereby small groups are treated as homogeneous entities or a small number of individuals are described as interacting within small groups, rather than complex patterns emerging from interactions across all of the individual agents (Levy and Wilensky, 2008). Learners, therefore, often make incorrect inter-level causal explanations (or confuse how levels are causally related) because ascribing aggregate-level patterns to agent-level interactions is complex, multiple levels may compete for limited attention, and considering multiple levels simultaneously may require a larger working memory than most learners have (Hmelo-Silver and Pfeffer, 2004; Chi, 2005).
Research suggests design principles that improve complex systems teaching. First, learners benefit from experiencing complex systems (Jacobson and Wilensky, 2006). For example, role-playing particles in a simulation of diffusion can develop improved complex systems schema (Resnick and Wilensky, 1998; Colella, 2000). Similarly, students acting out honey bee behavior show improvements in complex systems reasoning (Danish, 2014). Students can also learn about complex systems by using agent-based computer models that show numerous distinct agents moving and interacting to result in a system that globally changes over time (Epstein and Axtell, 1996; Wilensky, 2001; Goldstone and Janssen, 2005; Railsback et al., 2006; Epstein, 2007; Miller and Page, 2007). Agent-based models perceptually ground learners’ understanding by visually displaying results so that learners can track the evolution of systems in time. These concrete representations often support learning and can even bolster abstract understanding (i.e., not tied to the physical instantiation or context of the original representation) when designed appropriately (Goldstone and Barsalou, 1998; Barsalou, 1999; Cheng, 2002). Concrete representations are grounded in perceptual and/or motor experiences and have identifiable correspondences between their form and referents, while abstract representations may not be tied to specific perceptual experiences.
Grounding in perception and action is at the core of our resolution to the discrepancy between fast scientific and slow neuro-evolutionary progress. Learners solve new cognitive tasks by reusing brain and cognitive functions that evolved for other purposes. One of the exciting prospects of teaching complex systems using NetLogo is that difficult concepts that would otherwise be taught using opaque formalisms can be taught in (sometimes literally) graspable ways by taking advantage of adaptive perceptual systems. In this context, we consider formalisms from math and logic to be more abstract than simulations in which system components are represented by visual objects. Formalisms are more abstract because their representational forms have a more arbitrary, less perceptually direct connection to the system elements that they are intended to model. However, we consider a particular mental representation to be neither abstract nor concrete in itself; rather, it depends on how the learner construes their representation. NeLogo models may give students an effective new vocabulary for interpreting situations and help students to interpret scenarios in new ways. Even though the situations are “concrete” in the sense that they are made up of colored shapes with particular sizes and locations, learners armed with NetLogo primitives can see them as less tied to their perceptual qualities.
The concrete, visual representations of the individual agents in a simulation encourage learners to analyze both the agent-level and aggregate behavior. Whereas equations that describe the macroscopic behavior often obscure agent-level interactions, agent-based modeling forms a bridge between agent-based and aggregate levels that learners can use to develop a deeper understanding of complex system concepts (Resnick, 1994; Wilensky and Resnick, 1999; Klopfer et al., 2005; Blikstein and Wilensky, 2009; Levy and Wilensky, 2009; Sengupta and Wilensky, 2009). Further, dynamic manipulation of agent-based models promotes hands-on, active exploration of agent-based interactions and fosters deep, multilevel explanations of complex phenomena (Papert, 1991; National Research Council, 1999). Manipulating agent-based models allows learners to form hypotheses about the impact of variables on individual and aggregate-level patterns, test their hypotheses, and revise their understanding (Cooper et al., 2010).
A second principle for instruction that improves understanding is to make the complex systems framework explicit. Even though some learning environments address complex systems by building and exploring models without the explicit teaching of “complexity” (Wilensky and Resnick, 1999; Sengupta and Wilensky, 2009), some research suggests that making the complex systems framework explicit helps learning. For example, instruction that directly stresses how emergence differs from centralization improves complex system understanding and remedies students’ lack of a general schema for emergent phenomena (Chi, 2005). Stressing how emergence differs from a directed, narrative story schema allows students to develop a new schema and connect it to existing knowledge (Bereiter, 1985). Making the emergence framework explicit has enhanced students’ abilities to apply this knowledge broadly (Chi, 2005).
Third, training students to analyze both the “agent-based” level (where students think about the behavior of individual agents) and the “aggregate” level (where students reason about the properties and rates of change of the macrolevel structures) supports complex system knowledge (Levy and Wilensky, 2009; Berland and Wilensky, 2015). Training in analysis of these two distinct levels supports deeper understanding of the meaning that emerges from their specific and causal relationships and promotes learning of scientific phenomena quickly and effectively (Levy and Wilensky, 2008). For example, training in the microscopic interactions that happen between molecules and how those interactions correspond to macroscopic physical changes results in better complex systems knowledge (Levy and Wilensky, 2008).
A different approach to teaching complex systems emphasizes analyzing the structural, behavioral, and functional aspects of the different agents. Breaking down complex systems into structural, behavioral, and functional components may make the implicit functions and behaviors of a system explicit and may instantiate a schema that can be used to understand a variety of complex systems (Hmelo-Silver and Pfeffer, 2004). In fact, experts are much better at breaking apart complex systems into the structures, behaviors, and functions of the interacting individual agents than are novices (Hmelo-Silver et al., 2007).
Transferring Complex Systems Principles is Particularly Difficult
Students are usually taught material in the classroom setting with the hope that they will apply the newly learned principles to novel, real-world situations (Reeves and Weisberg, 1994; Barnett and Ceci, 2002). However, transfer, especially involving complex systems knowledge, has proven difficult to achieve. New knowledge of complex systems can be very fragile and revert to non-complex ways of thinking when applied to novel situations (e.g., Day et al., 2010; Day and Goldstone, 2011). Across many different paradigms, learners fail to spontaneously transfer knowledge to new situations (Gick and Holyoak, 1980, 1983; Detterman, 1993). Advocates of “situated learning” argue that knowledge is grounded in the concrete, contextualized situation in which it was learned, and decontextualizing this knowledge in order to apply it across situations is impossible (Lave, 1988; Brown et al., 1989).
Superficial similarity often drives reminding, such that learners are highly influenced by a previous solution of a problem if it involves the same superficial “cover story” (e.g., both problems involve race cars) (Ross, 1984, 1987; Tullis et al., 2014). When surface features differ across events, even if the deep structure is similar, learners fail to notice the applicability of a prior experience in new contexts (Hayes and Simon, 1977; Gick and Holyoak, 1980, 1983; Spencer and Weisberg, 1986). If learners notice the structural similarity between situations, or are told to use the prior situation to help solve the novel problem, most learners correctly apply their knowledge to solve the new problem (Gick and Holyoak, 1980, 1983). Transfer, then, seems to be most impeded by a lack of “noticing” the applicability of prior knowledge in new situations (Lobato, 2012).
Transferring complex systems knowledge appropriately may prove to be particularly difficult, as complex systems phenomena rarely share superficial features. For instance, similar complex systems models have been recruited to explain predator-prey dynamics and business cycles, and these two situations share few superficial features (Ball, 1999). When the phenomena share few superficial features, students are unlikely to notice the underlying structural principles that connect complex systems. Consequently, transferring across complex systems phenomena has proven very difficult (Wilensky, 1996).
Research provides hints about what does and does not foster appropriate transfer. For example, learning pure abstract and logical formalisms does not consistently foster far transfer. General formalisms provided by algebra and logic might be expected to be powerful because they can be applied across an infinite number of situations; however, the connection between specific scenarios and equations is typically difficult for students to notice (Ross, 1987, 1989). Therefore, students who learn abstract formalisms often fail to consistently apply their knowledge to new situations.
However, student interactions with physical elements during modeling has produced transferable knowledge, especially when the models are relatively idealized (Goldstone and Sakamoto, 2003; Goldstone and Wilensky, 2008). For example, students who learned about “competitive specialization” in a situation involving abstract ants and food transferred that knowledge to a situation involving neurons learning to differentially respond to patterns (Goldstone and Son, 2005). Similarly, student participation in classroom simulations involving complex systems has shown some ability to create transferrable knowledge (Wilensky and Abrahamson, 2006). When learners view events as manifestations of general principles, this learning prepares them to see future events in terms of the same basic principles and they can apply their knowledge to the new events (Goldstone and Sakamoto, 2003; Goldstone and Son, 2005). Further, providing multiple, different cases of the same principle can allow learners to identify the deep principles involved, view the events as manifestations of general principles (Bransford and Schwartz, 1999), and mentally discard the superficial characteristics (Gick and Holyoak, 1980, 1983; Gentner, 2005).
Transfer can be enhanced through training that alters students’ perceptions of novel situations. Through well-designed experiences, the perceived similarity between instances can be adapted so that formerly dissimilar situations seem similar (Goldstone and Wilensky, 2008; Goldstone et al., 2011). Subjective similarities between situations are malleable rather than fixed. Experience and training can give learners new tools to interpret novel situations and ultimately shift their perceptions of similarity. Transfer can best happen when students’ psychological spaces become tailored so that superficially dissimilar situations that instantiate the same complex systems principle become more closely related. For example, prompts can help students see abstract commonalities between situations that they would have otherwise missed (Gentner, 2003). Likewise, experience sorting objects into task or culturally relevant categories changes learners’ assessments of similarities (Goldstone, 1994; Livingston et al., 1998; Roberson et al., 2000). Further, long-term experience shifts judgments of similarities among problems, as experts shift from relying upon superficialities to structural components (Chi et al., 1981).
Programming Should Promote Complex Systems Transfer
Programming and computational modeling have been used as effective tools for learning difficult science and math concepts (diSessa, 2000; Sherin, 2001; Wilensky and Abrahamson, 2006; Kynigos, 2007; Guzdial, 2008; Blikstein and Wilensky, 2009). Here, we examine whether high school students can acquire complex systems knowledge through computer programming training and apply it to domains far beyond those involved in training. Because spontaneous far transfer has been difficult to achieve and transfer as a central goal of education, pedagogical methods that demonstrate far transfer are of great importance to the learning sciences research community (Jacobson and Wilensky, 2006).
Teaching an agent-based modeling computer programming language may both impart complex systems knowledge and foster transferable knowledge across superficially distant instantiations of complex systems for several reasons, which are summarized in Table 1. First, programming an agent-based model combines abstraction with concrete grounding (i.e., it combines formal logical rules with perceptual, physical representations); this combination has been shown to help foster far transfer. Programming necessitates abstraction, as programmers must abstractly define variables and routines before a simulation can run. However, learners also must interact with the concrete representation of the system in order to build up, debug, and explore the program. Interactions with the spatiotemporal visual representations can ground learners’ knowledge. Programming an agent-based model, then, combines the formal abstractions of programming with the physical, concrete instantiation of modeling in order to produce transportable knowledge. For example, when learners are programming a complex systems representation of the Ising model of ferromagnetism in statistical mechanics, they must first code the abstract rules that govern the interactions among neighboring atoms. In an Ising model, each atom has a directional magnetic spin (i.e., clockwise or counterclockwise) that is influenced by the direction of the magnetic spins of the atoms around it. In NetLogo, the two basic rules in an Ising model are as follows: (1) each patch (which represents a single atom) starts with a random state of blue or yellow (which represents a clockwise or counterclockwise spin) and (2) each patch counts how many of its eight neighboring batches are blue. If more than four of its neighbors are blue, the patch turns blue; if less than four of its neighbors are blue, the patch turns yellow. Step 2 repeats indefinitely, and the patches typically form a stable color configuration. When students are finished with the abstract coding, they can experience the visual and temporal representation of spin arrangements and spin changes as graphically depicted by the colors of patches in NetLogo (Wilensky, 1999a), and shown in Figure 1. Modelers receive both the benefits of grounding and abstracting.

Table 1. Summary of the programming mechanics and corresponding cognitive benefits of teaching an agent-based model.

Figure 1. Example images from the initial setup (left) and the final arrangement (right) of patches in the Ising spin model from the fourth day′s project.
Second, computer programming develops the practice of problem decomposition, whereby learners must represent complex programs simply. Programmers must break down complicated systems into simple line-by-line computer commands [but see Palumbo (1990)]. Decomposing a situation into simple line-by-line commands forces learners to see the underlying structure of a problem. These simple commands may be used across different programs and situations, such that problem decomposition helps programmers identify the structural similarities between superficially distant phenomena and thereby adjust their constructs to emphasize similarities across complex systems principles. In fact, programmers often borrow code from one program to use in a structurally similar new program. Computer programming training may allow learners to apply their knowledge broadly because they notice the shared, fundamental principles that govern superficially distant situations. For example, when learners code the Ising model of an array of atoms with magnetic spins that mutually influence one another, they may realize that magnetic spins of atoms are aligned through interactions among neighbors. If learners also program a model of geographical distributions of two-party political opinions, they can easily notice that the structure of both models (i.e., the code involved) relies solely upon interactions among neighbors. Noticing this common structure can allow learners to generalize a schema and support broad application of it.
Third, programmers must explicitly create agents and their interactions. By clearly articulating and instantiating objects and their relations (without providing aggregate-level commands or creating a special object that leads the others), learners are encouraged to recognize how the complex patterns that form in their simulations do not require complex, aggregate-level rules (Wilensky, 2001; Wilensky and Reisman, 2006). Students often do not appropriately reason about causal structures between multiple levels; in fact, “slippage” between different levels is one impediment to complex systems understanding (Wilensky and Resnick, 1999). Agent-based programming forces the learners to differentiate between the simple agent-level rules, which they have programmed, and the complex aggregate behavior, which they have witnessed (Blikstein and Wilensky, 2004). Learners may be more likely to correctly distinguish between the levels when they have programmed only agent-level interactions but perceive the resulting macroscopic effects. Learners may understand they are programming rules for individuals and also observe that large-scale patterns emerge “for free.” For example, when programming the Ising model, learners only code rules for individual patches, yet various patterns of large blocks of color quickly emerge. Learners know the simple interactions among neighbors that they programmed, yet observe a novel and unanticipated structured arrangement that occurs at the population level.
Fourth, agent-based models reduce the cognitive load placed upon students who are learning complex systems by computing the complex interactions among agents and presenting the results in a helpful visual modality. Learners do not need to use cognitive resources to mentally simulate the interactions among hundreds of independent agents because the program computes these quickly and easily. The learner can offload the mental burden of simulating the complexity and variability of a complex system to the computer program (Cooper et al., 2010). Learners can enact countless simulations by manipulating parameters to test hypotheses, allowing the program to compute the interactions, and observing the results. This allows learners to connect aggregate behavior with the relevant agent-level variables. Further, agent-based models easily illuminate how complex patterns arise in ways that other methods (e.g., differential equations) cannot (Penner, 2000; Sherin, 2001). For example, agent-based models can clearly present how complex patterns arise by visually displaying the individual agents and their interactions (Scaife and Rogers, 1996). In this manner, agent-based models extend students’ ability to perceive and encode complex systems, even when the complex phenomena may be otherwise unobservable (Quellmalz et al., 2012). For instance, learners who have programmed the Ising model can easily modify the temperature and variability parameters in order to observe how the overall patterns change. The NetLogo program does the complex work of simulating the individual interactions among thousands of turtles, and the learner can reflect on why the patterns change with changes in variables.
Fifth, students are more likely to build new knowledge when they actively create external artifacts, even when those artifacts are virtual. By creating an agent-based model, learners are engaged in an active, hands-on process and active processes foster deep understanding (National Research Council, 1999).
Sixth, computer modeling languages offer new cognitive tools for describing complex systems phenomena (Goldstone and Wilensky, 2008). Teaching children relational language, language that emphasizes relations between objects, prompts them to notice abstract commonalities (Loewenstein and Gentner, 2005); teaching students a new computer modeling language may shift how they view and describe situations. A high-level programming language may allow learners to see connections among various complex systems that they could not perceive before training, which should help them apply their knowledge broadly. For instance, in the Ising model, students learn to use the code “sum [spin] of neighbors4.” This code may give students new tools and language (e.g., “neighbors”) to analyze and describe the fundamental causes of complex systems.
Seventh, under the assumption that the computational programming constructs acquired by students will shape their mental models, student-generated agent-based models can eliminate irrelevant distractions and focus student attention on central principles of complex systems. For example, variations in elements’ appearances can be eliminated in order to focus attention on the interactions among the agents, rather than absolute properties of the agents themselves (Goldstone and Son, 2005). The agent-to-agent interactions can be made visually salient, while the distracting, superficial details can be downplayed. By eliminating irrelevant characteristics in the models (e.g., shape of the agents), students will be able to form more general mental models that apply to a broader array of novel situations. For example, in the Ising model, the spins of individual atoms are simply represented by colors. This minimalistic representation eliminates irrelevant distractions and allows learners to focus on the overall emergent patterns; plus, a similar abstract color arrangement can also be aptly employed in the geographic model of political party opinions.
Finally, teaching programming allows students to interact with several different models of complex systems. Learners who encounter multiple varied exemplars of the same structural principles begin to mentally discard the superficial characteristics and focus on the deeper principles underlying all of the exemplars (Gick and Holyoak, 1980; Catrambone and Holyoak, 1989; Bransford and Schwartz, 1999). Interactions with multiple examples of a deep principle allows learners to identify the core, consistent deep principle that underlies the varied instantiations because learners discard inconsistent superficial features across examples. By modeling several different exemplars of complex systems phenomena, students’ identification of the structural principles underlying them should be promoted. For example, learners who build both the Ising model and the model of geographical distributions of two-party political opinions should be able to identify the common structure between these two superficially distinct instances, namely, that spatially clustered regions of patches with the same property arise when each patch has tendency to adopt the same property as most of its neighbors.
In the quasi-experiments reported here, we implemented a NetLogo training program across two high school classes. We relied upon the eight principles outlined above to create 1 week of instruction centered on coding and creating models in NetLogo. Our main question was whether training in NetLogo programming would support student understanding of complex systems and allow them to accurately answer novel complex systems questions.
Current Research
Intervention 1
In the first study, we tested the idea that teaching an agent-based modeling language can foster application of complex systems knowledge across superficially different situations (Wilensky and Reisman, 2006; Blikstein and Wilensky, 2010). We taught a high school class how to program agent-based models in NetLogo (Wilensky, 1999a) for 1 week. During the training, students created several different agent-based models that illustrated complex systems concepts such as positive and negative feedback loops and self-organized cluster formation. Students took a complex systems knowledge inventory before and after the NetLogo training, and we measured how their knowledge changed and analyzed their programs.
Participants
Twenty-eight students participated as a part of the “Computer Science: Principles” course at a local public high school. Computer Science: Principles is a class that stresses computational thinking and abstraction, and students took the class as an elective. It was the first time that the class was taught at this high school. Fourteen students were seniors, 12 were juniors, and 2 were sophomore. Only five participants were female. The high school was located in a mid-size city, 80% of its students were white (with the biggest minority—Hispanic—comprising 6% of the students), and 21% of its students qualified for free or reduced lunch. Our agent-based modeling intervention occurred toward the end of their school year, and addressed one of the course’s core goals—using models and simulations to generate new understanding and knowledge. The class lasted 65 min long and met 5 days a week. Most students had very little or no experience writing code; none had experience writing code in NetLogo.
Ethics
The interventions in this manuscript were ruled Exempt under Category 1 from the Indiana University IRB, as it only involved research conducted in established or commonly accepted educational settings, involving normal educational practices.
Materials
We chose to use NetLogo (Wilensky, 1999a) as our agent-based modeling language because it enables learners to write meaningful models in a short amount of time with little training and without focusing on (and struggling with) syntax. NetLogo is a free, domain-independent modeling language that can represent thousands of basic agents (i.e., turtles, which can move, and patches, which are stationary) spatially, dynamically, and visually. It has powerful capabilities for modeling wide-ranging phenomena, and it has a large built-in library of models that can be used as code examples. Students can simply specify how the turtles and patches behave and interact with one another, and then observe the aggregate-level patterns that visually evolve over time. NetLogo has been used widely in both educational and research contexts (Blikstein and Wilensky, 2004; Abrahamson et al., 2006; Sengupta and Wilensky, 2009). However, in much of the prior research, learners interacted with prebuilt NetLogo simulations designed to improve student understanding on specific target concepts [e.g., GasLab (Wilensky, 1999b), Connected Chemistry (Stieff and Wilensky, 2003; Levy and Wilensky, 2009), BEAGLE (Rand et al., 2007), and the NEILS project (Sengupta and Wilensky, 2009)]. The minimal existing literature on training computer modeling skills has shown that learners can effectively create a computer model to represent emergent complex systems building from simple principles (Wilensky and Reisman, 2006). Similarly, students can modify existing models, and doing so can shift their thinking about complex systems (Blikstein and Wilensky, 2010). Through modifying complex systems models, students developed fewer, simpler rules that governed relevant complex systems phenomena, which enabled them to better understand and extend models with new rules. The current research extends the existing research in two significant ways: (1) we trained an entire classroom of students to create their own programs and complex systems models in NetLogo and (2) we measured far transfer among complex systems knowledge. We also developed and employed a complex systems inventory to assess learners’ complex system knowledge, and this is located in Section “Complex Systems Concepts Inventory” in Appendix.
Procedure
The first author acted as the instructor throughout each intervention. Each day’s lesson had a similar structure. First, some review of the previous day’s programming commands was conducted (except on the first day). Second, the instructor introduced new programming commands that were needed for the day’s assignment by projecting some sample code onto a screen in the front of the classroom. Students experimented with the new commands on their own computers as the commands were introduced. Students predicted how changing the commands would alter the model’s output, and in doing so, engaged in a hypothesis/test routine. Third, the day’s modeling project was given to students. The project explicitly detailed the specific rules that the individual turtles or patches needed to follow, without revealing what complex aggregate patterns could emerge. Students individually wrote their models with NetLogo on personal computers, but often asked their neighbors (or instructor) for help. Within each project, students were also given “challenges,” which involved more sophisticated adaptations of their original projects. These “challenges” were given so that students who finished the basic project quickly would continue to be engaged, while the other students finished the basic project. The instructor walked through the class during this time to make sure students were on task and helped students solve coding problems. Students were very interested and active during the individual project times; most students were motivated to solve the challenge problem. For the last 10 min of each class session, the instructor, with participation from the students, wrote one possible method (out of infinite different possible methods) of coding the program and explained why some alternatives would not work. During this wrap-up time, the instructor summarized what commands were covered. The instructor questioned students about the individual-level commands they coded and the subsequent aggregate-level behavior they witnessed. Finally, students emailed their code to the instructor to earn participation credit for the day. The content of the individual days is detailed below.
Day 1—Basic Turtle Commands
Students first took the pretest. Then, in order to motivate and capture the attention of students, an example NetLogo program that used the computer’s camera to sense motion was introduced. In the program, individual butterflies interacted with the real-life motion of a student volunteer, which was displayed on Netlogo’s graphical window. Next, the basics of NetLogo were described, including the capability of representing individual turtles (independent mobile agents) and patches (stationary sections of the background). Finally, a few basic turtle and patch commands (e.g., creating and killing turtles, assigning colors and shapes, assigning specific x and y coordinates to turtles) were described. Students created very simple programs that created turtles in various colors and shapes.
Day 2—Advanced Turtle Commands
On their second day, students created a new program from scratch that allowed the movement of turtles to be controlled through the model’s interface. They learned how to utilize control flow commands (e.g., if, ifelse) in NetLogo’s language. Further, they learned how to create variables (e.g., turning angle and speed) that could be adjusted once the program had started and how to create switches that hide or show the individual turtles. For an extra challenge, some students created a routine that made the turtles move toward the on-screen location where the mouse was clicked.
Day 3—Cluster Formation Model
The instructor introduced commands that allowed turtles to see if there were any other turtles ahead of them. Students programmed a model that randomly distributed turtles across the patches. Turtles were then programmed to look ahead of them by an adjustable distance (and angle). If a turtle saw another turtle in front of it, it moved toward the other turtle. If a turtle did not see another turtle, it did not move. Then, all the turtles rotated a small, random amount to the left or right. The model illustrated how a few simple rules caused several small, dense groups of turtles to form from the initially randomly spaced turtles, as shown in Figure 2. Further, the model illustrated the need for small random changes in the turtles’ headings, as these clusters only formed if some randomness in turtles’ headings was included.

Figure 2. Example images from the initial setup (left) and the emergent groups (right) from the third day’s project. The entire code for the project is displayed on the bottom.
Day 4—Ising Spin Model
Students learned the commands needed for having patches count the number of their neighbors with a certain property. In day 4’s project, students created an Ising model that represented the spatial arrangement of magnetic moments associated with the spins of atoms. First, patches were randomly assigned one of two colors, which represented the clockwise or counterclockwise electron spin of an atom. When the model started, the patches would switch their color to the color favored by the majority of their neighboring patches. Over successive rounds of color updating, this would lead to short-lived cascades of color switching because once one patch changed its color, it might change the balance of spins for a neighboring patch. Students then incorporated a variable amount of noise into the model, whereby the individual patches only probabilistically assumed the color of the majority of their neighbors. Students interacted with the simulation to see how different spin patterns emerged based upon the initial density of colors and the amount of randomness in the model. For an extra challenge, students coded the patches to be influenced by eight random patches, rather than their eight immediately surrounding neighbors.
Day 5—Conway’s Game of Life
No new commands were introduced on day 5. Similar to day 4, students programmed a world where each patch was impacted by the number of neighboring patches with a certain variable. Specifically, students programmed J. H. Conway’s game, Life, which has three simple rules: (1) a living patch with two or three alive neighbors remains alive, (2) a dead patch with three neighboring alive cells becomes alive, and (3) all other alive patches become dead. The three simple rules can lead to complex, self-sustaining or apparently chaotic patterns and provide considerable potential for exploring emergence (Penner, 2000; Beer, 2014). Students programmed the model so they could click on individual patches to switch them between being alive and dead. Finally, students took the posttest.
Tests
Students were administered a 11-question Complex Systems Concepts Inventory (CSCI), as shown in Section “Complex Systems Concepts Inventory” in Appendix, on the first and last days of the intervention. Students were not informed that they would take the same test at the end of the week. The test covered a wide array of principles central to complex systems understanding (e.g., dynamic equilibrium, non-linear influences, and emergence). Importantly, in order to test the ability of learners to transfer complex systems knowledge, the content of the test questions was superficially unrelated to the content covered during the training. The domains covered during the training were largely abstract, while those on the tests were mostly applied, natural phenomena. Test questions included diverse domains that naturally and intrinsically instantiated principles of complex systems (e.g., fireflies flashing in synchrony, spiral formations of pine cones), with different domains than those covered in class. It included seven multiple-choice and four short answer questions and was developed by the authors based upon preliminary complex systems research. Students earned 1 point for each multiple-choice question correct. Students earned 0, 1/2, or 1 point for each of the short answer questions, based on the depth and correctness of their answers. If students mentioned that the observed complex patterns can arise from a simple rule, they earned half a point. If students explicitly described what the underlying rule was (e.g., fireflies look to their neighbors and adjust the timing of their flash to be in greater synchrony with their neighbors), students earned a full point.
Results
Students seemed very engaged throughout the training, and many students attempted to complete the extra “challenge” projects. Students’ scores on the pre- and posttests are displayed in the left panel of Figure 3. Students earned more points [M = 5.46 (SD = 2.05)] on the posttest than on the pretest [M = 3.93 (SD = 1.88); t(25) = 4.54, p < 0.001, Cohen’s d = 0.91]. Twenty-one (out of 26) of the students (81%) showed improvement from the pretest to the posttest. The log odds of a correct answer on each question were predicted using a multilevel logit model. The model included the fixed effect of pretest or posttest and included random intercepts for subjects and items. The model was fit in the R software package (R Core Team, 2008) with Laplace estimation using the lmer() function of the lme4 package (Bates et al., 2008). The beta weights (and corresponding t values) of the model are shown in Table 2. This model of performance shows that students answered significantly more questions correctly on the posttest than on the pretest. The odds of correctly responding to a question after training were 1.15 times greater than correctly answering before training.
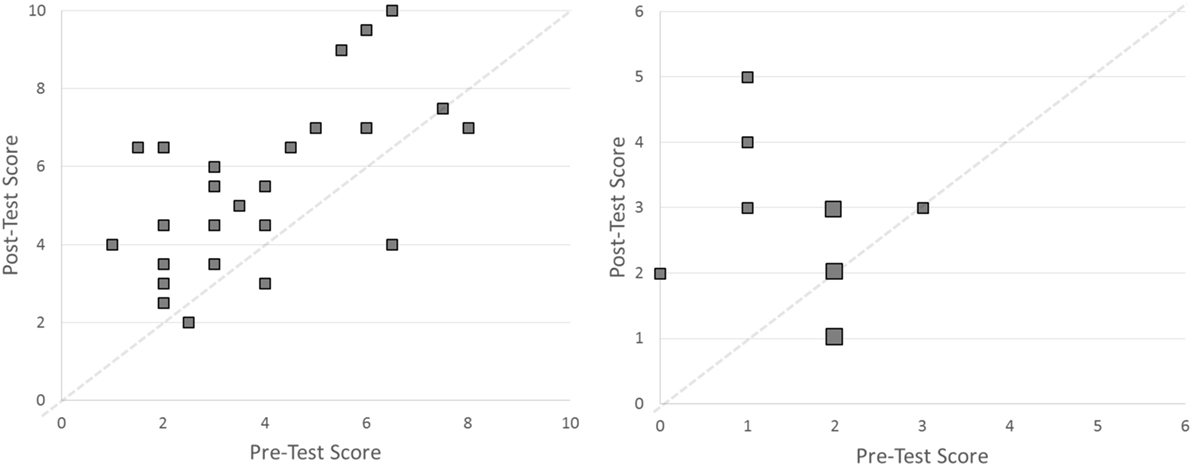
Figure 3. Scatter plots of total answers correct on the pre- and posttests in Intervention 1 (left panel) and Intervention 2 (right panel). In the right panel, larger points represent two participants each. Points above the dashed diagonal line indicate better performance on the posttest than the pretest.
Students’ answers to the short response questions revealed a significant shift in thinking across the week of training. Students initially invoked the centralized, deterministic mindset to describe several complex natural phenomena. For example, when describing how zebra stripes and cheetah spots can form, students often suggested that high-level master plans (i.e., genes) were needed to form complex patterns. Jason suggested that DNA is needed to specify the spiral shaped pattern in pinecones “because the designs are complicated.” Similarly, Calvin responded, “the individual traits that create the spirals are part of the DNA.” To describe the appearance of cheetah fur, Marcus answered “some genes are dominant in certain places.” Jacob described that emergent patterns of lightning bugs flashing in synchrony and birds flying in V patterns arise because “it is inherent in their genes.”
After training, students focused almost all of their explanations on the agent-level interactions that could underlie the complex aggregate-level patterns. For example, when describing how color patterns form on animal fur, Beth answered, “the cells want to be different than the ones next to them” and Will wrote “the cells avoid their neighbors’ choices.” When describing how the spirals of pinecones form, Erol explained that “it only takes simple rules to create a pattern” and Jacob stated “sometimes simple commands result naturally in complex patterns.” Even when describing the similarities between lightning bug flashes and the V pattern of flying geese, students ascribed the aggregate-level patterns to agent-level interactions. Abe suggested “they both observe their neighbors’ motions and make similar ones themselves.” Jacob conjectured “it might change what it is doing depending on what the organism next to it is doing.” Trey wrote “they arise from neighbors communication – that’s what makes them similar.”
Students sometimes broke down the problems into pseudocode to describe the agent-level interactions that could result in complex aggregate-level patterns. For example, when describing how zebra stripes can arise, Nathan wrote “if cell = black, set all neighbors white.” To describe the spiral pattern in pinecones, Abe answered, “if cells are told to grow out and clockwise from their parent, then they would hopefully form a spiral, just from a simple rule.”
Intervention 2
We repeated the intervention with a new class of students at the same high school the following year. Instead of answering the same questions on the pre- and posttest, as in the first intervention, students involved in this intervention answered different questions before and after training. While this design gives less statistical power and suffers from more statistical noise than Intervention 1, any improvement from pre- to posttests cannot be driven by re-exposure to the same questions in Intervention 2. We measured the change in performance across two different versions of a complex systems inventory to assess the development of complex systems understanding. Other than the tests, the intervention followed the same procedure as Intervention 1.
Participants
Fifteen high school students enrolled in the “Computer Science: Principles” course participated; three students were absent at the time of the posttest and one student was absent for the pretest. Eight students were seniors and seven students were juniors. Six were female and nine were male.
Content of the Intervention
The content of the intervention was the same as in the first year.
Tests
Two versions of a complex systems inventory were developed based on the results from the first intervention and are found in Appendices B and C. Each version included five short answer questions and one multiple-choice question that probe the same complex systems knowledge and abilities. The superficial features of the questions varied between test versions, but the deep structure of the problems were consistent. For example, on Form A, students were asked how geese form V patterns when flying, while on Form B, students were asked how groups of fireflies synchronize their flashing. While these are superficially distinct questions, both answers are that the animals change their behavior based upon the behavior of their neighbors. In this way, questions about each specific topic were yoked to each other across versions of the test. Students were randomly assigned to version A or B at the pretest. After training, all subjects completed the other version of the inventory. Students’ answers were graded blind to their condition, and answers were awarded either full or no credit. If students identified the complex systems principle associated with the question (e.g., emergence of complex patterns from simple local interactions), they earned full credit for the question.
Results
As in the first year, students seemed very excited and engaged throughout the weeklong training. Individual student performance is displayed in the right panel of Figure 3. Students earned marginally more points [M = 2.67 (SD = 1.11)] on the posttest than on the pretest [M = 1.57 (SD = 0.73); t(10) = 2.06, p = 0.06, Cohen’s d = 0.65]. Only 11 students were present for both the pre- and posttest, which limits the power of a traditional paired t-test. We also used a multilevel model to compare pre- and posttest performance because multilevel models can provide us with more power. The log odds of a correct answer on each question were predicted using a multilevel logit model, as in Intervention 1. The model included the fixed effect of pretest or posttest and included random intercepts for subjects, the 12 individual questions, and the 6 fundamental complex systems principles that were repeated across test versions. As in the first intervention, the model was fit in the R software package (R Core Team, 2008) with Laplace estimation using the lmer() function of the lme4 package (Bates et al., 2008). The beta weights (and corresponding Z values) of the model are shown in Table 3. This model of performance shows that students answered significantly more questions correctly on the posttest than on the pretest. The odds of correctly responding to a question after training were 2.51 times greater than correctly answering before training.
Similar to the first intervention, students’ answers to the short response questions revealed a significant, medium sized, shift in thinking across the week of training. Students initially invoked the centralized, deterministic mindset to describe several complex natural phenomena. For example, before the intervention, when describing how fireflies could synchronize their flashing, Avery wrote “the fireflies could sync by having a central firefly work as a timer, using external stimuli or possibly by using a form of internal clock.” Sam invoked the idea of DNA to describe how animals form seashells in complex spiral patterns, when she wrote “how else would the seashell make such complex spiral patterns?” Similar, Holly explained animal stripes by arguing that “cells at specific locations code for only 1 color. However, the cells can be dispersed in different patches, which results into the making of stripes.”
Students’ thinking shifted after training to invoke ideas of repeated simple patterns and decentralization. To describe how seashells can be formed in complex spiral patterns, Michael wrote “it simply tells the next part of the shell to be bigger and at a certain angle.” Similarly, Avery explained the spirals in pinecones by stating, “it is just the algorithm repeated over and over.” Students also invoked the importance of agent-agent interactions in the development of complex systems. To describe how fireflies can synchronize their flashing, Ethan wrote “they may be influenced by others’ patterns over a certain amount of time and larger groups would hold more influence” and Sam wrote “they look at others.” Garrett described how geese can form a V pattern while flying by arguing the rule is to “follow a goose in any direction of a cone around itself and a v pattern will emerge.”
Discussion
Students’ ability to apply complex systems knowledge across a wide variety of situations improved by learning an agent-based modeling language. A brief 1-week intervention which targeted NetLogo programming and modeling skills boosted students’ scores on a CSCI, even though the training intervention covered models in different domains than those tested. Whereas prior interactions with agent-based models have sometimes resulted in situated learning [Day et al., 2010; Day and Goldstone, 2011; but see Wilensky (1996) and Goldstone and Son (2005)], the current intervention based on computational modeling produced broadly applied knowledge of the core concepts of complex systems. In fact, both interventions produced medium to large sized improvements (Cohen, 1988) in students’ learning that lasted across multiple days. Students utilized the centralized mindset less and agent-level interactions more often to describe complex patterns following the intervention.
The specific combination of agent-based modeling and programming supported students’ ability to transfer their complex systems knowledge to distant new situations. The intervention supported application of complex systems knowledge broadly for many reasons. First, learners developed computational formalisms sufficient to express several different models (through learning a formal programming language), but also experienced the concrete grounding of the visual representation of the outcome (through running the agent-based model). Providing learners with yoked concrete and formal representations likely led to transportable knowledge. Second, students also seemed to gain new tools to analyze the novel situations. After training, some students used a spontaneously created pseudocode to describe new natural phenomena. Gaining this new expressive language apparently enables learners to connect superficially distinct situations that would be implemented using similar code. Further, students adopted certain, specific linguistic forms (e.g., “complex patterns”) when describing phenomena during the posttest. Having new phrases, at minimum, shows that students have acquired “prospective indexicals” (Goodwin, 1996) that can ease learning of the concept in the future (Zemel and Koschmann, 2014). Learners likely would not have experienced the same cognitive benefits from using ready-made models because they would be less likely to internalize formalizations of rules, gain new language to describe phenomena, and connect the abstract rules to concrete outcomes.
Learners also experienced multiple, varied examples of emergent phenomena throughout the week. Learners saw complex spatial arrangements emerge from uncomplicated rules in the Cluster Formation model, the Ising Spin model, and Conway’s Game of Life. While the superficial features of these models vary drastically, the underlying principles of macroscopic patterns emerging from a few simple rules governing the local interactions of basic agents remained consistent.
While evidence for far transfer has historically been controversial, we believe that this intervention suggests a sound pedagogical method for promoting transfer of complex systems principles. We argue transfer can occur when well-designed activities increase the perceived similarity of situations, transforming once dissimilar situations into instantiations of the same underlying principles. Moreover, while the term “principle” often connotes abstract and purely formal knowledge, the concrete implementation of the formal programming language into Netlogo code provides a cognitively accessible inroad into construing phenomena in transferable fashion. Experience with programming changes the perceived similarity among situations because it gives learners a new tool for analyzing situations (i.e., a programming language), focuses learners’ attention on the deep structure, and forces them to engage with the essential rules sufficient for generating phenomena. Further, modeling different projects gave students experience with multiple varied systems embodying the emergence principle and likely primed their ability to see vastly different natural systems as embodying the same principle. This agent-based modeling training, then, likely made distant things seem more similar, and allowed learners to use knowledge gained in a model of electron spin when answering a question about a zebra’s stripes, for example. Through the intervention, students began to identify important, meaningful components of a complex system, and connect the commonalities between superficially distinct events. This intervention adds to the literature that suggests how students can transfer scientific principles across superficially dissimilar domains (Simon, 1980; Bransford and Schwartz, 1999; Jacobson, 2001).
Programming, even when not coupled with agent-based models, may provide extensive benefits for cognition. Some have argued that computational thinking can foster broad cognitive gains because it because it provides a general analytic approach to problem solving, which involves problem representation, decomposition, abstraction, prediction, simulation, and verification (Wing, 2006; National Research Council, 2010). Some even argue that learning to program means learning to construct mechanisms and explanations (Soloway, 1993). In order to construct the mechanisms and explanations involved in programming, learners must explicitly decompose problems into their constituent rules (Nersessian, 1992; Ho, 2001). Learners must identify the basic rules of interaction that are important, which requires explicitly articulating and instantiating objects and their relations (Penner et al., 1998). This need for problem decomposition is inherent in all scientific and engineering disciplines (Qualls and Sherrell, 2010). In fact, Swan and Black (1987) show a significant increase in performance on subgoal formation, forward chaining, backward chaining, systematic trial and error, alternative representations, and analogy from programming language instruction. Computational thinking also involves conceptualizing via abstraction (Wing, 2006). Learners need to think through multiple layers of abstraction simultaneously, which may promote broad generalization of instantiated concepts.
However, others have argued that computer programming produces few general cognitive benefits (see Palumbo, 1990). Although transfer of specific problem-solving skills may occur through programming language instruction, improvements in general problem-solving domains are very difficult to achieve (Reed and Palumbo, 1988). In fact, Pea and Kurland (1984) found no benefits of programming language instruction on general problem-solving abilities or planning performance.
The intervention we developed may not have fully taken advantage of the benefits of computer programming. Throughout the training, learners were given the basic agent-level rules that they needed to instantiate in their code. Many programming interventions require learners to “reverse engineer” a system (Wilensky and Reisman, 2006). Learners start with a description of the macroscopic behavior; then, they have to break down the problem, determine the underlying rules that govern the elements and their interactions, build their model, and verify that their model recreates the macroscopic behavior. Our intervention did not require learners to decompose an event into its basic rules; rather, learners built the models from the given rules. Problem decomposition may be beneficial to explaining natural complex systems phenomena because both involve breaking down the aggregate-level pattern into agent-level interactions. Incorporating an explicit process of problem decomposition into agent-based modeling may further bolster student understanding. Problem decomposition may be especially relevant for our assessment instrument, which requires learners to “reverse engineer” a natural system. Additionally, we did not prompt learners to borrow relevant existing model components when building new models. Requiring learners to incorporate aspects of prior models into new, superficially different models may help learners make deep connections across the structural principles of the models.
Despite its significant influence across math and science fields, pre-college curricula have largely neglected complex systems principles. In the practice of modern biology, complex systems models have added precision to scientific theories and have been important sources of hypothesis formation and testing. Yet, the high school and undergraduate biology curriculum often remains centered on the memorization of classification schemas and established theories (Wilensky and Reisman, 1998, 2006). As education shifts to address fewer, more integrated core ideas (College Board, 2009; National Research Council, 2011), many argue that a modeling perspective needs to take an increasingly pronounced place in the curriculum.
Teaching agent-based programming can remedy this gap, present the fundamentals of scientific modeling, and support both computational thinking and science knowledge (Sengupta and Wilensky, 2009). Through instruction in NetLogo, students receive benefits associated with both interacting with agent-based models and learning to program. Interacting with agent-based models allows students to visualize complex phenomena, manipulate variables, test hypotheses, and connect agent-based interactions to aggregate-level behavior. Programming helps students to explicitly state the actions and interactions of the agents in a situation. Learners are then confronted with the complex patterns that can arise from simple rules that govern agent-level interactions. Programming naturally encourages students to think about a phenomenon from the perspective of what set of rules would minimally suffice to generate the phenomenon. Further, modeling supports students’ understanding of a wide range of key mathematical and scientific concepts and “should be fostered at every age and grade… as a powerful way to accomplish learning with understanding in mathematics and science classrooms” (Romberg et al., 2005, p. 10). Incorporating complex systems principles through agent-based modeling into standard science curricula can provide numerous opportunities to engage in the prevalent scientific pursuits of model building, hypothesizing, and testing. Further, an appreciation of complex systems schema can build links between disparate domains, provide unifying and coherent conceptual frameworks, and encourage students to look at natural phenomena in new and insightful ways. Teaching computer programming can foster knowledge transfer among superficially dissimilar disciplines, support valuable cross-fertilization of ideas and approaches, and ultimately unify scientific domains that would otherwise be fractionated.
Ethics Statement
This study was ruled exempt by the Indiana University Institutional Review Board because it is “research conducted in established or commonly accepted educational settings, involving normal educational practices, such as (i) research on regular and special educational instructional strategies, or (ii) research on the effectiveness of or the comparison among instructional techniques, curricula, or classroom management methods [45CFR46.101(b)(1)].”
Author Contributions
JT conceptualized the project, designed the instruction, taught the classes, wrote the tests, collected the data, analyzed the data, and wrote the manuscript. RG conceptualized the project, contributed to the design the experiments, thought of the test questions, helped analyze the data, and edited the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
This research was in part supported by National Science Foundation REESE grant 0910218, Institute of Education Sciences, US Department of Education Grant # R305A1100060, and start-up funding provided to the first author by the University of Arizona.
References
Abrahamson, D., Janusz, R. M., and Wilensky, U. (2006). There once was a 9-block … a middle-school design for probability and statistics. J. Stat. Educ. 8. Available at: http://www.amstat.org/publications/jse/v14n1/abrahamson.html
Barnett, S. M., and Ceci, S. J. (2002). When and where do we apply what we learn? A taxonomy for far transfer. Psychol. Bull. 128, 612–637. doi:10.1037/0033-2909.128.4.612
Barsalou, L. W. (1999). Perceptual symbol systems. Behav. Brain Sci. 22, 577–660. doi:10.1017/S0140525X99532147
Bates, D., Maechler, M., and Dai, B. (2008). Ime4: Linear Mixed Effects Models Using S4 Classes. R Package Version 0.999375 17. Available at: http://lme4.r-forge.r-project.org/
Beer, R. D. (2014). The cognitive domain of a glider in the game of life. Artif. Life 20, 183–206. doi:10.1162/ARTL_a_00125
Bereiter, C. (1985). Toward a solution of the learning paradox. Rev. Educ. Res. 55, 201–226. doi:10.3102/00346543055002201
Berland, M., and Wilensky, U. (2015). Comparing virtual and physical robotics environments for supporting complex systems and computational thinking. J. Sci. Educ. Technol. 24, 628–647. doi:10.1007/s10956-015-9552-x
Bishop, B. A., and Anderson, C. W. (1990). Student conceptions of natural selection and its role in evolution. J. Res. Sci. Teach. 27, 415–427. doi:10.1002/tea.3660270503
Blikstein, P., and Wilensky, U. (2004). MaterialSim Model-Based Curriculum. Evanston, IL: Northwestern University, Center for Connected Learning and Computer Based Modeling. Available from: http://ccl.northwestern.edu/rp/materialsim/models.shtml
Blikstein, P., and Wilensky, U. (2009). An atom is known by the company it keeps: a constructionist learning environment for materials science using agent-based modeling. Int. J. Comput. Math. Learn. 14, 81–119. doi:10.1007/s10758-009-9148-8
Blikstein, P., and Wilensky, U. (2010). “MaterialSim: a constructionist agent-based modeling approach to engineering education,” in Designs for Learning Environments of the Future: International Perspectives from the Learning Sciences, eds M. J. Jacobson and P. Reimann (New York: Springer), 17–60.
Bransford, J. D., and Schwartz, D. L. (1999). Rethinking transfer: a simple proposal with multiple implications. Rev. Res. Educ. 24, 61–101. doi:10.2307/1167267
Brown, J. S., Collins, A., and Duguid, P. (1989). Situated cognition and the culture of learning. Educ. Res. 8, 32–42. doi:10.3102/0013189X018001032
Catrambone, R., and Holyoak, K. J. (1989). Overcoming contextual limitations on problem-solving transfer. J. Exp. Psychol. Learn. Mem. Cogn. 15, 1147–1156.
Charles, E. S. (2002). Using Complex Systems Thinking to Facilitate Shifts in Ontological Beliefs: A Qualitative Case Study Systematically Investigating a Learning and Teaching Context that Employs “StarLogo” Simulations and a One-on-One Coaching Methodology. Paper Presented at the 83rd Annual Meeting of the American Educational Research Association. New Orleans, LA.
Charles, E. S. (2003). An Ontological Approach to Conceptual Change: The Role that Complex Systems Thinking May Play in Providing the Explanatory Framework Needed for Studying Contemporary Sciences. Unpublished Doctoral [Dissertation], Concordia University, Montreal, Canada.
Cheng, P. C. H. (2002). Electrifying diagrams for learning: principles for complex representational systems. Cogn. Sci. 26, 685–736. doi:10.1207/s15516709cog2606_1
Chi, M. T. H. (2005). Commonsense conceptions of emergent processes: why some misconceptions are robust. J. Learn. Sci. 14, 161–199. doi:10.1207/s15327809jls1402_1
Chi, M. T. H., Feltovich, P. J., and Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cogn. Sci. 5, 121–152. doi:10.1207/s15516709cog0502_2
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences, 2nd Edn. Hillsdale, NJ: Erlbaum.
Colella, V. (2000). Participatory simulations: building collaborative understanding through immersive dynamic modeling. J. Learn. Sci. 9, 471–500. doi:10.1207/S15327809JLS0904_4
College Board. (2009). Science: College Boards Standards for College Success. Available at: http://professionals.collegeboard.com/profdownload/cbscs-science-standards-2009.pdf
Cooper, S., Perez, L. C., and Rainey, D. (2010). K-12 computational learning. Commun. ACM 53, 27–29. doi:10.1145/1839676.1839686
Danish, J. A. (2014). Applying an activity theory lens to designing instruction for learning about the structure, behavior, and function of a honeybee system. J. Learn. Sci. 23, 100–148. doi:10.1080/10508406.2013.856793
Day, S. B., and Goldstone, R. L. (2011). Analogical transfer from a simulated physical system. J. Exp. Psychol. Learn. Mem. Cogn. 37, 551–567. doi:10.1037/a0022333
Day, S. B., Goldstone, R. L., and Hills, T. (2010). The Effects of Similarity and Individual Differences on Comparison and Transfer. Proceedings of the Thirty-Second Annual Conference of the Cognitive Science Society. Portland, Oregon: Cognitive Science Society, 465–470.
Deneubourg, J., Aron, S., Goss, S., Pasteels, J., and Duerinck, G. (1986). Random behavior, amplification processes, and number of participants: how they contribute to the foraging properties of ants. Physica D 22, 176–186. doi:10.1016/0167-2789(86)90239-3
Detterman, D. R. (1993). “The case for prosecution: transfer as an epiphenomenon,” in Transfer on Trial: Intelligence, eds D. K. Detterman and R. J. Sternberg (Norwood, NJ: Ablex), 1–24.
Epstein, J. M. (2007). Generative Social Science: Studies in Agent-Based Computational Modeling. Princeton, NJ: Princeton University Press.
Epstein, J. M., and Axtell, R. (1996). Growing Artificial Societies: Social Science from the Bottom Up. Washington, DC: Brookings Institution Press.
Feltovich, P. J., Spiro, R. J., and Coulson, R. L. (1989). “The nature of conceptual understanding in biomedicine: the deep structure of complex ideas and the development of misconceptions,” in The Cognitive Sciences in Medicine, eds D. Evans and V. Patel (Cambridge, MA: MIT Press), 113–172.
Gentner, D. (2003). “Why we’re so smart,” in Language Inmind: Advances in the Study of Language and Thought, eds D. Gentner and S. Goldin-Meadow (Cambridge, MA: MIT Press), 195–236.
Gentner, D. (2005). “The development of relational category knowledge,” in Building Object Categories in Developmental Time, eds L. Gershkoff-Stowe and D. H. Rakison (Hillsdale, NJ: Erlbaum), 245–275.
Gick, M. L., and Holyoak, K. J. (1980). Analogical problem solving. Cogn. Psychol. 12, 306–355. doi:10.1016/0010-0285(80)90013-4
Gick, M. L., and Holyoak, K. J. (1983). Schema induction and analogical transfer. Cogn. Psychol. 15, 1–39. doi:10.1016/0010-0285(83)90002-6
Goldstone, R. L. (1994). Influences of categorization on perceptual discrimination. J. Exp. Psychol. Gen. 123, 178–200. doi:10.1037/0096-3445.123.2.178
Goldstone, R. L., and Barsalou, L. (1998). Reuniting perception and conception. Cognition 65, 231–262. doi:10.1016/S0010-0277(97)00047-4
Goldstone, R. L., and Janssen, M. A. (2005). Computational models of collective behavior. Trends Cogn. Sci. 9, 424–430. doi:10.1016/j.tics.2005.07.009
Goldstone, R. L., Landy, D., and Brunel, L. (2011). Improving perception to make distant connections closer. Front. Percept. Sci. 2:385. doi:10.3389/fpsyg.2011.00385
Goldstone, R. L., and Sakamoto, Y. (2003). The transfer of abstract principles governing complex adaptive systems. Cogn. Psychol. 46, 414–466. doi:10.1016/S0010-0285(02)00519-4
Goldstone, R. L., and Son, J. Y. (2005). The transfer of scientific principles using concrete and idealizedsimulations. J. Learn. Sci. 14, 69–110. doi:10.1207/s15327809jls1401_4
Goldstone, R. L., and Wilensky, U. (2008). Promoting transfer by grounding complex systems principles. J. Learn. Sci. 17, 465–516. doi:10.1080/10508400802394898
Goodwin, C. (1996). “Transparent vision,” in Interaction and Grammar, eds O. Elinor, E. A. Schegloff, and T. Sandra (Cambridge: Cambridge University Press), 370–404.
Guzdial, M. (2008). Paving the way for computational thinking. Commun. ACM 51, 25–27. doi:10.1145/1378704.1378713
Hayes, J. R., and Simon, H. A. (1977). “Psychological differences among problem isomorophs,” in Cognitive Theory, Vol. 2, eds N. J. Castellan Jr., D. B. Pisoni, and G. R. Potts (Hillsdale, NJ: Erlbaum), 21–41.
Hmelo-Silver, C. E., Marathe, S., and Liu, L. (2007). Fish swim, rocks sit, and lungs breathe: expert-novice understanding of complex systems. J. Learn. Sci. 16, 307–331.
Hmelo-Silver, C. E., and Pfeffer, M. G. (2004). Comparing expert and novice understanding of a complex system from the perspective of structures, behaviors, and functions. Cogn. Sci. 28, 127–138. doi:10.1207/s15516709cog2801_7
Ho, C. H. (2001). Some phenomena of problem decomposition strategy for design thinking: differences between novices and experts. Des. Stud. 22, 27–45. doi:10.1016/S0142-694X(99)00030-7
Hughes, R. L. (2003). The flow of human crowds. Annu. Rev. Fluid Mech. 35, 169–182. doi:10.1146/annurev.fluid.35.101101.161136
Jacobson, M. J. (2001). Problem solving, cognition, and complex systems: differences between experts and novices. Complexity 6, 41–49. doi:10.1002/cplx.1027
Jacobson, M. J., and Wilensky, U. (2006). Complex systems in education: scientific and educational importance and research challenges for the learning sciences. J. Learn. Sci. 15, 11–34. doi:10.1207/s15327809jls1501_4
Klopfer, E., Yoon, S., and Um, T. (2005). Teaching complex dynamic systems to young students with StarLogo. J. Comput. Math. Sci. Teach. 24, 157–178.
Kynigos, C. (2007). Using half-baked microworlds to challenge teacher educators’ knowing. J. Comput. Math Learn. 12, 87–111. doi:10.1007/s10758-007-9114-2
Lave, J. (1988). Cognition in Practice: Mind, Mathematics, and Culture in Everyday Life. New York: Cambridge University Press.
Levy, S. T., and Wilensky, U. (2008). Inventing a “mid-level” to make ends meet: reasoning through the levels of complexity. Cogn. Instr. 26, 1–47. doi:10.1080/07370000701798479
Levy, S. T., and Wilensky, U. (2009). Students’ learning with the connected chemistry (CC1) curriculum: navigating the complexities of the particulate world. J. Sci. Educ. Technol. 18, 243–254. doi:10.1007/s10956-009-9145-7
Livingston, K. R., Andrews, J. K., and Harnad, S. (1998). Categorical perception effects induced by category learning. J. Exp. Psychol. Learn. Mem. Cogn. 24, 732–753.
Lobato, J. (2012). The actor-oriented transfer perspective and its contributions to educational research and practice. Educ. Psychol. 47, 232–247. doi:10.1080/00461520.2012.693353
Loewenstein, J., and Gentner, D. (2005). Relational language and the development of relational mapping. Cogn. Psychol. 50, 315–353. doi:10.1016/j.cogpsych.2004.09.004
Miller, J. H., and Page, S. E. (2007). Complex Adaptive Systems: An Introduction to Computational Models of Social Life. Princeton, NJ: Princeton University Press.
Narayanan, N. H., and Hegarty, M. (1998). On designing comprehensible interactive hypermedia manuals. Int. J. Hum. Comput. Stud. 48, 267–301. doi:10.1006/ijhc.1997.0169
National Research Council. (1999). How People Learn: Brain, Mind, Experience, and School. Washington, DC: The National Academy Press.
National Research Council. (2010). Report of a Workshop on the Scope and Nature of Computational Thinking. Washington, DC: The National Academies Press.
National Research Council. (2011). Learning Science through Computer Games and Simulations. Washington, DC: The National Academies Press.
Nersessian, N. J. (1992). “How do scientists think? Capturing the dynamics of conceptual change in science,” in Cognitive Models of Science, ed. R. N. Giere (Minneapolis, MN: University of Minnesota Press), 3–45.
Palumbo, D. B. (1990). Programming language/problem-solving research: a review of relevant issues. Rev. Educ. Res. 1, 65–89. doi:10.3102/00346543060001065
Papert, S. (1991). “Situating constructionism,” in Constructionism, eds I. Harel and S. Papert (Norwood, NJ: Ablex), 1–11.
Pea, R. D., and Kurland, D. M. (1984). On the cognitive effects of learning computer programming. New Ideas Psychol. 2, 137–168. doi:10.1016/0732-118X(84)90018-7
Penner, D. E. (2000). Explaining systems: investigating middle school students’ understanding of emergent phenomena. J. Res. Sci. Teach. 37, 784–806. doi:10.1002/1098-2736(200010)37:8<784::AID-TEA3>3.0.CO;2-E
Penner, D. E. (2001). “Complexity, emergence, and synthetic models in science education,” in Designing for Science, eds K. Crowley, C. D. Schunn, and T. Okada (Mahwah, NJ: Lawrence Erlbaum Associates, Inc.), 177–208.
Penner, D. E., Lehrer, R., and Schauble, L. (1998). From physical models to biomechanics: a design-based modeling approach. J. Learn. Sci. 7, 429–449. doi:10.1080/10508406.1998.9672060
Qualls, J., and Sherrell, L. (2010). Why computational thinking should be integrated into the curriculum. J. Comput. Sci. Coll. 25, 66–71.
Quellmalz, E. S., Timms, M. J., Silberglitt, M. D., and Buckley, B. C. (2012). Science assessments for all: integrating science simulations into balanced state science assessment systems. J. Res. Sci. Teach. 49, 363–393. doi:10.1002/tea.21005
R Core Team. (2008). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available at: https://www.R-project.org/
Railsback, S., Lytinen, S., and Jackson, S. (2006). Agent-based simulation platforms: review and development recommendations. Simulation 82, 609–623. doi:10.1177/0037549706073695
Rand, W., Novak, M., and Wilensky, U. (2007). BEAGLE Curriculum. Evanston, IL: Center for Connected Learning and Computer-Based Modeling, Northwestern University.
Reed, W. M., and Palumbo, D. B. (1988). The effect of the BASIC programming language on problem-solving skills and computer anxiety. Comput. Sch. 4, 91–101. doi:10.1300/J025v04n03_11
Reeves, L., and Weisberg, R. W. (1994). The role of content and abstract information in analogical transfer. Psychol. Bull. 115, 381–400. doi:10.1037/0033-2909.115.3.381
Resnick, M. (1994). Turtles, Termites and Traffic Jams: Explorations in Massively Parallel Microworlds. Cambridge, MA: MIT Press.
Resnick, M. (1996). Beyond the centralized mindset. J. Learn. Sci. 5, 1–22. doi:10.1207/s15327809jls0501_1
Resnick, M., and Wilensky, U. (1998). Diving into complexity: developing probabilistic decentralized thinking through roleplaying activities. J. Learn. Sci. 7, 153–171. doi:10.1207/s15327809jls0702_1
Roberson, D., Davies, I., and Davidoff, J. (2000). Color categories are not universal: replications and new evidence in favor of linguistic relativity. J. Exp. Psychol. Gen. 129, 369–398. doi:10.1037/0096-3445.129.3.369
Romberg, T., Carpenter, T., and Kwako, J. (2005). “Standards based reform and teaching for understanding,” in Understanding Mathematics and Science Matters, eds T. Romberg, T. Carpenter, and F. Dremock (Mahwah, NJ: Erlbaum), 3–26.
Ross, B. H. (1984). Remindings and their effects in learning a cognitive skill. Cogn. Psychol. 16, 371–416. doi:10.1016/0010-0285(84)90014-8
Ross, B. H. (1987). This is like that: the use of earlier problems and the separation of similarity effects. J. Exp. Psychol. Learn. Mem. Cogn. 13, 629–639.
Ross, B. H. (1989). Distinguishing types of superficial similarities: different effects on the access and use of earlier problems. J. Exp. Psychol. Learn. Mem. Cogn. 15, 456–468.
Scaife, M., and Rogers, Y. (1996). External cognition: how do graphical representations work? Int. J. Hum. Comput. Stud. 45, 185–213. doi:10.1006/ijhc.1996.0048
Sengupta, P., and Wilensky, U. (2009). Learning electricity with NIELS: thinking with electrons and thinking in levels. Int. J. Comput. Math. Learn. 14, 21–50. doi:10.1007/s10758-009-9144-z
Sherin, B. (2001). A comparison of programming languages and algebraic notation as expressive languages for physics. Int. J. Comput. Math. Learn. 6, 1–61. doi:10.1023/A:1011434026437
Simon, H. A. (1980). “Problem solving and education,” in Problem Solving and Education: Issues in Teaching and Research, eds D. T. Tuma and R. Reif (Hillsdale, NJ: Erlbaum), 81–96.
Soloway, E. (1993). Should we teach students to program? Commun. ACM 36, 21–24. doi:10.1145/163430.164061
Spencer, R. M., and Weisberg, R. W. (1986). Context-dependent effects on analogical transfer. Mem. Cognit. 14, 442–449. doi:10.3758/BF03197019
Stieff, M., and Wilensky, U. (2003). Connected chemistry – incorporating interactive simulations into the chemistry classroom. J. Sci. Educ. Technol. 12, 285–302. doi:10.1023/A:1025085023936
Swan, K., and Black, J. B. (1987). The Cross-Contextual Transfer of Problem Solving Skills (CTT Report 87-3). New York: Teachers College, Columbia University, Department of Communication, Computing, and Technology.
Tullis, J. G., Braverman, M., Ross, B. H., and Benjamin, A. S. (2014). Remindings influence the interpretation of ambiguous stimuli. Psychon. Bull. Rev. 21, 107–113. doi:10.3758/s13423-013-0476-2
Wilensky, U. (1996). Modeling rugby: kick first, generalize later? Int. J. Comput. Math. Learn. 1, 124–131.
Wilensky, U. (1997). What is normal anyway? Therapy for epistemological anxiety. Educ. Stud. Math. 33, 171–202. doi:10.1023/A:1002935313957
Wilensky, U. (1999a). NetLogo. Evanston, IL: Center for Connected Learning and Computer-Based Modeling, Northwestern University. Available at: http://ccl.northwestern.edu/netlogo/
Wilensky, U. (1999b). “GasLab: an extensible modeling toolkit for exploring micro-and-macro-views of gases,” in Computer Modeling and Simulation in Science Education, eds N. Roberts, W. Feurzeig, and B. Hunter (Berlin: Springer Verlag), 151–178.
Wilensky, U. (2001). “Modeling nature’s emergent patterns with multi-agent languages,” in Proceedings of EuroLogo 2001, Linz, Austria.
Wilensky, U., and Abrahamson, D. (2006). Is a Disease Like a Lottery? Classroom Networked Technology that Enables Student Reasoning about Complexity. Paper Presented at the Annual Meeting of the American Educational Research Association. San Francisco, CA. Available at: http://ccl.northwestern.edu/papers.shtml
Wilensky, U., and Reisman, K. (1998). ConnectedScience: learning biology through constructing and testing computational theories – an embodied modeling approach. Int. J. Complex Syst. 234, 1–12.
Wilensky, U., and Reisman, K. (2006). Thinking like a wolf, a sheep or a firefly: learning biology through constructing and testing computational theories – an embodied modeling approach. Cogn. Instr. 24, 171–209. doi:10.1207/s1532690xci2402_1
Wilensky, U., and Resnick, M. (1999). Thinking in levels: a dynamic systems perspective to making sense of the world. J. Sci. Educ. Technol. 8, 3–19. doi:10.1023/A:1009421303064
Zemel, A., and Koschmann, T. (2014). ‘Put your fingers right in here’: learnability and instructed experience. Discourse Stud. 16, 163–183. doi:10.1177/1461445613515359
Appendix
A. Complex Systems Concepts Inventory
1. There is a world made of black and white squares. Each square has four neighbor squares: one above, one below, one to the left, and one to the right. The squares all change color from one time to the next by the following rule: if a square has more than one black square neighbor, then it will be black. Otherwise, it will be white. All of the squares change at the same time. If the world starts with the pattern:

2. Wherever there is an A in this world, on the next generation it grows a B below it (if there is not already one there). Wherever there is a B, on the next generation, it grows a B to its left and an A below it (if these letters are not there already). What does a world that initially looks like this:

3. There are four kinds of soda in a city: Yaz, Jot, Mup, and Fet. The people in the city are very influenced by each other, and if somebody sees another person drinking a soda, they will then drink the same soda next time. If every person drinks a soda every day in a café, but the four soft drinks start off equally popular, then in three years, what is the likely outcome?
A. Everybody will be drinking the same soft drink.
B. All four of the soft drinks will still be about equally popular.
C. One of the soft drinks will be drunk by about 70% of the citizens and the three other soft drinks will be drunk by about 10% of the citizens.
D. The four soft drinks will be ordered in their popularity: 40, 30, 20, and 10%.
4. There is a machine that produces 10 spiky blobs per minute. The machine is the box at the bottom of the scene below. Each of the spiky blobs pops about 2 min after it has been created. Once created, the blobs randomly move around the scene. If more than four blobs fall on the circular sensor at the top of the scene at the same time, then the sensor turns off the machine and it stops producing blobs. Whenever there are fewer than four blobs on the sensor, the machine will be on. What will happen in the scene over time?
A. There will be more and more blobs in the scene over time, until the machine or the sensor breaks.
B. The number of blobs will increase until a certain number of blobs is reached, and then this will roughly be the stable number of blobs in the scene.
C. There will be fewer and fewer blobs in the scene because they pop after awhile.
D. As more and more blobs appear in the scene, the sensor will cause the machine to produce even more blobs, until the space is completely filled with blobs.
5. The trees in the forest below follow the following rule: they will catch fire if a tree above, below, left or right of them catches fire. Diagonally positioned trees (e.g., a tree above and to the left) are too far away to spread a fire. If the tree in the lower left hand corner of this forest catches fire, how many trees in all will eventually catch fire?
_______ trees will catch fire in all.
6. Two balls rolling the same speed start off heading in random directions. As they roll, the black ball turns slightly toward the white ball and the white ball turns slightly toward the black ball, but neither slows down. What pattern will they end up forming?
A. Each ball will trace out a circle, but the two circles may be different.
B. Both of the balls will trace out the same circle.
C. Both balls will end up converging on a single point.
D. The balls will trace out a single line and oscillate back and forth on this line.
7. The hiker below wants to get to the highest peak on the mountain range. Unfortunately, it is very foggy and he can only see a couple of feet in any direction. He decides to walk in whatever direction will raise him up the highest amount. What does adding in a bit of randomness to his movements cause him to do?
A. Adding randomness will make it more likely that he will end up in a valley between two peaks.
B. Adding randomness to his movements will make the trip more interesting for him and will probably help him to stay motivated.
C. Randomness in his movements will help him move past peaks that are not highest overall.
D. If the peak is located in a surprising location, then randomness is needed to find the location. Moving randomly is the only strategy that will work if the peak could be anywhere.
8. Instead of storing the exact pattern of zebra stripes in zebra DNA, how could cells interact that could cause stripes to eventually be formed?
9. [continued from #8] In what simple way could this interaction be slightly altered to create spotted cheetah fur rather than striped zebra fur?
10. Do biological organisms need complex, high-level rules (i.e., “grow in a spiral pattern”) to form the following intricate designs?
(circle one) YES or NO. If so, why? If not, why not?
11. Some species of fireflies will begin to synchronize their flashing after spending some time together in an area. Canadian geese typically fly in a V formation. In what ways might the formation of these reliable patterns be similar?
B. Version A
1. Wherever there is an A in this world, on the next generation it grows a B below it (if there’s not already one there). Wherever there is a B, on the next generation it grows a B to its left and an A below it (if these letters are not there already). What does a world that initially looks like this:

2. large group of children live in a neighborhood. Each child randomly prefers a red, blue, orange, or green toy, so that these colors are equally preferred across the neighborhood. The children are constantly moving around the neighborhood and playing with other kids. As they randomly move about, they look to see the preferred color of the most other kids around them. They switch their toy preference to the one preferred by the most children that they see at any moment. What will happen to toy preferences over time?
A. Everyone will eventually come to prefer the same toy
B. Toy preferences will not shift much at all
C. Toy preferences will shift back and forth a lot, but the four toy colors will always return to an equal balance
D. The toy preferences will have popularities of about 60, 20, 15, and 5%
3. A pattern of ridges and troughs can be formed when varnish begins to wrinkle and lift off of wood, as shown below. How can this complex pattern occur?
4. You are dropping a set of balls through an obstacle course (as shown below). You want all the balls to fall all the way through the obstacles (the black arcs). Why might it be important to add in a bit of random movement to the balls as they fall?
5. Seashells are often formed in very complex spiral patterns. Do you think the plans for these elaborate spirals are present in an animal’s DNA like a blueprint? (circle one) YES or NO. If so, why? If not, why not?
6. Some groups of fireflies will begin to synchronize their flashing after spending some time together in an area. How might large groups synchronize their flashing?
C. Version B
1. There is a world made of black and white squares. Each square has four neighbor squares: one above, one below, one to the left, and one to the right. The squares all change color from one time to the next by the following rule: if a square has more than one black square neighbor, then it will be black. Otherwise, it will be white. All of the squares change at the same time. If the world starts with the pattern:

2. There are four kinds of soda in a city: Yaz, Jot, Mup, and Fet. The people in the city are very influenced by each other, and if somebody sees another person drinking a soda, they will then drink the same soda next time. If every person drinks a soda every day in a café, but the four soft drinks start off equally popular, then in 3 years, what is the likely outcome?
A. Everybody will be drinking the same soft drink.
B. All four of the soft drinks will still be about equally popular.
C. One of the soft drinks will be drunk by about 70% of the citizens and the three other soft drinks will be drunk by about 10% of the citizens.
D. The four soft drinks will be ordered in their popularity: 40, 30, 20, and 10%.
3. Instead of storing the exact pattern of zebra stripes in zebra DNA, what is a simple rule for how cells interact that could cause stripes to eventually be formed?
4. The hiker below wants to get to the highest peak on the mountain range. Unfortunately, it is very foggy and he can only see a couple of feet in any direction. He decides to walk in whatever direction will raise him up the highest amount. Why might it be important to add in a bit of randomness to his movements?
5. Do biological organisms need complex, high-level rules (i.e., “grow in a spiral pattern”) to form the following intricate design? (circle one) YES or NO If so, why? If not, why not?
6. Canadian geese typically fly in a V formation. If there is no special geese leader, how might they arrange themselves in these patterns?
Keywords: complex systems, programming, transfer, agent-based modeling, computational thinking
Citation: Tullis JG and Goldstone RL (2017) Instruction in Computer Modeling Can Support Broad Application of Complex Systems Knowledge. Front. Educ. 2:4. doi: 10.3389/feduc.2017.00004
Received: 19 December 2016; Accepted: 13 February 2017;
Published: 06 March 2017
Edited by:
Jesus de la Fuente, University of Almería, SpainReviewed by:
Dor Abrahamson, University of California Berkeley, USANicole D. Anderson, MacEwan University, Canada
Copyright: © 2017 Tullis and Goldstone. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jonathan G. Tullis, dHVsbGlzQGVtYWlsLmFyaXpvbmEuZWR1
 Jonathan G. Tullis
Jonathan G. Tullis Robert L. Goldstone
Robert L. Goldstone