What’s the matter in phytoplankton? Highlighting the importance of stoichiometric traits in lake ecosystem models

Introduction: Accurate models of lake primary production are crucial for understanding ecosystem function and predicting ecosystem responses to global change. However, current research in lake ecosystem modeling has emphasized environmental characteristics while less work has considered phytoplankton stoichiometric traits. Importantly, these traits link resource availability to primary production via organismal metabolism and thus are critical to predicting ecosystem function.

Methods: Here, we use an existing database of phytoplankton traits and lake ecosystem models to demonstrate that phytoplankton minimum quotas for nitrogen and phosphorus significantly influence predictions of lake gross primary production. Additionally, we compare how different parameterizations of phytoplankton stoichiometry affect modeled gross primary production. Finally, we evaluate the ability of the models to capture observed patterns in gross primary production and seston stoichiometry for lakes in the Northern Hemisphere.

Results and discussion: We argue that parameterization and calibration of phytoplankton stoichiometric traits will improve lake ecosystem models and are critical for obtaining better estimates of lake primary production.

1 Introduction

Primary production is a globally important biological process that influences all three major biogeochemical cycles - carbon (C), nitrogen (N), and phosphorus (P). Because lakes are found at relatively low points in the landscape and tend to have high hydrologic residence times, their primary production significantly regulates biogeochemical cycles (Schindler, 2009; Williamson et al., 2009), for example, while lakes cover 2-3% of Earth’s surface they bury more C per year than all the oceans combined (Dean and Gorham, 1998; Mendonça et al., 2017). Specifically, lake phytoplankton integrate materials from across the landscape via metabolic processes such as primary productivity (Dokulil and Qian, 2021). However, rates of lake primary productivity are changing in response to environmental stressors and these changes have important implications for lake food web productivity and carbon sequestration (Heathcote et al., 2015; Mendonça et al., 2017).

Since macronutrients, such as N and P, often limit phytoplankton growth (Elser et al., 2007; Harpole et al., 2011), nutrient uptake and usage traits can influence rates of primary productivity and should be included in our understanding of lake primary productivity (Tilman, 1977; Litchman and Klausmeier, 2008; Litchman, 2022). While nutrient supply controls primary production across broad spatial scales (Hanson, 2004; Kelly et al., 2018; Olson and Jones, 2022), the ability of phytoplankton to take up and convert available nutrients to growth and biomass links nutrient supply to organismal-scale processes via supply and demand and, thereby, to broader patterns of primary productivity (Litchman et al., 2007). Therefore, traits that determine nutrient uptake and resource use and efficiency connect resource availability and growth at the organism level and primary production at the ecosystem scale. We refer to these traits as “stoichiometric traits”.

A common way to conceptualize nutrient limitation is Liebig’s law of the minimum, which states that growth rates of primary producers will be limited by the single nutrient that is the least environmentally available in relation to biological demand (von Liebig, 1855; Sterner and Elser, 2002). A change in the limiting element directly affects the biomass yield or rate of production (Reynolds, 1992; Kaspari and Powers, 2016). Stoichiometric traits describe how nutrients limit organismal metabolic processes and have roots in nutrient limitation theory, e.g. properties such as minimum cell quota, half saturation constants for growth and uptake, maximum growth and uptake rates. These traits can then be mathematically represented using functional responses. The advantage of these mathematically defined physiological responses is that they can be easily incorporated into ecosystem models.

Our understanding of lake primary productivity has primarily focused on physical and chemical drivers such as nutrient loading, climate, hydrology, light availability and lake morphology (Vollenweider, 1968; Mooij et al., 2010; Kelly et al., 2018; Olson and Jones, 2022; Puts et al., 2022) while less attention has been paid to phytoplankton physiology. For example, process-based lake ecosystem models like MyLake or PCLake+ prioritize catchment and physical factors such as land use and lake mixing dynamics (Saloranta and Andersen, 2007; Janssen et al., 2019). While phytoplankton traits are commonly studied in marine ecosystem models (Neumann, 2000; Allen et al., 2001; Finkel et al., 2010; Bonachela et al., 2016), few studies address trait-based models in freshwaters [but see Zwart et al. (2015); Krishna et al. (2021); Litchman and Thomas (2023)]. Thus, a deeper exploration of the effect of phytoplankton stoichiometric traits in lake ecosystem models of primary productivity is warranted.

Phytoplankton growth can be modeled with static and dynamic stoichiometric formulations that differ in their determinants: external nutrient supply and internal cellular quotas. The static approach is typically represented using Monod kinetics (Huisman and Weissing, 1994) where external nutrient supply determines phytoplankton specific growth rate. In reality, phytoplankton growth is a function of a dynamic intracellular stoichiometry and changes with nutrient supply concentrations (Hillebrand et al., 2013; Isanta-Navarro et al., 2024; Klip et al., 2024). Dynamic phytoplankton stoichiometry can be represented using the Droop formulation where internal cellular nutrient quotas govern phytoplankton growth rate. This allows phytoplankton to accumulate higher internal nutrient quotas under nutrient replete conditions.

Since choices regarding model structure and parameterization can bias predictions (Skogen et al., 2021), modeling choices require more careful consideration. Thus, in this paper we explore how model structure and trait parameterization affect lake primary productivity by integrating process-models with data. We have three objectives:

1. Assess how phytoplankton stoichiometric traits drive patterns of lake primary productivity across P- and N:P supply gradients.

2. Identify phytoplankton trait parameters that dictate patterns of lake primary productivity.

3. Evaluate the ability of our static and dynamic model structures that differ in their representation of phytoplankton stoichiometry to generate observed patterns in lake primary productivity and seston stoichiometry.

We extend a rich body of research using these particular models to understand lake ecosystem primary productivity (Klausmeier et al., 2004b; Jäger and Diehl, 2014; Kelly et al., 2018; Olson and Jones, 2022; Oleksy et al., 2022) by evaluating how model structure and phytoplankton stoichiometry influence lake primary productivity across gradients of both N and P. We compare model predictions to observational data from three lake data sets from the Northern Hemisphere to qualitatively assess how well the models replicate observed gross primary productivity and seston stoichiometry. We then highlight further modeling efforts and data requirements for confronting these models to better address the role of phytoplankton traits in ecosystem function.

2 Methods

2.1 Methods overview

To accomplish Objective 1, we simulated gross primary productivity (GPP) and phytoplankton stoichiometry across P- and N:P supply gradients with two model structures representing static and dynamic phytoplankton stoichiometry. We parameterized these models using stoichiometric traits representing diatoms, green-algae, cyanobacteria, and an “emergent” group. We then conducted a parameter sensitivity analysis with both model structures to assess which traits most strongly influence lake GPP and phytoplankton stoichiometry (Objective 2). Finally, we leveraged three pre-existing data sets of lakes in the Northern Hemisphere to compare how well the two model structures replicated observed patterns in lake GPP and phytoplankton stoichiometry (Objective 3).

2.2 Objective 1: model simulation experiments to assess how phytoplankton stoichiometric traits drive patterns of lake primary productivity

2.2.1 Trait database

To explore how phytoplankton trait parameterization influenced model predictions of GPP and phytoplankton stoichiometry we leveraged a previously compiled dataset of phytoplankton stoichiometric traits (Edwards et al., 2015). Traits of interest included nutrient half-saturation constants for N and P (K_N mg N m^-3; K_P mg P m^-3), minimum cell quotas of N and P relative to cell C content (N,P:C quota = Q_minN,P mg N,P mg C^-1) and maximum uptake rates for N and P (Vmax_N,P mg N,P mg C^-1). This dataset compiles trait data on 384 phytoplankton strains, of which 211 freshwater and 173 marine entries, derived from culture experiments where the limiting nutrient was ammonium, nitrate, or phosphate. The five most common taxa were diatoms (134), green-algae (120), and cyanobacteria (47); all other taxa had less than ten entries.

We selected only freshwater taxa of the green-algae, cyanobacteria, and diatom groups since these are considered major groups of freshwater phytoplankton (Dodds, 2002) and they had the most abundant trait data in the database. Several traits, including Q_minN,P and Vmax_N,P, were reported as µmol N,P cell^-1 which differ from units required in our models (Table 1). Consequently we converted them to mg N,P mg C^-1 using the median C per cell^-1 for each group: green-algae = 3. 9 * 10^-6 mg C cell^-1 and cyanobacteria = 0.37 * 10^-6 mg C cell^-1. Data for freshwater diatoms C cell^-1 were unavailable and in its place, we utilized the median of marine diatoms: 1.2 * 10^-6 mg C cell^-1. For each group, we obtained the median trait parameters described above. In addition, we calculated median trait values across all groups to represent “emergent phytoplankton traits” (Table 1; Figure 1). As the Edwards et al. (2015) data set did not include maximum growth rates (µ_max) this information was extracted from Schwaderer et al. (2011) and median values for each group were calculated as above.

Table 1

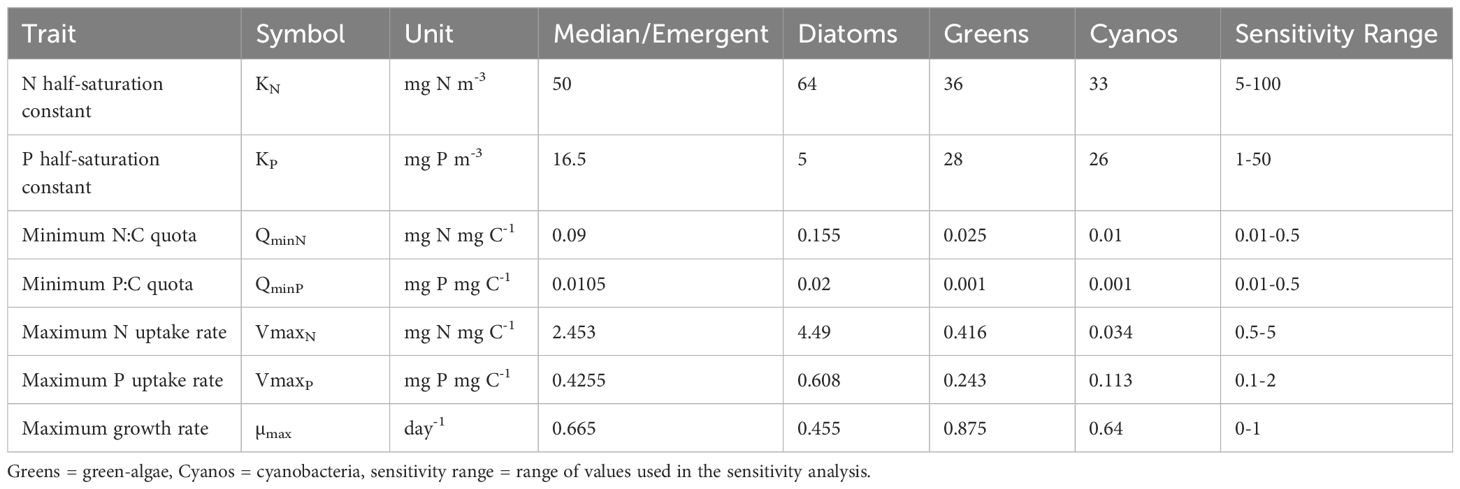
Table 1. Overview of group-specific phytoplankton stoichiometric traits used to parameterize the two model structures.

Figure 1

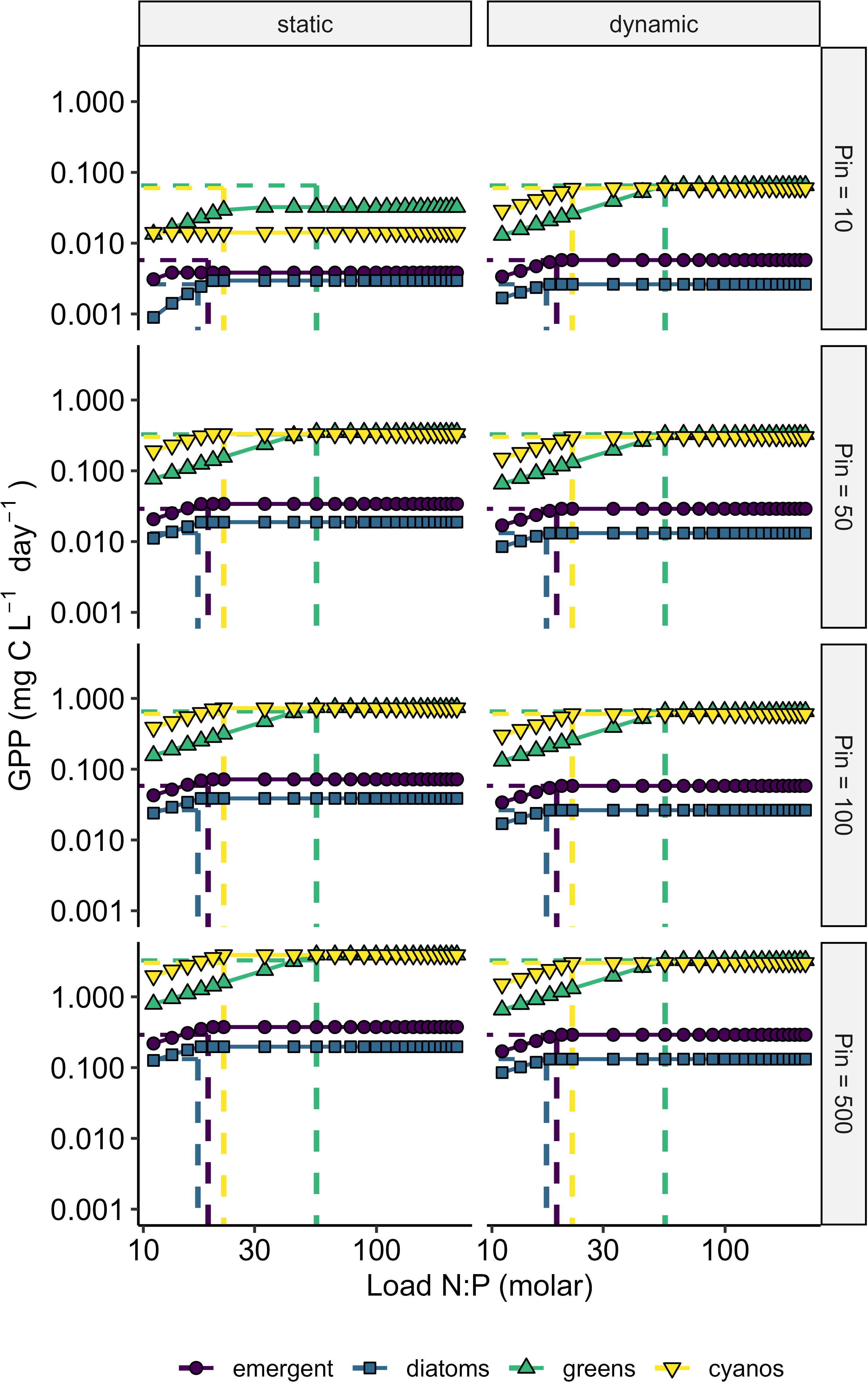
Figure 1. Static and dynamic model simulations showing variation in lake gross primary productivity (GPP; mg C L^-1 day^-1) as a function of nutrient loads, stoichiometry, and model structure. Gross primary productivity increases linearly with load N:P before plateauing once load N:P is equal to the minimum cell N:P quota. Dashed vertical lines show the minimum cell N:P quotas for the respective algae groups. Columns show the static vs. dynamic structure and rows show the different P-loading scenarios (Pin = 10, 50, 100, and 500 ug L^-1). Greens = green algae and cyanos = cyanobacteria.

Phytoplankton trait parameters showed considerable variation, frequently extending across multiple orders of magnitude within and between phytoplankton groups (Supplementary Figure S1; Table 1). Generally, parameters for P (n = 267) were better represented than those for N (n = 114), and green-algae (n = 230) were better represented than diatoms (n = 123 including three marine diatoms with measured carbon cell content) or cyanobacteria (n = 80). While parameters describing affinity and efficiency for nutrients and maximum growth rates were well described (K_P = 92, K_N = 44, Q_minP = 83, Q_minN = 26, Vmax_P = 83, Vmax_N = 44), there were very few measurements of cell C content (n = 6 across all phytoplankton groups). Similarly, there was only one observation of cell C content for green-algae. These missing data measurements likely biased our conversions of phytoplankton trait parameters from µmol cell^-1 to mg C^-1.

2.2.2 Model structure overview

The first model (static model) treats phytoplankton stoichiometry statically. Lake morphology is defined by a mix-depth layer ($zmix$) and surface area ($SA$) with a hydrologic inflow and outflow ($Q_{in}$=$Q_{out}$) and constant volume. Algal biomass is a function of a homogenous phytoplankton community evenly distributed throughout the water column (A; Equation 1). Phytoplankton are lost via sedimentation (v), mortality (l_A) and removal through hydrologic outflows (Q_out).

$\begin{array}{ll}\frac{dA}{dt}=A\ast \left(r_{s,d}-l_A-\frac{v}{z_{mix}}-\frac{Q_{out}}{SA\ast z_{mix}}\right)& (1)\end{array}$

Phytoplankton biomass increases through nutrient-limited growth. Specific growth rate ($r_s$; Equation 2) is a function of maximum growth rate (${\mu }_{max}$) and is strictly limited by N or P ($N,P$) following Liebig’s Law of the minimum. Nitrogen or P limitation is determined by the nutrient-specific half-saturation constants for growth ($K_N, K_P$).

$\begin{array}{ll}{r}_s={\mu }_{max}\ast min\left(\frac{N}{K_N+N},\frac{P}{K_P+P}\right)& (2)\end{array}$

Phytoplankton have access to bioavailable N and P in the well-mixed water column ($N$, $P$; Equation 3). These nutrient pools increase via external supply of nutrients supplied via hydrologic inflows ($N_{in}$, $P_{in}$), partial remineralization of dead phytoplankton ($l_A$) and nutrients are lost through uptake for phytoplankton growth and hydrologic outflow. Remineralization and uptake parameters are multiplied by a static minimum N or P quota (Q_minN, Q_minP).

$\begin{array}{ll}\frac{dN}{dt}=\frac{Q_{in}}{SA\ast z_{mix}}\ast (N_{in}-N)+Q_{minN}\ast l_A\ast A-Q_{minN}\ast r_s\ast A& \text{(3a)}\end{array}$

$\begin{array}{ll}\frac{dP}{dt}=\frac{Q_{in}}{SA\ast z_{mix}}\ast (P_{in}-P)+Q_{minP}\ast l_A\ast A-Q_{minP}\ast r_s\ast A& \text{(3b)}\end{array}$

The second model (dynamic model) treats phytoplankton stoichiometry dynamically (Klausmeier et al., 2004b; Hall, 2009). Phytoplankton growth follows the Droop formulation (Droop, 1968) where growth is a function of a dynamic internal cellular quota rather than external nutrient supply as in the static model ($r_d$; Equation 4).

$\begin{array}{ll}{r}_d={\mu }_{max}\ast min\left(1-\frac{Q_{minN}}{Q_N},1-\frac{Q_{minP}}{Q_P}\right) & (4)\end{array}$

Following Leibig’s law of the minimum phytoplankton growth is limited by either N or P where $Q_{minN}$ and $Q_{minP}$ are minimum cell quotas necessary to sustain growth. Cell quotas are dynamic and increase in response to external nutrient concentrations and decrease in response to demand for growth ($Q_N$, $Q_P$; Equation 5). Where $Vma{x}_N$ and $Vma{x}_P$ are maximum nutrient uptake rates for N and P, respectively.

$\begin{array}{ll}\frac{d{Q}_N}{dt}=Vma{x}_N\ast \left(\frac{N}{K_N+N}\right)-r_d\ast Q_N& \text{(5a)}\end{array}$

$\begin{array}{ll}\frac{d{Q}_P}{dt}=Vma{x}_P\ast \left(\frac{P}{K_P+P}\right)-r_d\ast Q_P& \text{(5b)}\end{array}$

Bioavailable N and P concentrations in the water column (Equation 6) are controlled by hydrologic inflows, partial remineralization, and phytoplankton uptake.

$\begin{array}{ll}\frac{dN}{dt}=\frac{Q_{in}}{SA\ast z_{mix}}\ast (N_{in}-N)+A\ast \left(-Vma{x}_N\ast \left(\frac{N}{K_N+N}\right)\right)+l_A\ast Q_N& \text{(6a)}\end{array}$

$\begin{array}{ll}\frac{dP}{dt}= \frac{Q_{in}}{SA\ast z_{mix}}\ast (P_{in}-P)+A\ast \left(-Vma{x}_P\ast \left(\frac{P}{K_P+P}\right)\right)+l_A\ast Q_P& \text{(6b)}\end{array}$

A full description of state variables and parameters can be found in Supplementary Table S1.

2.2.3 Model simulation experiments

We performed two model experiments to evaluate how static and dynamic phytoplankton stoichiometry and differences in phytoplankton traits influenced patterns of modeled GPP and phytoplankton stoichiometry across gradients of N and P. First, we ran model simulations using the emergent trait parameterization for different P inflow concentrations (P_in) representing nutrient-poor to nutrient-rich lakes (P_in = 10, 50, 100, and 500 µg L^-1). N inflow concentrations (N_in) were scaled to P_in using N:P ratios ranging from 10 to 50 molar. We chose this range of N:P supply ratios as it represents the range where phytoplankton N:P increases linearly with supply N:P (Klausmeier et al., 2004b).

Second, we performed the same set of simulations with different stoichiometric trait parameterizations reflecting the median trait values for the three major groups of phytoplankton, green-algae, cyanobacteria, and diatoms, as well as the emergent phytoplankton group (Edwards et al., 2015; Table 1; Supplementary Figure S1). In this second experiment, our goal was to investigate whether changes in group-specific trait values influenced patterns of modeled GPP and phytoplankton stoichiometry and how this may interact with the static and dynamic model structures.

2.3 Objective 2: sensitivity analysis to identify key phytoplankton trait parameters

Using both model structures, we performed a parameter sensitivity analysis to determine which stoichiometric traits had the strongest effect on modeled GPP and phytoplankton stoichiometry. Holding all other parameters constant at the emergent trait parameterization, we ran each model across a gradient of nutrient supply, Pin ranged from 5 to 500 µg P L^-1 with Nin inflow concentrations scaled to Pin using N:P ranging from 10 to 50 molar, and a gradient of trait values: $K_P$ = 1-50 mg P m^-3, $K_N$ = 5-100 mg N m^-3, $min{Q}_P$ = 0.01-0.5 mg P mg C^-1, $min{Q}_N$ = 0.01-0.5 mg N mg mg C^-1, $Vma{x}_P$ = 0.1-2 mg P mg C^-1, $Vma{x}_N$ = 0.5-5 mg N mg C^-1, ${\mu }_{max}$=0-1 day^-1 (Table 1). These trait ranges were informed by the range of trait parameter values from Edwards et al. (2015). This resulted in a total of 37,960 simulations. We evaluated parameter sensitivity by comparing GPP and phytoplankton stoichiometry estimates to baseline scenarios parameterized with the emergent phytoplankton trait values for a given P supply and N:P supply ratio. To standardize the effect of different traits and units, we calculated z-scores based on the difference between the simulations with varying trait parameters and baseline simulations.

2.4 Objective 3: evaluation of the models’ ability to generate patterns in GPP and seston stoichiometry

2.4.1 Data for generating observed patterns of GPP

To assess the performance of our models, we qualitatively compared model outputs of GPP and phytoplankton C:N:P stoichiometry to observed patterns. To the best of our knowledge, fully comprehensive datasets required to force and assess these models do not exist publicly. Thus, we used three publicly available datasets that jointly have the required data (described below). The first dataset is from Corman et al. (2023a) which was previously compiled from the Global Lake Ecological Observatory Network, and has the required data to force the model, including inflow stream nutrient concentrations, and GPP for validation, but it does not have seston C:N:P stoichiometry - a model output in the dynamic structure that is ideal for model validation. In contrast, the NEON and Flathead data sets (see description below) include seston stoichiometry but not inflow stream nutrient concentrations or GPP estimates for validation.

We used Corman’s dataset to assess the two model structures’ ability to generate observed patterns of GPP. These data include lake morphological characteristics, in situ high frequency data required to generate GPP estimates, and inflow stream TN and TP concentration for 16 lakes in the Northern Hemisphere (Corman et al. (2023a); Supplementary Table S2). Gross primary production rates and inflow stream nutrient concentrations were aggregated at a monthly resolution resulting in a total of 91 observations. Missing monthly data (GPP = 12, stream N and P concentrations = 4) were imputed using the median of the respective lake. We converted GPP estimates from mg O₂ L^-1 day^-1 to mg C L^-1 day^-1 using a C:O₂ ratio of 12:32 (Wetzel and Likens, 2000). As we were only modeling primary production in the mixed layer, we approximated the mixed layer water residence time by multiplying whole-lake water residence time by the ratio of the mixed-layer:lake volume. Lake inflow was then calculated from the mixed layer volume (product of surface area and mixed-layer depth) and the approximated water residence time for the mixed layer. We obtained mixed-layer depths from Oleksy et al. (2022).

2.4.2 Data for generating observed patterns of seston stoichiometry

We used data from seven lakes from the U.S. National Ecological Observatory Network (NEON) comprising seston stoichiometry and standard lake physicochemical information to assess the two model structures’ ability to generate observed patterns of seston stoichiometry. These data were collected following standard NEON protocols (NEON, 2024c, NEON, 2024a, NEON, 2024b). The lakes span a range of trophic status, size, and ecoregions within the United States (Supplementary Table S3; Supplementary Figure S2): Lake Barco (BARC), Crampton Lake (CRAM), Prairie Lake (PRLA), Prairie Pothole (PRPO), Little Rock Lake (LIRO), Lake Suggs (SUGG), and Toolik Lake (TOOK). Each lake was sampled at least once per season from January 2014 to December 2022, however, seston stoichiometry was only sampled/released from January 2014 to December 2019. We subset the data to include samples taken in the middle of the lake at the water surface. Inflow stream nutrient concentrations were unavailable for the NEON lakes, so we estimated them using a linear relationship between in-lake and stream inflow nutrient concentrations from the Corman dataset (Supplementary Figure S3). To obtain the mixed layer depth for each lake, we used surface area and in-lake dissolved organic carbon (DOC) concentrations following Equation 7 (Pérez-Fuentetaja et al., 1999; Kelly et al., 2018):

$\begin{array}{ll}{z}_{mix} = {10}^{-0.515 + lo{g}_{10}(DOC) + 0.115 * lo{g}_{10}(2 \ast \sqrt{\frac{SA}{\pi } + 0.991)}}& (7)\end{array}$

We complemented the NEON dataset with data from Flathead Lake (Supplementary Figure S2; Supplementary Table S3) for which most data are publicly available apart from the seston stoichiometry: https://flbs.umt.edu/newflbs/research/flbs-public-data/. The remaining seston elemental composition data set is published in Dryad (https://doi.org/10.5061/dryad.hdr7sqvkw). Samples from this large oligotrophic lake were collected at the deepest point in the lake at 5, 50 and 90 m depth. Sampling and analytical methods are listed in the Flathead Lake Biological Station Public Data Portal (Flathead Monitoring Program: https://flbs.umt.edu/PublicData). We focused on the four consecutive sampling years from June 2016 through mid September 2019 in which the program started to collect additional suspended particulate stoichiometry data. The summer season from 2016-2019 is available in the same repository (Elser, 2022). The mixed-layer depth from Flathead Lake was obtained from lake thermal data presented in Evans et al. (2024). In absence of robust hydrological data we assumed that the epilimnion had a water residence time of 1 year for the NEON lakes and Flathead Lake. We believe this is a reasonable assumption as many of these lakes stratify and mix annually.

2.4.3 Model simulations

As data sets containing both lake GPP and seston stoichiometry were unavailable to us, we chose to conduct two separate sets of simulations to evaluate the ability of the models to replicate observed patterns of GPP and seston stoichiometry (see descriptions of Corman and NEON data above). For the Corman data set, we assessed the ability of the models to reproduce patterns of observed GPP by comparing the distributions of observed and modeled GPP. For the Flathead Lake/NEON data set, we extracted modeled seston stoichiometry and compared it to observed data using ternary plots (see below).

We ran all simulations, including the model simulation experiments (above), for 2,000 timesteps at a daily resolution to obtain equilibrium values using the LSODA integration solver with the ode() function in the R package deSolve (Soetaert et al., 2010). All analyses and simulations were conducted using the R statistical software (version 4.3.3) (R Core Team, 2024), and model and simulation code are available on Github (https://github.com/diatomdaniel/getting_droopy_with_it_woodstoich24) and Zenodo (DOI: 10.5281/zenodo.13886190).

2.4.4 Variability in seston stoichiometry

We visualized variation in observed and modeled seston stoichiometry using a ternary plot diagram. Ternary plots are powerful visualization tools for stoichiometric data as they allow for 3-dimensional systems to be represented in 2-dimensional space along three axes. We plotted relative seston composition ratios by first Redfield-normalizing the molar C, N and P following Smith et al. (2017) for both the modeled and observed data. We then plotted those relative proportions in Ternary Plots using the software SigmaPlot (version 15.0, Graffiti LLC, Palo Alto, CA, USA). To aid interpretation of the data, we included the established Redfield ratio of 106C:16N:1P and Sterner ratio of 166C:20N:1P as reference ratios (Redfield, 1958; Sterner et al., 2008). We followed the interpretation as described in Smith et al. (2017). The composition of each average of field data per lake or model output varied between 0-100% with the sum of the three elements adding up to 100%. When a value falls below the 20% line for one of the three macro-elements, it can be interpreted as that element being depleted with the corners creating room for co-depletion of two elements.

3 Results

3.1 Objective 1: model simulation experiments of phytoplankton nutrient utilization and stoichiometric traits

3.1.1 Gross primary productivity

P inflow concentration limits the maximum rate of GPP (Figure 1). Across a gradient of N:P supply ratio, the rate at which GPP saturates is highest with the highest P inflow concentration. Additionally, P inflow interacts with phytoplankton traits; for example, phytoplankton groups parameterized with higher growth rates, such as cyanobacteria and green-algae, reach higher GPP at the same P inflow (Figure 1). At low P-supply, green-algae had a higher maximum GPP than cyanobacteria in the static model but not in the dynamic model. This result stems from the combination of low half-saturation constant for P and high maximum growth rate for green algae (Table 1). In contrast, growth is not related to half-saturation constants but is determined by Q_minN and Q_minP in the dynamic model. The N:P supply ratio at which this maximum GPP is reached is independent of P inflow and coincides with the parameterization of phytoplankton Q_minN: Q_minP (Figure 1). Differences in GPP between the static and dynamic model structures were minimal (Figure 1).

3.1.2 Phytoplankton stoichiometry

In the dynamic model structure, phytoplankton C:N and C:P demonstrate a threshold-type response to N:P inflow with the shift occurring at the Q_minN: Q_minP for that particular phytoplankton group (Figures 2A, B). Physiologically, this threshold is driven by a shift in limitation where phytoplankton carbon:nutrient stoichiometry increases to compensate for shifts in nutrient limitation. This result is consistent with classic chemostat studies (Rhee, 1978; Goldman, 1986). Phytoplankton N:P linearly increases with inflow N:P with all P inflow concentrations and across all phytoplankton groups (Figure 2C) which is consistent with theory demonstrating the effect of low dilution rate on phytoplankton quota (Klausmeier et al., 2004b).

Figure 2

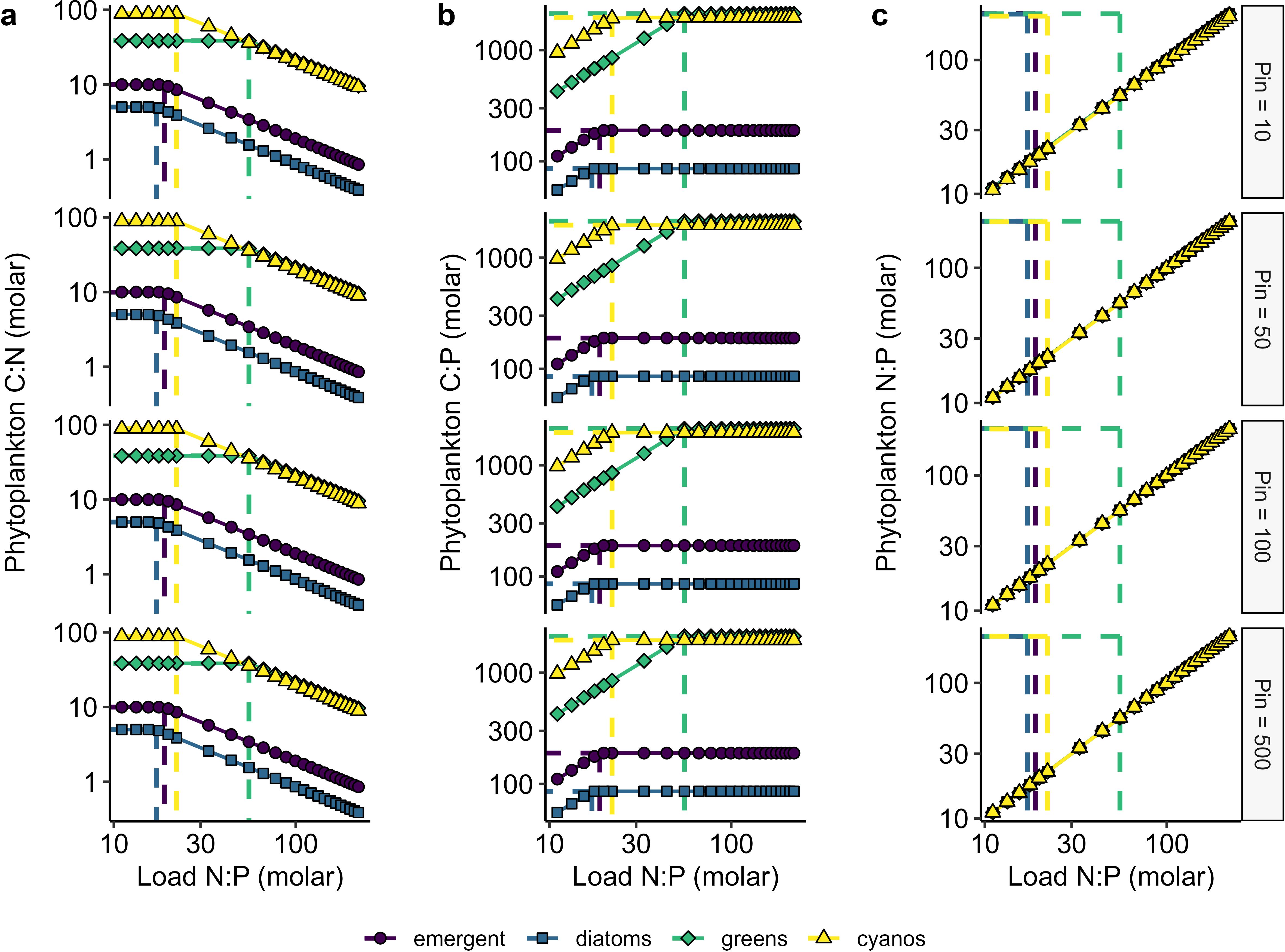
Figure 2. 'Dynamic model simulations highlighting variation in seston (A) C:N, (B) C:P, and (C) N:P (molar) as a function of nutrient loads and N:P stoichiometry (molar). Dashed vertical lines show the minimum cell N:P quotas for the respective algae groups. Rows show different P-loading scenarios (Pin = 10, 50, 100, and 500 µg L^-1. Greens = green-algae and cyanos = cyanobacteria.

3.2 Objective 2: sensitivity analysis to identify key phytoplankton trait parameters

3.2.1 Gross primary productivity

Gross primary production was most sensitive to Q_minN and Q_minP in both model structures (Figure 3A). Gross primary production increased with lower values of Q_minN and Q_minP as lower minimum cell quotas result in more efficient nutrient use. Any change in Q_minN had a larger effect on GPP at low N:P supply compared to high N:P supply (Figure 3A). Reciprocally, GPP increased at low Q_minP across the entire N:P supply gradient, however, this effect reached a threshold at a Q_minP of 0.1 mg P mg C^-1 (Figure 3A). Gross primary production was minimally sensitive to K_N and K_P in the static model and insensitive to half saturation constants in the dynamic model (Figure 3). In the static model, increasing K_P decreased GPP, particularly at high N:P supply while lower values of K_N increased GPP at low N:P supply. In both models, higher maximum growth rates increased GPP. In the dynamic model, GPP was insensitive to maximum uptake rates (Figure 3A).

Figure 3

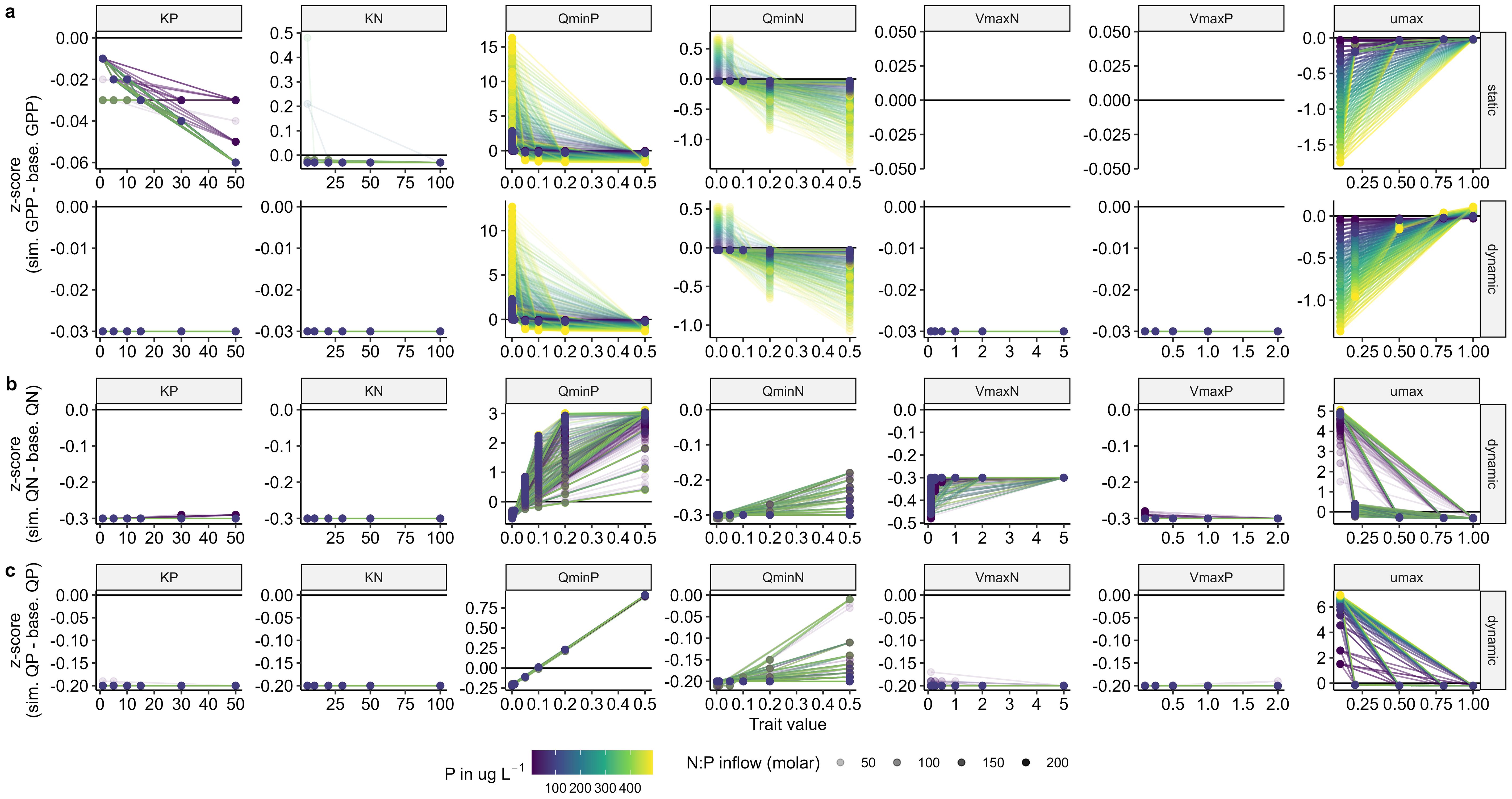
Figure 3. Parameter sensitivity analysis for (A) gross primary production (GPP; mg C L^-1 day^-1), (B) cell N quota (mg N mg^-1 C), and (C) cell P quota (mg P mg^-1 C). The Y-axis shows the standardized z-scores of the difference between the simulation using different trait parameter values and the baseline simulation using the emergent trait values. Positive values denote increases in the response variable relative to the baseline simulation and vice versa. Each of the dots is a single model simulation. Shaded lines connect simulations with the same P supply (Pin μg L^-1) and load N:P. Parameter units: KN and KP = mg m^-3, Q_minN and Q_minP = mg N, P mg^-1 C, Vmax_N and Vmax_P = mg N, P mg^-1 C, umax = days^-1.

3.2.2 Phytoplankton intracellular nutrient content

As with GPP, phytoplankton intracellular nutrient contents in the dynamic model, Q_N and Q_P, were most sensitive to Q_minN and Q_minP and this sensitivity was contingent on N:P supply (Figures 3B, C). Intracellular N increased with increasing Q_minN and Q_minP particularly at low and high N:P supply, respectively. Intracellular P also increased with increasing Q_minN and Q_minP, however, with respect to Q_minP, this increase was insensitive to N:P supply.

Both intracellular nutrient contents were insensitive to K_N, K_P, and Vmax_P, but both were sensitive to ${\mu }_{max}$ as cell N and P quotas decreased with increasing growth rates (Figures 3B, C). This change in cell nutrient quota under high growth rates represents a greater allocation of internal nutrient supplies to biomass accumulation. Interestingly, only Q_N was sensitive to Vmax_N, and increased with increasing Vmax_N at high N:P supply.

3.3 Objective 3: evaluation of models’ ability to generate patterns

3.3.1 Gross primary production

The static model better captured the distribution of observed GPP compared to the dynamic model particularly when parameterized using green-algae (static: R² = 0.41, p-value< 0.001) and cyanobacteria traits (static: R² = 0.41, p-value< 0.001; Figure 4). However, the static model tended to over-predict GPP at the high end of the range of observed GPP and under-predict GPP at the low end (Figure 4). All other model structures and parameterizations were poor predictors of modeled GPP (Figure 4). The emergent (static: R² = 0.30, p-value< 0.001; dynamic: R² = 0.25, p-value< 0.001), diatom (static: R² = 0.76, p-value< 0.001; dynamic: R² = 0.25, p-value< 0.001), green-algae (dynamic: R² = 0.30, p-value< 0.001), and cyanobacteria (dynamic: R² = 0.30, p-value< 0.001) parameterizations all underpredicted GPP for most of the observations. In many cases modeled rates of GPP approached zero suggesting a severe mismatch between nutrient supply and demand. However, both models and all phytoplankton trait parameterizations were able to capture the bimodal distribution of observed GPP (Figure 4), suggesting that the models can capture qualitative patterns in lake productivity across nutrient supply gradients.

Figure 4

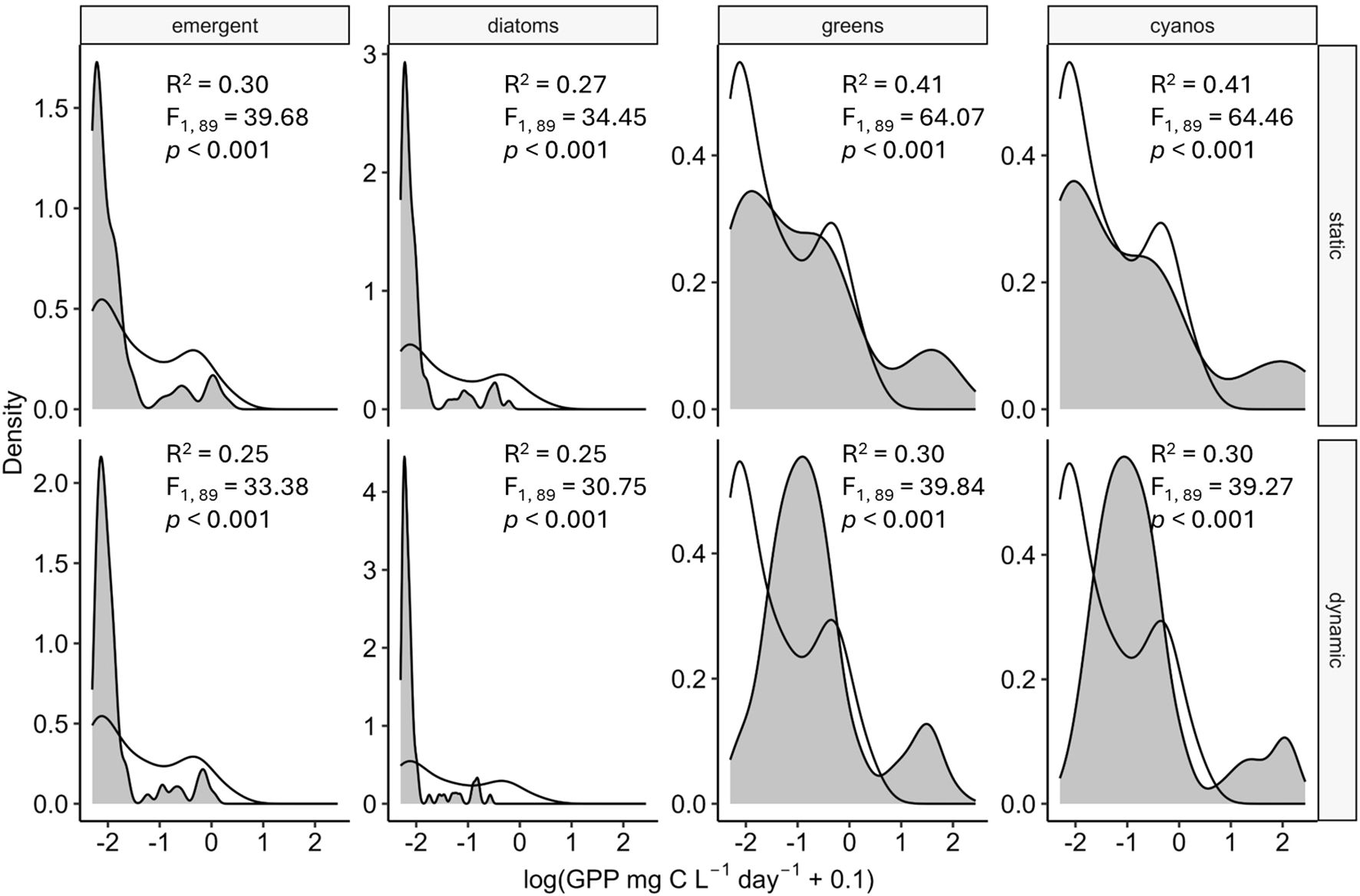
Figure 4. Density distributions of the observed gross primary production (white; GPP mg C L^-1 day^-1 for 16 lakes from the Northern Hemisphere (Corman et al., 2023a) compared to modeled GPP (gray) for the static and dynamic model strucutres and the four algae group parameterizations. Inset text shows summary statistics describing the linear relationship between observed and modeled log-transformed GPP. Greens = green-algae and cyanos = cyanobacteria.

3.3.2 Seston stoichiometry

The dynamic model was unable to capture observed patterns of seston C:N:P stoichiometry across a diverse range of lake types, but did produce some biologically reasonable seston estimates (Figure 5). Modeled seston stoichiometry varied within phytoplankton groups as well as lakes, resulting in a wide range of phytoplankton C:N:P ratios. Several taxa mostly grouped together: green algae, cyanobacteria, diatoms, and the emergent algae produced clusters of similar estimates of seston C:N:P ratios. Although model estimates generally diverged from the Redfield and Sterner ratios, the model produced biologically reasonable estimates for 7 of the 32 parameterizations. Modeled diatoms were C-depleted and green-algae were N-depleted. Modeled emergent seston ratios were split in that five were balanced and 3 were C-depleted. Finally, modeled cyanobacteria were both N and P co-depleted (5) and C and P co-depleted (3).

Figure 5

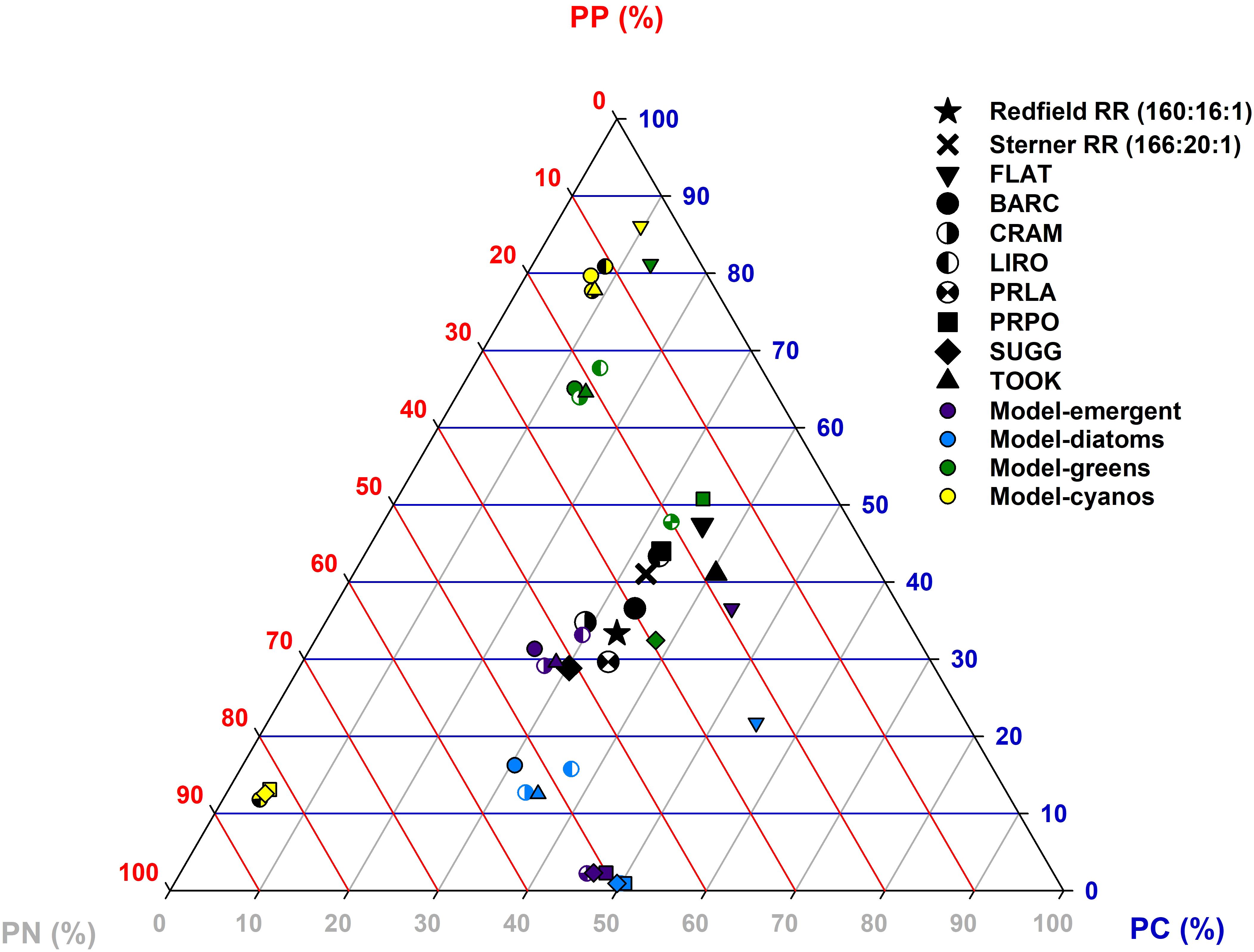
Figure 5. Summary ternary plot of the mean relative seston stoichiometry for modeled and observed data. The plot shows the average relative percentages of the molar Redfield-normalized seston stoichiometry of the seston sampling per particulate carbon (PC), particulate nitrogen (PN) and particulate phosphorus (PP) in the seven NEON lakes complemented with the larger Flathead lake during the summer. The lake abbreviations represent the following lakes: FLAT is Flathead Lake, BARC is Lake Barco, CRAM is Crampton Lake, LIRO is Little Rock Lake, PRLA is Prairie Lake, PRPO is Prairie Pothole, SUGG is Lake Suggs and TOOK is Toolik Lake. We added the relative Redfield and Sterner ratios (black star and cross respectively) as literature reference ratios. Model outputs for each algae group are represented with smaller symbols (lake) in color (phytoplankton groups). The composition of each model output or average of field data per lake varied between 0-100% with the sum of the three elements adding up to 100%. When a value gets below the 20% line for one of the three macro-elements, it can be interpreted as that element being nutrient-limited with the corners creating room for co-limitation of two elements, following Smith et al. (2017).

The observed Flathead Lake and NEON lake seston values were centered on the ternary diagram and cluster close to the Redfield ratio (Figure 5). The deepest lakes, Flathead and Toolik Lake, had P-depleted seston compositions (i.e., they are below the 20% PP line; Smith et al., 2017), while the remaining six lakes had a well-balanced seston stoichiometric composition (i.e., being above 20% of PP, PN, and PC).

4 Discussion

We used a combination of model simulations, parameter sensitivity analysis, and model-data comparison to assess the role of phytoplankton stoichiometric traits in lake ecosystem models. Our objectives were to (1) assess how phytoplankton nutrient utilization and stoichiometric traits drive patterns of lake primary productivity across P- and N:P supply gradients, (2) identify key phytoplankton trait parameters that dictate patterns of lake primary productivity, and (3) evaluate the ability of model structures that differ in their representation of phytoplankton stoichiometry to generate observed patterns in lake primary productivity and seston stoichiometry. With regards to Objectives 1 and 2, model simulations and sensitivity analysis revealed that phytoplankton stoichiometric traits, specifically Q_minN and Q_minP, significantly influence patterns of GPP by setting demand for N and P that interact with nutrient supply (Figures 1–3). With regards to Objective 3, our models qualitatively captured patterns of GPP, but were unable to capture patterns in observed seston stoichiometry (Figures 4, 5). We find that stoichiometric traits are important drivers of GPP and seston nutrient stoichiometry and interact strongly with supply N:P across gradients of P availability. Specifically, phytoplankton traits that describe nutrient use efficiency, i.e. Q_minN and Q_minP, determine model performance. Going forward lake ecologists would benefit from the collection and generation of data that will effectively parameterize lake ecosystem models to improve predictive capacity and generate reliable estimates of ecosystem processes under global change.

4.1 Objectives 1 + 2: phytoplankton traits drive GPP and seston stoichiometry

The maximum rate of GPP that can be attained was primarily controlled by P loading, a finding that is consistent with the P-paradigm in lakes that the long-term production of biomass is ultimately limited by P (Schindler et al., 2008; Higgins et al., 2018). Similarly, our models provide theoretical support for the role of N:P stoichiometry and N availability in distinguishing between capacity and rate limitation of biomass production in lentic systems. Although the biomass carrying capacity of a lake is ultimately set by P, the effects from limitation by light, CO₂ or N as well as species-specific differences in resource affinity and requirements may prevent this maximum from being obtained (Reynolds, 1992). In addition to P-related parameters, maximum growth rate parameter resulted in contrasting patterns of GPP across algal groups (Figure 1). Ultimately, differences in growth rate are a result of different resource acquisition and competition strategies that are associated with phytoplankton size, cellular composition, and trait expression (Litchman et al., 2007; Brandenburg et al., 2018; Klip et al., 2024). For example, high growth rates are often associated with low cell N:P ratios (Hillebrand et al., 2013) as demand for P increases according to the growth rate hypothesis that relates P content to organismal rRNA content and ultimately growth (Sterner and Elser, 2002).

The N:P supply ratio at which maximum GPP is attained was dictated by Q_minN and Q_minP (Figure 1). These traits determine the efficiency at which N and P are converted to biomass (or carbon). Consequently, phytoplankton stoichiometric traits directly link nutrient availability to biomass production in our models and provide a critical link between nutrient availability and C-cycling across broad nutrient inputs. For example, cyanobacteria and green-algae had the lowest Q_minN and Q_minP in our dataset (Table 1), indicating they required the least N and P to fix the same amount of C and thus, were able to build the most biomass at a higher N:P supply. Similarly, the ratio of minimum quotas for N and P dictate the supply N:P at which limitation shifts from N to P, highlighting how phytoplankton cellular composition (in terms of N and P) determines nutrient limitation (Figure 1). Conceptually, the ratio of Q_minN to Q_minP is equivalent to nutrient use efficiency (Vitousek, 1982), optimal N:P ratio (Klausmeier et al., 2004a), threshold elemental ratios (Frost et al., 2006), and consumption vectors of resource ratio theory (Tilman, 1985). Other studies have demonstrated that cellular quotas of P are important in models of lake primary production (Olson and Jones, 2022; Kelly et al., 2018). Thus, we provide further support for the importance of supply N:P and phytoplankton stoichiometry in shaping patterns of primary production and C-cycling across freshwater landscapes.

4.2 Objective 3: deviations between observations and theory

Both our models failed to adequately capture the relationships between nutrient supply and GPP in 16 lakes across the Northern Hemisphere (Corman et al., 2023b), resulting in underestimates of GPP. In contrast, Corman et al. (2023b) found strong support for nutrient loads as a driver of lake GPP. The incongruence between models and reality arises from the high N:P of the supply in our models. Aggregation of streamflow on a monthly basis resulted in low median P concentrations compared to N (N: median = 764 µg L^-1, ± 1sd = 2,822; P: median = 19 µg L^-1, ± 1sd = 54) and high supply N:P across all lakes (median = 91 by moles, ± 1sd = 173). As maximum obtainable GPP in our models is set by P supply (Figure 1), P-limitation is inevitable under conditions of low P-supply, and our models result in areas of near-zero GPP. Potential reasons for the failure of our models to capture observed rates of GPP is the lack of reliable nutrient loads and inability to account for internal cycling of P. Other models have circumvented this problem by (1) adjusting nutrient inputs to minimize differences between modeled and observed quantities (Kelly et al., 2018), (2) explicitly modeling internal P recycling (Olson and Jones, 2022), or (3) utilizing data assimilation techniques to determine parameter values that maximize model performance (Oleksy et al., 2022; Edwards et al., 2013).

The static and dynamic models differed in their ability to capture patterns of GPP (Figure 4). Surprisingly, the static model parameterized with cyanobacteria and green-algae performed the best but still captured less than 50% of the variation between observed and modeled GPP. The performance of the static model arises from the relatively high Q_minN: Q_minP ratios of the green-algae and cyanobacteria (55 and 22 by moles respectively) compared to the diatom and the emergent parameterization. This stoichiometric trait, Q_minN: Q_minP, interacts with the high affinity for P (K_P) to allow phytoplankton demand to match the high supply N:P of the inflow. Moreover, algal growth in the static model is independent of minimum quotas as nutrient uptake is translated into growth following Michaelis-Menten uptake kinetics (Equation 2). In contrast, the minimum cell quotas in the dynamic model require algae to meet “maintenance costs” before growth is permitted (Equations 4, 5), representing less efficient conversion of nutrients to biomass at low nutrient concentrations.

4.3 Caveats and future directions

Growth in our models is determined by a single limiting resource (either N or P) following Liebig’s Law of the Minimum (von Liebig, 1855), resulting in strict N- or P-limitation. In reality, nutrient limitation of phytoplankton is complex and subject to considerable spatiotemporal variation. For example, large-scale surveys, meta-analyses of experiments and field studies have found that freshwater phytoplankton are frequently characterized by co-limitation of N and P (Elser et al., 2007; Paerl et al., 2016; McCullough et al., 2024), and high rates of primary production can be observed under strong stoichiometric imbalances in eutrophic systems (Kelly et al., 2018), but see Sterner et al. (2007), and Elser et al. (2022) for large, oligotrophic lakes. Similarly nutrient supplies are often interactive, and the effects of increasing N or P depends on context and supply rate of the other element (Harpole et al., 2011; Frost et al., 2023). Our models did not include other factors that affect primary production in freshwater lakes, such as temperature, mixotrophy, zooplankton grazing or limitation by trace elements (Kimmel and Groeger, 1984; Hammer and Pitchford, 2005). Since light plays a crucial role in phytoplankton ecology (Richardson et al., 2017), assessment of the interaction between stoichiometric and light utilization traits on GPP and phytoplankton stoichiometry is necessary. We hypothesize that light limitation would reduce both GPP and phytoplankton C:nutrient ratios because phytoplankton will grow less under light limitation and will therefore accumulate nitrogen and phosphorus, but this will depend on nutrient supply (Tilman, 1977; Liu et al., 2017; Isanta-Navarro et al., 2024). Future work could also address how different representations of nutrient limitation influence model outputs and interact with trait parameterization.

Our models do not account for phytoplankton trait flexibility in response to nutrient limitation at the individual or the community level which adds a phenotypic or genotypic level of variation to model parameterization (Edwards et al., 2011; Andersen et al., 2020; Blows and Hoffmann, 2005). Minimum nutrient cellular quotas can be contingent on environmental context and growth phase (Rhee and Gotham, 1981; Daines et al., 2014; Jiang and Nakano, 2022). For example, elevated temperatures lead to lower cellular demand for P-rich ribosomal DNA via more efficient enzymatic kinetics resulting in lower cellular P quota and increased C:P and N:P ratios (Moreno and Martiny (2018) and reference therein). Additionally, seasonal and diurnal variation in seston elemental composition can reflect variation of minimum nutrient cellular quotas in natural communities (Kreeger et al., 1997; Garcia et al., 2022). Stoichiometric traits are also flexible due to trade-offs. For example, phytoplankton cells enlarge or form spines to avoid predation altering surface area:volume ratios and nutrient uptake efficiency and growth rate (Litchman et al., 2007; Edwards et al., 2011). Additionally, growth rate itself is associated with elemental stoichiometry due to a tripartite relation among higher P content with higher growth rate due to the need for more P-rich ribosomal RNA to support elevated protein synthesis rates, as described by the generally supported growth rate hypothesis (Elser et al., 2000; Flynn et al., 2010; Isanta-Navarro et al., 2022, Isanta-Navarro et al., 2024; Klip et al., 2024). Finally, the difference between acclimation and adaptation in driving variation in these traits is not trivial (Moreno and Martiny, 2018). In summary, it is important to use environmental gradients, flexible trait values, growth rate gradients and for as far as possible ecological-evolutionary physiological shifts. In contrast, we used static minimum quota of N and P to represent phytoplankton demand for N and P. Allowing this trait to vary with phenotypic, genotypic, or community composition change may allow for more realistic representation of phytoplankton stoichiometric traits and would embed ecological-evolutionary feedback into model structure. This variation in trait parameterization will likely improve model performance but it would be computationally complex and require challenging data collection.

Other work should focus on improving representations of external nutrient loading and representation of internal P recycling in lake ecosystem models. The parameterization of phytoplankton traits is often merely calibrated so that model predictions match observations and effectively serves to capture any variation in P cycling the model does not represent. Ultimately, these approaches lead to ecologically irrelevant parameter values for traits (Franks, 2009; Port et al., 2015; Golosov et al., 2021). There are three ways one can deal with this over-parameterization and equifinality of traits: (1) improve estimates of nutrient inputs into the system via better data collection or modeling approaches, (2) adjust model structure so that internal P cycling of lakes is more realistic, for example, by including processes such as internal P loading or lake turnover events, and (3) a combination of 1 and 2 that balances model simplicity and realism.

These improvements will require targeted data collection and compilation of existing data sets that allow models to be forced, calibrated and validated. How do we do these things? First, we need more detailed trait information to provide realistic parameterizations. For example, while parameters describing nutrient utilization and stoichiometry were well described (Supplementary Figure S1), there were very few measurements of cellular C content to help convert trait measurements into units consistent with our model. Second, we need to develop methods to relate observations of phytoplankton community composition to lab-derived trait data to improve trait parameterization. Many of these traits, including phytoplankton stoichiometry itself, are not observable in the field (Sieburth et al., 1978; Finkel et al., 2010). Additionally, model calibration exercises often result in parameter estimates that are not ecologically realistic. Thus, data sets that include phytoplankton community composition are extremely valuable. Unfortunately, these are rare, and even more rare are data sets that also have nutrient loading, GPP, and seston stoichiometry. Finally, lakes exhibit considerable vertical and spatial heterogeneity of their phytoplankton stoichiometry (Bucci et al., 2012). Thus, field data across space, both within and between lakes, and across depths would facilitate more informative parameter distributions. A wider geographic spread would also be desirable: due to data availability, our current study only contains lakes from North America, which matches the majority of global scientific publications on phytoplankton from 2012 to 2022 (Adhiambo et al., 2023). This sampling bias can increase modeling uncertainty around the globe (Kwiatkowski et al., 2017).

5 Conclusion

Our approach tested how phytoplankton traits shape patterns of lake productivity across nutrient supply gradients. We found that models were highly sensitive to the parameterization of phytoplankton minimum cell quotas for N and P, a finding that provides a critical link between nutrient-limited organismal growth and ecosystem-scale primary production. However, our models failed to predict observed patterns of lake primary production or phytoplankton C:N:P stoichiometry as we were unable to parameterize our models with informative trait values and reliable nutrient and hydrological inflows. This finding highlights how the mismatch between supply and demand impacts our ability to predict changes in ecosystem function to environmental change. We suggest that future research should focus on appropriate data collection and compilation for parameterizing, calibrating, and validating these models with special attention paid to phytoplankton traits. In conjunction with these data collections, data assimilation techniques should be employed to allow for distribution-informed parameterization. These efforts will move us closer to better capturing the ecological and evolutionary feedbacks that we expect to observe with ongoing global change.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: Elser et al. (2022). Nutrient concentrations, loading, and N:P stoichiometry (1983–2020) and impacts in Flathead Lake (Montana, USA). doi: https://doi.org/10.5061/dryad.hdr7sqvkw. Elser et al. (2007). Flathead Lake longterm dataset, Flathead Lake Biological Station, University of Montana. Available at: http://flbs.umt.edu/publicdata NEON: https://data.neonscience.org/data-products/explore data products DP1.20163.001, DP1.20166.001, DP1.20093.001. Corman et al. (2023a). Source code: Response of lake metabolism to catchment inputs inferred using high-frequency lake and stream data from across the northern hemisphere. doi: 10.5281/zenodo.8408298. Edwards et al. (2015). Nutrient utilization traits of phytoplankton. Ecol. 96, 2311–2311. doi: 10.1890/14-2252.1. Model and simulation code are available on Github (https://github.com/diatomdaniel/getting_droopy_with_it_woodstoich24) and Zenodo (https://doi.org/10.5281/zenodo.13886191).

Author contributions

CO: Writing – original draft, Writing – review & editing, Conceptualization, Investigation, Formal analysis, Methodology, Project administration. DG: Writing – original draft, Writing – review & editing, Conceptualization, Formal analysis, Methodology, Validation, Visualization. AD: Writing – original draft, Writing – review & editing, Conceptualization, Data curation, Methodology, Investigation. JM: Writing – original draft, Writing – review & editing, Conceptualization, Data curation, Validation, Visualization, Investigation. HK: Conceptualization, Data curation, Validation, Visualization, Writing – original draft, Writing – review & editing, Methodology.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. AD was supported by funding from the European Union (ERC: BLOOMTOX, 101044452). HK was supported by the National Science Foundation (grant DEB-2113783) and the Bierman Fund (Jessie M. Bierman Professorship, FLBS). CO and DG were supported by the National Science Foundation (OID OIA 2019596). DG was additionally supported by the Daugherty Water for Food Institute. We thank the AWI for providing access to the guest research facilities of the Biologische Anstalt Helgoland during the Woodstoich Workshop (grant number AWI_BAH_34).

Acknowledgments

We thank the following groups of people: (1) the Woodstoich organizers for their work: Cédric Meunier and Maarten Boersma (Alfred-Wegener-Institut, Helmholtz Zentrum für Polar- und Meeresforschung), Lienne Sethna (Science Museum of Minnesota), Robert Buchkowski and Genevieve Metson (Western University), and Jim Elser (Flathead Lake Biological Station, University of Montana), with extra thanks to Lienne Sethna for her mentorship and feedback on earlier versions of the manuscript, and to Jim Elser to proofreading the final version; (2) the senior scientists at Woodstoich for their guidance: Cecilia Laspoumaderes, Dieter Wolf-Gladrow and Karen Wiltshire; (3) the staff of the Alfred Wegener Institute at Helgoland for kindly hosting us; and (4) the advisors of all authors: Celia Symons, Jessica Corman, Jim Elser and Dedmer van de Waal. We especially thank the reviewers for this special edition’s quick turnaround time and we are grateful for their insightful suggestions and constructive comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2024.1505018/full#supplementary-material

References

Adhiambo R., Mensah P. K., Acheampong E. (2023). Widespread geographical disparities in phytoplankton ecology research in the face of climate change: A review. Water 15:4288. doi: 10.3390/w15244288

Crossref Full Text | Google Scholar

Allen J. I., Blackford J., Holt J., Proctor R., Ashworth M., Siddorn J. (2001). A highly spatially resolved ecosystem model for the North West European Continental Shelf. Sarsia 86, 423–440. doi: 10.1080/00364827.2001.10420484

Crossref Full Text | Google Scholar

Andersen I. M., Tanner J., Williamson, Maria J. G., Michael J. V. (2020). Nitrate, ammonium, and phosphorus drive seasonal nutrient limitation of chlorophytes, cyanobacteria, and diatoms in a hyper‐eutrophic reservoir. Limnology and Oceanograph 65(5), 962–978.

Google Scholar

Blows M. W., Hoffmann A. A. (2005). A reassessment of genetic limits to evolutionary change. Ecology 86(6), 1371.–1384.

Google Scholar

Bonachela J. A., Klausmeier C. A., Edwards K. F., Litchman E., Levin S. (2016). The role of phytoplankton diversity in the emergent oceanic stoichiometry. A. J. Plankton Res. 38, 1021–1035. doi: 10.1093/plankt/fbv087

Crossref Full Text | Google Scholar

Brandenburg K. M., Wohlrab S., John U., Kremp A., Jerney J., Krock B., et al. (2018). Intraspecific trait variation and trade-offs within and across populations of a toxic dinoflagellate. Ecol. Lett. 21, 1561–1571. doi: 10.1111/ele.13138

PubMed Abstract | Crossref Full Text | Google Scholar

Bucci V., Nunez-Milland D., Twining B. S., Hellweger F. L. (2012). Microscale patchiness leads to large and important intraspecific internal nutrient heterogeneity in phytoplankton. Aquat. Ecol. 46, 101–118. doi: 10.1007/s10452-011-9384-6

Crossref Full Text | Google Scholar

Corman J. R., Zwart J. A., Klug J., Bruesewitz D. A., de Eyto E., Klaus M., et al. (2023a). Source Code: Response of lake metabolism to catchment inputs inferred using high-frequency lake and stream data from across the northern hemisphere. doi: 10.5281/zenodo.8408298

Crossref Full Text | Google Scholar

Corman J. R., Jacob A., Zwart J. K., Denise A. B., Elvira de Eyto., Marcus K., et al. (2023b). Response of lake metabolism to catchment inputs inferred using high‐frequency lake and stream data from across the northern hemisphere. Limnology and Oceanography 68(12):2617–2631.

Google Scholar

Daines S. J., Clark J. R., Lenton T. M. (2014). Multiple environmental controls on phytoplankton growth strategies determine adaptive responses of the N : P ratio. Ecol. Lett. 17, 414–425. doi: 10.1111/ele.12239

PubMed Abstract | Crossref Full Text | Google Scholar

Dean W. E., Gorham E. (1998). Magnitude and significance of carbon burial in lakes, reservoirs, and peatlands. Geology 26, 535–538. doi: 10.1130/0091-7613(1998)026<0535:MASOCB>2.3.CO;2

Crossref Full Text | Google Scholar

Dodds W. K. (2002). Freshwater ecology: concepts and environmental applications. 3rd Edn (Amsterdam: Elsevier).

Google Scholar

Dokulil M. T., Qian K. (2021). Photosynthesis, carbon acquisition and primary productivity of phytoplankton: a review dedicated to Colin Reynolds. Hydrobiologia 848, 77–94. doi: 10.1007/s10750-020-04321-y

Crossref Full Text | Google Scholar

Droop M. R. (1968). Vitamin B12 and marine ecology. IV. The kinetics of uptake, growth and inhibition in Monochrysis lutheri. Journal of the Marine Biological Association of the United Kingdom 48(3), 689–733.

Google Scholar

Edwards K. F., Klausmeier C. A., Litchman E. (2011). Evidence for a three-way trade-off between nitrogen and phosphorus competitive abilities and cell size in phytoplankton. Ecology 92, 2085–2095. doi: 10.1890/11-0395.1

PubMed Abstract | Crossref Full Text | Google Scholar

Edwards K. F., Litchman E., Klausmeier C. A. (2013). Functional traits explain phytoplankton community structure and seasonal dynamics in a marine ecosystem. Ecol. Lett. 16, 56–63. doi: 10.1111/ele.12012

PubMed Abstract | Crossref Full Text | Google Scholar

Edwards K. F., Klausmeier C. A., Litchman E. (2015). Nutrient utilization traits of phytoplankton. Ecology 96, 2311–2311. doi: 10.1890/14-2252.1

Crossref Full Text | Google Scholar

Elser J. (2022). Nutrient concentrations, loading, and N:P stoichiometr- 2020) and impacts in flathead lake (Montana, USA: Dryad). doi: 10.5061/dryad.hdr7sqvkw

Crossref Full Text | Google Scholar

Elser J. J., Bracken M. E. S., Cleland E. E., Gruner D. S., Harpole W. S., Hillebrand H., et al. (2007). Global analysis of nitrogen and phosphorus limitation of primary producers in freshwater, marine and terrestrial ecosystems. Ecol. Lett. 10, 1135–1142. doi: 10.1111/j.1461-0248.2007.01113.x

PubMed Abstract | Crossref Full Text | Google Scholar

Elser J. J., Devlin S. P., Yu J., Baumann A., Church M. J., Dore J. E., et al. (2022). Sustained stoichiometric imbalance and its ecological consequences in a large oligotrophic lake. Proc. Natl. Acad. Sci. 119, e2202268119. doi: 10.1073/pnas.2202268119

PubMed Abstract | Crossref Full Text | Google Scholar

Elser J. J., Sterner R. W., Galford A. E., Chrzanowski T. H., Findlay D. L., Mills K. H., et al. (2000). Pelagic C:N:P stoichiometry in a eutrophied lake: responses to a whole-lake food-web manipulation. Ecosystems 3, 293–307. doi: 10.1007/s100210000027

Crossref Full Text | Google Scholar

Evans K. A., Peoples L. M., Ranieri J. R., Wear E. K., Church M. J. (2024). Mixing-driven changes in distributions and abundances of planktonic microorganisms in a large, oligotrophic lake. Limnol. Oceanogr. 69, 604–620. doi: 10.1002/lno.12509

Crossref Full Text | Google Scholar

Finkel Z. V., Beardall J., Flynn K. J., Quigg A., Rees T. A. V., Raven J. A. (2010). Phytoplankton in a changing world: cell size and elemental stoichiometry. J. Plankton Res. 32, 119–137. doi: 10.1093/plankt/fbp098

Crossref Full Text | Google Scholar

Flynn K. J., Raven J. A., Rees T. A. V., Finkel Z., Quigg A., Beardall J. (2010). Is the growth rate hypothesis applicable to microalgae? J. Phycol. 46, 1–12. doi: 10.1111/j.1529-8817.2009.00756.x

Crossref Full Text | Google Scholar

Franks P. J. S. (2009). Planktonic ecosystem models: perplexing parameterizations and a failure to fail. J. Plankton Res. 31, 1299–1306. doi: 10.1093/plankt/fbp069

Crossref Full Text | Google Scholar

Frost P. C., Benstead J. P., Cross W. F., Hillebrand H., Larson J. H., Xenopoulos M. A., et al. (2006). Threshold elemental ratios of carbon and phosphorus in aquatic consumers. Ecol. Lett. 9, 774–779. doi: 10.1111/j.1461-0248.2006.00919.x

PubMed Abstract | Crossref Full Text | Google Scholar

Frost P. C., Pearce N. J. T., Berger S. A., Gessner M. O., Makower A. K., Marzetz V., et al. (2023). Interactive effects of nitrogen and phosphorus on growth and stoichiometry of lake phytoplankton. Limnol. Oceanogr. 68, 1172–1184. doi: 10.1002/lno.12337

Crossref Full Text | Google Scholar

Garcia N. S., Talmy D., Fu W.-W., Larkin A. A., Lee J., Martiny A. C. (2022). The diel cycle of surface ocean elemental stoichiometry has implications for ocean productivity. Glob. Biogeochem. Cycles 36, e2021GB007092. doi: 10.1029/2021GB007092

Crossref Full Text | Google Scholar

Goldman J. C. (1986). On phytoplankton growth rates and particulate C: N: P ratios at low light. Limnol. Oceanogr. 31, 1358–1363. doi: 10.4319/lo.1986.31.6.1358

Crossref Full Text | Google Scholar

Golosov S., Zverev I., Terzhevik A., Palshin N., Zdorovennova G., Efremova T., et al. (2021). On the parameterization of phytoplankton primary production in water ecosystem models. J. Phys. Conf. Ser. 2131, 32079. doi: 10.1088/1742-6596/2131/3/032079

Crossref Full Text | Google Scholar

Hall S. R. (2009). Stoichiometrically explicit food webs: feedbacks between resource supply, elemental constraints, and species diversity. Annual Review of Ecology, Evolution, and Systematics 40(1), 503–528.

Google Scholar

Hammer A. C., Pitchford J. W. (2005). The role of mixotrophy in plankton bloom dynamics, and the consequences for productivity. ICES J. Mar. Sci. 62, 833–840. doi: 10.1016/j.icesjms.2005.03.001

Crossref Full Text | Google Scholar

Hanson C. E. (2004). Oceanographic forcing of phytoplankton dynamics in the coastal eastern Indian Ocean (University of Western Australia). Available online at: https://research-repository.uwa.edu.au/files/3246187/Hanson_Christine_Elizabeth_2004.pdf (Accessed September 30, 2024).

Google Scholar

Harpole W. S., Ngai J. T., Cleland E. E., Seabloom E. W., Borer E. T., Bracken M. E. S., et al. (2011). Nutrient co-limitation of primary producer communities. Ecol. Lett. 14, 852–862. doi: 10.1111/j.1461-0248.2011.01651.x

PubMed Abstract | Crossref Full Text | Google Scholar

Heathcote A. J., Anderson N. J., Prairie Y. T., Engstrom D. R., del Giorgio P. A. (2015). Large increases in carbon burial in northern lakes during the Anthropocene. Nat. Commun. 6, 10016. doi: 10.1038/ncomms10016

PubMed Abstract | Crossref Full Text | Google Scholar

Higgins S. N., Paterson M. J., Hecky R. E., Schindler D. W., Venkiteswaran J. J., Findlay D. L. (2018). Biological nitrogen fixation prevents the response of a eutrophic lake to reduced loading of nitrogen: evidence from a 46-year whole-lake experiment. Ecosystems 21, 1088–1100. doi: 10.1007/s10021-017-0204-2

Crossref Full Text | Google Scholar

Hillebrand H., Steinert G., Boersma M., Malzahn A., Meunier C. L., Plum C., et al. (2013). Goldman revisited: Faster-growing phytoplankton has lower N : P and lower stoichiometric flexibility. Limnol. Oceanogr. 58, 2076–2088. doi: 10.4319/lo.2013.58.6.2076

Crossref Full Text | Google Scholar

Huisman J., Weissing F. J. (1994). Light-limited growth and competition for light in well-mixed aquatic environments: an elementary model. Ecology 75, 507–520. doi: 10.2307/1939554

Crossref Full Text | Google Scholar

Isanta-Navarro J., Peoples L. M., Bras B., Church M. J., Elser J. J. (2024). Elemental and macromolecular plasticity of Chlamydomonas reinhardtii (Chlorophyta) in response to resource limitation and growth rate. J. Phycol. 60, 418–431. doi: 10.1111/jpy.13417

PubMed Abstract | Crossref Full Text | Google Scholar

Isanta-Navarro J., Prater C., Peoples L. M., Loladze I., Phan T., Jeyasingh P. D., et al. (2022). Revisiting the growth rate hypothesis: Towards a holistic stoichiometric understanding of growth. Ecol. Lett. 25, 2324–2339. doi: 10.1111/ele.14096

PubMed Abstract | Crossref Full Text | Google Scholar

Jäger C. G., Diehl S. (2014). Resource competition across habitat boundaries: asymmetric interactions between benthic and pelagic producers. Ecol. Monogr. 84, 287–302. doi: 10.1890/13-0613.1

Crossref Full Text | Google Scholar

Janssen A. B. G., Teurlincx S., Beusen A. H. W., Huijbregts M. A. J., Rost J., Schipper A. M., et al. (2019). PCLake+: A process-based ecological model to assess the trophic state of stratified and non-stratified freshwater lakes worldwide. Ecol. Model. 396, 23–32. doi: 10.1016/j.ecolmodel.2019.01.006

Crossref Full Text | Google Scholar

Jiang M., Nakano S. (2022). The crucial influence of trophic status on the relative requirement of nitrogen to phosphorus for phytoplankton growth. Water Res. 222, 118868. doi: 10.1016/j.watres.2022.118868

PubMed Abstract | Crossref Full Text | Google Scholar

Kaspari M., Powers J. S. (2016). Biogeochemistry and geographical ecology: embracing all twenty-five elements required to build organisms. Am. Nat. 188, S62–S73. doi: 10.1086/687576

PubMed Abstract | Crossref Full Text | Google Scholar

Kelly P. T., Solomon C. T., Zwart J. A., Jones S. E. (2018). A framework for understanding variation in pelagic gross primary production of lake ecosystems. Ecosystems 21, 1364–1376. doi: 10.1007/s10021-018-0226-4

Crossref Full Text | Google Scholar

Kimmel B. L., Groeger A. W. (1984). Factors controlling primary production in lakes and reservoirs: A perspective. Lake Reserv. Manage. 1, 277–281. doi: 10.1080/07438148409354524

Crossref Full Text | Google Scholar

Klausmeier C. A., Litchman E., Daufresne T., Levin S. A. (2004a). Optimal nitrogen-to-phosphorus stoichiometry of phytoplankton. Nature 429, 171–174. doi: 10.1038/nature02454

PubMed Abstract | Crossref Full Text | Google Scholar

Klausmeier C. A., Litchman E., Levin S. A. (2004b). Phytoplankton growth and stoichiometry under multiple nutrient limitation. Limnol. Oceanogr. 49, 1463–1470. doi: 10.4319/lo.2004.49.4_part_2.1463

Crossref Full Text | Google Scholar

Klip H. C. L., Meunier C. L., Boersma M. (2024). Less variability when growing faster? Experimental assessment of the relationship of growth rate with functional traits of the marine diatom Phaeodactylum tricornutum. Hydrobiologia 851, 2173–2187. doi: 10.1007/s10750-023-05444-8

Crossref Full Text | Google Scholar

Kreeger D., Goulden C., Kilham S., Lynn S., Datta S., Interlandi S. (1997). Seasonal changes in the biochemistry of lake seston. Freshw. Biol. 38, 539–554. doi: 10.1046/j.1365-2427.1997.00233.x

Crossref Full Text | Google Scholar

Krishna S., Ulloa H. N., Kerimoglu O., Minaudo C., Anneville O., Wüest A. (2021). Model-based data analysis of the effect of winter mixing on primary production in a lake under reoligotrophication. Ecol. Model. 440, 109401. doi: 10.1016/j.ecolmodel.2020.109401

Crossref Full Text | Google Scholar

Kwiatkowski L., Bopp L., Aumont O., Ciais P., Cox P. M., Laufkötter C., et al. (2017). Emergent constraints on projections of declining primary production in the tropical oceans. Nat. Clim. Change 7, 355–358. doi: 10.1038/nclimate3265

Crossref Full Text | Google Scholar

Litchman E. (2022). Understanding and predicting harmful algal blooms in a changing climate: A trait-based framework. Limnol. Oceanogr. Lett 6:2297–246. doi: 10.1002/lol2.10294

Crossref Full Text | Google Scholar

Litchman E., Klausmeier C. A. (2008). Trait-based community ecology of phytoplankton. Annu. Rev. Ecol. Evol. Syst. 39, 615–639. doi: 10.1146/annurev.ecolsys.39.110707.173549

Crossref Full Text | Google Scholar

Litchman E., Klausmeier C. A., Schofield O. M., Falkowski P. G. (2007). The role of functional traits and trade-offs in structuring phytoplankton communities: scaling from cellular to ecosystem level. Ecol. Lett. 10, 1170–1181. doi: 10.1111/j.1461-0248.2007.01117.x

PubMed Abstract | Crossref Full Text | Google Scholar

Litchman E., Thomas M. K. (2023). Are we underestimating the ecological and evolutionary effects of warming? Interactions with other environmental drivers may increase species vulnerability to high temperatures. Oikos 2023, e09155. doi: 10.1111/oik.09155

Crossref Full Text | Google Scholar

Liu J., Li Z., Guo J., Xiao Y., Fang F., Qin R., et al. (2017). The effect of light on the cellular stoichiometry of Chlorella sp. in different growth phases: implications of nutrient drawdown in batch experiments. J. Appl. Phycol. 29, 123–131. doi: 10.1007/s10811-016-0962-9

Crossref Full Text | Google Scholar

McCullough I. M., Sun X., Hanly P. J., Soranno P. A. (2024). Knowing your limits: Patterns and drivers of nutrient limitation and nutrient–chlorophyll relationships in US lakes. Limnol. Oceanogr. Lett. doi: 10.1002/lol2.10420

Crossref Full Text | Google Scholar

Mendonça R., Müller R. A., Clow D., Verpoorter C., Raymond P., Tranvik L. J., et al. (2017). Organic carbon burial in global lakes and reservoirs. Nat. Commun. 8:1694. doi: 10.1038/s41467-017-01789-6

PubMed Abstract | Crossref Full Text | Google Scholar

Mooij W. M., Trolle D., Jeppesen E., Arhonditsis G., Belolipetsky P. V., Chitamwebwa D. B. R., et al. (2010). Challenges and opportunities for integrating lake ecosystem modelling approaches. Aquat. Ecol. 44, 633–667. doi: 10.1007/s10452-010-9339-3

Crossref Full Text | Google Scholar

Moreno A. R., Martiny A. C. (2018). Ecological stoichiometry of ocean plankton. Annu. Rev. Mar. Sci. 10, 43–69. doi: 10.1146/annurev-marine-121916-063126

PubMed Abstract | Crossref Full Text | Google Scholar

NEON (2024a). Chemical properties of surface water (DP1.20093.001), RELEASE-2024. (Boulder, Colorado USA: NEON). doi: 10.48443/fdfd-d514

Crossref Full Text | Google Scholar

NEON (2024b). Periphyton, seston, and phytoplankton chemical properties (DP1.20163.001), RELEASE-2024. (Boulder, Colorado USA: NEON). doi: 10.48443/25wy-9f31

Crossref Full Text | Google Scholar

NEON (2024c). Periphyton, seston, and phytoplankton collection (DP1.20166.001). RELEASE-2024. (Boulder, Colorado USA: NEON). doi: 10.48443/25wy-9f31

Crossref Full Text | Google Scholar

Neumann T. (2000). Towards a 3D-ecosystem model of the baltic sea. J. Mar. Syst. 25, 405–419. doi: 10.1016/S0924-7963(00)00030-0

Crossref Full Text | Google Scholar

Olson C. R., Jones S. E. (2022). Chlorophyll–total phosphorus relationships emerge from multiscale interactions from algae to catchments. Limnol. Oceanogr. Lett. 7, 483–491. doi: 10.1002/lol2.10281

Crossref Full Text | Google Scholar

Oleksy I. A., Solomon C. T., Jones S. E., Olson C. R., Bertolet B. L., Adrian R., et al (2022). Chlorophyll–total phosphorus relationships emerge from multiscale interactions from algae to catchments. Controls on lake pelagic primary productivity: formalizing the nutrient-color paradigm. J. Geophys. Res. In press.

Google Scholar

Paerl H. W., Scott J. T., McCarthy M. J., Newell S. E., Gardner W. S., Havens K. E., et al. (2016). It takes two to tango: when and where dual nutrient (N & P) reductions are needed to protect lakes and downstream ecosystems. Environ. Sci. Technol. 50, 10805–10813. doi: 10.1021/acs.est.6b02575

PubMed Abstract | Crossref Full Text | Google Scholar

Pérez-Fuentetaja A., Dillon P. J., Yan N. D., McQueen D. J. (1999). Significance of dissolved organic carbon in the prediction of thermocline depth in small Canadian shield lakes. Aquat. Ecol. 33, 127–133. doi: 10.1023/A:1009998118504

Crossref Full Text | Google Scholar

Port A., Bryan K. R., Pilditch C. A., Hamilton D. P., Bischof K. (2015). Algebraic equilibrium solution of tissue nitrogen quota in algae and the discrepancy between calibrated parameters and physiological properties. Ecol. Model. 312, 281–291. doi: 10.1016/j.ecolmodel.2015.05.034

Crossref Full Text | Google Scholar

Puts I. C., Ask J., Siewert M. B., Sponseller R. A., Hessen D. O., Bergström A. (2022). Landscape determinants of pelagic and benthic primary production in northern lakes. Glob. Change Biol. 28, 7063–7077. doi: 10.1111/gcb.16409

PubMed Abstract | Crossref Full Text | Google Scholar

R Core Team (2024). R: A language and environment for statistical computing (Vienna, Austria: R Foundation for Statistical Computing). Available at: https://www.R-project.org/.

Google Scholar

Redfield A. C. (1958). The biological control of chemical factors in the environment. Am. Sci. 46, 230A–2221.

Google Scholar

Reynolds C. S. (1992). Eutrophication and the management of planktonic algae: what Vollenweider couldn’t tell us. Available online at: https://aquadocs.org/handle/1834/22792 (Accessed September 12, 2024).

Google Scholar

Rhee G. Y. (1978). Effects of N:P atomic ratios and nitrate limitation on algal growth, cell composition, and nitrate uptake. Limnol. Oceanogr. 23, 10–25. doi: 10.4319/lo.1978.23.1.0010

Crossref Full Text | Google Scholar

Rhee G. Y., Gotham I. J. (1981). The effect of environmental factors on phytoplankton growth: Temperature and the interactions of temperature with nutrient limitation1. Limnol. Oceanogr. 26, 635–648. doi: 10.4319/lo.1981.26.4.0635

Crossref Full Text | Google Scholar

Richardson D. C., Melles S. J., Pilla R. M., Hetherington A. L., Knoll L. B., Williamson C. E., et al. (2017). Transparency, geomorphology and mixing regime explain variability in trends in lake temperature and stratification across northeastern north americ[amp]]ndash;2014). Water 9, 442. doi: 10.3390/w9060442

Crossref Full Text | Google Scholar

Saloranta T. M., Andersen T. (2007). MyLake—A multi-year lake simulation model code suitable for uncertainty and sensitivity analysis simulations. Ecol. Model. 207, 45–60. doi: 10.1016/j.ecolmodel.2007.03.018

Crossref Full Text | Google Scholar

Schindler D. W. (2009). Lakes as sentinels and integrators for the effects of climate change on watersheds, airsheds, and landscapes. Limnol. Oceanogr. 54, 2349–2358. doi: 10.4319/lo.2009.54.6_part_2.2349

Crossref Full Text | Google Scholar

Schindler D. W., Hecky R. E., Findlay D. L., Stainton M. P., Parker B. R., Paterson M. J., et al. (2008). Eutrophication of lakes cannot be controlled by reducing nitrogen input: results of a 37-year whole-ecosystem experiment. Proc. Natl. Acad. Sci. U. S. A. 105, 11254–11258. doi: 10.1073/pnas.0805108105

PubMed Abstract | Crossref Full Text | Google Scholar

Schwaderer A. S., Yoshiyama K., De Tezanos Pinto P., Swenson N. G., Klausmeier C. A., Litchman E. (2011). Eco-evolutionary differences in light utilization traits and distributions of freshwater phytoplankton. Limnol. Oceanogr. 56, 589–598. doi: 10.4319/lo.2011.56.2.0589

Crossref Full Text | Google Scholar

Sieburth J., Smetacek V., Lenz J. (1978). Pelagic ecosystem structure: Heterotrophic compartments of the plankton and their relationship to plankton size fractions 1. Limnol. Oceanogr. 23, 1256–1263. doi: 10.4319/lo.1978.23.6.1256

Crossref Full Text | Google Scholar

Skogen M. D., Ji R., Akimova A., Daewel U., Hansen C., Hjøllo S. S., et al. (2021). Disclosing the truth: Are models better than observations? Mar. Ecol. Prog. Ser. 680, 7–13. doi: 10.3354/meps13574

Crossref Full Text | Google Scholar

Smith D. R., Jarvie H. P., Bowes M. J. (2017). Carbon, nitrogen, and phosphorus stoichiometry and eutrophication in river thames tributaries, UK. Agric. Environ. Lett. 2, ael2017.06.0020. doi: 10.2134/ael2017.06.0020

Crossref Full Text | Google Scholar

Soetaert K., Petzoldt T., Setzer R. W. (2010). Solving differential equations in R: package deSolve. J. Stat. Software 33, 1–25. doi: 10.18637/jss.v033.i09

Crossref Full Text | Google Scholar

Sterner R. W., Anagnostou E., Brovold S., Bullerjahn G. S., Finlay J. C., Kumar S., et al. (2007). Increasing stoichiometric imbalance in North America’s largest lake: Nitrification in Lake Superior. Geophys. Res. Lett. 34. doi: 10.1029/2006GL028861

Crossref Full Text | Google Scholar

Sterner R. W., Andersen T., Elser J. J., Hessen D. O., Hood J. M., McCauley E., et al. (2008). Scale-dependent carbon:nitrogen:phosphorus seston stoichiometry in marine and freshwaters. Limnol. Oceanogr. 53, 1169–1180. doi: 10.4319/lo.2008.53.3.1169

Crossref Full Text | Google Scholar

Sterner R. W., Elser J. J. (2002). Ecological stoichiometry: the biology of elements from molecules to the biosphere (Princeton: Princeton University Press). Available online at: http://catdir.loc.gov/catdir/samples/prin031/2002072262.html (Accessed January 18, 2023).

Google Scholar

Tilman D. (1977). Resource competition between plankton algae: an experimental and theoretical approach. Ecology 58, 338–348. doi: 10.2307/1935608

Crossref Full Text | Google Scholar

Tilman D. (1985). The resource-ratio hypothesis of plant succession. Am. Nat. 125, 827–852. doi: 10.1086/284382

Crossref Full Text | Google Scholar

Vitousek P. (1982). Nutrient cycling and nutrient use efficiency. Am. Nat. 119, 553–572. doi: 10.1086/283931

Crossref Full Text | Google Scholar

Vollenweider R. A. (1968). Scientific fundamentals of the eutrophication of lakes and flowing waters, with particular reference to nitrogen and phosphorus as factors in eutrophication. Paris Fr. 192, 14.

Google Scholar

von Liebig J. F. (1855). Principles of agricultural chemistry: With special reference to the late researches made in England (Walton & Maberly). Available online at: https://books.google.com/books?hl=en&lr=&id=8RcAAAAAQAAJ&oi=fnd&pg=PP7&dq=Justus+von+Liebig,+1855&ots=PkcYk5EMnc&sig=NMh_DkWOsiJkSVmljZ34K7DMMNg (Accessed September 30, 2024).

Google Scholar

Wetzel R. G., Likens G. E. (2000). Limnological analyses (New York, NY: Springer). doi: 10.1007/978-1-4757-3250-4

Crossref Full Text | Google Scholar

Williamson C. E., Saros J. E., Vincent W. F., Smol J. P. (2009). Lakes and reservoirs as sentinels, integrators, and regulators of climate change. Limnol. Oceanogr. 54, 2273–2282. doi: 10.4319/lo.2009.54.6_part_2.2273

Crossref Full Text | Google Scholar

Zwart J. A., Solomon C. T., Jones S. E. (2015). Phytoplankton traits predict ecosystem function in a global set of lakes. Ecology 96, 2257–2264. doi: 10.1890/14-2102.1

PubMed Abstract | Crossref Full Text | Google Scholar