Evaluation and Analysis of Bridge Modal Parameters Under Intelligent Monitoring Environment

After the bridge is completed, the structural materials will be gradually eroded or aged under the influence of climate, temperature, and building environment. Under long-term static and dynamic loads, the structural strength and stiffness of bridge structures, including bridge deck and bridge support, will decrease with the accumulation of time. Bridge modal parameter identification is not only the premise and foundation of health monitoring, but also the main part of bridge structure dynamic identification. Therefore, this paper proposes a bridge modal parameter identification model based on Bayesian method. The model fully considers the uncertainty of parameters and the selection of modal parameters, and identifies more local information through the probability distribution of model parameters and a posteriori confidence. The reliability of the bridge is monitored in real time through the Bayesian dynamic model, and the monitoring error is only 0.01, which can realize high-precision bridge modal parameter identification.

Introduction

Large bridges are not only key facilities on highway and railway transportation lines, but also key nodes in urban transportation networks (Jahan, 2020). They are usually expensive and have a long lifespan. Once an accident occurs, it will cause huge economic losses and even casualties. Therefore, it is necessary to timely understand the health of bridges through appropriate means and discover hidden dangers that endanger the safety of bridges (Mitsuru and Yuhu, 2019). However, safety detection of bridges has long been based on manual methods. People either inspect bridges regularly, or perform inspection and evaluation in special cases (Wu et al., 2020), which is not only time-consuming and labor-intensive, but also fails to detect many important structural defects in time, and cannot issue emergency warnings in advance, especially, it is difficult to the safety reserves and functional degradation paths of bridges are systematically assessed.

Once quality defects such as cracks, pits, and corrosion of steel bars appear in bridge engineering, the bearing capacity of the structure is often reduced and the improvement of engineering stability and reliability is restricted. In order to repair these problems in time, it is necessary to take measures to strengthen bridge modal monitoring and master the correct data processing methods. This cannot only fully understand the quality of the project, but also make up for the quality problems existing in the bridge construction, which is conducive to prolonging the service life of the project and laying a foundation for the smooth passage of vehicles.

In recent years, with the rapid development of sensor technology, data remote transmission technology, computer software and hardware technology, signal analysis and processing technology, and artificial intelligence technology, people have begun to research and develop automatic, continuous, and even real-time bridge health monitoring systems. The successful development of bridge health monitoring technology will play a role in ensuring the safe operation of bridges and extending the service life of bridges. At the same time, the early detection of bridge damage can effectively save the maintenance cost of the bridge, reduce the waste of resources, and avoid the inconvenience and loss caused by frequent maintenance (Zhang et al., 2022) and traffic closure.

The results of some environmental stimulation tests at this stage show that the changes of modal parameters caused by environmental factors are very significant, far greater than the changes caused by structural damage. Researchers at home and abroad have done a lot of work in this area. Kaloop et al. (2015), wavelet principal component analysis (WPCA) and spectral analysis methods were used to establish the time and frequency domains of bridge deformation, and to analyze the behavior and motion of bridges under working traffic loads. Peeters and Roeck (2001) studied the monitoring data of the Z24 Bridge in Switzerland for 1 year. The results show that the annual relative change rate of the first fourth-order modal frequencies of the structure caused by environmental changes is about 14–18%. It is considered that temperature is the main factor affecting the modal parameters, and the relationship between temperature and frequency is basically bilinear. Min et al. (2009) processed the 1-year structural condition monitoring data of Donghai Bridge, main channel, and cable-stayed bridge. According to the analysis of coherence and correlation analysis, it is considered that the ambient temperature and structural vibration level are the main factors affecting the modal frequency of the bridge in the 1-year analysis period. Wiberg (2006) prepared a reliable 3D Bernoulli-Euler girder finite element model for the new RSTA railway bridge for a comprehensive dynamic analysis using on-site bridge monitoring for correlation analysis (Peeters and Roeck, 2001; Wiberg, 2006; Min et al., 2009; Kaloop et al., 2015).

At present, there are still many difficulties in the research of bridge modal monitoring and damage identification technology based on environmental impact (Shull et al., 2015). How to distinguish the variability of structural modal parameters caused by environmental factors and structural damage, and quantify the impact of environmental factors on structural modal parameters is one of the most noteworthy difficulties. This paper mainly explores the influence of environmental factors on the modal parameters of the structure, and deeply reveals the influence mechanism of the environment on the modal parameters of the structure. Dynamic prediction of bridge performance is done through Bayesian dynamic linear models (Wang et al., 2010). The dynamic linear model cannot only monitor information, but also make real-time online prediction of bridge structural reliability.

Current Status of Bridge Modal Monitoring

With the development of science and technology and the improvement of people’s aesthetic requirements for bridge construction, bridge construction has put forward new requirements and challenges to bridge engineers in my country (Asadollahi and Jian, 2016). On the one hand, modern bridges require large spans, new materials, strong coordination with the environment, and practicality and beauty. On the other hand, our bridge builders need to start with bridge design, engineering, construction, operation, and maintenance to keep our bridges safe.

Throughout the bridge safety accidents at home and abroad, the reasons are many, mainly including: poor dynamic design of bridge structures, lack of strict control during construction, cutting corners (Hamdi et al., 2021), inadequate maintenance and management during operation, The real-time monitoring technology is immature and bears instantaneous loads. Many bridge collapse accidents have caused widespread concern in the society. How to ensure the construction safety and operation safety of the bridge, how to realize the real-time monitoring of the bridge structure, how to improve the service life of the bridge (Maity et al., 2022), are a major social issue at present.

At present, the main means of bridge real-time monitoring is to establish an effective bridge structural health monitoring system. The health monitoring system is mainly composed of a sensor system, a signal transmission system, a computer hardware system, a computer software system, and a signal analysis and processing system (Wang and Liu, 2018). The health monitoring system installed on the bridge structure can monitor the overall and local operation of the bridge structure in real time, and through the system to measure the key indicators affecting the operation of the bridge structure, to achieve qualitative analysis, location analysis and quantitative analysis of bridge structure damage, and give an early warning when the operating conditions of the bridge are abnormal to prevent problems before they occur. At the same time, the static and dynamic behavior of the actual bridge structure obtained by the bridge health monitoring system (Franken, 2017) can verify the rationality of the structural finite element analysis model, various basic assumptions, design standards and design methods, and provide decision-making and guidance for maintenance. Based on this, an in-depth study on the maintenance and management of bridges, the unknown areas and uncertainties of large and complex bridges in the process of bridge operation is carried out to provide a reliable basis for future design and construction.

Because the identification of bridge modal parameters in the environment is extremely important, scholars at home and abroad have done a lot of research on it, and have made great progress. At present, some influential research results are as follows: Qiyuan (2009) focuses on the identification of modal parameters of large structures based on modern time-frequency analysis theory, focusing on the identification of environmental modal parameters based on continuous wavelet transform and Hilbert-Huang transform. Simulation analysis and engineering example analysis show that the method can be applied in practical engineering. Ubertini et al. (2013) proposed an automatic mode recognition method. The basic idea of this method is to use SSI to identify the modal parameters of the system, and then introduce the pedigree clustering analysis method into the modal parameter screening process. Engineering examples show that the method can automatically identify the modal parameters of the system (Qiyuan, 2009; Ubertini et al., 2013).

After decades of development, researchers at home and abroad have made great progress in the identification of structural modal parameters. Comprehensive analysis of the research results of domestic and foreign scholars, it can be seen that SSI has its unique advantages in the identification of structural modal parameters under environmental conditions, which are mainly reflected in: SSI does not need to convert time domain data when identifying structural modal parameters, and can directly For time domain data without frequency resolution error. It has strong anti-interference ability to output noise, and has good identification accuracy to structure frequency, mode shape and damping. Based on this, the modal parameter identification method of SSI structure is widely favored by civil engineering researchers at home and abroad (Yang et al., 2014), and has become a commonly used structural modal parameter identification algorithm.

Although researchers at home and abroad have made great achievements in the identification method of structural modal parameters based on SSI (Snaebjörnsson et al., 2016), there are still a series of problems: How to automatically determine the system order, how to realize the automatic screening of physical mode and pseudo mode, avoid the subjectivity of manual screening, and how to solve the numerical control identification error caused by the interference of environmental factors in the identification of time-varying structure modal parameters. In order to improve the efficiency and accuracy of modal parameter identification, the above problems still need further research.

Based on the shortcomings of the previous analysis, this paper makes up for the previous shortcomings. Therefore, this paper mainly studies how to apply Bayesian reasoning to the correlation analysis of the relationship between bridge modal parameters and environmental factors, such as ambient temperature, relative humidity, wind speed and traffic flow, establish the probability mapping relationship between modal parameters and environmental factors representing the structural system, realize the uncertainty quantification of model parameters and prediction residuals, and realize the bridge modal parameters and the overall condition of the structure early warning, assessment and analysis.

Bayesian Model Analysis

Bayes’ theorem is the core tool of Bayesian reasoning (Le et al., 2021). Its function is to revise and update beliefs about unknown parameters based on observed sample data. The calculation of Bayesian inference requires the introduction of Bayes’ theorem, so it is necessary to introduce Bayes’ theorem.

The event form of Bayes’ theorem is first introduced: suppose A₁,A₂,⋯,A_n is an incompatible event, ${\bigcup }_{i=1}^{n}A$ is an unavoidable event, and any event B has:

$P\left(A_i\right|B)=\frac{P\left(A_i\right)P\left(B|A_i\right)}{{\sum }_j^{n}P\left(A_j\right)P\left(B|A_j\right)}(i=1,2,\mathrm{\cdots }n)(1)$

where P(A_i) is the prior probability of event A_i, P(B|A_i) is the conditional probability of event B under the premise of event A_i, and P(A_i|B) is the posterior probability of event A_i.

From the point of view of conditional probability, P(A_i|B) is the conditional probability of event A_i when event B occurs. This situation is common in everyday life: what was considered impossible is made possible by events, and vice versa. And Bayes’ theorem describes this change mathematically.

If P(B|A_i) is viewed as a forward probabilistic reasoning (positive problem) from A_i to B, then P(A_i|B) can be viewed as an inverse probabilistic reasoning (inverse problem) from B to A_i. The inverse problem is usually more difficult to solve than the corresponding positive problem. In practical applications, the observation data inevitably contains noise, and there will be accumulated errors in the calculation process, which makes the solution of the inverse problem often encounter difficulties such as non-uniqueness, instability, and non-existence of the solution. However, Equation (1) directly transforms the difficult inverse problem solution into the easier forward problem solution, which also makes Bayesian inference attract extensive attention in inverse problem research and is applied to ecosystems, heat conduction, medicine, the universe Inverse problem solving in various fields such as parameter estimation, urban environment, etc.

Many scientists and engineering problems are more concerned with the solution and prediction of uncertain parameters, which usually appear in the form of random variables. Discrete events can be obtained in the form of parameter vectors, and can also be obtained in the form of Bayes’ theorem random variables.

Assuming that parameter θ is a continuous random variable, X₁,X₂,⋯,X_n is an observable random vector of IID (Li et al., 2005), x = x₁,x₂,⋯,x_n is a sample observation, and the joint density of sample x (Abramowicz et al., 2020) is recorded as parameter θ of the conditional density f(x|θ) of sample x, It represents the conditional distribution of a random variable when the random variable θ is given a certain value. Then for the observed sample x, the value of the parameter θ is:

$f\left(\mathrm{\theta }|x\right)=\frac{f\left(\mathrm{\theta }\right)f\left(x|\mathrm{\theta }\right)}{{\int }_{\mathrm{\chi }}f\left(\mathrm{\theta }\right)f\left(x|\mathrm{\theta }\right)\mathit{d}\mathrm{\theta }}(2)$

In the formula, f(θ) is the prior probability density function of the parameter θ, which represents the distribution law of the parameter θ before the sample data is obtained, and f(θ) is generally determined according to scientific and engineering experience.

$f\left(x|\mathrm{\theta }\right)=f(x_1,x_2,\mathrm{\cdots },x_n|\mathrm{\theta })=\prod _{i=1}^{n}f\left(x_i|\mathrm{\theta }\right)(3)$

The above formula expresses the likelihood function after a given parameter θ, and expresses how well the model fits the observed data, where each observed data x_i(i = 1,2,⋯,n) is independent of each other. χ is the parameter space, and different θ correspond to different distributions. f(θ|x) is the posterior probability density function of the parameter θ, which integrates the prior information of the parameter θ and the information about θ provided by the sample x. Therefore, it can be understood that after obtaining the sample observation x = x₁,x₂,⋯,x_n, it integrates the prior information and data information to obtain a more realistic distribution. It can also be understood as the posterior distribution obtained by updating the prior distribution, that is, the θ distribution obtained by improving the understanding of θ.

Classical statistics treats the parameter θ as a definite unknown constant rather than a random variable. In Bayes’ theorem, the parameter θ is not a constant, but a random variable, which can take on different values. The uncertainty of the value of θ can be represented by a distribution, and f(θ) represents the confidence of the parameter value. For example, the defective rate p-value of products produced by a factory per day can be estimated by testing all products produced on a given day or by sampling some products (Pingfan, 2013). On a certain day, p is an unknown constant, but over a long period of time, there is a defect rate every day whose value fluctuates under the influence of random factors. Therefore, the defect rate on a given day can reasonably be regarded as one possible value of the random variable p. If the inspection record is long, the probability distribution of p can be determined.

The posterior probability density function of parameter θ is f(θ|x), which is determined after observing the data and can be understood as the updated confidence distribution of the unknown parameter. For example, p is the reject rate of factory products. Before sampling, one can assume that p is uniformly distributed between the interval [0,1], that is, one knows very little about p, and assume that p is equally likely to take on different values. When n products are selected for inspection and m substandard products are found, the understanding of p can be corrected. p can still take any value in the interval [0,1], but the chance sizes are no longer equal everywhere. Conversely, it can be argued that p is more likely to be close to m/n and less likely to be close to 0 or 1.

The denominator ∫χf(θ)f(x|θ)dθ of formula (2) only depends on the sample observation value x_i(i = 1,2,⋯,n), and has nothing to do with the parameter θ. It only acts as a regularization factor when computing θ. Therefore, formula (2) can be simplified to:

$f\left(\mathrm{\theta }|x\right)\mathrm{\infty }f\left(\mathrm{\theta }\right)f\left(x|\mathrm{\theta }\right)(4)$

where ∞ is the scale number, which means there is only one constant factor on both sides independent of θ, and f(θ)f(x|θ) is called the kernel of the posterior distribution f(θ|x). The corresponding constant can be determined by integrating the kernel of the distribution density over the entire space. Therefore, the key to obtaining the distribution density function of random variables is to obtain the kernel of the distribution density.

Bayesian-Based Intelligent Monitoring Bridge Modal Parameter Evaluation

Bayesian dynamic linear models build a dynamic model by combining subjective and objective information. The model is tested with the detected structural information so that the final result is close to the actual situation. Bayesian dynamic linear models have many advantages. For example, stability is not assumed, and at the same time, real-time online predictions can be made based on prior knowledge and sample data. At present, Bayesian dynamic linear models have been successfully applied in the fields of bridge evaluation and dam deformation.

The dynamic linear model can be used to describe how the observed variable depends on the state variable (Zhu et al., 2012) and how the state variable changes with time, which mainly represents random disturbances and dynamic state changes inside the system. Assuming that the state variables and observed variables obey a normal distribution, this model can be regarded as a normal linear model, and its observation equation can be expressed as follows:

$y_t=F_T^t+v_t,v_t\sim N[0,v_t](5)$

${\mathrm{\theta }}_t=G_t{\mathrm{\theta }}_{t-1}+{\mathrm{\omega }}_t,{\mathrm{\omega }}_t\sim N[0,{\mathrm{\omega }}_t]t=1,2,\mathrm{\cdots },T(6)$

$\left({\mathrm{\theta }}_{t-1}|D_{t-1}\right)\sim N[m_{t-1},C_{t-1}](7)$

In the formula: y_t observation variable; θ_t state variable, both are normal random variables. v_t observation error vector; ω_t state error vector, the same as a zero-mean normal random variable; D_t−1−(t−1) and all its previously valid information. The model pair has a quaternion element combination {F,G,V,W}t = {F_t,G_t,V_t,W_t} at each time t, where F_t is the known moment matrix; G_t is the known state transition moment matrix; V_t is the squared difference matrix, with known and unknown two kinds Case; W_t known variance matrix, which mainly represents the uncertainty in the whole process from time (t−1) to time t. v_t and w_t represent observation error and state error, respectively, and they can be assumed to be independent. From formulas (5) to (7), the relationship between observation and state variables can be deduced:

$\left(y_t|{\mathrm{\theta }}_t\right)=N[F_t^T{\mathrm{\theta }}_t,V],\left({\mathrm{\theta }}_t|{\mathrm{\theta }}_{t-1}\right)=N[G_t{\mathrm{\theta }}_{t-1},W_t](8)$

If y_t represents the observed value of resistance to degradation at timet, x_t represents the mean value at time t (anti-degradation; Sinsamutpadung and Sasaki, 2019; Li et al., 2021a,b), and v_t represents the observation error, the established observation equation is:

$y_t=x_t+{\mathrm{\beta }}_t+v_t,v_t\sim N[0,V_t](9)$

Equation (9) corresponds to (5), then there is $F_t=\left(\begin{array}{c}1\\ 0\end{array}\right)$

In fact, the average value of resistance levels changes over time. β_t shows the actual change in the mean resistance level at time t. State variables mainly include the mean value of resistance and its changes. The degradation resistance state equation can be expressed as:

$x_t=x_{t-1}+{\mathrm{\beta }}_{t-1}+{\mathrm{\omega }}_{t1},{\mathrm{\omega }}_{t1}\sim N[0,{\mathrm{\omega }}_{t1}](10)$

${\mathrm{\beta }}_t={\mathrm{\beta }}_{t-1}+{\mathrm{\omega }}_{t2},{\mathrm{\omega }}_{t2}\sim N[0,{\mathrm{\omega }}_{t2}](11)$

Equations can be established from (10) to (11):

$\left(\begin{array}{c}\hfill X_t\hfill \\ \hfill {\mathrm{\beta }}_t\hfill \end{array}\right)=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\left(\begin{array}{c}\hfill X_{t-1}\hfill \\ \hfill {\mathrm{\beta }}_{t-1}\hfill \end{array}\right)+\left[\begin{array}{c}\hfill {\mathrm{\omega }}_{t1}\hfill \\ \hfill {\mathrm{\omega }}_{t2}\hfill \end{array}\right](12)$

Substitute into (6), we can get:

$G_t=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right],{\mathrm{\theta }}_t=\left(\begin{array}{c}\hfill X_t\hfill \\ \hfill {\mathrm{\beta }}_t\hfill \end{array}\right),{\mathrm{\omega }}_t=\left[\begin{array}{c}\hfill {\mathrm{\omega }}_{t1}\hfill \\ \hfill {\mathrm{\omega }}_{t2}\hfill \end{array}\right](13)$

In the formula, ω_t1 and ω_t2 are state variables, mainly referring to the state uncertainty in the process from time (t−1) to time t. The state uncertainty value can represent a normal random variable. From the above formula, we can derive the equation of state:

$y_t=F_T^t\mathrm{\theta }+v_t,v_t\sim N[0,v_t](14)$

${\mathrm{\theta }}_t=G_t{\mathrm{\theta }}_{t-1}+{\mathrm{\omega }}_t,{\mathrm{\omega }}_t\sim N[0,w_t]t=1,2,\mathrm{\cdots },T(15)$

$\mathrm{In}\mathrm{the}\mathrm{formula}:F_t=\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right),G_1=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right],{\mathrm{\theta }}_t=\left(\begin{array}{c}\hfill X_t\hfill \\ \hfill {\mathrm{\beta }}_t\hfill \end{array}\right),{\mathrm{\omega }}_t=\left[\begin{array}{c}\hfill {\mathrm{\omega }}_{t1}\hfill \\ \hfill {\mathrm{\omega }}_{t2}\hfill \end{array}\right],W=\left(\begin{array}{cc}\hfill {\mathrm{\sigma }}_X^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{\sigma }}_{\mathrm{\beta }}^2\hfill \end{array}\right)$

The above is that we intelligently monitor and analyze bridge modal parameters through Bayesian method, and monitor bridge parameters in real time to ensure stability and safety (He and Kusiak, 2017; Cui et al., 2021; Li et al., 2021a,b, 2022; Zhou et al., 2021; Li, 2022a,b).

Simulation

For a reinforced concrete bridge with a span of 192.3 m, the numerical control real-time monitoring is shown in Table 1. Bridge monitoring programs include resistance and strain assessments of specific components of the structure, as well as long-term safety assessments of the entire bridge structure. The monitoring data only consider the stress changes caused by vehicle load, temperature, shrinkage and creep and structural changes, and do not include the stress information caused by the dead load of steel plates and concrete. Set the bridge location to crack.

TABLE 1

Table 1. Real-time monitoring data.

According to the monitoring data and the above formula, the prediction equation is established as follows:

$y_t=m_t+v_t,v_t\sim N[0,V](16)$

The equation of state is:

$m_t=m_{t-1}-0.0321+{\mathrm{\omega }}_t,{\mathrm{\omega }}_t\sim N[0.W_t](17)$

The initial information is as follows:

$m_{t-1}|D_{t-1}\sim N[24.5102,{4.5615}^2],\mathrm{LN}[3.1812,{0.1861}^2](18)$

In the formula, y_t is the monitoring limit resistance at time t. m_t is the state value at t. V can be approximated by using stochastic information from monitoring extreme data and smoothing trend terms.

It can be approximated by formula (18):

$W_t=-C_{t-1}+C_{t-1}/\mathrm{\delta }(19)$

N[⋅] is the normal probability distribution and LN[⋅] is the log-normal probability distribution.

As shown in Figure 1, the lower structure of the bridge is the first and second parts in the figure, and the structure mainly includes the pier part. The temperature around the bridge pier changes greatly, and it is eroded and worn for a long time, and the foundation settlement is uneven, resulting in the shrinkage and expansion of the concrete. For a long time, the pier part will appear cracks, corrosion, falling off and so on. The superstructure is shown in the Figure 1(3–5) parts are bridge supports, Figure 1(6) parts are bridge hangers and Figure 1(7) parts are bridge deck structures. The cracks in the upper part of the bridge are mainly caused by improper design of the bridge deck web size, unreasonable specifications and quantity of steel bars, unsatisfactory concrete mix ratio, and overloaded vehicles. The damage of the bridge support is caused by the poor manufacturing process of the bridge bottom plate and the wet environment around the bridge deck steel bars, resulting in uneven resistance on the support and changes in the bearing capacity of the bridge. The main reason for the corrosion of the boom is that the boom is exposed to the atmospheric environment for a long time, the oxidation reaction occurs, the protective layer on the surface of the boom is damaged, and the maintenance of the boom is not timely, resulting in serious corrosion of the boom.

FIGURE 1

Figure 1. Simple diagram of bridge damage.

By observing Figure 2A, it can be seen that there is a measurement error at point 2, which is 0.01 different from the actual damage position, and the monitoring errors at points 6 and 7 are 0.005 and 0.01; Bias, but the error is small, relatively speaking, the accuracy is high. It can be seen from Figure 2B that during monitoring, the damage location has obvious frequency fluctuations, up to 45 Hz, and the fluctuation is irregular, indicating that the parameters of the bridge have changed in the intelligent monitoring environment, and the damage location has obvious fluctuations, so that we can clearly know The damage location tends to be consistent with the actual damage location, which can monitor the problem well, reduce the degree of bridge damage, reduce economic losses, and ensure the safety of the masses. From the analysis results and the actual situation, it can be seen that some damages of the bridge have a certain influence on the bearing capacity of the bridge, but do not affect the load requirements of the bridge. After intelligent monitoring, the overall strength and stiffness of the bridge meet the requirements of the basic design specifications, but the deflection coefficient of some positions is very close to the specification value, indicating that its stiffness is weak and there is a certain risk.

FIGURE 2

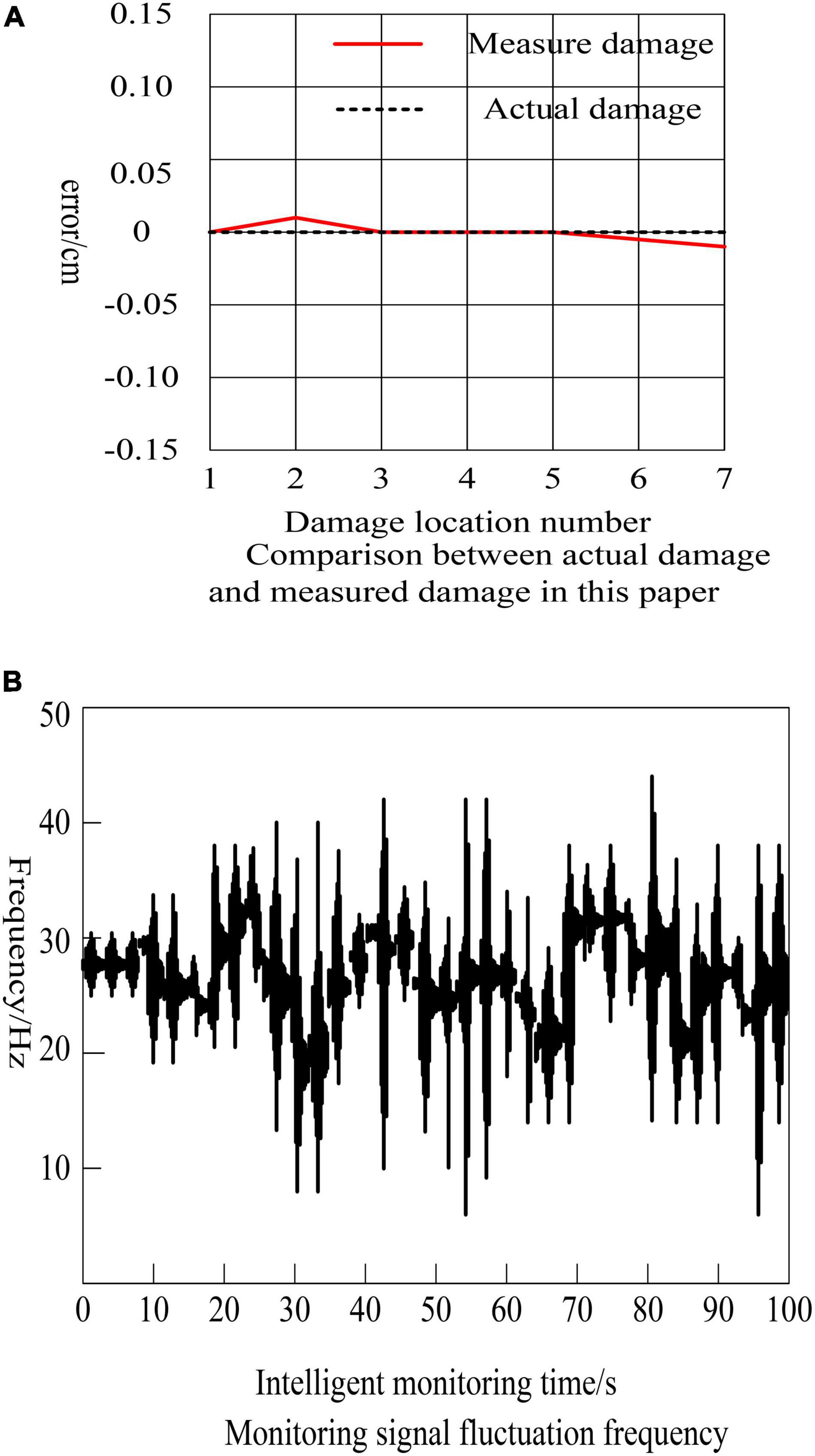
Figure 2. Intelligent monitoring bridge damage curve and signal fluctuation frequency. (A) Comparison between actual damage and measured damage in this paper. (B) Monitoring signal fluctuation frequency.

Conclusion

During the operation of bridge engineering, due to the quality defects of the project itself, coupled with the influence of vehicle load and natural environment, it may cause problems such as cracks, settlement, corrosion of steel bars, reduce the quality of the project, and have an adverse impact on vehicle traffic. In order to achieve timely repair and treatment of these problems, it is necessary to take measures to strengthen bridge monitoring and master the correct data processing methods. Correct bridge monitoring methods can help to deeply understand the quality of bridge engineering and promote the improvement of monitoring level.

This paper proposes a Bayesian-based bridge modal parameter identification model. The uncertainty of model parameters and model selection can be fully considered, and the posterior probability distribution and posterior confidence of model parameters can be obtained. Compared with the traditional parameter monitoring method, this method overcomes the defects in the static model, contains more information, has better application value, and can better provide the basis for the subsequent monitoring of bridge modal parameters. In the actual engineering application process, the Bayesian dynamic model can be used to monitor the bridge reliability in real time to further improve the parameter accuracy.

The future research directions of intelligent monitoring of bridge modal parameters mainly include four aspects. One is to effectively control the influence of noise and unstable factors. The second is to improve the accuracy of bridge damage diagnosis methods. The third is to develop a low-cost and practical bridge health monitoring system and the fourth is to actively identify the degree of damage.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

TW, XG, and GL conceived the idea and designed the experiments. XL and XG led the experiments. TW and XG contributed to data analysis and interpretation. All authors read and approved the final manuscript.

Funding

This work was supported by the National Key R&D Plan Project (2021YFB1600300), the Key Science and Technology Project in Transportation Industry (2021-ZD1-011), and the Science and Technology Plan Project of Shandong Provincial Department of Transportation (2021b51).

Conflict of Interest

GL was employed by the Shandong Hi-speed Group Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abramowicz, M., Berczyński, S., and Wróblewski, T. (2020). Modelling and parameter identification of steel–concrete composite beams in 3D rigid finite element method. Archiv.Civ.Mech.Eng. 20:103. doi: 10.1007/s43452-020-00100-7

CrossRef Full Text | Google Scholar

Asadollahi, P., and Jian, L. (2016). “Statistical analysis of modal properties of a cable-stayed bridge through long-term structural health monitoring with wireless smart sensor networks,” in Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Bellingham, WA: SPIE. doi: 10.1117/12.2219517

CrossRef Full Text | Google Scholar

Cui, S., Pei, X., Jiang, Y., Wang, G., Fan, X., Yang, Q., et al. (2021). Liquefaction within a bedding fault: understanding the initiation and movement of the daguangbao landslide triggered by the 2008 Wenchuan Earthquake (Ms = 8.0). Eng. Geol. 295:106455. doi: 10.1016/j.enggeo.2021.106455

CrossRef Full Text | Google Scholar

Franken, A. (2017). Application and Environmental Evaluation of Fibre Reinforced Polymers in Movable Bridge Design. Delft: TU Delft Industrial Design Engineering.

Google Scholar

Hamdi, S. E., Sbarta, Z. M., and Elachachi, S. M. (2021). Performance assessment of modal parameters identification methods for timber structures evaluation: numerical modeling and case study. Wood Sci. Technol. 55, 1593–1618. doi: 10.1007/s00226-021-01335-0

CrossRef Full Text | Google Scholar

He, Y., and Kusiak, A. (2017). Performance assessment of wind turbines: data-derived quantitative metrics. IEEE Trans. Sustain. Energy 9, 65–73. doi: 10.1109/TSTE.2017.2715061

CrossRef Full Text | Google Scholar

Jahan, S. (2020). Steel bridges structural health monitoring based on operational modal analysis accommodating evaluation of uncertainty. J. Struct. Constr. Eng. 4, 5–17.

Google Scholar

Kaloop, M. R., Elbeltagi, E., and Elnabwy, M. T. (2015). Bridge monitoring with wavelet principal component and spectrum analysis based on GPS measurements: case study of the Mansoura bridge in Egypt. J. Perform. Constr. Facil. 29. doi: 10.1061/(ASCE)CF.1943-5509.0000559

PubMed Abstract | CrossRef Full Text | Google Scholar

Le, S., Wu, Y., Guo, Y., and Del Vecchio, C. (2021). “Game theoretic approach for a service function chain routing in NFV with coupled constraints,” in Proceedings of the Circuits and Systems II: Express Briefs, Piscataway, NJ: IEEE, 3557–3561. doi: 10.1109/TCSII.2021.3070025

CrossRef Full Text | Google Scholar

Li, H. (2022a). Short-term wind power prediction via spatial temporal analysis and deep residual networks. Front. Energy Res. 10:920407. doi: 10.3389/fenrg.2022.920407

CrossRef Full Text | Google Scholar

Li, H. (2022b). SCADA data based wind power interval prediction using LUBE-based deep residual networks. Front. Energy Res. 10:920837. doi: 10.3389/fenrg.2022.920837

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D., and Cheng, Q. (2021a). Short-term nacelle orientation forecasting using bilinear transformation and ICEEMDAN framework. Front. Energy Res. 9:780928. doi: 10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. (2021b). Monitoring and identifying wind turbine generator bearing faults using deep belief network and EWMA control charts. Front. Energy Res. 9:799039. doi: 10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Li, H., He, Y., Xu, Q., Deng, j, Li, W., and Wei, Y. (2022). Detection and segmentation of loess landslides via satellite images: a two-phase framework. Landslides 19, 673–686. doi: 10.1007/s10346-021-01789-0

CrossRef Full Text | Google Scholar

Li, Z., Swanson, J. A., Helmicki, A. J., and Hunt, V. J. (2005). Modal contribution coefficients in bridge condition evaluation. J. Bridge Eng. 10, 169–178. doi: 10.1061/(ASCE)1084-0702(2005)10:2(169)

CrossRef Full Text | Google Scholar

Maity, S., Maiti, R., and Senapati, T. (2022). Evaluation of spatio-temporal variation of water quality and source identification of conducive parameters in Damodar River, India. Environ. Monit. Assess. 194:308. doi: 10.1007/s10661-022-09955-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, Z.-H., Sun, L.-M., and Dan, D. (2009). Analysis of environmental factors affecting modal parameters changes of cable-stayed bridges. Vib. Shock 28:7.

Google Scholar

Mitsuru, T., and Yuhu, W. (2019). Mayer-type optimal control of probabilistic boolean control network with uncertain selection probabilities. IEEE Trans. Cybernetics. 51, 3079–3092. doi: 10.1109/TCYB.2019.2954849

PubMed Abstract | CrossRef Full Text | Google Scholar

Peeters, B., and Roeck, G. D. (2001). One-year monitoring of the Z24-bridge: environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 30, 149–171. doi: 10.1002/1096-9845(200102)30:2<149::AID-EQE1>3.0.CO;2-Z

CrossRef Full Text | Google Scholar

Pingfan, F. U. (2013). Evaluation and Analysis of Yang Wangli’s Observational Narrative. Yuxi: Yuxi Normal University.

Google Scholar

Qiyuan, H. (2009). Research on the Identification Method of Environmental Excitation Modal Parameters Based on Modern Time-Frequency Analysis. Chongqing: Chongqing University.

Google Scholar

Shull, P. J., Shabbir, F., and Omenzetter, P. (2015). “Application of firefly algorithm to the dynamic model updating problem,” in Proceedings of the Spies Conference on Smart Structures & Materials/Nondestructive Evaluation & Health Monitoring, Bellingham, WA: SPIE, the International Society for Optics and Photonics, 94370Y. doi: 10.1117/12.2083573

CrossRef Full Text | Google Scholar

Sinsamutpadung, N., and Sasaki, E. (2019). Strain-based evaluation of bridge monitoring using numerical model analysis. IOP Conf. Ser. Mater. Sci. Eng. 639:012023. doi: 10.1088/1757-899X/639/1/012023

CrossRef Full Text | Google Scholar

Snaebjörnsson, J., Cheynet, E., and Jakobsen, J. B. (2016). “Performance evaluation of a suspension bridge excited by wind and traffic induced action,” in Proceedings of the 8th European Workshop on Structural Health Monitoring (EWSHM 2016), Bilbao.

Google Scholar

Ubertini, F., Gentile, C., and Materazzi, A. L. (2013). Automated modal identification in operational conditions and its application to bridges. Eng. Struct. 46, 264–278. doi: 10.1016/j.engstruct.2012.07.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., and Liu, P. (2018). Analysis and Evaluation of Water Quality Monitoring Results in Dongliao River. Jilin: Jilin Water Resources.

Google Scholar

Wang, Z., Ma, Y., Cheng, F., and Yang, L. (2010). Review of pulse-coupled neural networks. Image Vis. Comput. 28, 5–13. doi: 10.1016/j.imavis.2009.06.007

CrossRef Full Text | Google Scholar

Wiberg, J. (2006). Bridge Monitoring to Allow for Reliable Dynamic FE Modelling : A Case Study of the New Årsta Railway Bridge. Stockholm: KTH Royal Institute of Technology.

Google Scholar

Wu, Y., Guo, Y., and Toyoda, M. (2020). Policy iteration approach to the infinite horizon average optimal control of probabilistic boolean networks. IEEE Trans. Neural Net. Learn. Syst. 32, 2910–2924. doi: 10.1109/TNNLS.2020.3008960

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Q., Du, S., Liang, C., and Yang, L. A. (2014). Universal model-independent algorithm for structural Damage Localization. Comput. Model. Eng. Sci. 100, 223–248.

Google Scholar

Zhang, Y., Qian, T., and Tang, W. (2022). Buildings-to-distribution-network integration considering power transformer loading capability and distribution network reconfiguration. Energy 244:123104. doi: 10.1016/j.energy.2022.123104

CrossRef Full Text | Google Scholar

Zhou, J., Wei, J., Yang, T., Zhang, P., Liu, F., and Chen, J. (2021). Seepage channel development in the crown pillar: insights from induced microseismicity. Int. J. Rock Mech. Min. Sci. 145:104851. doi: 10.1016/j.ijrmms.2021.104851

CrossRef Full Text | Google Scholar

Zhu, Y., Xiao-Tao, G., Wang, X. B., Guo, H. S., Li, W., Wang, S. Y., et al. (2012). Evaluation of pollution status and analysis of water environmental capacity for Zhuyin Reservoir flowing in Zhuhai. Ecol. Sci. 31, 97–103.

Google Scholar