Development of ann-based data-driven ground motion model for Azerbaijan using temporal earthquake records of 2022–2024

Babayev, T.; Babayev, G.; Irawan, S.; Bayramov, E.

doi:10.3389/feart.2025.1571640

ORIGINAL RESEARCH article

Front. Earth Sci., 18 March 2025

Sec. Geohazards and Georisks

Volume 13 - 2025 | https://doi.org/10.3389/feart.2025.1571640

Development of ann-based data-driven ground motion model for Azerbaijan using temporal earthquake records of 2022–2024

T. Babayev¹*

G. Babayev¹

S. Irawan²*

E. Bayramov²

¹Institute of Geology and Geophysics, Ministry of Science and Education, Baku, Azerbaijan
²School of Mining and Geosciences, Nazarbayev University, Astana, Kazakhstan

This study evaluates the Soviet-era ground motion prediction equation (named as A&K-1979) and introduces an Artificial Neural Network (ANN)-based GMM specifically designed for Azerbaijan to improve prediction accuracy. Ground motion models (GMMs) are essential for predicting earthquake-induced ground motions, aiding seismic hazard assessments and engineering designs. While traditional linear empirical models have been widely used, they often struggle to capture complex nonlinear ground motion behaviors. The performance of A&K-1979 was assessed using a strong-motion dataset comprising 500 records collected between 2022 and 2024. Two variants of A&K-1979 were tested: A&K-1979-1 for PGA ≥160 cm/s² and A&K-1979-2 for PGA <160 cm/s². An ANN-based GMM was developed using earthquake magnitude and hypocentral distance as inputs, followed by three hidden layers (32-32-16 neurons) with the Rectified Linear Unit (ReLU) activation function. The model was validated with a separate dataset of 268 records, evaluated using metrics such as bias, standard deviation of residuals (σ), mean absolute error (MAE), root mean squared error (RMSE), and R². The A&K-1979 model exhibited notable prediction biases: A&K-1979-1 overestimated PGA values, while A&K-1979-2 underestimated them. The ANN-based GMM achieved improved performance metrics, with a bias of -0.0076, σ of 0.5971, MAE of 0.4416, RMSE of 0.5972, and an R² of 0.4601. The improved accuracy of the ANN-based GMM highlights its potential as a valuable tool for seismic hazard assessments in Azerbaijan. By providing enhanced prediction capabilities, the ANN model demonstrates greater reliability and practical value than A&K-1979, reinforcing the need for updated predictive models in the region and supporting its use in preliminary hazard analysis.

1 Introduction

Throughout history, earthquakes have been a leading cause of human casualties and severe economic losses, especially in earthquake-prone regions. From antiquity to the modern era, these catastrophic events have consistently posed a major threat, resulting in widespread destruction of infrastructure and significant loss of life in vulnerable areas. Seismic hazard assessment is a fundamental scientific discipline dedicated to quantifying the potential ground motion induced by earthquakes. Its significance stems from its role in informing earthquake-resistant design, guiding land-use planning, and enhancing disaster preparedness strategies, all of which are crucial for safeguarding public safety and fostering sustainable infrastructure development (Wang, 2011). Seismic hazard assessment integrates multiple critical factors, including understanding seismic sources, employing appropriate strong-motion models and selecting representative scenarios, to provide a comprehensive evaluation of potential ground shaking (Benito and Gaspar-Escribano, 2007). Two primary approaches, Deterministic Seismic Hazard Analysis (DSHA) and Probabilistic Seismic Hazard Analysis (PSHA), are widely employed (Gürboğa and Sarp, 2013) for over 50 years (Abrahamson, 2006). Both deterministic seismic hazard analysis (DSHA) and probabilistic seismic hazard analysis (PSHA) are established methods in this field, each offering distinct approaches and analytical tools to address seismic hazard challenges (Wang, 2011; Babayev and Babayev, 2024). DSHA focuses on simulating the worst-case scenario by modeling an individual target earthquake-based ground motion from a defined maximum credible earthquake, incorporating site-specific geological and seismotectonic conditions (Abrahamson, 2006; Babayev and Babayev, 2024; Bulajic and Manic, 2006). DSHA is particularly suitable for assessing seismic hazards for critical infrastructure such as dams, power plants, and tunnels, where worst-case scenarios must be considered (Sawires et al., 2023). In contrast, PSHA is widely applied in seismic design levels, hazard mapping, and the development of seismic building codes worldwide (Sawires et al., 2023; McGuire, 2008). PSHA calculates the probability of exceeding a certain ground motion level over a specified time period, integrating statistical models of earthquake recurrence and ground motion attenuation accounting all possible earthquake scenarios (Wang, 2011; Abrahamson, 2006; Cornell, 1968). Both approaches rely heavily on Ground motion models (GMMs). GMMs form the analytical foundation for both PSHA and DSHA, providing essential tools for quantifying seismic hazard levels across different regions with accuracy and consistency.

Ground motion models (GMMs) are widely utilized in civil and earthquake engineering for applications such as deterministic and probabilistic seismic hazard analyses, as well as the development of hazard maps for building code designs (Mohammadi et al., 2023). These models estimate various levels of ground motions based on seismological parameters, including earthquake magnitude, fault mechanism, focal depth, and source-to-site distance measures (Karimzadeh et al., 2024). Empirical GMMs proposed at both global and regional scales on basis of regression analysis (Mohammadi et al., 2023) are represented in the form of equations that are known as ground motion prediction equations (GMPEs). GMPEs are central to seismic hazard assessment, modeling peak ground motion parameters predictions such as peak ground acceleration, velocity and displacement (Wang, 2011; Babayev and Babayev, 2024), derived empirically by the regression of earthquake magnitude, distance and site-specific conditions (Boore and Atkinson, 2008). The region-specific GMPEs take part as important element of the seismic hazard analysis (Anbazhagan et al., 2013). Classically, empirical GMPEs are derived through linear regression and have been widely used in ground motion prediction studies (Douglas, 2011; Campbell and Bozorgnia, 2008; Bozorgnia et al., 2014; Zalachoris and Rathje, 2019). These models effectively capture first-order relationships between seismic and ground motion parameters, but struggle to account for complex nonlinear behaviors observed in real earthquake records. Although additional terms and regression coefficients are often introduced to address these limitations, the predefined mathematical forms of regression-based approaches still pose challenges in accurately representing intricate source, site, and path effects (Luco and Cornell, 2007; Güllü and Erçelebi, 2007; Alavi and Gandomi, 2011).

In recent years, seismological parameters, such as seismic moment (Gencoglu and Sayil, 2019) and earthquake ground-motion duration (Yaghmaei-Sabegh, 2018), have been utilized in the development of ground motion models.

There is a vast repository of empirical GMPEs (Douglas, 2019). While BA08 (Boore and Atkinson, 2008) is a globally applied GMPE, AC10 (Akkar and Cagnan, 2010), ASB14 (Akkar et al., 2014) are GMPEs proposed for Middle Eastern and European regions and KAAH15 (Kale et al., 2015) is proposed for Türkiye and Iran, the border countries of Azerbaijan. Moreover, Bindi et al. (2007); Gülkan and Kalkan (2002); Akinci et al. (2006); Akyol and Karagöz (2009); Kayabali and Beyaz (2011) are some of the Türkiye-specific empirical GMPEs.

To overcome such limitations in regression-based empirical GMMs, machine learning algorithms are utilized to form GMMs that can train the nonlinear complex behaviors of ground motions (Karimzadeh et al., 2024; Khosravikia and Clayton, 2021). Machine learning algorithms might be considered as an effective tool for seismic hazard assessment (Trugman and Shearer, 2018; Kong et al., 2019). A significant popularity is observed in ML-based studies in geosciences (Asencio-Cortes et al., 2018; Zhou et al., 2018; Sudakov et al., 2019; Achieng, 2019). Similarly, while machine learning has a long-standing history in seismology, its applications have expanded significantly in recent years (Mousavi and Beroza, 2023). In ground motion parameters prediction, ML algorithms are used in different places of the world, such as in Türkiye (Güllü and Erçelebi, 2007), in Europe (Ahmad et al., 2008), in Taiwan (Kerh and Ting, 2005), in Japan (Derras et al., 2012; Asencio-Cortes et al., 2017), in Poland (Wiszniowski, 2019), in some states of USA (Khosravikia et al., 2018). Artificial Neural Network (hereafter, ANN), Random Forest (hereafter, RF), Support Vector Machine (hereafter, SVM), extreme gradient boosting (hereafter, XGBoost), gradient boosting (hereafter, Gb) are well known machine learning algorithms which handle nonlinear feature influence and interaction effectively (Mohammadi et al., 2023; Khosravikia and Clayton, 2021; Kong et al., 2019). Khosravikia and Clayton, (2021) suggest that the provision of accuracy is fine in sufficient amount of data. The above-mentioned ML-techniques were tested by several authors for various regions (Khosravikia and Clayton, 2021; Seo et al., 2022). Mohammadi et al. (2023) describes the drawback of the ML-algorithms as “black boxes”, emphasizing that, the difficulty lies in understanding and interpreting the underlying processes.

ANNs are complex systems made up of interconnected neural units, which can process input data and adjust to their surroundings through a learning process (Karimzadeh et al., 2024). ANN-based GMMs are proposed by several authors for Türkiye by various authors Mohammadi et al. (2023); Karimzadeh et al. (2024); Temiz et al. (2024). Furthermore, Thomas et al. (2013), Derras et al. (2014), Khosravikia et al. (2019) and Derakhshani and Foruzan (2019) are some other studies suggesting data-driven GMMs using ANN.

In Azerbaijan, comprehensive seismic hazard assessment studies remain largely unexplored, with existing research primarily focusing on multi-scenario-based deterministic assessments for specific seismic regions such as the eastern slope of the Greater Caucasus (Babayev et al., 2010; Babayev et al., 2020a; Babayev G. R. et al., 2023; Babayev et al., 2024; Babayev and Telesca, 2016), the Middle Kur Depression (Babayev and Babayev, 2024; Babayev, 2024) employing Soviet-era GMM–A&K-1979 (Aptikayev and Kopnichev, 1979). However, the validity of ground motion prediction equation suggested by Aptikayev and Kopnichev (1979) has never been systematically tested against modern seismic data.

This present study aims to address this gap by evaluating the performance of A&K-1979 using the most up-to-date dataset, covering earthquakes from 2022 to 2024. We introduce a novel approach for Azerbaijan, developing GMM applying ANN implementation in Python. We selected ANN-based modeling since the training database contain small to moderate earthquakes which is easier for ANN to handle rather than, for instance, XGBoost (Karimzadeh et al., 2024). The suggested model estimates the horizontal peak ground acceleration (PGA) based on input parameters, including local magnitude (M_L) and hypocentral distance (R_hyp). The developed model is made available as a supplementary resource in a GitHub repository, allowing end-users to input parameters such as magnitude, focal depth, and epicentral distance. The model automatically calculates the hypocentral distance and incorporates it as an input parameter, alongside the magnitude.

2 Study area

Azerbaijan, officially known as the Republic of Azerbaijan, is a transcontinental country situated at the intersection of West Asia and Eastern Europe. Covering an area of approximately 86.6 thousand km², it is part of the South Caucasus region. The country is bordered by the Caspian Sea to the east, Russia’s Republic of Dagestan to the north, Georgia to the northwest, Türkiye to the southwest, Armenia to the west, and Iran to the south. As of the end of 2024, Azerbaijan’s population exceeds 10 million. The historical monuments and archaeological findings in the region reflect Azerbaijan’s rich historical and cultural heritage. Baku, the capital and largest city of Azerbaijan, is a coastal urban center situated on the Absheron Peninsula along the Caspian Sea, covering an area of 2,140 km². With a population approaching 2.5 million as of 2023, it serves as the country’s political, economic, and cultural hub.

Azerbaijan is situated on six tectonic structures: the Samur (Gusar)–Devechi (Shabran) zone, the Eastern Greater Caucasus, the Kur intermountain depression, the Outer Lesser Caucasus, the Inner Lesser Caucasus, and the Talysh mountains (Alizadeh et al., 2016). The Samur-Devechi and Eastern Greater Caucasus megazones form part of the Greater Caucasus Fold-Mountain System, with the Eastern Greater Caucasus megazone encompassing the southern and southeastern slopes. Similarly, the Outer Lesser Caucasus and Inner Lesser Caucasus megazones belong to the Lesser Caucasus region (Alizadeh et al., 2016). The Caucasus region, part of the Alpine belt, has a complex geological history and was formed as a result of the closure of the Neotethys Ocean (Adamia et al., 2011; Barrier and Vrielynck, 2008). The Greater Caucasus represents the highest mountain belt in Europe, formed due to the collision between the Arabian and Eurasian plates (Mosar et al., 2010). It is a fold-and-thrust belt separated from the Lesser Caucasus with the Kur foreland sedimentary basin (Mosar et al., 2010; Tibaldi et al., 2024).

The Samur-Devechi is characterized by Quaternary rocks (Alizadeh, 2024). The Eastern Greater Caucasus formed by various geological content, encompassing mainly Jurassic, Cretaceous, Paleogene, and Neogene rocks. We observe Jurassic, Albian to Maastrichtian sediments in the border with Kur depression, where Kur depression is subducted under the Eastern Greater Caucasus forming post-Eocene thrusts (Sosson et al., 2016). Kur basin is covered by Pliocene and Quaternary sediments and volcanites (Alizadeh, 2024; Sosson et al., 2016). In Outer Lesser Caucasus is mostly characterized by Bajocian to Upper Jurassic volcanogenic series with Upper Jurassic-Lower Cretaceous intrusions, Middle Jurassic to Lower Cretaceous ophiolitic series, Paleocene to Oligocene molasses and volcanites and for the Inner Lesser Caucasus the characterization can be similarly seen with Paleocene to Oligocene molasses and volcanites and Bajocian to Upper Jurassic volcanogenic series with Cretaceous and Cenozoic intrusions, furthermore, with Devonian to Permian plateform formations and Miocene volcagenics (Alizadeh, 2024; Sosson et al., 2016). Talysh mountains show up mainly with Paleogene rocks (Alizadeh, 2024).

The complex tectonic structure of Azerbaijan results in significant seismic activity (Babayev et al., 2020b). The study of seismicity in Azerbaijan is divided into two periods: the pre-instrumental (historical) and instrumental periods (Babayev T. H. et al., 2023). During the historical period, records of destructive and strong earthquakes were documented in ancient Arabic chronicles, manuscripts, and travel writings (Ashurbeyli and Bakuvi, 1958). Several significant historical earthquakes have been noted in Azerbaijan, including the earthquake of 427, the Ganja (Goygol) earthquake of 1139, the Ganja earthquake of 1235, the East Caucasus earthquake of 1667, the Mashtaga earthquake of 1842, and multiple Shamakhi earthquakes (1192, 1667, 1668, 1669, 1828, 1859, 1868, 1872, 1902). Other notable events include the Ardabil earthquake of 1924, the Lankaran earthquake of 1913, and several Caspian Sea earthquakes (957, 1812, 1842, 1852, 1911, 1935, 1961, 1963, 1986, 1989, 2000). These earthquakes are well known for their intensity, often resulting in surface deformations, widespread building destruction, and significant human casualties (Babayev and Agayeva, 2021). These historical events highlight the necessity of enhancing seismic hazard assessment methodologies to improve the understanding of earthquake risks and develop more effective mitigation strategies in Azerbaijan. Extensive seismic monitoring activities have been regularly conducted across various regions of Azerbaijan under the Republican Center of Seismic Survey (RCSS, 2024) (Yetirmishli et al., 2013; Yetirmishli et al., 2015; Yetirmishli et al., 2016; Yetirmishli et al., 2018). Additionally, various local and international scientists contributed in the analyses of seismicity (Telesca et al., 2013; Telesca et al., 2017), assessment of seismic hazard (Babayev et al., 2010; Babayev et al., 2020a; Babayev et al., 2024) across various regions of Azerbaijan. Bondar et al. (2024) proposed a comprehensive instrumental catalog for the period 1951–2019, combining the bulletins of local and international agencies, with relocation performed using the iLoc algorithm (Bondár et al., 2024). Similarly, Gunnels et al. (2021) proposed a double-difference (DD) relocated earthquake catalog for the period 2011–2016 and generated high-resolution 3D seismic velocity models for the Eastern Greater Caucasus and Kur basin (Gunnels et al., 2021). 57 seismic stations serve in Azerbaijan for the seismic monitoring studies under RCSS (RCSS, 2024).

Figure 1 illustrates six tectonic structures on geological map of Azerbaijan (Alizadeh et al., 2016; Budagov, 1993a; Budagov, 1993b), the fault map of Azerbaijan (Yetirmishli et al., 2017) and seismic stations distribution of the RCSS network. This study evaluates the existing GMPE used in seismic hazard analyses for Azerbaijan and proposes an ANN-based GMM, derived from a 2022–2024 database created using local station data.

Figure 1

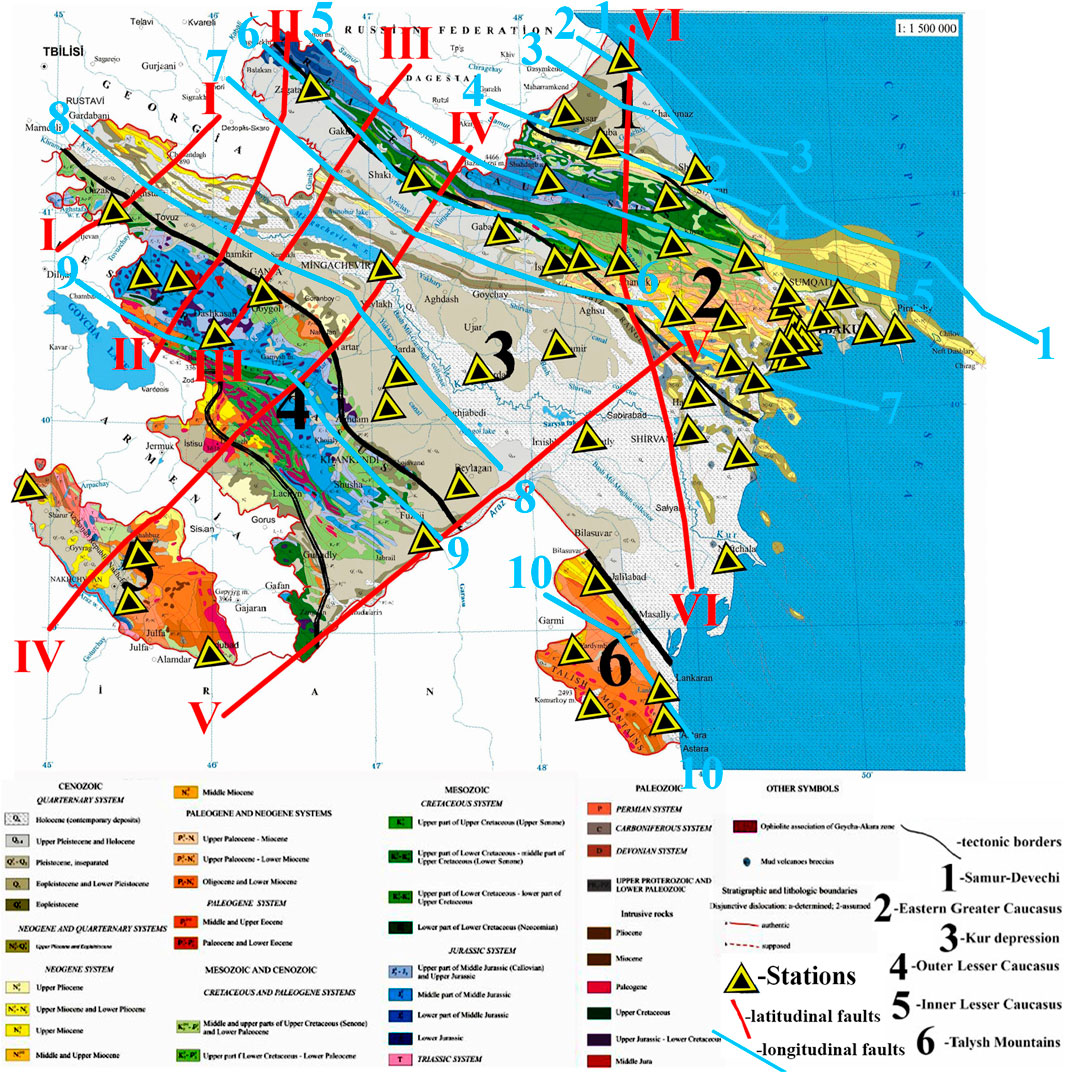
Figure 1. Combined tectonic, geological and fault map of Azerbaijan with the representation of 57 seismic stations of the RCSS network [adapted from (Alizadeh et al., 2016; Budagov, 1993a; Budagov, 1993b)]. Tectonic zones: 1 – Samur (Gusar)–Devechi (Shabran), 2 – Eastern Greater Caucasus, 3 – Kur, 4 – Outer Lesser Caucasus, 5 – Inner Lesser Caucasus, 6 – Talysh. Generalized depth faults of Azerbaijan are adapted from Yetirmishli et al. (2017). Longitudinal faults: 1–1 Makhachkala–Turkmenbashi; 2-2 Khudat–Gilazi; 3–3 Akhti-Nugadi-Gilazi; 4–4 Siyezen; 5–5 Qaynar-Zengi; 6–6 Vandam; 7–7 Ajichay-Elet; 8-8 Kur; 9–9 Lesser Caucasus; 10–10 Talysh. Latidudinal faults: I-I Gazakh-Siqnakh; II-II Sharur-Zagatala; III-III Ganjachay; IV-IV Arpa-Samur; V-V Palmir-Absheron; VI-VI West-Caspian.

3 Dataset acquisition and processing

3.1 Acquisition

The GMM validation and derivation starts with the dataset of earthquake recordings that could be used for regression analysis in empirical models (Bommer et al., 2010). Accurate validation of Ground Motion Prediction Equations (GMPEs) requires a robust dataset composed of reliable earthquake records and associated ground motion parameters. In this study, we developed a comprehensive dataset spanning seismic events from 2022 to 2024 in Azerbaijan, ensuring consistency and quality through systematic data selection and processing. The initial dataset was based on a seismic catalog containing essential parameters for each event, including local magnitude (M), date and time (UTC), longitude, latitude, and depth. The catalog was sourced from the Republican Center of Seismic Survey of Azerbaijan online database (RCSS, 2024). Events with incomplete metadata or poor location accuracy were eliminated during the selection process to ensure dataset integrity. The dataset was further refined to include only earthquakes for which station records were accessible via the IRIS FDSN web service [IRIS, 2024 (I. R. I. for Seismology)]. Since some of the Azerbaijani seismic stations became operational on the IRIS network only after mid-2022, our dataset covers seismic events from June 2022 to December 2024. A total of 183 earthquake events, with magnitudes ranging from 3.0 to 6.1, were initially included (Figure 2).

Figure 2

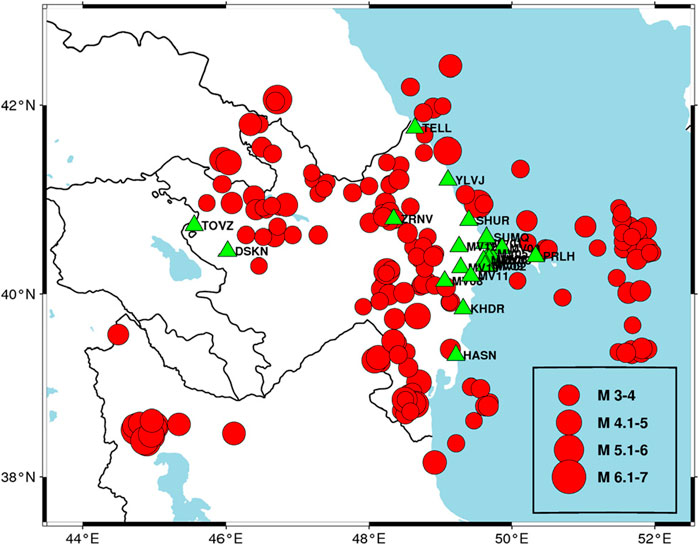
Figure 2. Map of the initial catalog (183 events) and 22 seismic stations used for event recordings.

Seismic waveform data were accessed and processed via the IRIS FDSN web service using the ObsPy Python library (Beyreuther et al., 2010). For each earthquake event, all seismic stations in Azerbaijan with available data on the IRIS network were queried based on the specific date and time of the event. Among the stations that successfully recorded the event, the five closest stations were selected. If five or fewer than five stations recorded the event, all available records were retained. However, 9 events with fewer than two valid station records were excluded to maintain reliability.

3.2 Processing

The raw waveform data from the selected stations underwent systematic preprocessing. For each earthquake, using the ObsPy library of Python, the script fetches waveform data from the selected stations within a specified time window (30 s before to 90 s after the earthquake) (Beyreuther et al., 2010). The instrument response is removed using the remove_response method, which converts the waveform to acceleration time series (m/s²). The remove_response method eliminates instrument response effects by deconvolving the instrument transfer function, ensuring that the recorded waveform accurately represents ground motion (Beyreuther et al., 2010). This method allows conversion of raw seismic data into acceleration (m/s²), velocity (m/s), or displacement (m), depending on the desired output. By applying this correction, the processed data more accurately reflect the true ground motion, independent of the specific characteristics of the recording instrument. The waveform data undergoes bandpass filtering with a frequency range of 1–48 Hz, effectively isolating the relevant seismic signals while attenuating low-frequency noise and high-frequency artifacts. This enhances the clarity of the recorded ground motion, ensuring a more accurate representation of the earthquake’s dynamic characteristics. From these processed records, the peak ground acceleration (PGA)—defined as the maximum absolute value in the acceleration time series—was extracted for each station. Additionally, both epicentral distance (R_epi) and hypocentral distance (R_hyp) were calculated using Python scripting. As the final step in dataset preparation, 74 events recorded by fewer than five stations were eliminated to enhance the reliability of the dataset, meanwhile this step serves the expansion of the dataset. The 100 events recorded at 5 stations present 5 PGA values at 5 hypocentral distances. Therefore, the dataset becomes of 500 records. The processed data were assembled into a structured dataset containing parameters such as magnitude (M_L), longitude, latitude, depth (km), date and time (UTC), station name, epicentral distance (km), hypocentral distance (km), and PGA (cm/s²). Finally, the dataset was exported as a CSV file for subsequent analysis, aimed at validating the GMPE–A&K-1979. Additionally, the dataset will be used to train an Artificial neural network (ANN) model to develop a new ground motion model (GMM), as discussed in the following sections (Figure 3). The 74 events recorded by at least 2, at most 4 stations are retained as a separate testing dataset to evaluate the performance of the new ANN model, after expanding them to 268 records with the same manner (Figure 4).

Figure 3

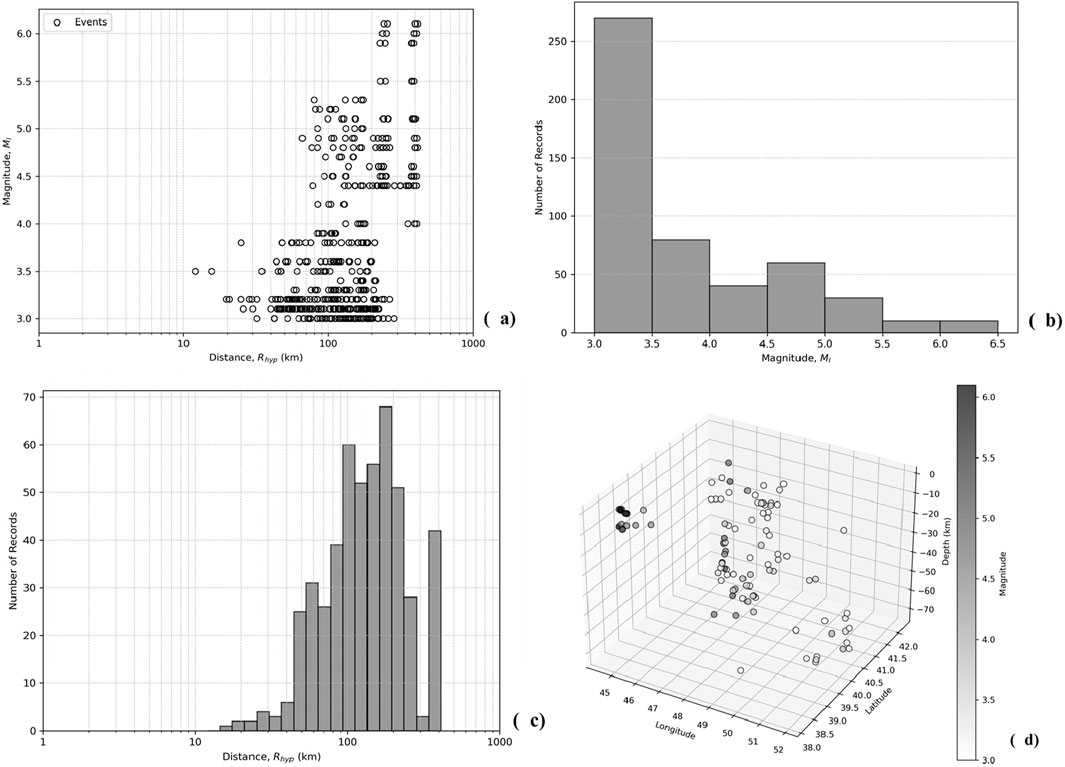
Figure 3. Training dataset representation. (a) Scatter plot of magnitude (M_L) versus hypocentral distance (R_hyp), histogram of number of events versus (b) magnitude (M_L) and (c) hypocentral distance (R_hyp), (d) the 3D representation of earthquake magnitudes in longitude, latitude and depth axes.

Figure 4

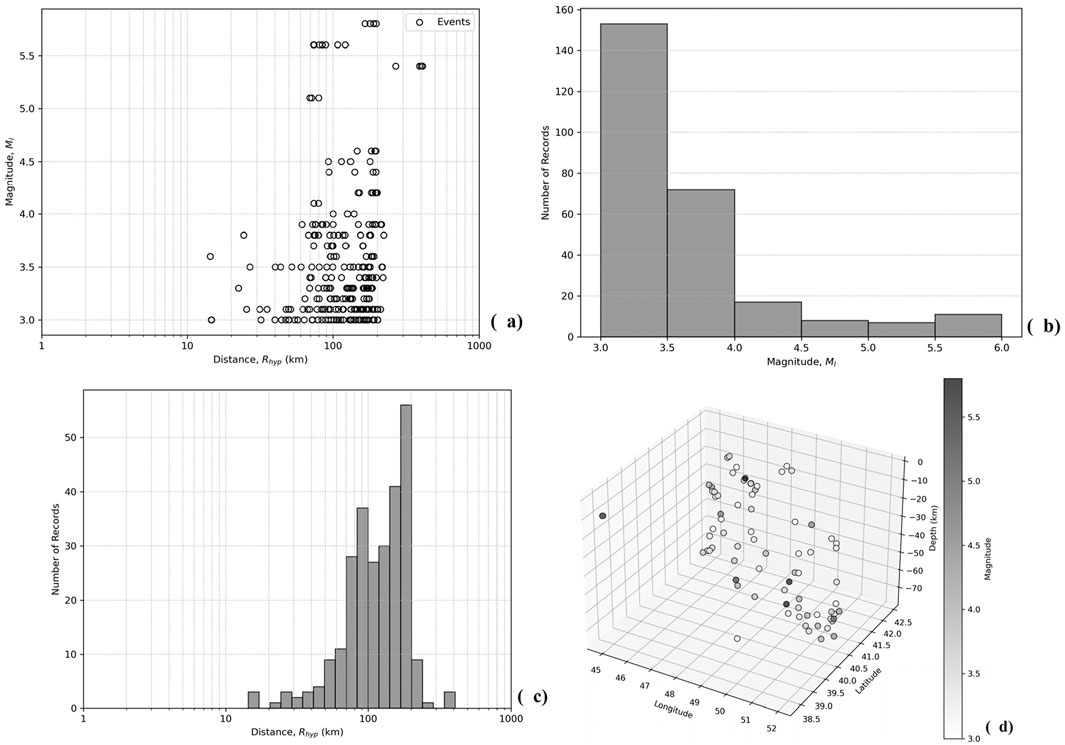
Figure 4. Testing dataset representation. (a) Scatter plot of magnitude (M_L) versus hypocentral distance (R_hyp), histogram of number of events versus (b) magnitude (M_L) and (c) hypocentral distance (R_hyp), (d) the 3D representation of earthquake magnitudes in longitude, latitude and depth axes.

To summarize, the dataset was divided into training and testing subsets based on the number of station recordings per event. Events recorded by five stations (100 events, 500 records) were used for training the ANN-based GMM. Meanwhile, events recorded by at least two but at most four stations (74 events) were retained for testing, and their records were expanded to 268 following the same methodology. This separation ensures a balanced and representative dataset for both training and evaluation, as illustrated in Figures 3, 4.

Figure 3A illustrates the relationship between magnitude (M_L) and hypocentral distance (R_hyp) for the earthquakes in the dataset. For the given dataset, the range of the magnitude is 3.0 ≤ M_L ≤ 6.1 and the range of the hypocentral distance is 12.05 km ≤ R_hyp ≤ 412.73 km. The dataset is typically characterized with low-magnitude events, since accelerograms are deficient in high magnitudes (Ml ≥ 5.5). When magnitude and distance distributions are considered together, the data are richer for 3.0 ≤ Ml ≤ 4.0 and R_hyp > 45 km (Kale et al., 2015). These are the results of some obstacles in the database forming: the stations from which data retrieved record only post-2022 earthquakes and the number of them in Azerbaijan are limited. Furthermore, the earthquake focal depths are changing from quite shallow till deep enough in range 2–72 km (Figure 3D). Therefore, the database contains mostly weak earthquakes in small magnitudes and high hypocentral distances (Figures 3B, C). The testing dataset elements also follow similar trends with magnitude, hypocentral distance and depth ranges of 3 ≤ M ≤ 5.8, 14.38 km ≤ R_hyp ≤ 408.60 km and 3 km ≤ h ≤ 75 km respectively (Figure 4).

These dataset characteristics indicate a significant predominance of low-magnitude and high-hypocentral-distance events, which may influence the model’s predictive performance. A statistical comparison between the training and testing datasets further highlights this trend. The training dataset has a mean magnitude of 3.73, with the majority of events clustered around Ml 3.0–4.0, and very few exceeding Ml 5.5, reinforcing the limited representation of strong-motion records. Similarly, the testing dataset exhibits an even stronger skew towards smaller magnitudes (mean Ml = 3.56) and a slightly lower maximum magnitude (Ml 5.8 vs. 6.1 in training). Regarding hypocentral distances, while both datasets share a broad range, the testing set is characterized by a slightly lower mean distance (128.15 km vs. 154.15 km) and reduced variability, suggesting that test events are somewhat more concentrated around intermediate distances. In terms of PGA, the testing dataset has a higher mean PGA (0.464 cm/s² vs. 0.268 cm/s²) and greater variability, though extreme values remain a challenge in both datasets due to high skewness. These statistical differences underscore potential biases in dataset composition, with the ANN model likely being more exposed to weak-to-moderate earthquakes occurring at mid-to-far distances, while having limited exposure to strong-motion events at short distances (Tables 1, 2).

Table 1

Table 1. Statistical metrics for the training dataset.

Table 2

Table 2. Statistical metrics for the testing dataset.

4 Methods

4.1 Testing A&K-1979

To evaluate the validity of the ground motion prediction equation (GMPE), we compare the predicted ground motion parameters with actual recorded data, which provides insight into the accuracy of the GMPE. In this study, we use PGA values from 500 station-recorded ground motions to assess the performance of the A&K-1979 GMPE for horizontal PGA predictions. This equation has been regarded as the most appropriate for Azerbaijani territory to date (Babayev et al., 2020a; Babayev et al., 2024). The comparison is conducted using the perfect alignment line and residuals analysis. The perfect alignment line, represented by the function y = x, serves as the ideal reference, where the observed and predicted PGA values are equal. This comparison allows for a quantitative assessment of the prediction accuracy. The residuals, defined as the difference between the observed and predicted PGA values, further quantify the predictive performance (Equation 1). Ideally, residuals should be zero, or as close to zero as possible, reflecting a high level of prediction accuracy:

R e s i d u a l s = \log {P G A}_{o b s} - \log {P G A}_{p r e d}, (1)

where $\log {P G A}_{o b s}$ and $\log {P G A}_{p r e d}$ represent the logarithms of the observed PGA values from real records and the PGA predictions from A&K-1979, respectively.

The GMM proposed by Aptikayev and Kopnichev (1979) is divided into two components and shown in the Equations 2, 3 respectively (Aptikayev and Kopnichev, 1979):

\log {P G A}_{A & K - 1979 - 1} = 0.28 M - 0.8 \log R + 1.70, (2)

where $R$ is the hypocentral distance, ${P G A}_{A & K - 1979 - 1}$ is predicted $P G A$ by A&K-1979 in cm/s², for $P G A$ ≥ 160 cm/s²;

\log {P G A}_{A & K - 1979 - 2} = 0.8 M - 2.3 \log R + 0.80, (3)

where $R$ is the hypocentral distance, ${P G A}_{A & K - 1979 - 2}$ is predicted $P G A$ by A&K-1979 in cm/s², for $P G A$ < 160 cm/s².

The perfect alignment and residual analysis will be shown in Results section.

4.2 Training ANN-based GMM

Given the characteristics of both the training and testing datasets in Tables 1, 2, the use of ANN for developing a GMM is justified due to the following key factors. First, the datasets exhibit significant non-linearity and complex interactions between magnitude, hypocentral distance and PGA. Traditional regression-based GMMs often struggle to capture these relationships, as discussed already, particularly in cases where the data distribution is skewed and contains a mix of near-field and far-field events. The high skewness and kurtosis values, especially for PGA (9.13 in training, 6.52 in testing), indicate that standard parametric models may not effectively generalize across the entire dataset.

Furthermore, the datasets contain imbalances in magnitude and distance distributions, with a predominance of small-magnitude and high-hypocentral-distance events. ANN models are well-suited for handling such imbalanced–non-linear datasets, as they can learn complex patterns from limited high-magnitude observations while avoiding overfitting to the dominant low-magnitude cases. Additionally, the ability of ANNs to approximate highly non-linear functions makes them advantageous when dealing with datasets that do not follow traditional empirical relationships, particularly given the wide range of hypocentral distances (12–412 km in training, 14–408 km in testing) and varying focal depths (2–72 km in training, 3–75 km in testing).

Moreover, the flexibility of ANN models allows them to integrate additional input parameters, such as site conditions (e.g., V_s30), which may further improve predictive accuracy. Given the dataset’s limitations—particularly the lack of strong-motion records—ANNs can leverage their ability to interpolate missing patterns and enhance predictions for rare, high-magnitude events. Therefore, an ANN-based approach provides a robust and data-driven alternative to traditional GMMs, ensuring greater adaptability and accuracy in predicting ground motion parameters.

ANN is a computational model that mimics the way the human brain processes information (Haykin, 2008). It consists of layers of interconnected neurons, where each neuron processes data and passes it to the next layer. ANNs have emerged as powerful computational tools for solving complex regression problems, particularly in applications where traditional empirical models struggle to capture intricate nonlinear relationships (Mohammadi et al., 2023). Inspired by the structure of biological neural networks, ANNs consist of interconnected computational units (neurons) arranged in layers: an input layer, one or more hidden layers, and an output layer (Karimzadeh et al., 2024). These networks learn from data by adjusting connection weights to minimize prediction errors, making them well-suited for ground motion modeling (Withers et al., 2020).

In this study, we develop an ANN-based ground motion prediction model specifically for Azerbaijan, leveraging a dataset of observed PGA values. The ANN model is trained to predict the logarithm of PGA values based on two key input parameters: earthquake magnitude and hypocentral distance. Following best practices in ANN-based ground motion modeling (Khosravikia and Clayton, 2021; Khosravikia et al., 2019), we divide the dataset into training and testing subsets, as 80% and 20% respectively, to optimize model performance while preventing overfitting.

The selection of input parameters for the ANN-based GMM was based on the available data and their relevance to ground motion prediction. Magnitude (M_L) and hypocentral distance (R_hyp) were chosen as the primary inputs, as they are fundamental factors influencing seismic ground motion. While V_s30 and depth are important for refining GMMs, we did not have consistent V_s30 data across the entire study area, and depth is implicitly accounted for in the calculation of hypocentral distance (Equation 4). Thus, magnitude and hypocentral distance were deemed the most reliable and relevant predictors given the dataset constraints. Future research could explore the inclusion of additional parameters for enhanced model accuracy.

R_{h y p} = \sqrt{R_{e p i}^{2} + h^{2}}, (4)

where $R_{h y p}$ and $R_{e p i}$ are hypocentral and epicentral distances respectively and $h$ is the focal depth of the earthquake.

The network is trained using backpropagation and the Adam optimizer with a learning rate of 0.01, which iteratively adjusts the model’s weights to minimize prediction errors. This approach allows for effective modeling of complex seismic relationships, providing a powerful tool for earthquake ground motion prediction. Backpropagation is a widely recognized multilayer neural network approach that employs a gradient-descent technique to minimize errors during the learning process (Karimzadeh et al., 2024; Adamowski and Karapataki, 2010). This method effectively reduces prediction errors, optimizing model accuracy while preventing overfitting. The model is trains using the TensorFlow Keras library. It consists of an input layer with two neurons corresponding to the earthquake magnitude and hypocentral distance, followed by two hidden layers with 32 neurons each, employing the Rectified Linear Unit (ReLU) activation function to introduce non-linearity and enhance learning capabilities. An additional hidden layer with 16 neurons is included to further refine feature extraction. The output layer consists of a single neuron representing $\log P G A$ with a linear activation function, allowing for unrestricted predictions. The model employs the Mean Squared Error (MSE) loss function for training while tracking the Mean Absolute Error (MAE) as an additional evaluation metric. The network is trained over 100 epochs (Withers et al., 2020) with a batch size of 32, ensuring convergence while maintaining computational efficiency. Epoch is the number of times the model has gone through the training dataset. We present the schematic view of the ANN structure used in this study in Figure 5.

Figure 5

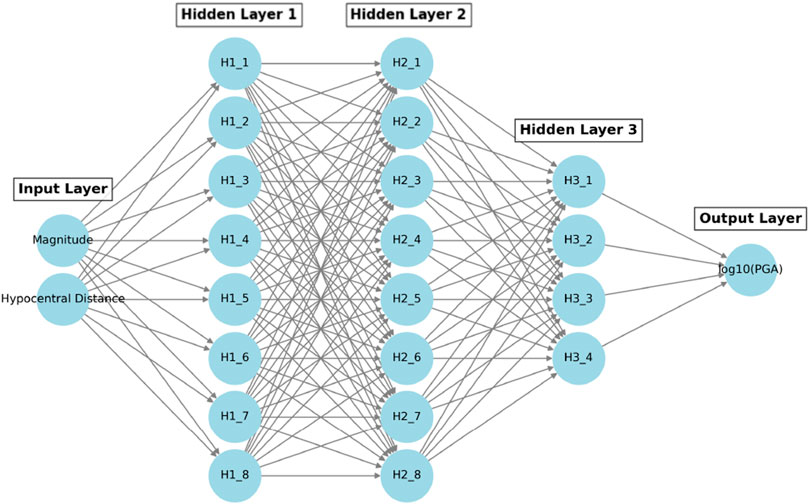
Figure 5. ANN Architecture for ground motion modeling. Predictive input layers are magnitude and hypocentral distance. Output layer is the logarithm of PGA. Hidden layers are shown as $\frac{N u m b e r o f H i d d e n l a y e r}{4}$ to avoid the mess in the scheme.

By leveraging ANN-based modeling, this study offers an alternative to traditional empirical GMMs, demonstrating the ability of machine learning techniques to capture complex seismic relationships that conventional models may not fully account for (Mohammadi et al., 2023; Karimzadeh et al., 2024).

5 Results

The following section presents the results of validating the A&K-1979 GMPE and developing the new ANN-based GMM using the respective methodologies outlined in Section 4.

5.1 Perfect alignment and residual analysis of A&K-1979 predictions

The perfect alignment (Figure 6A) and residual analysis (Figure 6B) of both versions of A&K-1979 expose the level of discrepancy between GMPE-suggested ground motion modeling and real strong motion dataset. A&K-1979-1 which is designed for high ground motion levels (≥160 cm/s²), predicts overestimated and low accurate PGA values for the area in comparison to the data. This is represented in Figure 6A with the position of the predicted points – they are positioned under the perfect alignment line. In Figure 6B we observe negative residual values with high frequencies. This means high number of residuals with overestimation. Residuals are too frequent between −3.5 and −1.5. Since the residual is simply the difference between observed (real data) PGA and predicted (by GMPE) PGA values (1), closer the residual to 0, more accurate it is. And the negative value means that predicted PGA values are greater than the values of real data. In the same manner, the plots of Figure 6 in green, for the low-level ground motion prediction equation–A&K1979-2 (<160 cm/s²) represent mainly underestimation. We observe satisfying modeling in the very low values of PGA (0–1 cm/s²), while the underestimation starts above the PGA > 1 cm/s².

Figure 6

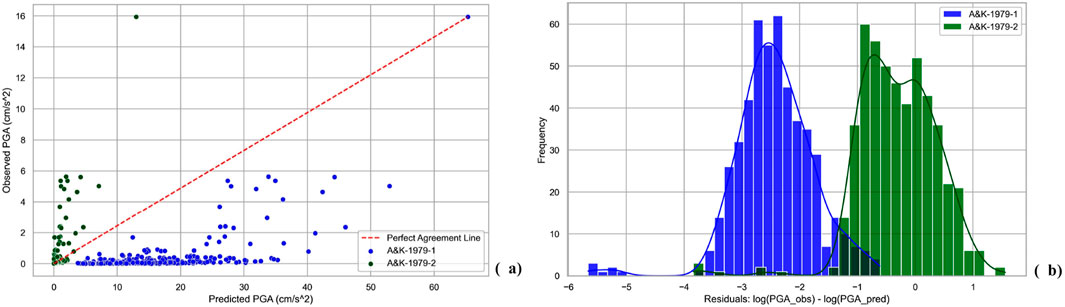
Figure 6. Observed PGA values versus prediction of A&K-1979. Blue for A&K-1979-1 (≥160 cm/s²), green for A&K-1979-2 (<160 cm/s²). (a) The scatter plot and perfect alignment line. (b) The logarithmic residuals.

5.2 ANN-based developed GMM

This section presents the results for the proposed ANN-based GMM for Azerbaijan. The model’s performance is evaluated using various statistical metrics, including Bias, Sigma, Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and R², as detailed in Table 3. Figures 7, 8 display the training, validation, and testing results. Figure 7 illustrates the trends for Mean Squared Error (MSE) and MAE during training and validation. Figure 8 highlights the predictive performance of the ANN-based model, showing scatter plots of predicted versus observed PGA (8a), residuals vs hypocentral distance (8b), and residuals vs the log of the model-predicted PGA (8c). Figures 8D, E show the performance comparisons of the ANN-based model and the A&K-1979 GMPE, using scatter plots and residuals histograms, respectively, for the testing dataset (analogous to Figures 6A, B).

Table 3

Table 3. Statistical metrics of the A&K-1979 GMPE and developed ANN-GMM.

Figure 7

Figure 7. Training and validation plots of ANN model. (a) MSE. (b) MAE.

Figure 8

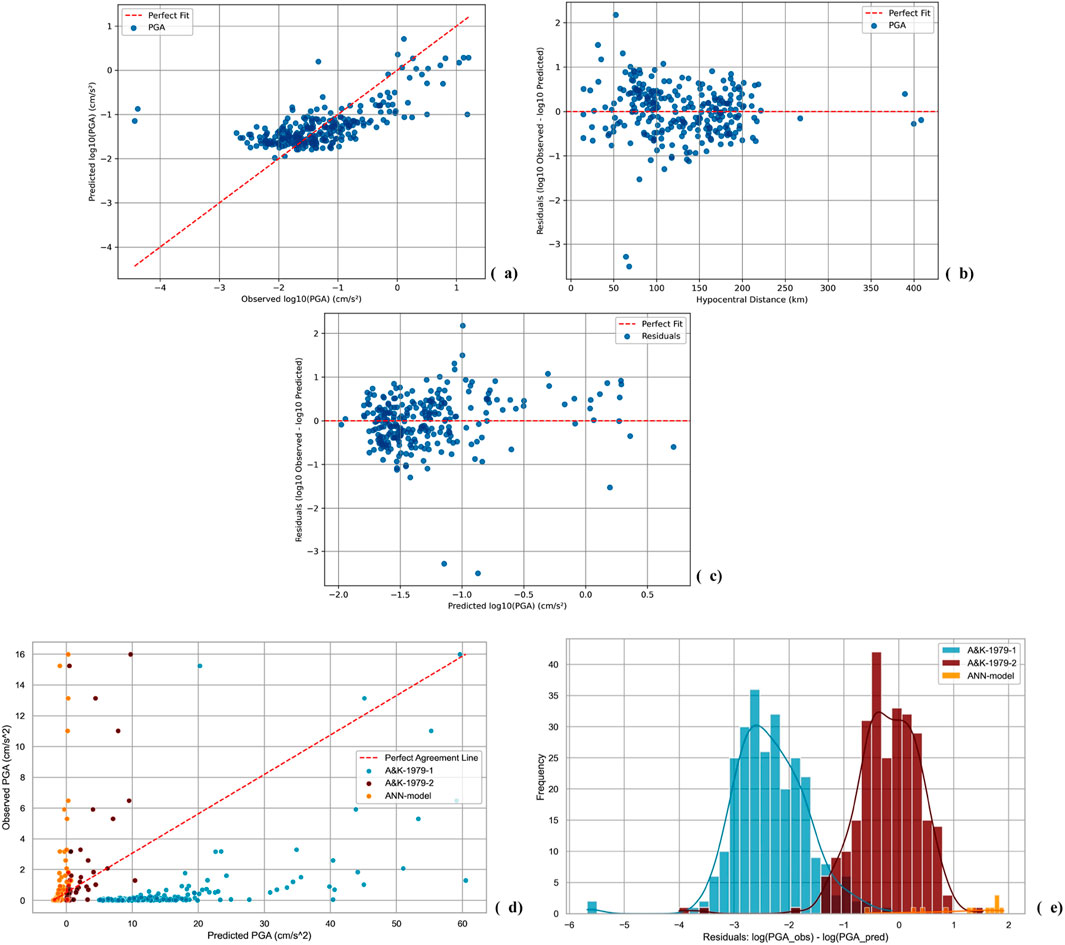
Figure 8. PGA Predictions of ANN-based GMM for Azerbaijan versus real PGA values of testing dataset. (a) Predicted vs. Observed PGA scatters around perfect fit line in logarithmic scale. (b) Logarithmic residuals vs. hypocentral distance scatters around perfect fit line. (c) Logarithmic residuals vs. predicted logarithmic PGA scatters around perfect fit line. (d) Scatters of observed PGA values based on testing set versus prediction of A&K-1979-1, A&K-1979-2, ANN-model around perfect line. (e) The logarithmic residuals.

The ANN-based model outperforms both versions of the A&K-1979 GMPE in terms of predictive accuracy and consistency. As shown in Table 3, the ANN model demonstrates significantly lower Bias (−0.0076), a reduced Sigma (0.5971), and a smaller RMSE (0.5972), indicating a more accurate and reliable prediction. Furthermore, the ANN model’s R² score of 0.4601 represents an improvement of 46% compared to A&K-1979-2, which has a R² of 0.4154. This suggests that the ANN model has a better overall fit to the data, with less variance in its predictions. In comparison, A&K-1979-1 exhibits much higher Bias (12.9530) and Sigma (9.0744), with a very low R² score of −73.5202, indicating poor predictive accuracy and significant deviation from observed values. In contrast, A&K-1979-2 shows a more reasonable performance with a small Bias (−0.0120), low Sigma (1.4008), and a higher R² score (0.4154), but it still falls short in comparison to the ANN model.

Figures 8D, E clearly illustrate these performance differences, where the scatter plot and residuals histogram show that the ANN-based model aligns more closely with observed PGA values, while A&K-1979-1, exhibits more variability and higher predictive uncertainty. This further highlights the superior predictive capability and consistency of the ANN-based GMM, making it a more robust alternative to the traditional A&K-1979 GMPE for seismic hazard assessment.

6 Discussion of proposed GMM

6.1 The validation of the GMM

Upon training completion, the ANN-model is tested on an unseen dataset to evaluate its predictive performance. For the validation, we used the secondary dataset in which 268 records of ground motion exist (Figure 4). Predicted $\log P G A$ values are converted back to PGA (cm/s²) for comparison with observed values. The model’s accuracy is assessed using standard statistical measures, including Bias, Sigma, Mean Absolute Error (MAE), Root Mean Squared Error (RMSE) and R² – coefficient of determination (Mohammadi et al., 2023). Figure 7 illustrates the training and validation Loss and MAE trends of the model. The training and validation loss (Figure 7A) is a plot of Mean Squared Error (MSE; y-axis) versus the epochs (x-axis). MSE is a measure of how far the model’s predictions deviate from the actual values. Decreasing training loss means that the model is learning and improving its predictions. Increasing validation loss means that this may indicate overfitting after a certain number of epochs. When a gap between training and validation loss is small, the case is normal, but a large gap suggests overfitting (the model is performing well on training data but poorly on unseen data). The training and validation MAE (Figure 7B) is a plot of Mean Absolute Error (MAE; y-axis) versus the epochs (x-axis). If both training and validation MAE decrease, the model is learning well. If validation MAE starts increasing while training MAE keeps decreasing, the model is overfitting. Ideally, both training and validation loss/MAE should gradually decrease and then stabilize at a low value. There should be a small gap between training and validation loss/MAE. If validation loss/MAE starts increasing while training loss/MAE keeps decreasing, the model is memorizing the training data but failing to generalize to unseen data, which is the case of overfitting. Similarly, if both training and validation loss/MAE remain high, the model is too simple and is failing to learn the data patterns, which is the case of underfitting. When it comes to our results, loss (Figure 7A) starts high at the beginning and rapidly decreases within the first few epochs, which is expected as the model learns. After about 10–20 epochs, both the training loss (blue line) and validation loss (orange line) stabilize around a similar level. The validation loss does not increase significantly, meaning there is no severe overfitting. Some fluctuations in the validation loss are visible, which is normal. The MAE (Figure 7B) follows a similar pattern to the loss. The validation MAE is slightly higher than the training MAE but remains stable. Some fluctuations in validation MAE indicate some variability in model performance, but overall, the difference is small. No major overfitting is observed. Overall, the model is relatively stable. Moreover, we present the predicted versus observed PGAs (Figure 8A) and residuals versus hypocentral distance (Figure 8B) obtained from secondary-testing dataset, where we observe grouping of scatters around the perfect line (red dashed line).

The performance of the developed artificial neural network ANN-based GMM was evaluated using statistical metrics, including bias, standard deviation of residuals (sigma), mean absolute error (MAE), root mean squared error (RMSE), and the coefficient of determination (R²). Table 3 shows the obtained estimations of the metrics. The model exhibited a near-zero bias of −0.0076, indicating minimal systematic over- or under-prediction of peak ground acceleration (PGA). The residuals showed a standard deviation (sigma) of 0.5971, reflecting moderate variability in prediction errors, which is expected given the inherent uncertainty in ground motion modeling. The MAE was found to be 0.4416, suggesting that, on average, the predicted PGA deviates by a factor of 10^0.4416 ≈ 2.75 from observed values. The RMSE, which penalizes larger errors more heavily, was 0.5972, further reinforcing the moderate dispersion of residuals. The ANN model achieved an R² score of 0.4601 (46%), indicating that the model explains 46% of the variance in the observed PGA values. While the R² value suggests room for improvement, the model remains acceptable given certain limitations, which will be discussed below. Given these results, the model provides a reasonable first approximation for PGA prediction and can be considered suitable for preliminary seismic hazard assessments, particularly in data-limited regions or as a complementary tool alongside traditional GMPEs.

Regarding the Figures 9, 10 we observe that model trained the dataset well and works in an acceptable level for both training (Figure 9) and testing (Figure 10) datasets. However, Figures 10C, D show that the ground motion model performs poorly during the tests for high-magnitude earthquakes. Reversely, the performance is moderate or even better for smaller magnitudes (Figures 10A, B). This is not actually about the model, but it is about the content of the database, which is discussed in the limitations section.

Figure 9

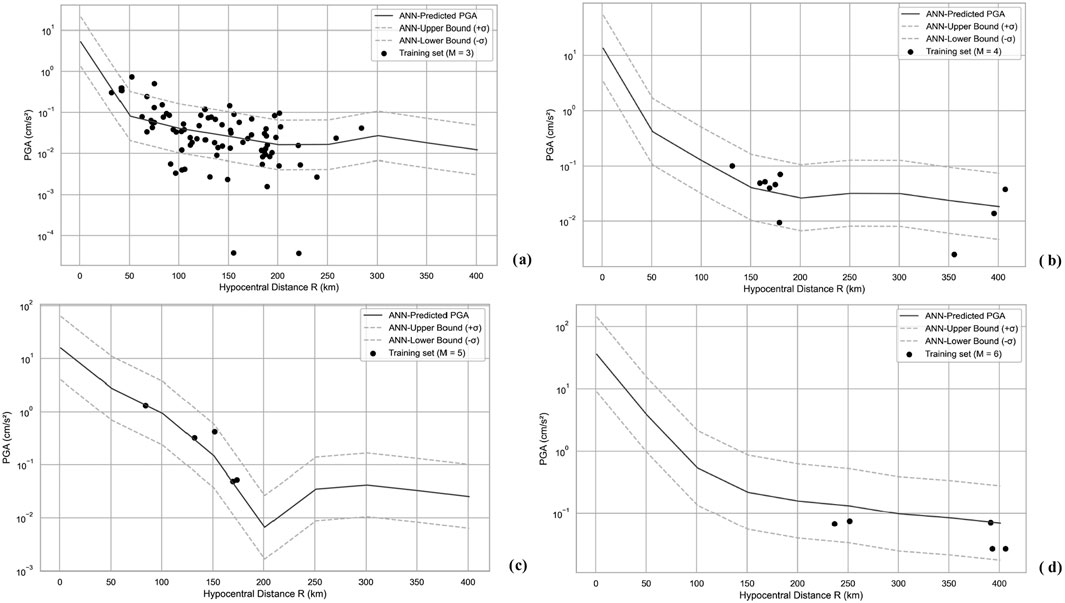
Figure 9. PGA vs. hypocentral distance for constant magnitude. Model predictions versus training set. Sigma ∼0.6. (a) M = 3. (b) M = 4. (c) M = 5. (d) M = 6.

Figure 10

Figure 10. PGA vs. hypocentral distance for constant magnitude. Model predictions versus testing set. Sigma ∼0.6. (a) M = 3. (b) M = 4, 4.1, 4.2. (c) M = 5.1. (d) M = 5.8.

6.2 Limitations of the GMM

During the 2022–2024 period, Azerbaijan experienced no significant earthquakes. The largest earthquakes, with magnitudes of M = 5.1, 5.5, 5.9, 6.0, and 6.1, occurred in Iran or along the Iranian-Azerbaijani border. An earthquake with a magnitude of M = 5.8 occurred in Dagestan. In the Caspian Sea, near the northeastern coast of Azerbaijan, two earthquakes with magnitudes of M = 5.6 occurred at depths of 66 and 70 km on 03.07.2023 and 07.12.2023, respectively. Although these events may appear significant due to their magnitudes, they were not felt strongly in Azerbaijan and in some cases, were practically undetectable. The nearest station in Azerbaijan recorded a peak ground acceleration (PGA) of 0.14 cm/s² from the strongest Iranian earthquake, with a magnitude of M = 6.1 and a depth of 10 km, which occurred 241 km away (Figure 11). As a result, the seismicity in Azerbaijan during this period was dominated by small-magnitude events. Our ANN-based model was trained on this database, where the highest recorded PGA was approximately 16 cm/s². The model, therefore, “recognized” the region as being relatively weak in terms of seismic hazard levels. This limitation affects the model’s ability to predict larger ground motions accurately. This issue stems from the composition of the dataset, but we chose not to exclude records with high magnitudes but low PGAs to avoid artificially reducing the dataset size during model training. Mohammadi et al. (2023) highlight the critical role of the dataset used in seismic hazard analysis, stressing its impact on the applicability of GMMs. Furthermore, Karimzadeh et al. (2024) identify this limitation as a key drawback of GMMs, especially in regions lacking recorded large-magnitude events, as also noted by Gianniotis et al. (2014). This concern is relevant to our study, where the absence of strong-motion records for large-magnitude events has influenced both the development and validation of the model. Similar challenges are discussed in the works of Temiz et al. (2024), Rezaeian et al., (2024), Yamamoto and Baker (2013).

Figure 11

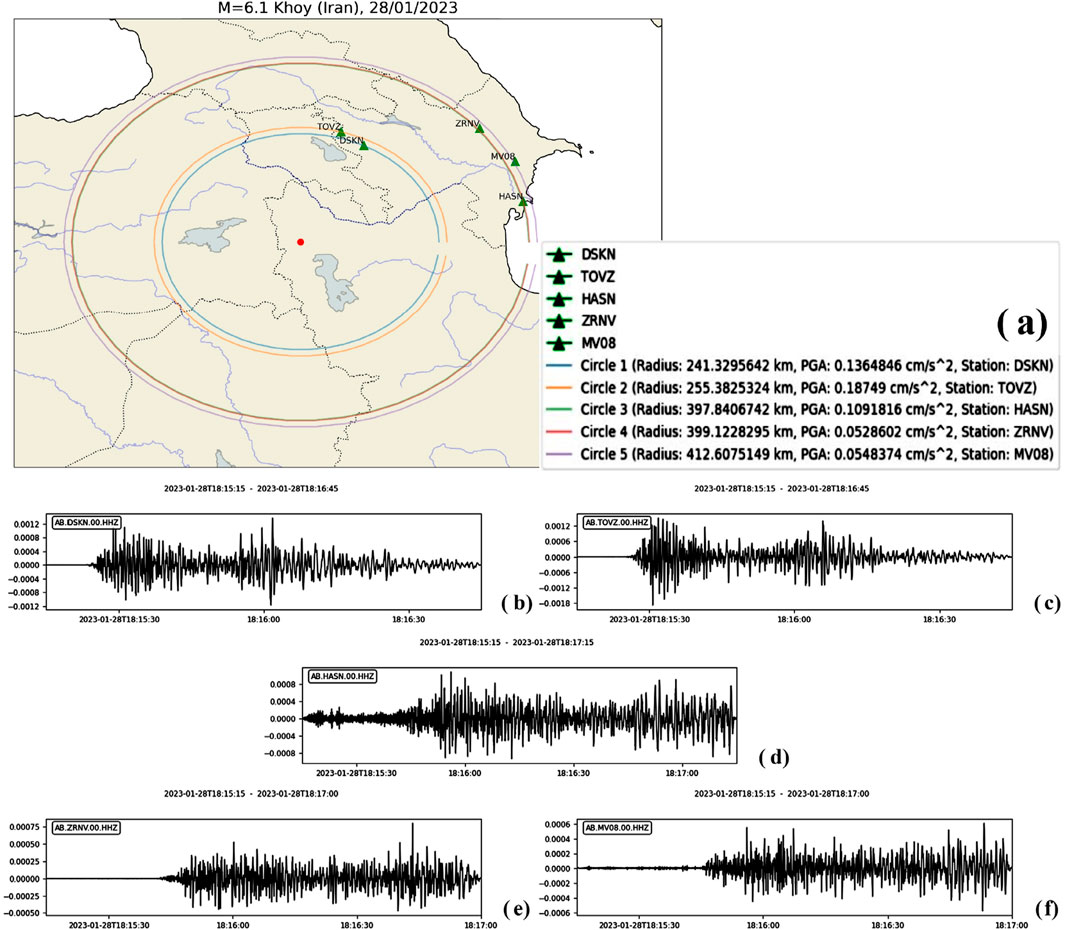
Figure 11. 28.01.2023 M = 6.1, h = 10 km, Iran Khoy earthquake. (a) Distance from Azerbaijan stations that recorded the earthquake. The records of Khoy earthquake from (b) DSKN, (c) TOVZ, (d) HASN, (e) ZRNV, (f) MV08 stations. The PGAs at DSKN, TOVZ, HASN, ZRNV, MV08 stations for this earthquake are 0.136, 0.187, 0.109, 0.053, 0.055 cm/s² respectively.

6.3 Future work

To overcome the limitations mentioned above, previous studies tend to generate synthetic dataset and conduct ground motion simulations based on them. Temiz et al. (2024) simulate ground motions for the North Tabriz Fault in northwest Iran, which exhibits a significant seismic gap (Temiz et al., 2024). Ground motion simulations offer critical insights into the potential effects of earthquakes, especially in areas with scarce recorded seismic data, facilitating more precise risk assessments and the formulation of effective mitigation strategies (Temiz et al., 2024). Rather than relying solely on future earthquakes, synthetic ground motion simulations can be used to expand recorded datasets by generating both historical and hypothetical events. These simulations have been extensively applied in various studies to reconstruct past earthquakes, explore potential seismic scenarios, assess structural demands across different building types, and GMMs (Temiz et al., 2024; Withers et al., 2020). Several studies have utilized ground motion simulations to reconstruct historical earthquakes and validate their results against empirical data. For instance, Tanırcan and Yelkenci-Necmioğlu (2020) modeled the 2017 Bodrum-Kos earthquake. More recently, Can et al. (2021) conducted simulations of the 2002 Çay earthquake in Türkiye, further demonstrating the applicability of such methods in seismic analysis. To mention further examples, Turkish authors such as Ugurhan and Askan (2010), Özmen et al. (2020), Askan et al. (2013), Karimzadeh and Askan (2018), Cheloni and Akinci (2020), Arslan Kelam et al. (2022) have employed stochastic simulation techniques to address the scarcity of recorded accelerograms for large-magnitude events by generating ground motions simulations (Ugurhan and Askan, 2010; Ozmen et al., 2020; Askan et al., 2013; Karimzadeh and Askan, 2018; Cheloni and Akinci, 2020; Arslan Kelam et al., 2022). They modeled several major historical earthquakes in Türkiye, including the 1999 Düzce (Mw 7.1), 1939 and 1992 Erzincan (Mw 7.8, 6.6 respectively) as well as more recent events such as the 2020 Elazığ (Mw 6.8) and 2023 Kahramanmaraş (Mw 7.8) earthquakes. Karimzadeh et al. (2024) produces ANN-based GMM for Türkiye using simulated records with stochastic method. Furthermore, several studies have focused on validating synthetic records from both seismological and engineering perspectives (Fayaz et al., 2020; Karimzadeh, 2019; Karimzadeh et al., 2019; Karimzadeh et al., 2020; Karimzadeh et al., 2021).

To conclude, ground motion simulations using synthesized acceleration data present an optimal approach to addressing the scarcity of recorded datasets, particularly for large-magnitude events, where data limitations are most pronounced.

7 Conclusion

This paper evaluates the applicability of A&K-1979 for Azerbaijan by comparing its predictions against a strong-motion dataset with 500 records. The analysis revealed significant discrepancies between the GMPE-suggested ground motion and observed data. The high ground motion version (A&K-1979-1, PGA ≥160 cm/s²) systematically overestimated PGA values, as indicated by the negative residuals concentrated between −3.5 and −1.5. In contrast, the low ground motion version (A&K-1979–2, PGA <160 cm/s²) exhibited underestimation. These findings underscore the limitations of applying A&K-1979 in the region, emphasizing the need for a more regionally adapted model.

To address this gap, we developed an ANN-based GMM for Azerbaijan training the 500 records-dataset and assessed its predictive performance using unseen testing set of 268 ground motion records for validation. The model exhibited a bias of −0.0076, indicating minimal systematic over- or under-prediction. The standard deviation of residuals (sigma) was 0.5971, while the mean absolute error (MAE) and root mean squared error (RMSE) were 0.4416 and 0.5972, respectively. The ANN-based GMM achieved an R² score of 0.4601 (46%), explaining nearly half of the variance in the observed PGA values. The training and validation loss curves confirm that the model avoided severe overfitting. While the ANN-GMM demonstrated satisfactory predictive capability for small to moderate magnitude events, its performance for high-magnitude earthquakes was influenced by the limited number of strong-motion records in the dataset. Despite this limitation, the proposed ANN-based GMM provides a more reliable alternative to A&K-1979 for Azerbaijan, particularly for preliminary seismic hazard assessments.

Future improvements may focus on expanding the dataset through synthetic ground motion simulations and incorporating additional seismological parameters to enhance model accuracy, especially for large-magnitude events.

8 Model provision

We provide the readers with the link to our GitHub repository where they can find the ANN-GMM model in. h5 format, a pkl-extension file that normalizes the input features of the model, two Python scripts in Jupyter notebook format to execute the model for single and multiple PGA predictions and a readme file for the detailed instructions. The link to the GitHub repository: https://github.com/turalbabaev/ANN_GMM_AZE_2025.git.

Data availability statement

The original contributions presented in the study, are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

TB: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. GB: Project administration, Supervision, Writing–review and editing, Resources. SI: Funding acquisition, Project administration, Supervision, Writing–review and editing. EB: Funding acquisition, Project administration, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was funded by the Nazarbayev University Collaborative Research Program 2025–2027 with project reference number 111024CRP2014.

Acknowledgments

The authors are grateful to RCSS and IRIS for providing public access to seismic data. Furthermore, we sincerely appreciate Nazarbayev University for their financial support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abrahamson, N. A. (2006). “Seismic hazard assessment: problems with current practice and future developments,” in First European Conference on Earthquake Engineering and Seismology (1st ECEES): Joint Event of the 13th European Conference on Earthquake Engineering and the 30th General Assembly of the European Seismological Commission, Geneva, 03-08 September 2006.

Google Scholar

Achieng, K. O. (2019). Modelling of soil moisture retention curve using machine learning techniques: artificial and deep neural networks vs support vector regression models. Comput. and Geosciences 133, 104320. doi:10.1016/j.cageo.2019.104320

Development of ann-based data-driven ground motion model for Azerbaijan using temporal earthquake records of 2022–2024

1 Introduction

2 Study area

3 Dataset acquisition and processing

3.1 Acquisition

3.2 Processing

4 Methods

4.1 Testing A&K-1979

4.2 Training ANN-based GMM

5 Results

5.1 Perfect alignment and residual analysis of A&K-1979 predictions

5.2 ANN-based developed GMM

6 Discussion of proposed GMM

6.1 The validation of the GMM

6.2 Limitations of the GMM

6.3 Future work

7 Conclusion

8 Model provision

Data availability statement

Author contributions

Funding

Acknowledgments

Conflict of interest

Generative AI statement

Publisher’s note

References

94% of researchers rate our articles as excellent or good