TBM shield mud cake prediction model based on machine learning

Introduction: During tunnel boring machine (TBM) shield tunneling in clayey strata, the excavated soil consolidates on the cutter head or cutting tools, forming mud cakes that significantly impact the efficiency of shield tunneling.

Methods: To predict mud cakes during shield tunneling, four distinct supervised machine learning models, including logistic regression, support vector machine, random forest, and BP neural network were employed. The optimal predictive model for mud cake formation was determined by assessing the precision, recall, and F1 scores of the models. Further analysis of feature dependencies and shapley additive explanations (SHAP) is conducted to pinpoint the critical risk factors associated with mud cake formation.

Results: The results indicate that among the four supervised machine learning models, the random forest model exhibited the best performance in predicting mud cake formation during shield tunneling, with an F1 score as high as 0.9934. Feature dependencies and SHAP information showed that the shield tunneling chamber temperature and average excavation speed had the most significant impact on mud cake formation, serving as crucial factors in determining mud cake formation. The rear earth pressure of the screw conveyor and the cutterhead penetration depth followed, constituting important elements in mud cake formation. The introduction of the interpretable method SHAP for analyzing the relationships between various factors extends beyond simple linear relationships, allowing for the examination of nonlinear patterns among factors.

1 Introduction

China is one of the countries with the largest distribution of karst in the world (Yang et al., 2020). Due to the long-term dissolution of surface water and groundwater on soluble rocks, karst caves, grooves and other unique karst landforms have been formed (Zhang et al., 2018; Ou et al., 2024). With the acceleration of urbanization and the increasing demand for transportation, the rational development and utilization of urban underground space have become key to alleviating urban traffic pressure. Due to its high safety level and excavation efficiency, the TBM shield tunneling method has become the preferred construction method for urban subway tunnels (Ou et al., 2025). However, caves are often filled with clayey soil in some karst areas. When the shield passes through soil layers with a high clay mineral content and weathered rock layers, the soil is prone to adhere to the surface of cutterheads and cutters made of metal, which forms mud cakes on the surface under the thrust of the shield. In milder cases, this will cause the cutter to lose its cutting ability, affecting the efficiency of shield tunneling. More severe consequences include surface subsidence, which endangers the safety of buildings and personnel. The shield mud cake formation is, in essence, the process of continuous soil compression and consolidation. In the early stage, the mud cake has a relatively low strength and is easier to handle. When the formation is complete, it may cause damage to the shield cutter, lower the efficiency of shield tunneling, and become much harder to treat (Langmaack and Lee, 2016; Yang et al., 2023). Therefore, early prediction of mud cakes is a prerequisite for ensuring safe and efficient shield tunneling and is also a hot topic actively studied by scholars. Some investigations indirectly determined the formation of shield mud cakes by monitoring the temperature or main tunneling parameters of shield tunneling (Zumsteg et al., 2016; Li et al., 2022). However, these methods failed to achieve early-stage prediction. Benefiting from the applications of emerging technologies such as machine learning and image recognition in civil engineering (Jin et al., 2022; Gao et al., 2021; Liu et al., 2020; Suwansawat and Einstein, 2006; Kohestani et al., 2017; Mahmoodzadeh et al., 2021), some studies developed early warning and monitoring systems for mud cake monitoring and identification. For instance, Fu et al. (2021) developed an early warning and monitoring system based on the Internet of Things technology, which monitored the temperature of TBM cutters in real time to identify the formation of mud cakes, thereby improving the shield machine’s operating efficiency and reducing construction risks. Zhai et al. (2022) analyzed the influencing factors of mud cake formation based on machine learning, established a mud cake prediction and early warning model, and developed a real-time mud cake early warning system. Most existing studies on the formation and prevention of mud cakes rely on traditional theories (Li et al., 2022), such as the summary of construction site experience, while the analysis of mud cake formation based on emerging machine learning technologies is still in its infancy and lacks methods with model interpretability (Kang and Chois, 2020). Beyond the model prediction accuracy, the reason for generating such prediction data also requires in-depth understanding since reasonable interpretability conclusions can help technicians apply the model more confidently and enhance generalization. Some commonly used model interpretability tools include permutation importance, SHAP, local interpretable model-agnostic explanations (LIME), and partial dependence plot (PDP).

This study targets one section of the Fuzhou Metro Binhai Express where a TBM shield passes through clayey strata in China. Based on the tunneling parameters before and after in-chamber processing of shield mud cakes, the model prediction results are analyzed using the SHAP analysis tool. The effects on a shield mud cake dataset of four supervised machine learning models, i.e., logistic regression, support vector machine (SVM), random forest (RF), and back propagation (BP) neural network, are compared. The optimum prediction model is selected for further feature dependency and SHAP analysis to identify key risk factors for mud cake formation. A mud cake formation prediction model is established to provide a reliable theoretical judgment basis for mud cake prevention in shield tunneling.

2 Project background and data preparation

2.1 Project background

As an essential intercity rail transit line in Fujian Province in China, the Fuzhou Metro Binhai Express connects the railways, Changle airport, and the urban rail transit network. As an inter-city railway tunnel project from Fuzhou to Changle Airport, the shield passes through dense ground structures multiple times along the route. The ground construction environment is complex, and the strata are diverse. The excavation diameter of the shield tunnel in this section is 8.6 m, and the tunnel cover soil has a thickness of 8.8–15.3 m. The shield tunneling section of this project is located in an alluvial plain with marine-terrigenous facies. The site surface is mostly covered by sand filling layers. The geology along the line is complex and diverse, mainly composed of silty clay and muddy fine sand, with a high content of clay particles. The shield section primarily passes through the strata of mucky soil, muddy fine sand, silty clay, and strongly weathered silty sand. The overlying soil is dominated by soft soil, such as shallow silt and fill. The compositions of soil mechanics particles in the strata are displayed in Table 1. Considering the high content of clay particles, an earth pressure balance (EPB) shield machine was used for excavation construction. The cutterheads and cutters often exhibit mud cakes during the construction process, greatly reducing the excavation efficiency. Moreover, multiple pressurized in-chamber mud cake treatment increase the risk of the project.

Table 1

Table 1. Soil mechanics parameters of strata.

2.2 Data preparation

The original data before and after cutterhead mud cake treatment from three shield tunneling sections were selected for analysis, with a total of 4,525 samples. Based on the existing research results about the influencing factors of shield mud cakes (Alberto-Hernandez et al., 2018; Zumsteg et al., 2016), characteristic factors related to the formation of shield mud cakes were screened. Each sample included ten numerical features, namely, total thrust of the propulsion cylinder, torque of the screw machine, front soil pressure of screw conveyor, rear soil pressure of screw conveyor, temperature of the sealed cabin, cutterhead torque, average driving speed, temperature of the motor cooling water, gear oil temperature, and cutterhead penetration. In addition, a binary label was used to indicate whether a mud cake was produced, where 0 indicated no presence of mud cake and 1 indicated the generation of mud cakes. Sorting and analysis of the original dataset finds 3,710 entries labeled as a normal class and 815 items labeled as mud cakes. Randomly divide the original 4,525 pieces of data into training and testing sets in an 8:2 ratio, with 3,620 data points in the training set and 905 in the testing set. The schematic diagram of the prediction model is presented in Figure 1.

Figure 1

Figure 1. Schematic diagram of the prediction model.

Statistical analysis of the shield tunneling parameters before and after mud cake treatment was performed. Measurement data that conformed to a normal distribution was expressed as mean ± standard deviation ($\overline{x}$ ± s), and the t-test was adopted for comparison among groups. Non-normally distributed measurement data was represented by its median [M(P₂₀, P₈₀)], and the non-parametric test was used for comparison among groups. Count data was expressed by the number of cases and percentage (%). Comparison between categorical data adopted the ${\chi }^2$ test. The test level was $\alpha$ = 0.05, and P < 0.05 indicated a statistically significant difference.

3 Establishment and evaluation of machine learning model

This study adopted the tools of Python 3.10 and Sklearn to establish the four different supervised machine learning models, i.e., logistic regression (Bisong et al., 2019), SVM (Cervantes et al., 2020), RF (Denisko and Hoffman, 2018), and BP neural network (Rumelhart et al., 1986), thereby evaluating the prediction accuracy of each model on the data validation set.

3.1 Logistic regression

As one of the most classic machine learning models, logistic regression is widely used in binary classification problems. It has advantages such as low computational complexity, rapid learning and prediction, and easy model interpretation, and its analysis model is:

$Z=W_0+W_1{X}_1+W_2{X}_2+\cdots +W_n{X}_n(1)$

$F\left(z\right)=\frac{1}{1+e^{-z}}(2)$

In Equation 1, X₁, X₂ … represent the features, while W₁, W₂ … represent the corresponding weights. Equation 2 is called the Sigmoid function, which features a monotonic increase, and its inverse function is also a monotonic increasing function. It is often used as a threshold function for neural networks, mapping variables to [0,1], and can be used for binary classification, which has good compatibility with logistic regression. When analyzing, substitute the calculated result Z from Equation 1 into Equation 2 to achieve data classification, where the output of Z is in the range of [0,1].

3.2 Support vector machine (SVM)

As a classic binary machine learning method, SVM can handle high-dimensional and nonlinear data well. It can obtain the optimum hyperplane in the sample feature space that separates all data points and maximizes their distance to it. Nonlinear SVM can solve nonlinear problems by introducing kernel functions to map data onto higher dimensional spaces. The operating principle of SVM is displayed in Figure 2.

Figure 2

Figure 2. Operating principle diagram of SVM.

The left and right samples closest to the red solid line at the center in Figure 2 are support vectors, and the goal of SVM is to maximize the distances from the support vectors to the center red line. SVM uses the hinge loss function (HingeLoss) as the objective function for optimizing the model, where f(x) represents the predicted results of SVM. The formula for calculating the hinge loss function is:

$HingeLoss\left(y,f\left(x\right)\right)={\displaystyle \sum _0^{\infty }}\left.\left[1-y*\left(f\left(x\right)\right)\right)\right]+=\left|\mathrm{z}\right|+(3)$

Equation 3 indicates that when z is greater than 0, the function has a value of 0. When z is smaller than 0, the function equals z.

3.3 Random forest (RF)

As an ensemble learning algorithm, RF is a widely used classifier in machine learning and has the advantages of anti-overfitting, anti-data noise, and high accuracy. Its core idea is to summarize the classification results of all independent small classifiers, namely, decision trees, and set the category with the most classification results as the final classification result, as displayed in Figure 3. Each decision tree adopts the Bootstrap class analysis method, which randomly selects a fixed number of samples from the training set with replacement and then takes them as the training set.

Figure 3

Figure 3. Structural diagram of the core idea of RF.

The core idea of RF classification decision-making can be represented by

$RF\left(X\right)=\mathit{ArgMax}\left(Ti\left(X\right)\right)(4)$

In Equation 4, Ti(x) denotes the prediction result of the i-th tree in the forest for the sample with input X; RF(X) represents the statistical analysis of all decision tree results where the highest result is taken as the final classification result of the entire RF for the sample with input X. Meanwhile, the Gini index is used as the basis for decision tree bifurcation to ensure higher dataset accuracy after each bifurcation. The formulas for the Gini index and RF algorithm bifurcation basis are

$\text{Gini}\left(\mathrm{D}\right)=1-{\displaystyle \sum _{k=0}^y}{P}_k^2(5)$

$Gini\_Index\left(D,x\right)={\displaystyle \sum _{v=0}^n}\frac{D^v}{D}\text{\hspace{0.17em}Gini}\left(D\right)(6)$

$\mathit{Argmin}Gini\_Index\left(D,x\right)(7)$

In Equation 5, Gini(D) represents the overall Gini index of dataset D. In this example, k takes the value of 2, representing a normal label and a label that displays the presence of mud cakes. P_k represents the probability of class k, which is the proportion of class k in the overall sample D. In Equation 6, Gini_Index (D,x) represents the Gini index after selecting feature x as the basis for bifurcation, $D^v$ denotes the size of the dataset obtained by using feature x as the basis for bifurcation. Finally, according to Equation 7, the working condition with the smallest Gini index is taken as the basis for the bifurcation of each decision tree.

3.4 BP neural network

BP neural network is a supervised machine learning algorithm, the core idea of which is the forward propagation of data and the backward propagation of errors. It continuously adjusts the weight of each feature through gradient descent to improve model accuracy. Its outstanding advantages are its strong nonlinear mapping capability and flexible network structure. The forward propagation structure of the BP neural network is presented in Figure 4.

Figure 4

Figure 4. Forward propagation structure diagram of BP neural network.

This study is based on the neural network module of PyTorch. The input feature X has 10 dimensions, the output category Y includes 2 classes, and the hidden layer has a total of 13 neurons (Karsoliya, 2012). The rectified linear unit (ReLU) function is used as the activation function, the cross entropy loss is used as the loss function, the learning rate is set to 0.01, and the model is trained 1,000 times. As shown in Figure 5, overfitting does not occur.

Figure 5

Figure 5. Variation graph of training loss using the cross entropy loss function.

The cross entropy loss function is used in machine learning to show the difference between the real sample label and the predicted probability, which is expressed by

$L=-\frac{1}{n}{\displaystyle \sum _x^{\hspace{0.17em}}}\left|ylogx+\left(1-y\right)\mathit{log}\left(1-x\right)\right|(8)$

In Equation 8, y represents the true label type, and x represents the predicted probability in the range of [0,1].

3.5 Model evaluation metrics

3.5.1 F1 Score

The F1 score is an accuracy metric used in statistics to measure the results of binary classification problems, considering the precision and recall of the model. The F1 score is in the range of [0,1]. The closer it is to 1, the higher the prediction accuracy. The F1 score is calculated by

$\mathrm{F}1=2\times \frac{Precision·recall}{Precision+recall}(9)$

$Precision=\frac{TP}{TP+FP}(10)$

$Recall=\frac{TP}{TP+FN}(11)$

In Equation 9, Precision represents the proportion of true positive cases among the samples predicted as positive by the model, Recall represents the proportion of samples correctly predicted as positive by the model to all true positive cases. In Equation 10, TP represents true cases (the number of samples correctly predicted as positive by the model), FP represents false positive cases (the number of samples incorrectly predicted as positive by the model). In Equation 11, FN represents false negative cases (the number of samples incorrectly predicted as negative by the model).

Taking the shield mud cake category as an example, Precision represents the proportion of samples that truly belong to the mud cake category among all the samples predicted by the model as mud cakes, and Recall represents the proportion of samples correctly predicted by the model as mud cakes among all samples that truly belong to the mud cake category.

3.5.2 Shapley additive explanations (SHAP)

SHAP is a game theory-inspired method for explaining the predictions of machine learning models. It was first proposed by Lundberg and Lee (2017). Its essence is the average marginal contribution of feature values in all possible alliances, which can reflect the influence of each feature in the sample. As a powerful model interpretability method, SHAP can transform the results calculated by the model into a more easily understandable one, which helps interpret the model. The SHAP value of each feature reflects its contribution to the final model prediction result; the larger the SHAP value, the greater the contribution.

$\varphi i={\displaystyle \sum _{S\in N}}\frac{\left|S\right|!\left(n-\left|S\right|-1\right)!}{n!}\left[\mathrm{v}\left(\mathrm{S}\mathrm{U}\left\{\mathrm{i}\right\}\right)-\mathrm{v}\left(\mathrm{S}\right)\right](12)$

where n denotes the total number of features, ϕi denotes the contribution of feature i to prediction, and S denotes all subsets that use feature i. Therefore, $\frac{\left|S\right|!\left(n-\left|S\right|-1\right)!}{n!}$ in Equation 12 represents the weight of subset S, and v(S) represents the prediction for S.

4 Experimental analysis

4.1 Overall experimental analysis

Using the metrics module in Sklearn, the statistics for the prediction accuracy of the four machine learning models are produced, as shown in Table 2, where the recall and precision of normal and mud cake categories are compared. The final experimental analysis results are shown in Figure 6.

Table 2

Table 2. Statistics of prediction accuracy for the four machine learning models.

Figure 6

Figure 6. Statistical bar charts of prediction accuracy for the four machine learning models.

According to Table 2 and Figure 6, the overall accuracy of the four models is above 90%. Among them, the RF algorithm performs the best, showing the highest prediction accuracy on the dataset, especially in terms of recall and precision of the normal category. The precision and recall of SVM and logistic regression in the mud cake category are significantly lower than those of the RF model and the BP neural network. Specifically, the recall of logistic regression in the mud cake category is 26% lower than that in the normal category, and a gap of over 7% in precision also appears. Similar phenomena also occur in SVM, where the recall of the mud cake category is 25% lower than that of the normal category, and there is a 13% difference in precision. The analysis results are consistent with the results obtained by Zhai et al (2022).

4.2 Model interpretability analysis

After model evaluation, the best prediction model for mud cake formation, i.e., RF, is selected for further analysis. Figure 7 displays the SHAP value feature importance map, the overall sample heat map, and the overall sample swarm plot of the RF model. In the heat map, the horizontal axis represents the specific samples, while the vertical axis represents the SHAP value of each feature. The importance of features decreases from top to bottom, with red indicating a positive impact on mud cake formation and blue the opposite. The swarm plot presents each sample in the form of points, and the importance of each feature for mud cake formation also decreases from top to bottom.

Figure 7

Figure 7. Analysis of various features of the RF model using the SHAP method. (A) Feature importance map in terms of SHAP value, (B) Overall sample heat map, (C) Overall sample swarm plot.

As shown in Figure 7, according to the SHAP value, the features in terms of importance are ranked as follows: temperature of the sealed cabin, average driving speed, cutterhead penetration, soil pressure behind the screw machine, soil pressure before the screw machine, cutterhead torque, temperature of the motor cooling water, gear oil temperature, total thrust of the propulsion cylinder, and torque of the screw machine. The temperature of the sealed cabin is the most important factor for the final judgment of the model since its increase facilitates the solidification of soils, such as crushed rock and soil, and their adherence to the cutter and cutterhead, increasing the probability of shield mud cake formation. The average driving speed of shield tunneling also plays an essential role in the final model prediction result. As can be seen from the overall feature distribution map in Figure 7, the average driving speed is positively correlated with mud cake formation. In the overall sample swarm plot in Figure 7C, a higher average driving speed corresponds to easier mud cake formation. This is mainly because as the shield tunneling speed increases, the shear rate generated by cutterhead rotation also increases. This increase in shear force will increase the contact area and adhesive force between soil particles, thereby increasing the probability of mud cake formation at the cutterhead. In addition, as the average driving speed increases, the soil is subjected to a large shear force, resulting in soil fluidization and a corresponding decrease in soil pressure. As for the feature of soil pressure behind the screw machine, its decrease increases the risk of mud cake formation. The factor that follows in terms of the influence on the final model judgment is the cutterhead penetration. With the increase of penetration, the compression and friction conditions for forming the cutterhead mud cake become more mature, so the formation probability increases. One reason is the increased contact area between the cutterhead and the soil. Meanwhile, the damage to soil particles increases the soil porosity, which promotes the entry of water into the soil and facilitates the generation of the cutterhead mud cake.

Besides these four most influential features, other factors have no decisive impact on the formation of mud cakes, most of which have a relatively small absolute SHAP value. For instance, the total thrust of the propulsion cylinder is nearly positively correlated with the probability of mud cake formation, but it is not a decisive factor. The same rule also applies to the soil pressure in front of the screw machine. As shown in Figure 8, the higher the soil pressure before the screw machine, the lower the risk of mud cake formation. This is mainly because the increase of this feature constrains the movement of soil particles and thus reduces the formation of mud cakes. Meanwhile, influenced by the soil moisture content, the increase in soil pressure before the screw machine will remove some water from the soil, indirectly reducing the risk of mud cake formation.

Figure 8

Figure 8. The overall heat map of mud cake and normal categories.

Figure 8 shows the contribution and influence direction (positive or negative) and the predicted value of each feature in the selected individual sample for mud cake formation, which can be used to determine the risk of mud cake formation in this sample. The base value represents the average of all model training samples, while f(x) represents the predicted risk of mud cake formation for a given sample. An f(x) below the sample average indicates a decreased mud cake formation risk, and an f(x) above average signifies an increased risk. The size of each arrow corresponds to a weight, indicating the level of impact of the feature on the prediction result. The red features and red arrows indicate a positive contribution to the formation of mud cakes, while the blue ones correspond to a negative contribution. The value of the weight characterizes the impact of the feature on sample prediction results.

Specifically, the average value of the overall sample set is 0.1752, as shown in Figure 8. In the first normal sample, the main influencing factors that turn the model prediction value from the base value to 0 include the temperature of the sealed cabin, the average driving speed, and the soil pressure after the screw machine. For a randomly selected mud cake sample, the main influencing factors that change the predicted value from the baseline to 1 are the temperature of the sealed cabin, the soil pressure behind the screw machine, and the penetration. These results mean that the temperature of the sealed cabin, the average driving speed, the soil pressure behind the screw machine, and the penetration are the primary influencing factors for the generation of shield mud cakes, which is consistent with the prediction results based on the SHAP value feature importance analysis shown in Figure 7.

4.3 Feature dependency analysis

As mentioned earlier, the temperature of the sealed cabin has a direct linear impact on the formation of mud cakes; the higher the temperature, the greater the risk of cutterhead mud cake formation. The second most important feature is the average driving speed, which does not show a clear gradient change pattern with mud cake formation. This is also true for the feature of soil pressure behind the screw machine. Therefore, it is necessary to conduct a feature dependency analysis for these two features. The analysis cloud maps are shown in Figures 9, 10, respectively.

Figure 9

Figure 9. Feature dependence analysis on average driving speed.

Figure 10

Figure 10. Feature dependence analysis on soil pressure after the screw machine.

Figures 9, 10 visualize the curve distribution relationships between the two features and the SHAP value. The left vertical axis represents the SHAP value of the feature, and each sample corresponds to a feature point in the figure. The color changing from blue to red indicates that the feature size gradually increases. According to the feature dependency analysis on the average driving speed in Figure 9, when the average driving speed of the shield machine is slower than 20 mm/min, the SHAP value of most samples is greater than 0. However, when the average driving speed is between 20 and 40 mm/min, the SHAP value is smaller than 0, indicating that the shield cutterhead is not prone to mud cakes. However, when the driving speed increases to above 40 mm/min, the SHAP value jumps to above 0, indicating a significant increase in the probability of mud cake formation within this speed range. A similar distribution pattern of feature points also appears for the feature of penetration. As known from the swarm plot in Figure 7C, the variations of the penetration and driving speed are consistent, both showing a linear pattern. This relationship can be explained by Equation 13.

$\text{Penetration}=\text{Driving\hspace{0.17em}speed}/\text{Cutterhead\hspace{0.17em}rotation\hspace{0.17em}speed}(13)$

Figure 10 shows the SHAP value variations of soil pressure behind the screw machine. The overall distribution of the curve demonstrates that as the soil pressure behind the screw machine increases, the SHAP value also increases. The feature distribution pattern reveals that the SHAP value is mostly smaller than 0 when the soil pressure behind the screw machine is in the range of 0–400 kPa. However, when this pressure is between 400 and 600 kPa, the SHAP value suddenly increases, peaking for some samples, which indicates that the soil pressure behind the screw machine has a positive effect on mud cake formation. When this pressure rises to above 600 kPa, the overall SHAP value is still greater than 0, though the absolute value is less than that in the range of 400–600 kPa. This indicates a pattern of first increasing and then decreasing effect for mud cake formation as the soil pressure behind the screw machine increases, which reaches the maximum at 400–500 kPa.

Figure 11 shows the distribution relationship between the average driving speed of the shield machine and the soil pressure behind the screw machine. According to Figures 9, 10, a nonlinear relationship exists between the average driving speed or the soil pressure behind the screw machine and the formation of shield mud cakes, but there is no relevant data to indicate the existence of an intrinsic relationship between these two features. Therefore, it is necessary to consider the curve distribution shown in Figure 11 to analyze the intrinsic relationship between the two. As can be seen from Figure 11, no intuitive relationship between the two features is present. However, when the soil pressure behind the screw machine is high, the SHAP value of the corresponding average driving speed is small. This may be because the excavated soil soil is squeezed around the screw machine during shield tunneling. When the shield tunneling speed is low, the soil soil will stay inside the screw machine for a relatively long time, which will lead to an increase in soil pressure behind the screw machine.

Figure 11

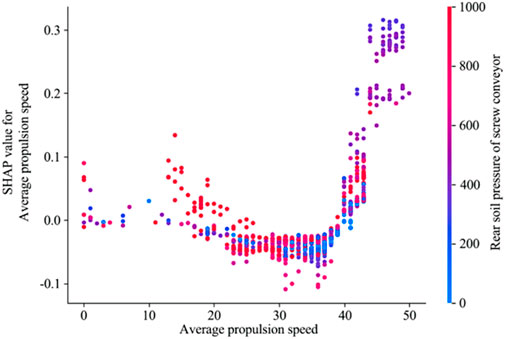
Figure 11. Relationship between the average driving speed and the soil pressure behind the screw machine.

5 Conclusion and outlook

This study is conducted based on the original excavation parameters of a double shield tunneling machine passing through the viscous strata in a section of the Fuzhou Metro Binhai Express before and after in-cabin shield mud cake treatment. By comparing four different supervised machine learning models (logistic regression, SVM, RF, and BP neural network), the best prediction model for mud cake formation, RF, is selected. Further feature dependence and SHAP analyses for the RF algorithm are conducted to identify key risk factors for mud cake formation, and the risk prediction model for mud cake formation is established. The research results have some guiding significance for preventing mud cake formation in shield cutterheads and controlling shield tunneling parameters. The main conclusions are as follows:

(1) Among the four supervised machine learning models, the RF model has good adaptability and the highest accuracy in predicting the formation of shield mud cakes. The high precision and recall metrics in normal and mud cake classes verify the robustness of the RF model.

(2) Among the ten listed features that affect the formation of mud cakes, the sealed cabin temperature and the average driving speed of the shield machine have the strongest impact on the formation of mud cakes, which are deemed the key factors in mud cake formation, followed by the soil pressure behind the screw machine and cutterhead penetration. It is recommended to monitor the real-time temperature of in-cabin soils during shield tunneling and dynamically adjust the tunneling speed to reduce the risk of mud cake formation.

(3) The interpretability method SHAP is introduced to analyze the relationships, linear or nonlinear, between the various factors. For example, the average driving speed is a key factor that has a nonlinear relationship with mud cake formation. This provides a new approach for preventing mud cake formation in shield tunneling by adjusting the driving speed.

There are two limitations to this study. (1) Only ten strongly related parameters are considered, so more features need to be integrated in the future to establish a more comprehensive analysis model of mud cake formation. (2) There are only 4,525 samples in the dataset, so more experimental samples need to be collected to complete a more accurate prediction model.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

QZ: Conceptualization, Data curation, Investigation, Methodology, Writing–original draft. PX: Resources, Validation, Writing–review and editing. JZ: Conceptualization, Methodology, Software, Writing–review and editing. ZY: Data curation, Project administration, Writing–review and editing. YL: Data curation, Formal Analysis, Writing–review and editing. XK: Resources, Validation, Writing–review and editing. XY: Formal Analysis, Visualization, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The financial support from the China Postdoctoral Science Foundation (Grant No. 2022M723536) is acknowledged and appreciated.

Conflict of interest

Authors QZ, ZY and YL were employed by CCCC Second Harbor Engineering Company Ltd. PX was employed by CCCC South China Construction and Development Co., Ltd. JZ was employed by Sichuan Tibet Railway Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alberto-Hernandez, Y., Kang, C., Yi, Y., and Bayat, A. (2018). Clogging potential of tunnel boring machine (TBM): a review. Int. J. Geotechnical Eng., 12 (3): 316, 323. doi:10.1080/19386362.2016.1277621

CrossRef Full Text | Google Scholar

Bisong, E. (2019). Building machine learning and deep learning models on google cloud platform: a comprehensive guide for beginners. 2019: 243–250. doi:10.1007/978-1-4842-4470-8

CrossRef Full Text | Google Scholar

Cervantes, J., Garcia-Lamont, F., Rodríguez-Mazahua, L., and Lopez, A. (2020). A comprehensive survey on support vector machine classification: applications, challenges and trends. Neurocomputing 408, 189–215. doi:10.1016/j.neucom.2019.10.118

CrossRef Full Text | Google Scholar

Denisko, D., and Hoffman, M. (2018). Classification and interaction in random forests. Proc. Natl. Acad. Sci. U. S. A. 115 (8), 1690–1692. doi:10.1073/pnas.1800256115

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, J., Xia, Y., Lan, H., Wu, D., and Lin, L. (2021). A case study on TBM cutterhead temperature monitoring and mud cake formation discrimination method. Sci. Rep. 11 (1), 19983. doi:10.1038/s41598-021-99439-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, B., Wang, R., Lin, C., Guo, X., Liu, B., and Zhang, W. (2021). TBM penetration rate prediction based on the long short-term memory neural network. Undergr. Space 6 (6), 718–731. doi:10.1016/j.undsp.2020.01.003

CrossRef Full Text | Google Scholar

Jin, Y., Qin, C., Tao, J., and Liu, C. (2022). An accurate and adaptative cutterhead torque prediction method for shield tunneling machines via adaptative residual long-short term memory network. Mech. Syst. Signal Process. 165, 108312. doi:10.1016/j.ymssp.2021.108312

CrossRef Full Text | Google Scholar

Kang, T.-H., Choi, S.-W., Lee, C., and Chang, S.-H. (2020). A study on prediction of EPB shield TBM advance rate using machine learning technique and TBM construction information. Tunn. Undergr. Space 30 (6), 540–550. doi:10.7474/TUS.2020.30.6.540

CrossRef Full Text | Google Scholar

Karsoliya, S. (2012). Approximating number of hidden layer neurons in multiple hidden layer BPNN architecture. Int. J. Eng. Trends and Technol.

Google Scholar

Kohestani, V., Bazargan-Lari, M., and Marnani, J. (2017). Prediction of maximum surface settlement caused by earth pressure balance shield tunneling using random forest. J. AI Data Min. 5, 127–135. doi:10.22044/jadm.2016.748

CrossRef Full Text | Google Scholar

Langmaack, L., and Lee, K. (2016). Difficult ground conditions? Use the right chemicals! Chances–limits–requirements. Tunn. Undergr. Space Technol. 57, 112–121. doi:10.1016/j.tust.2016.01.011

CrossRef Full Text | Google Scholar

Li, X., Yang, Y., Li, X., and Liu, H. (2022). Criteria for cutting head clogging occurrence during slurry shield tunneling[J]. Appl. Sci., 12(3): 1001–1001. doi:10.3390/app12031001

CrossRef Full Text | Google Scholar

Liu, Q., Wang, X., Huang, X., and Yin, X. (2020). Prediction model of rock mass class using classification and regression tree integrated Ada Boost algorithm based on TBM driving data. Tunn. Undergr. Space Technol. 106, 103595. doi:10.1016/j.tust.2020.103595

CrossRef Full Text | Google Scholar

Lundberg, S., and Lee, S. (2017). A unified approach to interpreting model predictions. Statistics 63, 4765–4774. doi:10.48550/arXiv.1705.07874

CrossRef Full Text | Google Scholar

Mahmoodzadeh, A., Mohammadi, M., Ibrahim, H., Abdulhamid, S., Mahmud, H., Mohammed Hasan, A., et al. (2021). Machine learning forecasting models of disc cutters life of tunnel boring machine. Automation Constr. 128, 103779. doi:10.1016/j.autcon.2021.103779

CrossRef Full Text | Google Scholar

Ou, X., Ouyang, L., Zheng, X., and Zhang, X. (2024). Hydrogeological analysis and remediation strategies for water inrush hazards in highway karst tunnels. Tunn. Undergr. Space Technol. 152, 105929. doi:10.1016/j.tust.2024.105929

CrossRef Full Text | Google Scholar

Ou, X., Tang, C., Qu, T., Xu, S., Zhou, Y., and Tian, J. (2025). Towards digitalized maintenance of operating tunnels: a text documents-based defect evaluation and visualization. Tunn. Undergr. Space Technol. 157, 106345. doi:10.1016/j.tust.2024.106345

CrossRef Full Text | Google Scholar

Rumelhart, D., Hinton, G., and Williams, R. (1986). Learning representations by back-propagating errors. Nature 323, 533–536. doi:10.1038/323533a0

CrossRef Full Text | Google Scholar

Suwansawat, S., and Einstein, H. (2006). Artificial neural networks for predicting the maximum surface settlement caused by EPB shield tunneling. Tunn. Undergr. Space Technol. 21 (2), 133–150. doi:10.1016/j.tust.2005.06.007

CrossRef Full Text | Google Scholar

Yang, J., Zhang, C., Fu, J. Y., Wang, S., Ou, X., and Xie, Y. (2020). Pre-grouting reinforcement of underwater karst area for shield tunneling passing through Xiangjiang River in Changsha, China. Tunn. Undergr. Space Technol. 100, 103380. doi:10.1016/j.tust.2020.103380

CrossRef Full Text | Google Scholar

Yang, Z., Liu, P., Chen, P., Li, S., and Ji, F. (2023). Clogging prevention of slurry - earth pressure balance dual-mode shield in composed strata with medium - coarse sand and argillaceous siltstone. Appl. Sci. 13, 2023. doi:10.3390/app13032023

CrossRef Full Text | Google Scholar

Zhai, J., Wang, Q., Yuan, D., Zhang, W., Wang, H., Xie, X., et al. (2022). Clogging risk early warning for slurry shield tunneling in mixed mudstone–gravel ground: a real-time self-updating machine learning approach[J]. Sustainability, 14(3): 1368–1368. doi:10.3390/su14031368

CrossRef Full Text | Google Scholar

Zhang, C., Fu, J., Yang, J., Ou, X., Ye, X., and Zhang, Y. (2018). Formulation and performance of grouting materials for underwater shield tunnel construction in karst ground.Constr. Build. Mater. 187, 327, 338. doi:10.1016/j.conbuildmat.2018.07.054

CrossRef Full Text | Google Scholar

Zumsteg, R., Puzrin, A., and Anagnostou, G. (2016). Effects of slurry on stickiness of excavated clays and clogging of equipment in fluid supported excavations. Tunn. Undergr. Space Technol. 58, 197–208. doi:10.1016/j.tust.2016.05.006

CrossRef Full Text | Google Scholar