Kui Chen
Minghao Zhao
Yansong Feng4
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
- 1Sinopec North China Petroleum Bureau, Zhengzhou, China
- 2State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum (Beijing), Beijing, China
- 3College of Geoscience, China University of Petroleum (Beijing), Beijing, China
- 4Exploration and Development Research Institute, PetroChina Changqing Oilfield Company, Xi’an, China
Tight sandstone reservoirs have become a focal area in the exploration and development of oil and gas in recent years. However, the complexity of their geological conditions and the significant heterogeneity of reservoir properties make the identification of sweet spots challenging. Traditional methods heavily rely on the experience and judgment of geologists and engineers, which introduces considerable subjectivity and uncertainty. The advent of artificial intelligence offers new avenues for identifying sweet spots in tight sandstone reservoirs. This study, based on an integrated geological-engineering perspective and utilizing data analysis and multiple machine learning methods, innovatively proposes a regression prediction model that integrates the Triangulation Topology Aggregation Optimizer (TTAO) algorithm, Random Forest (RF), and Multi-Head Self-Attention Mechanism (MSA), aiming to enhance the accuracy of oil and gas sweet spot identification. The case study utilizes actual data from the He8 section in the Ordos Basin, China. The results indicate that sweet spots are influenced by a combination of geological, rock mechanical parameters, and hydraulic fracturing operation parameters. The dominant reservoir properties affecting post-fracture productivity include gas saturation, porosity, and permeability, while the principal rock mechanics factors are fracture toughness and the difference in horizontal stresses. The critical fracturing operation factors are total fluid volume, total sand volume, and pre-pad fluid. Based on the analysis of dominant factors affecting productivity, the proposed hybrid machine learning model achieved an accuracy of 86.7% in identifying sweet spots. A three-dimensional geological-engineering sweet spot model considering lithology, physical properties, and rock mechanics characteristics was established, offering targeted areas for future well placement. Future applications of this model could achieve cross-regional adaptability by adjusting input parameters according to specific geological and engineering conditions.
1 Introduction
Tight sandstone gas reservoirs, a key component of unconventional oil and gas resources, have garnered significant attention amid the global transformation of energy structures and the increasing demand for clean energy, particularly in regions such as the Ordos Basin (Yang et al., 2012; Li, 2004). However, due to the low porosity and permeability of tight sandstone reservoirs, their development poses considerable challenges. Horizontal well with volumetric fracturing is a crucial technique for enhancing production (Wang et al., 2009; Wang et al., 2014; Han et al., 2019). Despite this, post-fracturing performance varies markedly among wells, with some failing to meet expectations (Jiang et al., 2017; Zou et al., 2013; Du et al., 2022). This uncertainty introduces risks in well placement and fracturing plan formulation. Consequently, accurately identifying the “sweet spot” areas within the reservoir—regions with high reservoir quality and production potential—is essential for optimizing drilling layouts, enhancing development efficiency, and reducing development costs (Zou et al., 2015). Thanks to the advancements driven by the North American shale gas revolution, sweet spot identification technology has seen notable improvements in recent years (Zou et al., 2020). Traditional methods of identifying sweet spots generally rely on geological interpretation and geophysical techniques, such as parameter truncation based on geological properties like porosity, permeability, and gas saturation, as well as engineering parameters such as Young’s modulus, brittleness index, and the stress difference coefficient (Clarkson et al., 2012; Buller et al., 2010; Liao, 2020; Rickman et al., 2008; Ross and Bustin, 2007), with additional approaches, including sedimentary diagenesis-reservoir facies analysis (You et al., 2014), petrophysical inversion of reservoir parameters (Zhou et al., 2019; He, 2018), and the integration of micro-core experimental data with high-resolution 3D seismic data (Sun et al., 2019), also depending on similar techniques for sweet spot identification and prediction. While traditional geological and geophysical approaches have achieved significant progress, they largely depend on expert judgment and qualitative analysis to assess reservoir physical properties and production potential. Although this approach works in small-scale datasets and simple geological settings, it often falls short in large-scale, complex geological environments due to its strong subjectivity and lack of quantitative analysis (Ji et al., 2019). Furthermore, while geophysical methods provide valuable reservoir insights, their resolution and accuracy are often limited in deep reservoirs and complex geological conditions. Traditional methods also struggle to efficiently handle multivariable, high-dimensional data, and fail to capture all the factors influencing sweet spot formation, making it difficult to quantify uncertainty.
To address these limitations, researchers have turned to new technological approaches. Machine learning algorithms, including random forests, support vector machines, and convolutional neural networks, are capable of extracting features from complex datasets. They demonstrate superior performance in handling large-scale and high-dimensional data and have been applied to sweet spot identification (Ji et al., 2019; Bansal et al., 2013; Zhong et al., 2015; Lolon et al., 2016; Bowie, 2018). For instance, data analysis has been used for sensitivity analysis of fracturing parameters influencing sweet spots (Jianmin et al., 2019; Wu et al., 2012; Yao et al., 2021; Wigwe et al., 2019; Hareland et al., 1993; Kolawole et al., 2019; Xinfang et al., 2005); fuzzy mathematics and support vector machines have been employed to correlate seismic attributes with petrophysical characteristics to identify sweet spots in unconventional reservoirs (Qian et al., 2018); adaptive boosting machine learning algorithms, neural network models, and other methods have been utilized to explore the correlation between productivity and factors such as rock mechanics, hydraulic fracturing, well completion data, and reservoir properties, providing a quantitative assessment of development impacts and refining sweet spot distribution (Wang and Chen, 2019; Luo et al., 2018; Han et al., 2020; Mohaghegh, 2013). Abdulaziz successfully predicted the porosity distribution of the tight sandstone reservoir in the Farrud field, Libya, by integrating artificial neural networks with well logging and seismic attributes, achieving 89% accuracy in handling reservoir heterogeneity (Abdulaziz et al., 2019). In the development of the Bakken Shale in North America, Cipolla proposed a method to separate the evaluation of reservoir quality from fracturing effectiveness, significantly improving single-well productivity through multi-objective optimization algorithms, thereby validating the necessity of engineering parameter optimization (Cipolla et al., 2010). In the Middle East, Balogun and Akintokewa conducted a quantitative risk assessment for drilling in the TM oilfield of the Niger Delta, demonstrating the feasibility of integrating geological characteristics with engineering parameters (Balogun and Akintokewa, 2023). Additionally, the rock brittleness evaluation criteria proposed by Boris and Potvin have been widely applied in tight gas reservoirs in Western Canada, emphasizing the critical role of rock mechanical parameters in sweet spot identification (Tarasov and Potvin, 2013). These cases illustrate that multidisciplinary, data-driven optimization strategies are a key trend in the development of complex reservoirs.
Despite these advances, machine learning methods still face challenges when processing geological data, particularly due to nonlinear relationships and complex spatial correlations between variables, compounded by limitations in sampling density and measurement accuracy, which introduce noise and uncertainty into the data. To counter these problems, a composite model is proposed that integrates the Triangulation Topology Aggregation Optimizer (TTAO), Random Forest (RF), and Multi-Head Self-Attention Mechanism (MSA), using the tight sandstone gas field in the Ordos Basin as a case study. This integrated approach fully leverages the TTAO algorithm’s ability to balance global and local search, the RF model’s stability and generalization capacity, and the MSA model’s sensitivity to key features. The combined framework enhances the accuracy of sweet spot identification and deepens the model’s understanding of the underlying data structure.
2 Geological background
The Ordos Basin, located on the North China Craton, is primarily a multi-cycle superimposed oil and gas cratonic basin. Its crystalline basement consists of metamorphic rock formations from the Archean to Proterozoic eras, with overlying sedimentary deposits from the Paleozoic, Mesozoic, and Cenozoic periods (Li, 2004; He et al., 2003; Li et al., 2014). Based on tectonic characteristics, the Ordos Basin is divided into six tectonic units the Yimeng Uplift, Western Thrusting Belt, the Weibei Uplift, the Tianhuan Depression, the Yishan Slope, and the Jinxi Folding Belt (Figure 1A) (Cao et al., 2013; Yang et al., 2012).
Figure 1
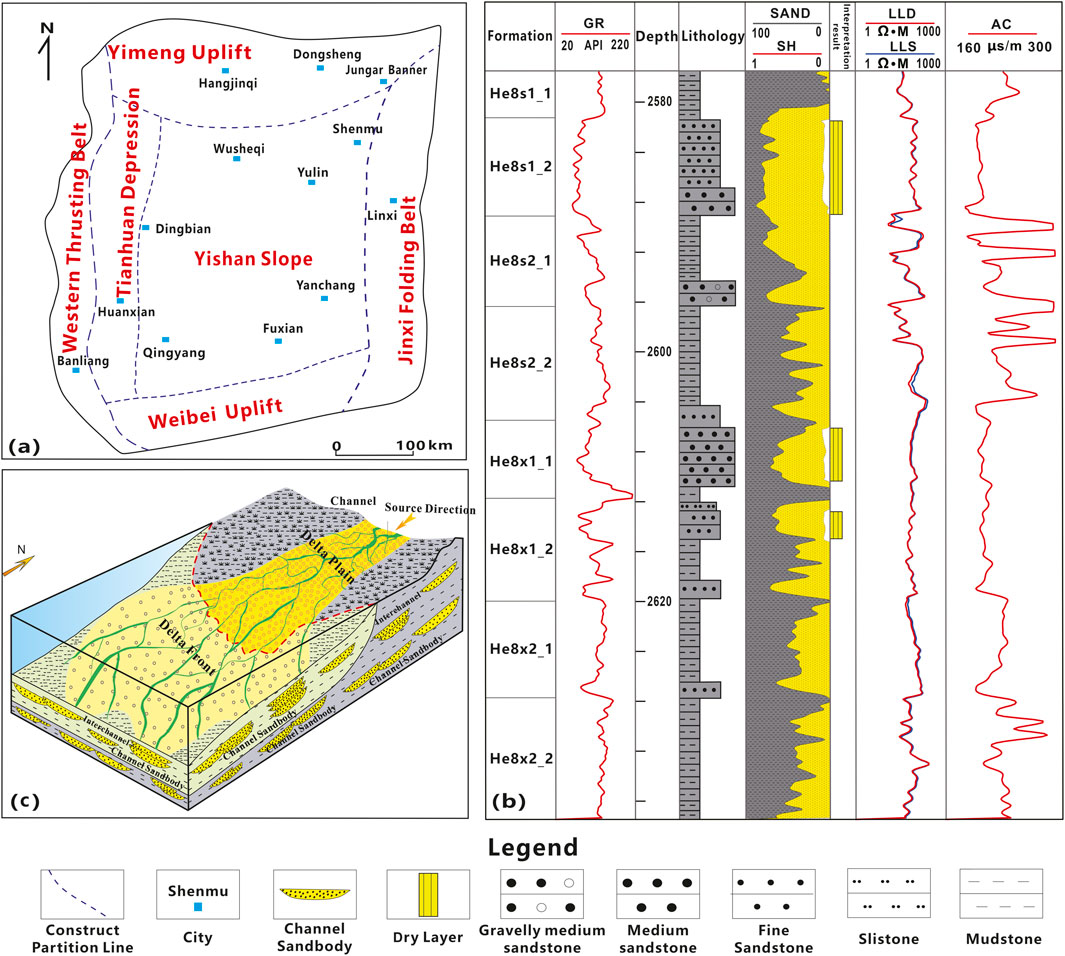
Figure 1. (A) Structural division and tectonic units of the Ordos Basin. (B) Comprehensive stratigraphic bar chart of the H8 Formation in the study area. (C) Sedimentary facies distribution model of the study area.
The study area is located in Ordos Basin. The primary stratigraphic units in this region include the Benxi Formation, Taiyuan Formation, Shanxi Formation, Lower Shihezi Formation, Upper Shihezi Formation, and the Shiqianfeng Formation. This study focuses on Section 8 of the Lower Shihezi Formation (Figure 1B), which is delimited by the Camel Neck Sandstone and the Shanxi Formation. The regional structure shows an eastward uplift and a westward depression, with localized development of gentle nose uplifts in the context of an overall monocline. During the sedimentary period of the Lower Shihezi Formation, as regional tectonic activity intensified, the northern source area of the basin continued to uplift, thereby increasing the supply of terrigenous detrital material. This led to the southward migration of the deltaic depositional system, which resulted in delta plain deposits dominating the study area. The primary sedimentary facies developed are distributary channel microfacies (Figure 1C), characterized by high sedimentary heterogeneity and complex superimposed relationships, which make sweet spot identification particularly challenging (Zhang and Lan, 2006).
3 Research data and methods
3.1 Data sources and processing
In this study, based on production capacity, the sweet spot areas of Section 8 of the Lower Shihezi Formation (He-8) are categorized into four types. Category I includes wells with a first-year gas production ecxeeding 10,000 m³/day; Category II includes wells with daily production in the range of 8,500 to 10,000 m³/day; Category III includes wells with daily production in the range of 7,500 to 8,500 m³/day; and Category IV includes wells with daily production less than 7,500 m³/day. Data from 20 coring wells in the study area were selected for this study, comprising 12 features (porosity, permeability, gas saturation, clay content, fracture toughness, minimum horizontal principal stress, brittleness index, total sand volume, total liquid volume, number of fracturing clusters, cluster spacing, and fracturing discharge), resulting in a dataset of 1,700 samples. Of these, 70% (1,190 sample points) were used for the training set, and 30% (510 sample points) were used for the test set. To ensure the quality and accuracy of the data and subsequent analysis, a series of data preprocessing steps were performed, including data cleaning and normalization.
3.2 TTAO-RF-MSA multivariable regression algorithm
To effectively identify the most influential factors on production capacity from a range of geological and engineering parameters, this study compares the feature importance scores to determine the key factors with a decisive impact on production capacity. Based on the selected key feature parameters, the TTAO algorithm is primarily designed to identify and filter the most significant factors influencing production capacity from a multitude of geological and engineering parameters through its unique triangular topology aggregation optimization strategy. This step ensures that only the most influential features are passed on to subsequent models, thereby reducing model complexity and mitigating the risk of overfitting. Subsequently, the feature subsets selected by the TTAO algorithm are input into the Random Forest (RF) model. The RF model then utilizes these optimized feature subsets to further enhance the accuracy of production capacity predictions by capturing nonlinear relationships and improving robustness against noise and outliers. This ensemble learning approach not only improves model stability but also strengthens the understanding of each feature’s contribution to sweet spots through a feature importance scoring mechanism. Finally, the Multi-Head Self-Attention (MSA) mechanism is incorporated to improve the model’s understanding of complex feature interactions. MSA learns multiple sets of attention weights in parallel, enabling the model to focus dynamically on different feature combinations and assign appropriate weights to each feature, thereby enhancing the accuracy of identification (Figure 2). During the model training phase, the dataset is divided into training and test sets (7:3), with the training set used for model learning and the test set used to evaluate model performance. Hyperparameters are tuned through cross-validation to achieve the best predictive performance. To validate the model’s identification accuracy, several evaluation metrics, including accuracy, recall, and F1 score, are employed.
Figure 2
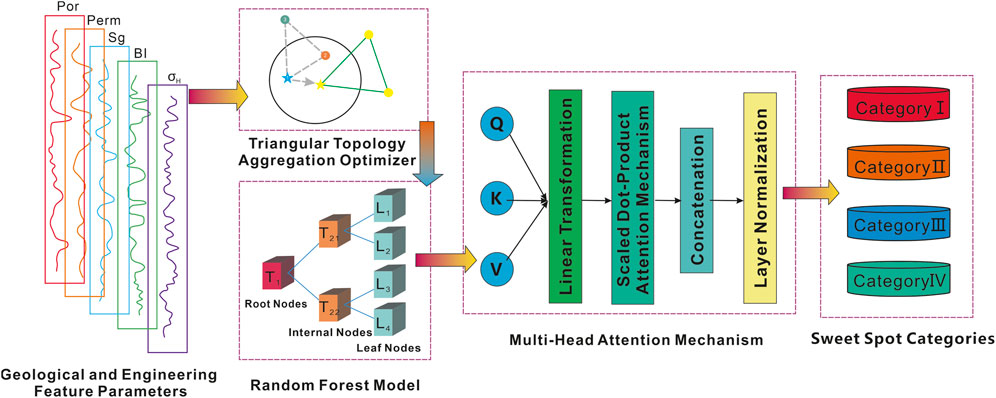
Figure 2. Integrated Geological-Engineering sweet spot identification framework combining TTAO, Random Forest, and Multi-Head Self-Attention Mechanism.
3.2.1 Triangular topology aggregation optimizer algorithm (TTAO)
The design inspiration for the TTAO algorithm is drawn from the stability and similarity of triangles in nature. In mathematics and engineering, triangular structures are widely used in various optimization problems due to their unique geometric properties. The TTAO algorithm aims to address this challenge by simulating the similarity of triangles, thereby enhancing the algorithm’s performance in multimodal, multi-objective, or large-scale optimization problems (Zhao et al., 2024). The TTAO algorithm transforms the optimization problem into a process of constructing and optimizing triangular topology units in high-dimensional space to simulate the search process. Each triangular unit consists of four vertices, with three vertices representing feature parameters that influence the sweet spot, and the fourth vertex, located inside the triangle, is generated by linearly weighting the three feature vertices. The addition of the internal vertex increases the flexibility of the triangular unit, enabling the algorithm to perform a more detailed search within the triangle (Zhao et al., 2024). These triangular topology units dynamically evolve through the iterative process in the search space, exploring and exploiting regions with potential optimal solutions.
The TTAO algorithm includes two primary aggregation strategies: generic aggregation and local aggregation. Generic aggregation focuses on global search by exchanging information between different triangular units to discover new solutions. Local aggregation focuses on local search by perturbing the optimal individual within a unit to precisely find local optimal solutions (Zhao et al., 2024). In each iteration, the algorithm first performs generic aggregation. In each triangular topology unit, the algorithm identifies the best-performing individual, which possibly represents the optimal feature combination or solution found in that unit during the current iteration. The algorithm then exchanges information between different units, typically involving the comparison of the optimal individuals in different units and generating new individuals through crossover strategies. Based on this information exchange, the algorithm generates new vertices that represent potential new solutions, which may be located in different regions of the search space, helping the algorithm explore areas that have not been fully explored. These newly generated vertices are added to the triangular topology units, and if they outperform the original vertices, they replace them. In this way, the algorithm explores the search space to find better solutions. Figure 3 illustrates the iterative exchange of information during the generic aggregation process, where the numbering of each vertex in the triangular unit represents its importance ranking. The information exchange in the algorithm involves three distinct movement methods. The first involves individuals generated after crossover that outperform the original optimal individuals (e.g., the upper right unit and the lower left unit, the upper left unit and the lower left unit). The second involves individuals generated after crossover that outperform the suboptimal individuals (e.g., the upper right unit with the lower right unit, and the second unit from the upper with the lower left unit). The third involves individuals generated after crossover that perform worse than the original individuals (e.g., the upper unit with the upper right unit, resulting in a worse solution).
Figure 3
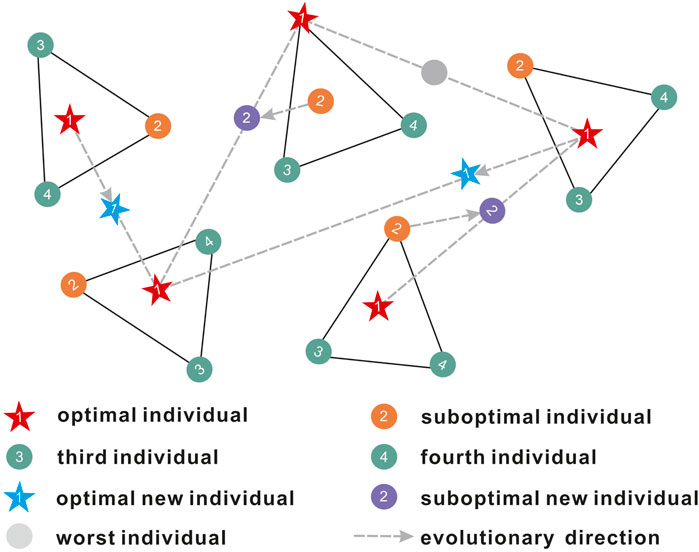
Figure 3. General aggregation information iteration update process (modified after Shijie Zhao et al., 2024).
Subsequently, the algorithm performs local aggregation. Within each triangular topology unit, the algorithm first identifies the current local optimal individual, which represents the best solution found in that unit during the current iteration. Centered on the local optimal individual, the algorithm defines a local search range to ensure that the search does not deviate too far from the optimal individual while allowing some degree of exploration. Within this local search area, the algorithm introduces new mutations by randomly perturbing the optimal individual through adding or subtracting a small random number to its feature values, thereby exploring the solution space near the optimal individual. Through this perturbation, the algorithm generates new individuals that represent other potential solutions in the vicinity of the local optimal individual. The generation of new individuals can be considered a minor adjustment to the local optimal solution, aimed at discovering better solutions. If a new individual’s fitness surpasses the fitness of the current local optimal individual, this new individual will replace the previous local optimal individual. This process is repeated until no further improvement is found within the local search range. Through local aggregation, the TTAO algorithm can perform a thorough exploration of local areas while retaining its global search capability. This strategy aids the algorithm in finding more accurate solutions in complex optimization problems, especially when multiple local optima are present, as local aggregation effectively prevents the algorithm from getting trapped in suboptimal solutions. Figure 4 shows a schematic of local aggregation for the triangular topology units, with the dashed triangular topology unit indicating the temporary topology structure formed by the optimal, suboptimal, and third vertexs after generic aggregation. Within a certain local area, the optimal individual in each unit is aggregated and updated to superior positions. After local aggregation of each temporary unit, new topology units (yellow dots) are constructed based on their optimal positions.
Figure 4
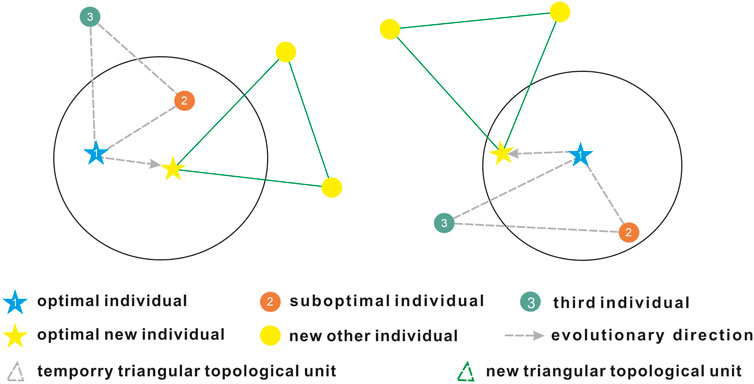
Figure 4. Iterative update process of local aggregation information (modified after Shijie Zhao et al., 2024).
3.2.2 Random forest with attention mechanism (RF-MSA)
The Random Forest algorithm improves prediction stability and accuracy by constructing multiple decision trees and integrating their prediction results. In this study, model performance is further optimized by incorporating an attention mechanism, enhancing the model’s capability to identify and assign weights to key features, thereby increasing the accuracy of sweet spot predictions.
Random Forest is an ensemble learning method that enhances model stability and accuracy by combining the prediction results from multiple decision trees (Lan, 2022; Fang et al., 2011). Each decision tree is trained on different random subsets of the dataset, using a method known as Bagging. In this process, assume the original dataset D comprises N samples. For each tree, N samples are randomly selected from D with replacement (Bootstrapping) to create a new training dataset Di. Each tree’s training set may contain duplicate samples, and roughly one-third of the samples are not included in Di; these unselected samples can then serve as Out-of-Bag (OOB) data, providing an unbiased estimate for model validation. Additionally, Random Forest increases model diversity and robustness by using a random subset of features, along with a random subset of data, at each decision node split (Lan, 2022).
In this study, the construction of the Random Forest follows these steps: First, multiple distinct training subsets are drawn from the original training set through sampling with replacement. Next, a decision tree is built for each training subset. A random subset of features is selected when determining split nodes, rather than using all available features. This process is repeated until the predefined number of trees is constructed. Finally, the prediction results from all decision trees are combined to make the final prediction (Figure 5).
Figure 5
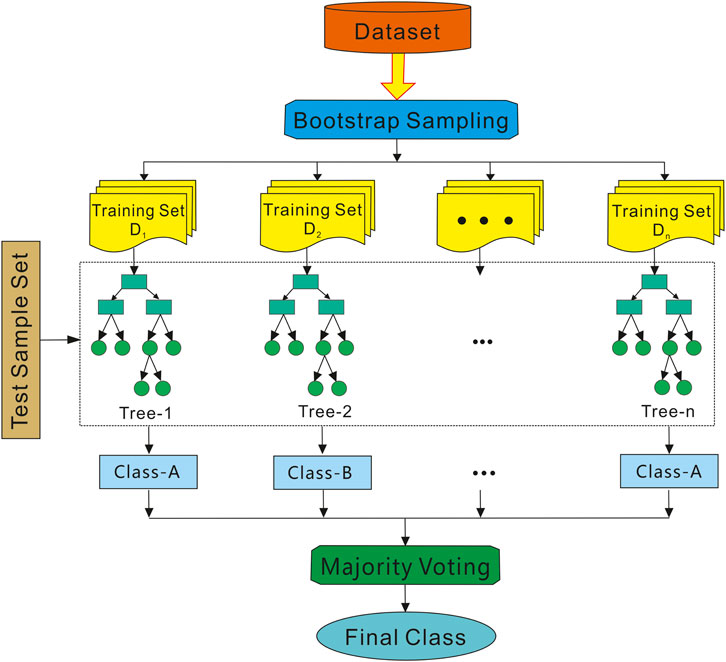
Figure 5. Schematic diagram of the Random Forest construction process illustrating bootstrap sampling, decision tree generation, and majority voting integration.
On the basis of Random Forest, we introduce the Multi-Head Attention (MSA) mechanism (Figure 6) to enhance the model’s capability to recognize key features. During each tree’s node split, the model can select the most informative features for splitting, based on attention weights, thereby improving the prediction performance of the tree.
Figure 6
Figure 6. Architecture of the Multi-Head Self-Attention mechanism with parallel query, key, and value transformations.
The attention mechanism is a computational framework that mimics human cognitive attention, enabling the model to focus on the key parts of the input data when processing information. In deep learning, the attention mechanism achieves this by assigning different weights to different portions of the input data, which reflect the importance of each part of the data. Multi-Head Attention is an extension of the attention mechanism, enhancing and combining the scaled dot-product attention mechanism. In this mechanism, the input vector is first transformed by multiple sets of linear projections into Query, Key, and Value spaces, resulting in three matrices Q, K, and V, where each transformation corresponds to a distinct “head.” As a result, each head learns different feature representations from the input data (Wang et al., 2024). Each head computes attention independently, producing a set of attention scores that determine the weighted sum of the value vectors in that head. Since each head focuses on distinct aspects of the data, this parallel computation enhances the model’s sensitivity to diverse input features. The attention outputs from all heads are concatenated, and finally, the concatenated output is passed through another set of linear projections to produce the final output of the multi-head attention layer. This output contains all the information the model has learned from the multiple “heads.”
4 Geological-engineering sweet spots identification example
4.1 Analysis of key factors influencing sweet spots
This study takes the Ordos Basin as a case example. First, rigorous preprocessing is applied to the raw dataset, including handling missing values and normalizing features, ensuring data quality and eliminating dimensionality effects. Next, we performed a Kendall correlation analysis to rank the importance of the 12 characteristic parameters affecting the gas reservoir’s production capacity. As shown in Figure 7, a bar chart of parameter importance is calculated based on correlation analysis. The results indicate that gas saturation, permeability, and porosity are the primary geological parameters affecting post-fracturing productivity. Additionally, rock mechanical parameters also have a significant impact on productivity. Specifically, fracture toughness and brittleness index refer to the resistance of rock to fracture propagation. Areas with a higher brittleness index and lower fracture toughness exhibit higher productivity. Furthermore, the minimum horizontal principal stress influences fracture propagation, which subsequently affects the well’s operational range and, consequently, productivity. In addition, fracturing operational parameters (such as total sand volume, total liquid volume, number of fracturing clusters, cluster spacing, and fracturing discharge) affect the effectiveness of the fracturing operation and, to a certain degree, influence post-fracturing productivity.
Figure 7
Figure 7. Importance Ranking of Main Control Factors for Multi factor Capacity.
Based on this, sweet spots are classified into four categories according to productivity. The TTAO algorithm is then applied to construct a triangular topological structure, mapping the feature space into an optimization problem. In this optimization problem, each vertex represents a feature, edges represent relationships between features, and triangles represent feature subsets. The algorithm evaluates the contribution of each feature subset to the sweet spot through an iterative search process and selects the optimal subset to reduce the complexity and overfitting risk of the subsequent model. The results show that porosity, permeability, gas saturation, clay content, minimum horizontal principal stress, brittleness index, fracture toughness, number of fracturing clusters, total sand volume, and total liquid volume form the optimal feature subset. Following this, a classification model is constructed using the Random Forest algorithm based on the feature subset selected by the TTAO algorithm. The integration of multiple decision trees enhances the model’s ability to capture non-linear relationships and improves robustness against noise and outliers. In this process, the Random Forest algorithm’s feature importance score mechanism further confirms each feature’s contribution to the sweet spot, providing a stable basis for prediction. Finally, the multi-head attention mechanism is introduced to enhance the model’s understanding of complex feature interactions. By learning in parallel from multiple attention weight sets, the model can dynamically focus on different feature combinations and assign corresponding weights to each feature. This coherent algorithmic fusion framework not only improves the accuracy of sweet spots identification but also enhances the model’s understanding of the underlying structure of the data.
4.2 Hyperparameter settings for the TTAO-RF-MSA model
To achieve optimal performance of the TTAO-RF-MSA model, its hyperparameters were carefully tuned, with particular focus on three key parameters that significantly influence model performance.
The first hyperparameter is the leaf size, also known as the minimum leaf size, which determines the minimum number of samples required in a leaf node. This parameter controls the growth of decision trees. A smaller leaf size enables the model to capture finer-grained data patterns but increases the risk of overfitting due to sensitivity to noise. Conversely, a larger leaf size enhances generalization ability but may result in underfitting. Experimental analysis compared model errors for leaf sizes of 3, 6, and 9 (Figure 8). The results indicate that a leaf size of three yields the smallest error, demonstrating optimal model performance.
Figure 8
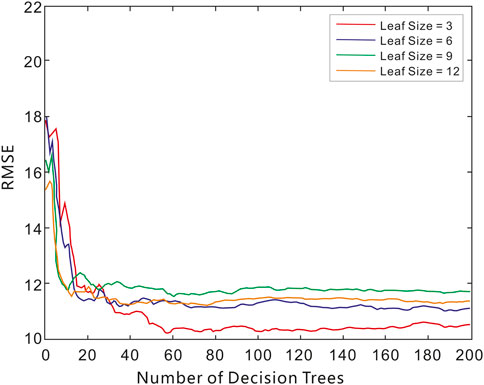
Figure 8. Comparison of training performance for the Random Forest model under varying minimum leaf sizes.
The second hyperparameter is the number of features. The dataset in this study includes 12 parameters related to geology, geomechanics, and engineering. Models were constructed using varying numbers of input features, ranging from 2 to 12 (Random feature selection), and their performance was evaluated (Figure 9). Each model underwent independent training and validation to ensure the accuracy and reliability of the results. Comparative analysis of performance metrics, including but not limited to relative error, revealed that the model achieved the lowest error when it included 10 features: porosity, permeability, gas saturation, clay content, minimum horizontal principal stress, brittleness index, fracture toughness, number of fracturing clusters, total sand volume, and total liquid volume. This indicates that this number of features provides the optimal balance for our model, allowing it to capture key information in the data while avoiding overfitting.
Figure 9
Figure 9. Impact of feature subset size on Random Forest model accuracy.
The third hyperparameter is the number of iterations, which defines the number of optimization cycles in the TTAO algorithm. Increasing the iteration count allows the algorithm to explore the search space more thoroughly, potentially identifying better solutions. However, excessive iterations can lead to significantly higher computational costs and may cause the algorithm to converge prematurely in a local optimum. Carefully determining the optimal number of iterations plays a critical role in achieving a balance between model performance and computational efficiency. Figure 10 presents the loss curves for the training and test sets at the highest accuracy. The analysis indicates that the optimal number of iterations is 138.
Figure 10
Figure 10. Training and validation loss curves of the TTAO-RF-MSA model.
4.3 Model evaluation metrics
To comprehensively assess the performance of the proposed TTAO-RF-MSA multivariable regression model, we employed multiple evaluation metrics to measure the model’s prediction accuracy and reliability, including but not limited to accuracy, recall, precision, and F1 score.
4.3.1 Accuracy
Accuracy is the ratio of correctly predicted samples to the total number of samples. It offers a straightforward evaluation of model performance, particularly in classification tasks. The formula is:
where TP refers to the number of true positive predictions, TN refers to the number of true negative predictions, FP refers to the number of false positive predictions, and FN refers to the number of false negative predictions.
4.3.2 Recall
Recall, or true positive rate, measures the model’s ability to correctly identify positive samples. It is calculated as the proportion of actual positive samples correctly predicted by the model. The formula is:
4.3.3 Precision
Precision is the proportion of positive predictions that are actually correct. t focuses on the accuracy of the model’s predictions, aiming to reduce false positives. The formula is:
4.3.4 F1 score
The F1 score is the harmonic mean of precision and recall, balancing the two metrics. It ranges from 0 to 1, with higher values indicating better model performance. The formula is:
4.4 Sweet spots identification results
In this study, the proposed TTAO-RF-MSA model was applied to identify sweet spots at the single-well scale. First, the TTAO algorithm was employed to optimize input features. By constructing and optimizing triangular topology units, the algorithm effectively selected the 10 factors most influencing productivity from geological and engineering parameters. These selected features were then used as inputs for the Random Forest (RF) model, which enhanced the ability to capture nonlinear relationships by integrating multiple decision trees, while improving robustness to noise and outliers. Building on the RF model, the Multi-Head Self-Attention mechanism (MSA) further refined the identification and weighting of key features, enabling the model to prioritize factors with decisive impacts on the output during sweet spot identification. Through this integrated framework, the TTAO-RF-MSA model successfully achieved single-well sweet spot identification. Analysis of the confusion matrix (Figure 11) revealed that the model accurately predicted 442 out of 510 samples, achieving an identification accuracy of 86.7%, which demonstrates good predictive performance. To further validate the model’s predictive capability, Horizontal Well A was selected as a case study. It is important to note that the data for Horizontal Well A is included in the dataset of the 20 coring wells mentioned earlier. This approach ensures the representativeness of the case study and allows a direct comparison between the model’s predictions and actual drilling data. Using the proposed TTAO-RF-MSA model, sweet spots in Horizontal Well A were identified. The results showed that the actual sweet spot length encountered in the horizontal section was 1,460 m, while the model predicted a sweet spot length of 1,510 m, resulting in a prediction error of less than 3% (Figure 12). This result demonstrates the model’s predictive accuracy at the single-well scale.
Figure 11
Figure 11. TTAO-RF-MSA model confusion matrix.
Figure 12
Figure 12. Comparison between actual drilling and predicted sweet spots in horizontal well A.
In practical applications, this paper integrates geological modeling techniques. Based on the existing sedimentary microfacies model, it samples the single-well sweet spot identification results into the model grid and performs variogram analysis. Sequential indicator simulation is employed 100 times, with the sweet spot type having the highest probability taken as the final result. This method utilizes the spatial correlation of geological features to provide reasonable estimates in areas with sparse well data. It achieves inter-well prediction of sweet spots and ensures the reliability of the prediction results, ultimately establishing a three-dimensional geological-engineering sweet spot model that comprehensively considers multiple factors and scales, such as lithology, physical properties, and rock mechanics characteristics (Figure 13). It not only depicts the spatial distribution of predicted sweet spots but also visualizes the spatial variations in different characteristic parameters, providing detailed and intuitive information for oil and gas exploration and development. As shown in the figure, Category I and II sweet spots are predominantly distributed in the central part of the channel, while Category III and IV sweet spots are mainly located along the channel edges.
Figure 13
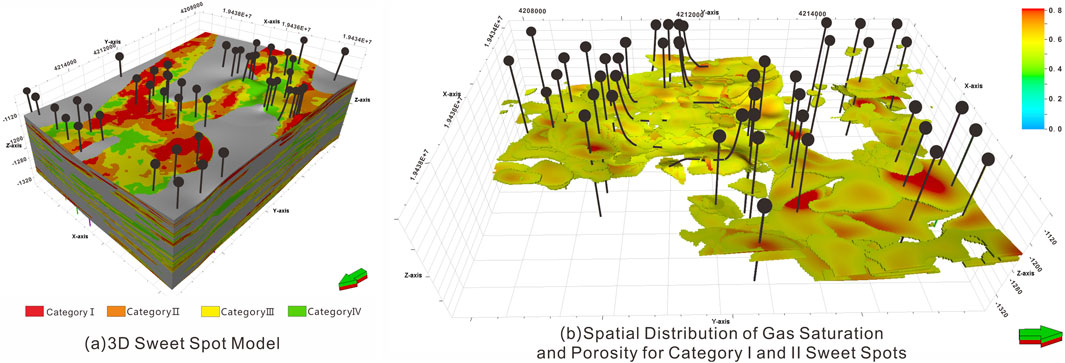
Figure 13. 3D sweet spot model. (A) 3D Sweet Spot Model. (B) Spatial Distribution of Gas Saturation and Porosity for Category I and II Sweet Spots.
4.5 Comparative experimental results of different models
Ensuring fairness in experimental setups and credibility of results is critical when comparing model performance. To this end, in addition to extensive hyperparameter optimization for the proposed TTAO-RF-MSA model, we performed similar hyperparameter tuning for other models used in the comparison (e.g., RF, KNN, CNN, XGBoost, and SVM). The selection of hyperparameters for each model was informed by comprehensive literature review and extensive experimental validation to ensure that all models operated under optimal or near-optimal configurations.
For the RF model, we adjusted the number of trees, maximum depth, and minimum leaf size. For the KNN model, different numbers of neighbors and distance metrics were tested. For the CNN model, adjustments were made to the number and size of convolutional layers and pooling strategies. The hyperparameters for the XGBoost model included learning rate, maximum tree depth, and regularization parameters. For the SVM model, we optimized the penalty parameter and kernel function types. All hyperparameter settings were determined through cross-validation and grid search to identify the best configurations for the dataset.
Following hyperparameter optimization, we reevaluated the models to ensure that each demonstrated its best performance. By calculating accuracy, precision, recall, and F1 scores for different sweet spot categories, we found that the TTAO-RF-MSA model consistently outperformed the other models across multiple evaluation metrics. These results not only demonstrate the superior performance of the TTAO-RF-MSA model but also highlight the critical role of hyperparameter optimization in enhancing model performance.
Table 1 summarizes the performance metrics of different models under their optimized hyperparameter configurations. The results of this detailed comparative experiment illustrate that the TTAO-RF-MSA model delivers the best sweet spot identification performance.
Table 1
Table 1. Accuracy, recall, and F1 score of sweet spot recognition for different models.
5 Discussion
In this study, the TTAO-RF-MSA model exhibited exceptional predictive performance, likely due to its innovative design in ensemble learning and optimization methodologies. Specifically, the TTAO algorithm balances global and local searches, enabling the discovery of optimal solutions across the entire search space. The stability and generalization capability of RF further enhanced prediction accuracy and robustness. Additionally, the incorporation of MSA assigned higher weights to critical features, enabling the model to prioritize factors with decisive impacts on the output during prediction. This approach partially emulates the decision-making processes of experienced geological engineers, enhancing the model’s adaptability to complex geological and engineering scenarios. The high accuracy (86.7%) of the TTAO-RF-MSA model proposed in this study for sweet spot identification is not only applicable to the Ordos Basin but also demonstrates methodological universality for other regions. For instance, Saputra identified fracturing fluid volume and rock brittleness index as critical parameters through an economic model in the Permian Basin, United States (Saputra et al., 2021), which aligns closely with the dominant controlling factors in this study. Research on the Volador Formation in the Gippsland Basin, Australia (Kamalrulzaman et al., 2024), revealed the control mechanism of sedimentary microfacies on sweet spot distribution, supporting the innovation of integrating sedimentary facies models with machine learning in this work. Additionally, the widely adopted “dual sweet spot” theory in North American shale gas development (Cipolla et al., 2010) shares similarities with the 3D modeling approach in this study, as both emphasize the synergistic optimization of reservoir physical properties and engineering fracability. Future applications could achieve cross-regional adaptability by adjusting input parameters (e.g., region-specific rock mechanical indices).
Although this study is exemplified by the actual conditions in the Ordos Basin in China, the proposed TTAO-RF-MSA model exhibits extensive applicability. The crux of the model is to capture the intricate relationships between geological and engineering parameters by integrating various algorithms, thereby precisely identifying the “sweet spots” within the reservoir.
This data-driven and machine learning-based methodology is not contingent upon specific geological conditions or reservoir types, and thus, in theory, it can be applied to other oil and gas fields with analogous complexities. For its application in other regions, it is merely necessary to gather corresponding data in accordance with local geological and engineering conditions, and to make suitable adjustments and train the model, in order to achieve accurate identification of the reservoir “sweet spots” in those areas.
6 Conclusion
(1) The TTAO-RF-MSA model integrates the Triangular Topology Aggregation Optimizer algorithm (TTAO), Random Forest (RF), and Multi-Head Attention Mechanism (MSA). This integrated framework effectively leverages the advantages of these algorithms, significantly improving the accuracy and reliability of reservoir sweet spots identification, with an identification accuracy of 86.7%.
(2) The study identified reservoir permeability, porosity, and gas saturation as the dominant geological parameters influencing post-fracturing productivity. Rock mechanical parameters, such as fracture toughness and minimum horizontal principal stress, were also found to have significant impacts on productivity.
(3) By combining geological modeling techniques with the TTAO-RF-MSA model, a three-dimensional geological-engineering sweet spot model was developed, accounting for a comprehensive range of factors. This model not only provides intuitive and detailed information for oil and gas exploration and development, but also extends sweet spot predictions from single-well to three-dimensional scales, demonstrating its potential applications in real-world oil and gas exploration and development.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
KC: Conceptualization, Methodology, Writing–original draft. MZ: Investigation, Writing–original draft. YF: Data curation, Writing–original draft. XF: Data curation, Writing–review and editing. YW: Writing–review and editing. HG: Writing–review and editing. JD: Investigation, Writing–review and editing. QC: Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study is supported by The National Natural Science Foundation of China (Nos 52104022, 42472205, 42172154).
Conflict of interest
Authors KC, HG, and JD were employed by Sinopec North China Petroleum Bureau. Authors YF, XF, and YW were employed by PetroChina Changqing Oilfield Company Exploration and Development Research Institute.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdulaziz, A. M., Mahdi, H. A., and Sayyouh, M. H. (2019). Prediction of reservoir quality using well logs and seismic attributes analysis with an artificial neural network: a case study from Farrud Reservoir, Al-Ghani Field, Libya. J. Appl. Geophys. 161, 239–254. doi:10.1016/j.jappgeo.2018.09.013
Balogun, O. B., and Akintokewa, O. C. (2023). Pre-rig mobilization hazard evaluation in offshore oil and gas prospect drilling: a case study of TM field, offshore Niger Delta. Energy Geosci. 4 (1), 158–178. doi:10.1016/j.engeos.2022.09.008
Bansal, Y., Ertekin, T., Karpyn, Z., Ayala, L., Nejad, A., and Suleen, F. (2013). Forecasting well performance in a discontinuous tight oil reservoir using artificial neural networks, in SPE unconventional resources conference/gas technology symposium. SPE. doi:10.2118/164542-MS
Bowie, B. (2018). Machine learning applied to optimize Duvernay well performance SPE Canada unconventional resources conference. SPE. doi:10.2118/189823-MS
Buller, D., Hughes, S., Market, J., Petre, E., Spain, D., Odumosu, T., et al. (2010). Petrophysical evaluation for enhancing hydraulic stimulation in horizontal shale gas wells. SPE Annu. Tech. Conf. Exhib. SPE. doi:10.2118/132990-MS
Cao, Q., Zhao, J., Fu, J., Yao, J., Liu, X., Zhao, H., et al. (2013). Gas source conditions of quasi-continuous accumulation of the upper paleozoic in Ordos Basin. Oil and Gas Geol. 34 (5), 584–591. doi:10.11743/ogg20130502
Cipolla, C. L., Williams, M. J., Weng, X., Mack, M., and Maxwell, S. (2010). Hydraulic fracture monitoring to reservoir simulation: maximizing value, in European Association of Geoscientists and Engineers second EAGE middle east tight gas reservoirs workshop. European Association of Geoscientists and Engineers. doi:10.3997/2214-4609.20145655
Clarkson, C. R., Wood, J. M., Burgis, S. E., Aquino, S. D., and Freeman, M. (2012). Nanopore-structure analysis and permeability predictions for a tight gas siltstone reservoir by use of low-pressure adsorption and mercury-intrusion techniques. SPE Reserv. Eval. and Eng. 15 (06), 648–661. doi:10.2118/155537-pa
Du, J., Zhu, G., Li, Y., Wu, P., Gao, J., Zhu, H., et al. (2022). Exploration and development challenges and technological countermeasures for tight sandstone gas reservoirs in Ordos basin margin: a case study of Linxing-Shenfu Gas Field. Nat. Gas. Ind. 42 (1), 114–124. doi:10.3787/j.issn.1000-0976.2022.01.011
Fang, K., Wu, J., Zhu, J., and Xie, B. (2011). A review of technologies on random forests. J. Statistics Inf. 26 (03), 32–38. doi:10.3969/j.issn.1007-3116.2011.03.006
Han, D., Jung, J., and Kwon, S. (2020). Comparative study on supervised learning models for productivity forecasting of shale reservoirs based on a data-driven approach. Appl. Sci. 10 (4), 1267. doi:10.3390/app10041267
Han, D., Kwon, S., Son, H., and Lee, J. (2019). Production forecasting for shale gas well in transient flow using machine learning and decline curve analysis Asia pacific unconventional resources technology conference, Brisbane, Australia, Unconventional Resources Technology Conference: 1510–1527. doi:10.15530/AP-URTEC-2019-198198
Hareland, G., Rampersad, P., Dharaphop, J., and Sasnanand, S. (1993). Hydraulic fracturing design optimization SPE eastern regional meeting. SPE. doi:10.2118/26950-MS
He, P. (2018). Comprehensive evaluation of the distribution of the dessert in the tight sandstone reservoir-zhenjing oilfield as an example. Beijing: China University of Petroleum.
He, Z., Fu, J., Xi, S., Fu, S., and Bao, H. (2003). Geological features of reservoir formation of Sulige gas field. Acta Pet. Sin. 24 (2), 6–12. doi:10.7623/syxb200302002
Ji, G., Jia, A., Meng, D., Guo, Z., Wang, G., Cheng, L., et al. (2019). Technical strategies for effective development and gas recovery enhancement of a large tight gas field: a case study of Sulige gas field, Ordos Basin, NW China. Petroleum Explor. Dev. 46 (3), 629–641. doi:10.1016/s1876-3804(19)60043-1
Jiang, T., Bian, X., Wang, H., Li, S., Jia, C., Liu, H., et al. (2017). Volume fracturing of deep shale gas horizontal wells. Nat. Gas. Ind. B 4 (2), 127–133. doi:10.1016/j.ngib.2017.07.018
Jianmin, L., Baocheng, W., Haiyan, Z., Ning, C., and Jialing, H. (2019). Adaptability of horizontal well volume fracturing to tight conglomerate reservoirs in Mahu oilfield. China Pet. Explor. 24 (2), 250. doi:10.3969/j.issn.1672-7703.2019.02.014
Kamalrulzaman, K. N., Shalaby, M. R., and Islam, M. A. (2024). Reservoir quality of the late cretaceous Volador Formation of the latrobe group, Gippsland Basin, Australia: implications from integrated analytical techniques. Energy Geosci. 5 (1), 100228. doi:10.1016/j.engeos.2023.100228
Kolawole, O., Esmaeilpour, S., Hunky, R., Saleh, L., Ali-Alhaj, H. K., Marghani, M., et al. (2019). Optimization of hydraulic fracturing design in unconventional formations: impact of treatment parameters, in SPE Kuwait oil and gas show and conference. SPE. doi:10.2118/198031-MS
Lan, Z. (2022). Data-driven sweet-spot prediction and fracturing optimization based on integrated reservoir model. Wuhan: China University of Geosciences.
Li, D. (2004). Return to petroleum geology of Ordos Basin. Petroleum Explor. Dev. 31 (6), 1–7. doi:10.3321/j.issn:1000-0747.2004.06.001
Li, Y., Tang, D., Xu, H., Meng, S., Liu, Y., and Zhang, W. (2014). Characteristics of structural controlled coalbed methane in East margin of Ordos Basin. Coal Sci. Technol. 42 (06), 113–117+129. doi:10.13199/j.cnki.cst.2014.06.024
Liao, D. (2020). Evaluation methods and engineering application of the feasibility of double sweet spotsin shale gas reservoirs. Pet. Drill. Tech. 48 (4), 94–99. doi:10.11911/syztjs.2020063
Lolon, E., Hamidieh, K., Weijers, L., Mayerhofer, M., Melcher, H., and Oduba, O. (2016). Evaluating the relationship between well parameters and production using multivariate statistical models: a middle bake and three forks case history, in SPE hydraulic fracturing technology conference and exhibition. SPE. doi:10.2118/179171-MS
Luo, G., Tian, Y., Bychina, M., and Ehlig-Economides, C. (2018). Production optimization using machine learning in bakken shale unconventional resources technology conference, Houston, Texas. Society of Exploration Geophysicists, American Association of Petroleum Geologists, Society of Petroleum Engineers, 2174–2197. doi:10.15530/URTEC-2018-2902505
Mohaghegh, S. D. (2013). Reservoir modeling of shale formations. J. Nat. Gas Sci. Eng. 12, 22–33. doi:10.1016/j.jngse.2013.01.003
Qian, K. R., He, Z. L., Liu, X. W., and Chen, Y. Q. (2018). Intelligent prediction and integral analysis of shale oil and gas sweet spots. Petroleum Sci. 15 (4), 744–755. doi:10.1007/s12182-018-0261-y
Rickman, R., Mullen, M., Petre, E., Grieser, B., and Kundert, D. (2008). A practical use of shale petrophysics for stimulation design optimization: all shale plays are not clones of the Barnett Shale. SPE Annual Technical Conference and Exhibition. SPE. doi:10.2118/115258-MS
Ross, D. J. K., and Bustin, R. M. (2007). Shale gas potential of the lower Jurassic Gordondale member, northeastern British Columbia, Canada. Bull. Can. petroleum Geol. 55 (1), 51–75. doi:10.2113/gscpgbull.55.1.51
Saputra, W., Kirati, W., and Patzek, T. (2021). Forecast of economic tight oil and gas production in Permian Basin. Energies 15 (1), 43. doi:10.3390/en15010043
Sun, W., Wang, Y., and Xu, W. (2019). Sweet spot prediction of tight reservoir of He 8 member in Leijiaqi area, eastern margin of Ordos Basin. Lithol. Reserv. 31 (1), 69–77. doi:10.12108/yxyqc.20190108
Tarasov, B., and Potvin, Y. (2013). Universal criteria for rock brittleness estimation under triaxial compression. Int. J. Rock Mech. Min. Sci. 59, 57–69. doi:10.1016/j.ijrmms.2012.12.011
Wang, H., Liao, X., Zhao, X., Zhao, D., Dou, X., and Chen, X. (2014). A study on productivity and flow regimes of segmented multi-cluster fractured horizontal well in ultra-low permeability reservoir-a case of Chang8 ultra-low permeability reservoir in Ordos Basin. Petroleum Geol. Recovery Effic. 21 (6), 107–110. doi:10.3969/j.issn.1009-9603.2014.06.027
Wang, S., and Chen, S. (2019). Insights to fracture stimulation design in unconventional reservoirs based on machine learning modeling. J. Petroleum Sci. Eng. 174, 682–695. doi:10.1016/j.petrol.2018.11.076
Wang, T., Wang, Z., Li, F., and Zhao, W. (2024). Lithology identification in optuna-BiGRU logging based on enhanced multi-head attention mechanism. J. Earth Sci. Environ. 46 (01), 127–142. doi:10.19814/j.jese.2023.07011
Wang, Z., Li, Z., and Zhao, Z. (2009). Analysis of influence factors on productivity of horizontal well. Fault-Block Oil and Gas Field 16 (3), 58–61.
Wigwe, M., Kolawole, O., Watson, M., Ispas, I., and Li, W. (2019). Influence of fracture treatment parameters on hydraulic fracturing optimization in unconventional formations, in ARMA-CUPB geothermal international conference. ARMA-CUPB.
Wu, Q., Xu, Y., Wang, X., Wang, T., and Zhang, S. (2012). Volume fracturing technology of unconventional reservoirs: connotation, design optimization and implementation. Petroleum Explor. Dev. Online 39 (3), 377–384. doi:10.1016/s1876-3804(12)60054-8
Xinfang, M., Fan, F., and Zhang, S. (2005). Fracture parameter optimization of horizontal well fracturing in low permeability gas reservoir. Nat. Gas. Ind. 25 (9), 61. doi:10.3321/j.issn:1000-0976.2005.09.020
Yang, H., Fu, J., Liu, X., and Meng, P. (2012). Accumulation conditions and exploration and development of tight gas in the Upper Paleozoic of the Ordos Basin. Petroleum Explor. Dev. 39, 315–324. doi:10.1016/s1876-3804(12)60047-0
Yao, J., Li, Z., Liu, L., Fan, W., Zhang, M., and Zhang, K. (2021). Optimization of fracturing parameters by modified variable-length particle-swarm optimization in shale-gas reservoir. SPE J. 26 (02), 1032–1049. doi:10.2118/205023-pa
You, L., Zhang, Y., Li, C., Zhang, S., and Zhao, Z. (2014). Based on analysis of sedimentary-diagenetic reservoir facies to determine “sweet spots” distribution in low permeability from wenchang 9 area. J. Jilin Univ. Earth Sci. Ed. 44 (5), 1432–1440. doi:10.13278/j.cnki.jjuese.201405104
Zhang, J., and Lan, C. (2006). Fractures and faults distribution and its effect on gas enrichment areas in Ordos Basin. Petroleum Explor. Dev. 33 (2), 172–177. doi:10.3321/j.issn:1000-0747.2006.02.010
Zhao, S., Zhang, T., Cai, L., and Yang, R. (2024). Triangulation topology aggregation optimizer: a novel mathematics-based meta-heuristic algorithm for continuous optimization and engineering applications. Expert Syst. Appl. 238, 121744. doi:10.1016/j.eswa.2023.121744
Zhong, M., Schuetter, J., Mishra, S., and LaFollette, R. F. (2015). Do data mining methods matter? a Wolfcamp “shale” case study, in SPE hydraulic fracturing technology conference and exhibition. SPE. doi:10.2118/SPE-173334-MS
Zhou, J., Ma, G., Sui, B., Xu, W., Zhang, W., Zeng, Y., et al. (2019). Application of reservoir parameters rock physics inversion in the prediction of Sweet Spot: a case study in W17 oilfield. Prog. Geophys. 34 (3), 1159–1169. doi:10.6038/pg2019CC0166
Zou, C., Pan, S., Jing, Z., Gao, J., Yang, Z., Wu, S., et al. (2020). Shale oil and gas revolution and its impact. Acta Pet. Sin. 41 (1), 1–12. doi:10.7623/syxb202001001
Zou, C., Yang, Z., Zhu, R., Zhang, G., Hou, L., Wu, S., et al. (2015). Progress in China's unconventional oil and gas exploration and development and theoretical technologies. Acta Geol. Sin. 89 (6), 979–1007. doi:10.3969/j.issn.0001-5717.2015.06.001
Keywords: ordos basin, tight sandstone reservoir, geological-engineering sweet spot, triangulation topology aggregation optimizer algorithm, random forest, multi-head self-attention mechanism
Citation: Chen K, Zhao M, Feng Y, Fu X, Wang Y, Guo H, Ding J and Chen Q (2025) Intelligent recognition of “geological-engineering” sweet spots in tight sandstone reservoirs - an application to a tight gas reservoir in Ordos Basin, China. Front. Earth Sci. 13:1535883. doi: 10.3389/feart.2025.1535883
Received: 28 November 2024; Accepted: 10 February 2025;
Published: 04 March 2025.
Edited by:
Yin Yanshu, Yangtze University, ChinaCopyright © 2025 Chen, Zhao, Feng, Fu, Wang, Guo, Ding and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qi Chen, Y3ExNDc1MTM2NjI1OUAxNjMuY29t