Research on damage and degradation of coal-bearing sandstone under freeze-thaw cycles

Comprehending the effect of freeze-thaw cycles on the damage and degradation of coal-bearing sandstones is crucial for the end-wall slope stability of open-pit mines in cold areas. In this study, freeze-thaw cycle tests on water-saturated coal-bearing sandstone samples under different freezing temperatures and different freeze-thaw cycles were conducted by a fully automatic low-temperature freeze-thaw testing system, and the effects of freeze-thaw cycle parameters on P-wave velocity and porosity of sandstone samples were obtained. With the assistance of CT scanning imaging technology, the microscopic damage and deterioration mechanism of sandstone samples under freeze-thaw cycles was further revealed, and a characterization method for the damage and deterioration of sandstone samples under freeze-thaw cycles was established, and damage and degradation effects of freeze-thaw cycles on the sandstone samples were predicted. The research results suggest that as the freezing temperature decreases and the number of freeze-thaw cycles increases, the P-wave velocity of the sandstone sample decreases, while the volume of the sandstone sample increases. The relative change rate of P-wave velocity and porosity increment of the sample are positively correlated with freezing temperature, and negatively correlated with the number of freeze-thaw cycles. The CT scan results show that with the decrease of the freezing temperature and the increase of the number of freeze-thaw cycles, the number and geometric size of pores on the sample cross section increase significantly. Additionally, the evolution equation of freeze-thaw damage factors was established with freezing temperature and number of freeze-thaw cycles as parameters, and the internal mechanism and physical characterization of freeze-thaw damage degradation of coal measure sandstone were revealed. This research provides a reference for the safety and stability evaluation and technology research and development of related rock engineering in cold areas.

1 Introduction

The large-scale open-pit coal mines in China are mainly distributed in high-latitude and seasonal frozen areas such as Inner Mongolia, Shanxi, Xinjiang, Liaoning, and Heilongjiang Provinces. The slope rock mass of the mining end-wall in the open-pit coal mines in high-latitude cold areas has long been subjected to temperature differences caused by seasonal changes and day-night changes (Lin et al., 2021; Yu et al., 2022); Coupled with the effect of ambient water, when the ambient temperature is lower than 0°C, the pore water in the rock mass undergoes a water-ice phase transition and then expands in volume. Under the combined action of ice segregation and water migration, the ice permeator in the pore structure expands, resulting in an enlargement of the initial rock body’s pore structure and emergence of new pore structures. When the ambient temperature rises above 0°C, the ice melts into water and penetrates into the new pore structure system of the rock mass and the softening of the rock mass occurs, which may induce the freezing damage and deterioration of the rock mass in the next freeze-thaw cycle. Under such reciprocating freeze-thaw cycles, the structure and physico-mechanical properties of the rock mass are significantly damaged and deteriorated (Li et al., 2023a; Li et al., 2023b). As a result, the damage and deterioration induced by repeated freeze-thaw cycles have emerged as an important cause of slope instability at the end-wall of open-pit coal mines in cold regions (Ke et al., 2021; Yuan et al., 2023).

The effect of rock damage and degradation can partially account for the changing patterns of macroscopic mechanical parameters of the slop rock (Chen et al., 2022; Jia et al., 2024; Shi et al., 2023a). However, the existing research on rock damage and degradation under freeze-thaw cycles mainly focuses on determining damage degree and its evolution mechanisms of rock mass. At present, the common detection methods for rock damage mainly include mercury intrusion measurement, CT non-destructive testing (Song et al., 2019), nuclear magnetic resonance (NMR) testing (Baldwin and Yamanashi, 1989) and electron microscopy measurement. Through mercury injection tests on limestone samples under freeze-thaw cycles, Fogue Djombou et al. (Fogue-Djombou et al., 2019) comparatively analyzed the relationship between the microstructure and macroscopic mechanical damage of the rock samples. V.G.R.D. Argandona et al. (Ruiz De Argandona et al., 1999) performed a three-dimensional reconstruction of the internal pore structure of Spanish dolomite samples under the freeze-thaw effect by using CT scanning and image processing techniques and obtained the porosity evolution of dolomite samples under the freeze-thaw effect. By scanning electron microscope (SEM) and CT scanning, J. Park et al. (Park et al., 2015) illustrated the changes in the internal microstructure of rocks after freeze-thaw cycles, and compared the three-dimensional pore structure of rocks. It was found that cracks are initiated and expanded around the central hole, indicating that the increase in rock porosity can be attributed to internal particle separation, crack formation and crack expansion. Li and Jiang et al. (Jiang, 2018; Jielin et al., 2018) conducted non-destructive tests on rock structures under freeze-thaw cycles by NMR and discussed the intrinsic relationship between the macroscopic mechanical properties and microstructural degradation of rock samples. Mousavi et al. (Mousavi et al., 2020) observed rock samples after freeze-thaw cycles by SEM. The results showed that the increase in rock porosity under freeze-thaw cycles is caused by the crack expansion and formation of new cracks and pores. In addition, techniques such as fluorescent agent calibration technique, acoustic emission (AE) detection testing, and laser scanning microscopy can also be used to analyze the microscopic porosity evolution of rock or rock-like material (Maji and Murton, 2020; Niu et al., 2021; Wang et al., 2024; Wu et al., 2020; Wu et al., 2024; Shi et al., 2023b).

The existing research mainly focuses on the rock media of geotechnical engineering within cold areas, such as red sandstone, mudstone, granite, limestone and dolomite (Ma et al., 2018; Berisavljević, 2019; Park et al., 2020; Yu et al., 2022). However, there is limited systematic research conducted on coal-bearing sandstone in open-pit mines. Different rocks exhibit distinct damage and degradation characteristics and mechanisms under freeze-thaw cycles. The coal-bearing sandstone in open-pit mines has low strength, weak cementation, development of primary/secondary cracks, high permeability coefficient, high porosity, and the presence of clay minerals (Yang et al., 2024). These characteristics aggravate the damage and deterioration effect of coal-bearing sandstone under freeze-thaw cycles, potentially leading to slope instability in open-pit mines during mining. The deterioration of the physical and mechanical properties of slope rocks in the freeze-thaw environment poses severe challenges to the stability and efficient operation of open-pit slope projects. In this study, the coal-bearing sandstone in open-pit mines in cold areas was taken as the research object, and the damage and deterioration of sandstone samples under the action of freeze-thaw cycles were investigated. Specifically, the effects of freeze-thaw cycles on the P-wave velocity and porosity of coal-bearing sandstone samples were obtained; the change rules of porosity and pore structure characteristics of coal-bearing sandstone samples before and after freeze-thaw cycles were analyzed by the microscopic imaging method of pore structure characteristics (CT scanning imaging technology); a characterization method for the damage and deterioration of coal-bearing sandstone samples under freeze-thaw cycles was established, and damage and degradation effects of freeze-thaw cycles on the sandstone samples were predicted. This research provides an important basis for the end-wall slop stability prediction, evaluation and design of open-pit mines in cold areas.

2 Freeze-thaw cycle tests on coal-bearing sandstone

2.1 Sample preparation

The sandstone samples used in the test were taken from the Antaibao Open-pit Coal Mine in Pingshuo City, Shanxi Province, China. This area is a typical high-latitude and seasonal frozen area, with an average annual minimum temperature of −14.9∼-26.7°C. According to the International Society of Rock Mechanics Test Procedures (ISRM 2007), sandstone samples were prepared into a standard cylinder with a diameter of 50 mm and a height of 100 mm. To reduce the discreteness of the test results, samples with obvious primary defects, cracks, and local defects were eliminated. Additionally, the P-wave velocity of the sample was measured by the P-wave velocity measuring instrument, and sandstone samples with similar P-wave velocity were used for the subsequent tests to reduce the test error. Figure 1A shows part of the sandstone samples after processing. Through X-ray diffraction testing (XRD), the material composition and content were as follows: quartz of 78.0%, feldspar of 6.8%, muscovite of 9.4%, and clay minerals of 5.8%. The clay minerals were composed of 76% illite, 21.3% kaolinite and 2.7% smectite, which was a typical medium-coarse sandstone, as shown in Figure 1B.

Figure 1

Figure 1. Sandstone samples and mineral composition.

The AutoPore IV 9520 fully automatic mercury intrusion meter was used to conduct mercury intrusion tests on rock samples^[14]. The results showed that the average porosity of the sandstone was 11.14%. In addition, uniaxial compression tests on sandstone samples were conducted, and the basic physical and mechanical parameters of sandstone were obtained, as shown in Table 1.

Table 1

Table 1. Basic physical and mechanical parameters of coal-bearing sandstone.

According to the composition structure characteristics and basic physical and mechanical properties of rock samples, the mechanical properties of the sample were weak, the pore structure was rich, and the rock mass was nearly weakly cemented (Wu et al., 2024). This type of rock mass is particularly sensitive to freeze-thaw cycles in high-latitude cold areas, especially under conditions with sufficient moisture content (Li et al., 2021; Chen et al., 2024). At present, there are abundant research results on the effects of moisture content on rock deformation and damage mechanisms under the action of freeze-thaw cycles. Existing research has shown that as the moisture content increases, the freeze-thaw cycle is more likely to induce the strength weakening, deformation and failure of the rock mass; Besides, the freeze-thaw cycle has the greatest weakening effect on saturated rocks (Yani et al., 2019; Liu J. et al., 2024). To obtain the weakening effect of freezing temperature and freeze-thaw cycles on coal-bearing sandstone, all rock samples were subjected to saturated treatment.

2.2 Experimental scheme

In this study, the effects of the number of freeze-thaw cycles and freezing temperature on the damage and deterioration of sandstone were mainly examined. The freezing temperature range was set to −5°C ∼ 20°C, −10°C ∼ 20°C, −15°C ∼ 20°C, −20°C ∼ 20°C, the number of freeze-thaw cycles was set to 5, 10, 15, 20. A total of 16 groups of tests were carried out, and eight samples were used for each test. The heating rate and cooling rate were both 0.5 °C/min. Once it reached freezing or thawing temperature (20°C), it was maintained for 2 h to avoid additional stress caused by excessive temperature gradient inside the sample. Figure 2 shows the specific test process.

(1) The sample is placed in a vacuum tank, and the air inside the vacuum tank is extracted to form a negative pressure environment. Open the valve and slowly inject distilled water into the vacuum tank until the water level is below the top of the sample. Continuous vacuum pumping for 24 h to ensure that water completely permeates the pores of sandstone samples.

(2) After vacuum saturation, the P-wave velocity, volume and other physical parameters of sandstone samples before the freeze-thaw cycles were measured by ultrasonic detectors and drainage methods as the control group. Subsequently, rock samples were wrapped with plastic film, and the ends were sealed with wax to ensure a constant state of water saturation within the rock sample.

(3) The saturated sample was put into the freeze-thaw cycles testing machine according to the designed freezing temperature range (such as −5°C∼20°C). Then the setup program was initiated until the desired number of freeze-thaw cycles was completed.

(4) After the completion of freeze-thaw cycles, the P-wave velocity, volume and other physical parameters of the sample were measured.

(5) By using CT scanning imaging technology, a rock core of ϕ 8 mm × 12 mm on the same sample was drilled, and the core was fixed on the sample platform for CT scanning. The visualization software Avizo was used to analyze the changes in pore structure characteristics under freezing temperature (−10°C and −20°C) and number of freeze-thaw cycles (5, 10, and 20).

Figure 2

Figure 2. Test flow chart.

3 Analysis of test results

3.1 Variation characteristics of P-wave velocity of coal-bearing sandstone under freeze-thaw cycles

The P-wave velocity is an important parameter that reflects the internal structural characteristics of the material, and the internal defects of the sample directly affect the P-wave propagation velocity (Zhang et al., 2018; Shen et al., 2020). When the sample contains a higher number of pores, its wave impedance experiences an increase, leading to a decrease in P-wave velocity; conversely, an increase in P-wave velocity is observed when the sample has fewer pores. Since the P-wave velocity of the sample after freeze-thaw cycles is related to the P-wave velocity before freeze-thaw cycles, the relative change rate of the P-wave rate of the sample is introduced to reflect the deterioration effect of the freeze-thaw cycle on the sample. The calculation function is shown in Equation 1.

${\eta }_{\mathrm{p}}=\frac{{\nu }_1-{\nu }_0}{{\nu }_0}\times 100\%(1)$

where η_p is the relative change rate of the P-wave velocity of the sample; ν₁ is the P-wave velocity of the sample after freeze-thaw cycles; ν₀ is the P-wave velocity of the sample before freeze-thaw cycles.

To reduce the impact of discreteness on the test results, the measured data of eight samples in each group were averaged. The test results are shown in Table 2. To analyze the influence of freezing temperature and the number of freeze-thaw cycles on the change of P-wave velocity of the sandstone sample, the relative change rate of P-wave velocity with freezing temperature and cycle number is plotted based on the data in Table 2, as shown in Figure 3.

Table 2

Table 2. Data of P-wave velocity of samples before and after freeze-thaw.

Figure 3

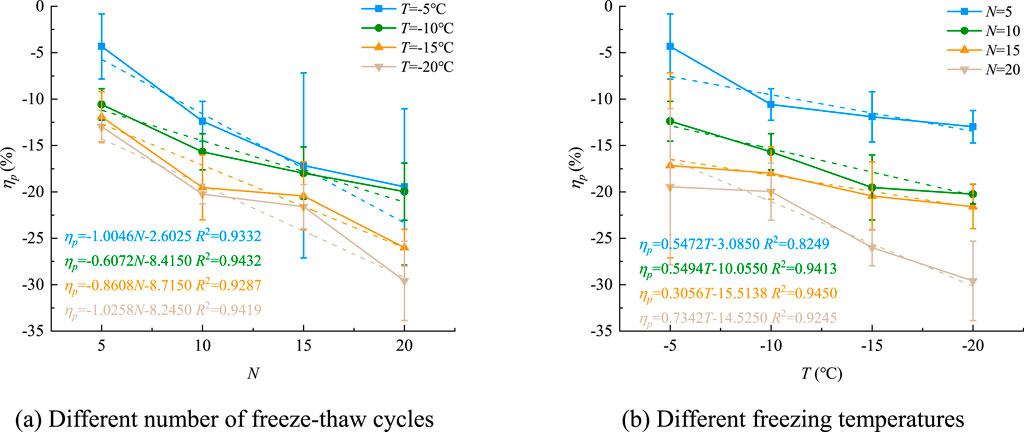
Figure 3. Curve of the relative change rate of P-wave rate with freezing temperature and cycle number. (A) Different number of freeze-thaw cycles (B) Different freezing temperatures.

As shown in Figure 3 and Table 2, ① the P-wave velocity v_p of the sample decreases as the decrease in freezing temperature T and the increase in the number of freeze-thaw cycles N. ② When the freezing temperature T is constant, as the number of freeze-thaw cycles N increases, the average relative change rate of the P-wave velocity before and after freeze-thaw cycles approximately decreases linearly, and its linear fitting correlation coefficient R² is greater than 0.92. ③ When the number of freeze-thaw cycles N is constant, as the freezing temperature T decreases, the average relative change rate of the P-wave velocity of the sample before and after freeze-thaw cycles decreases approximately linearly, and its linear fitting correlation coefficient R² ranges from 0.82 to 0.95. The above test results show that the freeze-thaw cycle has a significant damage and deterioration effect on the coal-bearing sandstone, and as the freezing temperature T decreases and the number of freeze-thaw cycles N increases, the deterioration damage effect is accumulated and intensified. ④ The slope of the fitted straight line a_N changes with the number of freeze-thaw cycles, ranging from −0.6072 to −1.0258, and the slope of the fitted straight line a_T changes with the change of freezing temperature, ranging from 0.3056 to 0.7342, and the absolute value of a_T is relatively small. This indicates that compared with freezing temperature, the number of freeze-thaw cycle is more likely to induce damage and deterioration of coal-bearing sandstone samples.

The above analysis and discussion were conducted on the damage and deterioration effects of freezing temperature and the number of freeze-thaw cycles on coal-bearing sandstone. In fact, these factors mutually influence the damage and degradation processes in coal-bearing sandstone. Figure 4 shows the change surface of the relative change rate of the P-wave velocity of the sample with the parameters of T and N. Figure 4A is the folded surface formed by the data in Table 2 and Figure 4B is the fitting surface of Figure 4A and its fitting function (surface equation):

${\eta }_p=0.0109T^2+0.0261N^2+0.7271T-1.4490N+0.0063NT+3.7819(2)$

Figure 4

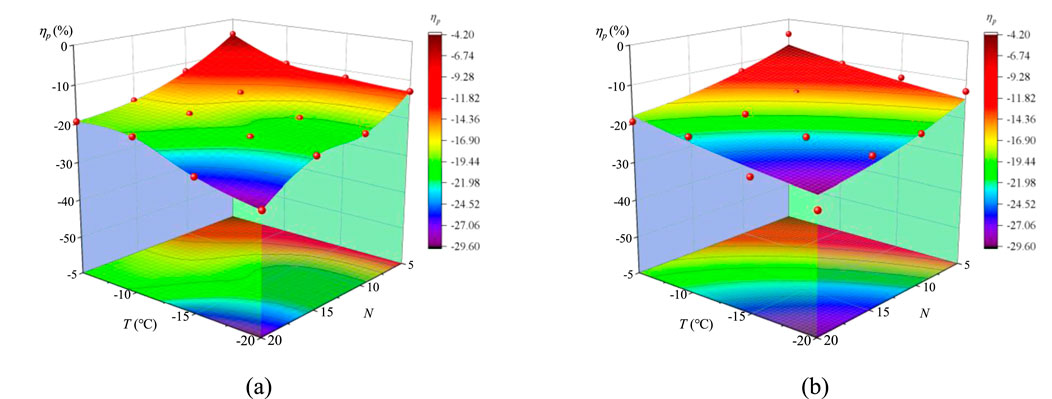
Figure 4. Surface plot of the relative change rate of P-wave velocity ${\eta }_p$ of the sample with the change of $T$ and $N$.

The fitting correlation coefficient R² of Equation 2 is 0.9368.

As shown in Figure 4 and Equation 2, ① η_p as the freezing temperature decreases and the number of freeze-thaw cycles increases, the damage and deterioration effect on the coal-bearing sandstone is increased. ② Examining the changing characteristics of the surface shape with the freezing temperature and the number of cycles, the coefficient values of T², T and N², N in Equation 2 are compared. It can be found that the number of freeze-thaw cycles has a higher deterioration effect on coal-bearing sandstone rather than freezing temperature. ③ The coefficient size of the NT term in Equation 2 reflects the coupling effect of the number of freeze-thaw cycles and freezing temperature. It should be noted that T is a negative value and the NT term is always negative. This indicates that the increase in the number of freeze-thaw cycles or the decrease in freezing temperature can increase the deterioration effect on coal-bearing sandstone.

3.2 Variation characteristics of porosity in the coal-bearing sandstone under freeze-thaw cycles

In addition to the P-wave velocity of the sample, the volume change of the sample is also a significant factor contributing to its degradation and damage under the action of freeze-thaw cycles. The change in sample volume indicates the rock deformation and the change in the internal microstructure. If the volume of the sample increases after freeze-thaw cycles (without considering the deformation effect of the sample matrix), it indicates that the internal porosity of the sample increases (Chu et al., 2023; Feng et al., 2023). In this section, the damage and deterioration effects of freeze-thaw cycles on the coal-bearing sandstone are studied based on the changes in sample volume and porosity. The porosity increment is introduced to reflect the deterioration effect of volume changes before and after freeze-thaw cycles on the sample. Its calculation function is shown in Equation 3.

$\Delta \mathrm{\Phi }=\frac{V_1-V_0}{V_0}\times 100\%(3)$

where ΔΦ is the porosity increment of the sample; V₁ is the volume of the sample after freeze-thaw cycles; V₀ is the volume of the sample before freeze-thaw cycles.

To reduce the impact of discreteness on the test results, the measured data of eight samples in each group were averaged. The test results are shown in Table 3. To analyze the effects of freezing temperature and the number of freeze-thaw cycles on the changes in the P-wave velocity of sandstone, the change curves of porosity increment with freezing temperature and cycle numbers are drawn based on the data in Table 3, as shown in Figure 5.

Table 3

Table 3. Sample volume and porosity increment before and after freeze-thaw cycles.

Figure 5

Figure 5. Change curves of sample porosity increment. (A) Different number of cycles (B) Different freezing temperatures.

As shown in Figure 5 and Table 3, ① the volume V of the sample before and after freeze-thaw cycles increases as the freezing temperature T decreases or the number of freeze-thaw cycles N increases. ② When the freezing temperature T is constant, as the number of freeze-thaw cycles N increases, the average porosity increment of the sample exhibits an approximately linear increase, and its linear fitting correlation coefficient R² is greater than 0.93. ③ When the number of cycles N is fixed, as the freezing temperature T decreases, the average porosity increment of the sample rises approximately linearly, and its linear fitting correlation coefficients R² are greater than 0.8. ④ The slope a_N of the fitted straight line of changes with the number of freeze-thaw cycles, ranging from 0.0864 to 0.1590, and the slope a_T of the fitted straight line changes with the freezing temperature. The variation range of a_T is 0.0332–0.1116, and its absolute value is relatively small. This indicates that the number of freeze-thaw cycles N has a significant effect on the deterioration and damage of coal-bearing sandstone, while the freezing temperature T has a relatively small effect on the deterioration and damage of coal-bearing sandstone.

Figure 6 shows the surface plot of the sample porosity increment $\Delta \varphi$ under the coupling effect of freezing temperature T and number of freeze-thaw cycles N. Figure 6A is the surface plot based on the $\Delta \varphi$ data in Table 3 and Figure 6B shows the fitting surface plot of Figure 6A, and the fitting equation of $\Delta \varphi$ can be expressed as follows:

$\Delta \varphi =0.0026N^2-0.0022T^2+0.1407N-0.0769T-0.0047NT-0.6500(4)$

Figure 6

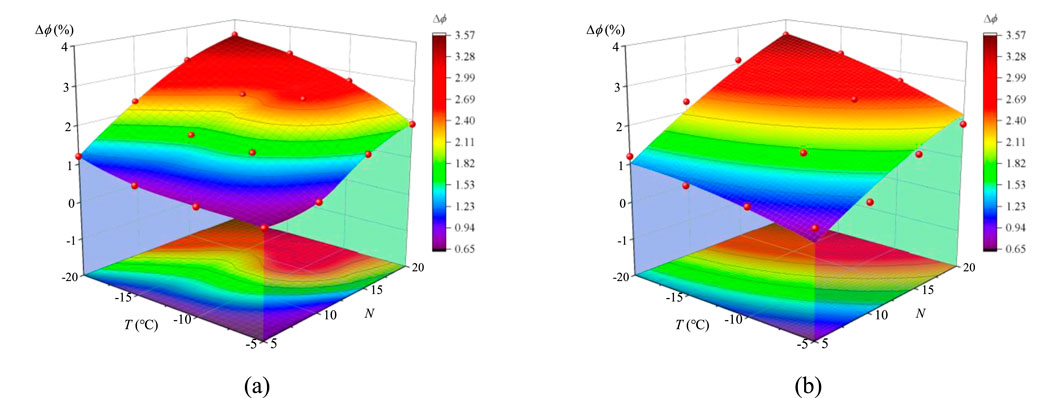
Figure 6. Surface plot of the relative change rate of porosity increment $\Delta \varphi$ of the sample with the change of $T$ and $N$.

The fitting correlation coefficient R² of Equation 4 is 0.9617.

As shown in Figure 6 and Equation 4, ① The porosity increment ∆Φ increases with the decrease of freezing temperature and the increase of cycle numbers. This indicates that the damage and deterioration effect of freezing temperature and cycle numbers on coal-bearing sandstone is enhanced. ② The variation characteristics of the surface shape with freezing temperature and cycle numbers are observed, and the coefficients of T², T, N² and N in Equation 2 are compared. It can be found that the coefficient of variable N is larger than that of variable T, indicating that the number of freeze-thaw cycles has a stronger deterioration effect on coal-bearing sandstone than freezing temperature. ③ The coefficient of the NT term in Equation 2 reflects the coupling effect of the number of freeze-thaw cycles and freezing temperature on the porosity increment ∆Φ of the sample. It is noted that T is negative, and the NT term is always positive, indicating that the increase of the number of freeze-thaw cycles and the decrease of freezing temperature both enhance the damage and deterioration on coal-bearing sandstone.

3.3 Microscopic mechanism of sample pore structure change

Based on the P-wave velocity, volume and other physical parameters of the sample, the change law of the freeze-thaw damage and deterioration of the coal-bearing sandstone with the freezing temperature T and cycle number N is predicted in a macroscopic way. In this section, the pore structure evolution characteristics of coal-bearing sandstone under freeze-thaw cycles were discussed through high-resolution CT microscopy imaging technology to reveal the microscopic mechanism of freeze-thaw damage of coal-bearing sandstone. Table 4 shows the CT test results of sample porosity.

Table 4

Table 4. Porosity of samples.

It can be seen from Table 4: ① When the number of freeze-thaw cycles N increases from 5 to 10, and 20 at the freezing temperature T of −10°C, the porosity ϕ of the sample increases by 1.52% and 3.22%, and the increasing amplitude is 12.4% and 23.4%; ② When the number of freeze-thaw cycles N increases from 5 to 10, and 20 at the freezing temperature T of −20°C, the porosity ϕ increases by 2.87% and 4.26%, with an increase of 22.2% and 26.9%; ③When the number of freeze-thaw cycle N is fixed, the porosity ϕ increases with the decrease of the freezing temperature T. For example, when the number of freeze-thaw cycles N is 5 and the freezing temperature T is between −10°C and -20°C, the increasing amplitude of porosity is 5.6%; when the number of freeze-thaw cycles N is 20, the freezing temperature T is between-10°C∼-20°C, the increasing amplitude of porosity 18.1%; ④ The sample porosity increment given in Table 3 is close to the CT test value, indicating that the data obtained from the freeze-thaw cycle test has high reliability.

Table 5 shows the cross-section and three-dimensional reconstruction of the pore structure of the sample by CT scanning. The black part in the picture represents the pores, and the other gray parts are the matrix structure. It can be seen from Table 5: ① When the freezing temperature is fixed, as the number of freeze-thaw cycles increases, the size and area of the pores in the sample section increase significantly, and the cracks on the surface of the three-dimensional reconstructed image increase significantly; ② When the number of freeze-thaw cycles is fixed, as the freezing temperature decreases, the size and area of the pores in the sample section also increase, and surface cracks in the three-dimensional reconstructed image also increase. It suggests that the freeze-thaw cycle leads to the progressive expansion and generation of internal cracks within the coal-bearing sandstone, resulting in the continuous deterioration of its deformation resistance and strength.

Table 5

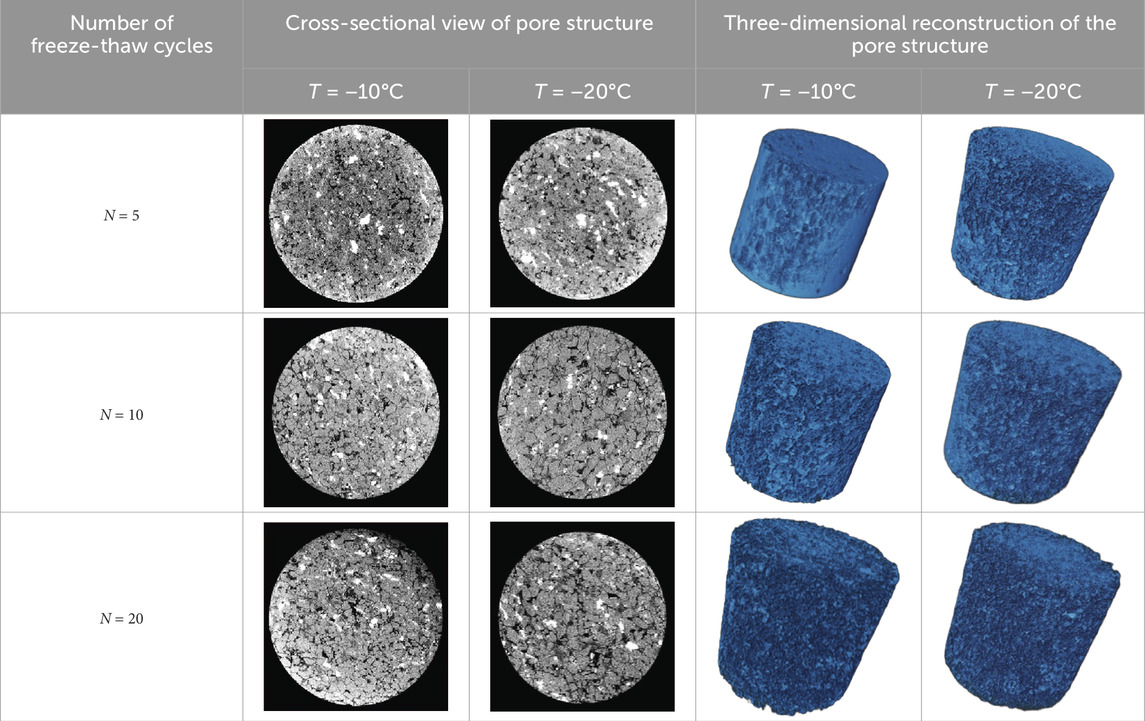
Table 5. Cross-section and three-dimensional reconstruction of the pore structure of the sample by CT scanning.

4 Discussion

4.1 Characterization methods of freeze-thaw damage

A large number of studies have shown that elastic modulus, mass density, porosity (ratio), resistivity, and other parameters can be used to describe or characterize material damage (Yani et al., 2019; Jiang et al., 2024; Liu M. et al., 2024; Liu J. et al., 2024). Elastic modulus is the most commonly used parameter, which is based on Lemaitre’s Strain equivalence principle: the strain caused by the full stress acting on the damaged material is equivalent to the strain caused by the effective stress ε acting on the non-destructive material.

$\epsilon =\frac{\sigma }{E^{\prime }}=\frac{{\sigma }^{\prime }}{E}(5)$

As shown in Equation 5, E and $E^{\prime }$ are the elastic moduli of the undamaged material and the damaged material respectively. However, since rock materials all have initial damage, the elastic modulus E of undamaged rock cannot be obtained. Later, researchers proposed the generalized strain equivalence principle (Zhang et al., 2003):

$\epsilon =\frac{{\sigma }_1}{E_2}=\frac{{\sigma }_2}{E_1}(6)$

where $E_1$ and $E_2$ are the elastic moduli of the material in the two damage states; ${\sigma }_1$ and ${\sigma }_2$ are the stresses in the two damage states. In this study, the state of the sample before freeze-thaw cycles is regarded as the first state, and a certain state of the sample after freeze-thaw cycles is regarded as the second state. Assuming that the damage deterioration of the sample before freeze-thaw cycles and after freeze-thaw cycles can be expressed by the damage factor $D_t$.

${\sigma }_2=\frac{{\sigma }_1}{1-D_t}(7)$

By substituting Equation 6 into Equation 7, we obtain:

$D_t=1-\frac{E_2}{E_1}(8)$

Equation 8 indicates that the damage factor D_t can be obtained as long as the elastic moduli E₁ and E₂ of the sample before and after freeze-thaw cycles are determined through experiments.

It should be noted that E₁ and E₂ in Equation 8 represent the static elastic moduli of the sample before and after freeze-thaw cycles, respectively. However, it is challenging to obtain the deformation and failure process of rock samples during freeze-thaw cycle tests, as well as E₁ and E₂. (Liu et al., 2015) suggested replacing the static elastic moduli E₁ and E₂ in Equation 8 with dynamic elastic moduli E_d and E_d'.

$D_t=1-\frac{E_d^{\prime }}{E_d}(9)$

In Equation 7, E_d and E_d' represent the dynamic elastic moduli of the sample before and after freeze-thaw cycles. The dynamic elastic moduli E_d and E_d' can be indirectly measured using non-destructive testing methods. Consequently, the damage and degradation characteristics of coal-bearing sandstone under freeze-thaw cycles can be obtained.

According to the theory of elastic dynamics, the dynamic elastic modulus E_d of a material has the following relationship with its P-wave velocity v_p, mass density ρ, and Poisson’s ratio μ:

$v_p=\sqrt{\frac{E_d\left(1-\mu \right)}{\rho \left(1+\mu \right)\left(1-2\mu \right)}}(10)$

From Equation 10, we can obtain:

$E_d=\frac{\rho v_p^2\left(1+\mu \right)\left(1-2\mu \right)}{\left(1-\mu \right)}(11)$

Equation 11 is substituted into Equation 9 to obtain the freeze-thaw damage factor, as shown in Equation 12:

$D_t=1-\frac{{\rho }^{\prime }{v^{\prime }}_p^2\left(1+{\mu }^{\prime }\right)\left(1-2{\mu }^{\prime }\right)}{\left(1-{\mu }^{\prime }\right)}\cdot \frac{\left(1-\mu \right)}{\rho v_p^2\left(1+\mu \right)\left(1-2\mu \right)}$

$=1-\frac{{\rho }^{\prime }}{\rho }\frac{{v^{\prime }}_p^2}{v_p^2}\frac{\left(1+{\mu }^{\prime }\right)\left(1-2{\mu }^{\prime }\right)}{\left(1-{\mu }^{\prime }\right)}\cdot \frac{\left(1-\mu \right)}{\left(1+\mu \right)\left(1-2\mu \right)}(12)$

Considering that the influence of Poisson’s ratio is very small during the freeze-thaw cycles, it can be neglected. Therefore, Equation 13 is obtained:

$D_t=1-\frac{{\rho }^{\prime }}{\rho }\frac{{v^{\prime }}_p^2}{v_p^2}(13)$

It can be concluded from Equation 13 that if the P-wave velocity ($v_p$ and $\left.v_p^{\prime }\right)$, mass density ($\rho$ and ${\rho }^{\prime }$) of the sample before and after freeze-thaw cycles are measured, the freeze-thaw damage factor $D_t$ can be easily obtained.

$\frac{{\rho }^{\prime }}{\rho }=\raisebox{1ex}{$\frac{m^{\prime }}{V^{\prime }}$}\!\left/ \!\raisebox{-1ex}{$\frac{m}{V}$}\right.(14)$

where $m$ and $m^{\prime }$ are the mass of the sample before and after freeze-thaw cycles; $V$ and $V^{\prime }$ are the volumes of the sample before and after freeze-thaw cycles, respectively. Considering that during the freeze-thaw cycle test, the sample is sealed with a thin film on the sides and wax on both ends, therefore, the mass of the sample changes little before and after freeze-thaw cycles. As shown in Equation 15,

$\frac{m^{\prime }}{m}\approx 1(15)$

Then Equation 13 can be modified as follows:

$D_t=1-\frac{V}{V^{\prime }}\frac{{v^{\prime }}_p^2}{v_p^2}(16)$

Based on the measured volume and P-wave velocity of the sample before and after the freeze-thaw cycles, the freeze-thaw damage factor $D_t$ can be obtained using Equation 16. The number of freeze-thaw cycles and freezing temperature change the pore structure inside the rock through different degrees of frost heave action, which causes changes in rock volume and P-wave velocity before and after freeze-thaw. Consequently, differences in damage factors can be caused.

4.2 Variation law of freeze-thaw damage factor

By substituting the longitudinal wave velocities v_p, v_p' and volumes V, V′ of the samples before and after freeze-thaw cycles from Tables 2 and 3 into Equation 14, the variation law of the average freeze-thaw damage factor D_t with the freezing temperature and cycle numbers can be obtained. As shown in Table 6, the average freeze-thaw damage factor is positively correlated with the number of freeze-thaw cycles. When the number of freeze-thaw cycles increases from 5 to 20, the average freeze-thaw damage factor D_t of the sample increases by 88.24% at each freezing temperature (0.1896–0.3569, T = −5°C), 82.61% (0.2059–0.3760, T = −10°C), 104.00% (0.2300–0.4692, T = −15°C) and 106.76% (0.2514–0.5198, T = −20°C). The average freeze-thaw damage factor D_t is negatively correlated with the freezing temperature. When the freezing temperature drops from −5°C to −20°C, the increasing amplitude in the average freeze-thaw damage factor of the sample under each freeze-thaw cycle is: 32.59% (0.1896–0.2514, N = 5),58.54% (0.2383–0.3778, N = 10), 28.06% (0.3147–0.4030, N = 15) and 45.64% (0.3569–0.5198, N = 20).

Table 6

Table 6. Variation of freeze-thaw damage factor D_t with freezing temperature and number of freeze-thaw cycles.

According to the data in Table 6, a surface plot of the sample freeze-thaw damage factor D_t with respect to the freezing temperature T and the number of freeze-thaw cycles N is drawn, as shown in Figure 7. Figure 7A shows the surface distribution diagram of the damage factor based on Table 6 and Figure 7B reveals the surface fitting diagram based on Figure 7A, and its fitting equation is described as follows:

$D_t=-0.0003T^2-0.0006N^2-0.0164T+0.0286N-1.6\times {10}^{-5}TN-0.0810(17)$

Figure 7

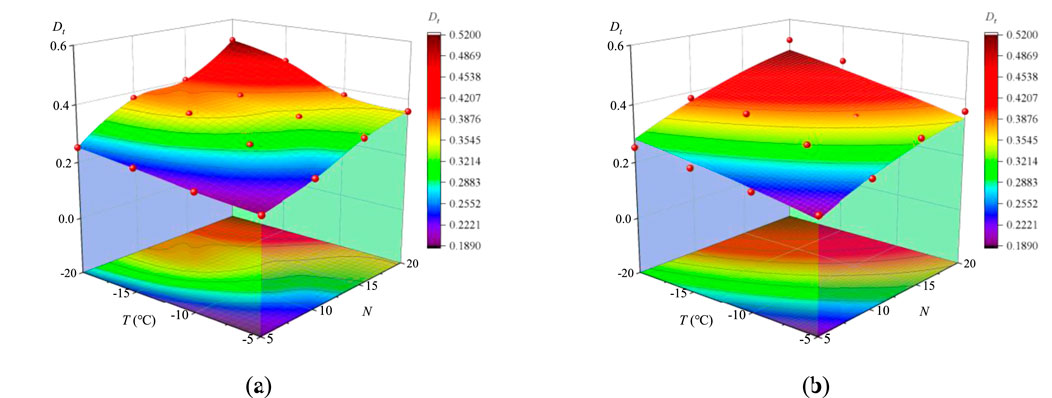
Figure 7. Surface plot of the variation of freeze-thaw damage factor with freezing temperature and number of freeze-thaw cycles.

The fitting correlation coefficient R² of Equation 17 reaches 0.9519. In other words, Equation 17 is approximately the damage evolution equation of coal-bearing sandstone with respect to freezing temperature T and number of freeze-thaw cycles N under freeze-thaw cycles.

From Equation 17, it can be observed that the coefficients of N² and N are larger than those of T² and T, indicating that the number of freeze-thaw cycles N has a higher effect on the freeze-thaw damage and degradation of coal-bearing sandstone than the freezing temperature T; the absolute value of the coefficient of the TN term is 1.6×10⁻⁵, which is much smaller than the coefficients of other terms. This indicates that the coupling effect of the freezing temperature T and the number of freeze-thaw cycles N is relatively weak.

5 Conclusion

(1) The results of the freeze-thaw cycle tests on coal-bearing sandstone show that the P-wave velocity of the sample decreases with the decrease of freezing temperature or the increase of the number of freeze-thaw cycles, and the relative change rate of the P-wave velocity of the sample before and after freeze-thaw cycles approximately linearly decreases with the decrease of freezing temperature or the increase of freeze-thaw cycles. The decrease in the P-wave velocity of the sample indicates that the P-wave propagation impedance in the sample increases. Therefore, the change in the P-wave velocity of the sample effectively reflects the damage degradation effects of freeze-thaw cycles on the coal-bearing sandstone.

(2) The volume of the sample before and after freeze-thaw cycles increases as the freezing temperature decreases, or the number of freeze-thaw cycles increases, and the sample porosity increment increases approximately linearly as the freezing temperature decreases or the number of freeze-thaw cycles increases. The increase in sample volume and porosity reflects the continuous development of internal cracks in the sample, indicating the inherent nature of the damage and deterioration development of coal-bearing sand samples.

(3) With the help of CT scanning imaging technology, the changing rules of porosity and pore structure characteristics of coal-bearing sandstone samples before and after freeze-thaw cycles were obtained. The results show that as the freezing temperature decreases and the number of freeze-thaw cycles increases, the porosity of the sample increases, the number of pores on the specimen cross section increases significantly, and the geometric size increases significantly. This reveals the microscopic mechanism of damage and deterioration of freeze-thaw cycles on coal-bearing sandstone to a certain extent.

(4) Based on Lemaitre’s strain equivalence principle and elastic dynamics theory, a calculation function for the freeze-thaw damage factor based on the P-wave velocity and volume of the sample before and after freeze-thaw cycles is proposed, and an evolution equation of freeze-thaw damage factors based on the freezing temperature and the number of freeze-thaw cycles is established, and the freeze-thaw damage degradation effect of coal-bearing sandstone is effectively characterized.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

YM: Conceptualization, Writing–original draft, Writing–review and editing. ML: Conceptualization, Data curation, Funding acquisition, Writing–original draft, Writing–review and editing. PW: Funding acquisition, Writing–original draft, Writing–review and editing. SG: Conceptualization, Data curation, Writing–review and editing. FZ: Conceptualization, Data curation, Formal Analysis, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (52304102, 52174090 and 52274140).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baldwin, B. A., and Yamanashi, W. S. (1989). Detecting fluid movement and isolation in reservoir core with medical NMR imaging techniques. SPE Reserv. Eng. 4, 207–212. doi:10.2118/14884-pa

CrossRef Full Text | Google Scholar

Berisavljević, Z. (2019). Comments on “Analysis of the effect of freeze-thaw cycles on the degradation of mechanical parameters and slope stability”. B. Eng. Geol. Environ. 78, 1295–1296. doi:10.1007/s10064-017-1048-x

CrossRef Full Text | Google Scholar

Chen, X., Du, W., Chen, L., Ma, B., Gong, S., Jiang, H., et al. (2022). Mechanical strength decay evaluation of excavation unloaded rock mass under freeze-thaw conditions. Appl. Sci. 12, 12205. doi:10.3390/app122312205

CrossRef Full Text | Google Scholar

Chen, Z., Liu, B., Liu, Y., and Xu, J. (2024). Surrounding rock pressure in the tunnel portal section through moraine under freeze-thaw action. J. Mt. Sci.-Engl. 21, 2480–2493. doi:10.1007/s11629-023-8412-z

CrossRef Full Text | Google Scholar

Chu, Y., Zhang, D., Song, S., Ouyang, K., and Liu, F. (2023). Experimental study on the evolution of pore structure of coal samples under freeze–thaw. Phys. fluids 35, 35. doi:10.1063/5.0145187

CrossRef Full Text | Google Scholar

Feng, Q., Hou, S., Liu, W., Zhang, S., Li, W., and Tian, M. (2023). Study on the simulation method and mesoscopic characteristics of rock freeze-thaw damage. Comput. Geotech. 153, 105038. doi:10.1016/j.compgeo.2022.105038

CrossRef Full Text | Google Scholar

Fogue-Djombou, Y. I., Corn, S., Clerc, L., Salze, D., and Garcia-Diaz, E. (2019). Freeze-thaw resistance of limestone roofing tiles assessed through impulse vibration monitoring and finite element modeling in relation to their microstructure. Constr. & Build. Mater. 205, 656–667. doi:10.1016/j.conbuildmat.2019.01.211

CrossRef Full Text | Google Scholar

Jia, S., Yu, Q., Yin, H., Dai, Z., Yin, S., Kong, Y., et al. (2024). Analysis of damage evolution and study on mesoscopic damage constitutive model of granite under freeze–thaw cycling. B. Eng. Geol. Environ. 83, 236. doi:10.1007/s10064-024-03741-7

CrossRef Full Text | Google Scholar

Jiang, H. (2018). The relationship between mechanical properties and gradual deterioration of microstructures of rock mass subject to freeze-thaw cycles. Earth Sci. Res. J. 22, 53–57. doi:10.15446/esrj.v22n1.66108

CrossRef Full Text | Google Scholar

Jiang, X., Xue, Y., Ren, X., Kong, F., and Liao, X. (2024). Dynamic response characteristics and damage calculation method of fractured rock mass under blasting disturbance. Int. J. Impact Eng. 192, 105036. doi:10.1016/j.ijimpeng.2024.105036

CrossRef Full Text | Google Scholar

Jielin, L., Kaunda, R. B., and Keping, Z. (2018). Experimental investigations on the effects of ambient freeze-thaw cycling on dynamic properties and rock pore structure deterioration of sandstone. Cold Reg. Sci. Technol. 154, 133–141. doi:10.1016/j.coldregions.2018.06.015

CrossRef Full Text | Google Scholar

Ke, B., Zhang, C., Liu, C., Ding, L., Zheng, Y., Li, N., et al. (2021). An experimental study on characteristics of impact compression of freeze–thawed granite samples under four different states considering moisture content and temperature difference. Environ. Earth Sci. 80, 661. doi:10.1007/s12665-021-09952-5

CrossRef Full Text | Google Scholar

Li, M., Yu, H., Zhang, J., Lin, G., Zhang, L. Y., Chen, Y., et al. (2023a). Study on dynamic mechanical response characteristics and fracture energy dissipation mechanism of sandstones with different saturations under real-time low temperature. Geomechanics Geophys. Geo-Energy Geo-Resources 9, 77. doi:10.1007/s40948-023-00622-3

CrossRef Full Text | Google Scholar

Li, M., Yu, H., Zhang, J., Lin, G., Zhu, F., Mao, Y., et al. (2023b). Dynamic tensile mechanical properties of thermally damaged sandstone under impact loads and the influence mechanism of composition. Eng. Fract. Mech. 289, 109388. doi:10.1016/j.engfracmech.2023.109388

CrossRef Full Text | Google Scholar

Li, Y., He, X., Sun, H., and Tan, Y. (2021). Effect of freeze-thaw on fatigue damage characteristics of cement emulsified bitumen mastic. Road. Mater. Pavement 22, 1543–1558. doi:10.1080/14680629.2019.1702584

CrossRef Full Text | Google Scholar

Lin, G., Li, M., Chen, Y., Zhang, J., Xu, L., Doan, D. V., et al. (2021). Dynamic tensile mechanical properties and fracture characteristics of water-saturated sandstone under the freezing effect. Int. J. Geomech. 21, 04021044(1)–04021044(16). doi:10.1061/(asce)gm.1943-5622.0001999

CrossRef Full Text | Google Scholar

Liu, J., Xuan, S., and Liu, G. (2024a). A study on the damage evolution law of layered rocks based on ultrasonic waves considering initial damage. Appl. Sci. 14, 9076. doi:10.3390/app14199076

CrossRef Full Text | Google Scholar

Liu, M., Ding, Y., Liu, Y., Zhang, Y., and Cheng, Y. (2024b). Macro-mesoscopic correlation investigation on damage evolution of sandstone subjected to freeze–thaw cycles. Rock Mech. Rock Eng. doi:10.1007/s00603-024-04201-0

CrossRef Full Text | Google Scholar

Liu, Q., Huang, S., Kang, Y., and Hunag, X. (2015). Fatigue damage model and evaluation index for rock mass under freezing-thawing cycles. Chin. J. Rock Mech. Eng. 34, 1116–1127. doi:10.13722/j.cnki.jrme.2023.0163

CrossRef Full Text | Google Scholar

Ma, Q., Ma, D., and Yao, Z. (2018). Influence of freeze-thaw cycles on dynamic compressive strength and energy distribution of soft rock specimen. Cold Reg. Sci. Technol. 153, 10–17. doi:10.1016/j.coldregions.2018.04.014

CrossRef Full Text | Google Scholar

Maji, V., and Murton, J. B. (2020). Micro-computed tomography imaging and probabilistic modelling of rock fracture by freeze-thaw. Earth Surf. Proc. Land 45, 666–680. doi:10.1002/esp.4764

CrossRef Full Text | Google Scholar

Mousavi, S. Z. S., Tavakoli, H., Moarefvand, P., and Rezaei, M. (2020). Micro-structural, petro-graphical and mechanical studies of schist rocks under the freezing-thawing cycles. Cold Reg. Sci. Technol. 174, 103039. doi:10.1016/j.coldregions.2020.103039

CrossRef Full Text | Google Scholar

Niu, C., Zhu, Z., Zhou, L., Li, X., Ying, P., Dong, Y., et al. (2021). Study on the microscopic damage evolution and dynamic fracture properties of sandstone under freeze-thaw cycles. Cold Reg. Sci. Technol. 191, 103328. doi:10.1016/j.coldregions.2021.103328

CrossRef Full Text | Google Scholar

Park, J., Hyun, C., and Park, H. (2015). Changes in microstructure and physical properties of rocks caused by artificial freeze-thaw action. B. Eng. Geol. Environ. 74, 555–565. doi:10.1007/s10064-014-0630-8

CrossRef Full Text | Google Scholar

Park, K., Kim, K., Lee, K., and Kim, D. (2020). Analysis of effects of rock physical properties changes from freeze-thaw weathering in ny-ålesund region: part 1-experimental study. Appl. SCIENCES-BASEL 10, 1707. doi:10.3390/app10051707

CrossRef Full Text | Google Scholar

Ruiz De Argandona, V. G., Rodriguez Rey, A., Celorio, C., Suarez Del Rio, L. M., Calleja, L., Llavona, J., et al. (1999). Characterization by computed X-ray tomography of evolution of the pore structure of a dolomite rock during freeze-thaw cyclic tests. Phys. Chem. earth. Part A, Solid earth geodesy 24, 633–637. doi:10.1016/S1464-1895(99)00092-7

CrossRef Full Text | Google Scholar

Shen, H., Li, X., Li, Q., and Wang, H. (2020). A method to model the effect of pre-existing cracks on P-wave velocity in rocks. J. Rock Mech. Geotechnical Eng. 12, 493–506. doi:10.1016/j.jrmge.2019.10.001

CrossRef Full Text | Google Scholar

Shi, H., Chen, W., Zhang, H., Song, L., Li, M., Wang, M., et al. (2023a). Dynamic strength characteristics of fractured rock mass. Eng. Fract. Mech. 292, 109678. doi:10.1016/j.engfracmech.2023.109678

CrossRef Full Text | Google Scholar

Shi, H., Zhang, H., Chen, W., Song, L., and Li, M. (2023b). Pull-out debonding characteristics of rockbolt with prefabricated cracks in rock: a numerical study based on particle flow code. Comput. Part. Mech. 11, 29–53. doi:10.1007/s40571-023-00607-9

CrossRef Full Text | Google Scholar

Song, R., Wang, Y., Liu, J., Cui, M., and Lei, Y. (2019). Comparative analysis on pore-scale permeability prediction on micro-CT images of rock using numerical and empirical approaches. Energy Sci. & Eng. 7, 2842–2854. doi:10.1002/ese3.465

CrossRef Full Text | Google Scholar

Wang, C., You, R., Lv, W., Sui, Q., Yan, Y., and Zhu, H. (2024). Damage evolution and acoustic emission characteristics of sandstone under freeze-thaw cycles. ACS Omega 9, 4892–4904. doi:10.1021/acsomega.3c08468

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, J., Jing, H., Yin, Q., Yu, L., Meng, B., and Li, S. (2020). Strength prediction model considering material, ultrasonic and stress of cemented waste rock backfill for recycling gangue. J. Clean. Prod. 276, 123189. doi:10.1016/j.jclepro.2020.123189

CrossRef Full Text | Google Scholar

Wu, J., Wong, H., Zhang, H., Yin, Q., Jing, H., and Ma, D. (2024). Improvement of cemented rockfill by premixing low-alkalinity activator and fly ash for recycling gangue and partially replacing cement. Cem. Con. Compos. 145, 105345. doi:10.1016/j.cemconcomp.2023.105345

CrossRef Full Text | Google Scholar

Yang, G., Chen, Y., Xie, Q., Wu, P., and Zhang, Y. (2024). Physical and mechanical characteristics deterioration and crack evolution of sandy mudstone in an open-pit mine under multiple freeze–thaw cycles. Geomechanics Geophys. Geo-Energy Geo-Resources 10, 87. doi:10.1007/s40948-024-00808-3

CrossRef Full Text | Google Scholar

Yani, L., Xinping, L., and Chan, A. (2019). Damage constitutive model of single flaw sandstone under freeze-thaw and load. Cold Reg. Sci. Technol. 159, 20–28. doi:10.1016/j.coldregions.2018.11.017

CrossRef Full Text | Google Scholar

Yu, Q., Lei, P., Dai, Z., Soltanian, M. R., Yin, S., Liu, W., et al. (2022). Damage characteristics of limestone under freeze–thaw cycle for tunnels in seasonal frozen areas. Iran. J. Sci. Technol. Trans. Civ. Eng. 1-9.

Google Scholar

Yuan, S., Jin, J., Liu, X., Li, S., and Liang, B. (2023). The influence of saturation and loading angle on sandstone damage characteristics after freeze-thaw cycle. Geomatics, Nat. hazards risk 14. doi:10.1080/19475705.2023.2250526

CrossRef Full Text | Google Scholar

Zhang, Q., Yang, G., and Ren, J. (2003). New study of damage variable and constitutive equation of rock. Chin. J. Rock Mech. Eng. 22, 30–34.

Google Scholar

Zhang, Y., Wenbo, Y., Peng, C., and Ming, Y.Jianhua (2018). A method to identify blasting-induced damage zones in rock masses based on the p-wave rise time. Geotech. Test. J. 41, 31.

Google Scholar