Yuwei Liu
Yuling Xu- Natural Resources Policy Investigation and Evaluation Center of Jiangxi Province, Nanchang, Jiangxi, China
Colluvial landslides widely developed in mountainous and hilly areas have the characteristics of mass occurrence and sudden occurrence. How to reveal the spatial distribution rules of potential landslides quickly and accurately is of great significance for landslide warning and prevention in the study area. Landslide susceptibility prediction (LSP) modeling provides an effective way to reveal the spatial distribution of regional landslides, however, it is difficult to accurately divide slope units and select prediction models in the processes of LSP modeling. To solve these problems, this paper takes the widely developed colluvial landslides in Dingnan County, Jiangxi Province, China as the research object. Firstly, the multi-scale segmentation (MSS) algorithm is used to divide Dingnan County into 100,000 slope units, to improve the efficiency and accuracy of slope unit division. Secondly, 18 environmental factors with abundant types and clear meanings, including topography, lithology and hydrological environment factors, were selected as input variables of LSP models. Then, a widely representative Support Vector Machine (SVM) and Random Forest (RF) models were selected to explore the difference characteristics of various machine learning models in predicting landslide susceptibility. Finally, the comprehensive evaluation method is proposed to compare the accuracy of various slope unit-based machine learning methods for LSP. The results show that the MSS algorithm can divide slope units in Dingnan County efficiently and accurately. The RF model (AUC = 0.896) has a higher LSP accuracy than that of the SVM model (AUC = 0.871), and the landslide susceptibility indexes (LSI) predicted by the RF model have a smaller mean value and a larger standard deviation than those of the SVM model. Conclusively, the overall performance of RF model in predicting landslide susceptibility is higher than that of SVM model.
1 Introduction
Landslide susceptibility prediction refers to the determination of the spatial probability distribution pattern of landslide occurrence at a specific location based on historical landslide cataloguing data, taking into account the nonlinear coupling effects of multiple disaster-causing environmental factors such as topography, hydrological environment, lithology, and surface coverage (Rohan et al., 2023). It is achieved through various quantitative methods including conventional mathematical statistics and machine learning. Landslide susceptibility prediction (LSP) is to calculate the nonlinear coupling rules of various disaster environmental factors such as topography, hydrology, stratigraphic lithology and land cover on slope evolution on the basis of historical landslide inventory data, using conventional mathematical statistics and machine learning quantitative methods, so as to predict the spatial probability of a specific slope evolving into a landslide. The crux of landslide susceptibility prediction modeling lies in establishing the intricate nonlinear statistical correlations between landslide inventory information and environmental factors (Sameen et al., 2020; Huang et al., 2024a). As of now, landslide susceptibility is among the most popular research topics worldwide. Scholars at home and abroad have attained remarkable achievements in the domain of regional landslide disaster monitoring and prevention and control.
The evaluation of landslide susceptibility began to be quantitatively analyzed after the 1990s. Pack (1985) draws the landslide susceptibility map (LSM) by analyzing the relevant environmental factors in the landslide area, and then using the discrete discrimination of a simple polynomial classification model. Al-Daghastani (1987); Gao (1992) initiated the introduction of remote sensing (RS) and geographic information system (GIS) platforms in the LSP, significantly improving the standardization, accuracy, and efficiency of the LSP. With the in-depth study of various prediction methods, numerous scholars have employed diverse mathematical statistics and machine learning models, such as the analytic hierarchy process (Kayastha et al., 2013; Shahabi et al., 2014), logistic regression (Felicisimo et al., 2013; Althuwaynee et al., 2014), and support vector machines (Kavzoglu and Teke, 2022) in LSP, thereby further enhancing the LSP performance. A Deep-Convolutional Neural Network was used to study the susceptibility of Isfahan Province in Iran with excellent results (Azarafza et al., 2021).
Hua et al. (2021) utilized multi-source and multi-temporal regional landslide monitoring data (such as geological, topographic, hydrological, and remote sensing images, etc.) to disclose the dynamic variation law of landslide susceptibility in the Badong-Zigui section of the Three Gorges Reservoir area over time. Huang et al. (2024a) employed diverse screening approaches to combine environmental factors and chose multiple classical machine learning models to train and test various types of environmental factor combinations in order to investigate the modeling rules of landslide susceptibility. Eventually, a well-developed environmental factor combination system was constructed. Ping et al. (2024) constructed a landslide susceptibility assessment model on the basis of integrating slope units and semantic segmentation methods, attaining the purpose of fully considering the impact of the geometric shape information of slope units on landslide susceptibility. Chang et al. (2023a) innovatively uses MSS method to divide slope units, realizes automatic divide of slope units and improves the prediction accuracy of LSP.
At present, the methods for LSP are increasing day by day, and the prediction accuracy of various machine learning and deep learning models is constantly improving. The selection of prediction units is of vital importance to the application of prediction results, while the intrinsic relationship between environmental factors and landslides remains unclear. Therefore, it is necessary to combine more environmental factors, select appropriate prediction unit, and adopt typical machine learning models to further deepen the research on LSP.
2 Research methods
2.1 LSP modeling process
Landslide susceptibility modeling is to predict and assess the probability and degree of landslide occurrence in a specific area by comprehensively analyzing the landslide inventory data, topography and geomorphology, and other related factors within the study area, using statistical analysis methods and machine learning models. The main modeling process is as follows (As illustrated in Figure 1).
(1) Basic Data Collection: Gather data to obtain the landslide inventory data of Dingnan County, and acquire the necessary data for the study by analyzing attributes such as topographic and geomorphic features, surface coverage, meteorological and hydrological conditions, and stratigraphic lithology.
(2) Extract environmental factors and divide slope units: Select well-defined and diverse hazard-causing environmental factors to construct a spatial data set, and employ the multi-scale segmentation (MSS) method to extract slope units and serve as the basic evaluation unit for the study.
(3) Landslide susceptibility modeling: Two machine learning models, namely, SVM and RF, are chosen for the LSP, thereby obtaining the LSM of the region.
(4) Susceptibility result analysis: An evaluation index system for landslide disaster susceptibility is constructed by analyzing the ROC curve and the distribution of susceptibility indices.
Figure 1. Modelling flow chart of this study.
2.2 The principle of multi-scale segmentation method
The MSS method is an image segmentation technique based on the principle of minimizing regional integration heterogeneity. The fundamental principle is to combine pixels or objects with similar features, such as color, shape, and texture, into continuous, uniform, and closed image objects. This approach aims to achieve the minimum heterogeneity within image objects and maximize the heterogeneity between them, in order to better reflect the actual structure and characteristics of the ground features (Huang et al., 2024e). Moreover, this approach enables the automatic division of slope units on a large regional scale and with high-precision data, significantly enhancing the efficiency of slope unit division.
The procedures of generating slope units by the MSS method mainly comprise basic data processing, acquisition of slope aspect and hill-shade, image segmentation, division of slope units, and post-processing (Yu and Xiong, 2020; Xie et al., 2024b). Firstly, the slope aspect map and hill-shade map are extracted from the DEM data, and the basic characteristics of the terrain are analyzed. Then, the MSS method is employed for image segmentation, merging pixels or objects with similar internal characteristics and significant external differences to form the preliminary main segmentation layer. Finally, in combination with the main segmentation layer, fine division of the slope units is conducted, along with post-processing operations such as smoothing and optimization to enhance the quality and practicability of the units. When generating slope units by applying the multi-scale segmentation algorithm, the selection of parameters is of paramount importance. The main parameters include the settings of scale, spectral factor, shape factor and its weight, compactness and smoothness and their weights (Chang et al., 2023b). These parameter settings directly determine the quality and accuracy of the segmentation results. When selecting parameters, an improved trial-and-error method is employed, combined with the morphological and scale characteristics of the landslide. The optimal parameter combination is sought by calculating relevant quantitative indicators. Specifically, the rationality of the segmentation is verified by comparing the mean and standard deviation of the extracted object with the corresponding values of the landslide area, and by evaluating whether the shape index is within a reasonable range. Additionally, the consistency between the position of the landslide and the position of the image object needs to be evaluated. Eventually, the reliable slope unit is confirmed by the image object that best matches the landslide record. This comprehensive optimization process not only enhances the accuracy and credibility of the ground features, but also provides guidance for the optimization of the multi-scale segmentation algorithm. The entire process is conducted using the eCognition Developer 8.7 software. The specific process is depicted in Figure 2.
Figure 2. Flowchart of slope units division by MSS method.
2.3 Evaluation model for landslide susceptibility
To avoid the uncertain impact of different machine learning models on the evaluation results of landslide susceptibility, it is proposed to adopt the random forest model based on the ensemble algorithm and the support vector machine model based on the kernel algorithm to carry out the research on landslide susceptibility (Wu et al., 2021; Wang et al., 2024).
2.3.1 Random forest model
RF is a potent ensemble learning model. The core concept is to construct multiple decision trees and integrate them to enhance the performance and generalization capacity of the overall model (Sun et al., 2021; Sahin, 2023). RF employs the bagging technique to generate multiple distinct training subsets from the original dataset through bootstrap sampling and constructs decision trees on each subset. When constructing each decision tree, instead of selecting the optimal splitting point from all features, RF randomly selects a portion of features and selects the optimal feature among these for tree splitting. Each decision tree is built based on different features and sample subsets, thereby being discrepant. Each decision tree in RF independently makes judgments and predictions on the input samples. Finally, by integrating the prediction results of all decision trees through methods such as voting or averaging, the final prediction outcome is obtained. Due to the integration of multiple decision trees, RF is typically capable of providing more accurate and stable predictions. The random forest model possesses several remarkable merits: (1) It can effectively mitigate the risk of overfitting and enhance the generalization ability of the model; (2) It demonstrates a considerable tolerance towards outliers and noise and is not readily influenced by individual trees; (3) Owing to the employment of Bagging technology and random feature selection, the random forest does not require feature selection when dealing with high-dimensional data and exhibits a strong adaptability to data sets; (4) The training speed of the model is relatively rapid, being applicable to large-scale data sets.
2.3.2 SVM model
Support Vector Machine (SVM) is a classification algorithm that is widely applied in the domain of machine learning. Its core concept is to seek an optimal hyperplane that maximizes the total distance of support vectors to the hyperplane, thereby separating data points of different classes (Huang et al., 2017; Luo et al., 2019; Huang et al., 2024c). During the training process, SVM emphasizes maximizing the margin between the hyperplane and the support vectors, among which the support vectors are the data points nearest to the hyperplane. This optimization issue can be addressed by means of convex optimization approaches. SVM incorporates regularization parameters to control the complexity of the model and prevent overfitting. SVM exhibits outstanding performance in addressing classification issues in high-dimensional spaces, particularly when the quantity of features far exceeds the number of samples. Suitable kernel functions can be selected based on the requirements of specific problems. Different kernel functions correspond to distinct feature mapping approaches, thereby facilitating the handling of various types of nonlinear problems (Wang et al., 2022).
2.4 Evaluation methods for the accuracy of susceptibility models
2.4.1 ROC curve accuracy
The ROC curve constitutes an essential instrument for assessing the performance of classification models, particularly in binary classification issues (Sun et al., 2020; Xie et al., 2024a). The ROC curve takes the True Positive Rate (TPR) as the ordinate and the False Positive Rate (FPR) as the abscissa, and assesses the accuracy of the model by comparing the performance indicators under different threshold values (Frattini et al., 2010; Pham et al., 2018). The area under the curve (AUC) characterizes the precision of the model, with its numerical range between 0 and 1. The closer the AUC value is to 1, the higher the precision of the model and the more superior its performance. Through the comparison of the magnitudes of AUC values, the performance of different machine learning models can be objectively evaluated. As indicated in Equation 1, where n0 denotes the number of negative samples, n1 indicates the number of positive samples, and ri represents the position sequence of the ith negative sample within the entire test sample.
2.4.2 Distribution law of landslide susceptibility index
The two statistical indicators, namely, the mean value and the standard deviation (SD), can embody the average level and dispersion degree of the LSI (Liu et al., 2022; Huang et al., 2024b). The mean is the average of the LSI prediction set, offering a measurement of the overall trend of the LSI and reflecting the average prediction level of the model for the overall landslide susceptibility. By comparing the magnitudes of the means, the average prediction effect of the model on the entire dataset can be preliminarily evaluated. The calculation method is as shown in Equation 2, where
The SD gauges the degree of dispersion of the LSI. The higher the SD, the lower the uncertainty in LSP and the stronger the ability to identify landslide samples. The calculation method is shown in Equation 3, which
3 Brief introduction of the study area and basic data
3.1 Brief introduction of the study area and basic data sources
Dingnan County is subordinate to Ganzhou City and lies at the southernmost end of Jiangxi Province, with its geographical location ranging from 114°46′ to 115°23′ east longitude and 24°32′to 25°03′ north latitude, as depicted in Figure 3. Dingnan County has a length of approximately 58.4 km in the east-west direction and about 56.2 km in the north-south direction. The landform within the county is dominated by low mountains and hills, and the majority of the altitude ranges from 300 m to 500 m. Dingnan County is affiliated with the mid-subtropical monsoon humid climate region, with an average annual rainfall reaching 1,593 mm. Based on relevant data statistics, during the 30-year period from 1980 to 2010, a total of 735 geological disaster points that occurred or had potential hazards were recorded, among which landslides accounted for as high as 89%, totaling 655. The landslides are mainly distributed in the eastern part of Dingnan County and mountainous areas in other regions. These landslides are mainly composed of accumulative soil landslides. In terms of scale, approximately 85% of the landslides are small shallow soil landslides, and large-scale landslides are relatively rare. The thickness of the soil layer on the slope is approximately between 2.0 m and 8.0 m. The basic data sources of the study area are presented as shown in Table 1.
Figure 3. Location map of Dingnan County.
Table 1. Basic data sources.
3.2 Selection of environmental factors for landslides
In this study, based on the geographical characteristics of the study area and by referring to relevant literature (Dou et al., 2019; Huang et al., 2024d), a total of 18 environmental factors in four categories, namely, topography and geomorphology, stratum lithology, hydrological environment, and surface cover factors, were ultimately selected. They are as follows: (1) Topography and geomorphology factors: elevation, slope, aspect, slope length, plan curvature, profile curvature, surface roughness, topographic relief, and valley depth; (2) Surface cover factors: normalized difference vegetation index, normalized difference built-up index, road density, and total radiation; (3) Hydrological environment factors: average annual rainfall, topographic wetness index, and modified normalized difference water index; (4) Stratum lithology factors: rock and soil types, and fault density. Partial environmental factors are shown in Figure 4.
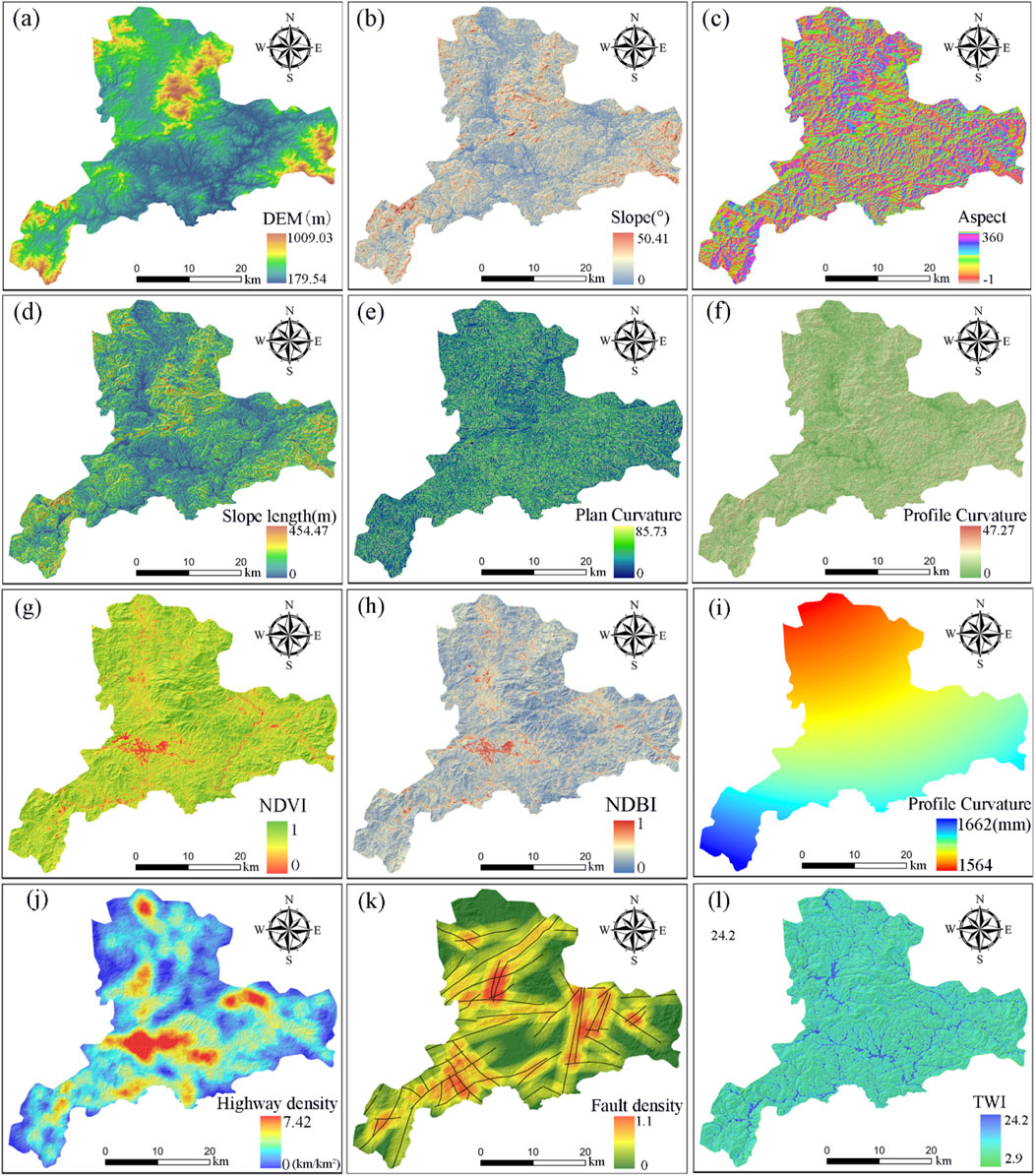
Figure 4. Part of the environmental factor diagram: (A) elevation; (B) Slope; (C) slope direction; (D) Slope length; (E) Plane curvature; (F) profile curvature; (G) NDVI; (H) NDBI; (I) Average annual rainfall; (J) Road density; (K) fault density; (L) topographic humidity index.
3.3 Results of slope unit division
In light of the topographic and geomorphological features as well as the landslide development characteristics of Dingnan County, the conventional trial-and-error approach was employed to establish five different scale magnitudes (10, 15, 20, 25, 30), five distinct shape parameters (0.5, 0.6, 0.7, 0.8, 0.9), and five compactness parameters (0.5, 0.6, 0.7, 0.8, 0.9), altogether constituting 125 parameter combinations. Under each set of parameter combinations, the MSS method was respectively adopted to divide the slope units. Through comparison with the statistical characteristics of the area and shape index of the landslides within the study area, it was discovered that when the parameters of scale, shape, and compactness were set at 20, 0.8, and 0.8 respectively, the division effect of the slope units was the most optimal. Due to the fact that the areas of some initial slope units were relatively small and their shapes were long and narrow, not conforming to the actual circumstances, further processing was conducted on these units. Ultimately, a total of 54,493 slope units in the study area were extracted using the MSS, as depicted in Figure 5.
Figure 5. Division diagram of slope units.
3.4 Construction of landslide susceptibility model
In this research, the SPSS Modeler 18.0 software was utilized for the modeling of the SVM, the widely employed Radial Basis Function (RBF) was chosen, and two significant parameters were determined: the penalty coefficient C and the kernel function parameter γ (Dou et al., 2019; Pham et al., 2019). The C parameter refers to the tolerance for errors. When the value of C is large, the tolerance of the model for misclassifications reduces, the classification margin narrows, and the generalization ability of the model may decline. The γ parameter governs the nonlinearity degree of the SVM model and the complexity of the model. When the value of the γ parameter is relatively large, the fitting degree of the model to the training samples increases and the complexity of the model rises, which might result in overfitting, that is, the model performs well on the training set but poorly on new data.
In order to determine the optimal C and γ parameters, the cross-validation approach was adopted. The dataset was partitioned into n subsets, followed by training the model and conducting evaluations. Subsequently, the results were analyzed to determine the final parameters. Eventually, the penalty coefficient C and the kernel function parameter γ were fixed at 10 and 0.1, respectively. Simultaneously, other parameters in this paper were set to default values to guarantee that the SVM model possessed both adaptability and generalization ability during the establishment process. Meanwhile, an RF model was established by utilizing the sklearn package in Python. Among them, the two parameters, namely, the number of decision trees and the optimal number of features, have a considerable influence on the performance of the model (Merghadi et al., 2020; Xiao et al., 2020). Increasing the number of decision trees in a random forest can improve the model’s accuracy, but it also increases the computing time. The optimal number of features refers to the maximum number of environmental factors considered by each tree during training. Increasing the value of the optimal number of features will increase the variance of the model, which may lead to overfitting; while the optimal number of features being too small may result in an increase in bias, thereby reducing the model’s accuracy. In the research presented herein, the grid search method was employed to determine the optimal parameters. Through defining the parameter range, splitting the dataset, training the model and evaluating the performance of the model, the number of decision trees in the random forest was ultimately determined as 600, the optimal number of features was set at 5, and the remaining parameters adopted the default values.
The well-trained SVM and RF models were applied to the pre-demarcated slope units to obtain the LSI of the study area, whose value range was between 0 and 1. Corresponding LSM were generated, and the natural breaks method was employed to classify the evaluation results of landslide susceptibility into five grades: very high, high, medium, low, and very low.
4 Uncertainty analysis of the modeling results of landslide susceptibility
4.1 The results of LSP based on SVM model and RF model
The results of landslide susceptibility based on the SVM model and the RF model are depicted in Figure 6. On the whole, the LSP results of the SVM and RF models exhibit certain similarities. In terms of the regional scope of susceptibility distribution, there are differences in the delineation of very high and high susceptibility areas between the RF model and the SVM model. Furthermore, the high and very high susceptibility areas identified by the RF model are relatively fewer. This implies that, under the prediction of the RF model, more regions are assessed as areas with lower landslide risk. Such a division might be more consistent with the actual situation, as in reality, landslide incidents tend to be concentrated in a few high-risk areas, while the risk in the majority of areas is relatively low. Consequently, the RF model yields better results in the evaluation of landslide susceptibility.
Figure 6. LSP divie diagram of SVM model and RF model.
4.2 Analysis on the results of LSP
4.2.1 Comparative analysis of AUC precision
In this study, the AUC value was employed as an indicator to assess the prediction accuracy of different models. As depicted in Figure 7, the AUC value of the RF model is 0.896, while that of the SVM model is 0.871. This suggests that in landslide susceptibility modeling, both the SVM and RF models have exhibited relatively good predictive capabilities. The RF model demonstrates superior predictive ability overall compared to the SVM model, which might be attributed to its stronger capacity in handling complex nonlinear relationships and data feature selection.
Figure 7. ROC curves of SVM model and RF model.
4.2.2 Comparison of the distribution of LSP index
In this research, by analyzing the mean and standard deviation of the LSI under the two machine learning models of RF and SVM, the uncertainty issues in the modeling process are explored. The distribution pattern of the landslide susceptibility index is shown in Figure 8. The mean value of the RF model is 0.258, and the mean value of the SVM model is 0.330, indicating that the LSI predicted by the RF model is relatively low. Meanwhile, the SD of the RF model (0.269) is greater than that of the SVM model (0.210), suggesting that the RF model has better discrimination and lower uncertainty when LSP. To sum up, in the process of LSP modeling, the RF model not only has higher prediction accuracy but also has lower uncertainty in assessing the susceptibility among different slope units.
Figure 8. Distribution of landslide susceptibility index: (A) SVM model; (B) RF model.
5 Conclusion
In this paper, by selecting the MSS method to divide slope units and using them as prediction units and choosing the SVM and RF models for LSP modeling, the main conclusions are as follows: The uncertainty laws of the LSP results are consistent. However, the LSP accuracy of the RF model is significantly higher than that of the SVM model, and the uncertainty is lower than that of the SVM model. The LSP accuracy of the RF model is 0.896, and the mean and SD are 0.258 and 0.269, respectively. The LSP accuracy of the SVM model is 0.871, and the mean and SD are 0.330 and 0.210, respectively. It can be seen that the RF model performs better in machine learning and can conduct predictions more effectively. In this study, only the RF and SVM models were utilized to investigate the landslide susceptibility in Dingnan County. In the subsequent research, more environmental factors and models will be employed to conduct a further study on the landslide susceptibility, and different methods will be adopted for its evaluation.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
YL: Writing–original draft, Writing–review and editing. YX: Writing–original draft, Writing–review and editing. JH: Data curation, Writing–review and editing. HL: Software, Writing–review and editing. YF: Validation, Writing–review and editing. YY: Data curation, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Special Fund Project for the Protection and Utilization of Natural Resources in Jiangxi Province in 2025, Subsidy Project for the Construction of the Disaster Prevention and Control System in 2024, Science and Technology Innovation Project of Jiangxi Provincial Department of Natural Resources in 2024 (No. ZRKJ20242413).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Al-Daghastani, N. S. (1987). The application of remote sensing to geomorphological mapping and mass movement study in the vicinity of Provo. Utah: Purdue University.
Althuwaynee, O. F., Pradhan, B., Park, H.-J., and Lee, J. H. (2014). A novel ensemble bivariate statistical evidential belief function with knowledge-based analytical hierarchy process and multivariate statistical logistic regression for landslide susceptibility mapping. Catena 114, 21–36. doi:10.1016/j.catena.2013.10.011
Azarafza, M., Azarafza, M., Akgun, H., Atkinson, P. M., and Derakhshani, R. (2021). Deep learning-based landslide susceptibility mapping. Sci. Rep. 11, 24112. doi:10.1038/s41598-021-03585-1
Chang, Z., Huang, F., and Jiang, S. J. A. E. S. (2023a). Slope unit extraction and landslide susceptibility prediction using multi-scale segmentation method. Adv. Eng. Sci. 55, 184–195.
Chang, Z., Huang, J., Huang, F., Bhuyan, K., Meena, S. R., and Catani, F. (2023b). Uncertainty analysis of non-landslide sample selection in landslide susceptibility prediction using slope unit-based machine learning models. Gondwana Res. 117, 307–320. doi:10.1016/j.gr.2023.02.007
Dou, J., Yunus, A. P., Bui, D. T., Merghadi, A., Sahana, M., Zhu, Z. F., et al. (2019). Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 662, 332–346. doi:10.1016/j.scitotenv.2019.01.221
Felicisimo, A., Cuartero, A., Remondo, J., and Quiros, E. (2013). Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: a comparative study. Landslides 10, 175–189. doi:10.1007/s10346-012-0320-1
Frattini, P., Crosta, G., and Carrara, A. (2010). Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 111, 62–72. doi:10.1016/j.enggeo.2009.12.004
Gao, J. (1992). Modeling landslide susceptibility from a DTM in Nelson County, Virginia: a remote sensing-GIS approach. University of Georgia.
Hua, Y., Wang, X., Li, Y., Xu, P., and Xia, W. J. L. (2021). Dynamic development of landslide susceptibility based on slope unit and deep neural networks. Landslides 18, 281–302. doi:10.1007/s10346-020-01444-0
Huang, F., Li, R., Catani, F., Zhou, X., Zeng, Z., and Huang, J. (2024a). Uncertainties in landslide susceptibility prediction: influence rule of different levels of errors in landslide spatial position. J. Rock Mech. Geotechnical Eng. 16, 4177–4191. doi:10.1016/j.jrmge.2024.02.001
Huang, F., Li, R., Catani, F., Zhou, X., Zeng, Z., Huang, J., et al. (2024b). Uncertainties in landslide susceptibility prediction: influence rule of different levels of errors in landslide spatial position. J. Rock Mech. 16, 4177–4191. doi:10.1016/j.jrmge.2024.02.001
Huang, F., Liu, K., Jiang, S., Catani, F., Liu, W., Fan, X., et al. (2024c). Optimization method of conditioning factors selection and combination for landslide susceptibility prediction. J. Rock Mech. Geotechnical Eng. doi:10.1016/j.jrmge.2024.04.029
Huang, F., Mao, D., Jiang, S.-H., Zhou, C., Fan, X., Zeng, Z., et al. (2024d). Uncertainties in landslide susceptibility prediction modeling: a review on the incompleteness of landslide inventory and its influence rules. Geosci. Front. 101886. doi:10.1016/j.gsf.2024.10188616749871
Huang, F., Xiong, H., Jiang, S.-H., Yao, C., Fan, X., Catani, F., et al. (2024e). Modelling landslide susceptibility prediction: a review and construction of semi-supervised imbalanced theory. Earth-Science Rev. 104700. doi:10.1016/j.earscirev.2024.104700
Huang, J., Fenton, G., Griffiths, D., Li, D., and Zhou, C. (2017). On the efficient estimation of small failure probability in slopes. Landslides 14, 491–498. doi:10.1007/s10346-016-0726-2
Kavzoglu, T., and Teke, A. (2022). Predictive performances of ensemble machine learning algorithms in landslide susceptibility mapping using random forest, extreme gradient boosting (XGBoost) and natural gradient boosting (NGBoost). Arabian J. Sci. Eng. 47, 7367–7385. doi:10.1007/s13369-022-06560-8
Kayastha, P., Dhital, M. R., and De Smedt, F. (2013). Application of the analytical hierarchy process (AHP) for landslide susceptibility mapping: a case study from the Tinau watershed, west Nepal. Comput. and Geosciences 52, 398–408. doi:10.1016/j.cageo.2012.11.003
Liu, L. L., Zhang, Y. L., Zhang, S. H., Shu, B., and Xiao, T. (2022). Machine learning with a susceptibility index-based sampling strategy for landslide susceptibility assessment. Geocarto Int. 37, 15683–15713. doi:10.1080/10106049.2022.2102221
Luo, X., Lin, F., Zhu, S., Yu, M., Zhang, Z., Meng, L., et al. (2019). Mine landslide susceptibility assessment using IVM, ANN and SVM models considering the contribution of affecting factors. PloS one 14, e0215134. doi:10.1371/journal.pone.0215134
Merghadi, A., Yunus, A. P., Dou, J., Whiteley, J., ThaiPham, B., Bui, D. T., et al. (2020). Machine learning methods for landslide susceptibility studies: a comparative overview of algorithm performance. Earth-Science Rev. 207, 103225. doi:10.1016/j.earscirev.2020.103225
Pack, R. (1985). “Multivariate analysis of relative landslide susceptibility,” in Davis county (Logan, Utah: Utah State University).
Pham, B. T., Jaafari, A., Prakash, I., and Bui, D. T. (2019). A novel hybrid intelligent model of support vector machines and the MultiBoost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 78, 2865–2886. doi:10.1007/s10064-018-1281-y
Pham, B. T., Shirzadi, A., Bui, D. T., Prakash, I., and Dholakia, M. (2018). A hybrid machine learning ensemble approach based on a radial basis function neural network and rotation forest for landslide susceptibility modeling: a case study in the Himalayan area, India. Int. J. Sediment Res. 33, 157–170. doi:10.1016/j.ijsrc.2017.09.008
Ping, Z., Siyi, Z., Yu, S., Xudong, R., Ning, W., and Shuheng, Z. (2024). Landslide susceptibility assessment in southern Anhui Province based on slope units and semantic segmentation. Chin. J. Geol. 59, 562–574.
Rohan, T., Shelef, E., Mirus, B., and Coleman, T. (2023). Prolonged influence of urbanization on landslide susceptibility. Landslides 20, 1433–1447. doi:10.1007/s10346-023-02050-6
Sahin, E. K. (2023). Implementation of free and open-source semi-automatic feature engineering tool in landslide susceptibility mapping using the machine-learning algorithms RF, SVM, and XGBoost. Stoch. Environ. Res. Risk Assess. 37, 1067–1092. doi:10.1007/s00477-022-02330-y
Sameen, M. I., Pradhan, B., and Lee, S. (2020). Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 186, 104249. doi:10.1016/j.catena.2019.104249
Shahabi, H., Khezri, S., Bin Ahmad, B., and Hashim, M. (2014). RETRACTED: landslide susceptibility mapping at central Zab basin, Iran: a comparison between analytical hierarchy process, frequency ratio and logistic regression models. Catena 115, 55–70. doi:10.1016/j.catena.2013.11.014
Sun, D., Shi, S., Wen, H., Xu, J., Zhou, X., and Wu, J. (2021). A hybrid optimization method of factor screening predicated on GeoDetector and Random Forest for Landslide Susceptibility Mapping. Geomorphology 379, 107623. doi:10.1016/j.geomorph.2021.107623
Sun, D. L., Wen, H. J., Wang, D. Z., and Xu, J. H. (2020). A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 362, 107201. doi:10.1016/j.geomorph.2020.107201
Wang, Y., Sun, X., Wen, T., and Wang, L. J. B. o.E. G. (2024). Step-like displacement prediction of reservoir landslides based on a metaheuristic-optimized KELM: a comparative study. Bull. Eng. Geol. Environ. 83, 322. doi:10.1007/s10064-024-03819-2
Wang, Y., Tang, H., Huang, J., Wen, T., Ma, J., and Zhang, J. (2022). A comparative study of different machine learning methods for reservoir landslide displacement prediction. Eng. Geol. 298, 106544. doi:10.1016/j.enggeo.2022.106544
Wu, R., Hu, X., Mei, H., He, J., and Yang, J. (2021). Spatial susceptibility assessment of landslides based on random forest:A case study from hubei section in the three Gorges reservoir area. Earth Sci. 46, 321–330.
Xiao, T., Segoni, S., Chen, L., Yin, K., and Casagli, N. (2020). A step beyond landslide susceptibility maps: a simple method to investigate and explain the different outcomes obtained by different approaches. Landslides 17, 627–640. doi:10.1007/s10346-019-01299-0
Xie, J., Huang, J., Zhang, F., He, J., Kang, K., and Sun, Y. (2024a). Enhancing the resolution of sparse rock property measurements using machine learning and random field theory. J. Rock Mech. Geotechnical Eng. 16, 3924–3936. doi:10.1016/j.jrmge.2024.03.016
Xie, J., Zeng, C., Huang, J., Zhang, Y., and Lu, J. (2024b). A back analysis scheme for refined soil stratification based on integrating borehole and CPT data. Geosci. Front. 15, 101688. doi:10.1016/j.gsf.2023.101688
Keywords: landslide susceptibility prediction, machine learning, multi-scale segmentation method, random forest, support vector machine
Citation: Liu Y, Xu Y, Huang J, Liu H, Fang Y and Yu Y (2024) A comparative study of intelligent prediction models for landslide susceptibility: random forest and support vector machine. Front. Earth Sci. 12:1519771. doi: 10.3389/feart.2024.1519771
Received: 30 October 2024; Accepted: 28 November 2024;
Published: 11 December 2024.
Edited by:
Faming Huang, Nanchang University, ChinaReviewed by:
Yankun Wang, Yangtze University, ChinaJiawei Xie, The University of Newcastle, Australia
Copyright © 2024 Liu, Xu, Huang, Liu, Fang and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuling Xu, eHV5dWxpbjEwMzBAMTI2LmNvbQ==