Divergence correction for three-dimensional magnetotelluric forward modelling with arbitrary electrical anisotropy

This paper presents an enhanced framework for three-dimensional (3D) magnetotelluric (MT) forward modeling that incorporates a current density divergence correction procedure for arbitrary anisotropic conditions. The method accelerates the convergence of iterative solvers in solving forward equations in anisotropic media. The divergence correction is adapted from techniques initially developed for isotropic MT modeling. Through four numerical examples—a 1D anisotropic model, a 2D anisotropic model with an infinite lateral fault overlying perfect conductor, a 2D anisotropic model with upper and lower structure and a challenging 3D anisotropic model with random parameters—the validity and efficiency of the proposed approach are demonstrated. The results show that the incorporation of divergence correction significantly reduces the number of iterations required for convergence, improving computational performance and stability. The framework proves robust even in demanding scenarios involving long periods and complex anisotropic structures.

1 Introduction

The magnetotelluric (MT) method is a passive geophysical exploration technique that measures natural electromagnetic (EM) fields at the Earth’s surface. These measurements are employed to infer subsurface resistivity distributions, enabling the mapping of geological structures at depths ranging from tens of meters to several hundred kilometers. In recent years, MT has been widely adopted across various resource exploration areas, including mineral, hydrocarbon, and geothermal exploration (Farquharson and Craven, 2009; Smith, 2014; Patro, 2017), as well as in tectonic studies (Xiao et al., 2017; 2018). Increasing attention has been directed towards electric anisotropy, with numerous three-dimensional (3D) EM forward modeling algorithms now incorporating anisotropic conditions (e.g., Jaysaval et al., 2016; Löwer and Junge, 2017; Wang et al., 2017; Han et al., 2018; Liu et al., 2018; Yu et al., 2018; Cao et al., 2018; Kong et al., 2021; Rivera-Rios et al., 2019; Xiao et al., 2019; Guo et al., 2020; Ye et al., 2021; Bai et al., 2022).

Initially, Smith (1996) observed that in the staggered-grid finite-difference (FD) solution of the magnetotelluric (MT) method, the convergence rate of the iterative solver considerably slowed at low frequencies. Smith attributed this to the reduced significance of the conductivity term in the electric-field equation as frequency decreased, which consequently lessened the necessity for the finite-difference approximation of the electric field corresponding to a divergence-free current density. To address this, Smith introduced a divergence correction technique that significantly improved the convergence rate of the FD solution. This correction procedure was subsequently adopted in other studies (e.g., Sasaki, 2001; Siripunvaraporn et al., 2002; Uyeshima and Schultz, 2000). Farquharson and Miensopust (2011) also applied this divergence correction approach to tackle a similar convergence issue in finite-element (FE) solutions for MT modeling. Notably, these methods were developed for use in isotropic media.

For anisotropic scenarios, several approaches have been proposed to avoid the current density divergence issue mentioned earlier. One such approach involves decomposing the electric field into discrete magnetic vector potential and electric scalar potential components. This transforms the forward equation system of the electric field into the form of vector and scalar potentials, commonly referred to as the A-φ system, which inherently includes the charge conservation equation (Han et al., 2018; Ye et al., 2021; Bai et al., 2022). The A-φ system has also been employed in isotropic cases (Everett and Schultz, 1996; Badea et al., 2001; Stalnaker et al., 2006; Yoshimura and Oshiman, 2002; Mitsuhata and Uchida, 2004; Mukherjee and Everett, 2011; Long, 2024). However, the primary focus here is on the electric-field method.

Liu and Yin (2013) applied a correction scheme similar to Smith’s (1996) to helicopter-borne EM finite-difference (FD) responses under arbitrary electrical anisotropy. Wang et al. (2017) employed this approach for a 3D tensor controlled-source audio-frequency magnetotelluric (CSAMT) FD solution with axial electrical anisotropy. Similarly, Cao et al. (2018) applied divergence correction to solve a 3D axial anisotropic MT forward problem, while Zhou et al. (2021) integrated a divergence correction technique in a 3D finite-element (FE) solver for axially anisotropic MT forward modeling. Xiao (2019) implemented a current density divergence correction method to enhance the convergence of the iterative solution for the 3D FE equation system in arbitrary anisotropic MT forward modeling. Building on this, Cheng et al. (2024) extended the approach by incorporating the divergence correction technique into a 3D MT algorithm that accounts for both electrical and magnetic anisotropy.

From the preceding discussion, it is evident that only a limited number of studies have addressed the issue of divergence correction in electromagnetic (EM) methods under conditions of electric anisotropy. In this paper, we focus on incorporating divergence correction into the FD solution for three-dimensional 3D MT with arbitrary anisotropy. The effectiveness and accuracy of the approach are demonstrated through three numerical examples, and its stability is validated through a highly challenging numerical computation, highlighting the robustness of the forward modeling with the divergence correction procedure. We also examine the impact of the forward iteration interval between successive divergence corrections on the overall computational time.

2 Methods

2.1 Basic theory

The frequency-domain Maxwell’s equations, in the MT quasi-stationary approximation, are in the form of Equations 1, 2,

$\nabla \times \mathbf{E}=i\omega \mu \mathbf{H},(1)$

$\nabla \times \mathbf{H}=\overline{\sigma }\mathbf{E}(2)$

where a time factor e^-iωμ is considered. The magnetic permeability μ is equal to the vacuum value, 4π × 10⁻⁷ H/m. The ω is the angular frequency. E and H denote electric and magnetic fields. In anisotropic medium, conductivity is a tensor expressed as 3 × 3 matrix in Equation 3,

$\overline{\sigma }=\left(\begin{array}{ccc}{\sigma }_{xx}& {\sigma }_{xy}& {\sigma }_{xz}\\ {\sigma }_{yx}& {\sigma }_{yy}& {\sigma }_{yz}\\ {\sigma }_{zx}& {\sigma }_{zy}& {\sigma }_{zz}\end{array}\right)(3)$

This matrix is symmetric and positive definite and can be rewritten with Equations 4, 5,

$\overline{\sigma }={\mathbf{R}}_z\left(\gamma \right){\mathbf{R}}_x\left(\beta \right){\mathbf{R}}_z\left(\alpha \right)\mathbf{\Lambda }{\mathbf{R}}_z^T\left(\alpha \right){\mathbf{R}}_x^T\left(\beta \right){\mathbf{R}}_z^T\left(\gamma \right),(4)$

$\mathbf{\Lambda }=\left(\begin{array}{ccc}{\sigma }_x& & \\ & {\sigma }_y& \\ & & {\sigma }_z\end{array}\right)(5)$

where σ_x, σ_y, σ_z, α, β, γ are three principle conductivity and three rotation angles (Pek and Verner, 1997; Martí, 2014). R_x and R_z are the rotation matrix for rotation around the σ_x and σ_z axis, respectively. In the following, the anisotropic parameters are expressed as σ_x/σ_y/σ_z/α/β/γ.

After some straightforward algebraic operations, we obtain an electric field governing equation,

$\nabla \times \nabla \times \mathbf{E}=i\omega \mu \overline{\sigma }\mathbf{E}(6)$

Based on a FD approximate, this equation can be written as a large linear system,

$\mathbf{A}\mathbf{x}=\mathbf{b},(7)$

where A, x and b respectively denotes coefficient matrix, unknown vector and right side vector. Upon obtaining the solution to Equation 7, H can be obtained via Equation 1.

We have developed a MT forward algorithm for calculating E and H fields on a 3D FD grid. Detailed information on the method can be found in Yu et al. (2018). In that earlier work, Equation 7 was solved using the direct solver PARDISO (Schenk and Gärtner, 2004; Kuzmin, Luisier, and Schenk, 2013). In this study, while the forward modeling framework remains the same as in Yu et al. (2018), the final linear system in Equation 7 is now solved using the preconditioned quasi-minimal residual (QMR) iterative method. The solver terminates when the normalized residual reaches 2 × 10⁻⁸ or the maximum number of iterations is reached. Additionally, we incorporate a current density divergence correction into the forward solution, which will be demonstrated in subsequent sections.

2.2 Current density divergence correction

As described by Smith (1996), the influence of the conductivity term in Equation 6 is weak even for what are considered high frequencies in geophysical electromagnetic methods, and becomes weaker as frequency decreases. Consider an approximate E solution at one certain iterative solution of Equation 7, such E would not satisfy the conservation of charge principle. As noted by Smith (1996), the impact of the conductivity term in Equation 6 is relatively weak, even at what are considered high frequencies in geophysical electromagnetic methods, and diminishes further as frequency decreases. In the case of an approximate E solution at a given iteration of Equation 7, this E would not fully satisfy the conservation of charge principle, which states that,

$\nabla ·\mathbf{J}=0,(8)$

where J is the current density corresponding to the approximate E,

$\mathbf{J}=\overline{\sigma }\mathbf{E}(9)$

The current density divergence cannot vanish. The residual divergence is computed,

$\mathbf{\psi }=\nabla ·\mathbf{J}(10)$

We solve the following divergence equation,

$\nabla ·\left(\overline{\sigma }\left(\nabla \phi \right)\right)=\nabla ·\mathbf{J}=\mathbf{\psi }(11)$

where φ is the static potential used to correct E. It takes too much less computation than solving Equation 7 does. When the static potential φ is determined, the corrected electric field E_c is given by the Equation 12,

${\mathbf{E}}_c=\mathbf{E}-\nabla \phi (12)$

Then, E_c is used as the starting solution for the new iterative loop of Equation 7, which significantly increase convergence of the forward iteration.

2.3 Current density divergence equation system

Figure 1 depicts the locations of the discretized electric fields and current density divergence points. The boundary and internal electric fields are represented by dashed and solid arrows, respectively, as shown in Figures 1A, B. Additionally, Figure 1B indicates that the static potential φ is defined at the grid cross nodes, denoted by cyan circles. With the discretization scheme, Equation 11 is approximated as the following linear equation system,

$\mathbf{D}\phi =\mathbf{t},(13)$

where D denotes the coefficient matrix and t is the right-hand vector composing of each node’s current density divergence computed by Equation 9 and Equation 10.

Figure 1

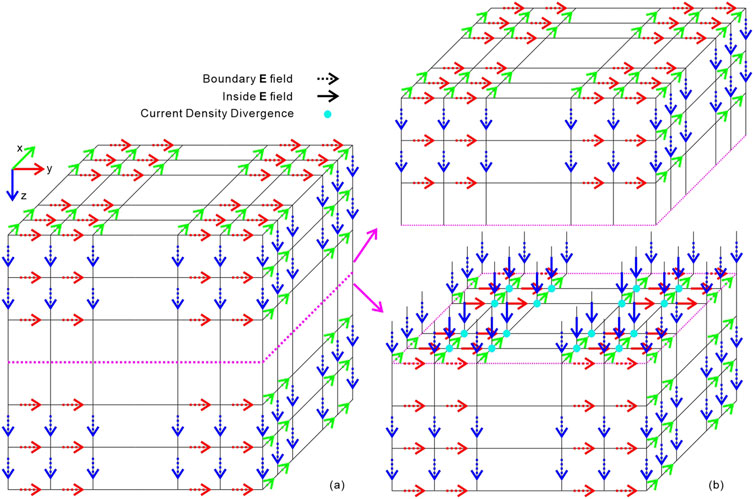
Figure 1. Discretization of electric fields and current density divergence points. (A) Boundary electric fields. (B) Inside electric fields and divergence points shown by separating the model from top to bottom at the plane corresponding to the dashed purple rectangular box.

Figures 2A, B illustrate the distribution of nonzero elements in the coefficient matrix D, discretized for isotropic and anisotropic media, respectively. To clearly present the nonzero element patterns, a simplified model subdivided into 5 (x-axis) × 5 (y-axis) × 9 (z-axis) cells is used. Both matrices exhibit a similar banded diagonal structure of nonzero elements. Due to the presence of 4 air layers within the 9 z-axis cells, the upper-left portion of the pattern in Figure 2B is identical to that in Figure 2A. However, when anisotropy is introduced in the subsurface, the number of nonzero elements increases slightly compared to the isotropic case, as the conductivity is represented by a 3 × 3 tensor in Equation 11. Equation 13 is solved using a preconditioned QMR iterative method with an incomplete LU preconditioner. Compared to solving Equation 7 for the electric field, the iterative solution of Equation 13 is more straightforward for this method.

Figure 2

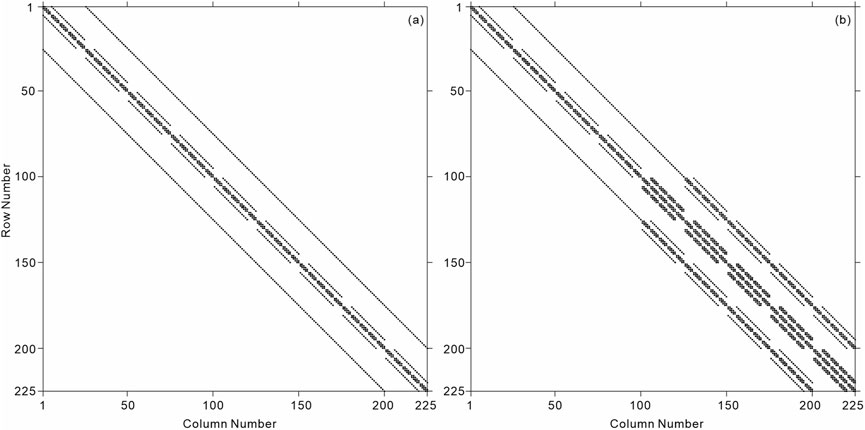
Figure 2. Nonzero element pattern of the coefficient matrix of the divergence correction linear equation. (A) Isotropy. (B) Anisotropy.

3 Numerical examples

In this section, three synthetic models in section 3.1, 3.2 and 3.4.1 are discretized on a 28 × 47 × 60 grid (along the x, y, and z-axis). The model discussed in Section 3.3 is discretized into a 28 × 88 × 120 grid, with the y- and z-axis dimensions matching those of the 2D model presented by Pek (as detailed in Section 3.3). The computational complexity of these models increases progressively. Both 1D and 2D anisotropic models are utilized to demonstrate the effectiveness of accelerating iterative convergence. The accuracy of the forward results is verified by comparison with analytical, quasi-analytical and numerical solutions. The last numerical example illustrates the stability of our forward framework, which incorporates the divergence correction procedure, in a highly challenging scenario involving a long-period computation and a random 3D fully anisotropic model. Furthermore, the impact of the interval between divergence corrections is analyzed in Section 3.4.2. All computations were performed on a PC equipped with 32 GB of RAM and two Intel (R) Xeon (R) Gold 5,218 CPUs (2.10 GHz).

In a 2D isotropic scenario, the polarizations in the north and east directions are commonly referred to as TE and TM modes, respectively. However, in a 3D anisotropic medium, these modes are not decoupled. In this paper, the polarizations in the north and east directions are designated as Mode1 and Mode2, corresponding to the TE and TM modes in the 2D case, respectively.

3.1 1D anisotropic model

Figure 3A illustrates a 1D model consisting of five anisotropic layers with significant variations, which was previously utilized in Yu et al. (2018). Figure 3B presents the iteration details for the forward solution at a period of 1325 s, with the divergence correction procedure applied every 100 iterations. Without divergence correction, convergence is achieved after 281 and 266 iterations for the Mode1 and Mode2 modes, respectively. In contrast, with divergence correction, the Mode1 and Mode2 residual curves reach their final levels after only 171 and 138 iterations. The iterative residuals exhibit significantly improved convergence after applying divergence correction in both Mode1 and Mode2 computations. Additionally, the total computational time is reduced from 186.467 s to 136.000 s with the incorporation of divergence correction. Figure 3C compares our results with the analytical solutions of Pek and Santos (2002), showing a high degree of agreement, consistent with the results from Yu et al. (2018).

Figure 3

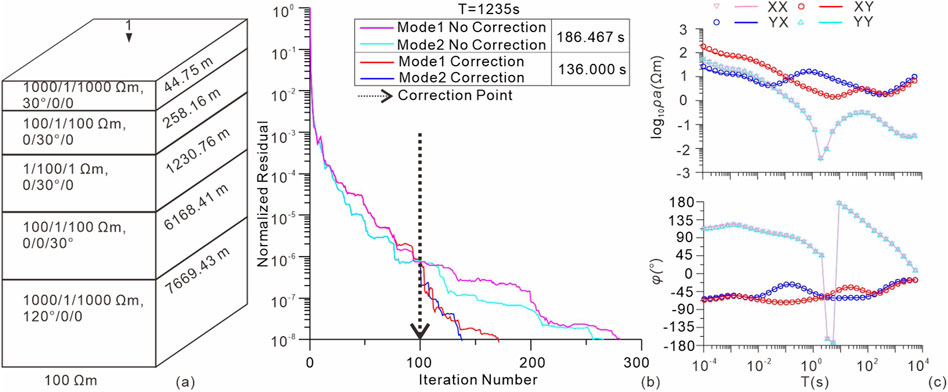
Figure 3. 1D numerical example. (A) 1D anisotropic model with five layers. Six anisotropic parameters are expressed as σ_x/σ_y/σ_z/α/β/γ. (B) Iterative information. Purple and cyan curves denote iterative information of Mode1 and Mode2 solutions, respectively, without applying divergence correction. Red and blue curves denote iterative information of Mode1 and Mode2 mode solutions, respectively, with applying divergence correction. The dashed line show the point when divergence correction is applied. The total computational time is 186.467 s without divergence correction and 136.000 s with divergence correction. (C) Comparison of the apparent resistivity and phase between the 3D numerical and 1D analytical solutions. The scattered points and solid lines indicate 1D analytical and 3D numerical results, respectively.

3.2 2D anisotropic model with infinite fault overlying a perfect conductor

As shown in Figure 4A, the model represents an infinite lateral fault with axially anisotropic conductivity structures overlying a perfect conductor, for which quasi-analytical MT solutions are available (Qin and Yang, 2016). Since a resistivity value of zero cannot be used in our numerical computations, a very low resistivity value of 10⁻⁵ Ωm is assigned to approximate the perfect conductor. All other electrical and geometrical parameters are set according to the model of Qin and Yang, 2016.

Figure 4

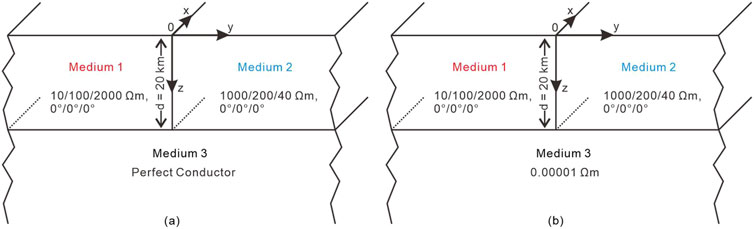
Figure 4. 2D model. (A) 2D model with a lateral infinite fault overlying a perfect conductor (Qin and Yang, 2016). (B) 2D model with a lateral infinite fault overlying a high conductor. A very low resistivity value of 10⁻⁵ Ωm is assigned to approximate the perfect conductor.

Figure 5 shows the iterative information of Mode2 mode at period 1,000 s. The divergence correction procedure works every 100 iterations. In the absence of divergence correction, the normalized residual decreases slowly, reaching only 7 × 10⁻⁷ by the 500th iteration (the maximum iteration number). However, similar to the previous example, convergence (10⁻⁸) is achieved rapidly with the application of the divergence correction procedure, requiring only 253 iterations. After the 100th and 200th iterations, the residual drops by nearly an order of magnitude following each application of divergence correction. The computation time is significantly reduced from 157.681 s to 98.500 s with the addition of divergence correction. This correction procedure notably accelerates the iterative solution of the forward problem.

Figure 5

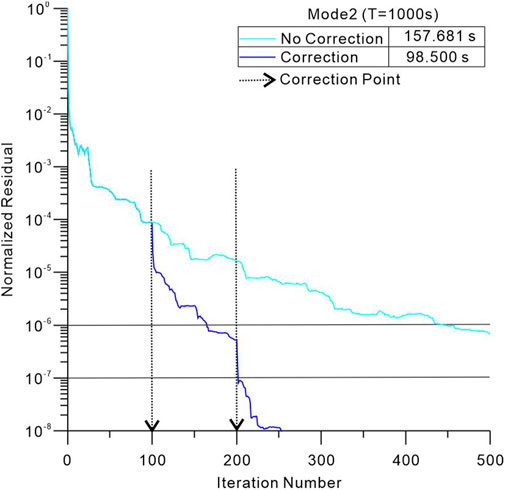
Figure 5. Iterative information of the Mode2 mode solution for 2D model (Figure 4) at a period of 1000 s. The blue and cyan curves denote the case with and without the application of divergence correction procedure, respectively. The total computational time is 157.681 s without divergence correction and 98.500 s with divergence correction.

Fourteen observation points are selected perpendicular to the infinite fault on both sides. As shown in Figure 6, the comparison of apparent resistivity and phase at a period of 10 s with quasi-analytical solutions (from Qin and Yang, 2016) indicates a strong agreement between our results (red circles) and the analytical solutions (blue squares). In Figure 7, two observation points, located on opposite sides of the infinite fault at an equal distance of 50 m, are selected to display the apparent resistivity and phase at different periods. The periods, ranging evenly from 10⁻³–10⁴ s, are referenced from Qin and Yang, 2016. As demonstrated in Figure 7, our results (red and blue circles) closely match the analytical solutions (red and blue squares). The comparisons presented in Figures 6, 7 validate the accuracy of our forward computations incorporating the divergence correction procedure.

Figure 6

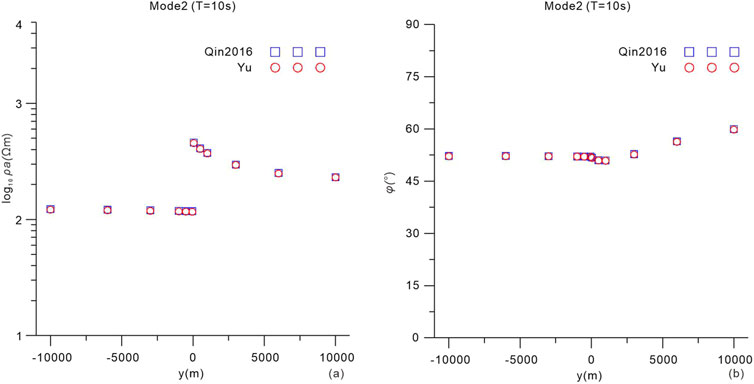
Figure 6. Comparison of the apparent resistivity (A) and phase (B) values perpendicularly across the fault between 3D numerical and quasi analytical (Qin and Yang, 2016) solutions at a period of 10 s.

Figure 7

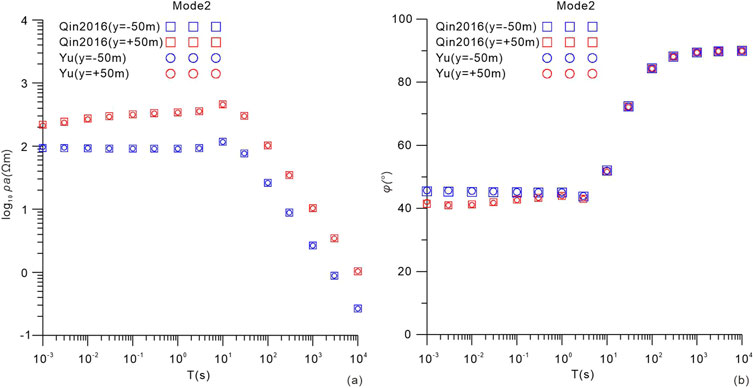
Figure 7. Comparison of the apparent resistivity (A) and phase (B) values of two observation points located on the opposite sides of the infinite fault at an equal distance of 50 m (y = −50 m and y = 50 m). The period varies from 10⁻³–10⁴ s.

3.3 2D anisotropic model with upper and lower structure

Figure 8A illustrates a classic 2D anisotropic model featuring upper and lower structure. The background resistivity is defined as 300 Ωm. The upper anisotropic body extends from 0.300 km to 5.943 km in depth, with a width of 2.260 km. The lower layer, which is in contact with the upper body, consists of a 9.600 km thick anisotropic layer. This model, initially presented by Pek and Verner (1997), was used to investigate the Phase Rolling Out of Quadrant (PROQ) phenomenon (Heise and Pous, 2003; Yu et al., 2019). Numerical solutions at the model’s center were provided by Pek’s 2D program (personal communication, 2017). As shown in Figures 8B, C, the comparison between Pek’s 2D results and our 3D numerical solutions further validates the accuracy of our algorithm, demonstrating high consistency.

Figure 8

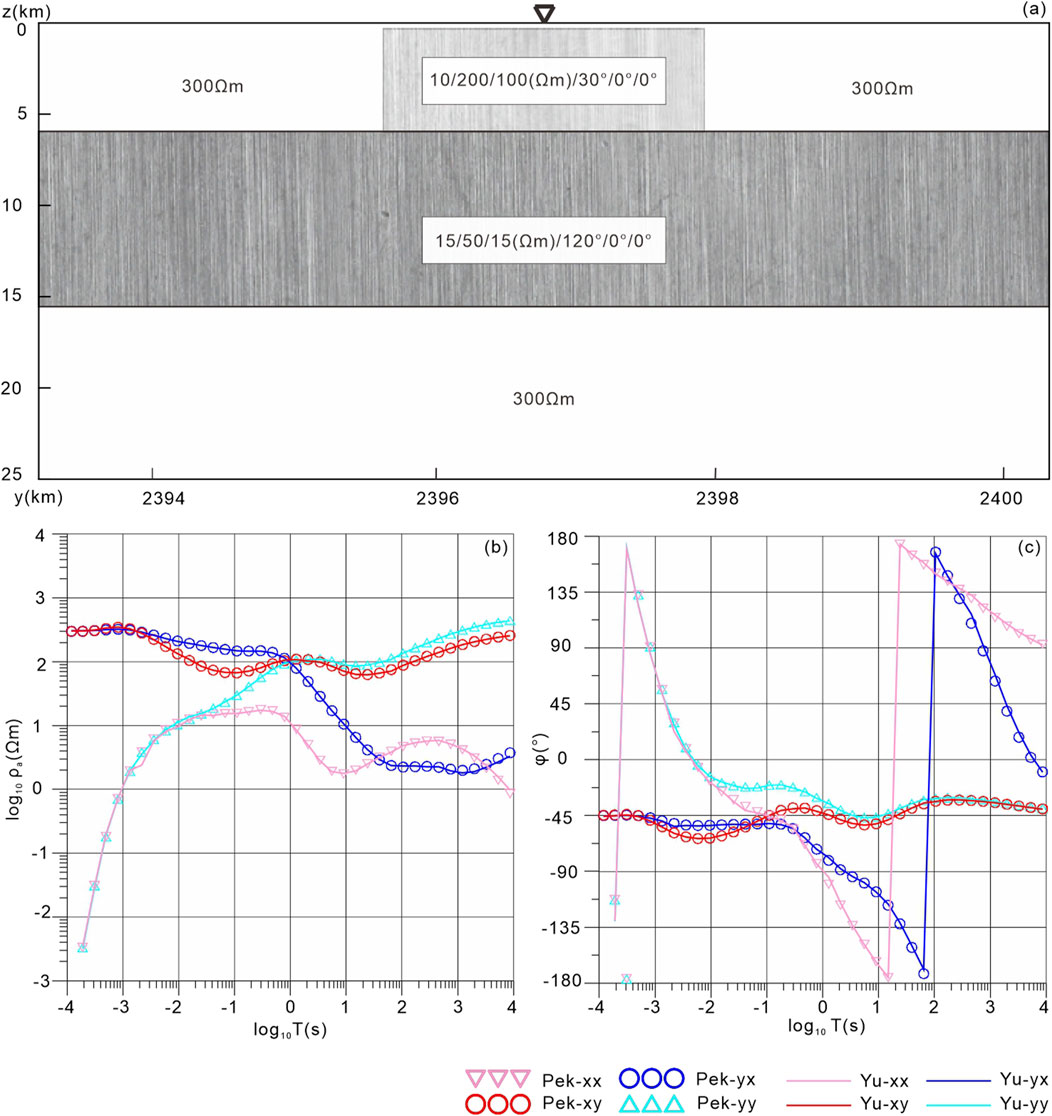
Figure 8. 2D model. (A) 2D model with upper and lower structure. (B) and (C) Comparison of apparent resistivity and phase between the 2D numerical results (Pek) and the 3D numerical results (this study) at the surface central point.

3.4 3D anisotropic model with random parameters

3.4.1 Robustness

An exceptionally complex model is designed to simulate a structure that is likely more challenging than what would typically be encountered in real-world scenarios. Six anisotropic parameters of each cell is defined randomly. As illustrated in Figure 9, a horizontal (red dashed line) and a vertical (blue dashed line) profile are selected to display the parameter distributions. Figures 10, 11 show that the three principal resistivity values range from 10⁻⁴ to 10⁴ Ωm, while the three rotation angles vary from 0° to 180°, respectively. The long period (10,000 s) and significant variations in the principal resistivity values exacerbate the ill-condition of the coefficient matrix A in Equation 7, thereby making convergence in the computations more difficult. We assert that this challenging numerical example serves as a rigorous test of the algorithm’s stability under extreme conditions. In this case, the maximum number of iterations is set to 10,000 to ensure that the forward iteration without divergence correction achieves an acceptable level of convergence.

Figure 9

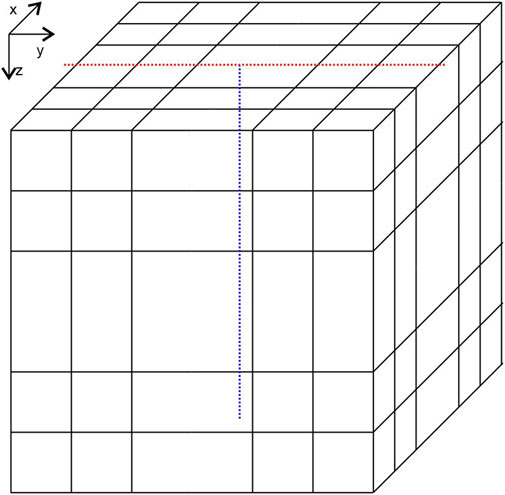
Figure 9. 3D model assigned with random anisotropic parameters. The red and blue dashed line denotes a horizontal and a vertical profiles selected to display the distribution of anisotropic parameters.

Figure 10

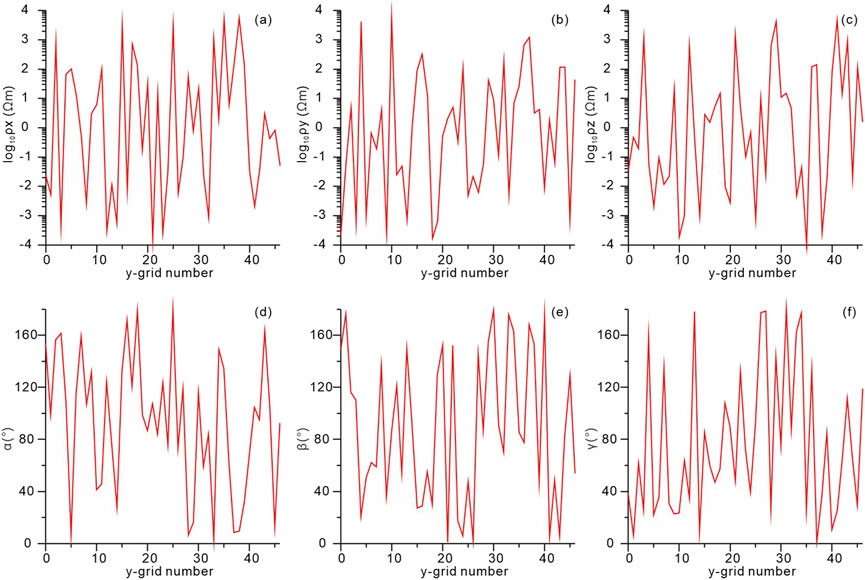
Figure 10. Distribution of six anisotropic parameters along the horizontal profile in 3D random model from Figure 9. (A) Distribution of ρ_x versus grid number in y-axis. (B) Distribution of ρ_y versus grid number in y-axis. (C) Distribution of ρ_z versus grid number in y-axis. (D) Distribution of α versus grid number in y-axis. (E) Distribution of β versus grid number in y-axis. (F) Distribution of γ versus grid number in y-axis.

Figure 11

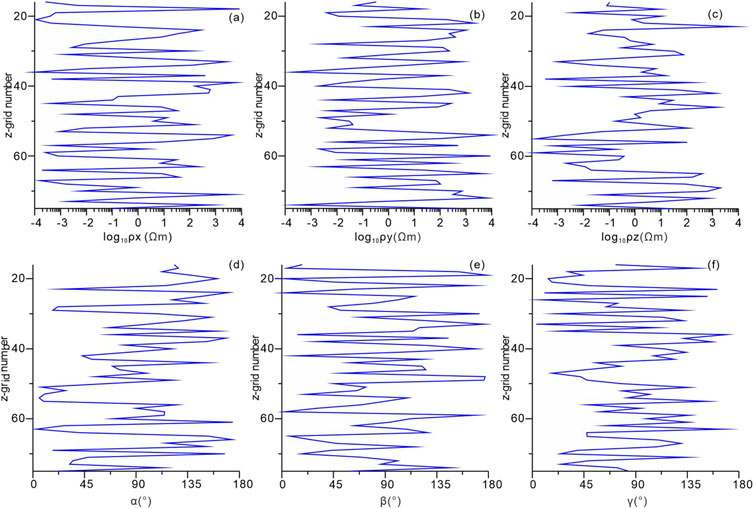
Figure 11. Distribution of six anisotropic parameters along the vertical profile in 3D random model from Figure 9. (A) Distribution of ρ_x versus grid number in z-axis. (B) Distribution of ρ_y versus grid number in z-axis. (C) Distribution of ρ_z versus grid number in z-axis. (D) Distribution of α versus grid number in z-axis. (E) Distribution of β versus grid number in z-axis. (F) Distribution of γ versus grid number in z-axis.

Figure 12A shows the iterative information. Without the application of divergence correction, the normalized residuals for the Mode1 and Mode2 modes decrease to 2.70 × 10⁻⁸ and 3.71 × 10⁻⁸, respectively, after 10,000 iterations. Seen from Figure 12B, following the 100th iteration, 900 additional iterations only result in a reduction of about two orders of magnitude. The residuals approach the termination criterion at the maximum of 10,000 iterations, with a total computation time of 4,417.662 s. The convergence of the residuals for both the Mode1 and Mode2 modes is exceedingly slow.

Figure 12

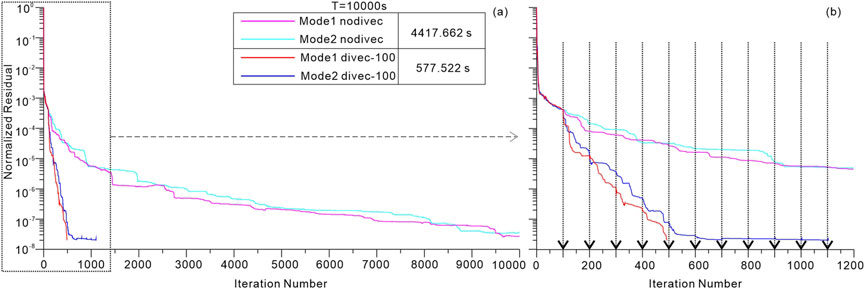
Figure 12. (A) Iterative information of the Mode1 and Mode2 mode solutions for 3D random model (Figure 9) at a period of 10,000 s. Purple and cyan curves denote iterative information of Mode1 and Mode2 solutions, respectively, without applying divergence correction. Red and blue curves denote iterative information of Mode1 and Mode2 mode solutions, respectively, with applying divergence correction. The dashed line shows the point when divergence correction is applied. The total computational time is 4,417.662 s without divergence correction and 577.522 s with divergence correction. (B) Details for the initial 1,200 iterations of (A).

In contrast, each application of divergence correction results in at least a one order of magnitude reduction (as indicated by the black dashed lines with arrows), significantly accelerating the iterative solution process with only 577.522 s. The residuals for the Mode1 and Mode2 modes finally reach 2.00 × 10⁻⁸ and 1.96 × 10⁻⁸ after 494 and 1,103 iterations, respectively, both basically satisfying the accuracy requirements around the 500th iteration. This challenging numerical example, characterized by the significant variation in anisotropic parameters and long period, demonstrates the stability of our MT forward modeling when integrated with the divergence correction procedure.

3.4.2 Interval of divergence correction

In the previous synthetic examples, the interval between successive divergence corrections, denoted as Nc, was consistently set to 100 forward iterations. These examples, particularly Figure 12A, demonstrate significant acceleration. However, while solving for divergence correction is computationally less demanding than forward computations, excessively frequent corrections can substantially increase the overall computation time in complex scenarios. Conversely, overly sparse divergence corrections may fail to effectively enhance the convergence rate of the forward iteration. Hence, an optimal interval Nc must be determined to balance the trade-off between iterative acceleration and the additional time required for divergence correction.

As illustrated in Figure 13A, a range of Nc values (50, 100, 150, 200, 300, 400) were tested. The dashed and solid lines represent the Mode1 and Mode2 iterations, respectively. Most curves achieve convergence within 1,000 iterations. Generally, more frequent divergence corrections result in fewer forward iterations needed for convergence, which is both reasonable and expected. However, as shown in Figure 13B, the minimum total computation time (444.355 s) occurs at Nc = 150, rather than at Nc = 50. This finding highlights that selecting an optimal Nc value enhances the efficiency of the forward framework with divergence correction, even though all curves in Figure 13A already demonstrate much faster convergence compared to the case without divergence correction (Figure 12A).

Figure 13

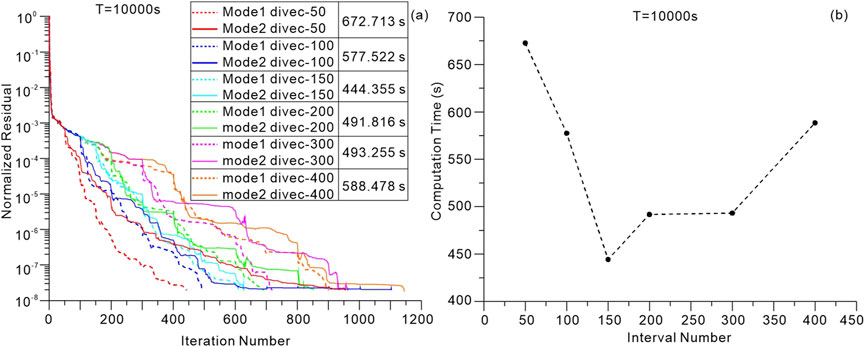
Figure 13. Interval Nc of forward iterations between successive divergence correction. (A) The total computational time is 672.713 s with Nc = 50 (red curves), 577.522 s with Nc = 100 (blue curves), 444.355 s with Nc = 150 (cyan curves), 491.816 s with Nc = 200 (green curves), 493.255 s with Nc = 300 (purple curves), 588.478 s with Nc = 400 (orange curves). (B) Distribution of the computational time with respect to the interval number Nc.

4 Discussion

Smith (1996) conducted pioneering work that significantly advanced iterative isotropic MT forward modeling, particularly in the context of limited computational resources at the time. This advancement proved especially valuable for MT forward computations at long periods, which are crucial for investigating deep earth’s structure. Since the divergence of a curl is identically zero, applying the divergence operator to the governing Equation 6 imposes the constraint described by Equation 8, which ensures the conservation of current density. However, Smith (1996) highlighted a critical limitation: as the frequency ω approaches zero, the only term in Equation 6 that carries information about the conductive structure (the right-hand side) vanishes. Consequently, although Equation 6 can be iteratively solved to a relatively low approximate error, the divergence condition in Equation 8 is not inherently satisfied at long periods. This failure undermines the accuracy of the approximate solution, particularly in reconstructing the correct charge distribution across interfaces with conductivity contrasts, thereby impeding iterative convergence. This issue was first addressed by introducing a static divergence correction (Smith, 1996), which enforces Equation 8 and significantly accelerates the convergence of Equation 6.

With the rapid advancement of computational techniques, various numerical methods have been employed to investigate increasingly complex structures, as discussed in Section 1, “Introduction”. In this study, the static divergence correction has been effectively integrated into the iterative MT forward modeling process to address fully anisotropic scenarios. Notably, we introduce, for the first time, an exceptionally complex model with randomly assigned anisotropic parameters. This novel approach is designed to closely emulate the inherent complexity of real-world scenarios, providing a rigorous test for the robustness and efficiency of our algorithm under challenging computational conditions.

While direct solvers, such as PARDISO, have become increasingly popular in recent years due to their convenience and reliability in solving forward problems, iterative methods retain a distinct advantage, particularly for large-scale computations performed on standard PCs. Iterative methods require significantly less memory compared to direct solvers. However, the primary challenge of incorporating divergence correction into iterative methods lies in the complexity of the implementation. This involves carefully managing the spatial locations of electric fields and divergence points, discretizing the divergence correction equation, etc. Despite these challenges, successfully integrating divergence correction into the iterative process enables substantial reductions in computational costs, making it a highly efficient solution for large-scale forward modeling.

5 Conclusion

The fundamental theory and technical aspects of the current density divergence correction procedure are well-established, having been originally applied in isotropic MT modeling. In this paper, we extend its application to 3D MT forward modeling under arbitrary anisotropic conditions. Three numerical examples are presented to demonstrate the performance of our framework, which integrates the divergence correction procedure.

In the first example, we compute the 3D results for a 1D model comprising five anisotropic layers. In the second and third example, we calculate the 3D results for a 2D anisotropic model with an infinite lateral fault overlying a perfect conductor and with an upper and lower structure. In both cases, the 3D forward results are compared with 1D analytical, 2D quasi-analytical and 2D numerical solutions, confirming the accuracy of our algorithm. For the first case, the corrected computation requires approximately half the iterations compared to the uncorrected case. In the second example, the case utilizing divergence correction converges after 253 iterations, whereas the uncorrected case fails to converge within the maximum of 500 iterations. The third example further verifies the accuracy of our algorithm. These three examples highlight the effectiveness of the divergence correction procedure, demonstrating a significant acceleration in iterative convergence.

In the final example, we introduce a challenging numerical problem involving a long period (10,000 s) and a fully anisotropic model with randomly assigned parameters. The effectiveness of the correction procedure is further validated in this scenario. The case with divergence correction (Nc = 100) achieves the target residual with 577.522 s, while the uncorrected case eventually reaches an accepted residual close to 10⁻⁸ after 10,000 iterations (the maximum allowed), with 4,417.662 s. Due to the divergence correction, the total computational time consuming significantly drops by 86.9%. This confirms that our 3D MT forward modeling framework, coupled with the divergence correction procedure, exhibits robust stability even in complex numerical computations. Furthermore, the analysis of varying Nc intervals between successive forward iterations reveals that selecting an optimal Nc value significantly enhances the efficiency of the forward framework incorporating divergence correction.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

GY: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. JH: Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research is supported by National Natural Science Foundation of China (42204073).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Badea, E. A., Everett, M. E., Newman, G. A., and Biro, O. (2001). Finite-element analysis of controlledsource electromagnetic induction using Coulomb-gauged potentials. Geophysics 66, 786–799. doi:10.1190/1.1444968

CrossRef Full Text | Google Scholar

Bai, N., Zhou, J., Hu, X., and Han, B. (2022). 3D edge-based and nodal finite element modeling of magnetotelluric in general anisotropic media. Comput. Geosci. 158, 104975. doi:10.1016/j.cageo.2021.104975

CrossRef Full Text | Google Scholar

Cao, H., Wang, K., Wang, T., and Hua, B. (2018). Three-dimensional magnetotelluric axial anisotropic forward modeling and inversion. J. Appl. Geophys. 153, 75–89. doi:10.1016/j.jappgeo.2018.04.015

CrossRef Full Text | Google Scholar

Cheng, X., Gong, C. Y., Wang, G. J., Xiao, T., Yang, B., Liu, J., et al. (2024). Efficient scalable three-dimensional magnetotelluric forward modeling method considering resistive anisotropy and magnetic resistivity. Prog. Geophys. 39 (5), 1963–1978. doi:10.6038/pg2024HH0511

CrossRef Full Text | Google Scholar

Everett, M. E., and Schultz, A. (1996). Geomagnetic induction in a heterogenous sphere: azimuthally symmetric test computations and the response of an undulating 660-km discontinuity. J. Geophys. Res. 101, 2765–2783. doi:10.1029/95jb03541

CrossRef Full Text | Google Scholar

Farquharson, C. G., and Craven, J. A. (2009). Three-dimensional inversion of magnetotelluric data for mineral exploration: an example from the McArthur River uranium deposit, Saskatchewan, Canada. J. Appl. Geophys. 68 (4), 450–458. doi:10.1016/j.jappgeo.2008.02.002

CrossRef Full Text | Google Scholar

Farquharson, C. G., and Miensopust, M. P. (2011). Three-dimensional finite-element modelling of magnetotelluric data with a divergence correction. J. Appl. Geophys. 75 (4), 699–710. doi:10.1016/j.jappgeo.2011.09.025

CrossRef Full Text | Google Scholar

Guo, Z., Egbert, G., Dong, H., and Wei, W. (2020). Modular finite volume approach for 3D magnetotelluric modeling of the Earth medium with general anisotropy. Phy. Earth. Planetary Inter. 309, 106585. doi:10.1016/j.pepi.2020.106585

CrossRef Full Text | Google Scholar

Han, B., Li, Y., and Li, G. (2018). 3D forward modeling of magnetotelluric fields in general anisotropic media and its numerical implementation in Julia. Geophysics 83 (4), F29–F40. doi:10.1190/geo2017-0515.1

CrossRef Full Text | Google Scholar

Heise, W., and Pous, J. (2003). Anomalous phases exceeding 90° in magnetotellurics: anisotropic model studies and a field example. Geophys. J. Int. 155, 308–318. doi:10.1046/j.1365-246X.2003.02050.x

CrossRef Full Text | Google Scholar

Jaysaval, P., Shantsev, D. V., de la Kethulle de, R. S., and Bratteland, T. (2016). Fully anisotropic 3-D EM modelling on a Lebedev grid with a multigrid pre-conditioner. Geophys. J. Intern. 207, 1554–1572. doi:10.1093/gji/ggw352

CrossRef Full Text | Google Scholar

Kong, W., Tan, H., Lin, C., Unsworth, M., Lee, B., Peng, M., et al. (2021). Three-dimensional inversion of magnetotelluric data for a resistivity model with arbitrary anisotropy. J. Geophys. Res. Solid Earth 126 (8), e2020JB020562. doi:10.1029/2020JB020562

CrossRef Full Text | Google Scholar

Kuzmin, A., Luisier, M., and Schenk, O. (2013). “Fast methods for computing selected elements of the Greens function in massively parallel nanoelectronic device simulations,” in Euro-par 2013 parallel processing. Editors F. Wolf, B. Mohr, and D. Mey (Berlin: Springer), 533–544.

Google Scholar

Liu, Y., Xu, Z., and Li, Y. (2018). Adaptive finite element modelling of three-dimensional magnetotelluric fields in general anisotropic media. J. Appl. Geophys. 151, 113–124. doi:10.1016/j.jappgeo.2018.01.012

CrossRef Full Text | Google Scholar

Liu, Y., and Yin, C. (2013). Electromagnetic divergence correction for 3D anisotropic EM modeling. J. Appl. Geophys. 96, 19–27. doi:10.1016/j.jappgeo.2013.06.014

CrossRef Full Text | Google Scholar

Liu, Y. H., and Yin, C. C. (2013). Electromagnetic divergence correction for 3D anisotropic EM modeling. J. Appl. Geophys. 96, 19–27. doi:10.1016/j.jappgeo.2013.06.014

CrossRef Full Text | Google Scholar

Long, J. (2024). meshfree modelling of magnetotelluric and controlled-source electromagnetic data for conductive earth models with complex geometries. Front. Earth Sci. 12, 1432992. doi:10.3389/feart.2024.1432992

CrossRef Full Text | Google Scholar

Löwer, A., and Junge, A. (2017). Magnetotelluric transfer functions: phase tensor and tipper vector above a simple anisotropic three-dimensional conductivity anomaly and implications for 3D isotropic inversion. Pure. Appl. Geophys. 174 (5), 2089–2101. doi:10.1007/s00024-016-1444-3

CrossRef Full Text | Google Scholar

Martí, A. (2014). The role of electrical anisotropy in magnetotelluric responses: from modelling and dimensionality analysis to inversion and interpretation. Surv. Geophys. 35, 179–218. doi:10.1007/s10712-013-9233-3

CrossRef Full Text | Google Scholar

Mitsuhata, Y., and Uchida, T. (2004). 3D magnetotelluric modeling using the T-Ω finite-element method. Geophysics 69, 108–119. doi:10.1190/1.1649380

CrossRef Full Text | Google Scholar

Mukherjee, S., and Everett, M. E. (2011). 3D controlled-source electromagnetic edge-based finite element modeling of conductive and permeable heterogeneities. Geophysics 76, F215–F226. doi:10.1190/1.3571045

CrossRef Full Text | Google Scholar

Patro, P. K. (2017). Magnetotelluric studies for Hydrocarbon and geothermal resources: examples from the Asian region. Surv. Geophys. 38 (5), 1005–1041. doi:10.1007/s10712-017-9439-x

CrossRef Full Text | Google Scholar

Pek, J., and Santos, F. A. M. (2002). Magnetotelluric impedances and parametric sensitivities for 1-D anisotropic layered media. Comput. Geosci. 28 (8), 939–950. doi:10.1016/s0098-3004(02)00014-6

CrossRef Full Text | Google Scholar

Pek, J., and Verner, T. (1997). Finite-difference modelling of magnetotelluric fields in two-dimensional anisotropic media. Geophys. J. Intern. 128, 505–521. doi:10.1111/j.1365-246x.1997.tb05314.x

CrossRef Full Text | Google Scholar

Qin, L., and Yang, C. (2016). Analytic magnetotelluric responses to a two-segment model with axially anisotropic conductivity structures overlying a perfect conductor. Geophys. J. Int. 205, 1729–1739. doi:10.1093/gji/ggw109

CrossRef Full Text | Google Scholar

Rivera-Rios, A. M., Zhou, B., Heinson, G., and Krieger, L. (2019). Multi-order vector finite element modeling of 3D magnetotelluric data including complex geometry and anisotropy. Earth Planets. Space 71 (1), 92. doi:10.1186/s40623-019-1071-1

CrossRef Full Text | Google Scholar

Sasaki, Y. (2001). Full 3-D inversion of electromagnetic data on PC. J. Appl. Geophys. 46, 45–54. doi:10.1016/s0926-9851(00)00038-0

CrossRef Full Text | Google Scholar

Schenk, O., and Gärtner, K. (2004). Solving unsymmetric sparse systems of linear equations with PARDISO. J. Future Gen. Com. Sys. 20, 475–487. doi:10.1016/j.future.2003.07.011

CrossRef Full Text | Google Scholar

Siripunvaraporn, W., Egbert, G., and Lenbury, Y. (2002). Numerical accuracy of magnetotelluric modeling: a comparison of finite difference approximations. Earth. Planets. Space 54, 721–725. doi:10.1186/bf03351724

CrossRef Full Text | Google Scholar

Smith, J. T. (1996). Conservative modeling of 3-D electromagnetic fields, Part II: Bi-conjugate gradient solution and an accelerator. Geophysics 61 (5), 1319–1324. doi:10.1190/1.1444055

CrossRef Full Text | Google Scholar

Smith, R. (2014). Electromagnetic induction methods in mining geophysics from 2008 to 2012. Surveys in Geophysics 35 (1), 123–156. doi:10.1007/s10712-013-9227-1

CrossRef Full Text | Google Scholar

Stalnaker, J. L., Everett, M. E., Benavides, A., and Pierce, C. J. (2006). Mutual induction and the effect of host conductivity on the EM induction response of buried plate targets using 3-D finite-element analysis. IEEE Transactions on Geoscience and Remote Sensing 44, 251–259. doi:10.1109/tgrs.2005.860487

CrossRef Full Text | Google Scholar

Uyeshima, M., and Schultz, A. (2000). Geoelectromagnetic induction in a heterogeneous sphere: a new three-dimensional forward solver using a conservative staggered-grid finite difference method. Geophysical Journal International 140, 636–650. doi:10.1046/j.1365-246x.2000.00051.x

CrossRef Full Text | Google Scholar

Wang, K. P., Tan, H. D., Zhang, Z. Y., Li, Z. Q., and Cao, M. (2017). Divergence correction schemes in finite difference method for 3D tensor CSAMT in axial anisotropic media. Explor. Geophys. 48 (4), 363–373. doi:10.1071/eg15074

CrossRef Full Text | Google Scholar

Wang, T., Wang, K.-P., and Tan, H.-D. (2017). Forward modeling and inversion of tensor CSAMT in 3D anisotropic media. Appl Geophys 14 (4), 590–605. doi:10.1007/s11770-017-0644-7

CrossRef Full Text | Google Scholar

Xiao, Q. B., Yu, G., Liu-Zeng, J., Oskin, M. E., and Shao, G. (2017). Structure and geometry of the Aksay restraining double bend along the Altyn Tagh Fault, northern Tibet, imaged using magnetotelluric method. Geophys. Res. Lett. 44, 4090–4097. doi:10.1002/2017GL072581

CrossRef Full Text | Google Scholar

Xiao, Q. B., Yu, G., Shao, G., Li, M., and Wang, J. (2018). Lateral rheology differences in the lithosphere and dynamics as revealed by magnetotelluric imaging at the Northern Tibetan Plateau. Journal of Geophys. Res. Solid Earth 123, 7266–7284. doi:10.1029/2017JB015285

CrossRef Full Text | Google Scholar

Xiao, T. (2019). Three-dimensional magnetotelluric and controlled-source audio-frequency magnetotelluric modeling in anisotropic media using finite-element method. China: Institutional Repository of University of Chinese Academy of Sciences.

Google Scholar

Xiao, T., Huang, X., and Wang, Y. (2019). 3D MT modeling using the T-Ω method in general anisotropic media. J. Appl. Geophys. 160, 171–182. doi:10.1016/j.jappgeo.2018.11.012

CrossRef Full Text | Google Scholar

Ye, Y., Du, J., Liu, Y., Ai, Z., and Jiang, F. (2021). Three-dimensional magnetotelluric modeling in general anisotropic media using nodal-based unstructured finite element method. Comput. Geosci. 148, 104686. doi:10.1016/j.cageo.2021.104686

CrossRef Full Text | Google Scholar

Yoshimura, R., and Oshiman, N. (2002). Edge-based finite element approach to the simulation of geoelectromagnetic induction in a 3-D sphere. Geophys. Res. Lett. 29, 1039–1045. doi:10.1029/2001gl014121

CrossRef Full Text | Google Scholar

Yu, G., Xiao, Q. B., and Li, M. (2019). Anisotropic model study for the phase roll out of quadrant data in magnetotelluric: with examples of upper-lower structure. Chinese J. Geophys. 62 (2), 763–778. doi:10.6038/cjg2019L0661

CrossRef Full Text | Google Scholar

Yu, G., Xiao, Q. B., Zhao, G., and Li, M. (2018). Three-dimensional magnetotelluric responses for arbitrary electrically anisotropic media and a practical application. Geophys. Prospecting 66 (9), 1764–1783. doi:10.1111/1365-2478.12690

CrossRef Full Text | Google Scholar

Zhou, J. J., Hu, X. Y., Xiao, T. J., Cai, H. Z., Li, J. H., Peng, R. H., et al. (2021). Three-dimensional edge-based finite element modeling of magnetotelluric data in anisotropic media with a divergence correction. J. Appl. Geophys. 189, 104324. doi:10.1016/j.jappgeo.2021.104324

CrossRef Full Text | Google Scholar