- 1 School of Mining, Liaoning Technical University, Fuxin, China
- 2 Shaanxi Huabin Yadian Coal Industry Co., Binzhou, China
The evolution of overlying strata structures significantly influences the manifestation of ground pressure behavior in working faces. The mechanism through which tectonic stress influences the evolution of overlying rock structures remains unclear. To address this, we established a nonlinear dynamic mathematical-mechanical model to analyse and propose a theory for the structural evolution of overlying rock structures under tectonic stress. Based on the 8,105 working face in Tongxin Mine, China, we used theoretical calculations and numerical simulations to analyse the influence of tectonic stress on the formation and evolution of the overlying rock “plate-shell” structure. Under similar coal and rock seam distribution conditions, higher tectonic stress led to larger first failure interval of the key stratum. Consequently, the scale of the “plate-shell” structure controlled by the key stratum increased, resulting in more pronounced ground pressure behavior. The EH-4 geomagnetic method and numerical simulations indicated that the damage height of the overlying strata at the working face was 170 m. In response to the intense manifestation of mineral pressure resulting from large-scale overlying strata structure above the working face, the implementation of pre-cracking blasting can significantly reduce the failure interval of the key stratum and alleviate surrounding rock stress.
1 Introduction
Coal mining disrupts the initial in-situ stress equilibrium, causing a redistribution of stresses around the mining area and within the overlying strata. This process results in the formation of a mining-induced stress field (Qian and Xu, 2010). Under the influence of the mining-induced stress field, various rock layers above the coal seam experience differing degrees of instability and damage. This instability and collapse of the overlying strata can lead to significant variations in the scale and morphology of the strata structure, which in turn cause intense ground pressure behavior at the coal wall. Additionally, this phenomenon can sometimes trigger dynamic mining disasters, such as coal mine tremors and rockbursts (Dou and He, 2001). In order to realize the timely prediction of the strong mine pressure behavior in the working face and ensure the safe and efficient production of coal, it isparticularly important to study the evolution law of the overburden structure in the working face.
In recent years, both Chinese and international researchers have conducted extensive research on the evolution patterns of overlying strata in mining areas and the characteristics of their damage. One notable theoretical framework in domestic studies is the “masonry beam” theory proposed by Qian Minggao. According to this theory, the rotational movement of rock blocks induced by coal mining forms a semi-arched masonry beam structure (Qian and Xu, 2019; Qian and Wang, 2018; Qian, 2017). Song Zhenqi proposed the “transferring rock beams” theory, which posits that as the working face advances, the overlying strata become exposed and bend and sink under their own gravity, transforming into simply supported beams. When these simply supported beams approximately move as a whole, they are referred to as transferring beams (Wen and Song, 2019; He et al., 2017). The hinge block hypothesis, proposed by Kuznetsov, suggests that the damage to the overlying strata layers above a working face can be divided into the caved and regular movement zones above it. Zeng et al. proposed that in the mining process of the working face, the additional stress generated by the fault changed the deformation and failure law of the roadway and the failure law of overlying rock, the “three zones” of overlying rock movement disappeared, and the settlement pattern changed from “trapezoid” to “inverted triangle” (Zeng, 2022). Zhang et al. by combining theoretical analysis, analog simulation and numerical simulation, foreign scholars conclude that with the increase of mining length, overlying rocks of fully mechanized caving face undergo a continuous dynamic subsidence process, and the initial rupture position of key strata is behind the working face, while the periodic rupture position of key strata is in front of the coal face (Zhang, 2023). Wang et al. used MATLAB and PFC 2D numerical simulation method, the fracture law and macroscopic mechanical response of overburden rock are analyzed. The overburden structure and load transfer evolution model of “four stages and three modes” in deep high stress stope is established, and the fracture effect of “beam, plate and arch” stage is proposed (Wang et al., 2023). The ground pressure behavior at the working face is closely related to the evolution of the overlying strata structure. Xu et al.through comparative analysis of the impact of mining pressure on the working face, revealed three different influence patterns of the “cantilever beam” structure of key stratum on mining pressure (Ju and Xu, 2023). Dou et al. believe that in the process of coal mining, the spatial structure of overlying strata exists and dynamically evolves with the change of mining scope (boundary condition), thus inducing rock burst (Dou et al., 2014). Cao et al. theoretically analysed the spatial structure of thick and hard overlying strata and their fracture movements at the isolated island working face of Baodian Coal Mine, as well as their impact on mining pressure dynamics. They concluded that the fracture movement during the evolution of the “T”-shaped overlying strata structure at the working face serves as the main source of mining-induced seismic activity (Cao and Zu, 2014). Zhou et al. believed that the initiation and expansion of cracks in rock mass are important factors affecting the stability of overlying rock structure (Zhou et al., 2019; Li et al., 2022; Wu et al., 2024). Li et al. through theoretical analysis and numerical simulation, show that the instability of the cantilever beam structure is the main reason for the ore pressure appearance of the working face during the excavation of the super-high mining face (Wang et al., 2022). Yang et al. proposed the “cutting block + squeezing balance arch” structural model based on extensive practical experience and theoretical research. Their analysis suggests that the localised overall cutting and falling of overlying strata result in the intensified ground pressure behavior at the working face and the continuous increase in support strength required for supporting the strata (Yang and Liu, 2021). The aforementioned scholars have contributed to the research on the evolution of the overlying strata structure and manifestation characteristics of mining pressure. However, the analysis of the overlying strata structure from the perspective of tectonic stress is relatively scarce. Considering the complex geological conditions in many Chinese coal mines, there are challenges associated with mining in structurally complex coal seams. During mining in such coal seams, the energy generated by complex geological structural movements increases the structural stress and energy of the coal-rock mass (Xiang and Ji, 2016), Crack propagation in rock mass (Zhao et al., 2021; Zhou et al., 2017; Wang et al., 2018; Bi et al., 2016). Under the influence of high tectonic stress environments, the overlying strata structure controlled by hard roof strata results in highly concentrated stress in the coal-rock mass. The combined effects often lead to accidents, such as roof collapses and floor bumps, in mining spaces, greatly affecting mine safety and production (Li, 2014). Therefore, there is an urgent need to investigate the evolution of overlying strata structures and mechanisms of the manifestation of intense ground pressure behavior under the influence of tectonic stress fields (Huang et al., 2017; Han and Wang, 2017).
In this study, we considered the aforementioned influencing factors and established a nonlinear dynamic mathematical-mechanical model to analyse the overlying strata structures under the influence of tectonic stress. We proposed a research method for studying the evolution of overlying strata structures under the influence of tectonic stress, focusing on the 8,105 working face of Tongxin Mine as the engineering background. From the perspectives of tectonic stress fields and overlying strata structures, we analysed the distribution characteristics of hard roof strata above the coal seam under the influence of tectonic stress fields. We determined the mechanism through which tectonic stress affects the formation and evolution of the “plate-shell” structure of overlying strata, and confirmed the scientific validity of the theory of evolution of the overlying strata structure under the influence of tectonic stress through theoretical calculations, numerical simulations, and field measurements. Our findings will provide theoretical and scientific bases for predicting and preventing the intense ground pressure behavior at the working face.
2 Project overview
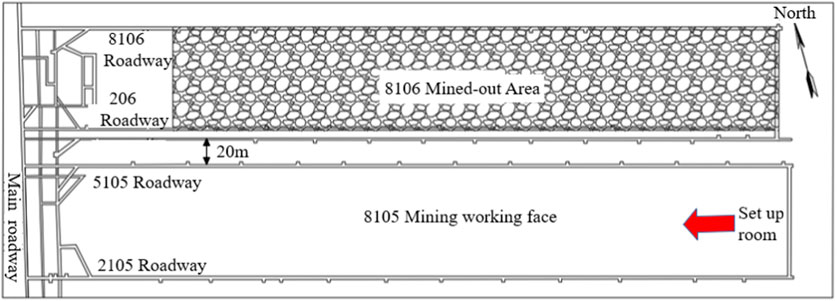
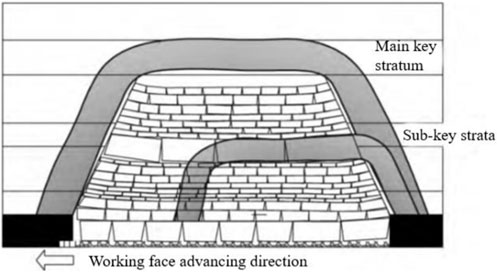
The Datong mining area is situated in the southwestern part of Datong City, Shanxi Province. Within this region lies the Tongxin coalfield, positioned on the eastern flank of the Datong syncline, wherein 3-5 coal seams are primarily extracted from the Carboniferous-Permian strata. Overall, the coalfield exhibits a relatively low number of faults; however, it features two significant folds. The stress concentration and energy accumulation induced by these folds provide the stress conditions and energy basis for the ground pressure behavior on the working face. We conducted in-situ stress measurements in the Tongxin coalfield using hollow inclusion cell measurements. The stress test results at the measured point in the return airway of North Section 8,107 are presented in Table 1; the calculated lateral pressure coefficient was 1.51. The 8,105 working face in Tongxin Mine is designed with a dip length of 200 m, strike length of 1,757 m, depth of 457 m, coal seam thickness of 16.42 m, and dip angle ranging from 1° to 3°. The majority of the roof of the 8,105 working face comprises hard sandstone, with the immediate roof being conglomeratic coarse sandstone. A completely mechanised top coal caving is employed in the 8,105 working face, which is developed with a cut-through entry in the southeast, advancing towards the northwest (Figure1). According to pressure monitoring, the first weighting interval of the working face is 84.8 m, and the periodic weighting interval ranges between 20 and 30 m. During the mining operations of the 8,105 working face, multiple instances of significant mine pressure were observed in Panel 5,105. Within a range of 10–40 m ahead of the working face in the return airway, the floor exhibited pronounced heaving, with a maximum heave of 0.5 m, and the roof experienced a maximum subsidence of 0.6 m. Additionally, severe cracking was observed in the concrete spray layer on both sides of the roadway, and the advanced-support single props suffered extensive damage (Figures 2, 3).
3 Theoretical evolution of the overlying rock structure under the influence of structural stress
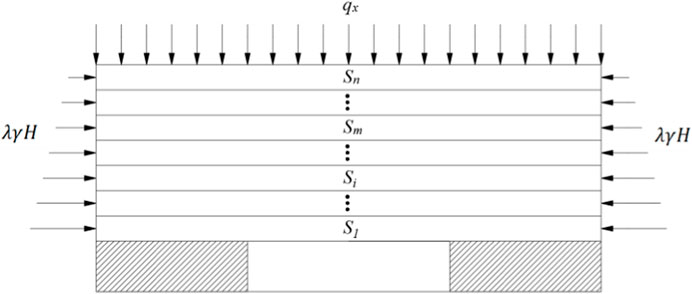
In 1990, Qian Minggao from the China University of Mining and Technology proposed the key stratum theory based on the analysis of the morphology and stress conditions of overlying strata. This theory posits that within the overlying strata of a mining site, there exist multiple hard rock layers that exert a controlling influence on the movement of the overlying strata either entirely or partially. The layers that control the overall movement of the overlying strata are termed key strata, whereas those that influence their partial movements are called sub-key strata. The key stratum theory can be utilised to study the fracture and movement patterns of overlying strata under specific geological and mining conditions. Considering that structural stress influences the collapse and structural evolution of overlying strata, the evolution theory of the overlying structure under the influence of structural stress has been developed based on the key stratum theory. The calculation equation is as follows (Key strata theory and practice, 2007; Hou, 2009):
Step 1: The positions of hard rock layers from the bottom to the top are identified. The first layer of rock is assumed to be a hard rock layer. The layers above it, up to the nth layer, deform in coordination with it. If the nth layer does not deform in coordination with the first layer, the nth layer is considered the second hard rock layer. Based on the combined-beam theory, the load acting on the first hard rock layer can be expressed as follows:
where h
i
is the thickness of the
Thus, the load formed by the m+1 th layer on the first hard rock layer is:
As the m+1 th layer is a hard rock layer, its deflection is less than that of the underlying rock layers; thus:
Substituting Equations 1, 2 into the above equation and simplifying yields the following:
Equation 4 is used to determine the position of hard rock layers. The calculation is conducted step-wise as follows: first, the first rock layer above the coal seam is considered. Subsequently, whether this layer satisfies Equation 4 is evaluated. If the layer satisfies Equation 4, this layer is determined as a hard rock layer and the calculation for this layer can be stopped.
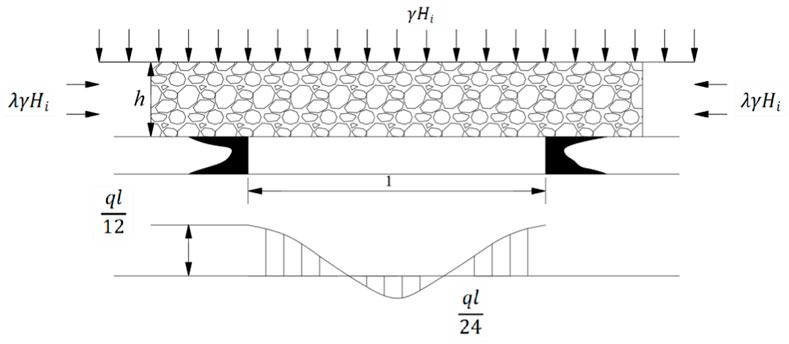
Step 2: The failure interval of each hard rock layer is calculated. For each stratification of surrounding rock, if the overlying load is
where q
Hi
is the horizontal load of the
λ is the lateral pressure coefficient;
γ is the bulk density;
H
i
is the burial depth of the
As shown in Figure 5, the stress induced by horizontal lateral pressure on the mid-span section of the fixed support beam model is expressed as:
For any point within the fixed support beam under the influence of structural stress, the normal stress can be expressed as:
where
J z is the sectional modulus about the neutral axis, measured in metres (m);
γ is the bulk density;
H
i
is the burial depth of the
If the calculation is based on the width of the beam, the sectional distance is
When
To simplify the calculation, we used a two-ended fixed support beam model to calculate the failure interval of the hard rock layer. In this case, the failure interval of the hard layer is expressed as:
where h
G
is the thickness of the Gth hard rock layer, measured in metres (
σ t is the tensile strength of the Gth hard rock layer, measured in megapascals (MPa);
q G is the load borne by the Gth hard rock layer, measured in kilonewtons per square metre (kN/m2);
λ is the lateral pressure coefficient;
γ is the bulk density;
H G is the burial depth of the Gth rock layer, measured in metres (m).
The critical mining length for the fracture of each key stratum is expressed as Equation 11 (Hou and Zang, 2004):
where L
G,j
is the working-face advance length at the fracture of the Jth key stratum, measured in metres (m);m is the number of rock layers from the roof of the coal seam to the lower part of the Jth key stratum;h
i
is the thickness of the i th rock layer, measured in metres (m);l
G,J
is the ultimate span of the J th key stratum at its initial fracture when not supported by the underlying strata, measured in metres (m);
Step 3: The key stratum position is determined by comparing the failure interval of each hard rock layer. The following principles are used to identify the key strata:
(i) If the kth hard rock layer is considered a key stratum, the failure interval of all hard rock layers above it must be greater than that of the kth layer, satisfying the following condition (Equation 12):
(ii) If the failure interval of the k+1th hard rock layer break, L k+1, is less than that of the k th hard rock layer break, L k, the load borne by the k+1th hard rock layer is added to the k th layer to recalculate the failure interval for the k th hard rock layer.
(iii) Based on the above two principles, the key stratum is determined layer-wise, moving upwards from the lowest hard rock layer and.
4 Study on the evolutionary pattern of the overlying structure under structural stress
4.1 Theoretical calculation of the overlying structure evolution under structural stress
4.1.1 Determination of key strata
Based on the borehole logs and physical-mechanical parameters obtained from drilling operations at the 8,105 working face in Tongxin Mine, the analysis based on the evolution theory of the overlying structure under structural stress was used to discern the positions of key strata. The calculation results indicated a total of four key strata within the overlying layers of the 8,105 working face. In particular, layers Y2, Y9, and Y22 were identified as sub-key strata, whereas layer Y25 was identified as the main key stratum. The detailed calculation results are presented in Table 2.
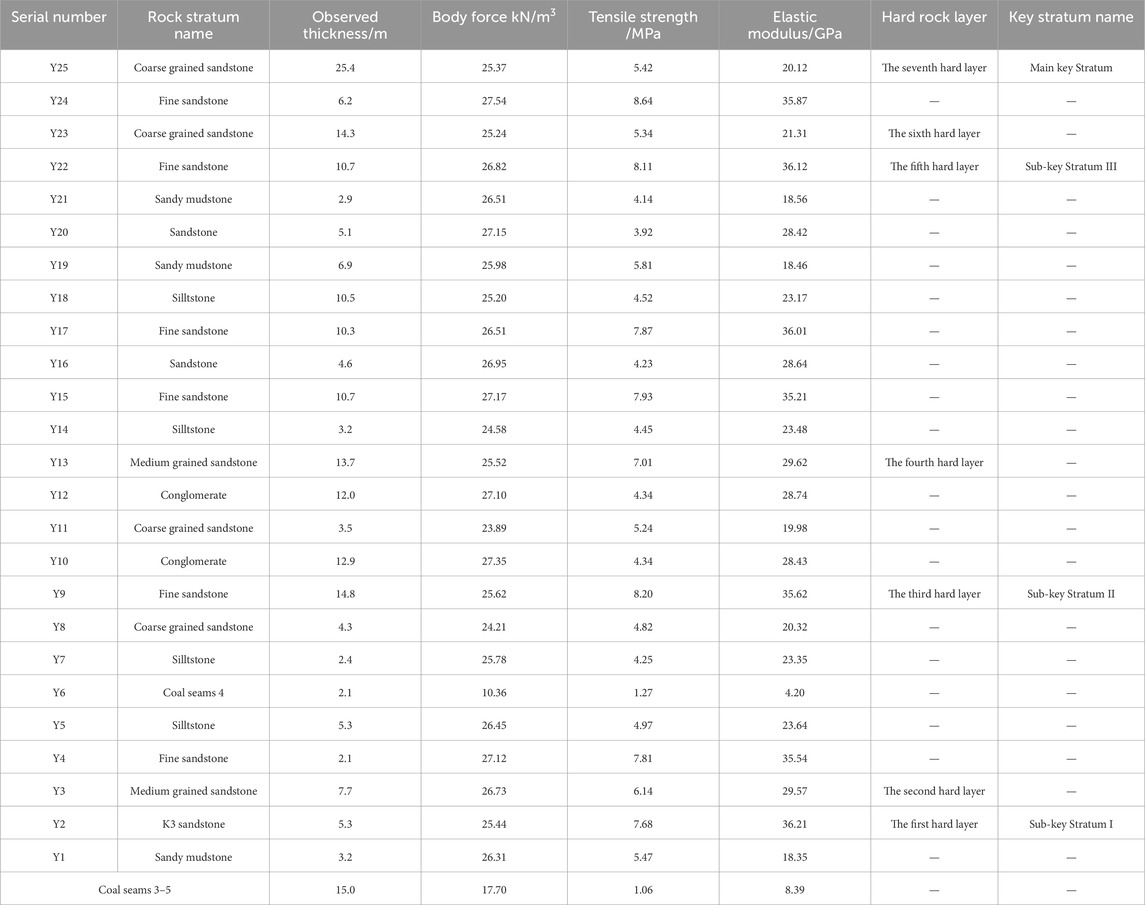
Table 2. Distribution of key strata and related physical and mechanical parameters in 8,105 working face of Tongxin Mine.
4.1.2 Analysis of the initial fracture of key strata under the influence of tectonic stresses
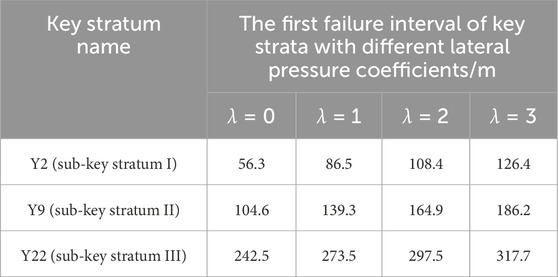
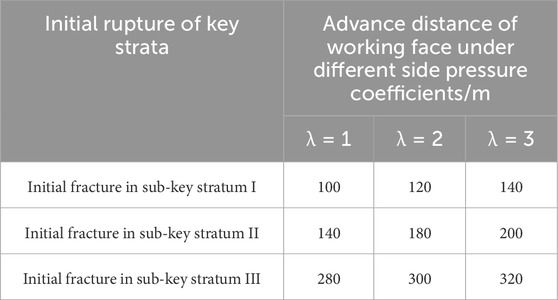
According to the data presented in Table 2 regarding the physical and mechanical parameters of the rock, along with the analysis based on the theory of structural evolution of the overlying rocks, we observed that when the lateral pressure coefficients were 0, 1, 2, and 3, the upper rock layers at Tongxin Mine, namely, Y2, Y9, and Y22, were identified as the first, second, and third key strata, respectively. This result is consistent under the influence of tectonic stresses. Meanwhile, as presented in Table 3, the first failure interval of each key stratum increased with increasing tectonic stress. In summary, the tectonic stress did not affect the determination of the location of key strata of the overlying rock formation on the working face, but has a greater influence on the first failure interval of each key stratum. In particular, the higher the tectonic stress, the greater is the first failure interval of the key stratum.
4.2 Numerical simulation analysis of the structural evolution of overlying rocks under the influence of tectonic stresses
4.2.1 Numerical modelling
The 8,105 working face of Tongxin Mine served as the backdrop for establishing a numerical model along its direction using the FLAC3D simulation software. The Mohr-Coulomb plastic model dimensions were 546.6 × 400 × 126.7 m, with a total of 764,100 model units. In the heading model, the boundaries of the model were kept fixed by applying gradient stresses ranging from 6.63 to 11.42 and 6.42–11.87 MPa along the Y- and Z-axes, respectively. The corresponding study of the lateral pressure coefficients of 1, 2, and 3 was achieved by varying the ratio of stresses in the X- to Z-axes directions, namely, 1, 2, and 3. The mechanical parameters of the model rock strata were set with reference to Table 2. The interface command of the software is used to simulate the interface between rock strata. The strength parameters given to the interface are shown in table 4.
4.2.2 Breakage of overlying rocks under tectonic stresses
Based on the influence of tectonic stresses, the distances of the advancement of the working face at the initial fracture of each key stratum are presented in Table 5. As presented in Table 4, the distance of the advancement of the working face at the initial fracture of each key stratum increased with increasing tectonic stress. When the lateral pressure coefficient was 1, the working face advanced by 100 m, and the sub-key stratum I underwent fracture for the first time; when the lateral pressure coefficient was 2, the working face advanced by 120 m, and the sub-key stratum I underwent fracture for the first time; when the lateral pressure coefficient was 3, the working face advanced by 140 m, and the sub-key stratum I underwent fracture for the first time. At the same degree of advance, the greater the tectonic stress, the less likely is the collapse of the top rock layer. Large areas of overhanging hard roof slabs elevate the stresses in the coal rock body and easily induce strong ground pressure behavior. The initial fracture of sub-key strata II and III is similar and will not be repeated here.
Figures 6–8 show the initial fracture of each key stratum under the influence of tectonic stress. Based on the damage characteristics of the overlying rock, with increasing tectonic stress, the lateral scale of overlying rock damage gradually increases, and the shape of the overlying rock structure gradually changes to an arch. Based on the distribution law of the stress peak, with increasing tectonic stress, the stress peak on both sides of the working face gradually increases, and the distance of the peak point from the coal face successively increases, and the influence range of the overrun of the working face also increases accordingly (Table 6). The above analysis indicates that the tectonic stress has an important influence on the structural evolution of the overlying rock, and the larger the tectonic stress, the larger is the lateral scale of overlying rock damage; thus, the larger the force acting on the coal wall, the more likely is the occurrence of the impact pressure and other dynamic disasters.

Figure 6. Breakage of sub-key stratum I under the influence of tectonic stresses. (A) Lateral pressure coefficient of I; (B) Lateral pressure coefficient of II; (C) Lateral pressure coefficient of III.
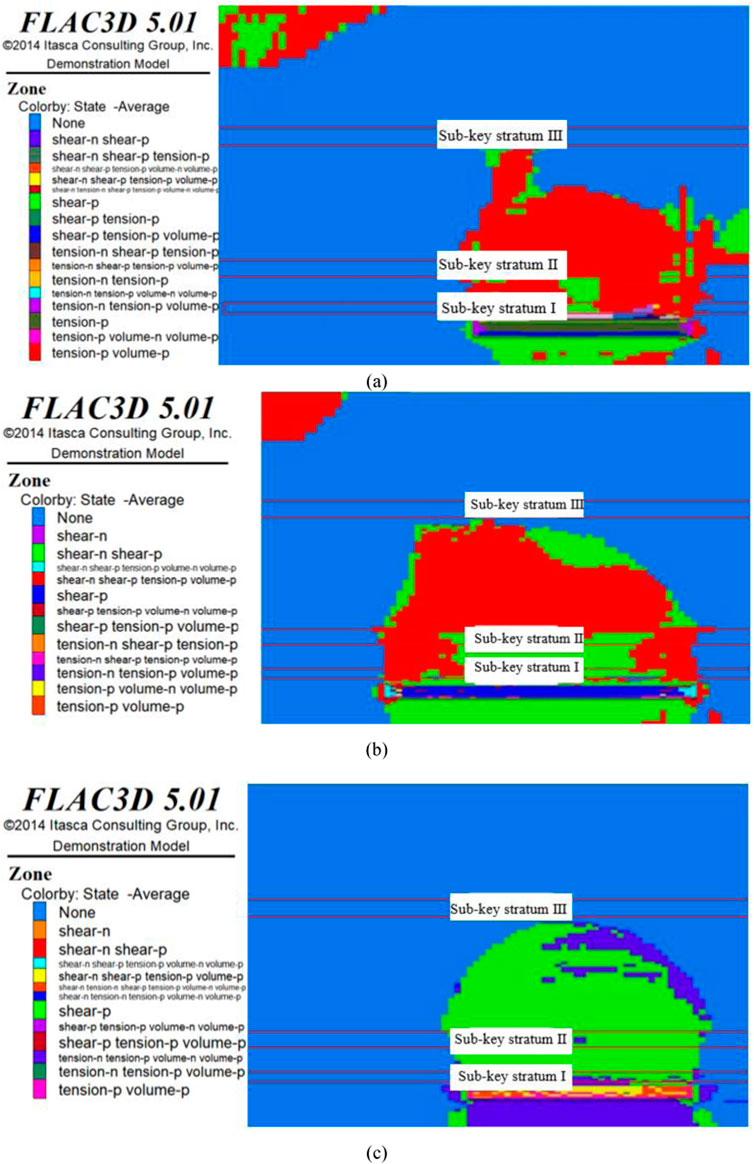
Figure 7. Breakage of sub-key stratum II under the influence of tectonic stresses. (A) Lateral pressure coefficient of I; (B) Lateral pressure coefficient of II; (C) Lateral pressure coefficient of III.
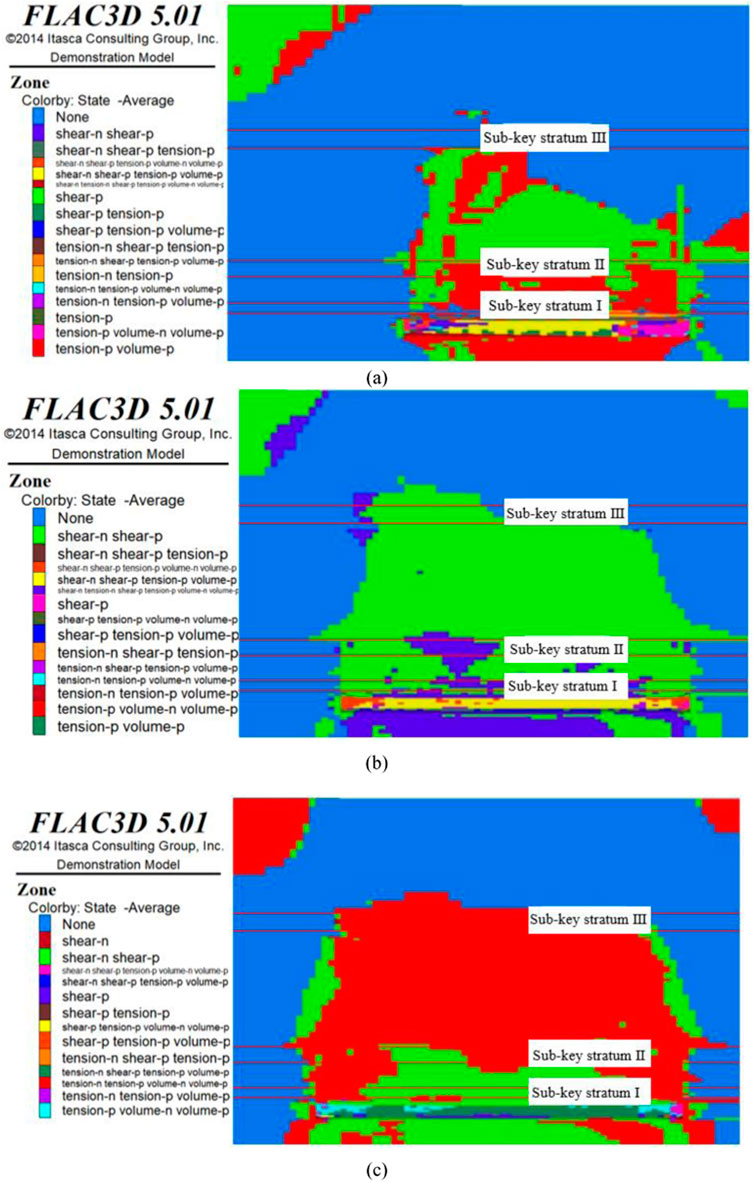
Figure 8. Breakage of sub-key stratum III under the influence of tectonic stresses. (A) Lateral pressure coefficient of I; (B) Lateral pressure coefficient of II; (C) Lateral pressure coefficient of III.
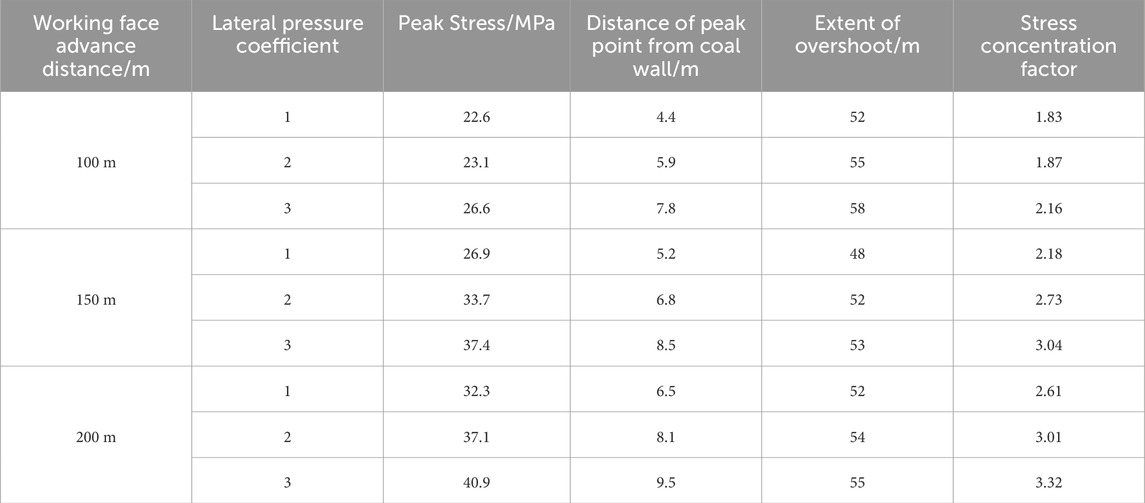
Table 6. Stress distribution under different lateral pressure coefficients at different distances of the advancement of the working wall.
4.3 Evolution of the overlying strata structure and characteristics of ground pressure behavior under the influence of tectonic stress
Based on the solid beam theory, the overlying quarry comprises key strata of rock beam structures and the weak rock layers above them that they support. The spatial structure of the overlying rock dynamically evolves as the working faces are mined. As shown in Figure 9, as the working face advances, the top rock layer collapses and the overlying rock collapses to the lower part of the key stratum, forming a “plate-shell” structure comprising the key-stratum rock plate structure and shell-shaped overlying space; this overlying structure bears most of the stresses before the key stratum is broken for the first time. The “clamping” effect of the tectonic stress level increases the first weighting interval of the working face, and the transverse scale of this large “plate-shell” structure also increases. When the area mined in the working face exceeds the critical value controlled by the sub-key stratum structure, this structure undergoes damaged and develops into the upper critical stratum, forming a larger scale “plate-shell” structure until it reaches the main critical layer. Notably, in the entire process of evolution, the greater the tectonic stress, the greater is the first failure interval of each key stratum; subsequently, the scale of the “plate-shell” structure controlled by the key stratum is larger, and the ground pressure behavior is also more intense.
5 The height of overlying damage and mine-pressure control technology of the 8,105 working face of Tongxin Mine
5.1 Comprehensive analysis of the height of overlying damage
5.1.1 Theoretical calculation of the height of damage to overlying rocks
The actual lateral pressure coefficient of Tongxin Mine is 1.51; combined with the theory of structural evolution of the overlying rock in the previous section, the calculation of the actual tectonic stress of Tongxin Mine under the influence of the key strata with the advancement of the breakage of the working face is presented in Table 7.
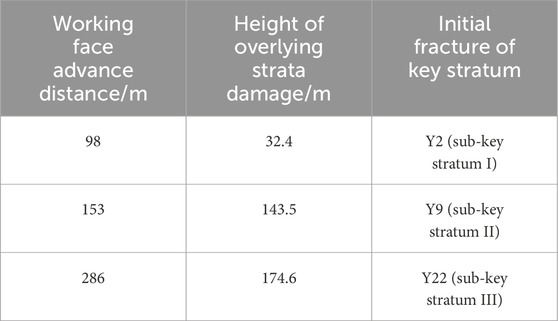
Table 7. Breakage of key strata under the influence of actual tectonic stresses in Tongxin Mine with the advancement of the working face.
As presented in Table 6, when the working face advanced by 98 m, the sub-key stratum I underwent fracture, and the height of overlying strata damage reached 32.4 m; when the working face advanced by 153 m, the sub-key stratum II underwent fracture, and the height of overlying strata damage reached 143.5 m; when the working face advanced 286 m, the sub-key stratum underwent fractured, and the height of overlying strata damage reached 174.6 m. As the working face advances forward, each key stratum gradually undergoes fractures, and the breakage of the lower key stratum causes the collapse of the overlying rock layer, and the damage of the overlying rock develops upwards until reaches the lower part of the main key stratum.
5.1.2 Numerical simulation analysis of the damage height of overlying strata
The distribution of overlying damage in the 8,105 working face of Tongxin Mine is shown in Figure 10. Along the direction of the working face, when the working face was mined back for 100 m, sub-key stratum I ruptured for the first time, and the overlying rock was damaged to 34 m; when the working face was mined back for 160 m, sub-key stratum II ruptured for the first time, and the overlying rock was damaged to 134 m; when the working face was mined back for 300 m, sub-key stratum III ruptured for the first time, and the overlying rock was damaged to 197 m. Therefore, the height of damage of the overlying rock layers on the 8,105 working face ranged from 34 to 197 m at the time of the initial fracture of each key stratum.
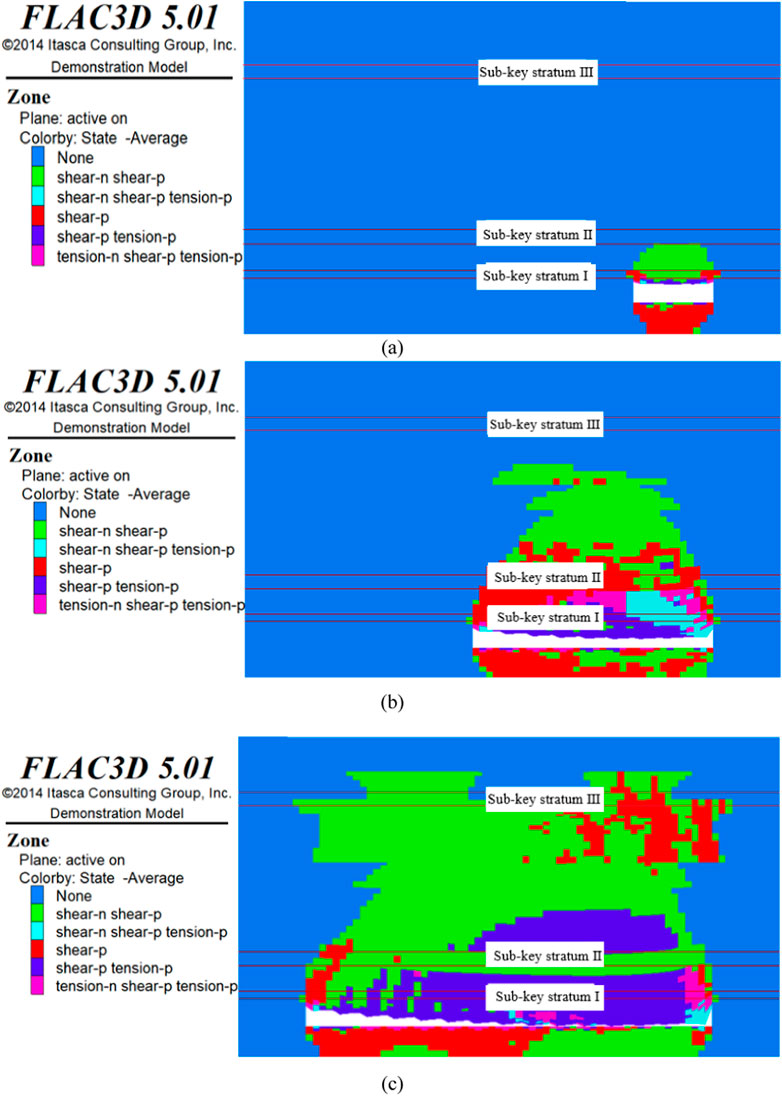
Figure 10. Distribution of overlying rock damage in the 8,105 working face of Tongxin Mine. (A) Initial fracture in sub-key layer I; (B) Initial fracture of sub-key layer II; (C) Initial fracture of sub-key layer III.
5.1.3 Physical detection of the overlying strata structure at the 8,105 working face
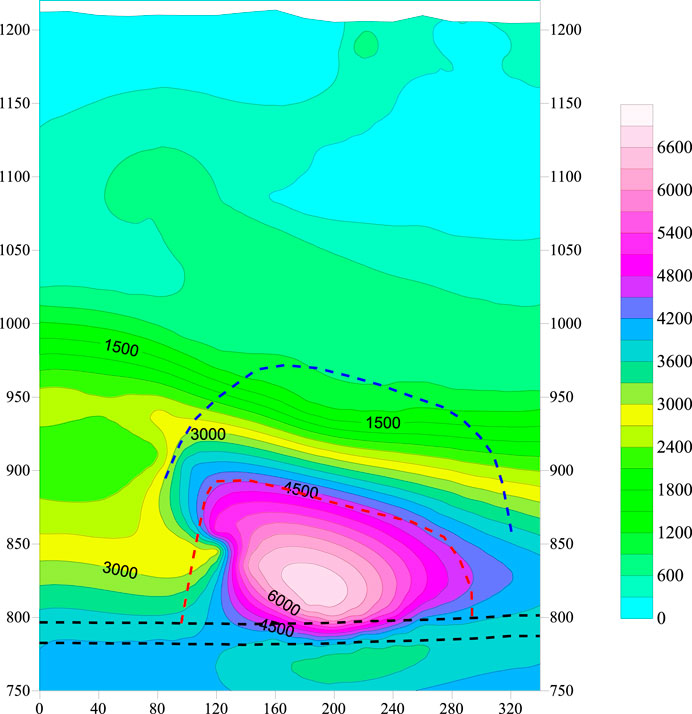
To precisely detect the caved zone in the goaf after the extraction of the fully mechanised mining face, we employed the EH-4 electromagnetic imaging system in the 8,105 working face of Tongxin Mine (as shown in Figure 11) to monitor the structure of overlying strata. The results are as follows.
The detection results shown in Figure 12 indicate that the upper resistivity contours are gentle and continuous, with a layer-like distribution, whereas the distribution of resistivity contours is very dense and irregular at the height and lateral scale ranges of approximately 780–880 and 100–320 m, respectively. The lateral scale range coincides with the range of the 8,105 working face; thus, we deduced that the resistive anomaly zone is the caved zone formed after the mining of the 8,105 working face. Therefore, we inferred that the resistive anomaly zone is a caved zone formed after the mining of the 8,105 working face, and the height of collapse is approximately 100 m. Additionally, the distribution of resistivity contours in the lateral scale ranges of approximately 880–950 and 100–320 m in height is highly dense and seems to be parallel. We inferred that this area is a fractured zone formed after the mining of the 8,105 working face, and consequently, that the collapsed fissure height of Tongxin Mine is approximately 170 m after the mining of the 8,105 working face.
5.1.4 Comparative analysis of the damage heights of overlying strata
To validate the accuracy of the theory of evolution of the overlying structure under the influence of tectonic stress, we comparatively analysed the overlying damage heights calculated from theoretical equations, numerical simulation, and field measurements. The specific findings are presented in Table 7. As presented in Table 8, when each key stratum of the 8,105 working face was first broken, the theoretically calculated overlying damage height was 32.4–174.6 m; the numerically simulated overlying damage height was 34–197 m, which coincided with the overlying damage height of 170 m that was accurately detected using the EH-4 system. These results proved the correctness and accuracy of the theory of evolution of the overlying structure under the influence of tectonic stresses.
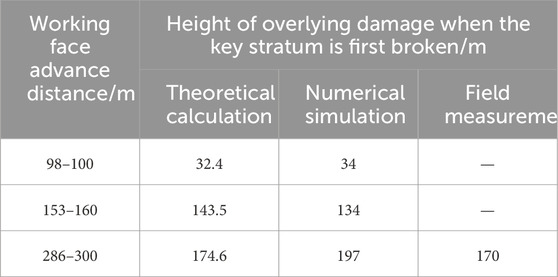
Table 8. Height of overlying damage during the initial fracture of each key stratum along the strike of the working face.
5.2 Characterisation of extractive stress evolution
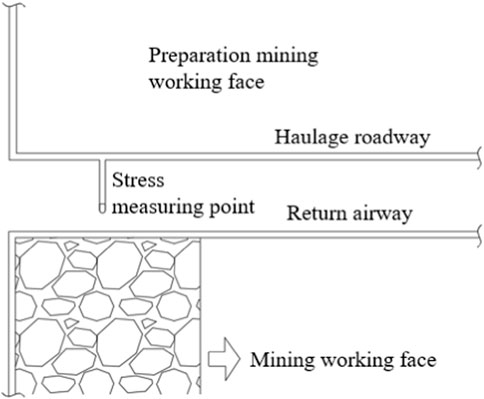
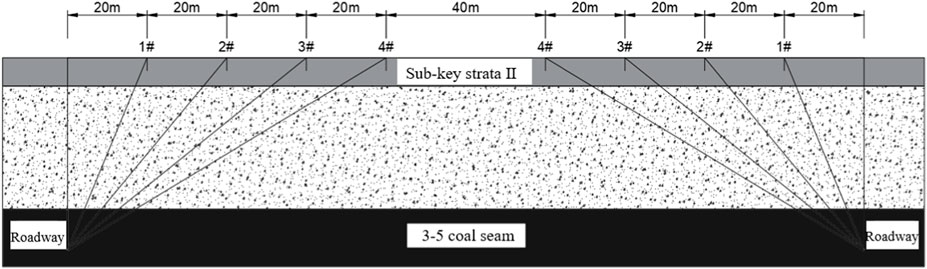
In the 8,105 working face of Tongxin Mine, we used a borehole deformation gage to monitor the surrounding rock stress of the roadway by analysing its change law at different stages of the working face mine. This was conducted to study the impact of the evolution of the overlying rock structure on the surrounding rock stress of the roadway and the ground pressure behavior, and ensure the continuity of the monitoring of the working face of the succession of sections of the coal pillar to be arranged within the monitoring probes (Figure 13).
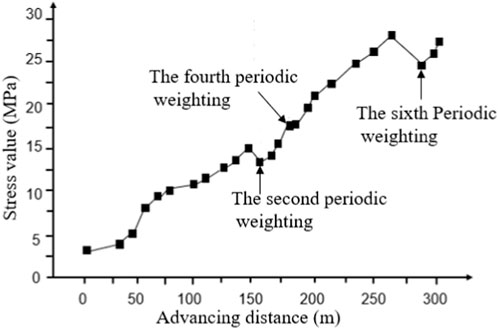
As shown in Figure 14, the stress acting on the surrounding rock increased with the advancement of the working face. However, during the second and sixth periodic weighting during the mining of the 8,105 working face, a sudden decrease was observed in the stress acting on the surrounding rock. Conversely, during the fourth periodic weighting, a sudden increase was observed in the stress acting on the surrounding rock. We inferred that this abrupt decrease is attributed to large structural instabilities in the formation of the basic top and sub-key strata. Simultaneously, the abrupt change in the increase is ascribed to the periodic rupture of the rock beneath the structure.
Considering the example of the second periodic weighting, when the 8,105 working face was mined back to approximately 160 m, sub-key stratum II (key block) collapsed for the first time, with rock layer 2 collapsing with it, and the overlying structure scale increased, as shown in Figure 15. Moreover, the overall height of the new overlying structure remained unchanged, but the scale in the horizontal direction increased, and the stress acting in the peripheral rock of the tunnel would be higher as the structure was still stable. As the structure was still stable, the stress on the perimeter rock of the roadway would be higher, and the fourth periodic weighting would be caused by the instability of the “plate-shell” structure.
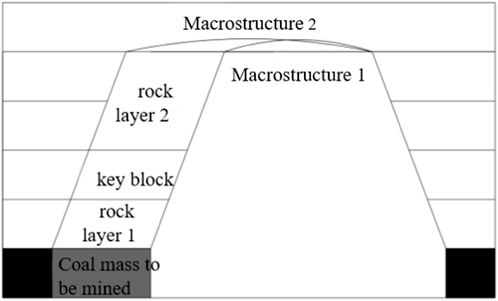
Figure 15. Structural changes in the overlying rock during a sudden change in stress at the 8,105 working face.
5.3 Strong mine pressure control technology
The hard top is one of the most important factors causing the ground pressure behavior. Effectively reducing the overhanging roof area and intensity of incoming pressure of the hard top plate of thick seams during mining can alleviate the strong ground pressure behavior during the mining of coal seams below from the root and source. Higher roof pre-cracking blasting is a type of blasting method used for higher key strata that can generate dynamic loads, and the high hard rock layers will be pre-cracked by overrunning, whole, and uniform blasting. Pre-cracking blasts for high tops are generally selected from the sub-key layers below the main critical layer. In the 8,105 working face of Tongxin Mine, the fine-grained sandstone, located 32.4 m above the coal seam, belongs to the thick and hard sub-key stratum II, and the rock layer does not easily collapse with the advance of the working face. Therefore, high level pre-cracking blasting is targeted at this critical layer (Figure 16).
We conducted mechanical analysis for sub-key strata I after the implementation of high level whole stratum pre-cracking blasting on the sub-key strata II, and analysed sub-key stratum II and its control on the formation of the overlying-rock-layer load on sub-key stratum I; thus, high-level whole layer pre-cracking blasting increased the overlying rock layer load borne by the lower key stratum to a certain extent, thereby making the periodic weighting interval to reduce. According to Equations 1–10, the load of the overlying rock stratum before artificial pre-cracking was 771.52 KPa, and the failure interval was 42.4 m; after the formation of the artificial pre-cracked layer, the load of the overlying rock layer was 1,216.03 KPa, and the failure interval reduced to 33.8 m, which was approximately 20.3% less than that before its formation. Therefore, the implementation of high-level roof pre-cracking blasting can effectively control the influence of the overlying structure on the working face with the ground pressure behavior.
6 Conclusion
In this paper, we established a nonlinear dynamic mathematical-mechanical model to analyse and propose a theory for the evolution of the overlying structure under the influence of tectonic stress. The main conclusions of the analysis of the fracture characteristics of the key strata by theoretical calculation and numerical simulation are as follows:
(1) Under the same conditions of the distribution of coal and rock seams, the higher the tectonic stress, the greater is the first failure interval of the key stratum. Moreover, the scale of the “plate-shell” structure controlled by the key stratum increases, and the ground pressure behavior more strongly.
(2) Under the influence of tectonic stress, the overburden failure height of 8,105 working face in Tongxin Mine is about 170 m. The theoretical calculation results are consistent with the field monitoring results. Thus, the accuracy of the theory of structural evolution of overlying rocks under the influence of tectonic stress was further verified.
(3) Stress monitoring of the surrounding rock at the working face revealed the presence of sudden upward and downward changes in the surrounding rock stress. Further analyses indicated that the periodic rupture of the rock layers beneath the overlying structure caused a sudden upward change in the stresses in the surrounding rock, and the destabilisation of the structure caused a sudden downward change in the stresses in the surrounding rock.
(4) In response to the strong ground pressure behavior caused by the large-scale overlying structure of the 8,105 working face, a pre-cracking blasting programme for the roof of the 8,105 working face was proposed. This solution increased the overburden loads on the critical layer and reduced the key stratum failure interval by 20.3%. This programme can effectively control the influence of the overlying structure on the ground pressure behavior in the working face, and provide references for the prediction and prevention of the ground pressure behavior of the working face under similar conditions.
7 Discussion
This paper mainly reveals the evolution law of overburden structure through macroscopic mechanical analysis. In fact, there are various holes and cracks distributed in the overlying strata on the working face. PFC discrete element can present the whole process of crack generation and expansion from the microscopic point of view, and deeply analyze the relationship between the crack expansion law of overburden rock and the characteristics of mine pressure behavior under the action of tectonic stress, so as to provide a theoretical basis for the prediction and prevention of mine pressure behavior in working face.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
ZZ: Supervision, Writing–review and editing. PW: Investigation, Methodology, Software, Writing–original draft. KC: Conceptualization, Validation, Writing–original draft. FL: Data curation, Writing–original draft. YH: Formal Analysis, Validation, Writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The basic scientific research project of the Liaoning Provincial Department of Education (LJ212410147007).
Conflict of interest
Authors KC and FL were employed by Shaanxi Huabin Yadian Coal Industry Co.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bi, J., Zhou, X. P., and Qian, Q. H. (2016). The 3D numerical simulation for the propagation process of multiple pre-existing flaws in rock-like materials subjected to biaxial compressive loads. Rock Mech. Rock Eng. 49, 1611–1627. doi:10.1007/s00603-015-0867-y
Cao, A. Y., and Zu, L. L. (2014). Mining ‘ T ’ type overburden structure and dynamic pressure evolution characteristics of island working face under thick and hard rock strata. J. china coal Soc. 39 (2), 328–335.
Dou, L. M., and He, X. Q. (2001). Rock burst prevention theory and technology. Xuzhou: China University of Mining and Technology Press.
Dou, L. M., He, X. Q., He, H., He, J., and Fan, J. (2014). Spatial structure evolution of overlying strata and inducing mechanism of rockburst in coal mine. Trans. Nonferrous Metals Soc. China 24, 1255–1261. doi:10.1016/s1003-6326(14)63187-3
Han, H. K., and Wang, X. C. (2017). Study on the motion characteristics and “ re-stability ” conditions of the key stratum structure of overburden rock after instability. J. Min. Saf. Eng. 10 (11).
He, M. Z., Song, Z. Q., and Wang, A. (2017). The theory of roof-cutting short-wall beam in longwall mining and its 110 method-the third revolution of mining science and technology. Coal Sci. Technol. (01), 1–9+13. doi:10.19896/j.cnki.mtkj.2017.01.002
Hou, Z. J. (2009). Application research and parameter determination of combined key strata theory. Shanxi: xi'an university of science and technology.
Hou, Z. J., and Zang, J. (2004). Overburden rock fracture criterion and span calculation of thick loose layer shallow coal seam. J. liaoning Tech. Univ. (05), 577–580.
Huang, B., Chen, S., and Zhao, X. (2017). Hydraulic fracturing stress transfer methods to control the strong strata behaviours in gob-side gateroads of longwall mines. Arabian J. Geosciences 10 (11), 236. doi:10.1007/s12517-017-3024-y
Ju, J. F., and Xu, J. L. (2023). The movement pattern of ' cantilever beam ' structure in key strata of large mining height stope and its influence on mine pressure. J. china coal Soc.
Key strata theory and practice of rock strata control. Jiangsu: China university of mining and technology. (2007).
Li, T., Li, Z., and Sun, J. (2022). Study on dynamic evolution of overburden rock movement and mining-induced stress of ultra-high working face. Shock Vib. 2022, 11–10. doi:10.1155/2022/2271635
Lu, Z. L. (2018). Study on mechanical model and stability of tunnel roof in horizontal ed surrounding rock. xi 'an technological university.
Qian, M. G. (2017). Strengthen the theoretical research of coal mining to achieve scientific mining. J. Min. Saf. Eng. 34 (04), 615.
Qian, M. G., and Wang, J. C. (2018). On scientific mining of coal. J. china coal Soc. 43 (01), 1–13. doi:10.13225/j.cnki.jccs.2017.4400
Qian, M. G., and Xu, J. L. (2010). Mining pressure and strata control,xuzhou. China University of Mining and Technology Press.
Qian, M. G., and Xu, J. L. (2019). Coal mining and strata movement. J. china coal Soc. 44 (04), 973–984. doi:10.13225/j.cnki.jccs.2019.0337
Wang, X. F., Zhang, Q., Liu, W., Wei, Y., Jiang, T., and Hao, F. (2023). Study on space–time evolution law and mechanism of instability failure of deep high-stress overburden rock. Appl. Sci. 13, 4573. doi:10.3390/app13074573
Wang, Y., Wu, J., and Pu, H. (2022). Effect of calcium formate as an accelerator on dilatancy deformation, strength and microstructure of cemented tailings backfill. Chemosphere 291, 132710. doi:10.1016/j.chemosphere.2021.132710
Wang, Y., Zhou, X., Wang, Y., and Shou, Y. (2018). A 3-D conjugated bond-pair-based peridynamic formula-tion for initiation and propagation of cracks in brittle solids. Int. J. Solids Struct. 134, 89–115. doi:10.1016/j.ijsolstr.2017.10.022
Wen, Z. J., and Song, Z. Q. (2019). Research on stope spatial structure model and related dynamic disaster control. Coal Sci. Technol. 47 (01), 52–61.
Wu, J., Wong, H. S., Zhang, H., Yin, Q., Jing, H., and Ma, D. (2024). Improvement of cemented rockfill by premixing low-alkalinity activator and fly ash for recycling gangue and partially replacing cement. Cem. Concr. Compos. 145, 105345. doi:10.1016/j.cemconcomp.2023.105345
Xiang, P., and Ji, H. G. (2016). Rock burst mechanism based on dynamic loading and unloading effect of two-body system. J. china coal Soc. 41 (11), 2698–2705.
Yang, J. Z., and Liu, Q. J. (2021). Study on the mine pressure law and overburden fracture structure of the super large mining height working face with 8. 8 m support. J. Min. Saf. Eng. 38 (04), 655–665.
Zeng, C. (2022). Study on overburden failure law and surrounding rock deformation control technology of mining through fault. Plose one.
Zhang, H. J. (2023). Research on structural evolution characteristics of overburden rock for shallow buried thick coal seam mining. E3S Web Conf. 406, 02006. doi:10.1051/e3sconf/202340602006
Zhao, Y., Bi, J., Wang, C., and Liu, P. (2021). Effect of unloading rate on the mechanical behavior and fracture charac-teristics of sandstones under complex triaxial stress conditions. Rock Mech. Rock Eng. 54, 4851–4866. doi:10.1007/s00603-021-02515-x
Zhou, X. F., Fan, L. F., and Wu, Z. J. (2017). Effects of micro-fracture on wave propagation through rock mass. Int. J. Geomech. 17 (9), 04017072. doi:10.1061/(asce)gm.1943-5622.0000947
Keywords: tectonic stress, overlying rock structure, overlying rock damage height, intense ground pressure behavior, key stratum
Citation: Zhu Z, Wang P, Chen K, Lv F and Hong Y (2024) Evolution of the overlying strata structure and characteristics of ground pressure behavior under the influence of tectonic stress. Front. Earth Sci. 12:1501631. doi: 10.3389/feart.2024.1501631
Received: 25 September 2024; Accepted: 30 October 2024;
Published: 03 December 2024.
Edited by:
Jiangyu Wu, China University of Mining and Technology, ChinaReviewed by:
Jing Bi, Guizhou University, ChinaVahab Sarfarazi, Hamedan University of Technology, Iran
Yiming Wang, Suzhou University, China
Copyright © 2024 Zhu, Wang, Chen, Lv and Hong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhijie Zhu, emh1emhpamllQGxudHUuZWR1LmNu
 Zhijie Zhu
Zhijie Zhu Peng Wang1
Peng Wang1