Frequency-broadening method of seismic data based on sparse reconstruction inversion strategy

To broaden the effective frequency bandwidth of seismic data and enhance its resolution, we investigate the high-resolution reconstruction method grounded in compressed sensing sparse theory, utilizing the characteristics of sparse decomposition of seismic signals. First, we examine the construction of an over-complete dictionary, which is then employed to sparsely represent the seismic data and derive the reflection coefficient, combined with noise, forms a mixed sparse component. By removing the noise sparse component from this mixture, we isolate a clean reflection coefficient. In the iterative reconstruction process of compressed sensing sparse decomposition, weak signal can easily be overwhelmed by the application of the maximum energy principle. To address this issue, we propose a useful signal control retention method incorporating lateral adjacent low-rank constraints. This approach increases the probability of optimizing weak signal dictionary atoms, mitigates the unbalanced reconstruction of strong and weak signals, and facilitates the comprehensive reconstruction of both signal types. Ensuring reconstruction accuracy is crucial, as the conditions for reconstruction significantly affect reliability. Therefore, we employ a signal-to-noise ratio estimation method to establish an adaptive iteration stop condition based on a residual threshold. During each iteration, the signal-to-noise ratio is recalculated, and the signal-to-noise ratio is multiplied by the residual to produce a weight residual. Finally, this new residual is used in the inner product calculations, allowing for the preferential selection of dictionary atoms. Both theoretical models and actual data validate the rationality and effectiveness of the proposed method. Analysis of real data demonstrates that our approach significantly enhances the seismic frequency band width and markedly improves the resolution of seismic data.

1 Introduction

Researches on improving the resolution of seismic data has been a prominent focus, with numerous technical methods developed, particularly those based on deconvolution and compensation (Haldorsen et al., 1994; Kaaresen and Taxt, 1998; Chang et al., 2000; Donoho, 2006; Gholami, 2014). The advancement of technology and the increasing demands of practical applications have driven the continuous evolution of methods and techniques aimed at enhancing seismic data resolution. Among various emerging technologies, compressed sensing has gained significant attention due to its advantages in sparse representation and perceptual reconstruction theory, particularly in terms of computational efficiency, feature analysis, and noise suppression (Herrmann and Hennenfent, 2008; Wang and Wang, 2014; Zhang et al., 2015; Sun et al., 2023; Ding et al., 2019; Bai et al., 2014). In the context of enhancing the seismic data resolution, compressed sensing sparse reconstruction primarily employs matching pursuit (MP) (Song et al., 2017), orthogonal matching pursuit (OMP), and their respective improvements. MP serves as the core algorithm within sparse reconstruction theory, while OMP and its variations are extensions of the MP framework. Although MP is characterized by its simplicity, it only facilitates local optimization. In contrast, OMP transitions from local to global optimization but suffers from calculational instability. Both methods aim to maximize the residual and the inner product of the dictionary as their optimization principle, yet a common limitation is the inability to update the dictionary. Addressing the stability problem of OMP (Zong Z. et al., 2023; Wang et al., 2024; Zhao et al., 2023; Huang, 2023), researchers have proposed various improved algorithms, such as the regularized OMP method. However, these methods primarily enhance the calculation of the inner product in the residual and atomic spaces without fundamentally resolving the stability problem. Inadequate atom selection can lead to significant oscillations in the residual, which means that even the improved regularized OMP method does not effectively mitigate the oscillation issue.

With the research and widespread application of compressed sensing theory, a series of challenges has emerged in its development and application, especially in the field of seismic exploration (Sun et al., 2024; Zong J. et al., 2023; Zong et al., 2022). These challenges can be categorized into two groups: those arising from the theoretical framework of compressed sensing itself, and those resulting from the integration of compressed sensing theory with specialized applications (Buchholtz, 1972; Zhang et al., 2017). This paper studies the use of seismic data by constructing a seismic wavelet dictionary, which is employed to project the observation signal and obtain a sparse representation of the reflection coefficient of the seismic record. Subsequently, the reflection coefficient is estimated to enhance the resolution of the seismic record. In addressing these practical challenges, we extend our focus to the issues faced by compressed sensing theory in sparse reconstruction of seismic signals. These include noise-containing approximate sparse reconstruction, redundancy and multiplicity in over-complete dictionaries, properties of the dictionaries, and the trade-off between reconstruction accuracy and sparsity (Herrmann and Li, 2012; Zhao et al., 2020; Anvari et al., 2017; Cai and Wang, 2011). Therefore, this paper conducts in-depth study from four aspects: dictionary construction, sparse representation, algorithm optimization, and reconstruction evaluation. By improvement of the over-complete dictionary and weighted sparse algorithm, we reduce the multiplicity of the reconstruction solution. To tackle the challenge of incorrect atom selection associated with the dictionary update corresponding to the reconstructed seismic reflection coefficient—especially for weak reflection coefficients—we explore a correlation control method for useful signals in adjacent traces. Finally, a signal-to-noise ratio estimation method is used to establish an adaptive iteration stop condition based on a residual threshold. This culminates in a frequency extension method suitable for effective sparse representation and reflection coefficient reconstruction of noisy seismic data.

2 Basic theory of sparse reconstruction

2.1 Sparse representation of signals

The sparse representation of signal y (mathematical problem) is shown in Equation 1:

$\min ‖x_0‖,s.t.y=Ax(1)$

where, A is a dictionary matrix of a*N, where the vectors of each column are the atoms in dictionary A. The solution to the optimization problem here is a coefficient vector that represents an accurate sparse representation of the target i signal y. The solution after optimization to the problem is X_opt, then the corresponding target signal is approximately expressed as Equation 2:

$\stackrel{\sim }{y}=A{x}_{opt}(2)$

The dictionary refers to a set of basis functions in sparse reconstruction inversion, so that any complex signal or data can be approximated by a linear combination of these basis functions. The dictionary atom is a single element in these basis functions. For sparse reconstruction inversion of seismic data, the dictionary can be regarded as a seismic wavelet library, which contains multiple seed wave forms to match different geological features in seismic data. The dictionary atom can be regarded as the sampling point of the wavelet, which is the specific element in the wavelet library for matching the characteristics of seismic data. They jointly construct the sparse form of seismic signals and help to extract and identify the characteristics of underground structures in the inversion process.

2.2 Sparse reconstruction of noisy signals

If the signal contains noise, reconstruction performance is degraded or even fails. The optimal dictionary cannot be obtained from the conventional sparse reconstruction method in the presence of noise. It was assumed that the observed signal is shown in Equation 3:

$y=\mathrm{\Phi }x+n(3)$

where, n represents noise. Sparse reconstruction theories under noise conditions are approximately sparse of the signal, that is, using the fewest dictionary atoms to achieve an approximate representation of the signal, so the optimization method is:

$\min {‖{\mathbf{w}}^{-1}\left(x+v\right)‖}_1,s.t.y=\mathrm{\Phi }\mathbf{W}\left(x+v\right)+n(4)$

In this case, the above Equation 4 can also be expressed as Equation 5:

$\min {‖{\mathbf{w}}^{-1}\left(x+v\right)‖}_1,s.t.{‖y-\mathrm{\Phi }\mathbf{W}\left(x+v\right)‖}_2<\epsilon (5)$

where, v represents the noise associated with the sparse coefficients. It is assumed that both the noise in the sparse coefficients and the noise arising from the seismic record are additive in nature. The design of an optimal dictionary under noisy conditions aims to enhance reconstruction performance. In the presence of noise, the reconstruction conditions of the signal are closely related to the amplitudes of the non-zero elements. When these amplitudes are small, conventional MP algorithms may not reliably identify the optimal dictionary atom. Consequently, the reconstruction constraint can be expressed as Equation 6:

${‖DX‖}_2+{‖Dn‖}_2<\left(\beta -u\left(k-1,\mathrm{\Phi },\psi \right)-u\left(k,\mathrm{\Phi },\psi \right)\right)(6)$

where, D is the actual dictionary matrix, $\beta ,u$ is the degree of coherence and cumulative correlation coefficient of atoms in each column of the dictionary. where, $\mathrm{\beta }\le \mathrm{\mu }$, based on practical experience, the value of $\mathrm{\mu }$ is generally between 0.5 and 1.

The atoms selected for optimal solutions in the context of noisy signals are not always orthogonal. It is important to recognize that Equation 1 forms a union of convex sets; thus, each minimization result maintains the same sparsity but yields different fitting errors, indicating that Equation 1 constitutes a multi-solution problem. The following optimization problem can be formulated to address such non-unique issues as shown in Equation 7:

$\min \left\{{‖x‖}_0+\frac{1}{2}{‖y-Ax‖}_2{\epsilon }^{-1}\right\},s.t.{‖y-Ax‖}_2<\epsilon (7)$

3 Frequency-broadening method of seismic data based on sparse reconstruction inversion strategy

3.1 Method for estimating reflection coefficient of sparse reconstruction of noisy seismic signals

Noisy seismic signals are expressed as Equation 8:

$y=A*r+n(8)$

Its matrix form is Equation 9:

$\mathbf{y}=\mathbf{\text{Ar}}+n(9)$

A sparse reflection coefficient model r was estimated based on a given seismic record. For the established objective function, the optimization process under the sparse reconstruction framework is Equation 10:

$\min {‖r‖}_0,s.t.y=Ar+n(10)$

To facilitate the solution of the problem, the above problem was transformed into the Equation 11 objective function problem:

$I={‖y-Ar‖}_2^2+\lambda {‖vr‖}_2^2(11)$

To address the issues discussed in this thesis, the overcomplete dictionary underwent sparse processing to reconstruct the sparse solution of the reflection coefficient. Both the sparse dictionary and the estimated reflection coefficient should exhibit sparsity. One method to enhance the sparsity of the reflection coefficient estimation involves applying a weight function to the reflection coefficient model as shown in Equation 12:

$v_i={\left|r_i\right|}^{\frac{2-p}{p}}+{\epsilon }_r(12)$

where, p changes between 0 and 2. In practical experience, p = 1 can work well in most cases, p < 1 indicates that a stronger sparsity is given, but it is easy to lose weak seismic signals, and p >1 indicates that less sparsity is given. The reflection coefficient is shown in Equation 13:

$r=s_{r}v(13)$

If the objective function is substituted, the transformed objective function is:

$I={‖y-A{S}_{r}v‖}_2^2+\lambda {‖vr‖}_2^2(14)$

where, λ is the weighting coefficient. The objective function in Equation 14 can be minimized by solving the system of equations as shown in Equation 15:

$\left({\mathbf{s}}_{\mathbf{r}}^{\mathbf{T}}{\mathbf{A}}^{\mathbf{T}}\mathbf{A}{\mathbf{s}}_{\mathbf{r}}+\lambda \mathbf{I}\right)\mathbf{v}={\mathbf{s}}_{\mathbf{r}}^{\mathbf{T}}{\mathbf{A}}^{\mathbf{T}}\mathbf{y}(15)$

If $A_s=A{S}_r$, the Equation 16 are obtained.

$\left({\mathbf{A}}_{\mathbf{s}}^{\mathbf{T}}{\mathbf{A}}_{\mathbf{s}}+\lambda \mathbf{I}\right)\mathbf{v}={\mathbf{A}}_{\mathbf{s}}^{\mathbf{T}}\mathbf{y}(16)$

This transformation reflects the sparsity and orthogonality of the overcomplete dictionary, aiming to reduce reconstruction multiplicity. In this study, the overcomplete dictionary was optimized under fixed sparsity conditions using a weighting method to enhance the sparsity or orthogonality of the dictionary atoms. The optimization procedure for the given overcomplete dictionary is shown in Equation 17:

$\min (\max {\displaystyle \sum }\left|〈A,A_s〉\right|+\frac{\max {\displaystyle \sum }\left|〈A,A_s〉\right|}{\min \left|〈A,A_s〉\right|}(17)$

It is very difficult to solve the above problem, considering the calculation problem, the optimized dictionary can satisfy (Equation 18):

$\min {‖{\mathbf{A}}^H\mathbf{A}‖}_2^2,s.t.A_{S,i}^H{A}_i=1,i=1,\cdots ,N(18)$

For each A_S*I, under the objective function $\mathrm{I}={‖\mathrm{y}-\mathrm{A}{\mathrm{S}}_{\mathrm{r}}\mathrm{v}‖}_2^2+\mathrm{\lambda }{‖\text{vr}‖}_2^2$, the Lagrange function can be constructed as:

$L\left(A_{s,i}{\lambda }_i\right)=\frac{1}{2}{‖A{s}^{H}A‖}_2^2+{\lambda }_i\left(A_{S,i}^H{A}_i-1\right)(19)$

Equation 20 can be obtained from the Equation 19:

$A_{s,i}=\frac{R^{-1}{A}_i}{A_i^{·}{R}^{-1}{A}_i}(20)$

Where R is shown in Equation 21,

$R=A{A}^H(21)$

If the probability of each optimal atom’s occurrence is determined, a weighted optimized dictionary can be constructed. In this case, $R={{AW}^{2}A}^H$ represents the weight coefficient. The inner product of the signal and the atoms in the overcomplete dictionary indicates the extent to which a corresponding atom constitutes the optimal atom for the signal. Therefore, the inner product of the overcomplete dictionary’s optimal signal can be utilized as the initialization weight as shown in Equation 22:

$W_0=diag\left\{\left|A^{H}y\right|\right\}(22)$

The calculation was conducted as Equation 23:

$R=A{W}^2{A}^H(23)$

The dictionary matrix was updated as Equation 24:

$A_{s,i}=\frac{R^{-1}{A}_i}{A_i^{·}{R}^{-1}{A}_i}(24)$

The weight was updated as Equation 25:

$W=diag\left\{\left|A^{H}y\right|\right\}(25)$

3.2 Dictionary construction and optimization methods

3.2.1 Dictionary construction

To fully utilize the prior information contained in actual seismic records, a wavelet dictionary was initially constructed based on these records. To accommodate the spatio-temporal variations in seismic data, we calculated the amplitude of the autocorrelation function at each sampling position from shallow to deep using a sliding time window. Similarly, we computed the envelope of the instantaneous phase. The amplitude of the autocorrelation function and the envelope of the instantaneous phase were then combined to create the actual seismic wavelet dictionary.

Although the extracted seismic wavelet is closest representation of the actual seismic record, it is impossible to extract a completely accurate actual wavelet dictionary due to various factors, including calculation methods and noise. To enhance the estimation performance of reflection coefficients reconstruction and improve the accuracy of weak reflection coefficients, a theoretical mixed-phase wavelet dictionary was constructed based on the previously extracted wavelet dictionary from actual seismic data. The construction method involves obtaining the dominant frequency by analyzing the seismic records, followed by employing a combination of time shifting, amplitude attenuation, and the dominant frequency to create the mixed-phase wavelet.

3.2.2 Dictionary update optimization

The optimization processes involved in compressed sensing sparse reconstruction fundamentally focus on the optimization and updating of the dictionary. Specifically, an optimal sparse representation is achieved through the iterative update and optimization of the dictionary, ultimately enhancing the reconstruction performance. To facilitate the accurate reconstruction of both strong and weak reflection coefficients corresponding to strong and weak amplitude seismic records, we employ a dictionary updating strategy that incorporates both a local dictionary and a public dictionary for previously constructed actual seismic wavelet and theoretical mixed-phase wavelet. For strong amplitude seismic records (or high signal-to-noise ratio), the OMP optimization algorithm can accurately effectively reconstruct strong reflection coefficients. However, for weak amplitude seismic records (or low signal-to-noise ratio), the application of the maximum inner product principle may result in the selection of incorrect atoms, leading to a degradation in reconstruction performance or even complete failure. To enhance the reconstruction performance of weak seismic signals, we utilize a shared dictionary along with a weighted constrained dictionary optimization strategy. This approach is based on two assumptions: first, that the wavelet of the wavelet of the adjacent trace seismic record remains constant over time, allowing the use of a common wavelet; and second, the seismic signals of adjacent traces are similar.

Under the above assumption, we employ updating methods for both the public dictionary and the lateral constrained dictionary to process r weak seismic signals. The specific design method involves calculating the correlation coefficients of the residuals from adjacent channels (3 or five channels) using a common dictionary. These correlation coefficient serve as both weighting coefficient and the update weights for the dictionary. Seismic signals from adjacent channels exhibit similarity and large correlation coefficients, while the noise from these channels tends to be dissimilar, resulting in lower correlation coefficients. Therefore, by integrating the residual correlation coefficients from adjacent channels as weight coefficients in the dictionary updating process, we enhance the weight of useful signals while diminishing the weight of noise. This approach effectively suppresses noise and reduces the likelihood of erroneously selecting dictionary atoms.

3.3 Analysis of sparse dictionary, sparsity and residual relation

For the sparse reconstruction of noisy signals, the residual during the iterative process can be divided into two components: $RC=RD+RN$. Here, $RD$ represents the residual between the reconstructed signal and the original effective signal, while $RN$ denotes the noise residual. The objective of noisy signal reconstruction is to minimize, $RD$ such that when the optimal dictionary is selected and the iterations reach an appropriate level of sparsity, $RD=0$ and $RC=RN$. This indicates that the residual consists solely of noise. However, since the sparsity is often unknown, selecting an appropriate dictionary and determining the suitable level of sparsity poses significant challenges, complicating the control of $RN$.Consequently, it is essential to conduct a thorough analysis of the relationships among sparsity, residuals, and dictionaries. Notably, as sparsity increases, the residual may not decrease as expected; instead, it may increase, suggesting that the initial atomic selection is inappropriate or that the initial dictionary is unsuitable for the weak reflection information at a certain iteration level. A monotonically decreasing minimum residual curve with increasing iterations indicates the suitability of the local dictionary, whereas a staggered curve with a minimum value suggests that the dictionary is inadequate. The correctness, redundancy, and sparse orthogonality of the dictionary are critical for optimizing the process and ensuring the convergence properties of the residuals. Figures 1A, B illustrate the variation characteristics of residuals under the seismic overcomplete dictionary, revealing that while the residuals decrease initially, they stabilize and do not converge with further iterations. Figures 1C, D depict the sparse orthogonalization of an overcomplete dictionary and its iteration results, demonstrating good convergence with noticeable changes in residuals. However, as the number of iterations increases, the changes in residuals become minimal, as shown in Figure 1E. To clarify, the results for the number of iterations in Figure 1D were cropped, as illustrated in Figure 1F, highlighting that greater changes in the number of iterations correspond to smaller changes in residuals. To further analyze the changes in residual errors and the dictionary, the inflection point in Figure 1D was examined, leading to the selection of the theoretical wavelet. Figures 2A, B present the iterative residual results under the theoretical mixed-phase dictionary and the mixed-phase dictionary, respectively, illustrating a monotonous decrease in residuals and a clear convergence effect.

Figure 1

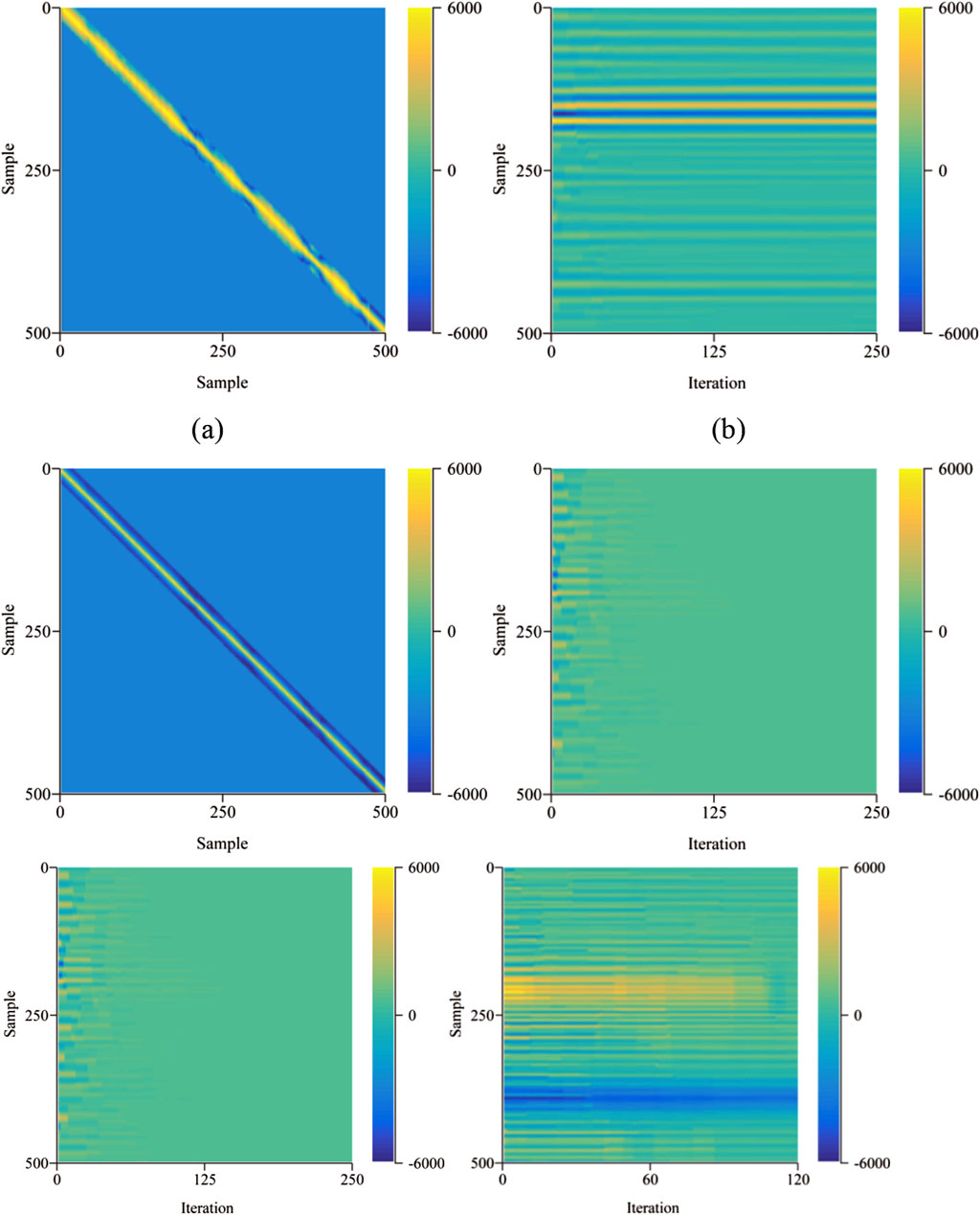
Figure 1. Different dictionary matrix and residual variation characteristics. (A) Overcomplete dictionary matrix. (B) Residual variation characteristics of Overcomplete dictionary. (C) Optimized overcomplete dictionary matrix. (D) Residual variation characteristics of optimized overcomplete dictionary. (E) Residual variation characteristics of optimized overcomplete dictionary (F) Residual variation characteristics of optimized overcomplete dictionary (The last 120 iterations result).

Figure 2

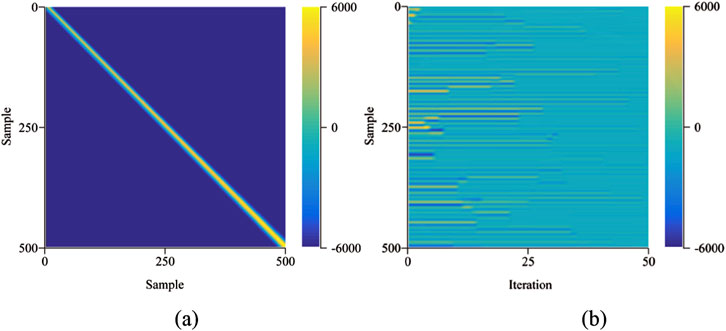
Figure 2. Mixed phase dictionary matrix and residual variation characteristics. (A) Mixed phase dictionary matrix. (B) The variation characteristics of residuals with the number of iterations.

3.4 An evaluation method for improving the accuracy and accuracy control of reconstructed reflection coefficient

In practical applications, the sparsity of the target signal is often unknown. Typically, substituting an estimated sparsity into algorithms such as MP, which require sparsity to be known, leads to a rapid decline in reconstruction performance. The research indicates that the size and distribution of the residual are determined by both the dictionary and the level of sparsity. The choice of residual threshold is crucial for determining reconstruction accuracy. Setting the residual threshold to zero for a noise-free signal maximizes reconstruction accuracy. Conversely, for noise-containing signals, minimizing the residual threshold enhances the reconstruction accuracy of effective signals. In the context of the evaluation method for seismic data frequency extension and reconstruction presented in this paper, sparsity is a key parameter that governs the algorithm’s iteration termination. Factors influencing sparsity include:

(1) The length of the seismic record;

(2) Residual size

(3) Dictionary features and number of dictionary atoms

(4) SNR of seismic signals

(5) Reconstruction accuracy and reconstruction precision

In the absence of noise, when the specified sparsity is less than the true sparsity of the signal, the OMP reconstruction algorithm selects K coefficients from largest to smallest based on their values, using the dictionary to generate the sparse signal YC. Conversely, when the specified sparsity is greater than or equal to the true sparsity of the signal, the reconstructed signal theoretically matches the actual signal. However, in the presence of noise, when the specified sparsity is greater than or equal to the true sparsity, the reconstructed signal diverges from the actual signal. As sparsity increases, the reconstructed signal will not only encapsulate all components of the original signal but will also incorporate noise. In the OMP algorithm, over-sparse representations are frequently misidentified as significant signal components. The distribution of these noise elements adheres to specific patterns. Following the decomposition of the seismic signal in the temporal (longitudinal) domain, the reflection coefficients of the useful signal exhibit a non-uniform distribution, while the noise is uniformly distributed. In contrast, in the spatial (lateral) direction, the reflection coefficients of the useful signal are uniformly distributed, whereas the noise distribution is irregular. These characteristics provide a theoretical foundation for estimating sparsity.

Research indicates that sparsity is directly proportional to signal length, inversely proportional to residual size, and proportional to dictionary capacity. These factors have a significant and direct relationship with sparsity. Additionally, sparsity is potentially linked to the dictionary, signal-to-noise ratio, and reconstruction accuracy. This study investigates the conditions for stopping the iteration of the noise-related residual threshold OMP algorithm. Based on the preceding analysis, seismic signal noise and its SNR are critical determinants of reconstruction accuracy and serve as the primary criteria for evaluating the stopping conditions of the iterative optimization algorithm. Given the characteristics of the problem addressed in this thesis, the singular value analysis method was employed to assess noise and SNR, and the threshold conditions for stopping iterations of the optimization algorithm were established based on these parameters.

Local matrix $P_{M\times N}$ is composed of N sample points in each adjacent M channel, and M singular values are obtained by singular value decomposition. Among them, the largest singular value Y₁ represents the energy of the signal, and other singular values represent the energy of the noise. M singular values were obtained by singular value decomposition of MN matrix, the largest singular value λ_max (the first singular value) represents the signal energy, and the other singular values represent the signal noise energy. The noise energy of the signal is:

The local matrix $P_{M\times N}$ consists of N sample points within each of the adjacent M channels. Singular value decomposition is employed to derive M singular values from the MN matrix. Among these singular values, the largest singular value λ_max (the first singular value) signifies the energy of the signal, while the remaining singular values represent the energy associated with noise. The noise energy of the signal can be defined as Equation 26:

$E_N=\frac{M}{M-1}{\displaystyle \sum _{I=2}^M}{\lambda }_i(26)$

The signal energy is Equation 27:

$E_s={\lambda }_1-\frac{M}{M-1}{\displaystyle \sum _{I=2}^M}{\lambda }_i(27)$

The SNR is Equation 28:

$SNR=\frac{{\lambda }_1-\frac{M}{M-1}{\displaystyle \sum _{I=2}^M}{\lambda }_i}{M-1{\displaystyle \sum _{I=2}^M}{\lambda }_i}(28)$

The relationship between noise energy and SNR was set as an iterative threshold as shown in Equation 29:

$TH=\frac{E_{N}SNR}{C}(29)$

Where, C is constant.

The stopping iteration condition of the algorithm is determined by the signal-to-noise ratio and the accompanying noise. It is important to recognize the distinction between the SNR of the original signal and the signal-to-noise ratio encountered during the calculation process; in this context, the signal-to-noise ratio refers to either the signal-to-noise ratio of the processed signal or the signal-to-noise ratio of the reconstructed signal. Noise encompasses not only the inherent noise of the original signal but also the noise introduced during the reconstruction process. Consequently, to achieve accurate and reliable signal reconstruction, it is essential to comprehensively optimize the stopping conditions, sparse dictionary, and computational methods. Accurate signal reconstruction depends on using the correct dictionary, an appropriate number of dictionaries, and an appropriate threshold for the residual size.

4 Analysis of theoretical model validation

The theoretical model was employed to validate and analyze the research method, as illustrated in Figure 3. Figures 3A–D present the reconstruction results of the reflectivity model, the synthetic seismic record model, the weighted matching pursuit method, and the joint optimization reconstruction method, respectively. The results indicate that the joint optimization method outperforms the weighted matching pursuit method. Furthermore, the correctness and rationale of the method were theoretically verified.

Figure 3

Figure 3. Reconstruction result of theoretical model. (A) Reflection coefficient model. (B) Synthetic seismic record. (C) Reconstruction result of theoretical model with weighted matching pursuit method. (D) Reconstruction result of theoretical model with joint optimization method.

5 Analysis of processing results of actual materials

The effectiveness of the research method for processing actual data was further validated through empirical analysis. Initially, various types of dictionaries were examined. Figure 4A illustrates the distribution of iteration residuals for overcomplete dictionaries, while (b) and (c) display the distribution of differences for optimized overcomplete dictionaries and mixed-phase dictionaries, respectively. A comparison of the three residual distributions reveals that the overcomplete dictionary constructed directly from seismic data exhibits slower changes in residuals, indicating a slower convergence rate. In contrast, the optimized overcomplete dictionary demonstrates reduced oscillation and achieves faster convergence.

Figure 4

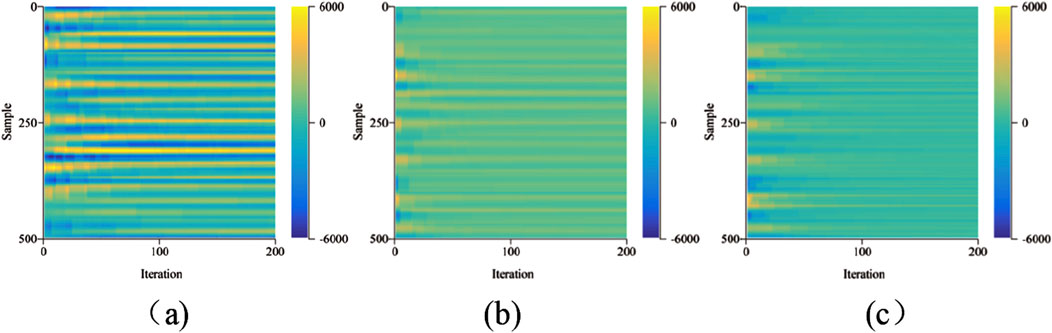
Figure 4. Iterative residual distribution of different dictionary reconstruction. (A) Iterative residual distribution by overcomplete dictionary. (B) Iterative residual distribution by optimized overcomplete dictionary. (C) Iterative residual distribution by mixed phase dictionary.

Sparsity serves as the stopping criterion for iterations in the algorithm, guiding the reconstruction outcome. In this study, noise levels and signal-to-noise ratios were derived by calculating the singular values of the reconstructed seismic signals during the algorithm optimization process. Consequently, an adaptive iterative stopping condition for the algorithm was established. The results illustrated in Figure 5 indicate that the threshold iteration stopping condition, determined through adaptive SNR analysis, significantly enhances both the continuity of the results and the effectiveness of noise control.

Figure 5

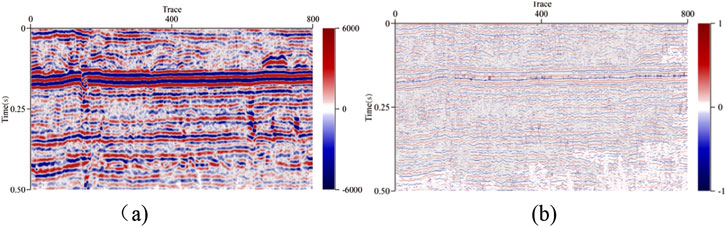
Figure 5. Reflection coefficient estimation result. (A) Original seismic profile. (B) Reflection coefficient estimation result with adaptive threshold stop condition.

To evaluate the effectiveness of the proposed method, actual seismic data were processed, and the results were subsequently compared and analyzed. Figures 6, 7illustrate the outcomes of sparse reconstruction across different frequency bandwidths. The comparative analysis indicates a significant enhancement in the resolution of the processed results, while effectively suppressing noise, particularly in the high-frequency range.

Figure 6

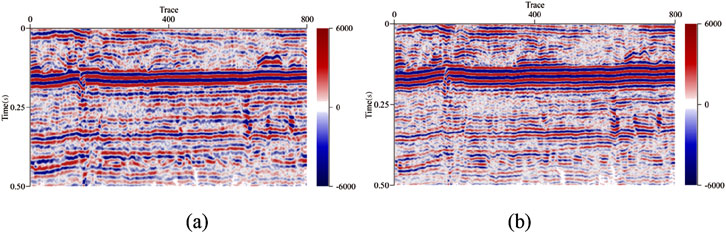
Figure 6. Result before and after seismic data processing. (A) Original seismic profile. (B) Seismic profile after processing.

Figure 7

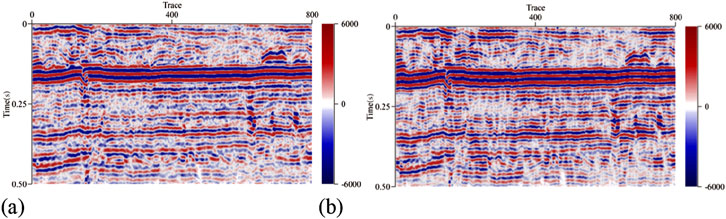
Figure 7. Result before and after seismic data processing (Broaden different frequency bandwidth). (A) Original seismic profile. (B) Seismic profile after processing.

6 Discussion

The seismic data bandwidth expansion technology, based on the theory of compressed sensing and sparse reconstruction, exhibits distinct characteristics compared to earlier methods. Notably, it offers improved noise suppression during the reconstruction process, which is crucial for high-frequency bandwidth expansion. Additionally, this technology encompasses various aspects that warrant further study and discussion.

6.1 Different stopping criteria

The primary objective of this technique is to utilize an overcomplete dictionary to sparsely project seismic signals, thereby achieving a relatively sparse estimation of reflection coefficients. By employing both forward and backward iterative approximation methods, reflection coefficients that converge towards the true solution are obtained, facilitating the reconstruction of seismic records. The stopping criteria for these iterative approximations vary based on the presence of noise in the signals. In theory, for noiseless signals, the stopping criterion is defined as the point at which the residual approaches zero. Conversely, for noisy signals, the stopping criterion must account for noise variance; specifically, the iterative residual should exceed the noise variance. As the reconstruction iterations progress, noise is progressively suppressed, resulting in a decreasing variance and, consequently, a smaller residual. This study correlates the residual in the iterative process with the signal-to-noise ratio of the seismic signal. By weighting the residual according to the signal-to-noise ratio, this approach not only addresses the magnitude of the residual but also considers the effective signal it contains. Testing this methodology in data processing has yielded encouraging results, as shown in Figure 8.

Figure 8

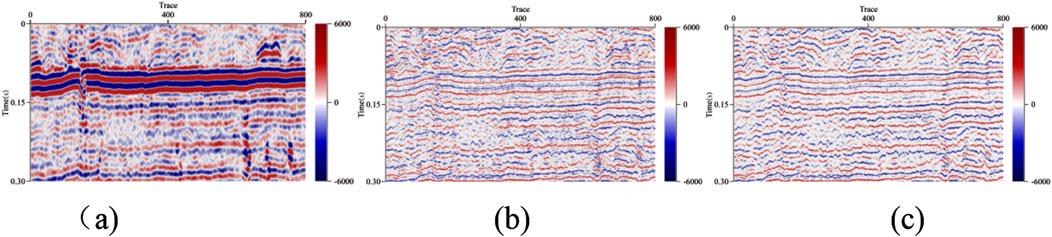
Figure 8. Reflection coefficient estimation result with different stopping criteria. (A) Original seismic profile. (B) Reflection coefficient estimation result with the coherent maximum stopping criterion. (C) Reflection coefficient estimation result with the weighted residual minimum stopping criterion.

6.2 Sparsity

In the matching pursuit algorithm, known sparsity is utilized as an input parameter to constrain the candidate atom set or to serve as a stopping criterion. However, in practical applications, the sparsity of the target signal is often unknown and is typically estimated. Feeding an inaccurately estimated sparsity into algorithms like matching pursuit, which require precise sparsity values, can lead to a rapid degradation in reconstruction performance. Research indicates that both the magnitude and distribution of the residual are influenced by the dictionary and the level of sparsity. The selection of a residual threshold is critical for determining reconstruction accuracy: for noiseless signals, the highest accuracy is achieved when the residual threshold is set to zero, while for noisy signals, optimal accuracy for reconstructing useful information occurs when the residual threshold matches the noise level. By optimizing this process, noise can be further suppressed, thereby enhancing the range of signal reconstruction, as shown in Figure 9. Furthermore, compressed sensing should be evaluated using different standards based on the specific application. In the context of seismic exploration, compressed sensing has found extensive applications, including noise suppression, missing seismic trace reconstruction, and bandwidth expansion of seismic data. In the problem of seismic data bandwidth expansion reconstruction addressed in this paper, sparsity plays a crucial role as a stopping criterion for the algorithm. Factors influencing sparsity include its established role as a known input parameter within the matching pursuit algorithm, where it constrains the capacity of the candidate atom set or serves as a stopping condition.

Figure 9

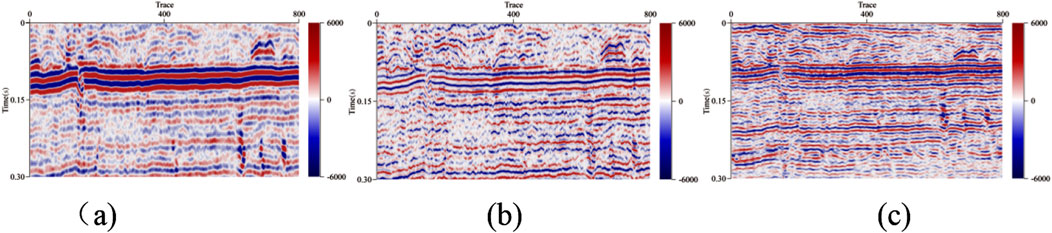
Figure 9. Reconstruction result of seismic data with different sparsity. (A) Original seismic profile. (B) Reconstruction result of seismic data with too small sparsity. (C) Reconstruction result of seismic data with appropriate sparsity.

6.3 Limited bandwidth

Sparse reconstruction-based bandwidth expansion enhances resolution while preserving a high signal-to-noise ratio. Overcomplete dictionaries more effectively capture the complex features of seismic data, enabling flexible bandwidth expansion. Both low and high-frequency bands can be expanded simultaneously or selectively according to specific needs. A potential relationship exists between bandwidth and sparsity; reduced sparsity facilitates the expansion of low-frequency components, while increased sparsity supports high-frequency expansion, as shown in Figure 10. Furthermore, bandwidth is inherently linked to the over complete dictionary, making accurate estimation of this dictionary crucial for achieving effective seismic bandwidth expansion.

Figure 10

Figure 10. Reconstruction result of seismic data with different frequency bandwidth. (A) Original seismic profile. (B) Reconstruction result of seismic data with too wide frequency bandwidth. (C) Reconstruction result of seismic data with appropriate frequency bandwidth.

6.4 Technical advantages

The seismic data compressed sensing sparse reconstruction frequency extension technology studied in this paper, compared with the traditional compressed sensing sparse reconstruction technology (Tang, 2010; Yin et al., 2014; Song and Wu, 2017),the technical advantages are reflected in two aspects. On the one hand, it can keep the low frequency band unchanged when broadening the high frequency, and can broaden the high frequency and low frequency at the same time. On the other hand, in the process of high-frequency broadening, high-frequency noise can be well suppressed, as shown in Figure 11. The comparison results show that the technical method in this paper has obvious effects in noise suppression, amplitude energy and resolution enhancement.

Figure 11

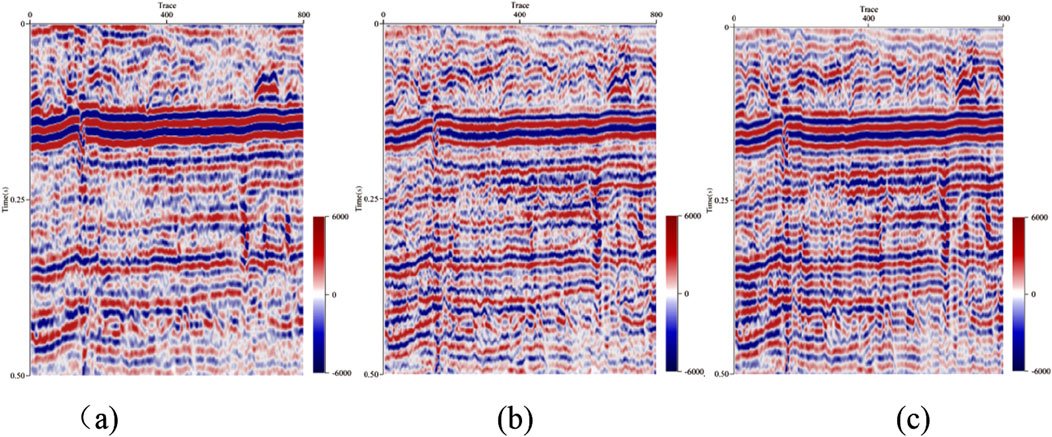
Figure 11. Reconstruction result of seismic data with different method. (A) Original seismic profile. (B) Reconstruction result of seismic data with traditional method. (C) Reconstruction result of seismic data with method in this paper.

7 Conclusion

Sparsity is a crucial factor influencing the reconstruction quality of strictly sparse, noise-free signals. In contrast, the reconstruction quality of noisy signals is affected by both sparsity and signal amplitude. This paper presents an approach that not only captures the complex characteristics of the signal but also minimizes the multiplicity of reconstruction solutions. We propose a reliable reconstruction method using an adaptive dictionary and constraint matching, specifically through an iterative residual evaluation mechanism. This approach enhances both the reconstruction quality and performance of seismic signals. Addressing the challenge of unknown sparsity in practical applications, we analyze the factors that influence sparsity and establish the conditions for algorithm termination based on signal-to-noise ratio and noise. By examining the relationships among sparse signal length, residual size, and signal-to-noise ratio, we determine optimal stopping criteria. Comparative analyses of processed data demonstrate a significant improvement in resolution and effective noise suppression.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SL: Writing–original draft. WS: Writing–original draft. AY: Writing–review and editing. SH: Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors SL, AY, and SH were employed by China National Offshore Oil Corporation.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anvari, R., Siahsar, M. A. N., Gholtashi, S., Kahoo, A. R., and Mohammadi, M. (2017). Seismic random noise attenuation using synchrosqueezed wavelet transform and low-rank signal matrix approximation. IEEE Trans. Geoscience Remote Sens. 55 (11), 6574–6581. doi:10.1109/TGRS.2017.2730228

CrossRef Full Text | Google Scholar

Bai, L. S., Liu, Y. K., Lu, H. Y., Wang, Y. B., and Chang, X. (2014). Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing. Chin. J. Geophys. 57 (9), 2937–2945. doi:10.6038/cjg20140919

CrossRef Full Text | Google Scholar

Buchholtz, H. (1972). A note on signal distortion due to dynamic (NMO) corrections. Geophys. Prospect. 20 (2), 395–402. doi:10.1111/j.1365-2478.1972.tb00642.x

CrossRef Full Text | Google Scholar

Cai, T. T., and Wang, L. (2011). Orthogonal matching pursuit for sparse signal recovery with noise. IEEE Trans. Inf. theory 57 (7), 4680–4688. doi:10.1109/TIT.2011.2146090

CrossRef Full Text | Google Scholar

Chang, S. G., Yu, B., and Vetterli, M. (2000). Spatially adaptive wavelet thresholding with context modeling for image denoising. IEEE Trans. image Process. 9 (9), 1522–1531. doi:10.1109/83.862630

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, Y., Du, Q., Liu, L., and Zhang, Q. (2019). Feature analysis and compensation of seismic low-frequency based on compressed sensing and broad-band Yu-type low-passing shaping filter. Chin. J. Geophys. 62 (6), 2267–2275. doi:10.6038/cjg2019M0096

CrossRef Full Text | Google Scholar

Donoho, D. L. (2006). Compressed sensing. IEEE Trans. Inf. theory 52 (4), 1289–1306. doi:10.1109/TIT.2006.871582

CrossRef Full Text | Google Scholar

Gholami, A. (2014). Non-convex compressed sensing with frequency mask for seismic data reconstruction and denoising. Geophys. Prospect. 62 (6), 1389–1405. doi:10.1111/1365-2478.12146

CrossRef Full Text | Google Scholar

Haldorsen, J. B. U., Miller, D. E., and Walsh, J. J. (1994). Multichannel wiener deconvolution of vertical seismic profiles. Geophysics 59 (10), 1500–1511. doi:10.1190/1.1443540

CrossRef Full Text | Google Scholar

Herrmann, F. J., and Hennenfent, G. (2008). Non-parametric seismic data recovery with curvelet frames. Geophys. J. Int. 173 (1), 233–248. doi:10.1111/j.1365-246X.2007.03698.x

CrossRef Full Text | Google Scholar

Herrmann, F. J., and Li, X. (2012). Efficient least-squares imaging with sparsity promotion and compressive sensing. Geophys. Prospect. 60, 696–712. doi:10.1111/j.1365-2478.2011.01041.x

CrossRef Full Text | Google Scholar

Huang, W. (2023). A genetic algorithm optimized undersampling method for seismic sparse acquisition and reconstruction. IEEE Trans. Geoscience Remote Sens. 61, 1–10. doi:10.1109/TGRS.2023.3252277

CrossRef Full Text | Google Scholar

Kaaresen, K. F., and Taxt, T. (1998). Multichannel blind deconvolution of seismic signals. Geophysics 63 (6), 2093–2107. doi:10.1190/1.1444503

CrossRef Full Text | Google Scholar

Song, W. Q., and Wu, C. D. (2017). Improve the resolution of seismic data with compression perception method. Oil Geophys. Prospect. 52 (2), 214–219. doi:10.13810/j.cnki.issn.1000-7210.2017.02.003

CrossRef Full Text | Google Scholar

Song, W. Q., Zhang, Y., Wu, C. D., and Hu, J. L. (2017). The method of weak seismic reflection signal processing and extracting based on multitrace joint compressed sensing. Chin. J. Geophys. 60 (8), 3238–3245. doi:10.6038/cjg20170828

CrossRef Full Text | Google Scholar

Sun, H., Gao, F., Huang, X., Zhang, J., Li, M., and Zhao, X. (2023). Time-frequency analysis method of seismic data based on sparse constraints for road detection. IEEE Trans. Intelligent Transp. Syst. 25 (3), 2748–2756. doi:10.1109/TITS.2023.3299353

CrossRef Full Text | Google Scholar

Sun, H., Zhang, J., Xue, Y., and Zhao, X. (2024). Seismic inversion based on fusion neural network for the joint estimation of acoustic impedance and porosity. IEEE Trans. Geoscience Remote Sens. 62, 1–10. doi:10.1109/TGRS.2024.3426563

CrossRef Full Text | Google Scholar

Tang, G. (2010). Seismic data reconstruction and denoising based on compressive sensing and sparse representation. Beijing: Tsinghua University.

Google Scholar

Wang, C., Zong, Z., Yin, X., and Li, K. (2024). Seismic resolution enhancement with variational modal-based fast-matching pursuit decomposition. Interpretation 12 (1), T77–T86. doi:10.1190/INT-2023-0002.1

CrossRef Full Text | Google Scholar

Wang, X. W., and Wang, H. Z. (2014). A research of high-resolution plane-wave decomposition based on compressed sensing. Chin. J. Geophys. 57 (9), 2946–2960. doi:10.6038/cjg20140920

CrossRef Full Text | Google Scholar

Yin, H., Li, J., Chai, Y., and Yang, S. X. (2014). A survey on distributed compressed sensing: theory and applications. Front. Comput. Sci. 8 (6), 893–904. doi:10.1007/s11704-014-3461-7

CrossRef Full Text | Google Scholar

Zhang, J. H., Zhang, B. B., Zhang, Z. J., Liang, H. X., and Ge, D. M. (2015). Low-frequency data analysis and expansion. Appl. Geophys. 12 (2), 212–220. doi:10.1007/s11770-015-0484-2

CrossRef Full Text | Google Scholar

Zhang, L., Han, L. G., Xu, D. X., Li, Y., and Li, H. (2017). Seismic data reconstruction with Shearlet transform based on compressed sensing technology. Oil Geophys. Prospect. 52 (2), 220–225. doi:10.13810/j.cnki.issn.1000-7210.2017.02.004

CrossRef Full Text | Google Scholar

Zhao, Z., Rao, Y., and Wang, Y. (2023). Structure-adapted multichannel matching pursuit for seismic trace decomposition. Pure Appl. Geophys. 180 (3), 851–861. doi:10.1007/s00024-023-03234-w

CrossRef Full Text | Google Scholar

Zhao, Z. Y., Li, Z. C., and Zhang, M. (2020). Reconstruction of discrete orthogonal S-transform seismic data using compressed sensing technology. Oil Geophys. Prospect. 55 (1), 29–35. doi:10.13810/j.cnki.issn.1000-7210.2020.01.004

CrossRef Full Text | Google Scholar

Zong, J., Chen, Y., Lu, C., Hu, G., and Wo, Y. (2022). Structure-oriented mapping of the subsalt fractured reservoir by reflection layer tomography from a perspective of the zero-offset vertical seismic profiling. IEEE Trans. Geoscience Remote Sens. 60, 1–11. doi:10.1109/TGRS.2022.3210046

CrossRef Full Text | Google Scholar

Zong, J., Stewart, R. R., Yang, J., Dyaur, N., and Wo, Y. (2023). Investigating seismic mode conversions from an ultra-high-velocity caprock by physical modelling, numerical simulations and a Gulf of Mexico salt proximity VSP survey. Geophys. J. Int. 234 (2), 1430–1446. doi:10.1093/gji/ggad151

CrossRef Full Text | Google Scholar

Zong, Z., Fu, T., and Yin, X. (2023). High-dimensional generalized orthogonal matching pursuit with singular value decomposition. IEEE Geoscience Remote Sens. Lett. 20, 1–5. doi:10.1109/LGRS.2023.3264623

CrossRef Full Text | Google Scholar