A comparative analysis of five land surface temperature downscaling methods in plateau mountainous areas

Land surface temperature (LST) is a crucial factor for reflecting climate change. High spatial resolution LST is particularly significant for environmental monitoring in plateau and mountainous areas, which are characterized by rugged landscapes, diverse ecosystems, and high spatial variability in LST. Typical plateau mountainous areas in Diqing Tibetan Autonomous Prefecture and Dali Bai Autonomous Prefecture were selected as study areas. Three machine learning models, including Back Propagation (BP) Neural Network, random forest (RF), and extreme gradient boosting (XGBoost), and two classic single-factor linear regression models (DisTrad and TsHARP) were compared. Particle Swarm Optimization (PSO) was introduced to optimize hyperparameters of three machine learning methods. Regression factors suitable for plateau mountainous areas, including normalized vegetation index (NDVI), normalized multi-band drought index (NMDI), bare soil index (BSI), normalized difference snow index (NDSI), elevation, surface roughness (SR), and Hillshade were selected. The performance of five models was analyzed from the perspective of different spatial resolutions and land cover types. The results revealed that the performance of machine learning models is better than traditional linear models in both study areas. Based on the coefficient of determination (R²), root mean square error (RMSE), and mean absolute error (MAE), XGBoost demonstrated the best performance. For study area A, the results were R² = 0.891, RMSE = 2.67 K, and MAE = 1.83 K, while for study area B, the values were R² = 0.832, RMSE = 1.98 K, and MAE = 1.54 K. In addition, among different land cover types, the XGBoost model has the best performance in both study areas. Moreover, the larger the ratio of initial resolution to target resolution, the lower the accuracy of downscaled LST (DLST). In summary, the XGBoost model is more suitable for downscaling LST in plateau mountainous areas.

1 Introduction

Land surface temperature (LST) is crucial for driving energy exchange between the land surface and the atmosphere (Li Z. L. et al., 2023). In plateaus and mountainous regions with complex terrain, LST plays a vital role. The scarcity of high spatial resolution LST data in these areas has significantly hindered environmental monitoring, fire prevention, long-term vegetation phenology tracking, and assessment of mountain vegetation’s impact on the global carbon cycle (He and Tang, 2023; Rao et al., 2019; Bibi et al., 2018). Therefore, obtaining high spatial resolution LST through downscaling is urgent to enhance environmental monitoring in plateaus and mountainous regions (Wang S. et al., 2017; Zhang et al., 2022).

Traditional methods of measuring LST, such as weather station monitoring, offer intuitive insights but are limited in their ability to describe LST data over large areas (Weng, 2009). In contrast, remote sensing satellites provide the latest, extensive, and long-term LST data (Li et al., 2013; Metz et al., 2014; Zhang et al., 2021; Long et al., 2020). However, the current methods for thermal infrared band inversion of LST face the challenge of achieving both high temporal and spatial resolution simultaneously. For instance, while the LST products from Moderate Resolution Imaging Spectroradiometer (MODIS) offer a daily temporal resolution, their spatial resolution is limited to 1 km (Wan et al., 2002). Similarly, the Landsat satellite’s thermal infrared band provides a spatial resolution of 100 m, but its temporal resolution is 16 days (Hough et al., 2020). Therefore, obtaining high-precision, low-cost LST data with high temporal and spatial resolution is key to the management and monitoring of ecological environment in plateau mountainous areas. The spatial downscaling method for LST has attracted wide attention due to its high practicality.

Recently, some LST spatial downscaling methods to enhance the resolution of LST data were proposed, which were classified into two main categories in terms of the employed algorithms: (Pu and Bonafoni, 2023) the fusion-based method and the scaling factor conversion-based method. In the first category, the image fusion technique is used to establish relationships between LST images. Although the obtained results are highly accurate and retain information from the original LST images, they often overlook explicit physical backgrounds and lack a physical mechanism (Zhan et al., 2011). In addition, it is essential to consider the impact of various factors such as sensor noise, LST retrieval error, and heterogeneous landscapes on high spatiotemporal LST data and evaluate the uncertainty associated with mixed pixels of different Land Use/Land Cover (LULC) coverage types (Pu and Bonafoni, 2023). Methods based on scaling factor conversion mainly include modulation allocation, spectral mixture model, and statistical regression (Zhan et al., 2011). The modulation allocation and spectral mixture methods are based on physical mechanisms and offer clear physical interpretations. However, due to their relatively complex implementation, their applications are limited (Xu and Cheng, 2021). Methods based on statistical regression establish linear or nonlinear relationships between LST and related physical parameters at low spatial resolution. These relationships are then applied to high spatial resolution data based on the principle of “scale invariance” (Deilami et al., 2018). It offers advantages such as easy operation and high accuracy, making it widely utilized (Duan and Li, 2016; Wu and Li, 2019). As a classic statistical regression model, the DisTrad model (Kustas et al., 2003) downscales LST by establishing a linear relationship between normalized difference vegetation index (NDVI) and low spatial resolution LST. Another classic statistical regression model, namely, the TsHARP model (Agam et al., 2007; Agam et al., 2008), improved upon the DisTrad model by using Fraction of Vegetation Cover (FVC) instead of the vegetation index to establish a regression relationship with LST, enhancing the downscaling effect. The aforementioned two single-factor linear regression methods have a straightforward process and quick execution. However, the relationships between NDVI, FVC, and LST vary across different land cover types, leading to complexities in areas with diverse land cover types, sparse vegetation, and regions lacking vegetation. Therefore, single-factor linear regression models may not be suitable for areas characterized by high heterogeneity (Hutengs and Vohland, 2016; Li Y. et al., 2023).

Many additional regression factors, such as surface albedo, elevation, slope, solar incidence angle, and land cover type, have been introduced for LST downscaling, achieving promising results (Dominguez et al., 2011; Zakšek and Oštir, 2012). In the context of LST downscaling involving multiple factors, machine learning regression prediction technology offers significant advantages due to its high efficiency, ease of operation, and high prediction accuracy. Consequently, an increasing number of downscaling studies were conducted utilizing machine learning models, including artificial neural networks (ANN) (Bindhu et al., 2013; Lemeshewsky and Schowengerdt, 2001; Yang et al., 2011; Pu, 2021), back propagation (BP) neural network, support vector machines (SVM) (Ghosh and Joshi, 2014; Ebrahimy and Azadbakht, 2019), random forest (RF) (Li et al., 2019; Ebrahimy et al., 2021), and extreme gradient boosting (XGBoost) (Xu et al., 2021; Tu et al., 2022). These studies have demonstrated the superiority of machine learning prediction models in LST downscaling. As a result, they have been widely applied to downscale LST in mountainous areas with complex terrain. Wang Z. et al. (2017) proposed a BP-based downscaling method, utilizing multiple scale factors as input variables. They demonstrated the robustness of the method in mountainous and mixed areas. Tu et al. (2022) utilized the TsHARP algorithm, RF model, and XGBoost model to conduct downscaling in karst areas. They pointed out that the XGBoost model exhibited superior performance compared to other methods. Bartkowiak et al. (2019) used the RF model to predict high-resolution LST, considering topographic features and land cover heterogeneity. These studies demonstrate that in the complex terrain of mountainous regions, machine learning can better capture the nonlinear relationships between LST and regression factors, resulting in improved LST downscaling effects.

Although machine learning models were extensively used for LST downscaling, there are two main limitations. Firstly, most experiments focused on downscaling between single-scale factors, namely, from one low-resolution to one high-resolution LST. However, evaluating performance at single-scale may not fully demonstrate the applicability of their methods. Secondly, different LST downscaling methods perform differently under various land cover types. Analyzing method performance across different land cover types can enhance the reliability of the results. Therefore, the study employed regression factors suitable for LST downscaling machine learning models in plateau mountainous areas. Three machine learning models (BP, RF, and XGBoost) and two classic single-factor linear methods (DisTrad and TsHARP) were utilized for LST downscaling in two typical plateau mountainous areas in Diqing Tibetan Autonomous Prefecture and Dali Bai Autonomous Prefecture. Hyperparameter optimization for three machine learning models was performed with the particle swarm optimization (PSO) method. The performance of spatial downscaling method under different land cover types was studied, and multi-level downscaling experiments on LST with varying target resolutions were conducted. The arrangement of the study is: In Section 2, the study areas and the used data are described. In Section 3, the used LST downscaling methods are introduced. In Section 4, the LST downscaling results are analyzed. Sections 5, 6 furnish the discussion and the conclusion of this study, respectively.

2 Study area and datasets

2.1 Study area

Two classical plateau mountainous areas in Yunnan Province, China were utilized in the study. Figure 1 displays the land covers, location, and elevation of two study areas.

Figure 1

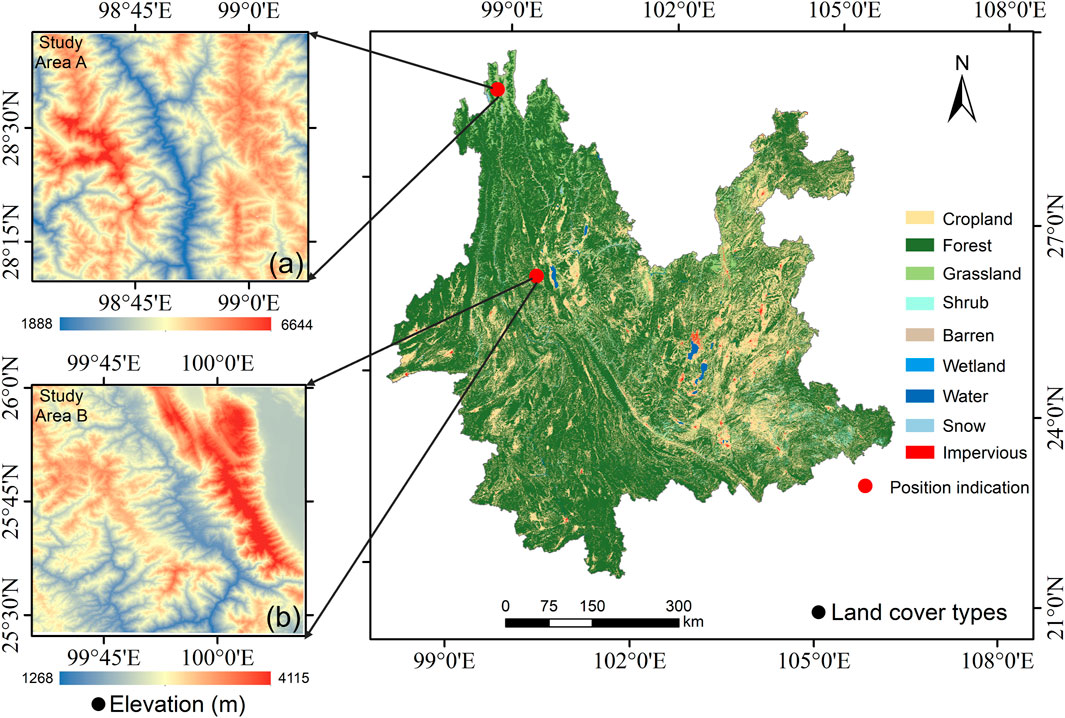
Figure 1. Overview of the study areas A and B, including location, land cover types, and surface elevation from ALOS World 3D-30 m elevation data (version 2.1).

Study Area A is situated in Deqin County, Diqing Tibetan Autonomous Prefecture, Yunnan Province. It lies at the confluence of Yunnan, Sichuan, and Tibet provinces, between the Nujiang River and Lancang River in the middle section of the Hengduan Mountains. The terrain of Deqin County is characterized by steep slopes, encompassing rugged mountains and valleys with varying elevations and complex geological structures. The longitude and latitude of study area A range from 98°30′to 99°3′east longitude and from 28°10′to 28°43′north latitude. The terrain is characterized by high elevations in the east and west, with a lower central region. The western part of study area A is the Meili Snow Mountain, which is covered by snow year-round. The predominant land cover types in study area A include snow, forests, grasslands, and barren.

Study Area B is situated in Dali Bai Autonomous Prefecture. It has a low-latitude plateau monsoon climate characterized by mild summers and winters with no extreme temperatures. Study Area B is located in the middle of Dali Prefecture and involves Cangshan-Erhai protected area. The terrain in study area B is undulating and varies in elevation. The longitude and latitude of study area B range from 99°35′to 100°8′east longitude and from 25°28′to 26°1′north latitude. The predominant land cover types of study area B include forests, shrubs, and grasslands.

The selection of these two study areas is based on several factors. Firstly, both study areas belong to typical plateau mountainous areas, making the study more representative. Secondly, the presence of diverse land cover types in both areas facilitates the verification of the downscaling model’s applicability to both single and complex land cover types. Finally, study area A features perennial snow, while study area B does not, despite both being located at high altitudes with significantly different elevation ranges. Conducting experiments in these two distinct areas ensures more sufficient and comprehensive results.

2.2 Data acquisition and processing

2.2.1 LANDSAT 9 satellite data

The study utilized various data products from the U.S. Geological Survey website https://earthexplorer.usgs.gov/, including Landsat 9 LST products, surface reflectance data, surface downwelling shortwave radiation products, and emissivity products. The spatial resolutions of them are 30 m. These datasets underwent systematic processing, including radiometric measurements and geometric corrections. Radiation calibration was performed based on the calibration coefficients provided in the documentation for each product. The Landsat 9 LST product served as the reference LST (RLST) and was also used to generate the upscaled low-resolution LST. Surface downwelling shortwave radiation products and emissivity products were incorporated as parameters in the radiative transfer equation for LST upscaling. Surface reflectance data were employed to calculate remote sensing indices essential for the study, including the NDVI which reflects vegetation coverage, Normalized Multi-band Drought Index (NMDI) which reflects the moisture content of soil and vegetation, Bare Soil Index (BSI) which reflects the bareness of the surface, and Normalized Difference Snow Index (NDSI) which reflects the snow cover. Given the requirement for remote sensing indices with varying resolutions, the study adopted the average aggregation method to upscale the surface reflectance to different spatial resolutions, followed by individual factor calculation. Detail information of each study area is shown in Table 1.

Table 1

Table 1. Detail information of study areas.

2.2.2 DEM data

Considering that the study area is a typical plateau mountainous area with complex terrain, and terrain factors significantly affect LST, the Advanced Surface Observation Satellite (ALOS) World 3D 30-m global digital ground model dataset (version 2.1) was adopted. These data are freely available from the website https://www.eorc.jaxa.jp/ALOS/en/aw3d30/. The DEM data was used to extract terrain factors, including altitude, surface roughness (SR), and Hillshade. DEM data of different resolutions was obtained through average aggregation, and then these terrain factors (i.e., altitude, SR, Hillshade) of different resolutions were calculated separately.

2.2.3 Land cover dataset

The land use data utilized is sourced from the CLCD dataset provided by Yang and Huang (Yang and Huang, 2021), which is based on Landsat’s annual China Land Cover Dataset (CLCD). The CLCD dataset is freely accessible at https://doi.org/10.5281/zenodo.4417810. It offers a spatial resolution of 30 m and has been updated up to the year 2022. This data was utilized to evaluate the accuracy of each downscaling approach under different land cover types.

3 Methodology

3.1 Multi-resolution upscaling of LST

To explore variations in LST downscaling results across different scales in plateau mountainous areas, four downscaling schemes were devised (see Figure 3). It is necessary to downscale LST to different target resolutions and adjust regressors to different resolutions. For regressors, remote sensing indices are upscaled to various spatial resolutions using the average aggregation method applied to Landsat 9 OLI data, and then computed individually. Similarly, terrain factors are obtained by averaging and aggregating ALOS data to each resolution, followed by the extraction of terrain factors at each resolution. In contrast, for LST, previous studies have utilized simple averaging aggregation methods (Guo et al., 2022), which neglect the physical mechanisms influencing LST. Notably, sensors observe that surface canopy radiance undergoes attenuation by the atmosphere, influencing the captured signal. Traditional spatial aggregation methods of LST do not account for the energy distribution across different scales. Directly aggregating LST can introduce uncertainty into the results and lack physical significance. Therefore, the direct averaging approach may not accurately reflect the true surface temperature. In order to obtain LSTs at different resolution levels, high-resolution LST products are used. Considering the atmospheric downward radiation, the average aggregation method is applied to estimate brightness of corresponding coarse-resolution pixels. Then, the Planck function is used to convert coarse-resolution pixels into LST. Calculation details are shown in Equations 1–3:

${\epsilon }_{c}B\left(T_c,\lambda \right)=\frac{1}{n}\left\{{\displaystyle \sum _{i=1}^n}\left[{\epsilon }_{i}B\left(T_i,\lambda \right)+\left(1-{\epsilon }_i\right){R_{atm,i}}^{\downarrow }\right]\right\}(1)$

$B\left(T_c,\lambda \right)=\frac{c_1{\lambda }^{-5}}{\mathit{exp}{\left(\frac{c_2}{\lambda T_c}\right)}^{-1}}(2)$

$T_c=\frac{c_2}{\lambda \ln \left[\frac{c_1}{B\left(T_{\mathrm{c}},\lambda \right){\lambda }^5}+1\right]}{c}^2(3)$

where B(T_c, λ) is the radiance; ε_c and T_c are the emissivity and LST corresponding to each pixel of the low spatial resolution image, respectively; ε_i and T_i stand for the emissivity and LST corresponding to the high spatial resolution image, respectively. n indicates the number of high spatial resolution image pixels corresponding to each ground spatial resolution pixel. ${R_{atm,i}}^{\downarrow }$ represents the atmospheric downward radiation corresponding to each high spatial resolution pixel. λ is the effective central wavelength, c₁ and c₂ are spectral constants (c₁ = 1.191 $\times$ 10⁸ W μm⁴·m^-2·sr⁻¹, c₂ = 1.43877 $\times$ 10⁴ μm K). T_c at each resolution can be derived from the above formula.

3.2 LST downscaling model

3.2.1 Classic downscaling model

To assess the performance of subsequent machine learning LST downscaling approaches, two widely used classic single-factor regression models (i.e., DisTrad and TsHARP) for LST downscaling were selected.

3.2.1.1 DisTrad

The DisTrad downscaling model, proposed by Kustas et al. (2003), relies on the observation that the NDVI and LST exhibit similar correlations across multiple spatial scales. This correlation is leveraged to construct a regression equation model between LST and vegetation index at low spatial resolution, which can then be extrapolated to construct a similar regression model at high spatial resolution. Any spatial variability in LST that is not captured by the fitting process is addressed by examining the residuals and adjusting accordingly. The downscaling process of the DisTrad method typically follows Equations 4–6:

${LST}_{\mathit{c}}=a_c*{NDVI}_c+b_c(4)$

$∆T=\text{LST}-{LST}_c(5)$

${LST}_f=a_c*{NDVI}_f+b_c+∆T(6)$

where LST_C and NDVI_C are low spatial resolution LST and NDVI, respectively. a_c and b_c are regression coefficients. ΔT is the error caused by soil moisture.

3.2.1.2 TsHARP

The TsHARP model proposed by Agam et al. (2007) is an improvement on the Distrad model. The basic principle of TsHARP model and DisTrad model is the same. Both of them improve the spatial resolution of LST through surface vegetation parameters related to LST, but the vegetation index used is different.

The TsHARP model shows superior performance compared to the DisTrad model. In other words, the TsHARP model’s predictive ability of the relationship between LST and fractional vegetation coverage (FVC) is superior to the DisTrad model’s predictive ability of the relationship between LST and NDVI (Norman et al., 1995). The vegetation coverage is calculated by the Equation 7:

$FVC=1-{\left(1-NDVI\right)}^{0.625}(7)$

3.2.2 Machine learning predictive models

3.2.2.1 Back propagation (BP)

The BP neural network model is a type of multi-layer feedforward network trained via error backpropagation algorithm. It’s one of the most popular neural network models in various fields (Li et al., 2012). The hyperparameters of the BP neural network include the size and number of hidden layers, learning rate, number of iterations, regularization parameters, etc. During training, it adjusts the connection weights by the backpropagation algorithm to reduce the error between the network’s output and the actual target values, thus improving the accuracy of the model. It has been widely recognized that the BP neural network has good regression and prediction performance (Zhu et al., 2021).

3.2.2.2 Random forest (RF)

The RF model was introduced by Breiman (2001). It operates as an ensemble learning model comprising decision trees as the fundamental classifiers. During training, various hyperparameters, including the number of trees, maximum tree depth, and minimum samples required for node splitting, can be adjusted to optimize performance. In regression tasks, the RF model computes the final output by averaging the predictions of individual trees. The RF model is robust against multicollinearity and effectively mitigates the risk of overfitting, making it widely utilized in multivariate regression prediction research (Wu and Li, 2019; Zhao and Duan, 2020).

3.2.2.3 Extreme gradient boosting algorithm (XGBoost)

The XGBoost model, introduced by Chen and Guestrin (2016), is built upon the gradient boosting decision tree model. Unlike the RF model, which averages the predictions of weak learners, the XGBoost model combines the weighted sum of each learner’s results to generate the final output. It leads to results with smaller deviations in most cases. Traditional boosting models, such as Gradient Boosting Machine (GBM), are susceptible to overfitting. To address this issue, the XGBoost model incorporates regularization parameters to regulate model complexity. Additionally, it employs first-order and second-order Taylor expansions to approximate the objective function. Moreover, the XGBoost model supports parallel computing, which significantly accelerates the training process. As a result, the XGBoost model has emerged as one of the state-of-the-art techniques in modern machine learning. Currently, the XGBoost model is widely used in LST downscaling simulation studies (Xu et al., 2021; Tu et al., 2022).

3.3 Particle swarm optimization (PSO)

Setting appropriate hyperparameters in machine learning prediction models is crucial for achieving high-quality results. However, manual adjustment of hyperparameters for each model is time-consuming, necessitating a faster method. The Particle Swarm Optimization (PSO) algorithm, known for its simplicity, ease of implementation, and strong global optimization capabilities, efficiently optimizes parameters in machine learning models. Therefore, the study employs the PSO algorithm to optimize the hyperparameters of machine learning models. It enables the study to concentrate on results rather than spending excessive time on determining optimal hyperparameters for each model.

Introduced by Eberhart and Kennedy (1995), the PSO algorithm operates by iteratively updating the velocity and position of particles, driving the particle swarm towards the global optimal solution. Each particle calculates new velocity and position based on its current state, historical experience, and information from global optimal solutions. Through continuous iteration, particle swarms can often discover improved solutions within the search space. Assuming there are N particles in a D-dimensional space, in which the position of particle i is represented as X_i = (x_i1, x_i2,.x_iD), and substituting x_i into the adaptation function f (x_i) yields the fitness value. The velocity of particle i is denoted as V_i = (v_i1, v_i2,.v_iD), with the best position experienced by the individual particle i as pbest_i = (p_i1, p_i2,. p_iD), and the best position experienced by the entire group as gbest_i = (g_i1, g_i2,. g_iD). Each particle updates its velocity and position based on Equations 8, 9:

$v_{id}^k=w{v}_{id}^{k-1}+{c_a}_1{r}_1\left(pbes{t}_{id}-x_{id}^{k-1}\right)+c_{a2}{r}_2\left(gbes{t}_d-x_{id}^{k-1}\right)(8)$

$x_{id}^k=x_{id}^{k-1}+v_{id}^{k-1}(9)$

where $x_{id}^k$ represents the D-dimensional component of the flight velocity vector of particle i in the $k_{th}$ iteration; $x_{id}^k$ denotes the D-dimensional component of the position vector of particle i in the kth iteration; c_a1 and c_a2 are acceleration constants that adjust the maximum learning step; r₁ and r₂ represent two random functions, with values ranging from [0,1] to rise the randomness; w is the inertia weight, which adjusts the search range of the solution space. The inertia weight w denotes the extent to which particles retain their original speed. If w is high, the global convergence ability is strong while the local convergence ability is weak. When combining three machine learning models, the hyperparameters of each model are treated as the position of the particles. The update process of particle velocity and position is then utilized to update these parameters. The position vector diagram of particle motion and the optimization process are summarized in Figure 2:

Figure 2

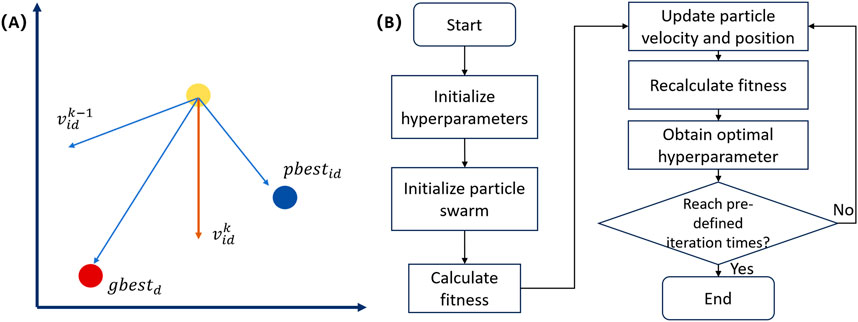
Figure 2. Particle motion position vector diagram (A) and particle swarm optimization hyperparameter process diagram (B).

3.4 Simulation schemes and technical route

All five LST downscaling models in the study employ regression techniques to achieve LST downscaling. By employing “scale invariance”, these models establish the relationship between LST and regression factors at low spatial resolutions. Specifically, three machine learning models establish the nonlinear relationship between LST and multiple regression factors at low resolution, which is then applied to high spatial resolution.

To evaluate the performance of the five downscaling methods, we implemented Scheme 1, which downscales the original LST from 960 m to 30 m. We assessed each method by comparing spatial details and analyzing performance indicators (R², RMAE, MAE), while also magnifying different land cover types for comparison. To examine the consistency of downscaling results across various scales, we introduced three additional schemes: downscaling to 60 m (Scheme 2), 120 m (Scheme 3), and 240 m (Scheme 4). All four schemes followed the same principle, utilizing identical technical procedures to reduce the size from 960 m to 30 m. The original 30 m LST, along with the upgraded 60 m, 120 m, and 240 m LSTs, served as reference values for accuracy evaluation at their respective scales, representing the actual LST. The entire experimental process is illustrated in Figure 3.

Figure 3

Figure 3. The research framework of the study.

4 Results

4.1 Spatial distribution of downscaling result

The XGBoost, RF, BP, DisTrad, and TsHARP models are applied to conduct Scheme 1 experiment, downscaling 960 m coarse LST (CLST) to the target resolution (30 m), with the Landsat 9 LST product serving as the RLST. Figures 4, 5 illustrate the spatial distribution of downscaling results for study areas A and B on 16 November 2021 and 1 February 2023, respectively. In each figure, (A) and (B) represent the spatial distribution of Landsat 9 LST with an upscaling of 960 m and 30 m RLST, respectively. (C) to (G) depict the LST downscaling results of DisTrad, TsHARP, BP, RF, and XGBoost models, respectively. The five DLST plots in both study areas closely resemble the RLST plots, exhibiting the same numerical range as the 30 m RLST and displaying similar spatial distribution patterns. However, the two classical downscaling methods both encounter challenges in accurately restoring LST spatial details with sufficient accuracy. While the temperature distribution with high spatial resolution can generally be captured, there are noticeable inaccuracies in certain areas. Particularly in the spatial distribution of study area A, noise is evident at the boundaries of water bodies along the river. The two classic downscaling methods experience significant overestimation in these regions. The three machine learning downscaling methods exhibit superior performance in terms of the spatial distribution of the downscaled results. They accurately capture the temperature distribution of LST at high spatial resolution and restore the spatial details of LST. The downscaled LST images depict features such as rivers and mountain edges. However, it’s evident that the BP neural network model shows notable overestimation at high temperatures and underestimation at low temperatures in the downscaled results. In comparison, the downscaled results of RF model and XGBoost model better represent the LST. Compared to machine learning models like BP neural network, RF, and XGBoost, the DisTrad and TsHARP models, as single-factor regression models, offer quicker and more concise results. However, they fall short in terms of spatial detail recovery compared to the aforementioned machine learning models.

Figure 4

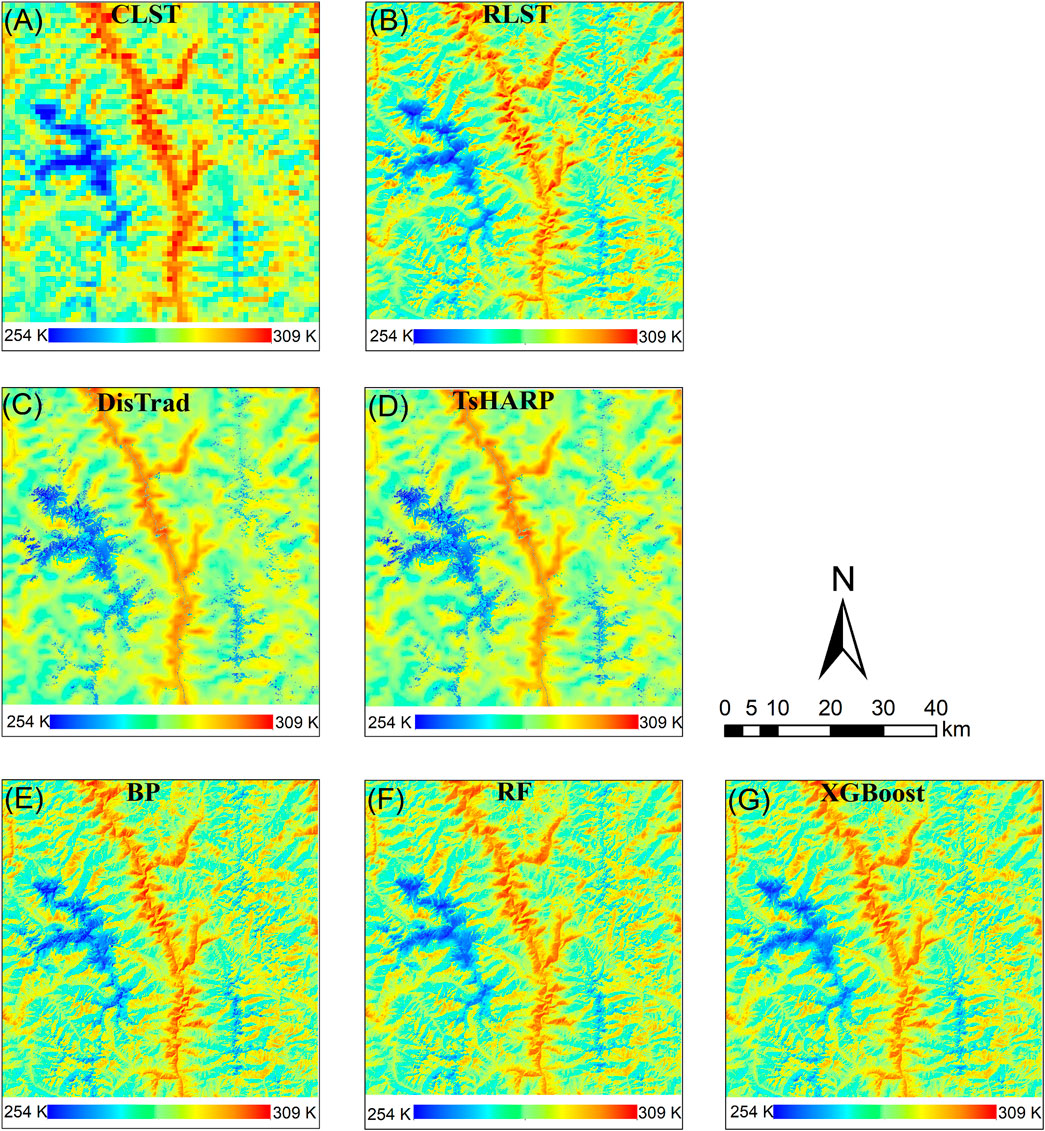
Figure 4. Comparisons of TsHARP, DisTrad-based, BP-based, RF-based, and proposed XGBoost-based algorithms for Study Area A (A) Landsat-9 LST (960 m), (B) Landsat-9 LST (30 m), (C) DisTrad downscaled LST (30 m), (D) TsHARP downscaled LST (30 m), (E) BP downscaled LST (30 m), (F) RF downscaled LST (30 m) and (G) XGBoost downscaled LST (30 m).

Figure 5

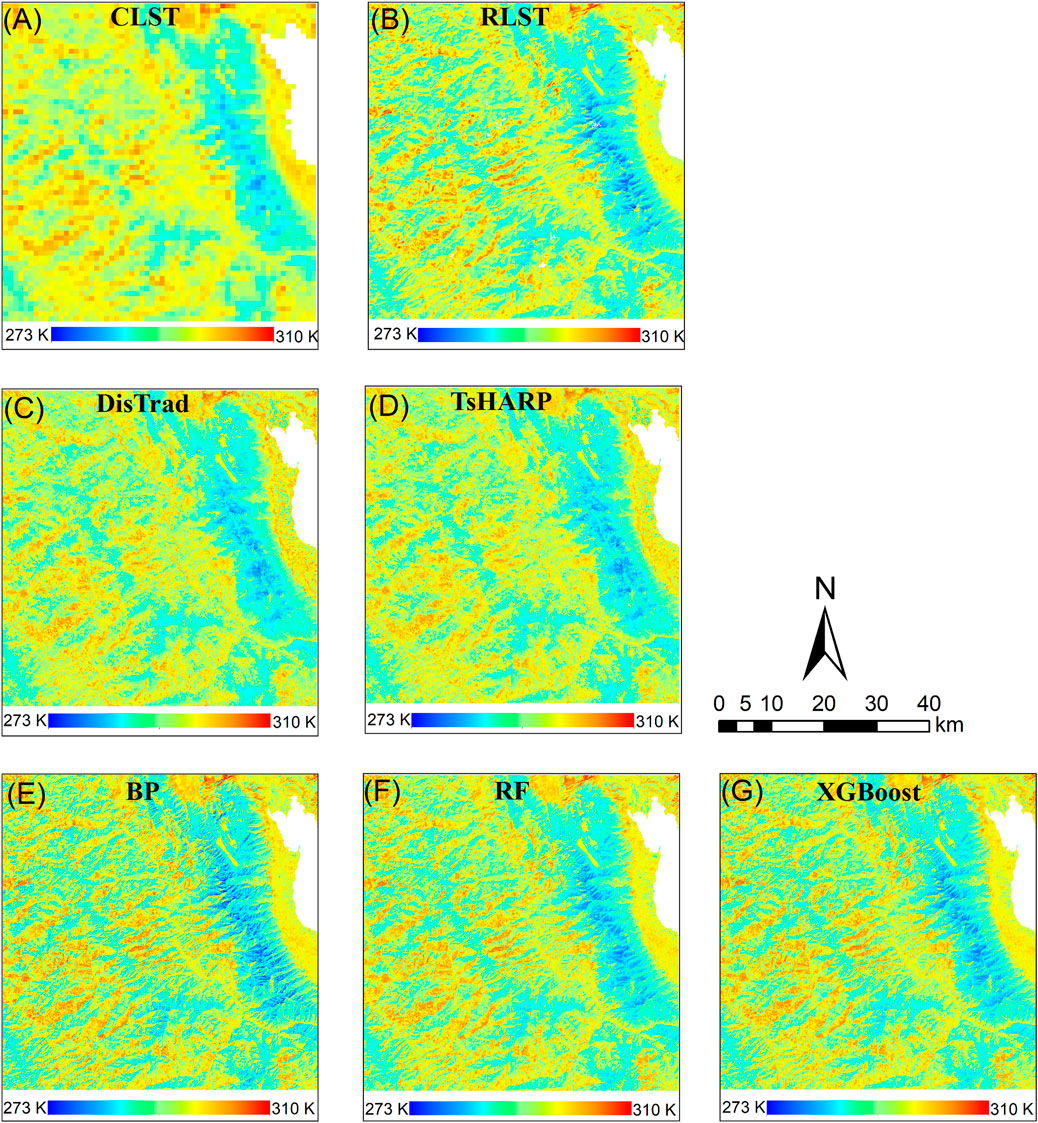
Figure 5. Comparisons of TsHARP, DisTrad-based, BP-based, RF-based, and proposed XGBoost-based algorithms for Study Area B (A) Landsat-9 LST (960 m), (B) Landsat-9 LST (30 m), (C) DisTrad downscaled LST (30 m), (D) TsHARP downscaled LST (30 m), (E) BP downscaled LST (30 m), (F) RF downscaled LST (30 m) and (G) XGBoost downscaled LST (30 m).

4.2 Quantitative analysis of accuracy of downscaling methods

To further assess the performance of the five downscaling methods, RMSE, R² and MAE are utilized for quantitative evaluation in Scheme 1. In addition, the distribution and anomalies of the downscaled data are observed by plotting DLST and RLST scatter plots. Similarly, the downscaling results of the images from study areas A and B on 16 November 2021 and 1 February 2023, respectively, are selected for detailed analysis.

Table 2 displays accuracy evaluation index of downscaling results at different dates in the two study areas. It clearly demonstrates that across study areas A and B, as well as different observation dates, the performance of machine learning models surpasses that of traditional single-factor regression models. Specifically, the XGBoost model exhibits the lowest RMSE, highest R², and minimal MAE, indicating that this approach not only enhances the spatial resolution of downscaled LST but also improves the accuracy of the downscaling process. For study area A, the RMSE of XGBoost model is 2.67 K, which is reduced by 0.10–0.40 K compared to the RF model (2.77 K) and BP neural network model (3.07 K). Similarly, compared to the DisTrad model (5.17K) and the TsHARP model (5.12 K), it is reduced by 2.45–2.50 K. The MAE values for the five models are 3.81 K, 3.77 K, 2.26 K, 2.18 K, and 1.83 K, respectively. The XGBoost model exhibits the smallest MAE values, reduced by 51.97%, 51.46%, 19.03%, and 16.06%, respectively. For study area B, the RMSE of the XGBoost downscaling model result is 1.98 K, reduced by 0.11–0.23 K compared to the RF model (2.09 K) and BP neural network model (2.21 K). Similarly, compared to the DisTrad model (2.78 K) and the TsHARP model (2.74 K), it is reduced by 0.76–0.80 K. The MAE values for the five models are 2.18 K, 2.13 K, 1.89 K, 1.61 K, and 1.54 K, respectively. The XGBoost model exhibits the smallest MAE values, reduced by 29.36%, 27.77%, 18.52%, and 4.35%, respectively. In addition, the coefficients of determination between the results of XGBoost model and RLST in the study areas A and B are 0.891 and 0.832 respectively, which are higher than the other four models, indicating that the XGBoost model has the highest correlation with the true value.

Table 2

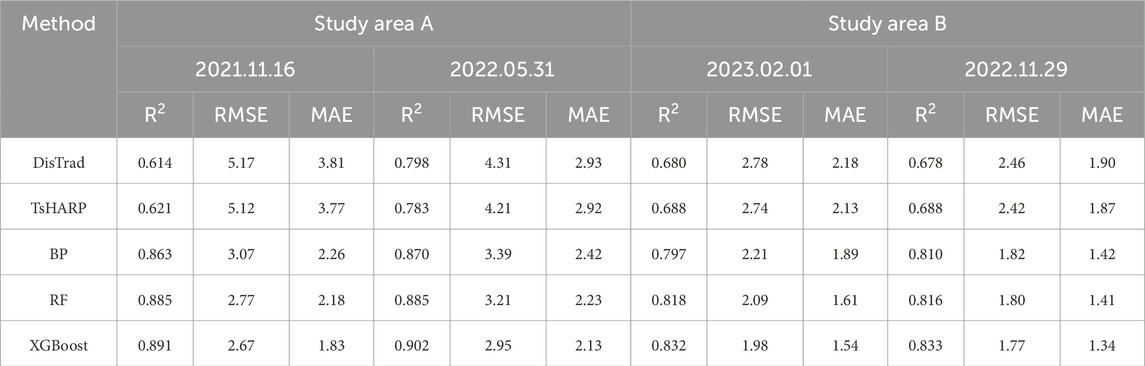
Table 2. Statistics of R², RMSE and MAE values between downscaled LST the Landsat-9 LST for study areas A and B.

Figure 6 displays the scatter plots of downscaling results and RST of the two study areas on 2021/11/16 and 2023/02/01. From a visual perspective, most of the scatter distributions for the five models follow a 1:1 relationship. However, in study area A, there are a large number of scattered points in the DisTrad and TsHARP models located both above and below the 1:1 reference line, indicating both overestimation and underestimation in the downscaled LST values. Although the scatter plot distribution of the two methods in study area B is better than that in study area A, there are still varying degrees of overestimation and underestimation. Due to the weak correlation between NDVI and LST in barren and snow-covered areas, accurate prediction of high-resolution LST is challenging. However, the extensive snow-covered areas in study area A significantly influence the overall results. Compared with the two classic methods, the scatter points corresponding to the three machine learning models are roughly distributed on both sides of the reference line in the two research areas. The three machine learning models generally exhibit better downscaling effects from the scatter plot. However, the BP neural network model also shows varying degrees of overestimation and underestimation, while the XGBoost model has the fewest outliers in the scatter plot.

Figure 6

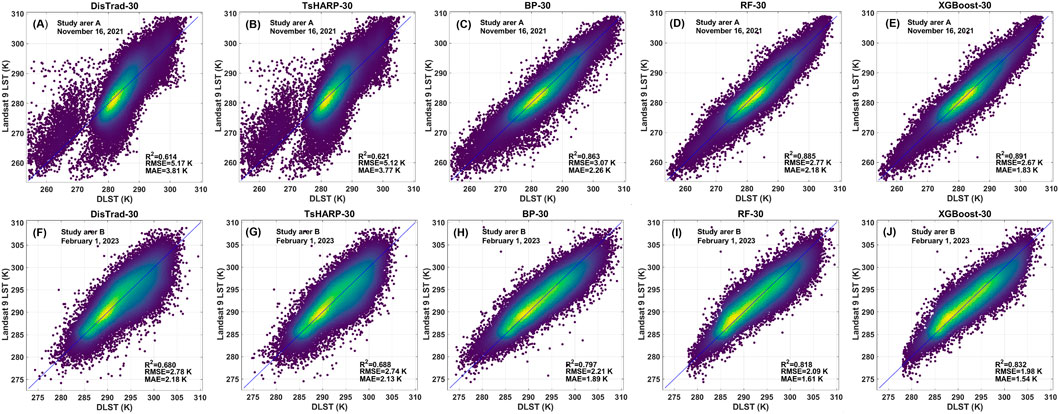
Figure 6. Density plots of the regression relationship between downscaled LST and Landsat 9 LST in Study Area A (first row) and B (second row); From left to right: DisTrad, TsHARP, BP, RF and XGBoost.

4.3 Analysis of downscaling accuracy for different land cover types

In areas where the natural landscape surface coverage type is uniform and the spatial heterogeneity is small, traditional single-factor downscaling methods (such as DisTrad and TsHARP) can be used to effectively achieve spatial downscaling of LST (Bisquert et al., 2016). However, for areas with diverse land cover types, complex topography, and patches, traditional methods may not achieve satisfactory downscaling effects. The study areas in the experiment feature various land cover types and complex terrain environments. Therefore, to further explore the accuracy of various methods used to restore high-spatial LST and delve into the performance of downscaled LST and RLST in different land cover types, we examine the differences in spatial distribution characteristics by selecting areas of interest based on different land cover types in two study areas for detailed analysis. Five rectangular areas of interest are selected in both study areas, as shown in Figures 7A and Figures 8A. In Figures 7A, these areas correspond to the following land cover types: Area (I), where barren is widely distributed; Area (II), where water is widely distributed; and Area (III), where grassland are widely distributed; Area (IV), where snow are widely distributed; and Area (V), where forest are widely distributed. In Figures 8–a, the corresponding areas are: Area (I), where cropland are widely distributed; Area (II), where grassland are widely distributed; Area (III), where impervious are widely distributed; Area (IV), where forests are widely distributed; and Area (V), where shrubs are widely distributed. In Figures 7, 8, (d) is the standard false-color composite diagram corresponding to the rectangular region of interest (I)-(V); (c), (e), (f), (g), (h) and (i) are the downscaling results of RLST, DisTrad, TsHARP, BP, RF and XGBoost models corresponding to the rectangular region of interest, respectively.

Figure 7

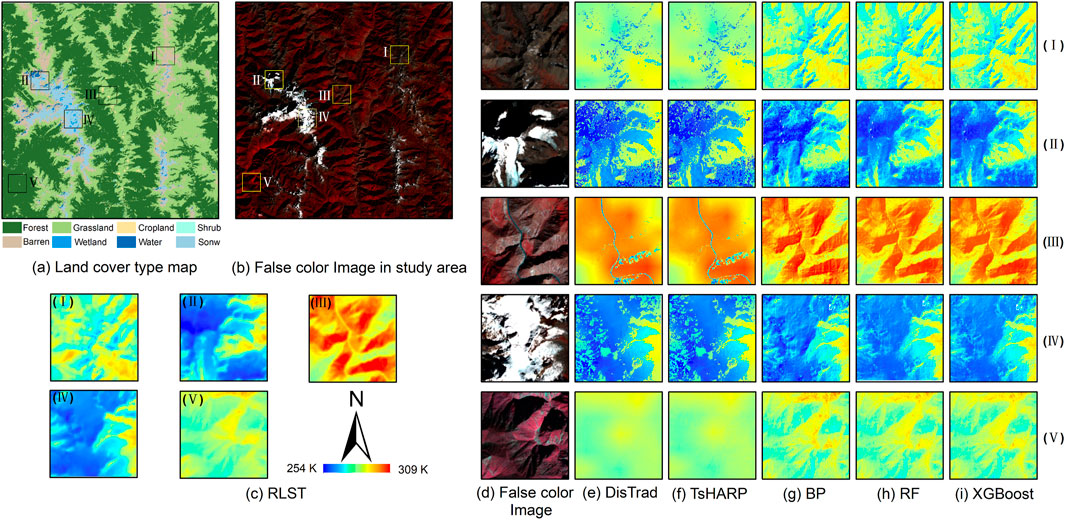
Figure 7. Enlarged view of downscaling results for different land cover types in selected areas of interest in study area A (A) land cover type map, (B) false color image, (C) enlargement of the five areas of interest RLST, (D) false color images in five areas of interest, (E)–(I) are the magnification of the downscaling results of the five region-of-interest models of DisTrad, TsHARP, BP, RF, and XGBoost, respectively.

Figure 8

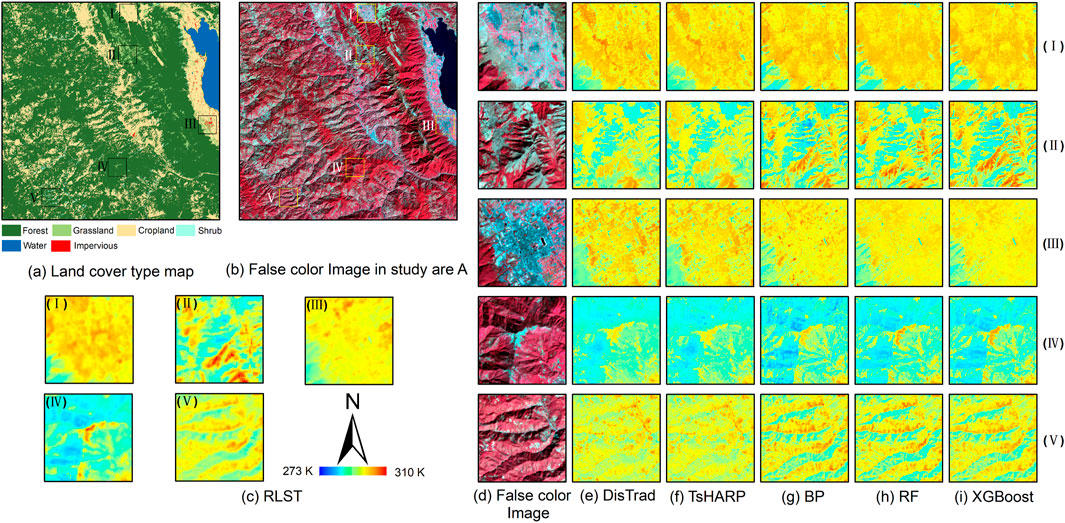
Figure 8. Enlarged view of downscaling results for different land cover types in selected areas of interest in study area B (A) land cover type map, (B) false color image, (C) enlargement of the five areas of interest RLST, (D) false color images in five areas of interest, (E)–(I) are the magnification of the downscaling results of the five region-of-interest models of DisTrad, TsHARP, BP, RF, and XGBoost, respectively.

As can be seen in Figures 7, 8, the machine learning model consistently outperforms the two classical downscaling methods for different land cover types. In study area A, the results of the two classical downscaling models only approximate the distribution of temperature, while lacking in detail, and in some cases there are obvious misestimates. In region (I), where the main vegetation cover is barren, the downscaling results of the two traditional models, TsHARP and DisTrad, perform poorly, while the machine learning model adds effective spatial information. This is related to the fact that the machine learning model takes into account the regressor BSI and is able to better model the relationship between barren and LST. In region (IV), the conventional model predicted the general contours of the snow and ice regions, while the machine learning model depicted the boundaries of snow and ice and non-snow regions more clearly. In region (II) (III) (V), the machine learning model takes into account the influence of topographic factors, which not only clearly and effectively represents the temperature difference between different features, but also the internal spatial details are closer to the actual surface conditions. In study area B, the three machine learning models still outperform the two traditional methods. In study area (I), the traditional models showed significant overestimation, especially in the edge areas of cropland and grassland. In addition, the traditional model also showed significant underestimation in the high temperature region in the middle of region (IV). In other regions of interest, it was also observed that the traditional model overestimated at high temperatures and underestimated at low temperatures. This is due to the fact that the traditional model considers only a single regressor and is unable to accurately capture the relationship between different land cover types and LST. The spatial distribution of downscaled temperatures realized by the machine learning model in different areas, both in study area A and B, is very similar to that of the RLST. The downscaled LST results from machine learning models are more consistent with changes in topography and are able to portray changes in LST at a much higher resolution, in line with natural patterns.

To further determine the accuracy of the five downscaling results, the RMSE, MAE, and R² of the downscaling results for each region are given in Tables 3, 4. The results further confirm that both the DisTrad and TsHARP methods perform poorly in areas with sparse vegetation. For example, in the study area A, where barrens are widely distributed, the R² values ​​are only 0.249 and 0.250, the RMSEs are 5.57 and 5.57, and the MAEs are 4.43 and 4.42, respectively. Similarly, in the study area B, the results obtained by the DisTrad and TsHARP methods in area C, which is dominated by impervious, and area E, which is characterized by widespread distribution of shrubs, are also unsatisfactory. Further analysis can confirm that the three machine learning models consistently outperform the two classical methods in different regions and corresponding areas of interest. It is worth noting that the XGBoost model achieves the highest R² and the lowest RMSE and MAE values.

Table 3

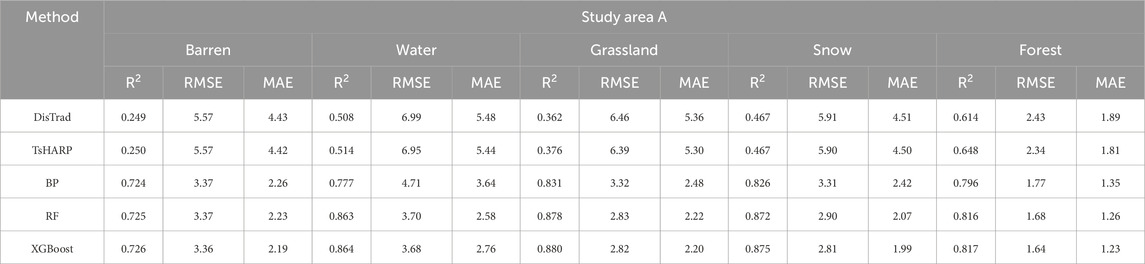
Table 3. R², RMSE and MAE of different downscaling model results for different land cover types in study area A.

Table 4

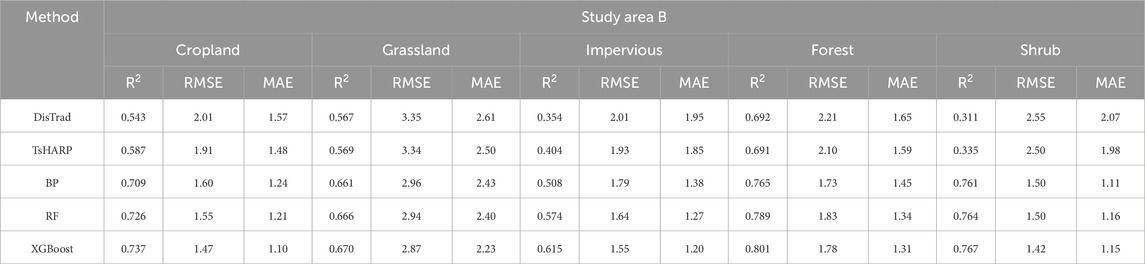
Table 4. R^2, RMSE and MAE of different downscaling model results for different land cover types in study area B.

4.4 Analysis of downscaling results at different resolution

To investigate whether the performance of the five downscaling methods varies across different target resolutions, we analyzed the experimental results of Schemes 2, 3 and 4. Figures 9, 10 illustrate the downscaling scatter density map and accuracy evaluation of the two regions under different schemes. As the downscaling spatial resolution and the spatial resolution of the reference temperature data increase for each method, both the RMSE and MAE of the LST downscaling results show a gradual increase, while R² exhibits a gradual decrease. This indicates that this outcome is associated with the increase in the number of pixels and the complexity of their temperature variations with the rise in resolution. Across different schemes in the two study areas, the XGBoost model consistently maintains higher R² values and lower RMSE and MAE values. Despite the good performance of the BP neural network model and RF model in various evaluation metrics, their downscaling effect still lags behind that of the XGBoost model. The DisTrad and TsHARP models continue to exhibit overestimation in low-temperature areas in study area A and underestimation in high-surface temperature areas. Similarly, in study area B, they display underestimation in high-temperature areas. This performance is consistent with that observed in Scheme 1. Across each downscaling scheme, the XGBoost model consistently outperforms the other four models and demonstrates strong robustness.

Figure 9

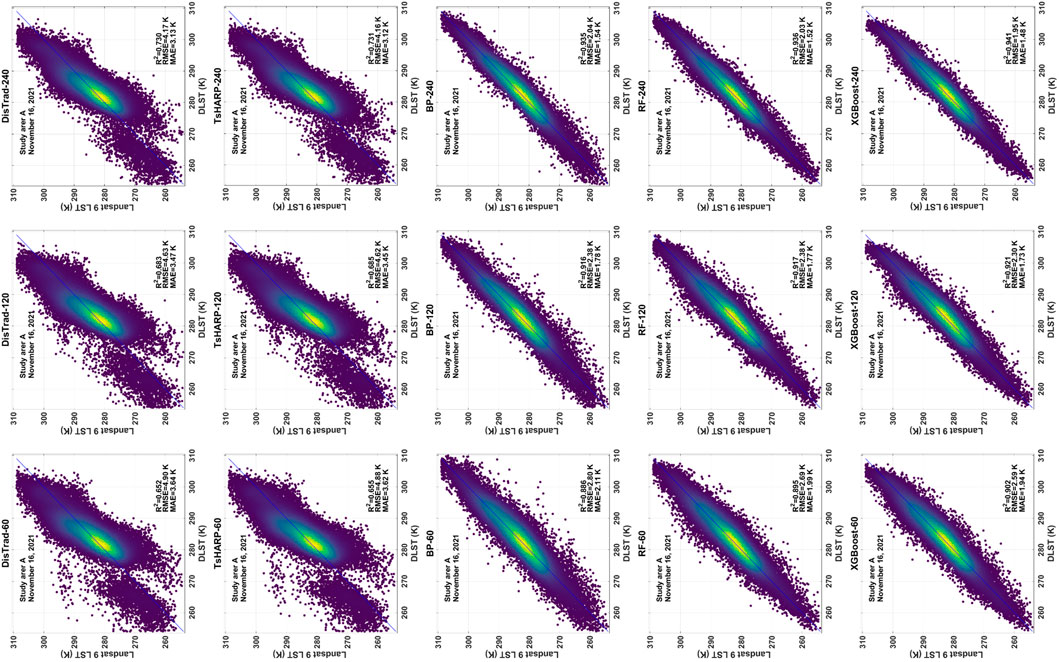
Figure 9. Scatter density plots depicting Landsat 9 LST products and downscaled LST for study area A, under Scheme 2, Scheme 3, and Scheme 4. From left to right are Scheme 2, Scheme 3, and Scheme 4, and from top to bottom are DisTrad, TsHARP, BP, RF, and XGBoost, respectively.

Figure 10

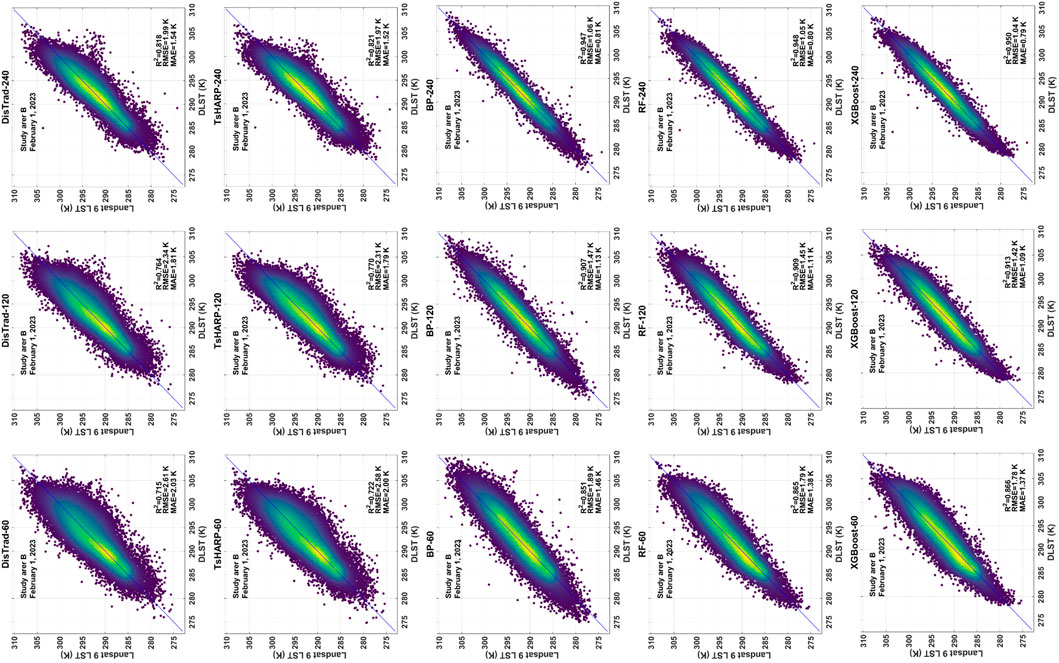
Figure 10. Same as Figure 9 for study area B.

4.5 Regression factor importance score analysis

In this study, five models were used to conduct LST downscaling in two typical plateau mountainous areas. The regression factors used in the three machine learning models are consistent. However, whether the importance of these factors is the same in different study areas requires further analysis. The RF model can evaluate the importance of its regression factors by calculating the Gini. the XGBoost model evaluates the importance of its regression factors through the built-in “weight”. The BP neural network does not inherently include a feature selection function. Regression factors were individually scrambled 1,000 times each to reduce uncertainty regarding their importance. This involved randomly rearranging one factor at a time. LST downscaling calculations were then performed. If a particular factor significantly influences the performance of the model, the performance will noticeably decline after the factor is replaced. Conversely, if the impact is minimal, it indicates lesser importance. This process helps determine the relative importance of variables in the BP neural network model. The importance score of regressors in the three machine learning models is illustrated in Figure 11.

Figure 11

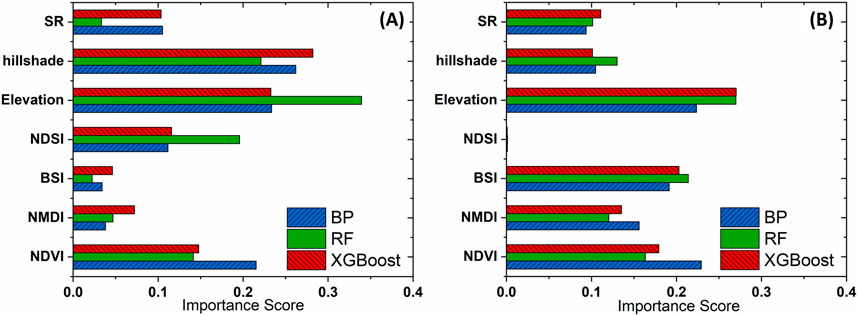
Figure 11. Comparison of the importance of regression factors for machine learning models in (A) study area A and (B) study area B.

Although NDVI demonstrated a certain degree of importance in each model, it was not the most crucial factor in the two study areas. This indicates that relying solely on NDVI to characterize vegetation is not suitable for plateau and mountainous regions with complex terrain. In addition, this explains why the DisTrad and TsHARP models, which consider only the single factor of NDVI, show poor fits in these two study areas. In the two study areas, topographic factors, particularly elevation, play the most significant role, surpassing other variables. This indicates that topographic have a substantial impact on the spatial variation of LST. In study area A, the importance of elevation factor corresponding to the RF model is obviously higher than that of the other two models, indicating that the elevation in the RF model is more sensitive. Different models calculate the importance of regression factors in different ways, so the relative importance of factors ultimately obtained is different. In study area A, NDSI showed a certain level of importance, whereas in study area B, NDSI was almost negligible across all three models. This discrepancy is due to the fact that in study area B, snow is not present year-round. During the selected study period, snow was confined to the higher altitudes of Cangshan Mountain, resulting in a very small snow-covered area. This underscores the necessity of considering NDSI in LST downscaling studies for plateau and mountainous areas with perennial snow cover.

Under the complex terrain conditions of plateau mountainous areas, altitude is a crucial surface parameter that influences the correlation characteristics between LST and terrain factors in the study area. To clarify the impact of altitude on LST, the elevations of the two study areas were divided into 200-m intervals, and the mean and standard deviation of LST for each interval were calculated. The elevation range of study area A is between 1888 m and 6,444 m. The study divides the study area A into 24 intervals, with pixels below 2000 m grouped into the 2000 m interval and those above 6,600 m grouped into the 6,600 m interval. For study area B, with elevations ranging from 1,268 m to 4,115 m, the study area B is divided into 14 intervals. Pixels below 1,400 m are grouped into the 1,400 m interval, while pixels above 4,000 m are merged into the 4,000 m interval. The statistical results for both study areas are presented in Figure 12.

Figure 12

Figure 12. Relationship between LST and elevation in (A) study area A and (B) study area B.

Overall, the average LST in each interval exhibits a clear downward trend as altitude increases, with study area A showing a more pronounced trend. Linear fitting of elevation and LST within these intervals reveals a determination coefficient of 0.970 for study area A and 0.878 for study area B, indicating that altitude has a significant impact on LST in plateau mountainous areas. The standard deviations in both study areas exceed 2 K, following a trend of initially increasing and then decreasing with altitude. In study area A, within the 4,200–5,000 m altitude range, there is a distinct “bulge” in the relationship between LST and altitude, where the standard deviation of LST is notably higher than in other intervals. Further analysis shows that the predominant land cover types at this altitude are grassland and farmland. Similarly, in study area B, within the 2,200–2,600 m altitude range, a “bulge” is also observed in the LST-altitude relationship, with a relatively large standard deviation. The main land cover types in this area are built-up land and farmland, suggesting that other factors influence LST within this altitude range.

5 Discussion

There are various methods available for LST downscaling. Compared to complex models based on physical mechanisms, such as modulation allocation and spectrum mixing models, statistical regression models offer a simpler implementation. Additionally, these models require fewer auxiliary parameters, which are generally easier to obtain while still providing high accuracy (Xu and Cheng, 2021; Li et al., 2022). Therefore, in this study, five statistical regression models—DisTrad, TIARP, BP, RF, and XGBoost—were used to perform LST downscaling experiments in Diqing and Dali. Machine learning prediction models utilized regression factors NDVI, NMDI, BSI, SR, DEM, Hillshade, and NDSI as downscaling variables tailored for plateau mountainous areas. Multi-scheme experiments were conducted to establish a LST downscaling model suitable for the complex terrain of plateau mountainous areas.

The downscaling results from the two study areas were analyzed and evaluated based on three indicators: R², RMSE, MAE, and visual inspection of spatial distribution. The findings indicate that machine learning models predict LST more accurately than the DisTrad and TsHARP models. While the downscaling results from all five methods closely approximate the spatial distribution of RLST, the DisTrad and TsHARP models, which rely solely on NDVI as a single explanatory variable, overlook terrain variations and fail to capture the complex spatial characteristics of LST. This highlights that traditional nonlinear methods do not achieve the accuracy required for LST downscaling in plateau mountainous areas. The machine learning model incorporates various terrain factors such as altitude, surface roughness, and mountain shadow specific to plateau mountain conditions. Additionally, it considers NDVI, NMDI, BSI, and NDSI to account for diverse land cover types and perennial snow presence in the study area. By utilizing these more appropriate factors, the model achieves more accurate LST downscaling results. Moreover, the machine learning model aligns better with terrain change patterns and exhibits sensitivity in predicting extreme temperature areas, thereby effectively enhancing spatial resolution. Among them, the XGBoost model demonstrates the most effective performance, achieving significantly higher accuracy in DLST compared to other models.

The downscaling results of the machine learning model in study area A generally outperform those in study area B, influenced by the respective land cover types. The LST downscaling results across different land cover types were magnified and analyzed. In densely vegetated areas of both study areas, the two traditional linear models showed better effectiveness compared to sparse areas but still fell short in capturing spatial changes accurately. Complex terrain and varied land cover types contribute to more mixed pixels. The advantage of the machine learning model lies in its ability to comprehensively learn the nonlinear relationship between different factors and LST, enabling adaptation to diverse land cover types. Notably, the XGBoost model exhibits superior adaptability and consistently achieves the best LST downscaling results across all areas of interest.

The results of LST downscaling using five methods across different schemes demonstrate that the accuracy of downscaled LST is closely tied to the ratio of initial resolution to target resolution. This relationship arises from the varying probability distributions of LST and its pixel values at different resolutions, contributing to scale dependence in the downscaling process. Essentially, higher ratios between initial and target resolutions yield more detailed information. Previous study (Zhou et al., 2016) indicated that efforts to mitigate scale effects marginally enhance the accuracy of downscaled LST, contingent upon errors inherent in the original data and downscaling process. Nonetheless, across various schemes, the XGBoost model consistently outperforms the other four models.

In the process of model building, we obtained the importance order of factors in different models in different study areas. The results show that the altitude is a very important factor in the LST downscaling study in the plateau mountain area. And it is necessary to consider NDSI as a factor in the plateau mountains with perennial snow cover.

In addition to prioritizing accuracy, minimizing time costs is also essential. Achieving higher accuracy in less time represents an ideal approach. Therefore, the PSO algorithm was applied to optimize hyperparameters of the three machine learning prediction models, eliminating the need for manual parameter adjustments. With optimized models, one can focus solely on interpreting results without the distraction of fine-tuning hyperparameters. Among the three machine learning models used, XGBoost was found to run the fastest following PSO, making it a more efficient and accurate choice compared to RF and BP.

These findings are significant for advancing environmental monitoring in plateau mountainous areas. Due to limited data availability in the study area, only four scene images were selected for training the downscaling models. The consistency of downscaling performance among the five models across different seasons in the study area was not considered. Additionally, the impact of varying study area sizes on the downscaling effectiveness of each method was not assessed. Future study should include supplementary experiments to address these limitations.

6 Conclusion

The research on LST downscaling in plateau mountainous areas remains a significant challenge in thermal infrared remote sensing. In the study, the LST downscaling effects of three machine learning models (BP, RF, and XGBoost) and two classic linear regression models (DisTrad and TsHARP) in plateau mountainous regions were compared. It is found that compared to traditional single-factor linear regression methods, the machine learning methods demonstrated higher accuracy in LST downscaling. Specifically, the XGBoost model outperformed others across different land cover types and resolutions, achieving the lowest RMSE and MAE and the highest R². This indicates that XGBoost is particularly well-suited for LST downscaling in plateau mountainous areas.

By upscaling the Landsat 9 LST product and conducting downscaling simulations at various resolutions, it was found that the downscaling results are influenced by the disparity between the original and target LST resolutions. The XGBoost model demonstrates more stable performance across different resolutions. The PSO algorithm was employed to optimize hyperparameters of three machine learning prediction models, resulting in reduced experimental time and enhanced efficiency.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JW: Writing–original draft. B-HT: Writing–review and editing. XZ: Writing–review and editing. DF: Writing–review and editing. ML: Writing–review and editing. JC: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the National Natural Science Foundation of China under Grant 42230109, in part by the Yunling Scholar Project of the “Xingdian Talent Support Program” of Yunnan Province under Grant 202221002, in part by the Platform Construction Project of High-Level Talent in the Kunming University of Science and Technology (KUST) under Grant 7202221001, and in part by the National Natural Science Foundation of China under Grant 42301454.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1488711/full#supplementary-material

Abbreviations

ASOS, Advanced Surface Observation Satellite; BP, Back Propagation Neural Network; BSI, Bare soil index, dimensionless; CLCD, China Land Cover Dataset; CLST, Coarse land surface temperature, K; DLST, Downscaled land surface temperature, K; FVC, Fractional vegetation coverage, dimensionless; LST, Land surface temperature, K; MAE, Mean absolute error, dimensionless; NDSI, Normalized difference snow index, dimensionless; NDVI, Normalized vegetation index, dimensionless; NMDI, Normalized multi-band drought index, dimensionless; PSO, Particle swarm optimization; R², Coefficient of determination, dimensionless; RF, Random forest; RLST, Real land surface temperature, K; RMSE, Root mean square error, dimensionless; SR, Surface roughness, dimensionless; XGBoost, Extreme gradient boosting.

References

Agam, N., Kustas, W. P., Anderson, M. C., Li, F., and Colaizzi, P. D. (2008). Utility of thermal image sharpening for monitoring field-scale evapotranspiration over rainfed and irrigated agricultural regions. Geophys. Res. Lett. 35, 2. doi:10.1029/2007gl032195

CrossRef Full Text | Google Scholar

Agam, N., Kustas, W. P., Anderson, M. C., Li, F., and Neale, C. M. (2007). A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 107 (4), 545–558. doi:10.1016/j.rse.2006.10.006

CrossRef Full Text | Google Scholar

Bartkowiak, P., Castelli, M., and Notarnicola, C. (2019). Downscaling land surface temperature from MODIS dataset with random forest approach over alpine vegetated areas. Remote Sens. 11 (11), 1319. doi:10.3390/rs11111319

CrossRef Full Text | Google Scholar

Bibi, S., Wang, L., Li, X., Zhou, J., Chen, D., and Yao, T. (2018). Climatic and associated cryospheric, biospheric, and hydrological changes on the Tibetan Plateau: a review. Int. J. Climatol. 38, e1–e17. doi:10.1002/joc.5411

CrossRef Full Text | Google Scholar

Bindhu, V. M., Narasimhan, B., and Sudheer, K. P. (2013). Development and verification of a non-linear disaggregation method (NL-DisTrad) to downscale MODIS land surface temperature to the spatial scale of Landsat thermal data to estimate evapotranspiration. Remote Sens. Environ. 135, 118–129. doi:10.1016/j.rse.2013.03.023

CrossRef Full Text | Google Scholar

Bisquert, M., Sánchez, J. M., López-Urrea, R., and Caselles, V. (2016). Estimating high resolution evapotranspiration from disaggregated thermal images. Remote Sens. Environ. 187, 423–433. doi:10.1016/j.rse.2016.10.049

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random forests. Mach. Learn. 45, 5–32. doi:10.1023/a:1010933404324

CrossRef Full Text | Google Scholar

Chen, T., and Guestrin, C. (2016). “Xgboost: a scalable tree boosting system,” in Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 785–794.

Google Scholar

Deilami, K., Kamruzzaman, M., and Liu, Y. (2018). Urban heat island effect: a systematic review of spatio-temporal factors, data, methods, and mitigation measures. Int. J. Appl. Earth Obs. Geoinf. 67, 30–42. doi:10.1016/j.jag.2017.12.009

CrossRef Full Text | Google Scholar

Dominguez, A., Kleissl, J., Luvall, J. C., and Rickman, D. L. (2011). High-resolution urban thermal sharpener (HUTS). Remote Sens. Environ. 115 (7), 1772–1780. doi:10.1016/j.rse.2011.03.008

CrossRef Full Text | Google Scholar

Duan, S., and Li, Z. (2016). Spatial downscaling of MODIS land surface temperatures using geographically weighted regression: case study in northern China. Remote Sens. 54 (11), 6458–6469. doi:10.1109/TGRS.2016.2585198

CrossRef Full Text | Google Scholar

Eberhart, R., and Kennedy, J. (1995). “A new optimizer using particle swarm theory. MHS'95,” in Proceedings of the sixth international symposium on micro machine and human science. Ieee, 39–43.

Google Scholar

Ebrahimy, H., Aghighi, H., Azadbakht, M., Amani, M., Mahdavi, S., and Matkan, A. A. (2021). Downscaling MODIS land surface temperature product using an adaptive random forest regression method and google earth engine for a 19-years spatiotemporal trend analysis over Iran. Remote Sens. 14, 2103–2112. doi:10.1109/jstars.2021.3051422

CrossRef Full Text | Google Scholar

Ebrahimy, H., and Azadbakht, M. (2019). Downscaling MODIS land surface temperature over a heterogeneous area: an investigation of machine learning techniques, feature selection, and impacts of mixed pixels. Comput. Geosci. 124, 93–102. doi:10.1016/j.cageo.2019.01.004

CrossRef Full Text | Google Scholar

Ghosh, A., and Joshi, P. K. (2014). Hyperspectral imagery for disaggregation of land surface temperature with selected regression algorithms over different land use land cover scenes. Isprs-J. Photogramm. Remote Sens. 96, 76–93. doi:10.1016/j.isprsjprs.2014.07.003

CrossRef Full Text | Google Scholar

Guo, F., Hu, D., and Schlink, U. (2022). A new nonlinear method for downscaling land surface temperature by integrating guided and Gaussian filtering. Remote Sens. Environ. 271, 112915. doi:10.1016/j.rse.2022.112915

CrossRef Full Text | Google Scholar

He, Z., and Tang, B. (2023). Spatiotemporal change patterns and driving factors of land surface temperature in the Yunnan-Kweichow Plateau from 2000 to 2020. Sci. Total Environ. 896, 165288. doi:10.1016/j.scitotenv.2023.165288

PubMed Abstract | CrossRef Full Text | Google Scholar

Hough, I., Just, A. C., Zhou, B., Dorman, M., Lepeule, J., and Kloog, I. (2020). A multi-resolution air temperature model for France from MODIS and Landsat thermal data. Environ. Res. 183, 109244. doi:10.1016/j.envres.2020.109244

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutengs, C., and Vohland, M. (2016). Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 178, 127–141. doi:10.1016/j.rse.2016.03.006

CrossRef Full Text | Google Scholar

Kustas, W. P., Norman, J. M., Anderson, M. C., and French, A. N. (2003). Estimating subpixel surface temperatures and energy fluxes from the vegetation index–radiometric temperature relationship. Remote Sens. Environ. 85 (4), 429–440. doi:10.1016/s0034-4257(03)00036-1

CrossRef Full Text | Google Scholar

Lemeshewsky, G. P., and Schowengerdt, R. A. (2001). Landsat 7 thermal-IR image sharpening using an artificial neural network and sensor model. Vis. Inf. Process. 4388, 181–192. SPIE. doi:10.1117/12.438256

CrossRef Full Text | Google Scholar

Li, J., Cheng, J., Shi, J., and Huang, F. (2012). Brief introduction of back propagation (BP) neural network algorithm and its improvement. Adv. Comput. Sci. Inf. Eng. 2, 553–558. doi:10.1007/978-3-642-30223-7_87

CrossRef Full Text | Google Scholar

Li, W., Ni, L., Li, Z., Duan, S., and Wu, H. (2019). Evaluation of machine learning algorithms in spatial downscaling of MODIS land surface temperature. Ieee J. Sel. Top. Appl. Earth Obs. Remote Sens. 12 (7), 2299–2307. doi:10.1109/jstars.2019.2896923

CrossRef Full Text | Google Scholar

Li, X., Zhang, G., Zhu, S., and Xu, Y. (2022). Step-by-step downscaling of land surface temperature considering urban spatial morphological parameters. Remote Sens. 14 (13), 3038. doi:10.3390/rs14133038

CrossRef Full Text | Google Scholar

Li, Y., Wu, H., Chen, H., and Zhu, X. (2023b). A robust framework for resolution enhancement of land surface temperature by combining spatial downscaling and spatiotemporal fusion methods. Ieee Trans. Geosci. Remote Sens. 61, 1–14. doi:10.1109/tgrs.2023.3283614

CrossRef Full Text | Google Scholar

Li, Z., Tang, B., Wu, H., Ren, H., Yan, G., Wan, Z., et al. (2013). Satellite-derived land surface temperature: current status and perspectives. Remote Sens. Environ. 131, 14–37. doi:10.1016/j.rse.2012.12.008

CrossRef Full Text | Google Scholar

Li, Z. L., Wu, H., Duan, S. B., Zhao, W., Ren, H., Liu, X., et al. (2023a). Satellite remote sensing of global land surface temperature: definition, methods, products, and applications. Rev. Geophys. 61, 1. doi:10.1029/2022RG000777

CrossRef Full Text | Google Scholar

Long, D., Yan, L., Bai, L., Zhang, C., Li, X., Lei, H., et al. (2020). Generation of MODIS-like land surface temperatures under all-weather conditions based on a data fusion approach. Remote Sens. Environ. 246, 111863. doi:10.1016/j.rse.2020.111863

CrossRef Full Text | Google Scholar

Metz, M., Rocchini, D., and Neteler, M. (2014). Surface temperatures at the continental scale: tracking changes with remote sensing at unprecedented detail. Remote Sens. 6 (5), 3822–3840. doi:10.3390/rs6053822

CrossRef Full Text | Google Scholar

Norman, J. M., Kustas, W. P., and Humes, K. S. (1995). Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 77 (3-4), 263–293. doi:10.1016/0168-1923(95)02265-y

CrossRef Full Text | Google Scholar

Pu, R. (2021). Assessing scaling effect in downscaling land surface temperature in a heterogenous urban environment. Int. J. Appl. Earth Obs. Geoinf. 96, 102256. doi:10.1016/j.jag.2020.102256

CrossRef Full Text | Google Scholar

Pu, R., and Bonafoni, S. (2023). Thermal infrared remote sensing data downscaling investigations: an overview on current status and perspectives. Remote Sens. Appl. Soc. Environ. 29, 100921. doi:10.1016/j.rsase.2023.100921

CrossRef Full Text | Google Scholar

Rao, Y., Liang, S., Wang, D., Yu, Y., Song, Z., Zhou, Y., et al. (2019). Estimating daily average surface air temperature using satellite land surface temperature and top-of-atmosphere radiation products over the Tibetan Plateau. Remote Sens. Environ. 234, 111462. doi:10.1016/j.rse.2019.111462

CrossRef Full Text | Google Scholar

Tu, H., Cai, H., Yin, J., Zhang, X., and Zhang, X. (2022). Land surface temperature downscaling in the karst mountain urban area considering the topographic characteristics. J. Appl. Remote Sens. 16 (3), 34515. doi:10.1117/1.JRS.16.034515

CrossRef Full Text | Google Scholar

Wan, Z., Zhang, Y., Zhang, Q., and Li, Z. (2002). Validation of the land-surface temperature products retrieved from terra moderate resolution imaging spectroradiometer data. Remote Sens. Environ. 83 (1-2), 163–180. doi:10.1016/s0034-4257(02)00093-7

CrossRef Full Text | Google Scholar

Wang, S., Wang, X., Chen, G., Yang, Q., Wang, B., Ma, Y., et al. (2017a). Complex responses of spring alpine vegetation phenology to snow cover dynamics over the Tibetan Plateau. China. Sci. Total Environ. 593, 449–461. doi:10.1016/j.scitotenv.2017.03.187

CrossRef Full Text | Google Scholar

Wang, Z., Sun, Y., Ren, H., Qin, Q., and Han, G. (2017b). “Downscaling research of remotely sensed land surface temperature,” in 2017 IEEE international geoscience and remote sensing symposium (IGARSS). IEEE, 6293–6296.

CrossRef Full Text | Google Scholar

Weng, Q. (2009). Thermal infrared remote sensing for urban climate and environmental studies: methods, applications, and trends. Isprs-J. Photogramm. Remote Sens. 64 (4), 335–344. doi:10.1016/j.isprsjprs.2009.03.007

CrossRef Full Text | Google Scholar

Wu, H., and Li, W. (2019). Downscaling land surface temperatures using a random forest regression model with multitype predictor variables. Ieee Access 7, 21904–21916. doi:10.1109/access.2019.2896241

CrossRef Full Text | Google Scholar

Xu, S., and Cheng, J. (2021). A new land surface temperature fusion strategy based on cumulative distribution function matching and multiresolution Kalman filtering. Remote Sens. Environ. 254, 112256. doi:10.1016/j.rse.2020.112256

CrossRef Full Text | Google Scholar

Xu, S., Zhao, Q., Yin, K., He, G., Zhang, Z., Wang, G., et al. (2021). Spatial downscaling of land surface temperature based on a multi-factor geographically weighted machine learning model. Remote Sens. 13 (6), 1186. doi:10.3390/rs13061186

CrossRef Full Text | Google Scholar

Yang, G., Pu, R., Zhao, C., Huang, W., and Wang, J. (2011). Estimation of subpixel land surface temperature using an endmember index based technique: a case examination on ASTER and MODIS temperature products over a heterogeneous area. Remote Sens. Environ. 115 (5), 1202–1219. doi:10.1016/j.rse.2011.01.004

CrossRef Full Text | Google Scholar

Yang, J., and Huang, X. (2021). 30 m annual land cover and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data Discuss. 2021, 1–29. doi:10.5194/essd-13-3907-2021

CrossRef Full Text | Google Scholar

Zakšek, K., and Oštir, K. (2012). Downscaling land surface temperature for urban heat island diurnal cycle analysis. Remote Sens. Environ. 117, 114–124. doi:10.1016/j.rse.2011.05.027

CrossRef Full Text | Google Scholar

Zhan, W., Chen, Y., Zhou, J., Li, J., and Liu, W. (2011). Sharpening thermal imageries: a generalized theoretical framework from an assimilation perspective. Ieee Trans. Geosci. Remote Sens. 49 (2), 773–789. doi:10.1109/TGRS.2010.2060342

CrossRef Full Text | Google Scholar

Zhang, K., Luo, J., Peng, J., Zhang, H., Ji, Y., and Wang, H. (2022). Analysis of extreme temperature variations on the yunnan-guizhou plateau in southwestern China over the past 60 years. Sustainability 14 (14), 8291. doi:10.3390/su14148291

CrossRef Full Text | Google Scholar

Zhang, X., Zhou, J., Liang, S., and Wang, D. (2021). A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote Sens. Environ. 260, 112437. doi:10.1016/j.rse.2021.112437

CrossRef Full Text | Google Scholar

Zhao, W., and Duan, S. (2020). Reconstruction of daytime land surface temperatures under cloud-covered conditions using integrated MODIS/Terra land products and MSG geostationary satellite data. Remote Sens. Environ. 247, 111931. doi:10.1016/j.rse.2020.111931

CrossRef Full Text | Google Scholar

Zhou, J., Liu, S., Li, M., Zhan, W., Xu, Z., and Xu, T. (2016). Quantification of the scale effect in downscaling remotely sensed land surface temperature. Remote Sens. 8 (12), 975. doi:10.3390/rs8120975

CrossRef Full Text | Google Scholar

Zhu, X., Li, J., Liu, Q., Yu, W., Li, S., Zhao, J., et al. (2021). Use of a BP neural network and meteorological data for generating spatiotemporally continuous LAI time series. Ieee Trans. Geosci. Remote Sens. 60, 1–14. doi:10.1109/tgrs.2021.3095535

CrossRef Full Text | Google Scholar