Spatiotemporal evolution and optimization analysis of investment efficiency in China’s agricultural water conservancy infrastructure based on a two-stage DEA model

The turbulent international political and economic situation has presented significant challenges to food and water security. Agricultural water conservancy infrastructure has garnered considerable attention due to its crucial role in the allocation and efficient utilization of water resources. Traditional research on the investment efficiency of agricultural water conservancy infrastructure often treats the intermediate impact pathways as a “black box”, neglecting the distinctions among various links. This article employs a two-stage DEA model to partition the impact of agricultural water conservancy infrastructure investment on agricultural output into two stages: water supply and water use. Utilizing data of 31 provinces in China from 2008 to 2022, we measured the efficiency of the two stages, as well as the spatiotemporal distribution and evolution characteristics. The findings reveal a spatial misalignment between water supply and water use efficiency: regions exhibiting higher water supply efficiency in the first stage are primarily those with abundant water resource endowments, whereas water use efficiency in the second stage is closely linked to regional economic development levels. Additionally, the spatial distribution and evolution characteristics of efficiency values indicate that the polarization of water use efficiency is more pronounced, with a significant spatial correlation observed between geographically adjacent areas and those within the same watershed. Conversely, water supply efficiency shows a significant correlation only within the context of watershed relationships. Based on the analysis of the sources of efficiency loss, recommendations include increasing investment in water-saving irrigation technologies, developing agricultural water conservancy infrastructure suitable for large-scale mechanized production, and designing investment compensation mechanisms. Future research is suggested to use econometric models to further examine and identify factors affecting efficiency, particularly the impacts of inter-basin water transfer projects.

1 Introduction

In the current global political and economic climate, the frequency of risk events has increased significantly, prompting nations to focus unprecedented attention on food and water security. Water resources are a crucial component of agricultural production; however, their distribution is often uneven. As an essential tool for managing these disparate water resources, agricultural water conservancy infrastructure plays a vital role in agricultural productivity. By constructing reservoirs, irrigation systems, and drainage facilities, societies can achieve a more equitable distribution of water resources. Additionally, precise irrigation techniques and effective management practices help minimize water waste, ensure that crops receive adequate hydration during their growth periods, and enhance the efficiency of water resource utilization.

China boasts a vast territory and a large population; however, its endowment of water resources is relatively limited and unevenly distributed both temporally and spatially, leading to a lack of coordination with land resource distribution (Liu and Wu, 2002). Most grain production areas in the northern region are experiencing significant water shortages. Currently, China’s grain production growth model heavily relies on increasing input factors, particularly water resources (Zhang et al., 2019). This ‘extensive’ production model inevitably results in low scale efficiency, redundant inputs, and resource waste (Yang et al., 2020). Consequently, the effective utilization of water resources in agricultural production presents considerable challenges. A thorough analysis focused on optimizing water resource allocation and enhancing utilization efficiency—particularly through improving the investment efficiency of agricultural water conservancy infrastructure—is crucial for advancing the efficiency of agricultural factor allocation and promoting output growth in China.

Research on the investment efficiency of agricultural water conservancy infrastructure is primarily conducted from three perspectives. The first perspective involves input-output analysis within the field of economics, focusing on the macro-level relationship between the inputs and outputs of agricultural water conservancy infrastructure in specific regions (Song et al., 2017; Pan et al., 2022; Zhang et al., 2022). The second perspective addresses the decision-making, design, construction, and management of such infrastructure, which is studied from a micro-level using relevant theories and tools, particularly from engineering management (Liu et al., 2014; Hatamkhani et al., 2021). The third perspective concerns the financing of agricultural water conservancy infrastructure, with research primarily examining investment sources and innovative methods, exploring diversified financing systems and capital structures. This article predominantly focuses on the first perspective (Lazurko and Venema, 2017; Du et al., 2019).

In the study of efficiency evaluation based on the input-output relationship, the selection of input-output variables is a crucial component. When examining the investment efficiency of agricultural water conservancy infrastructure, it is essential to clarify the logic and pathways through which such infrastructure affects agricultural production. Agricultural water conservancy infrastructure facilitates the supply of water resources essential for agricultural production through processes such as water storage, diversion, lifting, and transfer (Acevedo Guerrero, 2018; Yan, 2019). By enhancing irrigation efficiency and promoting the rational utilization of water resources, it improves agricultural production conditions and fosters soil moisture stability, thereby augmenting crop growth potential and yield (Guo and Zhang, 2024). Additionally, this infrastructure mitigates the risks associated with drought and flood disasters, enhances land use efficiency, and contributes to the sustainable development of agricultural.

The selection of efficiency evaluation methods represents another critical issue. The existing methods for evaluating efficiency primarily include Input–Output Analysis (IOA), Difference-in-Differences Analysis (DID), Vector Autoregressive (VAR), Stochastic Frontier Analysis (SFA), and Data Envelopment Analysis (DEA) models, among others (Yuan, 2020). The DEA model does not require a priori setting of weights, and it has demonstrated unique advantages in various efficiency measurements and performance evaluations resulting from its objectivity and flexibility. An increasing number of scholars are choosing the DEA model to measure the agricultural production efficiency (Zhang et al., 2022) and agricultural green ecological efficiency (Sun and Yu, 2023), thereby reflecting the carrying capacity of agriculture for sustainable development. Additionally, several studies concentrate on the efficiency of specific input factors in the agricultural production process, such as agricultural water conservancy infrastructures efficiency (Yan, 2019; Liu et al., 2013; Wang et al., 2022), water resource utilization efficiency (Xie et al., 2022) logistics efficiency (Hao et al., 2022) and machinery efficiency (Xu, 2023).

Currently, several studies have utilized the DEA model to assess the efficiency of investments in water conservancy infrastructure, with most research frameworks employing the DEA-Tobit model (Xu, 2023). In the framework, the DEA model is employed in the first stage to assess the efficiency of each Decision-Making Unit (DMU), while the Tobit regression model is applied in the second stage to analyze the factors influencing efficiency. Furthermore Pan et al. (2022) made a dynamic and static analysis on the agricultural efficiency of the Yangtze River Economic Belt from 2010 to 2019 through a three-stage DEA Malmquist model. The three stages primarily encompass the static efficiency of agricultural production, the application of SFA to mitigate the influence of environmental variables and statistical noise on the effectiveness of DMU, and the utilization of the DEA-Malmquist model to assess the impact of environmental variables on agricultural production efficiency.

Existing research indicates that the impact of agricultural water conservancy infrastructure investment on agricultural production is highly complex. However, the current measurement and evaluation of its efficiency often treat the intermediate impact processes and pathways as a “black box,” neglecting the specific role differences among various links. In most studies, investment in agricultural water conservancy infrastructure is merely considered an input variable, while agricultural output is treated as the output variable. This oversimplified perspective fails to fully capture the differential roles of each link in overall efficiency. Even when examining influencing factors, the results are frequently too general, making it challenging to identify the specific sources of efficiency loss. Therefore, further in-depth research and detailed analysis of efficiency performance across different links are necessary to elucidate the clearer sources of efficiency losses. The two-stage DEA method serves as a powerful tool for evaluating the efficiency of complex systems, as it decomposes overall efficiency into efficiencies across two distinct stages, where the output variables of the first stage are utilized as input variables for the second stage. Compared to traditional DEA models (Kim et al., 2015), the two-stage DEA model unveils the “black box” of the input-output relationship (Kord et al., 2022), allowing for a more precise delineation of the intricate logical relationships between various input variables and output variables. This technique is primarily applied in areas such as supply chains (Zhao et al., 2022), the financial sector (Tsai et al., 2020), and the technological innovation processes of high-tech companies. In this study, the two-stage DEA model is employed to decompose the relationship between investment in agricultural water conservancy infrastructure and agricultural output into two stages: the water supply stage and the water utilization stage. The amount of irrigation water is used as an intermediate variable for both stages to reflect the differing efficiencies in the allocation of water resources and water-saving irrigation practices.

Research on the investment efficiency of agricultural water conservancy infrastructure has been well-documented, with a focus on methodological and empirical aspects. Variations in existing studies primarily stem from differences in input-output indicators, evaluation methods, and evaluation objects. However, some studies have overlooked the fact that water conservancy infrastructure serves as a crucial input variable for water resources, land resources, and the overall production environment, rather than a direct input factor for agricultural production. As shown in Figure 1, this study examines the contribution of agricultural water conservancy infrastructure to agricultural production by dividing it into two stages: water supply and water use. A two-stage system for evaluating the investment efficiency of agricultural water conservancy infrastructure is established, utilizing a two-stage DEA model for evaluation. The efficiency of the water supply stage mainly focuses on the provision of agricultural irrigation water and the protection of water and soil resources through infrastructure. On the other hand, the water use stage efficiency evaluates the relationship between factor input and output in agricultural production. Efficiency values at different stages are analyzed using methods such as kernel density estimation and Moran’s I index to illustrate their distribution and evolution characteristics in time and space. By calculating input redundancy and output deficiency in the input-output relationship between the two stages, the study identifies the root causes of efficiency losses and proposes optimization suggestions.

Figure 1

Figure 1. Research framework.

2 Methodology and data

2.1 Efficiency measurement method—Two-stage DEA model

The DEA model is commonly used in analyzing the investment efficiency of agricultural water conservancy infrastructure. The types and definitions of related efficiencies are primarily based on Farrell (1957) proposed categories. This model assesses the relative effectiveness of DMUs by comparing their deviation from the frontier while maintaining input or output constant. There are two main DEA models: the CCR model (also known as the CRS model) by Charnes et al. (1978), which assumes constant returns to scale; and the BCC model, a modification of the CCR model by Banker et al. (1984) that does not require the constant returns to scale assumption.

Due to variations in regional water resources, fiscal levels, and competitive conditions, it may not be feasible for regions to internally operate at the optimal scale. Consequently, when evaluating the impact of regional agricultural water conservancy infrastructure investment on agricultural output, a variable return is employed to scale the DEA model, specifically the DEA-BCC model (Cheng and Jin, 2024).

Suppose there are n DMUs, with each DMU undergoing two stages. Let X_j represent the inputs of the j-th DMU in the first stage, which includes m inputs, expressed as X_ji = (X_j1, X_j2, … , X_jm)^T for the j-th DMU. Let Z_j denote the outputs of the j-th DMU in the first stage, encompassing n outputs, formulated as Z_jd = (Z_j1, Z_j2, … , Z_jn)^T for the j-th DMU. Furthermore, let Y_j signify the final outputs of the j-th DMU in the second stage, comprising p outputs, articulated as Y_jk = (Y_j1, Y_j2, … , Y_jp) for the j-th DMU.

To ensure alignment between the outputs of the first stage and the inputs of the second stage, an input-oriented DEA-BCC model is utilized in the first stage, whereas an output-oriented DEA-BCC model is applied in the second stage.

$\begin{array}{l}\min E_1=\frac{{\displaystyle \sum _{i=1}^m}{\omega }_i{x}_{ji}+{\beta }_1}{{\displaystyle \sum _{d=1}^n}{g}_d{z}_{jd}}\\ s.t.\left\{\begin{array}{l}\frac{{\displaystyle \sum _{d=1}^n}{g}_d{z}_{jd}}{{\displaystyle \sum _{i=1}^m}{\omega }_i{x}_{ji}+{\beta }_1}\le 1\left(j=1,2,\cdots ,r\right)\\ {\omega }_i\ge 1,g_d\ge 1,{\beta }_1\in R\end{array}\right.\end{array}(1)$

$t=\frac{1}{{\displaystyle \sum _{d=1}^n}{g}_d{z}_{jd}};t{w}_i={\omega }_i;t{g}_d={\lambda }_d;t{\beta }_1={\eta }_1$

Applying the Charnes et al. (1978) transformation to Equation 1, we can derive the final linear model Expression Equation 2 for the first stage:

$\begin{array}{l}\min E_1={\displaystyle \sum _{i=1}^m}{\omega }_i{x}_{ji}+{\eta }_1\\ s.t.\left\{\begin{array}{l}{\displaystyle \sum _{d=1}^n}{\lambda }_d{z}_{jd}-{\displaystyle \sum _{i=1}^m}{\omega }_i{x}_{ji}+{\eta }_1\le 0\left(j=1,2,\cdots ,r\right)\\ {\displaystyle \sum _{d=1}^n}{\lambda }_d{z}_{jd}=1\end{array}\right.\end{array}(2)$

where ω_i represents the weight coefficient of the input indicator for the first stage; λ_d represents the weight coefficient of the output indicator for the first stage; η₁ is an unrestricted slack variable, reflecting the returns to scale characteristics of the j-th DMU in Expression Equation 3. η₁ = 0 indicates that the DMU is at the optimal production scale; that is, there are constant returns to scale; η₁≠ 0 indicates that the DMU is in a state of increasing or decreasing returns to scale.

In the second phase, the DEA-BCC model (output-oriented) is used, aiming for maximum output and minimum input, with the evaluation index being the output/input ratio, and the optimal value being the maximum of this index.

$\begin{array}{l}\max E_2=\frac{{\displaystyle \sum _{k=1}^p}{u}_k{y}_{jk}-{\beta }_2}{{\displaystyle \sum _{d=1}^n}{g}_d{z}_{jd}}\\ s.t.\left\{\begin{array}{l}\frac{{\displaystyle \sum _{k=1}^p}{u}_k{y}_{jk}-{\beta }_2}{{\displaystyle \sum _{d=1}^n}{g}_d{z}_{jd}}\le 1\left(j=1,2,\cdots ,r\right)\\ u_i\ge 1,g_d\ge 1,{\beta }_2\in R\end{array}\right.\end{array}(3)$

$t=\frac{1}{{\displaystyle \sum _{d=1}^n}{g}_d{z}_{jd}};t{u}_k={\mu }_k;t{g}_d={\lambda }_d;t{\beta }_2={\eta }_2$

Applying the Charnes et al. (1978) transformation to Equation 3, we can derive the final linear model of Expression Equation 4 for the second stage:

$\begin{array}{l}\max E_2={\displaystyle \sum _{k=1}^p}{\mu }_k{y}_{jk}-{\eta }_2\\ s.t.\left\{\begin{array}{l}{\displaystyle \sum _{k=1}^p}{\mu }_k{y}_{jk}-{\displaystyle \sum _{d=1}^n}{\lambda }_d{z}_{jd}+{\eta }_2\le 0\left(j=1,2,\cdots ,r\right)\\ {\displaystyle \sum _{d=1}^n}{\lambda }_d{z}_{jd}=1\end{array}\right.\end{array}(4)$

where λ_d is the weight coefficient of the input variables in the second phase; μ_k is the weight coefficient of the output variables in the second phase; η₂ is an unconstrained real variable, reflecting the scale return characteristics of the jth DMU state in Expression Equation 4. η₂ = 0 indicates that the DMU is at the optimal production scale state; that is, constant returns to scale; η₂ ≠ 0 indicates that the DMU is in a state of increasing or decreasing returns to scale.

2.2 Kernel nuclear density and the dynamic evolution

In the existing literature, the traditional Gini coefficient and Theil index are frequently utilized to examine regional disparities. However, the precision of the Gini coefficient is often questioned, and the magnitude of the Theil index is highly sensitive to the base of the logarithm and the data distribution. Kernel density estimation offers a means to depict the distribution of random variables as a continuous density function, capturing not only the location but also shape and flexibility of the distribution. Assuming that the variables “R₁, R₂, … , R_n” represent sample points from an independent F-distribution with a probability density function denoted as f_ℎ(R), the corresponding kernel density estimation formula is presented in Equation 5:

$\stackrel{\wedge }{f_h}\left(R\right)=\frac{1}{nh}{\displaystyle \sum _{i=1}^n}K\left(\frac{R_i-\overline{R}}{h}\right)(5)$

Allowing R_i=WI_i, where WI_i represents the water conservancy infrastructure investment efficiency for a given sample province in China, we can compute the kernel density of the water conservancy infrastructure investment efficiency. The kernel function, denoted as K, is a non-negative function that integrates to 1, aligning with the properties of a probability density function, and it has a mean of 0. The term “h” (which is greater than zero) refers to the bandwidth, serving as a smoothing parameter.

$\mathit{f}\left(x\right)=\frac{1}{Nh}{\displaystyle \sum _{i=1}^N}K\left(\frac{X_i-x}{h}\right)(6)$

In this context, as shown in Equation 6. N denotes the total count of observations, with each X_i representing an independently and identically distributed observation across the dataset. The symbol x signifies the mean of these observations. The term K embodies the kernel density function, which is a type of estimator used for the probability density function of a random variable. Meanwhile, h stands for the bandwidth, a parameter that controls the smoothness of the estimation. As a function that serves both as a smoothing and weighting mechanism, the kernel density estimation typically meets the criteria shown in Equation 7:

$\left\{\begin{array}{l}\underset{x\to \infty }{\lim }K\left(x\right)·x=0\\ K\left(x\right)\ge 0{\displaystyle {\int }_{-\infty }^{+\infty }}K\left(x\right)dx=1\\ \sup K\left(x\right)<+\infty {\displaystyle {\int }_{-\infty }^{+\infty }}{K}^2\left(x\right)dx<+\infty \end{array}\right.(7)$

2.3 Spatial autocorrelation measure—Moran’s I

Moran’s I is an index that can be utilized to assess the spatial correlation among variables. The formula for calculating Moran’s I is presented in Equation 8:

$\begin{array}{ll}\hfill & \mathit{M}ora{n}^{\prime }sI=\frac{n{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{W}_{ij}\left(AW{I}_i-\overline{AWI}\right)\left(AW{I}_j-\overline{AWI}\right)}{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{W}_{ij}{\displaystyle \sum _{i=1}^n}{\left(AW{I}_i-\overline{AWI}\right)}^2}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{W}_{ij}\left(AW{I}_i-\overline{AWI}\right)\left(AW{I}_j-\overline{AWI}\right)}{S^2{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{W}_{ij}}\hfill \end{array}(8)$

$S^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\left(AW{I}_i-\overline{AWI}\right),\overline{AWI}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}AW{I}_i$, where n represents the total number of spatial units; W_ij is the spatial relationship value between spatial unit i and spatial unit j within the spatial weight matrix; AWI_i and AWI_j are the degrees of agricultural water conservancy infrastructure for provinces i and j, respectively; and the bar above a variable indicates the average value across the entire country. The value of Moran’s I index is in the range of [−1, 1]. A value greater than 0 signifies positive spatial correlation, while a value less than 0 indicates negative spatial correlation between the variables of the two provinces. The greater the absolute value, the stronger the correlation. During the measurement process, it is essential to define the spatial weight matrix and to apply different spatial weight matrices to measure variable correlation under specific spatial relationships. A scatter plot of Moran’s I can be employed to visualize the spatial correlation characteristics of the observations.

The spatial matrix defines the fundamental spatial relationships that are integral to the measurement of Moran’s I index and serves as the foundation for constructing a spatial model. Commonly utilized matrices include the adjacency matrix (W₁), the geographical distance matrix (W₂), the economic matrix (W₃). The principles for calculating these matrices are outlined in Table 1. Furthermore, this paper innovatively proposes a watershed matrix to improve the construction of agricultural water conservancy infrastructure, which relies on rivers and other water sources. According to the classification standards outlined in the China Water Conservancy Yearbook, China is divided into ten river basins: Songhua River Basin, Liao River Basin, Hai River Basin, Yellow River Basin, Huai River Basin, Yangtze River Basin, Southeast River Basins, Pearl River Basin, Southwest Rivers, and northwest rivers. The provinces included in each river basin are then determined. The watershed matrix is defined in detail (refer to W₄ in Table 1).

Table 1

Table 1. Calculation principles for designing spatial matrices.

2.4 Variable selection and data

To systematically and comprehensively assess the efficiency of investment in water conservancy infrastructure, it is essential to establish a scientific and practical input–output indicator system that aligns with the mechanisms of how water conservancy infrastructure impacts agricultural production, utilizing a two-stage DEA model. Agricultural water conservancy infrastructure is primarily designed to prevent and address disasters such as drought, flood, waterlogging, and salinization in farmlands, thereby improving the conditions for agricultural production through irrigation, drainage, and other related projects. Consequently, within the realm of agricultural production, these infrastructure types predominantly influence the provision of water resources and high-quality arable land, which are key input elements for farming activities.

Based on this analysis, an input–output variable system for the two-stage DEA model has been constructed, as depicted in Figure 2. In the first stage, the input variables include the stock of investment in agricultural water conservancy infrastructure and the workforce employed within the water conservancy sector. The outputs for this stage are the volume of water used in agriculture and the area of effective sowing. These output variables are the inputs for the second stage. Additionally, the second stage encompasses input variables such as the number of individuals engaged in agricultural work, the total power of agricultural machinery, the quantity of fertilizer used, and the volume of applied pesticide.

Figure 2

Figure 2. The input-output variable in two-stage DEA model.

By consulting the water conservancy databases from the China Water Conservancy Yearbook spanning from 2009 to 2023, as well as utilizing the EPS platform, the data for the aforementioned input–output indicators have been compiled and adjusted for the period from 2008 to 2022. Owing to the lack of data regarding effective irrigation areas, the final sample for analysis encompasses 31 provinces (including municipalities and autonomous regions), with the exclusion of Hong Kong, Macao, and Taiwan. Descriptive statistics for each variable are shown in Table 2.

Table 2

Table 2. Statistical description of variables.

3 Results

3.1 Basic situation and spatial characteristics

In this study, MAXDEA 8 software is employed to input the two-stage input–output panel data into the DEA model, wherein a multi-stage algorithm is used to evaluate the impact of investment in agricultural water conservancy infrastructure on agricultural output in a phased manner. This approach yields comprehensive efficiency information on both the water supply and the land protection and water use phases, including the efficiency of each individual phase. The results are presented in Table 3, where Score represents the overall efficiency. Stage1 reflects the first stage efficiency, which includes water supply and soil-water conservation efficiency. Stage2 represents the second stage efficiency, specifically water use efficiency. The relationship between the various efficiency values is as follows: $Score=Stage1\times Stage2$.

Table 3

Table 3. Average efficiency of each province from 2008 to 2022.

Looking at the average efficiency of input–output for agricultural water conservancy infrastructure investments from 2008 to 2022, there is a significant disparity among provinces. Only a few provinces achieve an efficiency of one in the Stage1. Since the overall efficiency is the product of the efficiencies from both stages, and there is a considerable difference in the efficiencies of the two stages across many provinces, it is rare that a province has high efficiency in both stages. Consequently, the overall efficiency values tend to be on the lower side. We now analyze the situation for each of the three efficiency values.

Firstly, regarding the overall efficiency, in addition to the generally low figures mentioned, there are also clear differences between provinces. Provinces with higher efficiency include Hainan, Shanghai, Henan, and Beijing. However, the results for Shanghai and Beijing are not statistically significant due to their smaller agricultural sectors. Henan and Hainan, being major agricultural provinces in China, not only benefit from economies of scale but also possess advanced agricultural production technologies, which contributes to their higher efficiency in water conservancy infrastructure investment.

Secondly, when examining Stage1, the differences between provinces are even more pronounced, with provinces such as Heilongjiang, Tibet, Qinghai, Ningxia Hui Autonomous Region, and Xinjiang Uygur Autonomous Region reaching a level of 1. Moreover, the Stage1 efficiency exceeds 0.85 in the case of Inner Mongolia Autonomous Region, Shanghai, Jiangxi, Chongqing, and Guizhou. A review of the geographical distribution of these provinces reveals that most are located in the southwest and northeast regions, which are relatively well endowed with water resources. In contrast, provinces in the water-scarce North China region and parts of the East China region have lower efficiency values for this stage. For instance, Shandong Province, which suffers from severe water scarcity, has an efficiency value of only about 0.49 for this stage.

Thirdly, from the perspective of the Stage2, which is the water use efficiency, the characteristics are entirely different from those of the Stage1. Provinces with efficiency values greater than 0.7 include Beijing, Shandong, Henan, and Hainan. The three provinces other than Beijing are major producers of grain, vegetables, and fruits in China. Shandong and Henan have relatively scarce water resources, and Hainan, despite its abundant rainfall, is often affected by typhoons. The higher water use efficiency indicates that the water conservancy infrastructure in these three regions is effective in water-saving irrigation and disaster prevention. Provinces in the lower efficiency bracket for this stage, with efficiency values below 0.2, mainly include Heilongjiang, Qinghai, and Ningxia Hui Autonomous Region.

In order to verify the correlation mentioned above, a test was conducted on the efficiency of two stages (Stage1 and Stage2) in the sample provinces, along with the actual GDP (GDP), annual water resources (R-water), and the cumulative stock of agricultural water infrastructure investment (AWI). The Pearson correlation test results, as depicted in Table 4, confirmed a significant correlation between stage1 and water resources, as well as between stage2 and the level of economic development.

Table 4

Table 4. Pearson correlation test.

In order to investigate the evolving characteristics of agricultural water conservancy infrastructure investment efficiency, a visual comparative static analysis was conducted on the efficiency values in 2008 and 2022. The efficiency distribution maps for these years are depicted in Figures 3–5.

Figure 3

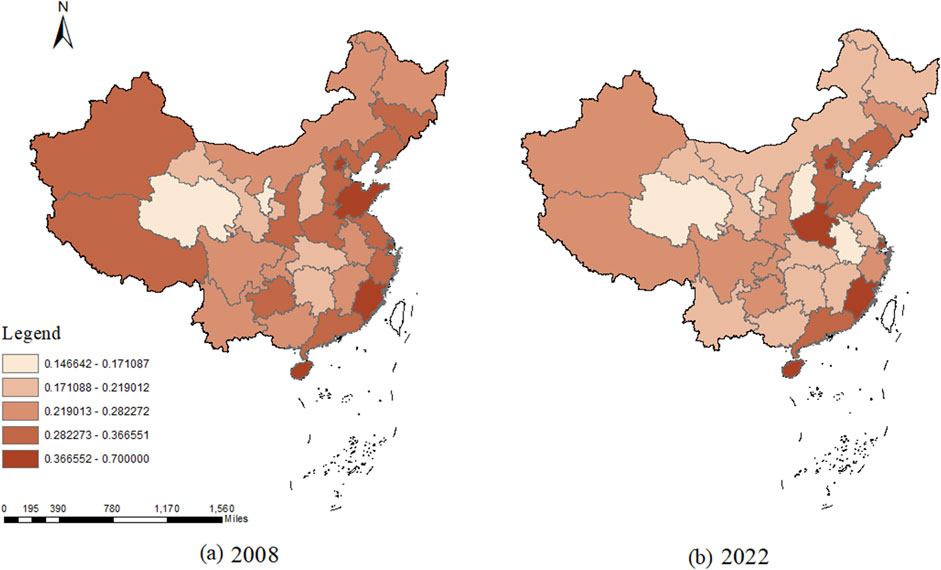
Figure 3. Distribution of Score of overall efficiency, (A) Distribution map for the year 2008. (B) Distribution map for the year 2022.

Figure 4

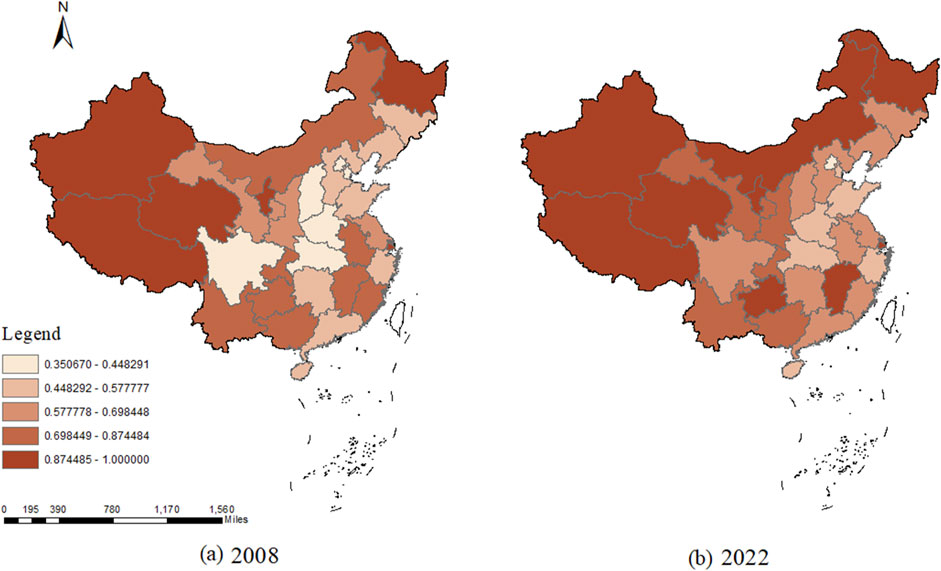
Figure 4. Distribution of Stage1 efficiency, (A) Distribution map for the year 2008. (B) Distribution map for the year 2022.

Figure 5

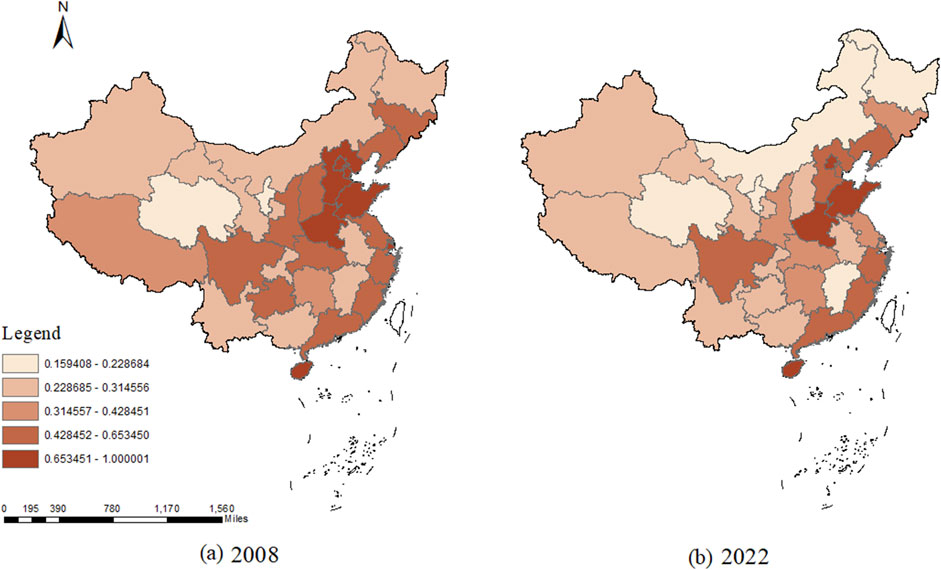
Figure 5. Distribution of Stage2 efficiency, (A) Distribution map for the year 2008. (B) Distribution map for the year 2022.

Overall, there has been a notable improvement in efficiency in certain areas of the central and eastern regions, such as Henan and Shandong provinces. Furthermore, the Stage1 analysis in Figure 4 reveals a significant enhancement in relative efficiency for the central and eastern regions, narrowing the gap with high-efficiency regions like the west and northeast. The increase in water supply efficiency in the central and eastern regions may be attributed to the expansion of agricultural irrigation infrastructure, the optimization of water resource allocation, and the more efficient utilization of water supply equipment by farmers and managers. Additionally, given that these areas are predominantly water-scarce, the agricultural water supply process is significantly influenced by the availability of water resources. In recent years, China’s inter-basin water transfer projects, such as the South-to-North Water Diversion Project, have improved regional water resource allocation to some extent, thereby alleviating the water scarcity challenges faced by these regions. Consequently, this is likely to have contributed to the enhancement of water supply efficiency. These considerations will be further validated in subsequent research. Examining Stage2 in Figure 5, a decline in efficiency is observed in the Inner Mongolia Autonomous Region, Shanxi in the northern region, Heilongjiang in the northeastern region, and Jiangxi in the central and southern regions, while other regions show minimal change. To more clearly delineate the distribution and evolution of the output efficiency of agricultural water conservancy infrastructure investment over the sample period, further clarification can be provided through the use of kernel density estimation methods.

The distribution and evolution of the output efficiency for agricultural water conservancy infrastructure investment over the sample period can be more clearly delineated on the basis of further clarification provided through the use of kernel density estimation methods.

3.2 Kernel density estimation

Kernel density estimation is performed on the overall and stage-wise efficiency results of water conservancy infrastructure investment from 2008 to 2022 as measured using the two-stage DEA, where kernel density estimation of the overall efficiency is shown in Figure 6, while Figures 7, 8 respectively illustrate the distribution and evolution of kernel density estimation for the efficiency of the first and second stages.

Figure 6

Figure 6. Kernel density estimation of the overall efficiency.

Figure 7

Figure 7. Kernel density estimation of Stage1 efficiency.

Figure 8

Figure 8. Kernel density estimation of Stage2 efficiency.

Firstly, examining the temporal evolution of the kernel density distribution curves for overall efficiency reveals that the curves for the sampled years are predominantly unimodal, with the peak predominantly in the range of 0.2–0.3 characterized by a noticeably shorter left tail compared to the right. Considering the overall efficiency values, it is important to note that the DEA model assesses relative efficiency, and since the total efficiency is the product of the kernel densities from both stages, it is expected that the values for total efficiency would be on the lower side.

Looking at the peak elevations, there is a clear upward trajectory over time. As the peaks rise, they also become narrower, indicating a convergence toward 0.2 regarding the total efficiency for most provinces. This convergence is also marked by a reduction in the length of the right tail, with a decreasing number of provinces exceeding a value of 0.5, which suggests a reduction in disparities between provinces. However, it is worth noting there is a concurrent decline in overall efficiency values.

Given that total efficiency is the multiplicative result of the efficiencies of both stages, it is likely that different provinces and regions will exhibit distinct characteristics at each stage. Therefore, it is imperative that kernel density estimation of efficiencies is also conducted for each stage. The outcomes of these estimations are depicted in Figures 6, 7.

The Stage1 kernel density estimation in Figure 7 and the distribution of overall efficiency exhibit considerable divergence, with the kernel density estimation curve demonstrating a markedly bimodal pattern for nearly all years. This pattern is characterized by two distinct peaks: one situated around 0.5 and the other around 0.9. Analyzing the movement of these peaks over time reveals a tendency for the left peak to drift toward the right, while the right peak remains stationary. This stability on the right is attributable to its nearness to 1, the upper limit of efficiency measurable by the DEA model, which implies a more confined space for further increase. The trajectory of the left peak’s shift underscores an upward trend in the initial efficiency of agricultural water conservancy infrastructure investments in provinces where lower efficiency levels were previously exhibited. This Stage1 predominantly pertains to the provisioning process of agricultural water and prime arable land, thereby indicating an enhancement in the aggregate supply efficiency of agricultural water conservancy infrastructure and a rise in the direct operational efficiency of these infrastructures.

Also noteworthy is the pronounced elevation of the nadir between the two peaks, which suggests a narrowing of disparities between provinces and a reduction in the degree of polarization as overall efficiency is enhanced. It should be acknowledged, however, that the input–output indicators designed for this study, for the Stage1, encompass only data on the region’s agricultural water supply and the extent of irrigation and do not account for the externalities affecting adjacent areas. Consequently, the observed rise in Stage1 efficiency signifies that with the diminishing proportion of central investments, there is a progressive rise in production efficiency concerning the natural resources essential for local agricultural production. The impact on external regions necessitates additional validation through assessments on further spatial spillover effects.

The rightward shift of the left tail also corroborates the aforementioned conclusions, indicating there is a collective improvement in the Stage1 efficiency of those provinces that were initially less efficient. This shift further substantiates the observed reduction in regional disparities.

As shown in Figure 8, the kernel density distribution of the Stage2 efficiency is found to be quite similar to those of the overall efficiency, exhibiting a distinct unimodal distribution. This, to some extent, indicates that the efficiency of the second stage contributes significantly to the total efficiency. Upon further observation of the temporal evolution of the Stage2 efficiency kernel density, it is noted that the peak has risen and slightly shifted to the left-over time. During the period from 2008 to 2010, the peak was broader and ranged between 0.3 and 0.6. From 2010 to 2017, the peak gradually consolidated between 0.3 and 0.4, with the unimodal feature becoming more pronounced. Post 2018, the unimodal characteristic has become even more evident, with the peak narrowing and the right tail extending closer to the horizontal axis, suggesting an overall decrease in efficiency and a pronounced polarization in the input–output relationship of the second stage. The efficiency characteristics of the second stage reflect, to a certain degree, the changes in the input–output efficiency of resources such as water and land. This indicates there is improved efficiency of water conservancy infrastructure in terms of water supply and irrigation area. However, no corresponding improvements are seen in the effectiveness of irrigation and the utilization efficiency of water resources. Therefore, the current policy direction in China, namely, to strengthen the construction of high-quality farmland and increase investment in infrastructure that enhances the utilization efficiency of water resources, appears to be the correct approach.

3.3 Moran’s I spatial autocorrelation test results

The Moran’s I test for spatial correlation is the basis of spatial analysis and is used to analyze the correlation of different location unit variables based on different spatial relations. It can test for similar, different, or independent relationships among regions under different spatial relationships. Based on the four spaces defined in Table 1, the agricultural output efficiency of China’s water conservancy infrastructure investment (including total efficiency and the efficiency of two stages) is tested based on the index Mollweide’s I, and the results are shown in Table 5.

Table 5

Table 5. Moran’s I index values of two-stage DEA scores for the 31 provinces.

Firstly, from the perspective of overall spatial correlation, with the exception of the economic matrix, the agricultural output efficiency of water conservancy infrastructure investment in each province shows a significant positive spatial correlation. However, under the economic matrix, most coefficients are negative and do not pass the significance test, indicating that the three types of efficiency scores are not significantly related to the relative economic levels between regions. Thus, it is more likely that there is autocorrelation based on geographical spatial relationships.

Secondly, regarding the differences in spatial correlation of the three types of efficiency, it is evident that second-stage efficiency has higher geographical spatial correlation than the first-stage and overall efficiency. Specifically, of these three types of efficiency, the spatial autocorrelation is weakest for overall efficiency. This is mainly due to the significant differences in the distribution characteristics of the Stage1 and Stage2 efficiencies. After multiplication, the spatial correlation of overall efficiency is weakened. The spatial autocorrelation coefficients of the Stage2 efficiency based on the three major spatial matrices of adjacency, geography, and river basin are all positive and highly significant, indicating that there is a positive demonstration effect and a mutually reinforcing relationship between the water use efficiency of each province in neighboring areas and within the same river basin. There is relatively strong spatial autocorrelation of the Stage1 efficiency based on the river basin matrix, all passing the significance test, and the results are positive. Based on the adjacency and geographical matrices, the significance of Stage1 efficiency is not high for half of the sample years. This confirms and illustrates that the efficiency of the water supply stage is greatly related to spatial location and water resource endowment, also indirectly demonstrating that economic development and technological improvement also depend on natural conditions. Thus, the protection and sustainable use of natural conditions is crucial.

Lastly, in terms of the trend of efficiency over time, the significance of the Stage1 efficiency gradually strengthens, and there is a trend of increasing coefficients. The spatial correlation coefficients of the second-stage efficiency show a slight downward trend under the adjacency, geographical, and river basin matrices. The above results indicate that the spatial relationships of efficiency are gradually weakening. Combined with the results from the analysis of kernel density estimation mentioned earlier, the main reason for this result appears to be intensification in the polarization of the second-stage efficiency level, the enhancement of regional differences, and the relative decrease in water use efficiency in additional areas.

4 Optimization analysis

In the two-stage DEA model, output slack and input slack are two important indicators for measuring the efficiency of DMUs. output slack refers to the gap between the actual output and the maximum possible output of a DMU under a given level of input. A positive output slack indicates that the DMU has not fully utilized its input resources toward producing more output. In terms of efficiency evaluation, output slack is considered unfavorable because it implies the potential to improve efficiency and output. On the other hand, input slack refers to the excess of input resources used by a DMU over the minimum input required to achieve the current level of output. A positive input slack means that the input resources of the DMU exceed the optimal level, which could lead to resource wastage.

4.1 Optimization analysis on Stage1

We will delve into the factors that contribute to the disparities in agricultural output efficiency resulting from investments in water conservancy infrastructure across different regions. By conducting calculations on the slack variables within a two-stage DEA model of 2022 (as detailed in Tables 5, 6), we aim to provide a deeper analysis into the reasons behind the observed inefficiencies. This will enable us to pinpoint the root causes of efficiency losses more precisely, all in the pursuit of enhancing overall efficiency.

Table 6

Table 6. Optimization analysis on Stage1.

From Table 6, it can be observed that in the Stage1 most provinces are experiencing a shortfall in output and redundancy in input. Firstly, from the input perspective, Investment redundancy is most prevalent in water infrastructure investment, indicating that current investment levels in these areas are already adequate. Instead of simply increasing investment in new projects, efforts should focus on enhancing efficiency through better utilization and management of existing infrastructures. The analysis shows that all provinces in China face shortages in water and land supply, with the exception of Shanghai and Xinjiang, where the shortages are limited to the sown area. This highlights the ongoing challenge of distributing water resources and preserving soil and water resources across all provinces in the country. In terms of spatial distribution, provinces with redundancy in the two input factors are spread out in all directions, without any obvious locational characteristics. The agricultural water supply deficiencies are particularly significant in Beijing, Tianjin, Qinghai, and Ningxia. A comparison of water endowment data shows that most of these regions face extreme water resource scarcity, indicating that the challenge of inter-basin water transfers remains daunting.

4.2 Optimization analysis on Stage2

Entering the optimization analysis of the Stage2 efficiency (Table 7), we find that there is still an overall deficiency in output, and this deficiency exists in all provinces, indicating that there is significant room for improvement in the efficiency of the agricultural production phase. Looking at the redundancy of other input factors, there is less redundancy in the input of agricultural labor and pesticides. Input redundancies are mainly concentrated in total machinery power and fertilizer usage, while these redundancies are also more geographically specific.

Table 7

Table 7. Optimization analysis on Stage2.

From a spatial distribution perspective, there is minimal input redundancy in Northeast and South China. In other regions, input redundancy is primarily seen in chemical fertilizers, particularly in the western region. South China shows input redundancy in total mechanical power. Taking into account the terrain, landform, and climate characteristics of different regions, the following observations can be made: firstly, there is generally no redundancy of agricultural labor in most areas of China; secondly, organic and natural growth of agricultural products is more suitable than heavy reliance on chemical fertilizers in western plateau areas and eastern megacity areas; thirdly, the mountainous and fragmented nature of South China makes mechanized planting impractical; finally, the northeast, central, and eastern regions, being key agricultural areas in China, have minimal investment redundancy, with a focus on chemical fertilizers, indicating the positive impact of ongoing land transfer and mechanized planting. Moving forward, the promotion of contiguous and large-scale planting should be continued, with increased emphasis on the efficient use of chemical fertilizers.

5 Conclusions and implications

In this study, we measured the agricultural output efficiency of water conservancy infrastructure investment in 31 provinces in China from 2008 to 2022 by analyzing the impact pathways of water conservancy infrastructure on agricultural production, combined with a two-stage DEA model. An index system for the two stages of water supply and soil conservation and water use has been established in the measurement of efficiency, with agricultural water use and sown area of arable land selected as intermediate variables. Based on measurements of the production efficiency of water conservancy infrastructure investment and the corresponding spatial visualization analysis, we also conducted kernel density estimation and spatial autocorrelation tests based on four types of spatial matrices: adjacency, geography, economy, and river basin. In this analysis, the distribution and evolution of total efficiency and the efficiency of the two stages are examined over space and time. Finally, based on the weights of output shortage and input redundancy of different stages and provinces measured in the two-stage DEA model, we have analyzed the causes of low efficiency and directions for optimization.

The study results demonstrate that there are significant regional differences in the overall output efficiency of China’s water conservancy infrastructure investment, and there is also large variation in the spatiotemporal characteristics of the two stages. Firstly, from the perspective of overall efficiency, the overall efficiency level is relatively low, and spatial correlation is not strong, with regional characteristics not being very pronounced. The main reason for the above results is that the first and second stages of efficiency exhibit completely different regional characteristics. Regions with high water supply efficiency in the Stage1 often do not have an advantage in water use efficiency, and regions with high water use efficiency often have lower efficiency in the Stage1. Coupled with the fact that total efficiency equals the product of the two partial efficiencies, the characteristics are not very distinct. Secondly, regarding the efficiency of the Stage1, provinces with higher efficiency are mainly distributed in areas rich in water resources and have a more pronounced spatial correlation, with no obvious polarization and a trend of decreasing regional disparities over time. Again, looking at the water use efficiency in the second stage, the kernel density distribution shows a significant unimodal pattern. The results of temporal evolution analysis indicate that the peak has risen and shifted slightly to the left-over time, suggesting a trend of declining efficiency and polarization in recent years. The above results indicate that China needs to further strengthen investment in water conservancy infrastructures with high water resource utilization rates, increasing the efficiency of water resource use while ensuring agricultural water supply. The current high-standard farmland construction being implemented in China is indeed the appropriate strategic choice to address the decline and polarization of water use efficiency. Agricultural water conservancy facilities do not serve as direct inputs in agricultural production; instead, they enhance yields by facilitating efficient irrigation, optimizing soil conditions, and protecting soil and water resources, thereby mitigating disaster-related losses. Unlike existing research, which typically analyzes the overall efficiency of these infrastructure investments, this paper distinguishes between the water supply and use stages, calculating efficiencies separately. This approach effectively opens the ‘black box’ of their influence on agricultural production. It clarifies efficiency and regional differences across various stages and analyzes spatial distribution and correlation. Using analytical software to identify efficiency loss sources through input redundancy and output deficiency provides valuable insights for formulating more targeted and practical countermeasures and recommendations.

After measuring the efficiency of water conservancy infrastructure investment and analyzing its influencing factors and spatial effects, we propose several policy recommendations to address the issues identified in this study: (1) We should continue to advance the construction of high-standard farmland, focusing on and increasing investment in infrastructure that improves the efficiency of water resource utilization, such as water-saving irrigation, to enhance the effective use of terminal water resources. (2) We should promote development and investment related to the construction of water conservancy infrastructure suitable for large-scale mechanized production. As the scale of investment continues to expand, the impact of management and technical factors of water conservancy infrastructure on the investment efficiency becomes increasingly significant. In the future, we should strengthen the control and promotion of investment project management and technology, placing more emphasis on improving their overall comprehensive benefits. (3) Due to the characteristics of water conservancy infrastructure that extend across regions and basins, together with the existence of certain externalities, various types of water conservancy infrastructures affect the efficiency of not only the local area but also related regions. We should therefore continue to advance research in this area and recommend that an interprovincial compensation mechanism be established for water conservancy infrastructure investment toward facilitating benefit compensation within river basins or economic cooperation frameworks, thereby mitigating the inefficiencies caused by market failures. Additionally, more attention should be paid to cross-regional “enclave” cooperation projects between adjacent provinces in the future to break the restrictions of administrative boundaries. (4) We should employ more market-oriented operational methods to attract more private capital into the construction of water conservancy infrastructure in addition to innovating investment, financing, and return methods toward better reflecting the social and cross-regional benefits of water conservancy infrastructure.

6 Implications and outlook

This study categorizes the contributions of agricultural irrigation infrastructure to agricultural production into two distinct phases: supply and utilization. A two-stage DEA model has been utilized to evaluate both overall efficiency and the efficiency of each phase. Furthermore, the spatial distribution characteristics have been described and assessed from the perspectives of visualization, evolutionary distribution traits, and spatial correlation. Finally, we examine the sources of efficiency loss across different regions and phases, drawing on input redundancy and output insufficiency data from both phases. It is well established that large-scale agricultural irrigation infrastructure exhibits cross-regional and watershed-based characteristics, along with possessing attributes of public goods (Anomaly, 2015). Investment in agricultural irrigation infrastructure is anticipated to generate spatial spillover effects concerning efficiency in both the supply and utilization phases, with notable distinctions between the spillover effects in each phase. Unfortunately, due to space limitations, a comprehensive discussion and verification of the existence and pathways of these spillover effects cannot be provided in this paper; this will be the focus of our future research.

Agricultural water infrastructure often involves large-scale projects that are capital-intensive and have extended payback periods, exhibiting characteristics of a quasi-public product. Particularly when it comes to major infrastructures, these projects cover broad areas and necessitate construction that transcends both river basins and regional boundaries. As a result, financing for agricultural water infrastructure cannot be addressed by market mechanisms alone and is typically supported by government public finance. Assessing and analyzing the efficiency of investment in such infrastructure as well as pinpointing the key determinants that affect it are essential for refining the investment structure of water conservancy projects, improving the utilization efficiency of water agricultural production.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LS: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. CZ: Methodology, Software, Writing–original draft. QL: Data curation, Funding acquisition, Methodology, Software, Visualization, Writing–review and editing. CX: Formal Analysis, Project administration, Writing–review and editing. MS: Methodology, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by the Social Science Planning Fund Program, Shandong Province (No. 23CCXJ06).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1452535/full#supplementary-material

References

Acevedo Guerrero, T. (2018). Water infrastructure: a terrain for studying nonhuman agency, power relations, and socioeconomic change. WIRES Water 5 (5), e1298. doi:10.1002/wat2.1298

CrossRef Full Text | Google Scholar

Anomaly, J. (2015). Public goods and government action. Philos and Econ. 14, 109–128. doi:10.1177/1470594x13505414

CrossRef Full Text | Google Scholar

Banker, R. D., Charnes, A., and Cooper, W. W. (1984). Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manage Sci. 30 (9), 1078–1092. doi:10.1287/mnsc.30.9.1078

CrossRef Full Text | Google Scholar

Charnes, A., Cooper, W., and Rhodes, E. (1978). Measuring the efficiency of decision-making units. Eur. J. Oper. Res. 2 (6), 429–444. doi:10.1016/0377-2217(78)90138-8

CrossRef Full Text | Google Scholar

Cheng, Q., and Jin, H. (2024). Spatial–temporal evolution characteristics and influence factors of extreme precipitation indices based on bias-corrected and gauge-measured precipitation data in the main river basins of China, 1980–2020. Theor. Appl. Climatol. 155, 3563–3580. doi:10.1007/s00704-024-04826-9

CrossRef Full Text | Google Scholar

Du, L., Xu, L., Li, Y., Liu, C., Li, Z., Wong, J. S., et al. (2019). China’s agricultural irrigation and water conservancy projects: a policy synthesis and discussion of emerging issues. Sustainability 11 (24), 7027. doi:10.3390/su11247027

CrossRef Full Text | Google Scholar

Farrell, M. J. (1957). The measurement of productive efficiency. J. R. Stat. Soc. 120 (3), 253. doi:10.2307/2343100

CrossRef Full Text | Google Scholar

Guo, Z., and Zhang, H. (2024). The important role of intelligent water conservancy in the construction of high-standard farmland. BOHR Int. J. Civ. Eng. Environ. Sci. 2 (1), 6–11. doi:10.54646/bijcees.2024.14

CrossRef Full Text | Google Scholar

Hao, H., Yin, S., Liu, Z., and Liu, Z. (2022). Research on agricultural logistics efficiency based on DEA and tobit regression models. J. Eur. des systèmes automatisés 55 (1), 71–79. doi:10.18280/jesa.550107

CrossRef Full Text | Google Scholar

Hatamkhani, A., Shourian, M., and Moridi, A. (2021). Optimal design and operation of a hydropower reservoir plant using a WEAP-based simulation–optimization approach. Water Resour. Manag. 35 (5), 1637–1652. doi:10.1007/s11269-021-02821-7

CrossRef Full Text | Google Scholar

Kim, K. T., Lee, D. J., Park, S. J., Zhang, Y., and Sultanov, A. (2015). Measuring the efficiency of the investment for renewable energy in Korea using data envelopment analysis. Renew. Sustain. Energy Rev. 47, 694–702. doi:10.1016/j.rser.2015.03.034

CrossRef Full Text | Google Scholar

Kord, A., Payan, A., and Saati, S. (2022). Network DEA models with stochastic data to assess the sustainability performance of agricultural practices: an application for sistan and baluchestan province in Iran. J. Math. 2022. doi:10.1155/2022/1119630

CrossRef Full Text | Google Scholar

Lazurko, A., and Venema, H. D. (2017). Financing high performance climate adaptation in agriculture: climate bonds for multi-functional water harvesting infrastructure on the Canadian prairies. Sustainability 9 (7), 1237. doi:10.3390/su9071237

CrossRef Full Text | Google Scholar

Liu, J., Zang, C., Tian, S., Liu, J., Yang, H., Jia, S., et al. (2013). Water conservancy projects in China: achievements, challenges and way forward. Glob. Environ. Chang. 23, 633–643. doi:10.1016/j.gloenvcha.2013.02.002

CrossRef Full Text | Google Scholar

Liu, X., Wang, S., Wang, Y., Kang, S., Hao, X., and Li, F. (2014). Comprehensive evaluation of farmland infrastructure in the arid area of north-west China. Irrig. Drain. 63, 561–572. doi:10.1002/ird.1858

CrossRef Full Text | Google Scholar

Liu, Y., and Wu, C. (2002). Situation of land-water resources and analysis of sustainable food security in China. J. Nat. Resour. 17 (3), 270–275. doi:10.3321/j.issn:1000-3037.2002.03.003

CrossRef Full Text | Google Scholar

Pan, Z., Tang, D., Kong, H., and He, J. (2022). An analysis of agricultural production efficiency of Yangtze River Economic Belt based on a three-stage DEA malmquist model. Int. J. Environ. Res. Public Health 19 (2), 958. doi:10.3390/ijerph19020958

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, M., Wang, Q., and Ji, X. Y. (2017). Research on regional differences and threshold effects of total factor farmland water conservancy efficiency in China. J. Hohai Univ. Philosophy Soc. Sci. Ed. 19 (04), 40–46+91. doi:10.3876/j.issn.1671-4970.2017.04.008

CrossRef Full Text | Google Scholar

Sun, Q., and Yu, S. (2023). Agricultural green ecological efficiency evaluation using BP neural network–DEA model. Systems 11 (6), 291. doi:10.3390/systems11060291

CrossRef Full Text | Google Scholar

Tsai, M. C., Cheng, C., Nguyen, V., and Tsai, M. I. (2020). The theoretical relationship between the CCR model and the two-stage DEA model with an application in the efficiency analysis of the financial industry. Symmetry 12, 712. doi:10.3390/sym12050712

CrossRef Full Text | Google Scholar

Wang, Q., Li, L., and Sun, J. (2022). Environmental efficiency of port and regional system: a two-stage network efficiency model. Comput. Ind. Eng. 171, 108462. doi:10.1016/j.cie.2022.108462

CrossRef Full Text | Google Scholar

Xie, Q., Ma, H., Zheng, X., Wang, X., and Wang, F. (2022). Evaluation and spatial–temporal difference analysis of urban water resource utilization efficiency based on two-stage DEA model. IEEE Trans. Comput. Soc. Syst. 9 (5), 1282–1296. doi:10.1109/tcss.2021.3116043

CrossRef Full Text | Google Scholar

Xu, Y. (2023). Impact of the Chinese allowance for purchasing agricultural machinery on the efficiency of agricultural machinery—an empirical analysis based on DEA-tobit two-stage method. Sustainability 13 (02), 607–621. doi:10.12677/sd.2023.132064

CrossRef Full Text | Google Scholar

Yan, J. (2019). Spatiotemporal analysis for investment efficiency of China’s rural water conservancy based on DEA model and Malmquist productivity index model. Sustain. Comput. Inf. Syst. 21, 56–71. doi:10.1016/j.suscom.2018.11.004

CrossRef Full Text | Google Scholar

Yang, S., Wang, H., Tong, J., Ma, J., Zhang, F., and Wu, S. J. (2020). Technical efficiency of China’s agriculture and output elasticity of factors based on water resources utilization. Water 12 (10), 2691. doi:10.3390/w12102691

CrossRef Full Text | Google Scholar

Yuan, J. (2020). Economic impact of investment in water conservancy construction in Hubei Province. Desalination Water Treat. 187, 79–86. doi:10.5004/dwt.2020.25292

CrossRef Full Text | Google Scholar

Zhang, C., Li, J., and Sun, J. (2022). Influence of investment gap in farmland water conservancy infrastructure on the loss of grain production efficiency. Resour. Sci. 44 (1), 169–180. doi:10.18402/resci.2022.01.13

CrossRef Full Text | Google Scholar

Zhang, S., Liu, Y., and Huang, D. H. (2019). Contribution of factor structure change to China’s economic growth: evidence from the time-varying elastic production function model. Ekonomska Istrazivanja-economic Res. 33 (1), 2919–2942. doi:10.1080/1331677x.2019.1697722

CrossRef Full Text | Google Scholar

Zhao, T., Xie, J., Chen, Y., and Liang, L. (2022). Coordination efficiency in two-stage network DEA: application to a supplier–manufacturer sustainable supply chain. Int. J. Logist. 25 (4-5), 656–677. doi:10.1080/13675567.2021.1895976

CrossRef Full Text | Google Scholar