A radiative transfer deep learning model coupled into WRF with a generic fortran torch adaptor

Advances in deep learning have created new opportunities for improving traditional numerical models. As the radiation parameterization scheme is crucial and time-consuming in numerical models, researchers sought to replace it with deep learning emulators. However, progress has been hindered at the offline emulation stage due to the technical complexity of the implementation. Additionally, the performance of the emulators when coupled with large-scale numerical models has yet to be verified. In this paper, we have developed a new tool called the Fortran Torch Adaptor (FTA) to facilitate this process and coupled deep learning emulators into the WRF model with it. The performance of various structured AI models was tested in terms of accuracy, generalization ability, and efficiency in different weather forecasting scenarios. Our findings revealed that deep learning models outperformed ordinary feedforward neural networks (FNN), achieving greater accuracy both online and offline, and leading to better overall forecasting results. When it came to unusual extreme weather events, all models were affected to some extent, but deep learning models exhibited less susceptibility than other models. With the assistance of FTA, deep learning models on GPU could achieve significant acceleration, ranging from 50x to 300x depending on the parameterization scheme replacing strategy. In conclusion, this research is crucial for both the theoretical and practical development of radiation transfer deep learning emulators. It demonstrates the emerging potential for using deep learning-based parameterizations in operational forecasting models.

1 Introduction

For a long time, meteorology research has been driven by physics-based mechanisms, with researchers relying on mathematical equations to explain geophysical and climatic phenomena. They have built deterministic computing systems to simulate and evaluate these processes. Recently, data-driven research methods represented by deep learning have made continuous progress, opening up new opportunities for the development of traditional numerical models (Irrgang et al., 2021). Increasing Data from Earth System Observations (ESO), advances in computing power, and powerful AI approaches have led to many innovative developments aimed at addressing numerical models’ shortcomings and enhancing their capabilities.

Currently, there are three types of approaches to combine AI with numerical models. The most common application is the post-processing of numerical model results using AI approaches (Krasnopolsky and Lin, 2012; Rasp and Lerch, 2018), which is favored for its simplicity. Another important scenario is the application of AI methods to the data assimilation process of numerical models (Lee et al., 2020). The most complex and probably most effective approach is integrating AI directly into the numerical model. Existing studies have explored replacing various components of the numerical model with AI emulators, including the dynamic core of the numerical model (Dueben and Bauer, 2018), sub-grid convection parameterization schemes (Brenowitz and Bretherton, 2018; Yuval and O’Gorman, 2020), planetary boundary layer parameterization schemes (Wang et al., 2019) and radiation parameterization schemes (Chevallier et al., 1998; 2000; Belochitski, 2011; Pal et al., 2019; Roh and Song, 2020) with AI emulators. Of all the components that can be replaced by AI emulators, radiation parameterization is one of the most popular options.

The radiation parameterization scheme is used to calculate the energy conversion during the process of radiation transmission in the Earth system. Although researchers have been able to build accurate line-by-line radiative models to simulate this (Clough et al., 1992), due to its expensive computational cost, the numerical models typically use simplified radiative models such as Rapid Radiation Transfer Model for GCM (RRTMG) to accomplish this task (Mlawer et al., 1997; Iacono et al., 2008; Pincus et al., 2019). Nevertheless, the computation of the radiation parameterization scheme remains the most time-consuming part of the entire numerical model running process (Krasnopolsky, 2020).

To accelerate the computation of the radiation parameterization scheme, researchers considered using neural networks to emulate and replace it even before the AI craze. Despite the slow training process of neural networks, they are much faster than traditional radiative transfer (RT) models based on kinetic equations in the inference stage. For the first time, the European Centre for Medium-Range Weather Forecasts (ECMWF) has utilized a neural network with a single hidden layer to simulate the RT computation process for each vertical layer in the radiation parameterization scheme (Chevallier et al., 1998). Moreover, the results have been incorporated into ECMWF’s four-dimensional variational data assimilation system (Chevallier et al., 2000). The National Center for Climate Prediction used neural networks to emulate longwave (LW) and shortwave (SW) radiation processes respectively, and successfully replaced the radiation parameterization scheme in the Global Forecast System (GFS) and the Climate Forecast System (CFS) for the online production environments, achieving significant speed improvements (Krasnopolsky et al., 2010). Pal et al. used a deeper neural network to compute radiation in the Super Parametric-Earth Energy System Model (SP-E3SM), which was an order of magnitude faster and produced stable results in a 1-year forecast (Pal et al., 2019). Song et al. extended this method to the study of weather forecasts with higher grid precision and stricter error requirement (Roh and Song, 2020). Replacing RT models with neural networks is a popular area of research not only in climate modeling and weather forecasting of the earth system but also in other scenarios such as remote sensing (Bue et al., 2019; Le et al., 2020; Liang et al., 2022).

All of the previous research employed the most basic feedforward neural network (FNN), which typically includes only one hidden layer. With the rise of deep learning techniques, deep neural networks (DNN) with complex network structures have achieved significant success in many fields (Wang, 2016; Ham et al., 2019). Some researchers have attempted to use DNN models to emulate the radiation parameterization scheme. For instance, Liu et al. (Liu et al., 2020) tested the performance of replacing the RRTMG long-wave module with a convolutional neural network (CNN) model, which is commonly used in the field of image recognition. Inspired by the internal calculation mechanism of the RT model, Ukkonen designed a deep learning model based on a recurrent neural network (RNN) enabling information exchange within the neural network layer to replace the whole radiation module (Ukkonen, 2022). Moreover, some scholars have achieved better results by incorporating domain knowledge or physical laws into neural network models, which are called Physics-informed neural networks (PINNs). Lagerquist applied U-Net, a more advanced CNN structure, to simulate the RRTM shortwave module and integrated physical relationships into the training process using a custom loss function (Lagerquist et al., 2021). Mishra et al. developed a novel algorithm based on PINNs that directly simulated the fundamental radiative transfer equation by minimizing the residual during training. (Mishra and Molinaro, 2021). Chen et al. applied PINNs to solve the radiative transfer equation and calculate a synthetic spectrum in cosmological studies (Chen et al., 2022).

The application of AI techniques to replace RT models can be divided into two steps. The first step is to train a radiation AI emulator on a radiation dataset, which is the offline simulation stage. The second step is the replacement stage, where the emulator is integrated into a large-scale numerical simulation system. These complex models (whether DNN or PINN) claimed to achieve good results in the simulation stage. However, the implementation complexity makes it challenging to integrate them into original numerical models compared with simple FNN. Currently, there are hardly any DNN emulators that can complete the second stage and operate online in real time.

Therefore, despite the impressive offline performance of DNN radiation emulators, there are still some arguments about their suitability for radiation emulators. Firstly, due to the lack of experimental data support for the online use of DNN radiation emulators, some researchers doubt whether they can maintain their good performance online as well (Ott, 2020). In other words, it is necessary to verify that good offline performance on the test dataset necessarily translates to good online performance when integrated into the numerical model. Furthermore, there are also doubts about the efficiency of DNN models. The “deep” of a deep learning model typically results in a more complex network structure with deeper layers, which can have a significant negative impact on performance, particularly when parallel acceleration provided by GPU is not available. As an example, the experimental results from Ukkonen (Ukkonen, 2022) indicate that the inference speed of deep learning models based on RNN models is 20 times slower than that of FNN inference under the same experimental conditions. Lastly, some researchers are concerned that the complexity and nonlinearity introduced by DNN structures might negatively impact generalization compared with FNN models (Belochitski and Krasnopolsky, 2021). Due to the black-box working mechanism of neural networks, although AI models can learn the underlying correlations contained in the data to some extent, they do not always follow the basic scientific rules of the physical system it models in their predictions (Reichstein et al., 2019). Therefore, they may not generalize well to unseen scenarios. While deep learning emulators can significantly improve the accuracy of radiation parameterization schemes, stable and reliable results are also necessary to make them practicable in the online operational environment.

To answer these controversial questions, we need to employ DNN models in online environments. Nevertheless, the primary issue is the lack of coupling tools to integrate complex DNN models into numerical models. Currently, popular numerical models are predominantly written in Fortran, but there is no mature AI ecological ecosystem in the Fortran language community. There do exist some tools, such as the popular NN Fortran library developed by Krasnopolsky (Krasnopolsky, 2014) and Fortran-Keras Bridge (FKB) (Ott, 2020) introduced by Irvine for porting trained NN models from Keras to the Fortran environment, that can be used to build AI applications in Fortran. But the restrictions are also apparent. For example, we are unable to use complex network structures like CNNs, let alone utilize GPU resources to accelerate computation. The separation between the AI and Fortran communities has become the primary obstacle to the application of deep learning to numerical models.

A generic tool called Fortran Torch Adaptor (FTA) was developed in this paper to solve the aforementioned technical challenges. FTA enables running AI models trained with PyTorch (a popular deep learning framework) directly in the Fortran environment using GPU resources. This tool is groundbreaking in bridging the gap between the Fortran environment and the AI ecosystem and is not limited to the radiation transfer AI modeling scenario. Moreover, it provides critical infrastructure for our subsequent experiments to test complex deep learning models in the online environment. A more in-depth introduction to it will be provided in Section 2.3.

In this study, we selected several NN models with different structures which have previously demonstrated good offline results (Belochitski and Krasnopolsky, 2021; Lagerquist et al., 2021; Ukkonen, 2022) and used them to emulate and replace the RRTMG-K radiation parameterization (both longwave and shortwave) in Weather Research and Forecasting Model (WRF). And these NN models will be evaluated both offline and online based on several weather forecast scenarios. Through these experiments, we will explore the following questions.

1. Whether the offline results of the AI model are consistent with the online results?

2. Is there an issue with the generalization ability of complex network models?

3. Considering both accuracy and efficiency, which model is more suitable for RT emulators? Particularly when GPU acceleration is enabled.

The contribution of this research is mainly reflected in two aspects. The first is the Fortran Torch Adaptor, which was created to incorporate deep learning models into the Fortran environment and served as the infrastructure for our experiments. The second is online validation experiments for deep learning radiation emulators. The performance of the deep learning emulators embedded into a large-scale model was evaluated through a series of experiments, demonstrating their superiority over traditional FNN models. In conclusion, this research is of great significance for the development of deep learning emulators in both theoretical and practical aspects.

The paper is organized as follows. The preparation of datasets for training and testing of the NNs is presented in Section 2.1. Section 2.2 presents different NN models we have used. In Section 2.3, we will introduce FTA and how we used it in the RT modeling experiment. Offline and online evaluation results are presented separately in Section 3.1 and Section 3.2. Finally, we present concluding remarks along with future works in Section 4.

2 Methods

2.1 Dataset

2.1.1 RRTMG-K in WRF

In this study, we used datasets of radiation simulations generated from the RRTMG-K radiation parameterization scheme in the WRF model (Skamarock et al., 2019). RRTMG-K (Baek, 2017) is an advanced version of the widely used RRTMG scheme, which enhances the efficiency and accuracy of radiation flux calculations for both spatial and angular integration of the RT equation. WRF is a leading mesoscale numerical weather prediction system that has been extensively used as the operational weather forecasting system, including the NCEP Global Forecast System (GFS) and the China Meteorological Administration (CMA) Global/Regional Assimilation and Prediction System (GRAPES).

Figure 1 presents the pseudocode for the original radiation module in the WRF model. Initially, the module initializes radiation-related variables. The primary radiation calculation logic takes place within a “for” loop, where each vertical column is independently processed following the rule of Independent Column Approximation rule. For each vertical column, some preprocessing work is carried out first to prepare the necessary input such as ozone properties, aerosol properties, optical cloud properties, and so on. Subsequently, the subroutines rrtmg_lwrad and rrtmg_swrad are called to perform the RRTMG SW and LW radiation calculations.

FIGURE 1

FIGURE 1. Pseudocode for the original radiation module presented in (A) and our proposed radiation module presented in (B). The blue part in the picture represents the replaced part in the module. The radiation AI emulator in this study only replaces the core radiation calculation logic and retains the module preprocessing part.

Unlike previous works (Roh and Song, 2020; Song and Roh, 2021), our approach did not involve replacing the entire radiation module radiation_driver. Instead, we emulated only the essential radiant calculation process, leaving the preprocessing logic untouched. This seems counterintuitive as it incurs additional adaptation workload and hinders performance improvement. However, we deemed it necessary to obtain some important preprocessed physical quantities, such as liquid particle effective radius, in-cloud liquid water path, and so on, which have been proven helpful in previous studies (Lagerquist et al., 2021). As a result, the input size of our model is significantly larger than that of typical models. The detailed input and output of the generated dataset are shown in Table 1. There are also some minor adjustments compared with similar studies. For example, we excluded some input variables of constant values because they provided no information for NN prediction. Furthermore, we included three additional input variables (longitude, latitude, and surface elevation) which were not present in the original scheme input. This geographical information is critical to help to capture similar characteristics between horizontally and vertically adjacent grids according to previous studies (Roh and Song, 2020).

TABLE 1

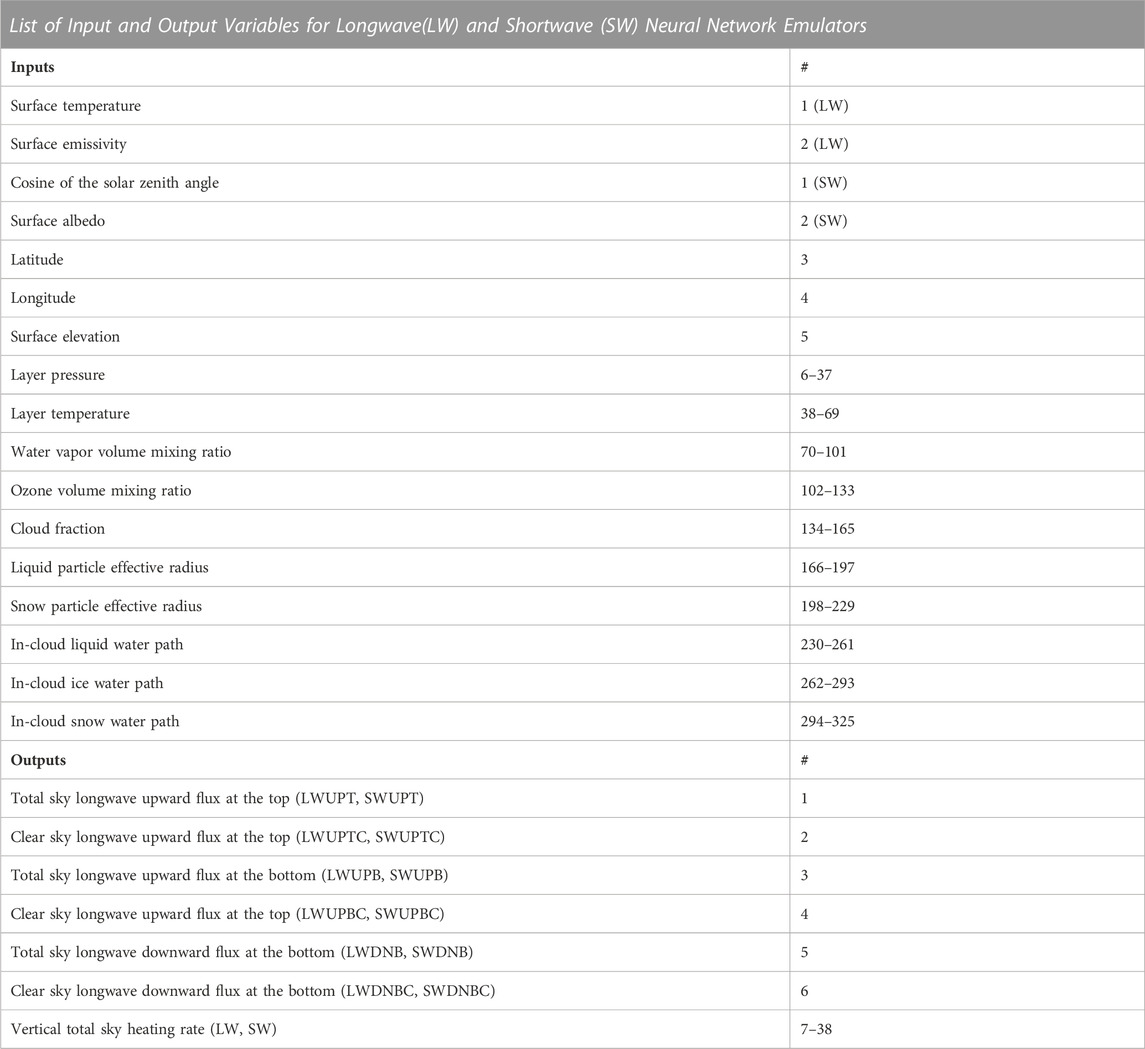
TABLE 1. List of input and output variables for the radiation simulation dataset. They are shown in a single table because the majority of variables in the longwave and shortwave datasets are the same. The input length for both datasets is 325, and the output length is 38. The longwave and shortwave datasets share most of the input variables, with only differences in the first two input variables (longwave: surface temperature and surface emissivity; shortwave: cosine of the solar zenith angle and surface albedo). The output of the two datasets is heat rates and related fluxes for longwave and shortwave, respectively.

2.1.2 Dataset generation process

It should be noted that the data in the dataset does not originate from the input and output of the WRF model, but rather from the input and output of the RRTMG-K scheme within the model. Since the input and output of the parameterization scheme are intermediate variables generated during model operation, they cannot be directly obtained from outside the model. Therefore, we modified the source code of the parameterization scheme to generate the dataset, ensuring that the input and output of the original module are not altered by other modules.

In addition to the standard set used for training, we created two testing sets for high-temperature and typhoon scenarios to test the AI emulator’s generalization ability in extreme weather conditions. The standard dataset is used to train AI models. Therefore, we aimed for it to learn from as many scenarios as possible, including different regions, seasons, and more. To accomplish this, we simulated the entire China region in 2021 using the WRF model to generate this dataset. For the two testing sets, we conducted simulations based on several typical extreme events that have occurred in recent years in China. Certain changes were applied to the WRF configurations dependent on the event characteristics, increasing the challenge of generalization for the NN models. The details are presented in Table 2. WRF4.2 was used to generate the radiation datasets used for NN training and testing in this survey. To approximate the real scene as much as possible, we chose a WRF setup comparable to the operational forecast. More specifically, Thompson Microphysics scheme was selected for the microphysics scheme, YSU boundary layer scheme was selected for the boundary layer scheme. Unified Noah Land-surface Model was selected for the land-surface scheme, and Kain-Fritsch Cumulus scheme was selected for the convection scheme. The experiments used NCEP FNL (final) operational global analysis data, which is compiled operationally on 1-degree by 1-degree grids every 6 hours. The reanalysis data provided by NCEP was processed by the WRF Preprocessing System as input to the WRF, and covers the entire China region with a horizontal resolution of 30 km and 33 vertical layers (or 34 levels) up to 50 hPa, with a grid size of 200 x 150. The WRF control run was integrated for 1 day every 180 s for both the time step (dt) and radiation time step (radt). As the optimal forecast time for WRF is between 24 and 48 h, the standard dataset was generated on a daily basis for all 365 days in 2021 to reflect the real-world usage scenario. For the RRTMG-K parameterization, it was set up with 256 g points for 16 bands over the LW spectrum and 224 g points for 14 bands over the SW spectrum using a two-stream correlated-k method and optimized Monte Carlo independent column approximation.

TABLE 2

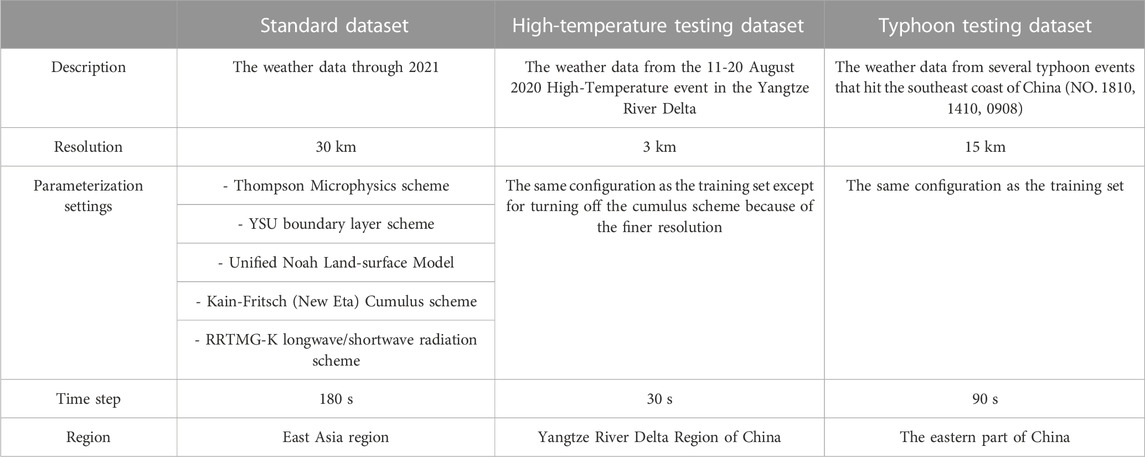
TABLE 2. The WRF configuration used to generate the three datasets. We have prepared a standard dataset for training and two extreme event datasets for testing. Different WRF configurations were used for each dataset based on their weather event characteristics. Only some important configuration items are listed here. Refer to the namelist file in the code repository for the complete configurations.

2.2 Neural network

In this subsection, we present three types of NN architecture for the RT emulator studied in this paper. Each network architecture has specific use scenarios, and we will focus on adapting various network models to the peculiarities of the radiation model to fully leverage their strengths. In the end, we’ll introduce the model training processes.

2.2.1 Feedforward neural network

A Feedforward Neural network (FNN) consists of three types of layers: an input layer, one or more hidden layers, and an output layer. Each layer usually has an activation function to introduce nonlinearity and acquire complex representations. As mentioned earlier, FNN is the most commonly used neural network for RT emulating, and there are already some successful cases of online FNN RT emulators in various fields, from climate simulation (Pal et al., 2019) to weather forecasting (Roh and Song, 2020).

Deciding on the network depth is an interesting issue when using FNNs. On the one hand, more hidden layers in a neural network are more conducive to extracting high-level semantic information about the features. On the other hand, Krasnopolsky et al. argued that (Belochitski and Krasnopolsky, 2021) controlling the stability and nonlinearity of deep networks is more challenging, and therefore, they are not suitable for building deterministic network models. Moreover, this concern is not limited to deeper FNNs but applies to all deep learning models. Therefore, we will investigate the performance of complicated models in the experiments, particularly in terms of generalization ability.

2.2.2 Convolutional neural network

CNN is a type of neural network designed for image-focused tasks. The convolutional layer in CNN is adept at capturing spatial features, such as the arrangement of pixels and their interrelationships in an image. This capability aids in accurately identifying an object’s position and its relationship to other objects in the image. In the context of RT, the localized features from the vertical column extracted by the convolutional layer are helpful to improve the offline prediction performance of deep neural networks compared with FNN, according to Liu’s experiments (Liu et al., 2020). For example, large local variations in the optical characteristics of the atmosphere are rather common because of the existence of clouds or horizontal advection of water vapor. FNN is not able to leverage this feature as it churns all the inputs together and ignores the spatial relations within.

In addition to the spatial characteristics of the input, the output of the radiation emulator also has a spatial structure, where a heating rate is calculated for each vertical layer. Such tasks fall into the category of pixel prediction in traditional AI research. U-net is a specialized type of convolutional neural network designed for such tasks (Lagerquist et al., 2021). It contains an encoding-decoding U-shaped structure, with skip connections that retain high-dimensional encoding feature information and pass it to the decoder side.

Since RT emulators produce both scalar outputs and vector outputs, we have made some modifications to the standard U-nets paradigm. The specific model design is shown in Figure 2. Our U-nets structure is designed with a conscious distinction between scalar and vector data and fully utilizes the spatial features of vector data while taking advantage of the convolutional network in extracting locality-dependent features. The vector features are layered into the U-nets network for feature extraction through the encoding path on the left. The U-nets structure fuses scalar features with embedding features extracted from vector-type features and predicts scalar output (fluxes-related information) through one fully connected layer. The vector-type output heating rate is obtained by layers from the decoding path of U-nets combined with the high-dimensional encoding information from skip connections on the same level.

FIGURE 2

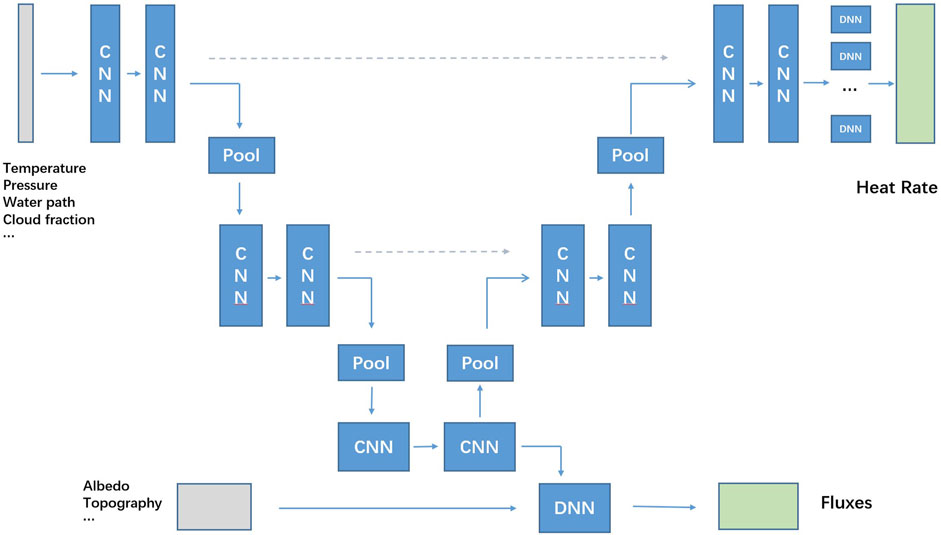
FIGURE 2. The model design of the CNN-based RT model. The overall framework of the model is based on a U-net model. The gray part represents the model input, the blue part is the model’s main structure, and the green part is the model output. The blue lines indicate the data flow, and the dotted lines are the skip connections.

2.2.3 Recurrent neural network

RNN is typically used for problems associated with temporal sequences. An RNN layer takes input at a specific point in a sequence, updates its internal state, and then moves on to the next point in the series. When dealing with a temporal problem, the internal state allows the RNN to have a memory so that prior inputs can influence the current forecast. Although radiative scenarios lack data with temporal dimensional characteristics, we can leverage this notion by describing the sequences as vertical layers. In the RNN layer, information travels down the sequence in the same way that radiative radiation propagates between vertical layers in numerical models. Additionally, since the fluxes can propagate in both directions, a bidirectional recurrent neural network (BiRNN) consisting of two RNNs of opposite directions was chosen to mimic this process (Ukkonen, 2022).

The model design of the RNN RT emulator is shown in Figure 3. The vector features are processed level by level through a fully-connected layer, fed into the BiRNN, and the heating rate for each layer is obtained from its output. Scalar features are also taken into account in predicting heating rates by affecting the initial hidden state of the BiRNN. For the scalar fluxes-related outputs, the layered DNN output combined with scalar features is used to predict them.

FIGURE 3

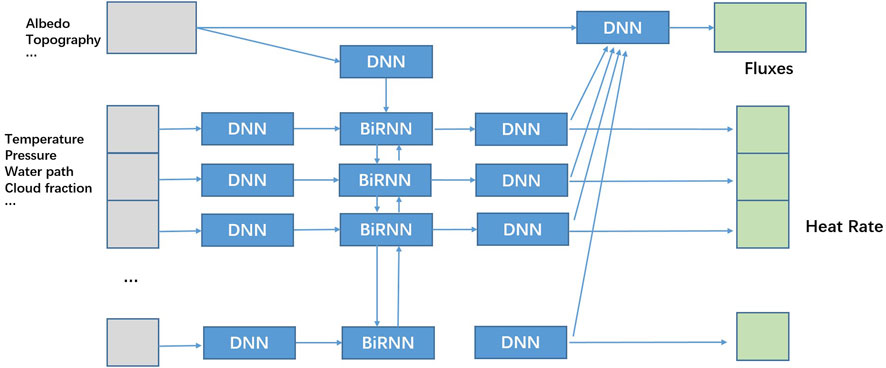
FIGURE 3. The model design of the RNN-based RT model. The main structure of the model is BiRNN, which is used to extract spatial features from vector inputs in the radiation dataset. The gray part represents the model input, the blue part is the main structure of the model, and the green part is the model output.

These are the three models which were used in the experiments. The CNN and RNN models share some similarities. For example, they both consider the spatial features of the data on the vertical column. The difference lies in how they handle these features: CNN extracts locality-dependent features of the vertical layer with convolutional kernels, while RNN treats the inputs of different vertical layers as a sequence and extracts features as a whole. Both CNN and RNN structures have been specifically designed based on the characteristics of RT, incorporating domain knowledge to help neural networks extract features more efficiently.

For the training process, we used the Adam optimizer to train all three types of models. Hyperparameters such as learning rate and batch size are tuned within a certain range through the grid search policy. Due to time and resource constraints, we can only try to tune the model as much as possible during training, since we need to test a lot of different types of models. It is worth noting that the goal of this study is not to find the best model but rather to test the performance of various model structures in the same scenario. For the same reason, we did not attempt to use overly complex structures like U-net++ as Lagerquist did (Lagerquist et al., 2021). Although the experiments may not reflect the best results for all types of structures, they are sufficient for this research.

2.3 Fortran Torch adaptor

Fortran Torch Adapter (FTA) is a generic tool developed to integrate deep learning models into the Fortran environment. It provides users with an interface to manipulate NN models directly in the Fortran language through FTA libraries. In this section, we will provide a detailed introduction to the background, implementation, and features of FTA. Furthermore, we will explain how this tool is used in our experiments.

2.3.1 Adaptor description

Deep learning has become increasingly popular in the earth system model community. However, since Python is the preferred language for AI, Fortran, which is commonly used for numerical models, lacks comparable libraries and tools. As a result, previous studies had to rely on a primitive and cumbersome implementation: training models in Python, importing model parameters into Fortran programs, and manually performing the forward propagation procedure in Fortran. This approach greatly limits the application of AI in earth system modes. There have also been some initiatives to address this issue, such as the Fortran-Keras Bridge (Ott, 2020), which automates the aforementioned operations. But some major limitations still exist, such as the inability to use complex model structures and the inability to access GPU resources for model inference.

We have developed a novel solution by creating a generic tool (Fortran Torch Adaptor) to utilize AI models in the Fortran environment based on language interoperability mechanisms. FTA enables PyTorch models to be used in the Fortran environment directly with GPU resources. FTA not only allows the Fortran projects to access the abundant deep learning resources from the Python community directly but also enables numerical models to use GPU-accelerated computation regardless of model architectures, which greatly helps to improve computational efficiency.

The implementation of FTA is based on the interoperability of Fortran and C++, as well as the complete C++ API support provided by the PyTorch community. The overall architecture is shown in Figure 4. It serves as an intermediary layer, providing simple and transparent interfaces for Fortran users to operate PyTorch models while hiding the underlying intricacies of connecting with C++ interfaces via language interoperability. In other words, the user only needs to use the interface provided by FTA as if calling a normal Fortran library function and FTA can automatically handle all the trivial inconsistencies between Fortran and C++ (such as data types, array memory models, etc.) which makes it extremely user-friendly.

FIGURE 4

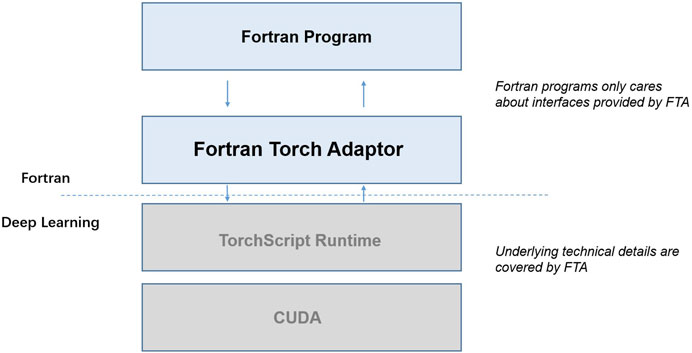
FIGURE 4. The role of FTA in the computer system. It serves as an intermediary layer, providing simple and transparent interfaces for Fortran users to operate PyTorch models while hiding the underlying intricacies of connecting with C++ interfaces via language interoperability.

FTA not only provides simple and transparent interfaces for Fortran users to operate PyTorch models but also offers flexibility that allows users to customize it to their specific needs. The customizable parameters include some system environment configuration options, such as the compiler used, the version of PyTorch, etc., as well as some usage options, such as the dimension and type of input and output data of the AI model, whether to use GPU resources, the storage location of AI models, etc. Comprehensive tests have been conducted to ensure the usability of FTA.

Lastly, FTA strives to ensure optimal performance. The performance advantages of Fortran have made it a popular language in the HPC field. If FTA were to suffer a significant performance loss, the cost of using it would outweigh the benefits. However, compared to other schemes, FTA may have a small drawback. This is because FTA requires an additional C++ runtime to run the TorchScript model compared to the native implementation of Fortran neural networks. Moreover, although FTA supports the use of GPU to accelerate calculation, the acceleration effect brought by GPU in the AI model reasoning stage is not significant, and it also incurs the additional cost of data transfer from memory to video memory. However, this issue is not unique to FTA; it affects all solutions that attempt to use the GPU. In the next subsection, we will introduce our solutions to overcome this challenge. Nevertheless, we still managed to maximize the performance of FTA during implementation. For example, FTA reduces unnecessary deep copy operations by sharing a single memory block among various languages.

All in all, FTA is an easy-to-use, flexible, and efficient tool to bridge the gap between the AI ecosystem and the Fortran environment. It is worth noting that this tool is not limited to integrating AI in earth system models. Any applications written in Fortran which aim to integrate AI models can benefit from it.

2.3.2 Implementation of WRF with embedded NN (WRF-NN)

In the experiments, we have trained a variety of deep learning models with different structures to emulate the RRTMG-K parameterization in the WRF model and coupled them into the WRF model via FTA to explore their online performance. This subsection introduces the implementation details of WRF-NN. As shown in Figure 1, what WRF-NN does is just get radiation results from NN inference instead of performing complex physical formula calculations. Though, there are some noticeable changes in the entire process.

First, the radiation calculation in WRF-NN is not performed column by column like the original scheme. Instead, all columns are directly computed together as a batch in the neural network which greatly improves efficiency. As mentioned earlier, the FTA solution has the drawback that its inference speed is not comparable to the native Fortran neural network due to the additional cost from C++ TorchScript runtime. To make it worse, when GPU is used, the flow cost from memory to video memory should also be considered. To address this performance loss issue caused by the flow cost, we developed a parallel implementation in our experiments. In the original RRTMG-K implementation, each column of grids is handled separately and all columns need to be traversed throughout the execution. If we strictly followed this computing strategy, each column’s radiation calculation would go through one data flow procedure, significantly negating the neural network’s performance advantages. To mitigate this issue, instead of performing the calculation separately, we perform it in batches, where a group of grid point calculations is carried out concurrently. Also, batch calculation can take advantage of the vector instructions of the CPU such as SIMD, or the parallel computing power of the GPU, which only incurs one extra cost of data transfer. It should be noted that the parallelism here is multiple-data parallelism and does not conflict with the WRF’s thread-level parallelism, implying that the acceleration effects can be stacked when sufficient resources are available. As demonstrated in the subsequent experimental section, the efficiency problem of FTA is eliminated after implementing this batch-processing technique.

Another point to note is the extra post-processing step. Since we normalized both the input and output when training NN models, we need to perform the same operations in WRF-NN to ensure compatibility. We must also denormalize the output when returning it. Furthermore, to prevent the neural network’s output results from violating physical constraints and causing the entire system to fail, we strictly limit the output results within the range prescribed by physics. For example, negative shortwave flux values are not permissible.

3 Experiments and results

Our experiments can be divided into two parts: offline and online. In the offline experiments, we trained several models with different structures on the generated dataset. For each type of structure, we examined the results under different scenarios. After that, we selected some representative models, coupled them into the WRF model with FTA to replace the original radiation scheme, and evaluated their online performance.

3.1 Offline results

To select the best models for online experiments, we tried various combinations of the network’s depth and width for each model type. The overall model results are presented in Figure 5. The complete results are presented in the Supplementary Material because of the large amount of experimental data.

FIGURE 5

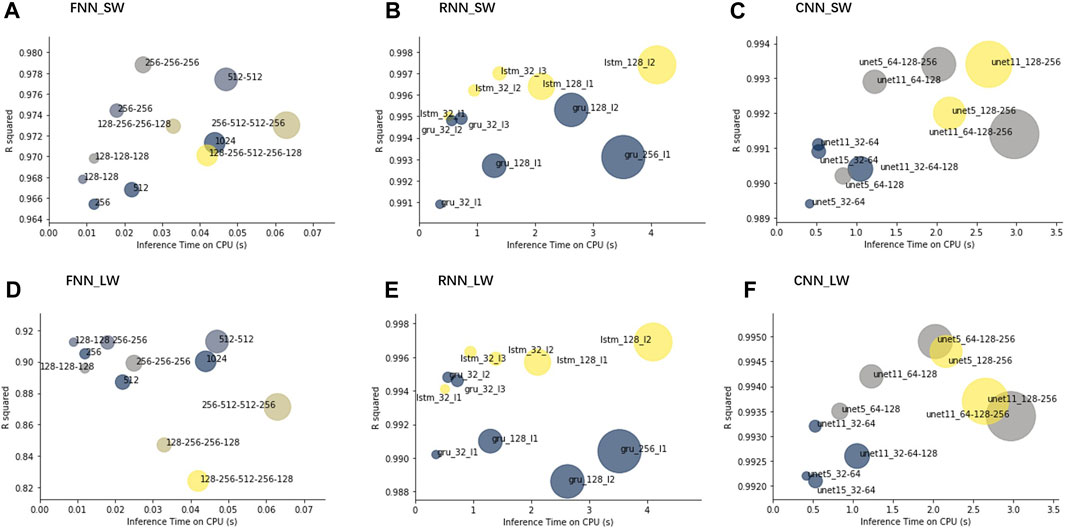
FIGURE 5. FNN, RNN, and CNN models’ performance on the SW standard dataset is presented in (A) (B) (C), on the LW standard dataset is presented in (D) (E) (F). A simplified notation to describe the model structure is used in Table 3. The horizontal coordinate indicates the inference time of the model in seconds on the CPU. The vertical coordinate indicates the performance of the correlation coefficient of the model on the test set. Therefore, the further to the top left, the better this model behaves. Additionally, model size measured by the number of parameters is represented by the area of the circle in the figure. Different types of models (FNNs, CNNs with different layers; RNNs using different units) are distinguished by different colors.

The FNN results are shown in the left column of Figure 5. In general, the SW FNN model’s performance improved as the model scale expands. And deeper models exhibited better performance than wider models at comparable scales. In other words, both depth and width were helpful to improve model performance, while broadening the model was less efficient than deepening it. This finding is in line with the mainstream opinion that a deeper model can learn more complicated transformations, leading to better nonlinear representation and useful feature inputs. However, the performance gains from depth came with a cost. The dividend delivered by additional layers decreased and might have negative impacts beyond a certain size. This law also applied to other model structures. For LW models, the situation was more complicated. The same rules applied to some extent, however, the tipping point where depth started to negatively contribute occurred much earlier than in SW models. The figure shows that the accuracy of LW models is not comparable to that of SW models, especially for large-scale models. Taking all the factors into account, a medium-sized FNN model which consists of two hidden layers of 512 neurons achieved the best results for both LW and SW.

For the RNN models, we experimented with two commonly used RNN units, namely, long short-term memory (LSTM) and gated recurrent unit (GRU), which are distinguished by different colors in Figure 5. LSTM has a powerful feature extraction capability and can yield better results with sufficient data, while GRU has fewer parameters and requires fewer data to generalize. With sufficient data generated by the numerical models in this experiment, the results of LSTM were better than those of GRU, but their inference efficiency was inferior to that of GRU. Under the same model structure, the results of LSTM were significantly better than those of GRU. Similar to the FNN results, the performance of layer stacking improved more efficiently than increasing neuron numbers within a single layer. The model based on GRU units reached its performance bottleneck at a very small scale, while the LSTM unit improved the performance upper limit of the model. At least within our testing range, larger LSTM models still performed better. The acceleration effect of GPU was much more obvious for RNN models. Due to the inherent recurrent characteristics of RNN structure, they were tens of times slower than FNN, even with GPU acceleration. Such performance would be completely unacceptable if FTA had not made GPU acceleration accessible. In addition, we noticed that the RNN structure brought substantial accuracy improvement compared with FNN. Even the simplest GRU model with only one layer and 32 hidden neurons in each unit performs better than the best FNN model, implying that the complexity of the deep learning model leads to better performance.

As we know, for CNN, convolution kernels play a critical role in CNN as they are responsible for extracting locality-dependent features which are the connections between vertical levels in the RT-emulating scenario. The kernel size corresponds to how many levels are considered in the CNN network. For example, when the kernel size is set to 1, the inputs from each level are encoded independently and the connection information between levels is lost. On the one hand, expansion of the kernel window helps to bring more inter-level association information when extracting features. On the other hand, it also introduces more noise which diminishes the advantage. When the kernel size is set to 32, which is the total number of levels, the CNN convolution layer degenerates into a dense layer, which is not desirable. After conducting some preliminary attempts, we determined two convolution kernels of sizes 5 and 11. Further experiments were conducted based on these kernel sizes. Building upon this, we conducted further investigations into the impact of U-Net network depth and width on the outcomes. In the case of the shortwave model, both 5 and 11 convolution kernel sizes yielded commendable results. The U-Net network with a three-layer encoder, featuring a first layer comprising 64 convolution kernels and a kernel size of 5, delivered the best correlation coefficient and MAE results. On the other hand, a network with the same three-layer encoder but with a first layer comprising 64 convolution kernels and a kernel size of 11 exhibited superior RMSE results. Moreover, when comparing specific indicators, the model with a kernel size of 5 demonstrated favorable performance in predicting heating rates, while the model with a kernel size of 11 excelled in predicting fluxes. Similar outcomes were obtained for the longwave model. However, due to the increased complexity of simulating longwave radiation, the larger U-Net with a kernel size of 11 reached its performance bottleneck earlier. Appendix Table 5 provides detailed results. Overall, when the model size was relatively small, larger kernel sizes substantially improved accuracy. Nevertheless, as the model size reached a certain threshold, smaller kernel sizes proved to be more effective. For instance, in our experiments, two models with identical structures except for the kernel size exhibited almost identical results, despite the model with a kernel size of 11 having twice the number of parameters as the model with a kernel size of 5.

In conclusion, we examined the effects of different model structures on the results under different architectures. For FNN, the depth of the model had a more significant impact on the results compared to the width of the model. For the CNN model, we focused on the effects of kernel size and the depth and width of the encoder-decoder path on the results. We found that models with larger convolution kernels had an advantage when the model size was relatively small. For the RNN model, the more advanced LSTM unit had a significant effect improvement compared to the GRU unit.

Throughout the model design process, we devoted a lot of effort to considering the spatial characteristics of the data. Therefore, we restored the model’s output results and visualized the spatial structure of which in Figure 6. The errors of the three model types shared some commonalities. They all performed better at the top of the atmosphere and worse near the surface. This distribution of errors can be explained from the perspective of atmospheric science. The complex interactions and energy exchange processes between the surface and the atmosphere, combined with the terrain and surface features, human activities, and other factors, make the radiation process of the surface more complex and challenging to simulate for AI models. Besides, the LW NN emulator exhibited much greater heating rate errors than SW. Comparing the three types of models, the FNN model performed the worst, with errors exceeding 0.25 and 1 $\mathrm{K}/\mathrm{d}\mathrm{a}\mathrm{y}$ for shortwave and longwave heating rates, respectively, in extreme cases. The CNN model was able to control the errors within 0.1 and 0.25, while the RNN model achieved the best results with errors of 0.05 and 0.15, respectively. This is consistent with the previous conclusion that the RNN model has the strongest spatial feature extraction capability.

FIGURE 6

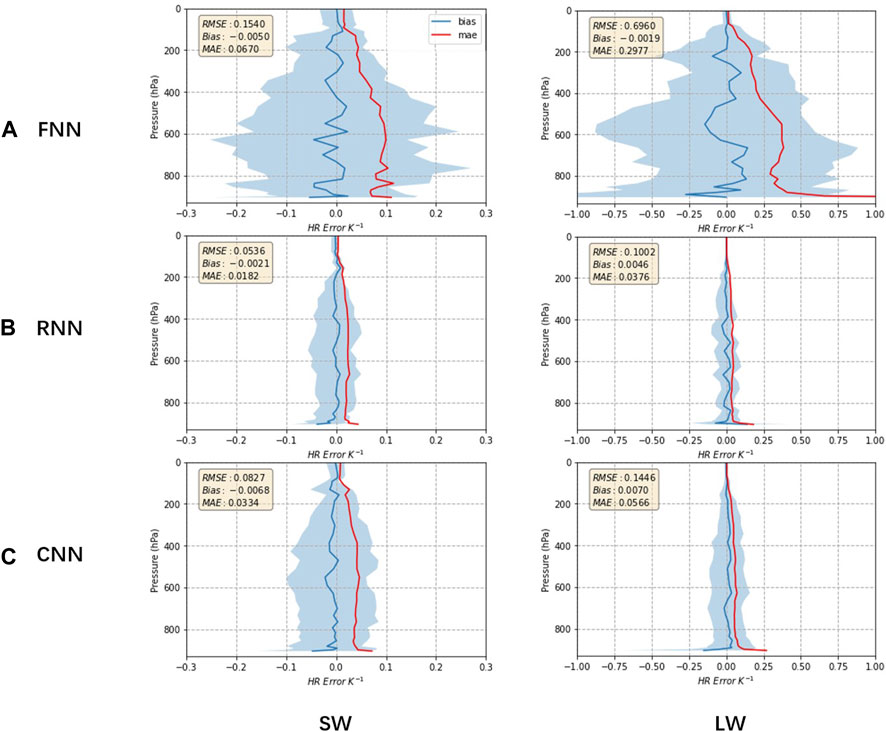
FIGURE 6. Vertical profiles of the error in heating rates using different NN models on the standard dataset (SW on the left and LW on the right). FNN used here is fnn_512-512 (A), RNN used is gru_32_l2 (B), and CNN used is unet11_32-64 (C). The red and blue lines show the mean absolute error and bias respectively, while the shaded area indicates the 5th and 95th percentile of differences (predicted - true value) at each level. Comparing the three models, the RNN-based radiation simulator exhibits the best spatial error distribution.

Based on the results presented above, we selected several representative NN models of each structure for further research. The models were selected based on two criteria: efficiency and accuracy. The most accurate model is certainly tempting, but a relatively accurate and efficient model may be more suitable for an operational model. In addition to the standard dataset used for model training and validating, we also prepared two additional testing datasets collected from extreme weather events to test the generalization ability of these models. From Table 3 and Table 4, we can see that models which achieve better results in the standard dataset are also better when faced with extreme conditions. For example, the selected LSTM model performed best in all metrics both for SW and LW. Compared to the FNN results, its RMSE error had decreased by 54% and 75% for SW and LW respectively. For extreme scenarios, all models showed some degradation in performance, especially for the Typhoon test set. Taking the LSTM shortwave simulation performance as an example, the error in the typhoon scenario was 1.8 times that of the standard dataset, while in the heatwave dataset, it was only 1.3 times. This is reasonable because there must be cases in the extreme events dataset that the model has not seen during training. Compared with high-temperature scenarios, typhoon events are much rarer in the standard dataset and more difficult to simulate. Among all the models, the LSTM model that performed the best on the standard dataset also performed the best on the extreme event dataset. That’s to say, models with higher accuracy on the standard dataset also had better generalization capabilities. This proves that concerns about the potential robustness risk introduced by the complex NN structure do not exist.

TABLE 3

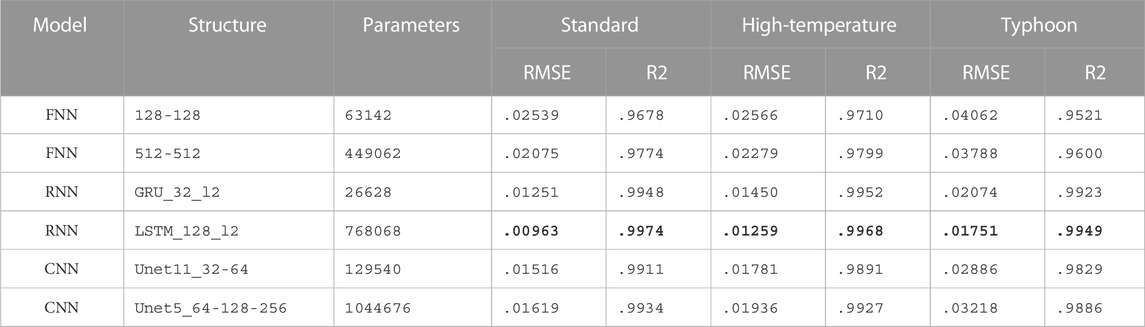
TABLE 3. Performance on all three datasets for the representative SW NN models. The bold fields represent the best results for that metric. We use a simplified notation to describe the model structure. For example, an FNN model with structure 256-256 has two hidden layers which both have 256 neurons; an RNN model with structure gru_32_l3 has three bidirectional RNN layers which all have 32 GRU units; a CNN model with structure unet5_32-64 has an encoder path with a depth of two layers (32 kernels in the first layer and 64 kernels in the second) and sets the convolutional kernel size as 5. Please note that the RMSE in the table is the error value obtained after standardizing several output variables and specific errors for each variable are provided in the results in the appendix. The RNN model LSTM_128_l2 achieved the best results in all metrics for all SW datasets.

TABLE 4

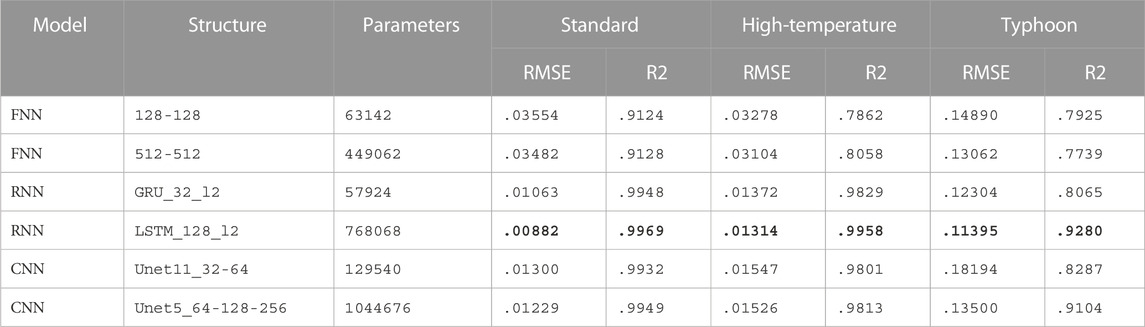
TABLE 4. Same as Table 3, but for LW datasets. The RNN model LSTM_128_l2 achieved the best results in all metrics for all LW datasets.

3.2 Online results

As mentioned earlier, we used FTA to replace radiation parameterization with selected NNs. Rather than emulating the entire radiation module, we chose to emulate only the core procedure of radiation calculations. Therefore, we separately measured the total runtime of the radiation module and the runtime of the radiation fluxes computation process, distinguishing between daytime (SW and LW running together) and nighttime (LW only) emulations. We also compared WRF’s multicore acceleration scheme with our schemes using the NN alternatives. The results are shown in Table 5.

TABLE 5

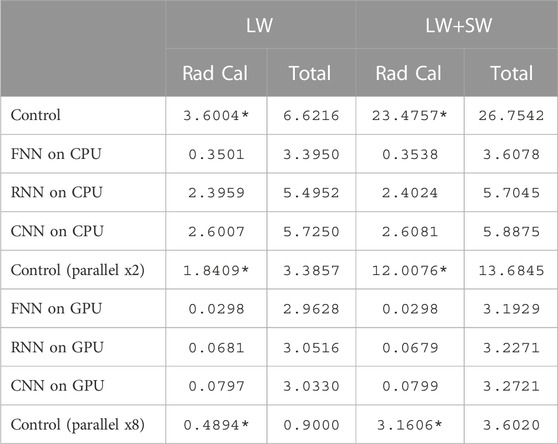
TABLE 5. The computation cost of different radiation schemes in seconds. The radiation AI simulator can greatly improve computational efficiency, especially with the support of GPUs. Control represents the original RRTMG-K radiation parameterization scheme and its results in parallel CPU acceleration are also provided as a reference. * indicates that the time is extrapolated rather than measured directly. FNN used here is fnn_512-512, RNN used is gru_32_l2, and CNN used is unet11_32-64.

All AI emulators provided some levels of acceleration depending on the architecture of the neural network and whether CPU or GPU is used. Specifically, when only CPU resources were used, the simple FNN network could achieve about 10 times acceleration for the LW radiation computation module, while the customized RNN and CNN could provide about 1.5 and 1.4 times acceleration, respectively. If both long-wave and short-wave parametrization schemes were replaced, the acceleration effect became more significant, FNN could reach a speedup ratio of 66 times, and both RNN and CNN reached a speedup of about 10 times. When the GPU was used for model inference, the speedup was significantly improved, with a 120-fold speedup using the FNN replacing only the long-wave radiation scheme, and a nearly 50-fold speedup for the RNN and CNN. When both the long-wave and short-wave schemes were replaced, the FNN speedup was further improved to about 800-fold, while the speedup ratio was around 300-fold for the more complex RNN and CNN. Compared to previous work, our FTA solution provides undiminished CPU acceleration, while the GPU acceleration even takes it a step further, boosting it by an order of magnitude.

The aforementioned results only pertain to the acceleration of the replaced flux computation module in the radiation parameterization scheme, and the overall acceleration of the entire radiation parameterization scheme is subject to the limitations of Amdahl’s Law. Our tests have shown that replacing only the long wave with AI resulted in an overall acceleration effect roughly equivalent to the MPI parallel scheme with two cores while replacing both the long wave and short wave simultaneously could outperform the acceleration effect of eight cores. As mentioned earlier, the AI parameterization scheme can be combined with the model’s parallelism scheme to provide a superimposed acceleration effect.

Improving computational efficiency alone is not enough. We also examined the actual impact of AI emulators on model operation. For this purpose, we selected several representative AI models and incorporated them into the WRF model using FTA, then verified their performance in realistic scenarios. To select the simulation scenarios, we utilized high-temperature and typhoon scenarios that generated extreme event datasets. This allowed us to test the performance of the model in extreme scenarios and compare its online and offline performance. Since WRF is mainly used for short-term weather forecasting, the extreme weather event scenarios were divided into several complete 24-h simulations, and average results were obtained. We extracted some key indicators, including LW/SW flux, LW/SW heating rate, skin temperature, and precipitation, for analysis. Flux and heating rate were obtained from the direct output of the parameterization scheme, while skin temperature and precipitation were obtained from the WRF output.

Figure 7 displays WRF-NN results under the heatwave scene. The simulation started at midnight, and was divided into three stages: the night before sunrise (LW alone 0–3 h), the day after sunrise (LW/SW runs together 3–17 h), and the night after sunset (LW runs alone 17–24 h). Let’s first examine the output from the parameterized scheme in the above four panels. The online error development trend for different AI models was roughly the same, with an increase followed by a decrease. The LW radiation scheme performed significantly better when LW works alone at night than when LW and SW worked together. During the day after sunrise, the simulation errors of both long wave and short wave radiation parameterization schemes experienced an explosive increase, reaching the peak in 12–16 h and then falling back to a lower level. This is very similar to the error accumulation mechanism of the autoregressive model. For example, there is a certain deviation in the heating rate output of the AI emulators, which affects the result of skin temperature. In the next iteration, the LW emulator would be affected because it requires a temperature input. Thus, a small error can have a lasting effect over time during online iterations. This is why online AI emulators are much less accurate than they are on the test set. In addition, by comparing the results of different models, RNN performed better than CNN and FNN most of the time. It can be seen that the accuracy of the AI model online and offline is the same, meaning that the model that performs better offline also performs better online, which is consistent with the conclusion of previous studies. Next, we examined the output of the WRF mode using the AI emulator. The performance of skin temperature was largely influenced by the LW heating rate, with a maximum error of about 1 $\mathrm{k}$. The deep learning model did not have a significant advantage during the daytime, but at night, the deep learning model outperformed the ordinary FNN model. In terms of precipitation, there was a discernible disparity in the performance of each model during the nighttime period after sunset, with the RNN demonstrating the lowest error at 0.4 mm/h. This discrepancy could potentially be attributed to the reduced occurrence of precipitation in high-temperature scenarios. We also conducted tests under typhoon scenarios; however, these results are not depicted in the figure due to all emulators’ online results rapidly shifting out of the valid range within a short duration.

FIGURE 7

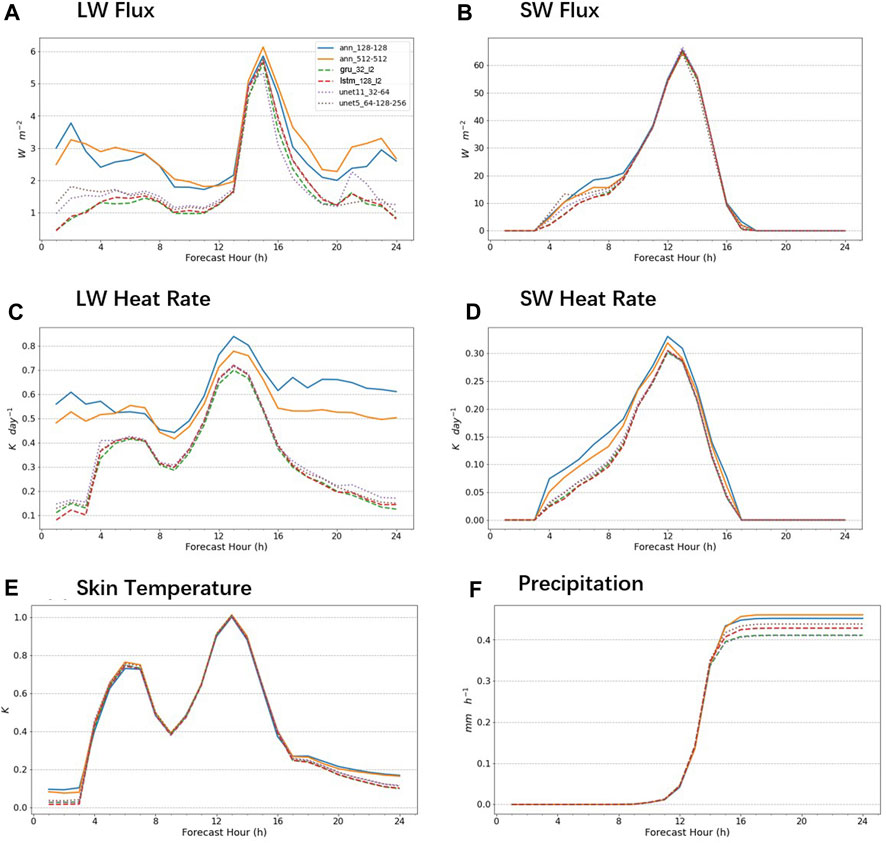
FIGURE 7. Performance of the WRF embedded with different NNs (WRF-NN) in simulating the heatwave event. The x-axis represents the simulation duration, and the y-axis represents the RMSE error compared to the original WRF model at that time for various indicators, including (A) longwave (LW) flux, (B) shortwave (SW) flux, (C) LW heating rate, (D) SW heating rate, (E) skin temperature, and (F) precipitation. The results of different models are differentiated by different line colors and styles. ANN is represented using solid lines, RNN using dashed lines, and CNN using dotted lines.

We did some further analysis for emulators’ online errors. Generally, it originates from two sources. The first is the error of the AI emulator itself, which refers to the error exhibited by the emulator in the offline dataset. Our experimental results show that the online error is much larger than the offline error mainly because of the second aspect. Therefore, if we can control the growth of the cumulative error we can significantly improve the results of online forecasting.

In the previously designed online experiments, AI emulators were used to replace both the LW and SW schemes, resulting in errors that interacted with each other, contributing to cumulative error growth. For example, the LW Flux error shown in Figure 7 was not only from the LW emulator but also from the deviation from the SW emulator output in the last time step, which affected the input vector in this iteration, thereby contributing to the error. To exclude the interaction of the LW and SW emulators, we attempted to replace the long- and short-wave parameterization schemes separately. The results are shown in Figure 8. The results of replacing the SW radiation parameterization scheme alone were close to those of replacing both LW and SW, while the results of replacing only the LW were significantly better than the former two. It was evident that the error when replacing both LW and SW came mainly from the cumulative error of the SW emulator. Even LW using the original physical parameterization scheme could not improve the overall results. Therefore, the accuracy of the SW radiation emulator has more significant effects on the results when the LW and SW radiation emulators are in use, and improving the SW radiation emulator will be more helpful to improve the overall output of the numerical model at this time.

FIGURE 8

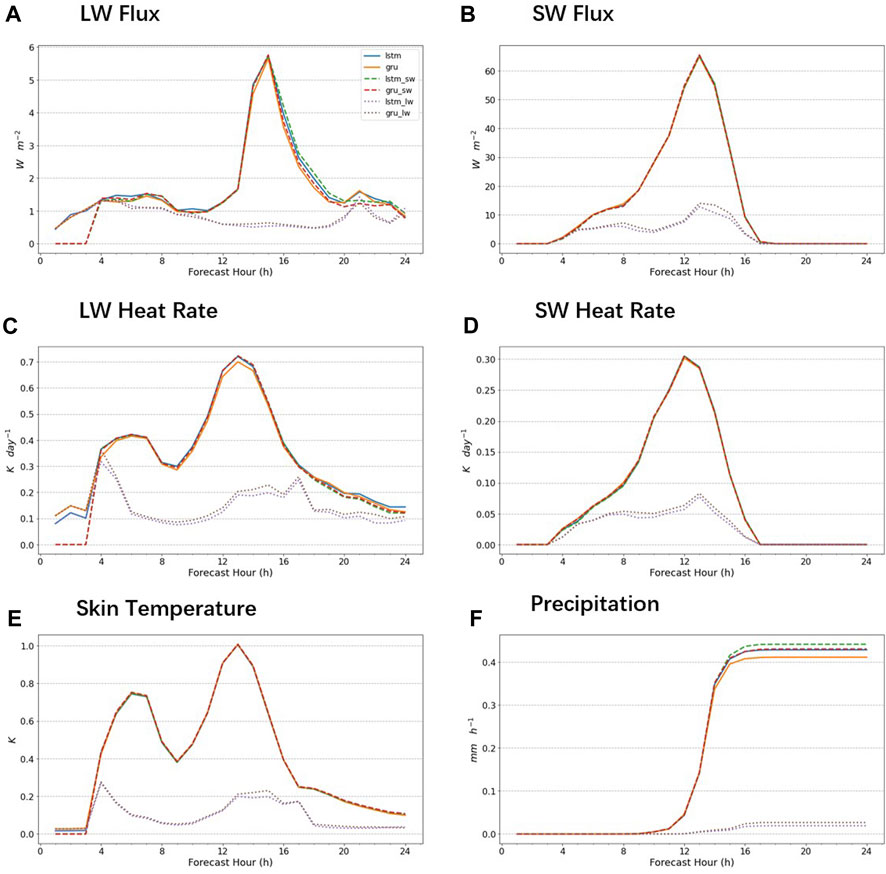
FIGURE 8. Performance of the WRF-NN using different simulating strategies in simulating the heatwave event. lstm indicates using LSTM to replace both SW and LW schemes, lstm_sw indicates that only the SW scheme is replaced and lstm_lw only replaces the LW scheme. The same applies to gru, gru_lw, and gru_sw. Different strategies are differentiated by different line styles, with replacing both SW and LW represented using solid lines, replacing SW using dashed lines, and replacing LW using dotted lines. Line colors are used to differentiate the replacement models. The selection of metrics and the layout of the graph are consistent with Figure 7, including (A) longwave (LW) flux, (B) shortwave (SW) flux, (C) LW heating rate, (D) SW heating rate, (E) skin temperature, and (F) precipitation.

4 Conclusion

In this paper, we introduced FTA, a generic tool designed to integrate deep learning models into the Fortran environment. This tool was then applied in the experiments of DNN radiation emulators for online weather simulation. The performance of DNN radiation emulators was evaluated from different perspectives. In terms of accuracy, the experiments showed that the DNN models significantly reduced simulation bias, with RNN outperforming CNN, which in turn outperforms FNN. The best-performing model was an LSTM model, which significantly reduced RMSE errors by 54% and 75% for SW and LW, respectively, compared to the FNN results. Moreover, models that performed better offline also exhibited superior performance online. This was not only reflected in the better results from the radiation scheme output but also positively affected the overall numerical model outputs such as skin temperature and precipitation in the 24-h simulations. Additionally, when faced with unseen events, all models exhibited some degree of performance deterioration. However, we found that the DNN models with better performance on standard datasets still outperformed others on two extreme event datasets, demonstrating their advantage in generalization ability. Lastly, with the aid of GPU acceleration provided by FTA, DNN emulators could deliver 50x or 300x acceleration, depending on whether only LW parameterization or both LW and SW were replaced. Although this cannot match the running speed of FNN on GPU, it is still a significant improvement compared to CPU solutions. In conclusion, our DNN emulators with GPU acceleration outperform the previous FNN on CPU scheme in all three aspects of accuracy, generalization ability, and efficiency, making them a promising tool for online weather forecasting.

This research also offers some valuable insights for future researchers dedicated to RT emulators for numerical models. In respect of model selection, our findings suggested that DNN models should be preferred when GPU resources are available, as even the simplest DNN model outperformed the best FNN model in our experiments. For FNN models, model depth is more beneficial than width for improving model accuracy. The size of the convolution kernel has a significant impact on the accuracy of CNN models when the model size is relatively small. When the number of convolution kernels and the depth of the convolution layers reach a certain size, relatively smaller convolution kernels are more advantageous. For RNN models, LSTM units show a significant performance improvement compared to GRU units. Taking into account the results of the three model categories, the bidirectional LSTM model has the highest overall accuracy, which is closely related to its strongest spatial feature extraction ability, reflected in its best vertical distribution of heating rate error. Additionally, we highlight the importance of controlling cumulative error growth to improve overall online error when applying AI emulators. Our results demonstrated that replacing only LW modules yielded significantly better outcomes than replacing both SW and LW modules.

It is important to note that these experiments were conducted under the premise that the issue of using AI in a Fortran environment had been resolved by the use of FTA. FTA eliminates barriers to integrating deep learning into numerical models, making various AI approaches available to researchers working with Fortran. To the best of our knowledge, this tool is the first publicly available generic solution to use interoperable techniques to address this issue. Since its release as an open-source tool last year, FTA has been adopted by numerous researchers from similar backgrounds. We believe that as the intersection of deep learning and meteorology deepens, FTA will receive more attention and be increasingly utilized by researchers in this field.

While this study represents a significant milestone, there is still ample room for improvement before a deep learning radiation emulator is ready for production use. To improve the accuracy of the model simulation, advanced PINN models could be used to achieve better results. Additionally, learning from higher-accuracy radiation parameterization schemes could also be considered, as the RRTMG-K model used in this research is an approximate model. Using the reference model’s results (line-by-line model) directly in AI training could help reduce bias. Moreover, the generalization ability of AI emulators still needs to be strengthened in some unusual extreme scenarios. Although we may address this issue by developing various models for different circumstances, a more comprehensive model is required for operational models that must deal with unpredictable scenarios at all times. To this end, our team is currently conducting research on online learning techniques that allow the AI emulator to adaptively adjust to different conditions.

Data availability statement

The datasets generated in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at A Radiative Transfer Emulator Dataset for WRFRRTMG-K (Chen, 2023). All codes in this study are publicly accessible onGitHub (FTA: https://github.com/luc99hen/FTA, WRF-NN: https://github.com/luc99hen/WRF).

Author contributions

LC developed the model code and performed the simulations. LC and BM prepared the manuscript with contributions from all co-authors. All authors contributed to the article and approved the submitted version.

Funding

This study is supported in part by the Key Project Fund of Shanghai 2020 “Science and Technology Innovation Action Plan” for Social Development under Grant 20dz1200702, in part by the National Natural Science Foundation of China under Grant 42075141, in part by the National Key Research and Development Program of China under Grant 2020YFA0608000, in part by the Meteorological Joint Funds of the National Natural Science Foundation of China under Grant U2142211, and in part by the first batch of Model Interdisciplinary Joint Research Projects of Tongji University in 2021 under Grant YB-21-202110.

Acknowledgments

The authors thank Deng at East China Meteorological Institute for her generous help with the extreme weather event cases.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1149566/full#supplementary-material

References

Baek, S. (2017). A revised radiation package of G-packed McICA and two-stream approximation: Performance evaluation in a global weather forecasting model. J. Adv. Model. Earth Syst. 9 (3), 1628–1640. doi:10.1002/2017MS000994

CrossRef Full Text | Google Scholar

Belochitski, A., Binev, P., DeVore, R., Fox-Rabinovitz, M., Krasnopolsky, V., and Lamby, P. (2011). Tree approximation of the long wave radiation parameterization in the NCAR CAM global climate model. J. Comput. Appl. Math. 236 (4), 447–460. doi:10.1016/j.cam.2011.07.013

CrossRef Full Text | Google Scholar

Belochitski, A., and Krasnopolsky, V. M. (2021). Robustness of neural network emulations of radiative transfer parameterizations in a state-of-the-art general circulation model. Geosci. Model. Dev. Discuss., 1–20. doi:10.5194/gmd-2021-114

CrossRef Full Text | Google Scholar

Brenowitz, N. D., and Bretherton, C. S. (2018). Prognostic validation of a neural network unified physics parameterization. Geophys. Res. Lett. 45 (12), 6289–6298. doi:10.1029/2018gl078510

CrossRef Full Text | Google Scholar

Bue, B. D., Thompson, D. R., Deshpande, S., Eastwood, M., Green, R. O., Natraj, V., et al. (2019). Neural network radiative transfer for imaging spectroscopy. Atmos. Meas. Tech. 12 (4), 2567–2578. doi:10.5194/amt-12-2567-2019

CrossRef Full Text | Google Scholar

Chen, L. (2023) ‘A radiative transfer emulator dataset for WRF RRTMG-K’. doi:10.5281/zenodo.7553218

CrossRef Full Text | Google Scholar

Chen, X., Jeffery, D. J., Zhong, M., McClenny, L., Braga-Neto, U., and Wang, L. (2022). ‘Using physics informed neural networks for supernova radiative transfer simulation’. arXiv. doi:10.48550/arXiv.2211.05219

CrossRef Full Text | Google Scholar

Chevallier, F., Chéruy, F., Scott, N. A., and Chédin, A. (1998). A neural network approach for a fast and accurate computation of a longwave radiative budget. J. Appl. meteorology 37 (11), 1385–1397. doi:10.1175/1520-0450(1998)037<1385:annafa>2.0.co;2

CrossRef Full Text | Google Scholar

Chevallier, F., Morcrette, J. J., Chéruy, F., and Scott, N. A. (2000). Use of a neural-network-based long-wave radiative-transfer scheme in the ECMWF atmospheric model. Q. J. R. Meteorological Soc. 126 (563), 761–776. doi:10.1002/qj.49712656318

CrossRef Full Text | Google Scholar

Clough, S. A., Iacono, M. J., and Moncet, J.-L. (1992). Line-by-line calculations of atmospheric fluxes and cooling rates: Application to water vapor. J. Geophys. Res. Atmos. 97 (D14), 15761–15785. doi:10.1029/92jd01419

CrossRef Full Text | Google Scholar

Dueben, P. D., and Bauer, P. (2018). Challenges and design choices for global weather and climate models based on machine learning. Geosci. Model. Dev. 11 (10), 3999–4009. doi:10.5194/gmd-11-3999-2018

CrossRef Full Text | Google Scholar

Ham, Y. G., Kim, J. H., and Luo, J. J. (2019). Deep learning for multi-year ENSO forecasts. Nature 573, 568–572. doi:10.1038/s41586-019-1559-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D. (2008). Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 113 (D13), D13103. doi:10.1029/2008jd009944

CrossRef Full Text | Google Scholar

Irrgang, C., Boers, N., Sonnewald, M., Barnes, E. A., Kadow, C., Staneva, J., et al. (2021). Towards neural Earth system modelling by integrating artificial intelligence in Earth system science. Nat. Mach. Intell. 3 (8), 667–674. doi:10.1038/s42256-021-00374-3

CrossRef Full Text | Google Scholar

Krasnopolsky, V. M., Fox-Rabinovitz, M. S., Hou, Y. T., Lord, S. J., and Belochitski, A. A. (2010). Accurate and fast neural network emulations of model radiation for the NCEP coupled climate forecast system: Climate simulations and seasonal predictions. Mon. Weather Rev. 138 (5), 1822–1842. doi:10.1175/2009mwr3149.1

CrossRef Full Text | Google Scholar

Krasnopolsky, V. M., and Lin, Y. (2012). A neural network nonlinear multimodel ensemble to improve precipitation forecasts over continental US, Adv. Meteorology 2012, 1–11. doi:10.1155/2012/649450

CrossRef Full Text | Google Scholar

Krasnopolsky, V. M. (2014). NN-TSV, NCEP neural network training and validation system; brief description of NN background and training software.

Google Scholar

Krasnopolsky, V. M. (2020). Using machine learning for model physics: An overview. arXiv:2002.00416 [physics, stat] [Preprint]. Available at: http://arxiv.org/abs/2002.00416 (Accessed October 8, 2021).

Google Scholar

Lagerquist, R., Turner, D., Ebert-Uphoff, I., Stewart, J., and Hagerty, V. (2021). Using deep learning to emulate and accelerate a radiative transfer model. J. Atmos. Ocean. Technol. 38 (10), 1673–1696. doi:10.1175/JTECH-D-21-0007.1

CrossRef Full Text | Google Scholar

Le, T., Liu, C., Yao, B., Natraj, V., and Yung, Y. L. (2020). Application of machine learning to hyperspectral radiative transfer simulations. J. Quantitative Spectrosc. Radiat. Transf. 246, 106928. doi:10.1016/j.jqsrt.2020.106928

CrossRef Full Text | Google Scholar

Lee, A., Sohn, B. J., Pavelin, E., Kim, Y., Kang, H. S., Saunders, R., et al. (2020). Assessment of cloud retrieval for IASI 1D-Var cloudy-sky assimilation and improvement with an ANN approach. Weather Forecast. 35 (4), 1363–1380. doi:10.1175/waf-d-19-0218.1

CrossRef Full Text | Google Scholar

Liang, X., Garrett, K., Liu, Q., Maddy, E. S., Ide, K., and Boukabara, S. (2022). A deep-learning-based microwave radiative transfer emulator for data assimilation and remote sensing. IEEE J. Sel. Top. Appl. Earth Observations Remote Sens. 15, 8819–8833. doi:10.1109/JSTARS.2022.3210491

CrossRef Full Text | Google Scholar

Liu, Y., Caballero, R., and Monteiro, J. M. (2020). RadNet 1.0: Exploring deep learning architectures for longwave radiative transfer. Geosci. Model. Dev. 13 (9), 4399–4412. doi:10.5194/gmd-13-4399-2020

CrossRef Full Text | Google Scholar

Mishra, S., and Molinaro, R. (2021). Physics informed neural networks for simulating radiative transfer. J. Quantitative Spectrosc. Radiat. Transf. 270, 107705. doi:10.1016/j.jqsrt.2021.107705

CrossRef Full Text | Google Scholar

Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A. (1997). Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 102 (D14), 16663–16682. doi:10.1029/97jd00237

CrossRef Full Text | Google Scholar

Ott, J. (2020). A fortran-keras deep learning bridge for scientific computing. Scientific Programming, e8888811. doi:10.1155/2020/8888811

CrossRef Full Text | Google Scholar

Pal, A., Mahajan, S., and Norman, M. R. (2019). Using deep neural networks as cost-effective surrogate models for super-parameterized E3SM radiative transfer. Geophys. Res. Lett. 46 (11), 6069–6079. doi:10.1029/2018GL081646

CrossRef Full Text | Google Scholar

Pincus, R., Mlawer, E. J., and Delamere, J. S. (2019). Balancing accuracy, efficiency, and flexibility in radiation calculations for dynamical models. J. Adv. Model. Earth Syst. 11 (10), 3074–3089. doi:10.1029/2019ms001621

PubMed Abstract | CrossRef Full Text | Google Scholar

Rasp, S., and Lerch, S. (2018). Neural networks for postprocessing ensemble weather forecasts. Mon. Weather Rev. 146 (11), 3885–3900. doi:10.1175/mwr-d-18-0187.1

CrossRef Full Text | Google Scholar

Reichstein, M., Camps-Valls, G., Stevens, B., Jung, M., Denzler, J., Carvalhais, N., et al. (2019). Deep learning and process understanding for data-driven Earth system science. Nature 566, 195–204. doi:10.1038/s41586-019-0912-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Roh, S., and Song, H.-J. (2020). Evaluation of neural network emulations for radiation parameterization in cloud resolving model. Geophys. Res. Lett. 47 (21), e2020GL089444. doi:10.1029/2020GL089444

CrossRef Full Text | Google Scholar

Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Liu, Z., Berner, J., et al. (2019). A description of the advanced research WRF model version 4. Boulder, CO, USA: National Center for Atmospheric Research, 145.

Google Scholar

Song, H.-J., and Roh, S. (2021). Improved weather forecasting using neural network emulation for radiation parameterization. J. Adv. Model. Earth Syst. 13 (10), e2021MS002609. doi:10.1029/2021MS002609

CrossRef Full Text | Google Scholar

Ukkonen, P. (2022). Exploring pathways to more accurate machine learning emulation of atmospheric radiative transfer. J. Adv. Model. Earth Syst. 14 (4), e2021MS002875. doi:10.1029/2021MS002875

CrossRef Full Text | Google Scholar

Wang, F.-Y. (2016). Where does AlphaGo go: From church-turing thesis to AlphaGo thesis and beyond. IEEE/CAA J. Automatica Sinica 3 (2), 113–120. doi:10.1109/JAS.2016.7471613

CrossRef Full Text | Google Scholar

Wang, J., Balaprakash, P., and Kotamarthi, R. (2019). Fast domain-aware neural network emulation of a planetary boundary layer parameterization in a numerical weather forecast model. Geosci. Model. Dev. 12 (10), 4261–4274. doi:10.5194/gmd-12-4261-2019

CrossRef Full Text | Google Scholar

Yuval, J., and O’Gorman, P. A. (2020). Stable machine-learning parameterization of subgrid processes for climate modeling at a range of resolutions. Nat. Commun. 11 (1), 3295. doi:10.1038/s41467-020-17142-3

PubMed Abstract | CrossRef Full Text | Google Scholar