Experimental study on whole process of river blockage and dam break under different hydrodynamic conditions

River blockage and dam break usually occur in mountainous areas with many valleys, and are frequent and extremely harmful natural disasters. With the construction of infrastructures in mountainous areas, the demand for disaster prevention and control has been further increased. Based on an innovative flume model for simulating whole process of river blockage and dam break, the present study carried out eight groups tests under different inflow rates. In the analysis, the whole process of river blockage and dam break was divided into four stages: ESBA (Early stage of blockage), LSBA (Late stage of blockage), ESBK (Early stage of breaking) and LSBK (Late stage of breaking). By analyzing the relationship between Q_in and Q_max, it is found that Q_max shows an overall trend of increase with the increase of Q_in while some contrarily decreasing Q_max cases exist when Q_in slightly increases. The cases of irregularities may come from the inflow condition impact and randomness during the dam formation process. In addition, the slope of the curve Q_in–Q_max/Q_in parameter shows a decreasing trend with the increase in the median particle size of the soil. The present study proposes a new method for model experiments, providing new ideas for subsequent model experiments. Furthermore, these conclusions can provide reference for disaster prevention and mitigation in mountainous areas.

Introduction

Due to natural disasters, such as earthquakes, rainstorms, typhoons and melting glaciers, destructive landslides or debris flows can easily form near mountain valleys (Coussot and Meunier, 1996; Cruden, 2005; Sassa, 2007; Chae et al., 2017; Chen et al., 2022). These material sources would very likely block river channels, causing these to stop flowing and form natural dams (Costa and Schuster, 1988; Fan et al., 2020; Zhong et al., 2021). The water volume of these resulting dammed lakes would gradually increase over time, and the threat to downstream human infrastructures and life would be self-evident.

Research on whole process of river blockage and dam break has been the basis and focus for solving the above problems. Research in this area has been mainly carried out from the perspective of field observation, model test, numerical simulation and theoretical analysis. Present studies generally divide the continuous process of river blockage and dam break into independent researches on the formation process of blocked rivers and its process of breaking. Recent developments in the field of formation process of river blockage have led to a renewed interest in the statistical analysis of field research data. Fan et al. (2014) developed an empirical method to predict coseismic landslide dam formation using landscape parameters obtained from digital elevation models. Chen and Wu. (2018) take Xinmo landslide for example, studied the post-failure behavior of the landslide using two-dimensional discontinuous deformation analysis (2D DDA). Li et al. (2020) proposed a discrete element simulation model to predict the geometry and formation process of landslide dams. In addition, Zhao et al. (2019b) and Wu et al. (2020) have explored the formation mechanism through model tests and numerical simulations. However, the results in this regard remains relatively lacking. For researches on whole process of river blockage and dam break, a large part of these researches adopt the method of combining the model test and theoretical analysis. The reason is because the model test can reproduce the actual block and break process in a small-scale model, allowing researchers to summarize the physical mechanism similar to the prototype. Rapid progress has been taken in the recent 30 years in the field of the experimental study on landslide dams. Coleman et al. (2002) made a detailed exploration of the overtopping process of homogeneous noncohesive embankments using model test. Awal (2008) identified the mechanism of landslide dams failure under different breaking modes through model tests. Schmocker and Hager. (2009) carried out a series of overtopping breach tests and indicated definite minimum dimensions for both the dike height and width, sediment diameter and overtopping discharge. Nian et al. (2020) proposed a dimensionless River Blockage Criterion (RBC) to judge the formation of landslide dams based on a series of model tests. And (Peng et al., 2021) investigated the breaching mechanisms of landslide dams composed of different materials under surge waves. However, the forming or breaking mechanism presents to be heterogeneous and highly test condition dependent, which greatly restricts the extrapolation. Although there are many reports in the above literature on the outcome of simple flume experiment, most are restricted to geometric similarity. Therefore, in recent years, there are a large number of published studies (Hanson et al., 2002; Höeg et al., 2004; Morris et al., 2007; Sheng-shui et al., 2014; Zhao et al., 2019; Li et al., 2021) that describe the landslide dam’ failure mechanism using large-scale field models or centrifugal models. Although the cost of this kind of experiment is high, this can better meet similar conditions, and the obtained test results are more similar to the prototype phenomenon, making this a better research method. Other approaches were performed through the establishment of the mathematical and physical model of a dam, and a high-performance computer simulates the dam breaking process, including the evolution process of breaches and floods (Cristofano, 1973; Fread, 1988; Chang and Zhang, 2010; Liu, 2018; Luo et al., 2019; Ruan et al., 2021; Tian et al., 2021; Zhang et al., 2021). However, these models have high simulation accuracy only when the input parameters are sufficiently large and accurate (Zhong et al., 2021).

In view of all that has been mentioned so far, one may suppose that a phenomenon or mechanism of river blockage or dam break is explained in depth. However, the above research has tended to focus on only one part of the whole process of river blockage and dam break rather than the continuous whole process. These studies have not able to convincingly confirm the relevance between model and prototype. The key issue is that the actual whole process of river blockage and dam break contains a number of uncertainties. First, the uncertainty of the occurrence time of natural disasters can lead to the triggering of landslides or debris flow that block the river, and this uncertainty puts forward more urgent time requirements for the prevention and control of such disasters. Second, after a landslide or debris flow forms, it is difficult to accurately predict whether and how the river would be blocked. Third, after the dam is formed, the breaking mode and the location of the breach have strong randomness. Finally, under the action of these above-mentioned random events, the outburst flood process would cause great changes. These suggests that a more realistic and continuous model test may lead to a more consistent conclusion with the actual prototype. Therefore, we developed a model that simulates the whole process in order to explore more valuable conclusions.

In addition, the impact of river flow on dam formation and break is a critical and interesting issue. The impact of the inflow on whole process of river blockage and dam break has strong uncertainties. For the same river, the flow may greatly vary at different time points of the year. For example, in the Jinsha River in China, where river blockage events frequently occur, the flood season from June to October accounts for 74–81% of the annual water volume (Wang et al., 2022). As a results, the consequences and prevention methods of river blockage events in different periods would be quite different. And the flow rate and water depth of the river would also affect the size of the formed dam (Chen et al., 2019). Therefore, considering only the inflow rate, there are a number of uncontrollable factors involved in the overall blockage and breakage process, and it would be difficult to fully grasp the key mechanism of the inflow rate on the whole process of river blockage and dam break. However, in recent years, some scholars have investigated the influence mechanism of inflow rate on the breaking process of natural dams through small-scale model tests. Xu et al. (2013) considered that the upstream inflow is the main factor that impacts the dam-break process through model tests with three groups of different inflow rates. Yang et al. (2015) investigated the change process of a breach under four different inflow rates. Zhou M. et al. (2019) concluded the relationship between the inflow rate and peak discharge of a breach through three groups of different inflow rates. These studies have carried out in-depth explorations on the impact of different flow rates on the breaking process, but the initial conditions were set too ideally. For example, the shape of the dam body have a fixed shape, the gradation was uniform, and the influence of water flow on the formation of the dam body was ignored. Based on some defects in the above tests, conducting the whole-process tests under different inflow rates are not only helpful to verify the reliability of previous research conclusions, but also to further explore the mechanism from a new perspective.

In summary, there are many uncertain factors in whole process of river blockage and dam break. Considering that the initial input quantity, such as initial hydrodynamic conditions, topographic conditions and provenance conditions, can be regarded as a definite initial quantity, the breaking flood flow and the change process of upstream and downstream water levels are correlated to the risk of this disaster chain. The present study used the newly developed model for the whole process of river blockage and dam break to explore new research methods for whole process of river blockage and dam break. In addition, under the condition of changing the initial inflow rate, the present study investigated the influence and internal mechanism of input parameters (inflow, topography, provenance, etc.) on output parameters (breach discharge, water level, etc.).

Methods

Model design

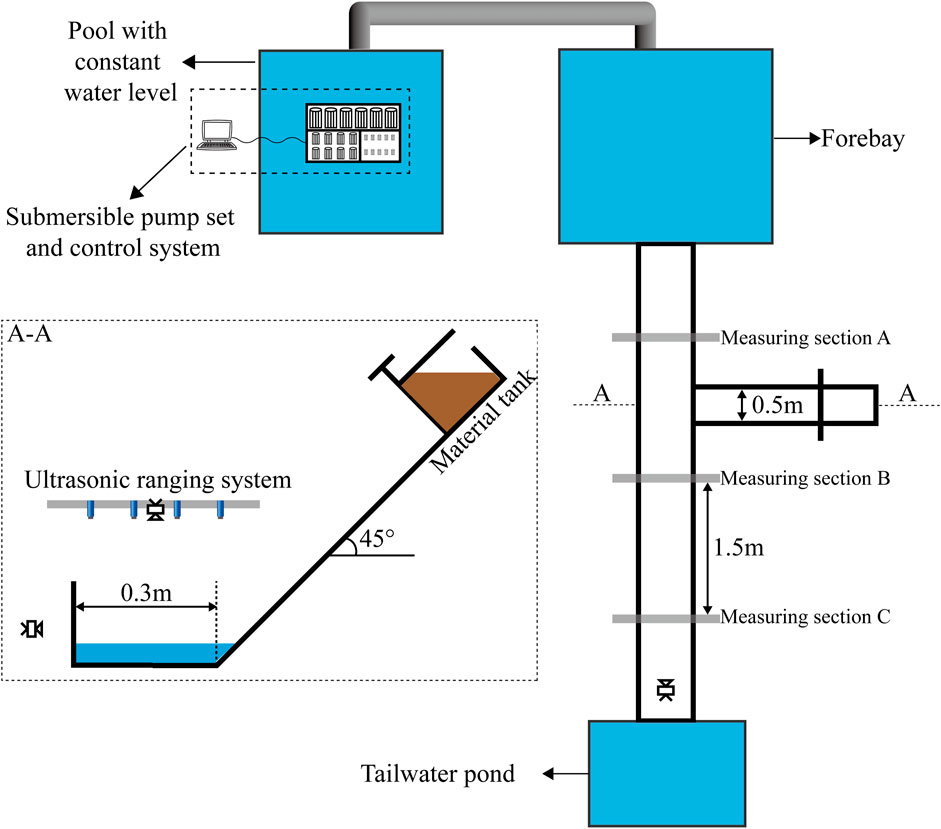
The experimental model is presented in Figure 1. The width and slope of the main channel, and the width and slope of the slope channel was adjusted according to the requirements. For the main channel, the length was 10.0 m, the height was 0.8 m, the width was adjusted between 0.1 m and 1.5 m, and the slope was adjusted between 1° and 15°. In the present experiment, the width was 30 cm and the slope was 1° for the main channel, while the width was 0.5 m, the height was 0.6 m, the length was 3.5 m, and the slope range was adjusted within 20°–70° for the slope channel. Furthermore, in the present experiment, the slope was 45°, the landslide material was stored in the material tank on the slope channel, and the maximum storage volume of the material tank was 0.3 m³. Furthermore, the mass of the landslide source was fixed at 80.0 kg. The water supply system included the laboratory water supply facilities, a pool with a constant water level, a forebay, a submersible pump set, and a control system. The storage capacity of the pool with a constant water level was 10.0 m³, and the maximum storage capacity of the forebay can reach up to 5.0 m³. When the laboratory water supply facility filled the pool up to the constant water level, the excess water flowed back to the large underground pool of the water supply facility after filling. Hence, the water level of the flat pool remained unchanged. The submersible pump set included three types of submersible pumps: six large water pumps with a maximum flow rate of 2 L/s, eight medium water pumps with a maximum flow rate of 1 L/s, and eight small water pumps with a maximum flow rate of 0.5 L/s. The pump set was fixed at the central position of the forebay, and the control system was used to integrate and control the switches of each water pump. The designed output flow range was 0.5–24.0 L/s. Due to the energy loss in the pumping process, the output flow was attenuated by 40%, and the actual output flow range was within 0.3–14.4 L/s.

FIGURE 1

FIGURE 1. Experimental setup.

During the experiment, the water level was measured using an ultrasonic ranging system. The ultrasonic wave was reflected after encountering the water surface. The measurement accuracy was high, and the maximum measurement frequency was 60 Hz. The phenomenon of the whole process of blocking and breaking was captured using a high-speed camera, as presented in Figure 1.

Materials

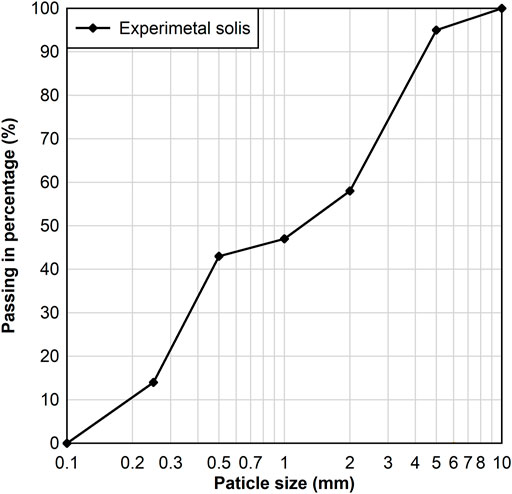
Grain size distribution has a great influence on whole process of river blockage and dam break. In order to make the gradation as consistent as possible with the actual situation, a wide-graded soil was used. Furthermore, in order to prevent more serious seepage phenomenon, fine particles were also present in the soil to fill the pores, allowing the experimental soil to have low permeability. The grain size distribution for the present experiment is presented in Figure 2.

FIGURE 2

FIGURE 2. Grain size distribution.

In traditional dam model experiments, researchers usually design the shape of the dam (dam height, dam width, etc.) in advance, and most of these are two-dimensional models. In order to achieve the design effect, the compaction of the dam body may be unintentionally affected, and the stacking method used is usually manual stacking or simple tool-assisted stacking, resulting in some errors. In the present study, the project of building a dam was abandoned in the experiment, and the initial parameters (mass, gradation, etc.) of the soil were entered to the designed landslide device. The landslide dam was formed by the sliding soil from the slope channel, which had authenticity and three-dimensionality. For example, the designed dam body is often a trapezoid or triangle with clear edges and corners (Figure 3A), but the actual accumulation geometry is irregular (Figures 3C,D). Comparing Figures 3B–D, we can see that the geometry of the naturally sliding landslide dam is more consistent with the prototype while the artificial dam is not.

FIGURE 3

FIGURE 3. Comparison of experimental landslide dams and prototypes: (A) manual stacked dam; (B) natural sliding dam in this paper; (C,D) are photographs of landslides blocking river.

For the random phenomenon of dam formation during the test, the dam geometry was calibrated in advance. The dam geometries measured in three tests under the same conditions are presented in Table 1. The dam’s geometry in the three pretests is presented in Figure 4. It can be observed that the change in shape was relatively small. Furthermore, since the dam’s geometry has influence on the experiment, and the dam height is an important parameter to control the process for breaking, the influence of the dam’s height on the dam’s geometry on the whole process of blocking and breaking was considered for the present study.

TABLE 1

TABLE 1. Dam body parameters.

FIGURE 4

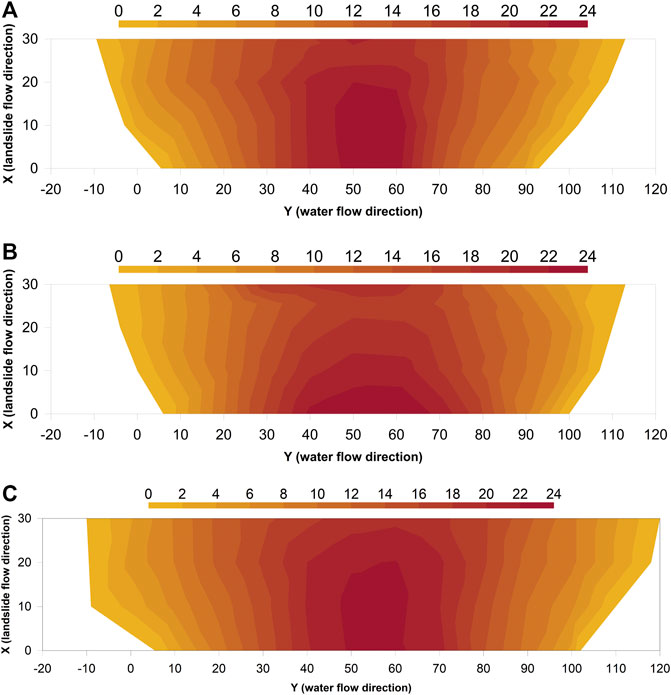
FIGURE 4. Dam geometry comparison: (A-C) are dam geometry obtained in three pre-experiments under the same conditions. All units are in centimeters. The sliding direction of the landslide along the horizontal direction is the same as the positive direction of the x-axis, the water flow direction is the same as the positive direction of the y-axis, and the exit position of the landslide into the main channel is between y = 50 and y = 60.

Costa and Schuster (1988) reported that the potential energy of water is an important parameter that affects dam breakage and flooding, and is correlated to the storage capacity of the impoundment (V_l). After field investigations, Korup (2004) considered that dam height (H_d) and dam volume (V_d) are the two key variables that can be used to assess the dam stability, and determine whether this would induce flood risk. Subsequently, Peng and Zhang (2012) proposed a set of dimensionless numbers, ($\frac{H_{\mathrm{d}}}{W_{\mathrm{d}}}$, $\frac{V_{\mathrm{d}}^{1/3}}{H_{\mathrm{d}}}$and$\frac{V_1^{1/3}}{H_{\mathrm{d}}}$),which can be used to define the geometric features of landslide dams and lakes. In order to verify whether experimental model dams can represent real landslide dams, Zhou G. G. D. et al. (2019) counted the dimensionless coefficients of 80 landslide dams from different regions of the world, and proposed that when the dimensionless numbers of a model experiment are close to the actual, the experiment models can be considered to represent real landslide dams. This conclusion helps to check whether the dimensions in the model experiment can meet the actual situation. Jiang et al. (2020) applied this conclusion in his research, proving that his model can satisfy the scale effect.

Therefore, the model designed for the present experiment comprehensively considered these parameters, and these key parameters were measured in multiple pre-experiments. The specific parameters are presented in Table 1. All parameters were within the feasible range (Zhou M. et al., 2019). This shows that the model, material and hydraulic properties of the present experiment can meet the actual situation.

Experimental procedure

The only initial variable in the present experiment is the inflow rate of the main channel. In order to simulate whole process of river blockage and dam break, the present experiment did not carry out human intervention after setting the initial parameters. The specific implementation process for the present experiment is, as follows:

(1) Clarify the initial conditions of the test;

(2) Initially place the preset landslide soil into the bearing device of the side slope, and turn on the pump set to make the river flow meet the preset flow;

(2) Arrange ultrasound sensors in the river to measure the upstream and downstream water levels;

(4) Arrange high-speed cameras around the model to measure the process of the landslide movement, the blocking process of the dam body, and the breaking process of the dam;

(5) After the measuring device is arranged and the river flow is stable, release the landslide;

(6) Wait for the end of the test, the sign at the end of the test is, the dam height is reduced to 1/2 of the maximum dam height.

Results and discussion

General description of whole process of river blockage and dam break

The test arrangements and results are presented in Table 2. In determining the breaking flow, the water balance equation is usually used to calculate the breach discharge, especially in model experiments and numeral calculations (Zhong et al., 2021). The simplified calculation equation used for the present study is, as follows:

$Q_{\text{out}}=-A\frac{d{L}_{\mathrm{w}}}{dt}+Q_{\text{in}}(1)$

where Q_out refers to the flow discharge, and can be considered as the breach discharge (due to the characteristics of the dam material, the influence of the seepage discharge on the calculation is ignored); Q_in refers to the inflow rate; A refers to the lake area; L_w refers to the upstream water level. Since the slope of the main channel is 1°, the variation of A with time is relatively low. In order to simplify the calculation in the absence of large errors, A is regarded as a constant. L_w can be obtained by the ultrasonic sensor, Q_in is a designed constant quantity, then the breach discharge can be calculated according to Eq. 1.

TABLE 2

TABLE 2. Test arrangements and results.

The variation process of the upstream water level and breach discharge with time is presented in Figure 5. According to the upstream water level, breach discharge, and actual observation results, the whole process of blocking and breaking was divided into four stages.

(1) Early stage of blockage (ESBA): At this time, the landslide has not blocked the main channel, the upstream flow is stable, and the water level at the measuring point remains unchanged, as shown in Figure 6A;

(2) Late stage of blockage (LSBA): At this time, the landslide just blocks the river, there is no discharge for the time being, and the upstream water level gradually increases, as shown in Figure 6B;

(3) Early stage of breaking (ESBK): At this time, the overtopping water flow gradually erodes the dam crest, forming a breach, which gradually expands, and the breach discharge gradually increases and reaches a peak value, as shown in Figure 6C;

(4) Late stage of breaking (LSBK): At this time, the shape of the landslide dam slightly changes, and the breach discharge gradually decreases to the initial inflow rate, as shown in Figure 6D.

FIGURE 5

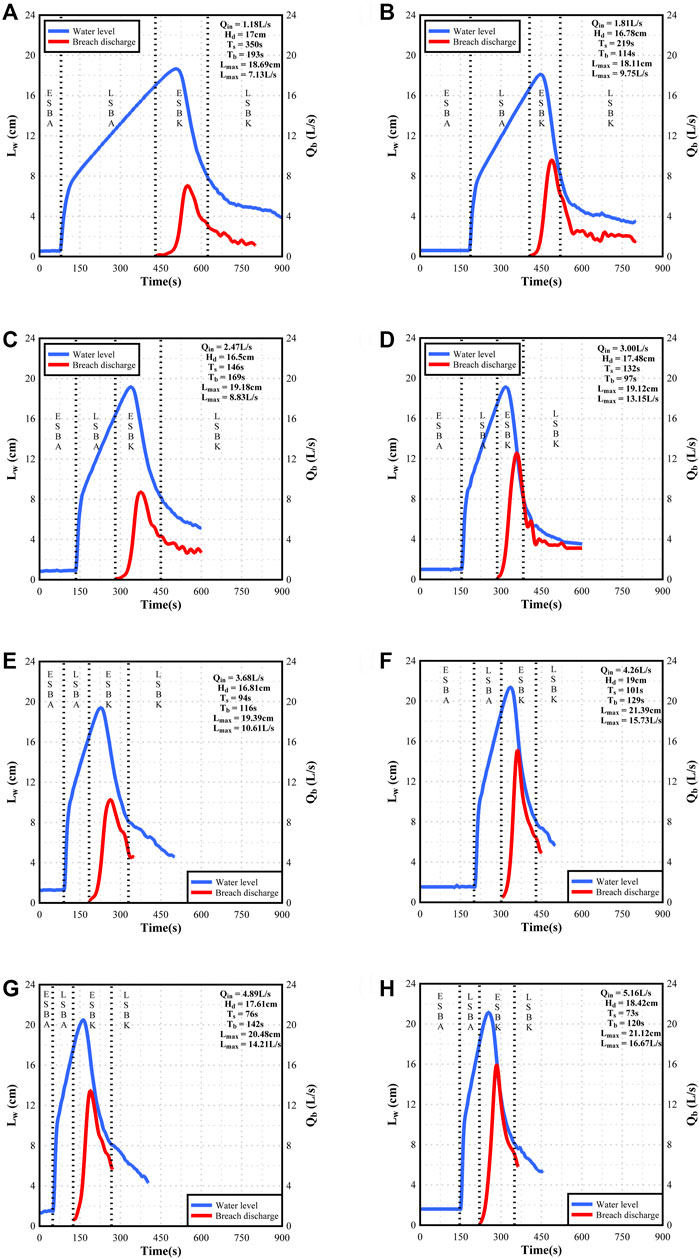
FIGURE 5. The upstream water level curve and the breach discharge curve at different stages: (A-H) expressed the water level and breach discharge process under different flow rates, respectively.

FIGURE 6

FIGURE 6. The four stages of the whole process of river blockage and dam breaking: (A) early stage of blockage; (B) Late stage of blockage; (C) Early stage of breaking; (D) Late stage of breaking.

Effect of Q_in on Q_max

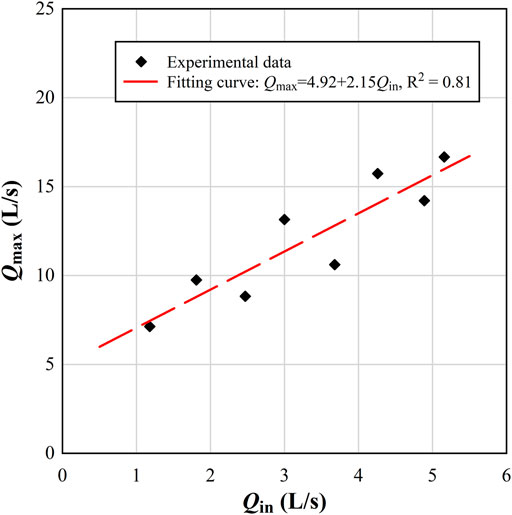
The relationship between Q_in and Q_max was drawn, as shown in Figure 7, and the test data was fitted. The fitting formula is, as follows:

$Q_{\max }=4.92+2.15Q_{in}(2)$

where Q_in refers to the inflow rate (L/s) and Q_out refers to the breach discharge (L/s). In the formula, R²=0.81, indicating that Q_max and Q_in have a high linear correlation. In the whole process, Q_max increased with the increase in Q_in.

FIGURE 7

FIGURE 7. The relationship between Q_in and Q_max.

The relational expression of L_w’ can be obtained from Eq. 1:

$L_{\mathrm{w}}^{\prime }=\frac{d{L}_{\mathrm{w}}}{dt}=\frac{Q_{\text{in}}-Q_{\text{out}}}{A}(3)$

where $L_{\mathrm{w}}$ refers to the upstream water level (cm) and $L_{\mathrm{w}}^{\prime }$ refers to the upstream water level growth rate (cm/s). In Eq. 3, it can be observed that the overall reason for the increase in Q_max with the increase in Q_in is that a larger Q_in can increase $L_{\mathrm{w}}^{\prime }$. This causes in the water level to be flow faster as it rises and flow slower as it falls.

A larger Q_in would cause the upstream water level at have a higher value when the flow just overtops, and this would have a higher flow area during the rising stage of the water level at ESBK. For the soil erosion rate in Eq. 4 (Hanson and Simon, 2001), it can be observed that a larger flow area would speed up the erosion process of the dam body, thereby shortening the breaking duration.

$E=K_{\mathrm{d}}\left(\tau -{\tau }_{\mathrm{c}}\right)(4)$

where E refers to the soil erosion rate (mm³/m²-s), K_d refers to the material property of the soil, and $\tau$ refers to the water flow shear force. The magnitude of the water flow shear force is positively correlated to the wet circumference.

Due to the rapid widening of the breach and slow drop in water depth, the outflow area would rapidly increase and become larger. According to experience and based on Eq. 5, this is often used to calculate the breach discharge in a dam breach model (Singh and Scarlatos, 1988). It can be observed that this case tends to have a larger peak discharge.

$Q_{\text{out}}=1.7\left[B+h_b\tan \alpha \right]h_b^{3/2}(5)$

where: B refers to the width of the bottom of the breach, h_b refers to the depth of the breach, and $\alpha$ refers to the angle of the side slope. B, h_b and $\alpha$ would gradually change with the erosion of the breach through the overtopping water flow. This is the fundamental reason that drives the change in breach discharge.

In summary, the influence of the increase in Q_in in the whole process mainly lies in two aspects. On one hand, the upstream water level at the beginning of ESBK would have a high value, resulting to a higher flow area during the rising stage before breaking. On the other hand, a larger flow area would accelerate the erosion process. In addition, Walder et al. (2015) explained that Q_max is an increasing function of initial water level through some theoretical analysis on a series of model tests. Therefore, combined with the experimental phenomenon, it can be observed that a higher water level and a faster erosion process causes the peak discharge to arrive earlier and become larger.

The investigators also considered that this is what contributed to the conclusion that the dimensionless peak discharge ($Q_{\max }/Q_{\text{in}}$) decreases with the inflow rate (Zhou M. et al., 2019). In the present study, the investigators fitted the relationship between $Q_{in}$ and $Q_{\max }/Q_{\text{in}}$, and compared this with previous studies. The fitting equation is presented in Eq. 6, and the fitting result is presented in Figure 8.

$Q_{\max }/Q_{\text{in}}=a\left(Q_{\text{in}}-b\right)(6)$

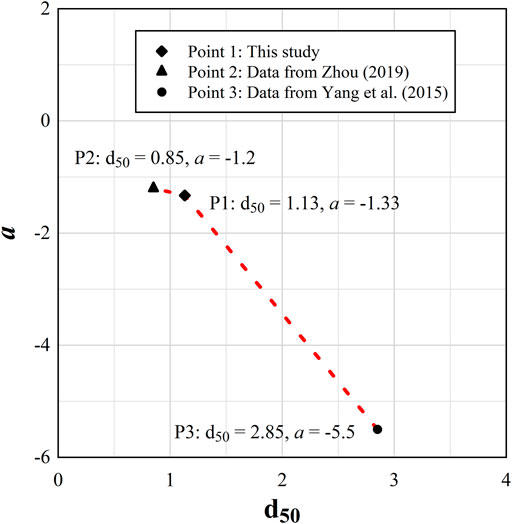
where a and b represent the fitting parameters, respectively. It was found that parameter a is correlated to d₅₀. As observed in Figure 9, a decreased as d₅₀ increased. This shows that the breach evolution of soil with a larger d₅₀ would be more sensitive to the influence of the inflow rate. For example, for Curve3 in Figure 8, the $Q_{\max }/Q_{\text{in}}$ decreased more when the same $Q_{\text{in}}$ increased.

FIGURE 8

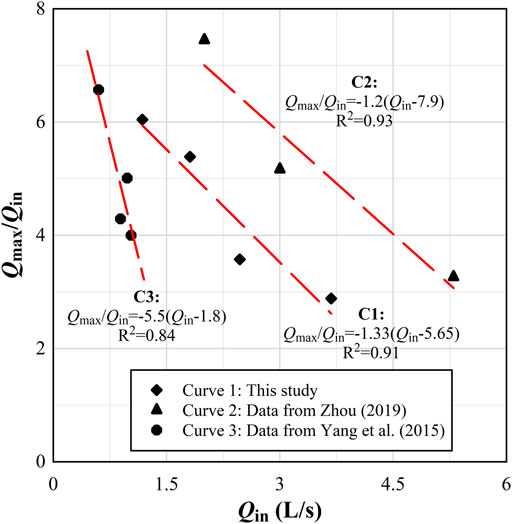
FIGURE 8. The relationship between Q_in and Q_max/Q_in. In order to avoid the influence of different dam heights, only four sets of data with the closest dam height are selected.

FIGURE 9

FIGURE 9. The relationship between d₅₀ and a.

Effect of Q_in and H_d on Q_max

Although Q_max increased with the increase in Q_in in the whole process, it was observed in Figure 7 that when the inflow rate only changed within a small range and Q_in increased, Q_max did not necessarily increase. This result was mainly caused by the randomness of friction and collision during the movement of soil particles during the sliding of the landslide. The short-term process of a landslide blocking the main channel to form a dam is shown in Figure 10. Dams with different shapes would lead to different subsequent processes. Hence, Q_max may not necessarily increase with the increase in inflow rate. However, the above phenomenon would only occur when the inflow rate changes in a relatively small range, because the dam height changes caused by randomness are limited. Therefore, when the inflow rate increases to a sufficient level, Q_max would increase with the increase in Q_in.

FIGURE 10

FIGURE 10. Short-term process of landslide blocking the main channel to form a dam: (A) At t = 0 s, the landslide is about to reach the channel; (B) At t = 0.4 s, the landslide just blocked the river; (C,D) the landslide dam is formed.

It would be relatively one-sided to only analyze the effect of Q_in on Q_max. Furthermore, it is given that multiple linear regression can help to analyze the relationship between multiple independent variables and dependent variables (Andrews, 1974; Aiken et al., 2003; Uyanık and Güler, 2013). In order to explain the influencing factors of Q_max, multiple linear regression was used to determine the effect of Q_in and H_d on Q_max. The analysis results are presented in Table 3, and the regression equation is presented in Eq. 7:

$Q_{\max }=-25.25+1.37Q_{\text{in}}+1.88H_{\mathrm{d}}(7)$

in this model, the interpretation degree of Q_in and H_d to Q_max is R²=0.93, which is higher than the interpretation degree for Q_in to Q_max. It is noteworthy that Q_in and H_d can predict Q_max very well. The coefficient of H_d was 1.88, and the coefficient of Q_in was 1.37, indicating that the increase in Q_max per unit of increase in H_d was higher, when compared to that of Q_max for each increase in unit of increase.

TABLE 3

TABLE 3. Multiple linear regression results.

The absolute value of Beta indicates the order of importance of the independent variables. As presented in Table 3, it can be observed that the Beta value of Q_in is slightly larger than the Beta value of H_d. This means that the independent value Q_in contributes more to the model, when compared to H_d. Although the significance of the constant was slightly larger than 0.05, the significance p for all three variables was less than 0.06. This means that the independent variable coefficient is statistically significant. The variance increase factors VIF in the present model were all lower than 10, as shown in Table 3. This means that there are no multiple correlations among variables.

Conclusion

The whole process of river blockage and dam break under different hydrodynamic conditions was investigated in a flume model for a range of inflow rates between 1.18 and 5.16 L/s. The phenomenon and process of river blockage and dam break were preliminarily demonstrated and the mechanism of how the inflow rate influences the whole process was explored. The main conclusions are summarized as follows:

Four stages including ESBA, LSBA, ESBK, and ESBK, can be distinguished during the whole process of river blockage and dam break due to significant differences in hydraulic properties. ESBA occurs at the initial stage of blockage and gradually evolves to LSBA when the soil accumulated dam cut off the river. It develops to ESBK as the stored water overtops and expands breaches. Followed by LSBK, the breach flow decreases after the peak breach flow. Among these stages, ESBK is the most violent period, Breaking flooding occurs at this time, and its duration and peak flow are important factors in assessing the risk; LSBK is the final stage in the whole process during when the change of the dam body becomes relatively slow, and the breaking process slows down.

The impact of Q_in on Q_out was explained theoretically. As is expected, the increase in Q_in will cause a relatively high upstream water level at the beginning of ESBK and accelerate the erosion process. Q_max shows an overall trend of increase with the increase of Q_in while some contrarily decreasing Q_max cases exist when Q_in slightly increases. The multiple regression analysis for Q_in and H_d on Q_max explained the cases of irregularities may come from the inflow condition impact and randomness during the dam formation process.

The present study investigated the effect of Q_in on Q_max/Q_in. The development trend of Q_in-Q_max/Q_in in this paper is consistent with that in the previous dam break flume experiment. By analyzing the soil gradation adopted in previous flume model experiments, we found that the slope of the curve Q_in-Q_max/Q_in parameter shows a decreasing trend with the increase in the median particle size of the soil.

The multiple regression equation for Q_in and H_d on Q_max was obtained. Q_in and H_d fits the Q_max multiple regression extremely well, and the goodness of fit reached 93%. And we found that when compared to the increase in Q_max per increase unit Furthermore, the increase in Q_max per increase unit of H_d was higher, when compared to the increase in Q_max per increase unit.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.

Author contributions

XW-L, NZ-P, DB-F, and MC-K contributed significantly to the conception of the study; MC-K, LY, and YH performed the experiment; NZ-P and MC-K contributed to analysis and manuscript preparation; XW-L and DB-F reviewed the original draft; NZ-P, MC-K, XW-L, DB-F, LY, and YH helped perform the analysis with constructive discussions.

Funding

This research was supported by the National Key Research and Development Plan of China (Grant No.2019YFC1510704-01) and CAS Light of West China Program (No. 2021160160).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

a, a fitting parameter in Equation 6; B, partial regression coefficient; Beta, standard regression coefficient; d₅₀, the particle size when the cumulative particle size distribution percentage reaches 50%; H_d, Dam height, the dam’s geometry is random due to particle collision and other reasons during the sliding movement of the soil, and there are slight differences in dam height under different initial parameters; k_d, downstream slope ratio; k_u, upstream slope ratio; L_d, Dam length; L_max, The highest water level in front of the dam; P, Significance; Q_in, Inflow rate, initial parameter manually set at the beginning of a test; Q_max, The maximum discharge of the breach; Std. Error, standard error; t₀, The moment when the landslide slides into the main channel just after it stabilizes; t₁, The moment when the flow just overtops; t₂, After the dam breaks, the upstream water level just drops to 8 cm, which refers to the end of breaking; T, results of t-test on regression coefficients; T_b, Breaking time, the breaking time is the difference between t₂ and t₁, and the formula to calculate this is T_b = t₂ - t₁; T_s, Water storage time, the water storage time is the difference between the time when the water flow just overtops and the time when the landslide just stabilizes after sliding into the main channel, and the formula to calculate this is T_s = t₁ - t₀; V_l, the maximum volume of the dam lake; V_d, Dam volume; VIF, Variance Inflation Factor; W_d, Dam width.

References

Aiken, L. S., West, S. G., and Pitts, S. C. (2003). Multiple linear regression. Hand. book. Psychol., 481–507. doi:10.1007/978-1-59745-530-5_9

CrossRef Full Text | Google Scholar

Andrews, D. F. (1974). A robust method for multiple linear regression. Technometrics 16, 523–531. doi:10.1080/00401706.1974.10489233

CrossRef Full Text | Google Scholar

Awal, R. (2008). Study on landslide dam failure due to sliding and overtopping. Kyoto, Japan: Kyoto University.

Google Scholar

Chae, B.-G., Park, H.-J., Catani, F., Simoni, A., and Berti, M. (2017). Landslide prediction, monitoring and early warning: A concise review of state-of-the-art. Geosci. J. 21, 1033–1070. doi:10.1007/s12303-017-0034-4

CrossRef Full Text | Google Scholar

Chang, D., and Zhang, L. (2010). Simulation of the erosion process of landslide dams due to overtopping considering variations in soil erodibility along depth. Nat. Hazards Earth Syst. Sci. 10, 933–946. doi:10.5194/nhess-10-933-2010

CrossRef Full Text | Google Scholar

Chen, H., Ruan, H., Chen, J., Li, X., and Yu, Y. (2022). Review of investigations on hazard chains triggered by river-blocking debris flows and dam-break floods. Front. Earth Sci. 10, 830044. doi:10.3389/feart.2022.830044

CrossRef Full Text | Google Scholar

Chen, K.-T., Chen, X.-Q., Hu, G.-S., Kuo, Y.-S., and Chen, H.-Y. (2019). Effects of river flow velocity on the formation of landslide dams. J. Mt. Sci. 16, 2502–2518. doi:10.1007/s11629-018-5319-1

CrossRef Full Text | Google Scholar

Chen, K.-T., and Wu, J.-H. (2018). Simulating the failure process of the Xinmo landslide using discontinuous deformation analysis. Eng. Geol. 239, 269–281. doi:10.1016/j.enggeo.2018.04.002

CrossRef Full Text | Google Scholar

Coleman, S. E., Andrews, D. P., and Webby, M. G. (2002). Overtopping breaching of noncohesive homogeneous embankments. J. Hydraul. Eng. 128128, 8299–8838. doi:10.1061/(asce)0733-9429(2002)128:9(829)

CrossRef Full Text | Google Scholar

Costa, J. E., and Schuster, R. L. (1988). The formation and failure of natural dams. Geol. Soc. Am. Bull. 100, 1054–1068. doi:10.1130/0016-7606(1988)100<1054:tfafon>2.3.co;2

CrossRef Full Text | Google Scholar

Coussot, P., and Meunier, M. (1996). Recognition, classification and mechanical description of debris flows. Earth-Science Rev. 40, 209–227. doi:10.1016/0012-8252(95)00065-8

CrossRef Full Text | Google Scholar

Cristofano, E. A. (1973). Method of computing erosion rate for failure of earthfill dams. Denver, CO, United States: US Department of the Interior, Bureau of Reclamation, Engineering and Research Center. 727.

Google Scholar

Cruden, D. (2005). Debris-flow hazards and related phenomena. Can. Geotech. J. 42, 1723. doi:10.1139/t05-075

CrossRef Full Text | Google Scholar

Fan, X., Dufresne, A., Siva Subramanian, S., Strom, A., Hermanns, R., Tacconi Stefanelli, C., et al. (2020). The formation and impact of landslide dams – state of the art. Earth-Science Rev. 203, 103116. doi:10.1016/j.earscirev.2020.103116

CrossRef Full Text | Google Scholar

Fan, X., Rossiter, D. G., van Westen, C. J., Xu, Q., and Görüm, T. (2014). Empirical prediction of coseismic landslide dam formation: Coseismic landslide dam formation. Earth Surf. Process. Landforms 39, 1913–1926. doi:10.1002/esp.3585

CrossRef Full Text | Google Scholar

Fread, D. (1988). BREACH, an erosion model for earthen dam failures. NOAA: Hydrologic Research Laboratory, National Weather Service.

Google Scholar

Hanson, G., Cook, K., and Temple, D. (2002). Research results of large-scale embankment overtopping breach tests. ASDSO Annu. Conf.

Google Scholar

Hanson, G. J., and Simon, A. (2001). Erodibility of cohesive streambeds in the loess area of the midwestern USA. Hydrol. Process. 15, 23–38. doi:10.1002/hyp.149

CrossRef Full Text | Google Scholar

Höeg, K., Løvoll, A., and Vaskinn, K. (2004). Stability and breaching of embankment dams: Field tests on 6 m high dams. Int. J. Hydropower. Dams 11, 88

Google Scholar

Jiang, X., Wörman, A., Chen, P., Huang, Q., and Chen, H. (2020). Mechanism of the progressive failure of non-cohesive natural dam slopes. Geomorphology 363, 107198. doi:10.1016/j.geomorph.2020.107198

CrossRef Full Text | Google Scholar

Korup, O. (2004). Geomorphometric characteristics of New Zealand landslide dams. Eng. Geol. 73, 13–35. doi:10.1016/j.enggeo.2003.11.003

CrossRef Full Text | Google Scholar

Li, D., Nian, T., Wu, H., Wang, F., and Zheng, L. (2020). A predictive model for the geometry of landslide dams in V-shaped valleys. Bull. Eng. Geol. Environ. 79, 4595–4608. doi:10.1007/s10064-020-01828-5

CrossRef Full Text | Google Scholar

Li, L., Yang, X., Zhou, J., Zhang, J., and Fan, G. (2021). Large-scale field test study on failure mechanism of non-cohesive landslide dam by overtopping. Front. Earth Sci. 9, 660408. doi:10.3389/feart.2021.660408

CrossRef Full Text | Google Scholar

Liu, W., and He, S. (2018). Dynamic simulation of a mountain disaster chain: Landslides, barrier lakes, and outburst floods. Nat. Hazards (Dordr). 19, 757–775. doi:10.1007/s11069-017-3073-2

CrossRef Full Text | Google Scholar

Luo, J., Xu, W., Tian, Z., and Chen, H. (2019). Numerical simulation of cascaded dam-break flow in downstream reservoir. Proc. Institution Civ. Eng. - Water Manag. 172, 55–67. doi:10.1680/jwama.15.00088

CrossRef Full Text | Google Scholar

Morris, M. W., Hassan, M. A. A. M., and Vaskinn, K. A. (2007). Breach formation: Field test and laboratory experiments. J. Hydraulic Res. 45, 9–17. doi:10.1080/00221686.2007.9521828

CrossRef Full Text | Google Scholar

Nian, T., Wu, H., Li, D., Zhao, W., Takara, K., and Zheng, D. (2020). Experimental investigation on the formation process of landslide dams and a criterion of river blockage. Landslides 17, 2547–2562. doi:10.1007/s10346-020-01494-4

CrossRef Full Text | Google Scholar

Peng, M., Ma, C.-Y., Chen, H.-X., Zhang, P., Zhang, L.-M., Jiang, M.-Z., et al. (2021). Experimental study on breaching mechanisms of landslide dams composed of different materials under surge waves. Eng. Geol. 291, 106242. doi:10.1016/j.enggeo.2021.106242

CrossRef Full Text | Google Scholar

Peng, M., and Zhang, L. M. (2012). Breaching parameters of landslide dams. Landslides 9, 13–31. doi:10.1007/s10346-011-0271-y

CrossRef Full Text | Google Scholar

Ruan, H., Chen, H., Wang, T., Chen, J., and Li, H. (2021). Modeling flood peak discharge caused by overtopping failure of a landslide dam. Water 13, 921. doi:10.3390/w13070921

CrossRef Full Text | Google Scholar

K. Sassa (Editor) (2007). Progress in landslide science (Berlin: Springer).

Google Scholar

Schmocker, L., and Hager, W. H. (2009). Modelling dike breaching due to overtopping. J. Hydraulic Res. 47, 585–597. doi:10.3826/jhr.2009.3586

CrossRef Full Text | Google Scholar

Sheng-shui, C., Xu-shun, F., Qi-ming, Z., and Yun-hui, L. (2014). Centrifugal model tests and numerical simulations for break of earth-rock dams due to overtopping. Chin. J. Geotech. Eng. 36, 922–932. doi:10.11779/CJGE201405017

CrossRef Full Text | Google Scholar

Singh, V. P., and Scarlatos, P. D. (1988). Analysis of gradual earth-dam failure. J. Hydraul. Eng. 1141141, 21–42. doi:10.1061/(asce)0733-9429(1988)114:1(21)

CrossRef Full Text | Google Scholar

Tian, Z., Yang, H., Wang, W., and Cao, D. (2021). Numerical analysis of sand bed degrading and sediment transport rate under tailings dam break. Front. Earth Sci. 9, 686277. doi:10.3389/feart.2021.686277

CrossRef Full Text | Google Scholar

Uyanık, G. K., and Güler, N. (2013). A study on multiple linear regression analysis. Procedia - Soc. Behav. Sci. 106, 234–240. doi:10.1016/j.sbspro.2013.12.027

CrossRef Full Text | Google Scholar

Walder, J. S., Iverson, R. M., Godt, J. W., Logan, M., and Solovitz, S. A. (2015). Controls on the breach geometry and flood hydrograph during overtopping of noncohesive earthen dams: DAM-BREACH hydraulics and hydrographs. Water Resour. Res. 51, 6701–6724. doi:10.1002/2014WR016620

CrossRef Full Text | Google Scholar

Wang, F., Bao, K., Huang, C., Liu, R., Han, W., Yi, C., et al. (2022). Distribution, characteristics, and research status of microplastics in the trunk stream and main lakes of the yangtze river: A review. China Geol. 5, 1–15. doi:10.31035/cg2022002

CrossRef Full Text | Google Scholar

Wu, H., Nian, T., Chen, G., Zhao, W., and Li, D. (2020). Laboratory-scale investigation of the 3-D geometry of landslide dams in a U-shaped valley. Eng. Geol. 265, 105428. doi:10.1016/j.enggeo.2019.105428

CrossRef Full Text | Google Scholar

Xu, F., Yang, X., Zhou, J., and Hao, M. (2013). Experimental research on the dam-break mechanisms of the jiadanwan landslide dam triggered by the wenchuan earthquake in China. Sci. World J., 1–13. doi:10.1155/2013/272363

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y., Cao, S., Yang, K., and Li, W. (2015). Experimental study of breach process of landslide dams by overtopping and its initiation mechanisms. J. Hydrodyn. 27, 872–883. doi:10.1016/S1001-6058(15)60550-9

CrossRef Full Text | Google Scholar

Zhang, J., Wang, W., Tian, Z., and Li, Y. (2021). An investigation of the characteristics of dam-break flood in a confluence channel based on the lattice Boltzmann method. AIP Adv. 11, 045320. doi:10.1063/5.0045256

CrossRef Full Text | Google Scholar

Zhao, T., Chen, S., Fu, C., and Zhong, Q. (2019). Centrifugal model test on the failure mechanism of barrier dam overtopping. KSCE J. Civ. Eng. 23, 1548–1559. doi:10.1007/s12205-019-0375-9

CrossRef Full Text | Google Scholar

Zhong, Q., Wang, L., Chen, S., Chen, Z., Shan, Y., Zhang, Q., et al. (2021). Breaches of embankment and landslide dams - state of the art review. Earth-Science Rev. 216, 103597. doi:10.1016/j.earscirev.2021.103597

CrossRef Full Text | Google Scholar

Zhou, G. G. D., Zhou, M., Shrestha, M. S., Song, D., Choi, C. E., Cui, K. F. E., et al. (2019a). Experimental investigation on the longitudinal evolution of landslide dam breaching and outburst floods. Geomorphology 334, 29–43. doi:10.1016/j.geomorph.2019.02.035

CrossRef Full Text | Google Scholar

Zhou, M., Zhou, G. G. D., Cui, K. F. E., Song, D., and Lu, X. (2019b). Influence of inflow discharge and bed erodibility on outburst flood of landslide dam. J.Mt. Sci. 16, 778–792. doi:10.1007/s11629-018-5312-8

CrossRef Full Text | Google Scholar