Landslide displacement prediction based on CEEMDAN and grey wolf optimized-support vector regression model

Landslide prediction is very important and challenging for reducing geological hazards. In the Three Gorges Reservoir area, landslides show stepped deformation due to seasonal rainfall and periodic fluctuation of reservoir water level. The purpose of this study is to use complete ensemble empirical mode decomposition with adaptive noise and grey wolf optimization to support the vector regression method for displacement prediction. Firstly, the cumulative displacement is decomposed by CEEMDAN to obtain both trend term and fluctuation term displacement. Secondly, according to the cumulative displacement, rainfall, and reservoir water level data, the influencing factors related to the displacement of the trend term and the fluctuation term are determined. Then, the GWO-SVR model is used to predict the trend and fluctuation displacement. The final prediction result is obtained by adding the calculated predicted displacement values of each component. The Shuizhuyuan landslide in the Three Gorges Reservoir area, China, was taken as an example, and the long-term displacement data of monitoring point SZY-03 were selected for analysis. The results show that the root mean square error (RMSE) and coefficient of determination (R²) between the measured displacement values and the prediction values were 0.9845 and 0.9964, respectively. The trained model has high computational accuracy, which proves that the GWO-SVR model can be used for displacement prediction of this type of landslide in the Three Gorges Reservoir area.

1 Introduction

As one of the common geological hazards, a landslide has the characteristics of widespread distribution, frequent occurrence, great harm, and difficult management. An improper response can cause a huge loss of life and property and have a major social impact (Zhang, 2000; Xu et al., 2008). Therefore, the landslide displacement prediction has become a research hotspot in order to achieve hazard prevention and reduction. (Du et al., 2009; Gao et al., 2019).

The systematic landslide research began in 1920 in Sweden (Chen, 2016). Up to now, the landslide prediction model has mainly gone through five stages: the empirical model, the statistical analysis model, the nonlinear model, the physical and mechanical model, and the comprehensive model (Chen, 2013). For the special step-like displacement observed under special geological conditions and the periodic fluctuation of the reservoir water level in the Three Gorges Reservoir area, its landslide deformation is caused by the superposition of internal and external factors like other landslide deformation (Li, 2010). The deformation process is complex and it is difficult to distinguish the deformation stage accurately (Zhou et al., 2022a; Luo et al., 2022). Therefore, the landslide displacement prediction model is no longer applicable, which relies on the division of landslide deformation stages to predict the landslide deformation time (Tang et al., 2012). The nonlinear models and the related combined models are applied to the landslide displacement prediction (Guo et al., 2018).

The nonlinear models have become the mainstream models nowadays. The multi-algorithm coupling model in the nonlinear model has been widely studied because the single algorithm model can no longer meet the needs of the landslide displacement prediction (Han et al., 2019). In these studies, in order to obtain better prediction results, most studies decompose the cumulative displacement of the landslide into the displacement components with different characteristics to predict the landslide displacements, respectively, by analyzing the deformation evolution mechanism of the landslide and considering the internal and external factors that induce the landslide deformation (Zhou et al., 2016; Zhou et al., 2022b). When decomposing the displacement, most scholars usually separate the displacement of the trend term first. The commonly used decomposition methods include: (Ayodele et al., 2019) the fitting method based on historical displacement, which is suitable for simple curves, such as the grey model (Deng, 2002; Wu et al., 2007), polynomial trend fitting, etc.; (Balogun et al., 2021) the filtering method based on the original displacement data, which is easy to use and difficult to determine the displacement type and periodic value of the trend term, such as sliding average method (Pei and Guo, 2001; Xu et al., 2011); (Chen, 2013) the wavelet analysis method, which can extract the multi-time scale information of the landslide displacement and needs to determine its basis function and wavelet order manually (Yang et al., 2014; Li et al., 2015, 2017, 2019); (Chen et al., 2018) the smoothness priors approach, which has a simple implementation process and need the multiple decompositions and comparisons to determine the decomposition parameters. Moreover, the displacement of the trend term obtained by this method will still have step property (Huang et al., 2014). In addition, in order to avoid the shortcomings of the above methods, the series of empirical mode decomposition (EMD) (Huang et al., 1998) and the ensemble empirical mode decomposition (EEMD) (Wu and Huang, 2009) appeared. These methods can completely decompose the cumulative displacement of the landslide and significantly improve the prediction accuracy, but they have the defects such as modal aliasing, low decomposition efficiency, and difficulty in completely eliminating noise. Therefore, Torres et al. proposed complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) (Torres et al., 2011). This method effectively solves the problems in the decomposition method mentioned above by adding the white noise at each stage and shows a very good decomposition effect in terms of the nonlinear time series (Tan et al., 2019; Wang et al., 2021).

In recent years, with the development of artificial intelligence and machine learning theories, more and more artificial intelligence algorithms have been widely applied to landslide displacement prediction, including the back propagation neural network (BPNN) model, the support vector regression (SVR) model, the extreme learning machine (ELM) model, and so on. BPNN is easy to fall into local optimization and is difficult to construct the appropriate network structure. So it is often difficult to obtain an ideal prediction effect (Hu et al., 2016; Zuan and Huang, 2018); ELM has simple parameter settings and good generalization in practical applications (Zhou et al., 2015; Zhao et al., 2018), but the input layer weights and hidden layer deviations are random, which reduces the model prediction accuracy. SVR has a strong generalization ability, a good prediction effect for small samples, and nonlinear and high-dimensional problems. Therefore, its popularization is strong (Ayodele et al., 2019; Liu et al., 2019), and it is widely used in landslide displacement prediction (Liu et al., 2013; Zhou et al., 2016; Miao et al., 2017). However, SVR has the problems such as difficulty in parameter selection. Adopting appropriate parameter optimization methods can effectively solve the problems of the above-mentioned algorithms and improve the accuracy of landslide displacement prediction. In the previous studies, parameter optimization was mainly realized by grid search method, gradient descent method, and meta-heuristic search algorithms, such as genetic algorithm (GA), particle swarm optimization (PSO), artificial bee colony (ABC), ant colony optimization (ACO) (Miao et al., 2016), whale optimization algorithm (WOA) (Mirjalili and Lewis, 2016), and so on. These traditional optimization algorithms take a long time to optimize and are relatively inefficient. As a new meta-heuristic algorithm, the grey wolf optimizer (GWO) (Mirjaliliet al., 2014) has the advantages of simple principle, less parameter adjustment, strong global search ability, etc. It has been proved to have significant advantages in the study of combinatorial optimization problems. It can effectively solve the joint optimization problems of multiple parameters and is widely used in various fields (Zhao, 2017; Liao et al., 2020; Guo et al., 2022).

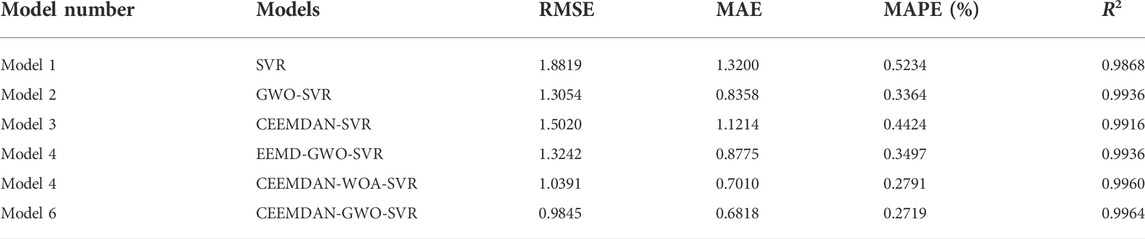
In summary, in this study, the Shuizhuyuan landslide in Wushan County of the Three Gorges Reservoir area is taken as an example and the CEEMDAN-GWO-SVR model is proposed. Firstly, the cumulative displacement is decomposed by CEEMDAN to obtain trend term and fluctuation term displacement. Secondly, according to the cumulative displacement, rainfall, and reservoir water level data, the influencing factors related to the displacement of the trend term and the fluctuation term are determined. Then, the GWO-SVR model is used to predict the trend and fluctuation displacement. The final prediction result is obtained by adding the calculated predicted displacement values of each component. In order to prove the superiority and applicability of the CEEMDAN-GWO-SVR model, the prediction accuracy of the model is compared with that of the SVR, GWO-SVR, CEEMDAN-SVR, EEMD-GWO-SVR, CEEMDAN-WOA-SVR models, root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) and coefficient of determination (R²) are used as evaluation indexes to compare and analyze the prediction results.

2 Methodology

2.1 Complete ensemble empirical mode decomposition with adaptive noise

The EMD is a signal decomposition method that can decompose the original signal into the different intrinsic mode functions (IMF) according to the fluctuation scale. The EEMD is obtained by adding the Gaussian white noise that obeys the normal distribution into the EMD, which solves the modal aliasing problem of the EMD and realizes the effective modal component separation. In order to further solve the problems in the decomposition of the original signal, the CEEMDAN algorithm is proposed based on the development of the EEMD. The adaptive Gaussian white noise is added to each stage of the decomposition, which effectively reduces the reconstruction error problem in the EEMD and improves the decomposition efficiency (Mousavi et al., 2020; Li et al., 2021; Song et al., 2021).

In CEEMDAN, X (t) represents the original signal, which is to be decomposed, E_k represents the k-th modal component generated by the decomposition of the original signal by the EMD, ${\omega }^i\left(t\right)$ is Gaussian white noise that obeys the normal distribution, and ${\epsilon }_k$ represents the signal-to-noise ratio coefficient of the k-th modal component. The specific decomposition steps of CEEMDAN are as follows:

Perform EMD decomposition on the original signal with Gaussian white noise, and get the first modal component:

$IM{F}_1\left(t\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}IM{F}_1^i\left(t\right)=\overline{IM{F}_1}\left(t\right)}(1)$

When $k=1$, calculate the first residual signal, which is:

$R_1\left(t\right)=X\left(t\right)-IM{F}_1\left(t\right)(2)$

Perform the i-th experiment, add Gaussian white noise to the residual signal, and decompose it by EMD until the first modal component of EMD is obtained, and then calculate the first modal component based on this:

$IM{F}_2\left(t\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{E}_1\left(R_1\left(t\right)+{\epsilon }_1{E}_1\left({\omega }^i\left(t\right)\right)\right)}(3)$

Similarly, when $k=2,\cdots ,K$, calculating the k-th residual signal and the k+1-th modal component according to the above process:

$R_k\left(t\right)=R_{k-1}\left(t\right)-IM{F}_k\left(t\right)(4)$

$IM{F}_{k+1}\left(t\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{E}_1\left(R_k\left(t\right)+{\epsilon }_{k}E{}_k\left({\omega }^i\left(t\right)\right)\right)}(5)$

When the residual signal does not meet the conditions, that is, the number of extreme points does not exceed two, the decomposition is terminated, the algorithm is completed, and $k$ modal components are obtained. The final residual component is:

$R\left(t\right)=X\left(t\right)-{\displaystyle \sum _{i=1}^{K}IM{F}_k\left(t\right)}(6)$

The final decomposition result of the original signal is:

$X\left(t\right)={\displaystyle \sum _{i=1}^{K}IM{F}_k\left(t\right)+R\left(t\right)}(7)$

2.2 Support vector regression machine optimized by grey wolf algorithm

Vapnik et al. (Vladimir, 2000) proposed the support vector machine (SVM) model for nonlinear problems based on statistical theory in 1995, and the SVR model is an important application branch of it. The main idea of SVR is to map the low-dimensional input vector to the high-dimensional feature space through the selected mapping function and find the regression function in the high-dimensional feature space. So the low-dimensional nonlinear regression problem is transformed into the high-dimensional linear regression problem. SVR effectively solves the problems of small samples, nonlinearity, and high dimensionality. It has strong robustness and has been widely used in prediction and other aspects. In this study, the radial basis function is taken as the kernel function of the SVR, which is used by many scholars. However, in the application process, the values of penalty factor C, kernel function parameter g, and insensitive parameter $\epsilon$ have a great influence on the predictive ability of the model. They directly determine the generalization ability of the model.

The GWO is a new heuristic algorithm proposed in 2014, which imitates the hunting behavior of wolves (Mirjaliliet al., 2014). The main content of this algorithm includes five parts: social level, surrounding prey, hunting, attacking prey, and looking for prey. The wolves are initialized to search for prey, each time the three wolves with the best adaptability in the population are retained, and the positions of other grey wolves are updated accordingly, then the optimal solution is finally found through the continuous iteration (Wang and Li, 2018; Balogun et al., 2021). Compared with traditional algorithms such as the PSO, GA, and ABC, the GWO has the advantages of simple parameter setting, strong convergence performance, and high optimization accuracy. At the same time, the wolves search randomly during the optimization process to avoid falling into the local optimum. Therefore, using the GWO to optimize the parameters of SVR can greatly improve the prediction accuracy of the SVR model and then achieve an accurate prediction of the landslide displacement.

The optimization process of GWO is as follows: a group of grey wolves is randomly generated in the search space. According to the fitness level, the wolves numbered α, β, and δ in the grey wolf group evaluate and locate the position of the prey. The rest of the individuals take this as the standard, calculate the distance between themselves and the prey to complete the prey capture, and realize the optimization process (Mirjalili et al., 2014).

(1) Social Hierarchy. The GWO model has a strict social class, which can be divided into α, β, δ, and ω wolves on the basis of the social class. The social class in the algorithm is reflected in the fitness level.

(2) Encircling Prey. In the process of wolf hunting, they need to s encircle the prey and determine the location of the prey. The mathematical equations of encirclement behavior are as follows:

$D=\left|C\times X_p\left(\omega \right)-X\left(\omega \right)\right|(8)$

$X\left(\omega +1\right)=X_p\left(\omega \right)-\mu \times D(9)$

$C=2\times r_1(10)$

$\mu =2\alpha \times r_2-\alpha (11)$

where $\omega$ is the current iteration number; $D$ is the distance between prey and grey wolf; $C$ is a coefficient vector; $X_p\left(\omega \right)$ is the position vector of the prey in a generation $\omega$; $X\left(\omega \right)$ is the position vector of the individual grey wolf in a generation $\omega$; $X\left(\omega +1\right)$ is the position vector of the individual grey wolf in a generation $\omega +1$; $r_1$ and $r_2$ belong to random vector, with the value range of [0,1]; $\mu$ is a vector of convergence; the value of $\alpha$ declines linearly from 2 to 0 during the iteration.

(3) Update the location and hunting. The hunting process of wolves on prey is represented by the constant replacement of hunting location information. The $\alpha$ wolf, $\beta$ wolf, and $\delta$ wolf are closest to the prey. The distance between the other grey wolves and these three wolves in the $\omega$ th generation is as follows:

$D_k=\left|C_i\times X_k\left(\omega \right)-X\left(\omega \right)\right|(12)$

$X_i=X_k-{\mu }_i\times D_k(13)$

The predation direction is determined according to the following formula:

$X_p\left(\omega +1\right)=\frac{X_1+X_2+X_3}{3}(14)$

where $k=\alpha , \beta ,\delta$; $i$= 1, 2, 3; $X_p\left(\omega +1\right)$ is the position vector of the prey in $\omega +1$ a generation.

The optimized SVR parameters C, g, and $\epsilon$ are obtained by outputting the position of the grey wolf $\alpha$ with the best fitness. The SVR prediction model is established by using the obtained optimal parameters.

2.3 Prediction method and process

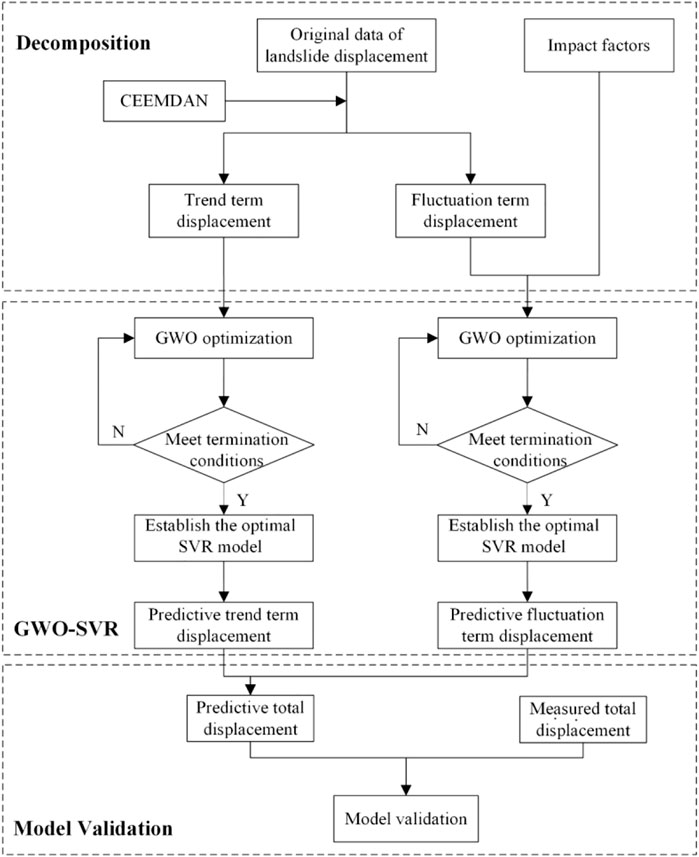
In order to realize the above algorithm, the following prediction process is designed. The specific steps are shown in Ayodele et al. (2019andChen (2016), which mainly include three major blocks: CEEMDAN decomposition, GWO-SVR model, and model validation. The specific process is shown in Figure 1.

(1) Preprocess the original displacement data, and use CEEMDAN to decompose the cumulative displacement of the landslide to obtain the displacement of the fluctuation term and the displacement of the trend term.

(2) Divide the decomposed displacement components into the training set and test set according to the characteristics of displacement deformation.

(3) Analyze the displacement component of the fluctuation term and the displacement component of the trend term, respectively, determine the respective input variables and output variables and judge the correlation between the input variables and the output variables.

(4) Initialize the wolves, set the initial parameters of GWO, optimize the parameters C, g, and $\epsilon$ of SVR, construct the GWO-SVR model, and use the model to predict the displacement of the fluctuation term and the displacement of the trend term, respectively.

(5) Superimpose the displacement of the fluctuation term and the displacement of the trend term to obtain the total landslide displacement data, and perform model verification.

FIGURE 1

FIGURE 1. Flow chart of displacement prediction.

2.4 Model performance evaluation index

In order to evaluate the predictive ability of the model more specifically, root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and coefficient of determination (R²) are selected as the evaluation indexes of the model performance in this study. The specific calculation formula is as follows:

$\text{RMSE}=\sqrt{\frac{1}{m}{\displaystyle \sum _{\text{i}=1}^m{\left({\widehat{y}}_i-y_i\right)}^2}}(15)$

$\text{MAE}=\frac{1}{m}{\displaystyle \sum _{\text{i}=1}^m\left|{\widehat{y}}_i-y_i\right|}(16)$

$\text{MAPE}=\frac{100\%}{m}{\displaystyle \sum _{i=1}^m\left|\frac{{\widehat{y}}_i-y_i}{y_i}\right|}(17)$

${\text{R}}^2=1-\frac{{\displaystyle \sum _{i=1}^m{\left({\widehat{y}}_i-y_i\right)}^2}}{{\displaystyle \sum _{i=1}^m{\left({\overline{y}}_i-y_i\right)}^2}}(18)$

where $y_i$ is the actual value, ${\widehat{y}}_i$ is the predicted value, ${\overline{y}}_i$ is the average value, and $m$ is the number of samples. The above four evaluation indexes integrate a variety of perspectives and can make a more comprehensive judgment on the prediction ability of the model.

3 Case study: Shuizhuyuan landslide

3.1 Geological conditions

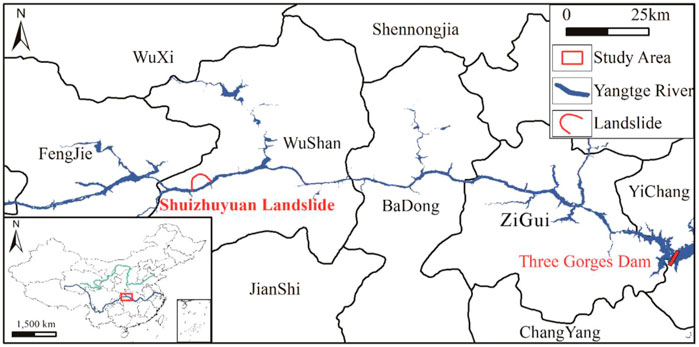
The Shuizhuyuan landslide is located in Group 1 of Ganju Village, Quchi Township, Wushan County, on the left bank of the Yangtze River (31°00′ 59.37″ E, 109°43 '27.33″ N). It is 14.82 km away from the new urban area of Wushan (Figure 2). The Shuizhuyuan landslide has a length of about 800m, a width of 360 ∼ 1200 m, an average thickness of 30 m, an area of 620, 000 m², and a volume of 18.5 million m³. The Yangtze River passes from west to east from the front edge of the landslide. The landslide area is characterized by an evolving steep slope-gentle slope. Especially, the slope of the front edge of the landslide below the elevation of 180 ∼ 250 m is relatively large, generally 30 ∼ 45^◦, and it is mostly in the reservoir water drawdown zone and its influence area; the middle and rear edge area of the landslide with an elevation of 250 ∼ 300 m is dominated by gentle slopes, the terrain slope is generally 10 ∼ 15^◦, and there are 3 platforms with different scales, which are the main farmland areas and villagers’ residential areas; the slopes with an elevation of more than 300 m are mainly steep slopes, which are the trailing edge of the landslide.

FIGURE 2

FIGURE 2. Location of the Shuizhuyuan landslide.

3.2 Monitoring situation

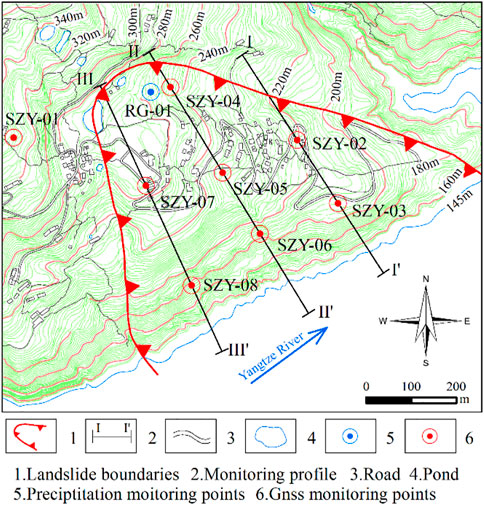
Through investigation and analysis, it is found that the Shuizhuyuan landslide is a large-scale retrogressive soil landslide. The rainfall and reservoir water level are the main inducing factors. The monitoring level of the landslide is level 2. The main monitoring contents are surface displacement, precipitation, and reservoir water level changes. The landslide is monitored by using the GNSS monitoring equipment to derive deformation, which distributes over the landslide area. The seven monitoring points and one datum point are arranged to form the three longitudinal monitoring profiles. A rainfall monitoring point is arranged. The data of reservoir water level change are measured by the measuring equipment arranged on-site at the monitoring point. The layout plan of the landslide monitoring network is shown in Figure 3.

FIGURE 3

FIGURE 3. Monitoring arrangement in the Shuizhuyuan landslide.

The monitoring curves of accumulated displacement, rainfall, and reservoir water level of SZY-03 of the Shuizhuyuan landslide are shown in Figure 4. For the displacement monitoring point studied in this study, it can be observed from Figure 4 that a combination of the successive rain pulses inducing landslide movement and the cumulative displacement increases in varying degrees according to the rainfall. During the 4 years studied in this study, the rainfall in 2017 was extremely rich, so the cumulative displacement increased sharply during the latter half of the rainy season in 2017. At the same time, the cumulative displacement increases obviously in the rainy season. After that, the cumulative displacement will still increase to a certain extent, which indicates that the impact of rainfall on landslide deformation has a certain hysteresis.

FIGURE 4

FIGURE 4. Monitoring curve of cumulative displacement, rainfall, and water level of the reservoir area of the landslide.

In addition, the reservoir water level of this monitoring point has an obvious periodicity and the time span is about 1 year. Within the time frame of this study, the reservoir water level has not undergone a significant change except the periodic fluctuation. In the first half of each year, the reservoir water level will decrease slightly. This means that the water pressure on the slope surface decreases and the supporting capacity on the slope is weakened. So the landslide deformation accelerates and the cumulative displacement increase rapidly. In the latter half of each year, the reservoir water level area rises and the water pressure on the slope surface is greater than the outward sliding force of the slope body, which inhibits landslide deformation. So the increase of the cumulative displacement becomes slow. The influence of the rainfall and reservoir water level on slope body is slow and continuous. So their influence of them on landslide displacement has hysteresis.

Analyzing the deformation rate of the landslides for many years, it is found that the deformation rate is higher in the rainy season or the reservoir water level adjustment period and the deformation rate is relatively lower in the non-rainy season or the reservoir water level is relatively flat period. These indicate that the precipitation and the wide adjustment of the reservoir water level are the main factors affecting landslide deformation.

4 Calculations and results

In this study, taking the SZY-03 surface displacement monitoring point of the Shuizhuyuan landslide in Wushan County of the Three Gorges Reservoir Area as an example, 1616 displacement, rainfall, and reservoir water level data of the SZY-03 monitoring point from July 2016 to November 2020 were selected for landslide displacement prediction. All of them were continuously monitoring data on a daily basis.

In order to make the data more representative and make a further study on the correlation between rainfall, reservoir water level, and landslide displacement, it is necessary to process the original data and obtain the new data with weeks as the number of monitoring periods. Specifically, the cumulative displacement took the average of the cumulative displacement in 1 week, the reservoir water level took the change of the reservoir water level in 1 week, and the rainfall took the sum of the rainfall in 1 week. Finally, the 230 sets of data for landslide displacement prediction were obtained. According to the periodic characteristics of the landslide deformation, the 190 sets of data from July 2016 to February 2020 were selected as the training sample set of the model, and the 40 sets of data from February 2020 to November 2020 were selected as the test sample set of the model.

4.1 Complete ensemble empirical mode decomposition with adaptive noise decomposition of landslide displacement

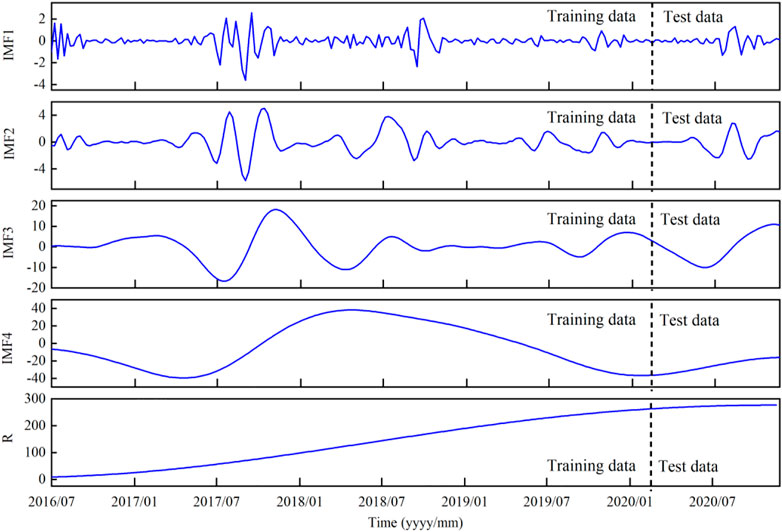
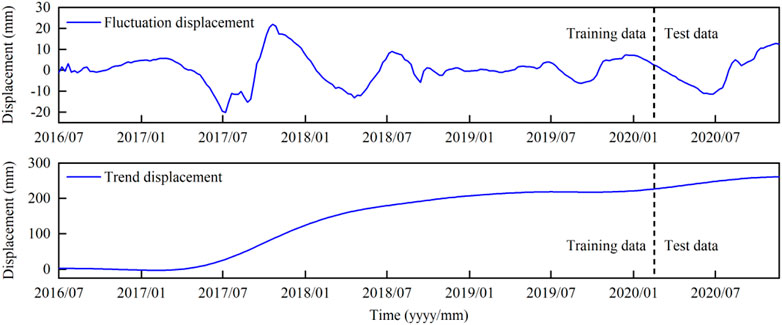
The factors affecting landslide displacement deformation mainly include internal factors caused by its own geological conditions and external factors caused by the external environment (Zhang et al., 2015a). In this section, CEEMDAN model was used to decompose the cumulative displacement of landslides into fluctuation term displacement and trend term displacement. The former is mainly determined by external factors (such as rainfall and reservoir water level changes) and the latter is mainly determined by internal factors (such as its own geological conditions) According to the above, the CEEMDAN decomposition program was written in Python language, the 230 sets of displacement data at the SZY-03 monitoring point of the Shuizhuyuan landslide was decomposed by using this program, the four IMF characteristic components with the significant differences and one residual component R were obtained, as shown in Figure 5. The component IMF4 and the residual component R change gently. So they can be considered as the actual displacement under the internal dynamic action of the landslide. Therefore, IMF4 and R are taken as the trend term of displacement, that is, the deformation displacement caused by the landslide itself, as shown in the lower part of Figure 6. The fluctuation term displacement is also obtained through the total displacement time series subtracted from the trend term displacement. This is the deformation displacement caused by the external factors, as shown in the upper part of Figure 6.

FIGURE 5

FIGURE 5. CEEMDAN decomposition results of displacement of the Shuizhuyuan landslide.

FIGURE 6

FIGURE 6. The fluctuant and trend displacement of the Shuizhuyuan landslide.

It can be seen from Figure 6 that the displacement of the trend term accounts for a relatively large proportion, and the peak is close to all the landslide displacements at the corresponding time. Thus, the accuracy of the trend term prediction is particularly important. Although the displacement of the fluctuation term occupies a relatively small part of the cumulative displacement, the accuracy of its predicted value will also affect the accuracy of the predicted result to a certain extent. Therefore, in order to obtain better prediction results, it is necessary to select the appropriate method based on the characteristics of the displacement deformation of the landslide to make the correct prediction.

4.2 Prediction of fluctuation term displacement

4.2.1 Determination of influence factors of the fluctuation item

The reservoir water level and rainfall are the main external factors inducing landslide deformation (Chen et al., 2018). The infiltration of rainfall will destroy the structure of the landslide, reduce the stability of the landslide, change the gravity field of the landslide, soften the soil and cause the deformation of the landslide surface, and affect the stability of the landslide (Jeonget al., 2017; Kuradusenge et al., 2020); the fluctuation of reservoir water level will reduce the shear strength of the landslide and also lead the deformation of the landslide (Liao et al., 2019). The influence of rainfall and reservoir water level on slope body is slow and continuous. So their influence of them on landslide displacement has hysteresis.

In addition, not only rainfall and reservoir water level will affect the fluctuation term displacement, but also the fluctuation term displacement itself. Therefore, referring to previous studies (Zhang et al., 2015b; Chen et al., 2018; Liao et al., 2019), combined with the monitoring period selected in this study, and considering the hysteresis, eight impact factors were determined. The data of the past week was regarded as the monitoring data of this period. The current period was set as the t-th period. Correspondingly, last week was set as the t-1-th period and the week before last week was set as the t-2-th period. The displacement of the fluctuation term, rainfall, and the change of the reservoir water level were, respectively, set to W, J, and K. Then W_t−1 represented last week’s fluctuation term displacement, and the rest could be done by analogy. Therefore, the eight influencing factors were W_t−1, W_t−2, W_t−3, J_t, J_t−1, K_t, K_t−1, and K_t−2, as shown in Table 1.

TABLE 1

TABLE 1. Inputs for the modeling of the fluctuation displacement.

In the prediction model, the input variables were the above-mentioned eight influencing factors, and the output variables were the displacement of the current period’s fluctuation term. In order to further determine the rationality of the selection of the input variables, the grey relational degree was used to evaluate the correlation between the influence factors and the displacement of the fluctuation term. The grey correlation coefficient was 0.5 and the grey relational degree was calculated (Qian et al., 2008). The results are shown in Table 2.

TABLE 2

TABLE 2. Grey relational degree (GRG) between each impact factor and fluctuation displacement.

Comparing the data in Table 2, it is found that the correlation between the impact factor and the displacement of the fluctuation item gradually decreases as the lag time increases. But the grey relational degree between each influencing factor and the displacement of the fluctuation term is greater than 0.6, so it is reasonable to select the lag time as 1∼3 weeks. At the same time, it is proved that the eight influence factors selected by the preliminary analysis have a strong correlation with the displacement of the fluctuation term. It is reasonable that the input variables were selected to predict the displacement of the landslide fluctuation term (Zhang et al., 2015b).

4.2.2 Modeling and prediction of fluctuation term displacement

The GWO-SVR model based on Python language was established to predict the displacement of the fluctuation term. Through analyzing the principle of GWO and comparative analysis of multiple experiments, the parameters of the GWO were finally determined. In this study, the population size N, the maximum number of iterations Max iter, and the dimension dim were set to 40, 100, and 3, respectively. The search intervals of optimizing the penalty factor C, the kernel function parameter g and the insensitive parameter ε of the SVR model were C = [10^–6, 10⁶], g = [10^–6, 10⁶], and ε = [10^–6, 10⁶]. The fitness function was set to the MAPE value of the test set. After the optimization calculation of GWO, the best fitness was obtained. Finally, the optimized parameter values are C = 802,455.4068, g = 1.4072 × 10^–5, $\epsilon$= 1.2246 × 10^–6.

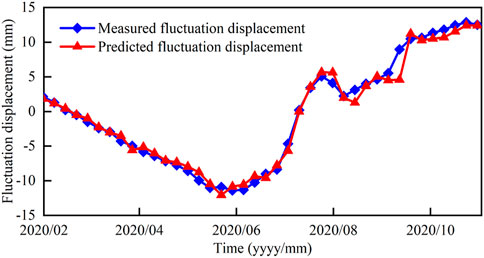
The optimized SVR model was used to predict the displacement of the fluctuation term, and the prediction result is shown in Figure 7. The RMSE of the prediction result of the fluctuation term displacement is 0.9900, the MAE is 0.6856, the MAPE is 16.5153% and the R² is 0.9835. Compared with the existing relevant literature, the prediction result is better and more accurate.

FIGURE 7

FIGURE 7. Prediction and comparison of the fluctuation displacement.

4.3 Prediction of trend item displacement

The trend item is determined by the landslide’s own geological conditions and reflects the overall development trend of the landslide (Wang et al., 2014). The trend item displacement has the characteristics of gentle change, strong regularity, and relatively simple influence factors, which are obtained by decomposing the cumulative displacement data of the SZY-03 monitoring point of the Shuizhuyuan landslide selected in this study.

Referring to the previous research results (Zhou et al., 2018), the t-1-th, t-2-th, and t-3-th period trend item displacements were used as the input variables, and the current trend item displacements were used as the output variables and the GWO-SVR model is still used for prediction. The grey wolf algorithm was used to find the optimal SVR parameters for this prediction, which were C = 94,093.2659, g = 2.0655 × 10^–5, and $\epsilon$= 1.9312 × 10^–6. The first 190 sets of data were used to train the optimized model and the trained model was used to predict the last 40 sets of data. The final prediction results are shown in Figure 8.

FIGURE 8

FIGURE 8. Prediction and comparison of the trend displacement.

The RMSE of the model is 0.0209, the MAE is 0.0176, the MAPE is 0.0069% and the R² is 0.999996. By observing Figure 8, it can be found that the actual displacement curve and the predicted displacement curve of the trend term displacement overlap to a great extent. The prediction results show that the prediction effect of the trend term is good and the CEEMDAN-GWO-SVR model established in this study also has good applicability for the trend item displacement prediction.

4.4 Prediction of cumulative displacement of landslide

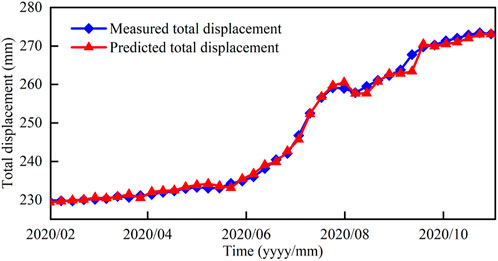
The prediction result of the cumulative displacement of the landslide was obtained by superimposing the predicted value of the landslide fluctuation item and the predicted value of the landslide trend item, as shown in Figure 9.

FIGURE 9

FIGURE 9. Prediction and comparison of the total displacement.

The RMSE of the total landslide displacement prediction result is 0.9846, the MAE is 0.6818, the MAPE is 0.2719% and the R² is 0.9964. From the final prediction results of the total landslide displacement, the overall fitting and prediction results are good and ideal, which meets the expectations of the model design.

5 Discussion

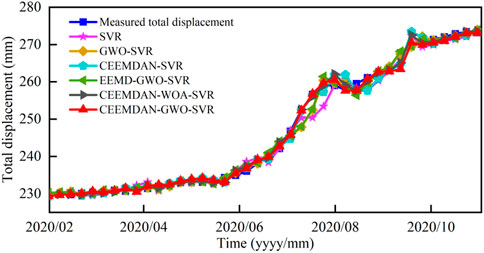
In general, the mechanism and the deformation characteristics of landslides in the Three Gorges Reservoir area are related to the comprehensive action of many influencing factors, including many geological and hydraulic factors. Through the analysis of monitoring data and macro deformation characteristics, it is proved that reservoir water level fluctuation and precipitation are the main influencing factors of Shuizhuyuan landslide deformation. In particular, the acceleration behavior of landslides is attributed to many heavy rainfall events and the rapid decline of water levels. In order to further test the superiority and accuracy of the model prediction, it is compared with the approximate prediction model. The prediction and comparison image is shown in Figure 10, and the comparison of evaluation indexes of each model is shown in Table 3.

FIGURE 10

FIGURE 10. Prediction and comparison of various models.

TABLE 3

TABLE 3. Comparison of prediction accuracy of different prediction models.

Combining the comparative analysis of each model in Figure 11 and the predictive index data in Table 3, the following results can be obtained:

(1) Comparing the GWO-SVR, CEEMDAN- SVR and SVR models, as shown in Figure 11A. The prediction accuracy of GWO-SVR and CEEMDAN-SVR has been significantly improved. The RMSE, MAE, and R² of GWO-SVR are 1.3054, 0.8358, and 0.9936, respectively, and the prediction effect is the best. This proves that the accuracy of the SVR model optimized by GWO has been greatly improved. In addition, the data analyzed by CEEMDAN significantly improves the prediction accuracy compared with the traditional SVR model.

(2) Compared with the prediction results of the EEMD-GWO-SVR model and the GWO-SVR model, as shown in Figure 11B, the prediction accuracy has not been improved, which reflects the limited decomposition effect of EEMD and the existence of reconstruction errors during decomposition. And for this monitoring point, the EEMD decomposition of the cumulative displacement of the landslide cannot improve the prediction accuracy of the model.

(3) Comparing the CEEMDAN-GWO-SVR model and GWO-SVR model, as shown in Figure 11C, it is found that the trend term displacement and fluctuation term displacement obtained by CEEMDAN decomposition are more regular than the original displacement data, which reduce the interference of random factors and noise on the prediction process and improve the prediction accuracy. Comparing the CEEMDA-GWO-SVR and EEMD-GWO-SVR models, it is found that RMSE and MAE are reduced by 0.3397 and 0.1957, respectively, MAPE is increased to 0.2719% and R² is increased to 0.9964. This shows that CEEMDAN has a better decomposition effect than EEMD and effectively reduces the problems of mode aliasing, low decomposition efficiency, and difficulty in completely eliminating noise.

(4) In order to further prove the superiority of GWO algorithm, GWO and WOA algorithms are compared. The data show that CEEMDAN-GWO-SVR has better prediction accuracy than the CEEMDAN-WOA-SVR model, as shown in Figure 11D. The RMSE, MAE, MAPE, and R² of the GWO algorithm are 0.9845, 0.6818, 0.2719%, and 0.9964, respectively, which is further improved than the WOA algorithm. The results show that the GWO algorithm has a stronger parameter optimization ability than the WOA algorithm when optimizing the three parameters C, g, $\epsilon$ of SVR, and the optimization effect is more in line with expectations. The model can significantly improve the prediction effect.

FIGURE 11

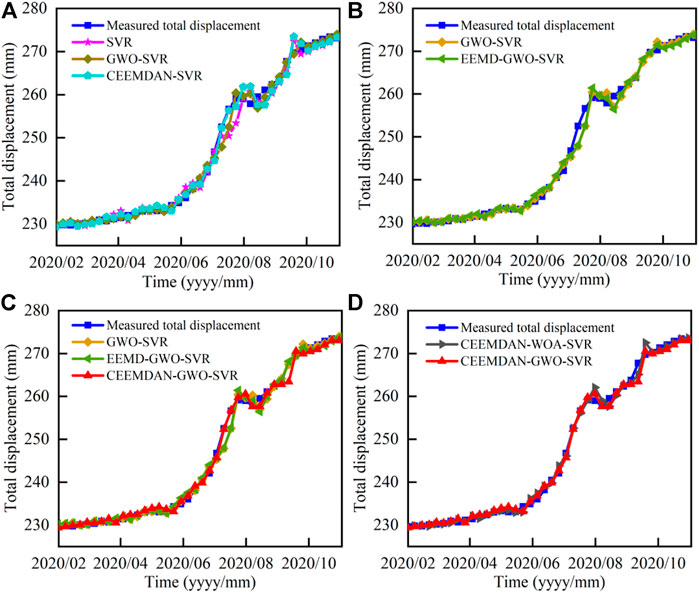
FIGURE 11. Prediction and comparison between different models. (A) Comparison of GWO-SVR, CEEMDAN-SVR and SVR models; (B) Comparison of GWO-SVR and EEMD-GWO-SVR models; (C) Comparison of GWO-SVR, EEMD-GWO-SVR and CEEMDAN-GWO-SVR models; (D) Comparison of CEEMDAN-WOA-SVR and CEEMDAN-GWO-SVR models.

In summary, for the prediction of the Shuizhuyuan landslide in the Three Gorges area, the CEEMDAN-GWO-SVR model proposed in this study has higher prediction accuracy and better results than other methods.

6 Conclusion

A new landslide displacement prediction method is proposed by combining CEEMDAN, GWO, and SVR models. Taking the Shuizhuyuan landslide in the Three Gorges Reservoir area as an example, the model was used to establish the cumulative displacement prediction model of the landslide. In addition, CEEMDAN-GWO-SVR is compared with other prediction models. The RMSE, MAE, MAPE, and R² of the predicted result are calculated as 0.9845, 0.6818, 0.2719%, and 0.9964, respectively. It demonstrates the applicability and superiority of the proposed model.

(1) CEEMDAN is used to replace the traditional EEMD, which solves the problems of modal aliasing, low decomposition efficiency, and difficulty in completely eliminating noise. The results obtained by CEEMDAN are more regular, and the prediction model can make more accurate predictions of the decomposed components. GWO algorithm is used to optimize the three model parameters of SVR, which effectively solves the problem of reducing the performance of the prediction model due to the randomness of parameters and significantly improves the prediction accuracy.

(2) The internal and external factors (rainfall factor, reservoir water level factor, and past cumulative displacement factor) affecting the displacement and deformation of the landslide are fully considered. Combined with previous research results, the changes in monitoring data were analyzed in detail and eight influencing factors were finally determined. The grey correlation degree between the eight influencing factors and the displacement of the fluctuation term is all greater than 0.6, indicating that the selection of the influencing factors of the fluctuation term is effective.

(3) The results show that the model has higher accuracy and better displacement prediction ability under the premise of effectively obtaining long-term landslide monitoring data. It can effectively solve the displacement prediction problem of step-like landslides similar to the Shuizhuyuan landslide and provide a new solution and research idea for studying the displacement prediction in the Three Gorges Reservoir area and other landslide-prone regions.

Data availability statement

The datasets presented in this article are not readily available because the datasets are under project protection. Therefore, the datasets cannot be made available to the public. Requests to access the datasets should be directed to mengqingjia@mail.cgs.gov.cn.

Author contributions

Conceptualization, CW, QM, and JJ; methodology, CW, GL, and QM; validation, CW, GL, QM, and JJ; formal analysis, CW, GL, WG, KY, and QM; investigation, CW, WG, and GL; resources, CW, GL, WG, QM, and JJ; data curation, CW, WG, KY, QM, and JJ; software, CW, GL, and JJ; writing—original draft preparation, CW, GL, QM, and JJ; writing—review and editing, CW, GL, QM, and JJ; supervision, CW, and QM; project administration, CW, and QM; all authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Key Research and Development Program of China (No. 2019YFC1509601 and No. 2018YFC1504805) and Geological Survey Projects of China Geological Survey (No. DD20190639, No. DD20221747 and No. DD20211369).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ayodele, T. R., Ogunjuyigbe, A., Amedu, A., and Munda, J. (2019). Prediction of global solar irradiation using hybridized k-means and support vector regression algorithms. Renew. Energy Focus 29 (JUN), 78–93. doi:10.1016/j.ref.2019.03.003

CrossRef Full Text | Google Scholar

Balogun, A. L., Rezaie, F., Pham, Q. B., Gigovic, L., Drobnjak, S., Aina, Y. A., et al. (2021). Spatial prediction of landslide susceptibility in Western Serbia using hybrid support vector regression (SVR) with GWO, BAT and COA algorithms. Geosci. Front. 12 (3), 101104104. doi:10.1016/j.gsf.2020.10.009

CrossRef Full Text | Google Scholar

Chen, H. (2013). Research on landslide prediction and controlling based on artificial neural net- works. Phd, Wuhan: Huazhong University of Science and Technology.

Google Scholar

Chen, L., Zou, Z., and Yuan, Y. (2018). Displacement prediction of reservoir landslide considering lag effect of inducing factors. Yangtze River 49 (10), 60–65. doi:10.16232/j.cnki.1001-4179.2018.10.012

CrossRef Full Text | Google Scholar

Chen, Q. (2016). Analyzing landslide susceptibility in the upper Mingjiang basin. Md: Fujian Normal University.

Google Scholar

Deng, J. (2002). Grey theory basis. Wuhan: Huazhong University of Science and Technology Press.

Google Scholar

Du, J., Yin, K., and Chai, B. (2009). Study of displacement prediction model of landslide based on response analysis of inducing factors. Chin. J. Rock Mech. Eng. (9), 1783–1789. doi:10.3321/j.issn:1000-6915.2009.09.007

CrossRef Full Text | Google Scholar

Gao, W., Dai, S., and Chen, X. (2019). Landslide prediction based on a combination intelligent method using the GM and ENN: Two cases of landslides in the three Gorges reservoir, China. Landslides 17 (1), 111–126. doi:10.1007/s10346-019-01273-w

CrossRef Full Text | Google Scholar

Guo, Z., Chen, L., Gui, L., Du, J., Yin, K., and Do, H. M. (2022). Landslide displacement prediction based on variational mode decomposition and WA-GWO-BP model. Landslides 17 (3), 567–583. doi:10.1007/s10346-019-01314-4

CrossRef Full Text | Google Scholar

Guo, Z., Yin, K., Huang, F., and Liang, X. (2018). Landslide displacement prediction based on surface monitoring data and nonlinear time series combination model. Chin. J. Rock Mech. Eng. 37 (S1), 3392–3399. doi:10.13722/j.cnki.jrme.2016.1534

CrossRef Full Text | Google Scholar

Han, H., Zhang, L., and Shi, B. (2019). Prediction of deep displacement of Majiagou land- slide based on optical fiber monitoring and PSO-SVM model. J. Eng. Geol. 27 (04), 853–861. doi:10.13544/j.cnki.jeg.2018-257

CrossRef Full Text | Google Scholar

Hu, J., Dong, J., and Wang, K. (2016). Research on CPSO-BP model of slope stability. Rock Soil Mech. 37 (S1), 577–582+590. doi:10.16285/j.rsm.2016.S1.075

CrossRef Full Text | Google Scholar

Huang, H., Yi, W., and Yi, Q. (2014). Smoothness priors approach in displacement decom- position and prediction of landslidesCNKI:SUN:SWDG.0.2014-05-018. HYDRO- Geol. Eng. Geol. 041 (005), 95–100.

Google Scholar

Huang, N. E., Shen, Z., and Long, S. R. (1998). The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the royal society A: Mathematical. Phys. Eng. Sci., 454. doi:10.1098/rspa.1998.0193

CrossRef Full Text | Google Scholar

Jeong, S., Lee, K., Kim, J., and Kim, Y. (2017). Analysis of rainfall-induced landslide on unsaturated soil slopes. Sustainability 9 (1280). doi:10.3390/su9071280

CrossRef Full Text | Google Scholar

Kuradusenge, M., Kumaran, S., and Zennaro, M. (2020). Rainfall-induced landslide pre- diction using machine learning models: The case of Ngororero District, Rwanda. Int. J. Environ. Res. Public Health 17 (11), 4147. doi:10.3390/ijerph17114147

CrossRef Full Text | Google Scholar

Li, D. (2010). Prediction study of landslides with step-like displacement deformation in the Three Gorges Reservoir. Phd: China University of Geosciences.

Google Scholar

Li, G., Xing, X., Huang, J., and Luo, D. (2021). A method of dissolved oxygen prediction based on CEEMDAN-LSTM combination. Inf. Technol. Netw. Secur. 40 (08), 47–52. doi:10.19358/j.issn.2096-5133.2021.08.008

CrossRef Full Text | Google Scholar

Li, H., Xu, Q., and Wang, S. (2017). Application of a novel predictive model integrating wavelet analysis, boosting regression tree and extreme learning machine to loess landslide displacement. J. Yangtze River Sci. Res. Inst. (09), 67–73. doi:10.11988/ckyyb.20160529

CrossRef Full Text | Google Scholar

Li, S., Wang, P., and Goel, L. (2015). Short-term load fore- casting by wavelet transform and evolutionary extreme learning machine. Electr. Power Syst. Res. 122, 96–103. doi:10.1016/j.epsr.2015.01.002

CrossRef Full Text | Google Scholar

Li, Y., Sun, R., Yin, K., Xu, Y., Chai, B., and Xiao, L. (2019). Forecasting of landslide displacements using a chaos theory based wavelet analysis-Volterra filter model. Sci. Rep. 9 (1), 19853853. doi:10.1038/s41598-019-56405-y

CrossRef Full Text | Google Scholar

Liao, K., Wu, Y., and Li, L. (2019). Displacement pre- diction model of landslide based on time series and GWO-ELM. J. Central South Univ. Sci. Technol. 50 (03), 619–626. doi:10.11817/j.issn.1672-7207.2019.03.015

CrossRef Full Text | Google Scholar

Liao, K., Wu, Y., Miao, F., Li, L., and Xue, Y. (2020). Using a kernel extreme learning machine with grey wolf optimization to predict the displacement of step-like landslide. Bull. Eng. Geol. Environ. 79 (2), 673–685. doi:10.1007/s10064-019-01598-9

CrossRef Full Text | Google Scholar

Liu, R., Huang, J., and Jian, X. (2019). Landslide deformation prediction based on EEMD -GA-SVM model. Yangtze River 50 (11), 134–139. doi:10.16232/j.cnki.1001-4179.2019.11.022

CrossRef Full Text | Google Scholar

Liu, Z., Shao, J., Xu, W., Chen, H., and Shi, C. (2013). Comparison on landslide nonlinear displacement analysis and prediction with computational intelligence approaches. Landslides 11 (5), 889–896. doi:10.1007/s10346-013-0443-z

CrossRef Full Text | Google Scholar

Luo, S., Huang, D., Peng, J., and Tomas, R. (2022). Influence of permeability on the stability of dual-structure landslide with different deposit-bedding interface morphology: The case of the three Gorges Reservoir area, China. Eng. Geol. 296, 106480. doi:10.1016/j.enggeo.2021.106480

CrossRef Full Text | Google Scholar

Miao, F., Wu, Y., and Xie, Y. (2016). Displacement prediction of Baishuihe landslide based on multi algorithm optimization and SVR model. J. Eng. Geol. 24 (06), 1136–1144. doi:10.13544/j.cnki.jeg.2016.06.013

CrossRef Full Text | Google Scholar

Miao, F., Wu, Y., Xie, Y., and Li, Y. (2017). Prediction of landslide displacement with step-like behavior based on multialgorithm optimization and a support vector regression model. Landslides 15 (3), 475–488. doi:10.1007/s10346-017-0883-y

CrossRef Full Text | Google Scholar

Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007

CrossRef Full Text | Google Scholar

Mousavi, A. A., Zhang, C., Masri, S. F., and Gholipour, G. (2020). Structural damage localization and quantification based on a CEEMDAN hilbert transform neural network approach: A model steel truss bridge case study. Sensors 20 (5), 1271. doi:10.3390/s20051271

CrossRef Full Text | Google Scholar

Pei, Y., and Guo, M. (2001). The fundamental principle and application of sliding average method. GUN LAUNCH & CONTROL J. 000 (001), 21–23. doi:10.3969/j.issn.1673-6524.2001.01.007

CrossRef Full Text | Google Scholar

Qian, M., Ren, R., and Zhang, S. (2008). Grey relational analysis of the factors influencing employment of college graduates——Taking jiangsu as an example. Liaoning Educ. Res. (05), 95–98. doi:10.16697/j.cnki.xdjygl.2008.05.031

CrossRef Full Text | Google Scholar

Song, Y., Yang, J., and Song, J. (2021). Concrete dam deformation prediction based on CEEMDAN- PE-LSTM model. HYDRO-SCIENCE Eng. (03), 41–49. doi:10.12170/20200520003

CrossRef Full Text | Google Scholar

Tan, M., Yin, K., Guo, Z., Zhang, Y., Yang, Y., Zhao, H., et al. (2019). Landslide displacement prediction based on CEEMDAN method and particle swarm optimized-extreme learning machine model. Geol. Sci. Technol. Inf. 38 (06), 165–175. doi:10.19509/j.cnki.dzkq.2019.0619

CrossRef Full Text | Google Scholar

Tang, S., Yin, K., and Du, J. (2012). Time prediction for landslides with step-style displacement characteristic. Geol. Sci. Technol. Inf. 31 (04), 106–110. https://en.cnki.com.cn/Article_en/CJFDTOTAL-DZKQ201204019.htm.

Google Scholar

Torres, M. E., Colominas, M. A., Schlotthauer, G., and Flandrin, P. (2011). “A complete ensemble empirical mode decomposition with adaptive noise,” in IEEE international conference on acoustics, Speech and Signal Processing (ICASSP), 4144–4147. doi:10.1109/ICASSP.2011.5947265

CrossRef Full Text | Google Scholar

Vladimir, N. V. (2000). The nature of statis- tical learning theory. New York, NY: Springer. doi:10.1007/978-1-4757-3264-1

CrossRef Full Text | Google Scholar

Wang, J., and Li, W. (2018). Ultra-short-term fore- casting of wind speed based on CEEMD and GWO. Power Syst. Prot. Control 46 (09), 69–74. doi:10.7667/PSPC170590

CrossRef Full Text | Google Scholar

Wang, J., Nie, G., Gao, S., Wu, S., Li, H., and Ren, X. (2021). Landslide deformation prediction based on a GNSS time series analysis and recurrent neural network model. Remote Sens. 13 (6), 1055. doi:10.3390/rs13061055

CrossRef Full Text | Google Scholar

Wang, Y., Zhao, Q., and Han, G. (2014). Prediction study on landslides with step-style displacement characteristics. YELLOW RIVER 36 (10), 106–109. doi:10.3969/j.issn.1000-1379.2014.10.032

CrossRef Full Text | Google Scholar

Wu, Y., Teng, W., and Li, Y. (2007). Application of grey- neural network model to landslide deformation prediction. Chin. J. Rock Mech. Eng. (03), 632–636. doi:10.3321/j.issn:1000-6915.2007.03.028

CrossRef Full Text | Google Scholar

Wu, Z., and Huang, N. E. (2009). Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 1 (1)–41. doi:10.1142/S1793536909000047

CrossRef Full Text | Google Scholar

Xu, F., Wang, Y., Du, J., and Ye, J. (2011). Study of displacement prediction model of landslide based on time series analysis. Chin. J. Rock Mech. Eng. (04), 746–751. http://www.en.cnki.com.cn/Article_en/CJFDTOTAL-YSLX201104014.htm.

Google Scholar

Xu, Q., Gao, T., Xu, K., and Huang, X. (2008). Research on space-time evolution laws and early warning-prediction of landslides. Chin. J. Rock Mech. Eng. 27 (6), 1104–1112. doi:10.3321/j.issn:1000-6915.2008.06.003

CrossRef Full Text | Google Scholar

Yang, H., Wu, B., Chen, M., and Li, Q. (2014). Wavelet analysis and support vector machine coupling mode based on particle swarm optimization for the displacement prediction of landslide. Saf. Environ. Eng. 21 (04), 13–18. doi:10.3969/j.issn.1671-1556.2014.04.004

CrossRef Full Text | Google Scholar

Zhang, J., Li, X., Chi, M., and Lu, T. (2015a). Analysis of formation mechanism and characteristics of landslide disasters. J. Nat. DISASTERS 24 (06), 42–49. doi:10.13577/j.jnd.2015.0605

CrossRef Full Text | Google Scholar

Zhang, J., Yin, K., Wang, J., and Huang, F. (2015b). Displacement prediction of Baishuihe landslide based on time series and PSO-SVR model. Chin. J. Rock Mech. Eng. 34 (02), 382–391. doi:10.13722/j.cnki.jrme.2015.02.017

CrossRef Full Text | Google Scholar

Zhang, Z. (2000). “The present status, technical advance and development trends of landslide remedial measures,” in CNKI:SUN:DZHB.0.2000-02-000, 89–97+181.J. Geol. Hazards Environ. Preserv.02.

Google Scholar

Zhao, D. (2017). Research and application of machine learning method based on swarm intelligence optimization. Phd: Jilin University.

Google Scholar

Zhao, L., Ma, L., and Wang, X. (2018). Prediction of thermal system parameters based on PSO-ELM hybrid algorithm. Electr. Power Sci. Eng. 34 (03), 70–74. CNKI:SUN:DLQB.0.2018-03-012.

Google Scholar

Zhou, C., Cao, Y., Hu, X., Yin, K., Wang, Y., and Catani, F. (2022b). Enhanced dynamic landslide hazard mapping using MT-InSAR method in the Three Gorges Reservoir Area. Landslides 19, 1585–1597. doi:10.1007/s10346-021-01796-1

CrossRef Full Text | Google Scholar

Zhou, C., Cao, Y., Yin, K., Intrieri, E., Catani, F., and Wu, L. (2022a). Characteristic comparison of seepage-driven and buoyancy-driven landslides in Three Gorges Reservoir area, China. Eng. Geol. 301, 106590. doi:10.1016/j.enggeo.2022.106590

CrossRef Full Text | Google Scholar

Zhou, C., Yin, K., Cao, Y., and Ahmed, B. (2016). Application of time series analysis and PSO–SVM model in predicting the bazimen landslide in the Three Gorges Reservoir, China. Eng. Geol. 204, 108–120. doi:10.1016/j.enggeo.2016.02.009

CrossRef Full Text | Google Scholar

Zhou, C., Yin, K., Cao, Y., Intrieri, E., Ahmed, B., and Catani, F. (2018). Displacement prediction of step-like landslide by applying a novel kernel extreme learning machine method. Landslides 15 (11), 2211–2225. doi:10.1007/s10346-018-1022-0

CrossRef Full Text | Google Scholar

Zhou, C., Yin, K., and Huang, F. (2015). Application of the chaotic sequence WA-ELM coupling model in landslide displacement prediction. Rock Soil Mech. 36 (09), 2674–2680. doi:10.1016/j.enggeo.2016.02.009

CrossRef Full Text | Google Scholar

Zuan, P., and Huang, Y. (2018). Prediction of sliding slope displacement based on intelligent algorithm. Wirel. Pers. Commun. 102 (4), 3141–3157. doi:10.1007/s11277-018-5333-1

CrossRef Full Text | Google Scholar