Sparse Gaussian Process Regression for Landslide Displacement Time-Series Forecasting

Landslide hazards are complex nonlinear systems with a highly dynamic nature. Accurate forecasting of landslide displacement and evolution is crucial for the prevention and mitigation of landslide hazards. In this study, a probabilistic landslide displacement forecasting model based on the quantification of epistemic uncertainty is proposed. In particular, the displacement forecasting problem is cast as a time-series regression problem with limited training samples and must be solved by statistical inference. The epistemic uncertainty of the landslide displacement series is depicted by the statistical properties of the function space constituted by the nonlinear mappings generated by the sparse Gaussian process regression. Data for our study was collected from the study area located in northwestern China. Other state-of-the-art probabilistic forecasting models have also been utilized for comparative analysis. The experimental results confirmed the superiority of the sparse Gaussian process in the modeling of landslide displacement series in terms of forecasting accuracy, uncertainty quantification, and robustness to overfitting.

1 Introduction

In southwest China, landslides are among the most devastating natural disasters, causing damage to life, property, and local infrastructure (Aggarwal et al., 2020; Fan & Cai 2021; Zhou et al., 2021). Over 7,000 landslides occurred in China in 2016 as reported in the annual report provided by the China Institute of Geo-Environment Monitoring (Tang et al., 2020). The factors that trigger landslides vary, including heavy rainfall, reservoir water fluctuations, earthquakes, and human activities (Fan et al., 2022; Li et al., 2022). Reliable early warning systems that accurately quantify future landslide deformation assist experts in the evaluation of incoming landslide hazards (Tang et al., 2021). Therefore, landslide displacement time-series forecasting plays an important role in the prevention of geo-hazards.

According to literature review, landslide displacement forecasting can be categorized into two major types: deterministic and probabilistic forecasting. Majority of the studies involving deterministic forecasting approaches were based on statistical models or machine-learning models in predicting the actual value of incoming landslide displacement. Lewis and Reinsel (1985) applied autoregressive time-series models to predict landslide displacement. Lu and Rosenbaum (2003) proposed using the GM (1,1) model to perform a multivariate regression analysis of landslide displacement. Liu et al. (2012) used an exponential model to conduct time-series regression on landslide displacement. With the advancement of artificial intelligence (AI) technologies, machine learning and deep learning have become more popular in recent years. For instance, Lian et al. (2015) trained an artificial neural network (ANN) to predict short-term landslide displacement. Zhu et al. (2017) used a least-squares support vector machine optimized by a genetic algorithm to predict landslide displacement empirically. Xu et al. (2019) compared multiple data mining algorithms on their performance in predicting landslide displacement in the Heifangtai Region, China. Li et al. (2018) proposed using an extreme learning machine (ELM) integrated with parametric copula models to forecast the faster seasonal landslide displacement. The tail correlation is quantified, and the risk boundaries are computed using value-at-risk and tail-value-at-risk. Li et al. (2020) applied a deep-learning algorithm called the deep belief network (DBN) to predict incoming landslide displacement in the temporal domain. The research utilized the exponentially weighted moving average (EWMA) model to set up decision boundaries for identifying faster seasonal displacement and achieved promising results. All the above studies were performed under deterministic forecasting and offered reliable solutions for determining future landslide research.

Compared with the deterministic forecasting approaches, probabilistic forecasting estimates the probability distribution of future landslide displacement and is more complicated in practice. Using the same input data as the deterministic forecasting models, the output of probabilistic forecasting models consists of a prediction interval (PI) with a probability density function. For a PI, the two independent quantiles are fitted to the upper and lower bounds, and an accurate prediction is defined as the actual value that falls within the PI. Ma et al. (2018) proposed using a bootstrap-based ELM to construct PIs for landslide incremental displacement. Xing et al. (2019) revised the structure of long short-term memory (LSTM) network to generate probabilistic forecasting of landslide displacement and produced high-quality PIs for future displacement. Jiang et al. (2021) proposed a hybrid grey wolf optimizer to optimize the ELM structure for PI construction and achieved improved probabilistic prediction performance using field data. However, there is currently limited studies on probabilistic forecasting of landslide displacement.

In recent years, Gaussian process regression (GPR) has demonstrated superior predictive strength in many regression tasks (He and Kusiak 2017; Schulz et al., 2018; Li et al., 2021a; Li et al., 2021b; Deringer et al., 2021; Jamei et al., 2021; West et al., 2021; Fuhg et al., 2022; Tamhidi et al., 2022). Generally, GPR is a nonlinear, nonparametric regression tool useful for interpolating data points scattered in a high-dimensional input space. GPR is based on the Bayesian probability theory and has very close connections with other regression techniques, such as kernel ridge regression (KRR) and linear regression with radial basis functions (Deringer et al., 2021).

In this study, a novel landslide displacement probabilistic forecasting model integrated with a sparse Gaussian process (SGP) is proposed. The SGP is a nonparametric approach based on Bayesian theory and has the advantage of requiring fewer training samples compared with other over-parametrized regression models. Compared with the original Gaussian process, SGP adopts inducing variable points and variational inference to approximate the model parameters. Gradient descent optimization was utilized to optimize the SGP for predicting probabilistic landslide displacement.

The main contributions of this paper can be concluded as follows:

• A new probabilistic landslide displacement model via the quantification of epistemic uncertainty is proposed.

• The SGP is incorporated within the probabilistic forecasting framework to tackle the interference complexity.

The remainder of this paper is organized as follows; Section 2 introduces the basics of the Gaussian process and the sparse Gaussian process, Section 3 describes the case study area and the data collection process, Section 4 summarizes the experimental results and Section 5 concludes the paper.

2 Methodology

2.1 Gaussian Process

The Gaussian process (GP) has been widely applied in probabilistic forecasting (Li et al., 2022a). A typical GP defines distribution over functions such that, if we pick any two or more points in a function, the observations of the outputs follow a joint multivariate Gaussian distribution (Schulz et al., 2018; Wen et al., 2022). In general, a Gaussian process states that in a multivariate dataset, any finite number of variables follows a joint Gaussian distribution.

In a regression type of a problem, a GP combined with a Gaussian likelihood generates a posterior GP over the model output. With a given input $\mathbf{x}$, and output $y$ of a function $f\left(\right)$, a GP model can be written as (1):

$\mathbf{y}=f\left(\mathbf{x}\right)+\mathit{ϵ}(1)$

where $f\left(\mathbf{x}\right)$ is the latent variable; $\mathcal{E}$ follows $\mathcal{E}\sim \mathcal{E}(0,{\sigma }_{\mathit{ϵ}}^2)$ and ${\sigma }_{\mathit{ϵ}}^2$ is the variance of the noise. Here, epistemic uncertainty is caused by the limited representation capability of displacements. Thus, we can specify the distribution of latent variable $\mathbf{f}=f\left(\mathbf{x}\right)$ as $\mathbf{f}\sim \mathcal{E}(0,C(\mathbf{x},\mathbf{x}))$ where $C\left(\right)$ is the covariance function.

In the GP, suppose $\widehat{{\mathbf{y}}_{\mathit{i}}}$ is the predicted value for a new input ${\mathbf{x}}_i$, the combination of $\mathbf{f}$ and $\widehat{{\mathbf{y}}_i}$ should follow a joint Gaussian distribution expressed as (2):

$p\left(\mathbf{f},\widehat{{\mathbf{y}}_i}\right)=\mathcal{N}\left(\left[\begin{array}{c}\mathbf{0}\\ 0\end{array}\right],\left[\begin{array}{cc}\mathit{C}& {\mathit{C}}_{\mathit{\ast }}\\ {\mathit{C}}_{\mathit{\ast }}^{\mathit{T}}& \tilde{\mathit{C}}\end{array}\right]\right)(2)$

where $\mathit{C} = C(\mathbf{x},\mathbf{x})$; ${\mathit{C}}_{\mathit{*}}=\mathit{C}({\mathbf{x}}_i,\mathbf{x})$; and $\tilde{\mathit{C}}=C({\mathbf{x}}_i,{\mathbf{x}}_i)$. According to Bayesian inference, the posterior distribution of the target prediction $\widehat{{\mathbf{y}}_i}$ conditioned on the training set $\mathbf{y}$ is expressed as (3)–(5).

$p\left(\widehat{{\mathbf{y}}_i}\text{|}\mathbf{y}\right)=\mathcal{N}\left({\mu }_{\ast },{\sigma }_{\ast }^2\right)(3)$

${\mu }_{\ast }={\mathit{C}}_{\mathit{\ast }}{\mathit{K}}^{-1}\mathbf{y}(4)$

${\sigma }_{\ast }^2=\tilde{\mathit{C}}-{\mathit{C}}_{\mathit{\ast }}^{\mathit{T}}{\mathit{K}}^{-1}{\mathit{C}}_{\mathit{\ast }}(5)$

where $\mathit{K} = \mathit{C}+{\sigma }_{\mathit{ϵ}}^2{\mathit{I}}_n$ and ${\mathit{I}}_n$ denotes the identity matrix of $n\times n$.

2.2 Sparse Approximation of the Gaussian Process

In practice, with a higher-dimensional dataset, the GP often faces the challenge of high computational cost (Li, 2022b). Sparse approximation offers a reliable solution to overcome the computational limitations of the GP model. Here, the principle behind sparse approximation is using a subset of the dataset to train the GP model. Within the SGP, the selection of the subset is performed repeatedly using greedy algorithms.

The scheme of GP approximation using a subset m of GP regression models with n data points can be achieved using (6)–(7):

$f_{SR}\left({\mathbf{x}}_i\right)={\displaystyle \sum }_{j=1}^m{\text{α}}_{j}C\left({\mathbf{x}}_i,\mathbf{x}\right)(6)$

${\mathbf{\alpha }}_{\mathit{m}}\sim \mathcal{N}(\mathbf{0},{\mathit{K}}_{\mathit{mm}}^{-1})(7)$

where the associated mean and variance of $f_{SR}\left({\mathbf{x}}_i\right)$ can be obtained using (8)–(9):

${\mu }_{SR}\left(f_{SR}\left({\mathbf{x}}_i\right)\right)={\mathit{C}}_{\mathit{m}}^{\mathit{T}}\left({\mathbf{x}}_i\right){\left({\mathit{C}}_{\mathit{mn}}{\mathit{C}}_{\mathit{nm}}+{\sigma }_n^2{\mathit{C}}_{\mathit{mm}}\right)}^{-1}{\mathit{C}}_{\mathit{mn}}\mathbf{y}(8)$

${\sigma }_{SR}\left(f_{SR}\left({\mathbf{x}}_i\right)\right)={\sigma }_n^2{\mathit{C}}_{\mathit{m}}^{\mathit{T}}\left({\mathbf{x}}_i\right){\left({\mathit{C}}_{\mathit{mn}}{\mathit{C}}_{\mathit{nm}}+{\sigma }_n^2{\mathit{C}}_{\mathit{mm}}\right)}^{-1}{\mathit{C}}_{\mathit{m}}\left({\mathbf{x}}_i\right)(9)$

and the posterior mean of ${\mathbf{\alpha }}_{\mathit{m}}$ can be computed by (10):

${\mathbf{\alpha }}_{\mathit{m}}={\left({\mathit{C}}_{\mathit{mn}}{\mathit{C}}_{\mathit{nm}}+{\sigma }_n^2{\mathit{C}}_{\mathit{mm}}\right)}^{-1}{\mathit{C}}_{\mathit{mn}}\mathbf{y}(10)$

2.3 Objective Function

To train the SGP model, a covariance function must be selected to define the similarity of any two sets of input points, giving rise to the covariance matrix. A popular selection of the covariance function is the squared exponential (SE) function, which is written by (11):

$C\left(x_i,x_j\right)={\eta }^{2}exp\left[-\frac{1}{2}{\displaystyle \sum }_{k=1}^d{\left(\frac{x_i-x_j}{l_k}\right)}^2\right](11)$

where ${\eta }^2$ is the signal variance, and $l$ is the characteristic length scale. Thus, to estimate the parameters $\mathbf{\Theta }=\left\{\eta ,l\right\}$, the objective function of SGP is to maximize the likelihood function expressed in (12):

$\mathbf{ℒ}\left(\mathbf{\Theta }\right)=\frac{1}{2}{\mathbf{y}}^{\mathit{T}}{\mathit{K}}^{-1}\mathbf{y}+\frac{1}{2}\mathbf{log}\left|\mathit{K}\right|+\frac{n}{2}\mathbf{log}\left|\mathbf{2}\mathit{\pi }\right|(12)$

2.4 State-Of-The-Art Probabilistic Forecasting Models

To demonstrate the outperformance of the proposed probabilistic forecasting approach using SGP, three popular state-of-the-art approaches were selected to perform a comparative analysis, including the quantile regression gradient boosting machine (QRGBM), the kernel density estimation (KDE), and the k-nearest neighbor (KNN). These state-of-the-art approaches are presented below.

QRGBM is a meta-algorithm technique that combines an ensemble of weak regression trees as a weighted sum to reduce both bias and variance (Landry et al., 2016). Similar to the traditional gradient boosting tree, it combines the advantages of both the regression and gradient boosting algorithms, which enables it to model complex nonlinear relationships that may include interactions among predictors.

KDE is a classic nonparametric estimation method used in a wide variety of probabilistic forecasting tasks (Botev et al., 2010; Kim & Scott 2012). It does not require a priori assumption that the data should follow a certain distribution, which is the key difference between the KDE and other parametric approaches.

KNN is a probabilistic forecasting approach that computes the probability distribution of the mean multiple nearest neighbors (Keller et al., 1985; Abu Alfeilat et al., 2019). The main advantage of KNN is that it does not assume the smoothness of the functions in forecasting tasks. It has been widely applied as a state-of-the-art forecasting algorithm in various engineering applications.

2.5 Measurement Metrics

To assess the quality of the tested algorithms in terms of probabilistic forecasting of landslide instant displacement, the evaluation metric namely Continuous Ranked Probability Score (CRPS) was utilized in this study. The CRPS was designed to quantify the difference between a continuous forecasted probability distribution (i.e., prediction) and a deterministic observation value (i.e., the ground truth value). The CRPS can be computed using (13)–(14) (Ton et al., 2018):

$\widehat{F}\left(y_i\right)=\underset{-\infty }{\overset{y_i}{{\displaystyle \int }}}p\left(\widehat{y_i}|x_i\right)d{x}_i(13)$

$H\left(y_i-\widehat{y_i}\right)=\{\begin{array}{cc}1& \mathrm{if}{y}_i\ge \widehat{y_i}\\ 0& otherwise\end{array}(14)$

where $x_i$ represents the input data, $y_i$ is the actual value of the ground truth, $\widehat{y_i}$ is the predicted mean value, $\widehat{F}\left(y_i\right)$ represents the cumulative density function (CDF) of the $\widehat{y_i}$; and $H\left(\right)$ denotes the binary step function with the observed sample at the step point. We can then compute the CRPS using (15) as follows:

$CRPS=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\underset{-\infty }{\overset{+\infty }{{\displaystyle \int }}}{\left[\widehat{F}\left(y_i\right)-H\left(y_i-\widehat{y_i}\right)\right]}^{2}d{y}_i(15)$

where $N$ represents total number of data points in the test dataset.

3 Dataset Collection

In this study, time-series displacement data were collected from our case study area, in southwest China. The case study area had landslide occurrences with a wide spatial distribution (Cui et al., 2021). The main material on the case study area slope were enormous deposits of silty clay and fragmented rubble, which are often loose and chaotic. The underlying bedrock of the case study landslide consisted of siltstones and mudstones. The major triggering factors of the landslide were heavy rainfall.

To obtain the displacement data, global positioning system (GPS) technology was used to monitor the landslides surface displacement, which is a useful and straightforward method for landslide evolution analysis. The GPS points recorded the cumulative displacement of the target landslide. In this study, a total of six GPS points were configured on the slide slope since the first reported initiation of slope failure. Continuous monitoring of the cumulative displacement was then conducted using the GPS points. The locations of the GPS points were relatively stable, enabling continuous and reliable acquisition of displacement data in the temporal domain. The six GPS points are shown in Figure 1.

FIGURE 1

FIGURE 1. Cracks measured by the GPS points on the front part of the slope.

As shown in Figure 1, the datasets contain multiple GPS time-series data monitoring the landslide deformation process. Within the figure, the label LF stands for the cracks measured by the GPS points. The evolution of the crack is the key indicator for quantify the landslide displacement on-site. The datasets display the cumulative displacement since the activation of slope failure. All data were recorded on a monthly basis, and the unit for the points was millimeters. In total, 6 years of data were provided by field experts for training and testing the probabilistic forecasting models.

4 Experimental Results

To achieve accurate probabilistic forecasting of landslide displacement, field data from six single GPS points from the study area were utilized in this study. In total, 6-year monthly data from 2014 to 2019 were considered for training and testing the proposed SGP model. All displacement data were transformed from cumulative displacement into instant displacement, which measures the absolute increment between the two-time stamps. For each GPS point, data collected between 2014 and 2018 were used to train the SGP, and the data collected in 2019 were used as the test dataset.

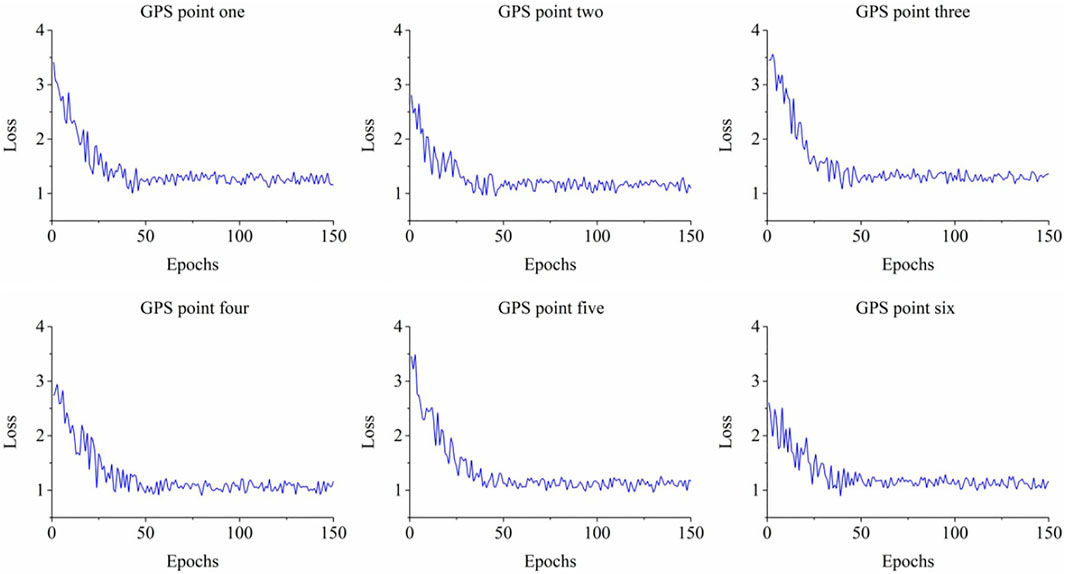
In our experiment, the training epochs for all GPS-collected displacement time series were set to 150. The loss function utilized for training was based on maximum likelihood, as described in Section 2.3. The average training time for all GPS points was 20 s. The average PI production time was less than 1 s. The convergence curves of the loss functions during the training process are shown in Figure 2.

FIGURE 2

FIGURE 2. Convergence curves of loss functions during the training process.

As illustrated in Figure 2, the loss curves of all six GPS monitoring points exhibit similar patterns. The loss function is based on the objective function expressed in (2) in Section 2.3 above. The starting value of the loss function varied depending on the random initialization of the experiment. The loss values converged at approximately 50 epochs on average, and the variance significantly reduced thereafter. This phenomenon confirms the reliability of the SGP in effectively learning patterns from the displacement time series.

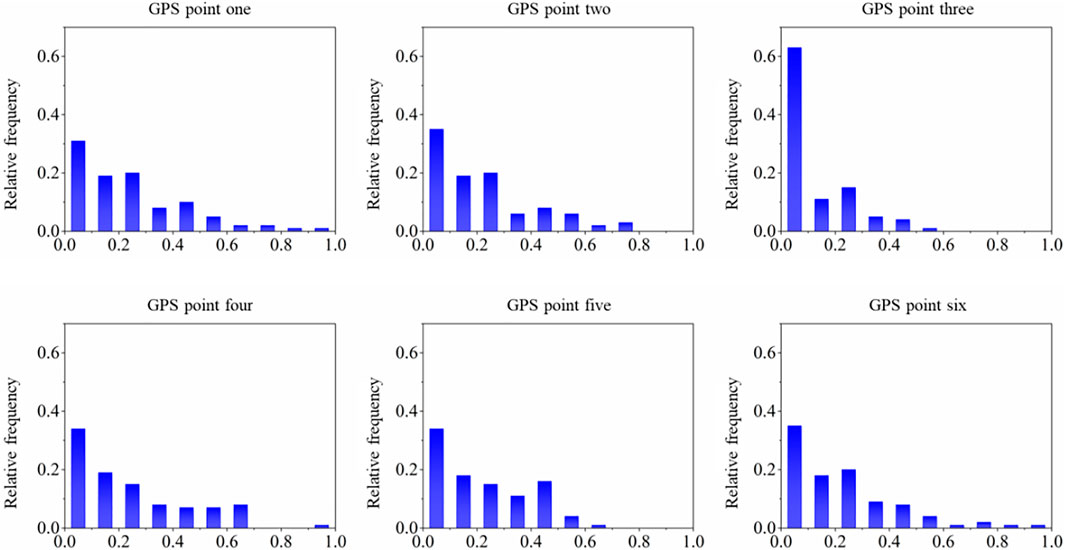
Prior to the performance evaluation of the proposed approach, the heterogeneity and sharpness of the test dataset were investigated. The test dataset contained the instant monthly displacement data collected in 2019. All test data per GPS point were rescaled between 0 and 1 via min-max scaling, and the histograms for the GPS points are presented in Figure 3. The vertical axis represents the scaled frequency and the horizontal axis denotes the scaled instant displacement between 0 and 1. Evidently, all instant displacements followed a right-skewed distribution, which confirms the field experts’ opinion that the majority of the displacements were under the mode of slow motion. However, occasional heavy rainfall or over-irrigation could trigger faster seasonal displacements on the slope over a few months, which contributes to occurrences above the median value.

FIGURE 3

FIGURE 3. Histograms of the scaled test dataset for all GPS points.

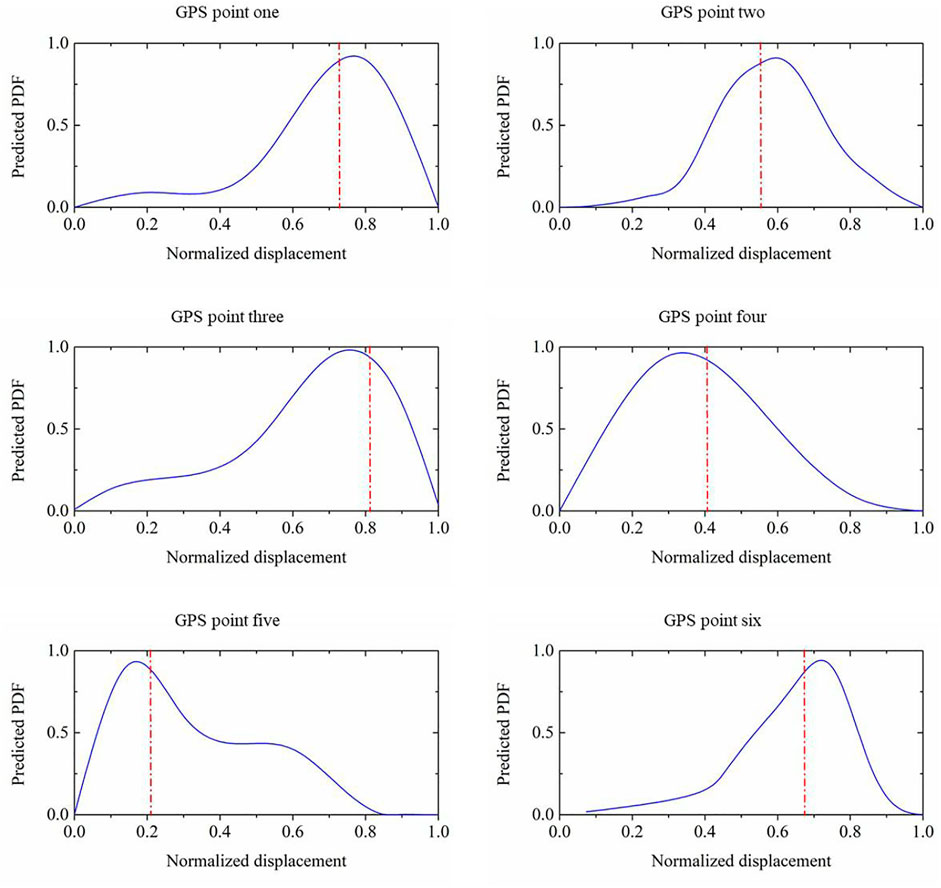
Figure 4 displays the six selected timestamps within the test dataset for each GPS point. The predicted probability density function (PDF) was the probabilistic forecast output generated by the SGP model. The vertical red line denotes the actual scaled value that corresponds to its intersection on the horizontal axis. For GPS points 1, 3, and 6, the selected instant displacement was from the mode of faster seasonal displacement. Correspondingly, the actual value were within the region with a high probability density. For the other three GPS points, the timestamps were selected from the mode of slow displacement. The actual value of the displacement was smaller than the group median value but was still within the region of high probability density. This demonstrates the reliability of SGP in probabilistic forecasting.

FIGURE 4

FIGURE 4. Constructed PIs and actual target instant displacement of the test dataset.

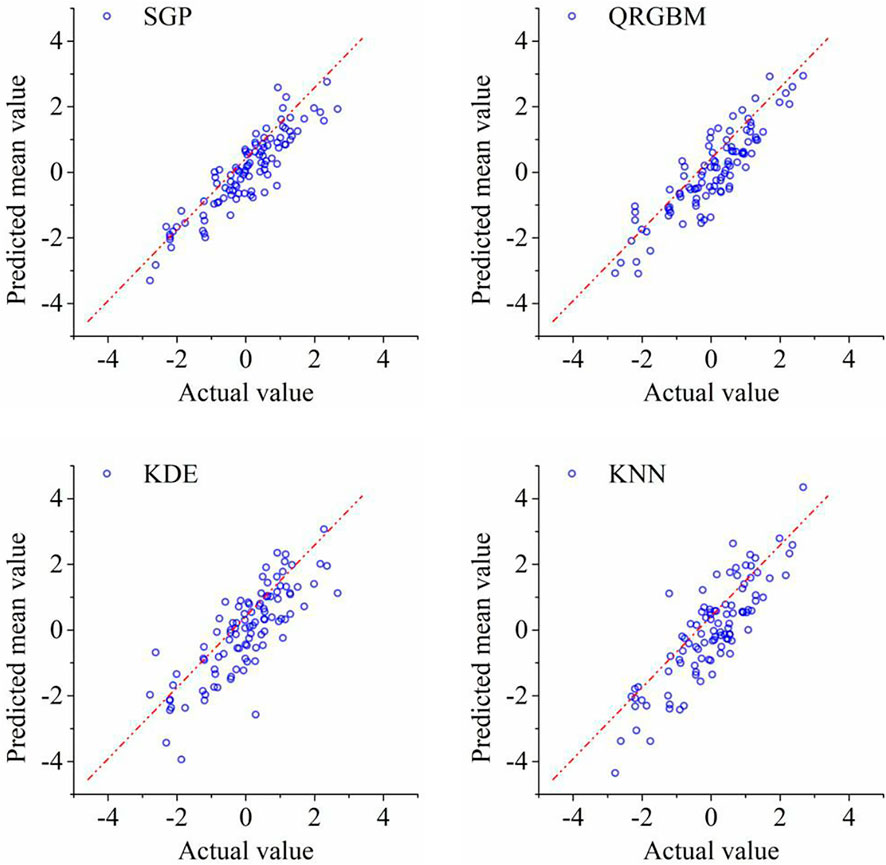
For comparative analysis, we merged all test data collected from the six GPS points and transformed the data into a Gaussian distribution that follows $\mathcal{E}\left(\mathrm{0,1}\right)$. The mean value of the predicted probability distribution per point was considered as the point estimate of the displacement. The mean predicted values generated by all probabilistic prediction algorithms versus the actual measured instant displacement are shown in Figure 5. It is notable that majority of the mean predicted values provided by SGP fall within a narrow band with respect to the diagonal red dashed line, which represents the corresponding actual value. In comparison, more outlier points were generated outside the narrow band provided by the other state-of-the-art algorithms, including, QRGMB, KDE, and KNN. This confirms that the SGP is outstanding in terms of probabilistic forecasting of landslide displacement (see Figure 5).

FIGURE 5

FIGURE 5. Actual value versus predicted mean value for all algorithms tested.

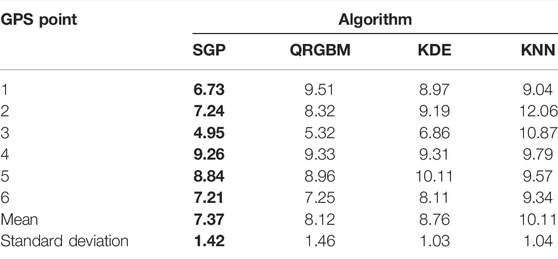
For a quantitative performance comparison, CRPS (see Section 2.5, Eq. 15) was adopted as the measurement metric to evaluate the quality of the estimated probability density. Table 1 presents the CRPS computed by all algorithms tested and in terms of all six GPS points. The proposed SGP model had the smallest CRPS score compared to the other state-of-the-art algorithms, which confirms the superiority of the proposed approach.

TABLE 1

TABLE 1. Summary of CRPS for all probabilistic algorithms tested.

5 Conclusion

In this study, the uncertainties of future landslide displacements were quantified and formulated using Bayesian theory. The sparse Gaussian process was adopted to derive the inducing variable, variational inference, and variational distribution of the future displacement, while significantly reducing the computational cost. Compared with other state-of-the-art probabilistic forecasting models, the proposed SGP approach demonstrated outstanding performance in terms of accuracy, reliability, and computational efficiency. The probabilistic forecasting of future displacement has improved remarkably. The proposed approach can provide practical assistance to field engineering geologists in the hazard estimation of future landslide occurrences.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

WY and LW contributed to the study methodology and wrote the original draft. WY and YF contributed to the study data curation. contributed to data analysis and investigation. JW contributed to conceptualize the study and writing-original draft. All authors have read and agreed to the published version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abu Alfeilat, H. A., Hassanat, A. B. A., Lasassmeh, O., Tarawneh, A. S., Alhasanat, M. B., Eyal Salman, H. S., et al. (2019). Effects of Distance Measure Choice on K-Nearest Neighbor Classifier Performance: a Review. Big data 7 (4), 221–248. doi:10.1089/big.2018.0175

PubMed Abstract | CrossRef Full Text | Google Scholar

Aggarwal, A., Alshehri, M., Kumar, M., Alfarraj, O., Sharma, P., and Pardasani, K. R. (2020). Landslide Data Analysis Using Various Time-Series Forecasting Models. Comput. Electr. Eng. 88, 106858. doi:10.1016/j.compeleceng.2020.106858

CrossRef Full Text | Google Scholar

Botev, Z. I., Grotowski, J. F., and Kroese, D. P. (2010). Kernel Density Estimation via Diffusion. Ann. Statistics 38 (5), 2916–2957. doi:10.1214/10-aos799

CrossRef Full Text | Google Scholar

Cui, S., Pei, X., Jiang, Y., Wang, G., Fan, X., Yang, Q., et al. (2021). Liquefaction within a Bedding Fault: Understanding the Initiation and Movement of the Daguangbao Landslide Triggered by the 2008 Wenchuan Earthquake (Ms = 8.0). Eng. Geol. 295, 106455. doi:10.1016/j.enggeo.2021.106455

CrossRef Full Text | Google Scholar

Deringer, V. L., Bartók, A. P., Bernstein, N., Wilkins, D. M., Ceriotti, M., and Csányi, G. (2021). Gaussian Process Regression for Materials and Molecules. Chem. Rev. 121 (16), 10073–10141. doi:10.1021/acs.chemrev.1c00022

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, Z., and Cai, J. (2021). Effects of Unidirectional In Situ Stress on Crack Propagation of a Jointed Rock Mass Subjected to Stress Wave. Shock Vib. 2021, 1–13. doi:10.1155/2021/5529540

CrossRef Full Text | Google Scholar

Fan, Z., Zhang, J., Xu, H., and Wang, X. (2022). Transmission and Application of a P-Wave across Joints Based on a Modified G-λ Model. Int. J. Rock Mech. Min. Sci. 150, 104991. doi:10.1016/j.ijrmms.2021.104991

CrossRef Full Text | Google Scholar

Fuhg, J. N., Marino, M., and Bouklas, N. (2022). Local Approximate Gaussian Process Regression for Data-Driven Constitutive Models: Development and Comparison with Neural Networks. Comput. Methods Appl. Mech. Eng. 388, 114217. doi:10.1016/j.cma.2021.114217

CrossRef Full Text | Google Scholar

He, Y., and Kusiak, A. (2018). Performance Assessment of Wind Turbines: Data-Derived Quantitative Metrics. IEEE Trans. Sustain. Energy 9 (1), 65–73. doi:10.1109/TSTE.2017.2715061

CrossRef Full Text | Google Scholar

Jamei, M., Ahmadianfar, I., Olumegbon, I. A., Karbasi, M., and Asadi, A. (2021). On the Assessment of Specific Heat Capacity of Nanofluids for Solar Energy Applications: Application of Gaussian Process Regression (GPR) Approach. J. Energy Storage 33, 102067. doi:10.1016/j.est.2020.102067

CrossRef Full Text | Google Scholar

Jiang, Y., Xu, Q., Lu, Z., Luo, H., Liao, L., and Dong, X. (2021). Modelling and Predicting Landslide Displacements and Uncertainties by Multiple Machine-Learning Algorithms: Application to Baishuihe Landslide in Three Gorges Reservoir, China. Geomatics, Nat. Hazards Risk 12 (1), 741–762. doi:10.1080/19475705.2021.1891145

CrossRef Full Text | Google Scholar

Keller, J. M., Gray, M. R., and Givens, J. A. (1985). A Fuzzy K-Nearest Neighbor Algorithm. IEEE Trans. Syst. Man. Cybern. SMC-15 (4), 580–585. doi:10.1109/tsmc.1985.6313426

CrossRef Full Text | Google Scholar

Kim, J., and Scott, C. D. (2012). Robust Kernel Density Estimation. J. Mach. Learn. Res. 13 (1), 2529–2565.

Google Scholar

Landry, M., Erlinger, T. P., Patschke, D., and Varrichio, C. (2016). Probabilistic Gradient Boosting Machines for GEFCom2014 Wind Forecasting. Int. J. Forecast. 32 (3), 1061–1066. doi:10.1016/j.ijforecast.2016.02.002

CrossRef Full Text | Google Scholar

Lewis, R., and Reinsel, G. C. (1985). Prediction of Multivariate Time Series by Autoregressive Model Fitting. J. Multivar. analysis 16 (3), 393–411. doi:10.1016/0047-259x(85)90027-2

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D. K., and Cheng, Q. (2021b). Short-Term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energy Res. 9, 780928. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. D. K. (2021a). Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energy Res. 9, 799039. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Li, H., He, Y., Xu, Q., Deng, j., Li, W., and Wei, Y. (2022). Detection and Segmentation of Loess Landslides via Satellite Images: a Two-phase Framework. Landslides 19, 673–686. doi:10.1007/s10346-021-01789-0

CrossRef Full Text | Google Scholar

Li, H. (2022a). SCADA Data Based Wind Power Interval Prediction Using LUBE-Based Deep Residual Networks. Front. Energy Res. 10, 920837. doi:10.3389/fenrg.2022.920837

CrossRef Full Text | Google Scholar

Li, H. (2022b). Short-term Wind Power Prediction via Spatial Temporal Analysis and Deep Residual Networks. Front. Energy Res. 10, 920407. doi:10.3389/fenrg.2022.920407

CrossRef Full Text | Google Scholar

Li, H., Xu, Q., He, Y., and Deng, J. (2018). Prediction of Landslide Displacement with an Ensemble-Based Extreme Learning Machine and Copula Models. Landslides 15 (10), 2047–2059. doi:10.1007/s10346-018-1020-2

CrossRef Full Text | Google Scholar

Li, H., Xu, Q., He, Y., Fan, X., and Li, S. (2020). Modeling and Predicting Reservoir Landslide Displacement with Deep Belief Network and EWMA Control Charts: a Case Study in Three Gorges Reservoir. Landslides 17 (3), 693–707. doi:10.1007/s10346-019-01312-6

CrossRef Full Text | Google Scholar

Lian, C., Zeng, Z., Yao, W., and Tang, H. (2015). Multiple Neural Networks Switched Prediction for Landslide Displacement. Eng. Geol. 186, 91–99. doi:10.1016/j.enggeo.2014.11.014

CrossRef Full Text | Google Scholar

Liu, Z., Xu, W. Y., and Shao, J. F. (2012). Gauss Process Based Approach for Application on Landslide Displacement Analysis and Prediction. Comput. Model. Eng. Sci. 84 (2), 99–122. doi:10.3970/cmes.2012.084.099

CrossRef Full Text | Google Scholar

Lu, P., and Rosenbaum, M. S. (2003). Artificial Neural Networks and Grey Systems for the Prediction of Slope Stability. Nat. Hazards 30 (3), 383–398. doi:10.1023/b:nhaz.0000007168.00673.27

CrossRef Full Text | Google Scholar

Ma, J., Tang, H., Liu, X., Wen, T., Zhang, J., Tan, Q., et al. (2018). Probabilistic Forecasting of Landslide Displacement Accounting for Epistemic Uncertainty: a Case Study in the Three Gorges Reservoir Area, China. Landslides 15 (6), 1145–1153. doi:10.1007/s10346-017-0941-5

CrossRef Full Text | Google Scholar

Schulz, E., Speekenbrink, M., and Krause, A. (2018). A Tutorial on Gaussian Process Regression: Modelling, Exploring, and Exploiting Functions. J. Math. Psychol. 85, 1–16. doi:10.1016/j.jmp.2018.03.001

CrossRef Full Text | Google Scholar

Tamhidi, A., Kuehn, N., Ghahari, S. F., Rodgers, A. J., Kohler, M. D., Taciroglu, E., et al. (2022). Conditioned Simulation of Ground-Motion Time Series at Uninstrumented Sites Using Gaussian Process Regression. Bull. Seismol. Soc. Am. 112 (1), 331–347. doi:10.1785/0120210054

CrossRef Full Text | Google Scholar

Tang, P., Chen, G.-Q., Huang, R.-Q., and Wang, D. (2021). Effect of the Number of Coplanar Rock Bridges on the Shear Strength and Stability of Slopes with the Same Discontinuity Persistence. Bull. Eng. Geol. Environ. 80 (5), 3675–3691. doi:10.1007/s10064-021-02180-y

CrossRef Full Text | Google Scholar

Tang, P., Chen, G.-Q., Huang, R.-Q., and Zhu, J. (2020). Brittle Failure of Rockslides Linked to the Rock Bridge Length Effect. Landslides 17 (4), 793–803. doi:10.1007/s10346-019-01323-3

CrossRef Full Text | Google Scholar

Ton, J.-F., Flaxman, S., Sejdinovic, D., and Bhatt, S. (2018). Spatial Mapping with Gaussian Processes and Nonstationary Fourier Features. Spat. Stat. 28, 59–78. doi:10.1016/j.spasta.2018.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, H., Ma, J., Gu, J., Yuan, L., and Jin, Z. (2022). Sparse Variational Gaussian Process Based Day-Ahead Probabilistic Wind Power Forecasting. IEEE Trans. Sustain. Energy 13 (2), 957–970. doi:10.1109/tste.2022.3141549

CrossRef Full Text | Google Scholar

West, A., Tsitsimpelis, I., Licata, M., Jazbec, A., Snoj, L., Joyce, M. J., et al. (2021). Use of Gaussian Process Regression for Radiation Mapping of a Nuclear Reactor with a Mobile Robot. Sci. Rep. 11 (1), 1–11. doi:10.1038/s41598-021-93474-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Xing, Y., Yue, J., and Chen, C. (2019). Interval Estimation of Landslide Displacement Prediction Based on Time Series Decomposition and Long Short-Term Memory Network. IEEE Access 8, 3187–3196. doi:10.1109/ACCESS.2019.2961295

CrossRef Full Text | Google Scholar

Xu, Q., Li, H., He, Y., Liu, F., and Peng, D. (2019). Comparison of Data-Driven Models of Loess Landslide Runout Distance Estimation. Bull. Eng. Geol. Environ. 78 (2), 1281–1294. doi:10.1007/s10064-017-1176-3

CrossRef Full Text | Google Scholar

Zhou, J., Wei, J., Yang, T., Zhang, P., Liu, F., and Chen, J. (2021). Seepage Channel Development in the Crown Pillar: Insights from Induced Microseismicity. Int. J. Rock Mech. Min. Sci. 145, 104851. doi:10.1016/j.ijrmms.2021.104851

CrossRef Full Text | Google Scholar

Zhu, X., Xu, Q., Tang, M., Nie, W., Ma, S., and Xu, Z. (2017). Comparison of Two Optimized Machine Learning Models for Predicting Displacement of Rainfall-Induced Landslide: A Case Study in Sichuan Province, China. Eng. Geol. 218, 213–222. doi:10.1016/j.enggeo.2017.01.022

CrossRef Full Text | Google Scholar