A Fast Quality Control of 0.5 Hz Temperature Data in China

Fast quality control (FQC) is important to deal with high-frequency observation records at meteorological station networks in time, and may check whether the records fall within a range of acceptable values. Threshold tests in the previous quality control methods for monthly, daily, or hourly observation data do not work well for 0.5 Hz data at a single station. In this study, we develop an algorithm for the automatic determination of maximum and minimum minute thresholds for 0.5 Hz temperature data in the data collection phase of the newly built stations. The fast threshold test based on the percentile threshold (0.1–99.9%) and standard deviation scheme is able to efficiently identify the incorrect data in the current minute. A visual graph is generated every minute, and the time series of the data records and the thresholds are displayed by the automated graphical procedures. The observations falling outside the thresholds are flagged and then a manual check is performed. This algorithm has the higher efficiency and lower computational requirement in identifying out the obvious outliers of 0.5 Hz data in real or near-real time observation. Meanwhile, this algorithm can also find problems in observation instruments. This method is applied to the quality control of 0.5 Hz data at two Tianjin experiment stations and hourly data at one Shenyang experiment station. The results show that this fast threshold test may be a viable option in the data collection phase. The advantage of this method is that the computation requires less memory and the computational burden is reduced for real or near-real time observations, so it may be extended to test other meteorological variables measured by high-frequency measurement systems.

Introduction

Observation data at meteorological surface stations are important to understanding weather and climate features and their evolutions, and to carry out meteorological services (Chen et al., 2011), scientific research, meteorological forecast, etc., (Xu et al., 2013). With the progress of meteorological observation technology, the observation accuracy and frequency of meteorological elements are increasing. The upload frequency of meteorological observation data ranges from once an hour to once a minute, and even reaches several times per second. This high-frequency sampling results in a large number of observation records with an increase of newly built stations. To ensure the completeness and accuracy of the observation records, their quality has to be checked (Ren et al., 2005; Hasu and Aaltonen, 2011). In addition, it is also important to develop a quality control (QC) procedure for the high-frequency original observation records (Houchi et al., 2015) in some specific situations. The major goal of QC is to identify incorrect data among the original observations. In QC techniques, thresholds are used for the identification of the abnormal records (Ren et al., 2005; Hasu and Aaltonen, 2011). The QC procedures for the current Automatic Surface Weather Observation System (AWS) include the station information check, the missing value and eigenvalue check, the climate extreme value behavior check, the climatological threshold check, the time consistency check, the spatial consistency check, and the interior consistency check among different variables (such as hourly, daily, monthly, and yearly temperature, humidity, pressure, wind direction and speed, and precipitation records) (e.g., Ren et al., 2005; Ren et al., 2007; Ren and Xiong, 2007; Wan et al., 2007; Wang et al., 2007; Tao et al., 2009; Jiménez et al., 2010; Wang and Liu, 2012; Xu et al., 2012; Roh et al., 2013; Houchi et al., 2015; Ren et al., 2015; Cheng et al., 2016; Kuriqi, 2016; Qi et al., 2016; Lopez et al., 2017; Ditthakit et al., 2021). These QC procedures can efficiently identify incorrect records.

Many studies have discussed QC techniques for meteorological observation data (e.g., Shafer et al., 2000; Fiebrich and Crawford, 2001; Qin et al., 2010; Liu et al., 2014; Oh et al., 2015; Xiong et al., 2017a; Xiong et al., 2017b; Ye et al., 2020). For example, one of the basic QC tests is to check whether the observational records fall within a range of acceptable values. This test proposes an algorithm for the automatic determination of daily maximum and minimum thresholds for new observations (Hasu and Aaltonen, 2011; Wang et al., 2014). Some studies used monthly threshold values that are determined on the basis of 30 years of climatic data (Hubbard et al., 2005; Hubbard and You, 2005; Hubbard et al., 2007). Thresholds and step change criteria were designed for the review of single-station data to detect potential outliers (Houchi et al., 2015). Xu et al. (2013) divided the national stations into eight parts according to the geographic and climatic characteristics, and proposed a QC method based on the extreme value, temporal consistency, and spatial consistency checks for surface pressure and temperature data at newly meteorological stations.

The above methods can identify outliers in the observations, paving the way for developing QC methods of high-frequency data (Vickers and Mahrt, 1997; Zhang et al., 2010; Li et al., 2012; Lin et al., 2017; Ntsangwane et al., 2019; Cerlini et al., 2020). The threshold methods are work by flagging suspicious observation values for further inspection. In addition, the flagged details have been discussed and the QC classes have been described (Vejen et al., 2002). Most of previous studies are focused on threshold methods on hourly or multiple time scales (Ye et al., 2020). However, a uniform QC method for high-frequency raw records is impractical (Hasu and Aaltonen, 2011), and also difficult. The threshold methods require more computation or depend on the observation record length. The high-frequency sampling (minutes or 0.5 Hz) data at a new station (with a short time series) are not easy to apply accurately for the current QC operation. Because of the large uncertainties of estimation related to the small samples (Hasu and Aaltonen, 2011; Ye et al., 2020), these QC methods cannot identify false records rapidly and well. Hence, it is necessary to develop an efficient method for the high-frequency observation data at some stations with short records for initial inspection of the data collection phase before the data are transmitted to the central server.

In recent years, some high-frequency observation stations have been established in China. Due to the cumulative amount of the acquired data, we need to develop a new QC method for the high-frequency data in advance and to find a simple and easily method which can rapidly isolate and flag outliers in the data collection phase before the data are transmitted to the central server and are checked with a strict QC operational procedure. This study proposes a simple and fast QC (FQC) algorithm to calculate maximum and minimum thresholds for short-time raw high-frequency (0.5 Hz) records gathered from newly meteorological stations. This algorithm has the higher efficiency in identifying outliers and isolating the maximal unrealistic instrumental records. Moreover, this algorithm offers a lower computational requirement and a graphical display. Thus the study’s novelty is that we demonstrate the effectiveness and feasibility of this algorithm in rapidly detecting and flagging outliers and instrumental problems for 0.5 Hz real or near-real time observations data. This algorithm may be used in the data collection phase before the data enters into the QC system and in these data processed locally on a remote data logger of an automatic and power-limited station.

This article is organized as follows. The details of the algorithm are given in Materials and Methods section. The application examples of the algorithm using the data at three newly built experiment stations and hourly data at one experiment station are given in Results section. Discussions and Conclusions section are given in the end. The appendix table is given in the end of the text (Table A1).

Materials and Methods

Data

We utilize surface (2-m) air temperature (SAT) raw observation records with a temporal resolution of 2 s at newly-built Shenyang experiment station (SA) and two Tianjin experiment stations (TA and TB) from 30 April to 29 May 2016 (when the data is continuous) (Table 1). These stations were in operation for a few months in 2016, and the raw data were collected for 1–2 months during the test. SA is the single surface meteorological operational station and has no information available about the neighboring stations for reference; and TA and TB are independent test sites, with a distance of approximately 10 km. The long-term (2002–2018) hourly SAT observation data at Shenyang station (with the station number 54342; SB) come from the National Meteorological Information Centre (NMIC), referred to as hourly data from surface meteorological stations (SMS) in China. Table 1 shows the related information. All 0.5 Hz observations are the original observation experimental data and have not been processed by standard QC systems at NMIC, but these data have subjected to a manual data integrity check and an extreme value check by using hourly climatic extremes based on the neighboring national climatological station. The hourly temperature data at Shenyang station have been checked with a strict QC operational procedure at NMIC, that is, they are reliable, and are used to evaluate the QC method developed in this study.

TABLE 1

TABLE 1. The temperature records at Shenyang and Tianjin stations.

Description of the Fast Threshold Method

For 0.5 Hz data at Shenyang and Tianjin experiment stations, we develop a QC method, that is, the fast threshold test method on the basis of the percentile threshold technique (e.g., Hasu and Aaltonen, 2011; Bonsal et al., 2001; Zhai and Pan, 2003) and the standard deviation at a given bin for a given moving time displacement interval (an updated threshold interval) (e.g., Houchi et al., 2015; Vickers and Mahrt, 1997; Zhang et al., 2010; Li et al., 2012). In this method, the maximum and minimum thresholds are used as the upper and lower limits of the test criteria at a given bin of the high-frequency records, respectively, and are calculated by tracking the time series of data in each bin. On the basis of the following two assumptions. One is that the descriptive statistics such as mean, standard deviation, and so on are possible to estimate at the given bin, and another is that the values are changing in time, the maximum and minimum thresholds can be calculated and cannot be the same, which enables a temporal averaging in the statistic determination (Hasu and Aaltonen, 2011).The maximum and minimum thresholds are calculated as follows.

$x_{imax}=x_m+a\sigma , a=\mathrm{0,1,2,3},\dots (1)$

$x_{imin}=x_{n-m}-a\sigma , a=\mathrm{0,1,2,3},\dots (2)$

$x_{imax}\ge x_i\ge x_{i\mathit{min}},(3)$

$\text{σ}=\sqrt{\frac{{{\displaystyle \sum }}_{i-1}^n\left(x_i-\overline{x}\right)}{n},}(4)$

$p=\frac{m-0.31}{n+0.38},(5)$

where $x_{imax}$ and $x_{imin}$ are the upper and the lower limits, respectively; $\sigma$ is the standard deviation; $\overline{x}$ is the mean value; $a$ is the magnification coefficient ($a=\mathrm{0,1,2,3},\dots$). In this study, $a$ is set to 1. $p$ is the given percentage; $n$ is the number of samples in a bin; 0.5 Hz temperature data for each bin is first ranked in ascending order $x_1, x_2, \dots ,x_n$; $m$ is the record number within the sample size $n$; $x_m$, $x_{n-m}$ are the initial values of the upper and the lower limits that are specified by percentile ranks $p$ (Bonsal et al., 2001; Li et al., 2008); and the probability $p$ that a random value is less than or equal to the rank of $x_m$ is estimated by Eq. 5. The percentile value is defined through a linear interpolation between the closest ranks (Houchi et al., 2015). For example, if a bin contains 900 values, the temperature representing the 99.9th percentile is linearly interpolated between the 900th-ranked value ($x_{900}$ , $p$ = 99.9234%) and the 899th-ranked value ($x_{899}$ , $p$ = 99.8123%). In Eq. 3, $x_i$ is accepted when the value falls within a range from $x_{imax}$ to $x_{imin}$; otherwise, $x_i$ will be classified as “flagged” data and flags will be assigned to records (Højstrup, 1993; Vickers and Mahrt, 1997). Meanwhile, the visual inspection will be displayed on a PC device simultaneously and the flagging data will further enter into a manual check. The reason for choosing Eq. 5 to estimate the percentiles (as opposed to fitting a statistical distribution such as gamma) include simplicity, as well as avoiding any assumptions of the underlying distribution (Jenkinson, 1977; Bonsal et al., 2001; Zhai and Pan, 2003).

The threshold values ($x_{imax}$ and $x_{imin}$) should be designed strictly, and the potential instrument problems or outliers will be highlighted during the visual inspection. In this study, we use the small and large percentages for the minimum and maximum thresholds respectively, when the observation history is short (Hasu and Aaltonen, 2011). The percentile levels (0.1–99.9%) are sufficient to remove the most unrealistic outliers from the statistics in the short-term observations (Houchi et al., 2015); and here the threshold values are defined as the 0.1th ($p$ = 0.1%) or the 99.9th ($p$ = 99.9%) percentile values minus (plus) 1.0 standard deviation ($a=1$) within a given bin. Considering the experiment observation history length used in this study, the bin size may be modified and adapted to obtain the desired amount of data in each bin for QC statistics at stations in a given time period. The threshold values are statistically dependent on both the data volume in each bin and the width of the percentiles (Houchi et al., 2015). Therefore, we test the sensitivity of the bin size in the range of 24 to 90 min.

It should be noted that the last step in our QC method is a manual check (that is, a visual inspection). The visual inspection of the raw data and the “flagged” records by the automated graphical procedures aims to identify an instrumental recording problem or a plausible physical behavior and may assess the accuracy of the flagging variable with simultaneously measurement from other instruments (Vickers and Mahrt, 1997). Moreover, the “flagged” records will be removed from the bin; otherwise, we do not update the subsequent thresholds (Hasu and Aaltonen, 2011). This is to make sure that false values do not affect the subsequent bin. The raw high-frequency sampling data at Shenyang and Tianjin experiment stations are used to verify the feasibility of the fast threshold test method, and the results may further reflect the accuracy of the instrument in the data collection phase. The fast threshold test method has a lower computational requirement that minimizes the rejection of physically real behavior and isolates the maximum unrealistic instrumental records in the data collection phase (Vickers and Mahrt, 1997; Wang et al., 2014). It reflects the efficiency of this method in the operation and resource occupancy.

In the following application of the fast threshold test method, we do not discuss the flagging rates in detail because of the lack of QC information, and we consider these data (after the manual data integrity check and the extreme value check) as “truth values”. Our purpose is to examine the functionality of the algorithm, to verify the feasibility of the combination scheme (Table 2) to newly built stations, to compare the operation efficiency of the different combination schemes, and to find out which combination scheme has smaller amounts of flagged data than others.

TABLE 2

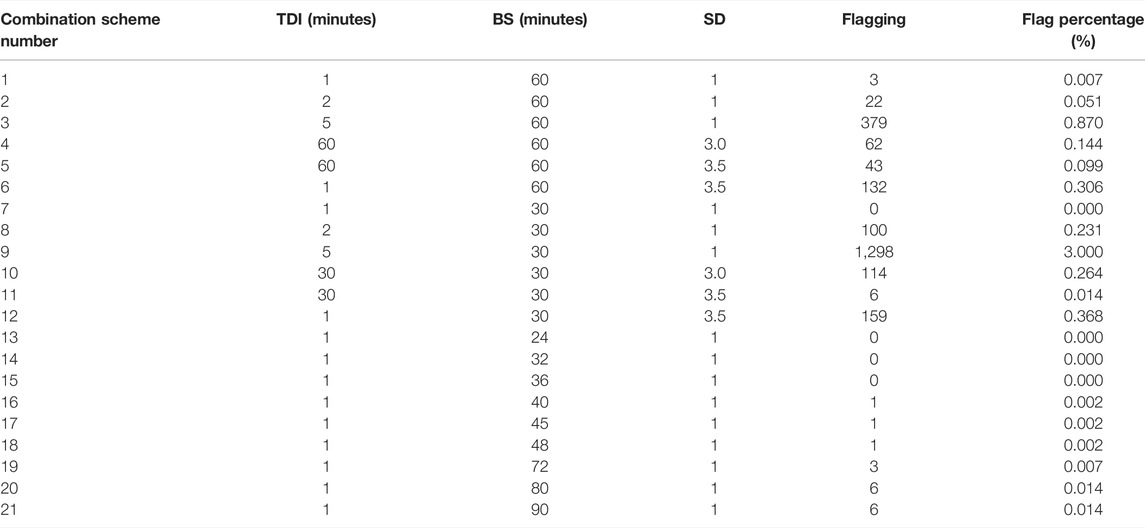
TABLE 2. The results of threshold tests at different bins and time displacement for raw temperature data at SA on 29 April 2016, in which TDI is for a time displacement interval (minutes), BS is for a bin size (minutes), and SD is for standard deviation.

Results

Test Examples

In this section, the fast threshold test is applied to the QC of both 0.5 Hz temperature data at three experiment stations and hourly data at one experiment station. The main results are shown as follow.

The Fast Threshold Test for 0.5 Hz Data

0.5 Hz observations are gathered at SA station from 29 April to 30 May 2016. The updated thresholds can be derived from the following tests, in which the number of data in each bin is determined by the given percentage ($p=99.9\%,n=690$/23 min). On the other hand, the adopted bin size is divided by 1,440 min with no remainder (that is, BS ≥ 24 min). Hence, the bin size may be modified and adapted to obtain the desired data amount in each bin for the FQC statistics, and the combination schemes are easy to be computed at SA station in a given period. Here, we test it in the range of 24 min (30 × 24 = 720 values; $x_{720}$ corresponds to $p$ = 99.9042%) to 90 min (30 × 90 = 2,700 values; $x_{2698}$ corresponds to $p$ = 99.9004%). In our tests, we obtain the maximum and minimum thresholds from 15 combination schemes. In addition, we adopt the threshold check schemes used in the previous studies based on 3 or 3.5 standard deviations and the mean value method to compute the thresholds for six combination schemes (Zhang et al., 2010; Li et al., 2012). On the basis of the flagged values, we finally choose the optimal combination scheme for further tests. The results are given in Table 2.

As shown in Table 2, the average flagging percentage of thresholds is 0.257%, which is significantly higher than the statistical expectation of 0.1% per threshold. The average flagging percentage of our method is 0.280%. At a 60-min bin size, scheme 3 has 0.870% of the maximum values. At a 30 min bin size, scheme 9 has 3.000% of the maximum values flagged. Scheme 8 has 0.231% of the maximum values flagged. On the contrary, schemes 1, 2, and 7 have 0.007, 0.051, and 0.000% of the corresponded maximum values flagged at 30 or 60 min bin sizes, respectively, schemes 13–15 have the same of the maximum values flagged as scheme 7, and the flagging percentages of schemes 13–21 are lower than the statistical expectation of 0.1% per threshold. The above results indicate that the thresholds derived from these schemes (e.g., scheme 3, scheme 9, etc.) are not updated frequently enough for 0.5 Hz data, i.e., the thresholds have not fully covered the time series, and thus more frequent updates are required. The results may be avoided by using a shorter given time displacement interval for the estimated thresholds. Accordingly, schemes 1, 7, 13–19 may update the thresholds more frequently, and the flagging percentages reach the minimal in all schemes. In contrast, when we apply the threshold test method in the previous studies, the average flagging percentage of thresholds is 0.199%. Scheme 5 has 0.099% of the maximum values flagged at a 60 min size, and scheme 11 has 0.014% of the maximum values flagged at a 30 min bin size. Compared to the result of our method, the difference in the flagging percentage is −0.092% between schemes 1 and 5 and is −0.014% between schemes 7, 13–15 and 11. It is evident that the flagging percentages of the new method are significantly lower than those of the previous threshold test method.

The selected scheme needs to provide easy and continuous computation and a graphical display conveniently when available, requires less memory, and can reduce the computational burden of the computer system. A further analysis shows that scheme 1 requires 1800 (30 × 60) values, scheme 7 requires 900 (30 × 30) values, scheme 13 requires 720 (30 × 24) values, scheme 14 requires 960 (30 × 32) values, scheme 15 requires 1,080 (30 × 36) values, scheme 16 requires 1,200 (30 × 40) values, scheme 17 requires 1,350 (30 × 45) values, scheme 18 requires 1,440 (30 × 48) values, and scheme 19 requires 2,160 (30 × 72) values for each given bin. These schemes have the same time displacement interval. The result indicates that the flagging percentages are 0–0.007% for schemes 1, 7, 13–19, and that there is only small differences between them. The memory savings are significant and the computational efficiency is higher for the computer system for schemes 7 and 13. Since the 30 min bin size is more conducive to make a calculation, and scheme 7 is selected in the subsequent tests.

Figure 1 shows a comparison of the thresholds test results between scheme 7 (Figure 1A) and scheme 11 (Figure 1B) at the same given bin. When temperature drops from 19 to 15°C within 15 min at 2–3 pm local time, scheme 7 has no flagging, but scheme 11 has six flagging. Then, which scheme is correct? The minutes-level precipitation this day are further investigated (figure not shown). We find that there is 0.1 mm precipitation at 2:57 pm local time (BJT). This temperature falling is likely caused by the occurrence of precipitation. Hence, scheme 7 avoids unnecessary false error flagging that is, type I flagging errors. Thus we may preliminarily judge that the temperature falling is a plausible physical behavior. On the other hand, the thresholds derived from scheme 11 are not updated frequently enough for 0.5 Hz data, so the thresholds have not covered the full time range at 3 pm local time.

FIGURE 1

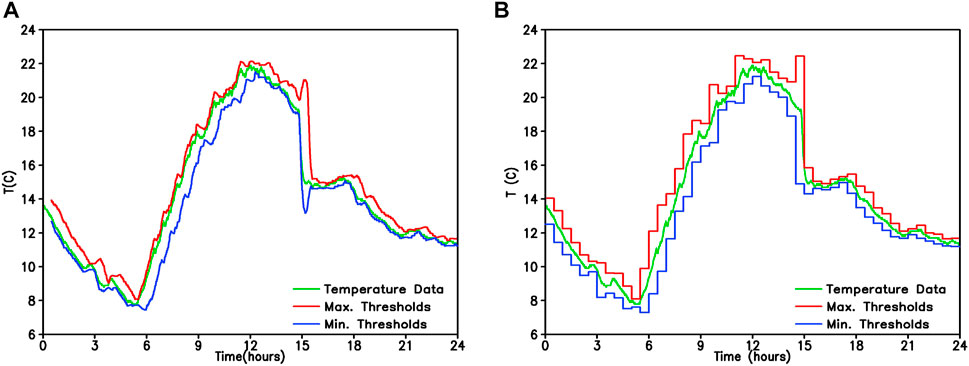
FIGURE 1. The fast threshold test results for raw temperature data at SA station on 29 April 2016 (Unit: °C). (A) Scheme 7; and (B) scheme 11 (The 0.5 Hz temperature data (green line); the upper limits per minute (the maximum thresholds, red line); and the lower limits per minute (the minimum thresholds, blue line)).

To investigate whether the bin size affects the feasibility of the fast threshold test, we adopt schemes 7 and 11 to inspect 0.5 Hz data from 30 April to 29 May 2016. Figure 2 shows the difference between the maximum/minimum threshold and the temperature based on the above two schemes. In Table 3, it is seen that the flagging percentage of thresholds is 0.000% for scheme 7 and is 0.054% for scheme 11. In Figure 2A and Table 3, no value (red line or blue line) goes through zero for scheme 7, and there are 703 values (red line or blue line) going through zero for scheme 11. After examing the minutes-level precipitation data (figure not shown), it is seen that most of the 703 flagging data are likely caused by precipitation. The other reasons need further investigation. We may also preliminarily judge that the temperature change is a plausible physical behavior. These threshold test examples show the advantages of this new algorithm, and the thresholds are statistically meaningful (Hasu and Aaltonen, 2011).

FIGURE 2

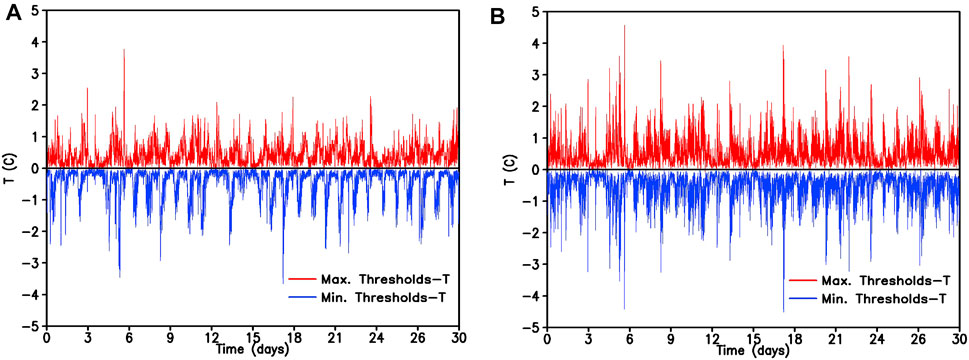
FIGURE 2. The difference between the maximum/minimum threshold and the temperature at SA station from 30 April to 29 May 2016 (Unit: °C), in which the maximum thresholds minus 0.5 Hz temperature (red line) and 0.5 Hz temperature minus the minimum thresholds (blue line).(A) Scheme 7; and (B) scheme 11.

TABLE 3

TABLE 3. The results of the fast threshold test method for raw temperature data at SA station from 30 April to 29 May 2016, in which TDI is for a time displacement interval (minutes), BS is for a bin size (minutes), and SD is for standard deviation.

Furthermore, we randomly change three values beyond the threshold for the time series in 30 days (from 30 April to 29 May 2016), and use scheme 7 to inspect them. As shown in Figures 3A–C, this scheme can flag the three artificial outliers exactly in the raw data series from the observations in the 30 day period. The flagging data exceed the thresholds at 1 May (Figure 3A), 9 May (Figure 3B), and 26 May (Figure 3C) 2016, respectively, and the visual inspection may further assess the accuracy of the flagging variable.

FIGURE 3

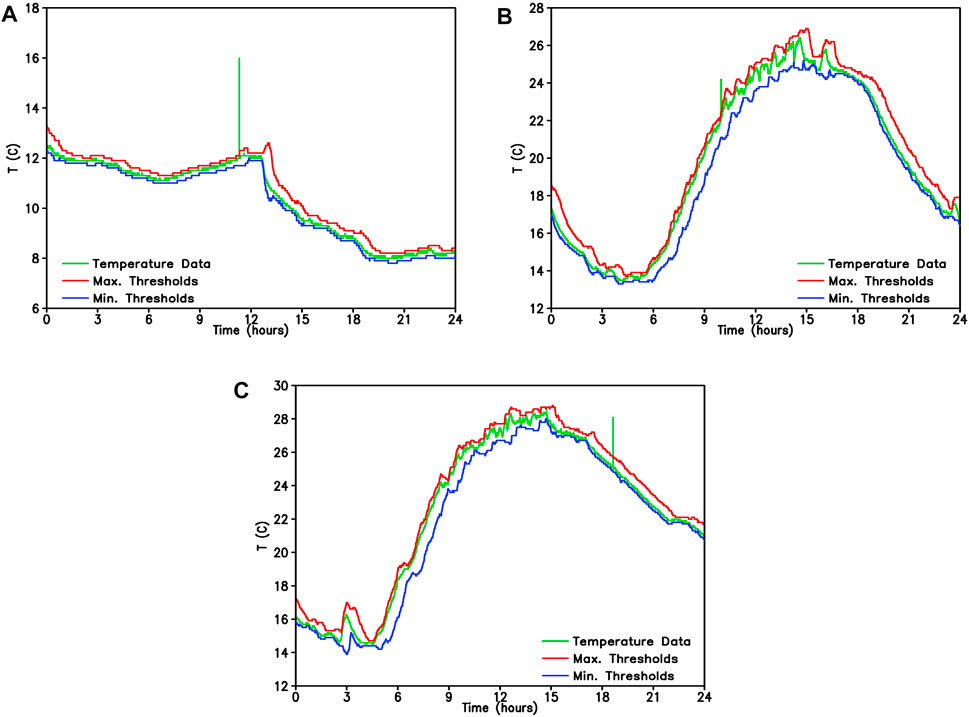
FIGURE 3. Same as in Figure 1, but for scheme 7 (Unit: °C) at SA station on 1 May, 9 May, and 26 May, 2016.

To investigate whether the fast threshold test method can be applied to the data at different stations, we use scheme 7 to inspect the 30 days data (from 30 April to 29 May 2016) at TA station. As a reference, we inspect the data at the neighboring TB station at the same time. It is seen from Figures 4A,B that the data at both stations pass the QC inspection, there is no value (red or blue line) going through zero when adopting scheme 7 at TA station as well as at TB station, which implies the suitability of the fast threshold test method at different stations. Scheme 7 verifies the feasibility of the fast threshold test method at these new stations, which demonstrates the efficiency of the QC scheme.

FIGURE 4

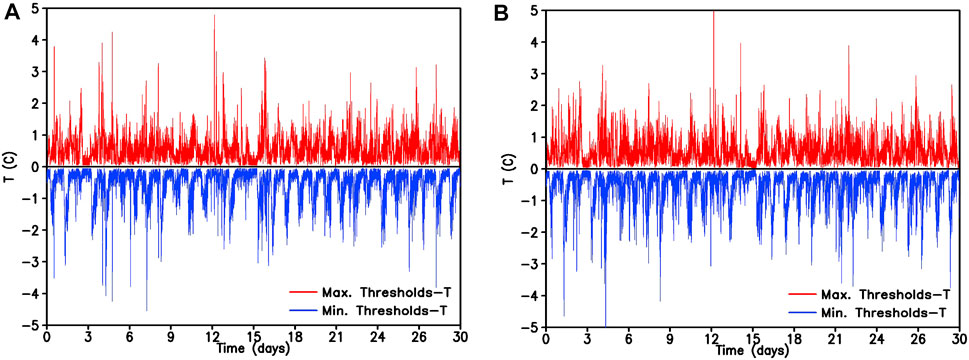
FIGURE 4. Same as in Figure 2, but for scheme 7 at TA (A); and TB (B) stations from 30 April to 29 May 2016.

The Fast Threshold Test for Hourly Temperature Data

This new algorithm is further applied in the hourly temperature data at SB station from 1 January 2002 to 31 December 2018, which indicates a change from seconds to hour level. As shown in Figure 5, the hourly data have passed to the strict quality control before our inspection. We test the hourly data by using the new algorithm to explore the possibility of misjudged or unrealistic observations existing in this dataset. Here, we still use small ($p$ = 0.1%) and large ($p$ = 99.9%) percentile values minus (plus) 1.0 standard deviation ($a$ = 1) for the respective minimum and maximum thresholds within a given bin. In view of the history length of the hourly temperature observation data, it is necessary to re-determine the bin size. For this purpose, a 30-days bin size (30 × 24 = 720 values) and a 1 h time displacement interval are used to test schemes. Meanwhile, we also adopt the threshold test method in the previous studies for the same bin size based on 3.5 standard deviations and the mean value method. The result indicates that our algorithm may be practically implemented for the temperature data. It is seen from Figure 5A that all data fall within the range of acceptable thresholds with the percentile levels of 0.1 and 99.9%. The thresholds derived from the previous method are not updated frequently enough for the data, i.e., the threshold series is not sufficiently smooth (Figure 5B).

FIGURE 5

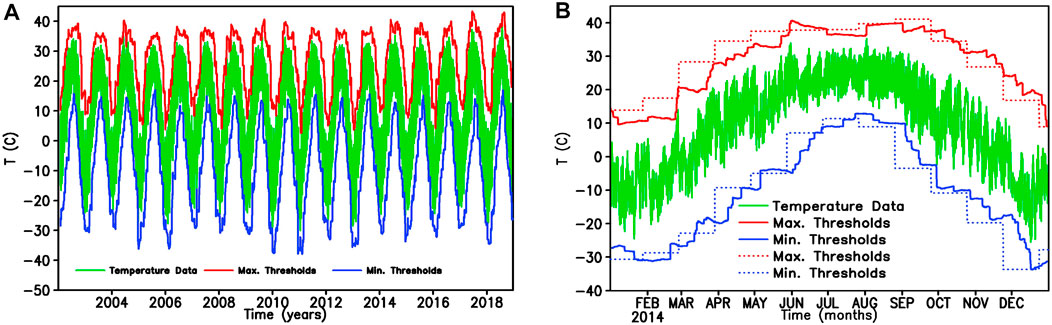
FIGURE 5. The results of the threshold test method for temperature (Unit: °C) at SB station (A) from 1 January 2002 to 31 December 2018 and (B) from 1 January 2014 to 31 December 2014.(The hourly temperature data (green line); the upper limits per hour (the maximum thresholds, red line) and the lower limits per hour (the minimum thresholds; blue line) obtained from our algorithm, the upper limits per 30 days (the maximum thresholds; the red dotted line) and the lower limits per 30 days (the minimum thresholds; the blue dotted line) obtained from the previous threshold test method).

Discussion

Our algorithm can successfully identify outliers for the high-frequency observation records in the data collection phase of the newly built meteorological stations. This method is based on three assumptions. The first one is that the descriptive statistics are possible to estimate for a given bin, the second one is that the values in each bin change with time (Hasu and Aaltonen, 2011), and the third one is that the majority of the 0.5 Hz data are “good” data (Long and Shi, 2008). Because of periodic variations of temperature measurement records, we need to know how the appropriate statistics for each moment are chosen. Moreover, when the history includes only a small number of samples of the assumed distribution, we need to know how the descriptive statistics are computed (Hasu and Aaltonen, 2011). In this study, we deal with these problems using Eq. 5 for estimating the percentiles, including the simplicity and avoiding any assumptions of the underlying distribution in the given bin (Jenkinson, 1977; Bonsal et al., 2001; Zhai and Pan, 2003).

Since this method is based on the statistics (such as data percentiles, the standard deviation, and a moving box filter), especially at new stations, we have not long observation series. Furthermore, because of the large estimation uncertainties in the small samples (Hasu and Aaltonen, 2011), we use a suitable percentile value minus (plus) standard deviation for the respective maximum and minimum thresholds within a given bin. Obviously, the minimum threshold is set according to a percentile related to a very small percentage ($p$ = 0.1%), and the maximum threshold is set using a very large percentage ($p$ = 99.9%). This may avoid unnecessary false error flagging (type $\text{I}$ flagging errors). Of course, the percentages may also be determined according to the user’s preference or the different types of sensors (e.g., sensor specifications, time response, resolution, etc.).

This FQC method is effective and feasible to rapidly detect and flag outliers and instrumental problems for 0.5 Hz real or near-real time records in the data collection phase before the data enter into the QC system. It is also useful to perform the data QC locally on a remote data logger of automatic and power-limited stations. The advantages of this method are as follows. Firstly, it does not need a priori knowledge of the climate, and therefore it enables the generation of statistically meaningful thresholds for newly built stations. Secondly, the approach enables the use of observation statistics for fast checking (Hasu and Aaltonen, 2011). Thirdly, this method does not need a lot of computing resources. Furthermore, the method splits data into fewer bins, which reduces the memory requirements for the computer system. The main computations are used in determining the thresholds and the thresholds can be updated more frequently (every minute). Updating more frequently thresholds is also an obvious advantage of this method. However, it is also noted that this method only describes the expected behavior of the measurement within a given bin period. When real or near-real time observation records have a systematic deviation, this method is inapplicable. Therefore, an accurate check at least a few days after using this method and a manual check for the flagged records are needed (Hasu and Aaltonen, 2011; Houchi et al., 2015). Otherwise, the thresholds are not reliable enough, this also implies that the automated algorithms should be under human supervision in the initial stages.

Because of differences in the meteorological measurements, not all similarly determined thresholds are meaningful to all measurements (Hasu and Aaltonen, 2011). Therefore, there is no one threshold value that cleanly separates all instrumentation problems from unusual physical situations. The manual checks (visual inspection) of individual flagged records are always required (Vickers and Mahrt, 1997), which can be implemented by investigation of the synoptic meteorological conditions occurring around the time of the flagged observations (Shulski et al., 2014).

Procedurally, the operation time control is also an important issue in QC for high-frequency observation data because the fast threshold test method needs to be performed in a short period. Our method is only a primary implementation that can help to screen out obvious outliers promptly in the data collection phase (Cheng et al., 2016). Since this method is developed based on the statistics, some uncertainties also exist. The short-term observational records are possibly not reliable enough when only using a basic threshold test method (Shulski et al., 2014). Thus, the data checked by this method should be further checked with a more strict QC operational procedure. Moreover, to handle unexpected problems such as misjudged observations in our method, more studies are needed (Houchi et al., 2015).

Conclusion

We propose an algorithm through the automatic determination of the maximum and minimum minute thresholds for the high-frequency meteorological observation data in the data collection phase of the newly built stations, and present an efficient statistical scheme to isolate and flag non-negligible outliers and instrumental problems from a large amount of 0.5 Hz raw data before they are introduced into the QC system (e.g., Houchi et al., 2015; Vickers and Mahrt, 1997; Zhang et al., 2010; Li et al., 2012). This method is based on the percentile threshold (0.1–99.9%) and standard deviation, which can identify the incorrect data in the current minute with a 30 min bin size and a 1 min time displacement interval. A visual graph is generated every minute, and the time series and the thresholds are displayed by the automated graphical procedures. Those observations that fall outside the thresholds are flagged and then a manual check (visual inspection) is performed (Cheng et al., 2016). The optimal thresholds will be derived from the corresponding tests (Houchi et al., 2015). This method is developed for the raw high-frequency (sampled every 2 s) surface temperature observation data. We demonstrates the effectiveness and feasibility of this algorithm in rapidly detecting and flagging outliers for an initial inspection of 0.5 Hz real or near-real time data in the data collection phase. A comparison at different experiment stations indicates that this fast threshold test may be a viable option in the data collection phase. Meanwhile, this method may also be applied to other high-frequency observation variables such as pressure, relative humidity (the beta-distributed, Yao 1974), wind speed (Weibull-distributed, Pang et al., 2001), and so forth .

Data Availability Statement

The data analyzed in this study is subject to the following licenses/restrictions: The analyzed data can only be accessed from inside China Meteorological Administration. Requests to access these datasets should be directed to RL, bGlhb3J3QGNtYS5nb3YuY24=.

Author Contributions

Conceptualization, formal analysis and writing–original draft, RL; Methodology, RL and DZ; Project administration, XF, LS, FY, and HL; Supervision, PZ; Writing–review and editing, RL, PZ and YC. All authors have read and agreed to the published version of the article.

Funding

This research is sponsored by the National Key Research and Development Program of China (Grant 2018YFC1505700), the National Natural Science Foundation of China (52078480) and the Basic Research Fund (2021Z001) of Chinese Academy Meteorological Sciences.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or any claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors acknowledge, with deep gratitude, the contribution of the reviewers whose comments has improved this article substantially. In the process of revising this paper, we have received the strong guidance from researcher Ding Minghu of Chinese Academy of Meteorological Sciences.

References

Bonsal, B. R., Zhang, X., Vincent, L. A., and Hogg, W. D. (2001). Characteristics of Daily and Extreme Temperatures over Canada. J. Clim. 14, 1959–1976. doi:10.1175/1520-0442(2001)014<1959:codaet>2.0.co;2

CrossRef Full Text | Google Scholar

Cerlini, P. B., Silvestri, L., and Saraceni, M. (2020). Quality Control and gap‐filling Methods Applied to Hourly Temperature Observations over central Italy. Meteorol. Appl. 27 (3). doi:10.1002/met.1913

CrossRef Full Text | Google Scholar

Chen, B. K., Xu, J. L., and Fang, W. Z. (2011). Quality Control of Minute Meteorological Observational Data. J. Meteorol. Res. Appl. 32 (3), 77–78. (In Chinese).

Google Scholar

Cheng, A. R., Lee, T. H., Ku, H. I., and Chen, Y. W. (2016). Quality Control Program for Real-Time Hourly Temperature Observation in Taiwan. J. Atmos. Ocean Technol. 33, 953–976. doi:10.1175/jtech-d-15-0005.1

CrossRef Full Text | Google Scholar

Ditthakit, P., Pinthong, S., Salaeh, N., Binnui, F., Khwanchum, L., Kuriqi, A., et al. (2021). Performance Evaluation of a Two-Parameters Monthly Rainfall-Runoff Model in the Southern Basin of Thailand. Water 13, 1226. doi:10.3390/w13091226

CrossRef Full Text | Google Scholar

Fiebrich, C. A., and Crawford, K. C. (2001). The Impact of Unique Meteorological Phenomena Detected by the Oklahoma Mesonet and ARS Micronet on Automated Quality Control. Bull. Amer. Meteorol. Soc. 82, 2173–2187. doi:10.1175/1520-0477(2001)082<2173:tioump>2.3.co;2

CrossRef Full Text | Google Scholar

Hasu, V., and Aaltonen, A. (2011). Automatic Minimum and Maximum Alarm Thresholds for Quality Control. J. Atmos. Ocean Technol. 28, 74–84. doi:10.1175/2010jtecha1431.1

CrossRef Full Text | Google Scholar

Højstrup, J. (1993). A Statistical Data Screening Procedure. Meas. Sci.Technol. 4, 153–157.

Google Scholar

Houchi, K., Stoffelen, A., Marseille, G.-J., and De Kloe, J. (2015). Statistical Quality Control of High-Resolution Winds of Different Radiosonde Types for Climatology Analysis. J. Atmos. Ocean Technol. 32, 1796–1812. doi:10.1175/jtech-d-14-00160.1

CrossRef Full Text | Google Scholar

Hubbard, K. G., Goddard, S., Sorensen, W. D., Wells, N., and Osugi, T. T. (2005). Performance of Quality Assurance Procedures for an Applied Climate Information System. J. Atmos. Ocean Technol. 22, 105–112. doi:10.1175/jtech-1657.1

CrossRef Full Text | Google Scholar

Hubbard, K. G., Guttman, N. B., You, J., and Chen, Z. (2007). An Improved QC Process for Temperature in the Daily Cooperative Weather Observations. J. Atmos. Ocean Technol. 24, 206–213. doi:10.1175/jtech1963.1

CrossRef Full Text | Google Scholar

Hubbard, K. G., and You, J. (2005). Sensitivity Analysis of Quality Assurance Using the Spatial Regression Approach-A Case Study of the Maximum/minimum Air Temperature. J. Atmos. Ocean Technol. 22 (10), 1520–1530. doi:10.1175/jtech1790.1

CrossRef Full Text | Google Scholar

Jenkinson, A. F. (1977). The Analysis of Meteorological and Other Geophysical Extremes. Synoptic Climatology Branch Memo. 58. Berkshire, United Kingdom: U.K. Met. Office, Bracknell, 41.

Google Scholar

Jiménez, P. A., Fidel, J., Navarro, J., Juan, P. M., and Elena, G. (2010). Quality Assurance of Surface Wind Observations from Automated Weather Stations. J. Atmos. Ocean Technol. 27, 1101–1122. doi:10.1175/2010JTECHA1404.1

CrossRef Full Text | Google Scholar

Kuriqi, A. (2016). Assessment and Quantification of Meteorological Data for Implementation of Weather Radar in Mountainous Regions. MAUSAM 67 (4), 789–802. doi:10.54302/mausam.v67i4.1408

CrossRef Full Text | Google Scholar

Li, H. M., Zhou, T. J., and Yu, R. C. (2008). Analysis of July-August Daily Precipitation Characteristics Variation in Eastern China during 1958-2000. Chin. J Atmos Sci 32 (2), 360–370. (in Chinese). doi:10.3878/j.issn.1006-9895.2008.02.14

CrossRef Full Text | Google Scholar

Li, M. S., Yang, Y. X., Ma, Y,M., Sun, F. L., Chen, X. L., Wang, B. B., et al. (2012). Analyses on Turbulence Data Control and Distribution of Surface Energy Flux in Namco Area of Tibetan Plateau. Plateau Meteorol. 31 (4), 875–884. (In Chinese).

Google Scholar

Lin, W., Portabella, M., Stoffelen, A., and Verhoef, A. (2017). Toward an Improved Wind Inversion Algorithm for RapidScat. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 10 (5), 2156–2164. doi:10.1109/jstars.2016.2616889

CrossRef Full Text | Google Scholar

Liu, Y. J., Chen, H. B., Jin, D. Z., Qi, Y. B., and Lian, C. (2014). Quality Control and Representativeness of Automatic Weather Station Rain Gauge Data. Chin. J Atmos Sci 38 (1), 159–170. doi:10.3878/j.issn.1006-9895.2013.13116

CrossRef Full Text | Google Scholar

Lopez, J. L. A., Uteuov, A., Kalyuzhnaya, A. V., Klimova, A., Bilyatdinova, A., Kortelainen, J., et al. (2017). Quality Control and Data Restoration of Metocean Arctic Data. Proced. Comp. Sci. 119, 315–324. doi:10.1016/j.procs.2017.11.190

CrossRef Full Text | Google Scholar

Ntsangwane, L., Mabasa, B., Sivakumar, V., Zwane, N., Ncongwane, K., and Botai, J. (2019). Quality Control of Solar Radiation Data within the South African Weather Service Solar Radiometric Network. J. Energy South. Afr. 30 (4), 51–63. doi:10.17159/2413-3051/2019/v30i4a5586

CrossRef Full Text | Google Scholar

Oh, G.-L., Lee, S.-J., Choi, B.-C., Kim, J., Kim, K.-R., Choi, S.-W., et al. (2015). Quality Control of Agro-Meteorological Data Measured at Suwon Weather Station of Korea Meteorological Administration. Korean J. Agric. For. Meteorology 17 (1), 25–34. doi:10.5532/kjafm.2015.17.1.25

CrossRef Full Text | Google Scholar

Pang, W.-K., Forster, J. J., and Troutt, M. D. (2001). Estimation of Wind Speed Distribution Using Markov Chain Monte Carlo Techniques. J. Appl. Meteorol. 40, 1476–1484. doi:10.1175/1520-0450(2001)040<1476:eowsdu>2.0.co;2

CrossRef Full Text | Google Scholar

Qi, Y., Martinaitis, S., Zhang, J., and Cocks, S. (2016). A Real-Time Automated Quality Control of Hourly Rain Gauge Data Based on Multiple Sensors in MRMS System. J. Hydrometeorol 17, 1675–1691. doi:10.1175/jhm-d-15-0188.1

CrossRef Full Text | Google Scholar

Qin, Z.-K., Zou, X., Li, G., and Ma, X.-L. (2010). Quality Control of Surface Station Temperature Data with Non-gaussian Observation-Minus-Background Distributions. J. Geophys. Res. 115, D16312. doi:10.1029/2009JD013695

CrossRef Full Text | Google Scholar

Ren, Z. H., Liu, X. N., and Yang, W. X. (2005). Complex Quality Control and Analysis of Extremely Abnormal Meteorological Data. Acta Meteorol. Sinica 63 (4), 526–533. (In Chinese). doi:10.11676/qxxb2005.052

CrossRef Full Text | Google Scholar

Ren, Z. H., and Xiong, A. Y. (2007). Operational System Development on Three-step Quality Control of Observations from AWS. Meteorol. Mon 33 (1), 19–24. (In Chinese). doi:10.7519/j.issn.1000-0526.2007.01.003

CrossRef Full Text | Google Scholar

Ren, Z. H., Xiong, A. Y., and Zou, F. L. (2007). The Quality Control of Surface Monthly Climate Data in China. J. Appl. Meteorol. Sci 18 (4), 516–523. (In Chinese).

Google Scholar

Ren, Z. H., Zhang, Z. F., Sun, C., Liu, Y. M., Li, J., Ju, X. H., et al. (2015). Development of Three-Levelquality Control System for Real-Time Observations of Automatic Weather Stations Nationwide. Meteorol. Mon 41 (10), 1268–1277. (In Chinese). doi:10.7519/j.issn.1000-0526.2015.10.010

CrossRef Full Text | Google Scholar

Roh, S., Genton, M. G., Jun, M., Szunyogh, I., and Hoteit, I. (2013). Observation Quality Control with a Robust Ensemble Kalman Filter. Mon Wea Rev. 141, 4414–4428. doi:10.1175/mwr-d-13-00091.1

CrossRef Full Text | Google Scholar

Shafer, M. A., Fiebrich, C. A., Arndt, D. S., Fredrickson, S. E., and Hughes, T. W. (2000). Quality Assurance Procedures in the Oklahoma Mesonetwork. J. Atmos. Oceanic Technol. 17, 474–494. doi:10.1175/1520-0426(2000)017<0474:qapito>2.0.co;2

CrossRef Full Text | Google Scholar

Shulski, M. D., You, J., Krieger, J. R., Baule, W., Zhang, J., Zhang, X., et al. (2014). Quality Assessment of Meteorological Data for the Beaufort and Chukchi Sea Coastal Region Using Automated Routines. Arctic 67 (1), 104–112. doi:10.14430/arctic4367

CrossRef Full Text | Google Scholar

Tao, S. W., Zhong, Q. Q., Xu, Z. F., and Hao, M. (2009). Quality Control Schemes and its Application to Automatic Surface Weather Observation System. Plateau Meteorol. 28 (5), 1202–1209. (In Chinese).

Google Scholar

Vejen, F., Jacobsson, C., Fredriksson, U., Moe, M., Andresen, L., Hellsten, E., et al. (2002). Quality Control of Meteorological Observations—Automatic Methods Used in the Nordic Countries. Nordklim. Rep. 8, 100. Available at: https://www.met.no/sokeresultat/_/attachment/inline/2fdbdbcf-2ae8-4bb3-86de-f7b5a6f11dae:b322c47c99e9a34086013dfa7e4a915a383d2b42/MET-report-08-2002.pdf.

Google Scholar

Vickers, D., and Mahrt, L. (1997). Quality Control and Flux Sampling Problems for tower and Aircraft Data. J. Atmos. Oceanic Technol. 14, 512–526. doi:10.1175/1520-0426(1997)014<0512:qcafsp>2.0.co;2

CrossRef Full Text | Google Scholar

Wan, H., Wang, X. L., and Swail, V. R. (2007). A Quality Assurance System for Canadian Hourly Pressure Data. J. Appl. Meteorol. Climatol 46, 1804–1817. doi:10.1175/2007jamc1484.1

CrossRef Full Text | Google Scholar

Wang, H. J., and Liu, Y. (2012). Comprehensive Consistency Method of Data Quality Controlling with its Application to Daily Temperature. J. Appl. Meteorol. Sci 23 (1), 69–76. (In Chinese).

Google Scholar

Wang, H. J., Yan, Q. Q., Xiang, F., and Pan, M. (2014). Algorithm Design of Quality Control for Hourly Air Temperature. Plateau Meteorol. 33 (6), 1722–1729. (In Chinese). doi:10.7522/j.issn.1000-0534.2014.00028

CrossRef Full Text | Google Scholar

Wang, H. J., Yang, Z. B., Yang, D. C., and Gong, X. C. (2007). The Method and Application of Automatic Quality Control for Real Time Data from Automatic Weather Stations. Meteorol. Mon 33 (10), 102–106. (In Chinese). doi:10.7519/j.issn.1000-0526.2007.10.015

CrossRef Full Text | Google Scholar

Xiong, X., Ye, X. L., Zhang, Y. C., Sun, N., Deng, H., and Jiang, Z. B. (2017a). A Quality Control Method for the Surface Temperature Based on the Spatial Observation Diversity. Chin. J Geophys-ch. 60 (3), 912–923. (In Chinese). doi:10.6038/cjg20170306

CrossRef Full Text | Google Scholar

Xiong, X., Ye, X., and Zhang, Y. (2017b). A Quality Control Method for Surface Hourly Temperature Observations via Gene‐expression Programming. Int. J. Climatol 37 (12), 4364–4376. doi:10.1002/joc.5092

CrossRef Full Text | Google Scholar

Xu, Z., Chen, X., and Wang, Y. (2013). Quality Control Scheme for New-Built Automatic Surface Weather Observation Station's Data. J. Meteorol. Sci 33 (1), 26–36. (In Chinese). doi:10.3969/2012jms.0120

CrossRef Full Text | Google Scholar

Xu, Z. f., Wang, Y., and Fan, G. Z. (2012). A Two-Stage Quality Control Method for 2-m Temperature Observations Using Biweight Means and a Progressive EOF Analysis. Mon Wea Rev. 141, 798–808. doi:10.1175/MWR-D-11-00308.1

CrossRef Full Text | Google Scholar

Yao, A. Y. M. (1974). A Statistical Model for the Surface Relative Humidity. J. Appl. Meteorol. 13, 17–21. doi:10.1175/1520-0450(1974)013<0017:asmfts>2.0.co;2

CrossRef Full Text | Google Scholar

Ye, X. L., Kan, Y. J., Xiong, X., Zhang, Y. C., and Chen, X. (2020). A Quality Control Method Based on an Improved Kernel Regression Algorithm for Surface Air Temperature Observations. Adv. Meteorol. 2020, 6045492. doi:10.1155/2020/6045492

CrossRef Full Text | Google Scholar

Zhai, P. M., and Pan, X. H. (2003). Change in Extreme Temperature and Precipitation over Northern China during the Second Half of the 20th Century. Acta Geogr. Sin 58 (7s), 1–10. doi:10.11821/xb20037s001

CrossRef Full Text | Google Scholar

Zhang, L., Li, Y. Q., Li, Y., and Zhao, X. B. (2010). A Study of Quality Control and Assessment of the Eddy Covariance System above Grassy Land of the Eastern Tibetan Plateau. Chin. J Atmos Sci 34 (4), 703–714. (In Chinese). doi:10.3878/j.issn.1006-9895.2010.04.04

CrossRef Full Text | Google Scholar

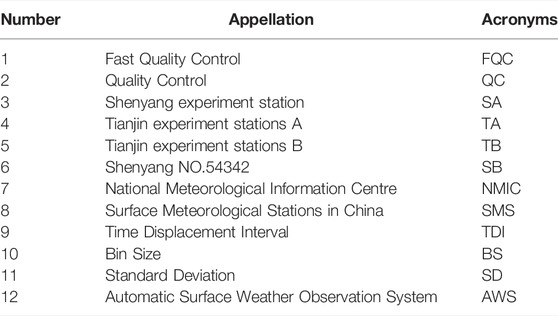
TABLE A1 | The list of acronyms.