Analysis of Energy Evolution Characteristics of Salt Rock Under Different Loading Rates

The existing uniaxial compression test results of salt rock under different loading rates are used to study its energy evolution characteristics during deformation and failure in this study. First of all, the influence of loading rate on the total energy density, elastic energy density, and dissipated energy density is analyzed. Afterward, the relationship between the number and size of fragments, crushing intensity after rock destruction, and energy density of each part is discussed. The results show that the energy evolution process of salt rock during deformation and failure contains three stages, namely, energy accumulation stage, energy dissipation stage, and energy release stage. With the increase in loading rate, the total energy density and dissipated energy density gradually decrease, whereas the elastic energy density increases. When the volume of rock remains constant, the greater the dissipated strain energy, the more the number of fragments will be produced after rock failure. When the dissipated strain energy remains unchanged, the larger the dissipated strain energy (surface free energy) is, the smaller the number and the larger the size of fragments will be produced. When the total strain energy is constant, the splash rate of the fragments increases with increasing elastic strain energy ratio.

Introduction

The deformation and failure process of rock under external loads is the generation and development process of new cracks. The generation of new cracks will absorb energy from the external environment, and the propagation and penetration process of cracks will consume energy. Namely, the process of rock deformation and failure is a process of energy accumulation and dissipation (Wang and Cui, 2018; Chen Z. et al., 2019; Wang et al., 2021a; Fan et al., 2022; Wang Y. et al., 2022). Therefore, studying the deformation and failure process of rocks from the perspective of energy is closer to its failure essence, and it is of great significance to reveal the mechanisms of rock failure and rock (body) engineering disasters (Carpinteri et al., 2004; Deng et al., 2016; He et al., 2018; Gong et al., 2021; Wang et al., 2021b; Wang et al., 2022b).

The deformation and failure of rocks under external load is the inevitable result of energy driving (Liu et al., 2019; Wang Y. et al., 2020; Li et al., 2021). Studying the deformation and failure process of rocks from the perspective of energy has always been a hot issue in the field of rock mechanics (Yang et al., 2019; Zhao et al., 2020; Li et al., 2022; Wang X. Y. et al., 2022; Zhang et al., 2022). Meng et al. (2019) carried out uniaxial cyclic loading tests on yellow sandstone, limestone, and marble under different loading rates, and analyzed the influence of loading rate on energy evolution during rock deformation and failure. Zhang and Gao (2015) analyzed the influence of water on energy evolution and distribution of sandstone based on the uniaxial cyclic loading and unloading test results. He et al. (2020) studied the evolution characteristics of the total energy, elastic energy, and dissipated energy for the fifteen rocks and then proposed a new method to determine the strength of rock using the dissipation energy coefficients. Gong et al. (2019) studied the relationship between total input energy and elastic strain energy under different unloading stress levels and proposed a new basis for judging rockburst tendency. Song et al. (2020) analyzed the influence law of loading mode on deformation characteristics, failure form, and energy evolution characteristics of the coal-rock combination. Wang et al. (2021c) and Yang D. et al. (2020) studied the energy evolution characteristics of rocks during fatigue deformation and pointed out that with the increase of load cycles, the elastic strain energy gradually increased, while the dissipated strain energy gradually decreased. Cao et al. (2020) studied the variation law of total strain energy, elastic strain energy, dissipated strain energy, and infrared radiation temperature of saturated sandstone under stress by using infrared thermal imaging technology. Zhang J. et al. (2021) studied the influence of joint inclination on the energy evolution characteristics of rock, the results showed that the total energy, elastic strain energy, and dissipated strain energy at the peak stress of rock first decreased and then increased with the increase of joint inclination. Zhang et al. (2017) studied the influence of confining pressure on the energy accumulation and dissipation of rocks and pointed out that confining pressure can promote energy input and accumulation and inhibit energy release. Huang and Li (2014) analyzed the influence of initial confining pressure and unloading rate on rock energy conversion and its failure characteristics based on the results of the triaxial cyclic loading test. Zhang et al. (2019) studied the energy evolution processes and mechanisms among three hard rocks using a strain energy analysis method under true triaxial compression. The results showed that the difference in the elastic and plastic deformation capacities, which influence the energy difference in different rocks, is influenced by the mineral compositions and microstructures of the different rocks when the external conditions are not considered. As aforementioned, a large number of research studies have been performed to examine the energy evolution characteristics of rocks under various experimental conditions for the past several years. However, there are only a few studies on the influence of loading rate on the energy evolution characteristics of salt rock.

The long-term operation process of salt cavern gas storage includes four stages: gas injection and pressurization, high-pressure operation, gas production, and depressurization, and low-pressure operation (Fan et al., 2019; Fan et al., 2020; Zhou et al., 2022). In the stage of gas production and depressurization stage, the pressure of the gas storage gradually decreases, and the unbalanced force of the surrounding rock gradually increases (Liu et al., 2020a; Wang et al., 2021d; Zhang X. et al., 2021; Wang et al., 2022d). With different gas recovery rates, the loading rates on the surrounding rock are also different. The energy evolution characteristics of salt rock under different loading rates exhibit some variation. Therefore, it is of great significance to study the energy evolution characteristics of salt rock under different loading rates to ensure the safety and stability of the salt cavern gas storage (Liu et al., 2020b; Wang J. et al., 2020; Kang et al., 2021; Wang et al., 2021e; Wang X. et al., 2022).

To study the influence of loading rate on the energy evolution characteristics of salt rock during deformation and failure, the total energy density, elastic energy, and dissipated energy density are calculated using the existing test results mentioned in this study. Based on the calculation results, the relationship between the energy density of each part and the loading rate is studied. Then, the relationship between the number and size of fragments after deformation and failure, crushing intensity, and energy is discussed. The results can provide some theoretical guidance for the long-term stability analysis of salt cavern gas storage.

Energy Calculation Method

According to the knowledge of thermodynamics, it is known that any physical process is the process of mutual conversion between various energies, such as mechanical energy and thermal energy, etc. Hence, the instability failure of an object under external loads is the inevitable result of energy driving. The whole process of deformation and failure of rock under external loads, such as compression density, elastic deformation, inelastic deformation, and post-peak damage stages is accompanied by the mutual conversion between various parts of energy. Therefore, it is conducive to understand the intrinsic mechanism of rock deformation and damage under external loads when thermodynamic knowledge is used to study the energy evolution process (Zhang et al., 2019).

Under the uniaxial or triaxial compression condition, the work done (total input energy) by the testing machine on the rock mainly includes three forms (as shown in Figure 1): 1) A part of the energy is stored inside the rock in the form of elastic strain energy, which can be released after unloading. Therefore, the elastic strain energy is reversible. 2) A part of the energy is mainly used for the closure of the original microcracks inside the rock, and the generation and development of new cracks. This part of energy is commonly called dissipated strain energy, which is irreversible. 3) A small part of the energy is released to the external environment in the form of heat and radiation energy (e.g., acoustic emission, infrared radiation, and electromagnetic radiation) due to the internal cracks, structural surfaces, and friction between mineral particles, which is also irreversible (Yang L. et al., 2020; Zhou et al., 2020).

FIGURE 1

FIGURE 1. Schematic diagram of energy conversion in rock.

The energy evolution process of rocks under external loads mainly undergoes three stages (as shown in Figure 2): namely, energy accumulation stage, energy dissipation stage, and energy release stage. 1) Energy accumulation stage: at the beginning of loading, the absorbed energy is mainly stored in the rock in the form of elastic strain energy, and only a small amount of energy is used to close the original defects inside the rock. Therefore, this stage is a process of energy accumulation. 2) Energy dissipation stage: after the external loads exceeds the yield stress of the rock, most of the absorbed energy is used for the nucleation, expansion, and penetration of microcracks, and only a small part of the absorbed energy is stored in the rock. Namely, the energy accumulation process also exists in this stage. However, the accumulated energy in this stage accounts for only a small proportion of the total absorbed energy, which can be ignored. Hence, this stage can be considered a process of energy dissipation. 3) Energy release stage: when the absorbed energy is sufficient to overcome the frictional effect of the critical failure surface, the rock is destabilized, and the energy stored in the rock is released to the outside in the form of kinetic energy (Li et al., 2017; Zhang L. et al., 2021).

FIGURE 2

FIGURE 2. Energy evolution process of rock.

Assuming that no heat exchange occurs between the interior of the rock and the external environment during the entire loading process that is, the testing machine and the rock are considered to be a closed system. Then, according to the first law of thermodynamics, the work done by the testing machine on the rock can be expressed as (Wang C. L. et al., 2020):

$U=U_{\mathbf{e}}+U_{\mathbf{d}}+U_{\mathbf{h}}.(1)$

Here, U is the stored energy of rock (total input energy), in mJ; U_e is the elastic strain energy, in mJ; U_d is the dissipated strain energy, in mJ; U_h is the energy consumed in the form of heat conduction, heat exchange, and heat radiation, etc. in mJ.

In Eq. 1, U_h accounts for a relatively small proportion of U, and can be ignored (Chen X. et al., 2019). Consequently, we can get:

$U=U_{\mathbf{e}}+U_{\mathbf{d}}.(2)$

For a rock mass unit, the energy evolution characteristics of rock under external loads are commonly characterized by energy density. Therefore, Eq. 3 is obtained according to Eq. 2, namely (Meng et al., 2016),

$u=u_{\mathbf{e}}+u_{\mathbf{d}},(3)$

where u is the total energy density, in mJ·mm⁻³; u_e is the elastic energy density, in mJ·mm⁻³; u_d is the dissipated energy density, in mJ·mm⁻³.

The energy evolution relationship of rock mass units during deformation and failure is also exhibited in Figure 2. The area under the loading stress–strain curve represents the stored energy density u, which is the total work performed by the testing machine on the rock specimen. The area under the unloading stress–strain curve (the green zone) is the elastic energy density u_e, which is recoverable from the rock mass unit. The area between the loading and unloading stress–strain curves represents the dissipated energy density u_d, which causes irreversible plastic deformation and internal damage.

The total energy density u can be calculated using Eq. 4, namely (Xie et al., 2011):

$u={\displaystyle \int {\sigma }_1\mathbf{d}{\epsilon }_1}+{\displaystyle \int {\sigma }_2\mathbf{d}{\epsilon }_2}+{\displaystyle \int {\sigma }_3\mathbf{d}{\epsilon }_3},(4)$

where σ₁, σ₂, and σ₃ are the principal stresses in the three directions, in MPa; ɛ₁, ɛ₂, and ɛ₃ are the principal strains in the three directions, respectively.

The elastic energy density u_e is obtained according to Eq. 5, that is (Tang et al., 2022):

$u_{\mathbf{e}}=\frac{1}{2}{\sigma }_1{\epsilon }_1+\frac{1}{2}{\sigma }_2{\epsilon }_2+\frac{1}{2}{\sigma }_3{\epsilon }_3.(5)$

For the uniaxial compression test (σ₂ = σ₃ = 0), the total energy density u can be expressed as:

$u={\displaystyle \int {\sigma }_1\mathbf{d}{\epsilon }_1}={\displaystyle \sum _i^n\frac{1}{2}\left({\sigma }_i+{\sigma }_{i-1}\right)\left({\epsilon }_i-{\epsilon }_{i-1}\right)},(6)$

where σ_i and σ_i−1 are the stresses at any point on the stress–strain curve, in MPa; ɛ_i and ɛ_i−1 are the strains corresponding to the stress points σ_i and σ_i−1, respectively.

The elastic energy density u_e can be expressed as:

$u_{\mathbf{e}}=\frac{1}{2}{\sigma }_1{\epsilon }_1=\frac{{\sigma }_1^2}{2E_{\mathbf{u}}},(7)$

where E_u is the unloading modulus, in MPa.

Here, the unloading modulus E_u can be replaced by the pre-peak elastic modulus E (Wang et al., 2017). Then Eq. 7 can be transformed as:

$u_{\mathbf{e}}=\frac{{\sigma }_1^2}{2E}.(8)$

Therefore, the concrete values of total energy density u, elastic energy density u_e, and dissipated energy u_d can be calculated by using Eqs 3, 6, 8.

Analysis of Energy Evolution Characteristics of Salt Rock Under Different Loading Rates

To study the influence of loading rate on the energy evolution characteristics of salt rock during deformation and failure, the uniaxial compression test results obtained by Wang et al. (2021f) is used to calculate the energy density of each part here. The loading rate selected in their study was u = 0.25, 1.00, 1.50, 2.00, 3.00, and 5.00 MPa·min⁻¹, respectively.

Figure 3 shows the macroscopic failure modes of salt rock under different loading rates and the corresponding sketch map. Figure 3 reveals that the macroscopic failure modes of salt rock under different loading rates and all show “X”-type conjugate shear failure, accompanied by a debris formed by dilatancy and spalling. Therefore, the loading rate has no effect on the macroscopic failure mode of salt rock, but it is closely related to its fragmentation degree. When the loading rate is low, the fragmentation degree of salt rock is high, and the fragments produced in the process of failure are small in volume and large in quantity. With the increase in the loading rate, the fragmentation degree of salt rock gradually decreases, and the fragments produced in the process of failure are larger in volume and less in quantity.

FIGURE 3

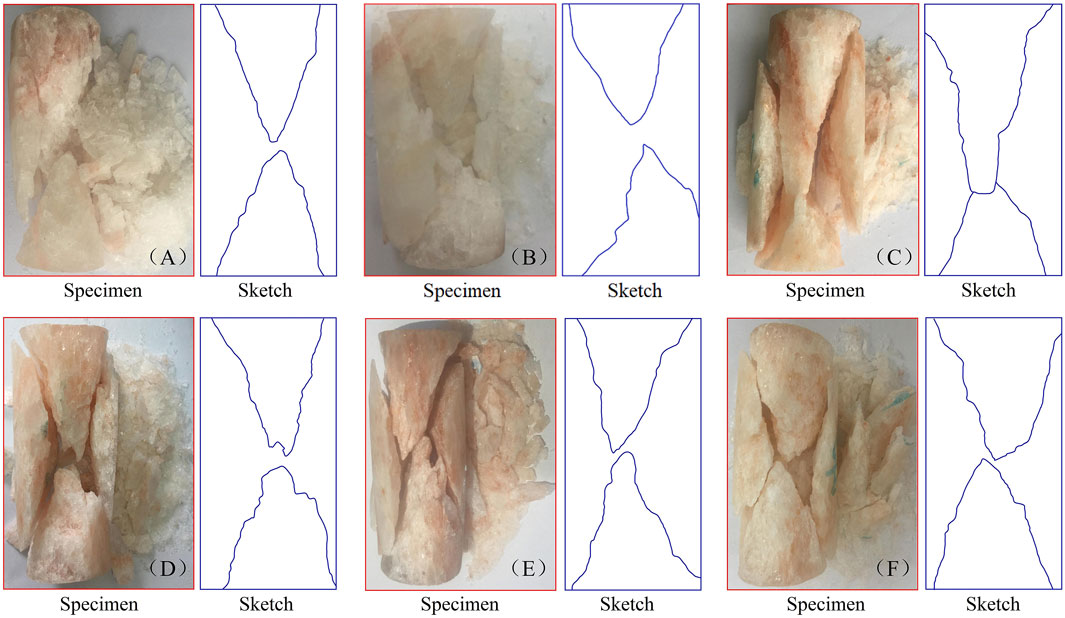
FIGURE 3. Macroscopic failure modes of salt rock and corresponding sketch map: (A) u = 0.25 MPa·min⁻¹, (B) u = 1.00 MPa·min⁻¹, (C) u = 1.50 MPa·min⁻¹, (D) u = 2.00 MPa·min⁻¹, (E) u = 3.00 MPa·min⁻¹, and (F) u = 5.00 MPa·min⁻¹ (Wang et al., 2021f).

Energy Evolution Characteristics of Salt Rock During Deformation and Failure

Figure 4 shows the variation in total energy density, elastic energy density, and dissipated energy density of salt rock with axial strain under different loading rates. Figure 4 reveals that with the increase in axial strain, the energy evolution process of salt rock during deformation and failure can be divided into the following three stages:

1) Energy accumulation stage (stage I), which corresponds to the compaction stage and elastic deformation stage of the axial stress–strain curve. In this stage, most of the absorbed energy is stored in salt rock in the form of elastic strain energy, and only a small amount of energy is used to close the initial defects. Generally speaking, the total energy density, elastic energy density, and dissipated energy density that occurred at this stage are all small. Through analysis, under different loading rates, the total energy density absorbed by salt rock is less than 0.1 mJ·mm⁻³; Among them, the releasable elastic energy density stored in salt rock accounts for more than 90% of the total energy density.

2) Energy dissipation stage (stage II), which corresponds to the inelastic deformation stage of the axial stress–strain curve. At the beginning of this stage, new cracks began to appear in salt rock, and the growth rate of new cracks is relatively stable. The absorbed energy was still mainly stored in the salt rock in the form of elastic strain energy, and the dissipated strain energy increased slowly. With the further increase of axial strain, the internal cracks in salt rock develop into an unstable expansion stage. Although the elastic energy density increases with the increase of axial strain, the increasing rate gradually slows down. At this time, the absorbed energy is mainly used in the form of dissipated strain energy for the propagation of internal cracks in salt rock, and the dissipated energy density increases faster and faster.

3) Energy release stage (stage III), which corresponds to the post-peak failure stage of the axial stress–strain curve. With the increase of axial strain, the internal cracks of salt rock expand and converge continuously, and then penetrate to form macroscopic cracks, which lead to the loss of bearing capacity of the salt rock. In this stage, the energy stored in salt rock is released to the outside in the form of kinetic energy and friction energy in a short time, and the elastic energy density rapidly decreases to zero, while the dissipated energy density increases rapidly.

FIGURE 4

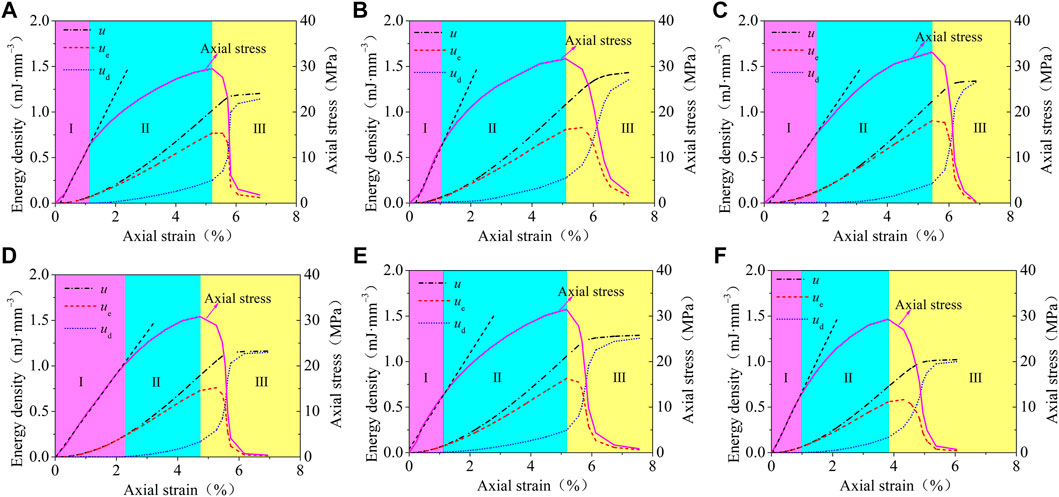
FIGURE 4. Stress-strain curve of salt rock and the variation law of energy under different loading rates: (A) u = 0.25 MPa·min⁻¹, (B) u = 1.00 MPa·min⁻¹, (C) u = 1.50 MPa·min⁻¹, (D) u = 2.00 MPa·min⁻¹, (E) u = 3.00 MPa·min⁻¹, (F) u = 5.00 MPa·min⁻¹.

Effect of Loading Rate on Energy Density of Each Part

Figure 5 shows the variation of total energy density, elastic energy density, and dissipated energy density of salt rock at peak point with loading rate. Figure 5 reveals that, in general, the total energy density and dissipated energy density gradually decrease with increasing loading rate, while the elastic energy density gradually increases. When the loading rate increased from 0.25 to 5 MPa·min⁻¹, the total energy density decreased from 1.12 to 0.87 mJ·mm⁻³, a decrease of 22.32%. The dissipated energy density decreased from 0.45 to 0.09 mJ·mm⁻³, a decrease of 80%, while the elastic energy density increased from 0.67 to 0.78 mJ·mm⁻³, an increase of 16.42%.

FIGURE 5

FIGURE 5. Relationship between energy density and loading rate.

Figure 6 shows the variation of the ratios of elastic energy density to total energy density (u_e/u) and dissipated energy density to total energy density (u_d/u) at peak point with loading rate. Figure 6 reveals that the ratio of elastic energy density to total energy density (u_e/u) gradually increases with the increase of loading rate, while the ratio of dissipated energy density to total energy density (u_d/u) gradually decreases. When the loading rate increased from 0.25 to 5 MPa·min⁻¹, the ratio of u_e to u increased from 0.6 to 0.9, an increase of 50%, while the ratio of u_d to u decreased from 0.4 to 0.1, a decrease of 75%.

FIGURE 6

FIGURE 6. Relationship between energy density ratio and loading rate.

It is known from the previous analysis that during the deformation and failure of rock, the elastic strain energy is stored in the rock during the loading process, and this part energy will release to the outside environment after unloading. The dissipated strain energy is mainly used for the closure of the original microcracks, and the nucleation and expansion of new cracks. The larger the dissipated strain energy, the more the number of fracture surfaces are formed in rock, and the higher the degree of fragmentation after deformation and failure (Zhang et al., 2014). It can be seen from Figure 5 that when the loading rate is slow, the dissipated strain energy used for the nucleation, expansion, and development of new cracks is relatively larger. In this case, the degree of the nucleation, expansion, and development of new cracks is adequate, the number of fracture surfaces formed in salt rock is relatively more, and the damage degree of salt rock is higher. Therefore, the fragmentation degree of salt rock is higher at lower loading rates, as shown in Figure 3A. With an increases of loading rate, on the whole, the dissipated strain energy decreases gradually. At this time, the degree of the nucleation, expansion, and development of new cracks decreases, and the number of fracture surfaces formed gradually decreases, resulting in the decrease in damage degree of salt rock. Consequently, the fragmentation degree of salt rock under higher loading rate is relatively lower, as shown in Figure 3F. This is consistent with the conclusion obtained by Zhang (2013).

Relationship Between the Number and Size of Fragments and Energy

The process of cracks expansion and development in the rock under external loads is the process from microscopic cracks to mesoscopic cracks, and then to macroscopic cracks. In the process of new cracks extension and development, it is necessarily accompanied by the increase of new free surfaces. Therefore, the dissipated strain energy U_d is mainly reflected in the form of surface free energy δ_s, which is used for the addition of new cracks on the surface. Assuming that the fragments produced by a rock after destruction are equal volume spheres, then (Zhang, 2013):

$U_{\text{d}}=\left({\displaystyle \sum 4\pi r^2-\pi dh-\frac{1}{2}\pi d^2}\right){\delta }_{\text{s}},(9)$

where d and h are respectively the diameter and height of the cylindrical rock specimen, in mm; r is the radius of the equivalent sphere of the rock fragment, in mm; and δ_s is the surface free energy, in mJ·mm⁻².

Noted that the surface free energy δ_s in Eq. 9 refers to the energy consumed to form a unit crack area, and this parameter is also a physical quantity reflecting the ability of the rock to resist crack expansion.

Since the volume of the rock before and after destruction is constant, we have:

${\displaystyle \sum \frac{4}{3}\pi r^3=\frac{1}{4}\pi d^{2}h}.(10)$

Assuming that the number of equal volume spheres formed after rock destruction is N, then according to Eqs 9, 10, we can get:

$N=\frac{{\left(\frac{U_{\mathbf{d}}}{{\delta }_{\mathbf{s}}}+\pi dh+\frac{1}{2}\pi d^2\right)}^3}{\frac{9}{4}{\pi }^3{d}^4{h}^2}.(11)$

With d = 50 mm and h = 100 mm, Figure 7 shows the variation of the number of fragments produced after the rock failure with dissipated strain energy under different surface energies (δ_s = 0.011, 0.012, 0.013, 0.014, and 0.015 mJ·mm⁻²). It reveals that under the condition of a certain rock volume, the greater the dissipated strain energy, the more fragments will be produced after rock failure, and the smaller the corresponding fragments will be. This is consistent with the macroscopic failure form of salt rock under different loading rates (as shown in Figure 3A). That is, the smaller the loading rate, the larger the dissipated strain energy, the more fragments produced after the salt rock failure, and the smaller the fragmented volume. Moreover, the larger the loading rate, the smaller the dissipated strain energy, the smaller the number, and the larger the volume of fragments after the salt rock failure (as shown in Figure 3F). The main reason for this phenomenon is that the larger the dissipated strain energy is, the more cracks and fracture surfaces are produced in the rock, and the more fragments are produced after failure, and the smaller the corresponding fragments are. In addition, under the condition that the dissipated strain energy remains unchanged, the larger the surface free energy δ_s is, the more energy is consumed to form the unit crack area, that is, the stronger the ability of the rock to resist crack propagation and development, the smaller the number of fragments produced after failure and the larger the fragment size.

FIGURE 7

FIGURE 7. Variation pattern of the number of rock fragments with dissipated strain energy.

Relationship Between the Crushing Intensity of Rock and Energy

The crushing intensity of rock is closely related to the kinetic energy of the fragments at the time of destruction, which is converted from the elastic strain energy stored in the rock. For the same mass of fragments, the more the elastic strain energy stored inside the rock, the more kinetic energy the fragments have, and the faster the splash rate of the fragments when broken. In order to analyze the relationship between the crushing intensity of rock and the elastic strain energy, the following assumptions are made here: 1) the total energy U input to the rock by the testing machine is constant, and the ratio of conversion into elastic strain energy is x, then the ratio of conversion into dissipated strain energy is 1-x; 2) the dissipated strain energy is all used for the expansion and development of new cracks inside the rock that is, the dissipated strain energy can be approximated as the surface free energy of cracks, then:

${\displaystyle \sum \frac{2}{3}\rho \pi r^3{v}^2}=xU,(12)$

$\left({\displaystyle \sum 4\pi r^2-\pi dh-\frac{1}{2}\pi d^2}\right){\delta }_{\mathrm{s}}=\left(1-x\right)U,(13)$

where ρ is the density of the rock, in g·mm⁻²; v is the splash rate of the fragments when the rock is damaged, in mm·s⁻¹.

In addition, assuming that the fragments produced by the rock after destruction are equal volume spheres and the number of equal volume spheres formed is N, then according to Eqs 10–13, we get:

$N=\frac{{\left[\frac{\left(1-x\right)U}{{\delta }_{\mathbf{s}}}+\pi dh+\frac{1}{2}\pi d^2\right]}^3}{\frac{9}{4}{\pi }^3{d}^4{h}^2},(14)$

$v={\left\{\frac{x}{1-x}\frac{\left[4\pi {\left(\frac{3}{16}{d}^{2}h\right)}^{2/3}{N}^{1/3}-\pi dh-\frac{1}{2}\pi d^2\right]{\delta }_{\mathbf{s}}}{\frac{1}{8}\rho \pi d^{2}h}\right\}}^{1/2}.(15)$

With d = 50 mm, h = 100 mm, δ_s = 0.015 mJ·mm⁻², and ρ = 2.14 × 10^–3 g·mm⁻³, Figure 8 shows the variation law of fragment splash rate with elastic strain ratio under different total input energies (U = 100, 200, 300, 400, and 500 mJ). It reveals that, under the condition of certain total input energy, with the increase of the proportion of elastic strain energy, the splash rate of fragments generally shows a changing trend in increase gradually, but the increasing range gradually decreases. In addition, when the proportion of elastic strain energy is constant, the greater the total input energy, the greater is the plastic strain energy, the smaller the mass of fragments produced after rock failure and the faster is the splash rate.

FIGURE 8

FIGURE 8. Variation pattern of splash rate of fragments with the ratio of elastic strain energy.

Conclusion

Based on the existing uniaxial compression test results of salt rock under different loading rates, the energy evolution characteristics of salt rock during deformation and failure are studied. The influence of the loading rate on the total energy density, elastic energy density, and dissipated energy density of salt rock is analyzed, and the relationship between the number, size of fragments, crushing intensity, and energy of each part is discussed. The main conclusions are as follows:

1) The energy evolution process of salt rock deformation and failure contains the energy accumulation stage, energy dissipation stage, and energy release stage. The energy accumulation stage corresponds to the compaction stage and the elastic stage of the stress–strain curve, the energy dissipation stage corresponds to the inelastic deformation stage of the stress–strain curve, and the energy release stage corresponds to the post-peak failure stage of the stress–strain curve.

2) With the increase in the loading rate, the total energy density and dissipated energy density of salt rock gradually decrease, while the elastic energy density gradually increases. At the same time, with the increase in the loading rate, the proportion of dissipated energy density to the total energy density gradually decreases, while the proportion of elastic energy density to the total energy density gradually increases.

3) When the volume of rock is constant, the greater the dissipated strain energy, the more the number of fragments produced after the rock failure and the smaller the size of the fragment. When the dissipated strain energy remains constant, the larger the surface free energy is, the smaller the number and the larger the size of fragments that will be produced after rock failure. When the total strain energy is constant, the splash rate of rock fragments increases with the increase of elastic strain energy ratio. When the proportion of elastic energy remains unchanged, the splash rate of rock fragments increases with the increase in total input energy.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author Contributions

JW conceived and designed the methods for the study and economically supported the project. XL provided the experimental materials and completed the data collection. QZ completed the data analysis and the writing of the study manuscript. ZS provided the guide for experiment and theoretical research for the study.

Funding

This study is supported by the National Natural Science Foundation of China (52178393, 52178354), the Housing and Urban–Rural Construction Science and Technology Planning Project of Shaanxi Province (No. 2019-K39), and the Innovation Capability Support Plan of Shaanxi—Innovation Team (No. 2020TD-005).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, K., Ma, L., Wu, Y., Khan, N. M., and Yang, J. (2020). Using the Characteristics of Infrared Radiation during the Process of Strain Energy Evolution in Saturated Rock as a Precursor for Violent Failure. Infrared Phys. Technol. 109, 103406. doi:10.1016/j.infrared.2020.103406

CrossRef Full Text | Google Scholar

Carpinteri, A., Lacidogna, G., and Pugno, N. (2004). Scaling of Energy Dissipation in Crushing and Fragmentation: A Fractal and Statistical Analysis Based on Particle Size Distribution. Int. J. Fracture 129 (2), 131–139. doi:10.1023/b:frac.0000045713.22994.f2

CrossRef Full Text | Google Scholar

Chen, Z., He, C., Ma, G., Xu, G., and Ma, C. (2019a). Energy Damage Evolution Mechanism of Rock and its Application to Brittleness Evaluation. Rock Mech. Rock. Eng. 52 (4), 1265–1274. doi:10.1007/s00603-018-1681-0

CrossRef Full Text | Google Scholar

Chen, X., He, P., and Qin, Z. (2019b). Strength Weakening and Energy Mechanism of Rocks Subjected to Wet-Dry Cycles. Geotech Geol. Eng. 37, 3915–3923. doi:10.1007/s10706-019-00881-6

CrossRef Full Text | Google Scholar

Deng, Y., Chen, M., Jin, Y., and Zou, D. (2016). Theoretical Analysis and Experimental Research on the Energy Dissipation of Rock Crushing Based on Fractal Theory. J. Nat. Gas Sci. Eng. 33, 231–239. doi:10.1016/j.jngse.2016.05.020

CrossRef Full Text | Google Scholar

Fan, J., Jiang, D., Liu, W., Wu, F., Chen, J., and Daemen, J. (2019). Discontinuous Fatigue of Salt Rock with Low-Stress Intervals. Int. J. Rock Mech. Mining Sci. 115 (3), 77–86. doi:10.1016/j.ijrmms.2019.01.013

CrossRef Full Text | Google Scholar

Fan, J., Liu, W., Jiang, D., Chen, J., Tiedeu, W. N., and Daemen, J. J. K. (2020). Time Interval Effect in Triaxial Discontinuous Cyclic Compression Tests and Simulations for the Residual Stress in Rock Salt. Rock Mech. Rock Eng. 53 (9), 4061–4076. doi:10.1007/s00603-020-02150-y

CrossRef Full Text | Google Scholar

Fan, S., Song, Z., Xu, T., and Zhang, Y. (2022). Investigation of the Microstructure Damage and Mechanical Properties Evolution of limestone Subjected to High-Pressure Water. Construction Building Mater. 316, 125871. doi:10.1016/j.conbuildmat.2021.125871

CrossRef Full Text | Google Scholar

Gong, F., Yan, J., Li, X., and Luo, S. (2019). A Peak-Strength Strain Energy Storage Index for Rock Burst Proneness of Rock Materials. Int. J. Rock Mech. Mining Sci. 117, 76–89. doi:10.1016/j.ijrmms.2019.03.020

CrossRef Full Text | Google Scholar

Gong, F., Zhang, P., Luo, S., Li, J., and Huang, D. (2021). Theoretical Damage Characterisation and Damage Evolution Process of Intact Rocks Based on Linear Energy Dissipation Law under Uniaxial Compression. Int. J. Rock Mech. Mining Sci. 146, 104858. doi:10.1016/j.ijrmms.2021.104858

CrossRef Full Text | Google Scholar

He, M., Huang, B., Zhu, C., Chen, Y., and Li, N. (2018). Energy Dissipation-Based Method for Fatigue Life Prediction of Rock Salt. Rock Mech. Rock Eng. 51 (5), 1447–1455. doi:10.1007/s00603-018-1402-8

CrossRef Full Text | Google Scholar

He, M. M., Pang, F., Wang, H. T., Zhu, J. W., and Chen, Y. S. (2020). Energy Dissipation-Based Method for Strength Determination of Rock under Uniaxial Compression. Shock and Vibration 2020, 8865958. doi:10.1155/2020/8865958

CrossRef Full Text | Google Scholar

Huang, D., and Li, Y. (2014). Conversion of Strain Energy in Triaxial Unloading Tests on Marble. Int. J. Rock Mech. Mining Sci. 66, 160–168. doi:10.1016/j.ijrmms.2013.12.001

CrossRef Full Text | Google Scholar

Kang, Y., Fan, J., Jiang, D., and Li, Z. (2021). Influence of Geological and Environmental Factors on the Reconsolidation Behavior of Fine Granular Salt. Nat. Resour. Res. 30 (1), 805–826. doi:10.1007/s11053-020-09732-1

CrossRef Full Text | Google Scholar

Li, M., Zhang, J., Zhou, N., and Huang, Y. (2017). Effect of Particle Size on the Energy Evolution of Crushed Waste Rock in Coal Mines. Rock Mech. Rock Eng. 50, 1347–1354. doi:10.1007/s00603-016-1151-5

CrossRef Full Text | Google Scholar

Li, X., Li, Q., Hu, Y., Teng, L., and Yang, S. (2021). Evolution Characteristics of Mining Fissures in Overlying Strata of Stope after Converting from Open-Pit to Underground. Arab. J. Geosci. 14 (24), 2795. doi:10.1007/s12517-021-08978-0

CrossRef Full Text | Google Scholar

Li, X., Li, Q., Hu, Y., Chen, Q., Peng, J., Xie, Y., et al. (2022). Study on Three-Dimensional Dynamic Stability of Open-Pit High Slope under Blasting Vibration. Lithosphere 2022, 6426550. doi:10.2113/2022/5426550

CrossRef Full Text | Google Scholar

Liu, W., Zhang, S., and Sun, B. (2019). Energy Evolution of Rock under Different Stress Paths and Establishment of a Statistical Damage Model. KSCE J. Civ. Eng. 23 (10), 4274–4287. doi:10.1007/s12205-019-0590-4

CrossRef Full Text | Google Scholar

Liu, W., Zhang, X., Fan, J., Zuo, J., Zhang, Z., and Chen, J. (2020a). Study on the Mechanical Properties of Man-Made Salt Rock Samples with Impurities. J. Nat. Gas Sci. Eng. 84, 103683. doi:10.1016/j.jngse.2020.103683

CrossRef Full Text | Google Scholar

Liu, W., Zhang, Z., Fan, J., Jiang, D., Li, Z., and Chen, J. (2020b). Research on Gas Leakage and Collapse in the Cavern Roof of Underground Natural Gas Storage in Thinly Bedded Salt Rocks. J. Energ. Storage 31, 101669. doi:10.1016/j.est.2020.101669

CrossRef Full Text | Google Scholar

Meng, Q., Zhang, M., Han, L., Pu, H., and Nie, T. (2016). Effects of Acoustic Emission and Energy Evolution of Rock Specimens under the Uniaxial Cyclic Loading and Unloading Compression. Rock Mech. Rock Eng. 49, 3873–3886. doi:10.1007/s00603-016-1077-y

CrossRef Full Text | Google Scholar

Meng, Q., Zhang, M., Zhang, Z., Han, L., and Pu, H. (2019). Research on Non-Linear Characteristics of Rock Energy Evolution under Uniaxial Cyclic Loading and Unloading Conditions. Environ. Earth. Sci. 78 (23), 650. doi:10.1007/s12665-019-8638-9

CrossRef Full Text | Google Scholar

Song, S., Liu, X., Tan, Y., Fan, D., Ma, Q., and Wang, H. (2020). Study on Failure Modes and Energy Evolution of Coal-Rock Combination under Cyclic Loading. Shock and Vibration 2020, 5731721. doi:10.1155/2020/5731721

CrossRef Full Text | Google Scholar

Tang, Y. J., Hao, T. X., Li, F., Zhao, L. Z., and Liu, J. (2022). Energy Evolution and Infrared Radiation Characterization of Coal Rocks Considering Strain Rate Effect. Chin. J. Rock Mech. Rock Eng. 41, 1–10. doi:10.13722/j.cnki.jrme.2021.0952

CrossRef Full Text | Google Scholar

Wang, Y., and Cui, F. (2018). Energy Evolution Mechanism in Process of Sandstone Failure and Energy Strength Criterion. J. Appl. Geophys. 154, 21–28. doi:10.1016/j.jappgeo.2018.04.025

CrossRef Full Text | Google Scholar

Wang, P., Xu, J., Fang, X., and Wang, P. (2017). Energy Dissipation and Damage Evolution Analyses for the Dynamic Compression Failure Process of Red-Sandstone after Freeze-Thaw Cycles. Eng. Geology. 221, 104–113. doi:10.1016/j.enggeo.2017.02.025

CrossRef Full Text | Google Scholar

Wang, Y., Feng, W. K., and Li, C. H. (2020a). On Anisotropic Fracture and Energy Evolution of marble Subjected to Triaxial Fatigue Cyclic-Confining Pressure Unloading Conditions. Int. J. Fatigue 134, 105524. doi:10.1016/j.ijfatigue.2020.105524

CrossRef Full Text | Google Scholar

Wang, J., Zhang, Q., Song, Z., and Zhang, Y. (2020b). Creep Properties and Damage Constitutive Model of Salt Rock under Uniaxial Compression. Int. J. Damage Mech. 29 (6), 902–922. doi:10.1177/1056789519891768

CrossRef Full Text | Google Scholar

Wang, C. L., He, B. B., Hou, X. L., Li, J. Y., and Liu, L. (2020c). Stress-Energy Mechanism for Rock Failure Evolution Based on Damage Mechanics in Hard Rock. Rock Mech. Rock Eng. 53 (3), 1021–1037. doi:10.1007/s00603-019-01953-y

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, B., Li, B., and Li, C. (2021a). A Strain-Based Fatigue Damage Model for Naturally Fractured Marble Subjected to Freeze-Thaw and Uniaxial Cyclic Loads. Int. J. Damage Mech. 30 (10), 1594–1616. doi:10.1177/10567895211021629

CrossRef Full Text | Google Scholar

Wang, Y., Han, J. Q., Song, Z. Y., and Zhu, C. (2021b). Macro-Meso Failure Behavior of Pre-Flawed Hollow-Cylinder Granite under Multi-Level Cyclic Loads: Insights from Acoustic Emission and Post-Test CT Scanning. Eng. Fracture Mech. 258, 108074. doi:10.1016/j.engfracmech.2021.108074

CrossRef Full Text | Google Scholar

Wang, Y., Feng, W. K., Hu, R. L., and Li, C. H. (2021c). Fracture Evolution and Energy Characteristics during marble Failure under Triaxial Fatigue Cyclic and Confining Pressure Unloading (FC-CPU) Conditions. Rock Mech. Rock Eng. 54 (2), 799–818. doi:10.1007/s00603-020-02299-6

CrossRef Full Text | Google Scholar

Wang, J., Zhang, Q., Song, Z., and Zhang, Y. (2021d). Experimental Study on Creep Properties of Salt Rock under Long-Period Cyclic Loading. Int. J. Fatigue 143, 106009. doi:10.1016/j.ijfatigue.2020.106009

CrossRef Full Text | Google Scholar

Wang, J., Wang, X., Zhang, Q., Song, Z., and Zhang, Y. (2021e). Dynamic Prediction Model for Surface Settlement of Horizontal Salt Rock Energy Storage. Energy 235, 121421. doi:10.1016/j.energy.2021.121421

CrossRef Full Text | Google Scholar

Wang, J., Zhang, Q., Song, Z., Zhang, Y., and Liu, X. (2021f). Mechanical Properties and Damage Constitutive Model for Uniaxial Compression of Salt Rock at Different Loading Rates. Int. J. Damage Mech. 30 (5), 739–763. doi:10.1177/1056789520983868

CrossRef Full Text | Google Scholar

Wang, Y., Zhu, C., Song, Z. Y., and Gong, S. (2022a). Macro-Meso Failure Characteristics of Circular Cavity-Contained Granite under Unconventional Cyclic Loads: A Lab-Scale Testing. Measurement 188, 110608. doi:10.1016/j.measurement.2021.110608

CrossRef Full Text | Google Scholar

Wang, J., Zhang, Q., Song, Z., Feng, S., and Zhang, Y. (2022b). Nonlinear Creep Model of Salt Rock Used for Displacement Prediction of Salt Cavern Gas Storage. J. Energ. Storage 48, 103951. doi:10.1016/j.est.2021.103951

CrossRef Full Text | Google Scholar

Wang, X. Y., Ma, Z., and Zhang, Y. T. (2022c). Research on Safety Early Warning Standard of Large-Scale Underground Utility Tunnel in Ground Fissure Active Period. Front. Earth Sci. 10, 828477. doi:10.3389/feart.2022.828477

CrossRef Full Text | Google Scholar

Wang, J., Zhang, Q., Song, Z., Liu, X., Wang, X., and Zhang, Y. (2022d). Microstructural Variations and Damage Evolvement of Salt Rock under Cyclic Loading. Int. J. Rock Mech. Mining Sci. 152, 105078. doi:10.1016/j.ijrmms.2022.105078

CrossRef Full Text | Google Scholar

Wang, X., Song, Q., and Gong, H. (2022e). Research on Deformation Law of Deep Foundation Pit of Station in Core Region of Saturated Soft Loess Based on Monitoring. Adv. Civil Eng. 2022, 848152. doi:10.1155/2022/7848152

CrossRef Full Text | Google Scholar

Xie, H., Li, L., JuPeng, Y. R. D., Peng, R., and Yang, Y. (2011). Energy Analysis for Damage and Catastrophic Failure of Rocks. Sci. China Technol. Sci. 54, 199–209. doi:10.1007/s11431-011-4639-y

CrossRef Full Text | Google Scholar

Yang, S., Wang, J., Ning, J., and Qiu, P. (2019). Experimental Study on Mechanical Properties, Failure Behavior and Energy Evolution of Different Coal-Rock Combined Specimens. Appl. Sci. 9 (20), 4427. doi:10.3390/app9204427

CrossRef Full Text | Google Scholar

Yang, D., Hu, J., and Ding, X. (2020a). Analysis of Energy Dissipation Characteristics in Granite under High Confining Pressure Cyclic Load. Alexandria Eng. J. 59 (5), 3587–3597. doi:10.1016/j.aej.2020.06.004

CrossRef Full Text | Google Scholar

Yang, L., Gao, F. Q., and Wang, X. Q. (2020b). Mechanical Response and Energy Partition Evolution of Coal-Rock Combinations with Different Strength Ratios. Chin. J. Rock Mech. Rock Eng. 39 (S2), 3297–3305. doi:10.13722/j.cnki.jrme.2020.0456

CrossRef Full Text | Google Scholar

Zhang, Z., and Gao, F. (2015). Experimental Investigation on the Energy Evolution of Dry and Water-Saturated Red Sandstones. Int. J. Mining Sci. Technol. 25 (3), 383–388. doi:10.1016/j.ijmst.2015.03.009

CrossRef Full Text | Google Scholar

Zhang, L. M., Gao, S., Ren, M. Y., Wang, Z. Q., and Ma, S. Q. (2014). Rock Elastic Strain Energy and Dissipation Strain Energy Evolution Characteristics under Conventional Triaxial Compression. J. China Coal Soc. 39 (7), 1238–1242. doi:10.13225/j.cnki.jccs.2013.1318

CrossRef Full Text | Google Scholar

Zhang, M., Meng, Q., and Liu, S. (2017). Energy Evolution Characteristics and Distribution Laws of Rock Materials under Triaxial Cyclic Loading and Unloading Compression. Adv. Mater. Sci. Eng. 2017, 5471571. doi:10.1155/2017/5471571

CrossRef Full Text | Google Scholar

Zhang, Y., Feng, X.-T., Zhang, X., Wang, Z., Sharifzadeh, M., Yang, C., et al. (2019). Strain Energy Evolution Characteristics and Mechanisms of Hard Rocks under True Triaxial Compression. Eng. Geology. 260, 105222. doi:10.1016/j.enggeo.2019.105222

CrossRef Full Text | Google Scholar

Zhang, Y. W., Fan, S. Y., Yang, D. H., and Zhou, F. (2022). Investigation About Variation Law of Frost Heave Force of Seasonal Cold Region Tunnels: A Case Study. Front. Earth Sci. 9, 806843. doi:10.3389/feart.2021.806843

CrossRef Full Text | Google Scholar

Zhang, J., Zhang, X., Huang, Z., Yi, Y., and Zhao, X. (2021a). Energy Evolution Mechanism of the Mechanical and Creep Properties of Layered Phyllite under Uniaxial Compression and Creep Tests. Arab. J. Geosci. 14 (22), 2437. doi:10.1007/s12517-021-08757-x

CrossRef Full Text | Google Scholar

Zhang, X., Liu, W., Jiang, D., Qiao, W., Liu, E., Zhang, N., et al. (2021b). Investigation on the Influences of Interlayer Contents on Stability and Usability of Energy Storage Caverns in Bedded Rock Salt. Energy 231, 120968. doi:10.1016/j.energy.2021.120968

CrossRef Full Text | Google Scholar

Zhang, L., Wang, G. L., Lei, R. D., Wen, X. X., Liu, B. L., and Sun, F. (2021c). Energy Damage Evolution Mechanism of Single Jointed Rock Mass with Different Lengths under Uniaxial Compression. China J. Highw. Transp. 34 (1), 24–34. doi:10.19721/j.cnki.1001-7372.2021.01.003

CrossRef Full Text | Google Scholar

Zhang, Z. Z. (2013). Energy Evolution Mechanism during Rock Deformation and Failure. China Uni. Min. Technol Doctoral Thesis, 22–25.

Google Scholar

Zhao, K., Yu, X., Zhou, Y., Wang, Q., Wang, J., and Hao, J. (2020). Energy Evolution of Brittle Granite under Different Loading Rates. Int. J. Rock Mech. Mining Sci. 132, 104392. doi:10.1016/j.ijrmms.2020.104392

CrossRef Full Text | Google Scholar

Zhou, Y., Sheng, Q., Li, N., and Fu, X. (2020). The Influence of Strain Rate on the Energy Characteristics and Damage Evolution of Rock Materials under Dynamic Uniaxial Compression. Rock Mech. Rock Eng. 53 (8), 3823–3834. doi:10.1007/s00603-020-02128-w

CrossRef Full Text | Google Scholar

Zhou, P. Y., Wang, J. B., Song, Z. P., Cao, Z. L., and Pei, Z. M. (2022). Construction Method Optimization for Transfer Section between Cross Passage and Main Tunnel of Metro Station. Front. Earth Sci. 10, 770888. doi:10.3389/feart.2022.770888

CrossRef Full Text | Google Scholar