Experimental study on shear wave velocity of sand-gravel mixtures considering the effect of gravel content

Sand-gravel mixtures are special engineering geological materials between soils and fractured rocks. This study performs a series of bending element tests to systematically investigate the shear wave velocity (V_s) of the sand-gravel mixtures, establish an effective evaluation method, and assess the influence of relative density and effective confining pressure on mixtures with a wide range of gravel contents. The results showed that the shear wave velocity increases and then decreases with the increase in gravel content and increases with the rise in relative density and effective confining pressure. Furthermore, a shear wave velocity prediction model is proposed in this study based on the intergranular contact state theory, including the stress parameter (n) and skeleton void ratio. The stress parameter can be described by a power function considering the uniformity coefficient. The model serves as a reference guide for estimating the shear wave velocity of sand-gravel mixtures with a wide range of gravel contents.

Introduction

Sand-gravel mixtures are special engineering geological materials between soils and fractured rocks, and the intergranular contact state of sand-gravel mixtures is the intermediate state between that of sand and gravel particles (Evans and Zhou, 1995; Yagiz, 2001; Lin et al., 2004; Hamidi et al., 2009). The sand-gravel mixtures with the advantages of low compressibility, high shear strength, abundant reserves, and convenient and economical extraction are widely used in highway roads, Earth and rock dams, soft ground treatments, artificial island buildings, offshore immersed tunnel mat foundations, etc., (Hara et al., 2004; Araei et al., 2012; Flora et al., 2012; Chang and Phantachang, 2016). The shear wave velocity (V_s) and associated small-strain (or maximum) shear modulus (G_max) play fundamental roles in soil deformation prediction, seismic liquefaction potential assessment, site response analyses, and the design of geotechnical structures subjected to dynamic or earthquake loadings (Andrus and Stokoe, 2000; Wang et al., 2012; Chen et al., 2019a). Simultaneously, the mechanical response of granular materials during scouring and erosion is an essential property that scholars have widely studied (Kuhnle et al., 2016; Pandey et al., 2019a; 2019b, 2020; de Leeuw et al., 2019). In this paper, the dynamic properties of sand-gravel mixtures are investigated from the view of V_s in laboratory tests aiming to establish a prediction method as a reference guide for geotechnical engineering.

Rollins et al. (1998) found that for a given void ratio (e) and effective confining pressure ${{\sigma }_0}^{\prime }$, G_max of sand-gravel mixtures with different gradations increases by 38% as the gravel content (G_c) increases from 0% to 60% during dynamic triaxial tests. Chang et al. (2014) showed that the V_s of gap-graded sand-gravel mixtures increase linearly with increasing G_c for the same skeleton void ratio by conducting a series of bending element tests. Menq (2003) found that for a given relative density (D_r), G_max of sand-gravel mixtures tended to increase with the rise in the non-uniformity coefficient (C_u) and average particle size (d₅₀), with the effect of d₅₀ on G_max being more significant than that of the C_u. Menq and Stokoe (2003) found that the combined effect of C_u and d₅₀ can be represented by the stress exponent (n), which gradually increases with the rise in C_u, and that the effect of n on the G_max of well-graded loose sand-gravel mixtures is more significant than that of gap-graded dense sand-gravel mixtures. Liu et al. (2020) performed bending element tests on pure sands, pure gravels, and sand-gravel mixtures with different gradations and highlighted that the values of G_max in sand-gravel mixtures could not be adequately quantified using e and ${{\sigma }_0}^{\prime }$. They also concluded that the G_max of pure sands and pure gravels is almost unaffected by d₅₀, instead of increasing with d₅₀ for well-graded sand-gravel mixtures. During the subsequent investigation (Liu et al., 2021), they found that C_u and d₅₀ have significantly opposite effects on the G_max of the sand-gravel mixtures, which contradicts the conclusion of Menq (2003).

Many methods are available for measuring soil V_s, such as the up-hole method, down-hole method, cross-hole method, indoor resonance column test, and bending element test method. (Wichtmann et al., 2015). The bending element test has been widely used in measuring V_s or G_max of various soils due to its simple principle, convenient operation, and non-destructive detection (Rahman et al., 2014; Yang and Liu, 2016).

This paper performs a series of bender element tests to study the V_s of the sand-gravel mixtures with a wider range of G_c in this study than that in previous studies. Within the study context, the effects of gravel content, relative density, and effective confining pressure are considered. Finally, a V_s prediction model of various mixed soil materials is proposed based on intergranular contact state theory. The applicability of the proposed model is validated using the published data of two types of coarse and fine granular mixtures.

Bender element test

Test material

The tested sand-gravel mixture was obtained from Nanjing, China. The gravel grains of the mixture are prismatic. The mixture’s gravel content (G_c) is 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 100%. The particle size distribution curves of various sand-gravel mixtures are shown in Figure 1. The basic properties of the mixtures are listed in Table 1. The mixtures’ particle size distribution curves and basic properties were measured according to the ASTM D4254-14, 2006 and ASTM D4254-16, 2006.

FIGURE 1

FIGURE 1. Particle size distribution curves of the tested sand-gravel mixtures.

TABLE 1

TABLE 1. Basic properties of the tested sand-gravel mixtures.

As shown in Table 1, the e_max and e_min of the mixtures both decrease and then increase with the rise in G_c, which is consistent with the findings of Evans and Zhou., (1995) and Amini and Chakravrty, 2004. In addition, the e_max and e_min reach the minimum value at G_c equals 50%.

Test apparatus and method

The measurement of shear wave velocity (V_s) and associated G_max was implemented using a pair of piezoceramic bender elements installed in the GCTS HCA-300 dynamic hollow cylinder-TSH testing system (Chen et al., 2019b). The test apparatus is shown in Figure 2. The confining and back pressure were measured using the standard pressure/volume controller. The axial static and dynamic force was controlled independently. Moreover, the maximum range of the dynamic force is 10 kN/5 Hz. The axial force and displacement sensors were placed at the top of the sample. Back pressure was applied at the top of the sample, and the excess pore water pressure was measured its bottom. Hardin and Black (1966), Goudarzy et al. (2016) detailed the testing principle of the bender element system.

FIGURE 2

FIGURE 2. Bender element test apparatus.

The V_s is calculated via Eq. 1:

$V_{\mathrm{s}}=\frac{d}{t}(1)$

where d is the effective distance of the shear wave propagation, and t is the time of the shear wave propagation.

The time domain method was used to determine t considering the simplicity and accuracy. Figure 3 shows the typical time histories of output signals from bender element tests, revealing that the received signals are always clear and efficient.

FIGURE 3

FIGURE 3. Typical time histories of output signals obtained from the bender element tests.

The cylindrical specimen has a diameter of 100 mm and a height of 150 mm. The specimen was prepared using a dry tamping method. This technique was adopted in several research works to test granular material. On the other hand, the well-mixed sand and grains were tamped into a cylindrical specimen creator for four layers in the apparatus using a dry tamping method. The pre-saturation was conducted after the specimen preparation. The pre-saturation consists of three steps: 1) permeating the specimen with CO₂ for 30 min; 2) flushing with de-aired water for 60 min; 3) flushing all water lines. After the pre-saturation, the back pressure saturation was initiated. Back pressure was gradually applied, and the Skempton B-value was checked until exceeding 0.95, which guaranteed the saturation of the tested sample. The saturated sample was consolidated under an effective target confining pressure until the strain was stable. After that, the bender element was conducted.

A series of bender element tests was conducted to study the V_s of the sand-gravel mixtures. The influence of relative density (D_r), effective confining pressure (${{\sigma }_0}^{\prime }$), and G_c were considered. The D_r of the mixtures was taken as 30%, 45%, and 70%. Additionally, the ${{\sigma }_0}^{\prime }$ of the mixtures was taken as 50, 100, 200, 300, and 400 kPa, and the G_c of the mixture was selected as 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 100%.

Test results and analysis

Vs analysis for sand-gravel mixtures

The relationship between the normalized effective confining pressure ${{\sigma }_0}^{\prime }/P_{\mathrm{a}}$ and V_s of the sand-gravel mixtures is shown in Figure 4, where the atmospheric pressure (P_a) is approximately equal to 100 kPa. It can be seen that for a given G_c and D_r, the mixtures' vs. increases with the rise in ${{\sigma }_0}^{\prime }/P_{\mathrm{a}}$. The reason may be that the greater the pressure, the greater the contact force between the particles, and the more the granular materials converge to a whole, which leads to easier shear wave propagation and increased propagation speed. Moreover, the V_s increases with the increase in D_r when the G_c and ${{\sigma }_0}^{\prime }/P_{\mathrm{a}}$ are given. The relationship between the V_s and ${{\sigma }_0}^{\prime }/P_{\mathrm{a}}$ can be described by Eq. 2:

$V_{\mathrm{s}}=A{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n(2)$

where A is the shear wave velocity value of the mixture when the ${{\sigma }_0}^{\prime }$ is 100 kPa, and n is the best-fit coefficient, which reflects the influence of ${{\sigma }_0}^{\prime }$ on the V_s.

FIGURE 4

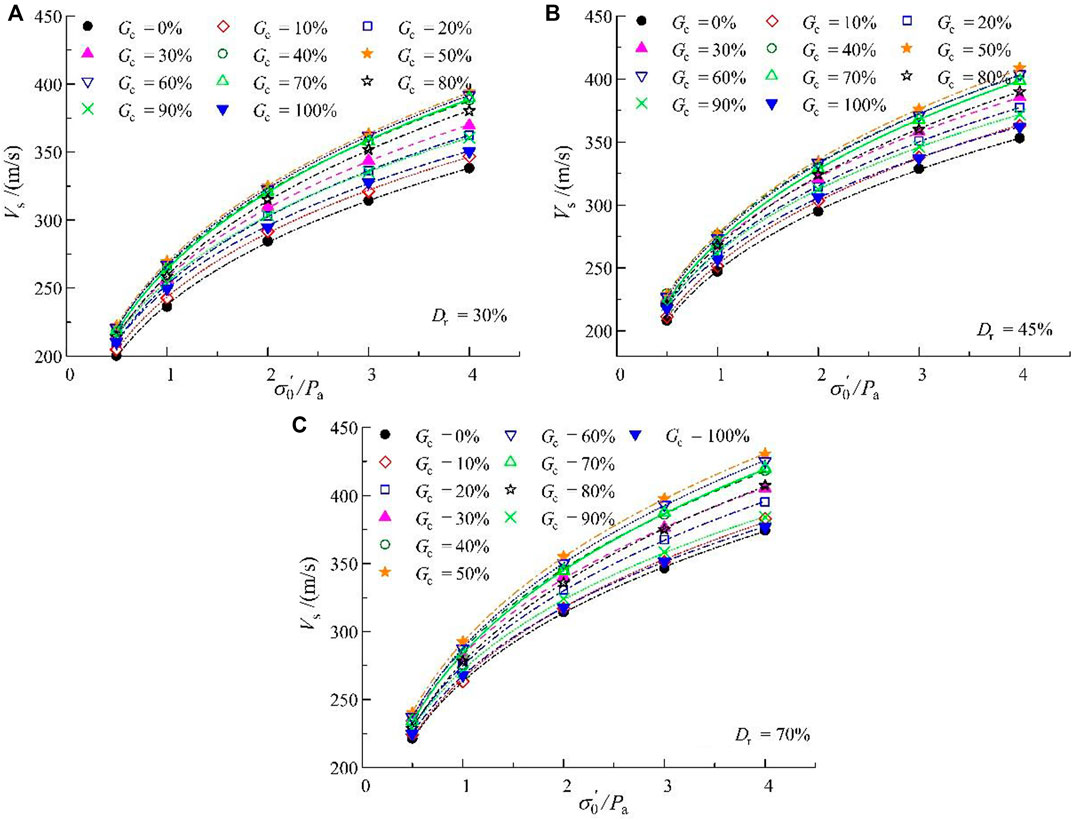
FIGURE 4. Relationship between the normalized effective confining pressure and V_s of the sand-gravel mixtures: (A) D_r = 30% (B) D_r = 45% (C) D_r = 70%.

The relationship between the fit coefficient n and coefficients of uniformity (C_u) for the mixtures is shown in Figure 5. It can be seen that the n increases with the increase in C_u. The relationship between the n and C_u can be described by Eq. 3:

$n=M{C}_{\mathrm{u}}^N(3)$

where M and N are the best-fit coefficients, which for the sand-gravel mixture of this test are defined as M is 0.24, and N is 0.04. The goodness of fit (R²) for this equation is 0.95.

FIGURE 5

FIGURE 5. Relationship between the fit coefficient n and coefficient of uniformity.

The relationship between the normalized shear wave velocity, $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ , and G_c of the sand-gravel mixtures is depicted in Figure 6. It can be seen that the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ increases and then decreases with the increase in G_c. The $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ reaches its peak when the G_c is 50%, meaning that the threshold gravel content value (G_cth) of the sand-gravel mixtures is 50%. The reason is that part of the force chain in sand particles is replaced by that of sand-gravel and gravel grains as the G_c increases. The contact area of the mixture grains increases, the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ increases first. However, the sand particles fill the void of the gravel grains, and the force chain of sand particles is invalid when the increase in G_c exceeds the G_cth. As a result, the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ decreases.

FIGURE 6

FIGURE 6. Relationship between the normalized shear wave velocity and the G_c of the mixtures.

The relationship between the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ and e of the sand-gravel mixtures is shown in Figure 7. Generally, the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ decreases with the rise in e. The relationship between the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ and e can be described using a power function when the G_c is given. However, the relationship between the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ and e described by a power function varies with respect to G_c. Accordingly, the e is not a reasonable parameter to describe the dense state of the sand-gravel mixtures.

FIGURE 7

FIGURE 7. Relationship between the normalized shear wave velocity and e of the mixtures.

Vs prediction method for sand-gravel mixtures

Sand-gravel mixture is composed of coarse gravel grain and fine sand particles, which is a fine-coarse grained mixture. Microstructural changes can affect the macro mechanical properties (Bai et al., 2019; Bai et al., 2021; Bai et al., 2022). The sand-gravel mixture’s force skeleton depends on the sand and gravel content, and the part that fills the void is invalid for the force skeleton. The force skeleton is composed of coarse gravel grain when the G_c is larger than G_cth. However, the force skeleton is composed of fine sand particles when the G_c is smaller than G_cth. The skeleton void ratio (e_sk) is defined as the volumetric ratio between the voids formed in the sand-gravel mixture skeleton and the volume of particles that make up the skeleton (Chang et al., 2014). This is used to describe the dense state of the fine-coarse-grained mixture. Thevanayagam (2007a, 2007b) proposed a binary intergranular contact theory of the fine-coarse-grained mixture and believed the particle contact state is divided into two types. The intergranular contact state of the sand-gravel mixture is shown in Figure 8.

FIGURE 8

FIGURE 8. Intergranular contact states of the mixtures.

The e_sk is calculated using Eqs 4, 5 when the intergranular contact state of the sand-gravel mixtures is in contact states 1 and 2, respectively. R_d is the average grain size ratio, which is the ratio of d_50-g and d_50-s. The d_50-g is the average size of the gravel, and d_50-s is the average size of the sand. b is the sand’s influence index, which ranges from 0 to 1. The sand particle is invalid for the force skeleton of the sand-gravel mixture when b is 0. Furthermore, the sand particles can be used in the force skeleton when b is 1. m is the gravel’s influence index that ranges from 0 to 1. The b and m can be determined using a back-fitting analysis (Thevanayagam, , ).

$e_{\text{sk}}=\frac{e+\left(1-b\right)\cdot \left(1-G_{\mathrm{c}}\right)}{1-\left(1-b\right)\cdot \left(1-G_{\mathrm{c}}\right)}(4)$

$e_{\text{sk}}=\frac{e}{1-G_{\mathrm{c}}+G_{\mathrm{c}}/R_{\mathrm{d}}^{\mathrm{m}}}(5)$

The relationship between the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ and e_sk of the sand-gravel mixtures is shown in Figure 9. It can be seen that the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ decreases with the increase in e_sk. The relationship between the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ and e_sk can be fitted by two curves using Eq. 6, and the G_cth is the critical value. The mechanical behavior of the sand-gravel mixtures under the same e_sk is similar to that of pure gravel (G_c = 100%) when the G_c is larger than G_cth. Moreover, the mechanical behavior of the sand-gravel mixtures under the same e_sk is similar to that of pure sand (G_c = 0) when the G_c is smaller than G_cth. As a result, the relationship between the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ and e_sk fitted by two curves using Eq. 6 is reasonable.

$V_{\mathrm{s}}=A_2{\left(\frac{{\sigma }_0^{\prime }}{P_{\mathrm{a}}}\right)}^{M\times C_{\mathrm{u}}^N}(6)$

where A₂ and B₂ are the best-fit parameters determined as A₂ is 210.29, B₂ is -0.41 when the G_c is smaller than G_cth, and A₂ is 216.48, and B₂ is -0.53 when the G_c is larger than G_cth.

FIGURE 9

FIGURE 9. Relationship between the normalized shear wave velocity and e_sk of the mixtures.

Applicability validation of V_s prediction method

A series of bending element tests were conducted by Choo and Burns (2015) and Oka et al. (2018) to investigate the effects of fine granular content (FC) on V_s of coarse and fine granular mixtures. In this section, test data published in the previous literature were used to further verify the applicability of Eq. 6 for two types of coarse and fine granular mixtures. The V_s versus e_sk curves for two types of coarse and fine granular mixtures are shown in Figure 10. It can be clearly observed that e_sk can normalize V_s, indicating that it is reasonable for e_sk to V_s of coarse and fine granular mixtures.

FIGURE 10

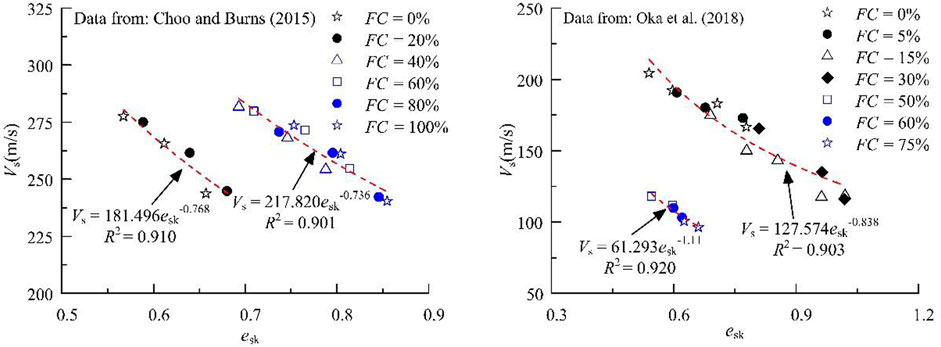
FIGURE 10. Relationship between V_s and e_sk for two types of coarse and fine granular mixtures obtained from the literature.

Conclusion

In this paper, a series of bending element tests are conducted to investigate the shear wave velocity V_s of the sand-gravel mixtures. Sand as the base soil and different contents of gravel are considered in the testing program. Moreover, bending element tests are performed at three relative densities of 30%, 45%, and 70% under an effective confining pressure of 50, 100, 200, 300, and 400 kPa.

Results of the tests illustrate that for a given D_r and ${{\sigma }_0}^{\prime }$, the V_s increases and then decreases with the rise in G_c. Moreover, the V_s increases with the increase in D_r and ${{\sigma }_0}^{\prime }$ under the same G_c. The relationship between the V_s and ${{\sigma }_0}^{\prime }$ can be described using an exponential function. The fitting parameter n increases with the increase in C_u, and the relationship between n and C_u can be described using a power function.

The e is not a reasonable parameter to describe the dense state of the sand-gravel mixtures. A new V_s prediction model is proposed based on intergranular contact state theory, including the skeleton void ratio e_sk. The $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ decreases with the increase in e_sk, and the relationship between the $V_{\mathrm{s}}/{\left({\sigma }_0^{\prime }/P_{\mathrm{a}}\right)}^n$ and e_sk can be described using a power function. The applicability of the proposed model is validated using published data regarding two types of coarse and fine granular mixtures.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

KC: Conceptualization, Methodology, Writing—original draft, Funding acquisition. HW: Data curation, Visualization. YF: Conceptualization, Writing—review and editing, Supervision. QW: Writing—review and editing, Funding acquisition.

Funding

This work is supported by the Natural Science Foundation of China (Grant No. 52208351), the Scientific and Technological Projects of Henan Province (Grant No. 222102320296), and the Start-Up Foundation of the Nanyang Institute of Technology (Grant No. NGBJ-2020-08).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amini, F., and Chakravrty, A. (2004). Liquefaction testing of layered sand-gravel composites. Geotechnical Test. J. 27 (1), 36–46.

Google Scholar

Andrus, R. D., and Stokoe, K. H. (2000). Liquefaction resistance of soils from shear-wave velocity. J. Geotech. Geoenviron. Eng. 126 (11), 1015–1025. doi:10.1061/(asce)1090-0241(2000)126:11(1015)

CrossRef Full Text | Google Scholar

Araei, A. A., Soroush, A., Tabatabaei, S. H., and Ghalandarzadeh, A. (2012). Consolidated undrained behavior of gravelly materials. Sci. Iran. 19 (6), 1391–1410. doi:10.1016/j.scient.2012.09.011

CrossRef Full Text | Google Scholar

ASTM D4253-16 (2006). Standard test methods for maximum index density and unit weight of soils using a vibratory table. Annu. Book ASTM Stand. 19, e782.

Google Scholar

ASTM D4254-14 (2006). Standard test methods for minimum index density and unit weight of soils and calculation of relative density. Annu. Book ASTM Stand. 45, 322.

Google Scholar

Bai, B., Wang, Y., Rao, D. Y., and Bai, F. (2022). The effective thermal conductivity of unsaturated porous media deduced by pore-scale SPH simulation. Front. Earth Sci. (Lausanne). 10, 943853. doi:10.3389/feart.2022.943853

CrossRef Full Text | Google Scholar

Bai, B., Yang, G. C., Li, T., and Yang, G. S. (2019). A thermodynamic constitutive model with temperature effect based on particle rearrangement for geomaterials. Mech. Mater. 139, 103180. doi:10.1016/j.mechmat.2019.103180

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Cai, G. P., Hu, W., and Yang, G. C. (2021). Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotechnics 137 (8), 104272. doi:10.1016/j.compgeo.2021.104272

CrossRef Full Text | Google Scholar

Chang, W. J., Chang, C. W., and Zeng, J. K. (2014). Liquefaction characteristics of gap-graded gravelly soils in K₀ condition. Soil Dyn. Earthq. Eng. 56, 74–85. doi:10.1016/j.soildyn.2013.10.005

CrossRef Full Text | Google Scholar

Chang, W. J., and Phantachang, T. (2016). Effects of gravel content on shear resistance of gravelly soils. Eng. Geol. 207, 78–90. doi:10.1016/j.enggeo.2016.04.015

CrossRef Full Text | Google Scholar

Chen, G. X., Kong, M. Y., Khoshnevisan, S., Chen, W. Y., and Li, X. J. (2019a). Calibration of Vs-based empirical models for assessing soil liquefaction potential using expanded database. Bull. Eng. Geol. Environ. 78 (2), 945–957. doi:10.1007/s10064-017-1146-9

CrossRef Full Text | Google Scholar

Chen, G. X., Zhao, D. F., Chen, W. Y., and Juang, C. H. (2019b). Excess pore water pressure generation in cyclic undrained testing. J. Geotech. Geoenviron. Eng. 145 (7), 04019022. doi:10.1061/(asce)gt.1943-5606.0002057

CrossRef Full Text | Google Scholar

Choo, H., and Burns, S. E. (2015). Shear wave velocity of granular mixtures of silica particles as a function of finer fraction, size ratios and void ratios. Granul. Matter 17, 567–578. doi:10.1007/s10035-015-0580-2

CrossRef Full Text | Google Scholar

De Leeuw, J., Lamb, M. P., Parker, G., Moodie, A., Haught, D., Venditti, J. G., et al. (2019). Entrainment and suspension of sand and gravel. Earth Surf. Dynam. 8 (2), 485–504. doi:10.5194/esurf-8-485-2020

CrossRef Full Text | Google Scholar

Evans, M. D., and Zhou, S. (1995). Liquefaction behavior of sand-gravel composites. J. Geotech. Engrg. 121 (3), 287–298. doi:10.1061/(asce)0733-9410(1995)121:3(287)

CrossRef Full Text | Google Scholar

Flora, A., Lirer, S., and Silvestri, F. (2012). Undrained cyclic resistance of undisturbed gravelly soils. Soil Dyn. Earthq. Eng. 43, 366–379. doi:10.1016/j.soildyn.2012.08.003

CrossRef Full Text | Google Scholar

Goudarzy, M., Rahman, M. M., Konig, D., and Schanz, T. (2016). Influence of non-plastic fines content on maximum shear modulus of granular materials. Soils Found. 56 (6), 973–983. doi:10.1016/j.sandf.2016.11.003

CrossRef Full Text | Google Scholar

Hamidi, A., Yazdanjou, V., and Salimi, N. (2009). Shear strength characteristics of sand-gravel mixtures. Int. J. Geotechnical Eng. 3 (1), 29–38. doi:10.3328/ijge.2009.03.01.29-38

CrossRef Full Text | Google Scholar

Hara, T., Kokusho, T., and Hiraoka, R. (2004). “Undrained strength of gravelly soils with different particle gradations,” in Proceedings of the 13 th World Conference on Earthquake Engineering, Vancouver, BC, August 1–6.

Google Scholar

Hardin, B. O., and Black, W. L. (1966). Sand stiffness under various triaxial stresses. J. Soil Mech. Found. Div. 92 (SM2), 27–42. doi:10.1061/jsfeaq.0000865

CrossRef Full Text | Google Scholar

Kuhnle, R. A., Wren, D. G., and Langendoen, E. J. (2016). Erosion of sand from a gravel bed. J. Hydraul. Eng. 142 (2), 04015052. doi:10.1061/(asce)hy.1943-7900.0001071

CrossRef Full Text | Google Scholar

Lin, P. S., Chang, C. W., and Chang, W. J. (2004). Characterization of liquefaction resistance in gravelly soil: Large hammer penetration test and shear wave velocity approach. Soil Dyn. Earthq. Eng. 24 (9-10), 675–687. doi:10.1016/j.soildyn.2004.06.010

CrossRef Full Text | Google Scholar

Liu, X. Y., Zou, D. G., Liu, J. M., and Zheng, B. W. (2021). Predicting the small strain shear modulus of coarse-grained soils. Soil Dyn. Earthq. Eng. 141, 106468. doi:10.1016/j.soildyn.2020.106468

CrossRef Full Text | Google Scholar

Liu, X. Y., Zou, D. G., Liu, J. M., Zhou, C. G., and Zheng, B. W. (2020). Experimental study to evaluate the effect of particle size on the small strain shear modulus of coarse-grained soils. Measurement 163, 107954. doi:10.1016/j.measurement.2020.107954

CrossRef Full Text | Google Scholar

Menq, F. (2003). Dynamic properties of sandy and gravelly soils. Austin: The University of Texas.

Google Scholar

Menq, F. Y., and Stokoe, K. H. (2003). IS Lyon, e23154.Linear dynamic properties of sandy and gravelly soils from large-scale resonant testsDeformation Charact. geomaterials

CrossRef Full Text | Google Scholar

Oka, L. G., Dewoolkar, M., and Olson, S. M. (2018). Comparing laboratory-based liquefaction resistance of a sand with non-plastic fines with shear wave velocity-based field case histories. Soil Dyn. Earthq. Eng. 113, 162–173. doi:10.1016/j.soildyn.2018.05.028

CrossRef Full Text | Google Scholar

Pandey, M., Chen, S. C., Sharma, P. K., Ojha, C. S. P., and Kumar, V. (2019a). Local scour of armor layer processes around the circular pier in non-uniform gravel bed. Water 11 (7), 1421. doi:10.3390/w11071421

CrossRef Full Text | Google Scholar

Pandey, M., Lam, W. H., Cui, Y. G., Khan, M. A., Singh, U. K., and Ahmad, Z. (2019b). Scour around spur dike in sand–gravel mixture bed. Water 11 (7), 1417. doi:10.3390/w11071417

CrossRef Full Text | Google Scholar

Pandey, M., Oliveto, G., Pu, J. H., Sharma, P. K., and Ojha, C. S. P. (2020). Pier scour prediction in non-uniform gravel beds. Water 12 (6), 1696. doi:10.3390/w12061696

CrossRef Full Text | Google Scholar

Rahman, M. M., Lo, S. C. R., and Dafalias, Y. F. (2014). Modelling the static liquefaction of sand with low-plasticity fines. Géotechnique 64 (11), 881–894. doi:10.1680/geot.14.p.079

CrossRef Full Text | Google Scholar

Rollins, K. M., Evans, M. D., Diehl, N. B., and Daily, W. D. (1998). Shear modulus and damping relationships for gravels. J. Geotech. Geoenviron. Eng. 124 (5), 396–405. doi:10.1061/(asce)1090-0241(1998)124:5(396)

CrossRef Full Text | Google Scholar

Thevanayagam, S. (2007a). Intergrain contact density indices for granular mixes—I: Framework. Earthq. Engin. Engin. Vib. 6 (2), 123–134. doi:10.1007/s11803-007-0705-7

CrossRef Full Text | Google Scholar

Thevanayagam, S. (2007b). Intergrain contact density indices for granular mixes—II: Liquefaction resistance. Earthq. Engin. Engin. Vib. 6 (2), 135–146. doi:10.1007/s11803-007-0706-6

CrossRef Full Text | Google Scholar

Wang, Z. J., Luo, Y. S., Guo, H., and Tian, H. (2012). Effects of initial deviatoric stress ratios on dynamic shear modulus and damping ratio of undisturbed loess in China. Eng. Geol. 143-144, 43–50. doi:10.1016/j.enggeo.2012.06.009

CrossRef Full Text | Google Scholar

Wichtmann, T., Hernández, M. A. N., and Triantafyllidis, T. (2015). On the influence of a non-cohesive fines content on small strain stiffness, modulus degradation and damping of quartz sand. Soil Dyn. Earthq. Eng. 69, 103–114. doi:10.1016/j.soildyn.2014.10.017

CrossRef Full Text | Google Scholar

Yagiz, S. (2001). Brief note on the influence of shape and percentage of gravel on the shear strength of sand and gravel mixtures. Bull. Eng. Geol. Environ. 60 (4), 321–323. doi:10.1007/s100640100122

CrossRef Full Text | Google Scholar

Yang, J., and Liu, X. (2016). Shear wave velocity and stiffness of sand: The role of non-plastic fines. Geotechnique 66 (6), 500–514. doi:10.1680/jgeot.15.p.205

CrossRef Full Text | Google Scholar