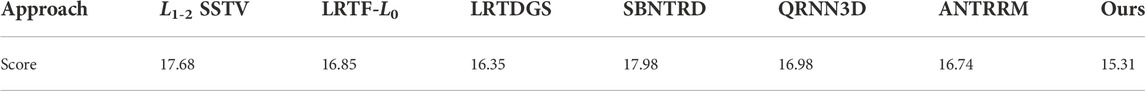Hyperspectral image restoration via hybrid smoothness regularized auto-weighted low-rank tensor ring factorization

Restoration of hyperspectral images (HSI) is a crucial step in many potential applications as a preprocessing step. Recently, low-rank tensor ring factorization was applied for HSI reconstruction, which has high-order tensors’ powerful and generalized representation ability. Although low-rank TR-based approaches with nuclear norm regularization achieved successful results for restoring hyperspectral images, there is still room for improved tensor low-rank approximation. In this article, we propose a novel Auto-weighted low-rank Tensor Ring Factorization with Hybrid Smoothness regularization (ATRFHS) for mixed noise removal in HSI. Nonlocal Cuboid Tensorization (NCT) is leveraged to transform HSI data into high-order tensors. TR factorization using latent factors rank minimization removes the mixed noise in HSI data. To highlight nuclear norms of factor tensors differently effective, an auto-weighted strategy is employed to reduce the more prominent factors while shrinking the smaller ones. A hybrid regularization combining total variation (TV) and phase congruency (PC) is incorporated into a low-rank tensor ring factorization model for the HSI noise removal problem. This efficient combination yields sharper edge preservation and resolves this weakness of existing pure TV regularization. Moreover, we develop an efficient algorithm for solving the resulting optimization problem using the framework of alternating minimization. Extensive experimental results demonstrate that our proposed method can significantly outperform existing approaches for mixed noise removal in HSI. The proposed algorithm is validated on synthetic and natural HSI data.

1 Introduction

Hyperspectral imaging is acquired by employing specialized sensors to capture data at numerous narrow wavelengths, ranging from 400 nm to 2500 nm in the same region. It is generally represented as a three-dimension image in which each image represents one of the tens or hundreds of narrow wavelength ranges or spectral bands. However, HSIs are frequently contaminated by various noises during the capture and transmission process, including Gaussian noise, stripes, deadlines, impulse noise, and hybrids (Bioucas-Dias et al., 2013), making further analysis and use of HSIs challenging. Therefore, the noise removal from HSI is an essential task as a preprocessing step and attracted lots of attention (Dabov et al., 2007; Zhang et al., 2013; Chen et al., 2017; Wu et al., 2017; Aggarwal and Majumdar, 2016; Wang et al., 2017; Zhang et al., 2014; Huang et al., 2017; Fan et al., 2017; Chen et al., 2018; Liu et al., 2012)).

Because a high-dimensional HSI is composed of hundreds of separate images banded together, each band of HSIs is regarded as a two-dimensional image. Then, traditional image restoration methods are applied to remove noise band-by-band, such as BM3D (Dabov et al., 2007) and low-rank matrix approximation (Zhang et al., 2013; Zhang et al., 2014; Chen et al., 2017). The matrix-based denoising approach uses conventional two-dimensional image denoising methods and unfolds the three-dimensional tensor into a matrix or treats each band independently. Traditional HSIs denoising algorithms can only evaluate the structural properties of each pixel or band separately, neglecting the significant relationships between all spectral bands and global structure information. Various improved approaches have been developed to compensate for the shortcomings by considering the correlation between all spectral bands.

An HSI is a three-dimensional image stack having two spatial dimensions and one spectral dimension. Therefore, tensors are realistic representations of HSIs data. For the past few years, to fully capture the spatial-spectral correlation of the HSIs, many researchers have employed tensor decompositions to analyze HSI, such as the low-rank tensor method with total variation regularization (Wu et al., 2017), tensor completion with three-layer transform via sparsity prior (Xue et al., 2019a) and Laplacian scale mixture (Xue et al., 2021; Xue et al., 2022), missing data recovery (Liu et al., 2014; Yokota et al., 2016), hyperspectral image super-resolution (Dian et al., 2019; Dian and Li, 2019), hyperspectral image restoration with low-rank tensor factorization (Zeng et al., 2020; Xiong et al., 2019; Chen et al., 2019a; He et al., 2022), and hyperspectral image denoising (Chen et al., 2022a; Chen et al., 2022b). These tensor decomposition approaches have the advantage of simultaneously investigating the spatial-spectral correlation between the HSIs inside all bands and better preserving the image’s spatial-spectral structure. Nevertheless, they fail to capture HSI’s intrinsic high-order low-rank structure and cannot keep a sharper edge.

Many studies have demonstrated the advantages of low-rank tensor approximation techniques in dealing with high-order tensor data. Recently, tensor-ring (TR) (Zhao et al., 2016; Huang et al., 2020) was developed to describe a high-order tensor as a sequence of cyclically contracted third-order tensors, which is the extensional version of tensor train (TT) (Oseledets, 2011). Due to its ability to promise to represent complex interactions within high-dimensional data, TR has received increasing attention. It was utilized in many high-dimensional incomplete data recovery applications, such as HSI CS reconstruction (Chen et al., 2020; He et al., 2019), tensor ring networks (Wang et al., 2018), tensor completion (Yuan et al., 2020; Ding et al., 2022), missing data recovery in high-dimensional images (Wang et al., 2021), and HSI denoising (Chen et al., 2019b; Xue et al., 2019b; Xuegang et al., 2022).

Compared to traditional tensor decomposition, TR decomposition imposed on the tensor approximation has two superiorities. First, the TR factor can be rotated equivalently and circularly in the trace operation, but the traditional tensor decomposition technique cannot turn the core tensor. Second, Since TR provides a tensor-by-tensor representation architecture, the original data structure can be better maintained.

Two representative works on the TR low-rankness characterization are low-rank TR decomposition (LTRD) and TR rank minimization (TRRM) (He et al., 2019). introduced a TR decomposition and total-variation regularized method for the missing information reconstruction of remote sensing images (Chen et al., 2020). described a nonlocal TR Decomposition for HSI denoising. Although the TRD-based approaches have shown good denoising results, TR rank parameter estimation is an NP-hard problem.

The TRRM-based methods, based on the nuclear norm, are a biased approximation to the TR rank and do not need to choose the optimal TR rank. It is more efficient than the former (Wang et al., 2021). presented a weighted TR decomposition model with TR factors nuclear norms and total variation regularization for missing data recovery in high-dimensional optical RS images (Chen et al., 2018). introduced the sum of nuclear norms of all unfolding matrices by the mode-k matricization as the convex surrogate of tensor Tucker rank for the tensor completion problem. To explore the latent features of the whole HSI data, a TRRM model with TR nuclear norm minimization is proposed by (Yuan et al., 2020) and elaborated by a convex surrogate of TR rank of circularly unfolding matrices for high-order missing data completion (Yu et al., 2019). proposed a TRRM-based method with nuclear norm regularization on the latent TR factors by exploiting the rank relationship between the tensor and the TR latent space. An improved version (Ding et al., 2022) by penalizing the logdet function onto TR unfolding matrices is proposed as remedies. However, these approaches are predicated on the convex relaxation by weight nuclear norm of the unbalanced TR unfolding matrices, which need manually choose the optimal weight values, resulting in poor solutions in execution. Furthermore, the conventional TR-based methods are inadequate to directly exploit the characteristics of low-rank by the original data and still have much room for improvement.

Due to the unfolding matrix with a much higher rank and larger size, the SVD operators of the rank minimization framework on the unfolding matrix in the TRRM-based methods are time-consuming (Wang et al., 2021). has employed three low-dimensional tensor factors of TR decomposition as a convex surrogate of TR rank for more convenient calculation. The SVD computation is considerably decreased due to the low dimension of TR factors. A better low-rank representation can be efficiently exploited by transforming lower-order tensors into higher-order tensors. As a result, TRRM-based approaches that leveraged low-rank and edge preservation on the original data were insufficient.

Inspired by the high effectiveness of rank minimization on TR latent factor for tensor completion, in this paper, to effectively promote the low-rankness of the solution, we introduce an auto-weight TR factors nuclear norm minimization with hybrid smoothness regularization by total variation (TV) and phase congruency (PC) to restore HSI image, which can more accurately approximate the TR rank and sharper promote edge preservation.

Contributions to this article are as follows.

1) To fully exploit the high-dimensional structure information and the low-rankness of HSI, an auto-weight TR nuclear norm, based on the convex relaxation by penalizing the weighted sum of nuclear norm of TR factors unfolding matrices, is proposed to recover the clean HSI part.

2) To highlight TR unfolding matrices differently effectively, an auto-weighted strategy is utilized to shrink the larger matrices while shrinking the smaller ones. By jointly regularizing TV and PC to promote local smoothness, this efficient combination yields sharper edge preservation and resolves this weakness of existing pure TV regularization.

3) An optimization algorithm with an alternating minimization framework is developed to solve the proposed approach efficiently. Experiments demonstrate that the proposed approach can effectively deal with gauss, strip, and mixed noise and outperform the state-of-the-art competitors in evaluation index and visual assessment.

This paper is organized as follows. To facilitate our presentation, we first introduce some notations, TR decomposition, tensor augmentation, and phase congruency regularization in Section 2. In Section 3, our proposed model is presented. We then develop an efficient framework of alternating minimization for solving the proposed model. In Section 4, extensive experiments on both simulated and real datasets were carried out to illustrate the merits of our model. We finally conclude this paper with some discussions on future research in Section 5.

2 Preliminaries

2.1 Background and notations

We deploy lowercase letters to denote scalars, e.g., $m\in \mathbb{R}$. And vectors are denoted by boldface lowercase letters, e.g., y. The upper case letters are represented for matrices, e.g., Y. An Nth-order tensor is given by lowercase letters calligraphic letters throughout this paper, e.g., $\mathcal{Y}\in {\mathbb{R}}^{I_{\mathbf{1}}\times {\mathit{I}}_{\mathbf{2}}...\times {\mathit{I}}_N}$ where I_j is the dimension of mode j and j=1,2 … , N. The (i₁, i₂, … , i_n) entry of tensor $\mathcal{Y}$ is given by $\mathcal{Y}\left(i_1,i_2,\dots ,i_{\mathrm{N}}\right)$. A tensor sequence is defined by the set $\{{\mathcal{Y}}^{\left(\mathit{k}\right)}{\}}_{k=1}^N:=\{{\mathcal{Y}}^{\left(1\right)},{\mathcal{Y}}^{\left(2\right)},...{,\mathcal{Y}}^{\left(N\right)}\}$, where ${\mathcal{Y}}^{\left(\mathit{k}\right)}$ is the kth tensor of the sequence. diag(Y) denoted a column vector consisting of the diagonal elements of Y. We use E to represent an identity matrix. The Frobenius norm of Y is defined as ${\Vert \mathit{Y}\Vert }_2^F=\sqrt{\langle \mathit{Y},\mathit{Y}\rangle }$. The nuclear norm ${\Vert \mathit{Y}\Vert }_{*}$ is the sum of singular values of a matrix Y.

2.2 Tensor ring low-rank factors

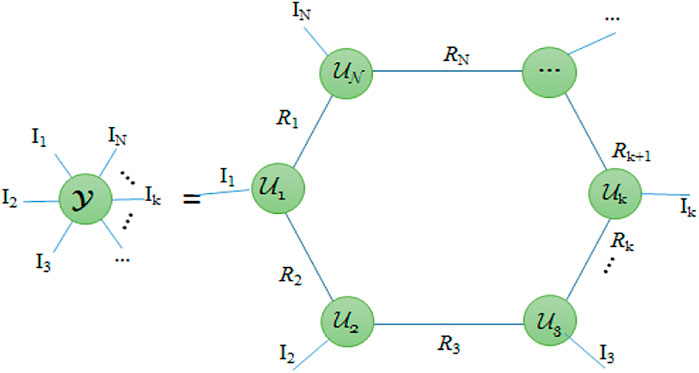
Tensor ring (TR) decomposition is briefly introduced in this subsection. TR representation is to decompose a tensor of higher order into a sequence of latent tensors. As shown in Figure 1, a linear tensor network can graphically represent the TR representation by circular multilinear products over a series of third-order tensors. The number of edges denotes the order of a tensor (which includes matrix and vector). The size of each mode is indicated by the number beside the edges (or dimension). A multilinear product operator between two tensors in a specific manner, also known as tensor contraction, corresponds to the summation over the indices of that mode when two nodes are connected.

FIGURE 1

FIGURE 1. Illustration of TR representation of an Nth-order tensor $\mathcal{Y}\in {\mathbb{R}}^{{\mathit{I}}_{\mathbf{1}}\times {\mathit{I}}_{\mathbf{2}}...\times {\mathit{I}}_{\mathit{N}}}$.

For i=1, … , N, the TR factors are denoted by a third-order tensor ${\mathcal{U}}_{\left(i\right)}\in {\mathbb{R}}^{r_{i-1}\times R_i\times r_i}$. The syntax {R₁, R₂, … , R_N, R_N+1}is indicated by the TR rank, which controls the model complexity of TR decomposition and satisfies the R₁= R_N+1. Then, $\mathcal{Y}$ can be estimated by tensor with TR format, as $\mathfrak{M}\left(\left[\mathcal{U}\right]\right)=<{\mathcal{U}}^{\left(1\right)},{\mathcal{U}}^{\left(2\right)},\dots ,{\mathcal{U}}^{\left(N\right)}>$. Therefore, the element-wise form can be expressed by $\mathcal{Y}\left(i_1,i_2,\dots ,i_{\mathrm{N}}\right)=\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({\mathcal{U}}^{\left(1\right)}\left(r_1,i_1,r_2\right),{\mathcal{U}}^{\left(2\right)}\left(r_2,i_2,r_3\right),\dots ,{\mathcal{U}}^{\left(N\right)}\left(r_N,i_N,r_1\right)\right)$. Trace(Y) is the matrix trace operation. $Y_{\left(n\right)}$ denotes the standard mode-n unfolding of tensor $\mathcal{Y}$.

The relationship between the tensor rank and the corresponding core tensor rank is elaborated, which can be explained by the following theorem. For the nth core tensor ${\mathcal{U}}^{\left(n\right)}$, according to the work of (Yuan et al., 2020; Chen et al., 2020), we define the $Y_{<n>}$ is another mode-n unfolding of tensor $\mathcal{Y}$ used in TR operations denoted by $Y_{<n>}\in {\mathbb{R}}^{I_n\times I_{n+1}...I_N{I_{1}I}_2\dots I_{n-1}}$. Thus, we have $Y_{<n>}=U_{\left(2\right)}^{\left(n\right)}{\left(U_{<2>}^{\left(\ne n\right)}\right)}^T$, where $U_{<2>}^{\left(\ne n\right)}$ is a matrix by the second unfolding along mode-2 by sequentially merging all core tensors except the nth one and $U_{\left(i\right)}^{\left(n\right)}\in {\mathbb{R}}^{R_i\times I_{n-1}{I}_n}$ is the mode-i unfolding of the nth core tensor. The relation of tensor ring rank and the corresponding factors rank have the following inequality for all n = 1, … , N.

$Rank\left(Y_{\left(n\right)}\right)\le Rank\left(U_{\left(2\right)}^{\left(n\right)}\right)(1)$

The detailed proof is available in (Yuan et al., 2020; Chen et al., 2020). The rank of the mode-n unfolding of the tensor $\mathcal{Y}$ is upper bounded by the rank of the dimension-mode unfolding of the corresponding core tensor ${\mathcal{U}}^{\left(n\right)}$, allowing us to impose a low-rank constraint on $\left[\mathcal{U}\right]$ to investigate the underlying tensor’s more low-rank structure.

2.3 Nonlocal cuboid tensorization for HSI augmentation

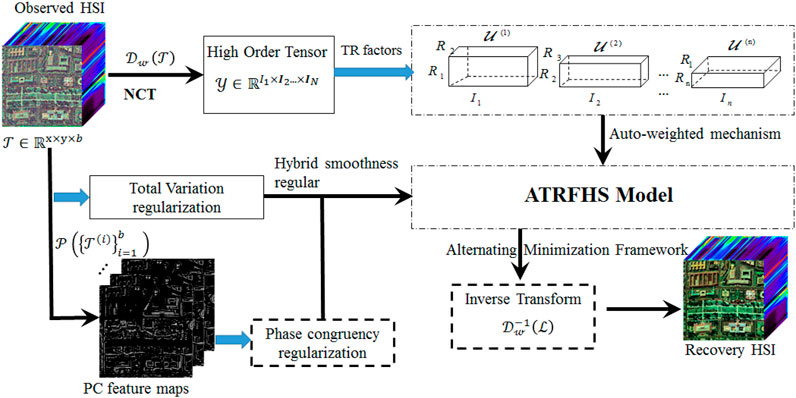
Tensor augmentation is an essential preprocessing step for exploiting the local structures and low-rank characteristics since higher-order tensors provide more significant image structure via TR decomposition. There are three main ways to transform a tensor into a higher-order one, namely the Reshape Operation (RO) (Yuan et al., 2019), high-order Hankelization (Yokota et al., 2018), and Ket Augmentation (KA) (Yuan et al., 2019). However, the recovered tensors applied RO and KA often have apparent blocking artifacts, while the data were permuted and rearranged without exploiting any neighborhood information. Patch Multiway Delay Embedding Transform (Yokota et al., 2018) is a high-order Hankelization approach, which provides a patch-wise procedure to extract more local information. But this technology increases the amount of HSI data, which makes high computational complexity. An augmented scheme called Nonlocal Cuboid Tensorization (NCT) (Xuegang et al., 2022) can represent HSI data into a high-order one for exploiting low-rank structure representation preferably, simultaneously exploring the nonlocal self-similarity and the spatial-spectral correlation. Therefore, our proposed ATRFHS approach leverages NCT to build HSI augmentation by grouping nonlocal similar cuboids in HSI.

Subsequently, we present the principle of the NCT method. For the recovery processing of an HSI image, $\mathcal{T}\in {\mathbb{R}}^{x\times y\times b}$ and $\mathcal{X}\in {\mathbb{R}}^{x\times y\times b}$ with x×y spatial size and b spectral bands denote the observed and recovered images, respectively. Firstly, for exhibiting rich redundancy in spectra, all cuboid patches ${\mathcal{C}}_i$ with the size of s×s×p across full bands ${\mathcal{C}\in \mathbb{R}}^{s\times s\times b}$ of HSI in the same spatial locations along the spectral direction with the interval $\frac{p}{2}$ are extracted, we search for its k²-1 nearest neighbors patches in a local window by Euclidean distance in the same spectra band for each cuboid patch. The k²-1 similar cuboid patches are stacked into a third-order tensor ${\mathcal{N}\in \mathbb{R}}^{sk\times sk\times p}$. There are $\left(\frac{2b}{p}-1\right)$ cuboid patches in the same spatial locations with different spectra bands. Thus, as shown in Figure 2, they are grouped into a four-order tensor ${\mathcal{M}}_i\in {\mathbb{R}}^{sk\times sk\times p\times \mathrm{h}}$ where $h=\left(\frac{2b}{p}-1\right)$.The part HSI with the size of x×y×p is divided into $T=$ $\frac{xy}{S^2}$ cuboid patches with the size of s×s×p.

FIGURE 2

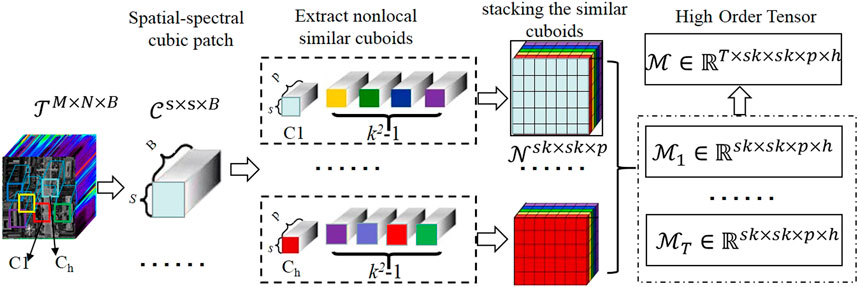
FIGURE 2. Illustration of the procedure to construct a high-order tensor by spatial and spectral similarities of HSI.

2.4 Phase congruency regularization

The regularization term can be regarded as the prior knowledge from underlying properties on recovered HS images. Total variation (TV) (Wang et al., 2017) is one of the prevalent regularization approaches applied for image restoration. TV regularization has long been acknowledged as a practical approach for improving image processing smoothness. For third-order hyperspectral data $\mathcal{T}$, the total variation of HSI is denoted by

${\Vert \mathcal{T}\Vert }_{TV}={\displaystyle \sum }_{x,y,b}\left(\left|{\mathcal{T}}_{x,y,b}-{\mathcal{T}}_{x-1,y,b}\right|+\left|{\mathcal{T}}_{x,y,b}-{\mathcal{T}}_{x,y-1,b}\right|+\left|{\mathcal{T}}_{x,y,b}-{\mathcal{T}}_{x,y,b-1}\right|\right)(2)$

The TV model can effectively remove noise while simultaneously preserving the fine details of the image’s edge. However, it is prone to misdiagnose the noises as the edge when the image edge is substantially contaminated by noise and cannot disentangle the noises from the edge. Furthermore, an edge-preserving regularization with gradient magnitudes diffusing along the edges rather than across them results in a staircase (blocky) effect.

To alleviate this shortcoming, phase congruency features are employed in this research to accurately preserve edge information and improve region structure smoothness from a noisy image. Since phase congruency (Morrone and Owens, 1987) is compatible with the properties of signals from corresponding points, it can adequately detect image features. Figure 3 compared the denoising results with TV regular and PC regular. We can see the discrepancy from Figure 3 that high-order information with PC feature maps from Figure 3C is more affluent than the first-order information with horizontal and vertical gradients from Compared to Figure 3D and Figure 3E, restored results in Figure 3F using hybrid smoothness regular combing TV and PC regularization can preserve more details of original images.

FIGURE 3

FIGURE 3. Comparison of the denoising results with TV regularization and PC regularization. (A) Noisy image from HYDICE urban HSI data, (B) Gradient magnitude maps, (C) PC feature maps,(D) Restored by the model with TV regularization [PSNR:33.58dB; SSIM:0.9345],(E) Restored by the model with PC regularization [PSNR:33.41dB; SSIM:0.9541] (F) Restored by the model with hybrid smoothness regularization combining TV and PC [PSNR:34.27dB; SSIM:0.9741].

Monogenic Phase Congruency (MPC) (Luo et al., 2015; Yuan et al., 2019) has recently increased the precision of feature localization and demonstrated superior computational efficiency and accuracy compared to standard phase congruency. At any specific point x in an image, MPC can be mathematically formulated as

$C\left(x\right)=E\left(x\right)\lfloor 1-\xi \times \mathrm{acos}\left(\frac{W^{\prime }\left(x\right)}{B^{\prime }\left(x\right)}\right)\rfloor \frac{\lfloor W^{\prime }\left(x\right)-M\rfloor }{B^{\prime }\left(x\right)+\eta }(3)$

where $E\left(x\right)$ is a weighting function constructed by applying a sigmoid function to the filter response spread value, which is given by (Luo et al., 2015) in detail. Both $\xi$ and $\eta$ are gain factors approximately from 1 to 2, which sharpen the edge response. M compensates for the influence of noise. $W^{\prime }\left(x\right)$ is local energy information. Similarly, $B^{\prime }\left(x\right)$ is the local amplitude at point x. MPC is capable of retaining both the irregular structure and being impervious to impulse noise. The l₁-norm with phase congruency regularization is generally employed in the fidelity term for impulse noise, similar to total variation regularization.

MPC feature maps are calculated by Eq. 3. Then, monogenic phase congruency regular is obtained by

${\Vert \mathcal{P}\left(\mathcal{T}\right)\Vert }_{\mathrm{P}\mathrm{C}}={\displaystyle \sum }_{i=1}^{b}C\left(\mathcal{T}\left(:,:,i\right)\right)(4)$

3 Proposed model and optimization solution

In this section, we propose a new model for HSI denoising based on weighted low-rank TR factorization using latent factors rank minimization with TV and PC regularization. Then, we introduce an auto-weighted mechanism to establish a tensor completion model and develop the corresponding algorithm based on an alternating minimization framework to solve the model. Figure 4 illustrates the proposed ATRFHS for HSI denoising.

FIGURE 4

FIGURE 4. Illustration of the proposed ATRFHS for HSI Denoising.

3.1 The proposed algorithm

To facilitate the presentation, for recovering a clean HSI from an observed HSI, by imposing the nuclear norm regularizations on the TR factors, we first review that a high-order tensor is decomposed into a sequence of 3-order tensors using the TR model to find the TR cores of an uncompleted tensor (Yuan et al., 2020), formulated as:

$\begin{array}{c}\underset{\mathcal{L},{\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{1:N}}{\mathit{min}}{\displaystyle \sum }_{n=1}^{N}Rank\left(L_{\left(n\right)}\right)+\frac{1}{2}{\Vert \mathcal{Y}-\mathcal{L}\Vert }_F^2\\ \mathrm{s}.\mathrm{t}.\mathcal{L}=\mathfrak{M}\left({\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N\right)\end{array}(5)$

Where $\mathcal{Y}={\mathcal{D}}_{\mathcal{w}}\left(\mathcal{T}\right)$ is a high-order tensor of the observed data $\mathcal{T}$ transformed by NCT, $\mathcal{L}$ is the reconstruction component and $L_{\left(n\right)}$ is the standard mode-n unfolding of tensor $\mathcal{L}$. The model can identify the data’s low-rank structure and approximate the recovered tensor. But the problem of determining the tensor rank is NP-hard. ANTRRM in (Xuegang et al., 2022) is based on mode-{d, l} unfolding with nuclear norm regularization via nonlocal tensor ring. Whereas, the local smoothness and consistency of the HSI in this approach is missed and the time-consuming of SVD computation of mode-{d, l} unfolding matrixes is more expensive than unfolding matrixes of low-rank TR factors.

To solve the above issue (Wang et al., 2021), enforced weight low-rankness on each TR factor. The optimization model can be reformulated as follows,

$\begin{array}{c}\underset{\mathcal{L},{\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{1:N}}{\mathit{min}}{\displaystyle \sum }_{n=1}^N{\displaystyle \sum }_{i=1}^3{\Vert {\mathcal{U}}_{\left(i\right)}^{\left(n\right)}\Vert }_{\ast }+\frac{1}{2}{\Vert \mathcal{Y}-\mathcal{L}\Vert }_F^2\\ \mathrm{s}.\mathrm{t}.\mathcal{L}=\mathfrak{M}\left({\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N\right)\end{array}(6)$

Where ${\mathcal{U}}_{\left(i\right)}^{\left(n\right)}$ is the mode-i unfolding matrix of the nth core tensor of ${\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1:N}$.

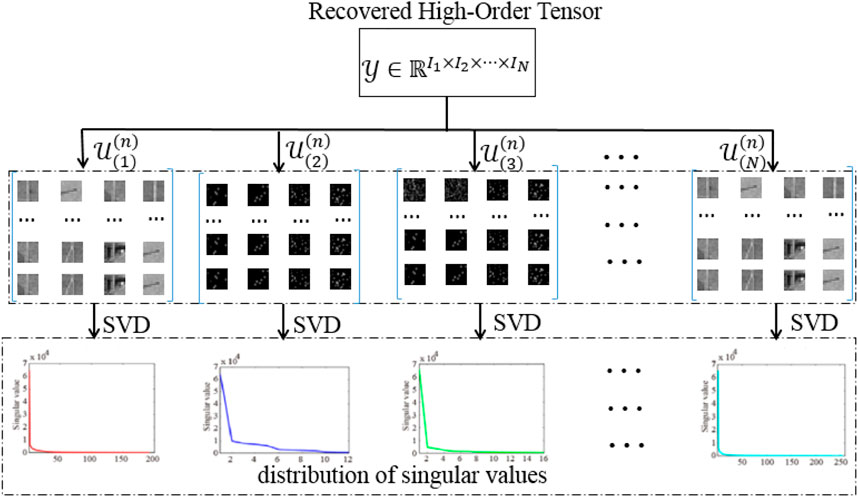
Model (6) can significantly reduce computational complexity compared to model (5). But as the decay distributions of singular values of the unfoldings of the TR factors along mode-n diverge. Appropriate weights should be constructed to determine the contributions of different nuclear norms in unfolding the TR tensor components. Therefore, the approach described above still has space for improvement because exploring low-rankness prior is rarely adequate to extract the underlying data by unreasonable weights. Furthermore, smoothness is another important prior that can be found in high-dimensional HSI data.

From Figure 5, the distribution of singular values significantly differs in the different unfolding matrixes. Weights for different unfolding parts should be treated differently. To reflect different contributions, the weight parameters $w$ play an essential role and need to tread carefully. To adapt the TR ranks of different modes, auto-weighted parameter optimization is utilized to measure the importance of different singular values voluntarily, thus minimizing the burden of failure caused by unreasonable weights.

FIGURE 5

FIGURE 5. The distribution of the singular values of unfolding matrixes.

Inspired by this nature, combining the auto-weighted strategy and hybrid smoothness regularization in our work, we can rewrite problem Eq. 6 as the following problem.

$\begin{array}{c}\underset{\mathcal{L},\mathit{w},{\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{1:N}}{\mathit{min}}{\displaystyle \sum }_{n=1}^N{w}_n{\displaystyle \sum }_{i=1}^3{\Vert {\mathcal{U}}_{\left(i\right)}^{\left(n\right)}\Vert }_{\ast }+\frac{1}{2}{\Vert \mathcal{Y}-\mathcal{L}\Vert }_F^2+\gamma {\Vert \mathit{w}\Vert }_F^2\\ +{\lambda }_{TV}{\Vert {\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)\Vert }_{\mathrm{T}\mathrm{V}}+{\lambda }_{PC}{\Vert \mathcal{P}\left({\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)\right)\Vert }_{\mathrm{P}\mathrm{C}}\mathrm{s}.\mathrm{t}.\mathcal{L}=\mathfrak{M}\left({\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N\right)\end{array}(7)$

Where $\gamma$, ${\lambda }_{TV}$ and ${\lambda }_{PC}$ are regularization parameters, ${\left\{w_n\right\}}_{n=1}^N$ are the weight of the nth norm satisfying $w_n\ge 0$ and ${\displaystyle \sum }_{n=1}^N{w}_n=1$.

To solve the above problem, auxiliary variables $\mathcal{M}$, $\mathcal{Z}$ and ${\left\{{\mathcal{G}}_{\left(i\right)}^{\left(n\right)}\right\}}_{i=1}^3$ are introduced, and the equivalent minimization problem is rewritten as

$\begin{array}{c}\underset{\mathcal{L},\mathit{w},\mathcal{M},\mathcal{Z},{\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{1:N}}{\mathit{min}}{\displaystyle \sum }_{n=1}^N{w}_n{\displaystyle \sum }_{i=1}^3{\Vert {\mathcal{U}}_{\left(i\right)}^{\left(n\right)}\Vert }_{\ast }+\frac{1}{2}{\Vert \mathcal{Y}-\mathcal{L}\Vert }_F^2\\ +\gamma {\Vert \mathit{w}\Vert }_F^2+{\lambda }_{TV}{\Vert \mathcal{M}\Vert }_{\mathrm{T}\mathrm{V}}+{\lambda }_{PC}{\Vert \mathcal{Z}\Vert }_{\mathrm{P}\mathrm{C}}\\ \mathrm{s}.\mathrm{t}.\mathcal{L}=\mathfrak{M}\left({\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1:N}\right),{\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)=\mathcal{M},\mathcal{P}\left({\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)\right)=\mathcal{Z}\end{array}(8)$

The abovementioned problem (8) is divided into two blocks for updating the variables $\mathcal{L},\mathit{w},\mathcal{G},\mathcal{M},\mathcal{Z},{\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{1:N}$. The first block is $\mathit{w}$, which is as follows the problem Eq. 9.

$\begin{array}{c}\underset{\mathit{w}}{\mathit{min}}{\displaystyle \sum }_{n=1}^N\left({\displaystyle \sum }_{i=1}^3{\Vert {\mathcal{U}}_{\left(i\right)}^{\left(n\right)}\Vert }_{\ast }\right)w_n+\gamma {\Vert \mathit{w}\Vert }_F^2\\ s.t.w^T\mathbf{1}=1,w_n\ge 0\end{array}(9)$

Then, the second block is the others (such as $\mathcal{L}$ and ${\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{1:N}$), which is as follows the problem Eq. 10.

$\begin{array}{c}\underset{\mathcal{L},\mathcal{M},\mathcal{Z},{\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{1:N}}{\mathit{min}}{\displaystyle \sum }_{n=1}^N{w}_n{\displaystyle \sum }_{i=1}^3{\Vert {\mathcal{G}}_{\left(i\right)}^{\left(n\right)}\Vert }_{\ast }+\frac{1}{2}{\Vert \mathcal{Y}-\mathcal{L}\Vert }_F^2\\ +{\lambda }_{TV}{\Vert \mathcal{M}\Vert }_{\mathrm{T}\mathrm{V}}+{\lambda }_{PC}{\Vert \mathcal{Z}\Vert }_{\mathrm{P}\mathrm{C}}\\ s.t.\mathcal{L}=\mathfrak{M}\left({\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N\right),{\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)=\mathcal{M},\\ \mathcal{P}\left({\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)\right)=\mathcal{Z}and{\mathcal{U}}_{\left(i\right)}^{\left(n\right)}={\mathcal{G}}_{\left(i\right)}^{\left(n\right)}\end{array}(10)$

3.2 Optimization for solving the proposed ATRFHS model

3.2.1 Auto-weighted mechanism

Through the problem solver (8), an auto-weighted mechanism can voluntarily balance the importance of different nuclear norms of TR factor matrices. The block coordinate descent (BCD) optimization framework can optimize the problem Eq. 9. When the variables ${\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{1:N}$ are fixed, the nuclear norms ${\left\{{\displaystyle \sum }_{\mathrm{i}=1}^3{\Vert {\mathcal{U}}_{\left(i\right)}^{\left(n\right)}\Vert }_{*}\right\}}_{n=1}^N$ are invariant. Namely, the indicator vector $\mathit{\eta }={\left[{\displaystyle \sum }_{i=1}^3{\Vert {\mathcal{U}}_{\left(i\right)}^{\left(1\right)}\Vert }_{*},{\displaystyle \sum }_{i=1}^3{\Vert {\mathcal{U}}_{\left(i\right)}^{\left(2\right)}\Vert }_{*},...,{\displaystyle \sum }_{i=1}^3{\Vert {\mathcal{U}}_{\left(i\right)}^{\left(n\right)}\Vert }_{*}\right]}^T$ is fixed. Then, the problem (9) for updating weighting coefficients $\mathit{w}$, automatically weighing the importance of the TR nuclear norm, can be defined as

$\mathcal{F}\left(\mathit{w}\right)={\displaystyle \sum }_{k=1}^N{\eta }_k{w}_k+\gamma {\Vert \mathit{w}\Vert }_F^2-\mu \left({\mathit{w}}^T\mathbf{1}-1\right)-{\mathit{\sigma }}^T\mathit{w}(11)$

where $\mu \ge 0$ and $\mathit{\sigma }={\left[{\sigma }_1,{\sigma }_2\cdots {\sigma }_N\right]}^T\ge 0$ are the Lagrangian multipliers. It is a convex Quadratic Programming (QP) problem with equality and non-equality requirements that any QP solver can solve. By taking the derivatives of Eq. 12 to $\mathit{w}$ and setting it as 0, ${\partial }_w\mathcal{F}=\mathit{\eta }+2\gamma \mathit{w}-\mu -\mathit{\sigma }=0$, we can get $w_i=\frac{\mu +{\sigma }_i-{\eta }_i}{2\gamma }$, The optimal solution $\mathit{w}$ satisfies the KKT condition. It can be discussed separately in three cases (Chen et al., 2021).

1) if ${\eta }_i-\mu >0$, since ${\sigma }_i>0$, from the condition $w_i^{*}{\sigma }_i=0$ and ${\sigma }_i=0$, then $w_i=\frac{\mu -{\eta }_i}{2\gamma }$

2) if ${\eta }_i-\mu =0$, then $w_i=\frac{{\sigma }_i}{2\gamma }$. Since $w_i^{*}{\sigma }_i=0$, so ${\sigma }_i=0$ and $w_i=0$ can be inferred

3) if ${\eta }_i-\mu <0$ and ${\sigma }_i>0$, we can find the positive integer $h=\underset{i}{argmax}\left({\eta }_i-\mu >0\right)$ satisfies the nonnegative constraint of $w_i$

Therefore, the optimal solution to the problem in Eq. 11 is given by

$w_{+i}=\{\begin{array}{cc}\frac{\mu -{\eta }_i}{2\gamma }& {,\eta }_i>\mu \\ 0& {,\eta }_i\le \mu \end{array}(12)$

Where $\mu =\frac{{\displaystyle \sum }_{i=1}^N{\eta }_i-2\gamma }{h}$.

3.2.2 Alternating minimization optimization framework

Problem Eq. 10 is transformed into the following unconstrained augmented Lagrangian function:

$\begin{array}{c}\mathcal{F}\left(\mathcal{W}\right)={\displaystyle \sum }_{n=1}^N{w}_n\left({\displaystyle \sum }_{\mathrm{i}=1}^3{\Vert {\mathcal{G}}_{\left(\mathrm{i}\right)}^{\left(\mathrm{n}\right)}\Vert }_{\ast }+\langle {\mathcal{A}}^{\left(n\right)},{\mathcal{G}}_{\left(\mathrm{i}\right)}^{\left(\mathrm{n}\right)}-{\mathcal{U}}_{\left(\mathrm{i}\right)}^{\left(\mathrm{n}\right)}\rangle +\frac{\beta }{2}{\Vert {\mathcal{G}}_{\left(\mathrm{i}\right)}^{\left(\mathrm{n}\right)}-{\mathcal{U}}_{\left(\mathrm{i}\right)}^{\left(\mathrm{n}\right)}\Vert }_{\mathrm{F}}^2\right)\\ +\frac{1}{2}{\Vert \mathcal{Y}-\mathfrak{M}\left({\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N\right)\Vert }_{\mathrm{F}}^2+{\lambda }_{TV}{\Vert \mathcal{M}\Vert }_1+\frac{\beta }{2}{\Vert {\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)-\mathcal{M}\Vert }_{\mathrm{F}}^2+\\ \langle \mathcal{B},{\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)-\mathcal{M}\rangle +{\lambda }_{PC}{\Vert \mathcal{Z}\Vert }_1+\frac{\beta }{2}{\Vert \mathcal{P}\left({\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)\right)-\mathcal{Z}\Vert }_{\mathrm{F}}^2+\langle \mathcal{C},\mathcal{P}\left({\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)\right)-\mathcal{Z}\rangle \end{array}(13)$

Where $\mathcal{W}=\left\{\mathcal{L},\mathcal{M},{\left\{{\mathcal{G}}^{\left(n\right)}\right\}}_{n=1}^N,\mathcal{Z},{\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N,{\left\{{\mathcal{A}}^{\left(n\right)}\right\}}_{n=1}^N,\mathcal{B},\mathcal{C}\right\}$, ${\left\{{\mathcal{A}}^{\left(n\right)}\right\}}_{n=1}^N,\mathcal{B},{\left\{{\mathcal{G}}^{\left(n\right)}\right\}}_{n=1}^N\mathrm{a}\mathrm{n}\mathrm{d}\mathcal{C}$ are auxiliary variables. Based on the framework of alternating minimization, the updates of $\mathcal{L},\mathcal{M},{\left\{{\mathcal{G}}^{\left(n\right)}\right\}}_{n=1}^N,\mathcal{Z},{\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N,{\left\{{\mathcal{A}}^{\left(n\right)}\right\}}_{n=1}^N,\mathcal{B},\mathcal{C}$ are given respectively as follows.

Step 1:. Update ${\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N$ and $\mathcal{L}$ with fixing other variables_, the ${\mathcal{U}}^{\left(n\right)}$ sub-problem is rewritten as

$\mathcal{F}\left({\mathcal{U}}^{\left(n\right)}\right)={\displaystyle \sum }_{i=1}^3\frac{\beta }{2}{\Vert {\mathcal{G}}^{\left(n,i\right)}-{\mathcal{U}}^{\left(n,i\right)}+\frac{1}{\beta }{\mathcal{A}}^{\left(n\right)}\Vert }_F^2+\frac{1}{2}{\Vert \mathcal{Y}-\mathfrak{M}\left({\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1:N}\right)\Vert }_{\mathrm{F}}^2$

This is a least-squares problem. So for n = 1, … , N, ${\mathcal{U}}^{\left(n\right)}$ can be updated by

${\mathcal{U}}_{+}^{\left(n\right)}=\mathrm{f}\mathrm{o}\mathrm{l}{\mathrm{d}}_2\left(\frac{{\displaystyle \sum }_{i=1}^3\left(\beta G_{\left(2\right)}^{\left(n,i\right)}+A_{\left(2\right)}^{\left(n,i\right)}\right)+T_{<n>}{U}_{<2>}^{\left(\ne n\right)}}{{U_{<2>}^{\left(\ne n\right)}}^T{U}_{<2>}^{\left(\ne n\right)}+3\mathbf{E}}\right)(14)$

where $\mathbf{E}$ is an identity matrix.By updated TR factors ${\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N$ for every iteration, then $\mathcal{L}$ is updated as

${\mathcal{L}}_{+}=\mathfrak{M}\left({\left\{{\mathcal{U}}_{+}^{\left(n\right)}\right\}}_{n=1}^N\right)(15)$

Step 2:. Update ${\mathcal{G}}^{\left(n\right)}$ with fixing other variables, by simplifying (13), for i = 1, 2, 3, the augmented Lagrangian functions w.r.t. [$\mathcal{G}$] is expressed as

$\mathcal{F}\left(G^{\left(n\right)}\right)=w_n{\displaystyle \sum }_{i=1}^3{\Vert G_{\left(i\right)}^{\left(n\right)}\Vert }_{\ast }+\frac{\beta }{2}{\Vert {\mathcal{G}}^{\left(n\right)}-\left({\mathcal{U}}^{\left(n\right)}-\frac{1}{\beta }{\mathcal{A}}^{\left(n\right)}\right)\Vert }_F^2$

Solving $G_{\left(i\right)}^{\left(n\right)}$ is a nuclear norm model and has led to a closed form. So for n = 1, … , N, ${\mathcal{G}}^{\left(n\right)}$ can be updated by

${\mathcal{G}}_{+}^{\left(n\right)}=\mathrm{f}\mathrm{o}\mathrm{l}{\mathrm{d}}_{\left(i\right)}\left({\mathbf{S}}_{\frac{w_n}{\beta }}\left({\mathcal{U}}^{\left(n\right)}-\frac{1}{\beta }{\mathcal{A}}^{\left(n\right)}\right)\right)(16)$

where ${\mathbf{S}}_{\frac{w_n}{\beta }}$ represents the thresholding SVD operation (Chen et al., 2018).

Step 3:. Update $\mathcal{M}$ by fixing other variables. The optimization model can be rewritten as

$\mathcal{F}\left(\mathcal{M}\right)={\lambda }_{TV}{\Vert \mathcal{M}\Vert }_1+\frac{\beta }{2}{\Vert \mathcal{M}-\left({\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)-\mathcal{B}\right)\Vert }_F^2(17)$

Optimizing (18) can be easily solved by a soft-thresholding operator.

${\mathcal{M}}_{+}={\mathbf{\Psi }}_{\frac{{\lambda }_{TV}}{\beta }}\left({\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)-\mathcal{B}\right)(18)$

where ${\mathbf{\Psi }}_{\mathit{v}}$ is defined by ${\mathbf{\Psi }}_{\mathit{v}}\left(x\right)=sgn\left(x\right).*\mathit{max}\left(\left|x\right|-v,0\right)$.

Step 4:. Fixing other variables to update $\mathcal{Z}$, the optimization model can be rewritten as

$\mathcal{F}\left(\mathcal{Z}\right)={\lambda }_{PC}{\Vert \mathcal{Z}\Vert }_1+\frac{\beta }{2}{\Vert \mathcal{Z}-\left(\mathcal{P}\left({\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)\right)-\mathcal{C}\right)\Vert }_F^2(19)$

Similarly, the closed-form solution is

${\mathcal{Z}}_{+}={\mathbf{\Psi }}_{\frac{{\lambda }_{PC}}{\beta }}\left(\mathcal{P}\left({\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)\right)-\mathcal{C}\right)(20)$

Step 5:. Update ${\left\{{\mathcal{A}}^{\left(n\right)}\right\}}_{n=1}^N,\mathcal{B},\mathcal{C}$: When the (t+1)-th iteration begins, the Lagrange multipliers are updated by the following

$\{\begin{array}{l}\begin{array}{l}{\mathcal{A}}_{t+1}^{\left(n\right)}={\mathcal{A}}_t^{\left(n\right)}+\beta \left({\mathcal{G}}_{t+1}^{\left(n\right)}-{\mathcal{U}}_{t+1}^{\left(n\right)}\right)\\ {\mathcal{B}}_{t+1}={\mathcal{B}}_t+\beta \left({\mathcal{M}}_{t+1}-{\mathcal{D}}_{\mathcal{w}}^{-1}\left({\mathcal{L}}_{t+1}\right)\right)\end{array}\\ {\mathcal{C}}_{t+1}={\mathcal{C}}_t+\beta \left({\mathcal{Z}}_{t+1}-\mathcal{P}\left({\mathcal{D}}_{\mathcal{w}}^{-1}\left({\mathcal{L}}_{t+1}\right)\right)\right)\end{array}(21)$

The specific process of the ADMM-based solver for the ATRFHS HSI reconstruction model and BCD-based solver for auto-weighting is introduced in Algorithm 1.

Algorithm 1. The whole procedure of the ATRFHS algorithm.

Input: observed HSI $\mathcal{T}\in {\mathbb{R}}^{x\times y\times b}$, TR rank {R₁,R₂, … R_N}, ${\lambda }_{TV}$, ${\lambda }_{PC},\beta$

Initialization: ${\left\{{\mathcal{A}}^{\left(n\right)}\right\}}_{n=1}^N=0,\mathcal{M}=\mathcal{Z}=\mathcal{B}=\mathcal{C}=0$ ,t=0, $\beta =0.01$, $\sigma =1.05$, ${\beta }_{\mathit{max}}={5\times 10}^2$,max_it=100,ter=1e-5, $\mathit{w}=\{w_j{\}}_{j=1}^N=\frac{1}{N}$, Grouping nonlocal similar cuboids by NCT to form tensor ${\mathcal{Y}=\mathcal{D}}_{\mathcal{w}}\left(\mathcal{T}\right)$; From n = 1 to N, randomly initialize for core tensors ${\mathcal{U}}^{\left(n\right)}$; Compute ${\mathcal{L}}_{\left(0\right)}=\Phi \left\{{\mathcal{U}}^{\left(1\right)},\dots ,{\mathcal{U}}^{\left(K\right)}\right\}$. Calculation MPC by $C\left(\mathcal{T}\left(:,:,i\right)\right)$ via (5) i=1, … ,b. While t ≤max_it and || $\mathcal{Y}$ -$\mathcal{L}$ _last||² < ter Update $\{w_j{\}}_{j=1}^N$ by Eq. 12 Update ${\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N$ by Eq. 14; Update $\mathcal{L}$ by Eq. 15; Update ${\left\{{\mathcal{G}}^{\left(n\right)}\right\}}_{n=1}^N$ by Eq. 16; Update $\mathcal{M}$ and $\mathcal{Z}$ by Eqs 18, 20; Update ${\left\{{\mathcal{A}}^{\left(n\right)}\right\}}_{n=1}^N,\mathcal{B},\mathcal{C}$ by (21), and the penalty parameter update $\beta =\mathit{min}\left(\sigma \beta ,{\beta }_{\mathit{max}}\right)$; t=t+1; End Transform $\mathcal{L}$ into a three-order tensor $\mathcal{X}={\mathcal{D}}_{\mathcal{w}}^{-1}\left(\mathcal{L}\right)$

return: restored HSI $\mathcal{X}$.

3.3 Computational complexity

The computational complexity of our ATRFHS method is analyzed as follows. For simplicity, we assume to transform HSI data into a high tensor $\mathcal{D}\in {\mathbb{R}}^{I\times I,\dots ,\times I}$ from by NCT and TR-rank with R1 = R2 = · · · = RN = R. The updating of $\{w_j{\}}_{j=1}^N$, ${\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N$, and ${\left\{{\mathcal{G}}^{\left(n\right)}\right\}}_{n=1}^N$ have closed-form solutions, as shown in Algorithm 1. It is obvious to observe that the most time-consuming parts are updating ${\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N$ and SVD operation of ${\left\{{\mathcal{G}}^{\left(n\right)}\right\}}_{n=1}^N$. Then the computational complexities of updating ${\left\{{\mathcal{U}}^{\left(n\right)}\right\}}_{n=1}^N$ and ${\left\{{\mathcal{G}}^{\left(n\right)}\right\}}_{n=1}^N$ are $\mathcal{O}\left(N{I}^N{R}^2\right)$ and $\mathcal{O}\left(N{I}^N{R}^3\right)$. The computational complexity of updating weighting $\{w_j{\}}_{j=1}^N$ is $\mathcal{O}\left(3TN\right)$. Thus, the overall complexity of our proposed algorithm can be written as $\mathcal{O}\left(TN{I}^N{R}^2\left(1+R\right)+3TN\right)$, where T is the number of iterations.

4 Experiments

Two simulated and two real datasets are utilized in the experiments to demonstrate the efficacy of the proposed algorithm with the auto-weight TR rank minimization regular on HSI restoration. Six representative state-of-the-art methods are considered for quantitative and visual comparison; namely, L_1-2 SSTV (Zeng et al., 2020) based on 3-D L_1-2 spatial-spectral total variation low-rank tensor recovery, LRTF-L₀ (Xiong et al., 2019) based on a spectral-spatial L₀ gradient regularized low-rank tensor factorization, LRTDGS (Chen et al., 2019a) based on weighted group sparsity-regularized low-rank tensor decomposition, SBNTRD (Chen et al., 2020; Oseledets, 2011) based on subspace nonlocal TR decomposition-based method, ANTRRM(Xuegang et al., 2022) based on nonlocal tensor ring rank minimization (Xuegang et al., 2022) and QRNN3D based on 3D Quasi-Recurrent RNN(Wei et al., 2020). All of our experiments are conducted on a Desktop computer with 16 GB of DDR4 RAM and a 3.2 GHz Intel Core i7-7700K CPU running MATLAB R2018b. All of the competitors’ parameters are adjusted following the literature’s guidelines.

4.1 Synthetic HSI experiments

Because the ground-truth HSI is provided for the simulated experiments, four quantitative quality indices: peak signal-to-noise ratio (PSNR), structure similarity (SSIM), feature similarity (FSIM), erreur relative global adimensionnelle de synthèse (ERGAS) (Chen et al., 2018) are adopted for validating the performance of the proposed model on two synthetic experiment datasets, namely, the Washington DC Mall and Indian Pines datasets. The MPSNR, MSSIM, and MFSIM, computed by taking the average of all bands, are used to evaluate performance.

The four indices evaluate spatial and spectral information retention, and the PSNR, SSIM, and FSIM values are generated by averaging all bands. The higher the PSNR, SSIM, and FSIM, the lower the ERGAS, and the better the HSI denoising outcome.

1) The WDC Mall dataset: The Washington DC Mall dataset was collected by the Hyperspectral Digital Imagery Collection Experiment (HYDICE) with the permission of the Spectral Information Technology Application Center of Virginia. The original size is 1208×307×210. A sub-image of 256×256×128 from this data set is extracted for our experiment.

2) The Indian Pines dataset: The Indian Pines dataset was collected by AVIRIS sensor over the Indian Pines test site in North-western Indiana. It contains 145×145 pixels and 224 spectral reflectance bands with wavelengths ranging from 0.4 to 2.5× 10⁻⁶ m. The Indian Pines dataset comprises 220 bands with a spatial size of 145×145 pixels. A sub-image of 145×145×128 from this data set is extracted for our experiment.

As for parameter settings, we empirically set the regularization parameter ${\lambda }_{TV}=0.02$, ${\lambda }_{PC}=0.05,\beta =0.03$. In NCT, we set s=5, k=7, and p=32. Five different types of noise cases were added to these two clean HSI datasets to simulate complicated noise cases in a real scene. The following is a detailed description of these cases.

Case 1. (i.i.d. Gaussian Noise): Entries in all bands were corrupted by zero-mean i.i.d. Gaussian noise N(0, σ²) with σ=0.05.

Case 2. (Non-i.i.d. Gaussian Noise): Entries in all bands were tainted by zero-mean Gaussian noise of different intensities. Each band’s signal noise ratio (SNR) is generated by a uniform distribution with a value between (Fan et al., 2017; Yokota et al., 2018)dB.

Case 3. (Gaussian+Stripe Noise): Based on Case 2, some stripes randomly selected from 20 to 75 are added from band 10 to band 98 in WDC Mall and Indian Pines datasets.

Case 4. (Gaussian+Deadline Noise): Based on Case 2, deadlines are added from band 76 to band 106 in WDC and Indian Pines datasets.

Case 5. (Gaussian+Impulse Noise): Based on Case 2, fifty bands in WDC and Indian Pines datasets were randomly chosen to add impulse noise with different intensities, and the percentage of impulse is from 30% to 60%.Table 1 displays the quantitative results of all comparable approaches in the Washington DC Mall and HYDICE urban data on various cases. The best results for each quality index are shown in bold. From Table 1, it is clear that our proposed approach and SBNTRD obtain the best results over the other compared methods in all cases, confirming our proposed method’s advantage over others. It is worth noting that SBNTRD fully exploits the spatial information by nonlocal prior and TR decomposition. Due to the considerations of auto-weight LR properties and efficiently exploiting the structure information of HSI by NCT in our proposed method, the proposed method obtains the best results over the other compared methods except for a small number of indicator cases.Regarding visual quality, Figure 6 and Figure 7 show the denoised results by seven different methods under Case 5 in the WDC dataset and Case 3 in the Indian Pines dataset, respectively. As shown in the white square from the enlarged red areas of restored images in Figure 6 and Figure 7C, QRNN3D methods can remove noises but fail to retain structure information. Moreover, it is clear to see that low-rank tensor recovery with prior information regularization methods L_1-2 SSTV, LRTDGS, SBNTRD LRTF-L₀, and ANTRRM can effectively remove random noise and stripe noise in Figure 5 and Figures 6B,D–G, but the image details cannot be preserved well shown in the enlarged box of Figure 6 and Figure 7. The proposed ATRFHS method, in contrast, can effectively remove all of the mixture noise and preserve more edges and details, as shown in Figure 6 and Figure7H. Because ATRFHS not only considers the more reasonable LR with auto-weight TR rank minimization for Gaussian noise and random noise in the HSI restoration task but the deadlines and stripe noise can be removed shown in Figure 6 and Figure7H by exploring high-order tensors structure, as a higher-order tensor makes it more efficient to exploit the local structures in transformed tensor. The our proposed approach outperforms all the evaluated methods in terms of four quantitative quality indices, eliminating all of the hybrid noise while keeping the detailed edges and texture information in the restored HSI. We further calculate the PSNR, SSIM, and FSIM values of different bands in all simulated data cases and show the curves of evaluation indices.Figure 8 and Figure 9 show the curves of PSNR and SSIM evaluation indices of each band on WDC Mall under Case 2 and INDIAN PINES under Case 4, respectively. As displayed in Figure 8A and Figure 9A, it is observed that the proposed method performs higher PSNR values than other methods for almost all bands in WDC Mall data and INDIAN PINES. For SSIM indices, the proposed method can outperform other methods in most bands, as demonstrated in Figure 8B and Figure 9B. From Figure 8C and Figure 9C, it can be seen that the proposed ATRFHS method achieves higher FSIM values than other methods in almost all bands, which verifies the robustness of the proposed method using the auto-weighted strategy of low-rank approximation and also demonstrates the superiority of the hybrid regularization compared with others. Our proposed method has obtained the best restoration performance among all competing methods, as evidenced by the distribution of evaluating index of the restoration image in Figures 8 and Figure 9.In conclusion, the proposed method outperforms the other methods in terms of visual quality and quantitative indices.

TABLE 1

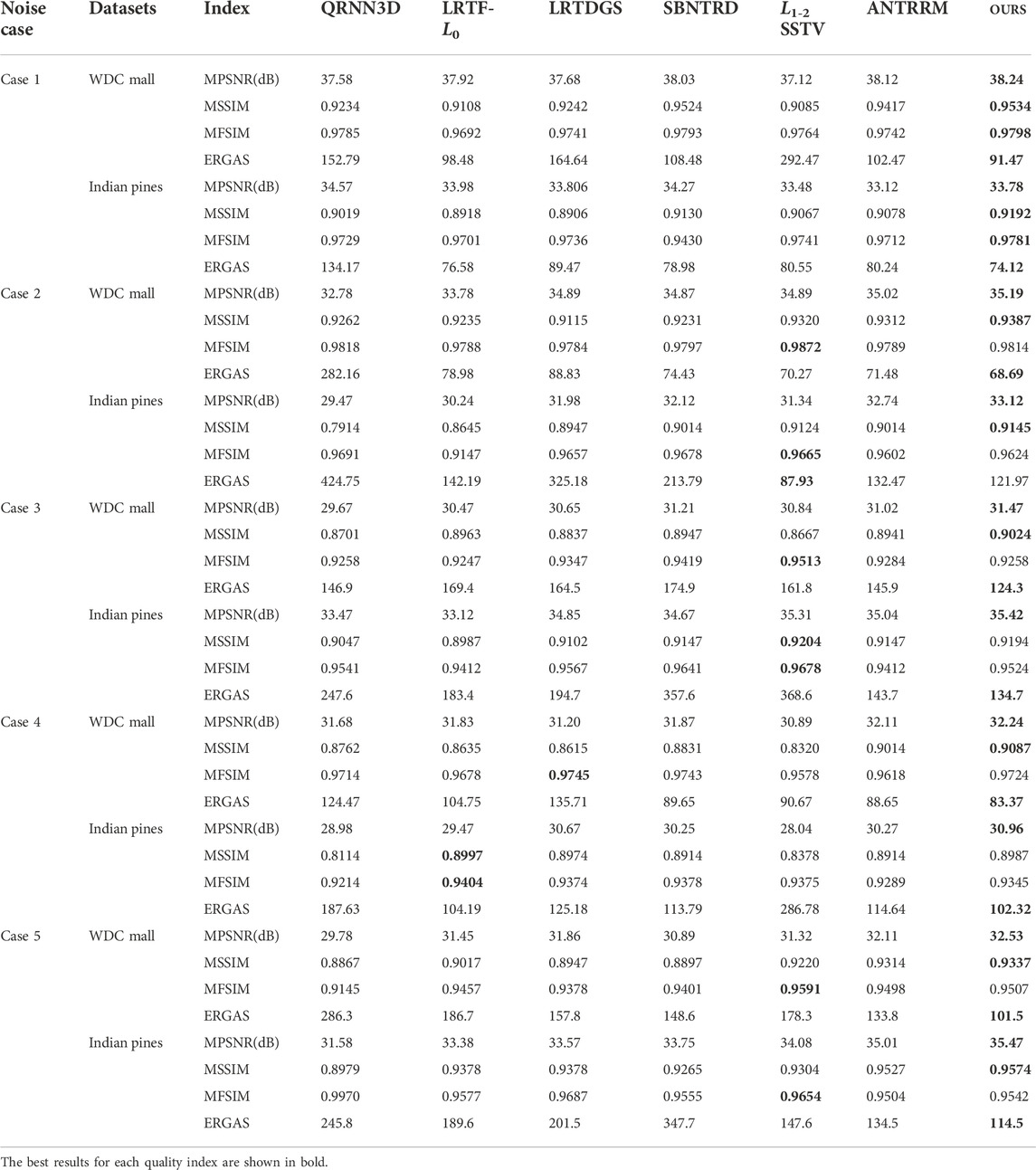
TABLE 1. Quantitative results of all the methods under different noise cases FOR WDC and urban DATASETs.

FIGURE 6

FIGURE 6. Restored results of all comparison methods for band 68 of WDC HSI data under Case 5: (A) Noisy, (B) L_1-2 SSTV, (C) QRNN3D, (D) LRTDGS, (E) SBNTRD, (F) LRTF-L₀, (G) ANTRRM, (H) OURS.

FIGURE 7

FIGURE 7. Restored results of all comparison methods for band 96 of INDIAN PINES data under Case 3: (A) Noisy, (B) L_1-2 SSTV, (C) QRNN3D, (D) LRTDGS, (E) SBNTRD, (F) LRTF-L₀, (G) ANTRRM, (H)OURS.

FIGURE 8

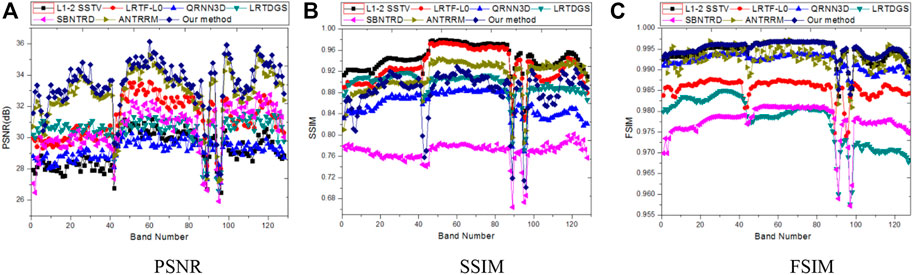
FIGURE 8. The comparative performance of different methods in terms of PSNR, SSIM, and FSIM under Case 2 on WDC Mall. (A) PSNR, (B) SSIM, (C) FSIM.

FIGURE 9

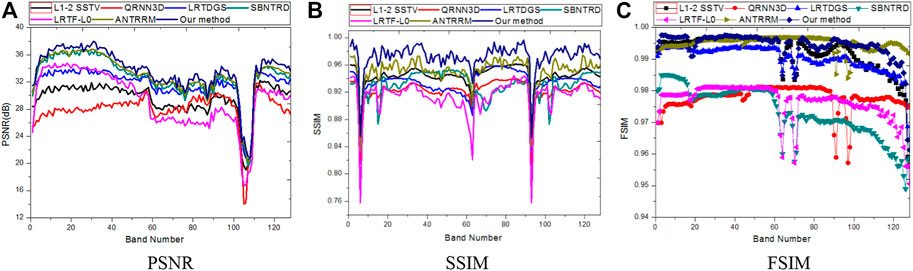
FIGURE 9. The comparative performance of different methods in terms of PSNR, SSIM, and FSIM under Case 4 on INDIAN PINES. (A) PSNR, (B) SSIM, (C) FSIM.

4.2 Real data experiments

The two GF-5 real-world hyperspectral data sets acquired by the GaoFen-5 satellite: Shanghai City and Baoqing (available URL: http://hipag.whu.edu.cn/resourcesdownload.html), were used in the real HSI data experiments. GaoFen-5 satellite was developed by the Chinese Aerospace Science and Technology Corporation and launched in 2018. The original size of the GF-5 dataset is 2100 × 2048 × 180, and 25 bands are miss information. This dataset is seriously degraded by the mixture of Gaussian, stripes, and deadlines noises.

The selected GF-5 Shanghai City image is 307 × 307 pixels in size and has 210 bands. The GF-5 Baoqing sub-image has a size of 300×300×305, with some abnormal bands removed. Both GF-5 images are extensively polluted by various stripes, including wide stripe noise that emerges at the same position on the continuous bands as dense stripe noise of varying widths. Furthermore, several of the bands have much-mixed noise. Before denoising, the gray values of authentic HSIs were band-by-band normalized to [0, 1]. After removing the miss bands and extracting a small region, a sub-HSI with the size of 300× 300×156 is chosen for experiments.

Both Equivalent Number of Looks (ENL) (Anfinsen et al., 2009)and Edge Preserving Index (EPI) (Sattar et al., 1997) were employed for performance evaluation. The larger the ENL and EPI values, the better the quality of the restored images.

The quantitative assessment indices ENL and EPI values and the running time of all competing methods are provided in Table 2 on the two GF-5 datasets. The best outcomes for each quality indicator are highlighted in bold. From the table, it is clear that our proposed approach achieves a significantly improved performance in both the ENL and EPI indexes, as compared with other competing methods. Because high-dimension tensor decomposition can capture the global correlation in the spatial-spectral dimensions, ATRFHS obtained better results than the other tensor-based format methods by combining auto-weighted low-rank tensor ring decomposition with total variation and phase congruency regularization. Meanwhile, the effectiveness of the suggested auto-weight TR nuclear standard is shown.

TABLE 2

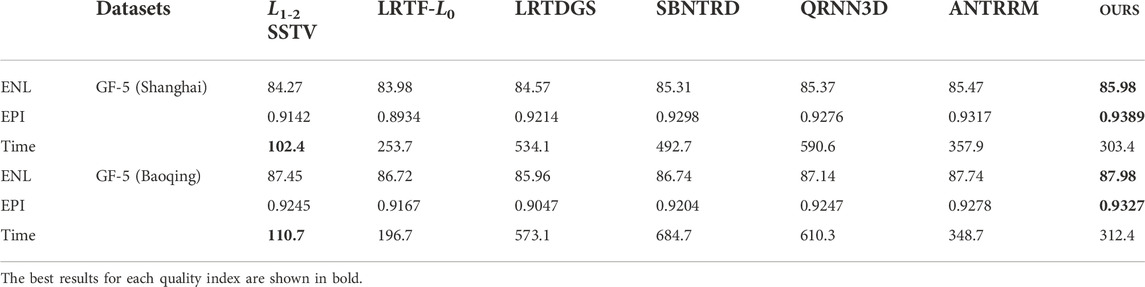
TABLE 2. Quantitative comparison of all competing methods on the two GF-5 datasets (time unit: second).

It can be observed from Table 2 that the L_1-2 SSTV method is the fastest method among all the compared methods. However, as the previous experimental work demonstrated, it cannot achieve good repair outcomes. Due to the use of updating $\mathcal{U}$ and SVD operation of $\mathcal{G}$ for higher-order data computation, the computational cost of the proposed ATRFHS is relatively higher than L_1-2 SSTV, QRNN3D including traning phase and LRTF-L₀ methods but significantly lower than other methods, namely, LRTDGS, ANTRRM and SBNTRD.

The restorations of band 96 in Shanghai City of GF-5 are presented in Figure 10. To clearly illustrate the visualization of the restoration results, a demarcated area in the subfigure is enlarged in the bottom right corner. Figure 10A shows that the image suffers from a mixture of Gaussian and sparse noise. It is straightforward to observe that L_1-2 SSTV, QRNN3D, and LRTDGS cannot efficiently maintain edge information to a certain extent. The approaches based on the low-rank prior perform more effectively than other competing methods, as seen in Figure 10. By combining the total variation and phase congruency into a unified TV regularization and utilizing the auto-weighted low-rank tensor ring decomposition to encode the global structure correlation, our proposed ATRFHS method can better remove the complex mixed noise. In particular, compared to other competing methods, our proposed method preserves the most significant detail edge, texture information, and image fidelity.

FIGURE 10

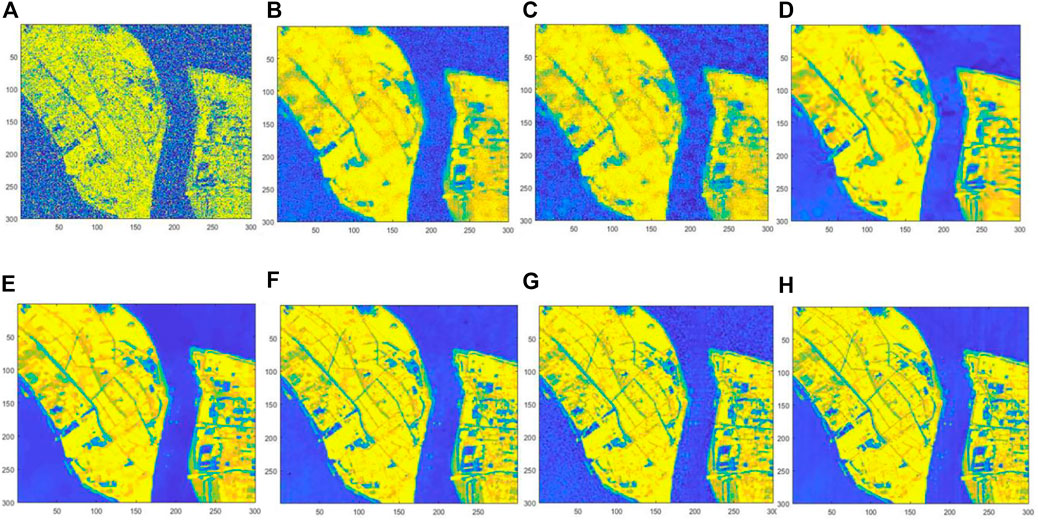
FIGURE 10. Restored results of GF-5 HSI data of Shanghai City: (A) Noisy, (B) L_1-2 SSTV, (C) QRNN3D, (D) LRTDGS, (E) SBNTRD, (F) LRTF-L₀, (G) ANTRRM, (H)OURS.

Figure 11 displays the restoration results of band 109 in Baoqing data of GF-5. From Figure 11A, one can see that the image is wholly contaminated by various noises, including Gaussian, random noise, and heavy structure noise, including stripes and deadlines. After denoising using the different HSI restoration methods, the noise is removed. As shown in Figures 11C,D, the QRNN3D and LRTDGS methods cannot eliminate the stripes in the results, as observed in the enlarged box on the image.

FIGURE 11

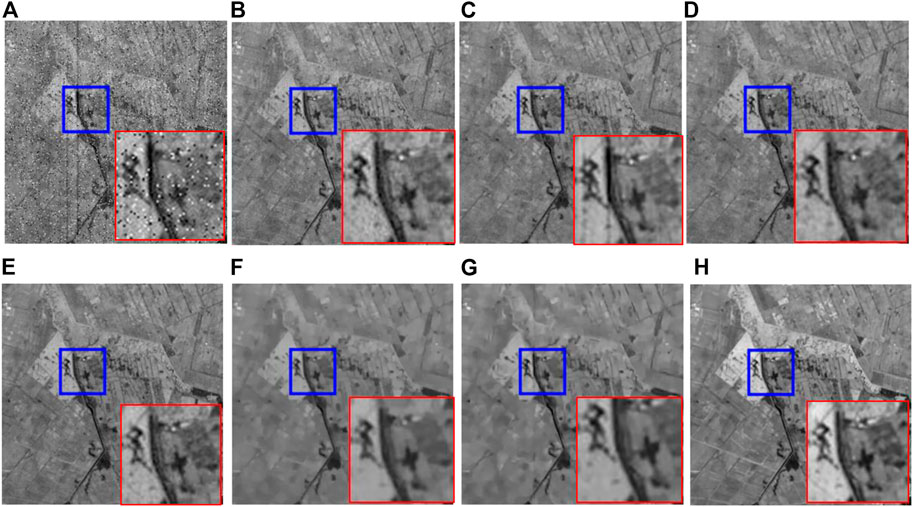
FIGURE 11. Restored results of GF-5 HSI data of Baoqing: (A) Noisy, (B) L_1-2 SSTV, (C) QRNN3D, (D) LRTDGS, (E) SBNTRD, (F) LRTF-L₀, (G) ANTRRM, (H)OURS. Please zoom in for better viewing.

The L_1-2 SSTV and SBNTRD can obtain a better visual result than the other methods, but some intrinsic information such as the local smoothness underlying the HSI cube, was not exploited, as shown in Figures 11B,E,F. LRTF-L₀ and the proposed method can remove much noise compared to the TV mentioned above, but LRTF-L₀ does not preserve edges and local detail information, as well as our proposed ATRFHS method. More detailed visual comparison results can be seen in such red boxes. To summarize, the proposed ATRFHS can still achieve the best performance for removing such heavy mixed noise from this dataset.

To further investigate the effect of our method, we provide a no-reference image quality assessment, as presented in (Yang et al., 2017), to evaluate the real-world hyperspectral data before and after denoising. The quality scores are presented in Table 3. A lower no-reference image quality assessment score indicates better denoising quality. The table shows that our proposed ATRFHS method has the lowest score, demonstrating ATRFHS’s superiority.

TABLE 3

TABLE 3. No-Reference Hyperspectral Image Quality Assessment on the GF-5 Baoqing image.

4.3 The impact of parameters

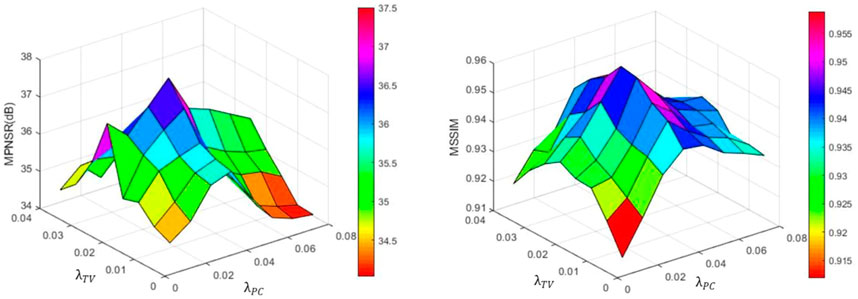
Three parameters in Eq. 9 need to be discussed, including two regularization parameters ${\lambda }_{TV}$ and ${\lambda }_{PC}$, and the penalty parameter $\beta$ .

1) The impact of parameters ${\lambda }_{TV}$ , ${\lambda }_{PC}$ and $\beta$:

TV and PC multichannel images have been widely exploited for their edge-preserving characteristics. To prevent the overfitting of the sharper edge of our proposed approach from influencing the experimental results, we present the MPSNR and MSSIM values achieved by a function of ${\lambda }_{TV}$ and ${\lambda }_{PC}$ for the WDC dataset in Case 1 as an example to identify the best parameter values. Figure 12 shows the change in MPSNR values for the proposed algorithm for these two regularization parameters ${\lambda }_{TV}$ and ${\lambda }_{PC}$. It is evident that when ${\lambda }_{TV}$ is equal to 0.02 and ${\lambda }_{PC}$ is set to 0.05, and the proposed method can reach the peak of MPSNR.

FIGURE 12

FIGURE 12. Sensitivity analysis of regularization parameter.

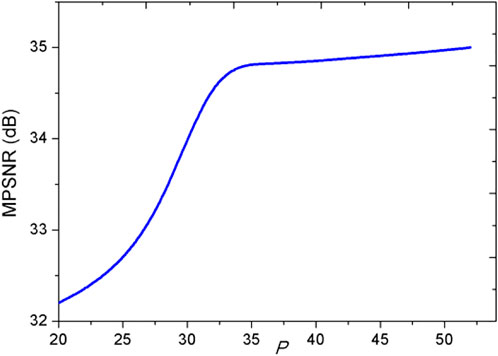
2) The impact of parameters spectral band length P:

Furthermore, P also is an important parameter for taking advantage of the spectral local low-rankness properties. As shown from Figure 13 in the simulated WDC data experiments, when P is equal to 32, the MPSNR value tends to be stable. Thus, we suggest the use of p=32.

FIGURE 13

FIGURE 13. Sensitivity analysis of spectral band length P

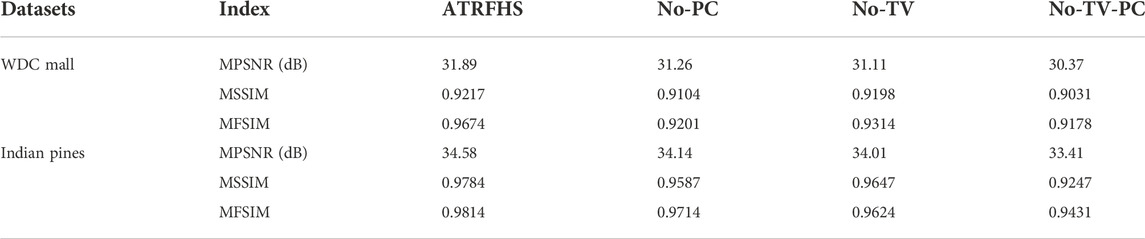
4.4 effectiveness of hybrid smoothness regularization terms

The proposed ATRFHS is a tensor ring-based method combining TV and PC priors. To verify the effectiveness of the two priors in our model, we further compare our approach with a simplified version of our model without the TV and PC regularization terms, that is, set the parameters ${\lambda }_{TV}=0$ and ${\lambda }_{PC}=0$ in our model (9). The test is conducted on two simulated datasets by the MPSNR, MFSIM, and MSSIM evaluation indices in Case 3 with a mixture noise. Experimental results are shown in Table 4. ATRFHS is our proposed method, and No-PC is a method using only TV prior without PC prior by ${\lambda }_{PC}=0$, No-TV is a method using only PC prior without TV prior by ${\lambda }_{TV}=0$ and No-TV-PC is the original weighted tensor ring-based method by ${\lambda }_{TV}=0$ and ${\lambda }_{PC}=0$. The metric scores listed in Table 3 obtained by ATRFHS are the highest among all the techniques. Hybrid smoothness regularization with TV and PC priors is more suitable for recovering HSIs with more texture information than pure TV methods. The performance of the ATRFHS method demonstrates the effectiveness of hybrid smoothness regularization terms.

TABLE 4

TABLE 4. Empirical analysis of each regularizer of the ATRFHS model.

4.5 Empirical analysis for convergence of the ATRFHS solver

The convergence behavior of the proposed algorithm is discussed. We present an empirical analysis of the proposed restoration approach convergence on the simulated WDC Mall data set. We offer a numerical experiment to show the convergence behavior in terms of relative error, the MPSNR values, and the MSSIM values. In Figure 14, we can observe that the curves of all assessment indexes come to a stable value when the algorithm reaches a relatively high iteration number, indicating that the proposed algorithm empirically converges well.

FIGURE 14

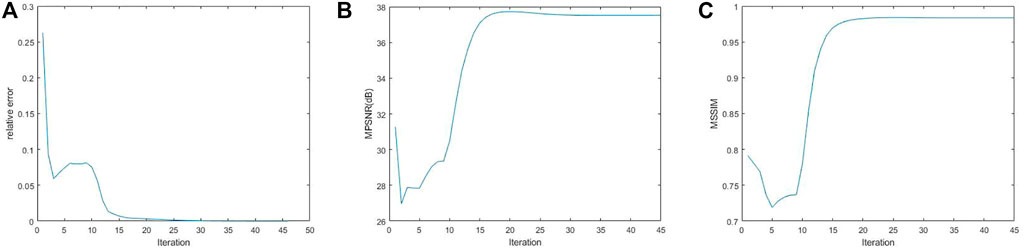
FIGURE 14. Convergence analysis of the algorithm in terms of (A) relative error, (B) the MPSNR values, and (C) the MSSIM values.

4.6 Classification application

In this sub-section, we examine the impact of HSI noise removal procedures as a preprocessing step for HSI classification. We employed Random Forest (RF) classifier (Athey et al., 2019) to make a comparison of the effectiveness of different restoration approaches. The main idea of the RF classifier is to classify an input vector by running down each decision tree in the forest. Each tree outcomes in a unit vote for a specific class, and the forest selects the final classification label based on the most votes. Classification accuracy is utilized to evaluate the effectiveness of different restoration approaches. Two metrics have been applied: Overall Accuracy (OA) and Average accuracy (AA). The percentage value of AA and OA is shown in Table 5. The metrics AA and OA are reported in percentage. Table 5 shows that denoising approaches improve the performance of the subsequent classification technique compared to directly using the raw data after the denoising procedure. The proposed ATRFHS approach achieves the highest OA and AA values among all the classification results achieved by the seven restoration approaches, indicating the best performance in HSI restoration.

TABLE 5

TABLE 5. Washington DC Mall-Classification accuracies obtained by different restoration approaches before using RF.

5 Conclusion

This article presents an auto-weighted low-rank Tensor Ring Factorization with Hybrid Smoothness regularization (ATRFHS) for HSI restoration. The global spatial structure correlation of HSI was efficiently depicted by the low-rank factorization of TR, which can embody the advantages of both rank approximations and high-dimension structures. An auto-weighted measure of factors rank minimization of TR factorization can more accurately approximate the TR rank and better promote the low-rankness of the solution. Moreover, we employed a hybrid regularization incorporating total variation and phase congruency to smooth the factor and preserve HSI’s spatial piecewise constant structure. A well-known alternating minimization framework was developed to solve the ATRFHS model efficiently. Both simulated and real-world datasets were used to demonstrate the performance and superiority of the proposed methods over state-of-the-art HSI denoising methods. In the future, we will try to incorporate more appropriate regularization and nonconvex tensor ring factor rank minimization into our tensor ring model to enhance its HSI restoration capability further.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: http://hipag.whu.edu.cn/resourcesdownload.html.

Author contributions

The project was suggested by JW. JL and XL did the analysis. Data and comments contributed by XL and DL. The article was written by XL, JL, and BW.

Funding

This work was supported in part by the Science and Technology Support Project of Panzhihua City of Sichuan Province of China under Grant 2021CY-S-6, in part by Sichuan Philosophy and Social Science Key Research Base Project under Grant ZGJS 2022-07, in part by Scientific research Project of Panzhihua University under Grant 2020ZD015, in part by Sichuan vanadium and Titanium Materials EngineeringTechnology Research Center Open project under Grant 2022FTGC03 and in part by Sichuan Meteorological Disaster Forecasting and Early Warning and Emergency Management Research center project under Grant 2022FTGC03 ZHYJ21-YB07.

Acknowledgments

The authors thank the Zhang Yanhong Project Group, which provided GaoFen-5 datasets for experiments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aggarwal, H. K., and Majumdar, A. (2016). Hyperspectral image denoising using spatio-spectral total variation. IEEE Geosci. Remote Sens. Lett. 13 (3), 1–5. doi:10.1109/lgrs.2016.2518218

CrossRef Full Text | Google Scholar

Anfinsen, S. N., Doulgeris, A. P., and Eltoft, T. (2009). Estimation of the equivalent number of looks in polarimetric synthetic aperture radar imagery. IEEE Trans. Geosci. Remote Sens. 47 (11), 3795–3809. doi:10.1109/tgrs.2009.2019269

CrossRef Full Text | Google Scholar

Athey, S., Tibshirani, J., and Wager, S. (2019). Generalized random forests. Ann. Stat. 47 (2), 1148–1178. doi:10.1214/18-aos1709

CrossRef Full Text | Google Scholar

Bioucas-Dias, J. M., Plaza, A., Camps-Valls, G., Scheunders, P., Nasrabadi, N., and Chanussot, J. (2013). Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 1 (2), 6–36. doi:10.1109/mgrs.2013.2244672

CrossRef Full Text | Google Scholar

Chen, C., Wu, Z. B., Chen, Z. T., Zheng, Z. B., and Zhang, X. J. (2021). Auto-weighted robust low-rank tensor completion via tensor-train. Inf. Sci. 567, 100–115. doi:10.1016/j.ins.2021.03.025

CrossRef Full Text | Google Scholar

Chen, Y., Guo, Y., Wang, Y., Wang, D., Peng, C., and He, G. (2017). Denoising of hyperspectral images using nonconvex low rank matrix approximation. IEEE Trans. Geosci. Remote Sens. 55 (9), 5366–5380. doi:10.1109/tgrs.2017.2706326

CrossRef Full Text | Google Scholar

Chen, Y., He, W., Yokoya, N., and Huang, T. Z. (2019). Hyperspectral image restoration using weighted group sparsity-regularized low-rank tensor decomposition. IEEE Trans. Cybern. 50 (8), 3556–3570. doi:10.1109/tcyb.2019.2936042

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., He, W., Yokoya, N., Huang, T. Z., and Zhao, X. L. (2019). Nonlocal tensor-ring decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 58 (2), 1348–1362. doi:10.1109/tgrs.2019.2946050

CrossRef Full Text | Google Scholar

Chen, Y., He, W., Zhao, X. -L., Huang, T. -Z., Zeng, J., and Lin, H. (2022). Exploring nonlocal group sparsity under transform learning for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 60 (5537518), 1–18. doi:10.1109/TGRS.2022.3202359(

CrossRef Full Text | Google Scholar

Chen, Y., Huang, T. -Z., He, W., Zhao, X. -L., Zhang, H., and Zeng, J. (2022). Hyperspectral image denoising using factor group sparsity-regularized nonconvex low-rank approximation. IEEE Trans. Geosci. Remote Sens. 60 (5515916), 1–16. doi:10.1109/TGRS.2021.3110769

CrossRef Full Text | Google Scholar

Chen, Y., Huang, T. Z., He, W., Yokoya, N., and Zhao, X. L. (2020). Hyperspectral image compressive sensing reconstruction using subspace-based nonlocal tensor ring decomposition. IEEE Trans. Image Process. 29, 6813–6828. doi:10.1109/tip.2020.2994411

CrossRef Full Text | Google Scholar

Chen, Y., Wang, S., and Zhou, Y. (2018). Tensor nuclear norm-based low-rank approximation with total variation regularization. IEEE J. Sel. Top. Signal Process. 12 (6), 1364–1377. doi:10.1109/jstsp.2018.2873148

CrossRef Full Text | Google Scholar

Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K. (2007). Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 16 (8), 2080–2095. doi:10.1109/tip.2007.901238

PubMed Abstract | CrossRef Full Text | Google Scholar

Dian, R., Li, S., and Fang, L. (2019). Learning a low tensor-train rank representation for hyperspectral image super-resolution. IEEE Trans. Neural Netw. Learn. Syst. 30 (9), 2672–2683. doi:10.1109/tnnls.2018.2885616

PubMed Abstract | CrossRef Full Text | Google Scholar

Dian, R., and Li, S. (2019). Hyperspectral image super-resolution via subspace-based low tensor multi-rank regularization. IEEE Trans. Image Process. 28 (10), 5135–5146. doi:10.1109/tip.2019.2916734

CrossRef Full Text | Google Scholar

Ding, M., Huang, T. Z., Zhao, X. L., and Ma, T. H. (2022). Tensor completion via nonconvex tensor ring rank minimization with guaranteed convergence. Signal Process. 194, 108425. doi:10.1016/j.sigpro.2021.108425

CrossRef Full Text | Google Scholar

Fan, H., Chen, Y., Guo, Y., Zhang, H., and Kuang, G. (2017). Hyperspectral image restoration using low-rank tensor recovery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 10 (10), 4589–4604. doi:10.1109/jstars.2017.2714338

CrossRef Full Text | Google Scholar

He, W., Yao, Q., Li, C., Yokoya, N., Zhao, Q., Zhang, H., et al. (2022). Non-local meets global: An iterative paradigm for hyperspectral image restoration. IEEE Trans. Pattern Anal. Mach. Intell. 44 (4), 2089–2107. doi:10.1109/TPAMI.2020.3027563

PubMed Abstract | CrossRef Full Text | Google Scholar

He, W., Yokoya, N., Yuan, L., and Zhao, Q. (2019). Remote sensing image reconstruction using tensor ring completion and total variation. IEEE Trans. Geosci. Remote Sens. 57 (11), 8998–9009. doi:10.1109/tgrs.2019.2924017

CrossRef Full Text | Google Scholar

Huang, H., Liu, Y., Liu, J., and Zhu, C. (2020). Provable tensor ring completion. Signal Process. 171, 107486. doi:10.1016/j.sigpro.2020.107486

CrossRef Full Text | Google Scholar

Huang, Z., Li, S., Fang, L., Li, H., and Benediktsson, J. A. (2017). Hyperspectral image denoising with group sparse and low-rank tensor decomposition. IEEE Access 6, 1380–1390. doi:10.1109/access.2017.2778947

CrossRef Full Text | Google Scholar

Liu, X., Bourennane, S., and Fossati, C. (2012). Denoising of hyperspectral images using the PARAFAC model and statistical performance analysis. IEEE Trans. Geosci. Remote Sens. 50 (10), 3717–3724. doi:10.1109/tgrs.2012.2187063

CrossRef Full Text | Google Scholar

Liu, Y., Shang, F., Jiao, L., Cheng, J., and Cheng, H. (2014). Trace norm regularized CANDECOMP/PARAFAC decomposition with missing data. IEEE Trans. Cybern. 45 (11), 2437–2448. doi:10.1109/tcyb.2014.2374695

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, X. G., Wang, H. J., and Wang, S. (2015). Monogenic signal theory based feature similarity index for image quality assessment. AEU - Int. J. Electron. Commun. 69 (1), 75–81. doi:10.1016/j.aeue.2014.07.015

CrossRef Full Text | Google Scholar

Morrone, M. C., and Owens, R. A. (1987). Feature detection from local energy. Pattern Recognit. Lett. 6 (5), 303–313. doi:10.1016/0167-8655(87)90013-4

CrossRef Full Text | Google Scholar

Oseledets, I. V. (2011). Tensor-train decomposition. SIAM J. Sci. Comput. 33 (5), 2295–2317. doi:10.1137/090752286

CrossRef Full Text | Google Scholar

Sattar, F., Floreby, L., Salomonsson, G., and Lovstrom, B. (1997). Image enhancement based on a nonlinear multiscale method. IEEE Trans. Image Process. 6 (6), 888–895. doi:10.1109/83.585239

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, M., Wang, Q., Chanussot, J., and Hong, D. (2021). Total variation regularized weighted tensor ring decomposition for missing data recovery in high-dimensional optical remote sensing images. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi:10.1109/lgrs.2021.3069895

CrossRef Full Text | Google Scholar

Wang, W., Sun, Y., Eriksson, B., Wang, W., and Aggarwal, V. (2018). “Wide compression: Tensor ring nets,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 9329–9338.

CrossRef Full Text | Google Scholar

Wang, Y., Peng, J., Zhao, Q., Leung, Y., Zhao, X. L., and Meng, D. (2017). Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 11 (4), 1227–1243. doi:10.1109/jstars.2017.2779539

CrossRef Full Text | Google Scholar

Wei, K., Fu, Y., and Huang, H. (2020). 3-D quasi-recurrent neural network for hyperspectral image denoising. IEEE Trans. Neural Netw. Learn. Syst. 32 (1), 363–375. doi:10.1109/tnnls.2020.2978756

CrossRef Full Text | Google Scholar

Wu, Z., Wang, Q., Jin, J., and Shen, Y. (2017). Structure tensor total variation-regularized weighted nuclear norm minimization for hyperspectral image mixed denoising. Signal Process. 131, 202–219. doi:10.1016/j.sigpro.2016.07.031

CrossRef Full Text | Google Scholar

Xiong, F., Zhou, J., and Qian, Y. (2019). Hyperspectral restoration via L₀ gradient regularized low-rank tensor factorization. IEEE Trans. Geosci. Remote Sens. 57 (12), 10410–10425. doi:10.1109/tgrs.2019.2935150

CrossRef Full Text | Google Scholar

Xue, J., Zhao, Y., Bu, Y., Chan, J. C. W., and Kong, S. G. (2022). When laplacian scale mixture meets three-layer transform: A parametric tensor sparsity for tensor completion. IEEE Trans. Cybern., 1–15. doi:10.1109/TCYB.2021.3140148

CrossRef Full Text | Google Scholar

Xue, J., Zhao, Y., Huang, S., Liao, W., Chan, J. C. W., and Kong, S. G. (2021). Multilayer sparsity-based tensor decomposition for low-rank tensor completion. IEEE Trans. Neural Netw. Learn. Syst. 33, 6916–6930. doi:10.1109/TNNLS.2021.3083931

CrossRef Full Text | Google Scholar

Xue, J., Zhao, Y., Liao, W., Chan, J. C. W., and Kong, S. G. (2019). Enhanced sparsity prior model for low-rank tensor completion. IEEE Trans. Neural Netw. Learn. Syst. 31 (11), 4567–4581. doi:10.1109/tnnls.2019.2956153

CrossRef Full Text | Google Scholar

Xue, J., Zhao, Y., Liao, W., and Chan, J. C. W. (2019). Nonlocal low-rank regularized tensor decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 57 (7), 5174–5189. doi:10.1109/tgrs.2019.2897316

CrossRef Full Text | Google Scholar

Xuegang, L., Lv, J., and Wang, J. (2022). Hyperspectral image restoration via auto-weighted nonlocal tensor ring rank minimization. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi:10.1109/LGRS.2022.3199820

CrossRef Full Text | Google Scholar

Yang, J., Zhao, Y. Q., Yi, C., and Chan, J. C. W. (2017). No-reference hyperspectral image quality assessment via quality-sensitive features learning. Remote Sens. 9 (4), 305. doi:10.3390/rs9040305

CrossRef Full Text | Google Scholar

Yokota, T., Erem, B., Guler, S., Warfield, S. K., and Hontani, H. (2018). “Missing slice recovery for tensors using a low-rank model in embedded space,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 8251–8259.

CrossRef Full Text | Google Scholar

Yokota, T., Zhao, Q., and Cichocki, A. (2016). Smooth PARAFAC decomposition for tensor completion. IEEE Trans. Signal Process. 64 (20), 5423–5436. doi:10.1109/tsp.2016.2586759

CrossRef Full Text | Google Scholar

Yu, J., Li, C., Zhao, Q., and Zhao, G. (2019). “Tensor-ring nuclear norm minimization and application for visual: Data completion,” in ICASSP 2019-2019 IEEE international conference on acoustics, speech and signal processing (ICASSP), 3142–3146.

CrossRef Full Text | Google Scholar

Yuan, L., Li, C., Cao, J., and Zhao, Q. (2020). Rank minimization on tensor ring: An efficient approach for tensor decomposition and completion. Mach. Learn. 109 (3), 603–622. doi:10.1007/s10994-019-05846-7

CrossRef Full Text | Google Scholar

Yuan, L., Zhao, Q., Gui, L., and Cao, J. (2019). High-order tensor completion via gradient-based optimization under tensor train format. Signal Process. Image Commun. 73, 53–61. doi:10.1016/j.image.2018.11.012

CrossRef Full Text | Google Scholar

Zeng, H., Xie, X., Cui, H., Yin, H., and Ning, J. (2020). Hyperspectral image restoration via global L_1-2 spatial-spectral total variation regularized local low-rank tensor recovery. IEEE Trans. Geosci. Remote Sens. 59 (4), 3309–3325. doi:10.1109/tgrs.2020.3007945

CrossRef Full Text | Google Scholar

Zhang, H., He, W., Zhang, L., Shen, H., and Yuan, Q. (2013). Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. geoscience remote Sens. 52 (8), 4729–4743.

Google Scholar

Zhang, Z., Ely, G., Aeron, S., Hao, N., and Kilmer, M. (2014). “Novel methods for multilinear data completion and denoising based on tensor-SVD,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 3842–3849.

CrossRef Full Text | Google Scholar

Zhao, Q., Zhou, G., Xie, S., Zhang, L., and Cichocki, A. (2016). Tensor ring decomposition. arXiv preprint arXiv:1606.05535.

Google Scholar