Using reinforcement learning to autonomously identify sources of error for agents in group missions

When deploying agents to execute a mission with collective behavior, it is common for accidental malfunctions to occur in some agents. It is challenging to distinguish whether these malfunctions are due to actuator failures or sensor issues based solely on interactions with the affected agent. However, we humans know that if we cause a group behavior where other agents collide with a suspected malfunctioning agent, we can monitor the presence or absence of a positional change and identify whether it is the actuator (position changed) or the sensor (position unchanged) that is broken. We have developed artificial intelligence that can autonomously deploy such “information acquisition strategies through collective behavior” using machine learning. In such problems, the goal is to plan collective actions that result in differences between the hypotheses for the state [e.g., actuator or sensor]. Only a few of the possible collective behavior patterns will lead to distinguishing between hypotheses. The evaluation function to maximize the difference between hypotheses is therefore sparse, with mostly flat values across most of the domain. Gradient-based optimization methods are ineffective for this, and reinforcement learning becomes a viable alternative. By handling this maximization problem, our reinforcement learning surprisingly gets the optimal solution, resulting in collective actions that involve collisions to differentiate the causes. Subsequent collective behaviors, reflecting this situation awareness, seemed to involve other agents assisting the malfunctioning agent.

1 Problem formulation

The group cooperation of agents is an important topic studied in the context of autonomous systems (Lee et al., 2018; Hu et al., 2020). Because it is likely that each agent will have individual biases in its actuator or sensor performance, it is an important autonomous ability to analyze these inherent biases and revise the control plan appropriately to continue the group mission. Such biases dynamically change over time during missions, occasionally leading to failures in some functions of an agent. When such changes occur, it is essential to promptly revise the transportation plan using methods such as reinforcement learning. However, this requires constructing a virtual environment that accurately reflects real-world conditions. Therefore, to properly update the operational plan using reinforcement learning, it is necessary to identify the causes of the biases, including any failures, in each agent as they occur.

Previous research on fault diagnosis methods in swarm robotic systems includes the work by O'Keeffe et al. (O’Keeffe et al., 2018). This approach adopts a fault diagnosis mechanism, inspired by biological immune systems, that learns from past diagnostic results to efficiently identify malfunctions based on the behavior of robots. However, the diagnostic tests assumed here only target predictable faults and may struggle when multiple faults occur simultaneously. This difficulty in diagnosis is an inevitable challenge in the advancement of robotic development.

One of the factors complicating this diagnosis is the difficulty in distinguishing the causes of faults.

Suppose that a command base, which controls a group of agents via each command $g_j$ (Figure 1A), has detected an anomaly in the position of an agent (e.g., no change in the position was observed). There are two possible causes for the observed anomaly: (1) actuator failures (agent is unable to move) or (2) sensor failures (agent can move, but the move is not captured by the sensor) (Figure 1B). Depending on the hypothesis [the failure may have occurred in the actuators $(h_a)$ or sensors $(h_s)$], the plan is subsequently calibrated and updated accordingly. However, it is generally difficult to identify which problem caused the anomaly solely through communication between the base and the agent. An intuitive method to identify the correct hypothesis is to execute a collision to the failure agent by other agents to check whether any displacement is observed by the sensor. Such a collision should demonstrate agent displacement; sensor failure would not detect that displacement. Thus, the correct hypothesis can be identified by “planning a group motion.” The question then arises as to whether such planning can be set up autonomously as a “strategy to acquire environmental information” (Friston, 2010).

Figure 1

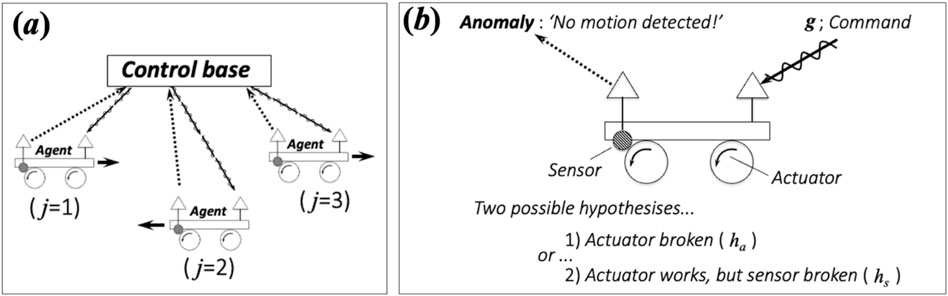
Figure 1. Agents perform group actions according to commands communicated from the “control base” (the figure depicts an example with three agents indexed by $j$). The wavy arrow denotes a command signal from the base, whereas the dotted arrows represent the return signals from each sensor on each agent [panel (A)]. When an anomaly is detected in a return signal, two hypotheses—$h_a$ or $h_s$—can be considered [panel (B)].

Such autonomous planning appears to be feasible given the following value function. Suppose that the command $\mathit{g}=\left(g_1,g_2,\cdots \right)$ is issued from the control base, directing the agent’s action to specify which of the hypotheses ($h_a$, $h_s$) is supported (Figure 1A). This command updates the agent state to $\mathit{R}\to \tilde{\mathit{R}}\left(\mathit{g}\right)$. The updated state $\tilde{\mathit{R}}$ should be denoted as ${\tilde{\mathit{R}}}^{\left(h_l\right)}\left(\mathit{g}\right)$ because it depends on the hypothesis about the state before the update $(l=a,s)$. As the expected results differ for different hypotheses, the following expression can be used to evaluate the distinction: $D=‖{\tilde{\mathit{R}}}^{\left(h_s\right)}-{\tilde{\mathit{R}}}^{\left(h_a\right)}‖$. To ensure appropriate planning $\mathit{g}$ that involves collisions between agents, a non-zero difference $D$ is obtained, and the likelihood of each hypothesis can be determined. We must, therefore, formulate a plan that maximizes $D=D\left(\mathit{g}\right)$ to ensure a significant difference. Accordingly, an autonomous action plan can be formulated to maximize $D\left(\mathit{g}\right)$ as a value function.

However, this maximization task is difficult to complete via conventional gradient-based optimization. Owing to the wide range of possibilities for $\mathit{g}$, interactions such as collisions are rare events, and for most of the planning phase $\mathit{g}$, $D\left(\mathit{g}\right)=0$, it is impossible to distinguish between hypotheses. Namely, sub-spaces with finite $D$ are sparse in the overall state space (sparse rewards). In such cases, gradient-based optimization is insufficient for the task of formulating appropriate action plans because the zero-gradient encompasses the vast majority of the space. For such sparse reward optimization, reinforcement learning, which has been thoroughly investigated in the applications of autonomous systems (Huang et al., 2005; Xia and El Kamel, 2016; Zhu et al., 2018; Hu et al., 2020), can be used as an effective alternative.

Reinforcement learning (Nachum et al., 2018; Sutton and Barto, 2018; Barto, 2002) is becoming an established field in the wider context of robotics and system controls (Peng et al., 2018; Finn and Levine (2017). Methodological improvements have been studied intensively, especially by verifications on gaming platforms (Mnih et al., 2015; Silver et al., 2017; Vinyals et al., 2019). Thus, the topic addressed in this study is becoming a subfield known as multi-agent reinforcement learning (MARL) (Busoniu et al., 2006; Gupta et al., 2017; Straub et al., 2020; Bihl et al., 2022; Gronauer and Diepold, 2021). Specific examples of multi-agent missions include unmanned aerial vehicles (UAV) (Bihl et al., 2022; Straub et al., 2020) and sensor resource management (SRM) Malhotra et al., 2017, 1997; Hero and Cochran, 2011; Bihl et al., 2022). The objective of this study can also be regarded as the problem of handling non-stationary environments in multi-agent reinforcement learning (Nguyen et al., 2020; Foerster et al., 2017). As a consequence of failure, agents are vulnerable to the gradual loss of homogeneity. Prior studies have addressed the problem of heterogeneity in multi-agent reinforcement learning (Busoniu et al., 2006; Calvo and Dusparic, 2018; Bihl et al., 2022; Straub et al., 2020; Gronauer and Diepold, 2021). The problem of sparse rewards has also been recognized and discussed as one of the current challenges in reinforcement learning (Wang and Taylor, 2017; Bihl et al., 2022). Recent advancements in reinforcement learning have introduced various innovative methods for handling single-agent or multi-agent scenarios. These approaches have focused on improving sample efficiency, computational costs, and learning stability across different frameworks. One such method is TD7, which utilizes state-action learned embeddings (SALE) for jointly learning embeddings of both states and actions Fujimoto et al., 2024). CrossQ is another approach that improves sample efficiency while significantly reducing computational costs by utilizing batch normalization (Bhatt et al., 2019). Continuous dynamic policy programming (CDPP) extends relative entropy regularized reinforcement learning from value function-based frameworks to actor-critic structures in continuous action spaces, achieving improved sample efficiency and learning stability (Shang et al., 2023). Furthermore, dropout Q-functions (DroQ) employs a small ensemble of dropout Q-functions to enhance computational efficiency while maintaining sample efficiency comparable to randomized ensembled double Q-learning (REDQ) (Hiraoka et al., 2021). In the realm of multi-agent reinforcement learning, multi-agent continuous dynamic policy gradient (MACDPP) has achieved high learning capability and sample efficiency by introducing relative entropy regularization to the centralized training with decentralized execution (CTDE) framework Miao et al., 2024).

The discussion thus far can be generalized as follows: Consider a scenario involving $N$ agents where some anomalies occur, and multiple hypotheses are conceivable. For instance, similar to the earlier example, there could be cases where only a sensor or only an actuator fails in a single agent. Alternatively, there could be scenarios involving multiple agents where anomalies occur in several sensors and actuators, among other various cases. Furthermore, let $\mathit{R}$ denote the state of these $N$ agents, which could be a vector obtained by concatenating the coordinates of $N$ robots. Under hypothesis $l$, the state $\mathit{R}$ is updated by a command $\mathit{g}$ to a new state ${\tilde{\mathit{R}}}^{\left(h_l\right)}$. The difference between the states under hypotheses $l$ and $l^{\prime }$ can be expressed as $D_{<l,l^{\prime }>}=‖{\tilde{\mathit{R}}}^{\left(h_l\right)}-{\tilde{\mathit{R}}}^{\left(h_{l^{\prime }}\right)}‖$, similar to earlier. If a virtual environment that faithfully reproduces these agents’ behavior is prepared, and $\mathit{g}$ that maximizes $D_{<l,l^{\prime }>}$ can be found through reinforcement learning, executing $\mathit{g}$ in real systems and observing the outcomes would allow for discrimination between hypotheses. To search for a $\mathit{g}$ that simultaneously discriminates all hypotheses, reinforcement learning should be conducted to maximize the sum of $D_{<l,l^{\prime }>}$ across all combinations of hypotheses.

As a prototype of such a problem, we considered a system composed of three agents moving on an $(x,y)$-plane, administrated by a command base to perform a cooperative task (Figure 2). In performing the task, each agent is asked to convey an item to a goal post individually. The second agent (#2) is assumed to be unable to move along the $y$-direction due to an actuator failure. By quickly verifying tiny displacements in each agent, the command base can detect the problem occurring in #2. However, it cannot attribute the cause to either the actuators or the sensors. Consequently, the control base sets hypotheses $h_a$ and $h_s$ and begins planning the best cooperative motions ${\mathit{g}}^{*}$ to classify the correct hypothesis via reinforcement learning.

Figure 2

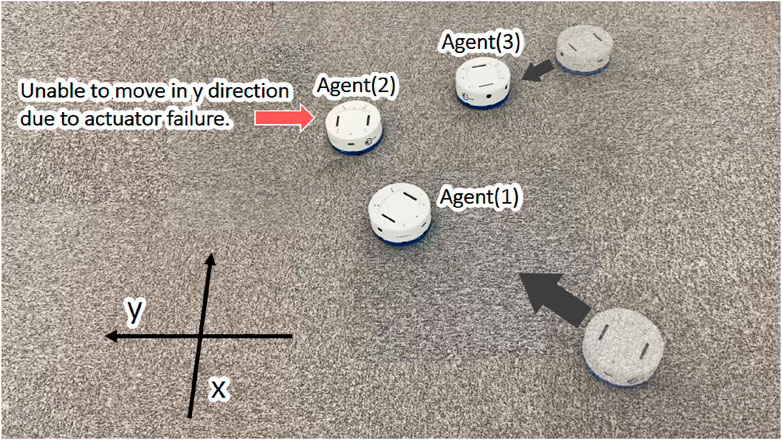
Figure 2. View of actual machines labeled as Agents #1–#3. Agent #2 is unable to move in the y-direction due to actuator failure. Agents #1 and #3 are on their way to rescue Agent#2 (see the main text about how the AI determines the action plan for the recovery of Agent #2).

Remarkably, the optimal action plan generated by reinforcement learning showed a human-like solution to pinpoint the problem by colliding other agents with the failed agent. By inducing a collision, the base could identify that #2 is experiencing problems with its actuators rather than sensors. The base then starts planning group motions to complete the conveying task, considering the limited functionality of #2. We observe that the cooperative tasks are facilitated by a learning process wherein other agents appear to compensate for the deficiency of #2 by pushing it toward the goal. In the present study, we employed a simple prototype system to demonstrate that reinforcement learning is extremely effective in setting up a verification plan that pinpoints multiple hypotheses for general cases of system failure.

2 Methodology

Let the state space for the agents be $\mathit{R}$. For instance, given three agents $(j=\mathrm{1,2,3})$ situated on a $xy$-plane at positions $\left(x_j,y_j\right)$, their states can be specified as $\mathit{R}=\left(x_1,y_1,x_2,y_2,x_3,y_3\right)$; that is, points in six-dimensional space. The state is driven by a command $\mathit{g}$ according to the operation plan generated in the command base. When $\mathit{g}$ is assigned to a given $\mathit{R}$, the state is updated depending on which hypothesis $h_l$ is taken, each of which restricts $\mathit{R}$ by individual constraint:

$\mathit{g}:\mathit{R}\to {\tilde{\mathit{R}}}^{\left(h_l\right)}\left(\mathit{g},\mathit{R}\right).$

The difference

$D\left(\mathit{g},\mathit{R}\right)={\displaystyle \sum _{<l,l^{\prime }>}}‖{\tilde{\mathit{R}}}^{\left(h_l\right)}\left(\mathit{g},\mathit{R}\right)-{\tilde{\mathit{R}}}^{\left(h_{l^{\prime }}\right)}\left(\mathit{g},\mathit{R}\right)‖$

can then be the measure to evaluate performance and thereby distinguish between the hypotheses. Therefore, the best operation plan for the distinction should be determined as

${\mathit{g}}^{*}={\mathrm{arg\hspace{0.17em}max}}_{\mathit{g}}D\left(\mathit{g},\mathit{R}\right).$

The naive idea of performing optimization using gradient-based methods is insufficient, owing to the sparseness described in the introduction. For $\mathit{g}$, $D(\mathit{g},\mathit{R})=0$, the gradient is zero for most of $\mathit{R}$ because it is incapable of selecting the next update. Accordingly, we employed reinforcement learning as an alternative optimization approach.

Suppose we can evaluate the reward $\rho \left(\mathit{R},\mathit{g}\right)$ for the action $\mathit{g}$ to be taken for a given state $\mathit{R}$. In reinforcement learning, decisions aim to maximize the action value $Q\left(\mathit{R},\mathit{g}\right)$, rather than maximizing the immediate reward $\rho \left(\mathit{R},\mathit{g}\right)$. Although the reward $\rho \left(\mathit{R},\mathit{g}\right)$ indicates the benefit obtained at that moment, the action value $Q\left(\mathit{R},\mathit{g}\right)$ represents the benefit accumulated over the future. The governing equation that links the given $\rho \left(\mathit{R},\mathit{g}\right)$ with $Q\left(\mathit{R},\mathit{g}\right)$ is known as the Bellman equation, being expressed in self-consistent manner. Users specify the reward function $\rho \left(\mathit{R},\mathit{g}\right)$ and the detailed specifications of the Bellman equation to self-consistently determine the action value $Q\left(\mathit{R},\mathit{g}\right)$ using a library. In this study, we employed the OpenAI Gym (Brockman et al., 2016) as such a library. Though the details of the reinforcement learning implementation are found in the general literature, we provide further details using our notation adopted in this paper in Section 1 of the Supplementary Material. In this research, the operational plans are finally determined by the converged action value, $\bar{Q}\left(\mathit{R},\mathit{g}\right)$, obtained by the self-consistent iterations as

$\begin{array}{ccc}\hfill {\bar{\mathit{g}}}_0& =\hfill & \arg {\mathrm{\hspace{0.17em}max}}_{\mathit{g}}\bar{Q}\left({\mathit{R}}_0,\mathit{g}\right)\hfill \\ \hfill & \hfill & {\bar{\mathit{g}}}_0:{\mathit{R}}_0\to {\mathit{R}}_1\hfill \\ \hfill {\bar{\mathit{g}}}_1& =\hfill & \arg {\mathrm{\hspace{0.17em}max}}_{\mathit{g}}\bar{Q}\left({\mathit{R}}_1,\mathit{g}\right)\hfill \\ \hfill & \hfill & {\bar{\mathit{g}}}_1:{\mathit{R}}_1\to {\mathit{R}}_2\hfill \\ \hfill \cdots & \hfill & .\hfill \end{array}(1)$

3 Experiments

The workflow required to achieve the mission for the agents, as described in §1, proceeds as follows:

[0a ] To determine if there are errors found in any of the agents, the base issues commands to move all agents by tiny displacements (and consequently, Agent #2 is found to have an error).

[0b ] Corresponding to each possible hypothesis ($h_a$ and $h_s$), the virtual spaces ${\left\{{\mathit{R}}^{\left(h_l\right)}\right\}}_{l=a,s}$ are prepared by applying each constraint.

[1 ] Reinforcement learning $(Q_{\alpha })$ is performed at the command base using the virtual space, generating “the operation plan $\alpha$” to distinguish the hypotheses.

[2 ] The plan $\alpha$ is performed by the agents. The command base compares the observed trajectory with that obtained in the virtual spaces in Step [1]. In the process, the hypothesis that yields the closest trajectory to that observed is identified as accurate $(h_a)$.

[3 ] By taking the virtual space ${\mathit{R}}^{\left(h_a\right)}$ as the identified hypothesis, another learning $Q_{\beta }$ is performed to get the optimal plan $\beta$ for the original mission (conveying items to goal posts).

[4 ] Agents are operated according to the plan $\beta$.

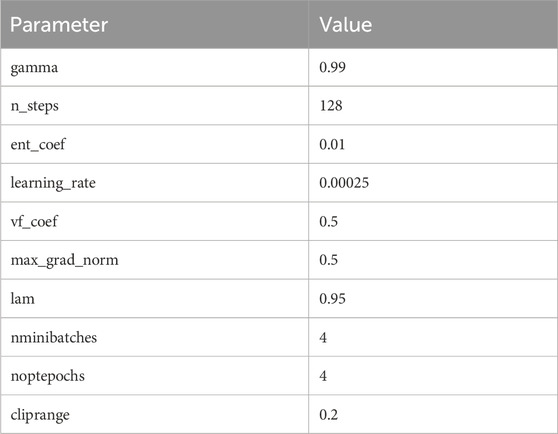
In this context, the term “virtual space” refers to an environment where physical computations are performed to simulate the movements of agents. In this study, it was implemented using Python. All learning processes and operations are simulated on a Linux server. The learning phase is the most time-intensive, requiring approximately 3 h to complete using a single processor without any parallelization. For the learning phase, we implemented the PPO2 (proximal policy optimization, version 2) algorithm Schulman et al., 2015) from the OpenAI Gym Brockman et al., 2016) library. Reinforcement learning $(Q_{\alpha })$ was benchmarked on the multilayer perceptron (MLP) and long short-time memory (LSTM) network structures, with performance compared between them. In the reinforcement learning described in [1], the state used comprised the positions of all agents, and the actions were defined as the direction of movement (x, y) for each agent. Conversely, in the reinforcement learning approach used in [3], the state included not only the positions of all agents but also the number of items each agent carried, the positions of all goal posts, and the number of items at each goal post. The actions remained the same, involving the direction of movement (x, y) for each agent. We did not conduct specific tuning for the hyperparameters as a default setting, as shown in Table 1. However, it has been pointed out that hyperparameter optimization (HPO) can significantly improve the performance of reinforcement learning (Henderson et al., 2018; Straub et al., 2020; Bihl et al., 2020; Snoek et al., 2012; Domhan et al., 2015; Bihl et al., 2022; Young et al., 2020). The comparison indicates that MLP performs better, with possible reasons given in the third paragraph of §4. The results described herein were obtained by the MLP network structure. Notably, LSTM also generated almost identical agent behaviors to those exhibited by the MLP (possible reasons are given in the Section 3 of the Supplementary Material.

Table 1

Table 1. PPO2 hyperparameters used in training.

The learning process $Q_{\alpha }$ in Step [1] is performed using two virtual spaces $V^{\left(h_s,a\right)}$, corresponding to the two hypotheses:

${\mathit{R}}^{\left(h_l\right)}\in V^{\left(h_l\right)}.$

Each ${\mathit{R}}^{\left(h_l\right)}$ can take such possibilities under each constraint of its hypothesis (e.g., $y_3$ cannot be updated due to the actuator error). For an operation $\mathit{g}$, the state on each virtual space is updated as

$\mathit{g}:\begin{array}{c}\hfill {\mathit{R}}^{\left(h_s\right)}\to {\tilde{\mathit{R}}}^{\left(h_s\right)}\left(\mathit{g},{\mathit{R}}^{\left(h_s\right)}\right)\hfill \\ \hfill {\mathit{R}}^{\left(h_a\right)}\to {\tilde{\mathit{R}}}^{\left(h_a\right)}\left(\mathit{g},{\mathit{R}}^{\left(h_a\right)}\right)\hfill \end{array}.$

Taking the value function,

$\begin{array}{ll}\hfill & {\rho }^{\left(\alpha \right)}\left(\mathit{g},{\mathit{R}}^{\left(h_1\right)},{\mathit{R}}^{\left(h_2\right)}\right)=‖{\tilde{\mathit{R}}}^{\left(h_1\right)}\left(\mathit{g},{\mathit{R}}^{\left(h_1\right)}\right)-{\tilde{\mathit{R}}}^{\left(h_2\right)}\left(\mathit{g},{\mathit{R}}^{\left(h_1\right)}\right)‖,\hfill \\ \hfill \end{array}(2)$

the two-fold $Q$-table is updated self-consistently as

$\begin{array}{ccc}\hfill & \hfill & Q\left(\mathit{g},{\mathit{R}}^{\left(h_1\right)},{\mathit{R}}^{\left(h_2\right)}\right)={\rho }^{\left(\alpha \right)}\left(\mathit{g},{\mathit{R}}^{\left(h_1\right)},{\mathit{R}}^{\left(h_2\right)}\right)\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{{\mathit{g}}^{\prime },{\mathit{R}}^{\prime \left(h_1\right)},{\mathit{R}}^{\prime \left(h_2\right)}}}F\left(\left\{Q\left({\mathit{g}}^{\prime },{\mathit{R}}^{\prime \left(h_1\right)},{\mathit{R}}^{\prime \left(h_2\right)}\right)\right\},\right.\left.\left\{\pi \left({\mathit{g}}^{\prime },{\mathit{R}}^{\prime \left(h_1\right)},{\mathit{R}}^{\prime \left(h_2\right)}\right)\right\}\right).\hfill \end{array}$

Denoting the converged table as ${\bar{Q}}_{\alpha }\left(\mathit{g},{\mathit{R}}^{\left(h_1\right)},{\mathit{R}}^{\left(h_2\right)}\right)$, the sequence of operations is obtained as given in Equation 1; in other words,

$\left\{{\bar{\mathit{g}}}_0^{\left(\alpha \right)},{\bar{\mathit{g}}}_1^{\left(\alpha \right)},\cdots {\bar{\mathit{g}}}_M^{\left(\alpha \right)}\right\}.(3)$

The operation sequence generates the two-fold sequence of (virtual) state evolutions as

$\left\{{\mathit{R}}_1^{\left(h_{s,a}\right)}\to {\mathit{R}}_2^{\left(h_{s,a}\right)}\to \cdots \to {\mathit{R}}_M^{\left(h_{s,a}\right)}\right\},(4)$

as shown in Figure 3A.

Figure 3

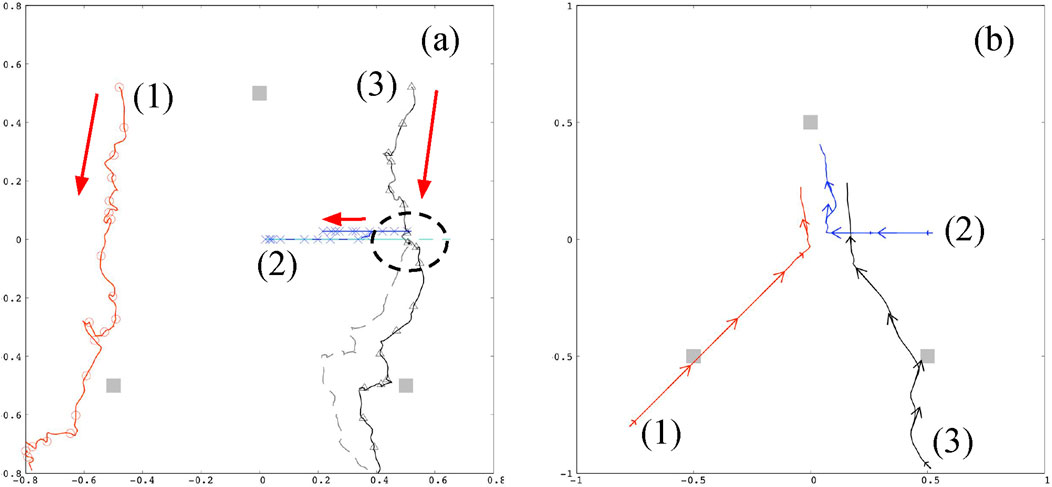
Figure 3. Agent trajectories are driven by each operation plan consequently generated via reinforcement learning (with the MLP neural network structure), $Q_{\alpha }$ first [panel (A)] and $Q_{\beta }$ [panel (B)]. The trajectories in (A) are the virtual states, ${\mathit{R}}^{\left(h_{s,a}\right)}$ (two-fold), branching for Agent #2 with respect to the hypothesis. Those given in (B) are the real trajectories, as obtained via Equation 6. The labels (1)–(3) indicate the agents, which move along the directions denoted by red arrows. Dotted circles indicate collisions between agents.

In Step [2], the agents operate according to the plan expressed by Equation 3 to update (real) states as

$\left\{{\mathit{R}}_1\to {\mathit{R}}_2\to \cdots \to {\mathit{R}}_M\right\},(5)$

to be observed by the command base. The base compares Equations 4, 5 to identify whether $h_s$ or $h_a$ is the cause of failure ($h_a$ in this case).

In Step [3], $Q_{\beta }$-learning is performed for reward ${\rho }^{\left(\beta \right)}$. The reward function ${\rho }^{\left(\beta \right)}$ calculates the sum of the individual agents’ rewards, where each agent gets a reward of $a/(r+1)+b\cdot \delta \left(r\right)$ depending on its distance $r$ from the goal post. Thus, a higher reward is realized when the agent gets closer to the goalpost. By setting $a=0.01$ and $b=100.0$, a much higher reward value $(a+b)$ is obtained when the agent reaches the goal post $(r=0)$. Although learning efficiency varies depending on the values of $a$ and $b$, a relatively high efficiency was achieved by setting $b\gg a$. The operation sequence is then obtained as

$\left\{{\bar{\mathit{g}}}_{M+1}^{\left(\beta \right)},{\bar{\mathit{g}}}_{M+2}^{\left(\beta \right)},\cdots {\bar{\mathit{g}}}_L^{\left(\beta \right)}\right\},$

by which the states of the agents are updated as

$\left\{{\mathit{R}}_{M+1}\to {\mathit{R}}_{M+2}\to \cdots \to {\mathit{R}}_L\right\},(6)$

as shown in Figure 3B.

4 Discussion

Figure 3A depicts two-fold trajectories, Equation 4, corresponding to the hypotheses $h_a$ and $h_s$. Although ${\mathit{R}}^{\left(h_a\right)}={\mathit{R}}^{\left(h_s\right)}$ for Agent #1, the branching ${\mathit{R}}^{\left(h_a\right)}\ne {\mathit{R}}^{\left(h_s\right)}$ occurs for Agent #2 during operations. The branching process earns a score via the value function ${\rho }^{\left(\alpha \right)}$ in Equation 2, which indicates that the learning $Q_{\alpha }$ was conducted properly. Thus, the ability to capture the difference between $h_a$ and $h_s$ has been realized. The red dotted circle shown in (a) represents a collision between Agents #2 and #3, inducing the difference between ${\mathit{R}}^{\left(h_a\right)}$ and ${\mathit{R}}^{\left(h_s\right)}$ (the trajectories only reflect the central positions of agents, while each agent has a finite radius similar to its size; therefore, the trajectories themselves do not intersect even when a collision occurs). In addition, the collision strategy is never generated in a rule-based manner, as the agents autonomously deduce their strategy via reinforcement learning.

Three square symbols (closed) situated at the edges of a triangle in Figure 3 represent the goalposts for the conveying mission. Figure 3B shows the real trajectories for the mission, where the initial locations of the agents are the final locations in the panel (a). From their initial locations, Agents #1 and #3 immediately arrived at their goals to complete each mission and subsequently headed to Agent #2 for assistance. Meanwhile, Agent #2 attempted to reach its goal using its limited mobility; that is, only along the $x$-axis. At the closest position, all three agents coalesced, and Agents #1 and #3 began pushing Agent #2 toward the goal. Though this behavior is simply the consequence of earning more from the value function ${\rho }^{\left(\beta \right)}$, it appears as if Agent #1 wants to assist the malfunctioning agent cooperatively (a video of the behavior shown in Figure 3B is available at the link Hayaschi, 2024). By identifying the constraint $h_a$ for the agents in the learning phase $Q_{\alpha }$, the subsequent learning phase $Q_{\beta }$ is confirmed to generate the optimal operation plans to ensure that the team maximizes their benefit through cooperative behavior as if an autonomous decision has been made by the team.

During training, if the target reward is not reached in the given number of training sessions, the training process is reset to avoid being trapped by the local solution. In Figure 4, the training curves of rejected trials are shown in blue, whereas the acceptable result is shown in red. Evidently, more learning processes were rejected in $Q_{\beta }$ (right panel) than in $Q_{\alpha }$ (left panel). This indicates that it is a more challenging task to perform transport planning with three malfunctioning agents than to plan the action to pinpoint a hypothesis between any two. However, under more complex failure conditions, more learning is expected to be rejected for $Q_{\alpha }$ as well, as the number of possible hypotheses increases.

Figure 4

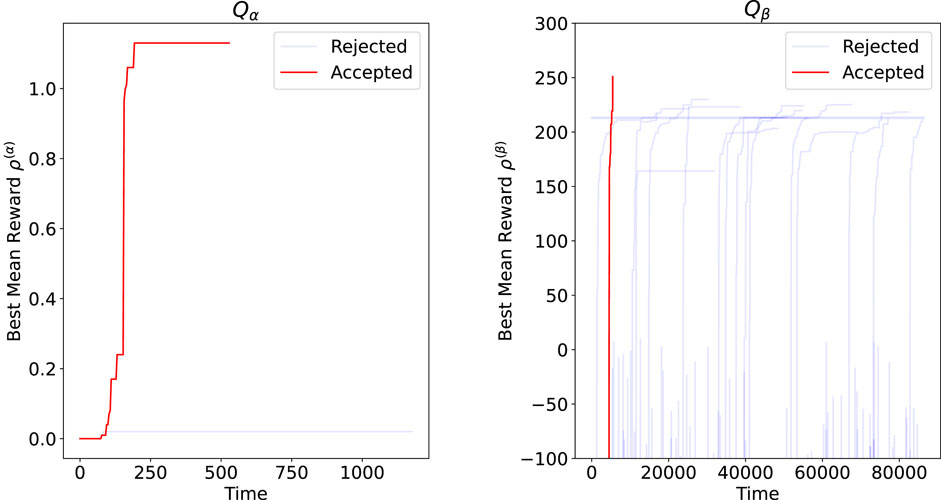
Figure 4. Learning curve evaluated for MLP network construction in terms of the reward function. Results for $Q_{\alpha }$ (left panel) and $Q_{\beta }$ (right panel) are shown. Blue and red curves correspond to trajectories that did not reach the target reward at the end of training and those that successfully reached the target reward, respectively.

The performance of LSTM and MLP was compared in terms of the success rate for obtaining working trajectories to distinguish between the hypotheses. Notably, even when applying the well-converged $Q$-table, there is a certain rate required for the non-working trajectories to eliminate the difference between the hypotheses. This is a result of the stochastic nature of the policy in generating the trajectories. In the present work, we took 50 independent $Q$-tables, each of which was generated from scratch, and obtained 50 corresponding trajectories. The rate required to obtain the trajectories required to distinguish among the hypotheses amounts to 94% for a learning management system (LMS) and 78% for LSTM. In the present comparison, we used the same iteration steps as for $Q$-table convergence. Because LSTM has a more complex internal structure, its learning quality was expected to be relatively lower than that of an LMS for the common condition, and its performance rate was likewise expected to be lower. In other words, a higher iteration cost is required for LSTM to achieve performance comparable to an LMS. As such, the results shown in the main text are those obtained by the LMS, whereas those obtained by LSTM are presented in the Supplementary Material for reference.

For a simulation in a virtual environment space, we must evaluate the distances between agents at every step. As this is a pairwise evaluation, its computational cost scales as $\sim N^2$ for $N$ agents. This cost scaling can be mitigated by using the domain decomposition method wherein each agent is evaluated according to its voxel, and the distance between agents is represented by that between corresponding voxels registered in advance. The corresponding cost scales linearly with $N$ at a much faster rate than the naive $\sim N^2$ evaluation method as the number of agents $N$ increases.

5 Conclusion

Agents performing group missions can suffer from errors during missions. Multiple hypotheses may be devised to explain the causes of such errors. Cooperative behaviors, such as collisions between agents, can be deployed to identify said causes. We considered the autonomous planning of group behaviors via machine-learning techniques. Different hypotheses explaining the causes of the errors lead to different expected states as updated from the same initial state by the same operation. The larger the difference becomes, the better the corresponding operation plan can distinguish between the different hypotheses. In other words, the magnitude of the difference can be the value function to optimize the desired operation plan. Gradient-based optimization does not work well because a tiny fraction among the vast possible operations (e.g., collisions) can capture the difference, leading to a sparse distribution of the finite value for the function. We discovered that reinforcement learning is the obvious choice for such problems. Notably, the optimal plan obtained via reinforcement learning was the operation that causes agents to collide with each other. To identify the causes of error using this plan, we developed a revised mission plan that incorporates the failure of another learning where the malfunctioning agent receives assistance from other agents. By identifying the cause of failure, the reinforcement learning process plans a revised mission plan that considers said failure to ensure an appropriate cooperation procedure. In this study, we conducted tests under the significant constraint that one of the three agents was malfunctioning. As described in §1, the framework can generally be formulated for $N$ agents. Future research will need to explore more detailed studies, including changes in the number of agents and variations in malfunctions. The findings presented in this paper provide initial insights into the capabilities of the proposed methods. Additional comparisons and results based on multiple trials, as well as comparisons with a greater number of baselines, are necessary to substantiate the conclusions of this study further.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

KU: conceptualization, methodology, validation, and writing–review and editing. K-tH: data curation, visualization, and writing–review and editing. TB: validation and writing–review and editing. KH: writing–review and editing. RM: funding acquisition, supervision, and writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by MEXT-KAKENHI (19H04692 and 16KK0097) and the Air Force Office of Scientific Research (AFOSR-AOARD/FA2386-17-1-4049; FA2386-19-1-4015).

Acknowledgments

The computations in this work were performed using the facilities at the Research Center for Advanced Computing Infrastructure at JAIST. RM is grateful for financial support from MEXT-KAKENHI (19H04692 and 16KK0097) and from the Air Force Office of Scientific Research (AFOSR-AOARD/FA2386-17-1-4049; FA2386-19-1-4015). The authors would like to thank Kosuke Nakano for his feedback as it significantly helped improve the overall paper. This work was cleared for public release under case AFRL-2023-3698. This work is the work of the authors and does not reflect any opinion or position of the U.S. government, the U.S. Air Force, or the Air Force Research Laboratory.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcteg.2024.1402621/full#supplementary-material

References

Barto, A. G. (2002). “Innovation and intellectual property rights,” in The handbook of brain theory and neural networks. Editor M. A. Arbib Second Edition (Cambridge, MA: The MIT Press), 963–972.

Google Scholar

Bhatt, A., Palenicek, D., Belousov, B., Argus, M., Amiranashvili, A., Brox, T., et al. (2019). Crossq: batch normalization in deep reinforcement learning for greater sample efficiency and simplicity. arXiv preprint arXiv:1902.05605

Google Scholar

Bihl, T., Jones, A., Farr, P., Straub, K., Bontempo, B., and Jones, F. (2022). “Assessing multi-agent reinforcement learning algorithms for autonomous sensor resource management,” in Proceedings of the 55th Hawaii international Conference on system Sciences (Hawaii international conference on system Sciences) (Honolulu, USA: HICSS). doi:10.24251/hicss.2022.695

CrossRef Full Text | Google Scholar

Bihl, T. J., Schoenbeck, J., Steeneck, D., and Jordan, J. (2020). “Easy and efficient hyperparameter optimization to address some artificial intelligence “ilities”,” in 53rd Hawaii international conference on system Sciences, HICSS 2020, maui, Hawaii, USA, january 7-10, 2020 ScholarSpace, 1–10.

Google Scholar

Brockman, G., Cheung, V., Pettersson, L., Schneider, J., Schulman, J., Tang, J., et al. (2016). Openai gym

Google Scholar

Busoniu, L., Babuska, R., and De Schutter, B. (2006). “Multi-agent reinforcement learning: a survey,” in 2006 9th international conference on control, automation, robotics and vision, 1–6. doi:10.1109/ICARCV.2006.345353

CrossRef Full Text | Google Scholar

Calvo, J., and Dusparic, I. (2018). Heterogeneous multi-agent deep reinforcement learning for traffic lights control. Proc. 26th Ir. Conf. Artif. Intell. Cogn. Sci., 1–12.

Google Scholar

Domhan, T., Springenberg, J. T., and Hutter, F. (2015). “Speeding up automatic hyperparameter optimization of deep neural networks by extrapolation of learning curves,” in Proceedings of the 24th international conference on artificial intelligence, 3460–3468.

Google Scholar

Finn, C., and Levine, S. (2017). “Deep visual foresight for planning robot motion,” in 2017 IEEE international conference on robotics and automation (ICRA), 2786–2793. doi:10.1109/ICRA.2017.7989324

CrossRef Full Text | Google Scholar

Foerster, J., Nardelli, N., Farquhar, G., Afouras, T., Torr, P. H. S., Kohli, P., et al. (2017). “Stabilising experience replay for deep multi-agent reinforcement learning,” in Proceedings of the 34th international conference on machine learning. (PMLR), vol. 70 of Proceedings of machine learning research. Editors D. Precup, and Y. W. Teh, 1146–1155.

Google Scholar

Friston, K. (2010). The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 11, 127–138. doi:10.1038/nrn2787

PubMed Abstract | CrossRef Full Text | Google Scholar

Fujimoto, S., Chang, W.-D., Smith, E., Gu, S. S., Precup, D., and Meger, D. (2024). For sale: state-action representation learning for deep reinforcement learning. Adv. Neural Inf. Process. Syst. 36.

Google Scholar

Gronauer, S., and Diepold, K. (2021). Multi-agent deep reinforcement learning: a survey. Artif. Intell. Rev. 55, 895–943. doi:10.1007/s10462-021-09996-w

CrossRef Full Text | Google Scholar

Gupta, J. K., Egorov, M., and Kochenderfer, M. (2017). “Cooperative multi-agent control using deep reinforcement learning,” in Autonomous agents and multiagent systems. Editors G. Sukthankar, and J. A. Rodriguez-Aguilar (Cham: Springer International Publishing), 66–83.

CrossRef Full Text | Google Scholar

Hayaschi, K. (2024). Video for fig. 3. Available at: https://www.dropbox.com/s/feejhj389h7p215/robot2_labeled.mp4?dl=0.

Google Scholar

Henderson, P., Islam, R., Bachman, P., Pineau, J., Precup, D., and Meger, D. (2018). “Deep reinforcement learning that matters,” in Aaai.

CrossRef Full Text | Google Scholar

Hero, A. O., and Cochran, D. (2011). Sensor management: past, present, and future. IEEE Sensors J. 11, 3064–3075. doi:10.1109/JSEN.2011.2167964

CrossRef Full Text | Google Scholar

Hiraoka, T., Imagawa, T., Hashimoto, T., Onishi, T., and Tsuruoka, Y. (2021). Dropout q-functions for doubly efficient reinforcement learning. arXiv Prepr. arXiv:2110.02034.

Google Scholar

Hu, J., Niu, H., Carrasco, J., Lennox, B., and Arvin, F. (2020). Voronoi-based multi-robot autonomous exploration in unknown environments via deep reinforcement learning. IEEE Trans. Veh. Technol. 69, 14413–14423. doi:10.1109/TVT.2020.3034800

CrossRef Full Text | Google Scholar

Huang, B.-Q., Cao, G.-Y., and Guo, M. (2005). Reinforcement learning neural network to the problem of autonomous mobile robot obstacle avoidance. 2005 Int. Conf. Mach. Learn. Cybern. 1, 85–89. doi:10.1109/ICMLC.2005.1526924

CrossRef Full Text | Google Scholar

Lee, H., Kim, H., and Kim, H. J. (2018). Planning and control for collision-free cooperative aerial transportation. IEEE Trans. Automation Sci. Eng. 15, 189–201. doi:10.1109/TASE.2016.2605707

CrossRef Full Text | Google Scholar

Malhotra, R., Blasch, E., and Johnson, J. (1997). Learning sensor-detection policies. Proc. IEEE 1997 Natl. Aerosp. Electron. Conf. NAECON 1997 2, 769–776. doi:10.1109/NAECON.1997.622727

CrossRef Full Text | Google Scholar

Malhotra, R. P., Pribilski, M. J., Toole, P. A., and Agate, C. (2017). “Decentralized asset management for collaborative sensing,” in Micro- and nanotechnology sensors, systems. Editors I. X. Applications, T. George, A. K. Dutta, and M. S. Islam (SPIE: International Society for Optics and Photonics), 10194, 403–414.

CrossRef Full Text | Google Scholar

Miao, C., Cui, Y., Li, H., and Wu, X. (2024). Effective multi-agent deep reinforcement learning control with relative entropy regularization. IEEE Trans. Automation Sci. Eng., 1–15doi. doi:10.1109/TASE.2024.3398712

CrossRef Full Text | Google Scholar

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. Nature 518, 529–533. doi:10.1038/nature14236

PubMed Abstract | CrossRef Full Text | Google Scholar

Nachum, O., Gu, S., Lee, H., and Levine, S. (2018). “Data-efficient hierarchical reinforcement learning,” in Proceedings of the 32nd international conference on neural information processing systems, 3307–3317.

Google Scholar

Nguyen, T. T., Nguyen, N. D., and Nahavandi, S. (2020). Deep reinforcement learning for multiagent systems: a review of challenges, solutions, and applications. IEEE Trans. Cybern. 50, 3826–3839. doi:10.1109/TCYB.2020.2977374

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Keeffe, J., Tarapore, D., Millard, A. G., and Timmis, J. (2018). Adaptive online fault diagnosis in autonomous robot swarms. Front. Robotics AI 5, 131. doi:10.3389/frobt.2018.00131

CrossRef Full Text | Google Scholar

Peng, X. B., Andrychowicz, M., Zaremba, W., and Abbeel, P. (2018). “Sim-to-real transfer of robotic control with dynamics randomization,” in 2018 IEEE international conference on robotics and automation (ICRA), 3803–3810. doi:10.1109/ICRA.2018.8460528

CrossRef Full Text | Google Scholar

Schulman, J., Levine, S., Mortiz, P., Jordan, M., and Abbeel, P. (2015). Trust region policy optimization. Proc. 32nd Int. Conf. Mach. Learn. 37, 1889–1897.

Google Scholar

Shang, Z., Li, R., Zheng, C., Li, H., and Cui, Y. (2023). Relative entropy regularized sample-efficient reinforcement learning with continuous actions. IEEE Trans. Neural Netw. Learn. Syst., 1–11doi. doi:10.1109/TNNLS.2023.3329513

CrossRef Full Text | Google Scholar

Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., et al. (2017). Mastering the game of go without human knowledge. Nature 550, 354–359. doi:10.1038/nature24270

PubMed Abstract | CrossRef Full Text | Google Scholar

Snoek, J., Larochelle, H., and Adams, R. P. (2012). Practical bayesian optimization of machine learning algorithms. Proc. 25th Int. Conf. Neural Inf. Process. Syst. - 2, 2951–2959.

Google Scholar

Straub, K. M., Bontempo, B., Jones, F., Jones, A. M., Farr, P., and Bihl, T. (2020). Sensor resource management using multi-agent reinforcement learning with hyperparameter optimization. Tech. Rep. White paper.

Google Scholar

Sutton, R. S., and Barto, A. G. (2018). Reinforcement learning: an introduction. second edn. The MIT Press.

Google Scholar

Vinyals, O., Babuschkin, I., Czarnecki, W. M., Mathieu, M., Dudzik, A., Chung, J., et al. (2019). Grandmaster level in starcraft ii using multi-agent reinforcement learning. Nature 575, 350–354. doi:10.1038/s41586-019-1724-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., and Taylor, M. E. (2017). “Improving reinforcement learning with confidence-based demonstrations,” in Proceedings of the twenty-sixth international joint conference on artificial intelligence (Darmstadt, Germany: IJCAI-17), 3027–3033. doi:10.24963/ijcai.2017/422

CrossRef Full Text | Google Scholar

Xia, C., and El Kamel, A. (2016). Neural inverse reinforcement learning in autonomous navigation. Robotics Aut. Syst. 84, 1–14. doi:10.1016/j.robot.2016.06.003

CrossRef Full Text | Google Scholar

Young, M. T., Hinkle, J. D., Kannan, R., and Ramanathan, A. (2020). Distributed bayesian optimization of deep reinforcement learning algorithms. J. Parallel Distributed Comput. 139, 43–52. doi:10.1016/j.jpdc.2019.07.008

CrossRef Full Text | Google Scholar

Zhu, D., Li, T., Ho, D., Wang, C., and Meng, M. Q.-H. (2018). “Deep reinforcement learning supervised autonomous exploration in office environments,” in 2018 IEEE international conference on robotics and automation (ICRA), 7548–7555. doi:10.1109/ICRA.2018.8463213

CrossRef Full Text | Google Scholar