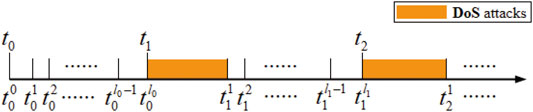Event-Based Resilient Control of Multi-Agent Systems in Non-Ideal Communication Networks

This article focuses on the consensus problem of linear multi-agent systems under denial-of-service attacks and directed switching topologies. With only intermittent communication, the leader-following consensus can be preserved by fully distributed event-triggered strategies. Theoretical analysis shows that the proposed event-triggered resilient controller guarantees the exponential convergence in the presence of denial-of-service attacks and the exclusion of Zeno behavior. Compared to the existing studies where continuous communication between neighboring agents is required, the event-triggered data reduction scheme is provided to tackle the effects of denial-of-service attacks on directed switching topology as well as to avoid continuous communication and reduce energy consumption. The obtained results can be extended to the scenario without a leader. Numerical simulations are finally given to illustrate the effectiveness of the proposed method.

1 Introduction

In past decades, cooperative control of multi-agent systems (MASs) has become one of the significant research interests in many areas, such as artificial intelligent, mathematics, biology, and control engineering (Olfati-Saber and Murray, 2004; Ren et al., 2007; Mei et al., 2016). Consensus control, one of the most important cooperative controls, is to guarantee the agents to achieve an agreement ultimately via neighborhood communication. Many related works on leaderless consensus and leader-following consensus (also known as consensus tracking) have been reported by Li et al., (2016),Qin et al., (2016), Li et al., (2018), and Zhu et al., (2021).

In Ma and Yang, (2016), Wang and Yang, (2016), Wang et al., (2020), and Zhang et al., (2021), continuous communication of neighbor agents and control is required to achieve the consensus for MASs. Recently, many efforts were devoted to the consensus problem for MASs with the event-triggered strategies. The event-triggered control method has obvious advantages which can effectively avoid continuous communication and reduce energy consumption and is widely applied in dealing with the scenario in which the bandwidth of the communication channel in a multi-agent system is limited. To design appropriate event-based control laws and the triggering functions are the main works in the event-triggered consensus problem. Event-triggered and self-triggered control schemes for single- or double-integrator agents have been developed by Dimarogonas et al., (2012), Meng and Chen, (2013), Seyboth et al., (2013), and Fan et al., (2015). For MASs with general linear dynamics, Yang et al., (2016), Cheng et al., (2017), Cheng and Li, (2019), Hu et al., (2020), and Xu and Wu, (2021) considered the consensus problem by designing event-triggered communication and control schemes. Specifically, Cheng et al., (2017) studied the leader-following consensus problem and eliminated the need of continuous communication between neighboring agents, where fixed and switching topologies are considered.

Among the studies on consensus of MASs, the security problem has attracted significant attention, as surveyed by Wang and Yang, (2018) and Wang et al., (2021), due to MASs being vulnerable to malicious attacks. The denial-of-service (DoS) attack is one of the common attacks on communication networks (Qin et al., 2018; Pelechrinis et al., 20212010), in which the legitimate members of MASs are unable to access information resources due to the malicious cyber threat actors. Some interesting results for MASs under DoS attacks have been obtained by Wang and Yang, (2018), Wang et al., (2021), Lu and Yang, (2018), and Zhang et al., (2019). To effectively alleviate needless waste of network resources, the event-triggering strategies for MASs under DoS attacks are proposed by Xu et al., (2019), Feng and Hu, (2020), Sun and Yang, (2020), and Tand et al., (2021). Note that the aforementioned results studied in the fixed topologies, though, for the unreliable communication environment under DoS attacks, the research results of using event-triggered methods to the systems under DoS attacks and directed switching topologies are relatively few.

Motivated by the aforementioned discussion, this article addresses the distributed event-triggered communication and control of linear MASs under DoS attacks, where directed switching topologies are considered. Although the control strategy under DoS attack is also studied by Wang et al., (2021), the continuous controller update is required. Moreover, unlike the result in Feng and Hu, (2020), assuming that the connection network is a fixed topology, a switching topology network including intermittent communication is considered, which is more reasonable in practical application. The contribution in this article is summarized as follows: First, an event-triggered secure approach, for solving the leader-following consensus problem of tracking a time-varying state of the leader agent in the presence of DoS attacks, has been developed. Moreover, while event-triggered control problem under DoS attack is considered in this article, the analysis is focusing on the switching topologies case. Furthermore, it is shown that the event-based control strategy is capable of reducing the frequency of communication and controller updates as well as excluding the Zeno behavior and event-triggered controller for leaderless multi-agent systems is further introduced.

The rest of the article is organized as follows: In Section 2, the necessary preliminaries are introduced. The achievement of the consensus and the exclusion of the Zeno behavior are presented in Section 3. Section 4 gives the simulation results, and finally the conclusions are drawn in Section 5.

2 Preliminaries and Problem Statement

2.1 Switching Communication Topologies

Among the N + 1 agents, the communication topology is modeled by a directed switching graph ${\mathcal{G}}^{\sigma (t)}$, of which one member is the leader (labeled by 0) and the rest N agents are the followers. ${\mathcal{G}}^{\sigma (t)}=\{{\mathcal{G}}^s:s\in \mathcal{S}\}$ is a set containing all possible directed connected graphs, where $\sigma (t):[0,+\infty )\to \mathcal{S}$ is defined as the switching signal with an index set $\mathcal{S}$. ${\mathcal{A}}^{\sigma (t)}=[a_{ij}^{\sigma (t)}]\in {\mathbb{R}}^{(N+1)\times (N+1)}$ is an adjacency matrix associated with nonnegative adjacency element a_ij and zero diagonal elements. Directed edge $(j,i)\in {\mathcal{E}}^{\sigma (t)}$ denotes that the agent i can obtain information from the agent j but not vice versa. ${\mathcal{L}}^{\sigma (t)}=[l_{ij}^{\sigma (t)}]\in {\mathbb{R}}^{(N+1)\times (N+1)}$ is a Laplacian matrix of ${\mathcal{G}}^{\sigma (t)}$, with $l_{ii}^{\sigma (t)}={\sum }_{j\ne i}{a}_{ij}^{\sigma (t)}$ and $l_{ij}^{\sigma (t)}=-a_{ij}^{\sigma (t)},i\ne j$. We partition the Laplacian matrix ${\mathcal{L}}^{\sigma (t)}\in {\mathbb{R}}^{(N+1)\times (N+1)}$ as ${\mathcal{L}}^{\sigma (t)}=[0,\mathbf{0};{\mathcal{L}}_1^{\sigma (t)},{\mathcal{L}}_2^{\sigma (t)}]$, where ${\mathcal{L}}_1^{\sigma (t)}=[{\mathcal{L}}_{1ij}^{\sigma (t)}]\in {\mathbb{R}}^{N\times 1}$ and ${\mathcal{L}}_2^{\sigma (t)}=[{\mathcal{L}}_{2ij}^{\sigma (t)}]\in {\mathbb{R}}^{N\times N}$. Note that ${\mathcal{L}}_2^s(s\in \mathcal{S})$ is a nonsingular M-matrix that satisfies ${\mathrm{\Sigma }}^s{\mathcal{L}}_2^s+{\mathcal{L}}_2^{sT}{\mathrm{\Sigma }}^s>0,\forall s\in \mathcal{S}$, where ${\mathrm{\Sigma }}^s=\mathrm{diag}\{{\xi }_1^s,{\xi }_2^s,\dots ,{\xi }_N^s\}$, ${\xi }^s={[{\xi }_1^s,{\xi }_2^s,\dots ,{\xi }_N^s]}^T={({\mathcal{L}}_2^{sT})}^{-1}{\mathbf{1}}_N$.

Assumption 1: The connection digraph ${\mathcal{G}}^{\sigma (t)}$ is fixed on every interval [t_m, t_m+1), m = 0, 1, 2, ⋯ . The leader node exists as a directed path to at least one follower.

Assumption 2: Topology-dependent average dwell time τ_as satisfies

$N_{\sigma }^s(t,T)\le N_0^s+\frac{T^s(t,T)}{{\tau }_{as}},(1)$

where $N_{\sigma }^s(t,T)$ represents the number of switching of the sth topology over (t, T), $s\in \mathcal{S}$, $N_0^s>0$ denotes the mode-dependent chattering bounds, and T^s (t, T) is the total running time of ${\mathcal{G}}^s$.

2.2 Intermittent DoS Attack Constraints

DoS attack refers to a class of attacks where an adversary renders certain or all components of an inaccessible control system. The DoS attacks can simultaneously affect both the measurement and control channels, which leads to the loss of data availability. One basic assumption of this article is that during the time DoS is active, only the exchange information among the group agents is interrupted, and thus the interaction information is inaccessible. The time series is shown in Figure 1.

FIGURE 1

FIGURE 1. Time series.

There are two states in a complete time sequence. One is the normal communication period without any malicious actions, and the other is the period interfered by DoS attacks. Here, the two states are defined as follows: when t ∈ Ω_I, intermittent communication failure occurs in the switching topologies, and thus the agent cannot obtain neighbor information; and when t ∈ Ω_C, all agents can receive neighbor information, in which ${\mathrm{\Omega }}_I={\bigcup }_{h\in {\mathbb{N}}_{+}}\left[t_h,t_h^1\right)$, ${\mathrm{\Omega }}_C=\bigcup \left[t_0,t_1\right){\bigcup }_{h\in {\mathbb{N}}_{+}}\left[t_h^1,t_{h+1}\right)$, and there exist the non-overlapping subintervals$[t_h^0,t_h^1),\dots$, $[t_h^{\ell },t_h^{\ell +1}),\dots ,[t_h^{l_h-1},t_h^{l_h})$ in each interval [t_h, t_h+1), with $t_h^0=t_h,t_h^{l_h}=t_{h+1}=t_{h+1}^0$, and $t_h^{\ell }(\ell =\mathrm{0,1},\dots ,l_h)$ are the topology switching time instants.

2.3 Problem Statement

Consider a group of N + 1 agents consisting of N followers and one leader. The dynamics of the ith follower agents are described by

${\dot{x}}_i(t)=A{x}_i(t)+B{u}_i(t),i=1,\dots ,N,(2)$

where $x_i(t)\in {\mathbb{R}}^n$ and $u_i(t)\in {\mathbb{R}}^m$ are the state and the control input of agent i, respectively. Matrices A and B are constant matrices with compatible dimensions. It is assumed that the matrix pair (A, B) is stabilizabie.

The dynamics of the leader agent are expressed as

${\dot{x}}_0(t)=A{x}_0(t),(3)$

where $x_0(t)\in {\mathbb{R}}^n$ is the state of the leader.

In this article, for the directed switching topological structure, our objective is to cope with the leader-following consensus problem of multi-agent systems under DoS attacks by designing event-triggered information transmission and control scheme, which leads x_i(t) − x₀(t) exponentially to converge to 0, and exclude the Zeno behavior.

3 Main Results

In this section, we study the consensus problem of multi-agent systems with directed switching topologies in the presence of DoS attacks and present the design of an event-triggered control scheme.

For each follower i, the state estimate is defined as ${\widehat{x}}_i(t)=e^{A(t-t_k^i)}{x}_i(t_k^i)$, $\forall t\in [t_k^i,t_{k+1}^i)$. The event-triggered controller for each follower agent i is proposed as

$u_i(t)=\varrho K\left[\sum _{j=1}^N{a}_{ij}^{\sigma (t)}({\widehat{x}}_i(t)-{\widehat{x}}_j(t))+a_{i0}^{\sigma (t)}({\widehat{x}}_i(t)-x_0(t))\right](4)$

with

$\varrho =\left\{\begin{array}{c}1,ift\in {\mathrm{\Omega }}_C,\hfill \\ 0,ift\in {\mathrm{\Omega }}_I,\hfill \end{array}\right.(5)$

where $K\in {\mathbb{R}}^{m\times n}$ is the feedback gain matrix to be determined and ${\widehat{x}}_0(t)=x_0(t)$.

The measurement error e_i(t) is defined as

$e_i(t)={\widehat{x}}_i(t)-x_i(t),i=1,\dots ,N.(6)$

The triggering time instant $t_{k+1}^i$ is determined by the following triggering mechanism:

$t_{k+1}^i=\left\{\begin{array}{c}{t}_h^{\ell },if{\mathcal{G}}^{\sigma (t)}switches,\hfill \\ \inf \{t>t_k^i:f_i^{\sigma (t)}(t)>0\},otherwise,\hfill \end{array}\right.(7)$

where the triggering function is given by

$\begin{array}{cc}\hfill f_i^{\sigma (t)}(t)=& \Vert e_i(t)\Vert -c\Vert \sum _{j=1}^N{a}_{ij}^{\sigma (t)}({\widehat{x}}_i(t)-{\widehat{x}}_j(t))\hfill \\ \hfill & +a_{i0}^{\sigma (t)}({\widehat{x}}_i(t)-x_0(t))\Vert ,\hfill \end{array}(8)$

with c is a positive constant to be determined.

Remark 1. The expression (Eq. 7) shows that agents update their communication when topology switches or event-triggering condition is satisfied.

Theorem 1. Consider the leader-following multi-agent systems (2) and (3). Suppose that controller (4) and event-triggered function (8) are applied with K = WP⁻¹ and $0<c<\sqrt{\frac{1}{{\lambda }_{\mathit{max}}(P^{-1})}}$. Then, the leader-following consensus problem can be solved if the following condition holds:

1) There exist matrices P > 0 and W such that

$\left[\begin{array}{cccc}\hfill {\mathrm{\Xi }}^s\hfill & \hfill {\mathrm{\Sigma }}^s{\mathcal{L}}_2^s\otimes BW\hfill & \hfill 0\hfill & \hfill {\mathcal{L}}_2^{\mathrm{s}T}\otimes P\hfill \\ \hfill *\hfill & \hfill -I_N\otimes P\hfill & \hfill {\mathcal{L}}_2^{\mathrm{s}T}\otimes P\hfill & \hfill 0\hfill \\ \hfill *\hfill & \hfill *\hfill & \hfill -\frac{1}{2N}{I}_{N\times n}\hfill & \hfill 0\hfill \\ \hfill *\hfill & \hfill *\hfill & \hfill *\hfill & \hfill -\frac{1}{2N}{I}_{N\times n}\hfill \end{array}\right]<0(9)$

and

$AP+P{A}^T-\alpha P<0,(10)$

with ${\mathrm{\Xi }}^s={\mathrm{\Sigma }}^s\otimes AP+{\mathrm{\Sigma }}^s\otimes P{A}^T+{\mathrm{\Sigma }}^s{\mathcal{L}}_2^s\otimes BW+{{\mathcal{L}}_2^s}^T{\mathrm{\Sigma }}^s\otimes W^T{B}^T+{\lambda }_s({\mathrm{\Sigma }}^s\otimes P)$, λ_s > 0 and α > 0.

2) Choose μ_s > b₀/a₀ such that $\sum _{s\in \mathrm{S}}({\lambda }_s-\frac{\ln {\mu }_s}{{\tau }_{as}})T^s(t_0,t_1)-\ln \frac{b_0}{a_0}>0$ and $\sum _{s\in \mathrm{S}}({\lambda }_s-\frac{\ln {\mu }_s}{{\tau }_{as}})T^s(t_h^1,t_{h+1})-\ln \frac{b_0}{a_0}>\alpha (t_h^1-t_h)$, where a₀ and b₀ will be given later.

Proof. Define the tracking error of each follower i as δ_i(t) = x_i(t) − x₀(t). Let δ(t) and e(t) be the column stack vectors of δ_i(t) and e_i(t), respectively. By combining Eq. 2, Eq. 3, and Eq. 4, the dynamics of the error closed-loop system can be expressed as

$\begin{array}{cc}\hfill \dot{\delta }(t)=& \varrho ((I_N\otimes A+{\mathcal{L}}_2^{\sigma (t)}\otimes BK)\delta (t)+({\mathcal{L}}_2^{\sigma (t)}\otimes BK)e(t))\hfill \\ \hfill & (1-\varrho )(I_N\otimes A)\delta (t).\hfill \end{array}(11)$

Consider the multiple topology-dependent Lyapunov function candidate

$V_{\sigma (t)}(t)=\varrho {\delta }^T(t)({\mathrm{\Sigma }}_{\sigma (t)}\otimes \bar{P})\delta (t)+(1-\varrho ){\delta }^T(t)(I_N\otimes \bar{P})\delta (t),(12)$

with $\bar{P}=P^{-1}$.

Denote a_s = λ_min (Σ^s), $a_0=\underset{s\in \mathrm{S}}{\min }\{a_s\}$, $\bar{a}=a_0{\lambda }_{\min }(\bar{P})$, b_s = λ_max (Σ^s), $b_0=\underset{s\in \mathrm{S}}{\max }\{b_s\}$, and $\bar{b}=b_0{\lambda }_{\max }(\bar{P})$. It follows from Eq. 12 that $\bar{a}\Vert \delta (t){\Vert }^2\le a_0{\delta }^T(t)(I_N\otimes \bar{P})\delta (t)\le a_s{\delta }^T(t)(I_N\otimes \bar{P})\delta (t)\le V_s(t)\le b_s{\delta }^T(t)(I_N\otimes \bar{P})\delta (t)\le b_0{\delta }^T(t)(I_N\otimes \bar{P})\delta (t)\le \bar{b}\Vert \delta (t){\Vert }^2$.

For t ∈ Ω_C, we assume σ(t) = s; at this time, the network communication is not subjected to attacks. Note that $V_{s1}(t)\le b_{s1}{\delta }^T(t)(I_N\otimes \bar{P})\delta (t)\le {\mu }_{s1}{V}_{s2}(t)$, where $s1,s2\in \mathcal{S}$.

Let $\zeta (t)={[{\delta }^T(t),e^T(t)]}^T$. The derivative of V_s(t) along the trajectories of Eq. 11 can be expressed as

$\begin{array}{cc}\hfill {\dot{V}}_s(t)=& 2{\delta }^T(t)({\mathrm{\Sigma }}^s\otimes \bar{P})\left[(I_N\otimes A)\delta (t)+({\mathcal{L}}_2^s\otimes BK)\delta (t)\right.\hfill \\ \hfill & \left.+({\mathcal{L}}_2^s\otimes BK)e(t)\right]\hfill \\ \hfill =& 2{\delta }^T(t)({\mathrm{\Sigma }}^s\otimes \bar{P}A)\delta (t)+2{\delta }^T(t)({\mathrm{\Sigma }}^s{\mathcal{L}}_2^s\otimes \bar{P}BK)\delta (t)\hfill \\ \hfill & +2{\delta }^T(t)({\mathrm{\Sigma }}^s{\mathcal{L}}_2^s\otimes \bar{P}BK)e(t)\hfill \\ \hfill \le & {\zeta }^T(t)M_1^s\zeta (t)-{\lambda }_s{\delta }^T(t)({\mathrm{\Sigma }}^s\otimes \bar{P})\delta (t)\hfill \\ \hfill & +{\lambda }_{\mathit{max}}(\bar{P})e^T(t)e(t),\hfill \end{array}(13)$

where

$\begin{array}{cc}\hfill M_1^s=& \left[\begin{array}{cc}\hfill {\mathrm{\Xi }}_1^s\hfill & \hfill {\mathrm{\Sigma }}^s{\mathcal{L}}_2^s\otimes \bar{P}BK\hfill \\ \hfill \ast \hfill & \hfill -I_N\otimes \bar{P}\hfill \end{array}\right],\hfill \\ \hfill {\mathrm{\Xi }}_1^s=& {\mathrm{\Sigma }}^s\otimes \bar{P}A+{\mathrm{\Sigma }}^s\otimes A^T\bar{P}+{\mathrm{\Sigma }}^s{\mathcal{L}}_2^s\otimes \bar{P}BK\hfill \\ \hfill & +{\mathcal{L}}_2^{sT}{\mathrm{\Sigma }}^s\otimes K^T{B}^T\bar{P}+{\lambda }_s({\mathrm{\Sigma }}^s\otimes \bar{P}).\hfill \end{array}$

By Eq. 7, one has

$\begin{array}{cc}\hfill \Vert e_i(t)\Vert \le & c\Vert \sum _{j=1}^N{a}_{ij}^s(e_i(t)-e_j(t))+a_{i0}^s{e}_i(t)\hfill \\ \hfill & +\sum _{j=1}^N{a}_{ij}^s({\delta }_i(t)-{\delta }_j(t))+a_{i0}^s{\delta }_i(t)\Vert ,\hfill \end{array}(14)$

which implies $\sum _{i=1}^N\Vert e_i(t){\Vert }^2\le 2N{c}^2(\Vert ({\mathcal{L}}_2^s\otimes I_n)e(t){\Vert }^2+\Vert ({\mathcal{L}}_2^s\otimes I_n)\delta (t){\Vert }^2)$. Furthermore, it follows that

$\Vert e(t){\Vert }^2\le {\zeta }^{\mathrm{T}}(t)\left[\begin{array}{cc}\hfill 2N{c}^2({\mathcal{L}}_2^{sT}{\mathcal{L}}_2^s\otimes I_n)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 2N{c}^2({\mathcal{L}}_2^{sT}{\mathcal{L}}_2^s\otimes I_n)\hfill \end{array}\right]\zeta (t).(15)$

According to the fact $0<c^2<\frac{1}{{\lambda }_{\mathit{max}}(P)}$, it can be derived from Eq. 13 and (Eq. 15) that

${\dot{V}}_s(t)\le {\zeta }^T(t)M_2^s\zeta (t)-{\lambda }_s{\delta }^T(t)({\mathrm{\Sigma }}^s\otimes \bar{P})\delta (t),(16)$

where

$\begin{array}{cc}\hfill M_2^s=& \left[\begin{array}{cc}\hfill {\mathrm{\Xi }}_2^s\hfill & \hfill {\mathrm{\Sigma }}^s{\mathcal{L}}_2^s\otimes \bar{P}BK\hfill \\ \hfill \ast \hfill & \hfill -I_N\otimes P+2N({\mathcal{L}}_2^{sT}{\mathcal{L}}_2^s\otimes I_n)\hfill \end{array}\right],\hfill \\ \hfill {\mathrm{\Xi }}_2^s=& {\mathrm{\Sigma }}^s\otimes \bar{P}A+{\mathrm{\Sigma }}^s\otimes A^T\bar{P}+{\mathrm{\Sigma }}^s{\mathcal{L}}_2^s\otimes \bar{P}BK\hfill \\ \hfill & +{\mathcal{L}}_2^{sT}{\mathrm{\Sigma }}^s\otimes K^T{B}^T\bar{P}+{\lambda }_s({\mathrm{\Sigma }}^s\otimes \bar{P})\hfill \\ \hfill & +2N({\mathcal{L}}_2^{sT}{\mathcal{L}}_2^s\otimes I_n).\hfill \end{array}$

Multiplying both sides of $M_2^s$ by   diag{I_N ⊗ P, I_N ⊗ P}, one gets that $M_2^s<0$ is equivalent to $M_3^s<0$ with $M_3^s=[{\mathrm{\Xi }}_3^s,{\mathrm{\Sigma }}^s{\mathcal{L}}_2^s\otimes BW;*,-I_N\otimes P+2N({\mathcal{L}}_2^{sT}{\mathcal{L}}_2^s\otimes PP)]$ and ${\mathrm{\Xi }}_3^s={\mathrm{\Sigma }}^s\otimes AP+{\mathrm{\Sigma }}^s\otimes P{A}^T+{\mathrm{\Sigma }}^s{\mathcal{L}}_2^s\otimes BW+{\mathcal{L}}_2^{sT}{\mathrm{\Sigma }}^s\otimes W^T{B}^T+{\lambda }_s({\mathrm{\Sigma }}^s\otimes P)+2N({\mathcal{L}}_2^{sT}{\mathcal{L}}_2^s\otimes PP)$. According to Schur complement lemma, from Eq. 9 one has $M_3^s<0$. Thus,

${\dot{V}}_s(t)\le -{\lambda }_s{V}_s(t).(17)$

For t ∈ [t₀, t₁), when the communication network switches among finite digraphs, it follows from Eq. 17 that

$V_{\sigma (t_0^{l_0-1})}(t_1^{-})\le \prod _{\ell =0}^{l_0-1}{\mu }_{\sigma (t_0^{\ell })}\exp \left\{-\sum _{\ell =0}^{l_0-1}{\lambda }_{\sigma (t_0^{\ell })}(t_0^{\ell +1}-t_0^{\ell })\right\}\times V_{\sigma (t_0)}(t_0).(18)$

For $t\in [t_h^1,t_h^{l_h})$, it follows from Eq. 17 that

$V_{\sigma (t_h^{l_h-1})}(t_h^{l_h-})\le \prod _{\ell =1}^{l_h-1}{\mu }_{\sigma (t_h^{\ell })}\exp \left\{-\sum _{\ell =1}^{l_h-1}{\lambda }_{\sigma (t_h^{\ell })}(t_h^{\ell +1}-t_h^{\ell })\right\}\times V_{\sigma (t_h^1)}(t_h^1).(19)$

When t ∈ Ω_I, the communication topology of MASs will be affected by DoS attacks, and thus the corresponding communication topology of the MASs will become paralyzed. Then, the time derivative of Eq. 12 along Eq. 11 becomes

${\dot{V}}_{\sigma (t)}(t)={\delta }^T(t)[I_N\otimes (A^T\bar{P}+\bar{P}A)]\delta (t)\le \alpha V_{\sigma (t)}(t).(20)$

It follows from Eq. 20 that

$V_{\sigma (t_h)}\left(t_h^{1-}\right)\le \exp \left\{\alpha \left(t_h^{1-}-t_h\right)\right\}{V}_{\sigma \left(t_h\right)}(t_h).(21)$

Next, analysis is given for t ∈ [t₀, t_h+1]. Note that $V_{\sigma (t_{h+1})}(t_{h+1})\le \frac{1}{a_0}{V}_{\sigma (t_h^{l_h-1})}(t_h^{l_h-})$ and $V_{\sigma (t_h^1)}\left.(t_h^1)\right)\le b_0{V}_{\sigma (t_h)}(t_h^{1-})$. Then, one gets

$\begin{array}{cc}\hfill V_{\sigma (t_{h+1})}(t_{h+1})\le & \exp \left\{\ln \frac{b_0}{a_0}+\alpha (t_h^1-t_h)+\sum _{\ell =1}^{l_h-1}\ln {\mu }_{\sigma (t_h^{\ell })}\right.\hfill \\ \hfill & \left.-\sum _{\ell =1}^{l_h-1}{\lambda }_{\sigma (t_h^{\ell })}(t_h^{\ell +1}-t_h^{\ell })\right\}{V}_{\sigma (t_h)}(t_h).\hfill \end{array}(22)$

Let ${\nu }_0=\exp \left\{{\sum }_{s\in \mathrm{S}}{N}_0^s\ln {\mu }_s\right\}$, ${\varphi }_h={\sum }_{s\in \mathrm{S}}({\lambda }_s-\frac{\ln {\mu }_s}{{\tau }_{as}})T^s(t_h^1,t_{h+1})-\ln \frac{b_0}{a_0}-\alpha (t_h^1-t_h)$, and ${\varphi }_0={\sum }_{s\in \mathrm{S}}({\lambda }_s-\frac{\ln {\mu }_s}{{\tau }_{as}})T^s(t_0,t_1)-\ln \frac{b_0}{a_0}$. For t ∈ [t₀, t_h+1], based on the aforementioned analysis, one gets

$V_{\sigma (t_{h+1})}(t_{h+1})\le {\nu }_0\exp \left\{-\sum _{h=1}^h{\varphi }_h-{\varphi }_0\right\}{V}_{\sigma (t_0)}(t_0).(23)$

Finally, for any t ≥ 0, there exists a constant ℏ ≥ 0 such that t_ℏ ≤ t ≤ t_ℏ+1. Let ${\varrho }_0={\max }_{\hslash \in \mathbb{N}}\{t_{\hslash +1}-t_{\hslash }\}$ and $\underline{\varphi }={\min }_{h\in \mathbb{N}}\{{\varphi }_h\}$, and then one has

$\begin{array}{cc}\hfill V_{\sigma (t_{\hslash })}(t)\le & {\nu }_0\exp \{\alpha (t-t_{\hslash })\}{V}_{\sigma (t_{\hslash })}(t_{\hslash })\hfill \\ \hfill \le & {\nu }_0\exp \{\alpha {\varrho }_0\}\exp \{-\hslash \underline{\varphi }\}{V}_{\sigma (t_0)}(t_0)\hfill \\ \hfill \le & \nu \exp \{-\chi (t-t_0)\}{V}_{\sigma (t_0)}(t_0),\hfill \end{array},(24)$

where $\nu ={\nu }_0\exp \{\alpha {\varrho }_0+\underline{\varphi }\}$ and $\chi =\underline{\varphi }/{\varrho }_0$. Moreover, one obtains $\Vert \delta (t){\Vert }^2\le \frac{\nu \bar{b}}{\bar{a}}{e}^{-\chi (t-t_0)}\Vert \delta (t_0){\Vert }^2$, which implies each follower agent follows the leader agent exponentially.

Remark 2. Note that under directed switching topologies and DoS attacks, the triggering mechanism design and the stability analysis of close-loop systems become even more difficult. Theorem 1 shows that the leader-following consensus problem is solved, for the situation with more practical significance; network intermittent DoS attacks are addressed in the directed switching topologies.

In the following, we show the feasibility of the proposed event-triggered protocol.

Theorem 2 There exists no Zeno behavior in the multi-agent systems (2) and (3).

Proof. Due to the average dwell-time property, they do not have Zeno behavior when the communication topology switches.

Then, considering two consecutive triggers which are induced by the triggering condition, let $\zeta (t)=\frac{\Vert e(t)\Vert }{\Vert q^{\sigma (t)}(t)\Vert }$ and the time derivative of $\frac{\Vert e(t)\Vert }{\Vert q^{\sigma (t)}(t)}$ for $t\in [t_k^i,t_{k+1}^i)$ is estimated to obtain $\dot{\zeta }(t)\le \frac{\Vert \dot{e}(t)\Vert }{\Vert q^{\sigma (t)}(t)\Vert }+\frac{\Vert e(t)\Vert \Vert {\dot{q}}^{\sigma (t)}(t)\Vert }{\Vert q^{\sigma (t)}(t){\Vert }^2}$ with the fact that $\Vert \dot{e}(t)\Vert \le \Vert I_N\otimes A\Vert \Vert e(t)\Vert +\Vert I_N\otimes BK\Vert \Vert q^{\sigma (t)}(t)\Vert$ and $\Vert {\dot{q}}^{\sigma (t)}(t)\Vert \le \Vert I_N\otimes A\Vert \Vert q^{\sigma (t)}(t)\Vert$. It follows that $\dot{\zeta }(t)\le c_1\zeta (t)+c_2$, where c₁ = 2‖I_N ⊗ A‖, c₂ = ‖I_N ⊗ BK‖. Then, ζ(t) satisfies the bound ζ(t) ≤ φ(t, φ₀), in which φ(t, φ₀) is the solution of $\dot{\phi }=c_1\phi +c_2,\phi (0,{\phi }_0)={\phi }_0$, given by $\phi (t,{\phi }_0)=-\frac{c_2}{c_1}+(\frac{c_2}{c_1}+{\phi }_0)e^{c_{1}t}$. Then, the inter-execution times are bounded by the solution ι ∈ R⁺ of $\phi (\iota ,0)=c\sqrt{N}$. Since $\phi (\iota ,0)=\frac{c_2}{c_1}(e^{c_1\iota }-1)$, we obtain $\iota =\frac{\ln ((c_1/c_2)c\sqrt{N}+1)}{c_1}$, which is strictly positive. So, Zeno behavior is excluded for the follower agent i.

Finally, the case that two consecutive triggers are brought by both switching topology and the condition of the triggers is studied. Based on the assumption that the triggering occurs when the topology switches and $e_i(t_h^{\ell })$ is reset to zero, so $t_h^{\ell }$ can be considered as the triggering time $t_k^i$. Thus, this interval $[t_h^{\ell },t_{k+1}^i)$ can be proven to be lower bounded by a positive constant. The inter-event interval $[t_k^i,t_h^{\ell })$ cannot be proven to be lower bounded since the switching may happen immediately after triggers induced by the condition of the triggers.. Assume that the next triggering times be $t_h^{\ell },\dots ,t_h^s,t_{k+1}^i$ with ℓ ≤ s < l_h − 1. We claim that no Zeno behavior occurs since the interval $[t_h^s,t_{k+1}^i)$ has a positive lower bound as discussed previously.

Remark 3. Note that the control strategies under DoS attack are also studied in many references, and the continuous controller update is required. In this article, an event-triggered control scheme is provided for MASs in the presence of denial-of-service attacks on directed switching topology.

With the aforementioned notations, this subsection is concluded by summarizing the algorithm for generating the u_i(t).

Algorithm 1 Initialization

(1) Set $t_k^i=0$ and k = 0;

(2) send $x_i(t_k^i)$ to its neighbors;

(3) compute $u_i(t)=K{q}_i^{\sigma (t)}(t_0)$;

while t < T, T is the desired lifespan of the system.

If t ∈ Ω_C,

send x_i(t) to its neighbors;

if $\Vert e_i(t_k^i)\Vert >c\Vert q_i^{\sigma (t)}\Vert$ or ${\mathcal{G}}^{\sigma (t)}$ switches,

(1) update k = k + 1 and $t_k^i=t$; and

(2) update $u_i(t)=K{q}_i^{\sigma (t)}(t_k^i)$;

end if

else (t ∈ Ω_I)

u_i(t) = 0;

end if

end while

Remark 4. The obtained results are then extended to achieve consensus for multi-agent systems without a leader. For a leaderless consensus problem, we assume that the undirected switching graph ${\mathcal{G}}^{\sigma (t)}$ is fixed and connected to each time interval [t_m, t_m+1), t₀ = 0, m ∈ N. The adjacency matrix and Laplacian matrix are denoted by ${\mathcal{A}}^{\sigma (t)}={[a_{ij}^{\sigma (t)}]}_{N\times N}$ and ${\mathcal{L}}^{\sigma (t)}={[l_{ij}^{\sigma (t)}]}_{N\times N}$, respectively.

The event-triggered controller for each follower agent i is proposed as

$u_i(t)=\varrho K\sum _{j=1}^N{a}_{ij}^{\sigma (t)}({\widehat{x}}_i(t)-{\widehat{x}}_j(t)),(25)$

where ${\widehat{x}}_i(t)=e^{A(t-t_k^i)}{x}_i(t_k^i)$, $\forall t\in [t_k^i,t_{k+1}^i)$, ϱ is defined in Eq. 5, and $K\in {\mathbb{R}}^{m\times n}$ is the feedback gain matrix to be determined.

The triggering time instant $t_{k+1}^i$ is determined by the following triggering mechanism:

$t_{k+1}^i=\left\{\begin{array}{c}{t}_h^{\ell },if{\mathcal{G}}^{\sigma (t)}switches\hfill \\ \inf \{t>t_k^i:f_i^{\sigma (t)}(t)>0\},otherwise.\hfill \end{array}\right.,(26)$

where the triggering function is given by

$f_i^{\sigma (t)}(t)=\Vert e_i(t)\Vert -c\Vert \sum _{j=1}^N{a}_{ij}^{\sigma (t)}({\widehat{x}}_i(t)-{\widehat{x}}_j(t))\Vert ,(27)$

with $e_i(t)={\widehat{x}}_i(t)-x_i(t)$ and $0<c<\sqrt{\frac{1}{{\lambda }_{max}(P^{-1})}}$.

The feedback gain matrix is defined as K = WP⁻¹. If there exist matrices p > 0 and W such that the following inequalities hold:

$\left[\begin{array}{cccc}\hfill {\mathrm{\Xi }}^s\hfill & \hfill {({\mathcal{L}}^s)}^2\otimes BW\hfill & \hfill 0\hfill & \hfill {\mathcal{L}}^s\otimes P\hfill \\ \hfill \ast \hfill & \hfill -I_N\otimes P\hfill & \hfill {\mathcal{L}}^s\otimes P\hfill & \hfill 0\hfill \\ \hfill \ast \hfill & \hfill \ast \hfill & \hfill -\frac{1}{2N}{I}_{N\times n}\hfill & \hfill 0\hfill \\ \hfill \ast \hfill & \hfill \ast \hfill & \hfill \ast \hfill & \hfill -\frac{1}{2N}{I}_{N\times n}\hfill \end{array}\right]<0(28)$

and

$AP+P{A}^T-\alpha P<0,(29)$

where ${\mathrm{\Xi }}^s={\mathcal{L}}^s\otimes AP+{\mathcal{L}}^s\otimes P{A}^T+{({\mathcal{L}}^s)}^2\otimes BW+{({\mathcal{L}}^s)}^2\otimes W^T{B}^T+{\lambda }_s({\mathcal{L}}^s\otimes P)$.As well as, we choose μ_s > b₀/a₀ such that $\sum _{s\in \mathrm{S}}\left({\lambda }_s-\frac{\ln {\mu }_s}{{\tau }_{as}}\right)T^s(t_0,t_1)-\ln \frac{b_0}{a_0}>0$ and $\sum _{s\in \mathrm{S}}\left({\lambda }_s-\frac{\ln {\mu }_s}{{\tau }_{as}}\right)T^s(t_h^1,t_{h+1})-\ln \frac{b_0}{a_0}>\alpha (t_h^1-t_h)$, where $a_0=\underset{s\in \mathrm{S}}{\min }({\lambda }_{\min }({\mathcal{L}}_s))$ and $b_0=\underset{s\in \mathrm{S}}{\max }({\lambda }_{\max }({\mathcal{L}}_s))$. Then, there exists the event-triggered controller (25) such that leaderless consensus objective is ensured.Denote $\xi (t)={({\xi }_1^T(t),\dots ,{\xi }_N^T(t))}^T$, where ${\xi }_i(t)=x_i(t)-\frac{1}{N}{\sum }_{j=1}^N{x}_j(t)$, then one has ξ(t) = (M ⊗ I_n)x(t), where $x={[x_1^T,\dots ,x_N^T]}^T$ and $M=I_N-\frac{1}{N}11^T$. Denote $e(t)={(e_1^T(t),\dots ,e_N^T(t))}^T$. The dynamics of the error closed-loop system can be further expressed as:

$\begin{array}{cc}\hfill \dot{\xi }(t)=& \varrho ((I_N\otimes A+{\mathcal{L}}^{\sigma (t)}\otimes BK)\xi (t)+({\mathcal{L}}^{\sigma (t)}\otimes BK)e(t))\hfill \\ \hfill & (1-\varrho )(I_N\otimes A)\xi (t),\hfill \end{array}.(30)$

Let $P={\bar{P}}^{-1}$. Using the following Lyapunov function candidate,

$V_{\sigma (t)}(t)=\varrho {\xi }^T(t)({\mathcal{L}}^{\sigma (t)}\otimes \bar{P})\xi (t)+(1-\varrho ){\xi }^T(t)(I_N\otimes \bar{P})\xi (t)(31)$

and following the similar step in the proof-of-leader-following consensus problem, the leaderless consensus of the multi-agent system can be obtained, and the Zeno behavior can be excluded.

4 Simulation Example

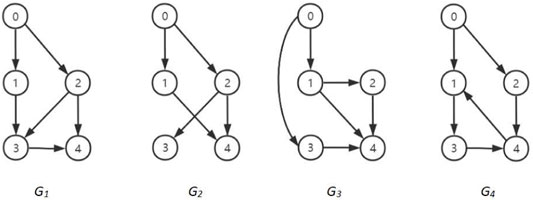
In this section, we present an example to verify the effectiveness of the theoretical results. A network of five agents with a communication graph ${\mathcal{G}}_{\sigma (t)}$ is shown in Figure 2.

FIGURE 2

FIGURE 2. Switching direct graphs among one leader and four follower agents.

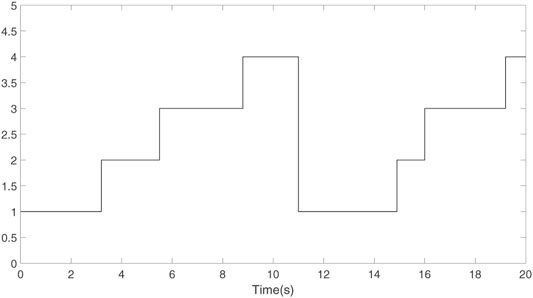
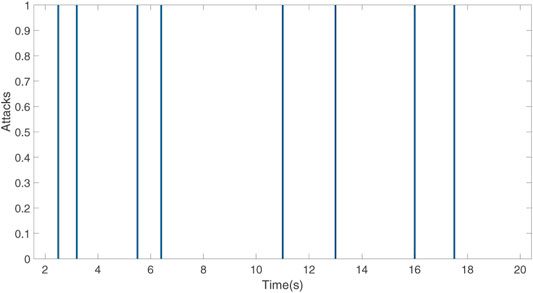
The topology switching signal and the DoS attack signal are determined by Figures 3, 4, respectively.

FIGURE 3

FIGURE 3. Topology switching signal.

FIGURE 4

FIGURE 4. DoS attack signal.

The parameters are selected as A = [ − 1.175, 0.987 1; −8.458, −0.877 6] and B = [ − 0.194, −0.035 93; −19.29, −3.803 6]. The initial conditions are given as x₀ (0) = [0,−0.5]^T, x₁ (0) = [−3,−6.8]^T, x₂ (0) = [0,−4.5]^T, x₃ (0) = [1, 2]^T, and x₄ (0) = [−1,−2.8]^T. The matrix K by solving Eq. 9 and Eq. 10 in Theorem 1 is derived as K = [23.792 3, −0.189 8; −120.689 0, 1.020 4], and the related parameters with controller design are selected as λ₁ = 1.45, λ₂ = 1.53, λ₃ = 1.62, λ₄ = 1.58, α = 2.5, and c = 0.15.

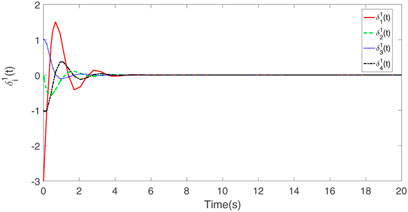
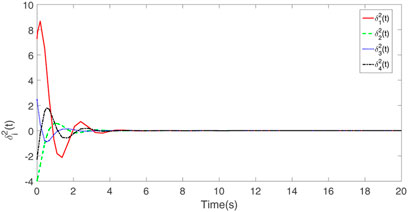
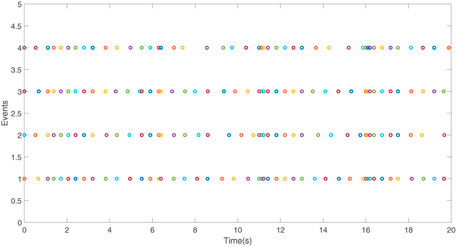
The consensus tracking errors are exhibited in Figures 5, 6, in which the multi-agent systems (2) and (3) are subjected to DoS attacks. The triggering instants of each agent are shown in Figure 7. Based on the aforementioned analysis, the event-triggered controller adopted in this article can effectively reduce the number of communications, and the leader-follower consensus can be achieved under DoS attack.

FIGURE 5

FIGURE 5. Trajectories of tracking errors ${\delta }_i^1,i=1,\dots ,4$.

FIGURE 6

FIGURE 6. Trajectories of tracking errors ${\delta }_i^2,i=1,\dots ,4$.

FIGURE 7

FIGURE 7. Triggering instants time for the agent i, i = 1, 2, 3, 4.

5 Conclusion

One kind of the typical consensus problem of the linear multi-agent system under DoS attacks has been developed in this article. With the directed switching communication topologies, fully distributed event-triggered strategies are proposed. It is shown that secure leader-following consensus can be achieved, and the Zeno behavior is ruled out in the presence of DoS attacks. The obtained results are then extended to achieve consensus for multi-agent systems without a leader. Future work will try to extend the event-based consensus control results to the nonlinear multi-agent system with a leader of nonzero inputs under DoS attack.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

JL contributed to methodology and writing—original draft preparation; LS contributed to conceptualization, methodology, and writing—original draft preparation; XW contributed to supervision and writing—review and editing; and DG contributed to software and validation.

Funding

This work was supported in part by the National Natural Science Foundation of China (No. 61873087), the Natural Science Foundation of Heilongjiang Province (No. YQ2021F014), the University Nursing Program for Young Scholars with Creative Talents in Heilongjiang Province (No. UNPYSCT-2020010), and the Outstanding Youth Fund of Heilongjiang University (No. JCL201903).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cheng, B., and Li, Z. (2019). Coordinated Tracking Control with Asynchronous Edge-Based Event-Triggered Communications. IEEE Trans. Automat. Contr. 64 (10), 4321–4328. doi:10.1109/tac.2019.2895927

CrossRef Full Text | Google Scholar

Cheng, T.-H., Kan, Z., Klotz, J. R., Shea, J. M., and Dixon, W. E. (2017). Event-triggered Control of Multiagent Systems for Fixed and Time-Varying Network Topologies. IEEE Trans. Automat. Contr. 62 (10), 5365–5371. doi:10.1109/tac.2017.2693824

CrossRef Full Text | Google Scholar

Dimarogonas, D. V., Frazzoli, E., and Johansson, K. H. (2012). Distributed Event-Triggered Control for Multi-Agent Systems. IEEE Trans. Automat. Contr. 57 (5), 1291–1297. doi:10.1109/tac.2011.2174666

CrossRef Full Text | Google Scholar

Fan, Y., Liu, L., Feng, G., and Wang, Y. (2015). Self-triggered Consensus for Multi-Agent Systems with Zeno-free Triggers. IEEE Trans. Automat. Contr. 60 (10), 2779–2784. doi:10.1109/tac.2015.2405294

CrossRef Full Text | Google Scholar

Feng, Z., and Hu, G. (2020). Secure Cooperative Event-Triggered Control of Linear Multiagent Systems under DoS Attacks. IEEE Trans. Contr. Syst. Technol. 28 (3), 741–752. doi:10.1109/tcst.2019.2892032

CrossRef Full Text | Google Scholar

Hu, W., Yang, C., Huang, T., and Gui, W. (2020). A Distributed Dynamic Event-Triggered Control Approach to Consensus of Linear Multiagent Systems with Directed Networks. IEEE Trans. Cybern. 50 (2), 869–874. doi:10.1109/tcyb.2018.2868778

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Shi, Y., and Yan, W. (2016). Distributed Receding Horizon Control of Constrained Nonlinear Vehicle Formations with Guaranteedγ-Gain Stability. Automatica 68, 148–154. doi:10.1016/j.automatica.2016.01.057

CrossRef Full Text | Google Scholar

Li, X., Soh, Y. C., and Xie, L. (2018). Robust Consensus of Uncertain Linear Multi-Agent Systems via Dynamic Output Feedback. Automatica 98, 114–123. doi:10.1016/j.automatica.2018.09.020

CrossRef Full Text | Google Scholar

Lu, A.-Y., and Yang, G.-H. (2018). Distributed Consensus Control for Multi-Agent Systems under Denial-Of-Service. Inf. Sci. 439-440, 95–107. doi:10.1016/j.ins.2018.02.008

CrossRef Full Text | Google Scholar

Ma, H.-J., and Yang, G.-H. (2016). Adaptive Fault Tolerant Control of Cooperative Heterogeneous Systems with Actuator Faults and Unreliable Interconnections. IEEE Trans. Automat. Contr. 61 (11), 3240–3255. doi:10.1109/tac.2015.2507864

CrossRef Full Text | Google Scholar

Mei, J., Ren, W., and Chen, J. (2016). Distributed Consensus of Second-Order Multi-Agent Systems with Heterogeneous Unknown Inertias and Control Gains under a Directed Graph. IEEE Trans. Automat. Contr. 61 (8), 2019–2034. doi:10.1109/tac.2015.2480336

CrossRef Full Text | Google Scholar

Meng, X., and Chen, T. (2013). Event Based Agreement Protocols for Multi-Agent Networks. Automatica 49 (7), 2125–2132. doi:10.1016/j.automatica.2013.03.002

CrossRef Full Text | Google Scholar

Olfati-Saber, R., and Murray, R. M. (2004). Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Trans. Automat. Contr. 49, 1520–1533. doi:10.1109/tac.2004.834113

CrossRef Full Text | Google Scholar

Pelechrinis, K., Iliofotou, M., and Krishnamurthy, S. V. (20212010). Denial of Service Attacks in Wireless Networks: The Case of Jammers. IEEE Commun. Surv. Tutorials 13 (2), 245–257.

Google Scholar

Qin, J., Li, M., Shi, L., and Yu, X. (2018). Optimal Denial-Of-Service Attack Scheduling with Energy Constraint over Packet-Dropping Networks. IEEE Trans. Automat. Contr. 63 (6), 1648–1663. doi:10.1109/tac.2017.2756259

CrossRef Full Text | Google Scholar

Qin, J., Yu, C., and Anderson, B. D. O. (2016). On Leaderless and Leader-Following Consensus for Interacting Clusters of Second-Order Multi-Agent Systems. Automatica 74, 214–221. doi:10.1016/j.automatica.2016.07.008

CrossRef Full Text | Google Scholar

Ren, W., Beard, R. W., and Atkins, E. M. (2007). Information Consensus in Multive- Hicle Cooperative Control. IEEE Control. Syst. Mag. 27 (2), 71–82.

Google Scholar

Seyboth, G. S., Dimarogonas, D. V., and Johansson, K. H. (2013). Event-based Broadcasting for Multi-Agent Average Consensus. Automatica 49 (1), 245–252. doi:10.1016/j.automatica.2012.08.042

CrossRef Full Text | Google Scholar

Sun, Y.-C., and Yang, G.-H. (2020). Event-triggered Distributed State Estimation for Multiagent Systems under DoS Attacks. IEEE Trans. Cybern., 1–10. to be published. doi:10.1109/TCYB.2020.3034456

PubMed Abstract | CrossRef Full Text | Google Scholar

Tand, Y., Zhang, D., Shi, P., Zhang, W., and Qian, F. (2021). Event-based Formation Control of Nonlinear Multiagent Systems under DoS Attacks. IEEE Trans. Automatic Control. 66 (1), 452–459.

Google Scholar

Wang, X., Park, J. H., Liu, H., and Zhang, X. (2021). Cooperative Output-Feedback Secure Control of Distributed Linear Cyber-Physical Systems Resist Intermittent DoS Attacks. IEEE Trans. Cybern. 51, 4924–4933. doi:10.1109/TCYB.2020.3034374

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Wang, G., and Li, S. (2020). Distributed Finite-Time Optimization for Integrator Chain Multiagent Systems with Disturbances. IEEE Trans. Automat. Contr. 65 (12), 5296–5311. doi:10.1109/tac.2020.2979274

CrossRef Full Text | Google Scholar

Wang, X., and Yang, G.-H. (2018). Adaptive Reliable Coordination Control for Linear Agent Networks with Intermittent Communication Constraints. IEEE Trans. Control. Netw. Syst. 5 (3), 1120–1131. doi:10.1109/tcns.2017.2687818

CrossRef Full Text | Google Scholar

Wang, X., and Yang, G. H. (2016). Distributed Reliable H_∞ Consensus Control for a Class of Multi-Agent Systems under Switching Networks: A Topology-Based Average Dwell Time Approach. Int. J. Robust Nonlinear Control. 26 (12), 2767–2787. doi:10.1002/rnc.3474

CrossRef Full Text | Google Scholar

Xu, W., Ho, D. W. C., Zhong, J., and Chen, B. (2019). Event/Self-Triggered Control for Leader-Following Consensus over Unreliable Network with DoS Attacks. IEEE Trans. Neural Netw. Learn. Syst. 30 (10), 3137–3149. doi:10.1109/tnnls.2018.2890119

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Y., and Wu, Z.-G. (2021). Distributed Adaptive Event-Triggered Fault-Tolerant Synchronization for Multiagent Systems. IEEE Trans. Ind. Electron. 68 (2), 1537–1547. doi:10.1109/tie.2020.2967739

CrossRef Full Text | Google Scholar

Yang, D., Ren, W., Liu, X., and Chen, W. (2016). Decentralized Event-Triggered Consensus for Linear Multi-Agent Systems under General Directed Graphs. Automatica 69, 242–249. doi:10.1016/j.automatica.2016.03.003

CrossRef Full Text | Google Scholar

Zhang, D., Liu, L., and Feng, G. (2019). Consensus of Heterogeneous Linear Multiagent Systems Subject to Aperiodic Sampled-Data and DoS Attack. IEEE Trans. Cybern. 49 (4), 1501–1511. doi:10.1109/tcyb.2018.2806387

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Yan, W., and Li, H. (2021). Distributed Optimal Control for Linear Multiagent Systems on General Digraphs. IEEE Trans. Automat. Contr. 66 (1), 322–328. doi:10.1109/tac.2020.2974424

CrossRef Full Text | Google Scholar

Zhu, J.-W., Gu, C.-Y., Ding, S. X., Zhang, W.-A., Wang, X., and Yu, L. (2021). A New Observer-Based Cooperative Fault-Tolerant Tracking Control Method with Application to Networked Multiaxis Motion Control System. IEEE Trans. Ind. Electron. 68 (8), 7422–7432. doi:10.1109/tie.2020.3001857

CrossRef Full Text | Google Scholar