IGSA-SAC: a novel approach for intrusion detection using improved gravitational search algorithm and soft actor-critic

Background: Network intrusion detection is a critical component of maintaining network security, especially as cyber threats become increasingly sophisticated. While deep learning-based intrusion detection algorithms have shown promise, they often struggle with high-dimensional datasets containing outliers, anomalies, or rare events. This study addresses these challenges by proposing a novel approach that combines the Improved Gravitational Search Algorithm (IGSA) with the Soft Actor-Critic (SAC) reinforcement learning algorithm, aiming to enhance detection accuracy and computational efficiency.

Methods: We introduce the IGSA-SAC intrusion detection model, which leverages an enhanced Gravitational Search Algorithm (IGSA) to improve robustness against outliers and dynamically adjust the exploration-exploitation balance. This is achieved through fitness normalization with an Adaptive Search Radius and a sigmoid function to modulate the gravitational constant. The IGSA-SAC method effectively navigates the search space to identify the most relevant features for intrusion detection, reducing dimensionality and computational complexity. Additionally, we design a reinforcement learning reward function to guide the learning process, encouraging the agent to improve detection effectiveness while minimizing false alarms and missed detections.

Results: Experiments were conducted on the NSL-KDD and AWID datasets to evaluate the performance of IGSA-SAC. The results demonstrate that IGSA-SAC achieves an accuracy of 84.15% and an F1-score of 84.85% on the NSL-KDD dataset. On the AWID dataset, IGSA-SAC surpasses 98.9% in both accuracy and F1-score, outperforming existing intrusion detection algorithms.

Conclusions: The proposed IGSA-SAC method significantly improves intrusion detection performance by effectively handling high-dimensional datasets and reducing computational complexity. The results highlight the potential of IGSA-SAC as a robust and efficient solution for real-world network intrusion detection systems, offering enhanced accuracy and reliability in identifying cyber threats.

1 Introduction

As the amount of data transmitted by network devices and communication protocols increases, the means of internet-oriented attacks become increasingly complex and diverse, posing more severe network security issues (Zhu et al., 2017). Current computer networks are facing security threats such as denial of service, viruses, trojans, and network sniffing (Chung and Wahid, 2012). Intrusion Detection Systems (IDS) have become a hot research topic in network security protection technology (Song et al., 2023).

The main function of intrusion detection systems is to conduct real-time monitoring of networks and computer systems, detecting and identifying intrusion behaviors or attempts within the system. However, a major issue faced by current intrusion detection systems is their low detection speed and high processing load, with handling excessive features being one of the main reasons for the decrease in speed. When the number of features exceeds a certain limit, it can lead to deterioration in classifier performance. Therefore, removing redundant features and retaining important features that reflect system state is an effective method for improving detection speed (Chatzoglou et al., 2022; Wang et al., 2024; Rani et al., 2024; Aljehane et al., 2024; Barbosa et al., 2024).

Intrusion detection involves sorting network or system activities into either “normal” or “intrusive” categories (indicating an attack), which can be simplified as a binary classification task solvable through machine learning (Belavagi and Muniyal, 2016; Wang et al., 2017; Liao and Vemuri, 2002). Researchers have suggested utilizing Support Vector Machine (SVM) with enhanced features for intrusion detection (Wang et al., 2017). Additionally, the k-Nearest Neighbor (kNN) classifier has been employed to distinguish program behavior as either normal or intrusive (Liao and Vemuri, 2002). Nevertheless, as the data's dimensionality expands, traditional machine learning algorithms encounter difficulties in effectively managing high-dimensional feature spaces. This can result in heightened computational complexity, extended training durations, and reduced performance due to sparse data distributions (Mishra et al., 2018).

Deep learning algorithm has the potential to surpass the constraints of traditional machine learning (ML) algorithms (Xie et al., 2018). Researchers used deep learning architectures including convolutional neural networks (CNNs; El-Ghamry et al., 2023), recurrent neural networks (RNNs; Sanju, 2023), long short-term memory (LSTM) networks (Altunay and Albayrak, 2023), and autoencoder-based models (Sarikaya et al., 2023) for intrusion detection. However, deep learning models have been shown to be vulnerable to adversarial attacks, where small, carefully crafted perturbations to input data can lead to misclassification. Adversarial attacks pose a significant threat to intrusion detection systems, as attackers could exploit vulnerabilities in the model to evade detection or trigger false alarms.

Reinforcement learning (RL) has surfaced as a promising framework for constructing intrusion detection systems (IDS) that possess the capability to autonomously learn and adjust to the ever-changing landscape of cyber threats within intricate network environments (Sethi et al., 2021). However, traditional RL encounters certain limitations, including issues with scalability and the inability to create sophisticated security models.

Deep Reinforcement Learning (DRL; Lavet et al., 2018) is an innovative field of study that offers the potential to develop intricate models capable of detecting highly sophisticated cyber threats (Nguyen and Reddi, 2019). This concept has been successfully applied in various domains such as computer vision, healthcare, and robotics (Sethi et al., 2021). DRL is gaining traction in the realm of network security as well, particularly in the advancement of next-generation IDS research and implementation. However, existing intrusion detection methods utilizing DRL suffer from a lack of feature selection, posing risks of inefficiency and performance decline.

In this paper, we introduce a new intrusion detection method based on Deep Reinforcement Learning with Soft Actor-Critic (SAC), in which an Improved Gravitational Search Algorithm (IGSA) is introduced to remove irrelevant data, thus reducing dimensionality and computational complexity. The main contributions are as follows.

(1) To solve the high dimensionality problem of the intrusion data, a new feature selection method based on IGSA is proposed, which reduces the influence of feature dimension on intrusion detection model and supports the model to better recognize the network intrusion.

(2) To improve the performance of the intrusion detection model, a new reward function is designed to guide the learning process by incentivizing the agent to take actions that lead to effective intrusion detection while minimizing false alarms and missed detections.

(3) A new hybrid approach combining two different optimization techniques is proposed, enhancing the robustness and reliability of the intrusion detection system. By focusing on relevant features and adapting detection strategies, the method improves detection accuracy while minimizing False Positive (FP) and False Negative (FN). Compared to other reinforcement learning algorithms, SAC can achieve better performance with fewer samples.

The rest of this paper is organized as follows. Section 2 mainly introduces related work. Section 3 develops the proposed improved Gravitational Search algorithm. Section 4 presents the description of SAC. Section 5 introduces the proposed intrusion detection method. Section 6 presents the experimental setup and discussion. Section 7 gives the conclusion.

2 Background of the study

The high-dimensional features of intrusion detection data contain lots of irrelevant features and redundant features. Some features either contain minimal system state information or do not contain it at all, having little to no impact on detection results. Therefore, removing redundant features and retaining important features that reflect system state is an effective method for improving detection speed. Feature selection aims to reduce the dimensionality of the feature space as much as possible without significantly decreasing classification accuracy. This involves selecting a subset of features from the original feature set based on certain evaluation criteria that are relevant to or important for the output results. Developing a lightweight intrusion detection system with fast detection speed while ensuring detection accuracy has become a hot topic in current research (Wang et al., 2024; Rani et al., 2024; Aljehane et al., 2024; Barbosa et al., 2024). Fang et al. devised a feature selection method for intrusion detection based on genetic algorithms. Their approach integrates a feature ranking fusion mechanism within the genetic algorithm to eliminate redundant features and accelerates global merit-seeking speed by incorporating the concept of growing tree clustering (Fang et al., 2024). Nasseh Barbosa et al. introduced a feature selection filtering method for intrusion detection, aiming to optimize both information quantity and linear correlation among resulting features. This method identifies Pareto dominant pairs of informative and correlated features, constructs a graph, and selects key features based on betweenness centrality within its connected components (Barbosa et al., 2024). Aljehane et al. (2024) introduced a novel model, GSAFS-OQNN (Gravitational Search Algorithm-based Feature Selection with Optimal Quantum Neural Network), for intrusion detection and classification. Rani et al. (2024) proposed a Deep Learning (DL) framework enabled by Archimedes Fire Hawk Optimization (AFHO), where feature selection is executed through AFHO—a combination of Archimedes Optimization Algorithm (AOA) and Fire Hawk Optimization (FHO).

Machine learning has become a vital tool in safeguarding networks from cyber threats (Mishra et al., 2018; Belouch et al., 2018; Ding et al., 2022; Azimjonov and Kim, 2024; Gu and Lu, 2021; Louk and Tama, 2023; Sathish and Valarmathi, 2022; Narayanan et al., 2023; Zhang et al., 2020). By analyzing network traffic patterns in real-time, machine learning-based Intrusion Detection Systems (IDSs) detect and respond to potential intrusions. Ding et al. (2022) proposed an IDS using the K-nearest neighbor method, while Azimjonov and Kim (2024) presented a lightweight, accurate IDS tailored for IoT networks, utilizing fine-tuned Linear Support Vector Machines (LSVMs) and feature selection techniques. Gu and Lu (2021) introduced an effective intrusion detection framework based on SVM with naïve Bayes feature embedding, enhancing the quality of data through feature transformation. Lestari Louk and Tama (2023) introduced a dual ensemble model for anomaly-based intrusion detection, employing various fine-tuned GBDT algorithms such as gradient boosting machine (GBM), LightGBM, CatBoost, and XGBoost. However, traditional ML algorithms face challenges in managing high-dimensional feature spaces as data dimensionality increases. This can lead to heightened computational complexity, longer training times, and reduced performance due to sparse data distributions.

For performance improvement, Deep learning-based models have emerged as promising approaches for network intrusion detection, offering the potential to effectively detect and mitigate various forms of cyber threats in complex network environments. These models leverage the power of neural networks to automatically learn hierarchical representations of network traffic data, enabling them to capture intricate patterns and anomalies indicative of malicious activities. Unlike traditional rule-based or signature-based intrusion detection systems (IDS), deep learning-based models can adapt to evolving threats and detect previously unseen attack patterns, making them well-suited for modern cybersecurity challenges. Some common deep learning architectures used for network intrusion detection include convolutional neural networks (CNNs; El-Ghamry et al., 2023), recurrent neural networks (RNNs; Sanju, 2023), long short-term memory (LSTM) networks (Altunay and Albayrak, 2023), and autoencoder-based models (Sarikaya et al., 2023). These architectures can effectively capture spatial and temporal dependencies in network data, allowing them to detect complex attack patterns and sequences across multiple network packets or sessions. However, Deep learning models are susceptible to adversarial attacks, where malicious actors manipulate input data to deceive the model into making incorrect predictions. Adversarial attacks pose a significant threat to the reliability and robustness of deep learning-based IDS, as attackers can exploit vulnerabilities in the model to evade detection. Deep learning models trained on historical data may struggle to generalize to new and unseen attack patterns or variations. Changes in network behaviors, evolving attack techniques, and zero-day vulnerabilities pose challenges for deep learning-based IDS to adapt and detect emerging threats effectively.

Reinforcement learning (RL) has emerged as a promising paradigm for building intrusion detection systems (IDS) capable of autonomously learning and adapting to evolving cyber threats in complex network environments (Sethi et al., 2021). RL-based IDS leverage dynamic learning algorithms to continuously refine their detection strategies based on feedback from the environment. In RL-based intrusion detection systems, an agent interacts with its environment, which represents the network environment being monitored, to learn an optimal policy for detecting and mitigating intrusions. The agent's objective is to maximize a cumulative reward signal by taking appropriate actions in response to observed network events and activities. These actions may include monitoring network traffic, analyzing system logs, deploying countermeasures, or raising alerts based on anomalous behavior. Some common RL algorithms used in intrusion detection include Q-learning, Policy Gradient methods, Actor-Critic architectures, and more advanced techniques such as Proximal Policy Optimization (PPO) and Trust Region Policy Optimization (TRPO). These algorithms enable RL-based IDS to learn complex decision policies from high-dimensional network data and adapt their detection strategies in real-time. However, traditional RL encounters certain limitations, including issues with scalability and the inability to create sophisticated security models.

Deep Reinforcement Learning (DRL; Lavet et al., 2018) is an innovative field of study that offers the potential to develop intricate models capable of detecting highly sophisticated cyber threats (Nguyen and Reddi, 2019). This concept has been successfully applied in various domains such as computer vision, healthcare, and robotics (Sethi et al., 2021). DRL is gaining traction in the realm of network security as well, particularly in the advancement of next-generation IDS research and implementation. Lopez-Martin et al. (2020) proposed a novel application of several deep reinforcement learning (DRL) algorithms to intrusion detection. Vadigi et al. (2023) presented a Federated Deep Reinforcement Learning-based IDS in which multiple agents are deployed on the network in a distributed fashion, and each of these agents runs a Deep Q-Network logic.

Deep Reinforcement Learning (DRL; Lavet et al., 2018) is an emerging area of research that holds promise for creating sophisticated models capable of identifying highly complex cyber threats (Nguyen and Reddi, 2019). This approach has found success across various fields including computer vision, healthcare, and robotics (Sethi et al., 2021). In the domain of network security, DRL is increasingly recognized for its potential, particularly in advancing next-generation Intrusion Detection Systems (IDS). Lopez-Martin et al. (2020) introduced a novel application of several DRL algorithms for intrusion detection. Vadigi et al. (2023) presented a Federated Deep Reinforcement Learning-based IDS, deploying multiple agents in a distributed manner across the network, each employing Deep Q-Network logic. However, existing intrusion detection methods utilizing DRL suffer from a lack of feature selection, posing risks of inefficiency and performance decline. Absence of feature selection means DRL algorithms may operate on raw or extraneous data, resulting in high-dimensional input spaces and heightened computational demands. This can lead to prolonged training durations, convergence challenges, and suboptimal model outcomes. Hence, integrating feature selection methods becomes imperative to enhance the effectiveness and efficiency of DRL-driven intrusion detection systems. By prioritizing relevant and informative features, this integration aims to bolster model accuracy and trim computational overhead. In this study, we introduce a novel intrusion detection approach leveraging the soft actor-critic deep reinforcement learning algorithm, in which we incorporate an IGSA-based feature selection method to weed out irrelevant data, thus reducing dimensionality and computational complexity.

3 Gravitational Search Algorithm (GSA)

3.1 Basic GSA

The Gravitational Search Algorithm (GSA) is a stochastic search method rooted in the principles of gravity and mass interaction (Rashedi, 2007; Rashedi et al., 2007, 2009). This algorithm orchestrates an iterative procedure that mimics mass interactions within a multi-dimensional search domain, guided by the force of gravity. In this framework, the performance of objects is evaluated based on their respective masses; these objects exert gravitational attraction on one another, inducing a collective movement toward those with greater mass.

Suppose there are k objects, where the position of the ith object is defined by Equation 1, with $x_i^d$ representing the position of the ith object along the dth direction.

$\begin{array}{ll}{X}_i=(x_i^1,\dots ,x_i^d,\dots ,x_i^n),i=1,2,\dots ,k& (1)\end{array}$

The force acting on object i from object j is described by Equation 2, where M_j signifies the mass associated with object j, M_i denotes the mass associated with object i, G represents the gravitational constant at time t, e is a small constant, and R_ij(t) stands for the Euclidean distance between objects i and j. The total force $F_i^d(t)$ exerted on object i along the dth direction is described by Equation 3, which is a randomly weighted sum of the dth components of the forces from other objects, in which rand_j is a uniform random variable in the interval [0, 1].

$\begin{array}{ll}{F}_{ij}^d(t)=G\frac{M_i(t)\times M_j(t)}{R_{ij}(t)+\epsilon }\left(x_j^d(t)-x_i^d(t)\right)& (2)\end{array}$

$\begin{array}{ll}{F}_i^d(t)={\displaystyle \sum _{j=1,j\ne i}^k}ran{d}_j{F}_{ij}^d(t)& (3)\end{array}$

The acceleration of object i, denoted as $a_i^d(t)$, at time t in the dth direction, is expressed by Equation 4, where M_ii represents the inertial mass of object i. The subsequent velocity $a_i^d(t)$ and position are determined by Equations 5, 6, respectively.

$\begin{array}{ll}{a}_i^d(t)=\frac{F_i^d(t)}{M_{ii}(t)}& (4)\end{array}$

$\begin{array}{ll}{v}_i^d(t+1)=ran{d}_i\times v_i^d(t)+a_i^d(t)& (5)\end{array}$

$\begin{array}{ll}{x}_i^d(t+1)=x_i^d(t)+v_i^d(t+1)& (6)\end{array}$

In Equation 5, rand_i represents a uniformly distributed random variable within the range [0, 1]. This randomness introduces a stochastic aspect to the search process, $v_i^d(t)$and $x_i^d(t)$ denote the current velocity and position of the object i along the dth direction, respectively.

The masses of the objects are determined by the fitness function. Assuming equivalence between gravitational and inertial mass, the mass M_i(t) undergoes updates according to Equations 8– 11, where fit_i(t) signifies the fitness function value of object i at time t. The flowchart depicting the gravitational search algorithm is illustrated in Figure 1.

$\begin{array}{ll}{M}_i=M_{ii},i=1,2,\dots ,k& (7)\end{array}$

$\begin{array}{ll}{m}_i(t)=\frac{fi{t}_i(t)-worst(t)}{best(t)-worst(t)}& (8)\end{array}$

$\begin{array}{ll}{M}_i(t)=\frac{m_i(t)}{\sum _{j=1}^k{m}_j(t)}& (9)\end{array}$

$\begin{array}{ll}best(t)=fi{t}_j(t)& (10)\end{array}$

$\begin{array}{ll}worst(t)=fi{t}_j(t)& (11)\end{array}$

Figure 1

Figure 1. The flow of GSA algorithm.

3.2 Improved GSA (IGSA)

The original iteration of GSA demonstrates significant potential as an optimization algorithm. However, it does present certain performance limitations. These include premature convergence resulting from a rapid decline in diversity and slower convergence rates when the global optimum closely aligns with the local search space's optimum. Furthermore, in real scenarios, where data often contains outliers, anomalies, or rare events indicative of potentially malicious activities, the presence of such outliers poses challenges. Recognizing this, and acknowledging the limitations of GSA, we introduce Fitness Normalization with Adaptive Search Radius. This approach enhances robustness to outliers and allows GSA to dynamically adjust its exploration-exploitation trade-off. By effectively balancing the exploration of diverse regions with the exploitation of promising solutions, this adaptation significantly improves optimization performance.

Moreover, the original GSA algorithm exhibits a rapid decline in the gravitational constant's value across various problem types, which contributes to premature convergence and a loss of diversity. To counteract these challenges, we propose the incorporation of a sigmoid function to modulate the gravitational constant. This adjustment aims to maintain exploration capabilities throughout the optimization process.

In the subsequent section, we delve into the details of Fitness Normalization with Adaptive Search Radius and Modulating the Gravitational Constant.

3.2.1 Fitness normalization with adaptive search radius

The masses of the particles are obtained through fitness normalization in the following way, replacing the original Equations 8, 9

$\begin{array}{ll}{m}_i(t)=\frac{fi{t}_i(t)-fi{t}_{median}}{fi{t}_{75}-fi{t}_{25}},i=1,2,\dots ,N& (12)\end{array}$

The fitness normalization of Equation 12 is more robust to outliers compared to Equation 8, as it uses the median and interquartile range for scaling, which makes it less sensitive to extreme values. Nonetheless, employing Equation 12 for mass computation during the iteration process reveals from experimental findings that the algorithm might encounter challenges in achieving smooth convergence during later stages. Moreover, there is a notable compromise in the accuracy of the ultimate optimal solution. This is because in the later stages of iteration, particles tend to converge toward a central point or region of the search space. When particles are predominantly attracted to each other, they tend to cluster around a central point, leading to center-biased convergence. To tackle this challenge and attain a better equilibrium between exploration and exploitation, we introduce an Adaptive Search Radius. This adjustment, incorporated into Equation 12, dynamically alters the radius based on the algorithm's convergence status and the density of particles in the vicinity. The primary goal is to smoothly transition from a state primarily governed by repulsion to one entirely dominated by attraction during the search phase, while ensuring attraction remains dominant during the exploitation phase. The computation of the Adaptive Search Radius is expressed as follows:

$\begin{array}{ll}R(t)=R_{min}+\frac{(R_{max}-R_{min})}{1+e^{-k·\frac{t-t_0}{\tau }}}& (13)\end{array}$

$\begin{array}{ll}{M}_i=m_i+R(t)& (14)\end{array}$

$\begin{array}{ll}{R}_{min}=\left|min\left\{m_1,m_2,\dots ,m_{\text{N}}\right\}\right|& (15)\end{array}$

$\begin{array}{ll}{R}_{max}=max\left\{m_1,m_2,\dots ,m_{\text{N}}\right\}& (16)\end{array}$

Where R(t) is the adaptive search radius at iteration. R_min and R_max are the minimum and maximum search radii, respectively, defining the range of possible values for the search radius. t is the current iteration number. t₀ is a parameter representing the starting iteration where the adaptation begins. τ is a time constant that determines the rate of adaptation. k is a parameter controlling the steepness of the sigmoid function.

R(t) gradually adjusts the search radius from R_min to R_max as the optimization progresses. Initially, the search radius is set to R_minto encourage exploration. As the iterations proceed, the function gradually increases the search radius, allowing the algorithm to exploit promising regions of the search space. Adjusting the parameters t₀, τ, and k allows to control the timing and rate of adaptation of the search radius according to the characteristics of the optimization problem and the desired balance between exploration and exploitation. This adaptive search radius equation enables the Gravitational Search Algorithm to dynamically adapt its exploration-exploitation trade-off, effectively balancing the exploration of diverse regions with the exploitation of promising solutions as the optimization progresses.

3.2.2 Modulating gravitational constant

In original GSA, the interaction force between masses is a function of the gravitational constant G(t) which determines the step size for mass movements. Maintaining control over G(t) is crucial for fostering diversification during the initial phases of the search process and enhancing concentration in the later stages. However, observations depicted in Figure 2 reveal a rapid decline in the gravitational constant's value across various problem types, leading to premature convergence and a swift loss of diversity. To mitigate these challenges, we propose the utilization of a sigmoid function to modulate the gravitational constant, as represented by Equation 17:

$\begin{array}{ll}G(t)=\frac{G_0}{1+e^{-\alpha (t-T)}}& (17)\end{array}$

Here, t represents the current iteration, T denotes the total number of iterations, and α regulates the curvature of the sigmoid curve. Figure 3 demonstrates how the gravitational constant evolves over iterations when employing the sigmoid function, illustrating that up to 50% of the total iterations can be dedicated to thorough exploration of the search space.

Figure 2

Figure 2. Value of gravitational constant with iteration in GSA.

Figure 3

Figure 3. Sigmoid gravitational function.

The primary aim of integrating the sigmoid function into the gravitational constant is twofold: firstly, to introduce disruption if diversity diminishes below a critical threshold during the initial search stages, and secondly, to facilitate gradual exploitation for identifying potential regions of interest in the later stages of the search.

In original GSA, G₀ remains consistent across all problems, ensuring uniformity in the search level of the GSA irrespective of the problem's nature. However, maintaining the same value of G₀ may result in excessive confusion and convergence challenges for problems with small solution spaces, while also causing slow progress and insufficient search efforts for problems with large solution spaces. To address this issue, G₀ is redefined in Equation 18 as a quantity proportional to the maximum distance between two particles in n-dimensional space:

$\begin{array}{ll}{G}_0=max\left\{\frac{2}{N(N-1)}{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=i+1}^N}dis(x_i,x_j),C_0\right\}& (18)\end{array}$

Here, N represents the total number of particles in the population, x_i and x_j denote the positions of particles i and j, respectively, dis(x_i, x_j) signifies the Euclidean distance between particles i and j in the solution space, and C₀ denotes the minimum limit of G₀ to ensure adequate search efforts.

The force exerting on the object i from the object j is redefined as Equation 19:

$\begin{array}{ll}{F}_{ij}^d(t)=G^m(t)\times \frac{M_i(t)\times M_j(t)}{R_{ij}(t)+\epsilon }\left(x_j^d(t)-x_i^d(t)\right)& (19)\end{array}$

$\begin{array}{ll}{G}^m(t)=\frac{max\left\{\frac{2}{N(N-1)}\sum _{i=1}^N\sum _{j=i+1}^{N}dis(x_i,x_j),C_0\right\}}{1+e^{-\alpha (t-T)}}& (20)\end{array}$

4 Soft actor-critic (SAC)

Soft Actor-Critic (SAC; Haarnoja et al., 2018) is a deep reinforcement learning algorithm operating within an off-policy framework, meaning it can learn from a separate data stream without needing to interact with the environment continuously. SAC aims to maximize the expected cumulative reward while also learning an approximation of the state-value function. At its core, SAC employs a soft policy update mechanism, which incorporates an entropy term in the objective function. This term encourages exploration by penalizing overly deterministic policies. By maximizing the entropy-adjusted expected return, SAC achieves a balance between exploration and exploitation, facilitating robust learning in complex environments.

One key feature of SAC is its use of twin Q-functions to estimate the state-action value (Q-value) function. This approach helps mitigate the overestimation bias commonly encountered in single Q-function methods, enhancing the stability and accuracy of the learned policies. Moreover, SAC utilizes a replay buffer to store and sample experiences, enabling efficient learning from past data. This buffer facilitates the decorrelation of samples and promotes data efficiency, making SAC suitable for real-world applications where data collection can be expensive or time-consuming.

As shown in Figure 4, Soft Actor-Critic (SAC) combines entropy regularization, twin Q-functions, off-policy learning, and experience replay to achieve effective and efficient learning in continuous action spaces, making it a powerful algorithm for a wide range of reinforcement learning tasks.

Figure 4

Figure 4. The framework of SAC algorithm.

5 Materials and methods

5.1 Overview of IGSA-SAC

Data sets of network intrusion are typically raw sensory inputs or high-dimensional state spaces. The presence of irrelevant features in the input data can increase the likelihood of False Positive (FP) in intrusion detection. Therefore, we propose the IGSA-SAC method for intrusion detection as illustrated in Figure 5, in which IGSA efficiently explores the search space to select the most relevant features for intrusion detection, reducing dimensionality and computational complexity, the classifier agent of SAC adapts its detection policy based on real-time feedback, enabling the system to respond dynamically to evolving threats and network conditions. The hybrid approach combines two different optimization techniques, enhancing the robustness and reliability of the intrusion detection system. By focusing on relevant features and adapting detection strategies, the method improves detection accuracy while minimizing False Positive (FP) and False Negative (FN). Algorithm 1 give the pseudo-code of the proposed IGSA-SAC method.

Figure 5

Figure 5. Flowchart of the IGSA-SAC intrusion detection.

Algorithm 1

Algorithm 1. The proposed IGSA-SAC method.

In the subsequent section, we delve into the details of feature selection based on IGSA, the state space and action space, the reward function, and the process training of the classifier agent of SAC.

5.2 Feature selection based on IGSA

The efficacy of intrusion detection systems, as measured by metrics such as accuracy, relevance, and redundancy, does not consistently yield superior outcomes. Situations may arise where both false alarm rates and detection rates are low, yet accuracy remains high. Moreover, reducing the number of features often results in decreased classification accuracy. Consequently, addressing intrusion detection in IoT networks presents a complex, multi-objective challenge that necessitates the utilization of multi-objective optimization algorithms (MOA) to deliver optimal solutions efficiently and promptly.

In this study, we leverage the Improved Gravitational Search Algorithm (IGSA) to select optimized features. IGSA is employed to minimize false alarm rates, enhance classification accuracy, reduce response time, and streamline computational complexity, thereby offering a holistic solution to intrusion detection challenges in IoT networks. Figure 6 presents a diagram of feature selection based on IGSA.

Figure 6

Figure 6. The diagram of feature selection based on IGSA.

5.2.1 Mass representation

In IGSA, trajectories denote alterations in position across various dimensions, with each dimension bearing binary values of 0 or 1. These trajectories represent changes in the probability of a coordinate adopting a 0 or 1 value. Moving along a dimension entail transitioning its value from 0 to 1 or vice versa.

The binary vector encoding for feature selection is illustrated in Figure 7. Each vector comprises binary values representing a subset of features. Within these vectors, elements can either be 1 or 0, signifying the inclusion or exclusion of a feature in the agent, respectively. Individuals in the search space represent potential feature subsets, utilizing a standardized notation: for a problem with d dimensions, each state comprises d bits, with each bit indicating the inclusion (1) or exclusion (0) of a feature. The length of the vector aligns with the total number of features, where the ith feature is included if the ith bit equals 1, otherwise, it's excluded.

Figure 7

Figure 7. Encoding of a binary vector for feature selection.

5.2.2 Fitness function definition

The fitness function is formulated considering two key criteria: classification accuracy and the quantity of selected features. A favorable fitness value indicates a balance between heightened classification accuracy and reduced feature dimensions. To address the challenge of multiple objectives, we devise a fitness function that amalgamates these two aims into a singular objective. The fitness function is expressed as Equation 21:

$\begin{array}{ll}fi{t}_i={\omega }_1\times acc{u}_i+{\omega }_2\times \left[1-\frac{\sum _{j=1}^p{f}_j}{p}\right]& (21)\end{array}$

Within the equation, two predefined weight factors, denoted as ω₁ and ω₂, are employed. ω₁ serves as the weight factor for Soft Actor-Critic (SAC) classification accuracy, represented by accui, while ω₂ corresponds to the weight factor for the quantity of selected features, with fj denoting the feature mask value. Adjusting the weight factor of accuracy to a higher value, such as 100%, is feasible if prioritizing accuracy is paramount. Objects with elevated fitness values possess a greater likelihood of influencing the positions of other objects in the subsequent iteration, underscoring the importance of setting these values judiciously. The accuracy accui is computed using Equation 22, where corr signifies the number of correctly classified examples, and incorr represents the number of incorrectly classified examples.

$\begin{array}{ll}acc{u}_i=\frac{corr}{corr+incorr}\times 100\%& (22)\end{array}$

5.3 State space and action space

The intrusion detection problem can be viewed as a reinforcement learning problem with a discrete action space. In this paper, we use the classifier agent of Soft Actor-Critic reinforcement learning approach to detect the network intrusions. The input of Soft Actor-Critic has two parts: state space and action space.

We consider the relevant features identified by improved GSA to be the state representation. This state encapsulates the essential characteristics of the network environment and provides the necessary information for the IDS to make decisions. The features selected through improved GSA ensure that the state representation captures relevant information about the network traffic while being suitable for consumption by the reinforcement learning model.

Actions typically correspond to the decisions or responses that the system can take in response to observed network traffic. These actions include classifying traffic as normal or malicious, applying specific security policies or rules, or triggering alerts or countermeasures. The feature labels, which indicate the ground truth classification of network traffic (e.g., benign or malicious), can be mapped to the set of actions that the IDS can take. Each action represents a distinct response or decision based on the observed network traffic characteristics.

We consider the selected features to be states and feature labels to be actions. As shown in the upper part of Figure 8, S = {s₀, s₁, …, s_n, s_n+1} is the selected feature and A = {a₀, a₁, …, a_n, a_n+1} is the feature label.

Figure 8

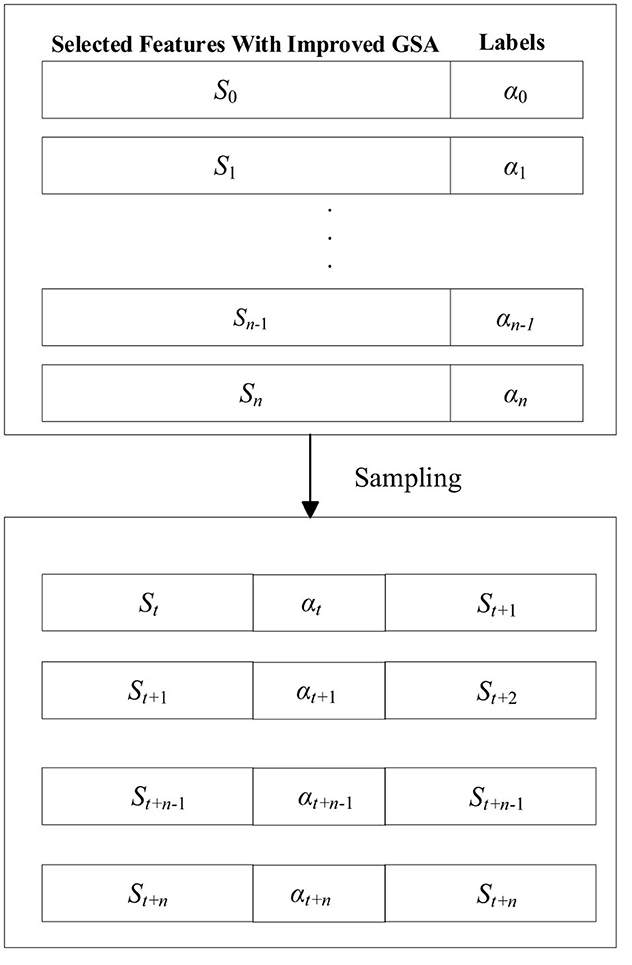
Figure 8. Sampling from selected features with improved GSA are mapped to the state space and labels are mapped to the action space.

5.4 Design of the reward function

To evaluate the performance of the intrusion detection model, we design a reward function to guide the learning process by incentivizing the agent to take actions that lead to effective intrusion detection while minimizing false alarms and missed detections. The formulation of the reward function along with the weighting of each component is designed as follows:

• Intrusion Detection Reward (Positive Reward): If the agent correctly identifies an intrusion in the network traffic data, it receives a positive reward. The magnitude of the positive reward can be fixed or proportional to the severity of the detected intrusion.

• False Positive Penalty (Negative Reward): If the agent incorrectly classifies benign network traffic as malicious (False Positive), it incurs a negative penalty. The magnitude of the negative penalty can be fixed or proportional to the severity of the False Positive.

• Resource Utilization Penalty (Negative Reward): If the agent's actions result in excessive resource utilization (e.g., high computational cost), it incurs a negative penalty. The magnitude of the negative penalty can be based on the amount of resources consumed.

• Exploration Reward: the agent can receive a positive reward for exploring new detection strategies or discovering new intrusion patterns. This encourages the agent to explore different actions and strategies.

The overall reward function is the weighted sum of these components, as illustrated below:

$\begin{array}{ll}\begin{array}{r}\hfill R\left(s,a,s\prime \right)=a_{instrusion}·R_{instrusion}\left(s,a,s\prime \right)\\ \hfill +{\beta }_{falsepositive}·R_{falsepositive}\left(s,a,s\prime \right)\\ \hfill -{\gamma }_{resource}·R_{resource}\left(s,a,s\prime \right)\\ \hfill +{\delta }_{exploration}·R_{exploration}\left(s,a,s\prime \right)\end{array}& (23)\end{array}$

The weights a_instrusion, β_{false positive}, γ_resource, and δ_exploration determine the importance of each component in the reward function and can be adjusted based on the specific requirements and characteristics of the network environment.

5.5 Training process of SAC

The selected features obtained from IGSA is then normalized by a data preprocessor to create a learned state representation. This preprocessed state vector serves as input to the classifier agent of SAC, which learns a policy directly and approximates the value function using a soft Q-function. Using the learned policy and value function, the model is rewarded with a reward r, facilitating weight updates to the SAC network. The precise steps followed by the agent are delineated in Algorithm 2.

Algorithm 2

Algorithm 2. Core algorithm for agent.

In each iteration of the training process for Soft Actor-Critic (SAC), the agent is provided with a batch of training samples. For each feature vector, the current vector is designated as the current state and is inputted into the agent's SAC algorithm. SAC learns a policy that maps states to actions. The agent predicts an action using the learned policy. The action chosen corresponds to the one with the highest expected return, as estimated by the soft Q-function, which approximates the value function in SAC.

If the action with the highest expected return corresponds to action 0, it signifies that the agent predicts the current state or sample belongs to the non-malicious category. Conversely, if action 1 yields the maximum expected return, it indicates that the agent predicts the current state belongs to an attack or malicious category. Following the prediction, the agent receives a reward r based on the original category of the sample from the dataset. Additionally, SAC employs a target Q-value network to stabilize training. The agent then updates the policy and value function parameters of its SAC algorithm using the reward obtained, applying the principles of reinforcement learning, which may involve maximizing expected return through gradient ascent.

In the training process of Soft Actor-Critic (SAC), an error metric is computed by measuring the discrepancy between the predicted value function and the target value function. This error metric is then utilized in the calculation of the weight assigned to each experience for prioritized experience replay. Specifically, the weight of each experience is computed as the summation of the elements in the error vector raised to the power of a hyperparameter ω, which governs the prioritization mechanism. At the onset of training, a replay buffer is allocated to store experiences for prioritized experience replay. Subsequently, each experience tuple, along with its associated state loss weight, is stored in this replay buffer. This iterative process contributes to the training of the agent's SAC algorithm. During training iterations, a batch of experiences is sampled from the replay buffer. The probability of selecting an experience for training is directly proportional to its loss weight, calculated earlier. This prioritized sampling strategy ensures that experiences with higher error metrics, and thus greater potential for learning, are more frequently included in the training batch. The training cycle continues iteratively, with sampled batches being used to update the parameters of the SAC algorithm, fostering improved learning from experiences that require greater attention.

6 Result and discussion

6.1 Experimental results for IGSA

This section evaluates the performance of the proposed IGSA using twenty-three standard benchmark functions (Supplementary Tables A.1–A.3). A comparison with five heuristic algorithms across different dimensions is presented in Section 6.1.3.

6.1.1 Benchmark functions

The benchmark functions used in the experiments are listed in Supplementary Tables A.1–A.3 (Rashedi et al., 2009, 2010; Yao et al., 1999). Here, n = 30 represents the function's dimension, and F(x^*) denotes its optimal value. The functions in Supplementary Tables A.1, A.2 generally have an optimum value of zero, except for F₈ in Supplementary Table A.2, which has an optimum of −418.9829 × n. A detailed description of Supplementary Table A.3 functions is provided in Appendix A.

6.1.2 Parameter settings

The IGSA is compared with five heuristic algorithms, with parameter settings adopted from their respective references. Table 1 summarizes the key parameters (Li and Zhou, 2011; Mahadevan and Kannan, 2010; Musharavati and Hamouda, 2011; Sarafrazi et al., 2011).

Table 1

Table 1. Parameter settings of compared heuristic algorithms.

To ensure a fair evaluation, all algorithms were independently run 30 times, using a maximum function evaluation limit (FEmax = 3.00E+05) or until the exact solution was found.

6.1.3 Comparison with other heuristic algorithms

The performance of IGSA is assessed using the mean fitness value (F_mean). Table 2 presents F_mean results for all six algorithms, with bolded values indicating the best performance.

Table 2

Table 2. F_mean values for the comparison of our proposed IGSA and five other heuristic algorithms.

The comparison is summarized using “w/t/l” and “#BMF”:

• w/t/l: Number of functions where IGSA wins (w), ties (t), or loses (l) against competitors.

• #BMF: Count of test functions where other algorithms achieved the best F_mean value.

Table 2 shows that IGSA outperforms its competitors in 18 out of 23 benchmark functions, demonstrating superior accuracy. While CLPSO achieved the best F_mean once (#BMF = 1), IGSA1 and IGSA2 each achieved it twice (#BMF = 2).

IGSA successfully identifies the global optima for all unimodal high-dimensional and multimodal low-dimensional functions, except F8, F16, and F22. In multimodal high-dimensional cases, overall accuracy declines, but IGSA remains the most effective, locating near-global optima for all such functions except F11.

6.2 Experimental results for IGSA-SAC method

6.2.1 Datasets and preprocessing

We evaluated the proposed IGSA-SAC method on three widely used intrusion detection datasets: NSL-KDD (Tavallaee et al., 2009), AWID (Kolias et al., 2015), and CICIDS2017 (GitLab, n.d.; Engelen et al., 2021). These datasets were chosen for their public availability, inclusion of anomalies, and sufficient sample sizes for training and testing.

• NSL-KDD: This dataset contains 41 features, including 38 continuous and three categorical variables. After preprocessing (max-min normalization and one-hot encoding), the dataset was expanded to 122 features. It includes five classes: Normal, DoS, Probe, R2L, and U2R (see Figure 9 and Table 3 for details).

• AWID: Collected from a real-world WiFi network, this dataset was reduced to 46 features after removing irrelevant attributes. It includes one normal class and three attack classes: Injection, Simulation, and Flooding (see Figure 10).

• CICIDS2017: This dataset was preprocessed to handle null values and normalize features, ensuring compatibility with the IGSA-SAC model.

Figure 9

Figure 9. Distribution frequency of each class of NSL-KDD.

Table 3

Table 3. Attack categories, including four types of attacks: Dos, Probe, R2L, and U2R.

Figure 10

Figure 10. Distribution frequency of each class of AWID.

Preprocessing Steps:

1. Data Cleaning: Infinity values were replaced with−1, and rows with NaN or NULL values were removed.

2. Data Conversion: Non-numeric features (e.g., protocol types, services) were converted to numeric data using one-hot encoding (Potdar et al., 2017).

3. Data Normalization: Features were scaled to the range [0, 1] using max-min normalization to ensure consistent value ranges, as illustrated in Equation 24.

$\begin{array}{ll}{f}_{new}=\frac{f_{old}-f_{min}}{f_{max}-f_{min}}& (24)\end{array}$

where f_old is a network traffic feature vector, and f_min and f_old are the minimum and maximum values of f_old, respectively.

6.2.2 Experiment setup

The experiments were conducted on a PC with an Intel Core i7-10750H CPU, 24 GB RAM, and libraries including Scikit-Learn, TensorFlow 2.0, and Keras. The SAC model used a neural network structure with three hidden layers of 100 neurons each, optimized using the Adam algorithm (see Table 4 for details).

Table 4

Table 4. Network structure of the classifier agent.

The SAC algorithm serves as the classifier agent. In this paper, the Actor network, Q Critic network, and V Critic network within the SAC model adopt a straightforward neural network structure. Table 4 presents the Network structure of the classifier agent. Below is a detailed explanation of the network structure notation “122(46)-100-100-100-5(4)”:

Input Layer: The first number, 122(46), represents the number of neurons in the input layer. 122 denotes the number of input features for the NSL-KDD dataset. 46 (in parentheses) denotes the number of input features for the AWID dataset. This indicates that the network is designed to handle both datasets, with the input layer dynamically adjusting based on the dataset used.

Hidden Layers: The notation 100-100-100 represents three fully connected hidden layers, each containing 100 neurons. These hidden layers are responsible for learning hierarchical features from the input data. All hidden layers use the ReLU (Rectified Linear Unit) activation function, which introduces non-linearity and helps the network learn complex patterns.

Output Layer: The final number, 5(4), represents the number of neurons in the output layer. 5 denotes the number of output classes for the NSL-KDD dataset. 4 (in parentheses) denotes the number of output classes for the AWID dataset. For the Actor network, the output layer uses the Softmax activation function to produce a probability distribution over the possible actions (classes). For the Critic networks, the output layer does not use any activation function, as it outputs a single value representing the estimated Q-value or state value.

Fully Connected Architecture: All networks (Actor, Q Critic, and V Critic) employ a fully connected (dense) architecture, meaning every neuron in one layer is connected to every neuron in the next layer.

Optimization: The parameters of all networks are optimized using the Adam algorithm, a popular stochastic optimization method known for its efficiency and adaptability.

Grid search was employed to identify the optimal hyperparameters for the SAC model. This method conducts a thorough search for specific hyperparameter values automatically, thereby conserving time and resources. The determination of the number of hidden layers and neurons in each layer was conducted through grid search. The chosen optimal values represent those yielding the highest accuracy across all parameters. Figures 11, 12 depict the outcomes of the grid search, revealing that the SAC model achieves satisfactory classification results with only three hidden layers, each comprising 100 neurons. While employing additional hidden layers and neurons may enhance classification performance, it would necessitate longer training times due to the increased complexity of the SAC model compared to other reinforcement learning models. It's important to note that the three network actors, Q Critic, and V Critic in the SAC model are solely utilized to approximate the probability distribution function, state-action value function, and state value function. In contrast, traditional deep learning networks typically directly learn a classifier, requiring more hidden layers and neurons.

Figure 11

Figure 11. Trend of accuracy with the number of hidden layers.

Figure 12

Figure 12. Trend of accuracy with the number of neurons.

The effectiveness of the proposed IGSA is evaluated by comparing it with existing methods such as GA (Ibrahim et al., 2011a), BPSO (Huang and Dun, 2008), QBPSO (Ibrahim et al., 2011b), and BGSA (Ibrahim et al., 2012). The aim of this comparison is to identify the most suitable feature selection algorithm for intrusion detection. To ensure fairness in the comparison, all optimization parameters are standardized, as outlined in Table 5, which presents the required parameter configurations for all optimization techniques employed in this study.

Table 5

Table 5. Parameter settings used in GA, BPSO, BGSA, QBPSO, and BIGSA.

6.2.3 Performance of IGSA-SAC

To assess the effectiveness of the method proposed in this paper, we utilize our IGSA for intrusion detection on NSL-KDD and AWID datasets. We conduct a comparative analysis by pitting our IGSA against other feature selection algorithms, namely GA (Ibrahim et al., 2011a), BPSO (Huang and Dun, 2008), QBPSO (Ibrahim et al., 2011b), and BGSA (Ibrahim et al., 2012), for intrusion detection tasks. Additionally, we select existing network intrusion detection models, including the AE-RL model (Caminero et al., 2019), AESMOTE model (Ma and Shi, 2020), SSDDQN (Dong et al., 2021), and SHIA (Vinayakumar et al., 2019), for comparison on NSL-KDD and AWID datasets. Throughout the remainder of this section, we delve into a detailed performance comparison between our proposed IGSA-SAC and the following models: SAC, GA-SAC, BPSO-SAC, QBPSO-SAC, BGSA-SAC, AE-RL, AESMOTE, SSDDQN, and SHIA.

To highlight the significance of our proposed method, we present a comprehensive comparison of the performance metrics (accuracy, precision, recall, and F1-score) of IGSA-SAC with other state-of-the-art methods on the NSL-KDD datasets. The results are summarized in Table 6.

Table 6

Table 6. Performance comparison of IGSA-SAC with existing methods on the NSL-KDD dataset.

Figure 13 presents the experimental comparison results concerning accuracy, precision, recall, and F1-score in the multi-classification scenario. Among the models compared, only BGSA-SAC attains an accuracy of 82.12%, whereas the remaining models achieve a maximum accuracy of 81.11%. Notably, our proposed IGSA-SAC model achieves an accuracy of 84.15%, outperforming all other models, including state-of-the-art methods such as SHIA and QBPSO-SAC. This represents a 2.73% improvement over the best-performing existing methods (SHIA and QBPSO-SAC) and a 5.51% improvement over the worst-performing method (GA-SAC).

Figure 13

Figure 13. Performance scores of IGSA-SAC compared to other methods (KDDTest+).

The IGSA-SAC model also demonstrates a clear advantage in terms of precision, recall, and F1-score. Specifically, it achieves precision and recall rates exceeding 84%, which are significantly higher than those of other models. While precision and recall are ideally both high, they are typically mutually constraining in practice. Therefore, we use the F1-score to evaluate these metrics collectively. The F1-score of our IGSA-SAC model is 84.85%, which is 2.73% higher than the best-performing existing methods (SHIA and QBPSO-SAC) and 5.51% higher than the worst-performing method (GA-SAC). These results underscore the robustness of our approach in handling multi-classification tasks.

The superior classification performance of our proposed method on the NSL-KDD dataset can be attributed to its ability to better distinguish between normal and malicious activities by eliminating irrelevant or redundant features. Generally, as the number of features increases, classifier performance improves initially but then declines. This indicates that having too many or too few features can significantly reduce a classifier's effectiveness. With too few features, data overlap is more likely; with too many features, the same category can become more distant and sparser in space, leading to the failure of many classification algorithms. After processing, the NSL-KDD dataset has 122 dimensions, which can severely impact classifier performance. Our IGSA-SAC method effectively addresses this challenge by optimizing feature selection, resulting in improved performance.

Figure 14 illustrates the accuracy of our proposed IGSA-SAC model compared to other models on the KDDTest21 dataset. Despite KDDTest21 being more challenging to recognize than KDDTest+, our IGSA-SAC model achieves an accuracy of 79.51%, outperforming other methods. This demonstrates the generalizability of our approach, even on more complex datasets.

Figure 14

Figure 14. Accuracy comparison of IGSA-SAC method and other methods on the KDDTest21 dataset.

Figure 15 highlights the performance of our proposed IGSA-SAC method compared to state-of-the-art methods on the AWID dataset. Our IGSA-SAC model achieves an accuracy of 98.9%, surpassing AESMOTE (97.1%) and SHIA (96.8%). Notably, all metrics (precision, recall, and F1-score) exceed 98.9%, representing a 1.8% improvement over the best-performing existing method (AESMOTE). Despite the processed AWID dataset having only 46 feature dimensions, feature selection remains a crucial factor influencing model performance, and our method demonstrates its effectiveness in this regard.

Figure 15

Figure 15. Performance scores of IGSA-SAC compared to other methods (AWID).

Figure 16 presents the experimental results comparing the accuracy of our proposed IGSA-SAC model with other methods on the CICIDS2017 dataset. Our IGSA-SAC model achieves an accuracy of 98.41%, surpassing that of the other methods. This further validates the robustness and generalizability of our approach across diverse datasets.

Figure 16

Figure 16. Accuracy comparison of IGSA-SAC method and other methods on the CICIDS2017.

The comparative analysis demonstrates that our proposed IGSA-SAC method consistently outperforms existing approaches across multiple datasets and evaluation metrics. The superior performance of IGSA-SAC can be attributed to its effective feature selection mechanism, which eliminates irrelevant or redundant features, thereby enhancing the model's ability to distinguish between normal and malicious activities. This is particularly evident in the NSL-KDD dataset, where IGSA-SAC achieves an accuracy of 84.15%, significantly higher than the next best model (BGSA-SAC at 82.12%). Similarly, on the AWID and CICIDS2017 datasets, IGSA-SAC achieves accuracy rates of 98.9% and 98.41%, respectively, further validating its robustness and generalizability.

In conclusion, the experimental results and comparative analysis highlight the significance of our proposed IGSA-SAC method in advancing the field of network intrusion detection. Its ability to consistently outperform state-of-the-art methods across multiple datasets, including NSL-KDD, AWID, and CICIDS2017, underscores its potential for real-world applications. The improvements in accuracy, precision, recall, and F1-score demonstrate the effectiveness of our approach in addressing the challenges of high-dimensional data and complex classification tasks.

6.2.4 Dimensionality reduction and computational efficiency

To further demonstrate the effectiveness of the proposed IGSA-SAC method, we quantify the improvements in dimensionality reduction and computational complexity. Table 7 shows the number of features before and after applying IGSA for the NSL-KDD, AWID, and CICIDS2017 datasets. The results indicate a significant reduction in dimensionality, which directly contributes to reduced computational complexity.

Table 7

Table 7. Dimensionality reduction achieved by IGSA.

The reduction in dimensionality not only improves the efficiency of the intrusion detection system but also reduces the computational overhead during training and inference. For instance, the NSL-KDD dataset, which originally contains 122 features, was reduced to 50 features after applying IGSA, resulting in a 59.02% reduction in dimensionality. This reduction significantly speeds up the training process and reduces the memory footprint of the model.

To evaluate the computational efficiency of the proposed IGSA-SAC method, we compare the training and inference times with other baseline methods, including GA-SAC, BPSO-SAC, QBPSO-SAC, and BGSA-SAC. Table 8 presents the training time, inference time, and computational complexity of each method.

Table 8

Table 8. Computational complexity comparison.

The results demonstrate that IGSA-SAC achieves the lowest training and inference times among all methods. For example, the training time for IGSA-SAC is 120 s, compared to 180 s for GA-SAC, representing a 33.33% improvement in computational efficiency. This improvement is attributed to the reduced dimensionality and the efficient exploration-exploitation balance achieved by IGSA.

The reduction in dimensionality achieved by IGSA directly impacts the computational complexity of the intrusion detection system. By selecting only the most relevant features, the training and inference times are significantly reduced. For instance, the NSL-KDD dataset, which originally contains 122 features, was reduced to 50 features after applying IGSA, resulting in a 59.02% reduction in dimensionality. This reduction not only speeds up the training process but also reduces the memory footprint of the model. Additionally, the improved exploration-exploitation balance in IGSA ensures faster convergence, further reducing the computational overhead. As shown in Table 8, the IGSA-SAC method achieves a training time of 120 s, compared to 180 s for GA-SAC, demonstrating a clear improvement in computational efficiency.

To visually demonstrate the relationship between dimensionality reduction and computational complexity, we plot the training time against the number of features for different methods. Figure 17 shows that as the number of features decreases, the training time also decreases, and IGSA-SAC consistently outperforms other methods in terms of computational efficiency.

Figure 17

Figure 17. Training time vs. number of features.

6.2.5 Discussion

The superior performance of IGSA-SAC can be attributed to:

1. Effective Feature Selection: IGSA eliminates irrelevant or redundant features, improving the model's ability to distinguish between normal and malicious activities.

2. Dynamic Exploration-Exploitation Balance: The use of an adaptive search radius and sigmoid function in IGSA ensures sustained exploration capabilities, leading to faster convergence and better optimization.

3. Reinforcement Learning Rewards: The designed reward function encourages the agent to improve detection effectiveness while minimizing false alarms and missed detections.

The results demonstrate that IGSA-SAC consistently outperforms state-of-the-art methods across multiple datasets, making it a robust and efficient solution for real-world intrusion detection systems.

7 Evaluation metrics

The performance of IGSA-SAC was evaluated using four metrics:

• Accuracy: Overall effectiveness of the model.

• Precision: Proportion of correctly identified intrusions.

• Recall (Detection Rate): Proportion of actual intrusions detected.

• F1-Score: Harmonic mean of precision and recall, providing a balanced measure of performance.

The formulas for these metrics are as follows:

$\begin{array}{ll}Accuracy=\frac{TF+TN}{TP+TN+FP+FN}& (25)\end{array}$

$\begin{array}{ll}Precision=\frac{TP}{TP+FP}& (26)\end{array}$

$\begin{array}{ll}Recall=\frac{TP}{TP+FN}& (27)\end{array}$

$\begin{array}{ll}F1-score=\frac{2\times Precision\times Recall}{Precision+Recall}& (28)\end{array}$

Where:

• TP (True Positive): Correctly identified intrusions.

• FP (False Positive): Incorrectly identified intrusions.

• TN (True Negative): Correctly identified normal traffic.

• FN (False Negative): Missed intrusions.

8 Conclusion

This paper proposes an improved Gravitational Search Algorithm (IGSA) with fitness normalization and an Adaptive Search Radius to enhance robustness against outliers and balance exploration and exploitation. To maintain sustained exploration, we introduce a sigmoid-modulated gravitational constant.

Based on IGSA, we develop the IGSA-SAC method for intrusion detection, where IGSA selects relevant features, and the SAC classifier adapts to evolving threats. Our experiments on 23 benchmark functions demonstrate IGSA's superior performance over five heuristic algorithms. For intrusion detection, IGSA-SAC achieves 84.15% accuracy on NSL-KDD and over 98.7% on AWID, with improved computational efficiency. The feature selection reduces dimensions from 122 to 50, cutting training time to 120 s, and inference time is the fastest among compared methods, making it suitable for real-time applications.

Despite these advancements, IGSA-SAC struggles with the U2R category due to limited training samples. Future work will explore SMOTE and generative adversarial networks to address this limitation.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: Data will be made available on request. Requests to access these datasets should be directed to c3hsemppbkB0eXVzdC5lZHUuY24=.

Author contributions

LJ: Writing – original draft, Writing – review & editing. RF: Software, Writing – review & editing. XH: Investigation, Writing – review & editing. XC: Validation, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Fundamental Research Program of Shanxi Province [Grant No. 202303021221144].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2025.1574211/full#supplementary-material

References

Aljehane, N. O., Mengash, H. A., Hassine, S. B. H., Alotaibi, F. A., Salama, A. S., and Abdelbagi, S. (2024). Optimizing intrusion detection using intelligent feature selection with machine learning model. Alex. Eng. J. 91, 39–49. doi: 10.1016/j.aej.2024.01.073

Crossref Full Text | Google Scholar

Altunay, H. C., and Albayrak, Z. (2023). A hybrid CNN+LSTM-based intrusion detection system for industrial IoT networks. Eng. Sci. Technol. Int. J. 38:101322. doi: 10.1016/j.jestch.2022.101322

Crossref Full Text | Google Scholar

Azimjonov, J., and Kim, T. (2024). Designing accurate lightweight intrusion detection systems for IoT networks using fine-tuned linear SVM and feature selectors. Comput. Secur. 137:103598. doi: 10.1016/j.cose.2023.103598

Crossref Full Text | Google Scholar

Barbosa, G. N. N., Andreoni, M., and Mattos, D. M. F. (2024). Optimizing feature selection in intrusion detection systems: Pareto dominance set approaches with mutual information and linear correlation. Ad Hoc Netw. 159:103485. doi: 10.1016/j.adhoc.2024.103485

Crossref Full Text | Google Scholar

Belavagi, M. C., and Muniyal, B. (2016). Performance evaluation of supervised machine learning algorithms for intrusion detection. Proc. Comput. Sci. 89, 117–123. doi: 10.1016/j.procs.2016.06.016

Crossref Full Text | Google Scholar

Belouch, M., El Hadaj, S., and Idhammad, M. (2018). Performance evaluation of intrusion detection based on machine learning using Apache Spark. Proc. Comput. Sci. 127, 1–6. doi: 10.1016/j.procs.2018.01.091

Crossref Full Text | Google Scholar

Caminero, G., Lopez-Martin, M., and Carro, B. (2019). Adversarial environment reinforcement learning algorithm for intrusion detection. Comput. Netw. 159, 96–109. doi: 10.1016/j.comnet.2019.05.013

Crossref Full Text | Google Scholar

Chatzoglou, E., Kambourakis, G., Kolias, C., and Smiliotopoulos, C. (2022). Pick quality over quantity: expert feature selection and data preprocessing for 802.11 intrusion detection systems. IEEE Access 10, 64761–64784. doi: 10.1109/ACCESS.2022.3183597

Crossref Full Text | Google Scholar

Chung, Y. Y., and Wahid, N. (2012). A hybrid network intrusion detection system using simplified swarm optimization (SSO). Appl. Soft Comput. 12, 3014–3022. doi: 10.1016/j.asoc.2012.04.020

Crossref Full Text | Google Scholar

Ding, H., Chen, L., Dong, L., Fu, Z., and Cui, X. (2022). Imbalanced data classification: A KNN and generative adversarial networks-based hybrid approach for intrusion detection. Future Gener. Comput. Syst. 131, 240–254. doi: 10.1016/j.future.2022.01.026

Crossref Full Text | Google Scholar

Dong, S., Xia, Y., and Peng, T. (2021). Network abnormal traffic detection model based on semi-supervised deep reinforcement learning. IEEE Trans. Netw. Serv. Manage. 18, 4197–4212. doi: 10.1109/TNSM.2021.3120804

Crossref Full Text | Google Scholar

El-Ghamry, A., Darwish, A., and Hassanien, A. E. (2023). An optimized CNN-based intrusion detection system for reducing risks in smart farming. Internet Things 22:100709. doi: 10.1016/j.iot.2023.100709

Crossref Full Text | Google Scholar

Engelen, G., Rimmer, V., and Joosen, W. (2021). “Troubleshooting an intrusion detection dataset: the CICIDS2017 case study,” in 2021 IEEE Security and Privacy Workshops (SPW) (Piscataway, NJ: IEEE), 7–12. doi: 10.1109/SPW53761.2021.00009

Crossref Full Text | Google Scholar

Fang, Y., Yao, Y., Lin, X., Wang, J., and Zhai, H. (2024). A feature selection based on genetic algorithm for intrusion detection of industrial control systems. Comput. Secur. 139:103675. doi: 10.1016/j.cose.2023.103675

Crossref Full Text | Google Scholar

GitLab (n.d.). CICFlowMeter [Computer software]. GitLab repository. Available online at: https://gitlab.com/hieulw/cicflowmeter (accessed June 8, 2024).

Google Scholar

Gu, J., and Lu, S. (2021). An effective intrusion detection approach using SVM with naïve Bayes feature embedding. Comput. Secur. 103:102158. doi: 10.1016/j.cose.2020.102158

Crossref Full Text | Google Scholar

Haarnoja, T., Zhou, A., Hartikainen, K., Tucker, G., Ha, S., Tan, J., et al. (2018). Soft actor-critic algorithms and applications. arXiv [Preprint]. doi: 10.48550/arXiv.1812.05905

Crossref Full Text | Google Scholar

Huang, C. L., and Dun, J. F. (2008). A distributed PSO–SVM hybrid system with features selection and parameter optimization. Appl. Soft Comput. 8, 1381–1391. doi: 10.1016/j.asoc.2007.10.007

Crossref Full Text | Google Scholar

Ibrahim, A. A., Mohamed, A., and Shareef, H. (2012). “Application of quantum-inspired binary gravitational search algorithm for optimal power quality monitor placement,” in Proceedings of the 11th WSEAS International Conference on Artificial Intelligence, Knowledge Engineering and Data Bases (AIKED ‘12), Cambridge, UK.

Google Scholar

Ibrahim, A. A., Mohamed, A., Shareef, H., and Ghoshal, S. P. (2011a). “Optimal placement of power quality monitors in distribution systems using the topological monitor reach area,” in Proceedings of the International Electric Machines and Drives Conference, Niagara Falls, Canada (New York, NY: IEEE Press). doi: 10.1109/IEMDC.2011.5994627

Crossref Full Text | Google Scholar

Ibrahim, A. A., Mohamed, A., Shareef, H., and Ghoshal, S. P. (2011b). “An effective power quality monitor placement method utilizing quantum inspired particle swarm optimization,” in Proceedings of the International Conference on Electrical Engineering and Informatics, Bandung, Indonesia (New York, NY: IEEE Press). doi: 10.1109/ICEEI.2011.6021845

Crossref Full Text | Google Scholar

Kolias, C., Kambourakis, G., Stavrou, A., and Gritzalis, S. (2015). Intrusion detection in 802.11 networks: empirical evaluation of threats and a public dataset. IEEE Commun. Surv. Tutor. 18, 184–208. doi: 10.1109/COMST.2015.2402161

Crossref Full Text | Google Scholar

Lavet, V. F., Henderson, P., Islam, R., Bellemare, M. G., and Pineau, J. (2018). An introduction to deep reinforcement learning. arXiv preprint, arXiv:1811.12560 [cs.LG]. doi: 10.1561/9781680835397

Crossref Full Text | Google Scholar

Li, C., and Zhou, J. (2011). Parameters identification of hydraulic turbine governing system using improved gravitational search algorithm. Energy Convers. Manage. 52, 374–381. doi: 10.1016/j.enconman.2010.07.012

Crossref Full Text | Google Scholar

Liao, Y., and Vemuri, V. R. (2002). Use of K-Nearest Neighbor classifier for intrusion detection. Comput. Secur. 21, 439–448. doi: 10.1016/S0167-4048(02)00514-X

Crossref Full Text | Google Scholar

Lopez-Martin, M., Carro, B., and Sanchez-Esguevillas, A. (2020). Application of deep reinforcement learning to intrusion detection for supervised problems. Expert Syst. Appl. 141:112963. doi: 10.1016/j.eswa.2019.112963

Crossref Full Text | Google Scholar

Louk, M. H. L., and Tama, B. A. (2023). Dual-IDS: A bagging-based gradient boosting decision tree model for network anomaly intrusion detection system. Expert Syst. Appl. 213(Part B):119030. doi: 10.1016/j.eswa.2022.119030

Crossref Full Text | Google Scholar

Ma, X., and Shi, W. (2020). AESMOTE: adversarial reinforcement learning with SMOTE for anomaly detection. IEEE Trans. Netw. Sci. Eng. 8, 943–956. doi: 10.1109/TNSE.2020.3004312

Crossref Full Text | Google Scholar

Mahadevan, K., and Kannan, P. S. (2010). Comprehensive learning particle swarm optimization for reactive power dispatch. Appl. Soft Comput. 10, 641–652. doi: 10.1016/j.asoc.2009.08.038

Crossref Full Text | Google Scholar

Mishra, P., Varadharajan, V., Tupakula, U., and Pilli, E. S. (2018). A detailed investigation and analysis of using machine learning techniques for intrusion detection. IEEE Commun. Surv. Tutor. 21, 686–728. doi: 10.1109/COMST.2018.2847722

Crossref Full Text | Google Scholar

Musharavati, F., and Hamouda, A. S. M. (2011). Modified genetic algorithms for manufacturing process planning in multiple parts manufacturing lines. Expert Syst. Appl. 38, 10770–10779. doi: 10.1016/j.eswa.2011.01.129

Crossref Full Text | Google Scholar

Narayanan, S. L., Kasiselvanathan, M., Gurumoorthy, K. B., and Kiruthika, V. (2023). Particle swarm optimization based artificial neural network (PSO-ANN) model for effective k-barrier count intrusion detection system in WSN. Measure. Sens. 29:100875. doi: 10.1016/j.measen.2023.100875

Crossref Full Text | Google Scholar

Nguyen, T. T., and Reddi, V. J. (2019). Deep reinforcement learning for cybersecurity. arXiv [Preprint]. doi: 10.48550/arXiv.1906.05799

Crossref Full Text | Google Scholar

Potdar, K., Pardawala, T. S., and Pai, C. D. (2017). A comparative study of categorical variable encoding techniques for neural network classifiers. Int. J. Comput. Appl. 175, 7–9. doi: 10.5120/ijca2017915495

Crossref Full Text | Google Scholar

Rani, B. S., Vairamuthu, S., and Subramanian, S. (2024). Archimedes Fire Hawk Optimization enabled feature selection with deep maxout for network intrusion detection. Comput. Secur. 140:103751. doi: 10.1016/j.cose.2024.103751

Crossref Full Text | Google Scholar

Rashedi, E. (2007). Gravitational search algorithm (M.Sc. thesis). Electrical Engineering Department, Shahid Bahonar University of Kerman, Iran.

Google Scholar

Rashedi, E., Nezamabadi-Pour, H., and Saryazdi, S. (2007). “Allocation of static var compensator using gravitational search algorithm,” in Proceedings of the First Joint Conference on Fuzzy and Intelligent Systems, Mashhad, Iran.

Google Scholar

Rashedi, E., Nezamabadi-Pour, H., and Saryazdi, S. (2009). GSA: a gravitational search algorithm. Inf. Sci. 179, 2232–2248. doi: 10.1016/j.ins.2009.03.004

Crossref Full Text | Google Scholar

Rashedi, E., Nezamabadi-Pour, H., and Saryazdi, S. (2010). BGSA: binary gravitational search algorithm. Nat. Comput. 9, 727–745. doi: 10.1007/s11047-009-9175-3

Crossref Full Text | Google Scholar

Sanju, P. (2023). Enhancing intrusion detection in IoT systems: a hybrid metaheuristics-deep learning approach with ensemble of recurrent neural networks. J. Eng. Res. 11, 356–361. doi: 10.1016/j.jer.2023.100122

Crossref Full Text | Google Scholar

Sarafrazi, S., Nezamabadi-Pour, H., and Saryazdi, S. (2011). Disruption, a new operator in gravitational search algorithm. Scientia Iranica 18, 539–548. doi: 10.1016/j.scient.2011.04.003

Crossref Full Text | Google Scholar

Sarikaya, A., Kiliç, B. G., and Demirci, M. (2023). RAIDS: Robust autoencoder-based intrusion detection system model against adversarial attacks. Comput. Secur. 135:103483. doi: 10.1016/j.cose.2023.103483

Crossref Full Text | Google Scholar

Sathish, N., and Valarmathi, K. (2022). Detection of intrusion behavior in cloud applications using Pearson's chi-squared distribution and decision tree classifiers. Pattern Recognit. Lett. 162, 15–21. doi: 10.1016/j.patrec.2022.08.008

Crossref Full Text | Google Scholar

Sethi, K., Madhav, Y. V., Kumar, R., and Bera, P. (2021). Attention based multi-agent intrusion detection systems using reinforcement learning. J. Inf. Secur. Appl. 61:102923. doi: 10.1016/j.jisa.2021.102923

Crossref Full Text | Google Scholar

Song, D., Yuan, X. Y., Li, Q. L., Zhang, J., Sun, M. F., Fu, X., et al. (2023). Intrusion detection model using gene expression programming to optimize parameters of convolutional neural network for energy internet. Appl. Soft Comput. 134:109960. doi: 10.1016/j.asoc.2022.109960

Crossref Full Text | Google Scholar

Tavallaee, M., Bagheri, E., Lu, W., and Ghorbani, A. A. (2009). “A detailed analysis of the KDD CUP 99 data set,” in 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications (Piscataway, NJ: IEEE), 1–6. doi: 10.1109/CISDA.2009.5356528

Crossref Full Text | Google Scholar

Vadigi, S., Sethi, K., Mohanty, D., Das, S. P., and Bera, P. (2023). Federated reinforcement learning based intrusion detection system using dynamic attention mechanism. J. Inf. Secur. Appl. 78:103608. doi: 10.1016/j.jisa.2023.103608

Crossref Full Text | Google Scholar

Vinayakumar, R., Alazab, M., Soman, K. P., Poornachandran, P., Al-Nemrat, A., and Venkatraman, S. (2019). Deep learning approach for intelligent intrusion detection system. IEEE Access 7, 41525–41550. doi: 10.1109/ACCESS.2019.2895334

Crossref Full Text | Google Scholar

Wang, H. W., Gu, J., and Wang, S. S. (2017). An effective intrusion detection framework based on SVM with feature augmentation. Knowl. Based Syst. 136, 130–139. doi: 10.1016/j.knosys.2017.09.014

Crossref Full Text | Google Scholar

Wang, Q., Jiang, H., Ren, J., Liu, H., Wang, X., and Zhang, B. (2024). An intrusion detection algorithm based on joint symmetric uncertainty and hyperparameter optimized fusion neural network. Expert Syst. Appl. 244:123014. doi: 10.1016/j.eswa.2023.123014

Crossref Full Text | Google Scholar

Xie, J., Song, Z., Li, Y., Zhang, Y., Hong, Y., Zhan, J., et al. (2018). A survey on machine learning-based mobile big data analysis: challenges and applications. Wireless Commun. Mobile Comput. 2018, 1–19. doi: 10.1155/2018/8738613

Crossref Full Text | Google Scholar

Yao, X., Liu, Y., and Lin, G. (1999). Evolutionary programming made faster. IEEE Trans. Evolut. Comput. 3, 82–102. doi: 10.1109/4235.771163

Crossref Full Text | Google Scholar

Zhang, W. A., Miao, Y., Wu, Q., Yu, L., and Shi, X. (2020). Intrusion detection of industrial control system based on double-layer one-class support vector machine. IFAC-PapersOnLine 53, 2513–2518. doi: 10.1016/j.ifacol.2020.12.226

Crossref Full Text | Google Scholar

Zhu, Y. Y., Liang, Y. W., Chen, Z. Y., and Ming, Z. (2017). An improved NSGA-III algorithm for feature selection used in intrusion detection. Knowl. Based Syst. 116, 74–85. doi: 10.1016/j.knosys.2016.10.030

Crossref Full Text | Google Scholar