WIMUSim: simulating realistic variabilities in wearable IMUs for human activity recognition

Introduction: Physics simulation has emerged as a promising approach to generate virtual Inertial Measurement Unit (IMU) data, offering a solution to reduce the extensive cost and effort of real-world data collection. However, the fidelity of virtual IMU depends heavily on the quality of the source motion data, which varies with motion capture setups. We hypothesize that improving virtual IMU fidelity is crucial to fully harness the potential of physics simulation for virtual IMU data generation in training Human Activity Recognition (HAR) models.

Method: To investigate this, we introduce WIMUSim, a 6-axis wearable IMU simulation framework designed to accurately parameterize real IMU properties when deployed on people. WIMUSim models IMUs in wearable sensing using four key parameters: Body (skeletal model), Dynamics (movement patterns), Placement (device positioning), and Hardware (IMU characteristics). Using these parameters, WIMUSim simulates virtual IMU through differentiable vector manipulations and quaternion rotations. A key novelty enabled by this approach is the identification of WIMUSim parameters using recorded real IMU data through gradient descent-based optimization, starting from an initial estimate. This process enhances the fidelity of the virtual IMU by optimizing the parameters to closely mimic the recorded IMU data. Adjusting these identified parameters allows us to introduce physically plausible variabilities.

Results: Our fidelity assessment demonstrates that WIMUSim accurately replicates real IMU data with optimized parameters and realistically simulates changes in sensor placement. Evaluations using exercise and locomotion activity datasets confirm that models trained with optimized virtual IMU data perform comparably to those trained with real IMU data. Moreover, we demonstrate the use of WIMUSim for data augmentation through two approaches: Comprehensive Parameter Mixing, which enhances data diversity by varying parameter combinations across subjects, outperforming models trained with real and non-optimized virtual IMU data by 4–10 percentage points (pp); and Personalized Dataset Generation, which customizes augmented datasets to individual user profiles, resulting in average accuracy improvements of 4 pp, with gains exceeding 10 pp for certain subjects.

Discussion: These results underscore the benefit of high-fidelity virtual IMU data and WIMUSim's utility in developing effective data generation strategies, alleviating the challenge of data scarcity in sensor-based HAR.

1 Introduction

The field of Human Activity Recognition (HAR) from wearable Inertial Measurement Units (IMUs) has experienced significant growth, driven by diverse applications across healthcare, fitness, and entertainment (Lara and Labrador, 2012; Liu et al., 2021). A challenge in this domain is the scarcity of high-quality ground truth data, which is particularly pronounced when using deep learning-based approaches (Plötz and Guan, 2018; Nweke et al., 2018). This challenge is compounded by the inherent variabilities in real-world usage, including differences in sensor placements, individual wearer body morphology, and hardware discrepancies (Roggen et al., 2010; Banos et al., 2014; Stisen et al., 2015; Mathur et al., 2018; Khaked et al., 2023). Collecting annotated datasets that encompass these variabilities is costly and time-consuming, requiring extensive participation from human subjects and laborious data annotation (Bulling et al., 2014; Plötz and Guan, 2018). As a result, datasets confined to controlled experimental conditions generally fail to capture the broad spectrum of real-world variabilities, making it difficult to create models that generalize well across diverse real-world settings (Garcia-Gonzalez et al., 2020, 2023). This highlights the need for more efficient and scalable data collection approaches.

Physics-based virtual IMU simulation has emerged as a promising approach to alleviate the cost of data collection by leveraging the vast amount of motion data available from other modalities (Kwon et al., 2020; Xia and Sugiura, 2022, 2023; Leng et al., 2023). Additionally, physics simulations can incorporate various realistic variabilities, including different sensor placements, diverse body morphologies, and varying hardware characteristics. Existing virtual IMU simulation methods generate synthetic IMU data using motion information from sources like motion capture systems or videos. However, the fidelity of the generated IMU data is fundamentally constrained by the quality of the source motion data. Lower fidelity introduces a domain shift between real and virtual IMU data, limiting the ability of HAR models trained with virtual IMU data to generalize to real-world scenarios. We hypothesize that improving the fidelity of virtual IMU data can significantly enhance its effectiveness in training HAR models, enabling better generalization by fully leveraging the ability of physics simulations to model realistic variabilities.

In this paper, we demonstrate that minimizing discrepancies between real and virtual IMU data is crucial for fully harnessing the potential of physics simulation in flexibly emulating real-world variabilities and generating virtual IMU data for training HAR models. For this purpose, we introduce WIMUSim, a wearable IMU simulation framework, which is designed to accurately parameterize real-world IMU properties when deployed on people and simulate realistic variabilities through physics simulation, thereby enhancing data collection efficiency and reducing the need for extensive data collection.

WIMUSim models wearable IMU data using four key parameters: Body (B), Dynamics (D), Placement (P), and Hardware (H). These parameters are designed to reflect the real-world variabilities that affect wearable IMU data, offering an intuitive and physically plausible wearable IMU simulation framework. B represents the human skeletal model as a directed tree, detailing each joint's position relative to its parent joint at the default posture. D describes the temporal evolution of body movement, with a sequence of rotation quaternions for each joint specifying relative orientation to its parent joint and a sequence of 3D vectors for the body's translation. P specifies each virtual IMU's position and orientation relative to its parent joint, enabling the simulation of IMU data from any location of the body. H characterizes each IMU's specific behaviors, such as noise levels and sensor biases. Based on these parameters, consisting of 3D vectors and quaternions, WIMUSim generates 6-axis virtual IMU data through differential vector manipulations and quaternion rotations. This design allows us to identify the parameters of real IMUs as they are deployed in specific wearable sensing scenarios using the B, D, P, and H parameters through gradient descent-based optimization, and introduce realistic variations to the virtual IMU data by varying the parameters around their identified point. Furthermore, WIMUSim is implemented in PyTorch, which enables fast simulation and seamless integration into the model training process, allowing for online data generation during the training of deep learning models.

WIMUSim is designed to be used as follows:

1. Data collection: prepare real IMU data and preliminary WIMUSim parameters. The B and D can be derived from various motion capture technologies, including optical-based, IMU-based, or video-based techniques. The P is manually specified to indicate where the real IMU is placed. The H can be obtained from device specifications or data collected at stationary positions. At this point, these parameters can be rough estimates.

2. High fidelity parameter identification: optimize these preliminary parameters by minimizing the error between the real and virtual IMU data to ensure that WIMUSim accurately parametrizes the real IMU data. This optimization is performed using a gradient descent-based method to minimize the error between the real and virtual IMU data.

3. Realistic parameter transformation: adjust the parameters around their identified points to introduce physically plausible variabilities, generating virtual IMU data that reflects a broad range of realistic conditions. This allows for the creation of diverse and enriched datasets, enhancing the training of HAR models without requiring extensive new data collection.

To illustrate the utility of WIMUSim, we present two use cases: (1) Comprehensive Parameter Mixing (CPM): This approach is designed to simulate a broad spectrum of possible variabilities by changing the combination of the WIMUSim parameter sets obtained from different subjects' data, aiming to enhance the diversity of the dataset. (2) Personalized Dataset Generation (PDG): This approach is designed to create datasets that are customized to individual profiles by selectively adjusting simulation parameters, thereby enhancing the personalization of HAR models.

We demonstrate the ability of WIMUSim to accurately parameterize real wearable IMU data and its effectiveness in improving HAR model training through a series of experiments using an in-house dataset and two public datasets, REALDISP and REALWORLD. Our evaluations are structured around two principal objectives: (1) Assessing the fidelity of WIMUSim in accurately replicating real IMU data and (2) Demonstrating the effectiveness of virtual IMU data generated with WIMUSim in enhancing HAR model performance in real-world scenarios.

The primary contributions of this work are as follows:

1. Review of virtual IMU simulation in HAR: we review virtual IMU simulation approaches in the context of wearable IMU-based HAR, examining their potential to address the data scarcity issue. We discuss the advantages and limitations of existing methods, highlighting the unique opportunities presented by virtual IMU simulation (Section 2).

2. Introduction of WIMUSim: we present WIMUSim: a wearable IMU simulation framework that simulates wearable IMU data based on B, D, P, and H parameters. Its implementation in PyTorch enables real-time data generation and seamless integration into deep learning model training pipelines. The implementation of WIMUSim is available at https://github.com/STRCWearlab/WIMUSim.git (Section 3).

3. Gradient descent-based parameter identification method: we design a gradient descent-based optimization method to identify WIMUSim parameters of real IMU data to closely align virtual IMU data with real IMU data, which enhances the realism of the generated virtual IMU data (Section 4).

4. Evaluation of the fidelity of virtual IMU data: we evaluate the fidelity of virtual IMU data generated by WIMUSim by assessing how accurately WIMUSim can parameterize real IMU data and how effectively modifications to the WIMUSim parameters reflect real-world changes in the wearable IMU data. This evaluation demonstrates the close alignment between the real and virtual IMU data (Section 6.1).

5. Evaluation of the effectiveness of WIMUSim in real-world scenarios: we evaluate the effectiveness of WIMUSim in improving HAR model performance in real-world scenarios. We test CPM to assess its potential to alleviate the need for extensive real-world data collection while enhancing model generalization to real-world variabilities. We also explore PDG for fine-tuning personalized models. These evaluations demonstrate significant enhancements in HAR model performance, highlighting the utility of WIMUSim (Section 6.2).

2 Related work

Virtual IMU generation using physics simulation typically involves placing virtual IMUs on an animated 3D human body model obtained from motion capture systems. Geometric transformations are then applied to the trajectories of these virtual IMUs to simulate inertial measurements (e.g., acceleration, angular velocity, and sometimes including magnetic field) that would be observed at the specified positions in the real world (Young et al., 2011; Asare et al., 2013; Lago et al., 2019; Pellatt et al., 2021). The flexibility of physics-based simulations to modify various settings enables researchers to conduct rigorous experiments, allowing them to explore and evaluate different scenarios in a controlled virtual environment, such as testing different configurations and optimizing sensor placements (Xia and Sugiura, 2021).

With advancements in pose estimation techniques in the vision domain, it has become possible to extract 2D and 3D poses from more easily accessible RGB videos, whereas traditionally, obtaining high-quality human motion data required specialized setups, such as optical motion capture, IMU-based motion capture, or depth cameras. Consequently, researchers have started leveraging the vast amount of human motion data available in RGB videos to address the scarcity of large labeled datasets by simulating virtual IMUs (Kwon et al., 2020, 2021; Rey et al., 2019, 2021).

To further enhance the diversity of virtual IMU data, Xia and Sugiura (2022) proposed a simulation-based data augmentation method using a virtual sensor module in Unity that utilizes spring joints. This module is designed to introduce variations, especially in acceleration in the vertical direction of the body, aiming to mimic accelerometer readings from the dynamic vertical movements typical of aerobic exercises. Moreover, Leng et al. (2023) have explored integrating generative models into virtual IMU simulation, leveraging T2M-GPT (Zhang et al., 2023), a model that generates various 3D human motion sequences from textual descriptions, to produce virtual IMU data with more motion variations.

However, a significant discrepancy still exists between real and virtual IMU data, as shown in previous studies (Kwon et al., 2020; Leng et al., 2023) where HAR models trained exclusively on virtual IMU data perform 10 to 20 percentage points lower—particularly when using deep learning models—compared to baselines trained on real IMU data. To address this gap, researchers have explored various approaches.

For instance, several works have explored leveraging shared features between real and virtual IMU data to train traditional machine learning models, improving performance despite the discrepancy between real and virtual IMU (Kang et al., 2019; Xia and Sugiura, 2022). Additionally, many studies incorporate virtual IMU data into their pipelines, either by mixing it with real IMU data or by pre-training on virtual data before fine-tuning with real data (Kwon et al., 2020; Rey et al., 2021; Leng et al., 2023). Notably, Multi³Net (Fortes Rey et al., 2024) adopts a multi-modal, multi-task, and multi-sensor framework to learn a shared latent representation across video descriptions, pose data, and synthetic IMU signals, addressing the limitations of poor-quality virtual IMU data. The pre-trained model is then fine-tuned with real IMU data, demonstrating improved performance, particularly for fine-grained activity recognition involving wrist-worn IMUs.

To enhance the fidelity of virtual IMU, CROMOSim (Hao et al., 2022) employs a BiLSTM-based model trained to map imperfect motion trajectories (e.g., from motion capture or video data) to realistic IMU readings. Similarly, Vi2IMU (Santhalingam et al., 2023) improves the fidelity of wrist-worn IMU data, specifically for American Sign Language (ASL) recognition, by incorporating two deep learning models into the simulation process: the first estimates wrist orientation by analyzing hand and arm joint positions extracted from pose estimation; then, the second predicts accelerometer and gyroscope signals by combining the estimated wrist orientation with motion dynamics specific to ASL gestures. Both methods demonstrate improved performance on HAR or ASL classification tasks, highlighting the importance of fidelity improvements in enhancing downstream applications.

These approaches provide promising solutions to address the scarcity of training data for wearable IMU-based HAR. However, little research has explored how improving the fidelity of virtual IMU data can fully leverage physics simulations to flexibly emulate real-world variations and generate virtual IMU data for training HAR models. To explore this, we introduce WIMUSim. Unlike methods such as CROMOSim and Vi2IMU, which rely on pre-trained deep learning models to deal with the misalignment between real and virtual IMU data, WIMUSim takes a fully analytical approach. It utilizes concurrently recorded real IMU and motion data to identify the B, D, P, and H parameters through gradient-descent optimization. This approach enables the accurate replication of real IMU data within the simulation environment while introducing realistic variability by adjusting the identified parameters.

3 WIMUSim framework

In this section, we explain how WIMUSim models and simulates 6-axis wearable IMUs using the Body (B), Dynamics (D), Placement (P), and Hardware (H) parameters:

• Body (B) defines the structural characteristics of the human body model, specifying the length of each limb to construct a skeletal representation as a directed tree. These measurements can be manually entered or derived from anthropometric databases (Gordon et al., 2014; OpenErg.com, 2020) for default values.

• Dynamics (D) represents the temporal sequence of movements using rotation quaternions for each joint, depicting their orientation over time relative to parent joints, alongside a sequence of 3D vectors for overall body translation. This can be extracted from motion capture data, whether sourced from IMUs or optical systems or analyzed from video sequences.

• Placement (P) specifies the position and orientation of the virtual IMUs relative to their associated body joints. This parameter is specified manually based on expected sensor placement in the target environment, but it may also be varied to simulate different sensor placement scenarios.

• Hardware (H) models each IMU's specific operational characteristics, such as sensor biases and noise levels. By incorporating these parameters, WIMUSim ensures that the generated virtual IMU data accurately reflects real-world IMU performances. These parameters can be manually specified based on device specifications.

The simulation of wearable IMUs in WIMUSim is fundamentally encapsulated in the following function: ${\widehat{X}}_{IMU}=f(B,D,P,H)$, where ${\widehat{X}}_{IMU}$ represents the virtual IMU data simulated based on the parameters B, D, P, and H. Figure 1 provides a visualization of the simulation environment to provide an overview of the WIMUSim simulation framework. The subsequent subsections will detail how each parameter—B, D, P, and H—contribute to the wearable IMU data simulation step by step as follows: Section 3.1 Animate the humanoid model defined by B using D, Section 3.2 Determine IMU position and orientation using P, and Section 3.3 Simulate IMU data from the determined sequence of IMU's positions, orientations, and H.

Figure 1

Figure 1. Visualization of WIMUSim's simulation environment, showcasing a humanoid model equipped with IMUs, generated and animated according to the Body, Dynamics, Placement, and Hardware parameters. The graphs on the right display virtual IMU readings from the right lower arm (RLA) and left lower arm (LLA).

3.1 Animate the humanoid model defined by B using D

The Body (B) parameter in WIMUSim captures variations in human physiques through a skeletal model using a tree structure of joints. It outlines the connections between joints, specifying their relative positions when all the joints are aligned to the world frame. By adjusting the B parameter, we can simulate virtual IMU data generated for a variety of humanoid body sizes. Formally, the skeletal tree is defined as B = (J, E), where J is the set of joints, and E is the set of edges. Each edge e ∈ E corresponds to a parent-child pair (j_p, j_c), where j_c, j_p ∈ J. For each joint pair, the relative position $B_{rp}^{(j_p,j_c)}$ is specified as a 3D vector from the parent joint j_p to its child j_c. Also, the range of motion (ROM) can be specified for each of the movable joints. Figure 2 visualizes this skeletal structure, illustrating the tree structure and the role of each joint within the system. This configuration can be customized to meet specific research needs or to reflect the granularity of available motion data. For example, additional joints may be added between the pelvis and the clavicles to reflect more detailed upper-body movements.

Figure 2

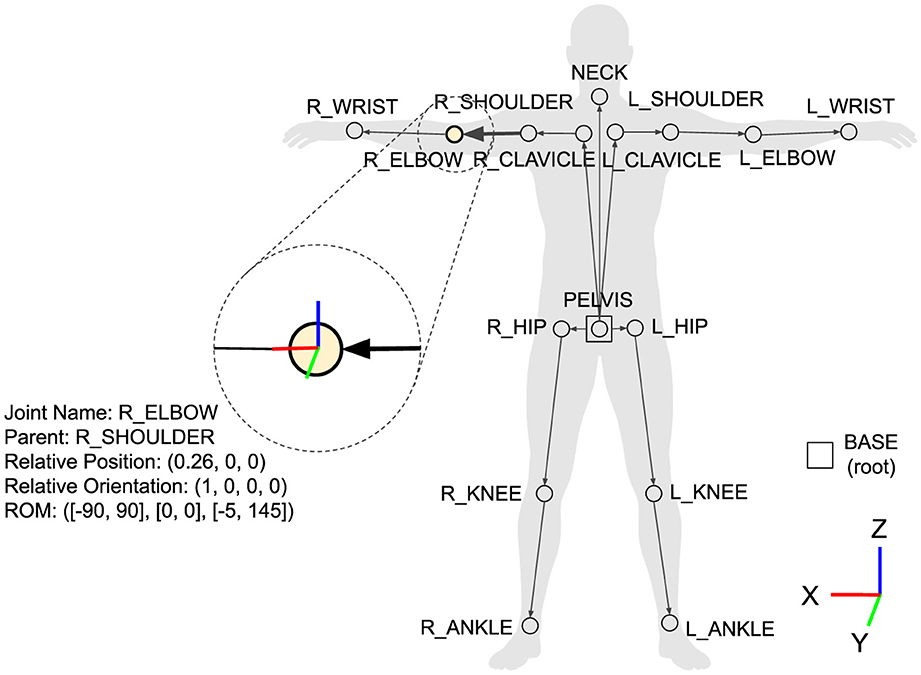
Figure 2. Example of the B parameter configuration, illustrating the skeletal tree structure. Each node represents a joint, detailing its relative position and range of motion (ROM) relative to its parent. All joints are aligned with the world frame, representing their default positions.

The Dynamics (D) parameter in WIMUSim is used to animate the skeletal model defined by the B parameter, simulating the temporal dynamics of human movement. For each movable joint j ∈ J, D^j specifies a series of quaternions representing the orientation of joint j over time $\left\{q_0^j,q_1^j,\dots ,q_{\left|T\right|-1}^j\right\}$, each relative to its parent joint's orientation, where |T| is the total number of time steps. Additionally, for the BASE joint, a distinct component $D_{(xyz)}^{BASE}$ provides a sequence of 3D vectors that specify the translational movement of the humanoid within the simulation environment.

For each joint j ∈ J, WIMUSim computes the position $p_t^j$ and orientation $q_t^j$ at every timestep t, starting from the root (BASE) joint and progressing through each child joint:

Position calculation at time t: The position of a child joint $p_t^{j^c}$ at time t is calculated by applying the orientation of the parent joint $q_t^{j_p}$ to the relative position vector defined in B, and then adding it to the parent joint's position:

$\begin{array}{ll}{p}_t^{j_c}=p_t^{j_p}+q_t^{j_p}{B}_{rp}^{(j_p,j_c)}{q_t^{j_p}}^{-1}& (1)\end{array}$

Note that the position of the BASE $p_t^{BASE}$ joint is directly defined by $D_{t,(xyz)}^{BASE}$, accommodating for translational movements within the simulation environment.

Orientation calculation at time t: Each child joint's orientation $q_t^{j_c}$ at time t is determined by applying its relative orientation $D_t^{j_c}$ to the current orientation of its parent joint $q_t^{j_p}$:

$\begin{array}{ll}{q}_t^{j_c}=q_t^{j_p}{D}_t^{j_c}& (2)\end{array}$

By applying these calculations to each joint in the body model, we now have the position and orientation for each joint at each time step t to animate the body. This animation process transforms the static posture derived from the B parameters into a dynamic representation of human motion, integrating the temporal aspects of movement as defined by the D parameters.

3.2 Determine IMU position and orientation with P

The Placement (P) parameter determines the positioning of IMUs on the human body. For each IMU u_i placed on the humanoid associated with a parent joint j_p ∈ J, $P_{rp}^{(j_p,u_i)}$ and $P_{ro}^{(j_p,u_i)}$ specify the IMU's relative position and orientation in 3D vector and orientation quaternion from j_p to u_i, respectively.

The global position of an IMU $p_t^{u_i}$ at time t is determined by transforming its relative position vector $P_{rp}^{(j_p,u_i)}$ using the orientation of its associated parent joint $q_t^{j_p}$. This transformation aligns the relative position vector to the world frame orientation of the parent joint, and then it is added to the world frame position of the parent joint:

$\begin{array}{ll}{p}_t^{u_i}=p_t^{j_p}+q_t^{j_p}{P}_{rp}^{(j_p,u_i)}{q_t^{j_p}}^{-1}& (3)\end{array}$

The global orientation of an IMU u_i at time t is computed by applying its relative orientation $P_{ro}^{(j_p,u_i)}$ to the current world frame orientation of its parent joint $q_t^{j_p}$:

$\begin{array}{ll}{q}_t^{u_i}=q_t^{j_p}{P}_{ro}^{(j_p,u_i)}& (4)\end{array}$

Figure 3 demonstrates a simplified arm model with IMUs placed on the lower arm, showcasing how the B, D, and P parameters determine sequences of IMU positions and orientations over time. This visualization illustrates how these parameters impose reasonable constraints on the IMU's possible trajectories, anchoring the simulation within the physical limits dictated by their attachment to the human body.

Figure 3

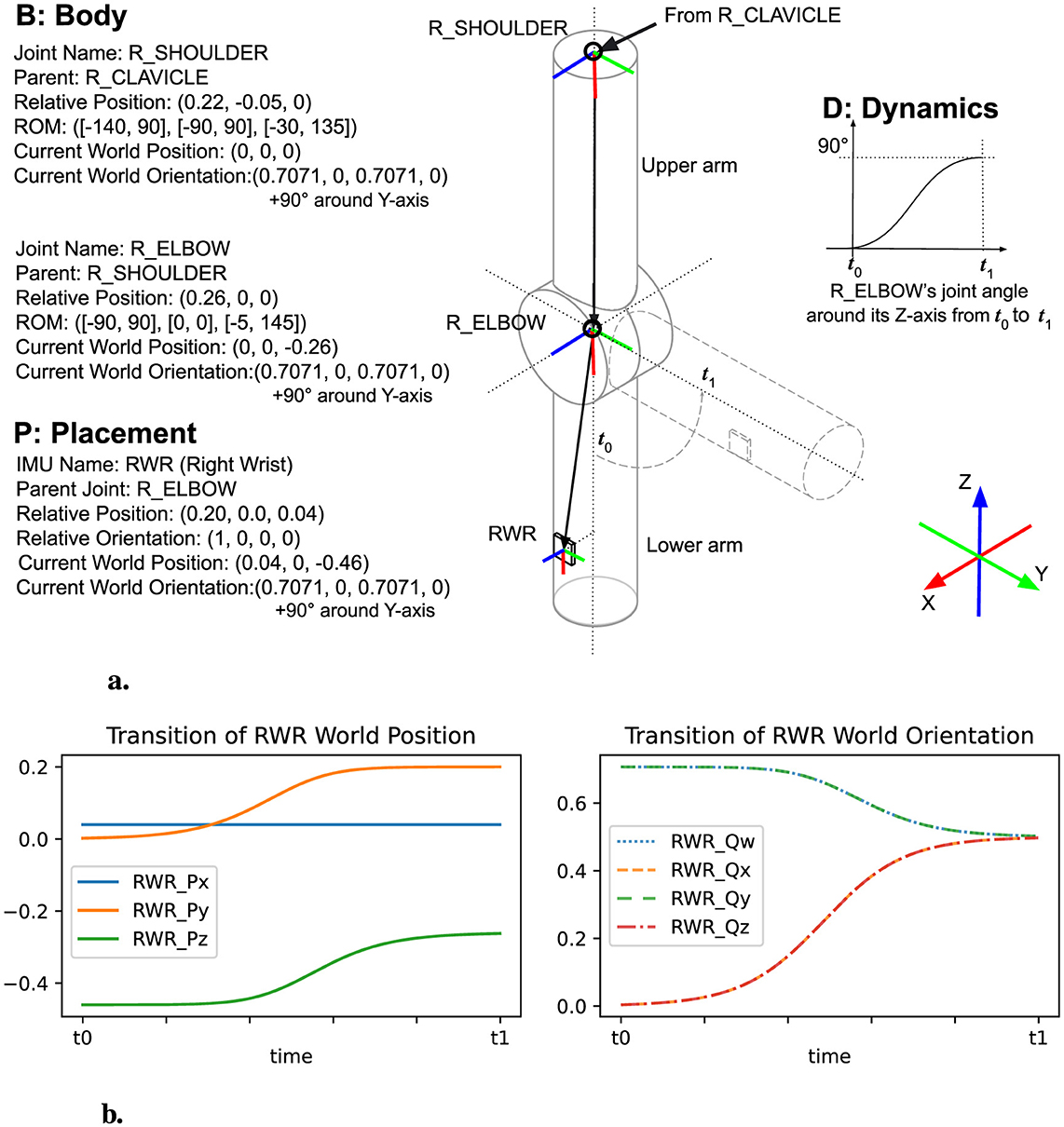
Figure 3. Visualization of IMU position and orientation generation based on B, D, and P parameters. This figure illustrates the simulation of an IMU's position and orientation on a right arm model, assuming the right shoulder joint is positioned at (0, 0, 0) in the world coordinate system, with an orientation of (0.7071, 0, 0.7071, 0) — indicating a rotation of 90 degrees from the default orientation along the Z-axis. (A) Right arm model with an IMU placed on the right wrist, moving the R_ELBOW joint 90 degrees around its Z axis from t₀ to t₁. (B) Transition of RWR's position and orientation.

3.3 Simulate IMU data from position, orientation, and hardware characteristics

The Hardware (H) parameter specifies the specific operational characteristics of IMU sensors. WIMUSim models it through a combination of bias vectors and standard deviations of the noise for each IMU sensor. Specifically, the H parameter includes bias vectors $b_{u_i}^{acc}$ for accelerometers and $b_{u_i}^{gyro}$ for gyroscopes, as well as standard deviations of the Gaussian noise, ${\sigma }_{u_i}^{acc}$ for accelerometers and ${\sigma }_{u_i}^{gyro}$ for gyroscopes, represented as $N(0,{\sigma }_{u_i}^2)$ for each IMU u_i.

WIMUSim generates virtual 6-axis IMU data (3-axis accelerometer and 3-axis gyroscope) for each IMU based on the sequence of positions and orientations determined by B, D, and P, with the H parameter introducing sensor-specific variations. The resulting IMU measurements are adjusted according to the specified biases and noise levels for each device, as detailed in the following:

Accelerometer simulation: the accelerometer simulation captures both linear and gravitational acceleration. The linear acceleration of an IMU u_i in the world frame, $a_t^{u_i,w}$, is computed as the second derivative of its position $p^{u_i}$:

$\begin{array}{ll}{a}_t^{u_i,w}=\frac{d^2{p}^{u_i}}{d{t}^2}& (5)\end{array}$

This is then adjusted for the IMU's local frame, factoring in gravitational acceleration g and the IMU's orientation, as well as the hardware-specific parameters—bias $b_{acc}^{u_i}$ and Gaussian noise $N(0,{{\sigma }_{acc}^{u_i}}^2)$:

$\begin{array}{ll}{a}_t^{u_i}={q_t^{u_i}}^{-1}(a_t^{u_i,w}-g)q_t^{u_i}+b_{acc}^{u_i}+N(0,{{\sigma }_{acc}^{u_i}}^2)& (6)\end{array}$

Gyroscope simulation: the gyroscope simulation focuses on measuring angular velocity. For each IMU u_i, the angular velocity ${\omega }_t^{u_i,w}$ in the world coordinate system is calculated based on the change in orientation from $q_{t-1}^{u_i}$ to $q_t^{u_i}$ over time:

$\begin{array}{ll}{\omega }_t^{u_i,w}=\frac{d{q}^{u_i}}{dt}=\frac{q_t^{u_i}{q_{t-1}^{u_i}}^{-1}}{T_t-T_{t-1}}& (7)\end{array}$

This angular velocity is then transformed to the IMU's local frame, and adjusted for the gyroscope's bias $b_{gyro}^{u_i}$ and Gaussian noise $N(0,{{\sigma }_{gyro}^{u_i}}^2)$:

$\begin{array}{ll}{\omega }_t^{u_i}={q_t^{u_i}}^{-1}{\omega }_t^{u_i,w}{q}_t^{u_i}+b_{gyro}^{u_i}+N(0,{{\sigma }_{gyro}^{u_i}}^2)& (8)\end{array}$

By incorporating these hardware-specific parameters, WIMUSim aims to model the real-world imperfections and variability observed in real IMUs, providing a flexible foundation for generating virtual IMU data that reflects real-world conditions.

While WIMUSim enables a flexible simulation of wearable IMUs using the parameters B, D, P, and H, these parameters must be carefully chosen to ensure high fidelity of virtual IMU data. In the next section, we explain how WIMUSim leverages its differentiable simulation process to iteratively refine these parameters, minimizing the discrepancy between virtual and real IMU data through gradient descent.

4 High fidelity parameter identification

WIMUSim simulates 6-axis wearable IMUs through differential vector manipulations and quaternion rotations. This simulation process is fully differentiable across all four key parameters: B, D, P, and H. By leveraging this differentiability, we propose a high-fidelity wearable IMU parameter identification method that refines these parameters through gradient descent optimization using real IMU and motion data collected concurrently. Initial estimates for the B and D parameters can be derived from motion capture methods, including optical-based, IMU-based, or video-based techniques, while P is manually specified based on the target sensor placement, and H is obtained from device specifications or stationary data collection. Although these initial parameters may be rough estimates, they are to be optimized using real-world measurements to minimize the discrepancy between real and virtual IMU data. Through gradient descent, WIMUSim ensures that the generated virtual IMU data ${\widehat{X}}_{\mathrm{\text{IMU}}}=f(B,D,P,H)$ closely matches real IMU measurements X_IMU.

To achieve this, we design a loss function that minimizes the error between virtual and real IMU data while maintaining physical plausibility by incorporating regularization terms specific to each WIMUSim parameter. The loss function used in this optimization process is defined as follows:

$\begin{array}{l}{L}_{\text{total}}=L_{\text{RMSE}}+{\lambda }_1{L}_{\text{D-ROM}}+{\lambda }_2{L}_{\text{B-range}}+{\lambda }_3{L}_{\text{P-range}}+{\lambda }_4{L}_{\text{H-range}}\\ +{\lambda }_5{L}_{\text{B-sym}}+{\lambda }_6{L}_{\text{D-temp}}+{\lambda }_7{L}_{\text{H-dist}}& (9)\end{array}$

The following details each component within this combined loss function.

4.1 RMSE loss

The primary objective is to minimize the discrepancy between the simulated IMU data and the target real IMU data. We use the RMSE as our metric of choice to quantify this discrepancy, penalizing larger errors more than smaller ones. The RMSE loss is defined as:

$\begin{array}{ll}{L}_{\text{RMSE}}=\sqrt{\frac{1}{\left|T\right|}{\displaystyle \sum _{i\in \left\{x,y,z\right\}}}{\displaystyle \sum _{t\in T}}\left[\alpha {(x_{t,i}^{\text{Acc}}-{\widehat{x}}_{t,i}^{\text{Acc}})}^2+\beta {(x_{t,i}^{\text{Gyro}}-{\widehat{x}}_{t,i}^{\text{Gyro}})}^2\right]}& (10)\end{array}$

where $x_{t,i}^{\mathrm{\text{Acc}}}$ and $x_{t,i}^{\mathrm{\text{Gyro}}}$ represent real IMU acceleration and gyroscopic data components along the axis i, ${\widehat{x}}_{t,i}^{\mathrm{\text{Acc}}}$ and ${\widehat{x}}_{t,i}^{\mathrm{\text{Gyro}}}$ represent their simulated IMU data components along the axis i, and α and β are weighting coefficients to account for the different scales of acceleration and gyroscopic data. |T| is the total number of time steps.

While the RMSE loss quantifies the discrepancy between simulated and real IMU data, optimizing WIMUSim parameters based solely on minimizing RMSE could result in unrealistic parameters. Therefore, the RMSE loss is supplemented with regularization terms designed to enforce physical realism and ensure that the optimized parameters remain reasonable within the context of wearable IMU simulations.

4.2 Parameter range regularization

Parameter range regularization is designed to ensure that the WIMUSim parameters stay within realistic boundaries. By integrating these regularization terms into the loss function, we guide the parameter tuning process to respect pre-defined limits, allowing us to inject prior knowledge about these parameters and making the simulated data more relevant to specific real-world scenarios.

Range of motion regularization: ROM regularization is calculated for each joint j within the set J, ensuring that the joint orientations in D remain within the specified range of motion (ROM) defined in the B parameter. Since the ROMs are defined in terms of Euler angles, joint orientations, originally represented as quaternions, are converted to Euler angles for this calculation. The ROM regularization term is formulated as follows:

$\begin{array}{l}{L}_{\text{ROM}}=\frac{1}{\left|T\right|}{\displaystyle {\sum }_{j\in J}{\displaystyle {\sum }_{i\in \{x,y,z\}}{\displaystyle {\sum }_{t\in T}[\max (0,\text{quat2euler}(D_t^{(j)},i)}}}\\ -B_{\text{max},i}^{(j)})+\max (0,B_{\text{min},i}^{(j)}-\text{quat2euler}(D_t^{(j)},i))]& (11)\end{array}$

where J is the set of joints; i denotes the individual x, y, andz component of the Euler angles; T represents the time steps; $\mathrm{\text{quat2euler}}(D_t^{(j)},i)$ represents the angle of joint j around axis i at time t, converted to Euler angles from its original quaternion representation; $B_{\mathrm{\text{max}},i}^{(j)}$ and $B_{\mathrm{\text{min}},i}^{(j)}$ are the maximum and minimum limits for each dimension of joint j, defining the joint's ROM.

Body, placement and hardware range regularization: similar to the ROM regularization, L_B-range, L_P-range, and L_H-range penalize deviations of the B, P, and H parameters outside their predefined limits. This regularization ensures that these parameters remain within realistic and physically plausible ranges.

For example, L_B-range penalizes deviations of each body parameter b ∈ B beyond its allowed range as follows:

$\begin{array}{ll}{L}_{\text{B-range}}={\displaystyle \sum _{b\in B}}{\displaystyle \sum _{i\in \left\{x,y,z\right\}}}\left[max(0,b_i-b_{\text{max},i})+max(0,b_{\text{min},i}-b_i)\right]& (12)\end{array}$

where b_i is the i-th component of the B parameter's relative position vector b, and b_{max, i} and b_{min, i} denote the upper and lower limits for each component, respectively.

Similarly, L_P-range penalizes relative position vectors and relative orientation quaternions that fall outside predefined limits, and L_H-range penalizes hardware-specific parameters (e.g., bias and standard deviation terms) outside of their expected operational range.

4.3 Symmetry regularization

In the WIMUSim framework, B parameters are defined independently for each side to account for potential misalignments between the left and right sides of the body. Although human limbs are generally similar in length, variations do occur, influenced by both genetic and behavioral factors (Auerbach and Ruff, 2006). While acknowledging these natural differences, it is also important to prevent the optimization process from exaggerating limb asymmetry beyond realistic and functional boundaries. This regularization term is thus designed to accommodate possible bilateral asymmetries while ensuring that their divergence remains within realistic limits. The symmetry regularization term is formulated as follows:

$\begin{array}{ll}{L}_{\text{B-sym}}={\displaystyle \sum _{(j_R,j_L)\in J_{\text{pair}}}}||B_{rp}^{(j_R)}-\text{mirror}(B_{rp}^{(j_L)})||& (13)\end{array}$

where J_pair is the set of key pairs representing corresponding points on the right and left sides of the body (e.g., right and left shoulders); j_R and j_L represent keys in the B parameter corresponding to a joint on the right and left side of the body, respectively; $B_{rp}^{(j)}$ denotes the relative position vector of the joint j in the B parameter; the function $\mathrm{\text{mirror}}(B_{rp}^{(j_L)})$ mirrors the left side position $B_{rp}^{(j_L)}$ across the sagittal plane to compare it with its right-side counterpart.

4.4 Temporal regularization

Temporal regularization smooths changes in joint orientations and humanoid translations over time, mitigating rapid and unrealistic fluctuations in the D parameter. This is formulated as:

$\begin{array}{ll}{L}_{\text{D-temp}}=\frac{1}{\left|T\right|}{\displaystyle \sum _{j\in J}}{\displaystyle \sum _{t\in T}}||{\Delta }^n{D}_t^{(j)}{||}^2& (14)\end{array}$

where J is the set of joints; T represents the time steps and |T| is the number of time steps; Δⁿ represents the n-th difference operation over time; $D_t^{(j)}$ indicates the joint parameters (either orientation or translation) of joint j at time t; n is the order of the difference (e.g., n = 3 for a third-order difference to target the smoothness of acceleration changes, avoiding jerky or abrupt transitions in joint movements), which specifies how many time steps are considered for calculating the change in joint parameters.

4.5 Noise distribution regularization

Noise distribution regularization is designed to estimate the noise characteristics of the target IMU data accurately. During parameter identification, we explicitly model the noise in the acceleration and gyroscopic signals as temporal noise matrices of shape [T, 3], where T represents the number of time steps, matching the shape of the target IMU data. These matrices are optimized to meet the following two conditions for each channel (x, y, and z): (1) the noise should follow a Gaussian distribution N(0, σ²) with zero mean and standard deviation within a predefined range; and (2) the noise should be uniformly distributed across all frequencies, reflecting the properties of random white noise typically found in real IMU sensors. The noise distribution regularization term is formulated as follows:

$\begin{array}{l}{L}_{\text{H-dist}}={\displaystyle {\sum }_{u\in \text{IMUs}}}{\displaystyle {\sum }_{s\in \left\{\text{Acc},\text{Gyro}\right\}}}\\ {\displaystyle {\sum }_{c\in \left\{x,y,z\right\}}}\left[||{\mu }_{\text{noise}}^{u,s,c}{||}^2+\frac{\text{std}(\mathcal{F}({\text{noise}}^{u,s,c}))}{\text{mean}(\mathcal{F}({\text{noise}}^{u,s,c}))}\right]& (15)\end{array}$

where ${\mu }_{\mathrm{\text{noise}}}^{u,s,c}$ is the mean of the noise matrices for IMU u, sensor type s (either accelerometer or gyroscope), and channel c (x, y, or z), enforced to remain close to zero, ensuring zero-mean noise for each channel. $\mathcal{F}({\mathrm{\text{noise}}}^{u,s,c})$ represents the Fourier transform of the noise vector for each IMU, sensor type, and channel, used to evaluate the spread of the noise frequencies. $\mathrm{\text{std}}(\mathcal{F}({\mathrm{\text{noise}}}^{u,s,c}))$ is the standard deviation of the energy of the noise's frequency components, and $\mathrm{\text{mean}}(\mathcal{F}({\mathrm{\text{noise}}}^{u,s,c}))$ is the mean energy of these frequency components. The ratio $\frac{\mathrm{\text{std}}(\mathcal{F}({\mathrm{\text{noise}}}^{u,s,c}))}{\mathrm{\text{mean}}(\mathcal{F}({\mathrm{\text{noise}}}^{u,s,c}))}$ promotes uniform distribution across all frequencies for each channel, encouraging the extracted noise to resemble a random white noise pattern.

After identifying these noise characteristics, only the estimated standard deviations of the learned noise matrices are used in the generation phase to produce realistic random noise N(0, σ²) during virtual IMU generation.

5 Realistic parameter transformation

Here, we illustrate how transforming WIMUSim parameters can introduce realistic variability into the simulated IMU data. By adjusting the parameters identified by the high-fidelity parameter identification, we generate virtual IMU data that reflects a broad range of realistic conditions. We present two use cases for applying realistic parameter transformation: Comprehensive Parameter Mixing (CPM) and Personalized Dataset Generation (PDG). These approaches showcase the flexibility and practicality of WIMUSim's parametric approach in generating diverse and enriched datasets, supporting both extensive data augmentation for broad generalization and fine-tuned personalization for subject-specific model refinement.

5.1 Comprehensive parameter mixing

CPM expands the dataset's diversity by changing the combinations of existing WIMUSim parameter sets—B, D, P, and H—collected from different subjects to augment the dataset without the need for complex manual intervention. This approach effectively introduces variations in body morphology, movement patterns, sensor placements, and hardware characteristics, generating diverse datasets aimed at improving the robustness of HAR models in real-world scenarios.

For example, CPM enables the simulation of scenarios where one subject's body size is combined with another's activity dynamics, a third subject's sensor placement preferences, and a fourth subject's hardware characteristics. Consider a dataset comprising n subjects, each having unique sets of WIMUSim parameters: B, D, P, and H. The number of possible combinations through parameter mixing can be quantified as n⁴, significantly increasing the size of the dataset and enriching variability without additional data collection. Figure 4A depicts a scenario involving three subjects, each providing distinct parameter sets. In this example, CPM generates 81 unique virtual IMU scenarios from just three subjects' data, demonstrating the scalability of this approach for expanding datasets.

Figure 4

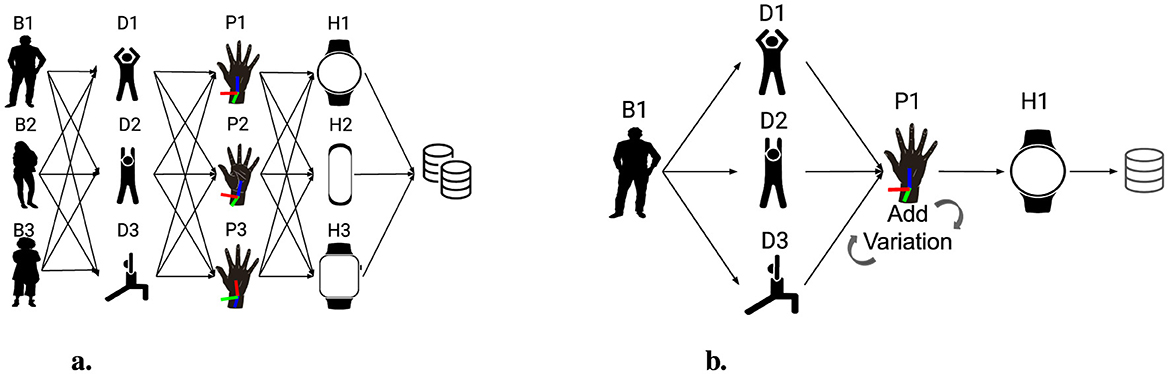
Figure 4. Visualization of (A) Comprehensive Parameter Mixing, illustrating the mixing of simulation parameters from three distinct subjects to enrich the variability of the dataset, and (B) Personalized Dataset Generation, depicting the tailored adjustment of simulation parameters to create personalized datasets.

5.2 Personalized dataset generation

PDG tailors the simulation to reflect individual profiles by selectively adjusting WIMUSim parameters. By fixing subject-specific B, P, and H parameters while varying D, PDG captures unique physical characteristics and typical sensor-wearing patterns for a given subject across a broad range of movement scenarios.

This method maintains personal relevance while introducing controlled variability in movement dynamics. Figure 4B provides a visual example of a scenario customized for an individual subject's specific body configuration, sensor placement, and the hardware used. This approach is designed for fine-tuning machine learning models.

6 Evaluations and results

In this section, we present evaluations conducted to assess the capabilities of WIMUSim in both simulating realistic virtual IMU data and enhancing HAR model performance through CPM and PDG. Our evaluations are twofold: Firstly, we assess the fidelity of virtual IMU data using our in-house dataset, focusing on the effectiveness of the parameter identification method to ensure its alignment with real-world data (Section 6.1). Secondly, we measure the impact of utilizing virtual IMU data generated with WIMUSim on the performance of HAR models using REALDISP and REALWORLD datasets, highlighting the benefits of high-fidelity virtual IMU data and the flexibility of physics simulation in simulating realistic variabilities (Section 6.2).

6.1 Fidelity assessment: sim-to-real alignment of WIMUSim virtual IMU data

We have conducted a fidelity assessment to verify WIMUSim's capability to accurately replicate real IMU data using the four sets of parameters: B, D, P, and H parameters. To facilitate this evaluation, an in-house dataset was collected to establish a reliable ground truth, detailed in Section 6.1.1. Subsequently, in Section 6.1.2, we describe the initial setup of the WIMUSim parameters and the configuration for optimization. The fidelity assessment is then carried out through two analyses:

1. Error analysis of virtual IMU data with optimized parameters: this analysis evaluates the accuracy of the optimized virtual IMU data by comparing the simulated data against real IMU data before and after parameter optimization. We quantify how closely WIMUSim can replicate actual IMU readings through the parameter identification process using error metrics such as Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) and supplement this quantitative assessment with visual comparisons (Section 6.1.3).

2. Sim-to-real alignment analysis via placement modification: this analysis examines how adjustments to the WIMUSim's Placement parameters effectively mirror real-world sensor movements, highlighting WIMUSim's close sim-to-real alignment (Section 6.1.4).

6.1.1 In-house digit drawing dataset

Our in-house digit drawing dataset features a single subject performing digit-drawing gestures, from 0 to 9, using their right arm. This selection of the task effectively isolates the intended motion by focusing exclusively on right arm movements, minimizing the influence of extraneous body movements. Data was collected using four BlueSense (Roggen et al., 2018) 9-axis IMUs positioned on the torso (TRS), right upper arm (RUA), and two on the right wrist (RWR1 and RWR2) at 100 Hz. Each IMU includes an accelerometer, gyroscope, and magnetometer, and also reports its orientation in quaternion format, which was utilized to derive initial D parameters for the simulation.

To assess the sim-to-real alignment when sensor displacement occurs, including shifts and rotations, the placements of RWR1 and RWR2 were adjusted for three experimental configurations: initially, with stacked IMUs on the right wrist to establish a baseline of nearly identical signals, followed by configurations where RWR2 was either rotated or shifted to mirror potential real-world displacements. Figure 5 illustrates these three configurations. The subject repeated each digit-drawing gesture, which takes about 3 s, at least three times, resulting in a total duration of 90 s for each sensor placement configuration.

Figure 5

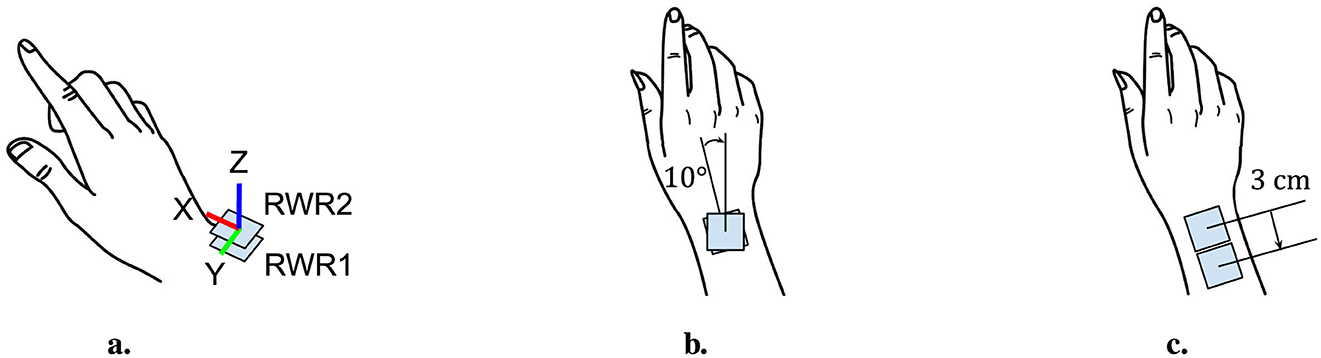
Figure 5. Illustration of IMU placement configurations used in the in-house dataset for fidelity assessment. (A) Stacked: Two IMUs are positioned directly on top of each other on the right wrist (RWR). (B) Rotated: The top IMU (RWR2) is rotated 10 degrees clockwise relative to the bottom IMU. (C) Shifted: The top IMU (RWR2) is displaced 3 cm toward the elbow from the original stacked position.

6.1.2 WIMUSim parameter preparation and optimization

Here, we describe how the initial WIMUSim parameters were defined for the evaluation. In this evaluation, we focus on right arm movements, limiting the B parameters to five joints: BASE, PELVIS, R_CLAVICLE, R_SHOULDER, and R_ELBOW, and defining P parameters for the TRS, RUA, and RWR1 IMUs. The B and P parameters are detailed in Tables 1, 2. Note that in Table 2, the relative orientations of the P parameter are presented in Euler angles for easier interpretation, although they are actually defined in quaternion format. The H parameters were initialized with a bias of (0, 0, 0), the mean of (0, 0, 0) and the standard deviation of (0.05, 0.05, 0.05) for each IMU sensor. The D parameter was derived from quaternion readings of the IMUs. This can be done in the reverse process of the virtual IMU simulation. In the simulation, we project joint dynamics into simulated sensor orientations. Conversely, here, we use actual sensor readings to backtrack and estimate the joint orientations. For each joint j ∈ J associated with an IMU u_j, we first compute its global orientation as $q^j=q^{u_j}{P_{ro}^{(j,u_j)}}^{-1}$, derived from Equation 4. The local orientation for each joint j is then determined by transforming the global orientation relative to its parent joint j_p in the kinematic chain, calculated as $D^j={(q^{j_p})}^{-1}{q}^j$, derived from Equation 2. In this dataset, the quaternions of TRS, RUA, and RWR1 IMUs correspond to the orientation of PELVIS, R_SHOULDER, and R_ELBOW joints, respectively; other joints' initial relative orientations are set to a unit quaternion (1, 0, 0, 0).

Table 1

Table 1. Initial relative positions of body parameter in meters.

Table 2

Table 2. Initial relative positions and orientations of Placement parameter.

For parameter identification, the Adam optimizer was used with learning rates set to 0.0001. The optimization was applied to B, P, D, and H parameters for the data collected in each of three IMU placement configurations: stacked, rotated, and shifted. The primary goal of the parameter identification was to align the three virtual IMU data (TRS_sim, RUA_sim, RWR1_sim) as closely as possible with the real-world counterparts. The coefficients for the loss function were adjusted to balance the scales between different regularizers and set as follows: ${\lambda }_1=10^{-3}$, ${\lambda }_2=10^2$, ${\lambda }_3=10^3$, ${\lambda }_4=10^0$, ${\lambda }_6=10^2$, and ${\lambda }_7=10^{-2}$. λ₅, corresponding to the symmetry regularization term, was not used in this experiment as it involved only the right arm. These values were chosen to ensure a balanced optimization process across the varying scales of the regularization terms.

6.1.3 Error analysis of virtual IMU data with identified parameters

In this analysis, we assess WIMUSim's capability to replicate real-world IMU data accurately, focusing on the “stacked” placement configuration. This evaluation compares the simulation accuracy of pre- and post-optimization for TRS, RUA, and RWR1. Additionally, for a reference of desired accuracy, we compare the data from two actual sensors, RWR1 and RWR2, placed on the right wrist. We quantify the degree of accuracy achieved using RMSE and MAE, alongside visual comparisons of real and simulated data, to detail the discrepancies and alignments between them.

Table 3 presents the comparison of RMSE and MAE values for acceleration and gyroscope data at the TRS, RUA, and RWR positions, both before and after optimization, alongside the real IMU comparison for RWR1 vs. RWR2. Notably, the optimization process results in a significant reduction in errors at the RWR position, with the post-optimization values for RWR1 vs. RWR1_sim (post-opt) even lower than those between the two real IMUs, RWR1 and RWR2, while maintaining high accuracy for TRS and RUA placements. These results underscore the capability of the WIMUSim framework in replicating real-world IMU data placed in different positions. Furthermore, Figure 6 visually compares the real and simulated IMU data at RWR1. The visual comparison underscores the close alignment of virtual IMU after optimization.

Table 3

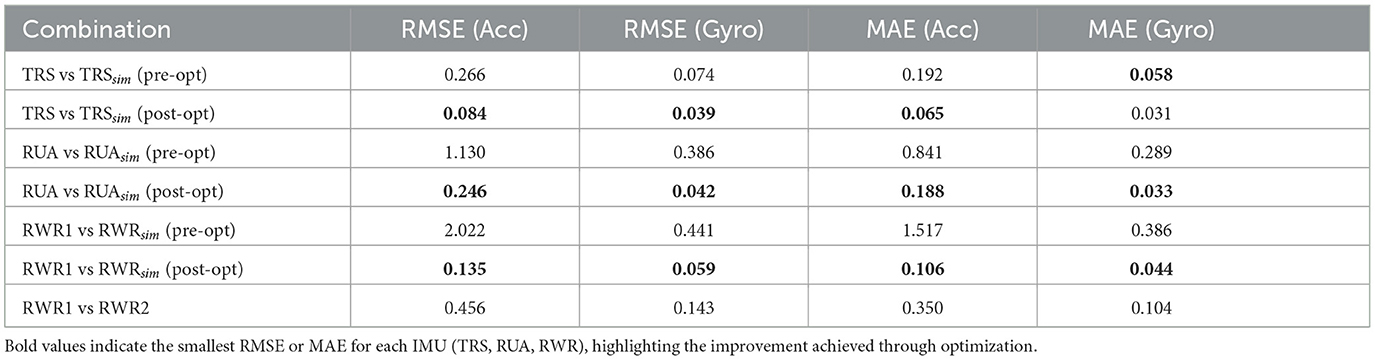
Table 3. Comparison of RMSE and MAE values for Acceleration (Acc) and Gyroscope (Gyro) data across different IMU positions, including pre-optimization and post-optimization of virtual IMU parameters and real IMU comparisons (for RWR).

Figure 6

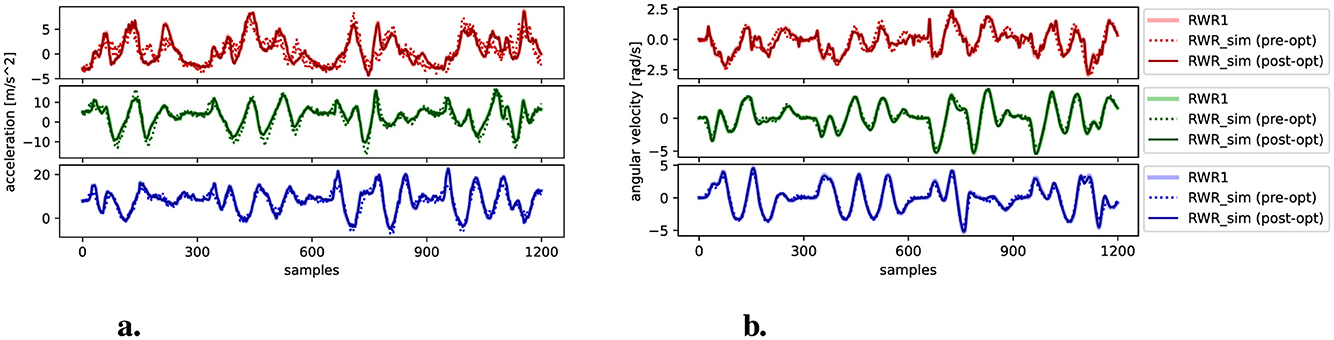
Figure 6. Visual comparisons between real RWR1 data and simulated IMU data with pre- and post-parameter optimization. X, Y, and Z axes from top to bottom, respectively; excerpts of 12 s, which corresponds to the motion of drawing digits from 2 to 5. This visualization highlights the close alignment achieved post-optimization, illustrating WIMUSim's capability in replicating real IMU data. (A) Accelerometer. (B) Gyroscope.

6.1.4 Sim-to-real alignment analysis via placement modification

We extend our fidelity assessment by examining WIMUSim's capability to simulate sensor placement changes, such as rotations and shifts, that mirror real-world modifications. Referring to the “rotated” and “shifted” configurations depicted in Figures 5B, C, we applied a 10-degree clockwise rotation and a 3-cm shift toward the elbow on the identified P parameter for RWR1. Note that these modifications were directly applied to the P parameter without re-optimizing it using RWR2 data, allowing us to test WIMUSim's sim-to-real alignment against actual sensor displacements. We then compared the modified RWR1_sim+rotate and RWR1_sim+shift against the real world counterparts, the rotated and shifted RWR2, respectively.

Table 4 presents the RMSE and MAE comparisons for the rotated and shifted configurations across three scenarios: RWR2 vs RWR1, RWR2 vs RWR1_sim, and RWR2 vs RWR1_sim+modified. The results show consistent error reductions when the placement values were modified to reflect the real-world changes, with the RMSE and MAE comparable to those observed between two stacked real IMUs in the previous experiment (in Table 3), indicating successful sim-to-real alignment. Additionally, Figure 7 contrasts the real and simulated IMU data pre- and post-rotation, visually demonstrating the sim-to-real alignment.

Table 4

Table 4. RMSE and MAE Comparison for Acceleration (Acc) and Gyroscope (Gyro): real IMU (RWR2) vs. simulated IMU (RWR1_sim) pre- and post-modification, demonstrating the close alignment between changes made in the real world and in WIMUSim.

Figure 7

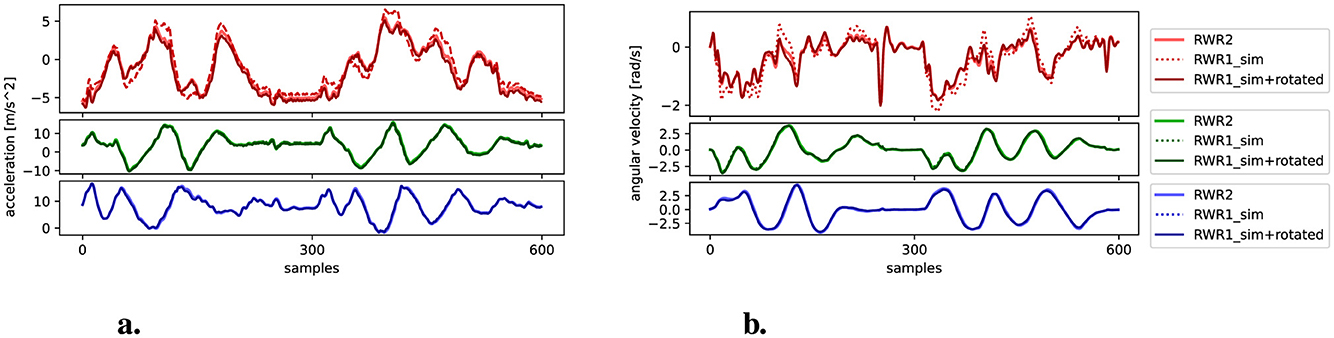
Figure 7. Visual comparison of real and simulated IMU data before and after applying −10 degrees rotation around Z axes to P parameter of RWR1, demonstrating the precise alignment between RWR2 and RWR1_sim+rotated. X, Y, and Z axes from top to bottom, respectively; excerpts of 6 s. (A) Accelerometer. (B) Gyroscope.

6.2 Performance assessment: impact of virtual IMU data on HAR model performance

In this section, we evaluate the effectiveness of WIMUSim in improving HAR model performance by examining the impact of optimized virtual IMU data through a series of experiments. Our objective is to explore WIMUSim's utility for generating realistic virtual IMU data that bridges the gap between real and simulated data.

We use the REALDISP and REALWORLD datasets to conduct our evaluations. In Section 6.2.1, we describe the datasets in detail and outline their role in the experiments. Our performance assessment is structured around three key experiments:

1. Examining the effectiveness of optimized virtual IMU on HAR model performance: this experiment assesses how the optimization of WIMUSim parameters can minimize the performance discrepancies caused by the differences between virtual and real IMU data, comparing HAR models trained on real IMU data with those trained on optimized or non-optimized virtual IMU data (Section 6.2.2).

2. Evaluating parameter mixing for reducing the data collection cost: this experiment investigates how much Comprehensive Parameter Mixing can effectively increase data diversity and enhance model performance, reducing the need for extensive real-world data collection (Section 6.2.3).

3. Testing fine-tuning with personalized augmented dataset: we examine the effectiveness of fine-tuning HAR models with Personalized Dataset Generation, assessing how well the models adapt to individual variations in sensor placements and body configurations (Section 6.2.4).

6.2.1 Datasets used in performance assessment

Realistic sensor displacement (REALDISP) dataset aims to investigate the effects of sensor displacement in HAR. It includes data from 33 fitness activities recorded with nine IMUs on 17 participants in three placement scenarios: (1) “ideal placement,” where the expert places the IMUs at desired positions with specific orientations; (2) “self-placement,” where the participants place the IMUs by themselves without specific instruction hence introducing natural placement variability, and (3) “mutual displacement,” where the expert explicitly displaces the IMUs. IMUs are placed on the back, upper arms, lower arms, thighs, and shins. For more details about the dataset, refer (Baños et al., 2012).

We use the dataset in two distinct scenarios:

1. User-independent scenario: “Ideal placement” data from subjects 1 to 10 are used for training, subjects 11 and 12 for validation, and subjects 13–17 for testing to evaluate the model's performance on unseen subjects.

2. Sensor displacement scenario: “Ideal placement” data from all subjects (1–17) are used for training. To assess the model's robustness against sensor displacement, “self-placement” data are used, with subjects 14–17 for validation, and subjects 1–5 and 7–12 for testing. Subjects 6 and 13 are excluded due to data unavailability in the self-placement setting.

In preparation for these experiments, we extracted the D parameters from the “ideal” placement data for all subjects, following the methods described in Section 6.1.2. For the B and P parameters, we estimated rough values from (Baños et al., 2012), using these same values for all subjects. The H parameters, including biases and noise levels, were initialized to zero by default. Subsequently, we optimized the B, D, P, and H parameters using the real IMU measurements. The coefficients for the loss function were adjusted to balance the scales between different regularization terms and set as follows: ${\lambda }_1,{\lambda }_4,{\lambda }_7,=10^0,{\lambda }_2=10^2,{\lambda }_3=10^3,{\lambda }_5=10^1,\mathrm{\text{and}}{\lambda }_6=10^{-2}$.

Throughout the experiments, we focus on accelerometer and gyroscope data from the Right Lower Arm (RLA) and Left Lower Arm (LLA) IMUs due to the commonality of these sensor placements. Both real and virtual data were downsampled from 50 to 25 Hz.

REALWORLD dataset is used to explore the applicability of virtual IMU data generated from 3D pose estimations extracted from RGB videos. It consists of sensor data collected from 15 participants (mean age 31.9 ± 12.4, eight males and seven females) performing eight distinct activities: walking, running, sitting, standing, lying, climbing stairs up, climbing stairs down, and jumping. Each activity was recorded for ~10 min per participant, except for jumping (up to 1.7 min) due to the physical exertion involved. The dataset includes data from seven IMU sensors placed on the head, chest, waist, upper arm, wrist, thigh, and shin, as well as corresponding video recordings for each session. For more details about the dataset, refer to (Sztyler and Stuckenschmidt, 2016).

In our experiments, we extracted the D parameters from these videos using MotionBERT (Zhu et al., 2023). The B parameters were obtained by first estimating each limb length ratio from the 3D pose estimation, followed by rescaling based on the subject's height information. The P parameters were manually set based on references to the photos provided in the dataset. The H parameters, including biases and noise levels, were initialized to zero by default.

To synchronize the sensor data, we aligned acceleration and gyroscope measurements across IMUs by maximizing the cross-correlation of acceleration magnitudes, followed by resampling the data to 30 Hz. We then synchronized the sensor data with the video recordings through cross-correlation minimization, again using acceleration magnitudes. Subsequently, we optimized the B, D, P, and H parameters using the real IMU measurements. The coefficients for the loss function were all set to 10⁰ except for λ₆, which corresponds to the temporal regularization on the D parameters. For stationary activities, such as lying, standing, and sitting, λ₆ was set to 10⁰, while for other activities, λ₆ was reduced to 10⁻² to account for increased movement dynamics.

For our evaluation, we adopted a single-subject hold-out split, following the setting used in (Kwon et al., 2020). Specifically, subjects 1–13 were used for training, subject 15 for validation, and subject 14 for testing. We used all of the seven devices, but only acceleration data was used for training the HAR models.

6.2.2 Examining the effectiveness of optimized virtual IMU on HAR model performance

This experiment assesses how the optimization of WIMUSim parameters can minimize the HAR model performance discrepancies caused by the differences between virtual and real IMU data. To evaluate this, we prepared training datasets with three distinct configurations in REALDISP's user-independent scenario and sensor displacement scenario, and REALWORLD's user-independent scenario:

• Real IMU (baseline): uses actual IMU data for training.

• Virtual IMU w/o Opt: uses virtual IMU data generated with the non-optimized WIMUSim parameters.

• Virtual IMU w/ Opt: utilizes optimized WIMUSim parameters for generating the virtual IMU dataset.

We trained the DeepConvLSTM (Ordóñez and Roggen, 2016) chosen for its relevance in HAR studies across these settings. The training was conducted with a batch size of 256 and for 100 epochs, using a sliding window with a window size of 100 (corresponding to 4 s of data after downsampling to 25 Hz) with a stride of 25 for the REALDISP scenarios and a window size of 30 with a stride of 15 for the REALWORLD scenario. An initial learning rate of 0.001 with a decay factor of 0.9 was applied, employing Adam as the optimizer. We selected the best-performing model on the validation set for final evaluation, focusing on the macro F1 score. The results were averaged over three different trials with different random seeds.

Table 5 showcases the macro F1 scores from employing the three training dataset configurations with the DeepConvLSTM model. This result confirms that virtual IMU data generated from optimized parameters can be used to train deep learning models to achieve classification performance comparable to that using real IMU data, thereby validating the efficacy of our WIMUSim's wearable IMU model and parameter identification method. It also establishes a foundation for the development of simulation-based data augmentation techniques using the optimized parameters for B, D, P, and H.

Table 5

Table 5. Comparison of HAR model performance (macro F1 score): assessing the effectiveness of parameter optimization.

Interestingly, in the REALDISP and REALWORLD user-independent scenarios, models trained on virtual IMU data generated with optimized parameters slightly outperformed those trained on real IMU data. This outcome may be due to WIMUSim's regularization effect on the training dataset, producing more consistent signals regulated by WIMUSim's simulation process, compared to the real IMU data, which likely contains local noise and some inconsistencies. As a result, the optimized virtual IMU data helped avoid overfitting to some specific patterns in the real training data, improving overall generalization.

In contrast, for the REALDISP dataset, virtual IMU data generated from non-optimized parameters underperformed by 15–18 percentage points (pp) compared to the real IMU data. For the REALWORLD dataset, the disparity in performance with non-optimized virtual IMU data was much more pronounced, with a drop in macro F1 score to 0.2035. This sharp decline can be attributed to the poor quality of pose data extracted from RGB videos, resulting from issues such as (1) camera movement unrelated to the subject's movement, (2) body segments being occluded or moving out of the camera's view, and (3) inaccuracies in pose estimation. Additionally, the REALWORLD dataset includes activities like walking, running, and jumping, where ground contact forces affect the IMU readings significantly—information that cannot be reliably inferred from the pose data alone. Since no optimization or refinement was applied to address these challenges, the resulting virtual IMU data could not effectively replicate the real-world dynamics, making it ineffective for training HAR models.

6.2.3 Enhancing inter-subject data diversity through comprehensive parameter mixing

This experiment explores the potential of Comprehensive Parameter Mixing (CPM) as a data augmentation technique to reduce the reliance on extensive real-world data collection for training robust HAR models. The primary objective is to demonstrate how CPM can effectively increase the diversity of training data, thereby enhancing model performance and reducing the need for costly, large-scale data collection.

We evaluated CPM within the REALDISP and REALWORLD user-independent scenarios. We created augmented virtual IMU datasets by varying the number of subjects involved in the mixing process, ranging from 1 to 10 for the REALDISP dataset and from 1 to 13 for the REALWORLD dataset. Unique sets of parameters—B, D, P, and H—were combined to simulate varied body configurations, movement patterns, sensor placements, and hardware characteristics. For each epoch, 256 unique parameter combinations were randomly sampled from the pool, generating the virtual IMU data online during training. For training, both the real and the augmented virtual IMU datasets were used.

Additionally, we generated another virtual IMU dataset using the same parameter mixing method but with non-optimized default D parameters. For the REALDISP dataset, B and P were still optimized to add variations, and for the REALWORLD dataset, initial B parameters set for each subject were used. The H parameters were kept at their default zero values. This comparison was implemented to assess the impact of parameter optimization within the CPM strategy, particularly the influence of accurate D parameters on HAR model performance.

The DeepConvLSTM model was trained for each scenario. The training was conducted with a batch size of 256 for the REALDISP dataset and 1,024 for the REALWORLD dataset over 100 epochs, retaining the model with the highest validation performance for testing. Other configurations remained consistent with those described in Section 6.2.2. We used the macro F1 score to measure performance.

Figure 8 illustrates how performance transitions as the number of subjects used in training for both datasets increases, contrasting those trained with the baseline dataset (without CPM), the dataset augmented with CPM optimized or non-optimized. The error bars represent standard deviations. For both datasets, the models trained with CPM-augmented virtual IMU data show substantial improvements over the baseline, demonstrating the effectiveness of CPM in enhancing model performance. Notably, the use of optimized parameter combinations yields superior results across all configurations. This indicates that leveraging the diversity in subjects' body sizes, movement dynamics, sensor placements, and hardware properties significantly enhances the generalization capability of the HAR models.

Figure 8

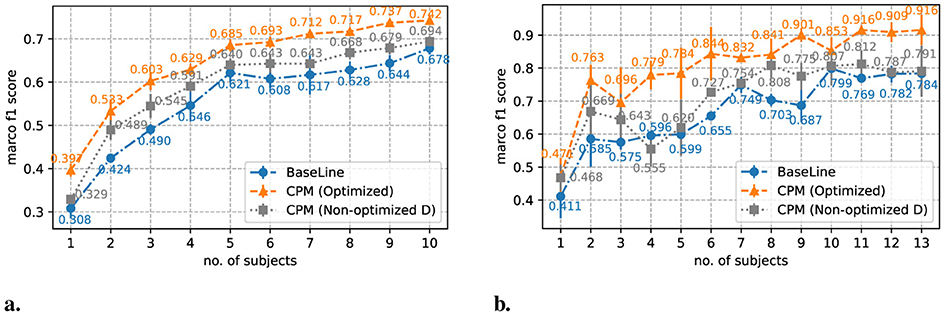
Figure 8. Performance Trends of HAR Models: The graphs (A) REALDISP and (B) REALWORLD illustrate macro F1 score transition as the number of subjects used in training increases. The blue line with circle markers represents the baseline with no augmentation, the orange line with triangle markers shows the performance with comprehensive parameter mixing (CPM), and the gray line illustrates the performance when using CPM with non-optimized D parameters.

For the REALDISP dataset (Figure 8A), the benefits of CPM with optimized parameters are observed consistently, with roughly 10 pp improvement when trained on data from just two to four subjects compared to the baseline. This trend continues, and the model trained using CPM with optimized parameters on just five subjects achieves performance comparable to the best baseline model trained with 10 subjects, resulting in a substantial reduction in the amount of real-world data required to reach similar performance. Even when all 10 subjects are included, CPM maintains a consistent six percentage point advantage over the baseline. This suggests that CPM can effectively reduce the need for extensive data collection by creating diverse synthetic training data that closely approximates the true distribution.

For the REALWORLD dataset (Figure 8B), the improvements are even more pronounced. Models trained with optimized CPM data consistently outperform the baseline. Specifically, a model trained with CPM data from just six subjects surpasses the best baseline performance, which required data from 10 subjects, reducing the need for real-world data by roughly half. Moreover, when using optimized CPM, the model achieves more than a 10 pp higher F1 score compared to both the best baseline and CPM with non-optimized parameters, highlighting the significant impact of high-fidelity simulation. Also, it is important to note that CPM with non-optimized parameters shows less consistent performance, with some initial gains over the baseline diminishing as the number of real IMU data used for training increases. This is likely due to the lower quality of D parameters extracted from videos, leading to less reliable virtual IMU data.

Overall, these results demonstrate the effectiveness of CPM in enhancing HAR model performance across datasets, significantly reducing the need for extensive real-world data collection in training scenarios. Moreover, the findings also emphasize the importance of maintaining high fidelity in virtual IMU data, particularly in scenarios like the REALWORLD dataset where available motion data quality is lower. Ensuring accurate parameter identification is essential for maximizing the benefits of virtual IMU dataset.

6.2.4 Fine-tuning with personalized augmented dataset

This experiment explores the potential of Personalized Dataset Generation (PDG) as detailed in Section 5.2. We aim to enhance HAR model performance by fine-tuning HAR models with personalized datasets tailored to individual subjects' body size and sensor placement preferences in the sensor displacement scenario of the REALDISP dataset.

For each subject, except for subjects 6 and 13, due to data unavailability, we generated personalized datasets using PDG. This process utilized the optimized B parameters for each specific subject and the D parameters from all training subjects (1–17) in the “ideal” placement scenario. The P parameters were extracted through an optimization process on the data from the “self” placement scenario, considering its relative ease of acquisition in real-world settings. We acknowledge that data leakage occurs during the P parameter extraction process; however, in this experiment, our focus is to demonstrate the potential benefits of PDG under the assumption that the user's placement preferences are known.

To establish a baseline for comparison, we first trained a generalized DeepConvLSTM model using both real IMU data and a virtual IMU dataset simulating a wide range of sensor displacements. For the virtual IMU data, a set of sensor misalignments was created using systematic rotations of 0°, 20°, and –20° along each axis (x, y, z), forming 3³ = 27 unique rotations. Additionally, extreme misalignments such as 180° rotations along each axis and ± 90° rotations along the x-axis were included to model more extreme placement deviations. This resulted in a total of 32 distinct rotations (27+3+2), ensuring that the dataset comprehensively covers both minor and significant misalignments. This model was expected to perform reasonably well across different subjects without specific personalization.

Following baseline training, we then fine-tuned the entire network of the baseline model for each subject using the personalized datasets. Given the adequate size of the personalized datasets, we chose not to freeze any part of the model during fine-tuning to allow comprehensive learning and adaptation to the unique characteristics and preferences of each subject. Due to the lack of dedicated validation data for each subject, we monitored model performance using a separate validation set (subjects 14–17 in the “self” placement scenario), determining that 150 epochs were a suitable cutoff, with a batch size of 1,024. Performance was evaluated based on the macro F1 score.

Table 6 demonstrates significant benefits from fine-tuning with personalized datasets generated with WIMUSim. DeepConvLSTM models showed an average macro F1 score improvement of 4 pp. Notably, some subjects experienced performance boosts exceeding 10 pp. A few cases showed slight declines; this might be due to the sub-optimal extraction of the P parameter from the “self” placement data or the need for improved validation methodologies during training.

Table 6

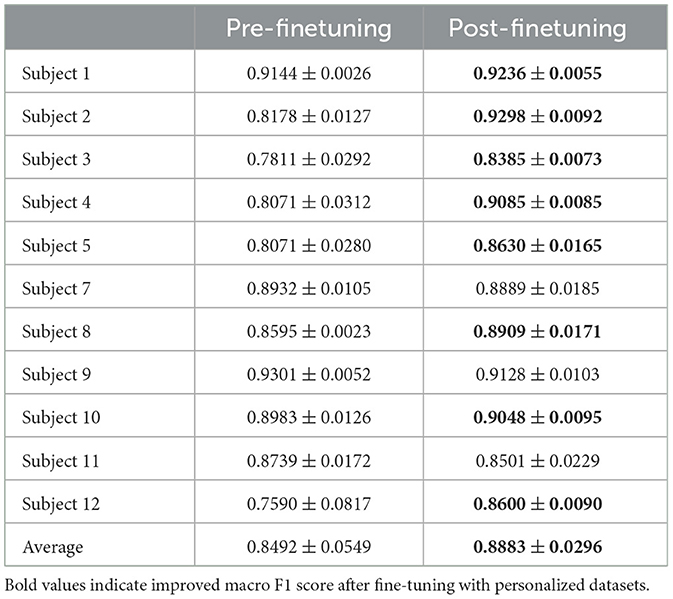
Table 6. Comparison of HAR model performance (macro F1 scores) before and after fine-tuning with personalized datasets generated using Personalized Dataset generation.

These findings confirm the utility of WIMUSim in generating personalized datasets for fine-tuning HAR models, attributed to the WIMUSim parameters' flexibility and reusability. By incorporating individual characteristics and potential variations extracted from the dataset, these personalized datasets provide highly relevant training data to specific subjects.

7 Discussion and limitations

The results of our experiments have demonstrated the effectiveness of WIMUSim in generating high-fidelity virtual IMU data through parameter identification and its utility in HAR model training. However, certain aspects of WIMUSim's implementation and the current modeling choices present limitations that need to be addressed for broader applicability. This section begins by comparing WIMUSim with IMUTube (Kwon et al., 2020) and CROMOSim (Hao et al., 2022) and discusses WIMUSim's positioning within HAR research. We then discuss the current limitations of WIMUSim and highlight potential future opportunities to enhance movement variability, wearable IMU modeling, and applicability beyond its reliance on real IMU data.

7.1 Positioning and benchmarking of WIMUSim against IMUTube and CROMOSim

To contextualize the performance of WIMUSim, we compared our results against IMUTube (Kwon et al., 2020) and CROMOSim (Hao et al., 2022). Following the protocols outlined in these papers, we conducted additional experiments on the REALWORLD dataset, the Opportunity dataset for a 4-class locomotion classification task (stand, walk, sit, and lie), and the PAMAP2 dataset for a reduced 8-class activity classification task (stand, walk, sit, lie, run, ascend stairs, descend stairs, and rope jump). For the REALWORLD dataset, virtual IMU data was generated using concurrently collected IMU and video data. For the Opportunity and PAMAP2 datasets, virtual IMU data was generated using video data from the REALWORLD dataset. The parameters identified from the REALWORLD dataset were used as a basis, with adjustments made to the P parameters to match the sensor configurations of these datasets. Although this setting goes beyond WIMUSim's originally intended use case, it allows us to evaluate how virtual IMU data generated with WIMUSim performs in cross-dataset scenarios, positioning WIMUSim among existing virtual IMU simulation methods. The reduction in PAMAP2's activity classes was made to align with the activity labels available in the REALWORLD dataset, which includes walking, running, sitting, standing, lying, climbing stairs (up and down), and jumping. The evaluation compared three configurations: R2R (Real-to-Real), V2R (Virtual-to-Real), and M2R (Mixed-to-Real).

The sensor placement settings varied across the methods for the Opportunity and PAMAP2 datasets. For the Opportunity dataset, IMUTube extracted virtual IMU data from 11 accelerometers. CROMOSim, in contrast, generated data from seven 6-axis IMUs. For the PAMAP2 dataset, IMUTube used 3 accelerometer placements on the chest, dominant wrist, and dominant ankle, while CROMOSim generated data from three 6-axis IMUs at the same locations. In our experiments with WIMUSim, we generated virtual IMU data for four 6-axis IMUs (left lower arm, left upper arm, back, and left foot) for Opportunity, as the D parameters were optimized only for the center and left side of the body using the REALWORLD dataset. For PAMAP2, we generated virtual IMU data for three 6-axis IMUs (chest, left ankle, and left wrist). For the V2R configuration of WIMUSim, we used virtual IMU data generated directly from the originally identified parameter sets without additional variation. For M2R, we applied CPM to introduce variations in virtual IMU data. For the rest of the configurations, we followed the same settings as explained in (Kwon et al., 2020), including CDF-based distribution mapping for virtual IMU data.

Table 7 presents the results of WIMUSim, IMUTube, and CROMOSim across three datasets: REALWORLD, Opportunity, and PAMAP2. Results for IMUTube and CROMOSim correspond to the scores reported in (Kwon et al., 2020; Hao et al., 2022).

Table 7

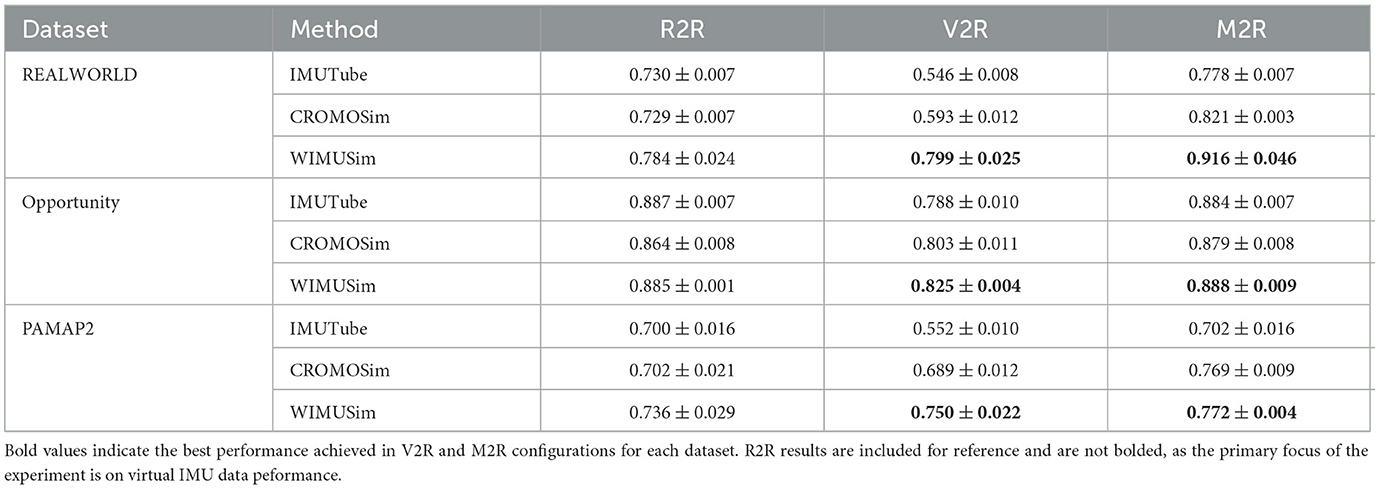
Table 7. Comparison of HAR model performance (F1 Score) across REALWORLD, Opportunity, and PAMAP2 datasets using IMUTube, CROMOSim, and WIMUSim for R2R (Real-to-Real), V2R (Virtual-to-Real), and M2R (Mixed-to-Real) configurations.

Due to differences in preprocessing and sensor placement settings, our baseline results differed from those reported for the other methods. For the REALWORLD dataset, where WIMUSim achieved 5 pp higher performance, this discrepancy can be attributed to differences in preprocessing. In our study, we employed cross-device synchronization to align IMU signals from multiple devices, ensuring consistent movement patterns for parameter identification. IMUTube, by contrast, did not explicitly mention such alignment, which may have contributed to less consistent training data and lower baseline performance. For the OPPORTUNITY and PAMAP2 datasets, differences in sensor placement settings may have also contributed to variations in these results.

For the V2R configuration, WIMUSim consistently outperformed the other methods, with particularly strong results on the PAMAP2 dataset. For the REALWORLD dataset, this performance is attributed to the parameter identification process, as detailed in Section 6.2.2. Remarkably, on the PAMAP2 dataset, WIMUSim even exceeded its R2R performance, underscoring the utility of high-fidelity virtual IMU data generated by WIMUSim. This result demonstrates that the realism of WIMUSim's virtual IMU data can contribute to superior performance, even in cross-dataset scenarios with differing data collection configurations.

For the M2R configuration, WIMUSim demonstrated significantly better performance on the REALWORLD dataset, where paired real IMU and video data were available. However, the performance gains were less pronounced on the Opportunity and PAMAP2 datasets. This may be due to the distribution mapping process, which aligns the distribution of the virtual IMU data to that of the real IMU dataset but could reduce the influence of the variations introduced by WIMUSim.

Overall, these results highlight WIMUSim's strength in generating high-fidelity virtual IMU data while capitalizing on the flexibility of virtual IMU simulation, particularly in scenarios where paired real IMU and motion data are available. Unlike deep learning-based virtual IMU simulation methods such as CROMOSim, which require substantial amounts of paired motion and IMU data for pre-training, WIMUSim avoids this dependency. This makes it especially advantageous for new sensor positions or devices, where such datasets are often scarce. For new applications—such as HAR models for rings, earbuds, or other emerging wearable devices, which are not well-represented in many existing datasets—it is reasonable to expect that real IMU data would be collected alongside video or pose estimation data during initial testing and evaluation. In these cases, WIMUSim can utilize this paired data to generate high-quality virtual IMU datasets with realistic variations, thereby reducing the need for extensive real-world data collection and enabling precise fine-tuning that is better aligned with specific use cases. In contrast, existing methods like IMUTube and CROMOSim are designed to leverage large-scale video datasets to generate virtual IMU data. These studies highlight the potential of utilizing lower-fidelity virtual IMU data in combination with real IMU data. Together, these approaches offer complementary roles for advancing the field of virtual IMU simulation for HAR.

7.2 Current limitations and future opportunities

Unexplored potential for simulating movement variability: While the two use cases of WIMUSim presented in this study—Comprehensive Parameter Mixing and Personalized Dataset Generation—successfully demonstrated their effectiveness in training HAR models, WIMUSim's potential for generating diverse movement patterns remains largely underexplored. Techniques such as time scaling, magnitude warping, and time warping could be applied directly to the Dynamics parameter to simulate variations in movement intensity and speed, thereby enhancing the diversity of the generated data and making it more reflective of real-world variations. Implementing these transformations would allow WIMUSim to capture a broader spectrum of IMU patterns observed in natural activities. Exploring such augmentation strategies could unlock the full potential of physics-based simulation, extending WIMUSim's utility and further reducing the need for extensive real-world data collection.

Expanding the wearable IMU model for further flexibility: currently, the Body parameter uses rigid bodies to model the human body, and the Placement parameter is fixed to the relative positions and orientations of the IMUs with respect to their parent joints. This simple modeling enables efficient simulation and has achieved satisfactory performance for our experiments; however, it may not sufficiently address the complexity of how wearable IMUs move in some real-world settings. For example, when sensors are embedded in loose clothing, as explored in recent studies such as (Jayasinghe et al., 2023), IMUs do not always move with their associated body joints, which cannot be accurately modeled using our current modeling approach. Addressing such scenarios would require more sophisticated models that account for the interaction between IMUs, clothing, and the body surface. This limitation highlights the need for more expansive validation across a broader range of activities and placements, as well as future work to investigate the potential benefits of a more complex model for accurately simulating virtual IMU data and enhancing HAR performance.

Streamlining coefficient selection process: the seven weight coefficients in Equation 9 are designed to allow researchers to tailor the parameter identification process based on prior knowledge of the dataset. For example, in controlled settings like the digit drawing dataset, larger coefficients (${\lambda }_2=10^2,{\lambda }_3=10^3$) were applied to strictly penalize deviations in B (Body) and P (Placement) parameters, reflecting higher confidence in their initial estimates. Conversely, for datasets like REALWORLD, where parameter ranges were less certain, default values of 1 were used in most cases. The only adjustment was to λ₆, which was decreased from 1 to 10⁻² for non-stationary activities to better accommodate fluctuations in Dynamics parameters (D-temp). However, the selection of these coefficients remains subjective, as no standardized guidelines currently exist for determining their values. This subjectivity reflects the intent to balance RMSE minimization with the physical plausibility of the identified parameters, rather than to maximize HAR performance. Future work could focus on developing systematic or automated methods for selecting coefficients to reduce the reliance on manual tuning.

Exploring the broader applicability of WIMUSim: the current WIMUSim framework relies on simultaneously collected real IMU data and motion data to identify its parameters—Body, Dynamics, Placement, and Hardware. This dependency can constrain WIMUSim's applicability to settings where such paired data is available. Though we have identified unique opportunities for WIMUSim in scenarios where small amounts of paired data can be collected, it would still be beneficial to explore methods for expanding its applicability. For example, in the M2R setting in Section 7.1, WIMUSim's CPM demonstrated less pronounced advantages for the Opportunity and PAMAP2 datasets, likely due to the distribution mapping method we used. To address this, future work could explore domain adaptation techniques that preserve the benefits of WIMUSim's flexibility in introducing meaningful variabilities into the virtual IMU data while improving its ability to generalize across diverse datasets.

8 Conclusion

In this work, we investigated the impact of improving the fidelity of virtual IMU data in training HAR models. To address the discrepancies between real and virtual IMU data, we introduced WIMUSim, a 6-axis wearable IMU simulation framework that models and simulates wearable IMU data using four parameters—Body, Dynamics, Placement, and Hardware. The fundamental novelty of our approach lies in leveraging gradient descent optimization to identify parameters that closely replicate real IMU data within the simulation environment, enabling the realistic simulation of variabilities in wearable IMU signals through physics-based modeling.

Our fidelity assessment (Section 6.1) using an in-house dataset demonstrated that WIMUSim could accurately replicate real IMU data through parameter optimization, achieving RMSE of 0.135[m/s²] for acceleration and 0.106[rad/s] for angular velocity for the IMU placed on the wrist. These results confirm WIMUSim's ability to generate realistic sensor outputs and accurately simulate changes such as shifts and rotations in sensor placements, validating its close sim-to-real alignment.

Our evaluations on the REALDISP and REALWORLD datasets demonstrated that HAR models trained on optimized virtual IMU data achieved performance comparable to those trained on real IMU data. In addition, we explored two primary use cases for WIMUSim: Comprehensive Parameter Mixing (CPM) and Personalized Dataset Generation (PDG). CPM improved HAR model performance by 6 pp on the REALDISP dataset and by 12 pp on the REALWORLD dataset compared to the baseline trained with real IMU data, while outperforming models trained with non-optimized virtual IMU data by 4–10 pp. PDG, designed for fine-tuning personalized models, achieved average improvements of 2–4 pp, with gains exceeding 10 pp for certain subjects in the sensor-displacement setting of REALDISP dataset.

These findings demonstrate the value of improving the fidelity of virtual IMU to fully leverage the flexibility of physics simulation for training HAR models and highlight the utility of WIMUSim in producing high-fidelity virtual IMU data. Our research showcases the benefits of improving the fidelity of virtual IMU data and positions WIMUSim as a tool for training HAR models in scenarios where real IMU data is collected alongside video recordings or other forms of pose information. Furthermore, WIMUSim offers the potential for developing more physically plausible data augmentation strategies that incorporate realistic variabilities influencing wearable IMU data, thereby contributing to mitigating the data scarcity issue in sensor-based HAR.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://github.com/STRCWearlab/WIMUSim.

Ethics statement

Ethical approval was not required for the studies involving humans because the data was collected from one of the authors. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

NO: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft. PB: Project administration, Supervision, Writing – review & editing. DR: Conceptualization, Funding acquisition, Resources, Supervision, Writing – review & editing. PL: Conceptualization, Resources, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work received support from the EU H2020-ICT-2019-3 project ‘HumanE AI Net' (grant agreement number 952 026).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Asare, P., Dickerson, R. F., Wu, X., Lach, J., and Stankovic, J. A. (2013). “BodySim: a multi-domain modeling and simulation framework for body sensor networks research and design," in Proceedings of the 11th ACM Conference on Embedded Networked Sensor Systems (New York, NY: ACM), 1–2. doi: 10.1145/2517351.2517392

Crossref Full Text | Google Scholar

Auerbach, B. M., and Ruff, C. B. (2006). Limb bone bilateral asymmetry: variability and commonality among modern humans. J. Hum. Evol. 50, 203–218. doi: 10.1016/j.jhevol.2005.09.004

PubMed Abstract | Crossref Full Text | Google Scholar

Baños, O., Damas, M., Pomares, H., Rojas, I., Tóth, M. A., and Amft, O. (2012). “A benchmark dataset to evaluate sensor displacement in activity recognition," in Proceedings of the 2012 ACM Conference on Ubiquitous Computing (New York, NY: ACM), 1026–1035. doi: 10.1145/2370216.2370437

Crossref Full Text | Google Scholar

Banos, O., Toth, M. A., Damas, M., Pomares, H., and Rojas, I. (2014). Dealing with the effects of sensor displacement in wearable activity recognition. Sensors 14, 9995–10023. doi: 10.3390/s140609995

PubMed Abstract | Crossref Full Text | Google Scholar

Bulling, A., Blanke, U., and Schiele, B. (2014). A tutorial on human activity recognition using body-worn inertial sensors. ACM Comput. Surv. 46, 1–33. doi: 10.1145/2499621

Crossref Full Text | Google Scholar

Fortes Rey, V., Ray, L. S. S., Xia, Q., Wu, K., and Lukowicz, P. (2024). “Enhancing inertial hand based har through joint representation of language, pose and synthetic IMUs," in Proceedings of the 2024 ACM International Symposium on Wearable Computers (New York, NY: ACM), 25–31. doi: 10.1145/3675095.3676609

Crossref Full Text | Google Scholar

Garcia-Gonzalez, D., Rivero, D., Fernandez-Blanco, E., and Luaces, M. R. (2020). A public domain dataset for real-life human activity recognition using smartphone sensors. Sensors 20:2200. doi: 10.3390/s20082200

PubMed Abstract | Crossref Full Text | Google Scholar

Garcia-Gonzalez, D., Rivero, D., Fernandez-Blanco, E., and Luaces, M. R. (2023). Deep learning models for real-life human activity recognition from smartphone sensor data. Internet Things 24:100925. doi: 10.1016/j.iot.2023.100925

PubMed Abstract | Crossref Full Text | Google Scholar

Gordon, C. C., Blackwell, C. L., Bradtmiller, B., Parham, J. L., Barrientos, P., Paquette, S. P., et al. (2014). 2012 Anthropometric Survey of US Army Personnel: Methods and Summary Statistics. Technical Report. Natick, MA: Army Natick Soldier Research, Development and Engineering Center.

Google Scholar

Hao, Y., Lou, X., Wang, B., and Zheng, R. (2022). CROMOSim: a deep learning-based cross-modality inertial measurement simulator. IEEE Trans. Mob. Comput. 23, 302–312. doi: 10.1109/CPHS56133.2022.9804560

Crossref Full Text | Google Scholar

Jayasinghe, U., Hwang, F., and Harwin, W. S. (2023). Inertial measurement data from loose clothing worn on the lower body during everyday activities. Sci. Data 10:709. doi: 10.1038/s41597-023-02567-4

PubMed Abstract | Crossref Full Text | Google Scholar

Kang, C., Jung, H., and Lee, Y. (2019). “Towards machine learning with zero real-world data," in 5th ACM Workshop on Wearable Systems and Applications (New York, NY: ACM), 41–46. doi: 10.1145/3325424.3329662

Crossref Full Text | Google Scholar

Khaked, A. A., Oishi, N., Roggen, D., and Lago, P. (2023). “Investigating the effect of orientation variability in deep learning-based human activity recognition," in Adjunct Proceedings of the 2023 ACM International Joint Conference on Pervasive and Ubiquitous Computing & the 2023 ACM International Symposium on Wearable Computing (New York, NY: ACM), 480–485. doi: 10.1145/3594739.3610742

Crossref Full Text | Google Scholar

Kwon, H., Tong, C., Haresamudram, H., Gao, Y., Abowd, G. D., Lane, N. D., et al. (2020). Imutube: automatic extraction of virtual on-body accelerometry from video for human activity recognition. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 4, 1–29. doi: 10.1145/3411841

Crossref Full Text | Google Scholar

Kwon, H., Wang, B., Abowd, G. D., and Plötz, T. (2021). Approaching the real-world: Supporting activity recognition training with virtual imu data. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 5, 1–32. doi: 10.1145/3478096

Crossref Full Text | Google Scholar

Lago, P., Takeda, S., Okita, T., and Inoue, S. (2019). “MEASURed: evaluating sensor-based activity recognition scenarios by simulating accelerometer measures from motion capture," in Human Activity Sensing: Corpus and Applications, eds. N. Kawaguchi, N. Nishio, D. Roggen, S. Inoue, S. Pirttikangas, and K. Van Laerhoven (Cham: Springer), 135–149. doi: 10.1007/978-3-030-13001-5_10

PubMed Abstract | Crossref Full Text | Google Scholar

Lara, O. D., and Labrador, M. A. (2012). A survey on human activity recognition using wearable sensors. IEEE Commun. Surv. Tutor. 15, 1192–1209. doi: 10.1109/SURV.2012.110112.00192

Crossref Full Text | Google Scholar

Leng, Z., Kwon, H., and Plötz, T. (2023). “Generating virtual on-body accelerometer data from virtual textual descriptions for human activity recognition," in Proceedings of the 2023 ACM International Symposium on Wearable Computers (New York, NY: ACM), 39–43. doi: 10.1145/3594738.3611361

Crossref Full Text | Google Scholar

Liu, R., Ramli, A. A., Zhang, H., Henricson, E., and Liu, X. (2021). “An overview of human activity recognition using wearable sensors: healthcare and artificial intelligence," in International Conference on Internet of Things (Cham: Springer), 1–14. doi: 10.1007/978-3-030-96068-1_1

Crossref Full Text | Google Scholar

Mathur, A., Zhang, T., Bhattacharya, S., Velickovic, P., Joffe, L., Lane, N. D., et al. (2018). “Using deep data augmentation training to address software and hardware heterogeneities in wearable and smartphone sensing devices," in 2018 17th ACM/IEEE international conference on information processing in sensor networks (IPSN) (Porto: IEEE), 200–211. doi: 10.1109/IPSN.2018.00048

Crossref Full Text | Google Scholar

Nweke, H. F., Teh, Y. W., Al-Garadi, M. A., and Alo, U. R. (2018). Deep learning algorithms for human activity recognition using mobile and wearable sensor networks: State of the art and research challenges. Expert Syst. Appl. 105, 233–261. doi: 10.1016/j.eswa.2018.03.056

Crossref Full Text | Google Scholar

OpenErg.com (2020). People Size Anthropometry Data - OpenErg. Online. Available at: https://www.openerg.com/psz/anthropometry_data.html (accessed October 21, 2024).

Google Scholar

Ordóñez, F. J., and Roggen, D. (2016). Deep convolutional and LSTM recurrent neural networks for multimodal wearable activity recognition. Sensors 16:115. doi: 10.3390/s16010115

PubMed Abstract | Crossref Full Text | Google Scholar

Pellatt, L., Dewar, A., Philippides, A., and Roggen, D. (2021). “Mapping Vicon motion tracking to 6-axis IMU data for wearable activity recognition," in Activity and Behavior Computing, eds. M. A. R. Ahad, S. Inoue, D. Roggen, and K. Fujinami (Singapore: Springer), 3–20. doi: 10.1007/978-981-15-8944-7_1

Crossref Full Text | Google Scholar

Plötz, T., and Guan, Y. (2018). Deep learning for human activity recognition in mobile computing. Computer 51, 50–59. doi: 10.1109/MC.2018.2381112

Crossref Full Text | Google Scholar

Rey, V. F., Garewal, K. K., and Lukowicz, P. (2021). Translating videos into synthetic training data for wearable sensor-based activity recognition systems using residual deep convolutional networks. Appl. Sci. 11:3094. doi: 10.3390/app11073094

Crossref Full Text | Google Scholar

Rey, V. F., Hevesi, P., Kovalenko, O., and Lukowicz, P. (2019). “Let there be IMU data: generating training data for wearable, motion sensor based activity recognition from monocular RGB videos," in Adjunct proceedings of the 2019 ACM international joint conference on pervasive and ubiquitous computing and proceedings of the 2019 ACM international symposium on wearable computers (New York, NY: ACM), 699–708. doi: 10.1145/3341162.3345590

Crossref Full Text | Google Scholar

Roggen, D., Förster, K., Calatroni, A., Bulling, A., and Tröster, G. (2010). “On the issue of variability in labels and sensor configurations in activity recognition systems," in Proc. “How to do Good Activity Recognition Research? Experimental Methodologies, Evaluation Metrics, and Reproducibility Issues” (Pervasive) (Berlin; Heidelberg: Springer-Verlag), 1–4.

Google Scholar

Roggen, D., Pouryazdan, A., and Ciliberto, M. (2018). “Poster: bluesense - designing an extensible platform for wearable motion sensing, sensor research and iot applications," in Proceedings of the 2018 International Conference on Embedded Wireless Systems and Networks, EWSN '18 (Junction, TX: Junction Publishing), 177–178.

Google Scholar

Santhalingam, P. S., Pathak, P., Rangwala, H., and Kosecka, J. (2023). Synthetic smartwatch imu data generation from in-the-wild asl videos. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 7, 1–34. doi: 10.1145/3596261

Crossref Full Text | Google Scholar

Stisen, A., Blunck, H., Bhattacharya, S., Prentow, T. S., Kjærgaard, M. B., Dey, A., et al. (2015). “Smart devices are different: assessing and mitigating mobile sensing heterogeneities for activity recognition," in Proceedings of the 13th ACM conference on embedded networked sensor systems (New York, NY: ACM), 127–140. doi: 10.1145/2809695.2809718

Crossref Full Text | Google Scholar

Sztyler, T., and Stuckenschmidt, H. (2016). “On-body localization of wearable devices: an investigation of position-aware activity recognition," in 2016 IEEE international conference on pervasive computing and communications (PerCom) (Sydney, NSW: IEEE), 1–9. doi: 10.1109/PERCOM.2016.7456521

Crossref Full Text | Google Scholar

Xia, C., and Sugiura, Y. (2021). Optimizing sensor position with virtual sensors in human activity recognition system design. Sensors 21:6893. doi: 10.3390/s21206893

PubMed Abstract | Crossref Full Text | Google Scholar

Xia, C., and Sugiura, Y. (2022). “Virtual IMU data augmentation by spring-joint model for motion exercises recognition without using real data," in Proceedings of the 2022 ACM International Symposium on Wearable Computers (Cambridge: ACM), 79–83. doi: 10.1145/3544794.3558460

Crossref Full Text | Google Scholar

Xia, C., and Sugiura, Y. (2023). Virtual sensors with 3d digital human motion for interactive simulation. Computer 56, 42–54. doi: 10.1109/MC.2023.3239344

Crossref Full Text | Google Scholar

Young, A. D., Ling, M. J., and Arvind, D. K. (2011). “IMUSim: a simulation environment for inertial sensing algorithm design and evaluation," in Proceedings of the 10th ACM/IEEE International Conference on Information Processing in Sensor Networks (Chicago, IL: IEEE), 199–210.

Google Scholar

Zhang, J., Zhang, Y., Cun, X., Huang, S., Zhang, Y., Zhao, H., et al. (2023). T2M-GPT: Generating human motion from textual descriptions with discrete representations. arXiv [Preprint]. arXiv:2301.06052. doi: 10.48550/arXiv.2301.06052

Crossref Full Text | Google Scholar

Zhu, W., Ma, X., Liu, Z., Liu, L., Wu, W., Wang, Y., et al. (2023). ‘Motionbert: a unified perspective on learning human motion representations," in Proceedings of the IEEE/CVF International Conference on Computer Vision (Paris: IEEE), 15085–15099. doi: 10.1109/ICCV51070.2023.01385

Crossref Full Text | Google Scholar