A new mathematical model to improve encryption process based on Split-Radix Fast Fourier Transform algorithm

This paper introduces a new encryption method aimed at improving the cryptography process through the use of splitting radix Fourier Transform technique called Split-Radix Fast Fourier Transforms (SRFFT). The proposed method is based on splitting the FFT radix-2 and radix-4 algorithms to achieve improved information assurance by SRFFT two phases. The first phase applies direct computation of SRFFT algorithm on input plaintext to produce a ciphertext and the second phase applies the reversing SRFFT algorithm to decipher. Several types of cryptoanalysis attacks such as brute-forcing, autocorrelation and dictionary attacks are comparatively evaluated and the end result of SRFFT evaluation indicates that SRFFT is preferable in many practical encryption applications since SRFFT complexity increases with the range of split-radix computations thus eliminating the potential chances of cryptanalysis attacks.

1 Introduction

In a time where preserving the interests in end-to-end encrypted communications via secure channels is vital, the cryptography proves as a stimulating foundation that upholds the purity of confidentiality that serves as the conduit through which information can be shielded from the prying eyes of unauthorized intruders (Manikandaprabhu and Samreetha, 2024).

Since secure communication channels have become pervasive in everyday arena with the increased intensity and sophistication of security-related attacks on the other side, there is apparently an imminent need for individuals and as well as organizations alike to embrace bridging that gap for achieving a comprehensive information security strategy backed up by use of specialized hardware and software and trained personnel (Shi et al., 2023).

Futher, in the age of ubiquitous digital information, ensuring data security turns out to be a pressing concern due to ithe available innovative mehods that can add farther fortifications to data security through hybridization techniques of encryption, involving the Length-Based Rewriting Systems and Advanced Encryption Standard (AES) and RSA, with the integration of kernel-based key storage (Srivastava and Kuma, 2023; Hughes and Tannenbaum, 2002).

To furnish this gap, numerous cryptography algorithms such as, covert channels, anonymity, and watermarking techniques projected on hidden and secret communication algorithms have been studied. Out of all these algorithms, due to reasons of popularities and versatilities, digital signal/image processing methods have been heavily applied by researchers for the purpose of secret communication and information assurance development during recent decades (Tan, 2008).

In digital image methods, Fourier transforms generally used to introduce the discrete domains of frequency representation for absolutely summable sequences with other transforms of generalized frequency-domain representation such as z-transforms. For arbitrary sequences, these transfer several properties to further improve the level of security of the hidden information (Proakis and Manolakis, 2008).

2 Related works

Due to pervasive need for data security and confidentiality, cryptosystem methods have emerged as popular encryption standards during recent decades and many researchers have worked in this filed to unveil number of such algorithms (Proakis and Manolakis, 2008; Diniz et al., 2010) proposed the most primitive and powerful method in this category and pioneered an approach that substantially reduces the amount of computations involved in the Discrete Fourier Transform (DFT) algorithms. This led to the explosion of other security applications under DFT and other development of security-efficient algorithms collectively known as Fast Fourier Transform (FFT) algorithms. The journey later led by Duhamel and disclosed application of FFT radix during 1986 and had been followed and redefined by several researchers during last two decades giving rise to several interesting encryption techniques (Hatem Majeed, 2021; Al-din Abed and Noaman, 2019).

Mishra et al. in 2012 developed a cryptosystem using the Fibonacci-Lucas Transformation (Kaur and Kumar, 2020) in which recursive sequence technique was applied. A paper on geometric series for encryption/decryption was proposed by Hatem Majeed (2021). Mathematical encryption model based on Taylor and McLaurin series was outlined as a new proposed methods by Al-din Abed and Noaman (2019), Noaman et al. (2020), and Gupta et al. (2020). Hughes made a study on Length-Based Attacks for Certain Group Based Encryption Rewriting Systems in which a probabilistic attack on public key cryptosystems that is based on the word/conjugacy problems (Hughes and Tannenbaum, 2002). In all such above schemes, Other encryption studies on properties of word problems while the conjugacy problem has no known polynomial solution was done by Wang et al. (2019), Hou et al. (2020), Abdalla et al. (2018), Belazi et al. (2018), Li et al. (2020), Wu et al. (2023), Ye et al. (2018), Özkaynak (2018), Song et al. (2021), Damrudi and Ithnin (2013), Hai et al. (2018), Zhang et al. (2021), and Kamara et al. (2012).

To achieve smarter encryption, extensive investigation was conducted on image processing encryption by Mishra et al. (2012), Kaur and Kumar (2020), Sher and Ahmad (2019), Ghafari (2024), Iqbal (2024), Li et al. (2017), and Gao et al. (2022) either on Fibonacci-Lucas Transformation techniques or non-dominated sorting genetic algorithm-based chaotic maps in order to review the comprehensive Encryption Techniques on computational Methods by Chaos based efficient selective image encryption properties by Gupta et al. (2020), Mishra et al. (2012), Kaur and Kumar (2020), Sher and Ahmad (2019), Ghafari (2024), Li et al. (2020), Wu et al. (2023), Ye et al. (2018), Özkaynak (2018), Iqbal (2024), and Lauter et al. (2011).

Since it is essential to ensure data security whether on transit or rest, the safety of the transferred and shared data remains predominantly in demand in today's comamercial worlds. Hence, some cryptography approaches employ different mathematical structural operations in substituting, replacing or permuting the input plaintext to achieve security mechanisms (Noaman et al., 2020; Gupta et al., 2020; Mishra et al., 2012; Kaur and Kumar, 2020; Sher and Ahmad, 2019; Wang et al., 2019; Hou et al., 2020; Belazi et al., 2018; Ghafari, 2024; Li et al., 2020; Wu et al., 2023; Ye et al., 2018; Özkaynak, 2018; Song et al., 2021; Oleksandr et al., 2022; Kamara et al., 2012).

In essence, encryption schemes employ security algorithms to deal with computer-related security incidents on assets that are subject to a variety of threats with varying time and space for which individuals and institutions have taken various measures to protect them, many of these security algorithms and applications were developed only to cover the trivial management aspects and other architectures of security mechanisms that inevitably proves core to prevent all sorts of vulnerabilities against the future chosen-plaintext and the chosen-ciphertext attacks. So, in a nutshell, single/dual key sensitivity is the bottom-line security feature while developing any cryptography algorithms (Stallings, 2018; Chillotti et al., 2019; Cash et al., 2015; Andreeva et al., 2024; Sakzad et al., 2018; Chen et al., 2021; Fan et al., 2022).

3 Properties of the Fast Fourier Transform

This section sketches out the theoretical background of FFT and their holistic contextual parameters as cryptography development process together with Split-Radix FFT algorithm.

Part A introduces the fundamental concepts of Fourier Transform properties geared toward enctyption process starting out with change variables of z-transform properties. Part B describes DFT Model. Part C discusses the configuration of FFT algorithm and finally part D presents the Proposed SRFFT Model.

3.1 Z-transforms parameters

The general z transform of a sequence x(n) is defined as

$\begin{array}{l}X(z)=Z\{x(n)\}={\displaystyle \sum _{k=-\infty }^{\infty }}x(n)z^{-n}\end{array}$

Where z is a complex variable whose function X(z) is only defined for the regions of the complex plane in which the summation on the right converges. Likewise, any discrete-time signal x(n) can become expressible as

$\begin{array}{ll}x(n)={\displaystyle \sum _{k=-\infty }^{\infty }}x(k)\delta (n-k)& (1)\end{array}$

Whose output function can be again defined as:

$\begin{array}{ll}y(n)={\displaystyle \sum _{k=-\infty }^{\infty }}x(k)h(n-k)& (2)\end{array}$

Provided with ordinary unit step of $(n)=\{\begin{array}{c}1,n\ge 0\\ 0,n<0\end{array}$, the unit step can be expressed as:

$\begin{array}{l}u(n)={\displaystyle \sum _{k=0}^{\infty }}\delta (n-k)\end{array}$

According to Hughes and Tannenbaum and Proakis and Manolakis (Hughes and Tannenbaum, 2002; Proakis and Manolakis, 2008), the change variable l = n − k can be embedded into Equation 1 and rewritten as:

$\begin{array}{l}y(n)={\displaystyle \sum _{k=-\infty }^{\infty }}x(n-l)h(l)\end{array}$

y(n) can now be interpreted as the result of the convolution of the excitation x(n) and the system impulse response h(n). The entire convolution operation shorthand notation, as given in Equations 1, 2 can be redefined as:

$y(n)=x{(n)}^{\ast }h(n)=h{(n)}^{\ast }x(n)$

Suppose now that the output y(n) of the system with impulse response h(n) becomes the new excitation for the system with impulse response h ´(n). In this case, the response outputs:

$\begin{array}{l}y(n)={\displaystyle \sum _{k=-\infty }^{\infty }}x(k)h(n-k)\\ ý(n)={\displaystyle \sum _{k=-\infty }^{\infty }}y(l)\acute{h}(n-l)\end{array}$

Obviously, substituting the impulse response output with the excitation, the following equation is generated.

$\begin{array}{l}ý(n)={\displaystyle \sum _{k=-\infty }^{\infty }}\left({\displaystyle \sum _{k=-\infty }^{\infty }}x(k)h(l-k)\right)\acute{h}(n-l)\\ ={\displaystyle \sum _{k=-\infty }^{\infty }}x(k)\left({\displaystyle \sum _{k=-\infty }^{\infty }}h(l-k)\acute{h}(n-l)\right)\end{array}$

In the end, by performing the change variable again of l = n − r, the above equation becomes the new convolution law of the combined two subsystems.

$\begin{array}{l}ý(n)={\displaystyle \sum _{k=-\infty }^{\infty }}x(n-k)(h{(k)}^{*}\acute{h}(k))\end{array}$

3.2 The fourier transforms

Based on Tan (2008), Diniz et al. (2010), and Kamara et al. (2012), different fields apply different Fourier transform laws to different paradigms. As was the case with z-transform, the Fourier transform X(e^jω) of a sequence x(n) equals to its z-transform X(z) at z = e^jω. Therefore, most properties of the Fourier transforms derive their applications from those of the z-transform with simple substitution of the z by ẽ^jω.

DFT corresponds to samples of the general Fourier transforms, its properties are closely related to those of the Fourier transform. However, one major difference being that N samples from the Fourier transform corresponding to the periodic repetition of the signal x(n) with period N can be reversibly recovered as shown by the following DFT and IDFT equations, respectively.

$\begin{array}{ll}X(k)={\displaystyle \sum _{k=-\infty }^{\infty }}x(n)W_N^{kn},for0\le k\le N-1& (3)\end{array}$

$\begin{array}{ll}x(n)=\frac{1}{N}{\displaystyle \sum _{k=-\infty }^{\infty }}X(k)W_N^{-kn},for0\le n\le N-1& (4)\end{array}$

From Equations 3, 4 observations, it becomes apparent that N² complex multiplications whose complexities grow with the square of the signal length might unavoidably be needed. This severely limits the application of DFT in practical sense particularly for lengthy computations. Fortunately, Cooley and Tukey (1965) proposed an efficient algorithm to compute the DFT, which requires lesser number of complex multiplications on the order of Nlog₂N called Fast Fourier Transform (FFT) that splits the N into N = 2ⁱ summation of two mutual parts, one part handling the even-indexed x(n) and the other dealing with the odd-indexed x(n) part. Based on Proakis and Manolakis (Proakis and Manolakis, 2008), the summation on the even/odd combination, each summation represents size N/2 of the distinct FFT size N and can be computed through the addition of two FFTs of size N/2 as elucidated by the following summation:

$\begin{array}{r}X(k)={\displaystyle \sum _{n=0}^{N-1}}x(n)W_N^{kn}\\ ={\displaystyle \sum _{k=0}^{(N/2)-1}}x(2n)W_N^{2nk}+{\displaystyle \sum _{k=0}^{(N/2)-1}}x(2n+1)W_N^{(2n+1)k}\end{array}$

Therefore, the overall FFT computation complexity of the DFT requires $2{(\frac{N}{2})}^2+N$ complex multiplications only. Since FFT's ${\frac{N}{2}}^2+N$ is smaller than N² for N > 2 the FFT provides a decrease in complexity when compared with the usual DFT computations and preferable in practical applications.

3.3 Proposed Split Radix FFT algorithm

According to Diniz et al., Hatem Majeed, and Al-din Abed and Noaman (Diniz et al., 2010; Hatem Majeed, 2021; Al-din Abed and Noaman, 2019), the Split Radix FFT (SRFFT) algorithm finds its way from the inspection of FFT with radix-2 decimation-in-frequency of accepting even-numbered data points of the FFT and can be computed independently of the odd-numbered data points. The SRFFT algorithm extends use of FFT radix-2 and FFT radix-4 by exploiting the idea of splitting them into a decomposition that allows to interleave in the same FFT radix-length algorithm. In radix-4 FFT, sample N = 2²ⁱ is used to acheive more space than radix-2 algorithms, radix-4 FFT algorithms can save us additional time economy in the required number of complex computations. The derivation of the radix-4 length-N sequence can also be divided into four sequences of length N/4 to be a parallel with those of the radix-2 algorithms.

The radix-2, radix-4 merged as split-radix for even and odd-numbered points of sample N can be given by Equations 5–7, respectively:

$\begin{array}{ll}X(k)={\displaystyle \sum _{n=0}^{N-1}}x(n)W_N^{kn}=X(2k)+X(4k+1)& (5)\end{array}$

$\begin{array}{ll}X(2k)={\displaystyle \sum _{n=0}^{\frac{N}{2}-1}}\left[x(n)+x+\left(n+\frac{N}{2}\right)\right]W_{\frac{N}{2}}^{nk}& (6)\end{array}$

$\begin{array}{l}fork=0,1,...\frac{N}{2}-1\end{array}$

The odd-numbered samples X(2k + 1) of the DFT requires the pre-calculations of phase factors of $W_N^n$ on radix-4 of N point of the DFT is given by:

$\begin{array}{l}X\left(4k+1\right)={\displaystyle \sum _{n=0}^{\frac{N}{4}-1}\{\left[x\left(n\right)-x\left(n+\frac{N}{2}\right)\right]}\\ -j\left[x\left(n+x+\frac{N}{2}\right)-x\left(n+\frac{3N}{4}\right)\right]\}{W}_N^n{W}_{N/4}^{kn}& (7)\end{array}$

Based on Oleksandr et al. and Hsue (Dobraunig et al., 2020; Oleksandr et al., 2022; Hsue, 2020), The technology of cryptography obtains signal spectrum components in detail, therefore, it has been theoretically and experimentally proven that the FFT provides sufficient guarantee for most practical applications since it is possible to reconstruct real signals of any data transmitted from the cloud or the other way round.

4 Data ciphering

Cipher is a method of securing data so that only a legitimate sender can cipher message through the encryption algorithm. A legitimate person, can on the other hand, decipher the message using the provided key, while illegal person, can't (Manikandaprabhu and Samreetha, 2024; Shi et al., 2023; Srivastava and Kuma, 2023; Tan, 2008). Most techniques to accomplish ciphering and deciphering fall into symmetrical and asymmetrical key cipher groupings. In the symmetrical key cipher system, one key is used for both to cipher and decipher the process. In asymmetrical key, two keys called public and private kays are used for in such a way that the first key is used for ciphering and the second key which is mathematically correlated is used for deciphering (Hughes and Tannenbaum, 2002; Diniz et al., 2010; Al-din Abed and Noaman, 2019). The proposed method utilizes the block cipher since SRFFT algorithm handle N block data size.

4.1 Calculation of SRFFT algorithm

SRFFT algorithm can be calculated via forward and backward computations to yield encryption/decryption process with arbitrarily N block plaintext. In some cases, SRFFT is derived repeatedly applying integration by parts or conveniently by use of algebraic systems to calculate encryption/decryption through the summations of the following Equation 8.

$\begin{array}{ll}X(k)={\displaystyle \sum _{n=0}^{N-1}}x(n)W_N^{kn},0\le k\le N-1& (8)\end{array}$

The summation can be expanded into matrix form with Polar coordination as follows:

$\begin{array}{l}\left[\begin{array}{c}X(0)\\ X(1)\\ X(2)\\ X(3)\\ \end{array}\right]=\left[\begin{array}{c}{W}_4^0{W}_4^0{W}_4^0{W}_4^0\\ W_4^0{W}_4^1{W}_4^2{W}_4^3\\ W_4^0{W}_4^2{W}_4^4{W}_4^6\\ W_4^0{W}_4^3{W}_4^6{W}_4^9\\ \end{array}\right]=\left[\begin{array}{c}x(0)\\ x(1)\\ x(2)\\ x(3)\\ \end{array}\right]\end{array}$

Substituting the Polar coordination periodicity directly into Euler theory:

$\begin{array}{l}\left[\begin{array}{c}X(0)\\ X(1)\\ X(2)\\ X(3)\\ \end{array}\right]=\left[\begin{array}{c}1111\\ 1-j-1j\\ 1-11-1\\ 1j-1-j\\ \end{array}\right]=\left[\begin{array}{c}x(0)\\ x(1)\\ x(2)\\ x(3)\\ \end{array}\right]\end{array}$

Proposed SRFF algorithm can exhibit efficient speed of encryption/decryption process on ordinary computer time and space resources and can better protect against unauthorized access to signals transferred to such computer systems (Oleksandr et al., 2022; Gao et al., 2022).

5 SRFFT algorithm description

5.1 Key generation phase

1. Choose first number N as a first key whose size is as large as the plaintext file.

2. Choose second number M as a second key whose size is as large as the ciphertext.

3. Send key M only without the SRFFT equation to the legitimate recipients.

5.2 Encryption phase

1. Generate first key N from the plaintext size.

2. Check the ASCII size of the plain text P(n)= N for 0 ≤ n ≤ N − 1.

3. Apply encryption equation of SRFFT algorithm.

$\begin{array}{l}C(k)=\left({\displaystyle \sum _{n=0}^{N-1}}P(n)W_N^{kn}\right)mod128\end{array}$

4. Compute k^th cipher of the plaintext.

$\begin{array}{r}C\left(k\right)=({\displaystyle \sum _{n=0}^{N-1}P(n)e^{jk}}=P(0)e^{jk}+P(1)e^{jk}\\ +\dots +P(N-1)e^{jk})mod128\end{array}$

5. Substitute the real and imaginary part of the complex quantities into equivalent ASCII code of cipher function C(k).

6. Repeat steps 1–5 until the end of the plain text message.

5.3 Decryption phase

1. Let the second key = M.

2. Check ASCII size of the cipher text.

3. Check ASCII code of the cipher text C(k)= M, for 0 ≤ k ≤ M− 1.

4. Apply decryption of SRFFT of the inverse equation formula.

$\begin{array}{l}P(n)=\left(\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}}C(k)W_M^{-kn}\right)mod128\end{array}$

5. Compute plaintext of the n^th ciphertext.

$\begin{array}{r}P(n)=(\frac{1}{M}{\displaystyle \sum _{n=0}^{M-1}C(k)e^{-jk}=C(0)}{e}^{-jk}\\ +C(1)e^{-jk}+C(2)e^{-jk}+\dots +C(N-1)e^{-jk})mod128\end{array}$

6. Substitute the real and imaginary parts of the complex quantities into equivalentt ASCII code of plain function P(n).

7. Repeat steps 1–5 until the end of the plain text message.

6 Examples

6.1 Generating keys

1. Choose first number N as a first key whose size is as large as the plaintext file.

2. Choose second number M as a second key whose size is as large as the ciphertext.

3. Send key M only without the SRFFT equation to the legitimate recipients.

6.2 Encryption phase

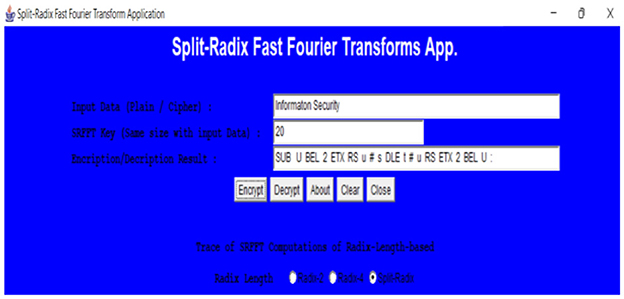
1. Let plaintext be “Information Security.”

2. Check ASCII values of all plaintext characters from I to y as: 73 110 102 111 114 109 97 116 105 1111~10 28 115 101 99 117 114 105 116 121 and check the key N = 20.

3. Compute the cipher using SRFFT equation starting from the first plain in the message.

4. Let n = 0 for 0 ≤ n ≤ N − 1 and

$\begin{array}{r}C(0)=\left({\displaystyle \sum _{n=0}^{19}P(n)e^{j0}}\right)mod128\\ =(P(0)e^{j0}+P(1)e^{j0}+P(2)e^{j0}+\\ \dots +P(19)e^{-j0})mod128\\ =P(0)+P(1)+P(2)+\dots +P(19)\\ =(73+110+102+\dots +121)mod128\\ =26\end{array}$

5. Compute ASCII of cipher c(0)=”SUB.”

6. Repeating steps 1-5 until end result of ciphertext message becomes:

26, 58.2 - 15.2i, 85.2 + 66.4i,−7.2 - 51.1i,−50.3 + 88.4i,−3.0 - 43.i,−30.4 + 79.9i,−117.3 - 94.4i, +35.8 + 61.2i,−115.6 - 47.2i, + 16.0,−115.6 + 47.2i, +35.8 - 61.2i,−117.3 + 94.4i,−30.4 - 79.9i,−3.0 + 43.i,−50.3 - 88.4i,−7.2 + 51.1i,−85.1 - 66.4i, + 58.2 + 15.2i.

6.3 Decryption phase

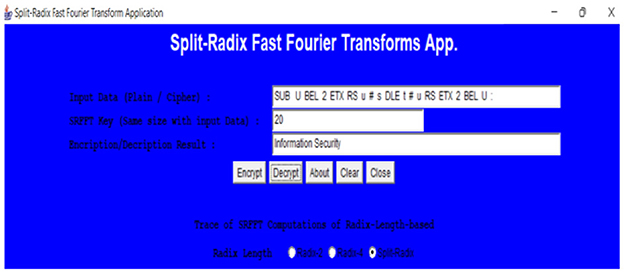
1. Let ciphertext be:

“SUB : U BEL 2 ETX RS u # s DLE t # u RS ETX 2 BEL U :” and set the key M = 20.

2. Set the the real and imaginary parts be equivalent numerically to the ciphertext strings from ASCII as:

26, 58.2 - 15.2i, 85.2 + 66.4i,−7.2 - 51.1i,−50.3 + 88.4i,−3.0 - 43.i,−30.4 + 79.9i,−117.3 - 94.4i, +35.8 + 61.2i,−115.6 - 47.2i, + 16.0,−115.6 + 47.2i, +35.8 - 61.2i,−117.3 + 94.4i,−30.4 - 79.9i,−3.0 + 43.i,−50.3 - 88.4i,−7.2 + 51.1i,−85.1 - 66.4i, + 58.2 + 15.2i.

3. Compute the first cipher using inverse SRFFT equation starting from the first cipher in the message.

4. Let k = 0 for 0 ≤ k ≤ N − 1 and

$\begin{array}{r}P(0)=\left(\frac{1}{M}{\displaystyle \sum _{n=0}^{19}C\left(k\right)e^{-j0}}\right)mod128\\ =(C(0)e^{-j0}+C(1)e^{-j0}+C(2)e^{-j0}+\\ \dots +C\left(19\right)e^{-j0})mod 128\\ =C(0)+C(1)+C(2)+\dots +C(19)\\ =(26+58.2-15.2i+85.2+66.4i,+\dots +58.2\\ +15.2i)mod128\\ =73\end{array}$

5. Compute ASCII of plain p(0)=”i.”

6. Repeating steps 1-5 until end result of plaintext message: “information security.”

7 Simulation results and performance evaluation

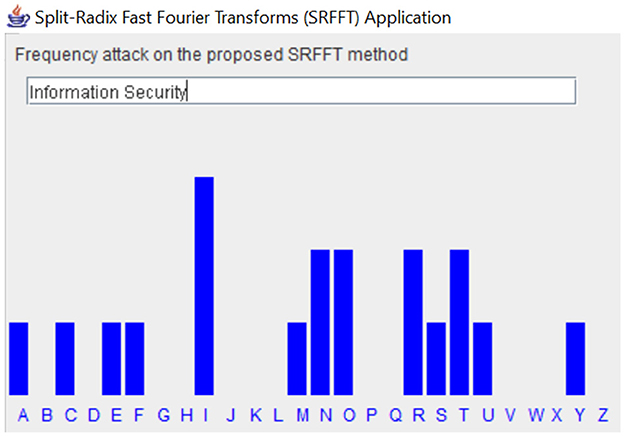
With regards to the standard cryptography technologies, the proposed method was simulated against majority cryptoanalysis attack techniques. Figure 1 aims to display simulated test possibility of breaking a SRFFT cipher code via the attacks of frequency of characters in the encrypted text. Through traces ran on comparative analysis with SRFFT encrypted text, the standard character frequency of the English language characters proves immaculate.

Figure 1

Figure 1. Frequency attacks.

Since polyalphabetic cipher worlds, the degree of improvement is measured on the size of the possible fixed keys, this mothod demonstrates that key to be used varies dynamically with input plain/cipher data sizes. Further, to appreciate both confidentiality and authentication under SRFFT, one can encrypt the plain message with N sized-key as private key which provides the complex quantities of intermediate real and imaginary numbers result as hashed digital signature output, and then use recipient's M sized-key to decrypt the cipher as public key for confidentiality purposes.

The design objective of SRFFT method, in fact, depends on the main SRFFT's permutation with sinusoidal waves as preferable over other cipher schemes. Figure 2 shows numerous traces of runs on SRFFT algorithm for encryption simulation showcasts, and as results, the plaintext along with variant key lengths produces remarkable cipher outputs of SRFFT computations with varied rounds of radix-lengths. In this way, SRFFT method becomes proven secure provided that the embedded complex hash functions of FFT algorithm bring with themselves some higher level of reasonable cryptographic strengths.

Figure 2

Figure 2. SRFFT algorithm encryption traces.

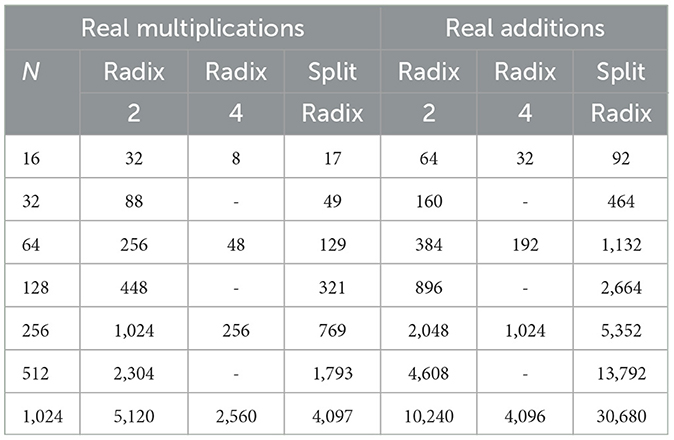
Therefore, for Radix-2 complexity, the total number of multiplication and addition achieved becomes $(\frac{N}{2}){log}_{2}N$ and Nlog₂N, respectively. While for Radix-4′s total complexity, in terms of number of multiplication and addition achieved becomes $(\frac{N}{4}){log}_{4}N$ and Nlog₄N while finally, the complexity of Split-Radix FFT total number of multiplication and addition achieved becomes $(\frac{N}{2}){log}_{2}N-N+1$ and (3N-4)log₂N + 4, respectively (Proakis and Manolakis, 2008; Diniz et al., 2010; Hatem Majeed, 2021; Al-din Abed and Noaman, 2019).

Likewise, numerious decryption traces run is displayed by Figure 3 and as results, the output plain of the decryption traces proves remarkable decryption.

Figure 3

Figure 3. SRFFT algotithm decryption traces.

While for Radix-4′s total complexity, in terms of number of multiplication and addition achieved becomes $(\frac{N}{4}){log}_{4}N$ and Nlog₄N while finally, the complexity of Split-Radix FFT total number of multiplication and addition achieved becomes $(\frac{N}{2}){log}_{2}N-N+1$ and (3N-4)log₂N + 4, respectively (Proakis and Manolakis, 2008; Diniz et al., 2010; Hatem Majeed, 2021; Al-din Abed and Noaman, 2019).

Table 1 presents main real part multiplications and additions output for N−Point FFT algorithms with complex valued data using Radix-2, Radix-4, and Split-Radix FFT comparisons. It is worth noting that of all algorithms, the Split-Radix FFT proves safer and smarter in producing the lowest numbers of multiplications/additions and preferable in many practical applications over the literature (Oleksandr et al., 2022; Gao et al., 2022).

Table 1

Table 1. Number of main real multiplications and additions for N point FFT algorithm.

8 Conclusion

This study introduces the splitting technique of two radix-methods through swapping mechanism for the sake of the enhancement of cryptography process. Based on SRFFT algorithm, as a hybridized method whose properties are drawn from Radix-2 and Radix-4FFT, the performance investigation achieves reliable encryption process with security traits of accuracy and efficiency as well as the practicality of the proposed algorithms are explored through analysis of comparative evaluations with other methods on engineering applications. Additionally, the following conclusions are summarized: (1) To demonstrate the use of key dynamically variant with input plain/cipher data sizes. (2) To appreciate SRFFT one can encrypt the plain message with M keys as a private key, which contains the complex quantities of intermediate real and imaginary numbers result hashed as digital signature output which the recipient can use sender's M key to decrypt the cipher as public key for confidentiality purposes.

Data availability statement

The datasets presented in this article are not readily available because, since this research is computer network simulation. Its data set is primarily input array of any data (alphanumeric). Requests to access the datasets should be directed to Abdulle Hassan Mohamud via Y2lnYWxlaEBnbWFpbC5jb20=.

Author contributions

AM: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research work was funded by CRD Unit of Simad University.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdalla, M., Bellare, M., and Neven, G. (2018). Robust encryption. J Cryptol. 2018, 308–312.

Google Scholar

Al-din Abed, B., and Noaman, S. (2019). McLaurin series as a new technique to improve encryption process. J Phys Conf Ser. 1294:e042008. doi: 10.1088/1742-6596/1294/4/042008

Crossref Full Text | Google Scholar

Andreeva, E., Bogdanov, A., Luykx, A., Mennink, B., Nandi, M., Tischhauser, E., et al. (2024). The COLM authenticated encryption scheme. J Cryptol. 37:15. doi: 10.1007/s00145-024-09492-8

Crossref Full Text | Google Scholar

Belazi, A., Khan, M., Abd El-Latif, A., and Belghith, S. (2018). Efficient cryptosystem approaches: S-boxes and permutation-substitution-based encryption. Nonlinear Dyn. 87, 337–361. doi: 10.1007/s11071-016-3046-0

Crossref Full Text | Google Scholar

Cash, D., Grubbs, P., Perry, J., and Ristenpar, T. (2015). Leakage-Abuse Attacks Against Searchable Encryption. ACM, 668–672.

Google Scholar

Chen, L., Huang, K., Manulis, M., and Sekar, V. (2021). Password-authenticated searchable encryption. Int J Inform Secur. 20, 675–693. doi: 10.1007/s10207-020-00524-5

Crossref Full Text | Google Scholar

Chillotti, I., Gama, N., and Georgieva, M. (2019). Malika Izabachène “Robust encryption.” J Cryptol. 3, 35–38. doi: 10.1007/978-3-642-14712-8_3

Crossref Full Text | Google Scholar

Cooley, J. W., and Tukey, J. W. (1965). An algorithm for the machine computation of complex Fourier series. Math. Comput. 19, 297–301.

Google Scholar

Damrudi, M., and Ithnin, N. Numerical analysis of parallel modular exponentiation for RSA using interconnection networks. ScienceAsia. (2013) 39S:103–106. doi: 10.2306/scienceasia1513-1874.2013.39S.103

Crossref Full Text | Google Scholar

Diniz, P., Silva, E., and Netto, S. (2010). Digital Signal Processing, 2nd edn (London: Pearson; Cambridge Press), 116–184.

Google Scholar

Dobraunig, C., Eichlseder, M., Mendel, F., and Schläffer, M. (2020). Lightweight authenticated encryption and hashing. J Cryptol. 34:33. doi: 10.1007/s00145-021-09398-9

PubMed Abstract | Crossref Full Text | Google Scholar

Fan, H., Li, K., Zhu, X., Zhang, L., and Liu, M. (2022). ATP-induced emergent circularly polarized luminescence and encryption. J Cryptol. 61:e202200727. doi: 10.1002/ange.202200727

PubMed Abstract | Crossref Full Text | Google Scholar

Gao, X., Mou, J., Xiong, L., Sha, H., Yan, H., Cao, Y. A., et al. (2022). fast and efficient multiple images encryption based on single-channel encryption and chaotic system. Nonlinear Dyn. 7, 613–636. doi: 10.1007/s11071-021-07192-7

Crossref Full Text | Google Scholar

Ghafari, A. (2024). Image encryption-compression method via encryption based sparse decomposition. Multimed Tools Appl. 6, 19129–19160. doi: 10.1007/s11042-023-16163-6

Crossref Full Text | Google Scholar

Gupta, A., Singh, D., and Kaur, M. (2020). An efficient image encryption using non-dominated sorting genetic algorithm-III based 4-D chaotic maps. J Ambient Intell Humaniz Comput. 11, 1309–1324. doi: 10.1007/s12652-019-01493-x

Crossref Full Text | Google Scholar

Hai, J., Li, T., Su, J., Liu, W., Ju, Y., Wang, B., et al. (2018). Reversible response of luminescent terbium(III)-nanocellulose hydrogels to anions for latent fingerprint detection and encryption. Stimuli-Responsive Mater. 130, 6902–6906. doi: 10.1002/ange.201800119

PubMed Abstract | Crossref Full Text | Google Scholar

Hatem Majeed, S. (2021). Cryptography model based on the principles of the geometric series. J Al-Qadisiyah Comput Sci Math. 13, 114–119. doi: 10.29304/jqcm.2021.13.3.851

Crossref Full Text | Google Scholar

Hou, Y., Zhang, Z., Lu, S., Yuan, J., Zhu, Q., Chen, W., et al. (2020). Highly emissive perylene diimide-based metallacages and their host–guest chemistry for information encryption. J Am Chem Soc. 4, 18763–18770. doi: 10.1021/jacs.0c09904

PubMed Abstract | Crossref Full Text | Google Scholar

Hsue, W. (2020). Enhancing security of double random phase encryption schemes based on discrete fractional Fourier transforms. 2020 IEEE Int Symp Circuit Syst. 2020, 2–5. doi: 10.1109/ISCAS45731.2020.9180524

Crossref Full Text | Google Scholar

Hughes, J., and Tannenbaum, A. (2002). Length-Based Attacks for Certain Group Based Encryption Rewriting Systems, Workshop SECI02 SEcurite de la Communication sur Intenet (Tunis), 2–6. doi: 10.48550/arXiv.cs/0306032

Crossref Full Text | Google Scholar

Iqbal, N. (2024). Image encryption using Queen. Multimed Tools Appl. 83, 10551–10585. doi: 10.1007/s11042-023-15674-6

PubMed Abstract | Crossref Full Text | Google Scholar

Kamara, S., Papamanthou, C., and Roeder, T. (2012). Dynamic Searchable Symmetric Encryption. CCS'12, October 16–18 (Raleigh, North Carolina), 965–969.

Google Scholar

Kaur, M., and Kumar, V. A. (2020). comprehensive review on image encryption techniques. Archiv Comput Methods Eng. 27, 15–43. doi: 10.1007/s11831-018-9298-8

Crossref Full Text | Google Scholar

Lauter, K., Naehrig, M., and Vaikuntanathan, V. (2011). Can Homomorphic Encryption Be Practical? CCSW'11, October 21 (Chicago, IL), 113–121.

Google Scholar

Li, C., Luo, G., and Qin, K. L. C. (2017). An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 87, 127–133. doi: 10.1007/s11071-016-3030-8

Crossref Full Text | Google Scholar

Li, J., Huang, X., Zhao, X., Chen, L., and Yan, X. (2020). pH-responsive torpedo-like persistent luminescence nanoparticles for autofluorescence-free biosensing and high-level information encryption. Angewandte Chemie. 133, 2428–2435. doi: 10.1002/ange.202011553

PubMed Abstract | Crossref Full Text | Google Scholar

Manikandaprabhu, P., and Samreetha, M. (2024). A review of encryption and decryption of text using the AES algorithm. Int J Sci Res Eng Trends. 10, 400–404.

Google Scholar

Mishra, M., Adhikary, P. C., and Kumar, S. (2012). Image encryption using Fibonacci-Lucas transformation. Int J Cryptogr Inform Secur. 2, 131–134. doi: 10.5121/ijcis.2012.2312

Crossref Full Text | Google Scholar

Noaman, A., Najim Al-din, A., and Abdul-Kader, S. (2020). A new mathematical model to improve encryption process using Taylor expansion. In: 1st International Conference of Information Technology to Enhance E-Learning and Other Application (IT-ELA 2020), 36–39.

Google Scholar

Oleksandr, M., Doukas, N., Alireza, M., and Bardis, N. (2022). Method of protecting data processed by the discrete Fourier transform in remote computer systems. In: 12th International Conference on Dependable Systems, Services and Technologies (DESSERT), 3–6.

Google Scholar

Özkaynak, F. (2018). Brief review on application of nonlinear dynamics in image encryption. Nonlinear Dyn. 92, 305–313. doi: 10.1007/s11071-018-4056-x

Crossref Full Text | Google Scholar

Proakis, J., and Manolakis, D. (2008). Digital Signal Processing, 4th edn (London: MIT Laboratories; Pearson), 518–533.

Google Scholar

Sakzad, A., Vo, V., and Nepal, S. (2018). Practical Backward-Secure Searchable Encryption from Symmetric Puncturable Encryption. CCS'18, October 15–19 (Toronto, ON), 965–969.

Google Scholar

Sher, J., and Ahmad, J. (2019). Chaos based efficient selective image encryption. Multidim Syst Sign Process. 18, 943–961. doi: 10.1007/s11045-018-0589-x

Crossref Full Text | Google Scholar

Shi, Q., Zhou, X., Xu, J., Zhang, J., Wang, N., Zhang, G., et al. (2023). Dendritic quaternary-encoded oligourethanes for data encryption. Angew Chem Int Ed. 62:e202214695. doi: 10.1002/anie.202214695

PubMed Abstract | Crossref Full Text | Google Scholar

Song, Y., Lu, M., Mandl, G. A., Xie, Y., Sun, G., Chen, J., et al. (2021). Energy migration control of multimodal emissions in an Er³⁺-doped nanostructure for information encryption and deep-learning decoding. Angew Chem Int Ed Engl. 60, 23791–23799. doi: 10.1002/anie.202109532

PubMed Abstract | Crossref Full Text | Google Scholar

Srivastava, A., and Kuma, A. (2023). Robust approach to secure data encryption: AES RSA hybrid with Kernel key protection. Res Sq. 1, 2–16. doi: 10.21203/rs.3.rs-3565782/v1

Crossref Full Text | Google Scholar

Stallings, W. (2018). Cryptography Network Security Principles and Practice, Global Edition, 7th edn (London: Pearson), 103–144.

Google Scholar

Tan, L. (2008). Digital Signal Processing Fundamentals and Applications, 1st edn (Amsterdam: Elsevier), 92–105.

Google Scholar

Wang, J., Ma, J., Zhang, J., Fan, Y., Wang, W., Sang, J., et al. (2019). Advanced dynamic photoluminescent material for dynamic anticounterfeiting and encryption. ACS Appl Mater Interfaces. 2019, 35871–35875. doi: 10.1021/acsami.9b10870

PubMed Abstract | Crossref Full Text | Google Scholar

Wu, Y., Chen, X., and Wu, W. (2023). Multiple stimuli-response polychromatic carbon dots for advanced information encryption and safety. Small. 19, 10551–10585. doi: 10.1002/smll.202206709

PubMed Abstract | Crossref Full Text | Google Scholar

Ye, G., Pan, C., Huang, X., and Me, Q. (2018). An efficient pixel-level chaotic image encryption algorithm. Nonlinear Dyn. 94, 745–756. doi: 10.1007/s11071-018-4391-y

Crossref Full Text | Google Scholar

Zhang, Z., Lin, Y., Jin, J., Gong, L., Peng, Y., Song, Y., et al. (2021). Crystalline-phase-recognition-induced domino phase transition and luminescence switching for advanced information encryption. Mol Recogn Hot Pap. 60, 23373–23383. doi: 10.1002/anie.202110088

PubMed Abstract | Crossref Full Text | Google Scholar