
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Comput. Sci., 20 June 2024
Sec. Computer Vision
Volume 6 - 2024 | https://doi.org/10.3389/fcomp.2024.1386514
Introduction: State-of-the-art multi-modal brain tumor segmentation methods often rely on large quantities of manually annotated data to produce acceptable results. In settings where such labeled data may be scarce, there may be value in exploiting cheaper or more readily available data through clinical trials, such as Response Assessment in Neuro-Oncology (RANO).
Methods: This study demonstrates the utility of such measurements for multi-modal brain tumor segmentation, whereby an encoder network is first trained to regress synthetic “Pseudo-RANO” measurements using a mean squared error loss with cosine similarity penalty to promote orthogonality of the principal axes. Using oriented bounding-boxes to measure overlap with the ground truth, we show that the encoder model can reliably estimate tumor principal axes with good performance. The trained encoder was combined with a randomly initialized decoder for fine-tuning as a U-Net architecture for whole tumor (WT) segmentation.
Results: Our results demonstrate that weakly supervised encoder models converge faster than those trained without pre-training and help minimize the annotation burden when trained to perform segmentation.
Discussion: The use of cheap, low-fidelity labels in the context allows for both faster and more stable training with fewer densely segmented ground truth masks, which has potential uses outside this particular paradigm.
Gliomas are one of the most common primary brain malignancies, typically classified by cell type, grade, and location. Low-Grade Glioma (LGG) tends to offer a better prognosis for patients, whereas High-Grade Glioma (HGG) is characterized by their amorphous structure and low survivability (Lefkovits et al., 2022). Extreme cases of HGG can be further categorized as Glioblastoma (GBM) with a median survival period of 14 months. Among this, patients experience a survival rate of 39.7% after a year, which shrinks to a rate of 5%–9% after 5 years (Villa et al., 2018; Chukwueke and Wen, 2019). Magnetic Resonance Imaging (MRI) is widely used in the diagnosis and longitudinal assessment of gliomas, which can be highly variable in terms of location, size, and morphology. Quantifying tumor burden remains a key technical and clinical challenge that has prompted the development of automated image analysis techniques applied to clinical imaging data. Segmentation is a critical step in many automated pipelines, whereby the tumor region is delineated to provide area or volume estimates that aid in treatment response monitoring, surgical planning, and prediction of overall survival.
There is an enormous clinical impact for accurate brain tumor segmentation; by giving clinicians access to clearly delineate tumor boundaries, treatment is both more effective and less risky to undergo, which improves patient survivability. However, there are challenges posed by limited amount of well-annotated data that are available for several reasons; for example, deep learning methods typically require large amount of raw input data to perform effectively, which often cannot be effectively acquired in medicine.
Convolutional neural networks (CNNs) have been widely demonstrated as state-of-the-art for the segmentation of medical images, where much of the focus is on large manually annotated datasets. Increasingly, greater attention is being placed on methods that can leverage lower fidelity annotations to train deep networks with clinically acceptable performance. Weakly supervised learning invokes the principle that models trained on noisy or imprecise annotations under supervision can still learn meaningful representations and alleviate the burden of manual annotation. This is particularly valuable in the context of the segmentation of complex structures in three dimensions, such as brain tumors.
This study proposes a weakly supervised learning pre-training task for annotating a tumor's principal axes. To validate the approach, we derive a pseudo-measure similar to RANO, “Pseudo-RANO,” from the labels supplied as part of the Brain Tumor Segmentation (BraTS) dataset (Menze et al., 2014). “Pseudo-RANO” is defined as the bi-dimensional measure of the whole tumor (WT), compared with classical RANO, which is applied to the enhancing tumor (though the same principle could be applied to any tumor region). Examples of these measures are shown in Figure 1. We show that encoder–decoder networks trained initially on weak labels provide an early improvement in segmentation results following fine-tuning, specifically in terms of robustness to outliers and overall model performance. The proposed solution aims to offset the model time and complexity issues of large-scale annotation by providing pre-training tasks based on more readily available and cheap-to-produce data that are still associated with the downstream task. The ultimate aim is to improve both the performance and clinical viability of such models and provide a framework that can be applied in many contexts with only minor changes in the architectures used. Our main contributions are as follows:
1. We derive the weak annotation, “Pseudo-RANO,” for use as ground truth, formulated similarly to a classical RANO annotation.
2. We produce a novel weakly supervised approach for pre-training a tumor segmentation model using “Pseudo-RANO” regression, promoting orthogonality through a novel dual loss function.
3. We demonstrate how a “Pseudo-RANO” pre-trained U-Net encoder can reduce the data requirement and time needed to train models to convergence.
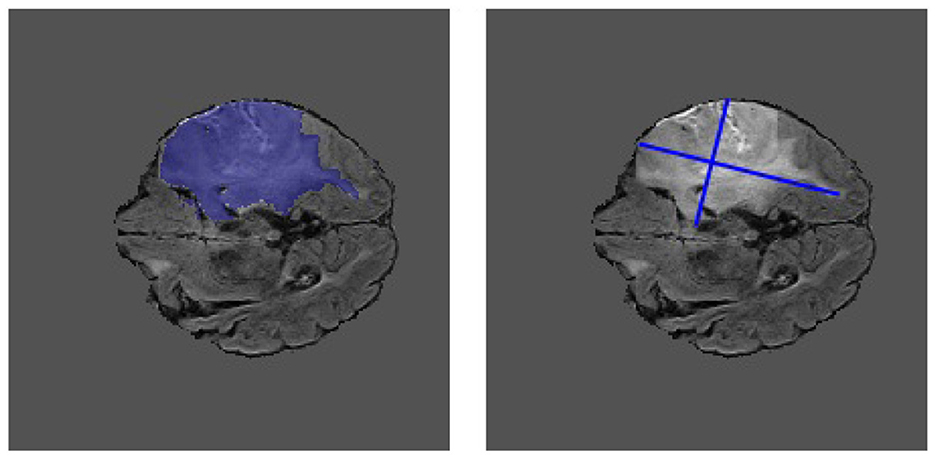
Figure 1. Example MRI slice from the BraTS 2018 dataset. The ground truth segmentation is shown overlaid on the image (left) alongside the extracted “Pseudo-RANO” measurement (right). The principal axes are approximately orthogonal to one another.
We discuss the application of pre-training, particularly in the context of weak supervision for medical deep learning approaches, so that we can gain a deeper understanding of the research area and the novel gaps that are available. Many methods for brain tumor segmentation provide high working results on medical images but have the downside of requiring either a large amount of input data to work effectively or complex or specialist annotations outside the clinical norm.
There is an increasingly more common requirement for computer-aided diagnosis (CAD) tools to include some form of artificial intelligence. In these cases, deep learning is integrated to reduce the long-term impact of time constraints, still utilizing specialist knowledge bases with a large number of innovative techniques and tools for brain tumor segmentation (Ranjbarzadeh et al., 2023; Panduri and Rao, 2024), including pipelines compromising of pre-processing, segmentation, and classification (Bhardawaj and Jain, 2024). These systems need to be in place in an evolving medical environment to complement clinicians as they work (Doi, 2007) rather than be used as an alternative to them.
Implementing a pre-training phase into a deep learning-based neural network is one of the ways that we can both offset and reduce performance loss, which can be observed within small data environments. In particular, we discuss using less involved medical data such as RANO, RECIST, or tumor circularity to support annotation, such as the study by Hu et al. (2020), which uses DICOM metadata such as probe type and study description as labels for adversarial training, alongside a context encoder trained to reconstruct missing patches of an ultrasound image. Methods have been shown to improve segmentation results and allow the model to converge much earlier while requiring fewer labeled examples. There is also research that has explored the use of encoder–decoder architectures to perform segmentation, specifically where the encoder is trained on lower fidelity labels, such as Hu et al. (2018) independently train the encoder as an optic disc localization network, where the weights are then frozen and the decoder trained for optic disc segmentation.
We compile a table showing methodological outputs and their reported evaluation measure and metric in Table 1 for the weak learning methods referenced in this study. Though the methods do not all uniformly improve on the quantitative results, those do not report similar outputs with much smaller quantities of fully annotated input data.
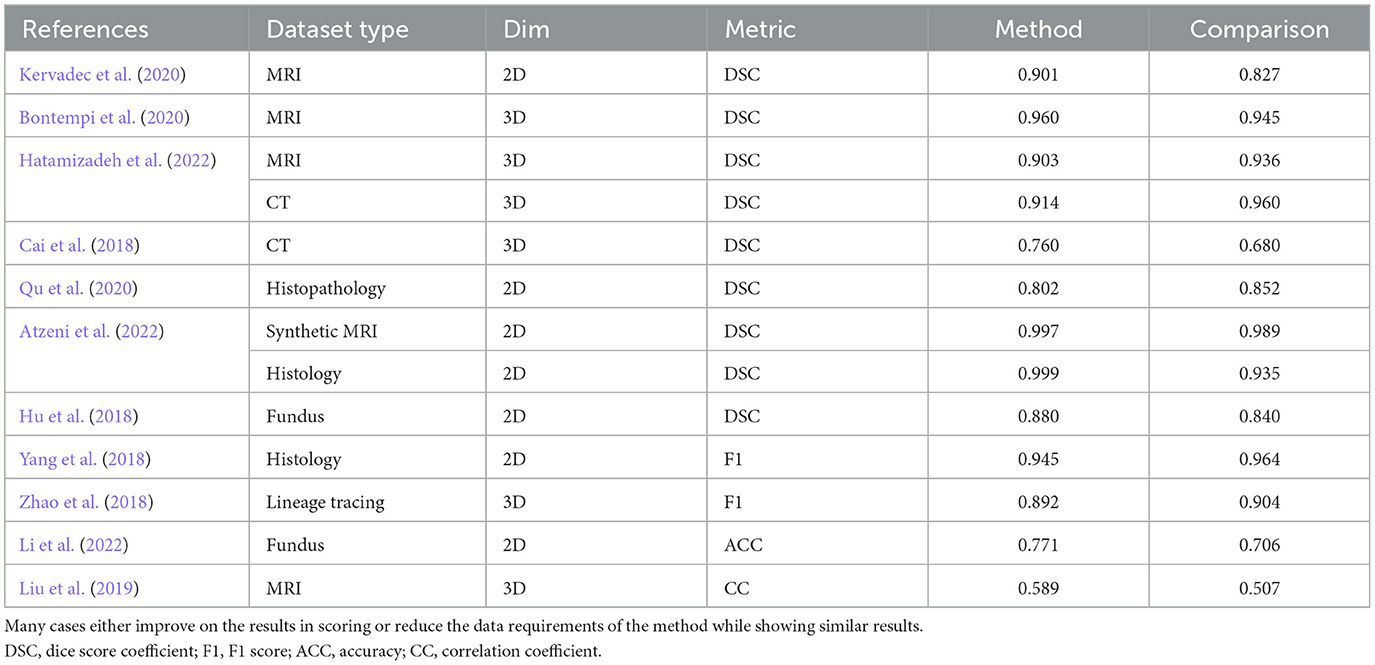
Table 1. A comparison of our results and those reported in the literature, showing data types, input dimensions, metrics reported, methods reported results, and the reported comparison results based on weakly supervised methods.
Weakly supervised pre-training tasks for medical image segmentation have been applied in different formats to solve many complex problems. Research completed by Kervadec et al. (2020) shows that global constraints and features derived from fixed bounding-box data can be utilized as pre-training tasks for segmentation, leveraging classical tightness as a setting and constraint for a deep learning model which is much more potent than standard cross-entropy. This method tested on MRI lesion data for both the prostate and glioma, approaching complete supervision levels and outperforming previously state-of-the-art methods. Alternatively, research by Bontempi et al. (2020) focuses on exploring both local and global spatial information, implementing segmentation for out-of-the-scanner volumetric T1-weighted data, exploiting an encoder–decoder structure with only convolutional blocks using atlas-based segmentation algorithms (FreeSurfer) to produce ground truth masks for the unknown data.
Similarly, others have explored the use of partial labels (i.e., only a subset of objects) to reduce the amount of annotated data needed for nuclei segmentation from histopathology images and Qu et al. (2020) extend point labels for cell nucleus into segmentation masks through a combination of regression models, probability maps, thresholding, and self-supervision, to train a deep CNN for lung cancer and multi-organ dataset segmentation. Utilizing bounding boxes to provide weak data for segmentation tasks in both 2D and 3D has applications within medical image processing; for example, Yang et al. (2018) produce a 2D deep learning method for extending extreme-point tilted bounding box annotations into rough segmentation masks, which are then further refined to fine masks using graph search methodologies, which is particularly useful in cases where multiple segmentations are present on a single image, reducing the potential for errors from bounding box overlap. The approach discussed by Zhao et al. (2018) provides better results in a similar amount of annotation time applied within the 3D domain in situations where only a tiny fraction of instances is required to have full volumetric annotations. At the same time, the remaining data comprise of 3D bounding boxes. This method proposes using a 3D instance segmentation model, including a mask-RCNN, to segment all objects of interest. Experimental results perform similarly to the best-known methods that use complete volumetric annotation for the same problem.
A wide variety of data can be considered “weak” in this context, such as those that use pixel-wise morphological features. The data leveraged in the study by Li et al. (2022) consist of gray-scale retinography images, which provide a baseline for coarse segmentation masks derived from gray-scale features. Several image segmentation algorithms are described, such as vessel segmentation and bright lesions, based on these gray-scale and morphological features to segment four variations of the mask, which are then applied to enhance the amount of labeled data from previously unlabeled datasets for the segmentation in a Residual-Attention U-Net (RAUNET). Solutions for clinical tasks outside of segmentation also remain essential for applying weak learning, data from the study by Liu et al. (2019), and leverage incomplete ground truth scores as data entries, estimating multiple clinical scores from several time points simultaneously. They define a neural network with weighted loss that can leverage all the data, where subject data with missing scores would previously be discarded.
In contrast to the bounding boxes previously outlined, Atzeni et al. (2022) use information directly from the input images, learning a single region of interest (ROI) per image, effectively creating a dense mask from weak annotations, then applying boundary image indices as an additional input label to improve training scores, optimizing dice rather than a proxy. Wang et al. (2020) present a quite different approach using pseudo-masks for training and then interatively learning pixel affinities and labeling information from weak, inaccurate data. This method uses energy minimization (EM) prediction as the proposed affinity, mining the confident regions of the generated map, where areas with a high confidence score (< 0.7) are expanded into a mask for the training of the model of a segmentation task.
Experimental methods were implemented using PyTorch-based architectures, consisting of a multi-stage learning pipeline and a regression-based encoder pre-training methodology. This is followed by a full tumor segmentation method that expands upon the previous study.
The BraTS dataset from 2018 was used for model development and evaluation (Menze et al., 2014; Bakas et al., 2017, 2018). The supplied data are comprised of four MRI sequences: T1-weighted (T1), T1 Contrast Enhanced (T1ce), T2-Fluid-attenuated inversion recovery (T2-FLAIR), and T2-weighted (T2), each of which reveals details of the tumor region, highlighting the edema, active tumor region and the necrosis to differing degrees. To account for the varying dynamic ranges of these acquisitions, zero-mean unit-variance normalization was applied to each channel separately. Multi-class ground truth segmentation masks (the enhancing tumor, edema, and tumor core) were merged into a single binary mask representing the WT. In total, 210 HGG and 75 LGG MRI volumes were used and randomly split into 70% for training, 10% for validation, and 20% for testing. Image augmentation was also used in the form of horizontal and vertical flips, rotation, and scaling.
“Pseudo-RANO” measurements of WT burden were utilized in training the encoder network, operating on individual slices such as those shown in Figure 1. Tumor principal axes are extracted using the approach outlined by Chang et al. (2019). For each slice, the largest object (based on the binary ground truth mask) was extracted, and pairwise distances were computed over all mask boundary pixels to find the major axis. The minor axis was then identified as the longest pairwise boundary pixel distance approximately orthogonal to the major axis. Any empty slices were removed from the dataset and not used in training. For any given slice, the “Pseudo-RANO” measurement is represented by a 1 × 8-dimensional vector representing the principal axes' start and end coordinates.
When pre-processing both the lung image database consortium (LIDC) dataset (Armato et al., 2011) and the DeepLesion dataset (Yan et al., 2018), each consisting of CT slices, we use the windowing procedure discussed in the original DeepLesion methodology by Yan et al. (2018). We rescale the houndfield units (HU) between −1,024 and 3,071 so that the major intensity ranges of lung, soft tissue, and bone are correctly covered. We continue the same pre-processing method to then normalize the resulting images to between 0 and 1 and ensure that the images are cropped to the correct dimensions of 512 × 512.
The model's U-Net architecture, shown in Figure 2, displays a symmetric encoder–decoder structure with skip connections to transfer information from the previous layers to the latter layers, i.e., the contracting layers to the mirrored expanding layers (Ronneberger et al., 2015).

Figure 2. The proposed U-Net architecture. The region separated by the dotted line is the pre-trained encoder path of the model that is used for “Pseudo-RANO” estimation as a regression output. This encoder is then extended into the full U-Net for segmentation.
Image slices, sized 240 × 240 pixels, comprise of four MRI sequences as channels. The architecture then consists of 16 hidden layer inputs with two convolutions at each resampling layer, with five down-sampling layers and four up-sampling layers to complete a full segmentation. Kernel dimensions are 3 × 3 except for the final (sigmoid) layer, which is 1 × 1.
The encoder portion of the U-Net architecture can be trained independently from the decoder to annotate “Pseudo-RANO” measurements, which is shown as the dotted outline in Figure 2. The encoder is used as a pre-training pathway before WT region segmentation, which fully utilizes the whole encoder–decoder architecture.
Equations 1–6 define the data structures and losses used within this work, while Equations 7 and 8 define the performance metrics that are leveraged to evaluate each of the experiments that we perform. We define and expand upon the reasons for introducing these structures and metrics. Each “Pseudo-RANO” measure is defined as a vector v ∈ ℝ8, which represents the principal axes of a tumor region,
where (xi, yi) represents the coordinates of a pixel on the tumor boundary. We formulate the “Pseudo-RANO” estimation as a regression problem by minimizing a mean squared error (MSE) loss and enforcing the orthogonality of the major and minor axes through minimizing cosine (dis)similarity. MSE loss is defined as follows:
where D defines the total number of samples in the batch, and defines the prediction and ground truth data items for each i index in the training set. We refer to the major and minor principal axes as line segments vmaj and vmin, respectively,
where ||vmin|| < ||vmaj||. The value v1, 2 is equal to the two coordinates for the first point of each axis, and v3, 4 is equal to the corresponding two coordinates for the second point of each axes. In addition to MSE, a cosine (dis)similarity loss is computed to enforce a degree of orthogonality between vmin and vmax,
where the variable ϵ, equal to 1 × 10−8, is used to avoid division by zero. The combined loss is then calculated with a weighting ω to balance the relative contributions of the two terms,
where ω is chosen as a value of 0 × , 3 × , or 5 × penalties to weight the regression training process toward a larger degree of orthogonality. For segmentation, DSC loss is used,
where X and Y are the predicted and ground truth masks, respectively. The variable ϵ, equal to 1 × 10−1, is used as a smoothing operator to avoid division by zero.
The “Pseudo-RANO” regression performance was evaluated employing the Jaccard score (JSC) similarity measure,
where X and Y are masks representing the oriented bounding-boxes defined by the predicted and ground truth “Pseudo-RANO” principal axes. For WT segmentation, the Dice-Sørensen Coefficient (DSC) similarity measure is used as follows:
where X and Y are the predicted and ground truth masks, respectively. We set the learning rate to 0.0003 (3e−4) for models training on MRI to 0.00003 (3e−5) for training on CT data, as the models do not learn at the larger learning rate.
Training and validation loss over time for “Pseudo-RANO” regression began uniformly with no cosine penalty for all models. The models then resumed at the varying levels of 0 × , 3 × , and 5 × cosine weighting from the 40th epoch. The loss continues to minimize to a similar level with little erraticism for all examples, converging at a similar point in training time compared with the JSC outputs shown in Figure 3 by the 100th epoch.
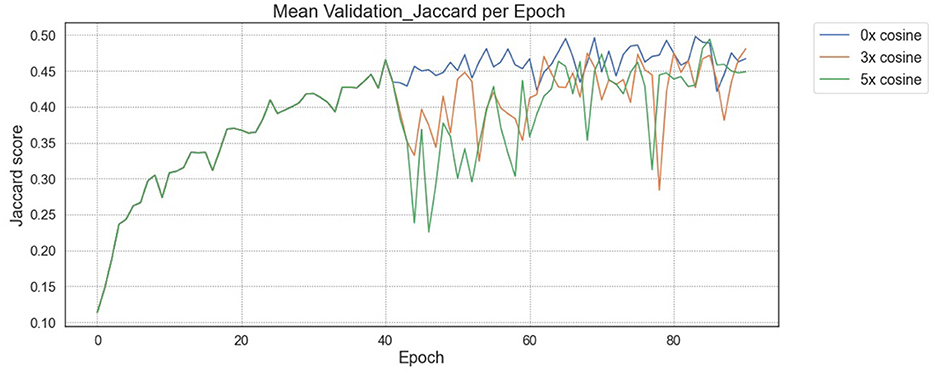
Figure 3. JSC during validation for “Pseudo-RANO” regression with initial baseline training. A drop is shown from the 40th epoch where cosine loss is reintroduced after initial training without cosine loss.
The utility of the additive cosine loss penalty is not directly apparent from the regression task results, producing lower JSC scores per increment. In many cases, however, the qualitative improvements shown in Figure 4 indicate that the localization of the predicted “Pseudo-RANO” measures improves with the individual line lengths, increasing as a trade-off. We show this in practice when comparing Figure 4 (Right) with Figure 4 (Center), having an overall higher quantitative score than the randomly initialized (RI) example Figure 4 (Left).
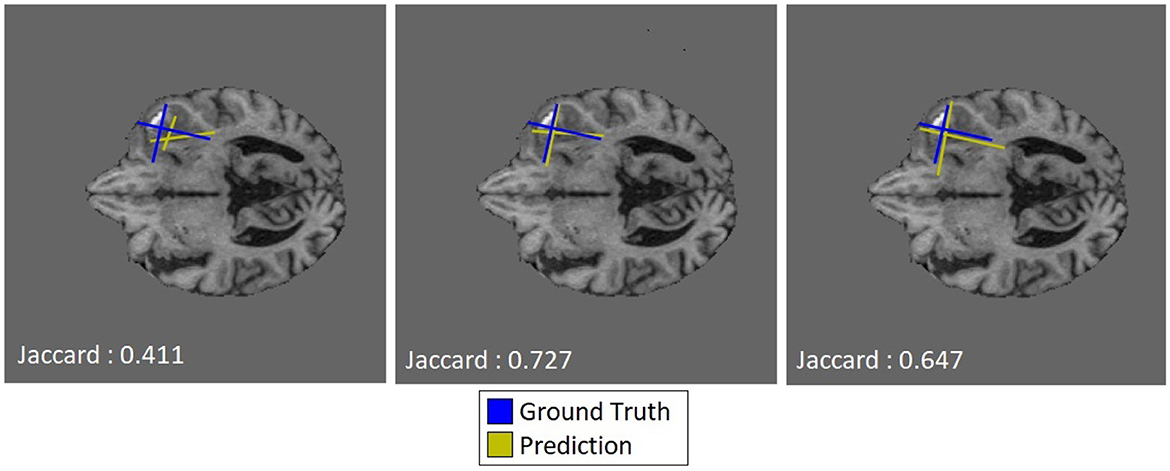
Figure 4. Qualitative examples of predicted “Pseudo-RANO” measurements with JSC calculated based on oriented bounding boxes of the same tumor slice at varying cosine penalty levels (0×, 3×, and 5× respectively), where ground truth is shown in blue and predicted is shown in yellow.
Training of the segmentation task utilizing the full U-Net model was investigated under three different schemes. In this study, they are defined as the baseline RI scheme, the pre-trained frozen encoder (PFE) scheme, and the pre-trained trainable encoder (PTE) scheme. Where the encoder undergoes no pre-training (RI), the encoder weights from the regression task are used and are not allowed to update during segmentation training (PFE), where the encoder weights are used and allowed to update (PTE), respectively.
Our study shows notable differences between the three schemes, with PTE performance peaking fastest and remaining consistently higher than the randomly initialized model. Additionally, pre-training appears to afford more stable training and fewer fluctuations in segmentation performance than RI. The different behaviors of the models are further highlighted in Figure 5, which shows the ground truth segmentation. While the RI scheme initially over-segments, the PTE and PFE schemes under-segment before eventually stabilizing on a shape which is more similar to the ground truth than what RI can achieve. The main benefit of this approach is that the PTE model produces a localized and detailed segmentation at an earlier point than the RI and with a higher overall DSC.

Figure 5. Example qualitative slice outputs for each multiple of 16 batches trained. Showing GT (A), RI (B), PFE (C), and PTE in (D). These are shown at the 50th step and the 550th step of 16 batches, at the end of the 1st epoch, and at the end of the 36th epoch, respectively. This shows a temporal progression of prediction quality between pre-training schemes.
The overall behavior of the three training schemes is shown in Figure 6. In general, we observe tighter distributions of DSC for PTE compared with the RI and PFE schemes. Some cases show that the PFE slightly outperforming the PTE for some examples early on, particularly between the 200th and 300th model batch, whereas the RI model is outperformed throughout training.
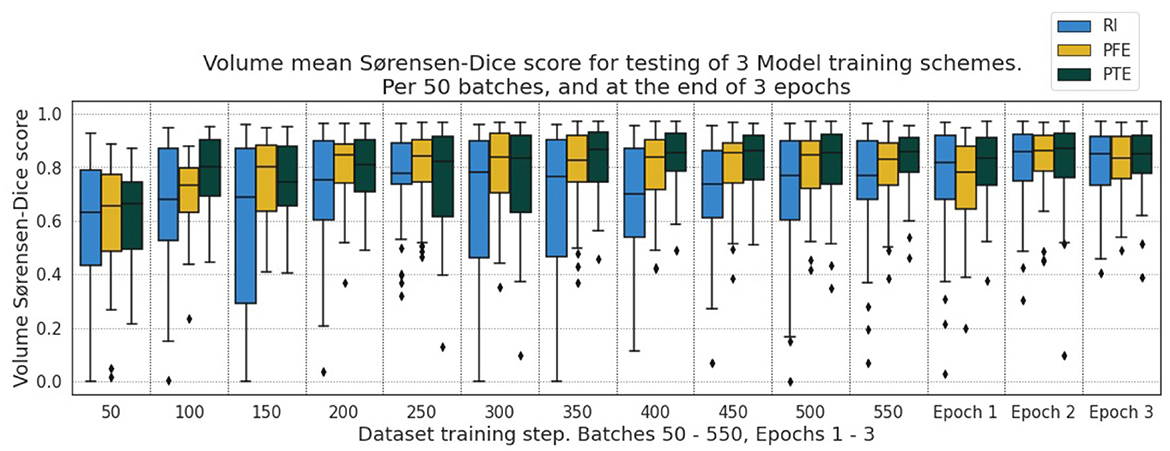
Figure 6. DSC for the testing dataset under the three pre-training schemes for every 50th batch up to the 550th and after the 1st, 2nd, and 3rd epochs.
We tested our approach to understand the impact of smaller datasets, as the ideal use of the method is to supplement segmentation data which are unavailable for smaller models or datasets. Using 10% of the original training dataset, Figure 7 shows large improvements in the calculated DSC per epoch of training for the PTE model when compared with using an RI model over all epochs. Further testing over 10 epochs included bounding box regression as an additional pre-training task.
We showed DSC outputs for testing when using models trained on fewer segmentation inputs (with full dataset utilized for the regression inputs), as shown in Table 2, for the best results over 10 epochs of training. Both bounding box regression and “Pseudo-RANO” regression produce a large improvement upon the randomly initialized model, with the additive cosine penalty having minimal positive impacts on the improvement in DSC, though it does lead to improvement in specificity and precision. “Pseudo-RANO” regression produces higher results than the utilization of bounding box, and although the results are similar, RANO is much more present and easily available within clinical contexts where bounding box data are comparably lacking.
We further evaluate this methodology on external CT datasets using the DeepLesion whole body dataset with RECIST measurements for the regression pre-training path of the model and the LIDC lung lesion dataset for segmentation training and testing. We show these evaluation results in Figure 8, where improvement upon the baseline remains consistent throughout testing. The RECIST-PTE results are almost uniformly better for DSC distribution than both the RI and the BBOX-PTE, though a few exceptions do occur, such as Epoch 29, where the BBOX-PTE results briefly exceed the RECIST-PTE results. This shows methodological generalisability and robustness across tasks and datasets.
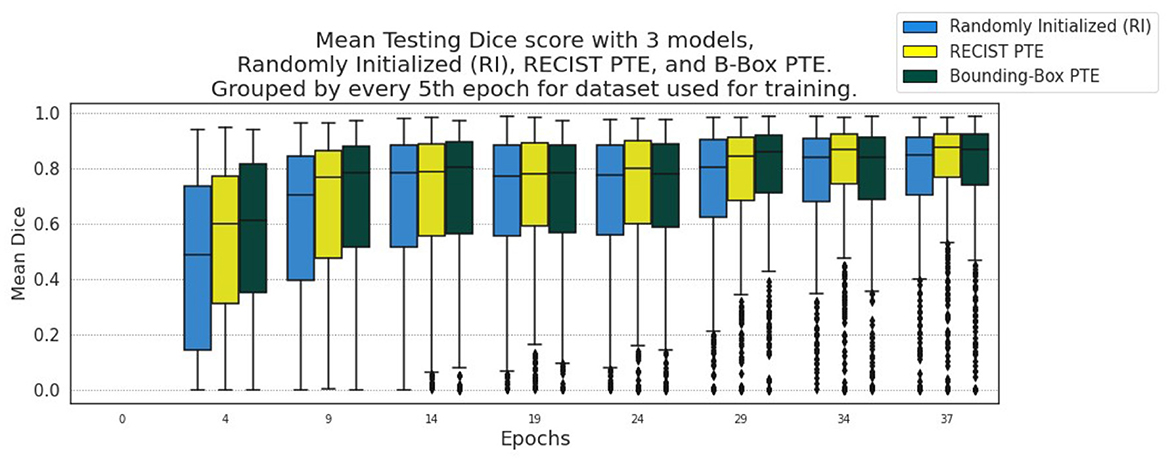
Figure 8. Segmentation results from every 5th Epoch for evaluation on LIDC using DeepLesion data for encoder pre-training.
Additionally, we evaluate the impact of noise with our approach by adding a random value between −33% and +33% of the sum between the length and width of the associated lesion in the CT slice to each of the eight values that make up the RECIST measurement. We can offset the measurement within a reasonable distance of the lesion, making the data less representative but still realistic in this manner. Training the regression model on this data and then comparing it with the RI baseline and the PTE non-noisy data at epoch 38 shows that there is still value in applying our method, sitting in between, above the baseline but below the accurate clinical data, as shown in Figure 9.
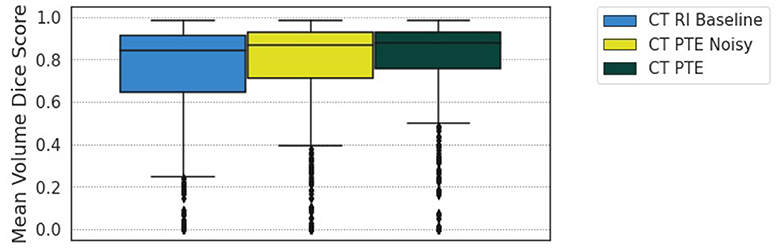
Figure 9. Comparison of the RI baseline, PTE noise model at 33% additional noise, and RECIST PTE for epoch 38 of training.
In this study, we demonstrate a pre-training approach for lesion segmentation based on the estimation of the lesion's principal axes. The “Pseudo-RANO” measures used in this study are relatively cheap and straightforward to obtain and could serve as an alternative to dense segmentation masks as training data. We further observe that U-Net encoder pre-training appears to facilitate the transfer of features to enable faster convergence and modest improvements in overall segmentation performance. In particular, we observe that a pre-trained, trainable encoder offers optimal performance when compared with randomly initialized models and those with a pre-trained frozen encoder. The proposed pre-training scheme allows for both faster and more stable training with fewer densely segmented ground truth masks.
Though bounding box implementations have been compared, future study will also continue to evaluate the proposed pre-training method with other weakly supervised training methods in terms of convergence, performance, impact on early training, and whether multi-task learning may afford further benefits. Additionally, the generalisability of the proposed approach to other modalities and diseases has been explored using other measures, such as Response Evaluation Criteria In Solid Tumors (RECIST) in the context of CT imaging.
Raw data availability without additional clinician time and expertise is the main benefit since this data are already available. This method of pre-training predisposes the network weights to understand a tumor representation; in this case, we can assume that the circularity and position of the tumor are estimated. Additional testing in the future will be applied to variable tumor shapes, though whole-body datasets for different organs will also be examined, particularly considering the DeepLesion dataset, which contains real RECIST measurements with CT input data.
Our methodology sits in a gap for weak segmentation where measurements that are already routinely produced within clinical practice can be used, particularly for tumor burden representation and estimation that are created but not actively used for this type of task. This application can have a huge impact when we consider how difficult medical data is to obtain, where very specialized equipment is required, particularly under specific patient conditions, and when we consider how specialized the annotations must be. This makes it a valuable research area for the development of weakly supervised deep learning. However, an approach has limitations where the length of time to train the model may be longer, though the small size of this data compared with high-fidelity alternatives should offset the impact of this quality difference.
Our approach takes advantage of an approach for splitting a model into encoder and decoder sections which are then unified to form a segmentation model, sharing similarities with that found in the study by Hatamizadeh et al. (2022) which uses masked CT and MRI modeling and Hu et al. (2018) which uses optic disc centroid estimation, where an encoder is pre-trained to solve this specific task. This study explores the value of weakly supervised learning on bi-dimensional measurements of tumor burden as a pretext task for segmentation, which is inspired by the RANO criteria and defined as a principal axis estimation for the active tumor region (Yang, 2016). The widespread adoption of such response evaluation measures within clinical trials (Cai et al., 2018) could provide a large amount of data for use in deep learning pipelines.
Publicly available datasets were analyzed in this study. This data can be found at: https://www.med.upenn.edu/sbia/brats2018/data.html.
JM: Writing – original draft. TL: Writing – review & editing. XY: Writing – review & editing. JB: Writing – review & editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study has been supported by the EPSRC Doctoral Training Partnership EP/T518177/1.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Armato III, S. G., McLennan, G., Bidaut, L., McNitt-Gray, M. F., Meyer, C. R., Reeves, E. A., et al. (2011). The lung image database consortium (LIDC) and image database resource initiative (IDRI): a completed reference database of lung nodules on CT scans. Med. Phys. 38, 915–931. doi: 10.1118/1.3528204
Atzeni, A., Peter, L., Robinson, E., Blackburn, E., Althonayan, J., Alexander, D. C., et al. (2022). Deep active learning for suggestive segmentation of biomedical image stacks via optimisation of dice scores and traced boundary length. Med. Image Anal. 81:102549. doi: 10.1016/j.media.2022.102549
Bakas, S., Akbari, H., Sotiras, A., Bilello, M., Rozycki, M., Kirby, J. S., et al. (2017). Advancing the cancer genome atlas glioma MRI collections with expert segmentation labels and radiomic features. Sci. Data 4, 1–13. doi: 10.1038/sdata.2017.117
Bakas, S., Reyes, M., Jakab, A., Bauer, S., Rempfler, M., Crimi, A., et al. (2018). Identifying the best machine learning algorithms for brain tumor segmentation, progression assessment, and overall survival prediction in the BRATS challenge. arXiv [Preprint] arXiv:1811.02629. doi: 10.48550/arXiv.1811.02629
Bhardawaj, F., and Jain, S. (2024). Cad system design for two-class brain tumor classification using transfer learning. Curr. Cancer Ther. Rev. 20, 223–232. doi: 10.2174/1573394719666230816091316
Bontempi, D., Benini, S., Signoroni, A., Svanera, M., and Muckli, L. (2020). Cerebrum: a fast and fully-volumetric convolutional encoder-decoder for weakly-supervised segmentation of brain structures from out-of-the-scanner mri. Med. Image Anal. 62:101688. doi: 10.1016/j.media.2020.101688
Cai, J., Tang, Y., Lu, L., Harrison, A. P., Yan, K., Xiao, J., et al. (2018). “Accurate weakly-supervised deep lesion segmentation using large-scale clinical annotations: slice-propagated 3D mask generation from 2D recist,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Cham: Springer), 396–404. doi: 10.1007/978-3-030-00937-3_46
Chang, K., Beers, A. L., Bai, H. X., Brown, J. M., Ly, K. I., Li, X., et al. (2019). Automatic assessment of glioma burden: a deep learning algorithm for fully automated volumetric and bidimensional measurement. Neurooncology 21, 1412–1422. doi: 10.1093/neuonc/noz106
Chukwueke, U. N., and Wen, P. Y. (2019). Use of the response assessment in neuro-oncology (RANO) criteria in clinical trials and clinical practice. CNS Oncol. 8:CNS28. doi: 10.2217/cns-2018-0007
Doi, K. (2007). Computer-aided diagnosis in medical imaging: historical review, current status and future potential. Comput. Med. Imaging Graph. 31, 198–211. doi: 10.1016/j.compmedimag.2007.02.002
Hatamizadeh, A., Xu, Z., Yang, D., Li, W., Roth, H., Xu, D., et al. (2022). Unetformer: a unified vision transformer model and pre-training framework for 3D medical image segmentation. arXiv [Preprint]. arXiv:2204.00631. doi: 10.48550/arXiv.2204.00631
Hu, S.-Y., Beers, A., Chang, K., Höbel, K., Campbell, J. P., Erdogumus, D., et al. (2018). Deep feature transfer between localization and segmentation tasks. arXiv [Preprint]. arXiv:1811.02539. doi: 10.48550/arXiv.1811.02539
Hu, S.-Y., Wang, S., Weng, W.-H., Wang, J., Wang, X., Ozturk, A., et al. (2020). “Self-supervised pretraining with DICOM metadata in ultrasound imaging,” in Proceedings of the 5th Machine Learning for Healthcare Conference, Volume 126 of Proceedings of Machine Learning Research, eds. F. Doshi-Velez, J. Fackler, K. Jung, D. Kale, R. Ranganath, B. Wallace, et al. (PMLR), 732–749.
Kervadec, H., Dolz, J., Wang, S., Granger, E., and Ayed, I. B. (2020). “Bounding boxes for weakly supervised segmentation: global constraints get close to full supervision,” in Proceedings of the Third Conference on Medical Imaging with Deep Learning, volume 121 of Proceedings of Machine Learning Research, eds. T. Arbel, I. B. Ayed, M. D. Bruijne, M. Descoteaux, H. Lombaert, and C. Pal (PMLR), 365–381.
Lefkovits, S., Lefkovits, L., and Szilágyi, L. (2022). HGG and LGG brain tumor segmentation in multi-modal mri using pretrained convolutional neural networks of amazon sagemaker. Appl. Sci. 12:3620. doi: 10.3390/app12073620
Li, Y., Zhu, M., Sun, G., Chen, J., Zhu, X., Yang, J., et al. (2022). Weakly supervised training for eye fundus lesion segmentation in patients with diabetic retinopathy. Math. Biosci. Eng. 19, 5293–5311. doi: 10.3934/mbe.2022248
Liu, M., Zhang, J., Lian, C., and Shen, D. (2019). Weakly supervised deep learning for brain disease prognosis using MRI and incomplete clinical scores. IEEE Trans. Cybern. 50, 3381–3392. doi: 10.1109/TCYB.2019.2904186
Menze, B. H., Jakab, A., Bauer, S., Kalpathy-Cramer, J., Farahani, K., Kirby, J., et al. (2014). The multimodal brain tumor image segmentation benchmark (BRATS). IEEE Trans. Med. Imaging 34, 1993–2024. doi: 10.1109/TMI.2014.2377694
Panduri, B., and Rao, O. S. (2024). A survey on brain tumour segmentation techniques in deep learning. Int. J. Intell. Syst. Appl. Eng. 12(7s), 412–425.
Qu, H., Wu, P., Huang, Q., Yi, J., Yan, Z., Li, K., et al. (2020). Weakly supervised deep nuclei segmentation using partial points annotation in histopathology images. IEEE Trans. Med. Imaging 39, 3655–3666. doi: 10.1109/TMI.2020.3002244
Ranjbarzadeh, R., Caputo, A., Tirkolaee, E. B., Jafarzadeh Ghoushchi, S., and Bendechache, M. (2023). Brain tumor segmentation of MRI images: a comprehensive review on the application of artificial intelligence tools. Comput. Biol. Med. 152:106405. doi: 10.1016/j.compbiomed.2022.106405
Ronneberger, O., Fischer, P., and Brox, T. (2015). “U-net: convolutional networks for biomedical image segmentation,” in International Conference on Medical image computing and computer-assisted intervention (Cham: Springer), 234–241. doi: 10.1007/978-3-319-24574-4_28
Villa, C., Miquel, C., Mosses, D., Bernier, M., and Stefano, A. L. D. (2018). The 2016 world health organization classification of tumours of the central nervous system. La Presse Méd. 47, e187–200. doi: 10.1016/j.lpm.2018.04.015
Wang, X., Liu, S., Ma, H., and Yang, M.-H. (2020). Weakly-supervised semantic segmentation by iterative affinity learning. Int. J. Comput. Vis. 128, 1736–1749. doi: 10.1007/s11263-020-01293-3
Yan, K., Wang, X., Lu, L., and Summers, R. M. (2018). Deeplesion: automated mining of large-scale lesion annotations and universal lesion detection with deep learning. J. Med. Imaging 5, 036501–036501. doi: 10.1117/1.JMI.5.3.036501
Yang, D. (2016). Standardized MRI assessment of high-grade glioma response: a review of the essential elements and pitfalls of the rano criteria. Neurooncol. Pract. 3, 59–67. doi: 10.1093/nop/npv023
Yang, L., Zhang, Y., Zhao, Z., Zheng, H., Liang, P., Ying, M. T., et al. (2018). Boxnet: deep learning based biomedical image segmentation using boxes only annotation. arXiv [Preprint]. arXiv:1806.00593. doi: 10.48550/arXiv.1806.00593
Zhao, Z., Yang, L., Zheng, H., Guldner, I. H., Zhang, S., Chen, D. Z., et al. (2018). “Deep learning based instance segmentation in 3D biomedical images using weak annotation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Cham: Springer), 352–360. doi: 10.1007/978-3-030-00937-3_41
Keywords: image segmentation, brain tumor, weak supervision, RANO, deep learning
Citation: Mckone JE, Lambrou T, Ye X and Brown JM (2024) Weakly supervised pre-training for brain tumor segmentation using principal axis measurements of tumor burden. Front. Comput. Sci. 6:1386514. doi: 10.3389/fcomp.2024.1386514
Received: 20 February 2024; Accepted: 31 May 2024;
Published: 20 June 2024.
Edited by:
Jing Yuan, Zhejiang Normal University, ChinaReviewed by:
Amina Benabid, Zhejiang Normal University, ChinaCopyright © 2024 Mckone, Lambrou, Ye and Brown. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joshua E. Mckone, Sk1ja29uZUBsaW5jb2xuLmFjLnVr
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.