Recovering manifold representations via unsupervised meta-learning

Manifold representation learning holds great promise for theoretical understanding and characterization of deep neural networks' behaviors through the lens of geometries. However, data scarcity remains a major challenge in manifold analysis especially for data and applications with real-world complexity. To address this issue, we propose manifold representation meta-learning (MRML) based on autoencoders to recover the underlying manifold structures without uniformly or densely sampled data. Specifically, we adopt episodic training, following model agnostic meta-learning, to meta-learn autoencoders that are generalizable to unseen samples specifically corresponding to regions with low-sampling density. We demonstrate the effectiveness of MRML via empirical experiments on LineMOD, a dataset curated for 6-D object pose estimation. We also apply topological metrics based on persistent homology and neighborhood graphs for quantitative assessment of manifolds reconstructed by MRML. In comparison to state-of-the-art baselines, our proposed approach demonstrates improved manifold reconstruction better matching the data manifold by preserving prominent topological features and relative proximity of samples.

1 Introduction

Challenges such as model transferability, explanability, and adversarial robustness prevent the application of deep learning to real-world problems with safety and mission importance. One research direction of growing interest is to address these challenges by studying deep learning from the perspective of geometry and topology (Watanabe and Yamana, 2022; Aktas et al., 2019). Based on the widely accepted assumption that high dimensional data often lie on a low dimensional manifold, manifold representation learning, which seeks to capture underlying manifold structure, serves as a critical first step towards principled geometric and topological analysis of deep learning (Tenenbaum et al., 2000; Bengio et al., 2013).

While autoencoders (Liou et al., 2014; Bank et al., 2020) have been widely adopted for learning intrinsic structure from high dimensional empirical data in an unsupervised manner, sample scarcity and sparsity remains a major challenge for capturing underlying manifolds especially for real-world problems. Existing solutions are often prone to issues of bad generalization and incorrect local geometry due to sparse sampling in high dimensional space and noisy samples of real-world complexity (Lee Y. et al., 2021). Meanwhile, meta-learning has been widely adopted as a technique to address the challenge of data scarcity and to learn models that are easy to adapt given few samples from new task domain (Hospedales et al., 2022; Snell et al., 2017; Finn et al., 2017).

In this work, inspired by model agnostic meta-learning (MAML) originally designed for domain adaptation and domain generalization (Finn et al., 2017; Li et al., 2018), we aim to combine the strength of autoencoders and meta-learning by proposing manifold representation meta-learning (MRML) to improve manifold representation learning considering training distributions containing low sampling density regions. We compare three different sampling schemes that mirror different types of shifts between training and testing distributions in an episodic training. Accordingly, we train models to achieve good generalization performance at different levels of difficulty. Thanks to the improved generalizability of meta-learned models, we demonstrate that manifold regions with low sample density can be faithfully recovered.

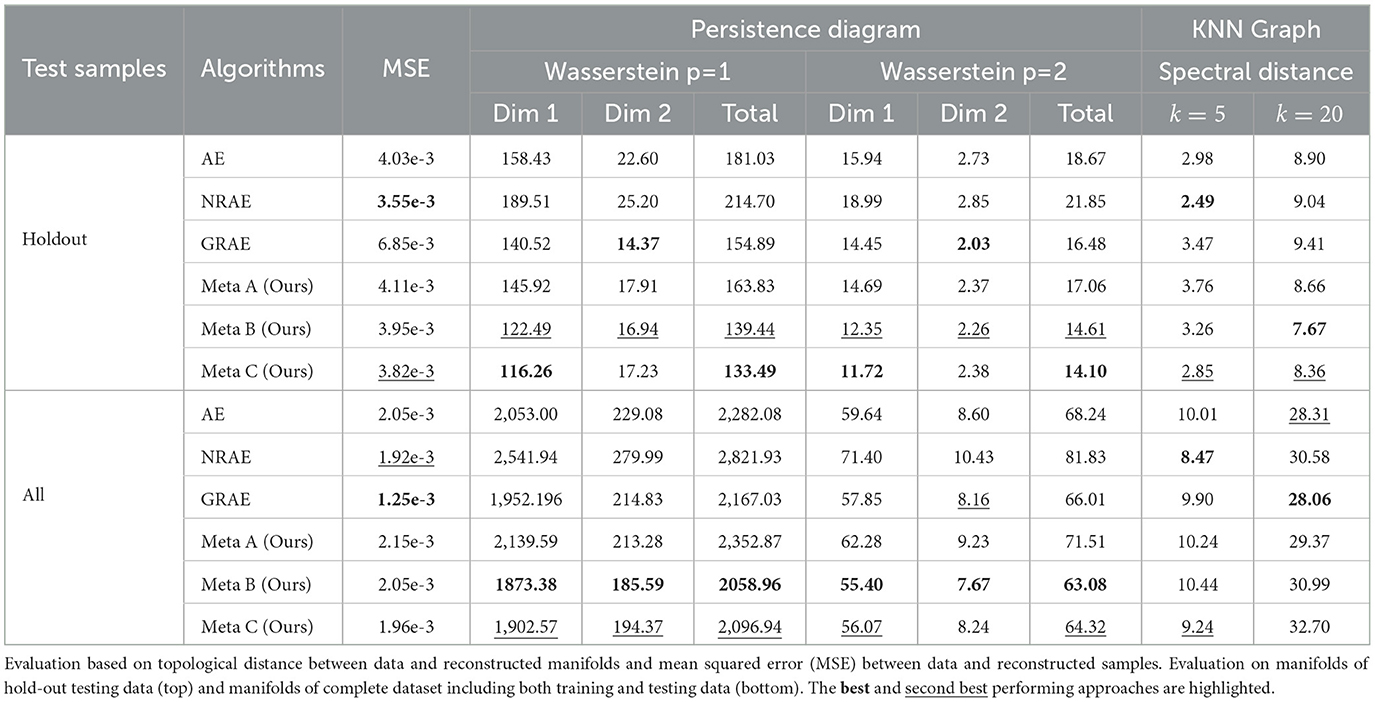
To evaluate the generalization performance of MRML, we tap into topological metrics based on persistent homology (Edelsbrunner and Harer, 2008) and neighborhood graphs to quantify the reconstructions at the manifold level. We perform experiments using the LineMOD dataset (Hinterstoisser et al., 2012) which is designed for 6-D pose estimation. We perform both qualitative and quantitative comparison between MRML under three different settings and multiple baseline methods including recent state-of-the-art autoencoders considering local connectivity (Lee Y. et al., 2021) and geometric regularization (Duque et al., 2022). We demonstrate consistent qualitative and quantitative improvement of manifold reconstruction against baselines with respect to topological metrics considering generalization to hold-out test samples corresponding to a missing gap/hole in the complete manifold. In comparison to baseline reconstruction, our best performing meta-learning procedure captures a manifold better matching the data manifold and leading to a relative reduction of topological distance at 14.44% considering the hold-out neighborhood and at 4.44% considering the entire manifold.

In summary, our major contributions include the following:

(1) We propose MRML (manifold representation meta-learning) with novel episodic sampling strategies to improve autoencoders' generalization performance in reconstructing manifold especially for regions with low sampling density.

(2) In addition to standard metrics focusing on sample-level reconstruction accuracy, we introduce topological and geometric metrics based on persistent homology and neighborhood graphs for quantitative evaluation of MRML with respect to manifold reconstruction.

(3) We demonstrate both qualitative and quantitative improvement via MRML against state-of-the-art baselines for manifold reconstruction evaluated based on topological and geometric metrics, using training data with low sampling density regions.

2 Related work

2.1 Manifold representation learning

Autoencoders (Liou et al., 2014; Bank et al., 2020) are commonly adopted for unsupervised representation learning where data in high dimensional input space is projected onto a lower dimensional latent space by an encoder and restored back to data dimension in the output space by a decoder. Several recent works are proposed to incorporate topological analysis in design of autoencoders for preserving the local geometry in unsupervised representation learning. Moor et al. (2020) propose Topological Autoencoder using topological loss to regularize the representation learning and thus improve the alignment between input and latent space based on persistent homology features. Schönenberger et al. (2020) propose Witness Autoencoder (W-AE) to improve the regularization by defining the alignment between input and latent space via geodesic distances computed based on witness complexes. Schonsheck et al. (2019) propose Chart Autoencoder (CAE) which use an ensemble of decoders to model a multi-chart latent space representing the manifold with a collection of overlapping local neighborhoods. With this formulation, the authors discuss the local proximity and manifold approximation theoretically. More recent works investigate the use of geometric regularization such as regularization based on local contraction and expansion of the decoder (Nazari et al., 2023) or isometry to preserve local distance (Gropp et al., 2020; Lee et al., 2022). In this work, we perform qualitative and quantitative comparison against two recent baselines addressing underlying geometry of autoencoders. Lee Y. et al. (2021) propose Neighborhood Reconstructing Autoencoder (NRAE) which seeks to correct local geometry and overfitting of autoencoders simultaneously with novel reconstruction loss leveraging neighborhood graph and local quadratic approximation of the decoder. Duque et al. (2022) propose Geometry Regularized Autoencoders (GRAE) which introduce regularization to specifically match latent representations of the autoencoder to representations from manifold learning computation. In comparison to existing works, our approach does not need explicit modeling or calculation of topological features at set or batch level during the training. It is based on meta-learning framework with episodic training and thus enables improved generalization of manifold learning with respect to topological metrics considering training manifolds consisting low sampling density regions.

2.2 Model agnostic meta learning

Meta-learning or 'Learning to Learn' techniques seek to extract generalizable knowledge from learning processes of diverse tasks to achieve fast adaptation or generalization to new tasks (Andrychowicz et al., 2016; Hospedales et al., 2022) and have demonstrated tremendous success in tasks such as few-shot learning (Snell et al., 2017; Hsu et al., 2019) and domain generalization (Li et al., 2019; Liu et al., 2021). Specifically model agnostic meta-learning (MAML) (Finn et al., 2017) is proposed to learn to achieve good adaptation to new tasks given a few samples with a few steps of gradient descent. The learned model serves an initial condition that is easy to fine-tune. MLDG (Li et al., 2018) extends the model agnostic episodic training framework and learns to achieve good zero-shot transfer by simulating domain shifts in supervised classification tasks. Recent works also apply meta-learning techniques to improve the training of generative models such as Variational AutoEncoders (VAE) where representation learning is performed considering a sets of related probabilistic models to achieve transferrable representation (Lee D. B. et al., 2021; Wu et al., 2020). Our proposed methods follow the episodic training framework in MLDG and explore novel episodic sampling strategies simulating data shifts in transfer learning based on local geometry without supervised labels. In comparison to recent works based on variational inference, our work does not make any prior assumption such as Gaussian or Gaussian Mixtures (Lee D. B. et al., 2021) about the latent distribution.

3 Method

3.1 Meta-learning for manifold representation learning

We develop unsupervised manifold representation learning based on autoencoders to capture meaningful representation of the data which faithfully encodes the underlying manifolds. To address the challenge of data scarcity, we propose a generalizable model which not only provides good reconstruction at sample level but also preserves underlying geometry of the data (e.g., relative proximity between samples; topological features highlights the shape of underlying manifolds) given unseen data corresponding to low sampling density region in the underlying manifold. We integrate autoencoders with meta-learning for domain generalization based on episodic training (MLDG) and examine novel sampling strategies specifically simulating low sampling regions in manifolds.

Following MLDG framework, we first split data into disjoint meta training set S and meta testing set S′. We adopt episodic training and at each training episode, we sample two disjoint batches from the meta training set S, namely episodic training batch S_train and episodic testing batch S_test. The split of episodic training batch and episodic testing batch is designed to resemble the distribution shift between source (S) and unseen target data (S′) so as to test models' generalization performance. We compute the gradient on S_train with respect to model parameters θ and compute the updated parameters θ^* after one step of gradient descent. At the episodic testing step, we perform a virtual evaluation of the updated model on the episodic testing set S_test with a task loss term $\mathcal{L}$. Herein, we adopt the Binary Cross Entropy (BCE) loss. Given input x, model f_θ with parameters θ, the task loss term is defined as

$\begin{array}{ll}L(x,\theta )=-\left[f_{\theta }(\text{x})log(\text{x})+(1-f_{\theta }(\text{x}))log(1-\text{x})\right].& (1)\end{array}$

At the meta-optimization step, we update the model parameters θ considering a meta-optimization loss as the weighted sum of task loss terms evaluated on the episodic training and episodic testing after one step of virtual update. The detailed meta-learning procedures are specified in Algorithm 1.

Algorithm 1

Algorithm 1. Meta-learning for manifold reconstruction.

In comparison to the original MLDG where the sampling of episodic training set and episodic testing set is designed based on different image domains (e.g., cartoon, painting, photo, etc.) for supervised object classification, in this work, we devise three sampling schemes specifically targeting the task of unsupervised reconstruction of data manifold given data scarcity. Figure 1 provides a notional depiction of sample distribution in 2D space which highlights the comparison between the different sampling strategies, where each dot referes to a sample. In each setting, we split the entire data space to meta training set S (light blue) and meta testing set S′ (light red). Specifically to simulate a low sampling density region in high dimensional data, we consider samples in a random local neighborhood as the S′ which is hold out from model training. Within S, at each episode, we consider uniformly sampled S_train and construct S_test to include (1) the nearest neighbor sample of each sample in S_train (Figure 1, Setting A), (2) a disjoint random batch uniformly sampled from the training data S (Figure 1, Setting B), or (3) a disjoint batch containing a random local neighborhood in S (Figure 1, Setting C). The three settings simulate different distribution shifts to encourage model generalization with increased difficulty. Correspondingly, the model is encouraged to generalize to (1) unseen test samples close to training samples in the Euclidean space in Setting A, (2) unseen test samples from the same training distribution in Setting B, and (3) unseen test samples from a low sampling density region corresponding to a hole or a gap in the training manifold in setting C.

Figure 1

Figure 1. Experimental setting A, B and C of MRML with increased difficulties in generalization. Each dot represents a sample when projected into 2D space. A Meta-test set (light red) is held out from Meta-train set (light blue) to simulate random hole in the manifold corresponding low-sampling density region. For each training episode, a random batch of episodic-train set (blue) and a disjoint batch of episodic-test set (red) are sampled from Meta-train set to simulate the data shift to encourage generalization of the model.

3.2 Topological metrics for manifold reconstruction

To quantitatively evaluate the performance of manifold reconstruction, we perform evaluation including metrics beyond classic reconstruction errors describing instance-level reconstruction quality. Based on various representation of manifolds adopted in topological data analysis, we adopt two sets of metrics to characterize reconstructions based on different types of topological and geometric features of learned manifolds.

For each manifold, we first compute its persistence diagram which characterizes the evolution of topological structures in persistent homology and provides a summarized description of the manifold shape (Cohen-Steiner et al., 2005; Pun et al., 2018; Agami, 2020; Watanabe and Yamana, 2022). We focus on the points in the diagrams describing 0-dimension homology (i.e., connected components) and 1-dimensional homology (i.e., holes) in the manifold. We adopt the Wasserstein distance metric (Mileyko et al., 2011) to compute the similarity between two persistence diagrams. Considering two persistence diagrams D₁ and D₂, the p-th Wasserstein distance W_p(D₁, D₂) is defined as:

$\begin{array}{ll}{W}_p(D_1,D_2)={({\displaystyle \underset{M}{inf}}{\displaystyle \sum _{x\in D_1}}||x-M(x){||}_{\infty }^p)}^{\frac{1}{p}}& (2)\end{array}$

where M denotes all bijection mappings from D₁ to D₂. The Wasserstein distance measures the distance between coupled points from an optimal matching between two diagrams and thus characterizes the similarity of topological features between two manifolds.

In addition to the persistence diagram, we further construct a k-nearest neighbor (KNN) graph for each of the manifolds as a representation characterizing the manifold from the perspective of local geometry at different resolutions. Considering each point in the manifold as a vertex in the graph, we connect vertices based on the Euclidean distance between corresponding samples (Omohundro, 1989). We describe each graph via its binary adjacency matrix and evaluate the similarity between two graphs based on adjacency spectral distance (Wills and Meyer, 2020). Let A₁ and A₂ denote the adjacency matrices of two KNN graphs G₁ and G₂ of size n. An adjacency matrix A is computed such that the (i, j)-th element in the matrix is labeled as 1 if i-th sample is one of the k-nearest neighbors to the j-th sample and is labeled as 0 otherwise. The adjacency spectral distance is computed as

$\begin{array}{ll}S(G_1,G_2)=\sqrt{{\displaystyle \sum _{i=1}^n}|{\lambda }_i^{A_1}-{\lambda }_i^{A_2}{|}^2}& (3)\end{array}$

with λ^A denoting the eigenvalues of matrix A and |·| computing the magnitude of values.

4 Experiment

4.1 Dataset

4.1.1 LineMOD

To demonstrate manifold reconstruction, we use the LineMOD dataset (Hinterstoisser et al., 2012) which is widely adopted for 6D object pose estimation. The dataset includes 3D object models and RGB-D images along with the ground-truth 6D object poses. There are 15 texture-less objects with discriminative colors, shapes, and sizes. For each of 15 objects, there are 1313 samples at 640x480 resolution which are obtained by rendering object mesh models with surface color and normal from a densely sampled view sphere. For our experiments, we use RGB data rescaled to 64x64. We train autoencoders to learn manifolds corresponding to data of single object class and data of all 15 object classes.

4.2 Experimental setting

To demonstrate manifold reconstruction with data scarcity, we perform multiple baseline experiments using vanilla autoencoder (AE) and recent approaches emphasizing preservation of geometry (Lee Y. et al., 2021; Duque et al., 2022). We perform experiments using MRML under three episodic sampling schemes as illustrated in Figure 1. We first split the data into (meta-) training and (meta-) testing set by randomly selecting a sample and holding out nearest k samples from the neighbor in Euclidean space. By holding out this random cluster away from training, we simulate a training manifold with a low density region corresponding to unseen latent variations. For all MRML experiments, we use the same encoder and decoder architectures. The encoder consists of 4 convolutional layers followed by 3 fully connected layers and the decoder consists of 3 fully connected layers followed by 4 deconvolutional layers. The latent space is set to 10 dimension. We use the Adam optimizer (Kingma and Ba, 2015) and batch size 64 for training all the models. We performed two sets of experiments, one for learning the manifold from images of a single object and one for learning the manifold from images of all 15 object classes. For single object experiment, we hold out a local neighborhood containing 100 images. We perform training with 1,000 iterations at learning rate 10⁻³. For experiments on multiple object classes, we hold out a local neighborhood containing 1,000 images. The hold out data are from the same object class. We use the same batch size, learning rate, episodic step size and episodic testing weight as used in the single object experiments. We set the episodic training step size α and weight on episodic testing loss β to be 10⁻⁷ and 10⁻³ for all three settings. For vanilla AE and NRAE experiments, we use the same encoder and decoder architecture, optimizer setting and learning rate as used in MRML experiments. For GRAE, we followed the reported implementation. The hyperparameters are selected based on the convergence of reconstruction accuracy.

4.3 Results and discussion

We compare MRML under three episodic training settings against the baselines. To qualitatively compare the learned manifolds, we show 3-dimensional t-SNE visualizations (van der Maaten and Hinton, 2008) of the manifolds in the data space, the latent space of the encoder and the reconstruction space of the decoder in Figure 2. We observe that for baselines and MRML, the contour of the manifold is largely preserved when projected to the latent space and the reconstructed space. Specifically focusing on the hold-out test samples unseen at training stage (red in Figure 2), we notice that in comparison to the ones learned via baselines, manifold representations learned via MRML produce more uniformly distributed samples in both the latent space and the reconstructed space, which better matches the original data manifold.

Figure 2

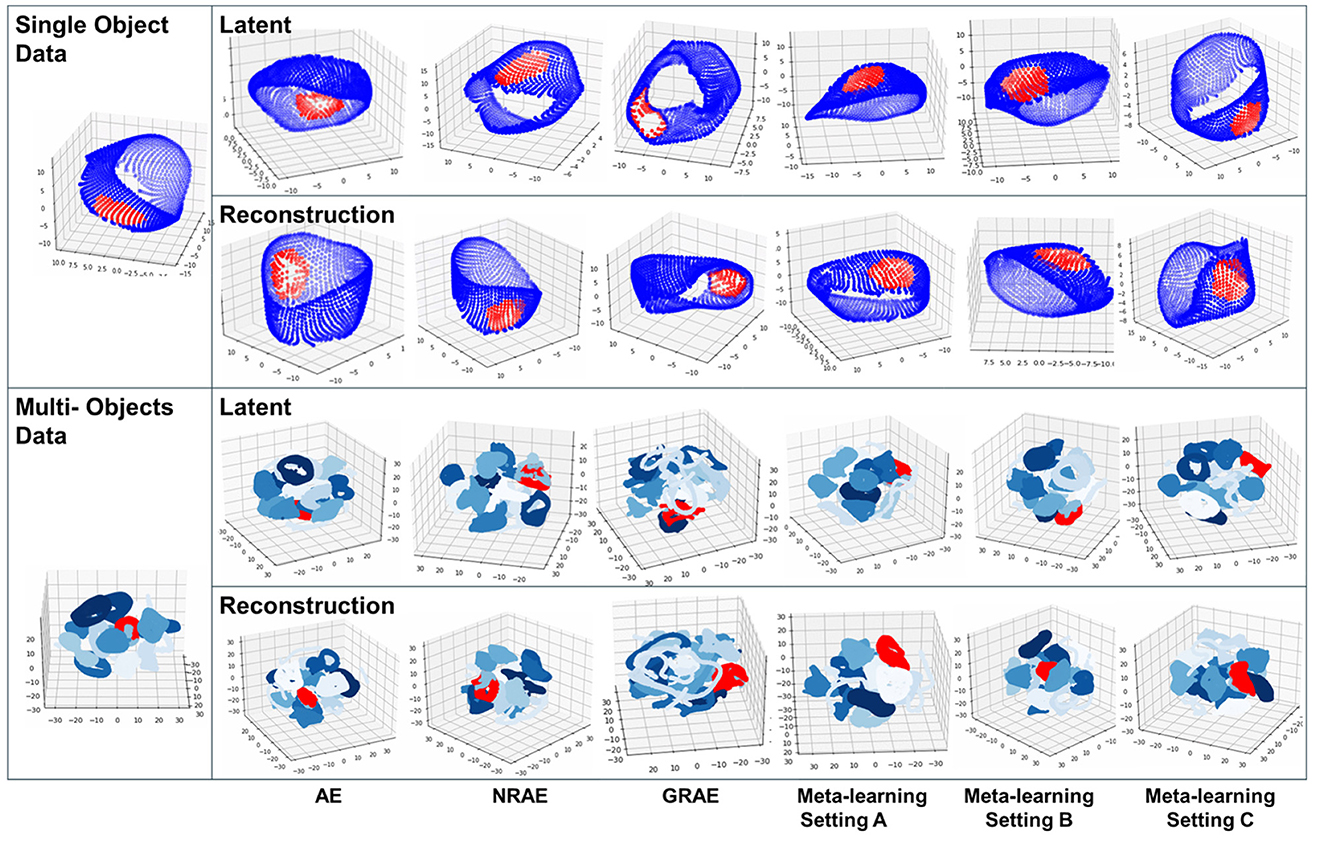
Figure 2. TSNE visualization of data and learned manifolds using LineMOD data of single object class (top panel) and all 15 object classes (bottom panel). In single object manifolds, blue represents meta-training samples and red represents hold-out meta-testing samples. In multiple object manifolds, blue with different shades represents meta-training samples of different objects and red represents hold-out meta-testing samples.

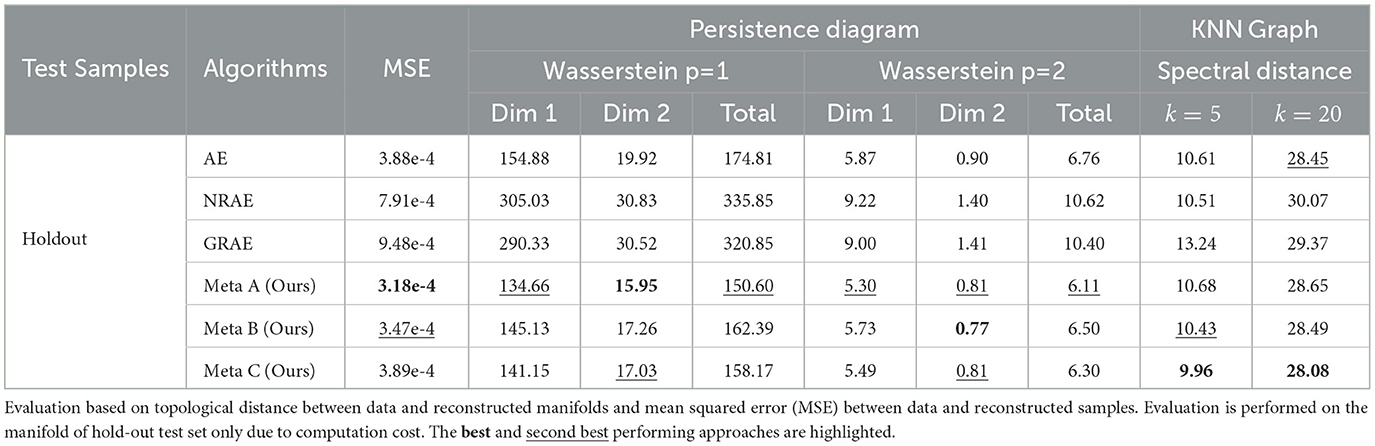
For qualitative comparison, in addition to sample-level reconstruction accuracy measured via mean square error (MSE), we measure the manifold-level reconstruction via the topological distance between learned manifold of the reconstructed images and the data manifold based on both persistence diagrams and KNN graphs. Table 1 shows the quantitative comparison for experiments on learning the manifold of a single object class. For comparison based on MSE, we observe that most methods have comparable sample-level reconstruction accuracy on average. While GRAE shows an edge in overall reconstruction accuracy but has considerably higher error when evaluated on the hold out test data. We would like to note that, while selected baselines were proposed to address local geometry, our problem setting pose further challenge in generalization as we consider holdout data specifically corresponding to holes/gaps in training manifolds as visualized in Figure 2, in opposed to, e.g., unseen samples following the same training distribution. Comparing performance over three sets of metrics, it is observed that for approaches with similar averaged reconstruction accuracy, its capability in preserving topological or geometric features can still vary. This emphasize the need for including topological and geometric metrics for examining representation learning to support the use of the representation in topological or geometric analysis. For comparison based on Wasserstein distance between persistence diagrams, we observe that MRML methods consistently achieve improved or comparative performance against baseline approaches over different orders of Wasserstein distance (p) and considering persistent homology features at different dimensions, especially for MRML setting B and setting C. This quantitative improvement is aligned with qualitative observation as shown in Figure 2. This improvement is consistent when we investigate manifold reconstruction of the local neighborhood that is held out from the training as well as the manifold reconstruction for the complete dataset including both training and hold-out testing samples. We also note that the improvement on reconstructing the manifold is demonstrated even against baselines showing higher average accuracy at sample level (e.g., comparing MRML against NRAE on holdout set and against GRAE on complete data). Specifically, MRML with best performing sampling strategy reduces the second order Wasserstein distance by a factor of 14.44% considering the hold-out neighborhood and by a factor of 4.44% considering the complete manifold against the best performing baseline.

Table 1

Table 1. Experiments on LineMOD dataset with single object class.

For comparison based on adjacency spectral distance between KNN graphs at different resolutions, we observe that when considering KNN graphs at finer granularity (k = 5), the comparison better correlates with the comparison based on averaged accuracy between pairwise samples. While proposed MRML methods, especially setting B and setting C on holdout test samples, demonstrate better match of KNN graphs at a coarser resolution (k = 20) which suggests the alignment on the intrinsic shape of the manifold. In this case, MRML with best performing sampling strategy demonstrates a reduction in adjacency spectral distance by a factor of 13.82% against the best performing baseline.

We also observe the improvement with proposed MRML approaches in both experiments of single object class where a manifold containing a single connected piece is considered and experiments of multiple object classes where the manifold of increased complexity contains multiple pieces, as shown in Table 2. Note that for the multi-class experiments, due to the computation cost, the comparison is only reported on the large holdout test set corresponding to the missing gap/hole in the manifolds. In this case, our proposed strategies again demonstrate consistent improvement with respect to topological metrics based on persistence diagrams and geometric metrics based on KNN graphs, comparing to baselines at similar or inferior generalization accuracy at sample level. Specifically, considering the hold-out neighborhood, MRML with best performing sampling strategy demonstrates a reduction in the second order Wasserstein distance by a factor of 9.62% against the best performing baseline.

Table 2

Table 2. Experiments on LineMOD dataset with multiple (15) object classes.

Finally, we compare the performance of MRML under different episodic sampling schemes. We observe that the comparison between MRML based strategies against baselines are mostly consistent. For single object experiments, we observe that Setting B and C yield relatively better generalization on the hold-out test samples and better reconstruction on the overall manifold. For experiments on multiple object classes where the overall manifold has higher complexity, setting A and C yield relatively better generalization. This comparison validate the use of sampling scheme specifically simulating a generalization to missing gaps/holes in the underlying manifold under setting C.

5 Conclusion

We propose manifold representation meta-learning to address data scarcity in manifold reconstruction. Our framework is based on model agnostic meta-learning, a state-of-the-art learning paradigm that utilize episodic training to achieve better performance given domain shifts. We specifically adapt the framework to address the challenge task of unsupervised manifold representation learning considering manifold regions with low sampling densities. We adopt two sets of topological and geometric metrics for quantitative comparison between data and model reconstruction at manifold level. The metrics are computed based on persistence diagrams characterizing homology features in the manifold and KNN graphs characterizing relative proximity of samples in the Euclidean space. We demonstrate that, in comparison to state-of-the-art baselines, our MRML can better preserve topological and geometric structures and better match the data manifold, especially for regions with low sampling densities. In our future work, we plan to integrate topological and geometric measures with model training to better capture the underlying manifold especially for real-world data with increasing complexity in shape and increasing noise level in the data samples.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YG: Writing – original draft, Writing – review & editing. JY: Writing – review & editing. RL: Writing – review & editing. XL: Writing – review & editing. CC: Writing – review & editing, Supervision. AD: Writing – review & editing. YY: Writing – review & editing, Supervision.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This material is based upon work supported by the Defense Advanced Research Projects Agency (DARPA) under Agreement No. HR0011-22-9-0077.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author disclaimer

Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of DARPA.

References

Agami, S. (2020). Comparison of persistence diagrams. Commun. Stat. Simulat. Comput. 52, 1948–1961. doi: 10.1080/03610918.2021.1894335

Crossref Full Text | Google Scholar

Aktas, M. E., Akbas, E., and Fatmaoui, A. E. (2019). Persistence homology of networks: methods and applications. Appl. Netw. Sci. 4, 1–28. doi: 10.1007/s41109-019-0179-3

Crossref Full Text | Google Scholar

Andrychowicz, M., Denil, M., Gomez, S., Hoffman, M. W., Pfau, D., Schaul, T., et al. (2016). “Learning to learn by gradient descent by gradient descent,” in Advances in Neural Information Processing Systems, 29.

Google Scholar

Bank, D., Koenigstein, N., and Giryes, R. (2020). Autoencoders. arXiv preprint arXiv:2003.05991.

Google Scholar

Bengio, Y., Courville, A., and Vincent, P. (2013). Representation learning: a review and new perspectives. IEEE Trans. Patt. Analy. Mach. Intell. 35, 1798–1828. doi: 10.1109/TPAMI.2013.50

PubMed Abstract | Crossref Full Text | Google Scholar

Cohen-Steiner, D., Edelsbrunner, H., and Harer, J. (2005). “Stability of persistence diagrams,” in Proceedings of the Twenty-First Annual Symposium on Computational Geometry, 263–271. doi: 10.1145/1064092.1064133

Crossref Full Text | Google Scholar

Duque, A. F., Morin, S., Wolf, G., and Moon, K. R. (2022). Geometry regularized autoencoders. IEEE Trans. Patt. Analy. Mach. Intell. 45, 7381–7394. doi: 10.1109/TPAMI.2022.3222104

PubMed Abstract | Crossref Full Text | Google Scholar

Edelsbrunner, H., and Harer, J. (2008). Persistent homology – a survey. Contemp. Mathem. 453, 257–282. doi: 10.1090/conm/453/08802

Crossref Full Text | Google Scholar

Finn, C., Abbeel, P., and Levine, S. (2017). “Model-agnostic meta-learning for fast adaptation of deep networks,” in International Conference on Machine Learning (PMLR), 1126–1135.

Google Scholar

Gropp, A., Atzmon, M., and Lipman, Y. (2020). Isometric autoencoders. arXiv preprint arXiv:2006.09289.

Google Scholar

Hinterstoisser, S., Lepetit, V., Ilic, S., Holzer, S., Bradski, G., Konolige, K., et al. (2012). “Model based training, detection and pose estimation of texture-less 3D objects in heavily cluttered scenes,” in Computer Vision-ACCV 2012: 11th Asian Conference on Computer Vision, Daejeon, Korea, November 5-9, 2012, Revised Selected Papers, Part I 11 (Springer Berlin Heidelberg), 548–562. doi: 10.1007/978-3-642-37331-2_42

Crossref Full Text | Google Scholar

Hospedales, T., Antoniou, A., Micaelli, P., and Storkey, A. (2022). Meta-learning in neural networks: a survey. IEEE Trans. Patt. Analy. Mach. Intell. 44, 5149–5169. doi: 10.1109/TPAMI.2021.3079209

PubMed Abstract | Crossref Full Text | Google Scholar

Hsu, K., Levine, S., and Finnl, C. (2019). Unsupervised learning via meta-learning. arXiv preprint arXiv:1810.02334.

Google Scholar

Kingma, D. P., and Ba, J. (2015). Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980.

Google Scholar

Lee, D. B., Min, D., Lee, S., and Hwang, S. J. (2021). “Meta-GMVAE: mixture of gaussian vaes for unsupervised meta-learning,” in International Conference on Learning Representations.

Google Scholar

Lee, Y., Kwon, H., and Park, F. C. (2021). “Neighborhood reconstructing autoencoders,” in Advances in Neural Information Processing Systems, 536–546.

Google Scholar

Lee, Y., Yoon, S., Son, M., and Park, F. C. (2022). “Regularized autoencoders for isometric representation learning,” in ICLR.

Google Scholar

Li, D., Yang, Y., Song, Y.-Z., and Hospedales, T. M. (2018). “Learning to generalize: meta-learning for domain generalization,” in Proceedings of the AAAI Conference on Artificial Intelligence. doi: 10.1609/aaai.v32i1.11596

Crossref Full Text | Google Scholar

Li, D., Zhang, J., Yang, Y., Liu, C., Song, Y.-Z., and Hospedales, T. M. (2019). “Episodic training for domain generalization,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 1446–1455. doi: 10.1109/ICCV.2019.00153

Crossref Full Text | Google Scholar

Liou, C.-Y., Cheng, W.-C., Liou, J.-W., and Liou, D.-R. (2014). Autoencoder for words. Neurocomputing 139, 84–96. doi: 10.1016/j.neucom.2013.09.055

Crossref Full Text | Google Scholar

Liu, Q., Chen, C., Qin, J., Dou, Q., and Heng, P.-A. (2021). “FEDDG: federated domain generalization on medical image segmentation via episodic learning in continuous frequency space,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 1013–1023. doi: 10.1109/CVPR46437.2021.00107

Crossref Full Text | Google Scholar

Mileyko, Y., Mukherjee, S., and Harer, J. (2011). Probability measures on the space of persistence diagrams. Inverse Problems 27:124007. doi: 10.1088/0266-5611/27/12/124007

PubMed Abstract | Crossref Full Text | Google Scholar

Moor, M., Horn, M., Rieck, B., and Borgwardt, K. (2020). “Topological autoencoders,” in International Conference on Machine Learning (PMLR), 7045–7054.

Google Scholar

Nazari, P., Damrich, S., and Hamprecht, F. A. (2023). Geometric autoencoders-what you see is what you decode. arXiv preprint arXiv:2306.17638.

Google Scholar

Omohundro, S. (1989). Five balltree construction algorithms. International Computer Science Institute Technical Report.

Google Scholar

Pun, C. S., Xia, K., and Lee, S. X. (2018). Persistent-homology-based machine learning and its applications - a survey. arXiv preprint arXiv:1811.00252.

Google Scholar

Schönenberger, S. T., Varava, A., Polianskii, V., Chung, J. J., Kragic, D., and Siegwart, R. (2020). “Witness autoencoder: shaping the latent space with witness complexes,” in NeurIPS 2020 Workshop TDA and Beyond.

Google Scholar

Schonsheck, S., Chen, J., and Lai, R. (2019). Chart auto-encoders for manifold structured data. arXiv preprint arXiv:1912.10094.

Google Scholar

Snell, J., Swersky, K., and Zemel, R. S. (2017). “Prototypical networks for few-shot learning,” in Advances in Neural Information Processing Systems, 30.

Google Scholar

Tenenbaum, J., de Silva, V., and Langford, J. (2000). A global geometric framework for nonlinear dimensionality reduction. Science 290, 2319–2323. doi: 10.1126/science.290.5500.2319

PubMed Abstract | Crossref Full Text | Google Scholar

van der Maaten, L., and Hinton, G. (2008). Visualizing data using t-SNE. JMLR 9, 2579–2605.

Google Scholar

Watanabe, S., and Yamana, H. (2022). Topological measurement of deep neural networks using persistent homology. Ann. Mathem. Artif. Intell. 90, 75–92. doi: 10.1007/s10472-021-09761-3

Crossref Full Text | Google Scholar

Wills, P., and Meyer, F. G. (2020). Metrics for graph comparison: a practitioner's guide. PLoS ONE 15:e0228728. doi: 10.1371/journal.pone.0228728

PubMed Abstract | Crossref Full Text | Google Scholar

Wu, M., Choi, K., Goodman, N., and Ermon, S. (2020). “Meta-amortized variational inference and learning,” in Proceedings of the AAAI Conference on Artificial Intelligence, 6404–6412. doi: 10.1609/aaai.v34i04.6111

Crossref Full Text | Google Scholar