Leveraging linear mapping for model-agnostic adversarial defense

In the ever-evolving landscape of deep learning, novel designs of neural network architectures have been thought to drive progress by enhancing embedded representations. However, recent findings reveal that the embedded representations of various state-of-the-art models are mappable to one another via a simple linear map, thus challenging the notion that architectural variations are meaningfully distinctive. While these linear maps have been established for traditional non-adversarial datasets, e.g., ImageNet, to our knowledge no work has explored the linear relation between adversarial image representations of these datasets generated by different CNNs. Accurately mapping adversarial images signals the feasibility of generalizing an adversarial defense optimized for a specific network. In this work, we demonstrate the existence of a linear mapping of adversarial inputs between different models that can be exploited to develop such model-agnostic, generalized adversarial defense. We further propose an experimental setup designed to underscore the concept of this model-agnostic defense. We train a linear classifier using both adversarial and non-adversarial embeddings within the defended space. Subsequently, we assess its performance using adversarial embeddings from other models that are mapped to this space. Our approach achieves an AUROC of up to 0.99 for both CIFAR-10 and ImageNet datasets.

1. Introduction

The rapid advancements in deep learning have led to remarkable breakthroughs in various tasks, such as image recognition, natural language processing, and autonomous driving. These achievements are widely attributed to increasingly innovative designs of neural network architectures, which are believed to enhance the quality of embedded representations. However, evidence from recent research into embedded representations has found results that counter this narrative. Specifically, McNeely-White et al. (2022) found that embedded representations of inputs within state-of-the-art models can be linked via a simple linear map. The existence of this simple map suggests that, despite the architectural diversity, the learned embedded representations may not be as distinctive as previously assumed.

In this study, we investigate the potential to harness this mapping to develop robust defenses against adversarial attacks (i.e., imperceptible perturbations added to input data that cause neural networks to incorrectly process inputs; Szegedy et al., 2014b). The crux of our proposed defense is that an adversarial defense can be established for specific neural network's embedded space—then, other neural network's embedded representations can be linearly mapped to that embedding space, leading to the detection of adversarial attacks. We define the neural network with the defense's embedding space as the canonical embedding space.

In order for the defense designed for the canonical embedding space to generalize to mapped inputs from other networks, adversarial inputs into other networks would need to map to the canonical space. We believe our work is the first to investigate if such a mapping would be accurate—McNeely-White et al. (2022) only experimented with mapping in-domain, unperturbed inputs from datasets like ImageNet and IJB-C. Mapping adversarial inputs between embedding spaces is a difficult problem because adversarial inputs are typically generated for a specific network. Thus, a source image that is adversarially perturbed by two different networks, resulting in one image per network, is distinct because each generated image is designed to fool a specific network. This makes the mapping problem more difficult, and requires that any adversarial defense for a canonical embedding space be robust to these differences.

Our work investigated a defense proposed by Gorbett and Blanchard (2022), utilizing a linear SVM to detect adversarial inputs specific to a particular network. The SVM training necessitates creating a dataset of potential attacks. While Gorbett and Blanchard (2022) demonstrates robustness with sufficient data, a drawback lies in the dataset requirement. By considering one network as the canonical reference and mapping other networks to that space, we overcome this limitation, needing training data solely for the canonical network. Figure 1 provides a high-level illustration of the concept.

FIGURE 1

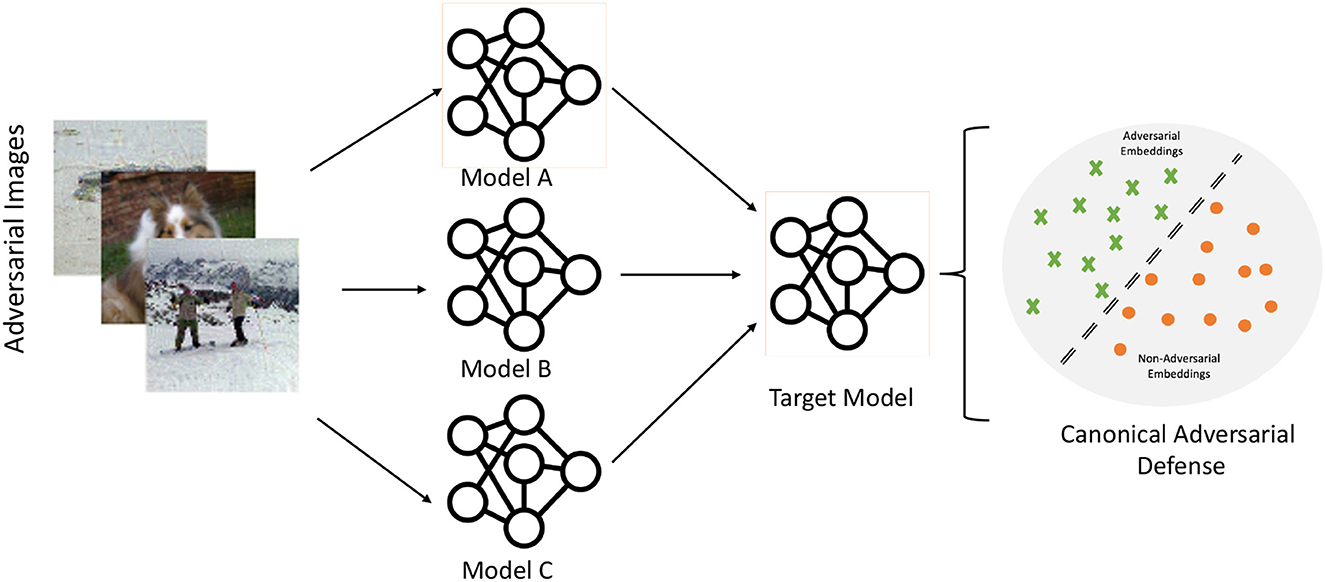
Figure 1. The idea of a model-agnostic defense: Adversarial embeddings from different models are mapped to a target model with a defended space. The mapped adversarial embeddings can then be effectively detected from non-adversarial embeddings using a simple linear classifier trained on the adversarial and non-adversarial embeddings of the target model.

In this research paper, we present the following key contributions:

• Successful Linear Mapping of Adversarial Inputs: We successfully establish connections between adversarial inputs across diverse CNNs using a simple linear mapping. By applying this technique to adversarial versions of MNIST, CIFAR-10, and ImageNet datasets, we achieve Mean Squared Error (MSE) scores, of mapped adversarial embeddings, going as low as approximately 0, highlighting significant similarities in the adversarial image embeddings of various CNN architectures.

• Robust Cross-Model Adversarial Detection: We develop a straightforward yet effective adversarial defense mechanism based on a linear SVM approach. Remarkably, this defense method, initially constructed for one model's embeddings, proves to be highly adept at detecting adversarial embeddings from other models as well. The achieved Area Under the Receiver Operating Characteristic (AUROC) scores, reaching up to 0.99, demonstrate the robustness and generalizability of our defense approach across different CNN architectures.

• By integrating linear mapping to build adversarial detection method, ultimately, we propose a canonical adversarial defense that accurately identifies adversarial inputs from a range of networks and adversarially manipulated datasets.

Our paper adheres to the following structure: Section 2 presents a comprehensive review of related literature concerning adversarial defense and linear mapping. In Section 3, we outline the experimental setup, encompassing the definition of linear mapping, selection of datasets, implementation of adversarial attacks, and the chosen evaluation metrics. Sections 4, 5, and 7 contain the details of conducted experiments, analysis of obtained results, and discussion. Lastly, in Section 8, we provide concluding remarks summarizing the overall findings and contributions of our research.

2. Related work

2.1. Adversarial defense

In recent years, the vulnerability of deep neural networks (DNNs) to adversarial attacks has sparked significant interest, leading to a growing body of research focused on interpreting adversarial attacks (Han et al., 2023) and devising defense and detection mechanisms (Khamaiseh et al., 2022). Various proposed methods include augmenting input images to enhance robustness against adversarial attacks (Frosio and Kautz, 2023), mapping adversarial images back to the clean distribution (Li et al., 2023), and using vector quantization (Dong and Mao, 2023). Several studies have delved into gradient-based methods, including leveraging sparse representation to counter adversarial attacks (Gopalakrishnan et al., 2018), constraining the hidden space of DNNs (Mustafa et al., 2019), and reducing the space of potential adversarial examples (Xu et al., 2017).

In parallel, researchers have also explored the utilization of manifold-related properties to address adversarial attacks. Notably, Jha et al. (2018) observed that adversarial examples tend to deviate from the data manifold as the intensity of attacks increases, and this increasing distance can serve as a valuable cue for detection. Moreover, Crecchi et al. (2019) employed the non-linear dimensionality reduction technique t-SNE to identify adversarial examples by detecting images lying outside the manifold in localized pockets. Additionally, Feinman et al. (2017) introduced kernel density and Bayesian uncertainty estimation methods for adversarial detection, using the representations of unknown data points in the last hidden layer to measure their distance within that feature space. These manifold-based approaches present promising avenues for fortifying DNNs against adversarial perturbations.

Another intriguing area for advancing adversarial defense techniques lies in the development of pre-processing methods. Recent studies by Blau et al. (2022) and Nie et al. (2022) have introduced innovative defense strategies based on diffusion processes, which prove effective in countering adversarial attacks. Qiu et al. (2021) in their work, have put forth pre-processing techniques aimed at mitigating gradient-based attacks. Additionally, Zheng et al. (2020) have proposed a model-agnostic defense approach that leverages affine transformations applied to images as a pre-processing step. Our work distinguishes itself from traditional pre-processing defense methods. Instead of modifying the input data prior to model inference, we harness the output of trained models as a foundation for constructing our adversarial defense.

The utilization of information from latent layers for detecting adversarial attacks has also received extensive attention. Bendale and Boult (2016) introduced OpenMax as an alternative to the softmax layer, leveraging penultimate layer information to identify unknown classes. Li and Li (2017) employed convolution layer outputs to develop a cascade method for detecting adversarial examples. In contrast, Gorbett and Blanchard (2022) demonstrated that only penultimate layers carry sufficient information to distinguish adversarial from non-adversarial images. Furthermore, Jamil et al. (2023) highlighted the utility of intermediate ReLU activation patterns for detecting adversarial images. These diverse approaches underscore the significance of using latent layer information for robust adversarial detection.

Our work aligns with the latter research endeavors, where we capitalize on information from the penultimate layer to construct a shared embedding space for various DNNs. This shared space exhibits potential as a robust fortress for adversarial defense. By mapping adversarial embeddings from different DNNs onto this canonical space, our aim is to create a generalized defense mechanism against adversarial attacks. This approach holds promise for strengthening the security and robustness of deep neural networks in the face of adversarial perturbations.

2.2. Linear mapping

Some researchers have directed their efforts toward emphasizing the commonalities existing between different DNN architectures concerning the learned features. For instance, in Lenc and Vedaldi (2015), a comparison of the hidden representations of DNNs in the convolutional layers was carried out through regression analysis. Notably, a series of studies conducted by McNeely-White et al. (2020), McNeely-White et al. (2021), and McNeely-White et al. (2022), established a relationship among DNNs by demonstrating that their hidden representations are essentially similar, up to a single linear transformation. McNeely-White et al. (2022) delved into the implications of these linear mappings in the context of biometric security.

In our work, we build upon this concept and extend it to the domain of adversarial attacks. We aim to investigate whether the hidden network representations for adversarial data can also be effectively mapped from one model's embedding space to another model's space. By exploring the feasibility of such cross-model mappings, we seek to uncover potential insights that may facilitate the development of more robust adversarial defense strategies.

3. Experimental setup

This section presents the methodology for establishing a linear mapping between a source network and a target network (see Section 3.1). Additionally, it encompasses the details of the datasets utilized in this study (see Section 3.2), the employed adversarial attacks (see Section 3.3), and the evaluation metrics (see Section 3.4) used to assess the transferability of adversarial features.

3.1. Linear mapping

Given f_A and f_B as the source and target networks, respectively, and X as the set of input images, we define a linear map denoted by M_A→B as follows:

$\begin{array}{ll}{\tilde{f}}_B\left(X\right)=M_{A\to B}{f}_A\left(X\right),& (1)\end{array}$

where ${\tilde{f}}_B\left(X\right)$ is the best approximation to f_B(x) across a given dataset, and the linear mapping M_A→B is computed by solving a least square regression problem as follows:

$\begin{array}{ll}\begin{array}{c}{\displaystyle \underset{{\tilde{M}}_{A\to B}}{minimize}}{\displaystyle {\sum }_{i=1}^m}\Vert {\tilde{M}}_{A\to B}{f}_A\left(x\right)-f_B\left(x\right){\Vert }_2.\end{array}& (2)\end{array}$

3.2. Datasets

To assess the transferability of adversarial information between different architectures, we conduct a series of experiments. We begin by testing with a simple dataset such as MNIST, and subsequently, we validate its generalizability by extending the evaluation to more complex datasets like CIFAR-10 and ImageNet. This section provides an overview of the datasets utilized in the experiments, as well as a detailed explanation of the methodology used for generating the adversarial attacks.

3.2.1. MNIST

The MNIST dataset comprises a collection of 70,000 grayscale images of handwritten digits, each measuring 28 × 28 pixels. The dataset is further partitioned into a training set, containing 60,000 images, and a test set, containing 10,000 images. These images are categorized into 10 classes, representing the digits from 0 to 9.

3.2.2. CIFAR-10

The CIFAR-10 dataset comprises 60,000 images that are organized into 10 distinct classes. For training purposes, there are 50,000 images, and an additional 10,000 images are allocated for testing. Each image within the dataset measures 32 × 32 pixels.

3.2.3. ImageNet

In this study, we utilized the validation set from the ImageNet dataset, consisting of 50,000 images spread across 1000 classes, with 50 images per class.

For the MNIST and CIFAR-10 datasets, we employed the training set to train the models. Subsequently, the test set was utilized to calculate the linear mapping and assess the transferability of adversarial attacks.

As for the Imagenet dataset, we performed a train-test split on the validation set. The training set was utilized to compute the linear mapping, while the test set was employed to evaluate the transferability of adversarial attacks.

3.3. Adversarial attacks

We generate adversarial datasets corresponding to MNIST, CIFAR-10, and ImageNet datasets using the following adversarial attack techniques.

3.3.1. Fast gradient sign method

The Fast Gradient Sign Method (FGSM) (Szegedy et al., 2014b) is an efficient one-step adversarial attack technique. It introduces small perturbations δ to the input data x based on the gradient ▽_x of the loss function J with respect to the input. The perturbations are scaled by a small positive scalar ϵ, and their direction is determined by the sign of the gradient. This method causes misclassification by the targeted machine learning model. The mathematical representation is as follows:

$\begin{array}{ll}\delta =ϵ·\text{sign}\left({▽}_{x}J\left(\Phi ,x,y\right)\right),& (3)\end{array}$

where ϵ is the scaling factor and sign denotes the sign function. This technique is widely used for crafting adversarial examples to evaluate the robustness of machine learning models.

3.3.2. Projected gradient descent

In contrast to FGSM, Projected Gradient Descent (PGD) (Madry et al., 2017) is an iterative adversarial attack method that computes perturbations using gradients and then restricts them within a specified perturbation bound. This iterative approach leads to more robust attacks as the perturbations are constrained to remain within an acceptable range. The iterative perturbation can be expressed as follows, where α represents the perturbation step size:

$\begin{array}{ll}{\delta }_{t+1}={\text{clip}}_{ϵ}\left({\delta }_t+\alpha ·\text{sign}\left({▽}_{x}J\left(\Phi ,x+{\delta }_t,y\right)\right)\right).& (4)\end{array}$

Here, clip_ϵ denotes a function that ensures the perturbations stay within the specified range, ϵ.

3.3.3. Carlini and Wagner attack

The Carlini and Wagner attack (Carlini et al., 2019) is an optimization-based adversarial technique that efficiently finds small perturbations to cause misclassification in a fixed input image. By minimizing a distance metric between the original and perturbed images, the attack strikes a balance between misclassification confidence, perturbation size, and the distance norm. This approach aims to generate potent and subtle adversarial perturbations for evading machine learning models effectively.

3.3.4. DAmageNet

DAmageNet (Chen et al., 2019) presents a transferable adversarial attack strategy that leverages attention heatmaps to create universal adversarial samples. By directing the attention to irrelevant regions in the image, it induces misclassification, taking advantage of shared attention patterns across diverse deep neural networks. This technique has proven to be effective in causing misclassification across a wide range of models, demonstrating its potency in generating robust adversarial samples.

In our experimental setup, we employed the Fast Gradient Sign Method (FGSM) attack to create adversarial datasets for the MNIST, CIFAR-10, and ImageNet validation datasets. For each dataset, we set the perturbation magnitude (ϵ) to the values of 0.02, 0.05, and 0.01, respectively.

However, for the ImageNet experiments, we extended our evaluation to include more sophisticated attacks, such as PGD, C&W attack, and the DamageNet attack. The adversarial dataset corresponding to the ImageNet validation set, generated with the DamageNet attack, was directly obtained from reliable source on the web.

3.4. Testing and evaluation metrics

3.4.1. Mean squared error

To evaluate the effectiveness of a linear mapping, we use the Mean Squared Error (MSE) metric. This involves calculating the MSE between the target embeddings and their corresponding linearly mapped source embeddings. For each pair of embeddings, we compute the squared differences between their elements, sum up these squared differences, and then take the average across all pairs. This resulting average MSE score represents how well the linear mapping transforms embeddings from one space to another. Lower MSE values indicate a more accurate and robust linear mapping.

3.4.2. Linear SVM classifier

To assess the effectiveness of linear mapping for deep neural networks with adversarial images, we adopt a linear SVM classifier. As demonstrated in a prior study (Gorbett and Blanchard, 2022), adversarial image embeddings can be distinguished from non-adversarial image embeddings using a linear SVM. To evaluate the mapping's efficacy, we train a linear SVM classifier on embeddings generated by one model to discern between adversarial and non-adversarial image embeddings. Additionally, we investigate whether the mapped adversarial embeddings, linearly transformed from a different network's embedding space to the target network's space, remain distinguishable from the non-adversarial image embeddings. To quantify the SVM's performance, we measure the area under the receiver operating characteristic curve (AUROC) metric.

4. Experiments

For CIFAR-10 and MNIST datasets, each comprising two sets: train and test. These sets consist of original images and their corresponding adversarial counterparts generated using the FGSM attack mentioned in Section 3.4.1.

In the case of ImageNet, we utilize pretrained models, leading to a dataset that solely contains test data. This dataset encompasses both original images and their corresponding adversarial images crafted through all the mentioned adversarial attacks given in Section 3.3.

For MNIST, we use two straightforward architectures: one comprising convolution layers and the other a feed-forward neural network (FFNN). For CIFAR-10, we employ EfficientNet (Tan and Le, 2020), ResNet-18 (He et al., 2015), MobileNetV2 (Sandler et al., 2019), GoogLeNet (Szegedy et al., 2014a), and VGG-19 (Simonyan and Zisserman, 2015) architectures. These networks were trained solely on the original images from the MNIST and CIFAR-10 training sets, respectively. In the case of ImageNet, we use pre-trained models, namely ResNet-50, ResNet-101, ResNet-152 (He et al., 2015), VGG-19, Inception-v3 (Szegedy et al., 2014a) and Vision Transformer (Dosovitskiy et al., 2020), which have been trained on the ImageNet training dataset. The classification accuracy on original test dataset and corresponding FGSM adversarial dataset of each of these models, evaluated using the test set, along with the size of the penultimate layer, are summarized in Table 1.

TABLE 1

Table 1. Classification accuracies for DNNs trained and evaluated on MNIST, CIFAR-10, and ImageNet and their corresponding adversarial datasets.

In these experiments, we initially construct a linear classifier trained to discriminate between the adversarial embeddings and original embeddings of a target model. Subsequently, we demonstrate that the trained classifier also effectively distinguishes these original embeddings from adversarial embeddings that are mapped from a source model to this target model.

To conduct this investigation, we designate a model as the target model and proceed to map the adversarial and original features from the embedding spaces of other models to the embedding space of this target model using MNIST and CIFAR-10 datasets with specified neural architectures. We then expand this approach to the ImageNet dataset, employing one neural architecture as the target model and several other architectures as source models. The experiment involves dividing the validation dataset into three distinct splits: map, svm, and val. For each split, we calculate the embeddings of the networks from their penultimate layer, which are denoted as $X_{\mathrm{\text{map}}}^A$, $X_{\mathrm{\text{svm}}}^A$, $X_{\mathrm{\text{val}}}^A$, with A representing the network under consideration.

Given two networks, a source network denoted by s and a target network denoted by t, we train a linear SVM using the embeddings $X_{\mathrm{\text{svm}}}^t$ from the target network. This SVM classifier is trained with binary labels to distinguish between adversarial and original data. Then, we learn a linear mapping denoted as M_s→t that aligns the embeddings $X_{\mathrm{\text{map}}}^s$ with $X_{\mathrm{\text{map}}}^t$ by solving model (2). Subsequently, we obtain the mapped embeddings $X_{\mathrm{\text{val}}}^{{}^{\prime }}$ by applying M_s→t to the validation data, $X_{\mathrm{\text{val}}}^s$, i.e., $X_{\mathrm{\text{val}}}^{{}^{\prime }}=M_{s\to t}{X}_{\mathrm{\text{val}}}^s$. We then measure the strength of this mapping using the MSE metric, as mentioned in Section 3.4.1.

To assess adversarial transferability, we replace the validation data of target network, $X_{\mathrm{\text{val}}}^t$, with $X_{\mathrm{\text{val}}}^{{}^{\prime }}$ obtained from linear mapping process. Next, we evaluate the modified data on the linear SVM trained on the target model's embeddings. The extent of transferability is quantified by measuring the SVM classification accuracy on the data which is the source model's adversarial and original embeddings after being linearly mapped to the target model's embedding space (see Section 3.4.2). The procedure is formally described in Algorithm 1.¹

ALGORITHM 1

Algorithm 1. Cross-network adversarial mapping and detection.

5. Results

5.1. Linear mapping for MNIST

Initially, we investigated the feasibility of linearly mapping adversarial images from the MNIST dataset and using a linear SVM to identify the adversarial images. Using a convolutional neural network (CNN) and a feed-forward neural network (FFNN) and evaluating mapping between both, we found the SVM was able to accurately identify adversarial images with 99.4% accuracy (CNN → FFNN) and 99.5% accuracy (FFNN → CNN) with ϵ = 0.02—notably, these results were consistent across various epsilon values. This mirrors the accuracy of the SVM's performance on the original embedding space (99.8% for CNN; 99.9% for FFNN).

5.2. Linear mapping for CIFAR-10

Table 2 presents the MSE scores between the adversarial embeddings of the target space and the ones mapped from the source model embedding space to the target model embedding space. The recorded lowest MSE values are 0.003 and 0.004 when adversarial embeddings are mapped to the space of GoogLeNet and MobileNet, respectively. Even when other models are considered as the target model, the MSE values remain remarkably low, indicating the overall efficiency of the linear mappings.

TABLE 2

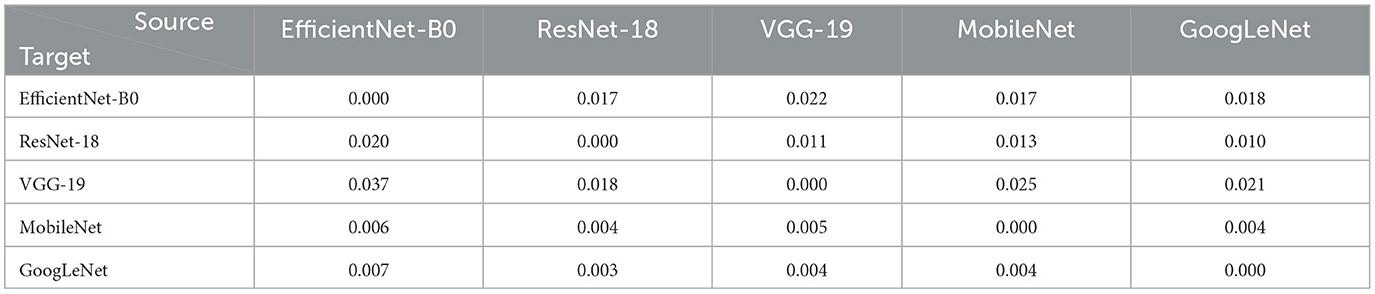
Table 2. MSE scores (3.4) for the trained linear mapping between source and target adversarial embeddings for CIFAR-10.

The architectures employed in the experiments demonstrate varying accuracies on non-adversarial and adversarial data (Table 1). EfficientNet-B0, with an accuracy of only 85%, is particularly vulnerable to adversarial attacks, achieving a mere 39.31% accuracy when exposed to such perturbations. Table 3 illustrates that when adversarial embeddings are mapped to the low-performing EfficientNet-B0, its ability to distinguish adversarial images from non-adversarial ones decreases. On the contrary, for ResNet-18, which exhibits better classification accuracy on original data, the mapped adversarial embeddings retain more distinctive features, enabling their effective separation from original images. These results show that the separability of adversarial embeddings seems to be contingent on the model's ability to classify the original data accurately. In other words, if the model performs well in classifying the original data, it tends to achieve better separability of adversarial embeddings as well.

TABLE 3

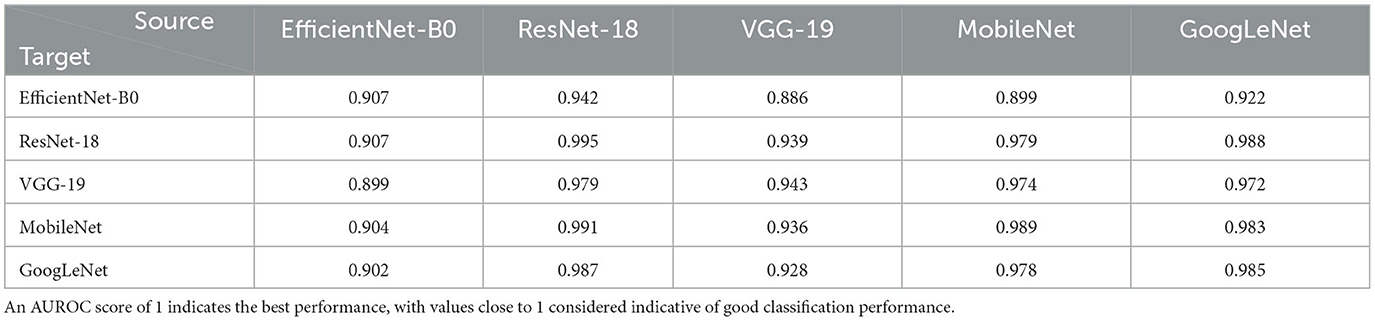
Table 3. AUROC scores for classification of mapped original and adversarial image embeddings from the source model using a linear SVM trained on target model's embeddings for CIFAR-10 dataset.

These findings were obtained using the FGSM adversarial attack with ϵ = 0.05. However, the transferability of adversarial features appears to be less dependent on the perturbation level, consistent with our observations from the MNIST experiments.

5.3. Linear mapping for ImageNet

Building upon the insights gained from MNIST and CIFAR-10, where linear mapping for adversarial data between different CNN architectures proved effective, we propose a shared embedding space concept, leveraging the ImageNet dataset. Specifically, we utilize ResNet-152's penultimate layer as the shared space, mapping adversarial embeddings from other networks onto it. Table 4 shows the MSE scores between the adversarial embeddings generated by ResNet-152 and the ones mapped to it from various CNNs. The overall MSE values are very low, except for VGG-19 where we observe notably higher MSE scores. We hypothesize that this discrepancy can be attributed to the high dimensionality of the VGG-19 embedding space. This trend appears to persist across our subsequent experiments, suggesting a consistent challenge posed by the intricately layered embedding space of VGG-19. Interestingly, the attention based model, ViT, shows very low MSE scores, signifying linear mapping can be easily learnt between CNN and attention based architectures.

TABLE 4

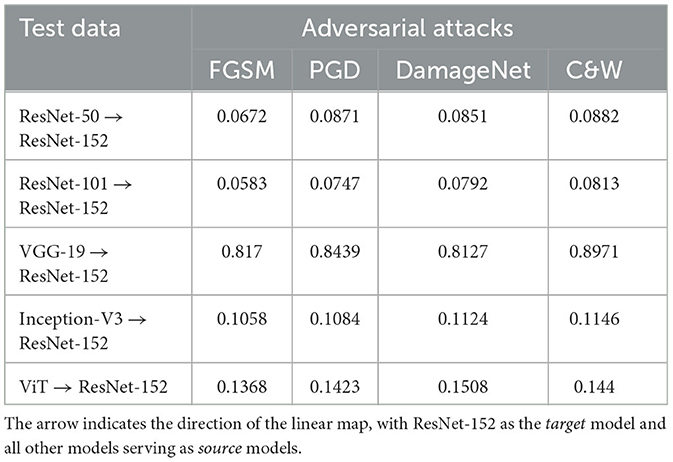
Table 4. MSE scores for the linear mapping trained on original and adversarial embeddings for ImageNet between various models and ResNet-152.

Moreover, Table 5 presents the AUROC values obtained from the linear SVM classification. Firstly, it shows the results for ResNet-152 generated using adversarial and non-adversarial embeddings (1st row). Subsequently, it demonstrates the performance of the linear SVM when applied to the adversarial embeddings mapped to ResNet-152 space from other models' embedding space. The AUROC scores range from 0.75 to 0.99, which represents an impressive range, highlighting the excellent performance of the linear SVM. These results demonstrate that different DNNs learn similar adversarial features, facilitating successful mapping and accurate detection using a binary classifier.

TABLE 5

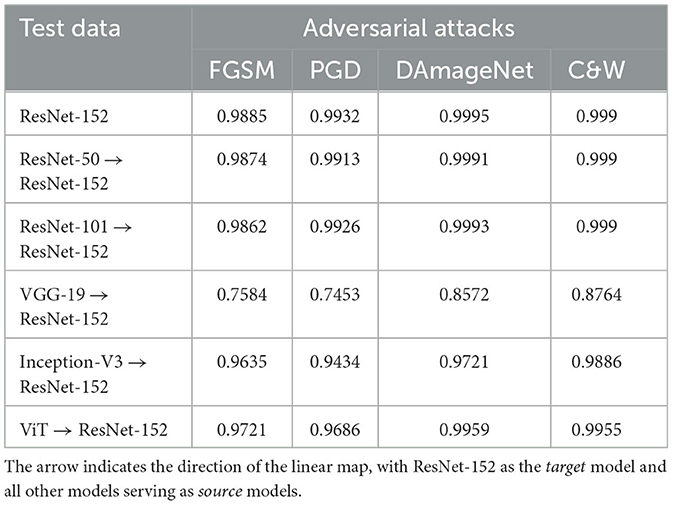
Table 5. AUROC scores for classification of mapped original and adversarial image embeddings from various models using a linear SVM trained on ResNet-152 model's embeddings.

We also perform the similar experiment while making the ViT as the target model and mapped the embeddings from all CNN architectures to its space. The AUROC scores for the SVM detection is given is Table 6. It is interesting to observe that the attention based architecture does not affect the quality of learnt linear map and the results are consistent with when the embeddings were mapped to ResNet-152's space.

TABLE 6

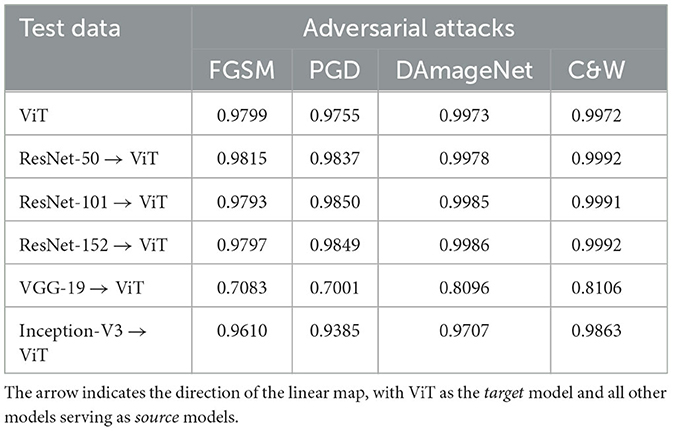
Table 6. AUROC scores for classification of mapped original and adversarial image embeddings from various models using a linear SVM trained on Vision Transformer (ViT) model's embeddings.

Remarkably, the linear mapping is trained exclusively on adversarial images; however, during detection, when differentiating adversarial embeddings from other models with non-adversarial embeddings from ResNet-152, the SVM performs comparably or even better. This observation indicates that adversarial information within an image can be linearly transferred, alongside the image embeddings themselves, to a different CNN space. Consequently, this idea hints at the potential for a unified and transferable representation of adversarial features across diverse DNN architectures within the ImageNet dataset.

5.4. Mapped embeddings adversarial classification accuracy

To assess whether the embeddings, once mapped to the target network, maintain their adversarial nature, we conducted an experiment to measure the classification accuracies achieved by the target models. Specifically, we recorded the classification accuracies of the target models when provided with embeddings mapped to their respective embedding spaces. The results are presented in Table 7, showcasing both the average accuracies across different source models and their standard deviations.

TABLE 7

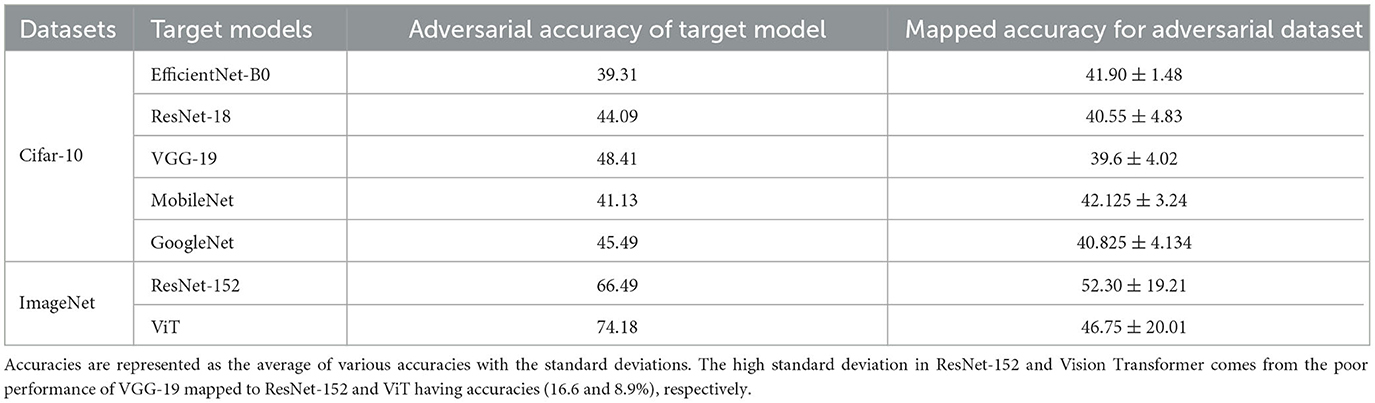
Table 7. Adversarial classification accuracies of embeddings from different models mapped to the target model for FGSM attack.

Table 7 reveals a notable trend—the classification accuracy of the target models closely aligns with their adversarial accuracies (as indicated in column 3 of Table 7). This observation underscores the effectiveness of our mapping approach in preserving adversarial characteristics during the transfer.

However, it's worth noting that when considering the ImageNet dataset, we observed a higher standard deviation, particularly due to the mapping process from the VGG-19 embedding space. This outcome can be attributed to the inherent challenges posed by the substantial disparity in dimensions between the source and target embeddings, a point previously discussed.

6. Comparison with other method

Our proposed method is the first to demonstrate the existence of a linear mapping between adversarial image representations of two models and leverages this insight to construct a model-agnostic adversarial defense.

We illustrate the possibility of this linear mapping using a simple baseline—a linear Support Vector Machine (SVM)—to create a model-agnostic detection method. We compare our baseline with the adversarial detection method proposed by Harder et al. (2021). The experiments in this section provide a comparative analysis. Specifically, we calculate the magnitude and phase of Fourier transforms for the penultimate layer embeddings and utilize them to establish a linear mapping. We then proceed to train a linear SVM classifier, following the procedure outlined in Algorithm 1.

To facilitate a comprehensive comparison, we selected ResNet-152 and Vision Transformer (ViT) as our target models, and mapped the Magnitude Fourier Spectrum (MFS) and Phase Fourier Spectrum (PFS) embeddings from various source models into the spaces of these target models. Our findings, as presented in Tables 8, 9, offer valuable insights.

TABLE 8

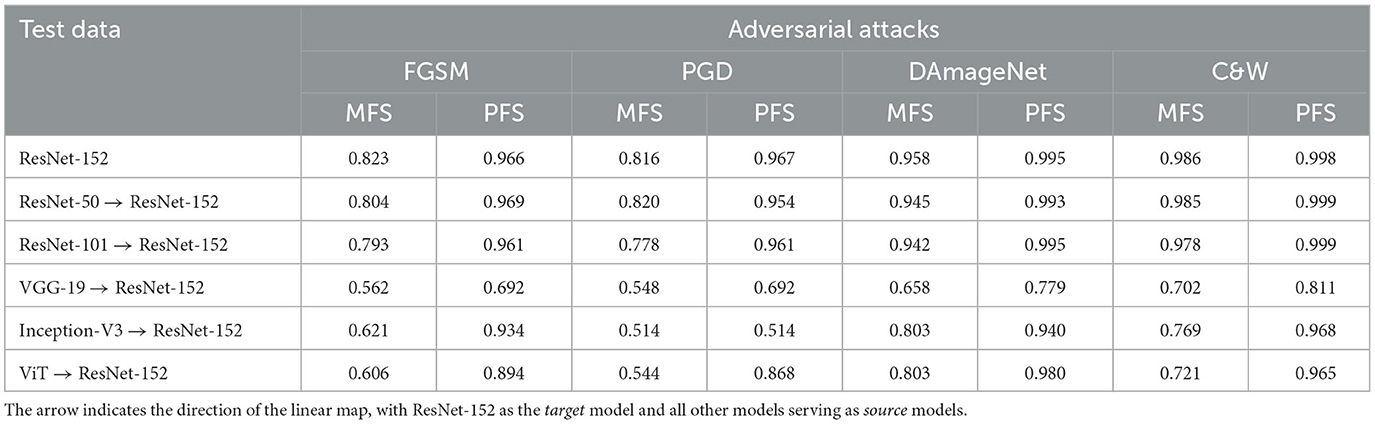
Table 8. AUROC scores for classification of mapped original and adversarial image magnitude Fourier spectrum (MFS) and phase Fourier spectrum (PFS) from various models using a linear SVM trained on ResNet-152 model's embeddings.

TABLE 9

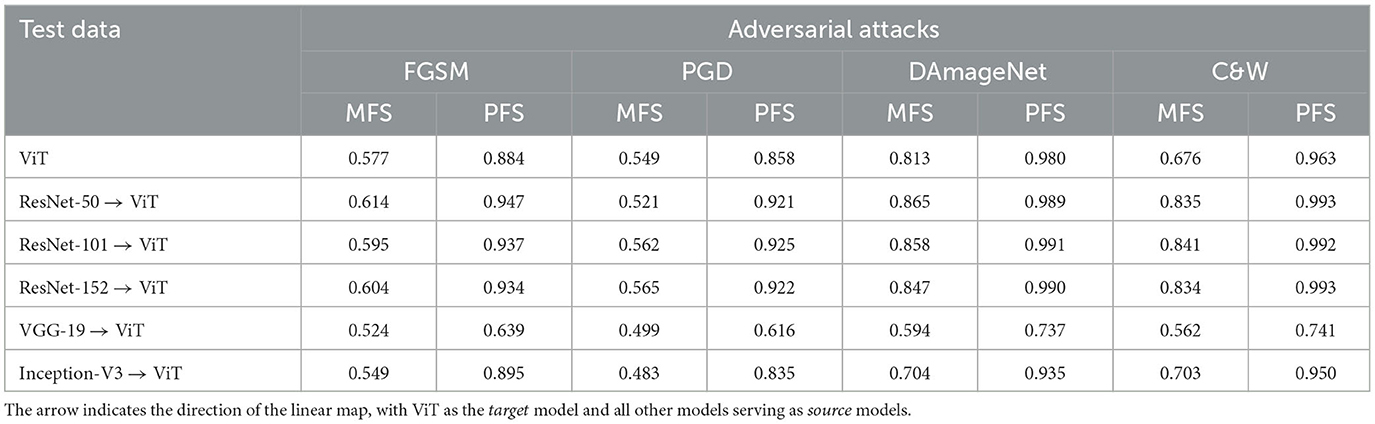
Table 9. AUROC scores for classification of mapped original and adversarial image magnitude Fourier spectrum (MFS) and phase Fourier spectrum (PFS) from various models using a linear SVM trained on Vision Transformer (ViT) model's embeddings.

Notably, when utilizing the mapped MFS embeddings, we observed that linear SVM did not exhibit strong performance, as indicated by relatively low AUROC scores across all adversarial attacks. In contrast, our method, which involves directly learning the linear mapping using the model's native embeddings, consistently outperformed the mapped MFS approach.

Furthermore, our analysis reveals that PFS presents an intriguing facet. It demonstrates superior performance when compared to mapped MFS embeddings, suggesting that phase information is amenable to linear mapping. However, it's worth highlighting an interesting observation: while PFS performs well within the realm of CNN-based architectures, its efficacy diminishes when applied to the mapping from attention-based architectures to CNN-based ones, as evidenced by lower AUROC scores in Table 8.

Notably, when all models are mapped to ViT space, the performance of PFS exhibits a slight decrease (see Table 9) compared to our proposed method. This underscores the adaptability and robustness of our approach, particularly in scenarios involving attention-based architectures.

In summary, our exploration of MFS and PFS mappings reveals interesting results. While PFS demonstrates promise, especially within the CNN domain, our method of direct linear mapping using model embeddings consistently delivers superior performance across various model architectures and adversarial attacks.

We also observed a notable variation in results when using different adversarial attack methods. For instance, the performance is better with DAmageNet images, likely due to their higher level of perturbation (MSE = 2.97 across the dataset) compared to FGSM (0.013), PGD (1.83), and C&W (1.05).

7. Discussion

To our knowledge, this is the first work to establish that adversarial features can be efficiently mapped between diverse DNN architectures. This novel discovery indicates the feasibility of creating a robust canonical embedding space that is resistant to adversarial inputs. This involves mapping adversarial embeddings from other DNNs to this canonical embedding and utilizing the canonical defense for identifying adversarial inputs. In this work, we establish the feasibility of a simple model-agnostic defense using an SVM—however, future work needs to explore the feasibility of alternative solutions for adversarial defense.

It is important to note that while this mapping does require data from the source model during its establishment, it subsequently enables the efficient detection of adversarial inputs. This detection process involves a minimal computational overhead, primarily consisting of matrix multiplication. The distinct advantage of our approach lies in its model-agnostic nature, allowing multiple models to achieve robustness against adversarial attacks through a shared and efficient detection mechanism. In contrast, model-dependent defense methods, although also requiring access to data, are inherently tied to specific model architectures and demand customization for each model.

These linear mappings raise intriguing possibilities for understanding the learned representations across different modalities, such as linking vision and language representations. Moreover, the implications extend to leveraging these mappings for practical purposes. For instance, mapping image embeddings to language embeddings may enhance the performance of language models in their respective tasks.

Our work also provide valuable insights into how one could consider the influence of architecture on a learned representation. If high performing models have ultimately learned similar representations, areas like neural architecture search (NAS) may consider shifting their focus to identifying higher performing representations—there is some work in this domain, such as the hypothesis by Blanchard et al. (2019) that learned representations that mirror biology, by grouping similar-looking objects in the embedded representations, enhance robustness. The methodology for evaluating this shift in focus has been established by works like Radford et al. (2021), who evaluated their learned representation by testing generalization to new tasks in a zero-shot context.

There are of course further investigations that need to be done for non-traditional training paradigms and architectures.² For example, what is the feasibility linear of mapping between generative models, such as Variational Autoencoders (VAEs), Generative Adversarial Networks (GANs), and CNNs? Do linear methods suffice for mapping from VAE spaces to CNN spaces, or are non-linear methods required? Despite initial appearances suggesting differences in the organization of VAEs' latent spaces, exploring the degree of dissimilarity from a linear relationship could yield valuable insights. Understanding the connections between these distinct embedding spaces will open avenues for leveraging the respective strengths of generative models and CNNs. Are there hybrid approaches that capitalize on the unique capabilities of each architecture? How can hybrid approaches facilitate the development of more powerful and adaptable AI systems?

Overall, our novel findings offer valuable insights into the interplay between adversarial features and neural network embeddings. This work paves the way for investigating novel model-agnostic defense strategies that transcend the limitations of individual architectures. Such defenses may enable more robust and reliable deep learning systems in the face of adversarial challenges.

8. Conclusion

In this study, we showcase the remarkable shared commonality in representations of adversarial images across a diverse set of deep neural networks (DNNs). This interchangeability is made possible through a straightforward linear mapping technique, typically using the DNNs penultimate layers. To our knowledge, this is the first work to establish that adversarial inputs are mappable across DNNs. Further, we capitalize on our novel finding to introduce the concept of a model-agnostic adversarial defense that leverages the transferability of adversarial features across representations. We develop a canonical adversarial defense, map adversarial embeddings from other models to that canonical space, and show adversarial inputs can be accurately identified without any additional training. The feasibility of linearly transforming adversarial features presents promising prospects for developing a more robust model-agnostic adversarial defense, provides insights for understanding and evaluating learned representations, and opens the door for a wealth of future research that capitalizes on these linear mappings.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HJ: Conceptualization, Methodology, Writing—original draft, Writing—review & editing. YL: Conceptualization, Supervision, Writing—review & editing. NB: Conceptualization, Formal analysis, Supervision, Writing—review & editing. MK: Funding acquisition, Project administration, Supervision, Writing—review & editing. CP: Supervision, Writing—review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the DARPA Geometries of Learning Program under Award No. HR00112290074.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^The “+” in step 1 of the Algorithm 1 indicates the concatenation of two sets.

2. ^Assuming the “traditional” paradigm is architectures trained for classification.

References

Bendale, A., and Boult, T. E. (2016). “Towards open set deep networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (LasVegas, NV).

Google Scholar

Blanchard, N., Kinnison, J., RichardWebster, B., Bashivan, P., and Scheirer, W. J. (2019). “A neurobiological evaluation metric for neural network model search,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (Long Beach, CA).

Google Scholar

Blau, T., Ganz, R., Kawar, B., Bronstein, A., and Elad, M. (2022). Threat model-agnostic adversarial defense using diffusion models. arXiv preprint arXiv:2207.08089. doi: 10.48550/arXiv.2207.08089

CrossRef Full Text | Google Scholar

Carlini, N., Athalye, A., Papernot, N., Brendel, W., Rauber, J., Tsipras, D., et al. (2019). On evaluating adversarial robustness. arXiv preprint arXiv:1902.06705. doi: 10.48550/arXiv.1902.06705

CrossRef Full Text | Google Scholar

Chen, S., Huang, X., He, Z., and Sun, C. (2019). DAmageNet: a universal adversarial dataset. arXiv preprint arXiv:1912.07160. doi: 10.48550/arXiv.1912.07160

CrossRef Full Text | Google Scholar

Crecchi, F., Bacciu, D., and Biggio, B. (2019). Detecting adversarial examples through nonlinear dimensionality reduction. arXiv preprint arXiv:1904.13094. doi: 10.48550/arXiv.1904.13094

CrossRef Full Text | Google Scholar

Dong, Z., and Mao, Y. (2023). Adversarial defenses via vector quantization. arXiv preprint arXiv:2305.13651. doi: 10.48550/arXiv.2305.13651

CrossRef Full Text | Google Scholar

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., et al. (2020). An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929. doi: 10.48550/arXiv.2010.11929

CrossRef Full Text | Google Scholar

Feinman, R., Curtin, R. R., Shintre, S., and Gardner, A. B. (2017). Detecting adversarial samples from artifacts. arXiv preprint arXiv:1703.00410. doi: 10.48550/arXiv.1703.00410

CrossRef Full Text | Google Scholar

Frosio, I., and Kautz, J. (2023). “The best defense is a good offense: adversarial augmentation against adversarial attacks,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (Vancouver, BC), 4067–4076.

Google Scholar

Gopalakrishnan, S., Marzi, Z., Madhow, U., and Pedarsani, R. (2018). Combating adversarial attacks using sparse representations. arXiv preprint arXiv:1803.03880. doi: 10.48550/arXiv.1803.03880

CrossRef Full Text | Google Scholar

Gorbett, M., and Blanchard, N. (2022). “Utilizing network features to detect erroneous inputs,” in Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (Waikoloa, HI), 34–43.

Google Scholar

Han, S., Lin, C., Shen, C., Wang, Q., and Guan, X. (2023). Interpreting adversarial examples in deep learning: a review. ACM Comput. Surv. 55, 1–38. doi: 10.1145/3594869

CrossRef Full Text | Google Scholar

Harder, P., Pfreundt, F.-J., Keuper, M., and Keuper, J. (2021). “Spectraldefense: detecting adversarial attacks on CNNs in the fourier domain,” in 2021 International Joint Conference on Neural Networks (IJCNN) (Shenzhen: IEEE), 1–8.

Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep residual learning for image recognition. arXiv preprint arXiv:1512.03385. doi: 10.1109/CVPR.2016.90

CrossRef Full Text | Google Scholar

Jamil, H., Liu, Y., Caglar, T., Cole, C., Blanchard, N., Peterson, C., et al. (2023). “Hamming similarity and graph Laplacians for class partitioning and adversarial image detection,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (Vancouver, BC), 590–599.

Google Scholar

Jha, S., Jang, U., Jha, S., and Jalaian, B. (2018). “Detecting adversarial examples using data manifolds,” in MILCOM 2018 - 2018 IEEE Military Communications Conference (MILCOM) (Los Angeles, CA).

Google Scholar

Khamaiseh, S. Y., Bagagem, D., Al-Alaj, A., Mancino, M., and Alomari, H. W. (2022). Adversarial deep learning: a survey on adversarial attacks and defense mechanisms on image classification. IEEE Access 10, 102266–102291. doi: 10.1109/ACCESS.2022.3208131

CrossRef Full Text | Google Scholar

Lenc, K., and Vedaldi, A. (2015). “Understanding image representations by measuring their equivariance and equivalence,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Boston, MA), 991–999.

PubMed Abstract | Google Scholar

Li, J., Zhang, S., Cao, J., and Tan, M. (2023). Learning defense transformations for counterattacking adversarial examples. Neural Netw. 164, 177–185. doi: 10.1016/j.neunet.2023.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., and Li, F. (2017). “Adversarial examples detection in deep networks with convolutional filter statistics,” in Proceedings of the IEEE International Conference on Computer Vision (ICCV) (Venice).

Google Scholar

Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and Vladu, A. (2017). Towards deep learning models resistant to adversarial attacks. arXiv preprint arXiv:1706.06083. doi: 10.48550/arXiv.1805.12152

CrossRef Full Text | Google Scholar

McNeely-White, D., Beveridge, J. R., and Draper, B. A. (2020). Inception and resnet features are (almost) equivalent. Cogn. Syst. Res. 59, 312–318. doi: 10.1016/j.cogsys.2019.10.004

CrossRef Full Text | Google Scholar

McNeely-White, D., Sattelberg, B., Blanchard, N., and Beveridge, R. (2021). Exploring the interchangeability of CNN embedding spaces. arXiv preprint arXiv:2010.02323. doi: 10.48550/arXiv.2010.02323

CrossRef Full Text | Google Scholar

McNeely-White, D., Sattelberg, B., Blanchard, N., and Beveridge, R. (2022). Canonical face embeddings. IEEE Trans. Biometr. Behav. Identity Sci. 4, 197–209. doi: 10.1109/TBIOM.2022.3155372

CrossRef Full Text | Google Scholar

Mustafa, A., Khan, S., Hayat, M., Goecke, R., Shen, J., and Shao, L. (2019). “Adversarial defense by restricting the hidden space of deep neural networks,” in Proceedings of the IEEE/CVF International Conference on Computer Vision (Seoul), 3385–3394.

Google Scholar

Nie, W., Guo, B., Huang, Y., Xiao, C., Vahdat, A., and Anandkumar, A. (2022). Diffusion models for adversarial purification. arXiv preprint arXiv:2205.07460. doi: 10.48550/arXiv.2205.07460

CrossRef Full Text | Google Scholar

Qiu, H., Zeng, Y., Zheng, Q., Guo, S., Zhang, T., and Li, H. (2021). An efficient preprocessing-based approach to mitigate advanced adversarial attacks. IEEE Trans. Comput. doi: 10.1109/TC.2021.3076826

CrossRef Full Text | Google Scholar

Radford, A., Kim, J. W., Hallacy, C., Ramesh, A., Goh, G., Agarwal, S., et al. (2021). “Learning transferable visual models from natural language supervision,” in International Conference on Machine Learning (Seoul: PMLR), 8748–8763.

Google Scholar

Sandler, M., Howard, A., Zhu, M., Zhmoginov, A., and Chen, L.-C. (2019). MobileNetV2: Inverted residuals and linear bottlenecks. arXiv preprint arXiv:1801.04381. doi: 10.1109/CVPR.2018.00474

CrossRef Full Text | Google Scholar

Simonyan, K., and Zisserman, A. (2015). Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556. doi: 10.48550/arXiv.1409.1556

CrossRef Full Text | Google Scholar

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., et al. (2014a). Going deeper with convolutions. arXiv preprint arXiv:1409.4842. doi: 10.48550/arXiv.1409.4842

CrossRef Full Text | Google Scholar

Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., et al. (2014b). Intriguing Properties of Neural Networks. Technical report.

Google Scholar

Tan, M., and Le, Q. V. (2020). EfficientNet: rethinking model scaling for convolutional neural e networks. arXiv preprint arXiv:1905.11946. doi: 10.48550/arXiv.1905.11946

CrossRef Full Text | Google Scholar

Xu, W., Evans, D., and Qi, Y. (2017). Feature squeezing: Detecting adversarial examples in deep neural networks. arXiv preprint arXiv:1704.01155. doi: 10.48550/arXiv.1704.01155

CrossRef Full Text | Google Scholar

Zheng, H., Zhang, Z., Gu, J., Lee, H., and Prakash, A. (2020). Efficient adversarial training with transferable adversarial examples. arXiv preprint arXiv:1912.11969. doi: 10.48550/arXiv.1912.11969

CrossRef Full Text | Google Scholar