Probabilistic and semantic descriptions of image manifolds and their applications

This paper begins with a description of methods for estimating probability density functions for images that reflects the observation that such data is usually constrained to lie in restricted regions of the high-dimensional image space—not every pattern of pixels is an image. It is common to say that images lie on a lower-dimensional manifold in the high-dimensional space. However, although images may lie on such lower-dimensional manifolds, it is not the case that all points on the manifold have an equal probability of being images. Images are unevenly distributed on the manifold, and our task is to devise ways to model this distribution as a probability distribution. In pursuing this goal, we consider generative models that are popular in AI and computer vision community. For our purposes, generative/probabilistic models should have the properties of (1) sample generation: it should be possible to sample from this distribution according to the modeled density function, and (2) probability computation: given a previously unseen sample from the dataset of interest, one should be able to compute the probability of the sample, at least up to a normalizing constant. To this end, we investigate the use of methods such as normalizing flow and diffusion models. We then show how semantic interpretations are used to describe points on the manifold. To achieve this, we consider an emergent language framework that makes use of variational encoders to produce a disentangled representation of points that reside on a given manifold. Trajectories between points on a manifold can then be described in terms of evolving semantic descriptions. In addition to describing the manifold in terms of density and semantic disentanglement, we also show that such probabilistic descriptions (bounded) can be used to improve semantic consistency by constructing defenses against adversarial attacks. We evaluate our methods on CelebA and point samples for likelihood estimation with improved semantic robustness and out-of-distribution detection capability, MNIST and CelebA for semantic disentanglement with explainable and editable semantic interpolation, and CelebA and Fashion-MNIST to defend against patch attacks with significantly improved classification accuracy. We also discuss the limitations of applying our likelihood estimation to 2D images in diffusion models.

1. Introduction

Understanding the complex probability distribution of the data is essential for image authenticity and quality analysis, but is challenging due to its high dimensionality and intricate domain variations (Gomtsyan et al., 2019; Pope et al., 2021). Seen images usually have high probabilities on a low-dimensional manifold embedded in the higher-dimensional space of the image encoder.

Nevertheless, the phenomenon that image embeddings encoded using methods such as a pretrained CLIP encoder (Ramesh et al., 2020) lie within a narrow cone of the unit sphere instead of the entire sphere (Gao et al., 2019; Tyshchuk et al., 2023), which degrades the aforementioned pattern of probability distribution. Hence, on such a manifold, it is unlikely that every point can be decoded into a realistic image because of the unevenly distributed probabilities. Therefore, it is important to compute the probability in the latent space to indicate whether the corresponding image is in a high-density region of the space (Lobato et al., 2016; Chang et al., 2017; Hajri et al., 2017; Grover et al., 2018; Papamakarios et al., 2021; Coeurdoux et al., 2022; Klein et al., 2022). This helps to distinguish seen images from unseen images, or synthetic images from real images. Some works train a discriminator with positive (real) and negative (synthetic) examples in the manner of contrastive learning (Liu et al., 2022) or analyze their frequency differences (Wang et al., 2020). However, they do not address this problem using the probabilistic framework afforded by modern generative models.

In this work, we calculate the exact log-probability of an image by utilizing generative models that assign high probabilities to seen images and low probabilities to unseen images. The confidence of such probabilities is usually related to image fidelity, we hence also introduce efficient and effective (with improved semantic robustness) generation strategies using hierarchical structure and large sampling steps with the Runge-Kutta method (RK4) (Runge, 1895; Kutta, 1901) for stabilization. Specifically, we use normalizing flow (NF) (Rezende and Mohamed, 2016; Papamakarios et al., 2021) and diffusion models (DMs) (Ho et al., 2020; Song et al., 2021; Luo, 2022) as image generators. NF models learn an image embedding space that conforms to a predefined distribution, usually a Gaussian. In contrast, DMs diffuse images with Gaussian noise in each forward step and learn denoising gradients for the backward steps. A random sample from the Gaussian distribution can then be analytically represented on an image manifold and visualized through an image decoder (for NF models) or denoiser (for diffusion models). In prior works, NF for exact likelihood estimation (Rezende and Mohamed, 2016; Kobyzev et al., 2019; Zhang and Chen, 2021) and with hierarchical structure (Liang et al., 2021; Hu et al., 2023; Voleti et al., 2023) have been explored in model training. To the best of our knowledge, however, it has not been studied by investigating such likelihood distribution of seen and unseen images with a hierarchical structure (without losing the image quality) from the manifold perspective. This is also applied to the diffusion models noting the difficulty of combining such exact likelihood with the mean squared error loss in diffusion training.

Samples from these image generators can be thought of having several meaningful semantic attributes. It is often desirable that these attributes be orthogonal to each other in the sample latent space so as to achieve a controllable and interpretable representation. In this work, we disentangle semantics in the latent space by using a variational autoencoder (VAE) (Kingma and Welling, 2013) in the framework of emergent languages (EL) (Havrylov and Titov, 2017; Kubricht et al., 2020; Pang et al., 2020; Tucker et al., 2021; Mu et al., 2023). This allows the latent representation on the manifold to be more robust, interpretable, compositional, controllable, and transferable. Although some VAE variant models such as β-TCVAE (Chen et al., 2018), GuidedVAE (Ding et al., 2020), and DCVAE (Parmar et al., 2021) achieve qualified semantic disentanglement results, we mainly focus on understanding the effectiveness of the emergent language framework for VAE based disentanglement inspired by Xu et al. (2022) and emphasizing the feasibility of our GridVAE (with mixture of Gaussian priors) under such an EL framework to study semantic distributions on the image manifold. We also evaluate their semantic robustness on such a manifold against adversarial and patch attacks (Carlini and Wagner, 2016; Brown et al., 2017; Tramer et al., 2017; Madry et al., 2018; Chou et al., 2019; Liu et al., 2020; Xiang et al., 2021; Hwang et al., 2023) and defend against the same attacks using semantic consistency with a purification loss.

We organize this paper into three sections, each with their own experiments: log-likelihood estimation for a given image under normalizing flows and diffusion models (see Section 2), semantic disentanglement in emergent languages for a latent representation of object attributes, using a proposed GridVAE model (see Section 3), and adversarial attacks and defenses in image space to preserve semantics (see Section 4).

2. Likelihood estimation with image generators

We evaluate the log-probability of a given image using (1) a hierarchical normalizing flow model, (2) a diffusion model adapted to taking large sampling steps, and (3) a diffusion model that uses a higher-order solution to increase generation robustness.

2.1. Hierarchical normalizing flow models

Normalizing flow (NF) refers to a sequence of invertible functions that may be used to transform a high-dimensional image space into a low-dimensional embedding space corresponding to a probability distribution, usually Gaussian. Dimensionality reduction is achieved via an autoencoding framework. For the hierarchical model, the latent vector corresponding to the image x_i at each level i is computed as

$\begin{array}{ll}{\text{z}}_i=g_i({\text{y}}_i)=g_i\circ f_i({\text{x}}_i)~N(0,1),& (1)\end{array}$

and the inversion of this process reconstructs the latent ${\text{z}}_i^{\prime }$ to ${\text{x}}_i^{\prime }$ as

$\begin{array}{ll}{\text{x}}_i^{\prime }=f_i^{\prime }\circ g_i^{\prime }({\text{z}}_i^{\prime }),& (2)\end{array}$

where the decoder $f_i^{\prime }$ and flow inverse function $g_i^{\prime }$ are inversions of the encoder f_i and flow function g respectively, and ${\text{z}}_i^{\prime }$ can be z_i or randomly sampled from $N$(0, 1). We illustrate hierarchical autoencoders and flows for rich and high-level spatial information with conditioning variables in either image space or latent space. In Figure 1, we show a 4-level hierarchical normalizing flow model, where each set of functions ($f_i,g_i,g_i^{\prime },f_i^{\prime }$) corresponds to one level and where $g_i^{\prime }$ and $f_i^{\prime }$ are conditioned on the higher-level reconstruction, that is

$\begin{array}{ll}{\text{x}}_1^{\prime }=f_1^{\prime }\circ g_1^{\prime }({\text{z}}_1^{\prime }|f_2^{\prime }\circ g_2^{\prime }({\text{z}}_2^{\prime }|f_3^{\prime }\circ g_3^{\prime }({\text{z}}_3^{\prime }|f_4^{\prime }\circ g_4^{\prime }({\text{z}}_4^{\prime })))).& (3)\end{array}$

The model is learned in two phases: joint learning of all autoencoders $\{f_i,f_i^{\prime }\}$ and then joint learning of all flows $\{g_i,g_i^{\prime }\}$ with the pretrained autoencoders, for all i ∈ {1, 2, 3, 4}. The loss function for autoencoder learning, denoted $L$_ae, is the mean squared error (MSE) between the reconstructed data and the processed data, and for the learning of flows the objective is to minimize the negative log-probability of y_i, denoted $L$_flow, such that the represented distribution of the latent variable is modeled to be the standard Gaussian distribution, from which a random latent variable can be sampled for data generation. Given N pixels and C channels (C = 3 for an RGB image and C = 1 for a greyscale image), x_i at level i can be represented as x_i = {x_ij} for all j ∈ {1, ..., N}, the autoencoder loss is then given by

$\begin{array}{ll}{L}_{\text{ae}}({\text{x}}_i^{\prime },{\text{x}}_i)=\frac{1}{CN}{\displaystyle \sum _{j=1}^N}\Vert {\text{x}}_{ij}^{\prime }-{\text{x}}_{ij}{\Vert }^2,& (4)\end{array}$

and the flow loss for the latent at level i is the negative log-probability of y_i, that is $L$_flow(y_i) = −log p_Y(y_i), using the change of variables as

$\begin{array}{l}log{p}_Y({\text{y}}_i)=log{p}_Z({\text{z}}_i)+log|det{\nabla }_Y{g}_i({\text{y}}_i)|\\ =log{p}_Z({\text{z}}_i)+log|J_Y(g_i({\text{y}}_i))|,& (5)\end{array}$

where

$\begin{array}{l}log{p}_Z({\text{z}}_i)=-\frac{1}{d_i}log\frac{1}{{(\sqrt{2\pi })}^{d_i}}exp\left(-\frac{1}{2}\Vert {\text{z}}_i{\Vert }^2\right)\\ =\frac{1}{2}log2\pi +\frac{1}{2d_i}\Vert {\text{z}}_i{\Vert }^2,& (6)\end{array}$

d_i is the dimension of the ith latent and J_X(·) computes the Jacobian matrix over the partial derivative X. Similarly, the log-probability of x_i at level i is

$\begin{array}{ll}\begin{array}{c}log{p}_X({\text{x}}_i)=log{p}_Z({\text{z}}_i)+log|det{\nabla }_X(g_i\circ f_i({\text{x}}_i))|\hfill \\ =log{p}_Z({\text{z}}_i)+log|det{J}_Y(g_i({\text{y}}_i))|+log|det{J}_X(f_i({\text{x}}_i))|.\end{array}\hfill & (7)\end{array}$

Then, the log-probability of an image at level i with hierarchical autoencoders and flows from multiple downsampling layers, x_i+1 = d(x_i) at level i, can be calculated with the chain rule as

$\begin{array}{ll}logp({\text{x}}_i)={\displaystyle \sum _{j=1}^i}log{p}_X({\text{x}}_j)+log|det{J}_X(d({\text{x}}_{j-1}))|·1\left[j>1\right],& (8)\end{array}$

where [·] is a binary indicator.

FIGURE 1

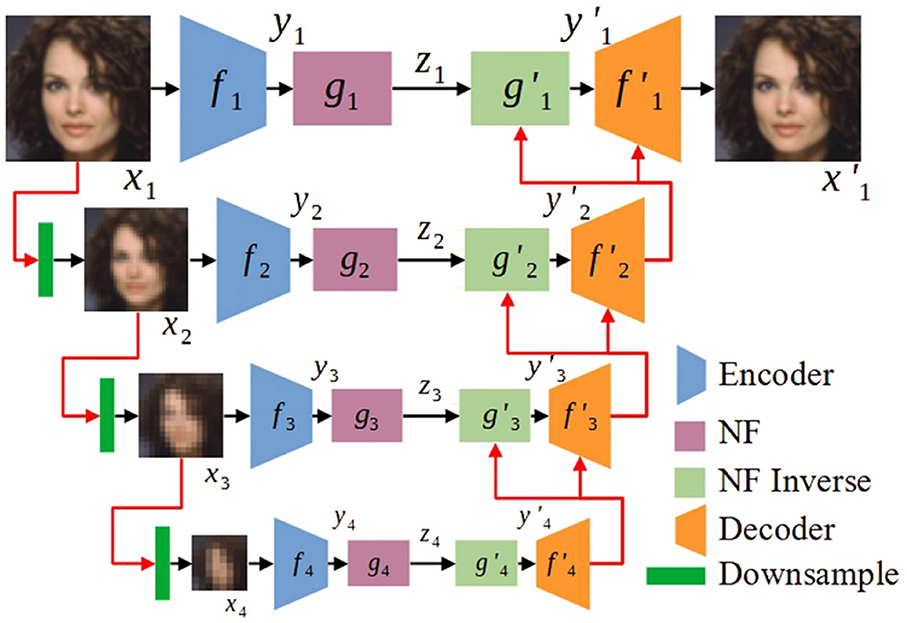
Figure 1. A 4-level hierarchical normalizing flow model, where each level involves the functions $(f_i,g_i,g_i^{\prime },f_i^{\prime })$. The normalizing flow (NF) model is based on Glow (Kingma and Dhariwal, 2018); the downsampling block decreases image resolution by a factor of two; and the output of each higher (i > 1) level is conditioned on the output of the lower level. We first train all autoencoders $\{f_i,f_i^{\prime }\}$ jointly, then train all flows $\{g_i,g_i^{\prime }\}$ jointly, to obtain the generated image ${\text{x}}_1^{\prime }$. The latent variable z_i conforms to the standard Gaussian distribution $N$(0, 1) during training; at test time, z_i is sampled from $N$(0, 1) for image generation.

2.2. Diffusion models

Differently from normalizing flow models that sample in a low-dimensional embedding space due to the otherwise large computational complexity, diffusion models diffuse every image pixel in the image space independently, enabling pixelwise sampling from the Gaussian distribution. We outline below a strategy and formulas to allow uneven or extended step diffusion in the backward diffusion process.

2.2.1. Multi-step diffusion sampling

2.2.1.1. Forward process

The standard description of denoising diffusion model (Ho et al., 2020) defines a sequence of random variables {x₀, x₁, …, x_T} according to a forward diffusion process

$\begin{array}{ll}{\text{x}}_{t+1}=\sqrt{{\alpha }_t}{\text{x}}_t+\sqrt{{\beta }_t}ϵ,& (9)\end{array}$

where β_t = 1 − α_t, x_t is a sample from a random variable X_t, and ϵ is a sample from the standard (multidimensional) Gaussian. The index t takes integer values between 0 and T, and the set of random variables form a Markov chain.

The idea can be extended to define a continuous family of random variables according to the rule

$\begin{array}{ll}{\text{x}}_t=\sqrt{{\bar{\alpha }}_t}{\text{x}}_0+\sqrt{{\bar{\beta }}_t}ϵ,& (10)\end{array}$

where ${\bar{\beta }}_t=1-{\bar{\alpha }}_t$, and for simplicity, we can assume that x_t is defined for t taking continuous values in the interval [0, 1]. Here, the values ${\bar{\alpha }}_t$ are a decreasing function of t with ${\bar{\alpha }}_0=1$ and ${\bar{\alpha }}_1=0$. It is convenient to refer to t as time.

It is easily seen that if {0 = t₀, t₁, ..., t_T = 1} are an increasing set of time instants between 0 and 1, then the sequence of random variables {X_t0, …X_tT} form a Markov chain. Indeed, it can be computed that for 0 ≤ s < t ≤ 1, the conditional probabilities p(x_t|x_s) are Gaussian

$\begin{array}{ll}p({\text{x}}_t|{\text{x}}_s)=N({\text{x}}_t|\sqrt{{\bar{\alpha }}_{st}}{\text{x}}_s,{\bar{\beta }}_{st}).& (11)\end{array}$

where ${\bar{\alpha }}_{st}={\bar{\alpha }}_t/{\bar{\alpha }}_s$ and ${\bar{\beta }}_{st}=1-{\bar{\alpha }}_{st}$. This is the isotropic normal distribution having mean $\sqrt{{\bar{\alpha }}_{st}}{\text{x}}_s$ and variance ${\bar{\beta }}_{st}$. Similarly to Eq. (9), one has

$\begin{array}{ll}{\text{x}}_t=\sqrt{{\bar{\alpha }}_{st}}{\text{x}}_s+\sqrt{{\bar{\beta }}_{st}}ϵ.& (12)\end{array}$

This applies in particular when s and t refer to consecutive time instants t_i and t_i+1. In this case, the joint probability of {X_t0, …, X_tT} is given by

$\begin{array}{ll}p({\text{x}}_{t_0},{\text{x}}_{t_1},\dots ,{\text{x}}_{t_T})=p({\text{x}}_{t_0}){\displaystyle \prod _{i=1}^T}p({\text{x}}_{t_i}|{\text{x}}_{t_{i-1}}).& (13)\end{array}$

One also observes, from Eq. (10) that p(x₁) is a standard Gaussian distribution. A special case is where the time steps are chosen evenly spaced between 0 and 1. Thus, if h = 1/T, this can be written as

$\begin{array}{ll}p({\text{x}}_0,{\text{x}}_h,{\text{x}}_{2h},\dots ,{\text{x}}_{Th})=p({\text{x}}_0){\displaystyle \prod _{i=1}^T}p({\text{x}}_{ih}|{\text{x}}_{(i-1)h}).& (14)\end{array}$

2.2.1.2. Backward process

The joint probability distribution is also a Markov chain, which can be written in the reverse order, as

$\begin{array}{ll}p({\text{x}}_{t_0},{\text{x}}_{t_1},\dots ,{\text{x}}_{t_T})=p({\text{x}}_{t_T}){\displaystyle \prod _{i=1}^T}p({\text{x}}_{t_{i-1}}|{\text{x}}_{t_i}).& (15)\end{array}$

This allows us to generate samples from X₀ by choosing a sample from X₁ = X_tT (a standard Gaussian distribution) and then successively sampling from the conditional probability distributions p(x_ti−1|x_ti).

Unfortunately, although the forward conditional distributions p(x_ti|x_ti−1) are known Gaussian distributions, the backward distributions are not known and are not Gaussian. In general, for s < t, the conditional distribution p(x_t|x_s) is Gaussian, but the inverse p(x_s|x_t) is not.

However, if (t − s) is small, or more exactly, if the variance of the added noise, ${\bar{\beta }}_{st}=1-{\bar{\alpha }}_{st}$ is small, then the distributions can be accurately approximated by Gaussians with the same variance ${\bar{\beta }}_{st}$ as the forward conditionals. With this assumption, the form of the backward conditional p(x_s|x_t) is specified just by determining its mean, denoted by μ(x_s|x_t). The training process of the diffusion model consists of learning (using a neural network) the function μ(x_s|x_t) as a function of x_t. As explained in Ho et al. (2020), it is not necessary to learn this function for all pairs (s, t), as will be elaborated below.

We follow and generalize the formulation in Ho et al. (2020). The training process learns a function ϵ_θ(x_t, t) that minimizes the expected least-squared loss function

$\begin{array}{ll}{E}_{{\text{x}}_0~X_0,ϵ~N}\left[\Vert ϵ-{ϵ}_{\theta }({\text{x}}_t,t){\Vert }^2\right],& (16)\end{array}$

where ${\text{x}}_t=\sqrt{{\bar{\alpha }}_t}{\text{x}}_0+\sqrt{{\bar{\beta }}_t}ϵ$. As such it estimates (exactly, if the optimum function ϵ_θ is found) the expected value of the added noise, given x_t (note that it estimates the expected value of the added noise, and not the actual noise, which cannot be predicted). In this case, following Ho et al. (2020),

$\begin{array}{ll}\mu ({\text{x}}_{t-1}|{\text{x}}_t)=\sqrt{\frac{{\bar{\alpha }}_{t-1}}{{\bar{\alpha }}_t}}\left({\text{x}}_t-\frac{1-{\bar{\alpha }}_t/{\bar{\alpha }}_{t-1}}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }({\text{x}}_t,t)\right).& (17)\end{array}$

In this form, this formula is easily generalized to

$\begin{array}{l}\mu ({\text{x}}_s|{\text{x}}_t)=\frac{1}{\sqrt{{\bar{\alpha }}_{st}}}\left({\text{x}}_t-\frac{1-{\bar{\alpha }}_{st}}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }({\text{x}}_t,t)\right)\\ =\frac{1}{\sqrt{{\bar{\alpha }}_{st}}}\left({\text{x}}_t-\frac{{\bar{\beta }}_{st}}{\sqrt{{\bar{\beta }}_t}}{ϵ}_{\theta }({\text{x}}_t,t)\right).& (18)\end{array}$

As for the variance of p(x_s|x_t), in Ho et al. (2020) it is assumed that the p(x_t−1|x_t) is an isotropic Gaussian (although in reality, it is not exactly a Gaussian, nor exactly isotropic). The covariance matrix of this Gaussian is denoted by ${\sigma }_{st}^2\text{I}$, and two possible choices are given, which are generalized naturally to

$\begin{array}{ll}{\sigma }_{st}^2={\bar{\beta }}_{st}\text{ or }{\sigma }_{st}^2=\frac{{\bar{\beta }}_s{\bar{\beta }}_{st}}{{\bar{\beta }}_t}.& (19)\end{array}$

As pointed out in Ho et al. (2020) both of these are compromises. The first choice expresses the approximation that the variance of the noise added in the backward process is equal to the variance in the backward process. As mentioned, this is true for small time steps.

Thus, in our work, we choose to model the reverse conditional as follows,

$\begin{array}{ll}{p}_{\theta }({\text{x}}_s|{\text{x}}_t)=N({\text{x}}_s|\mu ({\text{x}}_s|{\text{x}}_t),{\sigma }_{st}^2\text{I}),& (20)\end{array}$

where μ(x_s|x_t) is given by Eq. (18) and ${\sigma }_{st}^2$ is given by Eq. (19). This is an approximation of the true conditional probability p(x_s|x_t).

2.2.2. Probability estimation

In the following, we choose a finite set of T time instances (usually equally spaced) {0 = τ₀, τ₁, …, τ_T = 1} and consider the Markov chain consisting of the variables X_τt, for t = {0, …, T}, at these time instances. For simplicity, we use the notation X_t instead of X_τt and x_t a sample from the corresponding random variable. Then, the notation corresponds to the common notation in the literature, but also applies in the case of unevenly, or widely sampled time instants.

To distinguish between the true probabilities of the variables X_t and the modeled conditional probabilities, the true probabilities will be denoted by q (instead of p which was used previously). The modeled probabilities will be denoted by p_θ(x_t−1|x_t), and the probability distribution of X_T, which is Gaussian, will be denoted by p(x_T).

The image probability can be calculated by using the forward and backward processes for each step of a pretrained diffusion model. The joint probability p(x_0:T) and the probability of clean input x₀ can be computed using the forward and backward conditional probability, q(x_t+1|x_t) and p_θ(x_t|x_t+1) respectively. Each sampling pair (x_t, x_t+1) where t ∈ S = {0, 1, 2, ..., T − 1}, follows the Markov chain rule resulting in the joint probability

$\begin{array}{ll}p({\text{x}}_{0:T})=q({\text{x}}_0){\displaystyle \prod _{t\in S}}q({\text{x}}_{t+1}|{\text{x}}_t)=p({\text{x}}_T){\displaystyle \prod _{t\in S}}{p}_{\theta }({\text{x}}_t|{\text{x}}_{t+1}),& (21)\end{array}$

so

$\begin{array}{ll}q({\text{x}}_0)=\frac{p({\text{x}}_T){\displaystyle {\prod }_{t\in S}}{p}_{\theta }({\text{x}}_t|{\text{x}}_{t+1})}{{\displaystyle {\prod }_{t\in S}}q({\text{x}}_{t+1}|{\text{x}}_t)}.& (22)\end{array}$

The negative log-probability of the input image x₀ is then

$\begin{array}{ll}-logq({\text{x}}_0)=-logp({\text{x}}_T)+{\displaystyle \sum _{t\in S}}\left({\displaystyle \underset{\text{forward process}}{{\displaystyle \underbrace{logq({\text{x}}_{t+1}|{\text{x}}_t)}}}}{\displaystyle \underset{\text{backward process}}{{\displaystyle \underbrace{-log{p}_{\theta }({\text{x}}_t|{\text{x}}_{t+1})}}}}\right).& (23)\end{array}$

Computing Eq. (23) can be decomposed into three steps:

(1) Calculating log p(x_T). Since x₀ is fully diffused after T forward steps, x_T follows the standard Gaussian distribution $N$(0, 1), and thus the negative log-likelihood only depends on the Gaussian noise.

(2) Calculating log q(x_t+1|x_t). Since q(x_t−1|x_t) is a Gaussian with known mean ${\bar{\alpha }}_t/{\bar{\alpha }}_{t-1}$, and variance $1-{\bar{\alpha }}_t/{\bar{\alpha }}_{t-1}$, the conditional probability is easily computed, as a Gaussian probability.

(3) Calculating log p_θ(x_t|x_t+1). Similarly, the probability p_θ(x_t−1|x_t) is modeled as a Gaussian, with mean and variance given by Eq. (18) and Eq. (19) (where s = t − 1) the backward conditional probabilities are easily computed.

2.2.3. Higher-order solution

With the hypothesis that high-fidelity image generation is capable of maintaining image semantics, in each of the diffusion inversion steps the x₀ estimation and log-likelihood calculation should be stable and reliable with a small distribution variance. The diffusion inversion, however, usually requires a sufficiently small sampling step h, where DDPM (Ho et al., 2020) only supports h = 1 and DDIM is vulnerable to h (Song et al., 2021) as evidenced in Figure 8. It is important to alleviate the effect of h on the generation step by stabilizing the backward process in diffusion models.

Without loss of generality, the Runge-Kutta method (RK4) (Runge, 1895; Kutta, 1901) can achieve a stable inversion process by constructing a higher-order function to solve an initial value problem. Different from the traditional RK4, the diffusion inversion requires inverse-temporal updates because of the denoising gradient direction from the initial noisy image at t = T to the clean image at t = 0. We provide the formulation of traditional RK4 and our inverse-temporal version in the Supplementary material.

2.3. Experiments

For each of the hierarchical normalizing flows (NFs) and diffusion models (DMs), we first show the effectiveness of likelihood estimation to analyze the image distribution (on 2D images for NFs and point samples for DMs). For likelihood estimation with image fidelity, we then illustrate the quality of images generated by our generation models (sampling on the manifold from a Gaussian distribution as well as resolution enhancement in NFs and sampling step exploration with RK4 stabilization in DMs).

2.3.1. Experiments on hierarchical normalizing flow models

2.3.1.1. Probability estimation

Figure 2 illustrates the probability density estimation on level 3 for an in-distribution dataset CelebA (Liu et al., 2015) and an out-of-distribution dataset CIFAR10 (Krizhevsky, 2009). The distribution of the latent variable z_i of CelebA is concentrated on a higher mean value than that of CIFAR10 due to the learning of z_i in the standard Gaussian distribution. Similarly, this distribution tendency is not changed in the image space illustrated by log p(x_i). In this case, outlier samples from the in-distribution dataset can be detected with a small probability in the probability estimation.

FIGURE 2

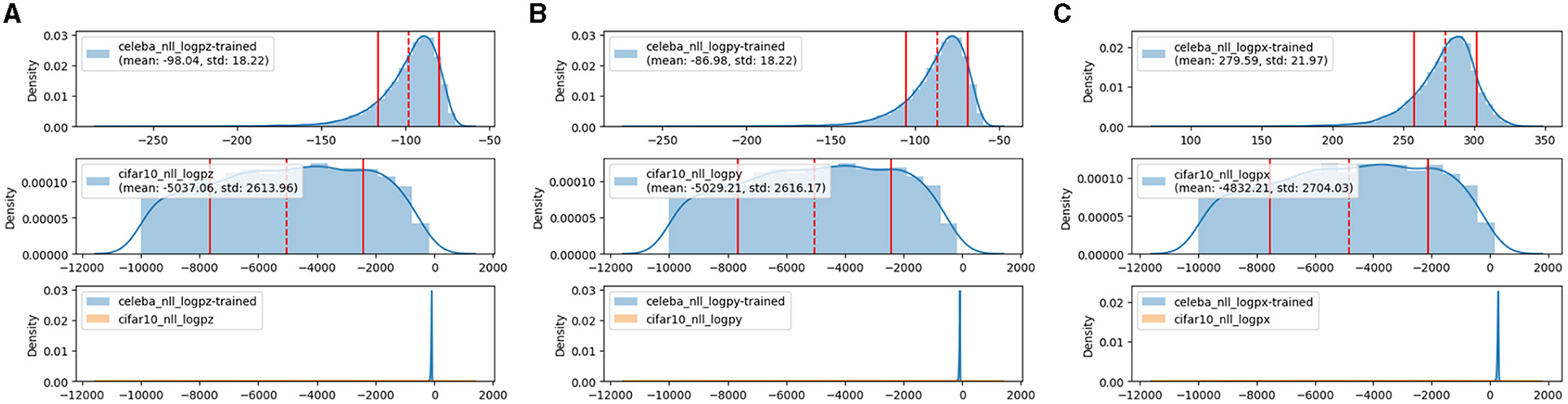
Figure 2. Log-likelihood estimation using hierarchical autoencoders and flows. The encoder and flow are trained on CelebA and evaluated on CelebA and CIFAR10. The x-axis is log p(·) and the y-axis is the histogram density. In each subfigure, the first row is on the in-distribution dataset CelebA and the second row is on out-of-distribution CIFAR10, both are in the last row. In (A), log p(z) can detect outlier samples, and adding log|det(·)| from NF and autoencoder does not significantly affect the distribution tendency, see (B) and (C). For better visualization, samples with log p(·) less than −10,000 are filtered out.

2.3.1.2. Random image generation

Image reconstructions with encoded latent variables and conditional images as well as random samples are provided in Figure 3. For the low-level autoencoder and flow, say at level 1, conditioned on the sequence of decoded x_i for i = {2, 3, 4}, the reconstruction of x₁ is close to the processed images although some human facial details are lost due to the downsampling mechanism, see Figure 3A. While randomly sampling {z_i} from the normal distribution at each level, the generated human faces are smooth but with blurry details in such as hair and chin and lack a realistic background.

FIGURE 3

Figure 3. Image reconstruction and generation on the end-to-end training of 4-level autoencoders and flows. For each of two columns from left to right in (A), the left is the real image and the right is the reconstructed image. (A) Reconstruction at level 1 with {z_i} from encoders {g_i} and conditioned on $\{f_i^{\prime }\}$. (B) Random generation at level 1 with latent variables {z_i} ~ $N$(0, 1) and conditioned on $\{f_i^{\prime }\}$.

2.3.1.3. Image super-resolution

With the jointly trained autoencoders and flows on CelebA, the images with low resolution, 3 × 8 × 8 (channel × height × width) and 3 × 16 × 16, are decoded to 3 × 64 × 64 with smooth human faces, see Figures 4A, B respectively. The low-resolution image x_i is used as a condition image for (1) NF inverse $\{g_i^{\prime }\}$ to generate embedding code to combine with the randomly sampled z_i ~ $N$(0, 1) and (2) decoders $\{f_i^{\prime }\}$ to concatenate with all upsampling layers in each decoder. This preserves the human facial details from either high levels or low levels for realistic image generation. As the resolution of the low-resolution images increases, the embedding code contains richer details.

FIGURE 4

Figure 4. Image super-resolution on dataset CelebA. The first column is low-resolution images, the second column is real images, and the rest are high-resolution images with latent variables {Z_i} ~ $N$(0, 1) conditioned on the low-resolution images and temperature 1.0. (A) Resolution: 3 × 8 × 8 to 3 × 64 × 64. (B) Resolution: 3 × 16 × 16 to 3 × 64 × 64.

2.3.2. Experiments on diffusion models

2.3.2.1. Log-likelihood estimation on point samples

We evaluate the log-probability of each point of point samples (Pedregosa et al., 2011) including Swiss roll, circle, moon, and S shown in Figure 5. Given a pretrained diffusion model on Swiss roll samples with 100 forward steps with each diffused by random Gaussian noise (see Figure 5A, the log-probability of the samples in Figure 5B follows Eq. (23) with h = 1 and indicates higher probability and density on seen or similar samples than unseen ones. In Figures 5B, C, the mean value of the Swiss roll sample achieves a higher mean value, −0.933, and a higher histogram density, 0.7, than the others. As the difference in the sample shape from the Swiss roll increases, the log-likelihood decreases, as shown in the bar chart in Figure 5C. It indicates that sampling from a low-density distribution is unable to reverse the diffusion step to obtain a realistic sample from the training set.

FIGURE 5

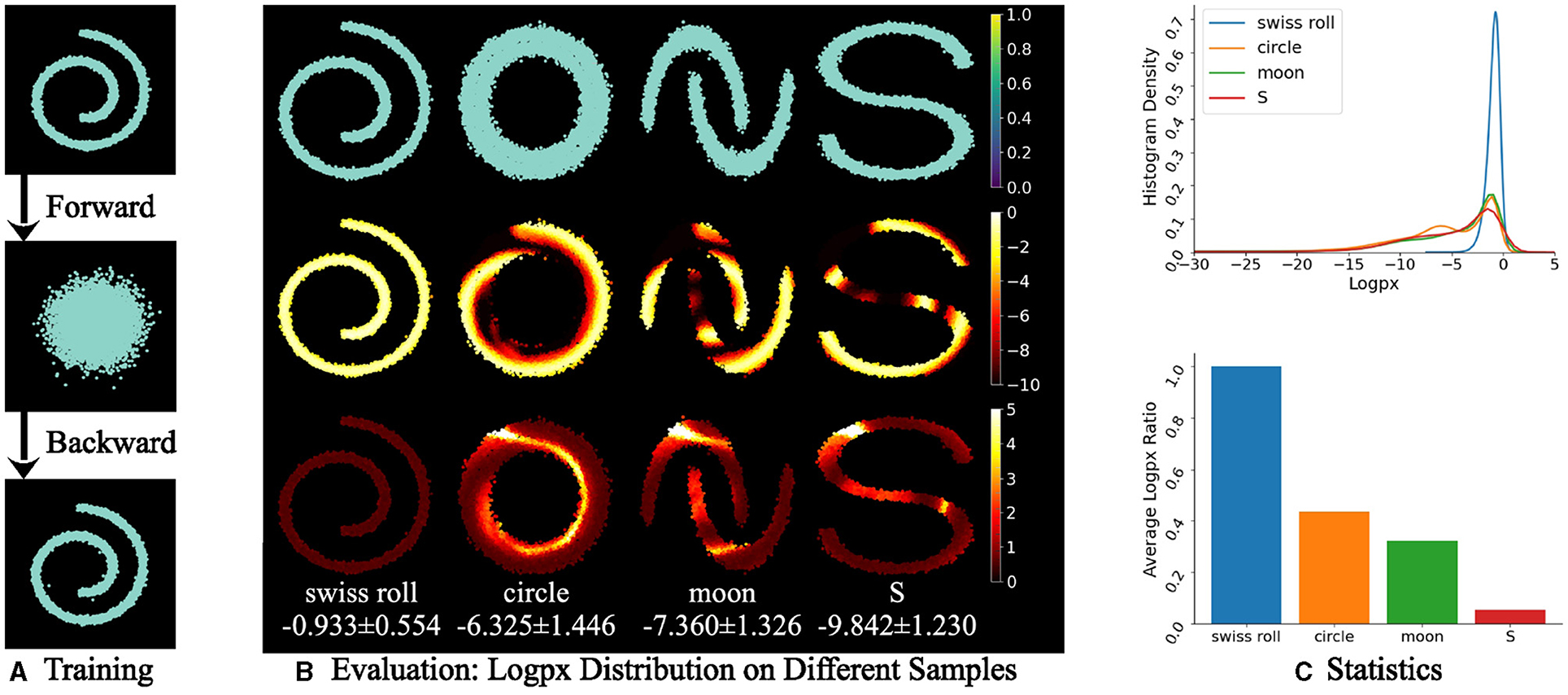
Figure 5. Evaluation of log-probability of x₀ on point samples with each of 10,000 points. (A) The training is on a Swiss roll sample and a diffusion model with forward (noising) and backward (denoising) processes. (B) At the evaluation phase, unseen samples, that is circle, moon, and S, have lower log p(x) values than the seen Swiss roll sample. In (B), the first row is sampled points and the middle and last rows are the mean value and the standard deviation of log p(x) for each point on 100 random rounds respectively, which is represented as “mean ± SD.” The randomness lies in the random noise in the forward and backward processes. A lighter color indicates a higher density. (C) Statistics indicates the higher density of a seen sample (Swiss roll) than an unseen one (circle, moon, or S) through the diffusion model by using the negative of Eq. (23) with log₁₀.

2.3.2.2. DDPM sampling with large steps

While Figure 5 uses h = 1 as the standard DDPM sampling process, it is feasible to sample with a fairly large step without losing the sample quality. This enables sampling from the Gaussian distribution for the log-likelihood estimation with less running time. To visualize the image quality, we evaluate the samples on CelebA dataset by using a pretrained diffusion model with 1,000 forward diffusion steps. In Figure 6, the sampling has an increase step h in {2, 10, 100} while the samples have a high quality for h = {2, 10} and a fair quality for h = 100.

FIGURE 6

Figure 6. Image generation from our modified DDPM with step size h. Samples follow a Gaussian distribution. Fine details are obtained even for very large steps (h = 100). (A) h = 1. (B) h = 2. (C) h = 10. (D) h = 100.

2.3.2.3. Higher-order solution stabilizes sampling

While sampling with a large step h can sometimes cause bias from the one with a small h, RK4 effectively alleviates such a bias. We evaluate both the point samples and human face images from CelebA. In Figure 7, compared with the sample by using DDPM, RK4 with DDPM inference achieves less noise at h = {2, 5, 10}. For h = 20, RK4 performs expectedly worse because it only applies five sampling steps while the training is on (T = 100) diffusion steps. In Figure 8, we apply DDIM as the inference method for RK4 to deterministically compare the samples with DDIM. As h increases from 1 to 100, many of the samples using DDIM lose the image consistency with the samples at h = 1; however, most of the samples using RK4 still retain the image consistency. This indicates the robustness of applying RK4 with a large sampling step.

FIGURE 7

Figure 7. Sampling robustness of DDPM and RK4 @ step h. With h being 5 or 10, RK4 still achieves clear sampling compared with DDPM. If h is too large, for instance 20, RK4 fails as expected. (A) DDPM. (B) RK4@2. (C) RK4@5. (D) RK4@10. (E) RK4@20.

FIGURE 8

Figure 8. Random image generation using DDIM and RK4 with DDIM as inference @ time step h={1, 2, 10, 100}. The RK4 sampling method is more robust than DDIM, especially at h = 100, with a higher image consistency than those at h = 1. (A) DDIM@1. (B) DDIM@2. (C) DDIM@10. (D) DDIM@100. (E) RK4@1. (F) RK4@2. (G) RK4@10. (H) RK4@100.

3. Semantic disentanglement on manifold

Semantics of object attributes are crucial for image distribution and spatial presentation. For instance, different shapes in Figure 5 represent different objects while those closer to the seen samples have high likelihood; in Figure 8 semantics such as human gender (see the 2nd row and 3rd column image with DDIM and RK4) are fundamental for controllable generation by sampling in high-density regions of specific semantic clusters on the manifold. These semantics, however, are usually entangled without independent distributions from each other for deterministic embedding sampling on the image manifold (Liu et al., 2018; Ling et al., 2022; Pastrana, 2022). Hence, regardless of image generation models, we exploit the popular and efficient variational autoencoder and introduce our GridVAE model for effective semantic disentanglement on the image manifold.

3.1. GridVAE for clustering and disentanglement

3.1.1. Formulation

A variational autoencoder (VAE) (Kingma and Welling, 2013) is a neural network that maps inputs to a distribution instead of a fixed vector. Given an input x, the encoder with neural network parameters ϕ maps it to a hidden representation z. The decoder with the latent representation z as its input and the neural network parameters as θ reconstructs the output to be as similar to the input x. We denote the encoder q_ϕ(z|x) and decoder p_θ(x|z). The hidden representation follows a prior distribution p(z).

With the goal of making the posterior q_ϕ(z|x) close to the actual distribution p_θ(z|x), we minimize the Kullback-Leibler divergence between these two distributions. Specifically, we aim to maximize the log-likelihood of generating real data while minimizing the difference between the real and estimated posterior distribution by using the evidence lower bound (ELBO) as the VAE loss function

$\begin{array}{l}L(\theta ,\varphi )=-log{p}_{\theta }(x)+D_{KL}(q_{\varphi }(z|x)\Vert p_{\theta }(z|x))\\ =-{𝔼}_{z~q_{\varphi }(z|x)}log{p}_{\theta }(x|z)+D_{KL}(q_{\varphi }(z|x)\Vert p_{\theta }(z)),& (24)\end{array}$

where the first term is the reconstruction loss and the second term is the regularization for q_ϕ(z|x) to be close to p_θ(z). The prior distribution of z is often chosen to be a standard unit isotropic Gaussian, which implies that the components of z should be uncorrelated and hence disentangled. If each variable in the latent space is only representative of a single element, we assume that this representation is disentangled and can be well interpreted.

Emergent language (EL) (Havrylov and Titov, 2017) is hereby introduced as a language that arises spontaneously in a multi-agent system without any pre-defined vocabulary or grammar. EL has been studied in the context of artificial intelligence and cognitive science to understand how language can emerge from interactions between agents. EL has the potential to be compositional such that it allows for referring to novel composite concepts by combining individual representations for their components according to systematic rules. However, for EL to be compositional, the latent space needs to be disentangled (Chaabouni et al., 2020). Hence, we integrate VAE into the EL framework by replacing the sender LSTM with the encoder of the VAE noting that the default LSTM encoder will entangle the symbols due to its sequential structure where the previous output is given as the input to the next symbol. In contrast, the symbols can be disentangled with a VAE encoder.

To achieve disentangled representations in EL, the VAE encoder must be able to cluster similar concepts into discrete symbols that are capable of representing attributes or concepts. The standard VAEs are powerful, but their prior distribution, which is typically the standard Gaussian, is inferior in clustering tasks, particularly the location and the number of cluster centers. In the EL setting, we desire a posterior distribution with multiple clusters, which naturally leads to an MoG prior distribution with K components

$\begin{array}{ll}p(z)=\frac{1}{K}{\displaystyle \sum _{k=1}^K}N(z|{\mu }_k,{\sigma }_k^2).& (25)\end{array}$

We choose the μ_k to be located on a grid in a Cartesian coordinate system so that the posterior distribution clusters can be easily determined based on the sample's distance to a cluster center. We refer to this new formulation as GridVAE, which is a VAE with a predefined MoG prior on a grid. The KL-divergence term in Eq. (24) can be re-written as

$\begin{array}{ll}{D}_{KL}(q_{\varphi }(z|x)\Vert p_{\theta }(z))={𝔼}_{x~p(x)}{𝔼}_{q_{\varphi }(z|x)}\left[logp(z)-log{q}_{\varphi }(z|x)\right].& (26)\end{array}$

The log probability of the prior can be easily calculated with the MoG distribution, and we only need to estimate the log probability of the posterior using a large batch size during training. By using a GridVAE, we can obtain a posterior distribution with multiple clusters that correspond to the same discrete attribute, while allowing for variations within the same cluster to generate different variations of the attribute.

3.1.2. Experiments

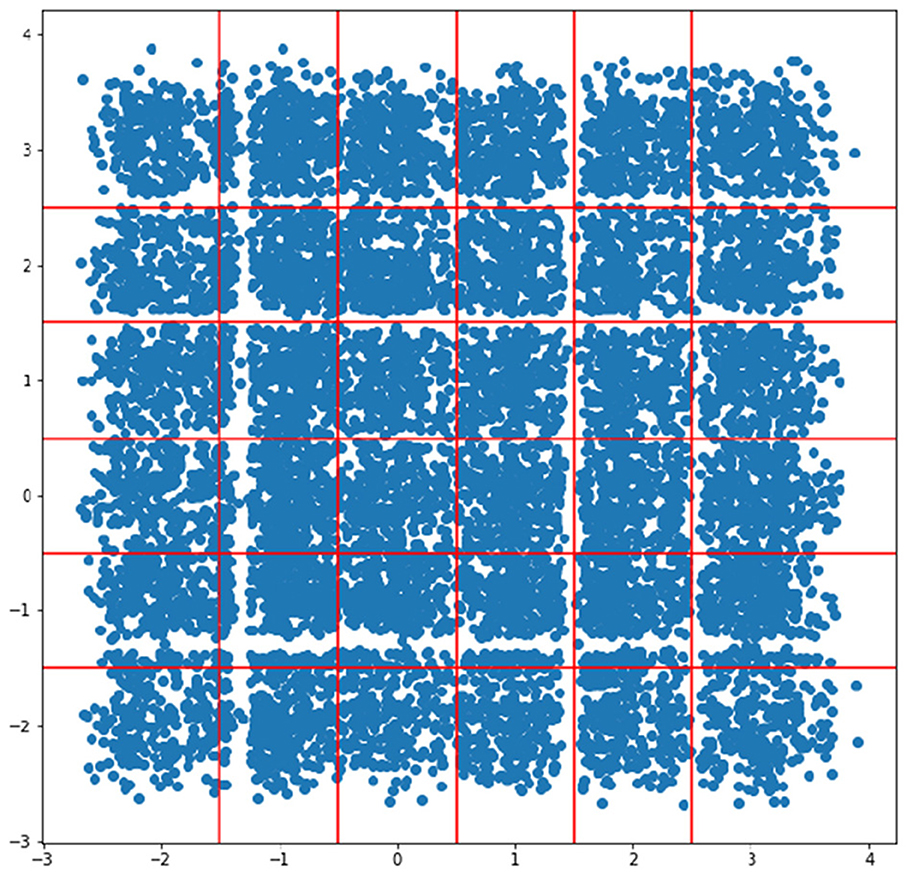
We evaluate the clustering and disentanglement capabilities of the proposed GridVAE model using a two-digit MNIST dataset (LeCun et al., 1998) consisting of digits 0 to 5. Each digit is from the original MNIST dataset, resulting in a total of 36 classes [00, 01, 02,..., 55].

To extract features for the encoder, we use a 4-layer ResNet (He et al., 2016) and its mirror as the decoder. The VAE latent space is 2-dimensional (2D), and if the VAE learns a disentangled representation, each dimension of the 2D latent space should represent one of the digits. We use a 2D mixture of Gaussian (MoG) as the prior distribution, with six components in each dimension centered at integer grid points from [−2, −1, 0, 1, 2, 3], that is the coordinates for the cluster centers are [(−2, −2), (−2, −1),..., (3, 3)]. The standard deviation of the mixture of Gaussian is 1/3.

After training the model, we generate a scatter plot of the test set latent space, as shown in Figure 9. Since the prior is a mixture of Gaussian on the grid points, if the posterior matches the prior, we can simply draw a boundary in the middle of two grid points, illustrated by the red lines in Figure 9.

FIGURE 9

Figure 9. Scatter plot of test set latent space with an MoG prior.

With the trained model, one can sample in the latent space for image generation. In Figures 10A, B, when we decode from the cluster centers (i, j): in (A) we keep j = 0 and change i from −2 to 3, while in (B) we keep i = 0 and change j from −2 to 3. The latent space is disentangled with respect to the two digits - the first dimension of the latent space controls the first digit, while the second dimension controls the second digit. Each of the cluster centers corresponds to a different number.

FIGURE 10

Figure 10. Generated images from sampling the latent space. (A) The second dimension is fixed at 0, changing the first dimension from −2 to +3. (B) The first dimension is fixed at 0 and the second dimension is changed from −2 to +3. (C) Around the cluster center(1, 1), keep the second dimension fixed and change the first dimension. (D) Around the cluster center(1, 1), keep the second dimension fixed and change the first dimension.

Figures 10C, D show images generated within the cluster centered at (1, 1), that is the pairs of number “44”. If we slightly modify one of the dimensions, it corresponds to different variations of the number “4” along this dimension, while keeping the other digit unchanged.

Overall, these results demonstrate the effectiveness of the proposed GridVAE model in clustering and disentangling the latent space on the two-digit MNIST dataset.

3.2. Scaling up GridVAE

In Section 3.1, the two-digit MNIST dataset lies in a 2-dimensional latent space. However, many real-world datasets would require a much higher dimensional space.

3.2.1. Addressing higher dimensional latent space

Discretizing a continuous space, such as in GridVAE, is challenging due to the curse of dimensionality (Bellman, 1957). This refers to the exponential growth in the number of clusters as the number of dimensions increases, which leads to a computational challenge when dealing with high-dimensional latent space. For example, when applying GridVAE to reconstruct images of the CelebA (Liu et al., 2015) dataset to learn the 40 attributes, we need a 40-dimensional latent space with two clusters in each dimension to represent the presence or absence of a given attribute. Firstly, parametrizing the mixture of Gaussian prior $p(z)=\sum _{k=1}^{K}N(z|{\mu }_k,{\sigma }_k^2)/K$ over 40 dimensions is prohibitively expensive as K = 2⁴⁰ ≈ 1.1 × 10¹². Secondly, the assumption of equal probability for the components, which was appropriate for the simple 2-digit MNIST dataset, is no longer valid. This is because the attributes in the CelebA dataset are not uniformly distributed, and some combinations may not exist. For instance, the combination of “black hair” + “blonde hair” + “brown hair” + “bald” is impossible due to attribute conflicts. To address this issue, we use the proposed loss function in Eq. (24) incorporating relaxation.

To avoid pre-parametrizing p(z) over 40 dimensions, we have implemented a dynamic calculation of the KL-divergence between q_ϕ and p_θ, whereby only the cluster that is closest to the latent space representation is considered, as illustrated in Figure 11. This means that clusters to which the data point does not belong do not affect its distribution, and the MoG distribution is simplified to a multivariate Gaussian as

$\begin{array}{l}{D}_{\text{KL}}(p_1\Vert p_2)=\frac{1}{2}[log\frac{|{\Sigma }_2|}{|{\Sigma }_1|}-n+\text{tr}({\Sigma }_2^{-1}{\Sigma }_1)\\ +{({\mu }_2-{\mu }_1)}^{⊺}{\Sigma }_2^{-1}({\mu }_2-{\mu }_1)],& (27)\end{array}$

where p₁ = q_ϕ(z|x) = $N$(z|μ₁, Σ₁), ${\Sigma }_1=\mathrm{\text{diag}}({\sigma }_1^2,\dots ,{\sigma }_n^2)$, p₂ = $N$(μ₂, Σ₂), μ₂ = R(μ₁), and ${\Sigma }_2=\mathrm{\text{diag}}({\sigma }_0^2,\dots ,{\sigma }_n^0)$ with the round function R(·) for the closest integer.

FIGURE 11

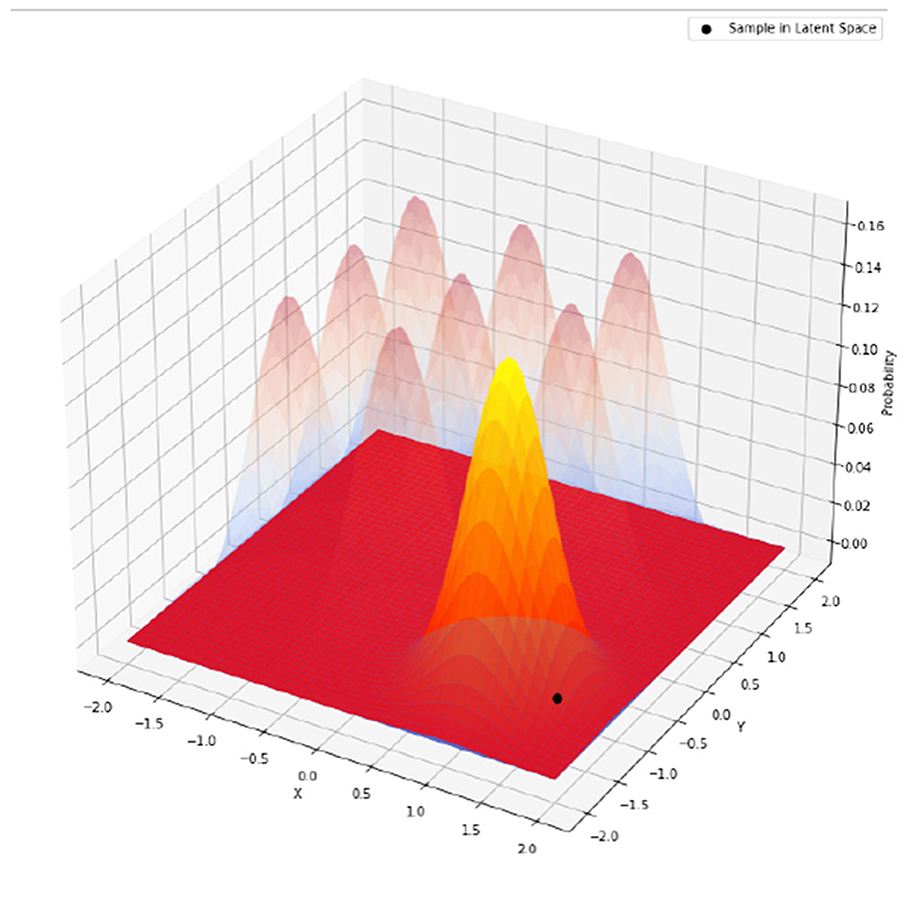
Figure 11. When calculating the KL-divergence, only the mixture component closest to the data (darker shade) is considered. Other components (lighter shade) are ignored. This can be generalized to multiple dimensions and multiple components in each dimension.

The key step here is that the round function dynamically selects the cluster center closest to μ₁, and σ₀ is a pre-defined variance for the prior distribution. It should be chosen so that two clusters next to each other have a reasonable degree of overlap, for example, σ₀ = 1/16 in some of our following experiments. The KL-divergence term becomes

$\begin{array}{ll}\begin{array}{c}{D}_{KL}(q_{\varphi }(z|x)\Vert p_{\theta }(z))=\frac{1}{2}[log\frac{|{\Sigma }_2|}{|{\Sigma }_1|}-n+\text{tr}({\Sigma }_2^{-1}{\Sigma }_1)\hfill \\ +{({\mu }_2-{\mu }_1)}^{⊺}{\Sigma }_2^{-1}({\mu }_2-{\mu }_1)]\hfill \\ =\frac{1}{2}[log{\displaystyle \prod _i}{\sigma }_0^2-log{\displaystyle \prod _i}{\sigma }_i^2-n+{\displaystyle \sum _i}\frac{{\sigma }_i^2}{{\sigma }_0^2}\hfill \\ +{\displaystyle \sum _i}\frac{{({\mu }_i-\text{R}({\mu }_i))}^2}{{\sigma }_0^2}]\hfill \\ =\frac{1}{2}[{\displaystyle \sum _{i=1}^n}(log{\sigma }_0^2-log{\sigma }_i^2-1)\hfill \\ +{\displaystyle \sum _{i=1}^n}\frac{{\sigma }_i^2+{({\mu }_i-\text{R}({\mu }_i))}^2}{{\sigma }_0^2}].\hfill \end{array}\hfill & (28)\end{array}$

By adopting Eq. (28), we can significantly reduce the computational complexity of the model, even for a high-dimensional latent space, bringing it to a level comparable to that of a standard VAE. It is worth noting that the global disentanglement may no longer be guaranteed. Rather, the model only provides local disentanglement within the proximity of each cluster.

Upon training the GridVAE with a 40-dimensional latent space by using the proposed Eq. (28) on the CelebA dataset, we observe some intriguing disentanglement phenomena. Figure 12 showcases the disentanglement of two latent space dimensions, where the first dimension governs one attribute and the second dimension determines another one. Combining these two dimensions leads to simultaneous attribute changes in the generated images.

FIGURE 12

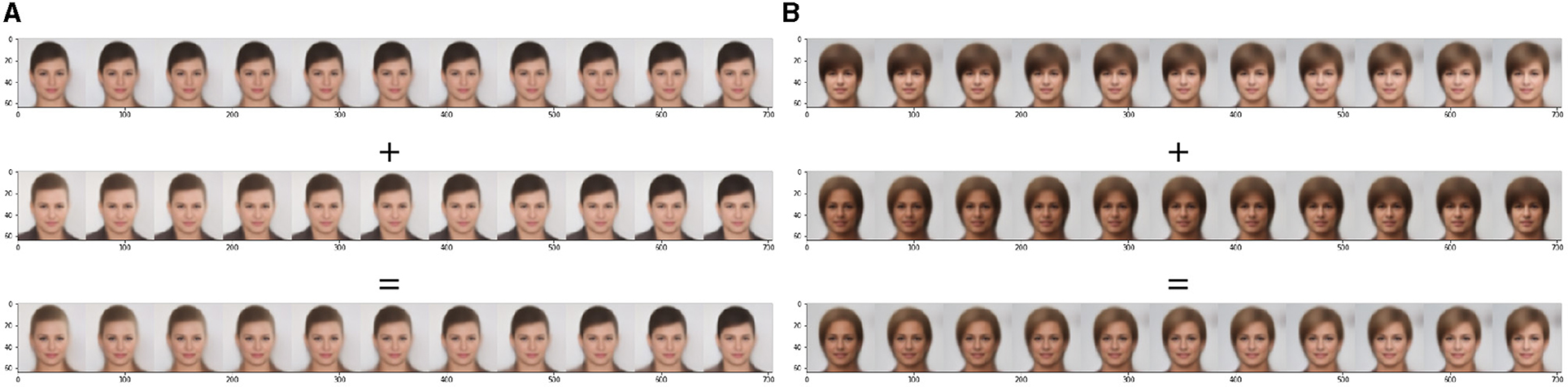
Figure 12. Two generated examples using linear sampling in the latent space. The top row fixes the dimensions and changes the first one, collar in (A) and skin color in (B), from −0.5 to +1.5. The middle row fixes the dimensions and changes the second one, hair color in (A) and hairstyle in (B), from −0.5 to +1.5. The bottom row changes the first and second dimensions from −0.5 to +1.5.

An inherent limitation of this unsupervised approach is that while the latent space appears to be locally disentangled for each image, the same dimension may have different semantic interpretations across different images. To address this issue, we introduce all 40 attributes of the dataset during the training. This should establish an upper bound on the disentanglement.

3.2.2. From unsupervised to guided and partially guided GridVAE

To this end, we described an unsupervised approach to learning the latent space representation of images. However, for datasets like CelebA with ground truth attributes, we can incorporate them into the latent space to guide the learning. Specifically, we extract the 40-dimensional attribute vector indicating the presence or absence of each feature for each image in a batch and treat it as the ground truth cluster center ${\mu }_i^{gt}$. Hence, instead of rounding the latent space representation μ_i in Eq. (28), we replace it with ${\mu }_i^{gt}$.

One limitation of this approach is the requirement of the ground truth attributes for all images, which may not always be available or feasible. Additionally, it is important to note that while we refer to this approach as “guided,” the given attribute information only serves in the latent space as the cluster assignment prior, and the VAE reconstruction task remains unsupervised. This differs from classical supervised learning, where the label information is the output. Furthermore, in our approach, no specific coordinate in the latent space is designated for the input. Instead, we provide guidance that the sample belongs to a cluster centered at a certain point in the latent space.

This guided learning framework can be extended to a subset of the 40 attributes or a latent space with more dimensions. For clarity, we will refer to the latter as “partially guided” to distinguish it from the commonly used “semi-supervised” by using a subset of the labeled dataset.

We conduct the experiments using attribute information as latent space priors and obtain the following findings for the guided approach: (a) GridVAE is able to cluster images accurately based on their attributes and the same dimension has the same semantic meaning across different images. For instance, dimension 31 represents “smile”. (b) GridVAE could not generate images for clusters that have little or no representation in the training set. For example, the attempt to generate an image of a bald female by constraining GridVAE to the “female” and “bald” clusters is not achievable for an accurate representation. (c) Some attributes are more universal across different images, such as their ability to add a smile to almost any face. However, other attributes, such as gender, are not always modifiable. This could be caused by attributes that are not independent and can be influenced by others. Universal attributes, such as “smile,” seem to primarily located locally in the image region without interruption from the other attributes, see Figure 13.

FIGURE 13

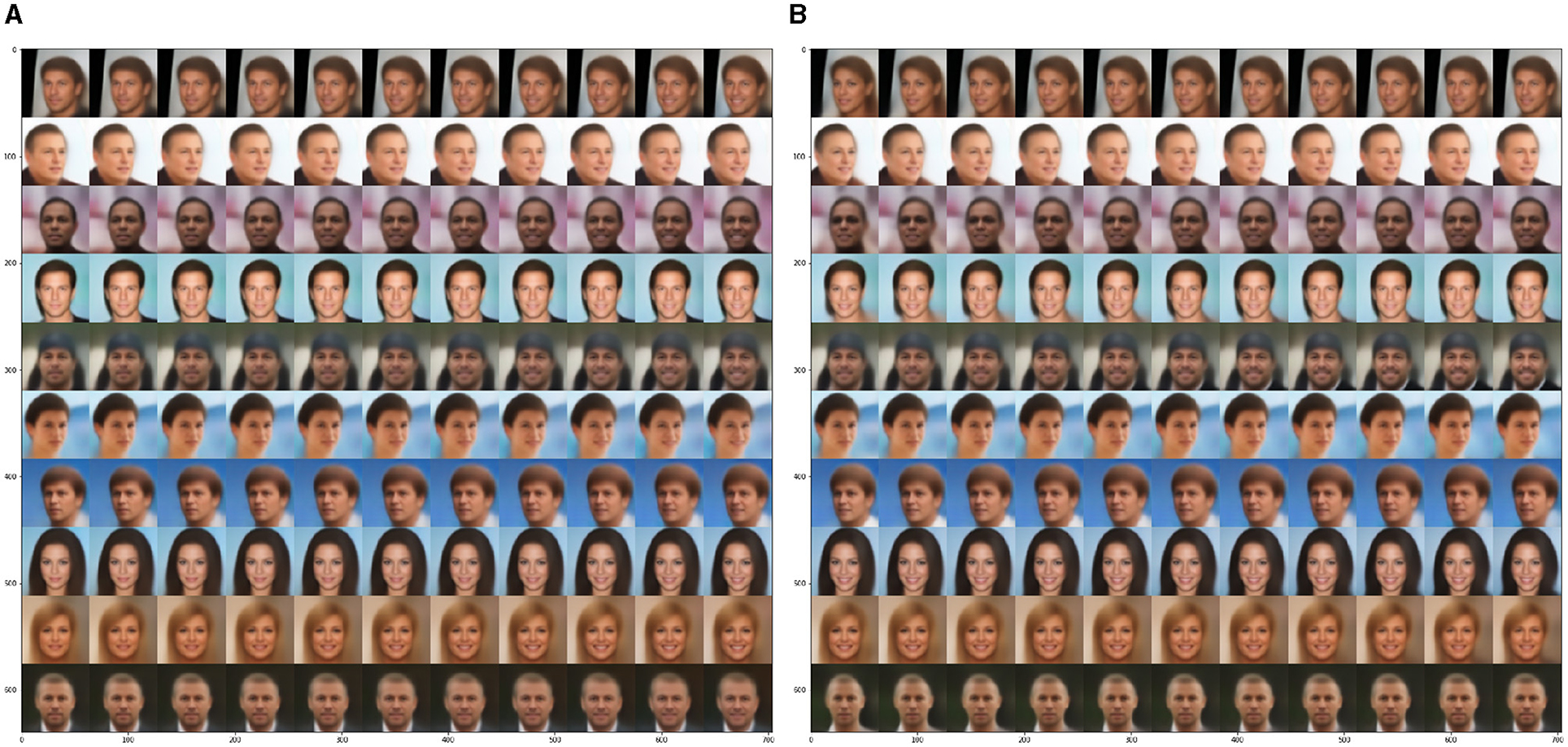
Figure 13. Generated images from sampling in the latent space. Keeping all other dimensions fixed and changing dimension (A) 31 (smile) from −0.5 to +1.5, or (B) 20 (male) from −0.5 to +1.5.

To further illustrate the incompleteness and correlation among the attributes in the CelebA dataset, we use a subset of the given attributes. We choose 38 out of the 40 attributes, excluding attributes 20 (female/male) and 31 (not smiling/smiling). Figure 14 shows that the GridVAE cannot learn the omitted attributes. This highlights the interdependence of different attributes in the latent space.

FIGURE 14

Figure 14. Partially guided GridVAE generation from the latent attributes which are not provided during training. The left and right subfigures (each with 11 images) are with the dimensions 20 and 31 respectively.

3.3. Combining manifolds of GridVAE disentangled attribute and facial recognition

After achieving a disentangled latent space, one may still wonder about the usefulness of a semantic description of a manifold. One can consider the scenario where another manifold, such as a facial recognition manifold, is learned. By studying these two manifolds jointly, we can gain insights to make the models more explainable and useful. One potential application is to better understand the relationship between facial attributes and facial recognition. By analyzing the disentangled latent space of facial attributes and the manifold learned for facial recognition, we can potentially identify which attributes are the most important for recognizing different faces. This understanding can then be used to improve the performance of facial recognition models as well as explain the model decisions.

For instance, FaceNet (Schroff et al., 2015) directly learns a mapping from face images to a compact Euclidean space where distances correspond to a measure of face similarity. To discover the semantic structure of this manifold with x as binary attributes, we can follow these steps:

1. Build a face recognition manifold using contrastive learning.

2. Use the CelebA dataset with ground truth attribute labels (40 binary values).

3. Insert CelebA samples onto the recognition manifold.

4. Find the nearest neighbor for each CelebA sample using the face recognition manifold coordinates.

5. For each attribute in x, compute p(x) over the entire CelebA dataset.

6. For each attribute in x, compute p(x|x of nearest neighbor = 0).

7. For each attribute in x, compute the KL divergence between p(x) and p(x|x of nearest neighbor = 0).

8. Identify attributes with the largest KL divergence.

Figure 15 demonstrates that the KL Divergence between p(x) and p(x|x of nearest neighbor = 0) is significantly larger for certain attributes, such as “male,” “wearing lipstick,” “young” and “no beard,” than the others. This indicates that the neighborhood structure of the facial recognition manifold is markedly different from the distribution of these attributes in the entire dataset. These findings highlight the importance of the joint study of different manifolds to gain a more profound understanding of the relationship between the attributes and the recognition tasks. By incorporating it into the models, we can potentially improve the performance of facial recognition models and also enhance their interpretability.

FIGURE 15

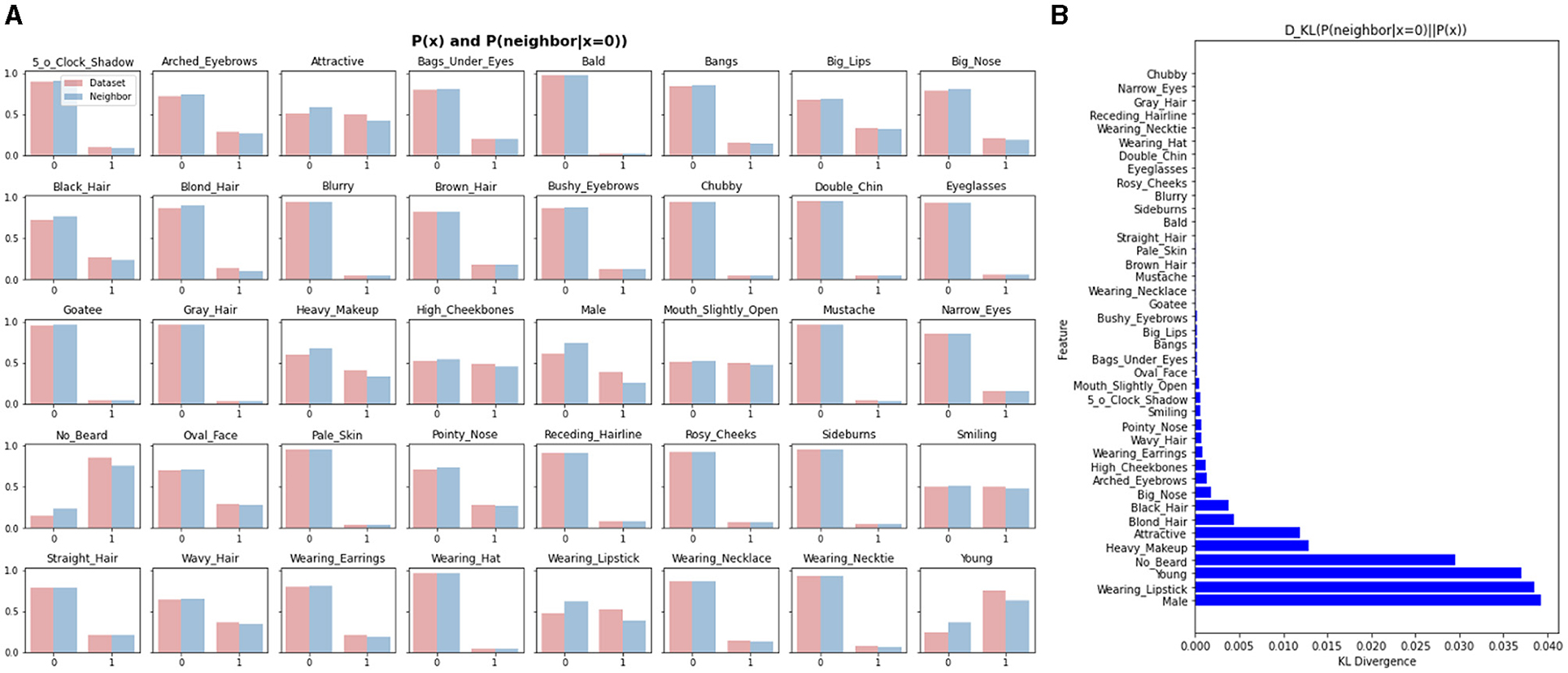
Figure 15. Semantic structure of the face recognition manifold by jointly studying the attribute manifold and the facial recognition manifold. (A) p(x) and p(x|xof nearest neighbor = 0) distributions. (B) KL divergence.

4. Application to defend patch attacks

To this end, interpretable and controllable samplings from each semantic distribution on the manifold can be achieved by using the semantic disentanglement in Section 3 toward high-fidelity and diverse image generation and probability distribution analysis in Section 2. It is also of strong interest to enhance the robustness of such semantic samplings under certain attacks. In this section, we present an adversarial robustness framework by enforcing the semantic consistency between the classifier and the decoder for reliable density estimation on the manifold.

4.1. Adversarial defense with variational inference

In Yang et al. (2022), adversarial robustness can be achieved by enforcing the semantic consistency between a decoder and a classifier (adversarial robustness does not exist in non-semantically consistent classifier-decoder). We briefly review the adversarial purification framework below. We define the real-world high-dimensional data as x ∈ ℝⁿ which lies on a low-dimensional manifold $M$ diffeomorphic to ℝ^m with m ≪ n. We define an encoder function f : ℝⁿ → ℝ^m and a decoder function f^† : ℝ^m → ℝⁿ to form an autoencoder. For a point x ∈ $M$, f^† and f are approximate inverses. We define a discrete label set $L$ of c elements as $L$ = {1, ..., c} and a classifier in the latent space as h : ℝ^m → $L$. The encoder maps the image x to a lower-dimensional vector z = f(x) ∈ ℝ^m and the functions f and h together form a classifier in the image space h(z) = (h ∘ f)(x) ∈ $L$.

A classifier (on the manifold) is a semantically consistent classifier if its predictions are consistent with the semantic interpretations of the images reconstructed by the decoder. Despite that the classifiers and decoders (on the manifold) have a low input dimension, it is still difficult to achieve high semantic consistency between them. Thus, we assume that predictions and reconstructions from high data density regions of p(z|x) are more likely to be semantically consistent and we need to estimate the probability density in the latent space with the variational inference.

We define three sets of parameters: (1) ϕ parametrizes the encoder distribution, denoted as q_ϕ(z|x), (2) θ parametrizes the decoder distributions, represented as p_θ(x|z), and (3) ψ parametrizes the classification head, given by h_ψ(z). These parameters are jointly optimized with respect to the ELBO loss and the cross-entropy loss as shown in Eq. (29), where λ is the trade-off term between the ELBO and the classification. We provide the framework in Figures 16A, B for the two-stage procedure and the trajectory of cluster center change after introducing our purification over attacks in Figure 16C. By adopting this formulation, we notice a remarkable semantic consistency between the decoder and the classifier. Specifically, on Fashion-MNIST (Xiao et al., 2017), when making predictions on adversarial examples, if the predicted label is “bag,” we observe that the reconstructed image tends to resemble a “bag” as well. This phenomenon is illustrated in Figures 16D, 17.

$\begin{array}{l}\underset{\theta ,\varphi ,\psi }{\max }\underset{\text{ELBO }(\text{lower bound of}log{p}_{\theta }(x)\text{)}}{\underbrace{{𝔼}_{z~q_{\varphi }(z|x)}\left[log{p}_{\theta }(x|z)\right]-D_{KL}[q_{\varphi }(z|x)\Vert p(z)]}}\\ +\lambda {\displaystyle \underset{\text{Classification loss}}{{\displaystyle \underbrace{{𝔼}_{z~q_{\varphi }(z|x)}\left[y^{⊺}log{h}_{\psi }(z)\right]}}}}.& (29)\end{array}$

FIGURE 16

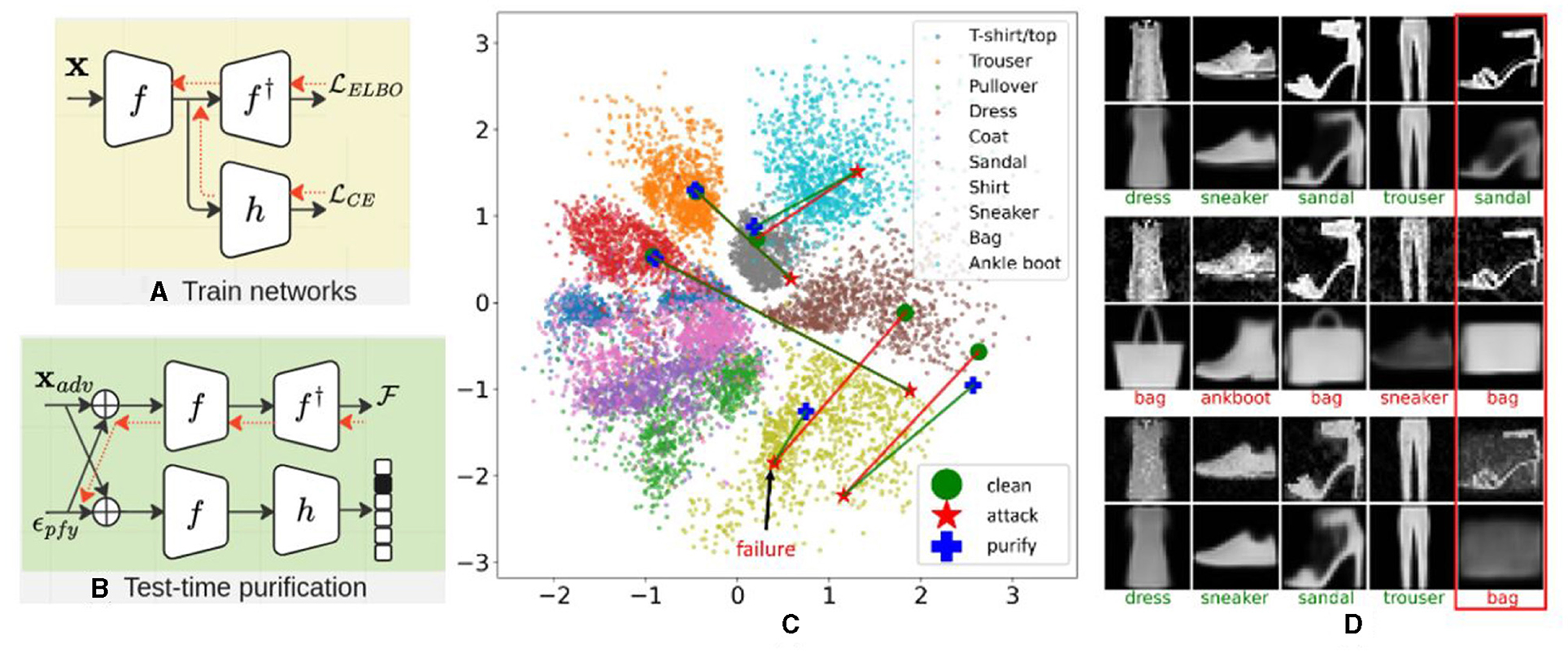
Figure 16. The framework of adversarial purification for image-level adversarial attacks. (A) Jointly train the classifier with the ELBO loss. (B) Test time adversarial purification with the ELBO loss. (C) Trajectories of clean (green)—attack (red)—purified (blue) images on a 2D latent space. (D) Input images and reconstruction images of samples in (C). The top two rows are the input and reconstruction of clean images, the middle two rows are the input and reconstruction of adversarial images. The bottom two rows are the input and reconstruction of purified images. The text represents predicted classes with green color for correct predictions and red color for incorrect predictions. The red box on the right corresponds to the failure case (purified process fails).

FIGURE 17

Figure 17. Class predictions from the VAE-Classifier models on clean, adversarial and purified samples of the CelebA gender attribute. The top two rows are the input and reconstruction of clean images, the middle two rows are the input and reconstruction of patch adversarial images. The bottom two rows are the input and reconstruction of purified images. The text represents the predicted classes with green color for correct predictions and red color for incorrect predictions. Since predictions and reconstructions from the VAE classifier are correlated, our test-time defenses are effective against adversarial attacks.

To defend against image-level attacks, a purification vector can be obtained through the test-time optimization over the ELBO loss. For example, given an adversarial example x_adv, a purified sample can be obtained by x_pfy = x_adv + ϵ_pfy with

$\begin{array}{ll}\begin{array}{c}{ϵ}_{\text{pfy}}={\displaystyle \underset{ϵ\in C_{\text{pfy}}}{arg max}}{𝔼}_{\text{z}~q_{\varphi }(\text{z}|{\text{x}}_{\text{adv}}+ϵ)}\left[log{p}_{\theta }({\text{x}}_{\text{adv}}+ϵ|\text{z})\right]\hfill \\ -D_{\text{KL}}\left[q_{\varphi }(\text{z}|{\text{x}}_{\text{adv}}+ϵ)\Vert p(\text{z})\right],\hfill \end{array}& (30)\end{array}$

where $C_{\text{pfy}}=\{ϵ\in {ℝ}^n\mid {\text{x}}_{\text{adv}}+ϵ\in {\left[0,1\right]}^n\mathrm{\text{and}}\Vert ϵ{\Vert }_p\le {ϵ}_{\text{th}}\}$ which is the feasible set for purification and ϵ_th is the purification budget. Since the classifier and the decoder are semantically consistent, the predictions from the classifier become normal to defend against the attacks upon normal reconstructions.

4.2. Bounded patch attack

In this work, we focus on the ℓ₀-bounded attacks (Papernot et al., 2016; Brown et al., 2017) from the manifold perspective which is not investigated in the prior work. In contrast to full image-level attacks like ℓ₂ and ℓ_∞ bounded attacks (Madry et al., 2018), patch attacks, which are ℓ₀ bounded attacks, aim to restrict the number of perturbed pixels. These attacks are more feasible to implement in real-world settings, resulting in border impacts. Below, we conduct an initial investigation into the defense against patch attacks by leveraging the knowledge of the data manifold.

When compared to ℓ_∞ attacks, ℓ₀ attacks, such as the adversarial patch attacks, introduce larger perturbations to the perturbed pixels. Therefore, we decide to remove the purification bound for the patch-attack purification. Without these constraints, the purified examples can take on any values within the image space. A purification vector can then be obtained through the test-time optimization over the ELBO loss as shown in Eq. (30).

4.3. Experiments

We use the gender classification model (Yang et al., 2022) to demonstrate the adversarial purification of ℓ₀ bounded attacks. To ensure that the adversarial examples do not alter the semantic content of the images, we restrict the perturbation region to the forehead of a human face. The patch for perturbation is a rectangular shape measuring 16 × 32, see Figure 17. For the patch attacks, we conduct 2,048 iterations with step size 1/255 using PGD (Madry et al., 2018) and PGD-NAG (Nesterov Accelerated Gradient) (Lin et al., 2020). In Table 1, the purification is carried out through 256 iterations with the same step size.

TABLE 1

Table 1. Classification accuracy of the model on clean and adversarial (patch) examples.

5. Limitation

The current version of log-probability estimation in diffusion models has limitations in evaluating high-dimensional images. Specifically, at early denoising steps (when t is small) the diffusion model serves as a denoiser such that x_t and x_t+h are similar while at large steps (when t moves toward T), their difference is still small due to the high proportion of the Gaussian noise in x_t. This leads to the proportion of the difference between x_t and x_t+h for effective out-of-distribution detection small compared with the log p accumulated in the processes. We keep this as an open problem for future work.

6. Conclusion

This work studies the image geometric representation from high-dimensional spatial space to low-dimensional latent space on the image manifold. To explore the image probability distribution with the assumption that real images are usually in a high-density region while not all samples from the distribution can be represented as realistic images, we incorporate log-likelihood estimation into the procedures of normalizing flows and diffusion models. Meanwhile, we explore the hierarchical normalizing flow structure and a higher-order solution in diffusion models for high-quality and high-fidelity image generation. For an interpretable and controllable sampling from the semantic distribution on the manifold, we then propose GridVAE model under an EL framework to disentangle the elements of the latent variable on the image manifold. To test the semantic and reconstruction robustness on the manifold, we first apply patch attacks and defenses in the image space and then effectively recover the semantics under such attacks with our purification loss. Experiments show the effectiveness of probability estimation in distinguishing seen examples from unseen ones, the quality and the efficiency with large sampling steps in image generation, meaningful representations of varying specific element(s) of the latent variable to control the object attribute(s) in the image space, and the well-preserved semantic consistency with patch attacks.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found at: https://mmlab.ie.cuhk.edu.hk/projects/CelebA.html, http://yann.lecun.com/exdb/mnist/, and https://github.com/zalandoresearch/fashion-mnist.

Ethics statement

Written informed consent was not obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article because these human face images are from the public dataset CelebA, which is widely used in computer vision community.

Author contributions

PT: Writing—original draft, Writing—review & editing. ZY: Writing—original draft, Writing—review & editing. RH: Writing—original draft, Writing—review & editing. ZX: Writing—original draft, Writing—review & editing. JZ: Writing—original draft, Writing—review & editing. YF: Writing—original draft, Writing—review & editing. DC: Writing—review & editing. JS: Writing—review & editing. TW: Writing—review & editing.

Funding

This work was supported by the DARPA geometries of learning (GoL) project under the grant agreement number HR00112290075.

Acknowledgments

We thank Amir Rahimi for his contribution to the code and discussion of the normalizing flow models.

Conflict of interest

PT, ZY, and YF are employed by General Electric.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2023.1253682/full#supplementary-material

References

Bellman, R. (1957). Dynamic Programming. Princeton, NJ: Princeton University Press.

Google Scholar

Brown, T. B., Mané, D., Roy, A., Abadi, M., and Gilmer, J. (2017). “Adversarial patch,” in Conference on Neural Information Processing Systems (NeurIPS) (Long Beach). Available online at: https://nips.cc/Conferences/2017

Google Scholar

Carlini, N., and Wagner, D. A. (2016). “Towards evaluating the robustness of neural networks,” in CoRR abs/1608.04644.

Google Scholar

Chaabouni, R., Kharitonov, E., Bouchacourt, D., Dupoux, E., and Baroni, M. (2020). Compositionality and generalization in emergent languages. arXiv. [preprint]. doi: 10.48550/arXiv.2004.09124

CrossRef Full Text | Google Scholar

Chang, L., Borenstein, E., Zhang, W., and Geman, S. (2017). Maximum likelihood features for generative image models. Ann. Appl. Stat. 11, 1275–1308. doi: 10.1214/17-AOAS1025

CrossRef Full Text | Google Scholar

Chen, R. T. Q., Li, X., Grosse, R., and Duvenaud, D. (2018). “Isolating sources of disentanglement in vaes,” in Conference on Neural Information Processing Systems (NeurIPS) (Montreal, QC). Available online at: https://nips.cc/Conferences/2018

Google Scholar

Chou, E., Tramer, F., and Pellegrino, G. (2019). “SentiNet: detecting localized universal attacks against deep learning systems,” in Deep Learning and Security Workshop (DLSW) (San Francisco, CA: IEEE). doi: 10.1109/SPW50608.2020.00025

CrossRef Full Text | Google Scholar

Coeurdoux, F., Dobigeon, N., and Chainais, P. (2022). “Sliced-Wasserstein normalizing flows: beyond maximum likelihood training,” in European Symposium on Artificial Neural Networks (ESANN) (Bruges). doi: 10.14428/esann/2022.ES2022-101

CrossRef Full Text | Google Scholar

Ding, Z., Xu, Y., Xu, W., Parmar, G., Yang, Y., Welling, M., et al. (2020). “Guided variational autoencoder for disentanglement learning,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Seattle, WA: IEEE). doi: 10.1109/CVPR42600.2020.00794

CrossRef Full Text | Google Scholar

Gao, J., He, D., Tan, X., Qin, T., Wang, L., Liu, T. Y., et al. (2019). “Representation degeneration problem in training natural language generation models,” International Conference on Learning Representations (ICLR) (New Orleans, LA). Available online at: https://iclr.cc/Conferences/2019

Google Scholar

Gomtsyan, M., Mokrov, N., Panov, M., and Yanovich, Y. (2019). “Geometry-aware maximum likelihood estimation of intrinsic dimension,” in Proceedings of Machine Learning Research. Asian Conference on Machine Learning (ACML). Available online at: https://www.acml-conf.org/2019/

Google Scholar

Grover, A., Dhar, M., and Ermon, S. (2018). “Flow-GAN: combining maximum likelihood and adversarial learning in generative models,” in AAAI Conference on Artificial Intelligence (AAAI). (New Orleans, LA). Available online at: https://dblp.org/db/conf/aaai/aaai2018.html

Google Scholar

Hajri, H., Said, S., and Berthoumieu, Y. (2017). “Maximum likelihood estimators on manifolds,” in International Conference on Geometric Science of Information (Cham: Springer). doi: 10.1007/978-3-319-68445-1_80

CrossRef Full Text | Google Scholar

Havrylov, S., and Titov, I. (2017). “Emergence of language with multi-agent games: learning to communicate with sequences of symbols,” in Conference on Neural Information Processing Systems (NeurIPS) (Long Beach, CA), 30. Available online at: https://dblp.org/db/conf/nips/nips2017.html

Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Las Vegas, NV: IEEE), 770–778. doi: 10.1109/CVPR.2016.90

CrossRef Full Text | Google Scholar

Ho, J., Jain, A., and Abbeel, P. (2020). Denoising diffusion probabilistic models. Conference on Neural Information Processing Systems (NeurIPS).

Google Scholar

Hu, H. Y., Wu, D., You, Y. Z., Olshausen, B., and Chen, Y. (2023). RG-Flow: a hierarchical and explainable flow model based on renormalization group and sparse prior. arXiv. [preprint]. doi: 10.48550/arXiv.2010.00029

CrossRef Full Text | Google Scholar

Hwang, R. H., Lin, J. Y., Hsieh, S. Y., Lin, H. Y., and Lin, C. L. (2023). Adversarial patch attacks on deep-learning-based face recognition systems using generative adversarial networks. Sensors 23, 853. doi: 10.3390/s23020853

PubMed Abstract | CrossRef Full Text | Google Scholar

Kingma, D. P., and Dhariwal, P. (2018). “Glow: generative flow with invertible 1x1 convolutions,” in Conference on Neural Information Processing Systems (NeurIPS) (Montreal, QC). Available online at: https://dblp.org/db/conf/nips/nips2018.html.

Google Scholar

Kingma, D. P., and Welling, M. (2013). Auto-encoding variational bayes. arXiv. [preprint]. doi: 10.48550/arXiv.1312.6114

CrossRef Full Text | Google Scholar

Klein, S., Raine, J. A., and Golling, T. (2022). Flows for flows: training normalizing flows between arbitrary distributions with maximum likelihood estimation. arXiv. [preprint]. doi: 10.48550/arXiv.2211.02487

CrossRef Full Text | Google Scholar

Kobyzev, I., Prince, S., and Brubaker, M. A. (2019). Normalizing flows: introduction and ideas. arXiv. [preprint]. doi: 10.48550/arXiv.1908.09257

CrossRef Full Text | Google Scholar

Krizhevsky, A. (2009). “Learning multiple layers of features from tiny images,” in Technical Report. University of Toronto. Available online at: https://learning2hash.github.io/publications/cifar2009learning/

Google Scholar

Kubricht, J. R., Santamaria-Pang, A., Devaraj, C., Chowdhury, A., and Tu, P. (2020). Emergent languages from pretrained embeddings characterize latent concepts in dynamic imagery. Int. J. Semant. Comput. 14, 357–373. doi: 10.1142/S1793351X20400140

CrossRef Full Text | Google Scholar

Kutta, W. (1901). Beitrag zur naherungsweisen integration totaler differentialgleichungen. Z. Math. Phys. 46, 435–453.

Google Scholar

LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). “Gradient-based learning applied to document recognition,” in Proceedings of the IEEE. doi: 10.1109/5.726791

CrossRef Full Text | Google Scholar

Liang, J., Lugmayr, A., Zhang, K., Danelljan, M., Gool, L. V., Timofte, R., et al. (2021). “Hierarchical conditional flow: a unified framework for image super-resolution and image rescaling,” in IEEE International Conference on Computer Vision (ICCV) (Montreal, QC: IEEE). doi: 10.1109/ICCV48922.2021.00404

CrossRef Full Text | Google Scholar

Lin, J., Song, C., He, K., Wang, L., and Hopcroft, J. E. (2020). “Nesterov accelerated gradient and scale invariance for adversarial attacks,” in International Conference on Learning Representations (ICLR). Available online at: https://iclr.cc/Conferences/2020

Google Scholar

Ling, J., Wang, Z., Lu, M., Wang, Q., Qian, C., Xu, F., et al. (2022). “Semantically disentangled variational autoencoder for modeling 3D facial details,” Transactions on Visualization and Computer Graphics. IEEE. doi: 10.1109/TVCG.2022.3166666. Available online at: https://ieeexplore.ieee.org/document/9756299

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, A., Wang, J., Liu, X., Cao, B., Zhang, C., Yu, H., et al. (2020). “Bias-based universal adversarial patch attack for automatic check-out,” in European Conference on Computer Vision (ECCV) (Cham: Springer). doi: 10.1007/978-3-030-58601-0_24

CrossRef Full Text | Google Scholar

Liu, B., Yang, F., Bi, X., Xiao, B., Li, W., Gao, X., et al. (2022). “Detecting generated images by real images,” in European Conference on Computer Vision (ECCV) (New York, NY: ACM). doi: 10.1007/978-3-031-19781-9_6

CrossRef Full Text | Google Scholar

Liu, Y., Wei, F., Shao, J., Sheng, L., Yan, J., Wang, X., et al. (2018). “Exploring disentangled feature representation beyond face identification,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Salt Lake City, UT: IEEE). doi: 10.1109/CVPR.2018.00222

CrossRef Full Text | Google Scholar

Liu, Z., Luo, P., Wang, X., and Tang, X. (2015). “Deep learning face attributes in the wild,” in Proceedings of International Conference on Computer Vision (ICCV) (Santiago: IEEE). doi: 10.1109/ICCV.2015.425

CrossRef Full Text | Google Scholar

Lobato, G. A., Mier, P., and Navarro, M. A. A. (2016). Manifold learning and maximum likelihood estimation for hyperbolic network embedding. Appl. Netw. Sci. 1, 10. doi: 10.1007/s41109-016-0013-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, C. (2022). Understanding diffusion models: a unified perspective. arXiv. [preprint]. doi: 10.48550/arXiv.2208.11970

CrossRef Full Text | Google Scholar

Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and Vladu, A. (2018). “Towards deep learning models resistant to adversarial attacks,” in International Conference on Learning Representations (ICLR). (Vancouver, CA). Available online at: https://iclr.cc/Conferences/2018

Google Scholar

Mu, Y., Yao, S., Ding, M., Luo, P., and Gan, C. (2023). “EC²: emergent communication for embodied control,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Vancouver, BC). doi: 10.1109/CVPR52729.2023.00648

CrossRef Full Text | Google Scholar

Pang, A. S., Kubricht, J., Chowdhury, A., Bhushan, C., and Tu, P. (2020). “Towards emergent language symbolic semantic segmentation and model interpretability,” in Medical Image Computing and Computer Assisted Intervention (MICCAI).

Google Scholar

Papamakarios, G., Nalisnick, E., Rezende, D. J., Mohamed, S., and Lakshminarayanan, B. (2021). Normalizing flows for probabilistic modeling and inference. J. Mach. Learn. Res. 2, 1–64. doi: 10.5555/3546258.3546315

CrossRef Full Text | Google Scholar

Papernot, N., McDaniel, P. D., Jha, S., Fredrikson, M., Celik, Z. B., Swami, A., et al. (2016). “The limitations of deep learning in adversarial settings,” in EuroS&P (Saarbruecken: IEEE), 372–387. doi: 10.1109/EuroSP.2016.36

CrossRef Full Text | Google Scholar

Parmar, G., Li, D., Lee, K., and Tu, Z. (2021). “Dual contradistinctive generative autoencoder,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Nashville, TN: IEEE). doi: 10.1109/CVPR46437.2021.00088

CrossRef Full Text | Google Scholar

Pastrana, R. (2022). Disentangling variational autoencoders. arXiv. [preprint]. doi: 10.48550/arXiv.2211.07700

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830. doi: 10.5555/1953048.2078195

CrossRef Full Text | Google Scholar

Pope, P., Zhu, C., Abdelkader, A., Goldblum, M., and Goldstein, T. (2021). “The intrinsic dimension of images and its impact on learning,” in International Conference on Learning Representations (ICLR). Available online at: https://iclr.cc/Conferences/2021

Google Scholar

Ramesh, A., Pavlov, M., Goh, G., Gray, S., Voss, C., Radford, A., et al. (2020). “Zero-shot text-to-image generation,” in International Conference on Machine Learning (ICML). Available online at: https://icml.cc/Conferences/2020

Google Scholar

Rezende, D. J., and Mohamed, S. (2016). “Variational inference with normalizing flows,” in International Conference on Machine Learning (ICML).

Google Scholar

Runge, C. D. T. (1895). Über die numerische auflösung von differentialgleichungen. Math. Annal. 46, 167–178. doi: 10.1007/BF01446807

CrossRef Full Text | Google Scholar

Schroff, F., Kalenichenko, D., and Philbin, J. (2015). “Facenet: a unified embedding for face recognition and clustering,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Boston, MA: IEEE), 815–823. doi: 10.1109/CVPR.2015.7298682

CrossRef Full Text | Google Scholar

Song, J., Meng, C., and Ermon, S. (2021). “Denoising diffusion implicit models,” in International Conference on Learning Representations (ICLR). Available online at: https://iclr.cc/Conferences/2021

Google Scholar

Tramer, F., Kurakin, A., Papernot, N., Goodfellow, I., Boneh, D., McDaniel, P., et al. (2017). “Ensemble adversarial training: attacks and defenses,” in International Conference on Learning Representations (ICLR) (Toulon). Available online at: https://iclr.cc/archive/www/doku.php%3Fid=iclr2017:main.html

Google Scholar

Tucker, M., Li, H., Agrawal, S., Hughes, D., Sycara, K., Lewis, M., et al. (2021). “Emergent discrete communication in semantic spaces,” in Conference on Neural Information Processing Systems (NeurIPS). Available online at: https://nips.cc/Conferences/2021

Google Scholar

Tyshchuk, K., Karpikova, P., Spiridonov, A., Prutianova, A., Razzhigaev, A., Panchenko, A., et al. (2023). On isotropy of multimodal embeddings. Information 14, 392. doi: 10.3390/info14070392

CrossRef Full Text | Google Scholar

Voleti, V., Voleti, V., Oberman, A., and Pal, C. (2023). Multi-resolution continuous normalizing flows. Res. Sq. Available online at: https://arxiv.org/abs/2106.08462

Google Scholar

Wang, S.-Y., Wang, O., Zhang, R., Owens, A., and Efros, A. A. (2020). “CNN-generated images are surprisingly easy to spot... for now,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Seattle, WA: IEEE). doi: 10.1109/CVPR42600.2020.00872

CrossRef Full Text | Google Scholar

Xiang, C., Bhagoji, A. N., Sehwag, V., and Mittal, P. (2021). “PatchGuard: a provably robust defense against adversarial patches via small receptive fields and masking,” USENIX Security Symposium 2021. Available online at: https://www.usenix.org/conference/usenixsecurity21

Google Scholar

Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms. arXiv. [preprint]. doi: 10.48550/arXiv.1708.07747

CrossRef Full Text | Google Scholar

Xu, Z., Niethammer, M., and Raffel, C. (2022). “Compositional generalization in unsupervised compositional representation learning: a study on disentanglement and emergent language,” in Conference on Neural Information Processing Systems (NeurIPS) (New Orleans, LA). https://nips.cc/Conferences/2022

Google Scholar

Yang, Z., Xu, Z., Zhang, J., Hartley, R., and Tu, P. (2022). Adaptive test-time defense with the manifold hypothesis. arXiv. [preprint]. doi: 10.48550/arXiv.2210.14404

CrossRef Full Text | Google Scholar

Zhang, Q., and Chen, Y. (2021). “Diffusion normalizing flow,” in Conference on Neural Information Processing Systems (NeurIPS). Available online at: https://nips.cc/Conferences/2021

Google Scholar