
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Comput. Sci. , 14 September 2023
Sec. Computer Vision
Volume 5 - 2023 | https://doi.org/10.3389/fcomp.2023.1154957
This article is part of the Research Topic Perceptual Organization in Computer and Biological Vision View all 14 articles
The standard physiological model has serious problems accounting for many aspects of vision, particularly when stimulus configurations become slightly more complex than the ones classically used, e.g., configurations of Gabors rather than only one or a few Gabors. For example, as shown in many publications, crowding cannot be explained with most models crafted in the spirit of the physiological approach. In crowding, a target is neighbored by flanking elements, which impair target discrimination. However, when more flankers are added, performance can improve for certain flanker configurations (uncrowding), which cannot be explained by classic models. As was shown, aspects of perceptual organization play a crucial role in uncrowding. For this reason, we tested here whether known principles of perceptual organization can explain crowding and uncrowding. The answer is negative. As shown with subjective tests, whereas grouping is indeed key in uncrowding, the four Gestalt principles examined here did not provide a clear explanation to this effect, as variability in performance was found between and within categories of configurations. We discuss the philosophical foundations of both the physiological and the classic Gestalt approaches and sketch a way to a happy marriage between the two.
Vision has been a mystery since ancient times. Intuitively, perception seems to give us ground truth about the outer world and its objects. Based on this intuition, direct realism proposes a one-to-one mapping (bijection) between the objects of the external world and our mental representations. When there is an apple in the external world, we perceive an apple, and when we perceive an apple, there is an apple in front of our eyes (leaving dreams and mental imagery aside). However, perception can hardly be direct. For example, according to the laws of optics, objects are projected upside-down (and left-right inverted) on the retinal image, but we perceive them upright, so there must be a second transformation undoing the laws of optics, for example, when we want to grasp these objects. Philosophically speaking, perception is not direct but indirect. Still, perception may give us ground truth about the external world, at least approximately. However, the situation is worse. We see many illusory things that are not out there. For example, we see blue spiral lines in the Munker-White illusion, which are simply not there (see Figure 2 of Herzog, 2022). In this case, a simple re-transformation cannot help.
For similar reasons, philosophers such as Berkeley, Kant, and Fichte, have abandoned reasoning about the external world. Ground truth is found in these approaches in the percepts and thoughts themselves. If I have the experience of an apple, there might be no corresponding apple out there, but my percept is undeniably true. Thus, focusing on the laws of perception and cognition is a first step toward a philosophy free of ontological commitments about an external world to which we have no direct access. The Gestaltists have largely subscribed to this continental approach of epistemology, with introspection being both the conceptual and methodological starting point. For many Gestaltists, there is more in the mind than in the world. There is information that goes “beyond the information given” (Kanizsa, 1979). For example, we clearly perceive a cross in Figure 1 (upper panel) even though there are only squares and disks.
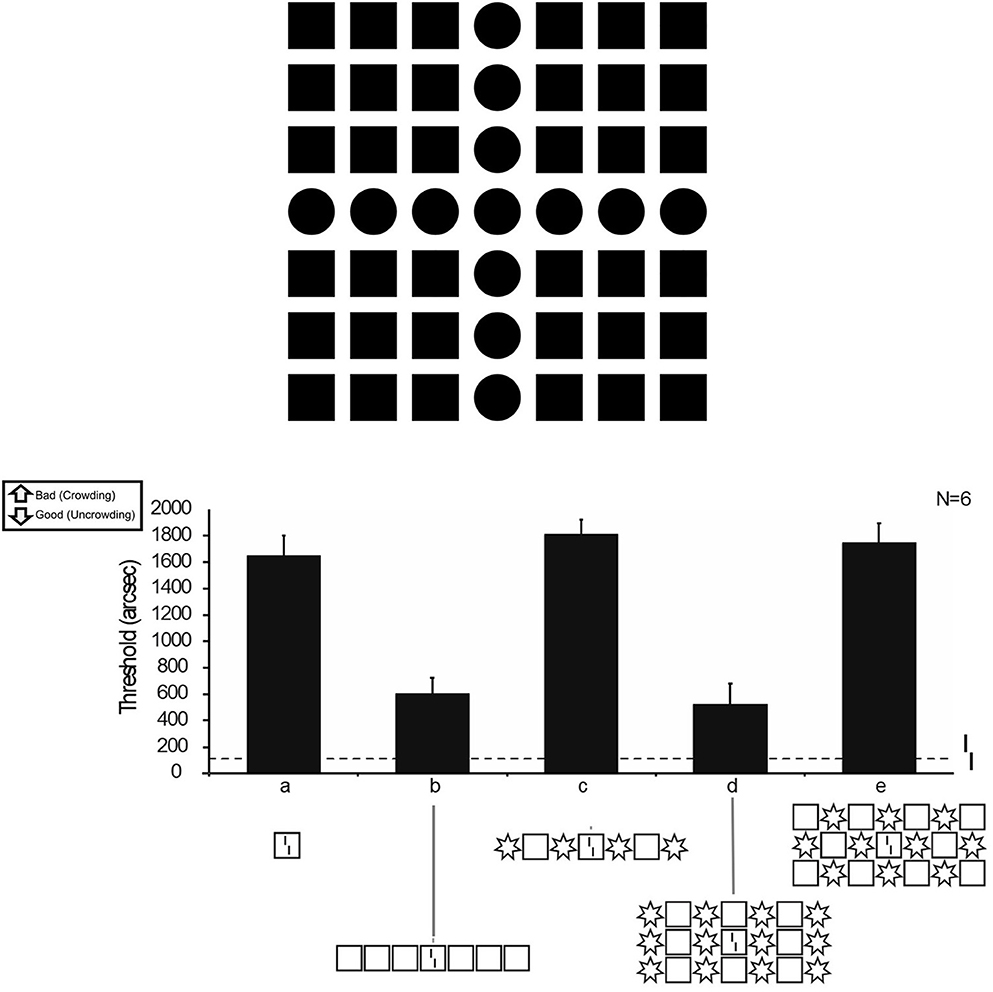
Figure 1. (Upper panel) We see a cross even though there are only squares and disks. (Lower panel) Classic models of vision fail to explain crowding in complex configurations. The x-axis shows different configurations. The y-axis shows the corresponding vernier threshold. A high value represents poor performance, a lower value represents good performance. The dashed line shows the performance of the vernier alone condition. When one square (a) is presented surrounding the vernier, performance deteriorates, i.e., crowding. When presenting 7 squares (b), performance improves drastically, i.e., uncrowding. When presenting squares and stars with different configurations (c–e), performances differ depending on the configuration. Note that the local configuration of all the conditions (a–e) is identical, i.e., a square surrounding a vernier. With permission, figure modified from Manassi et al. (2016).
Gestalt theory disappeared as quickly as it arose and was replaced by the physiological approach subscribing (implicitly) to indirect realism. This approach has dominated vision science for almost a century, aiming for a causal theory of perception. Physiology systematically studies how the presentation of an object affects neural responses, starting with phototransduction at the retina and continuing up the hierarchy of brain processing. One crucial aspect is that perception is genuinely ill-posed. The light that arrives at the retina (luminance) is always the product of the light shining on an object (illuminance) and the material properties of that object (reflectance). Hence, there are infinitely many possibilities for how a given luminance may have occurred (e.g., white light on a red tomato leads to the same luminance as red light shining on a white tomato). To perceive the true object properties, one needs to reconstruct the object. Because solving the ill-posed problems is mathematically not fully possible, this reconstruction may fail. Illusions and alike are rather evidences for the physiological approach than challenges.
Whereas the physiological approach has made great progress in explaining the first steps of vision (retina, LGN, V1), the processing of subsequent stages has turned out to be less straightforward. One reason may simply be that perception is not as one-to-one as assumed, i.e., perception is not only indirect, but percepts do not systematically match the objects of the external world, as in the case of the cross of Figure 1.
Predictions of the standard physiological model of perception fail, also in many classic psychophysical paradigms. Crowding is one example. In crowding, perception of a target strongly deteriorates when presented within clutter (Figure 1, lower panel, a). Crowding is the usual situation in daily life since elements are rarely presented alone (Weymouth, 1958; Bouma and Andriessen, 1968; Bouma, 1970, 1973; Strasburger et al., 1991; Levi, 2008). Crowding is traditionally explained by feature pooling or averaging (e.g., Parkes et al., 2001; Solomon et al., 2004; Pelli, 2008; Greenwood et al., 2009, 2017; Dakin et al., 2010; Rosenholtz et al., 2012). Whereas, pooling can well explain results with simple stimuli, it fails as soon as stimulus configurations become slightly more complex (Figure 1, lower panel).
For example, vernier offset discrimination drops drastically when the vernier is presented within a square well in line with pooling and other low-level physiological explanations. However, adding more squares improves performance almost to the level of the no crowding condition (Figure 1, lower panel; Manassi et al., 2012, 2013, 2015, 2016; Herzog and Manassi, 2015; Herzog et al., 2015, 2016; Choung et al., 2021). We argued that the Vernier information is recovered because the target and the squares are in different perceptual groups (Figure 1, lower panel, b and d), which is not the case when only one square is presented (Figure 1, lower panel, a). We call this release from crowding “uncrowding,” even when performance in the uncrowding condition does not reach the performance level in the no crowding, baseline condition. These results are not restricted to crowding and vernier stimuli but occur all over the place in vision as well as in audition and haptics (e.g., peripheral vision: Bouma and Andriessen, 1968; Toet and Levi, 1992; Chung et al., 2001; foveal vision: Flom et al., 1963; Danilova and Bondarko, 2007; Lev et al., 2014; Coates et al., 2018; verniers: Malania et al., 2007; Saarela and Herzog, 2008, 2009; Sayim et al., 2008, 2010, 2011, 2014; Saarela et al., 2009, 2010; Gabors: Chicherov et al., 2014; Chicherov and Herzog, 2015; Jastrzȩbowska et al., 2021; audition: Oberfeld and Stahn, 2012; touch: Overvliet and Sayim, 2016). Thus, we are back to square one, i.e., the Gestalt times.
Here, we asked whether Gestalt principles can do better than explanations from the physiological approach. Gestalt principles have been studied over centuries and are considered fundamental of perceptual organization (von Ehrenfels, 1890; Wertheimer, 1912, 1922, 1923; Köhler, 1920; Koffka, 1935; Metzger, 1936; Metzger et al., 2006; reviews: Todorović, 2007; Wagemans et al., 2012a,b). Gestalt principles include symmetry, proximity, similarity, common fate, good continuation, closure, parallelism, synchrony, common region, element, and uniform connectedness. In this study, we applied four such principles that pertain to the structure of the configuration (rather than the isolated principle), namely, symmetry, good continuation, closure, and repetition. Note that while the classic displays used by the earlier Gestaltists depicted specific instances of these principles, modern studies have offered more examples that are easier to apply in complex configurations such as the ones employed in our study (symmetry: Sasaki et al., 2005; good continuation: e.g., Lezama et al., 2016; closure: e.g., Han et al., 1999; repetition: Treder and van der Helm, 2007; van der Helm, 2014). Specifically, our displays depicted configurations of stars and squares, assuming grouping by shape similarity occurs in all of them. Our grouping manipulation, then, concerned other principles that were imposed on the similarity grouping (see Figure 1). The rationale of the following experiments is that uncrowding should occur when the central square is grouped with other squares. Consequently, we hypothesized that Gestalt principles could explain (un)crowding, as crowding would affect performance in a similar manner in configurations that employed the same Gestalt principle. Moreover, we tried to further categorize our configurations as more nuanced instances (e.g., symmetry with 1 or 2 axes), to potentially uncover more subtle effects of these principles on (un)crowding. However, this was not what we found. Our results only showed symmetry to have a minor advantage in our study, with no other systematic difference in performance.
Thirty-one participants took part in the experiments. Eleven out of the 31 participants were excluded after a calibration session because they did not show strong crowding in the basic one-square condition, which is a prerequisite for a release of crowding (see Calibration session). Hence, we retained the data of 20 participants (mean age: 21.6 ± 1.6, 10 females, all right-handed, 7 with left eye dominance). All participants had normal or corrected to normal visual acuity in the Freiburg Visual Acuity Test, as indicated by a binocular score greater than 1.0 (Bach, 1996). Observers gave written consent before the experiments. All experiments were conducted in accordance with the Declaration of Helsinki (World Medical Association, 2013), except for preregistration, and were approved by the local ethics committee (Beritashvili Centre of Experimental Biomedicine, Georgia).
Stimuli were displayed on a gamma-calibrated 24-inch ASUS VG248QE LCD monitor (1,920 x 1,080 px, 120 Hz). The room was dimly illuminated (~0.5 lux). The viewing distance was 75 cm, and the participant's chin and forehead were positioned on a chin rest. Responses were collected using wireless hand-held push buttons. In the Vernier discrimination task, when no response was registered within 3 s, the trial was repeated randomly within the same block. A feedback tone was given for incorrect responses (high tone, 600 Hz) and omissions (low tone, 300 Hz).
Three tasks (Figure 2) were carried out with 40 flanker configurations (Figure 3). The three tasks were a vernier discrimination task (VCrowd), a vernier standout ranking task (VRank), and a rating task (Rate). The VRank and the Rate tasks were tested twice. The experiment was conducted on 5 days within 2 weeks (day 1–3: calibration and VCrowd, day 4: VRank twice and Rate, day 5: Rate). Before the first experimental session, all participants went through a calibration session to adjust flanker-target distance individually.
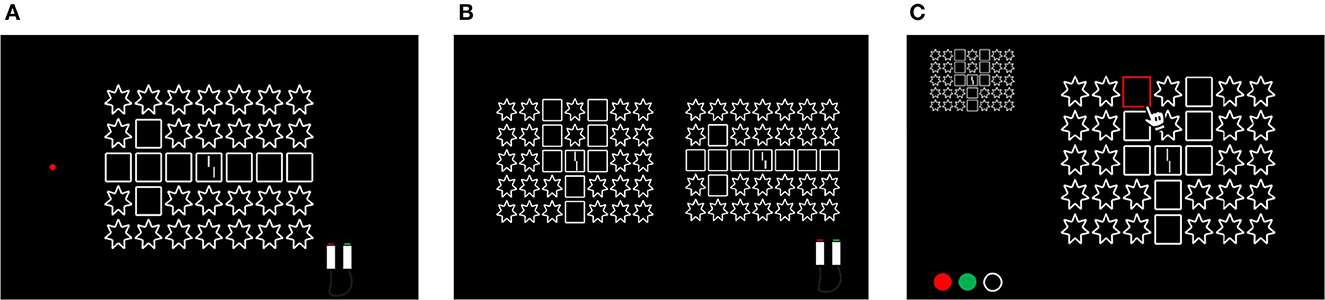
Figure 2. (A) VCrowd task: The task was to discriminate whether the lower Vernier bar is offset to the left or right compared to the upper bar. (B) VRank task: Vernier standout ranking task. Two stimuli were presented side-by-side with the same size. The task was to choose in which flanker configuration the Vernier target stands out more strongly. All possible pairwise comparisons, i.e., 40 x 39/2 pairs of configurations, were tested. (C) Rating task: Participants were asked to rate how much the vernier stands out (i) from the other elements, (ii) how much the center group stands out from the other elements, and (iii) how strongly the elements of the center group are grouped with each other.

Figure 3. Flanker configurations. Red lines indicate the tested Gestalt principle; these lines are for illustration purposes only and were not presented during the experiment; Symmetry- a1-b6 [a1-a6- symmetry with 2 axis (Symm2); b1-b6 – symmetry with 1 axis (Symm1)]; good continuation- c1-d4 [c1-c4 – stretched (contStret); d1-d4-curled (ContCurl)]; Closure- e1-f5 [e1-e3-closure only (Close); f1-f5-closure with symmetry (CloseSymm)]; repetition- g1-h4 [g1-g4- repetition on cardinal axes (Repeat); h1-h4-repetition diagonal (RepeatDia)]; random- i1-i4 [i1andi2-random spaced (RandSpace) and random condense (i3&i4: RandCond) group]. Note that the RandCond configurations could also be considered as grouping by proximity, which is another grouping principle. Most of the configurations were composed of 9 squares and 26 stars (*indicates three configurations, which had 10 squares and 25 stars, b6, d3, and h2). Therefore, low-level features, such as pixel values, were roughly the same across configurations.
Stimuli were white (100 cd/m2), presented on a black background with a luminance below 0.3 cd/m2. Participants were asked to fixate on a red fixation dot (diameter = 8 arcmin, 20 cd/m2). Each stimulus was composed of a Vernier target, flanking squares and stars. The Vernier target was composed of two 40 arcmin long, 1.8 arcmin wide vertical bars. The gap between the two bars was 4 arcmin. Left/right offsets were balanced within a block. The Vernier target was surrounded by 35 flanker elements, which were mostly composed of 9 squares and 26 stars, except for 3 configurations which contained 10 squares and 25 stars. Squares and stars were positioned in 5 rows and 7 columns, as in Figure 3, and there were 40 different configurations. Each flanker configuration followed one of four Gestalt principles; symmetry (in 1 or 2 axes), good continuation (stretched or curled), closure (only or with symmetry), repetition (on cardinal axis or on diagonal axis), or were chosen to not include any obvious grouping principle. The central flanker was always a square, and the Vernier target was always located within this square. Except for the VCrowd task, each square was composed of four 120 arcmin long lines, and each star was composed of seven 48 arcmin long lines. The center-to-center distance between flankers was 150 arcmin. For the VCrowd task, the square and star sizes and the gap between flankers were individually adjusted in a calibration session (details in Calibration session). The side length of the squares was 84–114 arcmin, and the gap between squares was 21–28.5 arcmin depending on observers.
Each configuration was presented at the center of the screen, and the fixation dot was presented at an eccentricity of 9 degrees to the left. Hence, stimuli were presented at 9 degrees in the visual periphery. The chin-rest was placed 75 cm from the fixation dot. Psychophysics Toolbox was used to present the stimuli (Brainard, 1997; Pelli and Vision, 1997; Kleiner et al., 2007). To avoid visual aftereffects, a small spatial jitter was applied to the entire stimulus within a 3 pixels range from trial to trial.
To avoid floor and ceiling effects, each participant went through a calibration session before the main experiment. The calibration session was composed of two conditions. First, 1 or 2 blocks with the Vernier alone condition (160 trial per block) were tested to familiarize observers with the Vernier task (only participants with thresholds larger than 200 arcsec were tested in the 2nd block). Second, up to 7 blocks with a vernier surrounded by one square (80 trial/block) were tested to find the spatial parameters that produce strong crowding and, thus, allow for a release from crowding, i.e., uncrowding. We reduced the flanker size and the flanker-to-flanker distance gradually, until the threshold of the one-square condition reached at least 6 times the threshold of the Vernier alone condition. We excluded participants whose thresholds were still below this criterion even after reducing the square size to 70%. In total, 11 of 31 participants were excluded. For the remaining 20 participants, the mean threshold for the vernier alone condition was 142.30 ± 45.48 and 935.84 ± 188.53 for the one square condition. Note that crowding effects existed in the 11 excluded participants as well, but not to the extent we requested, which is at least 6 times the threshold in the one-square condition. We had this high threshold to make sure that a missing release of crowding is a clear indication of a null result.
The vernier discrimination task (Figure 2A), the stimulus (Vernier + flankers) was presented for 150 ms in the center of the screen, and participants were asked to discriminate whether the lower bar was offset either to the left or right compared to the upper bar, by pressing the left or right button, respectively. Each configuration was tested in a block of 100 trials. The vernier target without flankers was presented in the first trial of each block to reduce target-location uncertainty. We used the PEST (Parameter Estimation by Sequential Testing) stair-case procedure (Taylor and Creelman, 1967) to determine testing levels (offsets). The PEST procedure changes the test levels depending on the recent history step-wise. Test levels are only changed when the hit rate is above or below the threshold criterion of 75%. The procedure ended after 100 trials, and a threshold (Thresh) was derived from post-hoc fitting of a psychometric function to the data (details in Data analysis).
The Vernier standout ranking task (Figure 2B), two flanker configurations were presented simultaneously side-by-side, and participants were asked to choose from which flanker configuration the Vernier target stands out more strongly, i.e., a “win” (Figure 2B). The stimulus was presented with unlimited time. Overall, 718 (20*39) pairs of configurations were tested twice. The responses from the two identical comparisons were averaged. We ranked the order of the configurations from 1 to 40, by counting the number of “wins” in each pair of comparisons. When two or more configurations had the same number of “wins,” the winner is the winner in the direct comparison between the configurations. In addition to the individual Rank order per participant, a global rank (GlobRank) was obtained by using a similar process, by pooling the number of “wins” from the 20 participants' responses.
The rating tasks (Figure 2C). As in the VCrowd task, the stimulus was presented for 150 ms. Four questions were asked. First, participants rated how much the vernier target stands out from the rest of the configuration on a scale from 1 to 5 (VStandRate). Second, the stimulus was presented with unlimited time, and the participants were asked to assign each flanker element to different sub-groups. Then, the observers were asked to rate on a scale from 1 to 5, first, how much each sub-group stands out from the other groups (GStandRate), and second, how strongly the elements in each group grouped together (GGroupRate)?
Hence, we determined five measures: crowding threshold (Thresh; from the VCrowd task), global vernier standout ranking (GlobRank; from the VRank task), vernier standout rating (VStandRate; from the Rate task), group standout rating (GStandRate; from the Rate task), and grouping strength (GGroupRate from Rate task).
We fitted a cumulative Gaussian function to the data and determined the vernier offset threshold (Thresh), for which 75% of correct responses were reached. High thresholds indicate inferior performance, and low thresholds indicate good performance. The Psignifit 2.5 toolbox (Fründ et al., 2011) was used for psychometric function fitting. We computed threshold elevation for each condition and each observer, i.e., we divided the threshold in each condition by the threshold in the Vernier alone condition. Data were log-transformed to bring the data closer to normality. No obvious violation was detected by visual inspection.
Using R (R Core Team, 2019) and lme4 package (Bates et al., 2015), we computed linear mixed-effects models (LMM) to account for random variations due to individual differences. The fixed and random effects are specified for each experiment. The model significance (p-value) was obtained through likelihood ratio tests (χ2) by comparing nested models. For each fitted model, using MuMIn package (Barton, 2020), we computed the effect size (r2), i.e. the explained variance, when including (conditional r) and excluding (marginal r) the random effects (Nakagawa and Schielzeth, 2013; Johnson, 2014; Nakagawa et al., 2017). Posthoc multiple comparisons of means were computed with multcomp package (Hothorn et al., 2008).
Intra-rater reliability for the Rate task was carried out by using ordinal alpha (Zumbo et al., 2007) to account for ordinality of the measures (VStandRate, GStandRate, and GGroupRate). The psych package was used (Revelle, 2021).
Correlations between the measures were computed using Spearman rank correlation (Spearman, 1904), as four measures among five were in ordinal scale. Moreover, to account for the individual variances and potential violation of normality of the data, the significance of the correlations was obtained through randomization tests (details in Supplementary Method Section; Mohr and Marcon, 2005; Bakdash and Marusich, 2017).
We computed ordinal alpha (Zumbo et al., 2007; Gadermann et al., 2012) to test intra-rater reliability for the three measures (VStandRate, GStandRate, GGroupRate) of the Rate Task and found good reliability for most configurations having alphas larger than 0.7 (Cohen, 1988; McHugh, 2012): VStandRate: α∈[0.730, 0.992]; GStandRate: α∈[0.708, 1]; GGroupRate: α∈[0.595, 1], except for two configurations for the GGroupRate. For this reason, we used the averaged rating values in the subsequent analyses.
Here, we tested to what extent perceptual grouping can be explained by the Gestalt principles used here, and whether certain principles contribute more strongly than others. For example, flanker configurations with 2 symmetry axes should lead to good performance, i.e., less crowding, whereas we expected poor performance, i.e., strong crowding, for irregular configurations. We tested 40 configurations, which followed five different Gestalt principles.
Performance was hardly explained by Gestalt principles. Figure 4 shows the crowding strength (Thresh) for each configuration. Importantly, crowding levels related to the same Gestalt principle were not consistent. For example, four configurations with two symmetry axes showed uncrowding (red bars' values smaller than that of the gray dotted line; Figure 4 a1, a2, a4, and a5), whereas the other two showed strong crowding (red bars' values larger than that of the gray dotted line; Figure 4 a3 and a6). We used a linear mixed effect model (LMM) with the fixed effect of Gestalt principles and random intercepts of configurations and participants. The fixed effect was significant (likelihood ratio test between models including and excluding the fixed effect: χ2(4) = 14.352, p < 0.01). However, post-hoc Tukey's HSD comparison showed that no Gestalt principle explains the data better than other ones in general, except that configurations with symmetry had better performance than that with closure (details in Supplementary Table 2). In addition, we wondered whether the performances between the configurations sharing the same Gestalt principle correlate with each other. As shown in Supplementary Figure 3, performances within the same Gestalt principles (Supplementary Figure 3, inside red dotted lines) did not have higher correlations than those from different principles (Supplementary Figure 3, outside red dotted lines).
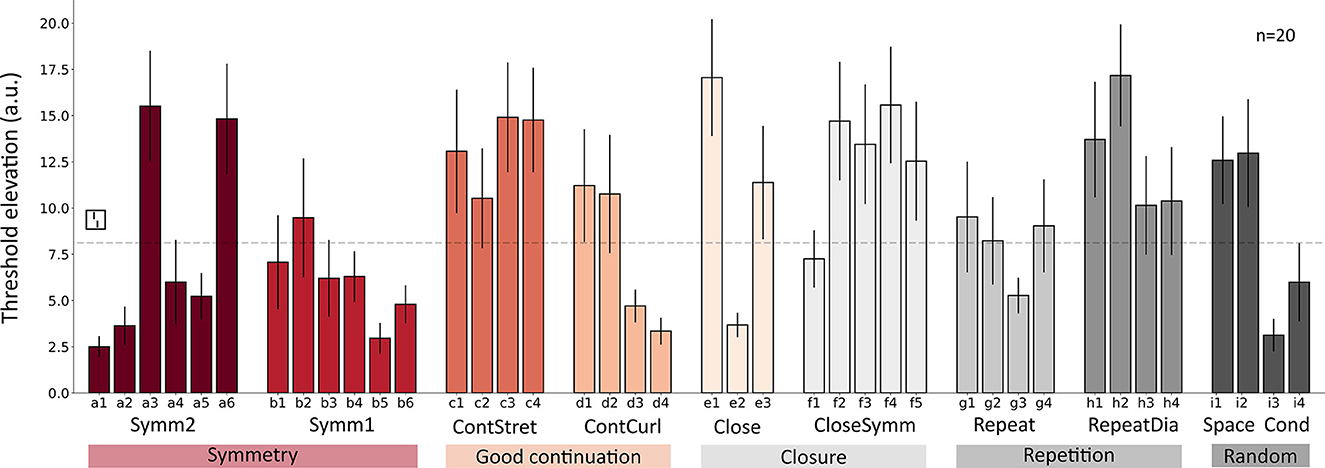
Figure 4. Performance for each configuration. Each color represents a different Gestalt principle. Configurations are presented in the same order as in Figure 3. The y-axis shows threshold elevation compared to the vernier only condition. Mean ± SEM. The hatched line shows performance in the one-square reference condition.
Thus, why do Gestalt principles not explain the performance in the VCrowd task? Two options come to mind: (1) Gestalt principles are not the major driver of grouping or (2) (un)crowding is not mediated by grouping.
First, we used LMMs to test if the Gestalt principles are a predictor for the grouping and segmentation measures (Rank, VStandRate, GStandRate, GGroupRate). An LMM with a fixed effect of Gestalt principles and random intercepts of configurations and participants was computed for each measure. Most of the models showed a significant fixed effect, except for VStandRate (GlobRank: χ2(4) = 19.969, pBonf < 0.01; VStandRate: χ2(4) = 7.406, pBonf = 0.464; GStandRate: χ2(4) = 18.662, pBonf < 0.001; GGroupRate: χ2(4) = 14.632, pBonf < 0.05; detailed estimates in Supplementary Table 4). However, similar to the previous experiment, no single Gestalt principle had high rates or low rates in general, except the symmetry configurations showed better ratings than other principles (post-hoc Tukey's HSD test; GlobRank: symmetry vs. closure p < 0.001; symmetry vs. contiunous p < 0.05; symmetry v.s. repetition p < 0.05; GStandRate: symmetry vs. closure p < 0.01, symmetry vs. random p < 0.001; GGropRate: symmetry vs. closure p < 0.05, symmetry v.s. random p < 0.01; details in Supplementary Table 5).
Next, we tested correlations between the performance measure (Thresh) and the grouping and segmentation measures. As expected, all the measures had significant correlations, even after Bonferroni correction (details in Table 1). We computed Spearman's Rank correlation to account for the ordinal scales; significance was obtained by randomization tests (details in Supplementary material). Figure 5 shows the average of absolute Spearman r coefficients. The full results for each configuration and the distributions of the randomization test are presented in Supplementary Figure 1. The correlation between (un)crowding (Thresh) and Vernier standout (GlobRank) measures was high; two Vernier standout measures had a strong correlation (GlobRank-VStandRate).
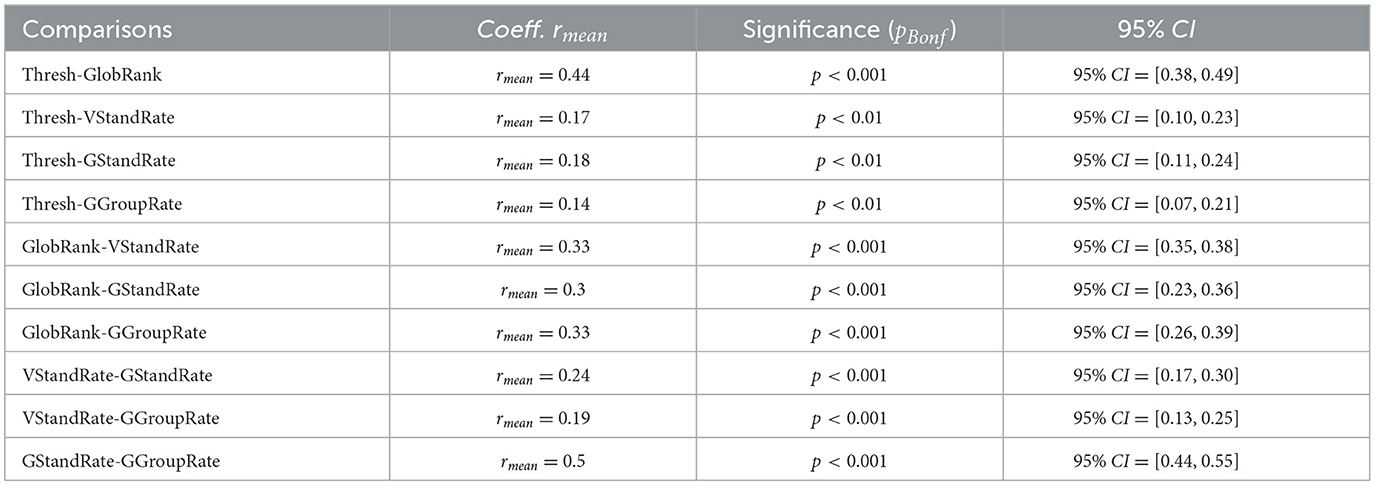
Table 1. Absolute values of correlation coefficients, significance, and 95% confidence interval (CI).
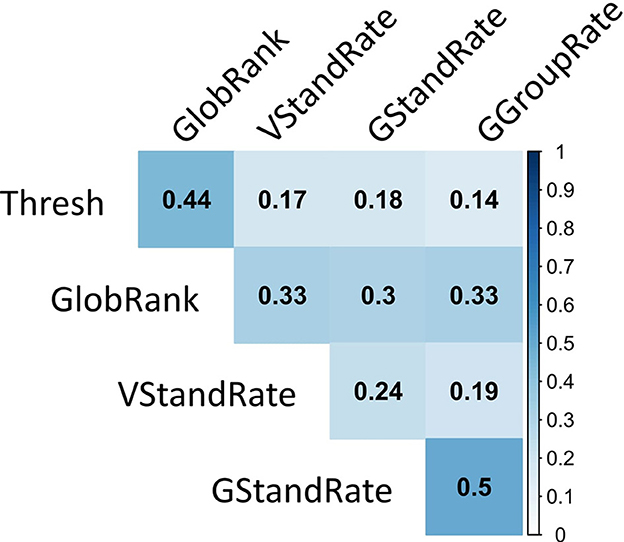
Figure 5. Correlations among measures. The color code represents the mean Spearman's absolute rank coefficient |r|. All correlations were significant after Bonferroni correction.
Altogether, these results indicate that subjective ratings of grouping and segmentation are indeed highly correlated with the (un)crowding performance. However, grouping processes could not be explained by classic Gestalt principles.
The correlation between the subjective ratings and the offset discrimination task suggests that higher-level grouping is crucial. To further support this claim, we show the number of squares neighboring the central square, a high-level feature, shows higher correlations with performance than the number of white pixels, a corresponding low-level feature.
Figure 6 shows the correlations between the mean performances across participants and model predictions. Correlations between threshold elevations and the number of connected squares, discounted by distance, show a strong correlation (rsquare (38) = −0.60, CI95% = [−0.75, −0.33], p < 0.001). However, flanker pixel values, regardless of the local crowding window restriction, show poor correlation (rpixel (38) = −0.03, CI95% = [−0.35, 0.29], p = 0.87).
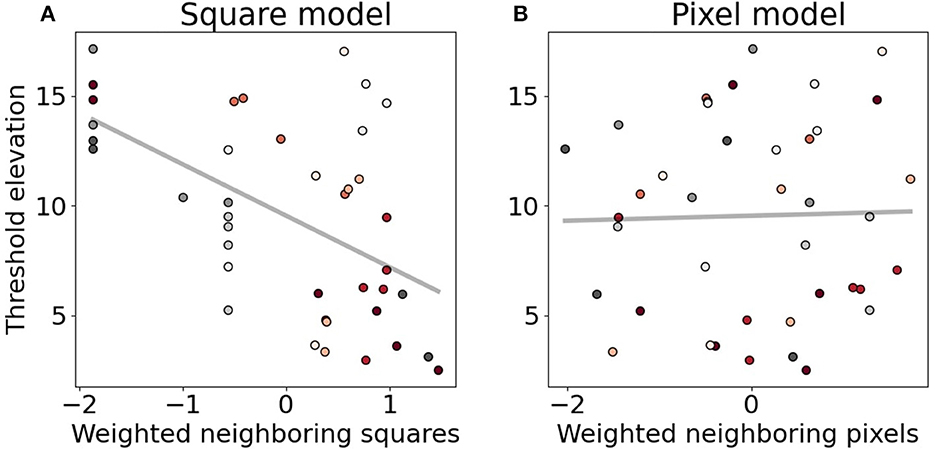
Figure 6. Correlations between model estimates and mean crowding level of each configuration for (A) the square model (higher-level feature) and (B) the pixel model (lower-level feature). The y-axis shows the mean threshold elevation, and the x-axis is the model estimates for each model. Dots represent configurations, the colors indicate Gestalt principles, corresponding to Figure 4.
We analyzed the predictability of the two models using two methods. First, we used LMMs, which had each of the model estimates as the fixed effects. We found that the number of connected squares has a significant effect on thresholds, unlike the number of pixels. For each LMM, the fixed effect was model estimates for each configuration, and each participant was considered a random intercept. There were significant fixed effects for the number of directly connected squares based models, but not for the pixel value based models (details in Supplementary Table 1). Although the effects could only explain 6.0 % of the variances (, square model; for the other models, see Supplementary Table 1), it was still better than the pixel estimators (0.0%, pixel model). Note that explained variances, including the random intercept across all the models, were comparable, 40%−45% ().
Next, we tested predictability with the leave-one-out cross-validation (LOOCV) method. Here, we validated the explained variance of each participant's performance from other participants' performances. We fitted the model estimates of threshold elevation of 19 participants. We obtained an r2-value (explained variance) by using data that was not included in model estimation. We repeated the computation 20 times (for each participant), then we averaged the r-squared values from 20 iterations to get the final explained variance of each model. As a result, similar to LMMs' estimates, the number of directed squares discounted by their distances predicted the crowding level partially ( = 0.164), whereas pixel values did not ( = 0.015).
These results indicate that none of the models can truly explain crowding and uncrowding. There were large performance variances across participants and across configurations. However, the number of directly connected squares and the remaining flankers' distances partly captured uncrowding. For full analyses of variations of these two models, see Supplementary Models Section.
(Un)crowding is ubiquitous. Still, there is no consensus about the underlying mechanisms. Classic explanations, such as pooling, fail to explain (un)crowding. As shown here and previously, the stimulus configuration across more or less the entire visual field matters. For example, the number of squares and stars is identical in almost all configurations in the experiments above, but performance varies strongly even though all configurations contain the central square. In addition, the size of all configurations is 17.5 deg in the horizontal and 12.5 deg arcmin in the vertical direction, spanning a large part of the visual field. Thus, the specific configuration across a large part of the visual field matters.
We proposed that the stimulus configuration is parsed into different groups and crowding occurs, if at all, only within a group (Herzog et al., 2016). Hence, grouping is key in crowding. Here, we asked whether specific Gestalt principles, aimed to explain grouping, can explain crowding and uncrowding (in this respect, crowding could have been an objective test for Gestalt processing replacing the subjective reports usually used in the field). However, we found no evidence that the examined Gestalt principles can explain (un)crowding. Our results showed some advantages for symmetry, but this result should be interpreted with caution, especially considering that configurations that combined symmetry with another principle did not necessarily show such an advantage, as we discuss below. The rationale of our experiments is that when the central square is part of a group according to Gestalt principles, it should ungroup from the vernier and, hence, performance should be good. However, for each category of configurations, we found that some configurations showed better performance compared to the one-central-square condition, indicating uncrowding, while other conditions showed clear crowding, often even stronger than in the one-square condition. Performances within one category correlated as strongly as across categories (Figure 4 and Supplementary Figure 3). Performance for configurations with more than two Gestalt principles was, overall, not better than for those with one principle (e.g., configurations with CloseSymm mostly lead to strong crowding, see Figures 3, 4, CloseSymm). Often, the combination of principles (e.g., Figure 4, ContStret and CloseSymm) rather led to an increase in crowding than a release, contrary to the spirit of previous findings that showed better grouping when two principles are combined (Hochberg and Hardy, 1960; Ben-Av and Sagi, 1995; Kubovy and Wagemans, 1995; Quinlan and Wilton, 1998; Claessens and Wagemans, 2005, 2008; Kubovy and van den Berg, 2008; Oyama and Miyano, 2008; Luna and Montoro, 2011; Luna et al., 2016; Rashal et al., 2017a,b; Rashal and Kimchi, 2022). Still, crowding level (Thresh) and subjective grouping ratings (GlobRank, VStandRate, GStandRate, and GGroupRate) correlated significantly (Figure 5). Correlations were highest with the Vernier standout (VStand) ratings, which supports our claim that uncrowding happens when the vernier stands out from the flankers.
Finally, model simulations showed that grouping among high-level features had a stronger correlation with crowding level (Thresh) than low-level features (Figure 6). We did not simulate the physiological approaches' model performances as exploring physiological models was out of the scope of the current work. Additionally, numerous publications have attempted to explain (un)crowding performance under physiological frameworks (Manassi et al., 2016; Doerig et al., 2020a,b; Bornet et al., 2021a,b; Choung et al., 2021). For instance, Manassi et al. (2016), using the Fourier model, evaluated similar flanker configurations that consist of squares and stars and failed to explain (un)crowding. However, we admit that our configurations might have affected physiological-based models, such as in Waugh et al. (1993) and Mussap and Levi (1997), which used Fourier analysis and showed that Vernier acuity changes depending on the orientations of masks.
What are the implications of our results? There are several aspects. First, the physiological approach may not be tenable in its current form but is correct in principle. Maybe we need to give up the feedforward aspects and allow recurrent, complex interactions. For example, Doerig et al. (2019) have shown that one-stage, feedforward models cannot explain uncrowding since target information is irretrievably lost during feedforward processing. This holds true for local pooling models (e.g., Parkes et al., 2001; Solomon et al., 2004; Pelli, 2008; Greenwood et al., 2009, 2017; Dakin et al., 2010; Rosenholtz et al., 2012), and models that can account for global configurations, such as a Fourier model (Waugh et al., 1993; Mussap and Levi, 1997; Manassi et al., 2016), epitomes model (for details see Jojic et al., 2003; Doerig et al., 2019), high dimensional feature pooling model (HD pooling; Rosenholtz et al., 2019; Bornet et al., 2021a; Choung et al., 2021), and deep networks (DNN; Doerig et al., 2020a). However, more complex models, employing recurrent processing, such as Capsule networks and the Laminart model, do not kill vernier-related information during feedforward and, therefore, can explain uncrowding results (Francis et al., 2017; Doerig et al., 2019, 2020b). In this models, indirect realism becomes even more indirect, including time-consuming, potentially idiosyncratic processing and the question arises whether these models adhere to spirit of the classic models.
Similar things can be said about the Gestalt approach. Indeed, the current Gestalt principles may be oversimplified. They work well for simple stimuli. However, future Gestalt cues may change the game (see for example, Todorović, 2011). For example, Gestalt principles may consider statistical principles, such as summary and ensemble statistics (Tiurina et al., 2022). In addition, it seems that our results do not argue against the Gestaltist's main credo: there is more in the mind than in the stimulus, and the whole is different from its parts. Perception is not one-to-one.
Maybe, these arguments are true. However, we think that the failures of both approaches show that there are deeper issues, related to the philosophical foundations of perception. As said, the Gestalt approach is rather silent about the external world because its main source of scientific reasoning comes from introspection, from how stimulus configurations look to us, and not from speculations about an external world, which is a latent variable because realism is indirect and, hence, we have no perceptual ground truth about it (Figure 1, upper panel). For this reason, Gestalt theory says very little about the world. Gestalt theory focuses on perception as a truly subjective science. However, detaching perception from an objective, mind-independent world opens up the possibilty that the Gestalt rules may be totally idiosyncratic. Hence, Gestalt theory loses its relationship to ground truth. This comes with quite some problems, in particular for an objective science of perception. From an evolutionary point of view, we may ask: why should there be more in the mind than what is in the world? Why should different people follow identical Gestalt principles if no constraints make some of the principles better than others?
Whereas the Gestalt approach is rather vague about its ontological commitments, the physiological approach clearly subscribes to indirect realism, includingthe ontological commitment to ordinary objects and a one-to-one mapping between the objects and their corresponding representations. As mentioned, mismatches are just unavoidable errors in the process because of the ill-posed problems of vision. However, the strong ontological commitment to the existence of everyday objects is not easily tenable. of course, one problem is that we can never verify this assumption since perception is indirect, i.e., we have no direct access to the world. However, we propose there is another main problem, namely, that the external world is much richer, i.e., there are much more fundamental entities (the physical particles), than mental representations. One can mathematically show that, in this situation, mind-independent ordinary objects cannot occur (Herzog and Doerig, 2021; Herzog, 2022). Apples are not the starting point of perception, they are the outcomes of perception. Perception is a mapping from fundamental physics directly to perception without an intermediate ontology of apples and alike. Hence, there is ground truth, as in the physiological approach, but the truth comes from physics (i.e., particles) as our primary source of knowledge, not by sensory or perceptual evidence of ordinary objects and a like. There is no accurate reconstruction of ordinary objects because there are no ordinary objects. In our view, the squares and disks are as mind-dependent as the cross in Figure 1.
In summary, as in the physiological approach, we propose that there is a mind-independent world of particles. Perception is a mapping from these particles into the world of mental representations, which are truly subjective in the spirit of the Gestaltists. For this reason, introspection is the tool of choice since there is no objectivity on the ordinary object level. Gestalt perception is realized by the neural wiring of each observer and hence may be fully idiosyncratic, i.e., different people do not employ Gestalt principles in an identical manner. This is evident by manifest differences, as in the case of the #theDress. These differences are not unavoidable errors of a reconstruction process of ordinary objects but the unavoidable consequence of the truly subjective nature of vision, i.e., Gestalt vision. We are now ready for a happy marriage of both perspectives on perception.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
The studies involving human participants were reviewed and approved by Beritashvili Centre of Experimental Biomedicine, Georgia. The participants provided their written informed consent to participate in this study.
OHC, ER, and MHH designed the experiment, interpreted the analyzed data, and wrote the initial version of the manuscript. MK collected the data. OHC and MK analyzed data. OHC designed and built the mathematical model. All authors contributed to the manuscript revision, read, and approved the submitted version.
OHC, MK, and MHH were supported by the Swiss National Science Foundation (SNF) 320030_176153 Basics of visual processing: from elements to figures. ER was supported by the European Union's Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement no. 708007.
We thank Greg Francis for the valuable discussions.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2023.1154957/full#supplementary-material
Bach, M. (1996). The freiburg visual acuity test-automatic measurement of visual acuity. Optom. Vis. Sci. 73, 49–53.
Bakdash, J. Z., and Marusich, L. R. (2017). Repeated measures correlation. Front. Psychol. 8, 456. doi: 10.3389/fpsyg.2017.00456
Barton, K. (2020). MuMIn: Multi-Model Inference. Available online at: https://CRAN.R-project.org/package=MuMIn (accessed September 1, 2023).
Bates, D., Machler, M., Bolker, B., and Walker, S. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Software 67, 1–48. doi: 10.18637/jss.v067.i01
Ben-Av, M. B., and Sagi, D. (1995). Perceptual grouping by similarity and proximity: experimental results can be predicted by intensity autocorrelations. Vision Res. 35, 853–866. doi: 10.1016/0042-6989(94)00173-J
Bornet, A., Choung, O-. H., Doerig, A., Whitney, D., Herzog, M. H., Manassi, M., et al. (2021a). Global and high-level effects in crowding cannot be predicted by either high-dimensional pooling or target cueing. J. Vision 21, 10–10. doi: 10.1167/jov.21.12.10
Bornet, A., Doerig, A., Herzog, M. H., Francis, G., and Van der Burg, E. (2021b). Shrinking Bouma's window: how to model crowding in dense displays. PLOS Comput. Biol. 17, e1009187. doi: 10.1371/journal.pcbi.1009187
Bouma, H. (1970). Interaction effects in parafoveal letter recognition. Nature 226, 177–178. doi: 10.1038/226177a0
Bouma, H. (1973). Visual interference in the parafoveal recognition of initial and final letters of words. Vision Res. 13, 767–782. doi: 10.1016/0042-6989(73)90041-2
Bouma, H., and Andriessen, J. J. (1968). Perceived orientation of isolated line segments. Vision Res. 8, 493–507. doi: 10.1016/0042-6989(68)90091-6
Brainard, D. H. (1997). The psychophysics toolbox. Spatial Vis. 10, 433–436. doi: 10.1163/156856897X00357
Chicherov, V., and Herzog, M. H. (2015). Targets but not flankers are suppressed in crowding as revealed by EEG frequency tagging. NeuroImage 119, 325–331. doi: 10.1016/j.neuroimage.2015.06.047
Chicherov, V., Plomp, G., and Herzog, M. H. (2014). Neural correlates of visual crowding. NeuroImage 93, 23–31. doi: 10.1016/j.neuroimage.2014.02.021
Choung, O-. H., Bornet, A., Doerig, A., and Herzog, M. H. (2021). Dissecting (un)crowding. J Vision Res. 21, 1–20. doi: 10.1167/jov.21.10.10
Chung, S. T. L., Levi, D. M., and Legge, G. E. (2001). Spatial-frequency and contrast properties of crowding. Vision Res. 41, 1833–1850. doi: 10.1016/S0042-6989(01)00071-2
Claessens, P. M. E., and Wagemans, J. (2005). Perceptual grouping in Gabor lattices: proximity and alignment. Percep. Psychophysics 67, 1446–1459. doi: 10.3758/BF03193649
Claessens, P. M. E., and Wagemans, J. (2008). A Bayesian framework for cue integration in multistable grouping: proximity, collinearity, and orientation priors in zigzag lattices. Vision Res. 8, 33–33. doi: 10.1167/8.7.33
Coates, D. R., Levi, D. M., Touch, P., and Sabesan, R. (2018). Foveal crowding resolved. Sci. Rep. 8, 1. doi: 10.1038/s41598-018-27480-4
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. Hillsdale, NJ: L. Erlbaum Associates.
Dakin, S. C., Cass, J., Greenwood, J. A., and Bex, P. J. (2010). Probabilistic, positional averaging predicts object-level crowding effects with letter-like stimuli. J. Vis. 10, 14–14. doi: 10.1167/10.10.14
Danilova, M. V., and Bondarko, V. M. (2007). Foveal contour interactions and crowding effects at the resolution limit of the visual system. J. Vis. 7, 25–25. doi: 10.1167/7.2.25
Doerig, A., Bornet, A., Choung, O-. H., and Herzog, M. H. (2020a). Crowding reveals fundamental differences in local vs. Global processing in humans and machines. Vision Res. 167, 39–45. doi: 10.1016/j.visres.2019.12.006
Doerig, A., Bornet, A., Rosenholtz, R., Francis, G., Clarke, A. M., Herzog, M. H., et al. (2019). Beyond Bouma's window: how to explain global aspects of crowding? PLOS Computat. Biol. 15, e1006580. doi: 10.1371/journal.pcbi.1006580
Doerig, A., Schmittwilken, L., Sayim, B., Manassi, M., and Herzog, M. H. (2020b). Capsule networks as recurrent models of grouping and segmentation. PLoS Comput. Biol. 16, e1008017. doi: 10.1371/journal.pcbi.1008017
Flom, M. C., Heath, G. G., and Takahashi, E. (1963). Contour interaction and visual resolution: contralateral effects. Science 142, 979–980. doi: 10.1126/science.142.3594.979
Francis, G., Manassi, M., and Herzog, M. H. (2017). Neural dynamics of grouping and segmentation explain properties of visual crowding. Psychol. Rev. 124, 483–504. doi: 10.1037/rev0000070
Fründ, I., Haenel, N. V., and Wichmann, F. A. (2011). Inference for psychometric functions in the presence of non-stationary behavior. J. Vis. 11, 16–16. doi: 10.1167/11.6.16
Gadermann, A. M., Guhn, M., and Zumbo, B. D. (2012). Estimating ordinal reliability for Likert-type and ordinal item response data: a conceptual, empirical, and practical guide. Practical Asses. Res. Evaluat. 17, 3. doi: 10.7275/n560-j767
Greenwood, J. A., Bex, P. J., and Dakin, S. C. (2009). Positional averaging explains crowding with letter-like stimuli. Proc. Nat. Acad. Sci. 106, 13130–13135. doi: 10.1073/pnas.0901352106
Greenwood, J. A., Szinte, M., Sayim, B., and Cavanagh, P. (2017). Variations in crowding, saccadic precision, and spatial localization reveal the shared topology of spatial vision. Proceed. Nat. Acad. Sci. 114, E3573–E3582. doi: 10.1073/pnas.1615504114
Han, S., Humphreys, G. W., and Chen, L. (1999). Parallel and competitive processes in hierarchical analysis: perceptual grouping and encoding of closure. J. Exp. Psychol. 25, 1411–1432. doi: 10.1037/0096-1523.25.5.1411
Herzog, M. H. (2022). The irreducibility of vision: gestalt, crowding and the fundamentals of vision. Vision 6, 35. doi: 10.3390/vision6020035
Herzog, M. H., and Doerig, A. (2021). Why our Best Theories of Perception and Physics Undermine Realism. Society for the Improvement of Psychological Science (SIPS) and the Center for Open Science (COS). doi: 10.31234/osf.io/r4sf9
Herzog, M. H., and Manassi, M. (2015). Uncorking the bottleneck of crowding: a fresh look at object recognition. Curr. Opin. Behav. Sci. 1, 86–93. doi: 10.1016/j.cobeha.2014.10.006
Herzog, M. H., Sayim, B., Chicherov, V., and Manassi, M. (2015). Crowding, grouping, and object recognition: a matter of appearance. J. Vis. 15, 5–5. doi: 10.1167/15.6.5
Herzog, M. H., Thunell, E., and Ögmen, H. (2016). Putting low-level vision into global context: Why vision cannot be reduced to basic circuits. Vision Res. 126, 9–18. doi: 10.1016/j.visres.2015.09.009
Hochberg, J., and Hardy, D. (1960). Brightness and proximity factors in grouping. Percept. Mot. Skills 10, 22. doi: 10.2466/PMS.10.1.22-22
Hothorn, T., Bretz, F., and Westfall, P. (2008). Simultaneous inference in general parametric models. Biomet. J. 50, 346–363. doi: 10.1002/bimj.200810425
Jastrzȩbowska, M. A., Chicherov, V., Draganski, B., and Herzog, M. H. (2021). Unraveling brain interactions in vision: the example of crowding. NeuroImage 240, 118390. doi: 10.1016/j.neuroimage.2021.118390
Johnson, P. C. (2014). Extension of Nakagawa and Schielzeth's R2GLMM to random slopes models. Methods Ecol. Evolut. 5, 944–946. doi: 10.1111/2041-210X.12225
Jojic, N., Frey, B. J., and Kannan, A. (2003). “Epitomic analysis of appearance and shape,” in Proceedings Ninth IEEE International Conference on Computer Vision (Nice: IEEE Computer Society), 34–34.
Kanizsa, G. (1979). Organization in Vision: Essays on Gestalt Perception. New York, NY: Praeger Publishers.
Koffka, K. (1935). Principles of gestalt psychology, international library of psychology. Philosophy Sci. Method 32, 8.
Köhler, W. (1920). Die physischen Gestalten in Ruhe und im stationaren Eine natur-philosophische Untersuchung [The physical Gestalten at rest and in steady state]. Wiesbaden: Vieweg+Teubner Verlag. doi: 10.1007/978-3-663-02204-6_6
Kubovy, M., and van den Berg, M. (2008). The whole is equal to the sum of its parts: a probabilistic model of grouping by proximity and similarity in regular patterns. Psychol. Rev. 115, 131–154. doi: 10.1037/0033-295X.115.1.131
Kubovy, M., and Wagemans, J. (1995). Grouping by proximity and multistability in dot lattices: a quantitative Gestalt theory. Psychol. Sci. 6, 225–234. doi: 10.1111/j.1467-9280.1995.tb00597.x
Lev, M., Yehezkel, O., and Polat, U. (2014). Uncovering foveal crowding? Scientific Rep. 4, 1. doi: 10.1038/srep04067
Levi, D. M. (2008). Crowding—An essential bottleneck for object recognition: a mini-review. Vision Res. 48(5), 635–654. 009. doi: 10.1016/j.visres.2007.12.009
Lezama, J., Randall, G., Morel, J-. M., and Grompone von Gioi, R. (2016). Good continuation in dot patterns: a quantitative approach based on local symmetry and non-accidentalness. Vision Res. 126, 183–191. doi: 10.1016/j.visres.2015.09.004
Luna, D., and Montoro, P. R. (2011). Interactions between intrinsic principles of similarity and proximity and extrinsic principle of common region in visual perception. Perception 40, 1467–1477. doi: 10.1068/p7086
Luna, D., Villalba-García, C., Montoro, P. R., and Hinojosa, J. A. (2016). Dominance dynamics of competition between intrinsic and extrinsic grouping cues. Acta Psychol. 170, 146–154. doi: 10.1016/j.actpsy.2016.07.001
Malania, M., Herzog, M. H., and Westheimer, G. (2007). Grouping of contextual elements that affect vernier thresholds. J. Vis. 7, 1–1. doi: 10.1167/7.2.1
Manassi, M., Hermens, F., Francis, G., and Herzog, M. H. (2015). Release of crowding by pattern completion. J. Vis. 15, 16–16. doi: 10.1167/15.8.16
Manassi, M., Lonchampt, S., Clarke, A., and Herzog, M. H. (2016). What crowding can tell us about object representations. J. Vis. 16, 35. doi: 10.1167/16.3.35
Manassi, M., Sayim, B., and Herzog, M. H. (2012). Grouping, pooling, and when bigger is better in visual crowding. J. Vis. 12, 13–13. doi: 10.1167/12.10.13
Manassi, M., Sayim, B., and Herzog, M. H. (2013). When crowding of crowding leads to uncrowding. J. Vis. 13, 10–10. doi: 10.1167/13.13.10
McHugh, M. L. (2012). Interrater reliability: the kappa statistic. Biochemia Medica 22, 276–282. doi: 10.11613/BM.2012.031
Metzger, W., Spillmann, L. T., Lehar, S. T., Stromeyer, M. T., and Wertheimer, M. T. (2006). Laws of seeing. Cambridge, MA: MIT Press. doi: 10.7551/mitpress/4148.001.0001
Mohr, D. L., and Marcon, R. A. (2005). Testing for a ‘within-subjects' association in repeated measures data. J. Nonparametric Stat. 17, 347–363. doi: 10.1080/10485250500038694
Mussap, A. J., and Levi, D. M. (1997). Vernier acuity with plaid masks: the role of oriented filters in vernier acuity. Vision Res. 37, 1325–1340. doi: 10.1016/S0042-6989(96)00192-7
Nakagawa, S., Johnson, P. C. D., and Schielzeth, H. (2017). The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. J. Royal Soc. Interface 14, 20170213. doi: 10.1098/rsif.2017.0213
Nakagawa, S., and Schielzeth, H. (2013). A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evolut. 4, 133–142. doi: 10.1111/j.2041-210x.2012.00261.x
Oberfeld, D., and Stahn, P. (2012). Sequential grouping modulates the effect of non-simultaneous masking on auditory intensity resolution. PLoS ONE 7, e48054. doi: 10.1371/journal.pone.0048054
Overvliet, K. E., and Sayim, B. (2016). Perceptual grouping determines haptic contextual modulation. Vision Res. 126, 52–58. doi: 10.1016/j.visres.2015.04.016
Oyama, T., and Miyano, H. (2008). Quantification of Gestalt laws and proposal of a perceptual state-space model. Gestalt Theory 30, 29.
Parkes, L., Lund, J., Angelucci, A., Solomon, J. A., and Morgan, M. (2001). Compulsory averaging of crowded orientation signals in human vision. Nature Neurosci. 4, 739–744. doi: 10.1038/89532
Pelli, D. G. (2008). Crowding: a cortical constraint on object recognition. Curr. Opin. Neurobiol. 18, 445–451. doi: 10.1016/j.conb.2008.09.008
Pelli, D. G., and Vision, S. (1997). The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat. Vis. 10.437–442. doi: 10.1163/156856897X00366
Quinlan, P. T., and Wilton, R. N. (1998). Grouping by proximity or similarity? Competition between the Gestalt principles in vision. Perception 27, 417–430. doi: 10.1068/p270417
R Core Team (2019). R: A Language and Environment for Statistical Computing (Vienna, Austria). R Foundation for Statistical Computing. Available online at: https://www.R-project.org/ (accessed September 1, 2023).
Rashal, E., and Kimchi, R. (2022). The competition between grouping cues can be resolved under inattention. Attent. Percept. Psychophysics 3, 1–12. doi: 10.3758/s13414-022-02576-2
Rashal, E., Yeshurun, Y., and Kimchi, R. (2017a). Attentional requirements in perceptual grouping depend on the processes involved in the organization. Attent. Percept. Psychophysics 79, 2073–2087. doi: 10.3758/s13414-017-1365-y
Rashal, E., Yeshurun, Y., and Kimchi, R. (2017b). The time course of the competition between grouping organizations. J. Exp. Psychol. Human Percep. Perform. 43, 608. doi: 10.1037/xhp0000334
Revelle, W. (2021). psych: Procedures for Psychological, Psychometric, and Personality Research (Evanston, Illinois). Northwestern University.
Rosenholtz, R., Huang, J., Raj, A., Balas, B. J., and Ilie, L. (2012). A summary statistic representation in peripheral vision explains visual search. J. Vis. 12, 14–14. doi: 10.1167/12.4.14
Rosenholtz, R., Yu, D., and Keshvari, S. (2019). Challenges to pooling models of crowding: implications for visual mechanisms. J. Vis. 19, 15–15. doi: 10.1167/jov.19.7.15
Saarela, T. P., and Herzog, M. H. (2008). Time-course and surround modulation of contrast masking in human vision. J. Vis. 8, 23–23. doi: 10.1167/8.3.23
Saarela, T. P., and Herzog, M. H. (2009). Size tuning and contextual modulation of backward contrast masking. J. Vis. 9, 21–21. doi: 10.1167/9.11.21
Saarela, T. P., Sayim, B., Westheimer, G., and Herzog, M. H. (2009). Global stimulus configuration modulates crowding. J. Vis. 9, 5–5. doi: 10.1167/9.2.5
Saarela, T. P., Westheimer, G., and Herzog, M. H. (2010). The effect of spacing regularity on visual crowding. J. Vis. 10.17–17. doi: 10.1167/10.10.17
Sasaki, Y., Vanduffel, W., Knutsen, T., Tyler, C., and Tootell, R. (2005). Symmetry activates extrastriate visual cortex in human and non-human primates. Proceed. National Acad. Sci. USA 102, 3159–3163. doi: 10.1073/pnas.0500319102
Sayim, B., Manassi, M., and Herzog, M. (2014). How color, regularity, and good Gestalt determine backward masking. J. Vision 14, 8. doi: 10.1167/14.7.8
Sayim, B., Westheimer, G., and Herzog, M. H. (2008). Contrast polarity, chromaticity, and stereoscopic depth modulate contextual interactions in vernier acuity. J. Vis. 8, 12–12. doi: 10.1167/8.8.12
Sayim, B., Westheimer, G., and Herzog, M. H. (2010). Gestalt factors modulate basic spatial vision. Psychol. Sci. 21, 641–644. doi: 10.1177/0956797610368811
Sayim, B., Westheimer, G., and Herzog, M. H. (2011). Quantifying target conspicuity in contextual modulation by visual search. J. Vis. 11, 6–6. doi: 10.1167/11.1.6
Solomon, J. A., Felisberti, F. M., and Morgan, M. J. (2004). Crowding and the tilt illusion: toward a unified account. J. Vis. 4, 9–9. doi: 10.1167/4.6.9
Spearman, C. (1904). The proof and measurement of association between two things. Am. JJ. Psychol. 15, 72–101. doi: 10.2307/1412159
Strasburger, H., Harvey, L. O., and Rentschler, I. (1991). Contrast thresholds for identification of numeric characters in direct and eccentric view. Percep. Psychophysics 49, 495–508. doi: 10.3758/BF03212183
Taylor, M. M., and Creelman, C. D. (1967). PEST: efficient estimates on probability functions. J. Acoust. Soc. America 41, 782–787. doi: 10.1121/1.1910407
Tiurina, N. A., Markov, Y. A., Choung, O-.H., Herzog, M. H., and Pascucci, D. (2022). Unlocking crowding by ensemble statistics. Curr. Biol. 32, 4975–4981.e3. doi: 10.1016/j.cub.2022.10.003
Toet, A., and Levi, D. M. (1992). The two-dimensional shape of spatial interaction zones in the parafovea. Vision Res. 32, 1349–1357. doi: 10.1016/0042-6989(92)90227-A
Treder, M. S., and van der Helm, P. A. (2007). Symmetry vs. repetition in cyclopean vision: a microgenetic analysis. Vision Res. 47, 2956–2967. doi: 10.1016/j.visres.2007.07.018
van der Helm, P. A. (2014). “Symmetry perception,” in The Oxford Handbook of Perceptual Organization ed J. Wagemans. Oxford University Press. doi: 10.1093/oxfordhb/9780199686858.013.056
von Ehrenfels, C. (1890). Über Gestaltqualitäten_About gestalt qualities. Vierteljahrsschrift Für Wissenschaftliche Philosophie, 14, 249–292.
Wagemans, J., Elder, J. H., Kubovy, M., Palmer, S. E., Peterson, M. A., Singh, M., et al. (2012a). A century of Gestalt psychology in visual perception: I. Perceptual grouping and figure–ground organization. Psychol. Bull. 138, 1172. doi: 10.1037/a0029333
Wagemans, J., Feldman, J., Gepshtein, S., Kimchi, R., Pomerantz, J. R., Van der Helm, P. A., et al. (2012b). A century of Gestalt psychology in visual perception: II. Conceptual and theoretical foundations. Psychol. Bull. 138, 1218. doi: 10.1037/a0029334
Waugh, S. J., Levi, D. M., and Carney, T. (1993). Orientation, masking, and vernier acuity for line targets. Vision Res. 33, 1619–1638. doi: 10.1016/0042-6989(93)90028-U
Wertheimer, M. (1922). Untersuchungen zur Lehre von der Gestalt I: Prinzipielle Bemerkungen [Investigations in Gestalt theory: I. The general theoretical situation]. Psychol. Forsch. 1, 47–58. doi: 10.1007/BF00410385
Wertheimer, M. (1923). Untersuchungen zur Lehre von der Gestalt II. [Investigations in Gestalt Theory: II. Laws of organization in perceptual forms]. Psychol. Forsch. 4, 301–350. doi: 10.1007/BF00410640
Weymouth, F. W. (1958). Visual sensory units and the minimal angle of resolution. Am. J. Ophthalmol. 46, 102–113. doi: 10.1016/0002-9394(58)90042-4
World Medical Association (2013). World Medical Association Declaration of Helsinki: ethical principles for medical research involving human subjects. JAMA 310, 2191–2194.
Keywords: visual perception, perceptual organization, Gestalt principle, crowding, grouping, vision model, recurrent processing
Citation: Choung OH, Rashal E, Kunchulia M and Herzog MH (2023) Specific Gestalt principles cannot explain (un)crowding. Front. Comput. Sci. 5:1154957. doi: 10.3389/fcomp.2023.1154957
Received: 31 January 2023; Accepted: 28 August 2023;
Published: 14 September 2023.
Edited by:
James Elder, York University, CanadaReviewed by:
Daniel Coates, University of Houston, United StatesCopyright © 2023 Choung, Rashal, Kunchulia and Herzog. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Oh-Hyeon Choung, b2hoeWVvbi5jaG91bmdAZ21haWwuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.