- Fraunhofer Institute for Cognitive Systems, Munich, Germany
There is increasing interest in the application of machine learning (ML) technologies to safety-critical cyber-physical systems, with the promise of increased levels of autonomy due to their potential for solving complex perception and planning tasks. However, demonstrating the safety of ML is seen as one of the most challenging hurdles to their widespread deployment for such applications. In this paper we explore the factors which make the safety assurance of ML such a challenging task. In particular we address the impact of uncertainty on the confidence in ML safety assurance arguments. We show how this uncertainty is related to complexity in the ML models as well as the inherent complexity of the tasks that they are designed to implement. Based on definitions of uncertainty as well as an exemplary assurance argument structure, we examine typical weaknesses in the argument and how these can be addressed. The analysis combines an understanding of causes of insufficiencies in ML models with a systematic analysis of the types of asserted context, asserted evidence and asserted inference within the assurance argument. This leads to a systematic identification of requirements on the assurance argument structure as well as supporting evidence. We conclude that a combination of qualitative arguments combined with quantitative evidence are required to build a robust argument for safety-related properties of ML functions that is continuously refined to reduce residual and emerging uncertainties in the arguments after the function has been deployed into the target environment.
1. Introduction
Recent advances in the field of artificial intelligence (AI), and in particular Machine Learning (ML), have led to increased interest in the application of ML to cyber-physical systems such as autonomous vehicles and industrial robotics. Such systems have the potential to increase safety through increased automation, for example by reducing the number of human-induced accidents, or allowing systems to operate in hazardous environments without direct human control. However, the malfunctioning of such systems can lead to severe harm to users, bystanders and the environment. There is therefore a clear need to demonstrate that safety-critical systems that utilize ML are acceptably safe. As a consequence, the field of trustworthy and safe AI is also receiving attention from a regulatory and standards perspectives. Examples of which are the EU proposal for regulations on AI1 and ongoing standardization efforts on safe AI2. Within the context of these regulations and standards, assurance arguments can be used to demonstrate that safety requirements have been met with sufficient confidence. However, there is still significant debate regarding whether or not a convincing argument for safety can be made at all for complex ML-based functions such as those used for camera-based obstacle detection in automated vehicles. In this paper, we provide a systematic examination of the underlying factors that make arguing the safety of ML so challenging. In doing so we build upon general definitions of complexity and uncertainty and demonstrate how these can be instantiated to explain the root causes of specification and performance insufficiencies of ML models and the resulting assurance uncertainty. We align our terminology with that of the standard ISO 21448 “Safety of the intended functionality” which provides a valuable conceptual perspective for reasoning about performance insufficiencies of complex, automated systems. We combine these viewpoints with notions of confidence in assurance cases to highlight which aspects of the safety argument contribute to assurance uncertainty and how the confidence in the argument can be increased. The result is a framework for reasoning about the residual uncertainty within assurance arguments for ML that can be used to provide a stronger foundation for determining for which applications and technical approaches a convincing safety argument can be made. The contributions of the paper can thus be summarized as follows:
• We provide a set of definitions with which safety assurance gaps for ML can be categorized and their severity evaluated.
• We apply these concepts to an assurance argument structure for ML based on previous work to identify which aspects of the argument contribute in which manner to assurance uncertainty.
• This leads us to identify measures for resolving these uncertainties which could form the focus of future research into ML safety assurance.
The paper is structured as follows: The following section provides an overview of previous work on assurance arguments for ML-based safety-critical functions and confidence in assurance arguments. In Section 3 we introduce a number of definitions of complexity and uncertainty that are used within this paper. Section 4 demonstrates how these definitions can be used to describe the manifestations of uncertainty with respect to the assurance of safety-critical ML functions in autonomous open-context systems. Section 5 introduces a safety assurance argument structure inspired by the previous work cited in Section 2 that addresses common areas of specification and performance insufficiencies. In Section 6, we apply notions of assurance confidence to examine areas of residual uncertainty in the assurance evidence as well as the argumentation structure itself. This leads to a set of conclusions regarding the current debate on safety of ML and the identification of areas of future research. The examples used to illustrate the concepts in this paper relate to supervised ML such as deep neural networks (DNNs). However the concepts could be extended as part of future work to other classes of ML techniques.
2. Background and related work
2.1. Safety assurance for machine learning
ISO (2019) defines assurance as grounds for justified confidence that a claim has been or will be achieved. A claim is defined as a true-false statement about the limitations on the values of an unambiguously defined property—called the claim's property—and limitations on the uncertainty of the property's values falling within these limitations. ISO (2019) also defines an assurance argument as a reasoned, auditable artifact that supports the contention that its top-level claim is satisfied, including systematic arguments and its underlying evidence and explicit assumptions that support the claim(s). As such, the assurance argument communicates the relationship between evidence and the safety objectives. A model-based graphical representation of the assurance argument can aid its communication and evaluation. Within this paper we make use of the Goal Structuring Notation (GSN)3 to visualize the assurance argument.
Previously, functional safety standards have not addressed the unique characteristics of ML-based software. Salay et al. (2017) analyze the standard ISO 26262 (functional safety of electrical/electronic systems for road vehicles) and provide recommendations on how to adapt the standard to accommodate ML. Burton et al. (2017) addressed the challenges involved in arguing the safety of ML-based highly automated driving systems and proposed a contract-based approach for demonstrating the fulfillment of a set of safety-related requirements (guarantees) for an ML function under a given set of assumptions. The Guidance on the Assurance of Machine Learning in Autonomous Systems (AMLAS) (Hawkins et al., 2021) provides an overview of different ML-lifecycle stages and guides the development of assurance cases for ML components by examining each stage in turn. The guideline emphasizes that the development of an effective safety argument requires an iterative process involving a large number of stakeholders. Furthermore it stresses the importance that the safety considerations are meaningful only when scoped within the wider system and operational context. Such an iterative approach is further developed in Burton et al. (2021) where a safety assurance argument for a simple ML-based function is discussed. The simplicity of the function and choice of ML technology (an adaptive approach to generalized learning vector quantization Sato and Yamada, 1995) allowed the authors to develop a convincing and comprehensive case by exploiting properties of the environment and model that could be determined with high certainty. Burton et al. (2022) present a safety assurance methodology for more complex ML-based perception functions. A particular focus is put on how evidences should be chosen, and how to show that the mitigation of insufficiencies was successful.
A diverse set of evidences based on constructive measures, formal analysis and test, are typically required to support the claims in the assurance case for complex software-based system. Work that has focused on the effectiveness of specific metrics and measures on providing meaningful statements regarding safety-related properties of ML models includes (Cheng et al., 2018, 2021; Henne et al., 2020; Schwaiger et al., 2021). In reality, an assurance argument will include a mixture of quantitative evidences as well as qualitative arguments. It is therefore not always obvious which level of residual risk has in fact been argued and is often dependent on expert judgement and the use of well-established chains of argument as laid out in safety standards. Although this paper references a number of works to illustrate various methods of evidence collection, we do not claim to provide a complete review in this area. For a more thorough review of evidences to support the safety of ML, we refer to dedicated survey papers such as Huang et al. (2020), Ashmore et al. (2021), and Houben et al. (2022).
There is currently no industry consensus for which set of methods are sufficient for evaluating the performance of an ML function in a safety critical context, with safety standards for ML still in development. This poses additional challenges when building an assurance case, as the validity of the evidences themselves can be called into question (Burton et al., 2019).
2.2. Assurance confidence arguments
Assurance confidence estimation aims to reduce uncertainties associated with validity of the assurance argument itself. Qualitative approaches to improving confidence in the assurance case aim to decrease uncertainty by strengthening the argument itself, e.g., through additional confidence-specific claims, sub-claims, and evidences. Hawkins et al. (2011) present the concept of assured safety arguments, an extension of conventional safety arguments as described above that separates safety argumentation from confidence argumentation. To this end, an assured safety argument consists of two separate components: (1) a conventional safety argument that is purely causal in nature, i.e., it only links claims, contextual information, and evidence without providing confidence values, and (2) a confidence argument that establishes confidence in the structure and context of the safety argument. Safety arguments and confidence arguments are connected through assurance claim points (ACPs) in the structural notation of the argument. ACPs can be assigned to the following types of assertions regarding the argument's confidence:
1. Asserted context: confidence in the validity of context information.
2. Asserted solution: confidence in the validity and integrity of evidence.
3. Asserted inference: confidence in the appropriateness of the deductive logic of the argument.
Confidence arguments aim to provide confidence in three particular aspects of the assertion:
1. There are grounds to support the probable truth of the assertion.
2. Residual uncertainties (termed assurance deficits) in the assertion have been identified.
3. Residual uncertainties in the assertion are insufficient to cause concern.
Whilst this approach aims to provide confidence in the overall safety argument through a separate set of confidence arguments, it does not allow for the assignment of a quantitative confidence metric for the whole safety argument, e.g., to quantify the risk of the overall claim being falsely stated as true. A range of quantitative approaches to assurance confidence have been presented, e.g., using eliminative induction and Baconian probabilities (Goodenough et al., 2013), Dempster-Shafer belief functions (Ayoub et al., 2013; Wang et al., 2019), or Bayesian inference (Guo, 2003; Denney et al., 2011; Hobbs and Lloyd, 2012). However, since these approaches depend on the availability of reliable confidence values that can be assigned to elements of the assurance argument and combined into an overall confidence score, they are themselves subject to uncertainty and subjective judgement.
3. Definitions of complexity and uncertainty
3.1. From complexity to uncertainty
In Burton et al. (2020), the authors discussed the notion of the semantic gap and its impact on the safety assurance of ML-based autonomous systems, in particular to express the difficulty of defining an adequately complete set of safe behaviors of the system. The authors make use of the following definition “Semantic gap: The gap between intended and specified functionality—when implicit and ambiguous intentions on the system are more diverse than the system's explicit and concrete specification” (Bergenhem et al., 2015). The semantic gap was described as a direct consequence of the following factors:
• the complexity and unpredictability of the environment in which the system operates,
• the complexity and unpredictability of the system as well as the system's interactions with other technical systems and human actors (including operators, users, and bystanders), and
• the increasing transfer of the decision-making responsibility from a human actor to the system, as the system will not have the semantic and contextual understanding of the decisions that the human does. This can also be considered as an expression of the inherent complexity and ambiguity of the task itself.
Complexity science would define a system as complex if some behaviors of the system are emergent properties of the interactions between the parts of the system, where it is not possible to predict those behaviors from knowledge of the parts and their interactions alone. The lack of knowledge about the causes of emergent behavior within complex systems is strongly related to the concept of uncertainty as illustrated in the following definition: “Any deviation from the unachievable ideal of completely deterministic knowledge of the relevant system” (Walker et al., 2003). Increasing levels of complexity severely limit the amount of a-priori knowledge about the system's behavior and thus the ability to model and predict its dynamics. Since emergent phenomena exist on a different semantic level than the system components themselves, their existence cannot be easily deduced from within the system, resulting in ontological uncertainty (Gansch and Adee, 2020). For example, from the perspective of an image represented as a set of pixel values, the concept of a “pedestrian” is an emergent phenomenon.
3.2. Dimensions of uncertainty
A number of taxonomies for uncertainty have been presented in the literature; for example, as provided in the surveys of Lovell (1995) and Rocha Souza et al. (2019). The work of Knight (1921) can be seen as the starting point for a formal treatment of uncertainty. Knight (1921) distinguished three types of decisions: decisions under certainty (type I) where the consequences of all options are known; decisions under risk (type II) where possible futures are known, probability distributions are known, and statistical analysis is possible; and decisions under uncertainty (type III) where the future states are known but the probabilities are unknown. The role of safety assurance can be seen as striving to facilitate decisions of type II wherever type I is not possible, whilst avoiding type III decisions.
Lovell (1995) proposes a taxonomy of uncertainty in the context of decision making. He classifies sources of uncertainty into the following categories, where complexity increases uncertainty in all three dimensions. However, for the purposes of this paper we will adapt the terminology to better align with language associated with cyber-phyiscal systems:
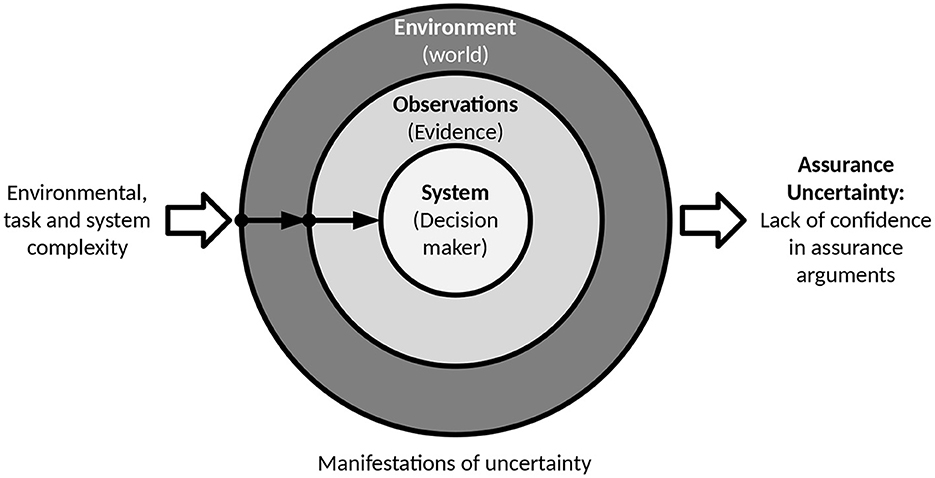
1. World: Uncertainty arising from the natural world (e.g., complexity, disorder, stochastic regularity, dynamism) and from actors within this world (e.g., actions, group decisions, unpredictable behavior). We will refer to this category of uncertainty within this paper as uncertainty in the environment.
2. Evidence: Uncertainty arising from data measurement (e.g., imprecision, incompleteness), from linguistic evidence (ambiguity, fuzziness), and from evidence from actors (possible error, possible deception). To avoid confusion with the term from the perspective of safety assurance, we will refer to this category from hereon as uncertainty of observations.
3. Decision maker: Uncertainty arising from processing capabilities (memory failure, time/resource limits), the ability to interpret evidence (linguistic ability, knowledge of context), and from mental models (incorrectness, incompleteness, conflicts). As we are concerned with assurance of technical systems rather than human behavior, we will refer to this category of uncertainty as uncertainty in the technical system.
For cyber-physical systems operating within an open context, the relationships between the categories can be summarized as follows: The environment (e.g., urban traffic) is inherently complex, unpredictable and difficult, if not impossible to completely model. This environment is observed via a set of imperfect sensors with inevitable limitations (e.g., resolution, field of view, signal noise, etc.). The system then attempts to make sense of these observations and decide on appropriate actions using a combination of algorithms, heuristics, and ML. Each of which include models with the potential for epistemic uncertainty.
Within the context of this paper we are primarily concerned with assurance uncertainty which is related to a lack of knowledge and thus confidence regarding the completeness and/or validity of an assurance argument for critical properties of the system. This can include a lack of confidence in the validity (including statistical confidence) of evidence supporting the assurance argument as well as the chain of reasoning itself. Assurance uncertainty can also include a lack of confidence in the validity and appropriateness of the overall claim of the assurance argument as well as the continued validity of the argument over time. Assurance uncertainty can thus be interpreted as a form of observation uncertainty regarding the determination of residual uncertainty in the technical system, which in turn can be a product of the inherent complexity of the environment, the task, and the system itself. The various categories of uncertainty used within this paper and their relationships are summarized in Figure 1.
3.3. Relative definitions of uncertainty
Uncertainty is not a binary property and when comparing different approaches to safety assurance, we would like to compare relative strengths of an argument. The taxonomies discussed so far refer to differences between types of uncertainty in purely qualitative terms. As much of the safety argument for ML will be based on quantitative properties and associated evidence, an obvious question is when quantifiability is possible and when it is not.
For example, probability theory is only applicable if probability is measurable and plausible distributions (or sets of distributions) can be given. As Dow (2012) clarifies, “for probability to be measurable, the range of possible outcomes must be known with certainty and the structure which generates these outcomes must also be known, either by logic or by empirical analysis.” Any probabilistic statement can thus be questioned in terms of its statistical significance. Any statement about significance can, in turn, be questioned in terms of the knowledge of the underlying structure. However, how much confidence can be associated with that knowledge itself? In theory, we may thus end up with an infinite “uncertainty escalator” (Williamson, 2014).
To structure this problem, Dow (2012) presents a taxonomy of uncertainty against the background of measurable and immeasurable probability. Table 1 summarizes the first four levels of the hierarchy. Each level can itself be subject to varying grades of uncertainty which, with increasing strength, indicate a transition to the next higher level in the hierarchy. For example, at level 2, the confidence interval around a data point might be narrower or wider depending on the grade of uncertainty associated with it. We refer to this orthogonal grade of uncertainty as severity, i.e., the difficulty of the judgement being made as originally proposed by Bradley and Drechsler (2014) and summarized in Table 2.
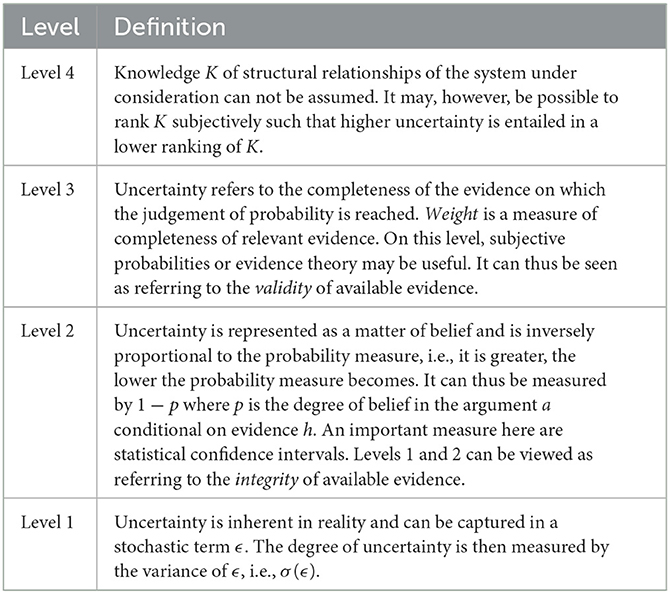
Table 1. Levels of uncertainty according to the Dow hierarchy (Dow, 2012).

Table 2. Definition of uncertainty severity classes according to Bradley and Drechsler (2014).
According to this scale, the difficulty of a judgement is defined by how much information is available to the decision maker. At levels 1 and 2 in the Dow hierarchy where probabilistic statements are possible, the severity of uncertainty is measured by the variance or the confidence interval associated with a data point, i.e., by the integrity of available evidence. At level 3, uncertainty is measured by the validity of evidence. At level 4, reliable quantitative statements are no longer possible and uncertainty management largely relies on qualitative judgement. Thus severe uncertainty or ignorance related to the knowledge reference at level 4 can be seen as a representation of unknown unknowns, ignorance or ontological uncertainty. This level of uncertainty is not possible to manage within the perspective of the system due to a fundamental lack of knowledge or availability of observations of relevant aspects of the system. It can therefore be termed unmanageable (Schleiss et al., 2022) and can only be resolved from an external perspective that has access to other knowledge of the system and its environment.
The Dow hierarchy in combination with the Bradley & Drechsler severity scale provide a useful guideline as to how different levels of uncertainty in assertions within an assurance argument can be assessed, by reasoning about the confidence that can be achieved within each level. For example, if confidence in quantitative evidence for robustness of the trained model could only be asserted at levels 1 and 2, then the robustness would be measured with a known statistical confidence interval. However, the relation of these measurements to the claim being investigated as well as the appropriateness of assumptions (such as i.i.d. assumptions on the sampled input space) that support the statistical relevance of the evidence cannot be demonstrated, thus undermining the assurance confidence. The hierarchy also illustrates that quantifiability of the uncertainty decreases with increasing levels until eventually only qualitative judgements will be possible, thus increasing the risk of severe uncertainty and ignorance. We will revisit the hierarchy when the question of assurance confidence is discussed in Sections 5, 6. A safety assurance argument with high confidence can therefore be defined as consisting of a number of assertions that are associated with only mild uncertainty within each of the first 4 levels of Dow's hierarchy.
4. Impact of complexity and uncertainty on ML safety assurance
The standard ISO 21448 “Road vehicles—Safety of the intended functionality (SOTIF)” addresses safety in terms of the absence of unreasonable risk due to functional insufficiencies of the system or by reasonably foreseeable misuse. The SOTIF approach considers hazards that are caused by latent insufficiencies of the function that are uncovered by triggering conditions in the operating environment at runtime. In comparison to functional safety, as defined by related standard ISO 26262, SOTIF does not require an explicit fault such as a systematic software bug or random hardware failure to trigger hazardous behavior. Instead, the focus of the standard is on inherent limitations of the system based on its specification or technical implementation. The standard requires the definition of acceptance criteria for each safety goal, which in turn are refined and allocated to subsystems such as perception or decision functions. Acceptance criteria can be expressed quantitatively, such as in terms of acceptable accident rates. Although originally motivated by safety issues associated with driving assistance systems, the concepts within the standard can be applied to a wide range of scenarios where insufficiencies of the functionality could lead to hazardous behavior.
The SOTIF model describes the task of risk reduction as maximizing the number of triggering conditions that are known to potentially lead to hazardous behavior (known unknowns) such that they can be made safe whilst minimizing the number of potentially hazardous residual unknown triggering conditions (unknown unknowns). In the context of ML, known triggering conditions could be considered as inputs that are known to reveal an insufficiency in the trained model, whilst unknown triggering conditions relate to inputs that were not considered within the training and test set, e.g., due to features considered irrelevant or distributional shift in the environment. SOTIF appears well suited as a basis for discussing the safety of ML functions where hazardous behaviors are caused by inaccuracies in the trained model itself rather than by faults during its execution. It therefore forms the basis of ISO PAS 8800 “Road vehicles - Safety and Artificial Intelligence,” currently in development.
Burton et al. (2019) express the task of assuring the safety of ML (according to the SOTIF model) in terms of demonstrating the fulfillment of a safety contract based on the following definition.
Where, for all inputs i that fulfill the set of assumptions A on the operational design domain and system context, the output of model M must fulfill a set of conditions defined by guarantees G. For realistic ML-based applications, residual errors in the model will inevitably remain. Assurance thus involves demonstrating that the probability with which this contract is fulfilled is in accordance to the risk acceptance criteria. Under these circumstances, the ML system can be considered “acceptably safe" under the following condition which also considers the probability distribution of potential triggering conditions (i) in the environment:
Where :I → [0, 1] is the input probability distribution function of the ODD that assigns every input i ∈ I with a probability value, with the condition that . In Equation 2, the left-hand side characterizes the probability of an input satisfying the guarantee G, conditional on the constraint that assumption A holds. Equation 2 states that so long as the failure rate (where the probability of (G(i, M(i)) = false) is small enough, the system is considered to be acceptably safe as defined by AC (acceptance criteria). This formulation of the assurance condition is related to type II uncertainty (decision under risk) according to Knight (1921), with the objective of demonstrating an acceptably low level of residual risk with high certainty related evidence in at least the first four levels of the Dow hierarchy.
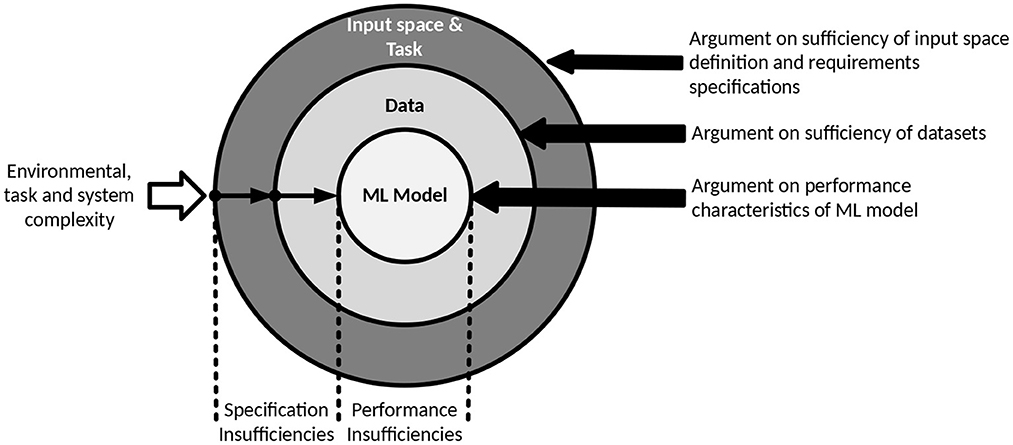
The SOTIF standard defines functional insufficiencies in terms of specification insufficiencies and performance insufficiencies, both of which can be described in terms of the uncertainty model introduced in Section 3. These insufficiencies can be seen as manifestations of uncertainty that eventually lead to uncertainty in the assurance argument and can then be classified along the following three dimensions:
1. Input space and task: uncertainty resulting from the complexity of the input space that data points are sampled from, and the inherent complexity of the tasks that the model is designed to perform (related to environment uncertainty from Figure 1),
2. Data: uncertainty resulting from potential inaccuracy or incompleteness of the sampled data points themselves that are used either in the training or verification of the model (related to observation uncertainty from Figure 1) and
3. ML model: uncertainty resulting from the complexity of the ML model, e.g., architecture or number of parameters (related to the system uncertainty from Figure 1).
4.1. Specification insufficiencies
Specification insufficiencies are related to the validity and completeness of appropriate safety acceptance criteria and the definition of acceptably safe behavior in all situations that can reasonably be anticipated to arise within the target environment. Specification insufficiencies can also be rooted in competing objectives and stakeholder-specific definitions of acceptable residual risk leading to unresolved questions related to ethical/socially acceptable system behavior. The inability to provide a complete specification of the (safe) behavior of the system is inherently linked to both the semantic gap and emergent properties of complex systems and can be broken into the following components based on the definitions in Equations 1 and 2:
• Uncertainty in the definition of a complete model of the input space I and associated assumptions A(i) which can also be used to reason about completeness and representativeness of training and test data.
• The guarantees G(i, M(i)), representing safety requirements allocated to the ML model, will typically be refined into a conjunction of safety-related properties P that may be quantitatively defined using associated metrics and target values. System-level safety goals (e.g., avoidance of collisions) must be refined into a set of ML-specific properties (e.g., precision, recall, bias, robustness, etc.). This set of properties should be derived based on an understanding of the potential performance insufficiencies and their causes (see below) of the ML model, which may only become apparent during test and operation. Identifying and refining safety requirements into measurable properties of the ML model and associated target values is a non-trivial task. Furthermore, for each property, a validation target derived from the acceptance criteria must be defined in terms of a quantitative threshold that can be measured during development.
• When operating within an open context, the assumptions A(i) made regarding the input space during design of the system may lose their validity over-time, either as the environmental context of the system changes, the system is adapted to different tasks, or a deeper understanding of the context is achieved through experience in the field (e.g., new sources of triggering conditions are discovered).
4.2. Performance insufficiencies
ML models work inductively by learning general concepts from sampled training data. The complexity of the learning task is a function of the complexity of the mapping between data points in the input or feature space (= the syntactic level) and concepts to be learned (= the semantic level). The idea of task complexity is thus closely related to the concept of learnability (Valiant, 1984). Based on this concept, one way to quantify the complexity is to revert to sample complexity, i.e., the number of samples required for a problem to be efficiently learnable. As, for example, discussed by Usvyatsov (2019), sample complexity depends on the underlying model complexity (described by the Vapnik-Chervonenkis (VC) dimension or VC density) which is itself a function of the number of weights in the model4. The relation between task complexity and required model complexity/expressiveness constitutes the achieved complexity of the trained model.
Performance insufficiencies relate to a lack of predictability in the performance of the technical system components. An example of performance insufficiencies in ML models are the unpredictable reaction of a system to previously unseen events (lack of generalization), or differences in the system behavior despite similar input conditions (lack of robustness). We argue that an ML model can only achieve optimal performance if task complexity, model expressiveness and achieved model complexity are in alignment. For example, using a highly complex model architecture (e.g., a DNN) and/or too much data for a comparatively simple task (e.g., low-dimensional polynomial regression), may cause the trained model to show high variance, i.e., to overfit to irrelevant noise; on the other hand, using a simple model (e.g., a shallow neural network) and/or too little data for a significantly more complex task (e.g., object detection) may cause the trained model to exhibit bias, i.e., to ignore relevant relations between features and target outputs.
Since the formal requirements of probably approximately correct (PAC) learning (Valiant, 1984) (e.g., iid samples, invariance between training and target distribution, or sufficiently large sample sizes) are often not satisfied in practice, the model output may be subject to prediction uncertainty. Predicted probabilities (e.g., softmax output value of a DNN-based classification task) may thus not necessarily be indicative of the actual probability of correctness and further confidence in the probabilities needs to be obtained.
In order to assess the performance of an ML model, the manner in which insufficiencies express themselves with respect to a set of measurable properties P (such as robustness, bias, prediction certainty etc.) needs to be expressed. The relevance of these properties to the fulfillment of guarantees G of the safety contract may be highly application and context specific. In addition, the root causes of these insufficiencies may depend on a number of factors and their presence may further exacerbate the difficulties in assessing the safety of the model.
4.3. Assurance uncertainty
Equation 2 was used to define an “acceptably safe” ML system. However, the input distribution function can never be perfectly characterized for complex systems such as autonomous driving due to input space uncertainty. This highlights one of the challenges in calculating realistic failures rates for such systems, as any measurements will ultimately be sensitive to the potentially unknown distribution of events (triggering conditions) in the input space. Any measurement of failure rates for such systems will therefore only ever be an approximation of the actual failure rates experienced during operation and sensitive to a number of assumptions made on the distribution of triggering conditions and the extrapolation of the properties observed using specific data samples (data uncertainty). This requires an inductive approach based on evidence that is collected regarding the design and performance of the ML model, which is the inherent nature of most forms of safety assurance.
Given that the conditions given in Equation 2 cannot be proven with absolute certainty, the assurance challenge therefore is to find a set of conditions that can be demonstrated with sufficient confidence from which we can infer that these conditions are met. This includes the concept of estimated failure rate λM of the ML-based system, where if we demonstrated that 1 − λM ≥ AC we might infer that the failure rate of the ML model represented by λM is sufficiently low. λM can be defined as follows:
Where j represents the unique observations or measured samples of the input space, which represent only a subset of the entire input space that could be theoretically experienced during operation. Here λM represents the estimated probability of failure on demand under the assumption that all inputs in the domain may occur with equal probability, which may not necessarily hold. Furthermore, it may not be possible to directly measure whether or not the conditions outlined in G are fulfilled, but instead these would be inferred by estimating a set of conditions P(j, M(j)) related to set a observable properties of M that are hypothesized to be related to the ability of the model to fulfill its guarantees G(j, M(j)). An expression of the assumption underlying this approach to safety assurance can therefore be expressed as follows.
Assurance uncertainty can thus manifest itself as a lack of knowledge of the difference between the estimated failure rate λM and the actual failure rate that occurs during operation (the left and right side of Equation 4). This “assurance gap” will typically need to be closed based on a combination of quantitative (e.g., related to statistical confidence) and qualitative arguments (e.g., based on the appropriateness of certain assumptions). As we will show later, the assurance gap is particularly sensitive to uncertainties at the levels 3 and 4 of the Dow model. In the definition above, the selection of samples is still restricted by a set of assumptions A over the input space. By loosening this definition, the robustness of the model against inputs outside of these constraints can be evaluated as well as the appropriateness of the assumptions themselves.
Based on the set of definitions defined within this Section, we can now express the objectives of ML safety assurance by adapting the definitions from Section 3 as described in Figure 2. In the following section we describe a typical assurance argument structure for addressing functional insufficiencies before examining assurance uncertainties within such an argument in more detail in Section 6.
5. Assurance argument structures
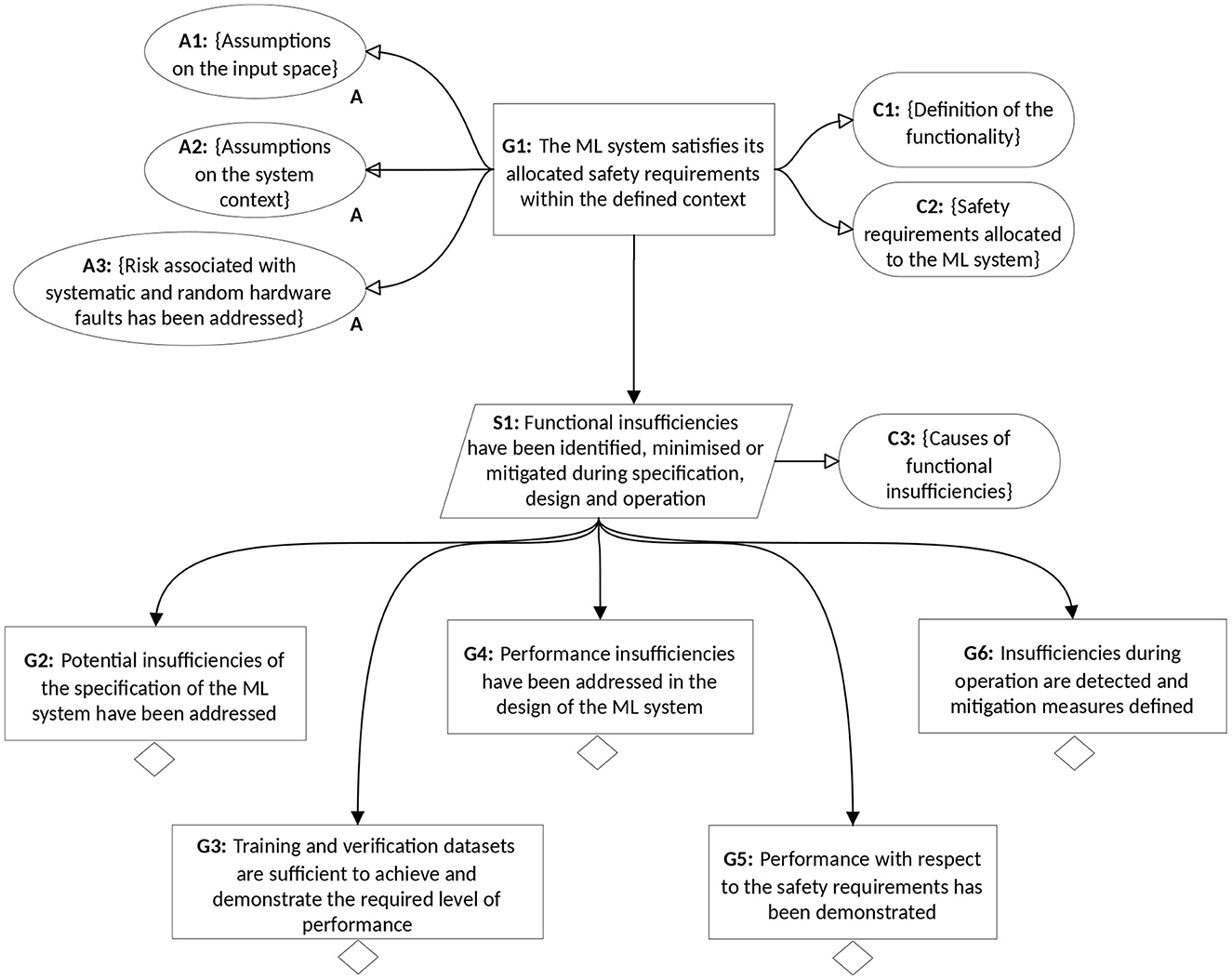
Figure 3 describes the structure of an assurance argument for a safety-relevant function implemented using supervised ML. The structure is based on a synthesis of previous work in this area in both structuring the assurance argument and defining associated evidences, including Burton et al. (2017), Ashmore et al. (2021), Burton et al. (2021), Hawkins et al. (2021) and Houben et al. (2022). This structure is used to reason about which manifestations of uncertainty are addressed by such arguments, whilst an evaluation of the effectiveness of this structure is provided in Section 6.
G1 and its associated elements represents the safety contract as expressed by Equation 1. The guarantees G are represented by C1 and C2 which define the functionality and associated safety requirements, e.g., “locate hazardous objects with a tolerance of +/- 20 cms” including a definition of an acceptable failure rate with respect to those requirements, e.g., how often a detection outside of the tolerance interval is permitted. A1 and A2 define the assumptions A on the input space related to the operating environment (e.g., distribution and types of critical objects to be identified, environmental constraints, etc.) and the system context (e.g., quality of sensor readings) respectively. Note, that the argument structure in Figure 3 does not reflect an argument over systematic faults or random hardware faults which are out of scope of this paper and would be covered by an additional argumentation strategy, as stated by A3. The assurance argument covers the functionality implemented by the ML model, which could also include pre- and post-processing operations such as data cleaning and output anomaly detection implemented using traditional (non-ML) approaches. This is referred to in the argument as the “ML system”.
Given these pre-requisites, the assurance strategy (S1) involves demonstrating that functional insufficiencies and their causes have been identified and either minimized or mitigated. Context C3 defines the set of potential causes of insufficiencies that are used to drive this argumentation strategy.
5.1. Addressing insufficiencies of the specification
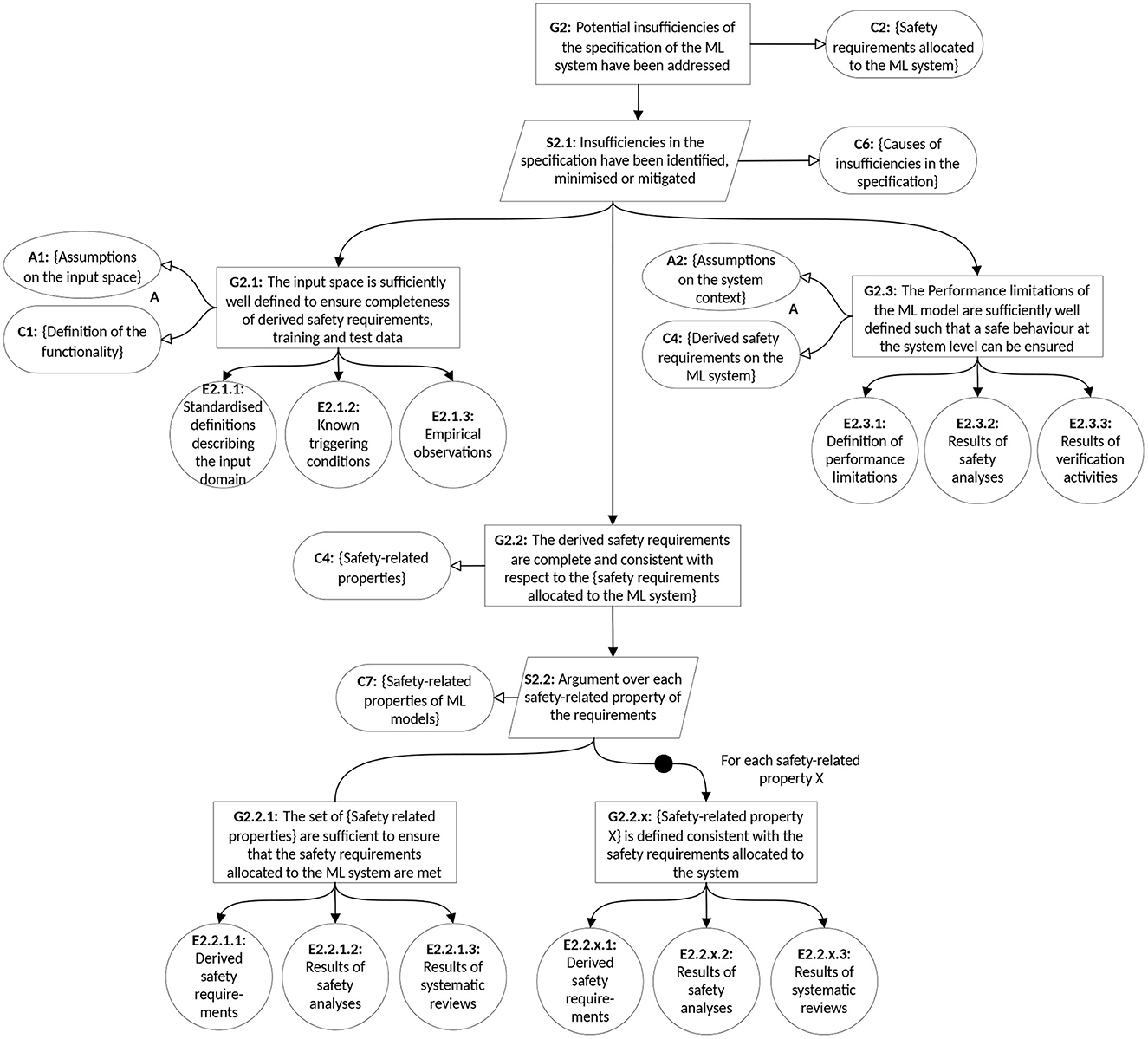
The objective of claim G2 is to demonstrate that a complete and consistent set of safety requirements on the ML model has been derived and is sufficient to ensure that the residual risk of system-level hazardous behavior due to residual errors is acceptably low. This section of the argument is focused on resolving semantic gaps and the reducing specification insufficiencies resulting from input space and task uncertainty. Figure 4 shows the development of G2 to illustrate how the GSN notation can be used to elaborate the assurance argument to the level of individual evidences. G2 is further refined into the subclaims:
• G2.1: The input domain is sufficiently well defined to ensure completeness of derived safety requirements, training and test data. Evidence to support this claim can include standardized ontologies for describing the semantic input space and known triggering conditions from previous experience.
• G2.2: The derived safety requirements are complete and consistent with respect to the safety requirements allocated to the AI system. Challenges associated with this claim include demonstrating that the selected set of safety-relevant properties (P in the formal definition given above) are sufficient to guarantee the overall requirements as well as selecting an appropriate set of metrics and thresholds to define measurable target values of the properties. An example of such a property could be robustness against sensor noise, with thresholds defined according to the L-infinity norm. The specification of such properties has been explored by a number of Bergenhem et al. (2015), Gauerhof et al. (2018), Hu et al. (2020), and Ashmore et al. (2021). The identification of safety-relevant properties of ML functions can be supported by causal safety analyzes to determine root causes of insufficiencies and therefore desirable properties of the function, as well as measures to minimizse or mitigate the insufficiencies to prevent them from leading to hazards. Salay et al. (2019) propose a novel safety analysis method—Classification Failure Mode Effects Analysis (CFMEA)—as a systematic way to assess the risk due to classification under adversarial attacks or varying degrees of classification uncertainty. Evidence to support this claim can include the results of safety analyzes to identify safety-relevant properties of the ML model and systematic (e.g., checklist-based) review.
• G2.3: The performance limitations of the AI system are sufficiently well defined such that a safe behavior at the system level can be ensured. This claim is critical to ensure that performance insufficiencies can be compensated for at the system level in order to avoid hazardous behavior, and correspond to a definition of the known unknowns associated with the trained model. Supporting evidence includes the results of performance analyzes against the derived safety requirements (e.g., tests and formal verification) and the results of safety analysis activities.
5.2. Addressing insufficiencies in the data
The objective of claim G3 is to demonstrate that the data used for training and verification of the ML model is sufficient to achieve and demonstrate the required performance of the ML model with respect to its derived safety requirements. This claim also addresses a form of specification insufficiency as defined by ISO 21448. However, in comparison to G2, this claim addresses the implicit specification as defined by the selected datasets. As such, the objective is to address observation uncertainties as defined in Section 3. The claim is further refined into the following subclaims:
• G3.1: The datasets consist of suitable selections of observations from the overall input space. This includes subclaims regarding the representativeness of the datasets regarding overall coverage of the input space, suitability of the dataset sources (e.g., are there potential geographical differences between where datasets were collected and the intended environment of use), the inclusion of sufficient data capable of revealing triggering conditions, as well as the independence between training and verification datasets. Evidence includes a specification of desirable properties of the datasets, a data selection policy, traceability between the specified dataset properties and the derived safety requirements on the ML model, dataset balance validation and a coverage analysis of the input space definition and known triggering conditions.
• G3.2: The metadata associated with the datasets is sufficiently accurate. This includes addressing insufficiencies in the labeling of ground truth data used for supervised learning and testing purposes. Manual labeling may lead to a high error rate in the metadata which in turn will impact the performance and accuracy of the verification of the ML model. It may also be affected by unconscious bias where specific classes of inputs are disproportionately impacted by the labeling errors. Insufficiencies may also be introduced by pre-processing techniques such as automated scaling and transformation in order to convert data from multiple sources into a common form.
Synthetic and augmented data (Shorten and Khoshgoftaar, 2019) can reduce the risk associated with data labeling (G3.2) but can increase the risk that the fidelity or distribution does not sufficiently match that of the target operating environment and therefore requires additional argumentation in G3.1. In particular, this can increase the risk of previously unknown triggering conditions remaining undetected during development. The use of publicly available and, therefore widely scrutinized datasets (e.g., Cordts et al., 2016; Kotseruba et al., 2016, can help to address potential issues of completeness and integrity of the datasets. However, where used in safety-critical applications, arguments would be required to demonstrate the integrity of the metadata associated with such datasets (Northcutt et al., 2021) as well as their representativeness of the actual target domain.
5.3. Addressing performance insufficiencies in the design
The objective of claim G4 is to demonstrate that the selected AI technology and design, including the selection of a suitable set of hyperparameters is inherently capable of meeting the safety requirements by minimizing the number of performance insufficiencies in the ML model. This can include reference to design measures that are identified in an iterative manner during the development of the system and informed by performance evaluation and subsequent safety analysis. As such, the objective is to address technical system uncertainties as defined in Section 3. The claim is further refined into a number of subclaims as follows:
• G4.1: The choice of ML technology and system design is inherently sufficient to fulfill the safety requirements. This claim includes a consideration of all necessary properties of the ML model as well as the relationship between the inherent task complexity, model expressiveness and achieved model complexity as described in Section 4.2. For example, if interpretability is required to achieve sufficient confidence in the model, models should be inherently interpretable by design (Rudin, 2019). Evidence to support this claim could include analytical and empirical analysis as well as reference to well-documented benchmarks for similar classes of tasks.
• G4.2: Measures during development are selected that reduce safety-relevant performance insufficiencies in the trained model. This claim includes reference to a set of measures during development, that given sufficient training data, minimize the occurrence of insufficiencies. Optimization of the hyperparameters (Feurer and Hutter, 2019) of the model and its training procedure can reduce insufficiencies, including a lack of robustness against adversarial perturbations (Wang et al., 2021). Model extensions such as reliable uncertainty estimation (Henne et al., 2020) may enable runtime mechanisms to better mitigate residual errors. Further measures may include the avoidance of overfitting to improve generalization properties (Anguita et al., 2012). Visual analytics (Haedecke et al., 2022) can be a powerful tool during development to explore the behavior on the trained model and to identify elements of the inputs space where performance insufficiencies still need to be addressed.
• G4.3: Architectural measures are defined to mitigate the impact of known residual insufficiencies in the model. For most realistic applications, it will not be possible to reduce the insufficiencies in the ML model to an acceptable level. Therefore, additional architectural measures may be necessary to mitigate remaining errors. These measures can include monitoring and plausibility checks based on redundant calculations or semantic knowledge of the input space (e.g., maximum rate of movement for detected objects from frame to frame). In addition, out-of-distribution detection (Hendrycks et al., 2021) can be used to detect inputs during runtime that are likely to lead to an erroneous result in the ML model. Evidence associated with this claim should include an evaluation of the effectiveness of the architectural measures in terms of the types and proportion of residual errors that can be mitigated.
• G4.4: Evaluation of the impact of the development environment and tool chain. This claim argues that the level of performance achieved and evaluated during development is representative of the performance that will be achieved during deployment within the technical system. This includes an investigation into the impact of target execution hardware on performance insufficiencies (e.g., due to differences in mathematical precision or pruning of the DNN due to resource restrictions). The claim will also include the evaluation of confidence in the development tools themselves to ensure that errors during training and deployment do not lead to performance insufficiencies that are difficult to detect. Supporting evidence may include target testing as well as tool qualification and certification.
5.4. Evaluation of performance
The objective of claim G5 is to demonstrate that the performance of the trained model is sufficient to meet the requirements and to do so with as much certainty as possible. As for claim G4 described above, this aims to address technical system uncertainty as defined in Section 3. In its simplest form, this step may consist of performing black-box testing against the safety requirements using a set of representative test data. However, due to limitations described in Section 4 this is unlikely to lead to a sufficient level of confidence without additional claims. G5 is therefore further structured as follows:
• G5.1: Evaluation has demonstrated that all safety requirements allocated to the ML have been met. This involves demonstrating direct compliance to requirements allocated to the ML model and can include executing the model within either a simulated or its target system context and typically involves black-box testing based on carefully selected datasets. However, due to properties such as (lack of) robustness, non-linearity, as well as complexity of the input space and potential deficiencies in the datasets themselves, the ability to extrapolate the results of the tests to all possible inputs may be limited. Nevertheless, requirements-based testing is essential also to validate that the derived safety-related properties used to drive the design and verification (see claims G5.x) of the model do indeed lead to a fulfillment of the safety requirements.
• G5.x: Evaluation has demonstrated that safety-related property X is fulfilled. This set of claims evaluates the individual properties P that are required in order to minimize the safety-related performance insufficiencies in the model. The estimated failure rate with respect to different properties P may be estimated using testing techniques or with formal verification (Huang et al., 2020; Abrecht et al., 2021). Formal verification can include an exhaustive exploration of a bounded hypersphere defining the vicinity of particular samples to demonstrate local robustness properties (Cheng et al., 2017; Huang et al., 2017) and several techniques have been put forward to apply constraint solving to this problem. In general, formal verification may provide a more complete estimation of specific properties but is currently limited in its scalability and may only be realistically applied to a small subset or an abstraction on the input space I. The selection of representative samples for the basis of verification is also reliant on a number of assumptions on and abstractions of the input space, thus increasing uncertainty at Dow's levels 3 and 4 for this type of evidence.
• A number of test case generation techniques have been proposed for generating efficient test data to verify specific properties of the model. These techniques can be directed by specific coverage metrics (Odena et al., 2019), making use of Generative Adversarial Networks (GANs) for synthesizing realistic scenarios (Zhang et al., 2018). Furthermore, test adequacy can be evaluated using both structural (Sun et al., 2018) and input space metrics (Gladisch et al., 2020).
5.5. Addressing insufficiencies during operation
The objective of claim G6 is to ensure that emerging insufficiencies during operation are adequately addressed. This can include addressing environmental/input space uncertainty, e.g., in the form of detecting distributional shift (Moreno-Torres et al., 2012) as well as observational/assurance uncertainty by addressing previously unknown triggering conditions detected during operation. Failures detected during operation can be due to both specification and performance insufficiencies. This claim is further structured as follows:
• G6.1: Technical measures are sufficient to detect and mitigate residual and emerging insufficiencies during operation. This claim involves justifying the effectiveness of technical measures for detecting effects such as distributional shift during operation. This may involve architectural measures specific to the ML approach that extend (G4.3) with the notion of resilience to previously unknown triggering conditions, such as anomaly detection (Schorn and Gauerhof, 2020). The claim could also be supported by technical measures at the system level such as fallback strategies upon receiving indications of insufficiencies or high uncertainty in the outputs of the model.
• G6.2: Procedural measures are sufficient to resolve residual and emerging insufficiencies during operation. This claim involves justifying the effectiveness of the operational response to discovering unacceptable safety risk during operation. This can include procedures for monitoring and data recording, halting or restricting the use of the system, as well as ensuring that updates to the model are implemented and deployed in a safe fashion. This includes a demonstration of monotonic safety improvements, i.e., changes in the model to improve specific properties do not lead to an unacceptable degradation in other properties.
6. Evaluating confidence in the assurance argument
In this section, we apply the principles of Hawkins et al. (2011) to identify areas of uncertainty within the argument itself. As proposed in their paper, assurance claim points can be identified within the assurance argument structure to indicate where an additional confidence argument is necessary for asserted context, solutions (related to evidences) and inference (related to the assurance strategy itself). The definitions of uncertainty with respect to the Dow hierarchy levels of Table 1 can be used to determine how much confidence has been achieved for each type of assertion. We illustrate this methodology by examining the three types of assertions applied to several aspects of the assurance argument as outlined in Section 5. Table 3 demonstrates how these types of analysis could be applied to the assurance argument for a DNN-based pedestrian recognition function.
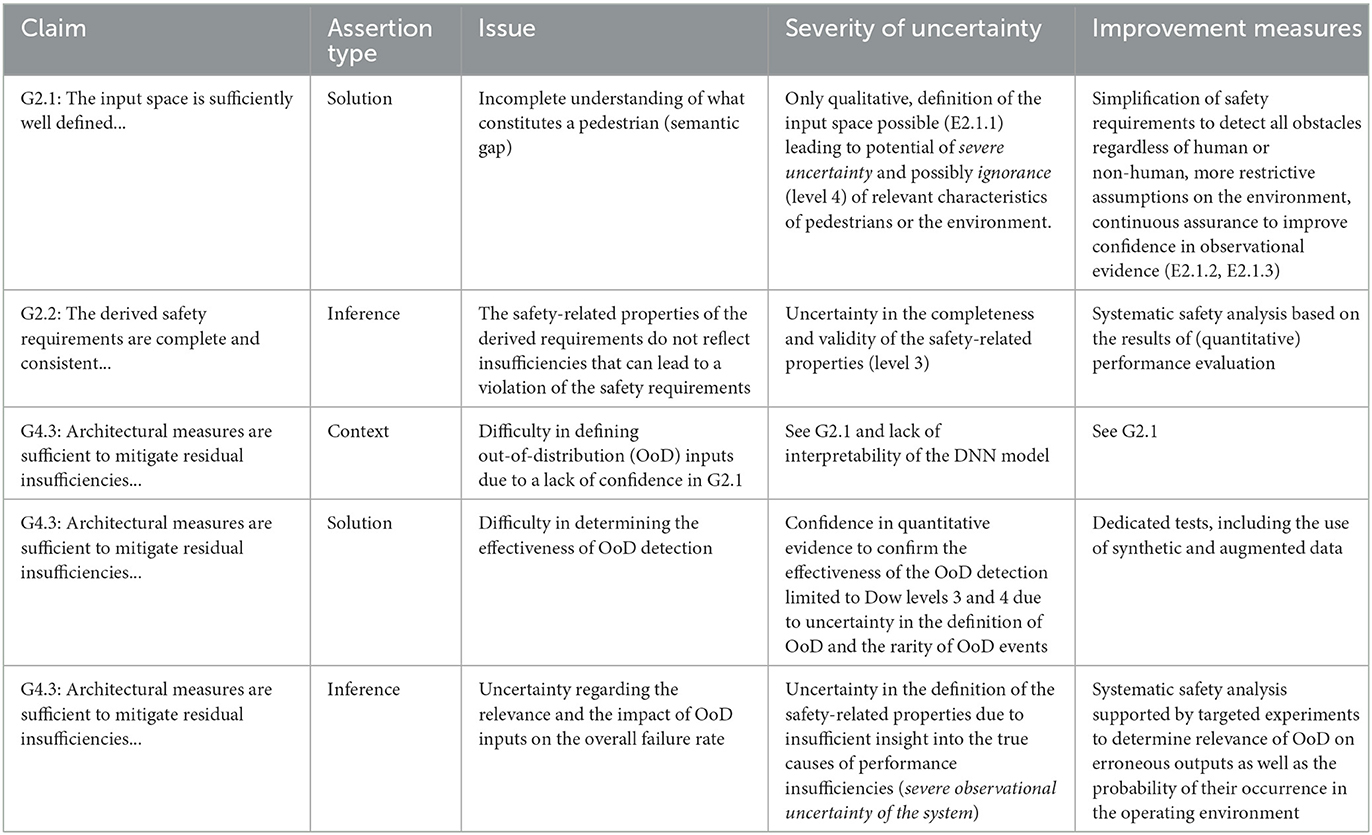
Table 3. Analysis of confidence in assurance claims and potential improvement measures for ML-based pedestrian recognition task.
6.1. Confidence in the reduction of specification insufficiencies
Specification insufficiencies are addressed within claim G2. Confidence in the related assurance argument can be evaluated as follows:
• Asserted context: A prerequisite to the formulation of sufficient set of detailed specifications on the ML model is a sufficient understanding of the system context and requirements allocated to the ML model as well as all associated assumptions. This corresponds to assumptions A1..A3 and contexts C1..C2. Insufficiencies in this asserted context would undermine the confidence in all subclaims of G2. The confidence with which these assertions can be stated will depend highly on the availability and nature of evidence provided at the system level.
• Asserted solution: Figure 4 proposes a number of evidences to support the subclaims of G2. Subclaim G2.1 expresses that the input space of the ML model is sufficiently well defined to ensure the completeness of derived safety requirements as well as training and test data. This corresponds to expressing that the input space uncertainty has been sufficiently reduced. Proposed evidence includes the use of standardized definitions to describe the semantic input space (E2.1.1), a set of known triggering conditions (E2.1.2) as well as empirical observations used to confirm the understanding on the input space (E2.1.3). Confidence arguments associated with these asserted solutions will involve demonstrating both the trustworthiness and appropriateness of the evidence as well as ensuring that potential deficits in the evidence have been identified and are found to be acceptable (Hawkins et al., 2011). E2.1.1 is inherently qualitative in nature leading to the potential for Level 4 uncertainty in the Dow hierarchy. In order to achieve confidence in the definition of the input space, evidences E2.1.2 and E2.1.3 should therefore ensure that direct observations can be called upon to confirm this definition, thus increasing the level of knowledge of structural relationships within the system. However, due to environmental complexity, it may be challenging to achieve confidence in these evidences unless sufficiently restrictive assumptions on the input space and system context can be made. Otherwise, the resulting ontological uncertainty would need to be resolved via external measures in the system or more extensive evidence in the form of E2.1.2 and E2.1.3 collected over a longer period of time as part of continuous assurance activities (see below) in order to reduce observational uncertainty.
• Asserted inference: Subclaim G2.2 claims the completeness and consistency of the derived safety requirements on the model, based on strategy S2.2 which makes use of a set of common properties associated with the safety of ML models (Context C4). Confidence in the validity of this strategy will depend upon determining that the fulfillment of the safety requirements can indeed be guaranteed by this set of properties. As described in Section 4, the identification of derived safety requirements and a suitable set of measurable properties depends on the task complexity. As above, achieving a confidence to Dow levels 1..4 of this assertion may require either restricting the complexity of the environment and task at the system level or collecting sufficient observations through continuous assurance in the target environment to argue confidence in the choice of properties.
6.2. Confidence in out-of-distribution detection to reduce performance insufficiencies
Subclaim G4.3 includes the definition of a number of architectural measures to minimize the impact of performance insufficiencies including out-of-distribution detection (OoDD) to detect to previously unseen inputs that lead to high uncertainty in the outputs of the model. The following conditions are of particular importance in ensuring confidence in this claim.
• Asserted context: The choice of OoDD as a measure depends on the assumptions that OoD inputs may be present during the operation phase of the ML model, and that these may lead to a measurable impact on the fulfillment of safety requirements. This requires two conditions to be fulfilled: the potential for OoD inputs to occur in the field, which itself requires confidence in the definition of in-distribution (ID) inputs and the contribution of such inputs to the overall system failure rate.
• Asserted solution: Evidence to confirm the effectiveness of the OoDD measure can include empirical experiments performed under well-defined conditions. However Dow levels 3 and 4 will be harder to achieve due to the difficulty in justifying the set of conditions under which the measurements are made. This is due to the need for a sufficiently precise specification of ID and OoD inputs as well as the ability to distinguish between failures caused by OoD inputs and failures caused by other insufficiencies present in the model. This can be seen as another manifestation of observational uncertainty.
• Asserted inference: Confidence in the assertion that the use of OoDD in itself is a relevant strategy can be undermined by the difficulty in demonstrating causalities between errors in the outputs of the ML and their respective causes. This is exacerbated by the difficulty in providing a sufficient definition of OoD inputs (see above) as well as the rarity of their occurrence.
6.3. Closing the assurance gaps
As described above, there are significant challenges involved in achieving a sufficient level of confidence in the assurance argument for ML models. This lack of confidence can be eventually traced back to the manifestations of uncertainty described in Figure 2 and Section 3. This inevitably leads to the question of whether or not it is realistic to expect that a sufficiently convincing assurance argument can be made for complex cyber-physical systems that make use of ML such as automated driving systems, mobile logistics robots or medical devices. We argue that the key to answering this question is to understand and acknowledge the uncertainties in the assurance argument by applying the definitions and approach described in this paper, combined with restricting the complexity of the conditions in which the system is deployed in order to counteract the resulting residual risk.
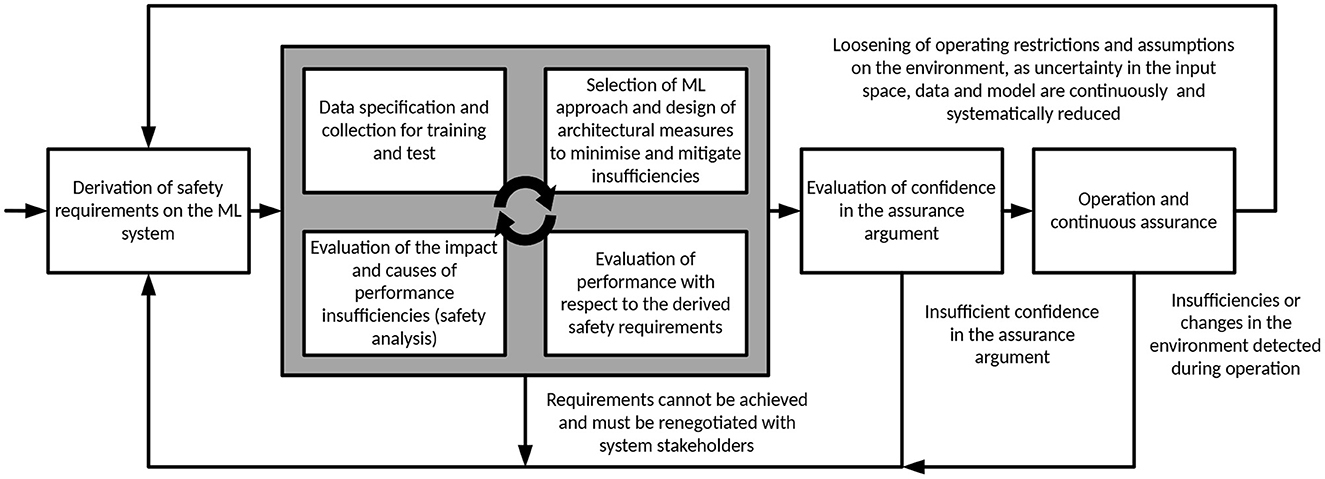
To operationalise this approach we propose an inherently iterative process of safety assurance as described in Figure 5. The process should be seen within the context of wider system development and deployment procedures, which are not detailed here. The ML safety lifecycle begins with the derivation of a set of safety requirements on the ML model based on the allocated system level requirements. The “inner” loop of the process follows repeated cycles of data collection, training, evaluation, and optimisation. This process is extended with an explicit safety analysis step to evaluate the impact and causes of performance insufficiencies on the safety requirements. The analysis can be deductive or inductive in nature or a combination of both and has the objective to analyze insufficiencies in the model that could lead to the violation of safety requirements and their underlying causes. Based on the result, a set of additional safety properties may be defined to extend safety requirements as well as additional measures for data selection, design and evaluation of the ML model. The safety analysis is therefore a key driver for understanding specification and performance insufficiencies and reducing the corresponding uncertainty. If a convergence on evidence to support the safety requirements cannot be achieved, a renegotiation of safety requirements themselves may be necessary. This includes communication of known residual insufficiencies in the ML model to the system integrator such that compensatory measures can be designed at the system level. For example, performance requirements on the ML model may be relaxed based on the introduction of redundant perception or planning mechanisms at the system level. The inner loop of the process is repeated until sufficient evidence is collected to form the safety assurance argument, as outlined in Section 5. Once complete, confidence in the assurance analysis can then be evaluated, e.g., based on the method described above. If deficits are identified in the argument, this could lead to a re-evaluation of the requirements and more repetitions of the inner loop. Once the confidence in the assurance argument has been confirmed, the ML model can be deployed within its operational context.
The “outer” loop is triggered by knowledge gained during operation which can take the following form. Observations are collected that either reduce environmental/input space and observational/data uncertainty or increase them, e.g., by observing previously unknown triggering conditions or contradictions in assumptions made regarding the environment or system context. In the former case, increased confidence in the assurance of the system and reduced uncertainty could allow for a loosening of operating restrictions and assumptions on the environment to increase utility of the system. This would nevertheless require a repetition of the assurance lifecycle and re-evaluation of the assurance argument. In the latter case, changes within the system or its context could lead to an increase in the actual achieved residual risk. Assurance arguments and evidence supporting the claim could lose their credibility over time if contradicting evidence comes to light, or assumptions under which claims were made no longer hold true. This could result in the removal from service or a restriction in the operating conditions until an assurance argument that takes this new knowledge into account can be constructed with sufficient confidence.
7. Discussion and future work
In this paper, we presented a framework for reasoning about confidence in the assurance of ML-based safety-critical functions. By applying a set of definitions of uncertainty to this problem we can evaluate which statements can be made about the safety of ML for a particular application and which cannot. In particular we show that certain claims of an assurance argument can be made with more confidence than others. ML itself is based on statistical modeling techniques, whilst the occurrence of properties of the input space (triggering conditions) that can lead to failures can often only be reasoned about in a restricted probabilistic manner due to the complexity of the environment and uncertainties in the observation. It should therefore come as no surprise that the safety assurance of ML will require statistical arguments regarding the residual failure rates of the system, but the strength of these statistical arguments rely on a number of qualitative assumptions. A safety assurance argument therefore inevitably needs to consist of a combination of quantitative and qualitative assertions all of which may be subject to different levels of uncertainty. An awareness of sources of uncertainty in the assurance argument is key to closing these gaps as more evidence is collected and a deeper understanding of the system and its environment is gained.
Arguing the absence (or sufficiently low probability) of specific manifestations of performance insufficiencies, e.g., lack of robustness to slight perturbations in the input, can rely on quantitative evidence collected during development. However, sufficient confidence across the Dow hierarchy is required to be able to make decisions under risk [as defined by Knight (1921)]. This can only be achieved if certain assumptions are met. On the other hand, arguing the absence of specification insufficiencies, including the absence of unknown unknowns in the definition of the input space might only be arguable qualitatively during development with indirect quantitative evidence (e.g., residual accident rates) being collected during operation to indicate the presence or absence of residual insufficiencies.
The level of achievable confidence for such arguments will inevitably be dependent upon the actual (rather than perceived or assumed) complexity of the environment, system and task itself. Specification insufficiencies also have a direct impact on the selection of training and testing data. As specification uncertainty is an expression of the semantic gap (Burton et al., 2020) and thereby complexity of the environment, the system and the inherent complexity of the task to be performed, restricting these factors will inevitably reduce the potential for resulting uncertainty in the assurance argument. Residual uncertainty in the assurance argument will, however inevitably remain. Therefore we describe the role of continuous assurance with a targeted focus on resolving assurance uncertainties to increase confidence in the system, thus allowing the restrictions on the environmental, task and system complexity to be incrementally lifted.
Based on these reflections, for which classes of ML systems can reliable safety assurance claims be made? The analysis in this paper leads to the unsurprising conclusions that where there is high uncertainty in the environment and task, but a high level of certainty in understanding the system behavior, a systematically and continuously developed and evaluated assurance argument may eventually lead to a sufficient level of confidence. Likewise, where there is low uncertainty in the specification but high uncertainty in understanding the system behavior (e.g., a DNN with an inherent lack of interpretability is used to learn a well defined, relatively low complexity task), a convincing assurance argument might also be developed. However, where there is a high level of uncertainty in the environment, task and the system itself, a convincing safety assurance argument in an acceptably low level of residual risk is not conceivable based on current methods and technologies. This also implies that there will be no “one size fits all” solution to safety assurance arguments for ML. This paper should therefore provide useful guidance when developing robust assurance arguments for ML and determining under which conditions such arguments cannot be made for specific applications and choice of ML technologies.
We see this paper an initial step in a systematic treatment of uncertainty in the safety assurance of ML-based systems and identify a number of areas of potentially interesting research. Firstly, a better definition and understanding of the inherent task and environmental complexity and environmental would provide means to determine whether or not an assurance argument for a specific problem can be conceivably achieved. This might include providing criteria for comparative evaluation of tasks to determine to which extent demonstratively successful assurance strategies can be transferred to new domains. This work could be supported by the application of the framework to a number of use cases with variations in environmental, task and system complexity to better understand the factors impacting confidence in the assurance argument. Secondly, we see the need to consider the problem of asserted inference when proposing new metrics or methods for providing evidence for the safety of ML. When developing innovative techniques, e.g., for improving robustness, OoD detection or prediction certainty, the set of assumptions on the impact of these properties on the safety requirements and means to demonstrate both the relevance and effectiveness of the techniques should be explicitly considered. Otherwise uncertainty in the assurance arguments making use of this evidence will inevitably remain. Lastly, we see potential for the extension and application of existing techniques for a quantitative evaluation of assurance argument confidence (see Section 2, but not applied here). A combination of these approaches with the categories and severity of uncertainty used in this paper may allow for improved tool support for constructing and evaluating assurance arguments. This may include support for impact analysis and automated re-evaluation based on newly collected observations during operation.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
Both authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was performed as part of the ML4Safety project supported by the Fraunhofer Internal Programs under Grant No. PREPARE 40-02702.
Acknowledgments
The authors would like to thank all colleagues that supported and inspired the development of this work, especially Adrian Schwaiger of Fraunhofer IKS for his detailed review comments.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^https://artificialintelligenceact.eu
2. ^https://www.iso.org/standard/81283.html and https://www.iso.org/standard/83303.html
4. ^Measuring the actual VC dimension of a model is hard and an area of active ongoing research. For example, Li et al. (2018) use measures such as intrinsic dimensions to compare the relative complexity of different ML tasks and Li et al. (2022) identify low dimensional properties of training trajectories with the goal of reducing the number of parameters required to achieve a particular level of performance and robustness.
References
Abrecht, S., Gauerhof, L., Gladisch, C., Groh, K., Heinzemann, C., and Woehrle, M. (2021). Testing deep learning-based visual perception for automated driving. ACM Trans. Cyber Phys. Syst. 5, 1–28. doi: 10.1145/3450356
Anguita, D., Ghelardoni, L., Ghio, A., Oneto, L., and Ridella, S. (2012). “The ‘k' in k-fold cross validation,” in 20th European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN) (Bruges), 441–446.
Ashmore, R., Calinescu, R., and Paterson, C. (2021). Assuring the machine learning lifecycle: Desiderata, methods, and challenges. ACM Comput. Surveys 54, 1–39. doi: 10.1145/3453444
Ayoub, A., Chang, J., Sokolsky, O., and Lee, I. (2013). “Assessing the overall sufficiency of safety arguments,” in 21st Safety-critical Systems Symposium (SSS'13) (Bristol, United Kingdom), 127–144.
Bergenhem, C., Johansson, R., Söderberg, A., Nilsson, J., Tryggvesson, J., Törngren, M., et al. (2015). “How to reach complete safety requirement refinement for autonomous vehicles,” in CARS 2015-Critical Automotive applications: Robustness and Safety (Paris).
Bradley, R., and Drechsler, M. (2014). Types of uncertainty. Erkenntnis 79, 1225–1248. doi: 10.1007/s10670-013-9518-4
Burton, S., Gauerhof, L., and Heinzemann, C. (2017). “Making the case for safety of machine learning in highly automated driving,” in Computer Safety, Reliability, and Security, eds S. Tonetta, E. Schoitsch, and F. Bitsch (Cham: Springer International Publishing), 5–16.
Burton, S., Gauerhof, L., Sethy, B. B., Habli, I., and Hawkins, R. (2019). “Confidence arguments for evidence of performance in machine learning for highly automated driving functions,” in Computer Safety, Reliability, and Security, eds A. Romanovsky, E. Troubitsyna, I. Gashi, E. Schoitsch, and F. Bitsch (Cham: Springer International Publishing), 365–377.
Burton, S., Habli, I., Lawton, T., McDermid, J., Morgan, P., and Porter, Z. (2020). Mind the gaps: Assuring the safety of autonomous systems from an engineering, ethical, and legal perspective. Artif. Intell. 279, 103201. doi: 10.1016/j.artint.2019.103201
Burton, S., Hellert, C., Hüger, F., Mock, M., and Rohatschek, A. (2022). Safety Assurance of Machine Learning for Perception Functions. Cham: Springer International Publishing.
Burton, S., Kurzidem, I., Schwaiger, A., Schleiss, P., Unterreiner, M., Graeber, T., et al. (2021). “Safety assurance of machine learning for chassis control functions,” in Computer Safety, Reliability, and Security, eds I. Habli, M. Sujan, and F. Bitsch (Cham: Springer International Publishing), 149–162.
Cheng, C.-H., Huang, C.-H., Ruess, H., Yasuoka, H., et al. (2018). “Towards dependability metrics for neural networks,” in 2018 16th ACM/IEEE International Conference on Formal Methods and Models for System Design (MEMOCODE) (Beijing: IEEE), 1–4.
Cheng, C.-H., Knoll, A., and Liao, H.-C. (2021). Safety metrics for semantic segmentation in autonomous driving. arXiv preprint arXiv:2105.10142. doi: 10.1109/AITEST52744.2021.00021
Cheng, C.-H., Nührenberg, G., and Ruess, H. (2017). “Maximum resilience of artificial neural networks,” in International Symposium on Automated Technology for Verification and Analysis (Springer), 251–268.
Cordts, M., Omran, M., Ramos, S., Rehfeld, T., Enzweiler, M., Benenson, R., et al. (2016). “The Cityscapes dataset for semantic urban scene understanding,” in CVPR (Las Vegas, NV).
Denney, E., Pai, G., and Habli, I. (2011). “Towards measurement of confidence in safety cases,” in 2011 International Symposium on Empirical Software Engineering and Measurement (Banff), 380–383.
Feurer, M., and Hutter, F. (2019). “Hyperparameter optimization,” in Automated Machine Learning (Cham: Springer), 3–33.
Gansch, R., and Adee, A. (2020). “System theoretic view on uncertainties,” in 2020 Design, Automation and Test in Europe Conference &Exhibition (DATE) (Grenoble: IEEE), 1345–1350.
Gauerhof, L., Munk, P., and Burton, S. (2018). “Structuring validation targets of a machine learning function applied to automated driving,” in International Conference on Computer Safety, Reliability, and Security (San Francisco, CA: Springer), 45–58.
Gladisch, C., Heinzemann, C., Herrmann, M., and Woehrle, M. (2020). “Leveraging combinatorial testing for safety-critical computer vision datasets,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (Seattle, WA: IEEE), 324–325.
Goodenough, J. B., Weinstock, C. B., and Klein, A. Z. (2013). “Eliminative induction: a basis for arguing system confidence,” in 2013 35th International Conference on Software Engineering (ICSE) (San Francico, CA), 1161–1164.
Guo, B. (2003). “Knowledge representation and uncertainty management: applying Bayesian Belief Networks to a safety assessment expert system,” in International Conference on Natural Language Processing and Knowledge Engineering, 2003. Proceedings. 2003 (Beijing), 114–119.
Haedecke, E., Mock, M., and Akila, M. (2022). “ScrutinAI: a visual analytics approach for the semantic analysis of deep neural network predictions,” in EuroVis Workshop on Visual Analytics (EuroVA) (Rome: The Eurographics Association), 73–775.
Hawkins, R., Kelly, T., Knight, J., and Graydon, P. (2011). “A new approach to creating clear safety arguments,” in Advances in Systems Safety (Southampton: Springer), 3–23.
Hawkins, R., Paterson, C., Picardi, C., Jia, Y., Calinescu, R., and Habli, I. (2021). Guidance on the Assurance of Machine Learning in Autonomous Systems (AMLAS). arXiv [Preprint]. arXiv: 2102.01564
Hendrycks, D., Basart, S., Mu, N., Kadavath, S., Wang, F., Dorundo, E., et al. (2021). “The many faces of robustness: a critical analysis of out-of-distribution generalization.,” in ICCV.
Henne, M., Schwaiger, A., Roscher, K., and Weiss, G. (2020). “Benchmarking uncertainty estimation methods for deep learning with safety-related metrics,” in Proceedings of the Workshop on Artificial Intelligence Safety (SafeAI) (New York, NY), 1–8.
Hobbs, C., and Lloyd, M. (2012). “The application of Bayesian Belief Networks to assurance case preparation,” in Achieving Systems Safety, eds C. Dale and T. Anderson (London: Springer London), 159–176.
Houben, S., Abrecht, S., Akila, M., Bär, A., Brockherde, F., Feifel, P., et al. (2022). “Inspect, understand, overcome: a survey of practical methods for AI safety,” in Deep Neural Networks and Data for Automated Driving (Cham: Springer), 3–78.
Hu, B. C., Salay, R., Czarnecki, K., Rahimi, M., Selim, G., and Chechik, M. (2020). “Towards requirements specification for machine-learned perception based on human performance,” in 2020 IEEE Seventh International Workshop on Artificial Intelligence for Requirements Engineering (AIRE) (Zurich: IEEE), 48–51.
Huang, X., Kroening, D., Ruan, W., Sharp, J., Sun, Y., Thamo, E., et al. (2020). A survey of safety and trustworthiness of deep neural networks: verification, testing, adversarial attack and defence, and interpretability? Comput. Sci. Rev. 37, 270. doi: 10.1016/j.cosrev.2020.100270
Huang, X., Kwiatkowska, M., Wang, S., and Wu, M. (2017). “Safety verification of deep neural networks,” in International Conference on Computer Aided Verification (Heidelberg: Springer), 3–29.
ISO (2019). Systems and software engineering – systems and software assurance. Technical Report ISO/IEC/IEEE 15026, 2019, International Organization for Standardization.
Knight, F. H. (1921). Risk, Uncertainty and Profit, volume 31. Boston, MA; New York, NY: Houghton Mifflin.
Kotseruba, I., Rasouli, A., and Tsotsos, J. K. (2016). Joint attention in Autonomous Driving (JAAD). arXiv [Preprint]. arXiv: 1609.04741
Li, C., Farkhoor, H., Liu, R., and Yosinski, J. (2018). Measuring the intrinsic dimension of objective landscapes. arXiv preprint arXiv:1804.08838. doi: 10.48550/arXiv.1804.08838
Li, T., Tan, L., Huang, Z., Tao, Q., Liu, Y., and Huang, X. (2022). Low dimensional trajectory hypothesis is true: DNNs can be trained in tiny subspaces. IEEE Trans. Pattern Anal. Mach. Intell. 45, 3411–3420. doi: 10.1109/TPAMI.2022.3178101
Moreno-Torres, J. G., Raeder, T., Alaiz-Rodríguez, R., Chawla, N. V., and Herrera, F. (2012). A unifying view on dataset shift in classification. Pattern Recognit. 45, 521–530. doi: 10.1016/j.patcog.2011.06.019
Northcutt, C. G., ChipBrain, M., Athalye, A., and Mueller, J. (2021). Pervasive label errors in test sets destabilize machine learning benchmarks. arXiv [Preprint]. arXiv: 2103.14749.
Odena, A., Olsson, C., Andersen, D., and Goodfellow, I. (2019). “Tensorfuzz: debugging neural networks with coverage-guided fuzzing,” in International Conference on Machine Learning (Long Beach, CA: PMLR), 4901–4911.
Rocha Souza, R., Dorn, A., Piringer, B., and Wandl-Vogt, E. (2019). Towards a taxonomy of uncertainties: analysing sources of spatio-temporal uncertainty on the example of non-standard German corpora. Informatics 6, 34. doi: 10.3390/informatics6030034
Rudin, C. (2019). Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 1, 206–215. doi: 10.1038/s42256-019-0048-x
Salay, R., Angus, M., and Czarnecki, K. (2019). “A safety analysis method for perceptual components in automated driving,” in 2019 IEEE 30th International Symposium on Software Reliability Engineering (ISSRE) (Berlin: IEEE), 24–34.
Salay, R., Queiroz, R., and Czarnecki, K. (2017). An analysis of ISO 26262: using machine learning safely in automotive software. arXiv preprint arXiv:1709.02435. doi: 10.4271/2018-01-1075
Sato, A., and Yamada, K. (1995). “Generalized learning vector quantization,” in Advances in Neural Information Processing Systems, Vol. 8 (Denver, CO).
Schleiss, P., Carella, F., and Kurzidem, I. (2022). “Towards continuous safety assurance for autonomous systems,” in Proceedings of 12th IEEE International Workshop on Software Certification at 33rd IEEE International Symposium on Software Reliability Engineering (ISSRE) (Venice: IEEE).
Schorn, C., and Gauerhof, L. (2020). “Facer: a universal framework for detecting anomalous operation of deep neural networks,” in 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC) (Rhodes: IEEE), 1–6.
Schwaiger, F., Küppers, M. H. F., Roza, F. S., Roscher, K., and Haselhoff, A. (2021). “From black-box to white-box: Examining confidence calibration under different conditions,” in Proceedings of the Workshop on Artificial Intelligence Safety (SafeAI), 1–8.
Shorten, C., and Khoshgoftaar, T. M. (2019). A survey on image data augmentation for deep learning. J. Big Data 6, 1–48. doi: 10.1186/s40537-019-0197-0
Sun, Y., Wu, M., Ruan, W., Huang, X., Kwiatkowska, M., and Kroening, D. (2018). “Concolic testing for deep neural networks,” in Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering (Montpellier: IEEE), 109–119.
Usvyatsov, A. (2019). On sample complexity of neural networks. arXiv preprint arXiv:1910.11080. doi: 10.48550/arXiv.1910.11080
Walker, W. E., Harremoës, P., Rotmans, J., Van Der Sluijs, J. P., Van Asselt, M. B., Janssen, P., et al. (2003). Defining uncertainty: a conceptual basis for uncertainty management in model-based decision support. Integrated Assess. 4, 5–17. doi: 10.1076/iaij.4.1.5.16466
Wang, C., Wang, J., and Lin, Q. (2021). “Adversarial attacks and defenses in deep learning: a survey,” in Intelligent Computing Theories and Application, eds D.-S. Huang„ K.-H. Jo, J. Li„ V. Gribova, and V. Bevilacqua (Cham: Springer International Publishing), 450–461.
Wang, R., Guiochet, J., Motet, G., and Schön, W. (2019). Safety case confidence propagation based on dempster-shafer theory. Int. J. Approx. Reason. 107, 46–64. doi: 10.1016/j.ijar.2019.02.002
Williamson, J. (2014). How uncertain do we need to be? Erkenntnis 79, 1249–1271. doi: 10.1007/s10670-013-9516-6
Keywords: machine learning, safety, assurance arguments, cyber-physical systems, uncertainty, complexity
Citation: Burton S and Herd B (2023) Addressing uncertainty in the safety assurance of machine-learning. Front. Comput. Sci. 5:1132580. doi: 10.3389/fcomp.2023.1132580
Received: 27 December 2022; Accepted: 20 March 2023;
Published: 06 April 2023.
Edited by:
Xiaowei Huang, University of Liverpool, United KingdomReviewed by:
Jianwen Li, East China Normal University, ChinaPanagiotis Katsaros, Aristotle University of Thessaloniki, Greece
Copyright © 2023 Burton and Herd. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Simon Burton, c2ltb24uYnVydG9uQGlrcy5mcmF1bmhvZmVyLmRl
 Simon Burton
Simon Burton Benjamin Herd
Benjamin Herd