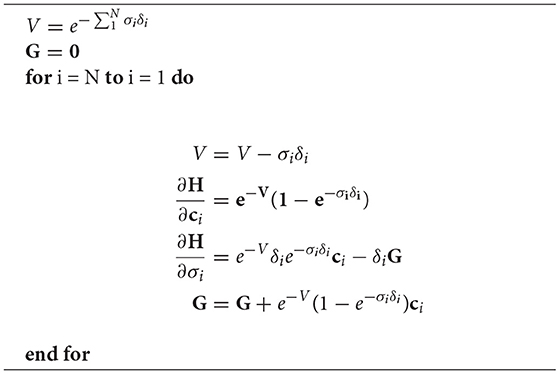PERF: Performant, Explicit Radiance Fields

We present a novel way of approaching image-based 3D reconstruction based on radiance fields. The problem of volumetric reconstruction is formulated as a non-linear least-squares problem and solved explicitly without the use of neural networks. This enables the use of solvers with a higher rate of convergence than what is typically used for neural networks, and fewer iterations are required until convergence. The volume is represented using a grid of voxels, with the scene surrounded by a hierarchy of environment maps. This makes it possible to get clean reconstructions of 360° scenes where the foreground and background is separated. A number of synthetic and real scenes from well-known benchmark-suites are successfully reconstructed with quality on par with state-of-the-art methods, but at significantly reduced reconstruction times.

1. Introduction

We present Performant Explicit Radiance Fields (PERF), a novel approach to image-based volumetric reconstruction of 360° scenes based on radiance fields. Unlike previous methods, our approach does not use an MLP solution, but instead solves the problem directly as a non-linear least-squares system. This system is minimized using a Gauss-Newton solver with higher rate of convergence than standard Stochastic Gradient Descent used for systems based on Neural Networks. As a result, the time until convergence for a given scene is significantly shorter than for comparable methods.

The NERF (Mildenhall et al., 2020) techniques present a simple formulation of the 3D reconstruction problem using volume rendering and neural networks. We ask the question if it is possible to solve this problem directly using pure ADAM-optimization (see Figure 1; Kingma and Ba, 2014). With this confirmed, and identifying the problem as non-linear least-squares, we can see that it is possible to achieve much higher convergence rates for the same volumetric formulation, without sacrificing much in terms of quality.

FIGURE 1

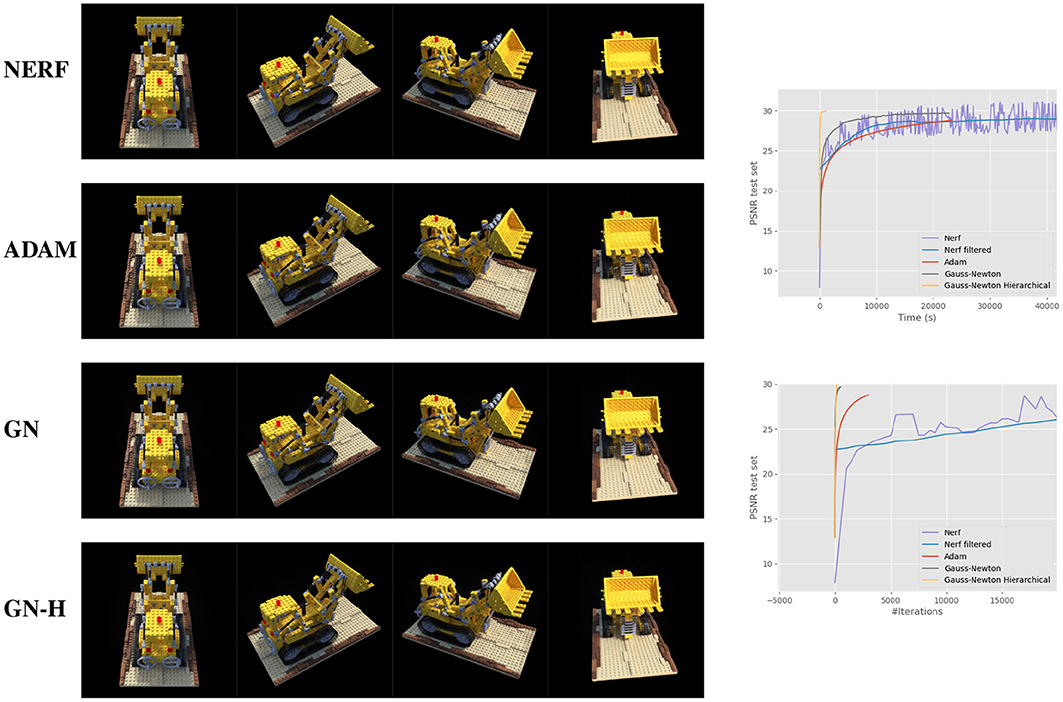
Figure 1. Hold out views for the lego scene comparing NERF (without view-dependence), pure ADAM-optimization, regular Gauss-Newton optimization and a hierarchical Gauss-Newton formulation; from top to bottom. To the top-right the corresponding PSNR-curves are shown vs. time; to the bottom-right PSNR is plotted vs. number of iterations.

The scene is represented using a grid of voxels containing color and opacity values. Additionally, surrounding the object of interest, is a hierarchical layer of environment maps (also with color and opacity), which enable efficient segmentation of foreground from background.

A ray is followed through each pixel of a given image, and color accumulated through the voxel grid and the surrounding environment maps according to classic volumetric rendering. The square of the difference between the accumulated ray and the value of the pixel is then computed for each pixel in each image. The sum of all these differences builds up to a non-linear least-squares system. In this system, each ray corresponds to three residuals (one for each color channel), and each voxel in the grid and texel in the environment maps corresponds to four variables each (three color channels and opacity).

This non-linear least squares system can be solved efficiently using the Gauss-Newton method. The Gauss-Newton method has several useful properties in being amenable to parallelization, while only requiring the computation of partial derivatives of the first degree. We show that these derivatives can be computed analytically with a simple iterative algorithm. Each Gauss-Newton step is computed using the iterative Preconditioned Conjugate Gradient algorithm.

Since rendering the volume only amounts to raymarching through the voxel grid and environment maps, inspecting and evaluating the reconstruction is possible in real-time during any stage of the computation.

To summarize, the contributions in this paper are:

• a solution of volumetric reconstruction based on a non-linear least squares formulation,

• efficient computation of analytical derivatives using an iterative algorithm,

• a fast GPU-based Gauss-Newton solver using Preconditioned Conjugate Gradient,

• the separation of foreground and background for 360° scenes using a hierarchical envelope of environment maps.

Note that we do not consider view-dependent effects in this work.

2. Related Work

2.1. Multi-View Stereo

Multi-view stereo (MVS) is a classical application of computer vision where a scene is reconstructed from a set of images taken from multiple viewpoints, typically using pairwise stereo matching algorithms. This is a well-researched topic that have been extensively treated the last few decades. For an overview, see Hartley and Zisserman (2004) and Seitz et al. (2006). In recent years, this approach have been successfully paired with neural networks in deep multi-view stereo (Yao et al., 2018, 2019).

2.2. Structure From Motion

Another classical approach for scene reconstruction is Structure from Motion (SfM) (Snavely et al., 2006; Özyeşil et al., 2017). In these systems images are paired by identifying image features, which works well given that there is enough overlap between the images. Camera poses (or motion) are estimated and 3D points corresponding to image features are computed. The output of such a reconstruction is sparse, but it can be paired with stereo matching techniques such as PatchMatch Stereo to create dense output (Bleyer et al., 2011; Schonberger and Frahm, 2016).

2.3. View Synthesis

View synthesis is a related research area where focus lies on synthesizing novel viewpoints given a set of images and their poses, not necessarily caring about the underlying geometry of the scene. This includes image-based rendering and lightfields, which have been explored thoroughly over the years (Shum and Kang, 2000).

One recent attempt at this problem is to use Multi-Plane Images (MPIs); a set of semi-transparent images that can be trained efficiently with neural networks and then rendered from a novel viewpoint (Zhou et al., 2018; Mildenhall et al., 2019).

Broxton et al. (2020) surround the scene with a hierarchical set of environment maps in a similar way to ours using MPIs, with the goal of representing a scene captured by a fixed rig of 46 synchronized action cameras. They, however, use MPIs as the primary data structure to represent their scenes, while in our work we use the surrounding environment maps as a tool to segment the background from the region of interest modeled with voxels. Our work does also not use neural networks to train MPIs, but instead use a layer of environment maps optimized explicitly in the same manner (and simultaneously) as the voxel grid.

2.4. Neural Rendering

Recently a popular approach have been to use neural networks as a key component in encoding the scene representation. In Neural Volumes (Lombardi et al., 2019), a semi-transparent voxel grid is coupled with a encoder-decoder network to create high quality reconstructions from a multi-view setup. While the scene is not explicitly stored in a network, they are still pivotal to its overall approach. In NERF (Mildenhall et al., 2020), the outgoing radiance f(x, ω) at any point, x, and direction, ω, is expressed as an MLP with a positional encoding for the inputs. The positional encoding has recently been shown to improve the ability of an MLP to reconstruct high frequency signals (Tancik et al., 2020b). Many improvements have been presented to the original NERF implementation to help with e.g., improved view synthesis and large scenes (Liu et al., 2020; Martin-Brualla et al., 2021).

Follow-up work has shown that it is possible to transform a trained NERF MLP into a format more suitable for real-time rendering (Rebain et al., 2020; Garbin et al., 2021; Hedman et al., 2021; Neff et al., 2021; Reiser et al., 2021; Yu et al., 2021). Some of these methods use voxels as part of their visualization but still use neural networks for their training. Due to the need of transforming the NERF model for rendering, these methods typically add even more time to the already time-consuming training.

For an overview of this growing field, we refer the reader to the STAR-paper by Tewari et al. (2020).

To our knowledge, only a few papers have tried to address one of the main caveats of the otherwise compelling approach used in NERF; namely the long reconstruction times.

Tancik et al. have demonstrated that, when the target function belongs to a known class, the network can be pre-initialized to make the final optimization faster (Tancik et al., 2020a). The authors show that when pretraining on a class of objects in the ShapeNet (Chang et al., 2015) dataset, the result after a few iterations is much better than, but the quality converges to the same value as for, a randomly initialized network after as many iterations. An important observation in our paper is that a discrete Radiance Field can be obtained much faster by optimizing the function, f(x, ω), directly rather than training an MLP representation.

MVSNerf (Chen et al., 2021) is an alternative approach to creating a Radiance Field, in which a few input views are processed through a CNN to create a feature vector that is projected into a cost volume defined by a reference camera. These feature vectors are passed, along with position and direction, to an MLP which is optimized as in previous work. This allows for much faster training of the network, but unfortunately only for the geometry directly seen by the reference camera.

In this work, we significantly improve the reconstruction times by identifying the problem of volumetric reconstruction as a non-linear least-squares problem, which can be solved directly with an efficient Gauss-Newton solver.

3. Methods

We represent the scene using a voxel grid, where each cell contains three color channels, C = {c_r, c_g, c_b}, and differential opacity (σ in Equations 1–4). The voxel grid is surrounded by a hierarchical set of environment maps, centered around the object of interest. These environment maps also contain a color and opacity per texel. The main purpose of these environment maps is not to try to reconstruct the background, but rather to improve convergence and allow for transparent voxels (see Figure 2).

FIGURE 2

Figure 2. Environment maps surround the scene, improving convergence and allowing for separation of foreground and background.

3.1. Volume Rendering

The render an image, the color of each pixel is computed by integrating over the ray going through the pixel and into the volume using the volume rendering equation:

$\begin{array}{ll}H(\text{r})={\displaystyle {\int }_{t_n}^{t_f}}T(t)\sigma \left[\text{r}(t)\right]\text{c}\left[\text{r}(t)\right]dt& (1)\end{array}$

where

$\begin{array}{ll}T(t)=e^{(-{\int }_{t_n}^t\sigma \left[\text{r}(s)\right]ds)}.& (2)\end{array}$

Given that the volume is discretized in a grid, the equation amounts to ray-marching through this grid according to:

$\begin{array}{ll}\widehat{\text{H}}={\displaystyle \sum _{t_n}^{t_f}}\widehat{T}(t)(1-e^{\left[-\sigma (t)\delta (t)\right]})\text{c}(t)& (3)\end{array}$

where

$\begin{array}{ll}\widehat{T}(t)=e^{\left[-{\displaystyle {\sum }_{t_n}^t}\sigma (t)\delta (t)\right]}.& (4)\end{array}$

The contribution from the environment maps are accumulated much in the same manner, but instead of ray-marching intersection testing is used, starting from where the ray exists the volume and going outwards, see Section 4.3 and Figure 3.

FIGURE 3

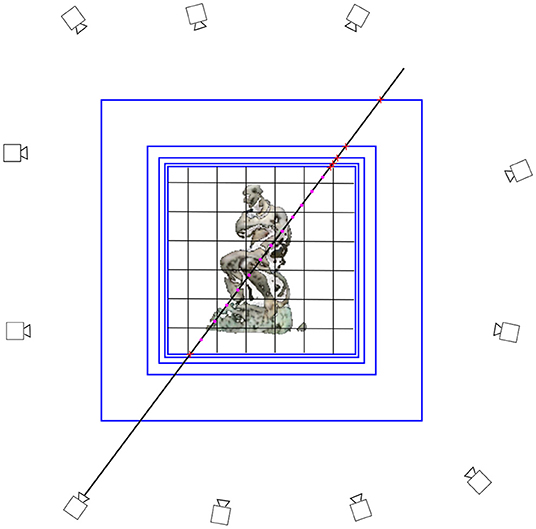
Figure 3. A sketch of how a ray is integrated through the scene representation. The main region of interest is surrounded by a voxel grid. This grid is hierarchichally surrounded by environment maps, their distance increasing with the square of the distance to the voxel grid. First, an intersection test is made between the ray and the grid to get the entry and exit points. While in the volume, the ray is raymarched using jittered steps. Upon exit, the ray is successively intersected with the environment maps in order. Intersection tests are marked with an x and raymarch steps with a dot.

3.2. Volumetric Reconstruction

Given a set of images of a scene, we wish to reconstruct the volume enclosed by the corresponding cameras in 3D. Using the formulation of volume rendering from Equation (3), we can formulate the reconstruction as an optimization problem that minimizes the sum of squares of the difference between the accumulated color for a ray sent through each pixel of every image, and the actual color sampled from the same pixel. The objective function that we want to minimize is:

$\begin{array}{ll}F\left[\text{c}(t),\sigma (t)\right]=0.5{\displaystyle \sum _{t_n}^{t_f}}{\displaystyle \sum _{i=1}^3}{({Ĥ}_i\left[c_i(t),\sigma (t)\right]-C_i)}^2,& (5)\end{array}$

with Ĥ_i[c_i(t), σ(t)] from Equation (3) and each pixel color C_i.

3.3. Non-linear Least-Squares Formulation

The objective function in Equation (5) is a non-linear least-squares equation, of which the general form is

$\begin{array}{ll}S(\text{x})=0.5{\displaystyle \sum _{i=1}^m}{r}_i{(\text{x})}^2,& (6)\end{array}$

where r_i are called residuals.

The problem of volumetric reconstruction can thus be formulated as the minimization of a non-linear least-squares problem of this form, where the residuals r_i correspond to the the difference between pixel color C and accumulated colors $\widehat{\text{H}}$ for each ray. For each pixel the three color channels are added independently to the sum, giving three residuals per ray.

3.4. Gauss-Newton Solver

The Gauss-Newton algorithm can be used to iteratively solve non-linear least-squares problems of the form in Equation (6) and Nocedal and Wright (2006). Starting with a value x₀, the update function for the algorithm is:

$\begin{array}{ll}{x}_{i+1}=x_i-{(J_r{}^T{J}_r)}^{-1}{J}_r{}^{T}r(x_i)& (7)\end{array}$

$\begin{array}{ll}={\text{x}}_i+\Delta & (8)\end{array}$

where x_i represent all color and opacity values, J_r is the jacobian and Δ is the update step.

The matrix J_r is very sparse, since only a fraction of all x_i's (corresponding to a voxel or texel) will actually be hit by a given ray, and thus be non-zero.

3.5. Computation of Partial Derivatives

For each ray that is marched through the volume, the partial derivatives need to be computed with respect to each variable in the voxels or texels that are encountered for Equation (3). We can rewrite (Equation 3) as:

$\begin{array}{l}\widehat{\text{H}}=e^0(1-e^{-{\sigma }_1{\delta }_1}){\text{c}}_1\\ +e^{-{\sigma }_1{\delta }_1}(1-e^{-{\sigma }_2{\delta }_2}){\text{c}}_2\\ +e^{-({\sigma }_1{\delta }_1+{\sigma }_2{\delta }_2)}(1-e^{-{\sigma }_3{\delta }_3}){\text{c}}_3\\ +\dots \\ +e^{-{\displaystyle {\sum }_1^{N-1}}{\sigma }_i{\delta }_i}(1-e^{-{\sigma }_N{\delta }_N}){\text{c}}_N\end{array}$

The partial derivatives can be efficiently computed with only two auxiliary variables if this equation is traversed backwards (Algorithm 1).

ALGORITHM 1

Algorithm 1. Iterative algorithm for computation of partial derivatives of Equation (3).

3.6. Update Step

The update step of Equation (8) requires an expensive matrix inversion of the large and sparse square matrix ${{\text{J}}_r}^T{\text{J}}_r$. Instead of performing this operation explicitly, it is possible to rewrite the step calculation as a linear system Ax = b, where $\text{A}={{\text{J}}_r}^{\top }{\text{J}}_r$, x = Δ and $\text{b}=-{{\text{J}}_r}^{\top }\text{r}$. Note that ${{\text{J}}_r}^{\top }\text{r}$ corresponds to the gradient of the residual ∇r.

A is a very large and sparse matrix (nxn where n is the total number of parameters in the voxel grid and environment maps). One efficient way of solving the linear system is to use the iterative Preconditioned Conjugate Gradient (PCG) algorithm (Algorithm 2).

ALGORITHM 2

Algorithm 2. The iterative Preconditioned Conjugate Gradient algorithm, with precondition matrix M (see Section 3.7).

The variables r, z, p and x are temporary variables with the same size and shape as the voxel grid (or environment maps if they are used). The vector addition (such as x_k + α_kp_k) and dot products (such as ${\text{r}}_k^{\top }{\text{z}}_k$) of Algorithm 2 are cheap and easy to compute in parallel on the GPU. The computation of Ap, however, requires some additional exposition. The matrix A itself is much too large to form explicitly (for a very modest 32³ grid it amounts to 4TB of data). To get around this, the following identity can be used:

$\begin{array}{ll}\text{A}\text{p}={\text{J}}_r^{\top }{\text{J}}_r\text{p}={\displaystyle \sum _i}\nabla {\text{r}}_i(\nabla {\text{r}}_i^{\top }\text{p}).& (9)\end{array}$

This enables each residual to add independently to the computation of Ap, resulting in efficient parallelization. For the computation of the gradients ∇r_i we use Algorithm 1. The algorithm is invoked twice; once to compute the sum of the dot product $\nabla {\text{r}}_i^{\top }\text{p}$, and once to compute the scalar-vector product with this sum and the gradient ∇r_i.

3.7. Preconditioner

For the precondition matrix M we use a simple diagonal Jacobi preconditioner. This can be computed jointly with the gradients since

$\begin{array}{l}diag(J_r{}^{\top }{J}_r)=\left[{\displaystyle \sum {(\frac{\partial r_i}{\partial x_1})}^2},{\displaystyle \sum {(\frac{\partial r_i}{\partial x_2})}^2},\dots ,{\displaystyle \sum {(\frac{\partial r_i}{\partial x_n})}^2}\right].\end{array}$

The size of these diagonal elements amounts to a total of n variables, the same as for the voxel grid. This also implies that each precondition with M⁻¹ simplifies to regular vector addition.

Since each iteration of Algorithm 2 is quite expensive, especially the computation of Ap, we strive to keep the number of iterations of the PCG algorithm low. If the convergence rate is not high enough, then we have found it preferable to exit early (the second condition in Algorithm 2) and continue with the next Gauss-Newton iteration. Typically, 1 − 3 iterations of the PCG algorithm is evaluated.

3.8. Line Search

In the Gauss-Newton method, there is no guarantee that the objective function will decrease at every iteration. It can however be shown that the direction $\Delta =-{({{\text{J}}_r}^{\top }{\text{J}}_r)}^{-1}{{\text{J}}_r}^T\text{r}$ is a descent direction. Therefore, taking a a sufficiently small step γ in this direction should take us closer to a solution. In the update function of the Gauss-Newton algorithm (Equation 8), there is no scaling of the step length. We therefore add a simple backtracking algorithm that starts at the initial step length γ = 1 and scales the step size by geometrical decimation with a factor of α = 0.7. We then use a simple heuristic to decide if decimation should continue based on evaluating (Equation 6) (see Algorithm 3).

ALGORITHM 3

Algorithm 3. The backtracking algorithm used to find a suitable step size.

3.9. Auxiliary Terms

One way for the algorithm to handle view-dependent surfaces is to add highlight-colored smoke-like artifacts in the volume (see Figure 4). To mitigate this problem, one extra residual is added per ray. This extra term penalizes the total accumulated opacity along a ray if it deviates from 0 or 1. The reasoning is that either the ray should see background and thus the path should be fully transparent, or that it hits the object of interest in which case it should be fully opaque. The following quadratic is used:

$\begin{array}{ll}L=\lambda \left[-4{(\widehat{T}-0.5)}^2+1\right]& (10)\end{array}$

with $\widehat{T}$ from Equation (4) and the factor λ = 0.1.

FIGURE 4

Figure 4. (Left) Smoke-like artifacts is a way for the algorithm to compensate for view-dependent surfaces. (Right) Result with a threshold on the accumulated opacity during rendering.

4. Implementation

The Gauss-Newton solver is implemented in CUDA. The grid data is stored in a 3D surface, while the environment maps are stored in cube maps. To facilitate the use of atomics in CUDA, the backing storage is copied to regular memory for some kernels, since this feature is not supported for surfaces. CUDA texture objects are bound to surfaces when sampling, giving access to hardware trilinear interpolation.

4.1. Hierarchical Formulation

To speed up reconstruction further, a simple hierarchical scheme is used, typically with 4–5 hierarchical levels. The resolution in each dimension is doubled for the voxel grid and the environment maps for each increasing level. A fixed number of iterations (typically N = 30) are performed per level, starting at a resolution of (32, 32, 32) for the voxel grid and (32, 32) for each cubemap. The initial values are typically random colors with low opacity. When a level is completed, the tentative result is stored temporarily while all buffers are reallocated. The new buffers are then populated with the old data using linear interpolation, and computation is resumed at the new hierarchical level. The optimization is sensitive to the initial state of the colors and opacity, and by priming each new hierarchical level with the result from the previous one, a reasonable start guess is acquired from start. Also, the algorithm only starts from random values for a very low resolution, where each iteration is cheap to compute and the extra time spent is negligible.

4.2. Jittering

The position within each pixel which the ray originates from is chosen randomly according to two uniformly distributed floats. Jittering is also applied along each ray, randomizing the position of which samples are taken within half a raymarch step before and after the uniform steps along the ray.

4.3. Rendering

Real-time rendering of a given scene is done with Equation (3). This allows for continuous inspection of a scene during training from any given viewpoint. First, an intersection test is made with the ray and bounding box of the voxel grid. The grid is then ray-marched with a step length equal to the shortest side of a voxel cell. Exiting the volume, the ray is intersected in order with the surrounding environment maps.

Upon convergence of a scene, some of flying artifacts are usually still present (Figure 4). To remove these, we simply add a minimum threshold (1.0−T) < 0.7 for the total opacity along a ray within the target volume when rendering the converged scene. Failing this test, the occupying volume is considered fully transparent.

5. Results

We have used our method on a number of different scenes among the NERF data sets, as well as for the Tanks and Temples data set (Knapitsch et al., 2017). As a reference, we compare our reconstructions with those from NERF with view-dependence disabled to make for a viable comparison. For the synthetic scenes we also compare with the voxel-based method SNerG (Hedman et al., 2021) rendered with the diffuse part only, as well as standard NERF.

The resolution of the final hierarchical level of the voxel grid is typically 256³ or 512³ (see Table 2). We use 10 environment maps surrounding the 360° scenes with corresponding resolutions of 256² or 512² for each cubemap face. The synthethic scenes are run with half image resolution, and all 360° scenes are run with quarter image resolution to conserve memory during NERF training.

For all 360° scenes, PSNR-scores are computed on a set of hold-out views, corresponding to every eighth image in the data set. These views are not part of the reconstruction step.

All results are computed on a single Nvidia Titan V GPU.

5.1. Reconstruction Quality

In Figure 5, our method is tested on a number of synthetic scenes from the NERF data set. In all these cases, we achieve similar or better results compared to the reference (see Table 1). We have purposefully excluded scenes with too much specularities from these sets, since that is not handled well by either us or NERF without view-dependence. The bottom microphone scene in Figure 5 is on the limit of what the methods without view-dependence can handle. In this case, our method manages to average out specularities in a more pleasing way compared to NERF.

FIGURE 5

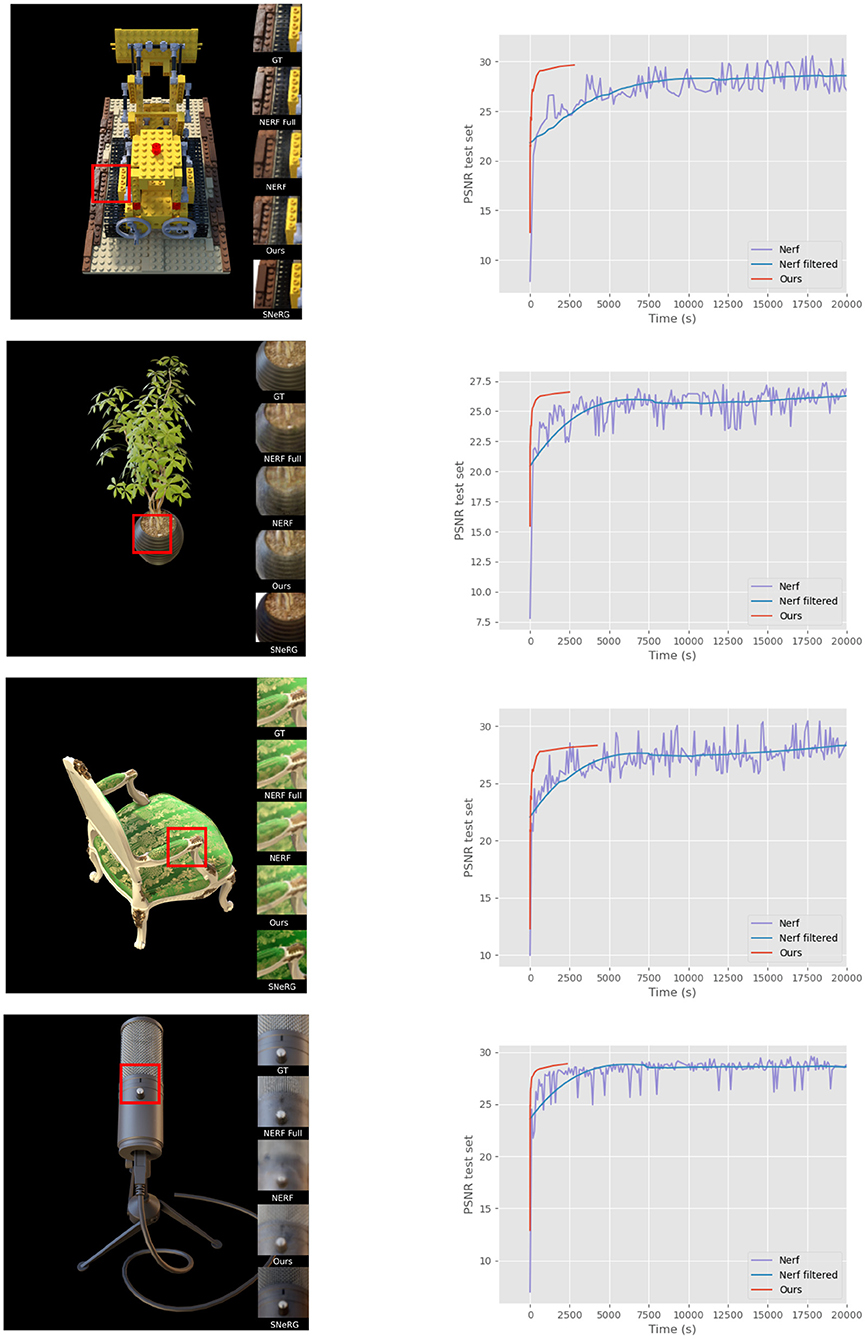
Figure 5. Results on scenes from the NERF synthetic data set. Our reconstructions are shown in comparison with full NERF, NERF without view dependence, and SNeRG. On the right curves of PSNR vs. training time are shown for our method and NERF without view dependence. We can see that our method converges much faster, while obtaining a comparable level of quality.

TABLE 1

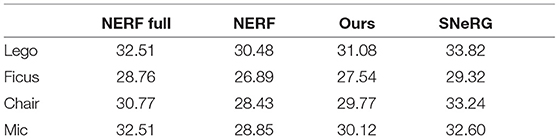
Table 1. PSNR-scores on holdout views of scenes from the NERF synthetic data set for original NERF, NERF without view-dependence, our method, and SNeRG.

SNeRG achieves overall good quality compared to ground truth, almost in parity with standard NERF. A direct comparison, however, is hard to make since we have used their pre-trained models including view-dependence. The scenes shown with SNeRG are therefore trained using the full model and then rendered with only diffuse components. For SNeRG, the scores shown in Table 1 are with view-dependence included since rendering with diffuse components only would skew the results in a negative way.

In Figure 6, we have reconstructed the two 360° scenes used in the NERF paper, as well as a number of scenes from the Tanks and Temples benchmark suite. To get a comparable metric, we have first masked out the foreground for each input image using our method. The PSNR metric have then been computed on the results of both our and NERF's reconstructions while applying these masks. We get similar quality using our method compared to the reference. By visual inspection, our result has a bit higher resolution but with more noise compared to NERF.

FIGURE 6

Figure 6. Results on the 360° scenes from the NERF data set as well as scenes from the Tanks and Temples data set. The cut-outs show the ground truth, our reconstruction and NERF without view-dependence. Corresponding average PSNR-scores computed over a set of hold out views are shown beneath each cut-out.

5.2. Performance

In the right side of Figure 5, corresponding PSNR-curves are shown for our method vs. the reference for some artificial scenes from the NERF data set. We can see that the convergence is much higher for our method while achieving a similar or better final PSNR-score.

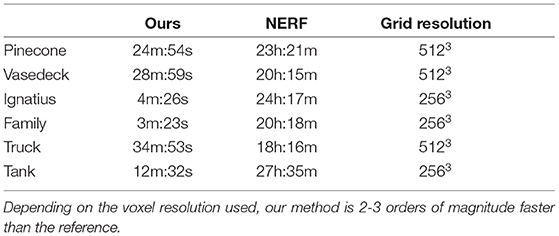
For the 360° scenes in Figure 6, the computation times are shown in Table 2. Since proper comparison requires the application of a foreground mask from our finished scene, we only show the final time until convergence for our method vs. NERF. We can see that our method is 30–400 times faster than the reference method at comparable quality. The main reason for the spread in computation time for our method is if it has required four or five hierarchical levels to achieve the same level of quality as the reference. This in turn is largely decided by the relative distance between the cameras and the object of reconstruction, since we use a fixed discretization using a voxel grid.

TABLE 2

Table 2. Reconstruction times for the 360° scenes.

The relative costs of the included CUDA kernels are shown in Figure 7. The kernels of the PCG algorithm are also shown. Note that the “gradient” post also includes computation of the preconditioner in each iteration as discussed in Section 3.7.

FIGURE 7

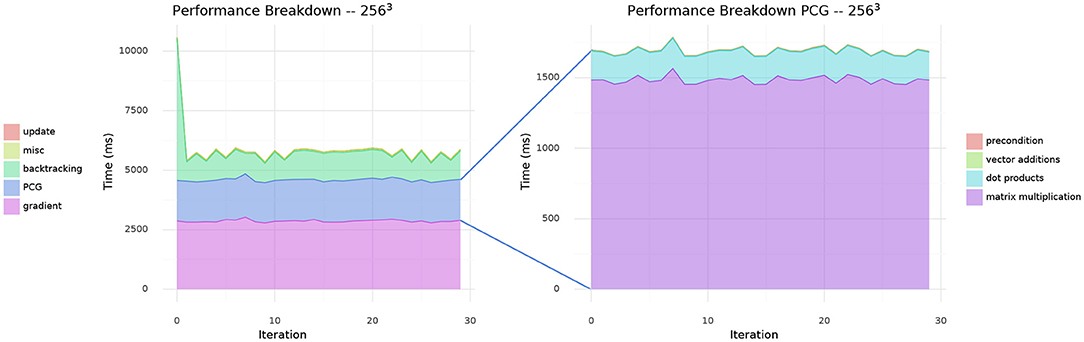
Figure 7. Performance breakdown of used CUDA kernels. The PCG algorithm is comprised of several kernels whose individual times are shown to the right.

5.3. Memory Usage

The memory usage of a dense grid that uses 32-bit floats, three color channels, and one density value is 2GB for a resolution of 512³. Using a preconditioner, the maximum number of live buffers for a given kernel is three (colors+density, gradient and preconditioner), otherwise two.

The memory usage for the 10 surrounding environment maps in 512² is 240MB.

Our dense representations makes it unfeasible to go to higher voxel resolutions, even though this would be necessary to get full quality out of the data sets used in this paper where the pixel resolution varies from 800 x 800 up to 4,032 x 3,024. A sparse implementation that would concentrate voxels around the surface boundary of objects (scaling quadratically instead of cubically) would be necessary for that to work.

The rendering and training times are memory bound and scales with the number of traversed voxels for each ray. Sparse implementations such as PlenOctrees (Yu et al., 2021) and SNeRG (Hedman et al., 2021) show that it is possible to get real-time rendering also for higher resolutions of voxels, which for us would also translate to faster training times.

5.4. Rendering Times

For a test view, rendering a voxel grid of 512³ in Full HD takes about 10–25 ms on an NVIDIA Titan V GPU, depending on how much of the scene that fills the camera view. For comparison, rendering a 400 x 400 image with NERF takes about 6 s on the same hardware. SNeRG has a structure very amenable to fast rendering, and can render scenes in ~64 fps on a Macbook Pro (Hedman et al., 2021).

6. Discussion

We present a novel method that can be used to reconstruct both real and artificial 360° scenes. We obtain comparable quality to the reference, both subjectively and with respect to PSNR (Figures 5, 6). Performance-wise, our reconstruction times are about two to three order of magnitudes faster then for the compared method (Figures 5, 6).

In this paper, we chose to limit our reconstruction to view-independent radiance fields, as we focused on the explicit reconstruction of the non-linear least-squares formulation, and the task of solving this with high performance. Even though the reconstruction show some robustness to view-dependant effects such as highlights, highly specular scenes from the NERF data set had to be omitted. This is true both for our method and for NERF without view-dependence. It would therefore be interesting to extend the ideas in this paper to incorporate view-dependence, to enable a true comparison between our method and NERF.

Another interesting idea to follow up on would be to exploit the fact our method requires about three order of magnitudes fewer iterations until convergence (see Figure 1). This makes our method a strong candidate for distributed computing, since that requires synchronization of intermediate results between nodes for each iteration.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

SR, ES, and UA contributed to the conception and design of the project. SR implemented the software and performed the experiments. All the authors contributed to writing the manuscript.

Funding

This work was supported by the Swedish Research Council under Grant 2014-4559.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bleyer, M., Rhemann, C., and Rother, C. (2011). Patchmatch stereo-stereo matching with slanted support windows. BMVC 11, 1–11. doi: 10.5244/C.25.14

CrossRef Full Text | Google Scholar

Broxton, M., Flynn, J., Overbeck, R., Erickson, D., Hedman, P., Duvall, M., et al. (2020). Immersive light field video with a layered mesh representation. ACM Trans. Graph. 39, 3392485. doi: 10.1145/3386569.3392485

CrossRef Full Text | Google Scholar

Chang, A. X., Funkhouser, T., Guibas, L., Hanrahan, P., Huang, Q., Li, Z., et al. (2015). Shapenet: an information-rich 3d model repository. arxiv:1512.03012. doi: 10.48550/arXiv.1512.03012

CrossRef Full Text | Google Scholar

Chen, A., Xu, Z., Zhao, F., Zhang, X., Xiang, F., Yu, J., et al. (2021). MVSNeRF: fast generalizable radiance field reconstruction from multi-view stereo. arXiv:2103.15595. doi: 10.1109/ICCV48922.2021.01386

CrossRef Full Text | Google Scholar

Garbin, S. J., Kowalski, M., Johnson, M., Shotton, J., and Valentin, J. (2021). Fastnerf: high-fidelity neural rendering at 200fps. arXiv preprint arXiv:2103.10380. doi: 10.1109/ICCV48922.2021.01408

CrossRef Full Text | Google Scholar

Hartley, R. I., and Zisserman, A. (2004). Multiple View Geometry in Computer Vision, Second edition. Cambridge: Cambridge University Press.

Hedman, P., Srinivasan, P. P., Mildenhall, B., Barron, J. T., and Debevec, P. (2021). “Baking neural radiance fields for real-time view synthesis,” in ICCV (Montreal, QC).

Kingma, D., and Ba, J. (2014). “Adam: a method for stochastic optimization,” in International Conference on Learning Representations (San Diego, CA).

Knapitsch, A., Park, J., Zhou, Q.-Y., and Koltun, V. (2017). Tanks and temples: benchmarking large-scale scene reconstruction. ACM Trans. Graph. 36, 3073599. doi: 10.1145/3072959.3073599

CrossRef Full Text | Google Scholar

Liu, L., Gu, J., Lin, K. Z., Chua, T.-S., and Theobalt, C. (2020). “Neural sparse voxel fields,” in NeurIPS.

Lombardi, S., Simon, T., Saragih, J., Schwartz, G., Lehrmann, A., and Sheikh, Y. (2019). Neural volumes: learning dynamic renderable volumes from images. ACM Trans. Graph. 38, 3323020. doi: 10.1145/3306346.3323020

CrossRef Full Text | Google Scholar

Martin-Brualla, R., Radwan, N., Sajjadi, M. S. M., Barron, J. T., Dosovitskiy, A., and Duckworth, D. (2021). “NeRF in the wild: neural radiance fields for unconstrained photo collections,” in CVPR.

Mildenhall, B., Srinivasan, P. P., Ortiz-Cayon, R., Kalantari, N. K., Ramamoorthi, R., Ng, R., et al. (2019). Local light field fusion: practical view synthesis with prescriptive sampling guidelines. ACM Trans. Graph. 38, 3322980. doi: 10.1145/3306346.3322980

CrossRef Full Text | Google Scholar

Mildenhall, B., Srinivasan, P. P., Tancik, M., Barron, J. T., Ramamoorthi, R., and Ng, R. (2020). NeRF: representing scenes as neural radiance fields for view synthesis. Lect. Notes Comput. Sci. 12346, 405–421. doi: 10.1007/978-3-030-58452-8_24

CrossRef Full Text | Google Scholar

Neff, T., Stadlbauer, P., Parger, M., Kurz, A., Mueller, J. H., Chaitanya, C. R. A., et al. (2021). DONeRF: towards real-time rendering of compact neural radiance fields using depth oracle networks. Comput. Graph. Forum 40, 45–59. doi: 10.1111/cgf.14340

CrossRef Full Text | Google Scholar

Nocedal, J., and Wright, S. J. (2006). Numerical Optimization, 2nd Edn. New York, NY: Springer.

Özyeşi, O., Voroninski, V., Basri, R., and Singer, A. (2017). A survey of structure from motion*. Acta Numer. 26, 305–364. doi: 10.1017/S096249291700006X

CrossRef Full Text | Google Scholar

Rebain, D., Jiang, W., Yazdani, S., Li, K., Yi, K. M., and Tagliasacchi, A. (2020). “Derf: decomposed radiance fields,” in 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 14148–14156.

Reiser, C., Peng, S., Liao, Y., and Geiger, A. (2021). “Kilonerf: Speeding up neural radiance fields with thousands of tiny mlps,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 14335–14345.

Schonberger, J. L., and Frahm, J.-M. (2016). “Structure-from-motion revisited,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Las Vegas, NV: IEEE), 4104–4113.

Seitz, S. M., Curless, B., Diebel, J., Scharstein, D., and Szeliski, R. (2006). “A comparison and evaluation of multi-view stereo reconstruction algorithms,” in 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'06), Vol. 1 (New York, NY: IEEE), 519–528.

Shum, H., and Kang, S. B. (2000). Review of image-based rendering techniques. Vis. Commun. Image Process. 4067, 2–13. doi: 10.1117/12.386541

PubMed Abstract | CrossRef Full Text | Google Scholar

Snavely, N., Seitz, S. M., and Szeliski, R. (2006). “Photo tourism: exploring photo collections in 3d,” in ACM Siggraph 2006 Papers (Boston, MA), 835–846.

Tancik, M., Mildenhall, B., Wang, T., Schmidt, D., Srinivasan, P. P., Barron, J. T., et al. (2020a). Learned initializations for optimizing coordinate-based neural representations. arXiv:2012.02189. doi: 10.48550/arXiv.2012.02189

CrossRef Full Text | Google Scholar

Tancik, M., Srinivasan, P. P., Mildenhall, B., Fridovich-Keil, S., Raghavan, N., Singhal, U., et al. (2020b). Fourier features let networks learn high frequency functions in low dimensional domains. Adv. Neural Inf. Process. Syst. 2020, 1–24. doi: 10.48550/arXiv.2006.10739

CrossRef Full Text | Google Scholar

Tewari, A., Fried, O., Thies, J., Sitzmann, V., Lombardi, S., Sunkavalli, K., et al. (2020). State of the art on neural rendering. Comput. Graph. Forum. 39, 701–727. doi: 10.1111/cgf.14022

CrossRef Full Text | Google Scholar

Yao, Y., Luo, Z., Li, S., Fang, T., and Quan, L. (2018). “Mvsnet: depth inference for unstructured multi-view stereo,” in European Conference on Computer Vision (ECCV) (Munich).

Yao, Y., Luo, Z., Li, S., Shen, T., Fang, T., and Quan, L. (2019). “Recurrent mvsnet for high-resolution multi-view stereo depth inference,” in Computer Vision and Pattern Recognition (CVPR) (Long Beach, CA).

Yu, A., Li, R., Tancik, M., Li, H., Ng, R., and Kanazawa, A. (2021). “PlenOctrees for real-time rendering of neural radiance fields,” in ICCV.

Zhou, T., Tucker, R., Flynn, J., Fyffe, G., and Snavely, N. (2018). Stereo magnification: Learning view synthesis using multiplane images. ACM Trans. Graph. 37, 3201323. doi: 10.1145/3197517.3201323

CrossRef Full Text | Google Scholar