On the Use of Efficient Projection Kernels for Motion-Based Visual Saliency Estimation

In this paper, we investigate the potential of a family of efficient filters—the Gray-Code Kernels (GCKs)—for addressing visual saliency estimation with a focus on motion information. Our implementation relies on the use of 3D kernels applied to overlapping blocks of frames and is able to gather meaningful spatio-temporal information with a very light computation. We introduce an attention module that reasons the use of pooling strategies, combined in an unsupervised way to derive a saliency map highlighting the presence of motion in the scene. A coarse segmentation map can also be obtained. In the experimental analysis, we evaluate our method on publicly available datasets and show that it is able to effectively and efficiently identify the portion of the image where the motion is occurring, providing tolerance to a variety of scene conditions and complexities.

1. Introduction

Biological perception systems are very skilled in processing efficiently and effectively a huge amount of visual information, bringing attention to attractive regions or objects that may be potentially relevant for higher-level understanding tasks. The same ability in artificial systems is related to the notion of visual saliency estimation (Cong et al., 2018), often the first step of more complex analysis pipelines. For this reason, it is convenient to address the task very efficiently to avoid an excessive burden in the computation. Motion, in particular, is known to be one of the most attractive visual features for human attention (Itti et al., 1998).

In this work, we explicitly focus on bottom-up motion-based visual saliency and we explore the use of Gray-Code Kernels (GCKs) (Ben-Artzi et al., 2007) as a tool for efficiently obtaining a projection of a video content on top of which a new unsupervised motion-based attention module is devised, to coarsely, but very efficiently, detect the moving objects in the scene.

We target scenarios where motion-based saliency estimation triggers attention toward regions of the image where the presence of relevant information can be detected. We are not necessarily interested in a very precise segmentation of the entire object, while it is necessary to gather very quickly hints on where and how the relevant motion is occurring. Application domains including robotics and video-surveillance are just two examples where this ability may be highly beneficial. Similarly to change detection methods (see for instance Bouwmans, 2011), we are mainly interested in an efficient way of detecting the presence of motion in the scene, but as with optical flow, we foresee a representation that can sustain different levels of analysis, from the detection to higher-level understanding (Weinzaepfel et al., 2013; Fortun et al., 2015). Also, a desired property for the method is the tolerance to different viewing and scene conditions.

Inspired by these motivations, we explored the use of GCKs, a family of filters that include the Walsh-Hadamard kernels and that can be used as a highly efficient filtering scheme for images and videos. Their efficiency is discussed in Ben-Artzi et al. (2007), where it is shown that, under appropriate conditions, successive convolutions of an image with a set of such filters only require two operations per pixel for each filtering, regardless of filter or image size.

In this work, we thoroughly discuss a pipeline for motion-based saliency detection based on GCKs—an early version of which has been presented in Nicora and Noceti (2022)—where the main goal is to reach a good compromise between effectiveness and efficiency. The pipeline is structured in two modules: we first apply the bank of GCKs to overlapping clips of video, obtaining a bank of projections compactly represented by means of pooling operations. We then introduce an attention module to estimate in an unsupervised way a saliency map that reflects the presence of motion in the scene and from which a coarse segmentation map can be derived.

In the experimental analysis, we compare our method with alternative solutions of comparable complexity and we perform an evaluation on benchmark datasets with different characteristics and complexity. To clarify, we did not include state-of-art deep learning approaches, very precise but also computationally demanding, instead, we considered basic motion detection and segmentation methods. In addition, we discuss a simple use of our motion-based attention map in combination with RGB information in case a more precise segmentation is required. With respect to Nicora and Noceti (2022), in this work, we provide a more comprehensive experimental analysis of the method, including an assessment of synthetic data to gather insights about the interpretation of the obtained projections, and thoroughly discuss the pros and cons of the methods, identifying scenarios where its use may be highly beneficial but also discussing its main limitations.

The remainder of this document is organized as follows. In Section 2, we review works related to ours, while in Section 3 we introduce the basics of GCKs and our 3D implementation. Section 4 provides an assessment of synthetic data, while in Section 5 we describe our motion saliency estimation method and how we exploit saliency to derive a coarse motion-based image segmentation. In Section 6, we experimentally evaluate our method on a publicly available dataset, while Section 7 concludes.

2. Related Works

Video object segmentation (VOS), motion detection, and saliency. The task of motion-based saliency estimation is tightly intertwined with motion detection and may take different shapes. As a consequence the existing literature is huge, and a comprehensive review is out of the scope of this work. Instead, we provide here an account of the main families of approaches.

Classical approaches to motion-based saliency estimation/detection can be categorized in feature-based and learning-based methods. The majority of feature-based methods (see e.g., Ren et al., 2012; Fang et al., 2014; Xi et al., 2016; Chen et al., 2017) rely on the extraction of appearance and motion features, later fused to obtain the final saliency map. Here, motion information is crucial, in particular, to refine temporal consistency (Guo et al., 2017). In learning-based methods, optical flow is often considered a meaningful starting point (Wang et al., 2015), but it can be time consuming. For this reason, some methods try to avoid optical flow computation and directly embed multiple frames into the network (see e.g., Wang et al., 2017). Recently, deep learning architectures have been proposed for salient object detection in video (Le and Sugimoto, 2017; Yang et al., 2021), sometimes in combination with attention mechanisms (Jian et al., 2021) or employing multiple sources of information (Zhao et al., 2021).

When the focus is on the segmentation of the moving objects—the foreground— with respect to the background, the problem is often referred to as VOS (or salient object segmentation).

Classical approaches shape the problem as a change detection (or foreground segmentation), in which the main idea is to segment moving objects by comparing the current scene with a model of the background, that may include indeed dynamic elements (Bouwmans, 2011; Stagliano et al., 2015). These type of methods may be computationally feasible at the price of limited generalization capabilities, as their use is usually constrained to settings where there is no camera motion and the lighting conditions are kept under control.

Motion detection and segmentation methods based on optical flow provide a higher degree of flexibility to scene conditions and acquisition settings (Fortun et al., 2015; Noceti et al., 2015; Vignolo et al., 2017; Rea et al., 2019), but, on the other hand, they typically are either very efficient but inaccurate or very effective to the price of high computational demand, especially when involving global optimization steps (Werlberger et al., 2010) or if based on deep architectures (Weinzaepfel et al., 2013).

Often, VOS methods aim at obtaining a mask of the entire salient object, even when only part of it is actually moving. In such circumstances, motion cues might not be enough. To overcome this problem, supervised and unsupervised solutions have been proposed to combine motion-based cues with complementary (usually appearance-based) sources of information that may help to provide a more precise segmentation of the salient object (Ochs et al., 2013; Papazoglou and Ferrari, 2013; Perazzi et al., 2016a, 2017; Xiao and Jae Lee, 2016; Zhuo et al., 2019), also including approaches based on deep architectures (as Jain et al., 2017; Voigtlaender and Leibe, 2017).

Our work belongs to the family of unsupervised VOS methods, but unlike the approaches we mentioned, we propose A motion-based attention module targeting a coarse space-time localization of the moving object, or part of it to be more precise, rather than an accurate segmentation that also includes non-moving parts. Indeed, we will show that our attention map can be used in combination with appearance information as an alternative to the classical optical flow.

Efficient filtering and the GCKs. Enhanced image resolution, large quantity of data, and, possibly, the need for real-time performance generated the necessity of increasing the efficiency and thus the sustainability of the image filtering process. To this end, in literature, different possible solutions can be identified. A popular choice relies on filtering in the frequency domain using Fast Fourier Transform (Fialka and Cadik, 2006). An alternative is to resort to the use of meta representations efficiently computable (as boxlets Simard et al., 1999 or integral images Viola and Jones, 2004) or to filter engineering, to design families of filters to speed up the entire process of cascade filtering (Gotsman, 1994).

The GCKs belong to this latter family, as they are a large set of filters that can be used in combination with a very efficient filtering scheme on general d-dimensional signals. More in detail, they are efficiently computable, inclusive—as they consist of an extremely large set of kernels—and informative—as they are also able to carry meaningful information about the signal.

In literature, GCKs have been mainly used in their 2D formulation as an efficient projection scheme for image matching based on hashing techniques (Korman and Avidan, 2015) to speed up existing approaches (as Patch Match Barnes et al., 2010). In Moshe and Hel-Or (2009), the same approach is extended to videos, using 2D GCKs for video block motion estimation by computing the distance between projections over blocks of frames instead of using single images.

To the best of our knowledge, there is only one available example of the application of 3D GCKs (Moshe et al., 2012), where they are used to create 3D space-time patches followed by dimensionality reduction for the identification of foreground objects. With respect to this approach, particularly focused on video surveillance scenarios, we are more interested in the inclusive task of motion-based saliency detection under general conditions.

3. The Gray-Code Kernels

The Gray-Code Kernels provide an elegant and efficient projection framework for filtering images and videos. If applied in the appropriate order, successive convolutions with a bank of GCKs only requires two operations per pixel regardless of image or kernel sizes.

In the following, we briefly review the main theory behind GCKs and introduce our implementation of a 3D video filtering based on them.

3.1. One-Dimensional GCKs

In this section, we will define GCKs and the efficient projection scheme in their simplest form, that is when both signal and kernels are a one-dimensional vector. For a more detailed discussion, we refer the interested readers to Ben-Artzi et al. (2007).

A family of GCKs is built according to a recursive definition, starting from a vector s of length t, also called the seed, and a parameter k ≥ 0. It is easy to show that these two parameters determine the final length of each one-dimensional kernel (composed of n = 2^kt elements) and the total number of kernels in the family (2^kD, with D = 1 in the one-dimensional setting). Starting from the seed, a family of GCKs can be recursively defined as follows:

$\begin{array}{ll}\begin{array}{l}{V}_s^{(0)}=\{[s]\}\\ V_s^{(k)}=\{[v_s^{(k-1)}{\alpha }_k\times v_s^{(k-1)}]\}\end{array}& (1)\end{array}$

with $v_s^{(k-1)}\in V_s^{(k-1)}\text{ and }{\alpha }_k\in \left\{+1,-1\right\}$. The notation […] refers to the concatenation between vectors.

This recursive definition can be represented as a binary tree of k levels, starting with a root equal to [s] and where the branches are labeled with the values of α used to create the kernels (see Figure 1A). The final family will be composed of the kernels on the leaves nodes.

FIGURE 1

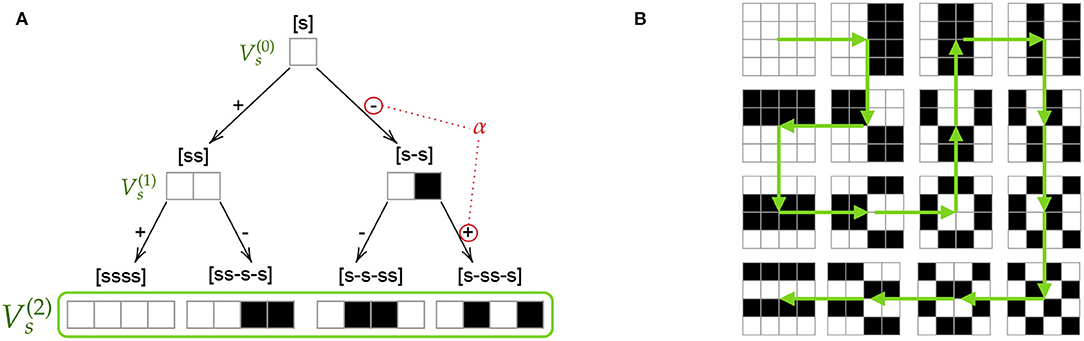
Figure 1. (A) Example of a binary tree with k = 2 generating one-dimensional Gray-Code Kernels (GCKs) of size 4. (B) Example of ordering (on 2D GCKs) that forms a Gray Code Sequence, hence enabling the efficient application of successive convolutions.

The efficiency of filtering with a family of GCKs is related to the ordering in which these filters are applied. An optimal ordering, also called Gray-Code Sequence (GCS), is defined with respect to the kernel's α-index, a code composed by the labels of the edges of the path going from the root of the tree to the leaf corresponding to such kernel. Two kernels are α-related if the hamming distance between their α-indices is one. A GCS is and sequence of kernels such that two consecutive kernels are always α-related.

To show the efficiency of filtering with sequences of α-related kernels, we may start defining as v₊ and v₋, respectively, the sum and difference of two kernels $v_1,v_2\in V_s^{(k)}$. It can be easily derived that, for construction, v₁ and v₂ share a common prefix of length Δ > 0, and the following relation holds:

$\begin{array}{ll}\left[0_{\Delta }{v}_{+}\right]=\left[v_{-}{0}_{\Delta }\right]& (2)\end{array}$

where 0_Δ is a vector of Δ zeros. If we expand $v_1,v_2\in V_s^{(k)}$ to an infinite sequence such that v₁(i) = v₂(i) = 0 for i < 0 and for i ≥ 2^kt, Eq.2 can be more specifically re-written as

$\begin{array}{ll}{v}_{+}(i-\Delta )=v_{-}(i).& (3)\end{array}$

It is now possible to introduce the core principle behind the efficient filtering scheme with GCKs. Indeed, exploiting the equality in Equation (3), we may derive that

$\begin{array}{ll}\begin{array}{c}{v}_1(i)=v_2(i)+v_2(i-\Delta )+v_1(i-\Delta )\\ v_2(i)=v_1(i)-v_1(i-\Delta )-v_2(i-\Delta )\end{array}& (4)\end{array}$

Let f₁ and f₂ be the results of convolving a signal ${X}$ respectively with the kernels v₁ and v₂. Then, by linearity of convolution we have the following:

$\begin{array}{ll}\begin{array}{c}{f}_1(i)=f_2(i)+f_2(i-\Delta )+f_1(i-\Delta )\\ f_2(i)=f_1(i)-f_1(i-\Delta )-f_2(i-\Delta )\end{array}& (5)\end{array}$

From the above formulas, it can be derived that, given the result of convolving the signal ${X}$ with one of the two kernels, only two operations per pixel are needed to obtain the result of convolving the signal with the other kernel.

It is worth noticing that the efficiency strictly depends on the relationship between pairs of consecutive filter kernels, meaning that the actual order of the kernels within the sequence is not relevant as long as the α-relation is maintained. For this reason, multiple orderings can be considered, valid GCSs and different strategies may be exploited depending on the task. One of the most common is to rely on sequency-based ordering: the term sequency is used to refer to the number of sign changes along each dimension of the kernel, in Figure 1B, we report a practical example of one of the most used sequency-based ordering, the “snake.”

3.2. Our 3D Implementation

As discussed in Ben-Artzi et al. (2007), the efficient properties of filtering with GCKs can be generalized to higher dimensions. As we are mainly interested in filtering video data, a natural choice is to employ 3D filter kernels to capture spatio-temporal information from an image sequence.

A family of 3D GCKs can be built by combining triplets of 1D GCKs. Considering the notation we used in Section 3.1, if v₁, v₂, and v₃ are three 1D kernels belonging to the same family, a 3D GCK ${V}$ can be computed as ${V}=v_1\times v_2\times v_3$ where ′ × ′ denotes the outer product between vectors. In this way, we may derive a bank of filters $𝕍={\{{{V}}^h\}}_{h=0}^{{M}-1}$, where ${M}=2^{kD}$ is the total number of filters with D = 3, of size n × n × n (where n = 2^kt is the length of the 1D filter, t being the length of the seed s).

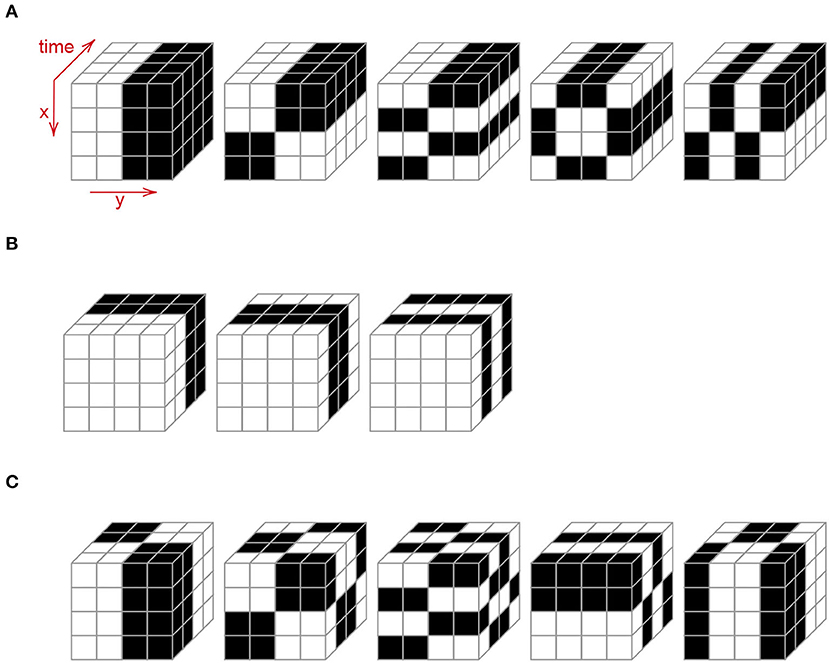
It is worth noting that even if one-dimensional kernels used to generate 3D GCKs are already ordered to form a 1D GCS, the resulting kernels are not necessarily in the right order, and further processing is needed to obtain a 3D GCS. In our implementation, we derive the GCS by reasoning on coherent temporal sequency. Given a kernel ${V}$ let $n_{{V}}$ be the number of changes between values of a kernel along the time component, i.e., the number of changes from 1 to −1 and vice versa. To give some examples, $n_{{V}}=0$ for kernels in Figure 2A, while $n_{{V}}=3$ for the rightmost kernel in Figure 2B. To obtain a GCS, when possible, we prefer to have kernels with the same $n_{{V}}$ covering consecutive positions in the sequence. In other words, we minimize the number of jumps between pairs of kernels ${{V}}_i$ and ${{V}}_j$ such that $n_{{{V}}_i}\ne n_{{{V}}_j}$.

FIGURE 2

Figure 2. Examples of (A) spatial, (B) temporal, and (C) spatio-temporal 3D kernels.

Our choice is motivated by computational considerations, as the extension from 2D to 3D GCKs brings non-trivial issues on the space computational complexity. For the efficient computation scheme, the previous Δ projections need to be stored in memory and available, with Δ = 2^(k−1)t corresponding to the length of the prefix that two α-related kernels have in common. Since we will need to access the projection values at most Δ pixels away from the location we are computing, in time this would require storing the previous Δ whole filtered images, unnecessarily burdening the memory requirement of the method.

According to the original work, we build a binary tree starting from an initial seed s = [1] (notice this corresponds to derive a family of Walsh-Hadamard kernels Pratt et al., 1969) and we set the number of levels of the tree to k = 2. The final GCS will be thus composed of 64 filters of size 4 x 4 x 4 of ±1 values.

Within the family of the considered GCKs, we can distinguish three main subgroups of filters, depending on their structure and the main properties that they are predominantly able to highlight: spatial (𝕍_S), temporal (𝕍_T), and spatio-temporal (𝕍_ST). The sets are non-overlapping, thus 𝕍 = 𝕍_S ∪ 𝕍_T ∪ 𝕍_ST. Examples from each subset can be found in Figure 2.

4. An Assessment on Synthetic Data

In this section, we provide an experimental investigation on synthetic data to discuss the properties of filtering with GCKs. The method starts from the assumption that the bank of filters may give us variability in the projection values depending on different factors, such as the type and quantity of information found in the image region and the structure of the specific kernel in use. GCKs used in this assessment are of size n × n × n and n = 4. As a testbed, we created ad-hoc sequences with a white dot (that we will also call “target”) moving on a black uniform background following rectilinear paths in 8 different directions. The target moves with a constant velocity (of magnitude $\frac{n}{2}$, n, 2n, or 4n) in each sequence, and it may be of size (diameter) equal to n, 2n, or 4n. We end up with a total of 96 sequences. The explicit connection between the sequence properties and the size of the kernels allows us to reason about the ability of the filters to highlight specific movement features.

In the following, we discuss the filter's behavior with respect to specific research questions.

[Q1] What is the benefit of 3D vs. 2D filtering? With respect to filtering with 2D kernels, the use of 3D kernels provides additional cues about temporal variations. The difference this extension can make, can be appreciated in Figure 3, where we computed the projection of four distinct yet connected kernels: the first one is an edge-like 2D kernel, applied to a single frame by means of a classical 2D convolution; the second is a 3D kernel that captures changes only on the time axis; the third one is the 2D kernel propagated in time, so that the resulting 3D kernel is applied simultaneously to n frames by means of a 3D convolution; the last projection (Figure 3D) is obtained by applying a 3D kernel that captures changes both in space and in time. The number of changes is indicated by the number of sign changes in the values of the kernel along the different axis. As one can see from the resulting projections, while the 2D kernel can only capture variations purely related to appearance, 3D kernels also incorporate the effect of the movement, providing a sort of blurred 2D projection of the target features in the different time instants. The temporal projection in particular (second one) provides a visual impression of the displacement of the target in the time window considered by the filter. We claim that, under appropriate conditions, this intermediate output can be used to derive a coarse estimate of the target velocity.

FIGURE 3

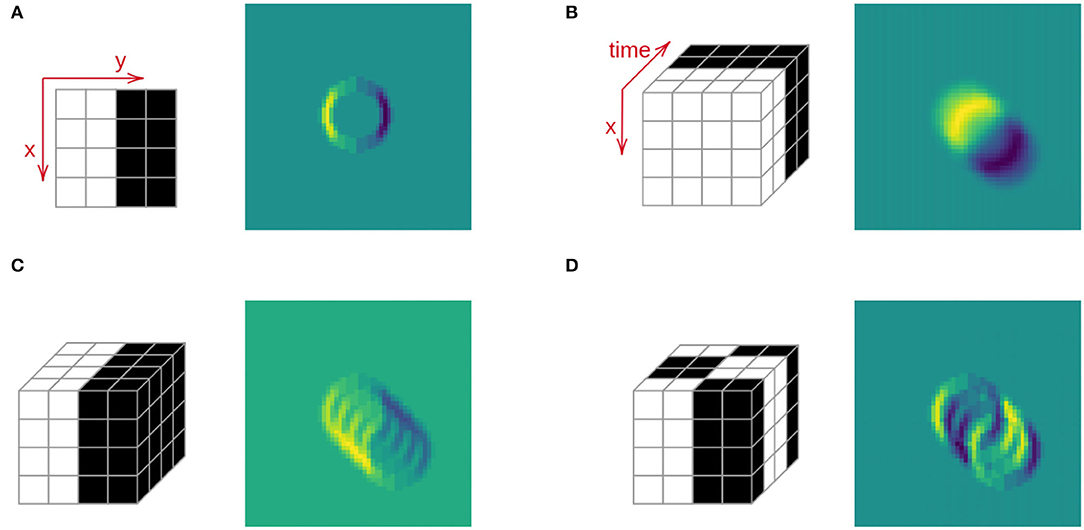
Figure 3. Filtering with 2D vs. 3D kernels. The target is moving in the direction north-west. The range of values goes from 0 (purple) to 1 (yellow). (A) 2D filtering (on a single frame). (B) 3D temporal filtering. (C) 3D spatial filtering. (D) 3D spatio-temporal filtering.

This simple experiment highlights how the 3D GCKs can efficiently and effectively enhance the presence of spatio-temporal variations in the signal and can thus be employed as a projection scheme for motion-based analysis.

[Q2] How can GCKs globally describe the dynamic event? We now consider both the local responses of single kernels and more global responses obtained by pooling the projection results at a pixel level. The popular max and average poolings are employed. More specifically, the pooling can be applied to the whole bank of filters or by grouping kernels according to the type of information they are predominantly able to capture.

Given a set of kernels 𝕎—that can be equal to 𝕍, 𝕍_S, 𝕍_T, or 𝕍_ST (see Section 3.2)—and a video clip ${C}$ more formal definitions of, respectively, max and average pooling are the following

$\begin{array}{ll}M{P}_{𝕎}({C})(i,j)={\displaystyle \underset{w\in 𝕎}{max}}{\Phi }_w({C})(i,j)& (6)\end{array}$

$\begin{array}{ll}A{P}_{𝕎}({C})(i,j)=\frac{1}{{{M}}_{𝕎}}{\displaystyle \sum _{w\in 𝕎}}{\Phi }_w({C})(i,j)& (7)\end{array}$

where Φ_w is the projection of the input clip with the kernel w ∈ 𝕎, while ${{M}}_{𝕎}$ represents the number of kernels in the considered set. We focus in particular on kernels with a time component and, to simplify the notation, in the following we call MP_𝕍ST=ST-MAX, MP_𝕍T=T-MAX, AP_𝕍ST=ST-AVG, and AP_𝕍T=T-AVG. A visual intuition of the effect of pooling is given in Figure 4: we may appreciate that ST-MAX (Figure 4A) and T-AVG (Figure 4D) maps are able to give us more general information about what happened in a limited amount of time. From ST-MAX, we derive a visual impression of where the motion occurred in the time span covered by the filtering. Since filtering acts on blocks of frames contiguous in time, rather than single images, the final projections provide a 2D impression of the movement evolution, with peaks in the regions where a significant amount of motion is occurring in the reference time instants. By maximizing the contributions we can gather a representation that, in spirit, is similar to the motion history (Ahad et al., 2012). With T-AVG instead, we focus on information purely related to motion, and we gather cues about how the motion evolves in time. Averaging the values, contributions in regions covered by the motion in past instants tend to smoothly decrease, while the values tend to increase in locations where the motion is mainly evolving in the current time instant (in fact, the position of the target in the reference frame overlaps with the yellow area of the average pooling while past positions are covered by the blue/purple “shadow.”

FIGURE 4

Figure 4. Example of pooling: (A) Spatio-temporal Max Pool (ST-MAX=MP_𝕍ST). (B) Spatio-temporal Avg Pool (ST-AVG=AP_𝕍ST). (C) Temporal Max Pool (T-MAX=MP_𝕍T). (D) Temporal Avg Pool (T-AVG=AP_𝕍T).

[Q3] Can GCKs help to discriminate events with different properties? We used dimensionality reduction to test the representative power of the pooling representations with respect to the direction of motion, velocity, and dimension of the target. We used the pooling maps obtained at each time instant and unrolled them to obtain the corresponding vectorial representations. Flattened representations are then collected in a set to which we apply principal component analysis, to derive a 2D representation that we can visualize. In Figure 5, we report the obtained representations for ST-MAX, ST-AVG, T-MAX, and T-AVG as we change the direction of the movement (Figure 5A), size of the target (Figure 5B), and its velocity (Figure 5C). For readability of the figure, we only consider a pair of possible values for each case (North-West vs. South direction in Figure 5A, size of the target set to 4 or 16 pixels in Figure 5B, and velocity equal to 4 or 16 pixels in Figure 5C). Each point in the pictures refers to a pooling map obtained at a certain time instant.

FIGURE 5

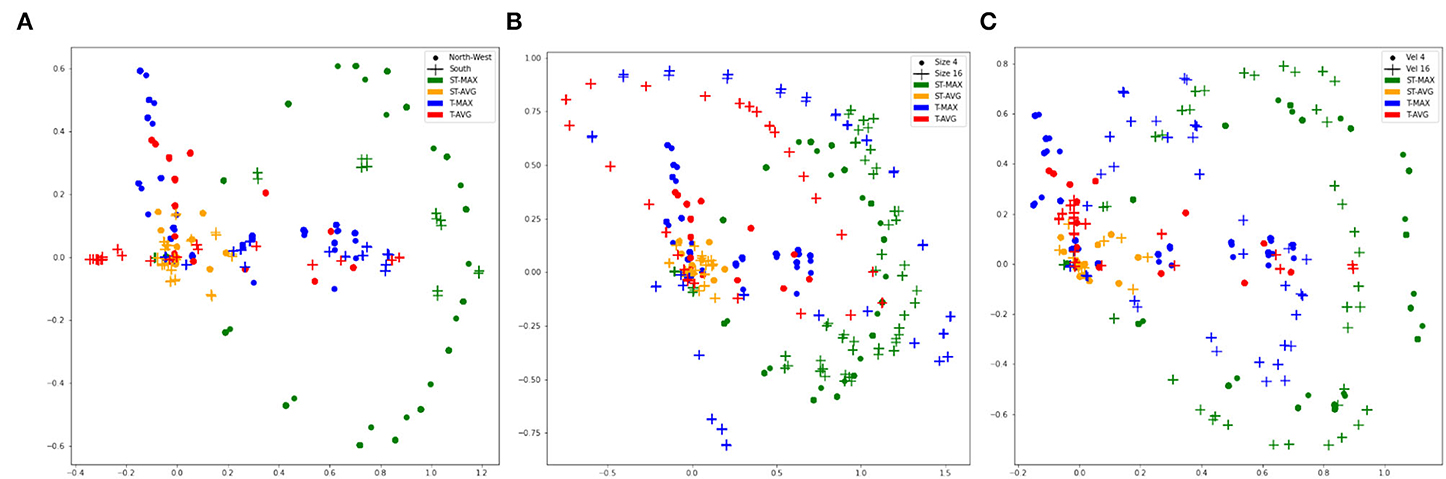
Figure 5. Test on pooling's representation power in the case of (A) movement in different directions. (B) Different target dimensions. (C) Different velocities. When fixed we refer to Direction NW, Velocity of magnitude 4 and Target dimension of magnitude 4.

For the direction of motion, GCKs are indeed able to highlight the main differences. In particular, in the case of T-MAX and T-AVG, it can be observed in Figure 5A how the GCKs nicely highlight the presence of one (crosses) or two (circles) main directions. Since spatial distribution of the representations is directly proportional to the target's dimension, with the exception of ST-AVG, every pooling is able to distinguish between different sequences, as it can be appreciated in Figure 5B. By varying the velocity, one can notice in Figure 5C that GCKs provide different patterns showing a temporal coherence that is learned autonomously, highlighting significant differences among different velocities.

In all the experiments, ST-AVG shows a poor descriptive power, as in all plots the orange dots and crosses are always located in a compact area.

Take-home messages Following this explorative analysis, we convey that the introduction of a third dimension in the structure of GCKs could be beneficial from several viewpoints. It could give us the opportunity to directly focus our attention on motion occurring in a scene without solely relying on the object's appearance. In a particular way, ST-MAX and T-AVG could be used as motion-based features, being able to highlight in a single filtering step where and how motion occurred in a scene, describing different aspects of it in a consistent but distinct way.

5. Proposed Method

In this section, we present our unsupervised motion saliency segmentation pipeline based on the computation of an efficient video projection. The overall pipeline (Figure 6A) is divided into two main modules: the first one, the Projection Module, coarsely identifies the region of the video containing salient motion and it is in charge of filtering and pooling the information; the Attention Module, instead, guides the segmentation refinement by combining temporal and spatio-temporal cues coming from the previous module in order to estimate a saliency map and a segmentation of the moving object.

Leveraging the empirical observations we made in Section 4, we focused our analysis on temporal and spatio-temporal features and designed a motion-based attention module with pooling operations able to exploit oscillations in the filter responses.

FIGURE 6

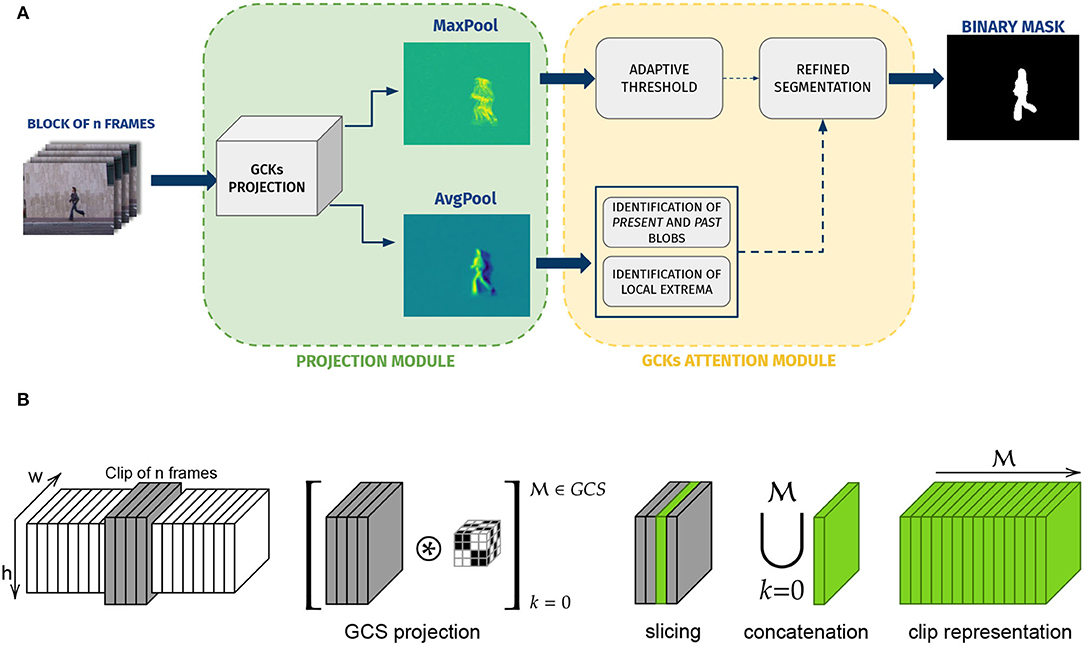
Figure 6. Visual description of our entire pipeline for unsupervised motion saliency segmentation. (A) A visual representation of the processing flow of our method. (B) Inside the Projection module: our procedure takes in input a clip of n video frames, computes the GCKs projections, and composes the representation.

5.1. Projection Module

Given an input video, we split the sequence in overlapping clips ${C}$ of size W × H × n, where W and H are, respectively, the width and height of the video frames, while n = 2^kt is the side of the 3D GCKs. We define a projection Φ that maps the original frame clip in a new space obtained by filtering it with the bank of GCKs. Thus $\Phi :{ℝ}^{W\times H\times n}\to {ℝ}^{W\times H\times {M}}$ is mathematically defined as

$\begin{array}{ll}\Phi ({C})={\{{C}⊛{{F}}^h\}}_{h=0}^{{M}-1}& (8)\end{array}$

where ⊛ denotes the convolution operator (notice that we need to perform a first full convolution and then continue with the remaining ${M}$-1 efficient convolutions). The GCKs projection is summarized in Figure 6B: each processed clip of frames is filtered with the ${M}$ kernels of the family ${F}$, each projection provides a three-dimensional result from which we select and normalize between 0 and 1 the central slice (at position $\frac{n}{2}$), ending with ${M}$ two-dimensional representations for each clip $\widehat{{C}}=\Phi ({C})$. In particular, the three-dimensional result of each convolution step finds in its central slice the maximization of the information about the whole block, i.e., how that filter responded in a span of n frames in time. At this point, we define two representations that, respectively, report the maximum (ST-MAX) and the average (T-AVG) values of, respectively, spatio-temporal and temporal filters, using Equations (6) and (7):

$\begin{array}{ll}M{P}_{{𝕍}_{ST}}({C})(i,j)={\displaystyle \underset{w\in {𝕍}_{ST}}{max}}{\Phi }_w({C})(i,j)& (9)\end{array}$

$\begin{array}{ll}A{P}_{{𝕍}_T}({C})(i,j)=\frac{1}{{{M}}_{{𝕍}_T}}{\displaystyle \sum _{w\in {𝕍}_T}}{\Phi }_w({C})(i,j)& (10)\end{array}$

5.2. Attention Module

Identification and segmentation of the salient part of the video are then left to the second module of the pipeline, the Attention Module, which combines temporal and spatio-temporal knowledge coming from the pre-computed poolings to perform multiple rounds of thresholds and segmentation refinements. First, Otsu's adaptive threshold method (Otsu, 1979) is applied to each ST-MAX to obtain a first, coarse segmentation. This initial result is refined by discarding connected components with an area smaller than 25, approximately a 5 × 5 pixel patch, and by applying a sequence of morphological operations of opening and closing, in order to discard detections caused by noise. The obtained map derived from max pooling (see Figure 7E) provides a comprehensive view of the movement that goes beyond the instantaneous variation and still it includes a significant amount of false positives. The second step of our segmentation aims at attenuating this effect.

FIGURE 7

Figure 7. Example of pooling and segmentation maps obtained by our method: (A) Reference frame, (B) ST-MAX, (C) T-AVG, (D) ground truth, (E) adaptive segmentation over ST-MAX (GCKs-A), (F) refined final map using information about “present” and “past” (GCKs-R).

As observed before, average pooling over temporal projections is able to convey information about the evolution of the movement in the scene in a limited amount of time frames. Roughly speaking, locations corresponding to past and present phases of the motion may be identified by detecting the local minima and maxima of T-AVG using a pair of threshold values σ₁ and σ₂. We then exploit this knowledge to refine the segmentation map, as follows (i) “present” blobs are exploited to consolidate the masks obtained from ST-MAX and (ii) positions belonging to the “past” are discarded from the refined map. An additional step of refinement is implemented by discarding blobs with no local extrema in the T-AVG pooling. The ultimate binary segmentation map B (see Figure 7) can finally be composed as

$\begin{array}{ll}B=B_{ST-MAX}-B_{T-AVG}^{past}+B_{T-AVG}^{present}.& (11)\end{array}$

where B_ST−MAX is the map obtained by thresholding ST-MAX, $B_{T-AVG}^{present}$ and $B_{T-AVG}^{past}$ are binary maps encoding, respectively, present and past blobs of T-AVG.

6. Experimental Analysis

In this section, we provide an experimental evaluation of our method on publicly available datasets. As already observed, motion saliency detection can be casted into different problem formulations, and, to the best of our knowledge, no single experimental protocol or benchmark dataset have been proposed for its specific and independent evaluation. For these reasons, we critically discuss the behavior of our method approaching the evaluation from two different perspectives.

Datasets On the one side, we started with a simple classical controlled dataset, the Weizmann dataset (Gorelick et al., 2007). It is a classic action recognition dataset that includes sequences recorded with a fixed camera and where, in each sequence, the background is static and mostly homogeneous, with only one salient moving subject. In this setting, we can therefore compare the ability of our method in providing segmentations in a controlled scenario where change detection can be performed.

On the other hand, we put to the test our method of VOS in challenging scenarios characterized by a higher variability in terms of acquisitions setting and scenes complexity. We considered two VOS benchmarks: SegTrackv2 (Li et al., 2013), which consists of 14 low-resolution videos, and DAVIS-2016 (Perazzi et al., 2016b), including 50 high-resolution sequences. Both of them include videos acquired in very challenging conditions including motion blur, complex deformations, occlusions slow and fast motion. In particular, in the DAVIS-2016, the number of videos for each scenario is unbalanced, with a strong presence of acquisitions where the camera is moving (in particular, there are no videos where the camera is fixed for the entire time) or where more than one moving object is present in the scene and annotated in the ground truth (in 37 videos out of 50 multiple objects are present). Overall, the DAVIS dataset is substantially more complex than SegTrackv2, and we decided to focus on specific subsets of its videos in order to investigate the ability of our model to cope with different classes of complex scenarios.

Evaluation metrics The ground truth is provided as a binary map for each frame, where important moving structures are highlighted. As common in VOS, we evaluate the segmentation quality by computing pixel-level measures—a natural choice to compare our method with other approaches—although this may be not in favor of our method. It is worth reminding that our goal is to quickly identify a coarse region where the motion is occurring, rather than precisely estimate the segmentation of the moving object at pixel-level precision (which is the main goal of VOS approaches). Indeed, one of the core contributions of our analysis is a discussion about the potentials and limitations of our approach depending on the scenario under analysis.

For each video, we evaluate our results in terms of mean Intersection over Union (mIoU)—both at a pixel level and considering the bounding boxes around each segmented region (see Figure 8, bottom)—Precision, Recall, and F₂-measure.

FIGURE 8

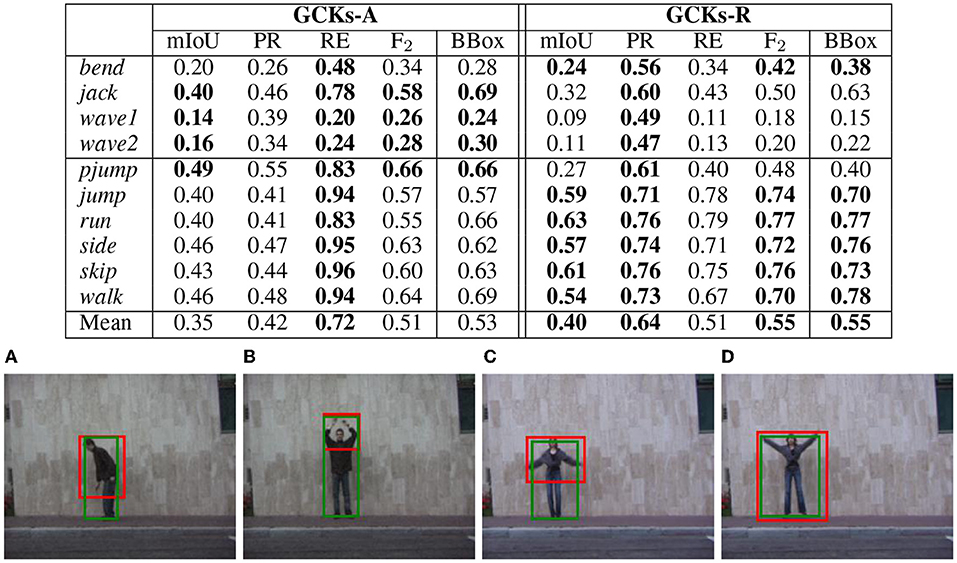
Figure 8. Above: evaluation of the two segmentation step on the Weizmann Dataset. Below: samples frames with the detection (red: our detection; green: ground truth). (A) Bend, (B) wave, (C) jumping jack, and (D) jumping jack.

6.1. Assessment on Fixed Camera Sequences

We start with an ablation study to show the influence of the refinement step on the quality of the obtained segmentation. For this purpose, we used the Weizmann dataset that despite being characterized by simple scenarios (uncluttered background and no camera motion) presents one of the main issues of motion-based saliency detection as it includes actions in which only part of the body is moving.

In the table, in Figure 8-top, we report video-wise mIoU, Precision, Recall, and F-measure derived on the segmentation maps obtained with the two steps included in the attention module, i.e., using first B_ST−MAX from the adaptive segmentation, and then B from the refinement step (see Eq. 11). We call the two methods, respectively, as GCKs-A and GCKs-R.

A first observation is that our method behaves nicely on actions involving the motion of the entire body (second group in the table), while on actions where only a part of the body is moving (first group in the table) it provides less accurate results, as it only detects the moving part (which is precisely its aim) instead of the whole body (see examples in Figure 8-bottom). In all cases, the refinement step brings improvement on the precision of the segmentation to the price of a lower recall, as the erosion in the refinement tends to also discard true positives. However, the F-measure—harmonic mean of precision and recall, and a complementary measure to mIoU although based on the same quantities—shows that in most cases the gain in terms of precision is higher or comparable to the loss on the recall side, leading to improvements on the measure. It is worth noting that the negative impact of the true positives we lose with the refinement is particularly evident in actions where the movement is only referring to arms or legs, as the small granularity of such changes is not captured by the refinement step of our method. With bend instead, where the whole upper body is moving, the performance improves with the refinement, as the scale of the moving part is more appropriately captured by the attention mechanism.

In the last column of the table, we report the mIoU value obtained by comparing the bounding boxes instead of the pixel-level segmentation. In both steps, the mIoU of the bounding boxes increases with respect to the corresponding value obtained from the segmentation; also, the improvement at the refinement step is consistently present.

6.2. Analysis on More Complex Scenarios

We now evaluate our method on more complex scenarios using the SegTrackv2 and DAVIS-2016 VOS benchmark datasets. We compare our approach with classical alternative strategies for motion detection showing an overall complexity comparable to the one of our approach. We consider in particular the following choices based on optical flow computation or background subtraction:

• Gunnar-Farneback algorithm (GF) Farnebäck (2003), a dense optical flow technique that computes intensity changes of all pixels¹.

• SIFT flow algorithm (SIFT), an optical flow techniques that exploits sift features to track changes between consecutive frames².

• Background Subtraction (BS), a foreground segmentation method based on Gaussian Mixture Models (Lee, 2005)³.

All the methods are followed by the thresholding strategy we use in our approach, for a fair comparison.

The results are summarized in Table 1. To enable a discussion about the influence of the complexity of the scenario—due in particular to the acquisition setting—on our results, we group them according to three acquisition types, i.e., using fixed, handheld, and dynamic camera. Overall, our approach has the average best performance across the different scenarios, with higher stability reflected by the lowest SD. In comparison to the other approaches, our method is less influenced by camera movements and achieves the best motion localization performances (indicated by the bounding box) with hand-held and dynamic cameras. Noticeably, it reaches slightly higher performances than the other approaches when the camera is tracking the moving object, a particularly challenging condition since the relative position of the subject within the scene appears to be almost the same in consecutive frames. On the negative side, with still cameras, the accuracy of our segmentation is not optimal, as already observed on the Weizmann dataset.

TABLE 1

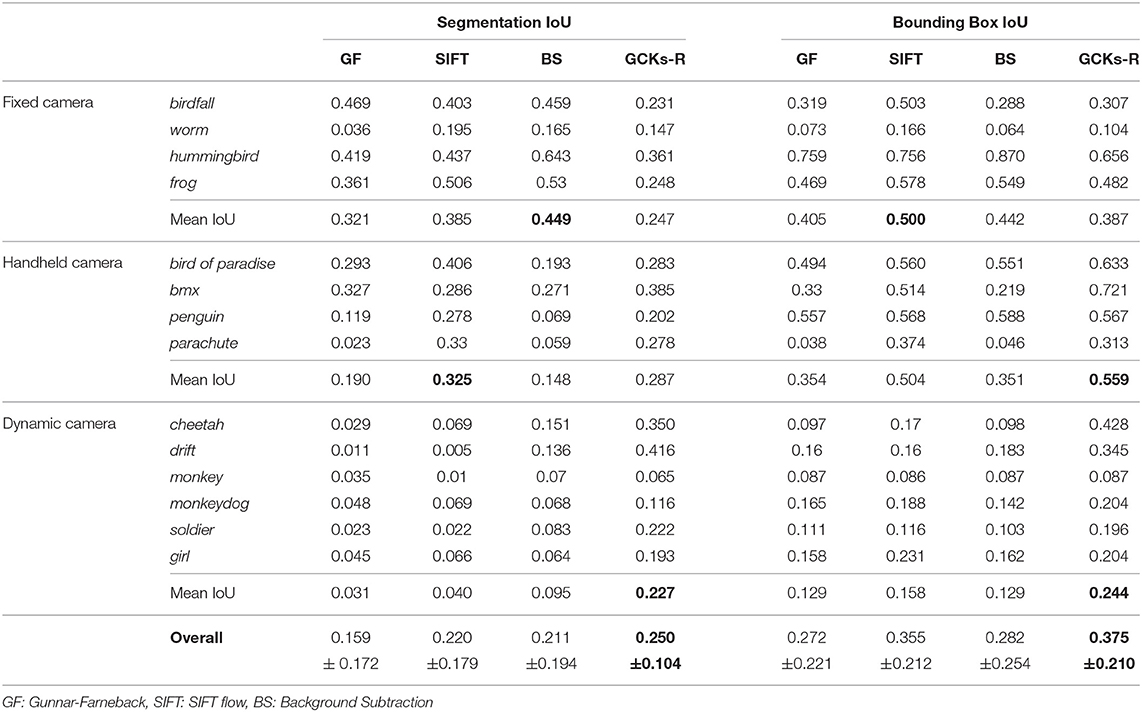
Table 1. Evaluation of our motion-based pipeline on SegTrackv2 with respect to basic motion detection approaches, “GCKs-R” refers to the result of the complete pipeline described in Section 5.

In Figure 9, we report a few samples from the dataset, together with our segmentation maps in the third column, to provide a qualitative evaluation of our results. As apparent, the segmentations we obtained are very much in line with the ground truth, also on sequences acquired with still cameras (as birdfall, frog, or hummingbird).

FIGURE 9

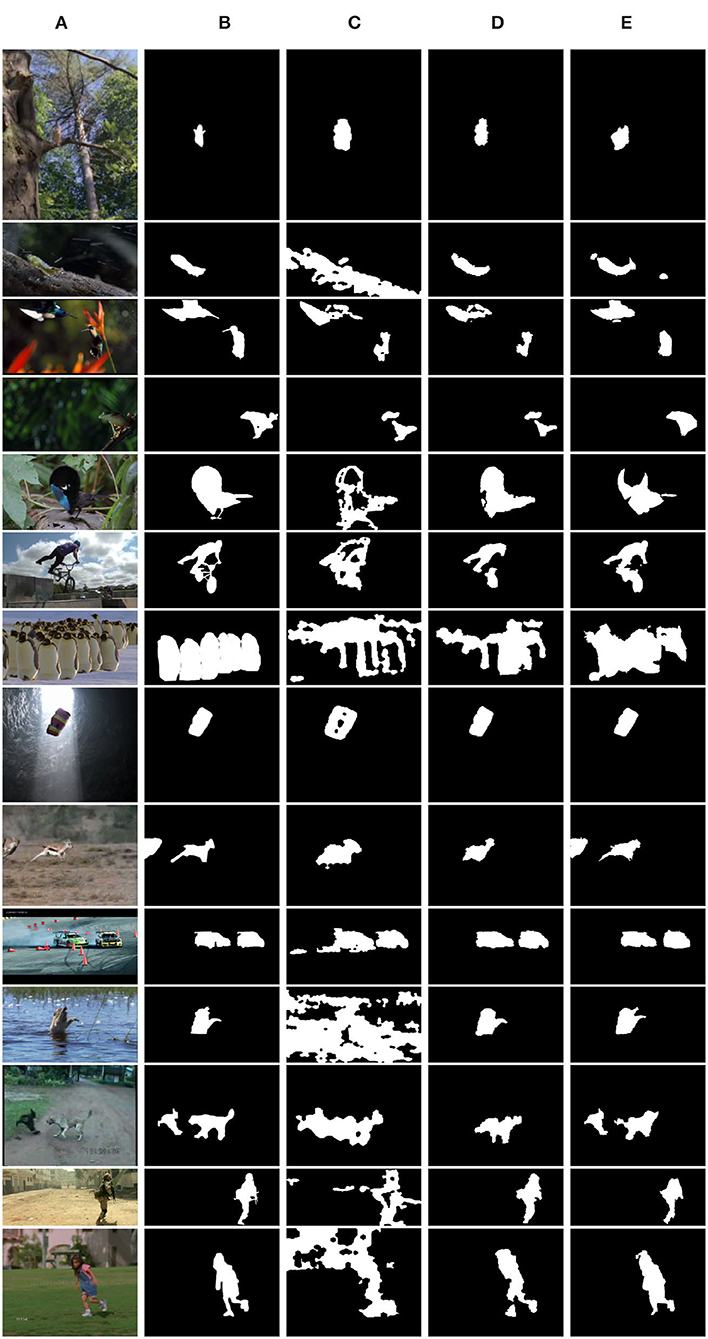
Figure 9. Sample results on SegTrackv2 dataset for sequences acquired with a fixed camera (from top birdfall, worn, hummingbird, and frog), hand-held camera (bird of paradise, bmx, penguin, and parachute), and dynamic cameras (cheetah, drift, monkey, monkeydog, soldier, and girl). (A) Reference frame, (B) ground truth, (C) our results (motion), (D) our results (motion+objectness), and (E) Zhuo et al. (2019).

More in detail, the strengths of our method are represented by a reliable detection in case of complex deformations (e.g., bmx) and appearance changes (as bird of paradise), especially if we consider that we do not rely on previous detections or prior information to determine the new segmentation masks, as done for instance by Zhuo et al. (2019). Another crucial challenge handled well by our pipeline is related to camouflaged motion (as for birdfall), in which purely appearance-based segmentation methods are likely to fail because there is no major distinction, from the appearance viewpoint, between the falling bird and the trees in the background. The same observation can be extended to changes in the illumination (parachute).

In the case of moving cameras, our results strongly depend on the mutual relationship between object and camera motion. In particular, we can distinguish two scenarios, depending on whether the camera and object move with a coherent velocity or not. Related to the latter case, in sequences like drift and cheetah, the motion of the target object deviates from the camera motion, and our method nicely detects such changes. Examples of the first type are instead the sequences girl and monkey: in both of them the difference in the relative positions of the object in successive frames is extremely small, hence no substantial movement is detected. On them, our method provides uneven results, coherently with the behavior of the other approaches. Relying solely on motion information, slow motion (as in frog) might represent a drawback in our method, since the actual movement in blocks of successive frames is very limited. This problem is compensated by the fact that GCKs are particularly able to identify the contours of the moving object. Thanks to this ability, we can still achieve a good detection in terms of motion localization at the bounding box level.

Concerning the use of the DAVIS-2016 dataset, we mention that in Perazzi et al. (2016b), different attributes have been assigned to each sequence. Among them, in our investigation, we are particularly interested in videos belonging to the following sets: camera shake (CS), similar to the hand-held camera of the SegTrackv2 dataset, dynamic background (DB), motion blur and fast motion (MBFM), background clutter (BC), and occlusions (OC). There is no distinct attribute that indicates the absence of camera motion. However, by visually inspecting the dataset, we manually assigned to the fixed camera (FC) group only 7 out of 50 videos (of which 3 of them can be considered only partially fixed, since they present an abrupt change in camera motion at some point in the sequence). We report in Table 2 a comparison of the results obtained with our method and the basic motion detection approaches we also considered in Table 1. In Figure 10 are included some examples (including segmentations of uneven quality) for each considered subset together with a visual comparison between segmentations obtained by our method at a different moment of the pipeline.

TABLE 2

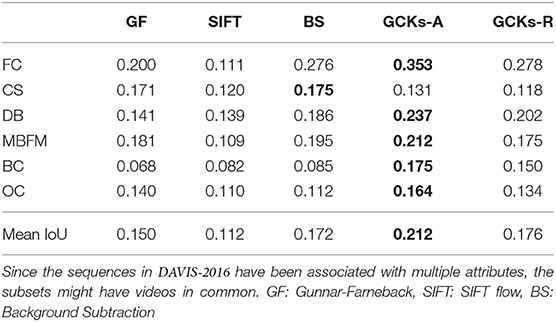
Table 2. Evaluation of our motion-based pipeline on a selection of sequences from the DAVIS-2016 dataset, in comparison with classical motion detection approaches.

FIGURE 10

Figure 10. Sample results on DAVIS-2016 dataset. From top to bottom: bus (OC), car-turn (FC), drift-chicane (FC), kite-walk (FC), soccerball (FC), motocross-bumps (MBFM), kite-surf (MBFM), motocross-jump (MBFM), mallard-fly (DB), goat (BC), dance-twirl (BC), camel (CS), motorbike (MBFM). (A) Reference frame, (B) ground truth, (C) GCKs-A, and (D) GCKs-R.

A first major observation is that, within these scenarios, our refinement step based on present and past blobs (GCKs-R) is not particularly beneficial (see Table 2 and fourth column in Figure 10). We hypothesize that there are two possible culprits in this situation. The first one is a considerable difference between kernel dimension and motion amplitude (both at appearance and temporal level) so that the size of the kernel might be too small to detect salient motion in its entirety (with some preliminary experiments, we empirically observed indeed that the results improve if we subsample the video frames). The other reason can be found in a camera motion overwhelming one of the moving targets. For instance, in the camel sequence (Figure 10), the camera moves around the animal while it only moves the paws. For this two-fold reason, refinement based on T-AVG pooling (GCKs-R) could result into limiting. Nevertheless, both GCKs-A and GCKs-R provide results higher that other approaches. This is further evidence than our method shows a higher tolerance to scene variability and challenges with respect to basic approaches of comparable complexity.

6.3. Using Appearance for Improving VOS

We now discuss a simple use of our motion-based attention map in combination with RGB information in situations where a more precise segmentation is required and motion is not sufficiently informative. For this purpose, we adapted the first part of the unsupervised VOS method proposed in Zhuo et al. (2019), where two appearances (objectness) and motion maps— derived, respectively, by Mask R-CNN (He et al., 2017) and the use of optical flow—are fused to obtain an improved segmentation. We replaced the use of the more classical, but also expensive, optical flow with our motion saliency map derived from the GCKs projection. In this sense, we are indeed evaluating the capability of our projections of being a viable, more efficient, alternative to the optical flow as a low-level, basic, motion representation. In this new solution, the final segmentation is achieved by computing the pixel-wise intersection of the two binary masks (our motion-based map + the Mask R-CNN one).

We compare the obtained results on SegTrackv2 with the performance reported in the original work (Zhuo et al., 2019) (UOVOS) (where a second step to enforce the coherency of the segmentation across time was included), and the state-of-art VOS method FusionSeg (Jain et al., 2017), a two-stream fully convolution neural network that fuses RGB appearance information and, again, optical flow motion information in a unified framework. The evaluation of the SegTrack dataset is reported in Table 3. For almost all sequences, the use of appearance leads to improvements in the segmentation quality, from a mIoU of 0.250 to 0.551. On some occasions (hummingbird), this does not happen, or the final accuracy does not get near other methods' results like for the other videos (frog, bird of paradise, penguin). The reason is 2-fold: sometimes the objectness masks retrieved for those sequences are not particularly accurate, we suppose Mask R-CNN failed at yielding an appropriate segmentation due to slow motion and motion blur in the first two sequences, and the fact that, originally, the sequence penguins was treated as a multiple object segmentation, one for each penguin in the first row (five in total, while the penguin in the sequence is way more). The other reason for unimproved segmentation accuracy might be due to the choice of obtaining the fused mask by intersecting the motion-based and Mask R-CNN segmentations. A weighted fusion might in fact improve the final result.

TABLE 3

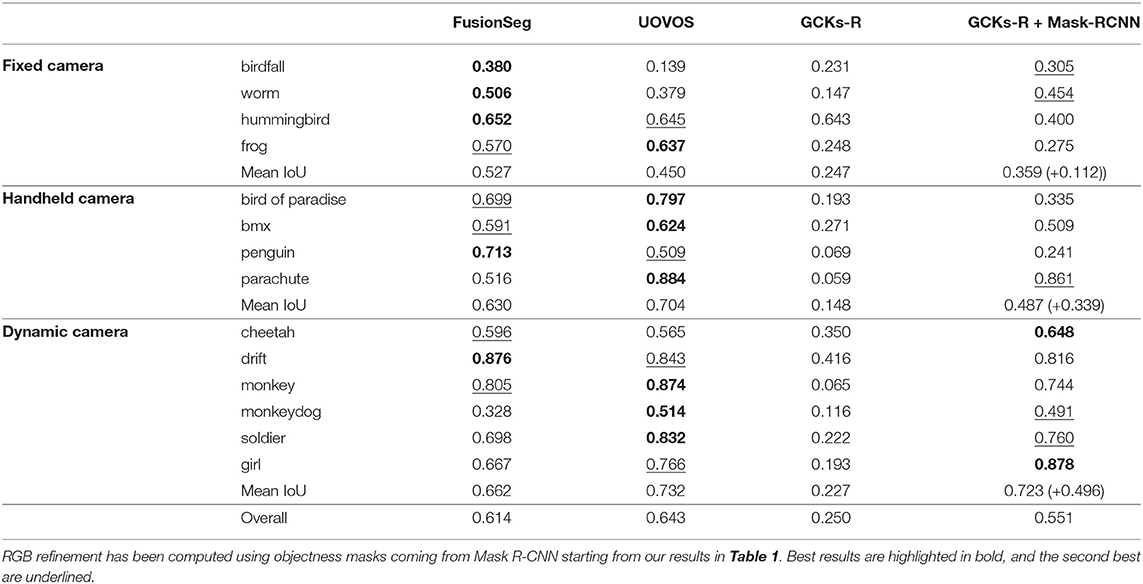
Table 3. Comparison with alternative approaches that also combine motion information with appearance information.

As expected, the segmentation quality in our method is below the level provided by the other two approaches: both of them start indeed from a motion map derived from the optical flow, more precise but also less efficient. Interestingly, we may notice how the methods seem to perform at best in different groups of videos: FusionSeg on fixed camera sequences, UOVOS on hand-held camera sequences, UOVOS and our method on dynamic camera sequences. As a consequence, we may observe that our solution may be beneficial in particular in the latter situation, where with a very simple approach we can achieve results comparable to the ones of more advanced methodologies. Often times, lower results for our method (especially in the hand-held camera setting) are due to the fact that either our motion-based segmentation or rgb-based objectness masks are not consistent throughout the entire sequence (this happens in particular in the case of bird of paradise, and penguin) and this may be partially counteracted including a time reasoning as on UOVOS.

Considering the scope of our work and the ambition to design a method that pursues computational efficiency, we may conclude our method is able to reach a trade-off between the quality of the segmentation and computational efficiency. An analysis of the latter is provided in the next section.

6.4. Computational Analysis

We start with a computational analysis of the GCKs filtering scheme with respect to classical 3D convolution. Here, we report the time consumption (expressed in seconds per frame) of alternative strategies for obtaining the same 64 projections with kernels of size 4 x 4 x 4 on the SegTrack dataset. All the tested solutions have been implemented in Python on a laptop with Intel(R) Core(TM) i5-8265U CPU @ 1.60GHz and 32GB RAM. With respect to full 3D convolution (11.45 s/frame) or FFT-based convolution (0.7 s/frame), our method is substantially more efficient: we employ the Scipy implementation of the 3D fft-based convolution on the first kernel of the family followed by 63 efficient projections and we obtain the 64 results with an average execution time of 0.061 s/frame⁴.

In terms of the number of operations, in order to obtain ${M}$ projections with a kernel of size n × n × n, using a full 3D convolution will require ${M}\ast n^3$ multiplications per pixel while using GCKs efficient filtering scheme we are able to obtain the same result at the cost of $2({M}-1)$ operations per pixel.

If we consider the full pipeline, our machines our implementation we must add to this estimate the cost of computing the two pooling maps that we employ in our final solution (it can be considered constant for each pixel) and the cost of combining the binary maps derived from the pooling maps to obtain the final segmentation map (a sequence of and/or operations, again the cost can be considered as a constant if we reason at the pixel level).

Concerning the comparison with alternative approaches, it does not make sense to consider complex deep architectures, as the level of complexity of the approaches (and so the results) is at a different scale. With respect to the baseline methods included in Table 1, the comparison in terms of computational time is not completely fair as the implementation we adopted were sometimes in different languages, although having similar characteristics⁵. To give an idea on our machines, our implementation runs approximately with the same computational time of Farnebäck (2003) and Zivkovic (2004) and is ~75 faster than the SIFT-Flow implementation included in Zhuo et al. (2019).

On a more theoretical side, we may reason on the fact that very simple background subtraction approaches may have a computational load that is comparable to ours (in the simplest case, the operation can be performed as a simple difference between images) to the price of a poor robustness to variable scene conditions. Improving the robustness also means burdening the computation and specific solutions are required to speed up the computation (see e.g., Gorur and Amrutur, 2011 for the Gaussian Mixture Models). On the other hand, optical flow algorithms have been studied for decades, with a significant number of existing solutions that differ in computational speed, quality of the estimation, and robustness to complex situations. It is worth noting that even in the case of “simple" solutions to the optical flow estimation the computational cost is significant. To make an example, we cite the very popular Lucas-Kanade algorithm that has a complexity in the order of O(n³) where n is the number of pixels in an image (Baker and Matthews, 2004). When the method relies on the global optimization step, the computational cost is designed to increase, and parallelization methods are often of help (Petreto et al., 2018). With these considerations in mind, we observe that the method we employ is an alternative—sometimes less accurate, but always more efficient and robust to different scene challenges—to such classical approaches, with no particular need for speedup strategies.

7. Discussion

In this work, we explored the use and properties of GCKs for efficiently addressing motion saliency estimation in videos. We showed that our method provides a good compromise between effectiveness and efficiency, with saliency maps that are able to reliably highlight the motion in a scene. Indeed, in our work, saliency estimation is an intermediate step in a more complex pipeline whose final goal is to address motion classification, and as such, we need a method that quickly provides us information on where to focus the attention for the next steps of analysis. A good property of the GCKs is that they also provide a powerful representation for such higher-level tasks: we are currently investigating their application to dynamic events segmentation and motion classification. This may open the door to an end-to-end pipeline in which the very same low-level features could be exploited in multiple stages of the analysis, from the detection to the higher-level understanding of a dynamic event.

Data Availability Statement

All real data supporting the conclusions of this article are already available. The synthetic dataset employed in Section 4 can be made available upon request.

Author Contributions

EN designed and implemented the method, implemented a novel version of 3D GCKs, carried out experiments in Section An Assessment of Synthetic Data and Proposed Method. NN designed the synthetic dataset and supervised the whole process. EN and NN carried out the state of the art analysis, contributed in the assessment and the design of experiments in Section An Assessment of Synthetic Data and took care of writing, revising, and editing the manuscript. Both authors contributed to the article and approved the submitted version.

Funding

This work has been carried out at the Machine Learning Genoa (MaLGa) Center, Università di Genova (IT). It has been supported by AFOSR, with the project Cognitively-inspired architectures for human motion understanding, grant no. FA8655-20-1-7035.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^We used the Python implementation available in openCV.

2. ^We used the MATLAB implementation included in Zhuo et al. (2019).

3. ^We employed the Python function available in openCV that implements (Zivkovic, 2004; Zivkovic and Van Der Heijden, 2006).

4. ^It needs to be mentioned that our pipeline is, at the moment, implemented in Python, therefore execution times could be further improved moving to a more efficient programming language.

5. ^Both Python and Matlab are interpreted languages, and as such their computational capabilities can be roughly considered as comparable.

References

Ahad, M. A. R., Tan, J. K., Kim, H., and Ishikawa, S. (2012). Motion history image: its variants and applications. Mach. Vis. Appl. 23, 255–281. doi: 10.1007/s00138-010-0298-4

CrossRef Full Text | Google Scholar

Baker, S., and Matthews, I. (2004). Lucas-kanade 20 years on: a unifying framework. Int. J. Comput. Vis. 56, 221–255. doi: 10.1023/B:VISI.0000011205.11775.fd

CrossRef Full Text | Google Scholar

Barnes, C., Shechtman, E., Goldman, D. B., and Finkelstein, A. (2010). “The generalized patchmatch correspondence algorithm,” in European Conference on Computer Vision (Heraklion: Springer), 29–43.

Google Scholar

Ben-Artzi, G., Hel-Or, H., and Hel-Or, Y. (2007). The gray-code filter kernels. IEEE Trans. Pattern. Anal. Mach. Intell. 29, 382–393. doi: 10.1109/TPAMI.2007.62

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouwmans, T. (2011). Recent advanced statistical background modeling for foreground detection-a systematic survey. Recent Patents Comput. Sci. 4, 147–176. doi: 10.2174/1874479611104030147

CrossRef Full Text | Google Scholar

Chen, C., Li, S., Wang, Y., Qin, H., and Hao, A. (2017). Video saliency detection via spatial-temporal fusion and low-rank coherency diffusion. IEEE Trans. Image Process. 26, 3156–3170. doi: 10.1109/TIP.2017.2670143

PubMed Abstract | CrossRef Full Text | Google Scholar

Cong, R., Lei, J., Fu, H., Cheng, M.-M., Lin, W., and Huang, Q. (2018). Review of visual saliency detection with comprehensive information. IEEE Trans. Circ. Syst. Video Technol. 29, 2941–2959. doi: 10.1109/TCSVT.2018.2870832

PubMed Abstract | CrossRef Full Text | Google Scholar

Fang, Y., Wang, Z., Lin, W., and Fang, Z. (2014). Video saliency incorporating spatiotemporal cues and uncertainty weighting. IEEE Trans. Image Process. 23, 3910–3921. doi: 10.1109/TIP.2014.2336549

PubMed Abstract | CrossRef Full Text | Google Scholar

Farnebäck, G. (2003). “Two-frame motion estimation based on polynomial expansion,” in Scandinavian Conference on Image Analysis (Halmstad: Springer).

Google Scholar

Fialka, O., and Cadik, M. (2006). “FFT and convolution performance in image filtering on GPU,” in Tenth International Conference on Information Visualisation (IV'06) (London: IEEE), 609–614.

Google Scholar

Fortun, D., Bouthemy, P., and Kervrann, C. (2015). Optical flow modeling and computation: a survey. Comput. Vis. Image Understand. 134, 1–21. doi: 10.1016/j.cviu.2015.02.008

CrossRef Full Text | Google Scholar

Gorelick, L., Blank, M., Shechtman, E., Irani, M., and Basri, R. (2007). Actions as space-time shapes. Trans. Pattern Anal. Mach. Intell. 29, 2247–2253. doi: 10.1109/TPAMI.2007.70711

PubMed Abstract | CrossRef Full Text | Google Scholar

Gorur, P., and Amrutur, B. (2011). “Speeded up Gaussian mixture model algorithm for background subtraction,” in 2011 8th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS) (Klagenfurt: IEEE), 386–391.

Google Scholar

Gotsman, C. (1994). Constant-time filtering by singular value decomposition. Comput. Graphics Forum 13, 153–163. doi: 10.1111/1467-8659.1320153

CrossRef Full Text | Google Scholar

Guo, F., Wang, W., Shen, J., Shao, L., Yang, J., Tao, D., et al. (2017). Video saliency detection using object proposals. IEEE Trans. Cybern. 48, 3159–3170. doi: 10.1109/TCYB.2017.2761361

PubMed Abstract | CrossRef Full Text | Google Scholar

He, K., Gkioxari, G., Dollár, P., and Girshick, R. (2017). “Mask R-CNN,” in Proceedings of the IEEE International Conference on Computer Vision (Venice: IEEE), 2961–2969.

Google Scholar

Itti, L., Koch, C., and Niebur, E. (1998). A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 20, 1254–1259. doi: 10.1109/34.730558

CrossRef Full Text | Google Scholar

Jain, S. D., Xiong, B., and Grauman, K. (2017). “Fusionseg: Learning to combine motion and appearance for fully automatic segmentation of generic objects in videos,” in 2017 IEEE conference on computer vision and pattern recognition (CVPR) (Honolulu, HI: IEEE), 2117–2126.

Google Scholar

Jian, M., Wang, J., Yu, H., and Wang, G.-G. (2021). Integrating object proposal with attention networks for video saliency detection. Inf. Sci. 576, 819–830. doi: 10.1016/j.ins.2021.08.069

CrossRef Full Text | Google Scholar

Korman, S., and Avidan, S. (2015). Coherency sensitive hashing. IEEE Trans. Pattern Anal. Mach. Intell. 38, 1099–1112. doi: 10.1109/TPAMI.2015.2477814

PubMed Abstract | CrossRef Full Text | Google Scholar

Le, T.-N., and Sugimoto, A. (2017). “Deeply supervised 3D recurrent FCN for salient object detection in videos,” in BMVC, Vol. 1 (London), 3.

Google Scholar

Lee, D.-S. (2005). Effective Gaussian mixture learning for video background subtraction. IEEE Trans. Pattern Anal. Mach. Intell. 27, 827–832. doi: 10.1109/TPAMI.2005.102

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, F., Kim, T., Humayun, A., Tsai, D., and Rehg, J. M. (2013). “Video segmentation by tracking many figure-ground segments,” in Proceedings of the IEEE International Conference on Computer Vision (Honolulu, HI: IEEE), 2192–2199.

Google Scholar

Moshe, Y., and Hel-Or, H. (2009). Video block motion estimation based on gray-code kernels. IEEE Trans. Image Process. 18, 2243–2254. doi: 10.1109/TIP.2009.2025559

PubMed Abstract | CrossRef Full Text | Google Scholar

Moshe, Y., Hel-Or, H., and Hel-Or, Y. (2012). “Foreground detection using spatiotemporal projection kernels,” in 2012 IEEE Conference on Computer Vision and Pattern Recognition (Providence, RI: IEEE), 3210–3217.

Google Scholar

Nicora, E., and Noceti, N. (2022). “Exploring the use of efficient projection kernels for motion saliency estimation,” in Image Analysis and Processing - ICIAP 2022. ICIAP 2022. Lecture Notes in Computer Science, Vol. 13233, eds S. Sclaroff, C. Distante, M. Leo, G. M. Farinella, and F. Tombari (Cham: Springer). doi: 10.1007/978-3-031-06433-3_14

CrossRef Full Text | Google Scholar

Noceti, N., Sciutti, A., and Sandini, G. (2015). “Cognition helps vision: Recognizing biological motion using invariant dynamic cues,” in International Conference on Image Analysis and Processing (Springer), 676–686.

Google Scholar

Ochs, P., Malik, J., and Brox, T. (2013). Segmentation of moving objects by long term video analysis. IEEE Trans. Pattern Anal. Mach. Intell. 36, 1187–1200. doi: 10.1109/TPAMI.2013.242

PubMed Abstract | CrossRef Full Text | Google Scholar

Otsu, N. (1979). A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man. Cybern. 9, 62–66. doi: 10.1109/TSMC.1979.4310076

CrossRef Full Text | Google Scholar

Papazoglou, A., and Ferrari, V. (2013). “Fast object segmentation in unconstrained video,” in Proceedings of the IEEE International Conference on Computer Vision (Sydney, NSW: IEEE), 1777–1784.

Google Scholar

Perazzi, F., Khoreva, A., Benenson, R., Schiele, B., and Sorkine-Hornung, A. (2017). “Learning video object segmentation from static images,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Honolulu, HI: IEEE), 2663–2672.

Google Scholar

Perazzi, F., Pont-Tuset, J., McWilliams, B., Van Gool, L., Gross, M., and Sorkine-Hornung, A. (2016a). “A benchmark dataset and evaluation methodology for video object segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Las Vegas, NV: IEEE), 724–732.

Google Scholar

Perazzi, F., Pont-Tuset, J., McWilliams, B., Van Gool, L., Gross, M., and Sorkine-Hornung, A. (2016b). “A benchmark dataset and evaluation methodology for video object segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Las Vegas, NV: IEEE), 724–732.

Google Scholar

Petreto, A., Hennequin, A., Koehler, T., Romera, T., Fargeix, Y., Gaillard, B., et al. (2018). “Energy and execution time comparison of optical flow algorithms on SIMD and GPU architectures,” in 2018 Conference on Design and Architectures for Signal and Image Processing (DASIP) (Porto: IEEE), 25–30.

Google Scholar

Pratt, W. K., Kane, J., and Andrews, H. C. (1969). Hadamard transform image coding. Proc. IEEE 57, 58–68. doi: 10.1109/PROC.1969.6869

CrossRef Full Text | Google Scholar

Rea, F., Vignolo, A., Sciutti, A., and Noceti, N. (2019). Human motion understanding for selecting action timing in collaborative human-robot interaction. Front. Rob. AI 6, 58. doi: 10.3389/frobt.2019.00058

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, Z., Gao, S., Rajan, D., Chia, L.-T., and Huang, Y. (2012). “Spatiotemporal saliency detection via sparse representation,” in 2012 IEEE International Conference on Multimedia and Expo (Melbourne, VIC: IEEE), 158–163.

Google Scholar

Simard, P., Bottou, L., Haffner, P., and LeCun, Y. (1999). “Boxlets: a fast convolution algorithm for signal processing and neural networks,” in Advances in Neural Information Processing Systems (Denver, CO), 571–577.

Stagliano, A., Noceti, N., Verri, A., and Odone, F. (2015). Online space-variant background modeling with sparse coding. IEEE Trans. Image Process. 24, 2415–2428. doi: 10.1109/TIP.2015.2421435

PubMed Abstract | CrossRef Full Text | Google Scholar

Vignolo, A., Noceti, N., Rea, F., Sciutti, A., Odone, F., and Sandini, G. (2017). Detecting biological motion for human-robot interaction: a link between perception and action. Front. Rob. AI 4, 14. doi: 10.3389/frobt.2017.00014

CrossRef Full Text | Google Scholar

Viola, P., and Jones, M. J. (2004). Robust real-time face detection. Int. J. Comput. Vis. 57, 137–154. doi: 10.1023/B:VISI.0000013087.49260.fb

CrossRef Full Text | Google Scholar

Voigtlaender, P., and Leibe, B. (2017). Online adaptation of convolutional neural networks for video object segmentation. arXiv preprint arXiv:1706.09364. doi: 10.5244/C.31.116

CrossRef Full Text | Google Scholar

Wang, W., Shen, J., and Shao, L. (2015). Consistent video saliency using local gradient flow optimization and global refinement. IEEE Trans. Image Process. 24, 4185–4196. doi: 10.1109/TIP.2015.2460013

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., Shen, J., and Shao, L. (2017). Video salient object detection via fully convolutional networks. IEEE Trans. Image Process. 27, 38–49. doi: 10.1109/TIP.2017.2754941

PubMed Abstract | CrossRef Full Text | Google Scholar

Weinzaepfel, P., Revaud, J., Harchaoui, Z., and Schmid, C. (2013). “DeepFlow: Large displacement optical flow with deep matching,” in Proceedings of the IEEE International Conference on Computer Vision (Sydney, NSW: IEEE), 1385–1392.

Google Scholar

Werlberger, M., Pock, T., and Bischof, H. (2010). “Motion estimation with non-local total variation regularization,” in 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (San Francisco, CA: IEEE), 2464–2471.

Google Scholar

Xi, T., Zhao, W., Wang, H., and Lin, W. (2016). Salient object detection with spatiotemporal background priors for video. IEEE Trans. Image Process. 26, 3425–3436. doi: 10.1109/TIP.2016.2631900

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, F., and Jae Lee, Y. (2016). “Track and segment: an iterative unsupervised approach for video object proposals,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Las Vegas, NV: IEEE), 933–942.

Google Scholar

Yang, S., Zhang, L., Qi, J., Lu, H., Wang, S., and Zhang, X. (2021). “Learning motion-appearance co-attention for zero-shot video object segmentation,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, (Montreal, QC: IEEE), 1564–1573.

Google Scholar

Zhao, X., Pang, Y., Yang, J., Zhang, L., and Lu, H. (2021). “Multi-source fusion and automatic predictor selection for zero-shot video object segmentation,” in Proceedings of the 29th ACM International Conference on Multimedia (Chengdu), 2645–2653.

Google Scholar

Zhuo, T., Cheng, Z., Zhang, P., Wong, Y., and Kankanhalli, M. (2019). Unsupervised online video object segmentation with motion property understanding. IEEE Trans. Image Process. 29, 237–249. doi: 10.1109/TIP.2019.2930152

PubMed Abstract | CrossRef Full Text | Google Scholar

Zivkovic, Z. (2004). “Improved adaptive Gaussian mixture model for background subtraction,” in Proceedings of the 17th International Conference on Pattern Recognition, 2004. ICPR 2004., Vol. 2 (Cambridge, UK: IEEE), 28–31.

Google Scholar

Zivkovic, Z., and Van Der Heijden, F. (2006). Efficient adaptive density estimation per image pixel for the task of background subtraction. Pattern Recognit. Lett. 27, 773–780. doi: 10.1016/j.patrec.2005.11.005

CrossRef Full Text | Google Scholar