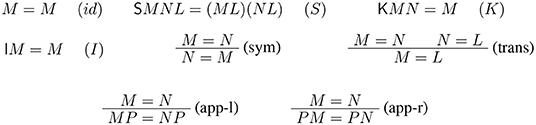Semantics for Combinatory Logic With Intersection Types

There is a plethora of semantics of computational models, nevertheless, the semantics of combinatory logic are among the less investigated ones. In this paper, we propose semantics for the computational system of combinatory logic with intersection types. We define extensional applicative structures endowed with special elements corresponding to primitive combinators. We prove two soundness and completeness results. First, the equational theory of untyped combinatory logic is proven to be sound and complete with respect to the proposed semantics. Second, the system of the combinatory logic with intersection types is proven to be sound and complete with respect to the proposed semantics. The usual approach to the semantics for calculi with types that can be found in the literature is based on models for the untyped calculus endowed with a valuation of type variables which enables the interpretation of types to be defined inductively. We propose, however, a different approach. In the semantics we propose, the interpretation of types is represented as a family of subsets that satisfies certain properties, whereas for a given valuation of term variables, the interpretation of terms is defined inductively. Due to the wide applicability of semantics of computational models, the presented approach could be further developed to other computational models and beyond—to current and foreseen application of semantics to large distributed systems and new challenging technologies.

1. Introduction

In the 1920s two models of computation were invented, combinatory logic and lambda calculus. The foundations of combinatory logic and lambda calculus was established in Curry (1930) and Church (1936), respectively. They were developed with the aim to describe functions, their behavior and properties. Nowadays they serve as a basis for the design of functional programming languages and programming languages at large. These two models of computation have the same computational power, they can express the same computational concepts; however the syntax of combinatory logic is much simpler. The basic idea of combinatory logic, introduced in Schönfinkel (1924), is to build functions without using variables. In order to control function application, type systems were introduced for both combinatory logic and lambda calculus. A recent comprehensive overview of combinators is given in Wolfram (2021). Apart from usual application in programming languages, typed combinatory logic has found its application in a wide range of different fields, such as machine learning, artificial intelligence, program synthesis. Developments of these fields urge for further investigation and development of the theory of combinatory logic.

In computation and type theory, intersection types characterize exactly all strongly normalizing lambda terms (Coppo and Dezani-Ciancaglini, 1978; Sallé, 1978; Pottinger, 1980) providing, on the computational side, a significant extension of simple types, which do not type even some normal forms, such as λx.xx. On the semantical side, intersection types became a powerful tool suitable for analysing lambda models (Barendregt et al., 1983, 2013). Intersection types for different systems have been studied (e.g., van Bakel et al., 2018; de'Liguoro and Treglia, 2019). Combinatory logic was equipped with intersection types in Dezani-Ciancaglini and Hindley (1992) with the same computational advantage of characterizing exactly all strongly normalizing combinatory terms, i.e., computations that always terminate.

The main contributions and results of this paper:

• We propose a novel semantics for combinatory logic with intersection types. We define extensional applicative structures endowed with special elements corresponding to primitive combinators S, K and I.

• We prove that the equational theory of untyped combinatory logic is sound and complete with respect to the proposed semantics.

• We then prove that combinatory logic with intersection types is sound and complete with respect to the proposed semantics.

1.1. Background and Motivation

There have been several approaches to semantics of lambda calculus with intersection types (Barendregt et al., 1983; Dezani-Ciancaglini and Margaria, 1984; Barbanera et al., 1995; Ong and Tsukada, 2012; de Carvalho, 2018) nevertheless none of them addresses combinatory logic. In Barendregt et al. (1983), the authors have introduced the filter models for lambda calculus and proved the soundness and completeness of the type assignment system with respect to the proposed semantics. Further, in Dezani-Ciancaglini and Margaria (1984) a modification of intersection type discipline has been considered, and it has been proved that this type system is sound and complete with respect to the F-semantics. The type assignment system with intersection and union types has been introduced in Barbanera et al. (1995), where authors proposed three semantics for the introduced system and proved soundness and completeness results. In de Carvalho (2018), the author introduced a non-uniform semantics of lambda calculus which allows to measure execution time and presented the intersection type system induced by these semantics, which can be seen as a reformulation of the system of Coppo et al. (1980). In Ong and Tsukada (2012), the two-level game semantics is used to model intersection types.

On the other hand, semantics for combinatory logic with intersection types has not been investigated as much as the semantics for lambda calculus with intersection types. An overview of models of combinatory logic is given in Bimbó (2012), however most of these models are models of untyped combinatory logic. Particularly, one class of models for combinatory logic with intersection types is presented based on theories of types which are in 1 − 1 correspondence with filters. Nevertheless, to the best of our knowledge filter models for combinatory logic with intersection types has not been published anywhere. The lack of study of models of combinatory logic has been our motivation for the present research.

1.2. Organization of the Paper

In Section 2, we briefly review basic notions of the untyped combinatory logic and intersection type assignment system for combinatory logic. We then define the semantics in Section 3. Section 4 presents the results of the paper: in Section 4.1, we prove the soundness and completeness of the equational theory of the untyped combinatory logic with respect to the proposed semantics; in Section 4.2, we prove the soundness and completeness of the combinatory logic with intersection types with respect to the proposed semantics. Section 5 concludes and contains the discussion of the related work.

2. Combinatory Logic With Intersection Types

We shortly review some basic notions of the untyped combinatory logic CL (Barendregt, 1985; Hindley and Seldin, 1986; Bimbó, 2012), and intersection types for combinatory logic (Dezani-Ciancaglini and Hindley, 1992).

2.1. Combinatory Logic

The language of combinatory logic is build up from a countable set of term variables V and a set of term constants using application, the only (binary) operation. Terms of combinatory logic, called CL-terms, are generated by the following grammar:

$\begin{array}{l}M,N::=x\mid \text{S}\mid \text{K}\mid \text{I}\mid MN\end{array}$

where x is a term variable and S, K, I are term constants, or constants for short. The set of all CL-terms is denoted by CL and is ranged over by capital letters M, N, …, M₁, …. The set of variables that occur in a term M is denoted by FV(M), and the result of substitution of the term N for variable x in the term M is denoted by M{N/x}. The use of parentheses is minimized by the convention that application associates to the left: M₁M₂…M_n means […(M₁M₂)…M_n].

The main objects of study in combinatory logic are the relations between terms. We will consider the equivalence relation generated by the equational theory ${E}{Q}$ given in Figure 1.

FIGURE 1

Figure 1. Equational theory ${E}{Q}$.

If M = N can be derived from the set of axioms and rules of Figure 1 we say that terms M and N are equal, and we write M = N. The equational theory obtained by adding the rule

$\begin{array}{l}\frac{Mx=Nxx\notin FV(M)\cup FV(N)}{M=N}(\text{ext})\end{array}$

to the equational theory ${E}{Q}$ will be denoted by ${{E}{Q}}^{\eta }$, and it represents the extensional equational theory. We write M =_η N, whenever M = N is provable in ${{E}{Q}}^{\eta }$. We use the notion of equivalence classes: $\left[M\right]=\left\{N\mid M=N\text{ is provable in }{{E}{Q}}^{\eta }\right\}$.

2.2. Intersection Types

Intersection types for combinatory logic were introduced in Dezani-Ciancaglini and Hindley (1992). The set of intersection types is generated by the following grammar:

$\begin{array}{l}\sigma ,\tau ::=a\mid \omega \mid \sigma \to \tau \mid \sigma \cap \tau \end{array}$

where a belongs to a countable set of type variables V_Type and ω is a type constant. There are two type forming operations: the arrow, →, which generates the simple types and the intersection, ∩, which provides the extension of the simple types. The set of all intersection types is denoted by Types and is ranged over by σ, τ, …, σ₁, …. We can omit parentheses in arrow types by removing outer parentheses and using the convention that, unless otherwise bracketed, nested arrows associate to the right: σ₁ → … → σ_n−1 → σ_n means (σ₁ → … → (σ_n−1 → σ_n)). Intersection types are associative: (σ ∩ τ) ∩ ρ is the same as σ ∩ (τ ∩ ρ), and an intersection type takes precedence over an arrow type: σ ∩ τ → ρ means (σ ∩ τ) → ρ.

Definition 2.1 (Dezani-Ciancaglini and Hindley, 1992; Barendregt et al., 2013).

(i) A statement is of the form M : σ, where M ∈ CL and σ ∈ Types. The term M is the subject and the type σ is the predicate of the statement.

(ii) A declaration is a statement with a term variable as subject, i.e., x : σ.

(iii) A basis (context) is a set of declarations with distinct term variables as subjects.

(iv) Let Γ = {x₁ : σ₁, …, x_n : σ_n} be a basis. The set dom(Γ) = {x₁, …, x_n} is the domain of the basis Γ.

(v) Let Γ = {x₁ : σ₁, …, x_n : σ_n} be a basis. Then |Γ| = {σ₁, …, σ_n}.

The subtyping (pre-order) relation on the set of intersection types is defined in the following way.

Definition 2.2 (Dezani-Ciancaglini and Hindley, 1992). The relation ≤ is the smallest binary relation satisfying:

(1) σ ≤ σ;

(2) σ ≤ σ ∩ σ;

(3) σ ≤ ω;

(4) σ ∩ τ ≤ σ, σ ∩ τ ≤ τ;

(5) ω ≤ ω → ω;

(6) (σ → ρ) ∩ (σ → τ) ≤ σ → (ρ ∩ τ);

(7) if σ ≤ τ, τ ≤ ρ then σ ≤ ρ;

(8) if σ ≤ σ₁, τ ≤ τ₁, then σ ∩ σ₁ ≤ τ ∩ τ₁;

(9) if σ ≤ σ₁, τ ≤ τ₁, then σ₁ → τ ≤ σ → τ₁,

The induced equivalence relation ~ is defined by

$\sigma ~\tau \text{ if and only if }\sigma \le \tau \text{ and }\tau \le \sigma .$

The type-assignment system for combinatory logic with intersection types, denoted by CL_∩, is presented in Figure 2. If the typing judgment Γ ⊢ M : σ can be derived by the rules in Figure 2, then it means that the statement M : σ is derivable from the basis Γ and that the term M is typable in the given basis Γ with type σ.

FIGURE 2

Figure 2. Type-assignment system CL_∩.

The rules (axiom S), (axiom K), and (axiom I) type the combinators S, K, and I, respectively. The rule (axiom ω) enables every combinatory term M to be typable. The rules (→ elim), (∩ elim-l), and (∩ elim-r) are the usual elimination rules for → and ∩, respectively. The rule (∩ intro) is the introduction rule for ∩. The rule (sub-type) is the subsumption rule induced by the subtyping relation on types and the rule (eq) is the rule which enables type preservation under equality.

Remark 2.3. The type-assignment system $T{A}_{CL{{B}}_1}$ of Dezani-Ciancaglini and Hindley (1992) is obtained from CL_∩ by omitting the rule (eq). Type-assignment statements in $T{A}_{CL{{B}}_1}$ are preserved by the equality generated by the equational theory ${E}{Q}$ (Dezani-Ciancaglini and Hindley, 1992, Theorem 3.12). In order to obtain a type-assignment system in which types are preserved by the equality generated by the extensional equational theory ${{E}{Q}}^{\eta }$, the rule (eq) has to be added.

Lemma 2.4 (Weakening lemma). If Γ ⊢ M : σ and Γ ⊆ Γ′ then Γ′ ⊢ M : σ.

Proof. By induction on the length of derivation of Γ ⊢ M : σ.□

3. Semantics for CL_∩

In this section, we introduce a semantics for combinatory logic with intersection types. We define a model for CL_∩ as an applicative structure equipped with an environment.

Definition 3.1. An applicative structure for CL_∩ is a tuple

${M}=\langle D,\left\{A^{\sigma }\right\},App\rangle$

which consists of:

(i) a non-empty set D, called domain,

(ii) a family {A^σ} of sets indexed by types σ, such that for every σ, τ ∈ Types,

• A^σ ⊆ D,

• A^ω = D,

• A^σ∩τ = A^σ ∩ A^τ,

• if σ ≤ τ, then A^σ ⊆ A^τ.

(iii) an application function App:D × D → D, such that for every σ, τ ∈ Types,

App↾(A^{σ → τ} × A^σ):A^{σ → τ} × A^σ → A^τ.

Definition 3.2. An applicative structure

${M}=\langle D,\left\{A^{\sigma }\right\},App\rangle$

has combinators if there exist elements s, k, i of the domain D such that

• s ∈ A^{(σ → (ρ → τ)) → ((σ → ρ) → (σ → τ))} for every σ, ρ, τ ∈ Types,

• k ∈ A^{σ → (τ → σ)} for every σ, τ ∈ Types,

• i ∈ A^{σ → σ} for every σ ∈ Types,

• for every a, b, c ∈ D the following equations hold:

$\begin{array}{ll}App(App(App(\text{s},a),b),c)=App(App(a,c),App(b,c))& (1)\end{array}$

$\begin{array}{ll}App(App(\text{k},a),b)=a& (2)\end{array}$

$\begin{array}{ll}App(\text{i},a)=a& (3)\end{array}$

Definition 3.3. An applicative structure

${M}=\langle D,\left\{A^{\sigma }\right\},App\rangle$

is extensional if for all f, g ∈ D it holds that

$\text{if }(\forall a\in D)(App(f,a)=App(g,a)),\text{then }f=g.$

Definition 3.4. An environment ρ for an applicative structure ${M}$ is a mapping from a set of term variables to the domain, ρ:V → D.

Although the proposed semantics is not Kripke-style semantics, its definition is inspired by the Kripke-style semantics introduced in Mitchell and Moggi (1991) and Kašterović and Ghilezan (2020), where a model is also defined as an applicative structure provided with an environment. The important difference between Definition 3.4 and the definition of an environment in Kašterović and Ghilezan (2020) is the fact that the environment in Kašterović and Ghilezan (2020) was a partial mapping, whereas herein it is a total mapping. The motivation for defining environments as total mappings will be explained in Remark 4.5.

Let ρ be an environment for ${M}$ and a ∈ D. By ρ(x: = a) we denote the environment for ${M}$ such that for all y ∈ V

$\begin{array}{l}\rho (x:=a)(y)=\{\begin{array}{cc}a,& y=x\\ \rho (y),& y\ne x\end{array}\end{array}$

Definition 3.5. A model for CL_∩ is a pair ${{M}}_{\rho }=\langle {M},\rho \rangle$, where ${M}=\langle D,\left\{A^{\sigma }\right\},App\rangle$ is an extensional applicative structure for CL_∩ with combinators, and ρ is an environment for ${M}$.

Definition 3.6. Let ${{M}}_{\rho }$ be a model for CL_∩. We define the meaning of a term M in the environment ρ, denoted by ⟦M⟧_ρ, inductively as follows:

1. ⟦x⟧_ρ = ρ(x),

2. ⟦S⟧_ρ = s,

3. ⟦K⟧_ρ = k,

4. ⟦I⟧_ρ = i,

5. ⟦MN⟧_ρ = App(⟦M⟧_ρ, ⟦N⟧_ρ).

Note that the meaning of a term does not depend on the meaning of the variables that do not occur in the term. Since an environment ρ is a total mapping and ρ(x) is defined for every variable x, the meaning of every term M, denoted by ⟦M⟧_ρ, is also well-defined.

Remark 3.7. An important difference between the applicative structure we define and the one introduced in Mitchell and Moggi (1991) is that we have a domain in the applicative structure. In Mitchell and Moggi (1991) the authors define the interpretation of the judgment Γ ⊢ M : σ, they interpret the term with its type. In turn, we wanted to be able to define the interpretation of a term independent of its type. For this reason we have introduced a domain as part of the applicative structure.

Lemma 3.8. Let ${M}$ be an extensional applicative structure for CL_∩ with combinators, ρ₁ and ρ₂ environments for ${M}$ and M a CL-term. If ρ₁(x) = ρ₂(x) holds for every variable x ∈ FV(M), then ⟦M⟧_ρ1 = ⟦M⟧_ρ2.

Proof. We prove the statement by induction on the structure of the term M.

• Let M be a variable x. If ρ₁(x) = ρ₂(x), then ⟦x⟧_ρ1 = ρ₁(x) = ρ₂(x) = ⟦x⟧_ρ2.

• If M is a term constant, then its interpretation does not depend on the environment, but only on the applicative structure. For example, let M be a term constant S, then ⟦S⟧_ρ1 = s = ⟦S⟧_ρ2.

• If M is an application NL, then by the induction hypothesis the statement holds for terms N and L, ⟦N⟧_ρ1 = ⟦N⟧_ρ2 and ⟦L⟧_ρ1 = ⟦L⟧_ρ2. Now, by Definition 3.6 we have

$\begin{array}{l}{⟦M⟧}_{{\rho }_1}={⟦NL⟧}_{{\rho }_1}=App({⟦N⟧}_{{\rho }_1},{⟦L⟧}_{{\rho }_1})=App({⟦N⟧}_{{\rho }_2},{⟦L⟧}_{{\rho }_2})\\ ={⟦NL⟧}_{{\rho }_2}={⟦M⟧}_{{\rho }_2}.\end{array}$

□

Lemma 3.9 (Substitution lemma). Let M, N be CL-terms and ρ an environment for an applicative structure ${M}$. Then,

${⟦M\left\{N/x\right\}⟧}_{\rho }={⟦M⟧}_{\rho (x:={⟦N⟧}_{\rho })}.$

The satisfiability of a statement M : σ in a model and the notion of semantical consequence are defined as follows.

Definition 3.10 (Kašterović and Ghilezan, 2020).

1. A statement M : σ is satisfied in a model M_ρ, denoted by ${{M}}_{\rho }\vDash M:\sigma$, if and only if ${⟦M⟧}_{\rho }\in A^{\sigma }$. In this case we say ${{M}}_{\rho }$ is a model of the statement M : σ. If a model ${{M}}_{\rho }$ does not satisfy the statement M : σ, we write ${{M}}_{\rho }⊭M:\sigma$.

2. A model ${{M}}_{\rho }$ is a model of a basis Γ, denoted by ${{M}}_{\rho }\vDash \Gamma$, if and only if every declaration x : σ from the basis Γ is satisfied in the model ${{M}}_{\rho }$, namely ${{M}}_{\rho }\vDash x:\sigma$.

3. A statement M : σ is a semantical consequence of a basis Γ, denoted by Γ ⊧ M : σ, if and only if every model of the basis Γ is also a model of the statement M : σ.

4. Soundness and Completeness Results

In this section we present the main results of the paper. We prove in Section 4.1 that the equational theory of the untyped combinatory logic ${{E}{Q}}^{\eta }$ is sound and complete with respect to the proposed semantics. In Section 4.2, we prove that the type-assignment system CL_∩ is sound and complete with respect to the proposed semantics.

4.1. Soundness and Completeness of Equational Theory ${{E}{Q}}^{\eta }$

In the previous section we have introduced models for CL_∩ such that the interpretation of every term is defined in a model. A fundamental question to ask is: if two terms are proven to be equal in the equational theory are their interpretations equal in a model?—this is referred to as the soundness of the equational theory with respect to the model. The other direction: if interpretations of two terms are equal in every model are the terms proven to be equal in the equational theory?—is referred to as the completeness.

In the sequel, we prove that the equational theory of untyped combinatory logic ${{E}{Q}}^{\eta }$ is sound and complete with respect to the proposed semantics.

Theorem 4.1 (Soundness of ${{E}{Q}}^{\eta }$). If M =_η N, then ⟦M⟧_ρ = ⟦N⟧_ρ for every model ${{M}}_{\rho }$.

Proof. The proof is by induction on the length of the proof of M = N in ${{E}{Q}}^{\eta }$.

If M = N is an instance of axiom (id), then terms M and N represent the same term L and it holds that ⟦M⟧_ρ = ⟦L⟧_ρ = ⟦N⟧_ρ for every model ${{M}}_{\rho }$.

If M = N is obtained by axiom (S), then there exist terms P, Q and R such that terms M and N are terms SPQR and (PR)(QR), respectively. Then, from Definitions 3.2 and 3.6 we obtain

$\begin{array}{l}{⟦\text{S}PQR⟧}_{\rho }=App(App(App({⟦\text{S}⟧}_{\rho },{⟦P⟧}_{\rho }),{⟦Q⟧}_{\rho }),{⟦R⟧}_{\rho })\\ =App(App(App(\text{s},{⟦P⟧}_{\rho }),{⟦Q⟧}_{\rho }),{⟦R⟧}_{\rho })\\ =App(App({⟦P⟧}_{\rho },{⟦R⟧}_{\rho }),App({⟦Q⟧}_{\rho },{⟦R⟧}_{\rho }))\\ ={⟦(PR)(QR)⟧}_{\rho }.\end{array}$

If M = N is obtained by axiom (K), then there exist terms P and Q, such that terms M and N are terms KPQ and P, respectively. Then, from Definitions 3.2 and 3.6 we obtain

$\begin{array}{l}{⟦\text{K}PQ⟧}_{\rho }=App(App({⟦\text{K}⟧}_{\rho },{⟦P⟧}_{\rho }),{⟦Q⟧}_{\rho })\\ =App(App(\text{k},{⟦P⟧}_{\rho }),{⟦Q⟧}_{\rho })\\ ={⟦P⟧}_{\rho }.\end{array}$

If M = N falls under axiom (I), then terms M and N are of the form IP and P, respectively, for some term P. In a similar way as in the previous two cases, we obtain

$\begin{array}{l}{⟦\text{I}P⟧}_{\rho }=App({⟦\text{I}⟧}_{\rho },{⟦P⟧}_{\rho })=App(\text{i},{⟦P⟧}_{\rho })={⟦P⟧}_{\rho }.\end{array}$

If M = N is obtained from N = M by rule (sym), then by induction hypothesis ⟦N⟧_ρ = ⟦M⟧_ρ and the statement holds.

If M = N is obtained from M = L and L = N by rule (trans), then ⟦M⟧_ρ = ⟦L⟧_ρ and ⟦L⟧_ρ = ⟦N⟧_ρ hold by induction hypothesis. Thus, ⟦M⟧_ρ = ⟦N⟧_ρ also holds.

Next, let us suppose that M = N is obtained from L = Q by rule (app-l), then terms M and N are of the form LP and QP, respectively, for some term P. By induction hypothesis ⟦L⟧_ρ = ⟦Q⟧_ρ. From the latter we obtain

${⟦LP⟧}_{\rho }=App({⟦L⟧}_{\rho },{⟦P⟧}_{\rho })=App({⟦Q⟧}_{\rho },{⟦P⟧}_{\rho })={⟦QP⟧}_{\rho }.$

Similarly to the previous case, if M = N is obtained by rule (app-r), then terms M and N are of the form PL and PQ, respectively, for some terms P, L, Q such that L = Q is provable in ${{E}{Q}}^{\eta }$. By induction hypothesis we obtain ⟦L⟧_ρ = ⟦Q⟧_ρ, and thus

${⟦PL⟧}_{\rho }=App({⟦P⟧}_{\rho },{⟦L⟧}_{\rho })=App({⟦P⟧}_{\rho },{⟦Q⟧}_{\rho })={⟦PQ⟧}_{\rho }.$

Finally, we consider the case where M = N is obtained by applying rule (ext) to Mx = Nx, with x being a variable which appears neither in M nor in N. Let ${{M}}_{\rho }$ be a model for CL_∩. In order to prove that ⟦M⟧_ρ = ⟦N⟧_ρ holds, it is enough to prove that for every d ∈ D it holds that App(⟦M⟧_ρ, d) = App(⟦N⟧_ρ, d), because of the extensionality of the applicative structure ${M}$. Let d ∈ D. Since by induction hypothesis ⟦Mx⟧_ρ = ⟦Nx⟧_ρ holds in any model, it also holds in model ${{M}}_{\rho (x:=d)}$, that is App(⟦M⟧_{ρ(x: = d)}, ⟦x⟧_{ρ(x: = d)}) = App(⟦N⟧_{ρ(x: = d)}, ⟦x⟧_{ρ(x: = d)}). From the assumption that x does not appear in M and Lemma 3.8, we obtain ⟦M⟧_ρ = ⟦M⟧_{ρ(x: = d)}. Similarly, ⟦N⟧_ρ = ⟦N⟧_{ρ(x: = d)}. Now, we have

$\begin{array}{l}App({⟦M⟧}_{\rho },d)=App({⟦M⟧}_{\rho (x:=d)},d)\\ =App({⟦M⟧}_{\rho (x:=d)},{⟦x⟧}_{\rho (x:=d)})\\ ={⟦Mx⟧}_{\rho (x:=d)}\\ ={⟦Nx⟧}_{\rho (x:=d)}\\ =App({⟦N⟧}_{\rho (x:=d)},{⟦x⟧}_{\rho (x:=d)})\\ =App({⟦N⟧}_{\rho },d).\end{array}$

Thus, ⟦M⟧_ρ = ⟦N⟧_ρ due to the extensionality of the applicative structure.

This concludes the proof.□

Recall that by [M] we denote the equivalence class of term M with respect to the equivalence relation generated by the equational theory ${{E}{Q}}^{\eta }$, $\left[M\right]=\left\{N\mid M=N\text{is provable in}{{E}{Q}}^{\eta }\right\}$.

In order to prove the completeness, we first prove the following property.

Lemma 4.2. Let ${M}=\langle D,\left\{A^{\sigma }\right\},App\rangle$ be an extensional applicative structure with combinators, such that D = {[M]∣M ∈ CL}, App([M], [N]) = [MN], s = [S], k = [K] and i = [I]. If an environment ρ^⋆ is defined by ρ^⋆(x) = [x], then ${⟦M⟧}_{{\rho }^{\star }}=\left[M\right]$.

Proof. The proof is by induction on the structure of M.

• If the term M is a variable x, then by Definition 3.6 we have ${⟦x⟧}_{{\rho }^{\star }}={\rho }^{\star }(x)=\left[x\right]$.

• If the term M is a term constant, for example S, then by Definition 3.6 we have ${⟦\mathsf{\text{S}}⟧}_{{\rho }^{\star }}=\mathbf{\text{s}}=\left[\mathsf{\text{S}}\right]$. Similarly, for term constants K and I.

• If the term M is an application NL, then by the induction hypothesis the statement holds for terms N and L, ${⟦N⟧}_{{\rho }^{\star }}=\left[N\right]$ and ${⟦L⟧}_{{\rho }^{\star }}=\left[L\right]$. Further, by Definition 3.6 we obtain ${⟦NL⟧}_{{\rho }^{\star }}=App({⟦N⟧}_{{\rho }^{\star }},{⟦L⟧}_{{\rho }^{\star }})=App(\left[N\right],\left[L\right])=\left[NL\right]$.

□

Theorem 4.3 (Completeness of ${{E}{Q}}^{\eta }$). If ⟦M⟧_ρ = ⟦N⟧_ρ holds in every model ${{M}}_{\rho }$, then M =_η N.

Proof. Suppose that ⟦M⟧_ρ = ⟦N⟧_ρ holds for any model ${{M}}_{\rho }$. We define a model ${{M}}_{{\rho }^{\star }}^{\prime }=\langle {{M}}_0,{\rho }^{\star }\rangle$ where ${{M}}_0$ is an applicative structure 〈D, {A^σ}, App〉 with the following components:

• the domain D is defined by D = {[M] ∣ M ∈ CL};

• for every σ ∈ Types, A^σ = {[M] ∣ M ∈ CL and ⊢ M : σ};

• App is a function defined by App([M], [N]) = [MN].

The environment ρ^⋆ is defined by ρ^⋆(x) = [x].

First we prove that the structure ${{M}}_0$ is an applicative structure, meaning that it satisfies conditions of Definition 3.1. The set D is a non-empty set. For every σ ∈ Types, the set A^σ = {[M] ∣ M ∈ CL and ⊢ M : σ} is a subset of the set D = {[M] ∣ M ∈ CL}. Since for every term M it holds that ⊢ M : ω, we have that A^ω = {[M] ∣ M ∈ CL and ⊢ M : ω} = {[M] ∣ M ∈ CL} = D. Next, we look at the sets A^σ and A^τ. By the definition of the applicative structure ${{M}}_0$ we have A^σ = {[M] ∣ M ∈ CL and ⊢ M : σ} and A^τ = {[M] ∣ M ∈ CL and ⊢ M : τ}. If [M] ∈ A^σ ∩ A^τ, then ⊢ M : σ and ⊢ M : τ. By rule (∩ intro) of Figure 2 we obtain ⊢ M : σ ∩ τ, which is equivalent to [M] ∈ A^σ∩τ, and we conclude A^σ ∩ A^τ ⊆ A^σ∩τ. Similarly, we prove that A^σ∩τ ⊆ A^σ ∩ A^τ and we conclude A^σ∩τ = A^σ ∩ A^τ. Let σ, τ ∈ Types such that σ ≤ τ. If [M] ∈ A^σ, then ⊢ M : σ holds, and since σ ≤ τ we obtain ⊢ M : τ by rule (sub-type). It follows that [M] ∈ A^τ and we can conclude that σ ≤ τ implies A^σ ⊆ A^τ. The function App defined by App([M], [N]) = [MN] maps D × D to D. If [M] ∈ A^{σ → τ} and [N] ∈ A^σ, then by the definition of the applicative structure ${{M}}_0$ we have ⊢ M : σ → τ and ⊢ N : σ. By rule (→ elim) of Figure 2 we obtain ⊢ MN : τ, thus we conclude [MN] ∈ A^τ and App ↾ (A^{σ → τ} × A^σ):A^{σ → τ} × A^σ → A^τ.

Next, we prove that the applicative structure ${{M}}_0$ has combinators. We consider the equivalence classes [S], [K], [I] ∈ D and denote them by s, k, i, respectively. Since ⊢ S:(σ → (τ → ρ)) → ((σ → τ) → (σ → ρ)) holds by (axiom S) of Figure 2, we have that s = [S] ∈ A^{(σ → (τ → ρ)) → ((σ → τ) → (σ → ρ))} for any σ, τ, ρ ∈ Types. Similarly, we obtain k = [K] ∈ A^{σ → (τ → σ)} and i = [I] ∈ A^{σ → σ}. We also have to prove that the elements s, k, and i satisfy the Equations (1)–(3). By the rules of the equational theory ${{E}{Q}}^{\eta }$ we obtain [SMNL] = [(ML)(NL)], [KMN] = [M] and [IM] = [M] and it follows that:

$\begin{array}{l}App(App(App(\left[\text{S}\right],\left[M\right]),\left[N\right]),\left[L\right])=\left[\text{S}MNL\right]=\left[(ML)(NL)\right]\\ =App(\left[ML\right],\left[NL\right])\\ =App(App(\left[M\right],\left[L\right]),App(\left[N\right],\left[L\right]))\end{array}$

$\begin{array}{l}App(App(\left[\text{K}\right],\left[M\right]),\left[N\right])=\left[\text{K}MN\right]=\left[M\right]\end{array}$

$\begin{array}{l}App(\left[\text{I}\right],\left[M\right])=\left[\text{I}M\right]=\left[M\right]\end{array}$

The extensionality of the applicative structure follows from the extensionality of combinatory logic. Let [M], [N] ∈ D such that for every [L] ∈ D, App([M], [L]) = App([N], [L]), i.e., [ML] = [NL]. Then, for a variable x, that does not appear in terms M and N, it holds that [Mx] = [Nx], that is Mx = Nx is provable in ${{E}{Q}}^{\eta }$. By rule (ext) we obtain M = N is provable in ${{E}{Q}}^{\eta }$, so [M] = [N].

We have proved that ${{M}}_{{\rho }^{\star }}^{\prime }$ is a model for CL_∩. If ⟦M⟧_ρ = ⟦N⟧_ρ in any model, then it also holds in the model ${{M}}_{{\rho }^{\star }}^{\prime }$. Hence, we have that ${⟦M⟧}_{{\rho }^{\star }}={⟦N⟧}_{{\rho }^{\star }}$. From Lemma 4.2 we get ${⟦M⟧}_{{\rho }^{\star }}=\left[M\right]$ and ${⟦N⟧}_{{\rho }^{\star }}=\left[N\right]$. Now we can conclude that [M] = [N] holds, that is M =_η N.□

Theorems 4.1 and 4.3 prove that the equational theory of untyped combinatory logic is both sound and complete with respect to the proposed semantics, hence the proposed semantics is a semantics of the untyped combinatory logic.

4.2. Soundness and Completeness of Type-Assignment System CL_∩

In the sequel we consider another fundamental question: if M : σ is (syntactically) derivable in the type system CL_∩, ⊢ M : σ, is it valid in all models, ⊧ M : σ?—this is referred to as the soundness of the type-assignment system with respect to the model. More general, if Γ ⊢ M : σ is (syntactically) derivable in the type system CL_∩, is it semantically derivable, Γ ⊧ M : σ? The other direction: if M : σ is valid in all models of CL_∩, is it derivable in CL_∩?—is referred to as the completeness. More general, does semantical derivability Γ ⊧ M : σ imply syntactical derivability Γ ⊢ M : σ?

We prove herein the type-assignment system CL_∩ to be sound and complete with respect to the proposed semantics.

Theorem 4.4 (Soundness of CL_∩). If Γ ⊢ M : σ, then Γ ⊧ M : σ.

Proof. We prove the statement by induction on the derivation of Γ ⊢ M : σ, considering the last rule used.

• Let $\frac{x:\sigma \in \Gamma }{\Gamma ⊢x:\sigma }$ be the last rule used. Assume that ${{M}}_{\rho }$ is a model, such that ${{M}}_{\rho }\vDash \Gamma$. By Definition 3.10, the latter implies that for every y : τ ∈ Γ, ${{M}}_{\rho }\vDash y:\tau$. From the premise we have x : σ ∈ Γ, thus ${{M}}_{\rho }\vDash x:\sigma$.

• If Γ ⊢ M : σ falls under (axiom S), then we have Γ ⊢ S:(σ₁ → (ρ₁ → τ₁)) → ((σ₁ → ρ₁) → (σ₁ → τ₁)) for some σ₁, τ₁, ρ₁ ∈ Types. Let ${{M}}_{\rho }$ be an arbitrary model for CL_∩. By Definition 3.6 we have that ${⟦\mathsf{\text{S}}⟧}_{\rho }=\mathbf{\text{s}}\in A^{({\sigma }_1\to ({\rho }_1\to {\tau }_1))\to (({\sigma }_1\to {\rho }_1)\to ({\sigma }_1\to {\tau }_1))}$. Thus, ${{M}}_{\rho }\vDash \mathsf{\text{S}}:({\sigma }_1\to ({\rho }_1\to {\tau }_1))\to (({\sigma }_1\to {\rho }_1)\to ({\sigma }_1\to {\tau }_1))$ and we can conclude Γ ⊧ S:(σ₁ → (ρ₁ → τ₁)) → ((σ₁ → ρ₁) → (σ₁ → τ₁)).

• If Γ ⊢ M : σ falls under (axiom K), then we have Γ ⊢ K : σ₁ → (τ₁ → σ₁) for some σ₁, τ₁ ∈ Types. Let ${{M}}_{\rho }$ be an arbitrary model for CL_∩. We have that ${⟦\mathsf{\text{K}}⟧}_{\rho }=\mathbf{\text{k}}\in A^{{\sigma }_1\to ({\tau }_1\to {\sigma }_1)}$. Thus, ${{M}}_{\rho }\vDash \mathsf{\text{K}}:{\sigma }_1\to ({\tau }_1\to {\sigma }_1)$ holds and we can conclude Γ ⊧ K : σ₁ → (τ₁ → σ₁).

• If Γ ⊢ M : σ falls under (axiom I), then we have Γ ⊢ I : σ₁ → σ₁ for some σ₁ ∈ Types. For an arbitrary model ${{M}}_{\rho }$ it holds that ${⟦\mathsf{\text{I}}⟧}_{\rho }=\mathbf{\text{i}}\in A^{{\sigma }_1\to {\sigma }_1}$. Hence, ${{M}}_{\rho }\vDash \mathsf{\text{I}}:{\sigma }_1\to {\sigma }_1$ and Γ ⊧ I : σ₁ → σ₁.

• If Γ ⊢ M : σ falls under (axiom ω), then we have Γ ⊢ M : ω. Let ${{M}}_{\rho }$ be an arbitrary model for CL_∩. We have that ⟦M⟧_ρ ∈ D and A^ω = D. From this we obtain ${⟦M⟧}_{\rho }\in A^{\omega }$, that is ${{M}}_{\rho }\vDash M:\omega$.

• Let $\frac{\Gamma ⊢M:\sigma \to \tau \Gamma ⊢N:\sigma }{\Gamma ⊢MN:\tau }$ be the last rule used and ${{M}}_{\rho }$ a model which satisfies Γ. By the induction hypothesis, we have that the statement holds for premises Γ ⊢ M : σ → τ and Γ ⊢ N : σ, i.e., Γ ⊧ M : σ → τ and Γ ⊧ N : σ. From the induction hypothesis and the assumption ${{M}}_{\rho }\vDash \Gamma$, we obtain ${{M}}_{\rho }\vDash M:\sigma \to \tau$ and ${{M}}_{\rho }\vDash N:\sigma$. The former implies ${⟦M⟧}_{\rho }\in A^{\sigma \to \tau }$ and the latter implies ${⟦N⟧}_{\rho }\in A^{\sigma }$. Thus, it holds that ${⟦MN⟧}_{\rho }=App({⟦M⟧}_{\rho },{⟦N⟧}_{\rho })\in A^{\tau }$, and we obtain ${{M}}_{\rho }\vDash MN:\tau$.

• Let $\frac{\Gamma ⊢M:\sigma \cap \tau }{\Gamma ⊢M:\sigma }$ be the last rule used and ${{M}}_{\rho }$ a model of Γ. By the induction hypothesis we have ${{M}}_{\rho }\vDash M:\sigma \cap \tau$, which implies that ${⟦M⟧}_{\rho }\in A^{\sigma \cap \tau }$ holds. Since A^σ∩τ = A^σ ∩ A^τ by Definition 3.1, we have ${⟦M⟧}_{\rho }\in A^{\sigma }\cap A^{\tau }\subseteq A^{\sigma }$. Thus, we conclude ${{M}}_{\rho }\vDash M:\sigma$.

• If the last rule used is $\frac{\Gamma ⊢M:\sigma \cap \tau }{\Gamma ⊢M:\tau }$ the proof proceeds similarly as in the previous case.

• Let $\frac{\Gamma ⊢M:\sigma \Gamma ⊢M:\tau }{\Gamma ⊢M:\sigma \cap \tau }$ be the last rule used and ${{M}}_{\rho }$ a model of Γ. By the induction hypothesis we obtain ${{M}}_{\rho }\vDash M:\sigma$ and ${{M}}_{\rho }\vDash M:\tau$. The former implies that ${⟦M⟧}_{\rho }\in A^{\sigma }$ holds, and the latter implies that ${⟦M⟧}_{\rho }\in A^{\tau }$ holds. Since A^σ ∩ A^τ = A^σ∩τ by Definition 3.1, we have ${⟦M⟧}_{\rho }\in A^{\sigma }\cap A^{\tau }=A^{\sigma \cap \tau }$. Finally, we conclude ${{M}}_{\rho }\vDash M:\sigma \cap \tau$.

• Let $\frac{\Gamma ⊢M:\sigma \sigma \le \tau }{\Gamma ⊢M:\tau }$ be the last rule used and ${{M}}_{\rho }$ a model which satisfies the basis Γ. By the induction hypothesis we obtain that the statement holds for the premise, i.e., Γ ⊧ M : σ and since ${{M}}_{\rho }\vDash \Gamma$ we have that ${{M}}_{\rho }\vDash M:\sigma$. The latter implies ${⟦M⟧}_{\rho }\in A^{\sigma }$. By Definition 3.1 we know that σ ≤ τ implies A^σ ⊆ A^τ. Hence, it holds that ${⟦M⟧}_{\rho }\in A^{\tau }$, and we can conclude ${{M}}_{\rho }\vDash M:\tau$.

• Let $\frac{\Gamma ⊢M:\sigma M{=}_{\eta }N}{\Gamma ⊢N:\sigma }$ be the last rule used and ${{M}}_{\rho }$ a model of Γ. By the induction hypothesis we have ${{M}}_{\rho }\vDash M:\sigma$, which implies that ${⟦M⟧}_{\rho }\in A^{\sigma }$ holds. From M =_η N, that is M = N is provable in ${{E}{Q}}^{\eta }$, and Theorem 4.1 we obtain ⟦M⟧_ρ = ⟦N⟧_ρ. Thus, we can conclude ${⟦N⟧}_{\rho }={⟦M⟧}_{\rho }\in A^{\sigma }$, that is ${{M}}_{\rho }\vDash N:\sigma$.

• This concludes the proof.

□

Remark 4.5. As pointed out in Section 3, we have defined an environment as a total mapping, whereas in Kašterović and Ghilezan (2020) an environment was defined as a partial mapping. Every combinatory term is typable with the type ω, i.e., Γ ⊢ M : ω for any basis Γ, and in order to obtain the soundness of the type-assignment system we need to prove that M : ω holds in every model. Thus, we had to define environments so that the meaning of every term M is defined in all models. This is specific to intersection type systems and is due to the rule (axiom ω) which ensures typability of all terms.

We define a class of canonical models, following the approach used in Kašterović and Ghilezan (2020), in order to prove the completeness of the type-assignment system CL_∩ with respect to the models presented in Section 3. Each canonical model is defined with respect to some basis, so that it satisfies only statements that can be derived from that basis. More precisely, we will define a model ${{M}}_{{\rho }^{\star }}^{\Gamma }$ such that

${{M}}_{{\rho }^{\star }}^{\Gamma }\vDash M:\sigma \text{ if and only if }\Gamma ⊢M:\sigma .$

Definition 4.6. Let Γ be a basis. A canonical model is a pair ${{M}}_{{\rho }^{\star }}^{\Gamma }=\langle {{M}}^{\Gamma },{\rho }^{\star }\rangle$, where

${{M}}^{\Gamma }=\langle D,\left\{A^{\sigma }\right\},App\rangle$

such that

• D = {[M] ∣ M ∈ CL},

• A^σ = {[M] ∣ M ∈ CL and Γ ⊢ M : σ},

• App([M], [N]) = [MN],

and ρ^⋆(x) = [x].

Lemma 4.7. The canonical model ${{M}}_{{\rho }^{\star }}^{\Gamma }$ is a model for CL_∩.

Proof. We need to prove that the tuple ${{M}}_{{\rho }^{\star }}^{\Gamma }$ introduced in Definition 4.6 satisfies the conditions of Definition 3.5. First, we prove that ${{M}}^{\Gamma }=\langle D,\left\{A^{\sigma }\right\},App\rangle$ is an applicative structure. The set D is a non-empty set. The set A^σ = {[M] ∣ M ∈ CL and Γ ⊢ M : σ} is a subset of D = {[M] ∣ M ∈ CL}. For every CL-term M we have Γ ⊢ M : ω, thus A^ω = {[M] ∣ M ∈ CL and Γ ⊢ M : ω} = {[M] ∣ M ∈ CL} = D. The proofs that the family {A^σ} and the application function App satisfy the conditions of Definition 3.1 are obtained similarly as in the proof of Theorem 4.3.

We have proved that the tuple ${{M}}^{\Gamma }=\langle D,\left\{A^{\sigma }\right\},App\rangle$ is an applicative structure. Next, we prove that it has combinators and that it is extensional. Similarly as in the proof of Theorem 4.3 we denote equivalence classes [S], [K], [I] by s, k, i, respectively. From the type-assignment system (Figure 2) we know that for the basis Γ, Γ ⊢ S:(σ → (τ → ρ)) → ((σ → τ) → (σ → ρ)). From the latter it follows that s = [S] ∈ A^{(σ → (τ → ρ)) → ((σ → τ) → (σ → ρ))}. Similarly, we obtain k = [K] ∈ A^{σ → (τ → σ)} and i = [I] ∈ A^{σ → σ}. The proof that elements [S], [K], [I] satisfy Equations (1)–(3) is given in the proof of Theorem 4.3.

We have proved that the applicative structure introduced in Definition 4.6 has combinators. The proof that the applicative structure is extensional is the same as in the proof of Theorem 4.3.

The mapping ρ^⋆ defined by ρ^⋆(x) = [x] is an environment for the applicative structure ${{M}}^{\Gamma }$.

This completes the proof that ${{M}}_{{\rho }^{\star }}^{\Gamma }$ is a model for CL_∩.□

Lemma 4.8. Let ${{M}}_{{\rho }^{\star }}^{\Gamma }$ be the canonical model. For every CL-term M, it holds ${⟦M⟧}_{{\rho }^{\star }}=\left[M\right]$.

Proof. This is a straightforward consequence of Lemma 4.2.□

Theorem 4.9. Let ${{M}}_{{\rho }^{\star }}^{\Gamma }$ be a canonical model. It holds that

${{M}}_{{\rho }^{\star }}^{\Gamma }\vDash M:\sigma \text{ if and only if }\Gamma ⊢M:\sigma .$

Proof. By Definition 4.6 and Lemma 4.8 we obtain

$\begin{array}{l}{{M}}_{{\rho }^{\star }}^{\Gamma }\vDash M:\sigma \text{ if and only if }{⟦M⟧}_{{\rho }^{\star }}\in A^{\sigma }\\ \text{ if and only if }\left[M\right]\in \left\{\left[N\right]\mid N\in CL\text{ and }\Gamma ⊢N:\sigma \right\}\\ \text{ if and only if }\Gamma ⊢M:\sigma .\end{array}$

□

Theorem 4.10 (Completeness of CL_∩). If Γ ⊧ M : σ, then Γ ⊢ M : σ.

Proof. Suppose that Γ ⊧ M : σ. Let ${{M}}_{{\rho }^{\star }}^{\Gamma }$ be a canonical model (Definition 4.6). First, we need to prove that ${{M}}_{{\rho }^{\star }}^{\Gamma }\vDash \Gamma$. Let x : σ be a declaration from the basis Γ. By Lemma 4.8 and Definition 4.6 we have

${⟦x⟧}_{{\rho }^{\star }}=\left[x\right]\in \left\{\left[N\right]\mid N\in CL\text{ and }\Gamma ⊢N:\sigma \right\}=A^{\sigma }$

It follows that ${{M}}_{{\rho }^{\star }}^{\Gamma }\vDash \Gamma$. From the latter and the assumption Γ ⊧ M : σ we obtain ${{M}}_{{\rho }^{\star }}^{\Gamma }\vDash M:\sigma$. By Theorem 4.9 we obtain Γ ⊢ M : σ.□

Theorems 4.4 and 4.10 prove that the type-assignment system CL_∩ is both sound and complete with respect to the proposed semantics. Hence the proposed semantics is a semantics of the combinatory logic with intersection types and of the untyped combinatory logic, as proven in Section 4.1.

5. Discussion and Conclusion

Combinatory logic, both typed and untyped, found its application in different scientific fields of computer science, e.g., machine learning (Liang et al., 2010) and artificial intelligence (e.g., Garrette et al., 2015), cognitive representation (e.g., Pierre Desclés, 2004), program synthesis (e.g., Düdder et al., 2012). The development of these fields urge for the further development of combinatory logic, typed, and untyped. Combinatory logic with intersection types has been the object of several studies (Dezani-Ciancaglini and Hindley, 1992; Bunder, 2002; Rehof and Urzyczyn, 2011; Bimbó, 2012). In Dezani-Ciancaglini and Hindley (1992), two different formulations of intersection types for combinatory logic are proposed and we consider in the paper one of these formulations. The authors proved that type-assignment statements are preserved by combinatory β-equality. A logic of intersection types is considered in Venneri (1994), by studying a logical characterization for the intersection-type discipline. The author presents a new formulation of the intersection type inference, equivalent to the original one, and then define a Hilbert-style axiomatization such that a formula is provable in the logical system if and only if it is an inhabited intersection type. Bunder (2002) also studies a logic of intersection types for lambda-terms and combinators by introducing a new system for intersection types, weaker than the one of Venneri (1994), and with the advantage that the logic of types can be obtained directly from the rules of the type-assignment system. None of these papers consider semantics for combinatory logic with intersection types. Models for combinatory logic with intersection types are presented in Bimbó (2012) along with the proof that the type-assignment system is sound and complete with respect to the presented models. Kripke-style semantics for lambda calculus and combinatory logic with types are introduced in Mitchell and Moggi (1991) and Kašterović and Ghilezan (2020). In Mitchell and Moggi (1991), calculi with simple types are considered, whereas in Kašterović and Ghilezan (2020) the authors considered full simply typed calculi. However, to the best of our knowledge the semantics we propose is novel.

We have introduced a semantics for combinatory logic with intersection types. As the main results of the paper we have proved that both the extensional equational theory of the untyped CL and the intersection type-assignment system CL_∩ are sound and complete with respect to the proposed semantics.

The usual approach to the semantics for calculi with types that can be found in the literature, e.g., filter models for lambda calculus with intersection types (Barendregt et al., 1983), is based on a model for the untyped calculus endowed with a valuation of type variables which enables the interpretation of types to be defined inductively. We propose a different approach. In the semantics we propose, the interpretation of types is represented as a family of subsets that satisfies certain properties. Moreover, for a given valuation of term variables, the interpretation of terms is defined inductively, whereas in the previously mentioned semantics the interpretation of terms is defined as a function that satisfies specified conditions.

We plan to further develop this approach to lambda calculus, to different frameworks in logic and computation, e.g., polymorphic types.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author/s.

Author Contributions

Both authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research reported in the paper is partly supported by the Science Fund Republic of Serbia #6526707 AI4TrustBC.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank the referees whose suggestions lead to major improvements.

References

Barbanera, F., Dezani-Ciancaglini, M., and de'Liguoro, U. (1995). Intersection and union types: syntax and semantics. Inf. Comput. 119, 202–230. doi: 10.1006/inco.1995.1086

CrossRef Full Text | Google Scholar

Barendregt, H. P. (1985). The Lambda Calculus - Its Syntax and Semantics, Volume 103 of Studies in Logic and the Foundations of Mathematics. Elsevier: North-Holland.

Google Scholar

Barendregt, H. P., Coppo, M., and Dezani-Ciancaglini, M. (1983). A filter lambda model and the completeness of type assignment. J. Symb. Logic. 48, 931–940. doi: 10.2307/2273659

CrossRef Full Text | Google Scholar

Barendregt, H. P., Dekkers, W., and Statman, R. (2013). Lambda Calculus With Types. Perspectives in Logic. Cambridge: University Press. doi: 10.1017/CBO9781139032636

CrossRef Full Text | Google Scholar

Bimbó, K. (2012). Combinatory Logic: Pure, Applied, and Typed. Boca Raton, FL: CRC Press; Taylor & Francis Group. doi: 10.1201/b11046

CrossRef Full Text | Google Scholar

Bunder, M. W. (2002). Intersection types for lambda-terms and combinators and their logics. Log. J. IGPL 10, 357–378. doi: 10.1093/jigpal/10.4.357

CrossRef Full Text | Google Scholar

Church, A. (1936). An unsolvable problem of elementary number theory. Am. J. Math. 58, 345–363. doi: 10.2307/2371045

CrossRef Full Text

Coppo, M., and Dezani-Ciancaglini, M. (1978). A new type assignment for λ-terms. Arch. Math. Log. 19, 139–156. doi: 10.1007/BF02011875

CrossRef Full Text | Google Scholar

Coppo, M., Dezani-Ciancaglini, M., and Venneri, B. (1980). “Principal type schemes and lambda-calculus semantics,” in H.B.Curry: Essays on Combinatory Logic, Lambda-Calculus and Formalism (San Diego, CA: Academic Press), 535–560.

Google Scholar

Curry, H. B. (1930). Grundlagen der kombinatorischen logik. Am. J. Math. 52, 509–536. doi: 10.2307/2370619

CrossRef Full Text

de Carvalho, D. (2018). Execution time of λ-terms via denotational semantics and intersection types. Math. Struct. Comput. Sci. 28, 1169–1203. doi: 10.1017/S0960129516000396

CrossRef Full Text | Google Scholar

de'Liguoro, U., and Treglia, R. (2019). “Intersection types for the computational lambda-calculus,” in Proceedings of the 20th Italian Conference on Theoretical Computer Science, ICTCS 2019, eds A. Cherubini, N. Sabadini, and S. Tini (Como), 184–189.

Google Scholar

Dezani-Ciancaglini, M., and Hindley, J. R. (1992). Intersection types for combinatory logic. Theor. Comput. Sci. 100, 303–324. doi: 10.1016/0304-3975(92)90306-Z

CrossRef Full Text | Google Scholar

Dezani-Ciancaglini, M., and Margaria, I. (1984). “F-semantics for intersection type discipline,” in Semantics of Data Types, International Symposium Sophia-Antipolis, Vol. 173 of Lecture Notes in Computer Science, eds G. Kahn, D. B. MacQueen, and G. D. Plotkin (Berlin; Heidelberg: Springer), 279–300. doi: 10.1007/3-540-13346-1_14

CrossRef Full Text | Google Scholar

Düdder, B., Martens, M., Rehof, J., and Urzyczyn, P. (2012). “Bounded combinatory logic,” in Computer Science Logic (CSL'12) - 26th International Workshop/21st Annual Conference of the EACSL, CSL 2012, Vol. 16 of LIPIcs, eds P. Cégielski and A. Durand (Fontainebleau: Schloss Dagstuhl - Leibniz-Zentrum für Informatik), 243–258.

Google Scholar

Garrette, D., Dyer, C., Baldridge, J., and Smith, N. A. (2015). “Weakly-supervised grammar-informed Bayesian CCG parser learning,” in Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, eds B. Bonet and S. Koenig (Austin, TX: AAAI Press), 2246–2252.

Google Scholar

Hindley, J. R., and Seldin, J. P. (1986). Introduction to Combinators and Lambda-Calculus. Cambridge: Cambridge University Press.

Google Scholar

Kašterović, S., and Ghilezan, S. (2020). Kripke-style semantics and completeness for full simply typed lambda calculus. J. Log. Comput. 30, 1567–1608. doi: 10.1093/logcom/exaa055

CrossRef Full Text | Google Scholar

Liang, P., Jordan, M. I., and Klein, D. (2010). “Learning programs: a hierarchical Bayesian approach,” in Proceedings of the 27th International Conference on Machine Learning (ICML-10), eds J. Fürnkranz and T. Joachims (Haifa: Omnipress), 639–646.

Google Scholar

Mitchell, J. C., and Moggi, E. (1991). Kripke-style models for typed lambda calculus. Ann Pure Appl. Logic 51, 99–124. doi: 10.1016/0168-0072(91)90067-V

PubMed Abstract | CrossRef Full Text | Google Scholar

Ong, C. L., and Tsukada, T. (2012). “Two-level game semantics, intersection types, and recursion schemes,” in Automata, Languages, and Programming - 39th International Colloquium, ICALP 2012, Vol. 7392 of Lecture Notes in Computer Science, eds A. Czumaj, K. Mehlhorn, A. M. Pitts, and R. Wattenhofer (Warwick: Springer), 325–336. doi: 10.1007/978-3-642-31585-5_31

CrossRef Full Text | Google Scholar

Pierre Desclés, J. (2004). “Combinatory logic, language, and cognitive representations,” in Alternative Logics. Do Sciences Need Them?, ed P. Weingartner (Berlin: Springer Verlag), 115–148. doi: 10.1007/978-3-662-05679-0_9

CrossRef Full Text | Google Scholar

Pottinger, G. (1980). “A type assignment for the strongly normalizable λ-terms,” in To H. B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism, eds J. P. Seldin and J. R. Hindley (London: Academic Press), 561–577.

Google Scholar

Rehof, J., and Urzyczyn, P. (2011). “Finite combinatory logic with intersection types,” in Typed Lambda Calculi and Applications - 10th International Conference, TLCA 2011, Volume 6690 of Lecture Notes in Computer Science, ed C. L. Ong (Novi Sad: Springer), 169–183. doi: 10.1007/978-3-642-21691-6_15

CrossRef Full Text | Google Scholar

Sallé, P. (1978). “Une extension de la théorie des types en lambda-calcul,” in 5th International Conference on Automata, Languages and Programming, ICALP'78, Vol. 62 of Lecture Notes in Computer Science, eds G. Ausiello and C. Böhm (Udine: Springer), 398–410. doi: 10.1007/3-540-08860-1_30

CrossRef Full Text | Google Scholar

Schönfinkel, M. (1924). Über die bausteine der mathematischen logik. Math. Ann. 92, 305–316. doi: 10.1007/BF01448013

CrossRef Full Text | Google Scholar

van Bakel, S., Barbanera, F., and de'Liguoro, U. (2018). Intersection types for the lambda-mu calculus. arXiv:1704.00272. doi: 10.48550/arXiv.1704.00272

CrossRef Full Text | Google Scholar

Venneri, B. (1994). Intersection types as logical formulae. J. Log. Comput. 4, 109–124. doi: 10.1093/logcom/4.2.109

CrossRef Full Text | Google Scholar

Wolfram, S. (2021). Combinators: a centennial view. CoRR, abs/2103.12811.

Google Scholar