Effects of Uncertainty Visualization on Map-Based Decision Making Under Time Pressure

Korporaal, Michelle; Ruginski, Ian T.; Fabrikant, Sara Irina

doi:10.3389/fcomp.2020.00032

ORIGINAL RESEARCH article

Front. Comput. Sci., 31 August 2020

Sec. Human-Media Interaction

Volume 2 - 2020 | https://doi.org/10.3389/fcomp.2020.00032

This article is part of the Research Topic Uncertainty Visualization and Decision Making View all 8 articles

Effects of Uncertainty Visualization on Map-Based Decision Making Under Time Pressure

$\nMichelle Korporaal$ Michelle Korporaal¹

Ian T. Ruginski²^*

Sara Irina Fabrikant²

¹Skyguide Inc., Zurich, Switzerland
²Department of Geography and Digital Society Initiative, University of Zurich, Zurich, Switzerland

Most of our daily activities in a highly mobile digital society require timely spatial decision-making. Much of such decision-making is supported by map displays on various devices with different modalities. Spatial information visualized on maps, however, is always subject to a multitude of uncertainties. If space-time decision-makers are not informed about potential uncertainties, misleading, or at worst, life-threatening outcomes might result from map-based decisions. Therefore, data uncertainties should be communicated to decision-makers, especially when they are made with limited time resources and when decision outcomes can have dramatic consequences. Thus, the current study investigates how data uncertainty visualized in maps might influence the process and outcomes of spatial decision-making, especially when made under time pressure in risky situations. Although there is very little empirical evidence from prior uncertainty visualization research that considered decision time constraints, we hypothesized that uncertainty visualization would also have an effect on decision-making under time critical and complex decision contexts. Using a map-based helicopter landing scenario in mountainous terrain, we found that neither time pressure nor uncertainty affected participants decision-making accuracy. However, uncertainty affected participants' decision strategies, and time pressure affected participants' response times. Specifically, when presented with two equally correct answers, participants avoided uncertainty more often at a cost of landing distance (an equally important decision criteria). We interpret our results as consistent with a loss-aversion heuristic and suggest implications for the study of decision-making with uncertainty visualizations.

Introduction

Data visualization is becoming more and more ubiquitous in society as a way of communicating complex phenomena to scientific experts and the general public alike. Along with this increase in availability comes a responsibility for scientists to visualize uncertainty, which includes a consideration of the accuracy of data from a variety of sources, such as measurement error, natural variation, and prediction error (Skeels et al., 2010; MacEachren et al., 2012). Since the launch of the “Visualization of Data Quality” research initiative by the National Center for Geographic Information and Analysis (NCGIA; Beard et al., 1991) in 1991, geographic information scientists have been working on the problem of uncertainty visualization in spatial data. Because uncertainty is a multi-faceted concept, there are many different uncertainties, and the visualization of uncertainties is applied in various contexts with different objectives, so there cannot be a single optimal uncertainty visualization technique. This calls for evaluation of uncertainty visualization methods in specific contexts.

The current research will focus on two specific contexts: making decisions using map-based geographic data with and without time pressure. Maps depicting geographic data offer a plethora of options to visualize uncertainty, but it is not often clear how (e.g., choice of color, texture, glyphs) to effectively communicate uncertainty information. Since the ultimate goal of uncertainty visualizations is for decision-makers to make “well-founded decisions based on imperfect information” (Pang et al., 1997), it is important to understand what influence uncertainty visualizations have on map-based decisions. In principle, there is agreement that geographic uncertainties influence decisions in some way (MacEachren et al., 2005). For a long time, however, it was simply assumed that uncertainty visualizations are useful for a decision-maker without empirical evaluation (MacEachren et al., 2005). The more uncertainty visualization techniques have developed, the more there has been a call for empirical evaluations and theoretical frameworks to test the effects uncertainty visualizations have on decision-making (Spiegelhalter et al., 2011; Kinkeldey et al., 2015a; Kay et al., 2016; Padilla et al., 2018).

Decision-Making With Uncertainty and Uncertainty Visualizations

Decisions can be divided into two basic elements: (1) the decision-making process and (2) the decision outcome (Keuper, 2004). A bounded rationality model of decision-making assumes that decision-makers cannot obtain complete and perfect information; their knowledge of all options, their cognitive abilities, and the time available are limited (Simon, 1956; Orquin and Mueller Loose, 2013). For this reason, decision-makers must break down the decision-making problem and prioritize certain information or apply specific strategies to reach a decision (Kahneman, 2011; Orquin and Mueller Loose, 2013). In the context of visualizations, Padilla et al. (2018) more recently have proposed two types of decision-making with visualizations, one that is fast and easy (type I) and one that is slower and more effortful (type II). Type I decisions occur if the visualization matches common preconceptions (e.g., “dark is more” on maps; Garlandini and Fabrikant, 2009) and processing is relatively simple, resulting in a fast and correct decision. Type II decisions occur if the visualization requires additional effort. Additional effort could be due to a variety of reasons, such as inconsistencies with the viewer's preexisting knowledge, a lack of knowledge about uncertainty, or difficulty integrating multiple sources of information. In these cases, processing is effortful and requires more time and working-memory resources to arrive at a correct decision.

Decisions can be difficult without uncertainties, but when uncertainties are involved in decisions, they can become many times more complicated. For decisions with uncertainties, each option can lead to different outcomes, with the results arriving with different probabilities (Joslyn and LeClerc, 2013). We argue this may result in more effortful type II processing, even if representations of uncertainty match pre-existing knowledge about graphs. Since the assessment and estimation of probabilities is extremely complex, decision-makers often resort to simpler procedures in order to assess and weigh different options against each other. Such simplifications are called heuristics, or strategies (Tversky and Kahneman, 1974). While heuristics are often useful in simplifying a very complex problem, they can also lead to serious, systematic errors (Padilla et al., 2018). For example, in the context of uncertainty visualization, this can take the form of an inside-outside heuristic, where decision-makers have no sense of risk for data located outside the borders of a hurricane forecast's “cone of uncertainty”—which indicates a 66% confidence interval of potential forecast tracks—even though those areas are still at risk of being affected by the hurricane (Cox et al., 2013; Ruginski et al., 2016; Padilla et al., 2017).

Empirical studies on uncertainty visualization comprehension often contain complex tasks in which not “only” values have to be retrieved or compared from a map, but which require a thorough analysis of the primary data as well as the uncertainties. In concrete terms, participants often have to decide which option is the most optimal from a selection of options, sometimes based on multiple sources of information (Kinkeldey et al., 2015b; Kübler et al., 2019). The effects of uncertainty visualizations on the decision can be analyzed in two ways. In the objective assessment of the effects, it is analyzed whether more correct decisions are made as a result of the uncertainty visualizations, whether the decision-makers arrive at a decision more quickly or whether the decisions differ in other ways (Kinkeldey et al., 2015a; Padilla et al., 2018). The objective assessment, especially regarding decision accuracy, can be challenging, depending on the study design, due to the “right decision, wrong result” problem. The problem says that under uncertainty a right decision (the most rational decision based on task-relevant information) can lead to a wrong result due to uncertainty (Cheong et al., 2016, 2020). In the subjective assessment of the effects, it is analyzed whether the uncertainty visualizations change the attitude of the decision-makers (e.g., their risk attitude) or their decision security. Subjective assessments are usually based on self-assessments of the participants (Kinkeldey et al., 2015a).

Overall, results are mixed concerning the effects of uncertainty visualizations: uncertainty visualizations can result in more accurate decisions (Andre and Cutler, 1998; Greis et al., 2018), but accuracy can also remain unchanged compared to decisions made without uncertainty (Leitner and Buttenfield, 2000; Riveiro et al., 2014). Results are likely mixed since visualization choice has a large effect on comprehension, as specific encodings of uncertainty visualizations have been shown to be more effective than others at facilitating accurate judgments and reducing misconceptions (Cheong et al., 2016; Ruginski et al., 2016; Hullman et al., 2018). Others have argued that individuals take specific decision strategies when presented with uncertainty, which may or may not change accuracy. For example, Hope and Hunter (2007b) found that participants chose significantly more regions with low uncertainty, often although these regions should not have been chosen due to the low soil suitability class or other rational considerations. The authors justify this behavior with the concept of loss aversion by Kahneman and Tversky (1979). The concept states that, for example, in a bet with the same chance of losing and winning, the participants suffer more from a possible loss than they are happy about the possible win, which is why they reject the bet. In terms of a decision made with map-based uncertainty, this means that the participants estimate the potential losses due to high uncertainty to be higher than the potential gains, and therefore do not select locations with high uncertainty (Hope and Hunter, 2007b).

Decision-Making With Time Pressure

Even if an optimal uncertainty visualization technique is chosen, gathering information for a decision and cognitively processing the information is a time-consuming process. Decision-makers therefore almost always have internal or external time constraints in real-world decisions made with uncertainty. While time limits place internal or external constraints on decision-making, time pressure, on the other hand, only exists if the time limitation triggers a feeling of stress (Ordóñez and Benson, 1997). Time pressure is therefore a subjective (often negative) reaction to a time limit associated with strong arousal (Svenson and Edland, 1987). In uncertainty visualization research, however, the aspect of time pressure has not received extensive research. With the exception of a few studies (e.g., Riveiro et al., 2014; Cheong et al., 2016), the participants in uncertainty decision-making studies typically have as much time as needed for their decisions, which does not always correspond to real-world decision-making scenarios.

The current study therefore focuses on the influence of time pressure, given that time pressure can affect decision-making processes and outcomes (Hwang, 1994) and is important for real-world scenarios under time pressure, such as emergency search and rescue operations (Wilkening and Fabrikant, 2011) and evacuation decisions (Cao et al., 2016; Cheong et al., 2016). Results are mixed as to the effects of time pressure on decision-making. Time pressure can facilitate decision-making by increasing engagement or arousal but hinders decision-making when time pressure is extreme and induces stress (Hwang, 1994; Ordóñez et al., 2015). Negative effects of time pressure on decision performance are often characterized by speed-accuracy trade-offs. Speed accuracy trade-offs occur when faster decisions result in less correct decisions (Ahituv et al., 1998; Wilkening and Fabrikant, 2011; Kyllonen and Zu, 2016; Cheong et al., 2020). These trade-offs may occur due to increasing task difficulty (Hwang, 1994; Crescenzi et al., 2016; Padilla et al., 2019) or speed-confidence trade-offs, where decision confidence decreases with increased time pressure (Maule and Edland, 1997; Wilkening, 2012). Further, time pressure results in users reporting a lesser amount of satisfaction overall with their task performance (Crescenzi et al., 2013, 2016).

Even if time pressure does not alter decision outcomes, it can alter decision strategies and information search. For example, individuals under time pressure tend to constrain their search and alter decision-making strategies. Time pressure can have a negative effect on decision performance because decision-makers use different decision strategies to reduce cognitive stress (Hwang, 1994). These strategies are heuristics, as are the strategies for decisions under uncertainty. Research suggests that individuals process information more quickly (e.g., more effective or scattered search per unit of time) and filter information (Maule and Edland, 1997; Maule et al., 2000). Generally, decision-makers under time pressure use fewer but more important attributes, give greater weight to negative or task-irrelevant aspects, take fewer risks, and consider fewer options than decision-makers with unlimited time (Ahituv et al., 1998; Forster and Lavie, 2008).

The Current Study and Hypotheses

While the effects of time-pressure on decision-making seem to be largely negative, very limited work has been done analyzing the effects of time pressure on geographic uncertainty data, especially when individuals must weigh multiple equally important sources of map information. To our knowledge, Wilkening and Fabrikant (2011) and Cheong et al. (2016) are the only studies that have studied the effects of time pressure on map-based decisions with uncertainty, even though individuals must make important, quick decisions with uncertainty every day. Yet it is critical to have a better understanding of how decision-making might change in these high pressure, information-dense situations, since decisions can have life-altering consequences in contexts such as search-and-rescue. Therefore, the current study will implement a search-and-rescue landing site selection task with uncertainty information, similar to Wilkening and Fabrikant (2011).

Wilkening and Fabrikant (2011) investigated the influence of time pressure on map-based decisions using various map representations of slope. In the study, the participants had to decide under low, medium or high time pressure, depending on the task, which of the six marked helicopter landing sites had a slope inclination of <14% and were therefore safe for a helicopter landing. Slopes were visualized using four different methods: (1) contour lines only, (2) contour lines plus light hill shading, (3) contour lines plus dark hill shading, and (4) contour lines plus colored slope classes. Wilkening and Fabrikant (2011) found that the participants performed significantly better with the slope color hue map (4) than with all other maps (see also Wilkening, 2012). Individuals also felt that this map was the safest way to make their decision. Participants performed best at medium time pressure, followed by coping under low time pressure. The worst performance was achieved by the participants under great time pressure. Further, when individuals had to make evacuation decisions under time pressure with uncertainty visualizations of forest fires, Cheong et al. (2016) found that individuals made the most accurate judgments under time pressure when uncertainty was encoded as color hue when compared to text, borders (simple solid and dashed lines), color value, and transparency. Due to the results of these studies, our study implements a diverging green-purple color hue to encode slope information. We chose to overlay uncertainty as a texture given texture's appropriateness to visualize uncertainty with a diverging color scale (Brewer, 2016; see section Preliminary Study Stimuli for more). The decision of texture type was driven by a preliminary study (section Preliminary Study), prior to our main study of interest (section Main Study).

Broadly the current study aims to determine whether and how map-based decisions under different conditions (without and under time pressure; with and without uncertainty) affect decision-making processes. To this end, we combine multiple measurements (accuracy, decision strategy, response time, decision confidence, self-assessed stress, eye-tracking) in order to determine where trade-offs occur in a search-and-rescue decision-making scenario and gain more targeted insights into how individuals process, perceive, and decide when viewing uncertainty visualizations. In order to achieve this goal, we propose the following research questions and associated hypotheses:

(1) How does uncertainty visualization affect complex map-based decisions made with and without time pressure?

H1a: Uncertainty visualizations will influence map-based decisions regardless of time pressure. This hypothesis is based on the previously mentioned research showing that uncertainty visualizations have an influence on map-based decisions without time pressure (e.g., Wilkening and Fabrikant, 2011; Hullman et al., 2018). In order to test this hypothesis, the results of complex map-based decisions are assessed both objectively (accuracy, response time) and subjectively (decision confidence). We expect uncertainty to be treated differently than certain data irrespective of time pressure due to its well-documented effects on decision-making. Specifically, we expect individuals to have less confidence in uncertainty information, take longer to answer due to more effortful decision-making and be less accurate than without uncertainty information.

A competing hypothesis, H1b, is that time pressure systematically changes the effect of uncertainty on decisions. This hypothesis based on the idea that uncertainty visualization comprehension is more effortful (type II decisions; Padilla et al., 2018). If this is the case, we would expect that time pressure will result in more errors with uncertainty, since time pressure would constrain the additional time necessary to arrive at an accurate decision. At the same time, we would expect that the control group takes more time to view uncertainty visualizations, relying less on fast heuristics, thus resulting in equal performance with and without uncertainty in the control group.

(2) How do uncertainty visualizations affect decision-making processes, such as visual search, with or without time pressure?

H2: Uncertainty visualizations influence the decision-making processes that precede decisions regardless of time pressure. Any effect of uncertainty on decision outcomes may be attributable to changes in the decision-making processes. The current hypothesis is based on the fact that decision research has shown that heuristics are used for decisions under uncertainties, which is why the decision-making process changes (Kahneman, 2011; Padilla et al., 2015; Ruginski et al., 2016). Eye tracking and decision strategies will be used to answer research question 2 and to test the related hypothesis. Specifically, we will determine whether gaze time for areas of interest (AOIs) in the display changes based on uncertainty and time pressure, and whether response strategy changes based on uncertainty or time pressure.

(3) How does decision-making with or without time pressure differ?

H3: Decisions made with time pressure will be faster, but less accurate, compared to decisions made without time pressure. This hypothesis is based on decision research, which has shown that time pressure can have negative effects on decisions when it induces stress in participants. In addition, it was shown that under time pressure very specific decision-making strategies are applied, which is why it is assumed that the decision-making processes differ. To test the hypothesis, we will utilize decision accuracy, response time, and eye tracker data. Specifically, we think that individuals with time pressure will answer more quickly, but less accurately, showing a classic speed-accuracy trade-off, compared to individuals making decisions without time pressure.

Preliminary Study

Prior to the main study, a preliminary online study was completed to determine: (1) the method of uncertainty visualization utilized for the main study and (2) the decision time limit for the experimental time pressure group. In our maps, uncertainties are communicated qualitatively, and past research suggests that extrinsic methods are better suited for depicting qualitative uncertainty information (Kunz et al., 2011). In addition, some researchers recommend using extrinsic methods when the primary information is of great variability (Kinkeldey et al., 2013, 2014). Our preliminary study sought to determine the most effective extrinsic depiction of uncertainty out of a few options.

Materials and Methods

The first part of the study consisted of a personality questionnaire, the second part consisted of eight map-based decision tasks, and the third part consisted of questions about the scenario and uncertainty visualizations.

Preliminary Study Stimuli

Eight map stimuli were shown to participants (further details on map production can be found in the main study methods, section 3.1.1). In two of these eight maps, no uncertainties are shown, and in each of three maps the uncertainties are visualized with one of two chosen methods. The first uncertainty visualization method is a black-and-white stitched texture developed by MacEachren et al. (1998) (see Figure 1, left). This method should be particularly suitable if the primary data are visualized with a diverging color scale (Brewer, 2016; Johannsen et al., 2018), which is the case here. The second visualization technique is a point texture that was used by Retchless and Brewer (2016), for example (see Figure 1, right). While Retchless and Brewer (2016) varied the arrangement and color of the dots, the dots in the current study's stimuli are always black and in the same arrangement.

FIGURE 1

Figure 1. The two extrinsic uncertainty visualization methods used in the preliminary study. Left: black and white stitched method according to MacEachren et al. (1998), right: dotted method according to Retchless and Brewer (2016) and Brewer (2016).

Measures

The primary measure of interest for the preliminary study was decision time in order to determine the time limit for the time pressure condition in the main study. We also asked participants about their preferences and thoughts on each of the two uncertainty visualization methods as a follow-up after the experiment.

Participants

Eleven individuals took part in the online preliminary study (6 female, 5 male). The average age of the pre-study participants is 34.8 years, ranging from 23 to 58 years.

Results

Participants answered dot stimuli the fastest [mean (M) = 33.9, standard deviation (SD) = 10.0], no uncertainty stimuli less fast (M = 36.1, SD = 10.6), and hatch stimuli the slowest (see Figure 2, M = 42.9, SD = 14.5).

FIGURE 2

Figure 2. Distributions of preliminary study decision times, grouped by visualization method.

Nested non-parametric Wilcoxon-Mann-Whitney tests for group differences using 10,000 sample Monte Carlo distribution approximations implemented with the coin package in R (Zeileis et al., 2008) showed that the mean values were not significantly different between dots and hatches (z = −1.94, p = 0.05), between dots and no uncertainty (z = −0.72, p = 0.48), or between hatches and no uncertainty (z = 1.5, p = 0.13). Still, the dots method was chosen for the primary study given the fastest mean response time, lowest variability in response time, and more positive feedback in the written follow-up amongst all visualizations.

Main Study

Materials and Methods

Stimuli

Map stimuli were based on randomly chosen and anonymized locations in Switzerland with mountainous terrain (see Supplementary Material for further detail on stimuli generation). Most of the operations are performed using ESRI's ArcMap 10.4.1 software, with the exception of uncertainty calculations, which are performed using Monte Carlo simulation in Java. The Java code used for calculating uncertainty is available for use with attribution on an Open Science Framework repository (available at https://osf.io/yz2s6/). The procedure and parameters for the code are described in further detail on the repository and in section Decision-Making With Time-Pressure of the Supplementary Material of this manuscript.

We systematically controlled four criteria that needed to be considered by decision-makers: (1) slope categories (°), including slope uncertainty, (2) distance (m) to an air navigation obstacle, (3) distance (m) to a ski lift, and (4) distance (m) to the person to be rescued. The person to be rescued was always marked near the center of the map, in a zone unsuitable for landing a helicopter.

We developed eight map stimuli, and a ninth for a practice trial (see Figure 3). To increase the map set, we additionally rotated and mirrored the eight original maps to generate 16 map stimuli in total. We randomized the labeling of the potential landing spots, to avoid potential response bias.

FIGURE 3

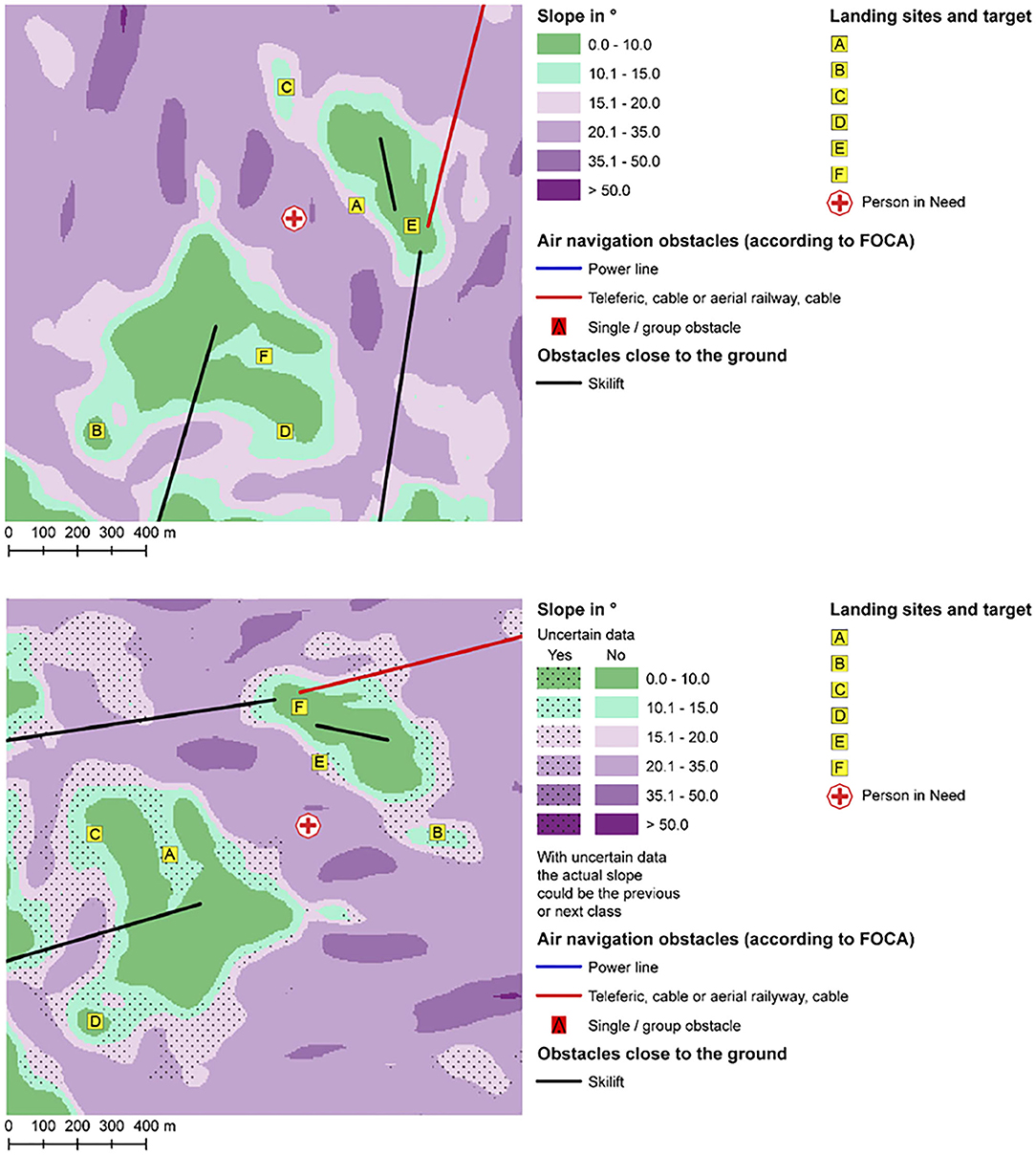
Figure 3. Example map stimuli (region: San Bernardino). Participants viewed the map key in German, but the keys have been translated to English for readers' convenience. An example map without uncertainty is illustrated in the top figure. An example map with uncertainty is illustrated in the bottom figure. Note how the map with uncertainty is a rotation and reflection of the same map without uncertainty above. Each map also features the same locations (with shuffled letterings). FOCA indicates the Federal Office for Civil Aviation in Switzerland.

To present stimuli, we utilized a 23-inch, 1,920×1,080 display and Onlineumfragen¹ for all participants.

Experimental Design

The experimental design was a mixed factorial (2 × 2) design, with a within-subject factor of uncertainty (with vs. without uncertainty) and a between-subject factor of time pressure (with vs. without time pressure). Repeated trials were presented for generalizability of study results to various decision contexts (see section Materials and Methods), resulting in 16 total trails (eight with uncertainty, eight without uncertainty).

The time limit for time pressure decisions was determined using the results from the preliminary study (described in section Preliminary Study). The method of Ordóñez and Benson (1997) is used to determine the time limit, and calculated as follows:

\begin{array}{l} T i m e l i m i t = M - 1^{*} S D \end{array}

Assuming that the decision times are normally distributed, this time limit would mean that about 84% of all participants would have to reach a decision faster than average (Ordóñez and Benson, 1997). It is therefore a rather short or strict time limit. Using the above equation (M decision time = 34.8 s, SD = 8.8), we calculated the time limit as 25.98. This was rounded to 25 to select a whole, even value, as two pilot participants reported confusion with a time limit of 26 s. Only 18.2% of preliminary study participants took on average <25 s to make decisions, so 81.8% of the pre-study participants with this time limit would have had to decide faster than their actual decisions, suggesting the time limit will result in pressure to decide more quickly than usual. The time limit was displayed as a countdown in the upper left corner of the map, which has been previously validated in map usability research (e.g., Wilkening and Fabrikant, 2011).

Decision Task

The scenario used for the decision tasks is a helicopter search and rescue scenario. The task was originally developed by Wilkening (2012) but adapted for the current study to consider multiple decision-criteria, whereas, Wilkening (2012) only required consideration of slope inclination information. The aim is for the participants to imagine themselves as helicopter pilots with Rega (Swiss Air Rescue). With the help of a map, participants decide between six marked landing places in order to rescue a person in an emergency whose position is also noted on the map. Some rules have to be observed, because off-field landings [definition: landings of aircraft outside of airports; AuLaV (Foreign Land Ordinance), 2014] are only possible under certain conditions. These conditions were presented to participants as decision criteria with a series of instructions. Note that the scenario descriptions of the experimental groups are not identical because the time pressure aspect was already introduced in the description of the time pressure group. All text passages that were not present in the description of the no time pressure group, but were added in the description of the time pressure group, are written in italics in the following scenario description. In both groups, however, particularly important aspects were written in bold in the description, presented below (presented to participants in German, translated to English here for convenience):

“Imagine you are a helicopter pilot at Rega and have to land in a mountainous area with no fixed mountain landing sites in order to rescue a person from an emergency situation as quickly as possible.

As a decision aid, you have a map of the area where you have to land. In this map, your inexperienced co-pilot has already drawn in six places which he proposes as landing sites. However, some of these places are completely unsuitable for a helicopter landing, on the others a landing is theoretically possible. It is your task to decide as quickly as possible where you want to land, because the sooner you are with the person in distress, the sooner he can be helped. Since safety comes first, you should always choose the position you think is best, not just any site that would be theoretically suitable. If several places are theoretically suitable, the site closest to the person in distress is the best possible site.

The map is a slope map with additional elements relevant for the landing. A slope map shows the slope of the terrain in degrees (°). The slope is classified into a total of six classes, so that the map shows six differently colored gradient classes.

The additional elements are, on the one hand, air navigation obstacles (teleferics, cables, cable railway, aerial railway, power lines). All air navigation obstacles are recorded, managed, and communicated to pilots by the Federal Office of Civil Aviation (FOCA). In mountainous areas they are at least 25 m high. Other additional elements are ski lifts that are <25 m high, but are also important for a helicopter landing.

(1) The slope should ideally be between 0 and 8°, between 8 and 15° a landing is a bit more difficult but still feasible, slopes above 15° are too steep for landings. Summarized: slope inclination > 10° ideal, 10–15° acceptable, >15° unsuitable.

(2) The distance to air navigation obstacles (single and group obstacles, cableways, cables, teleferics) must be at least 100 m.

(3) The distance to ski lifts must be at least 200 m, as there can be large crowds outside.

If several positions meet all three criteria, the position with the closest distance to the person in distress shall be selected.

Since you should decide as quickly as possible, the time available to you for your decision is limited by a timer. Decide on a landing site before time runs out.”

Because the participants do not necessarily have an intuitive understanding of uncertainties as in many other studies [e.g., those of Kübler (2016) or McKenzie et al. (2016)], but should make decisions with a knowledge of how uncertainties arise and what effects they can have, the participants read a description of the concept of uncertainties in digital elevation maps in the introduction to the decision tasks, similar to Scholz and Lu (2014) (presented to participants in German, translated to English here for convenience):

“The slope gradient values in the slope gradient map you will be using have been calculated from elevation data. Altitude values cannot be measured exactly for every point in Switzerland. Therefore, precise measurements are carried out at selected locations and the elevation values for the whole of Switzerland are calculated on this basis.

This procedure has the consequence that there are uncertainties in the area-wide height data. This means that the specified value may differ from the actual value. Consequently, there are also uncertainties in the slope inclination values calculated from this. In regions with particularly high uncertainties, the actual slope gradient may deviate to such an extent that it falls into a different slope class than that indicated on the slope gradient map.

In some of the maps you will see, these regions are now marked with particularly high uncertainty in the slope inclination values in addition to the other elements. The actual slope inclination value in regions with marked uncertainties may deviate by more than 5° from the indicated value, which may result in the value being in the previous or next class.

The decision task that you have to solve, as well as all criteria for it, remain exactly the same even on maps with marked uncertainty.”

This training ensures that everyone has similar prior knowledge about uncertainties, regardless of their background. In addition, the uncertainty is noted in the legend of the map (see Figure 1).

Measures of decision-making

Accuracy and response time were our two measures of decision-making. Accuracy was determined by a complex decision analysis based on the decision criteria provided to participants. Similar to Kübler (2016), the landing sites are categorized so that the decisions for the different categories can be compared. Overall, we classified landing-site decisions into “very wrong,” “wrong,” and “correct” based on a combination of slope inclination and obstacle proximity. A summary of slope suitability for landing is presented in Table 1.

TABLE 1

Table 1. Suitability of the different slope categories for landing.

The reason for differences in classification between no uncertainty and uncertainty is because the slope may have differed from the category depicted by one unit. Our classifications of suitability for landing thus reflect this ambiguity in information. Of nine possible combinations of slopes and obstacles, a total of eight combinations occur in the maps (a “bad/very bad” slope inclination in combination with “2 × too close” distance to the obstacles does not occur), which is why there are a total of eight categories. These categories are listed together with the characteristic values in Table 2.

TABLE 2

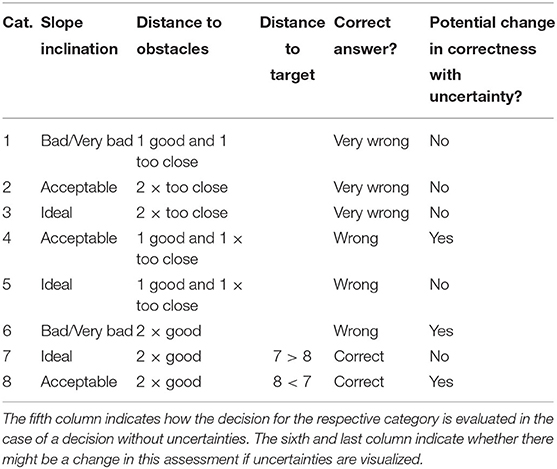
Table 2. Categorization of the landing sites into eight categories (short: cat.) for the analysis of decisions.

To summarize, landing site categories 1, 2, and 3 are regarded as “Very wrong”; categories 4, 5, and 6 as “wrong”; and categories 7 and 8 as correct.

Response time was calculated as the time to make a decision in seconds. If participants in the time pressure group did not make a decision within the maximum time limit (25 s), this trial was considered missing and not included in analyses (for both decision accuracy and response time).

Eye tracking

To obtain information about participant's decision-making process, the eye movements of the participants were recorded with the aid of an eye tracker. We utilized the Tobii TX3008 model, which has a recording rate of 300 Hz and an accuracy of 0.4° of visual angle. The Eye Tracker was used with Tobii Studio 3.4.7 software.

In order to examine the decision times of the two decision types in more detail using the eye tracker data, the map stimuli were divided into different AOIs. AOIs are regions in the stimulus in which the researcher is particularly interested. The seven AOIs include (1) the map, (2) the scale, (3) the legend for the slope inclination, (4) the legend for the obstacles, (5) the legend for the landing sites, (6) the six selection options, and (7) the answer button (Figure 4). The AOIs are exactly the same for maps with and without uncertainty, with the exception of a more detailed legend of slope inclination for maps with uncertainty, resulting in a slightly larger AOI for this legend compared with maps without uncertainty.

FIGURE 4

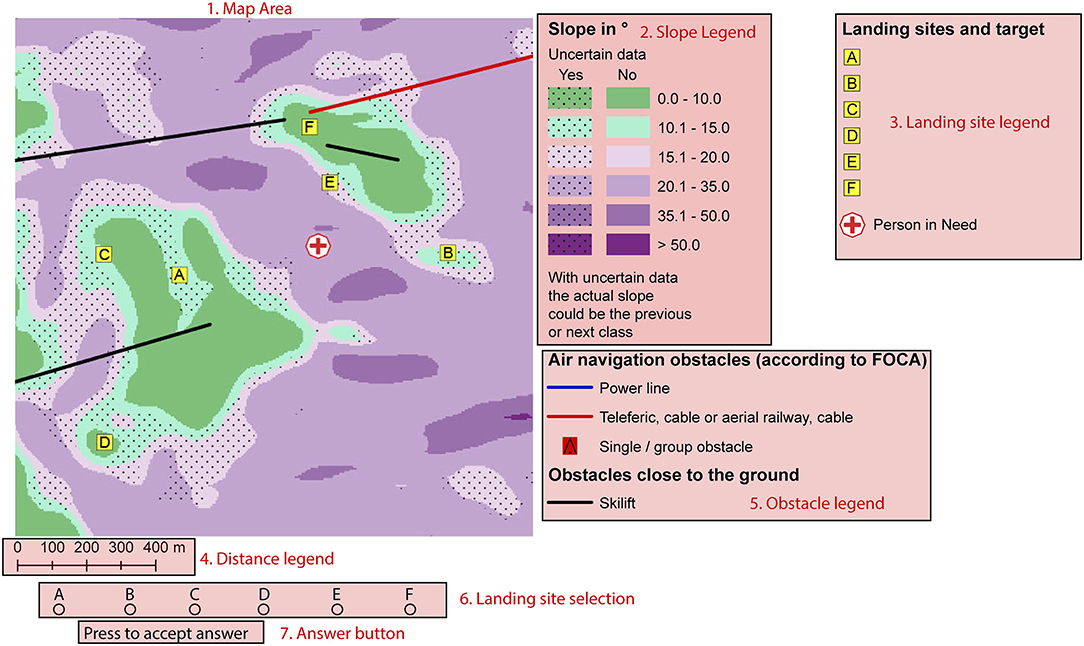
Figure 4. Subdivision of the view into seven different AOIs, numbered and labeled in red (example region: San Bernadino). The AOIs are shaded in pink, aside from the map. (1) the map, (2) the slope legend, (3) the landing site legend, (4) the distance legend, (5) the obstacle legend, (6) the six selection options, and (7) the answer button.

Visit Count and Total Visit Duration (in seconds) were calculated for each trial, participant, and AOI using Tobii Studio 3.4.7.

Assessment of spatial ability: paper-folding test

Spatial ability was assessed using the paper-folding test (Ekstrom et al., 1976) and was collected to ensure that experimental groups were homogenous with respect to spatial ability.

Assessment of stress: short-state stress questionnaire (SSSQ)

Because an imposed time limit does not mean that a person is necessarily stressed, a measure is needed to quantify the extent to which the time limit used in this study puts the participants group under stress. The SSSQ measures the current emotional state of the participants using 24 questions (Helton, 2004). The questionnaire measures three dimensions of subjective stress perception: (1) Task Engagement, (2) Distress, and (3) Worry. The task engagement factor describes feelings that are related to the commitment that is applied to a task. These include the sensations of motivation and concentration. The distress factor includes uncomfortable feelings such as tension or cognitive interference. Worry is a cognitive factor that is mainly derived from self-attention, self-esteem, and cognitive interference (Helton, 2004).

In order to detect a change in emotions using the SSSQ, we utilized the SSSQ before and after the main decision-making tasks in the study. Each question is answered using a five-part Likert scale, where 1 means “not true at all” and 5 means “fully true.” Due to a procedural error, all participants answered only 23 of the 24 questions. The missing question is question 12 (part of the task engagement factor) and was excluded from all analyses.

Procedure

The first part of the main study consisted of the Pre-SSSQ (Helton, 2004) and a paper-folding test that measured spatial thinking ability (Ekstrom et al., 1976). The first questionnaire was conducted using the survey tool Onlineumfragen, and the paper-folding test was solved on paper. After the SSSQ pre-test, participants received training, completed the decision task, and took an SSSQ post-test.

Participants

Thirty-four participants (17 with time pressure, 17 without time pressure) were recruited broadly without any specific background relevant to the decision-making scenario and volunteered to participate in the study. Of the 34 participants, 18 were female and 16 male. The gender distribution was the same in both experimental groups (9 female, 8 male). The average age of all participants together was 27.7 years (SD = 10.2; time pressure M = 27.5, time pressure SD = 10.3; No time pressure M = 27.9, SD = 10.5).

Participants were randomly assigned to the time-pressure and control groups. A non-parametric Exact Wilcoxon-Mann-Whitney Test from the coin package in R revealed that participants did not differ in spatial ability assessed with the paper-folding test (see section Decision Making Results) between the experimental groups (z = −0.36, p = 0.72).

Results

Data Analyses

Given the non-normal nature of the data, all basic group comparisons reported in the following sections were completed using non-parametric Exact Wilcoxon-Mann-Whitney Tests from the coin package in R version 3.6.

Analyses and hypothesis testing related to decision-making and response time were completed using multilevel models. Multilevel modeling is a generalized form of regression appropriate for nested study designs (multiple trials and uncertainty groups nested within participants, in this case; Gelman and Hill, 2006). Multilevel models were implemented using the lme4 package and marginal effects plotted using sjPlot and ggplot2 in R version 3.6 (Wickham, 2011; Bates et al., 2015; Lüdecke, 2020). We utilized the following multilevel model:

\begin{array}{l} Y_{i j} = β_{00} + {β_{01} * T i m e P r e s s u r e}_{j} + {β_{10} * U n c e r t a i n t y}_{i} + β_{11} \\ {* T i m e P r e s s u r e}_{j} * U n c e r t a i n t y_{i} + u_{0 j} + r_{i j} \end{array}

where i represents trials, and j represents individuals. This model was adapted as appropriate dependent on distributions of outcomes, but predictors remained the same throughout all models.

The mixed two-level regression model tested whether the effect of uncertainty (level 1, within person), varied as a function of time pressure (level 2, between person). Groups were contrast coded such that −0.5 corresponded to no uncertainty trials and 0.5 to uncertainty trials, while −0.5 corresponded to the control group and 0.5 to the time pressure group. With these codings, hypothesis tests reflect whether the difference between variables is different than 0 (e.g., Is the time pressure group mean minus the control group mean significantly different from 0?). Note that the accuracy effects (β) are reported using odds-ratios in the text for easier interpretation. Odds are defined as the ratio of correct responses to incorrect responses, and an odds-ratio is calculated as the ratio of the odds of two groups. An odds-ratio of 1 indicates the same odds of answering correctly between the groups, an odds-ratio below 1 indicates that the group coded 0.5 has lesser odds of answering correctly, and an odds-ratio above 1 indicates that the group coded 0.5 has greater odds of answering correctly.

Prior to running the accuracy model (section Decision Making Results), we noted that the percentage of very wrong (6.8%) and wrong (3.9%) decisions was very small in comparison to the percentage of correct answers (89.3%). Because of this, we treated very wrong and wrong decisions as the same (total wrong = 10.9%) in accuracy analyses, coding correct answers as 1 and wrong answers as 0. We thus analyzed the effects of decision accuracy using a multilevel logistic regression model, appropriate for binary data (correct vs. incorrect).

We analyzed decision response time (section Eye Tracking Results) using a multilevel model with a Gaussian distribution. Participants were included as random effects in all models. The full output of our models is available in Supplemental Materials, along with the associated data and code.

Overall, the participants of the time pressure group were not able to decide on a landing site before the timer expired for 28 decision tasks (10.29%). Each participant did this at least once, but not more than four times. In addition, we noted that participants took much longer to complete trial 1 than other trials (M response time = 37, SD = 21.8, compared to M response time = 23, avg SD = 13 for all other trials). During experimentation, we noted that this was due to participants becoming familiar with the task and interface, and thus considered this an additional practice trial rather than experimental trial. Uniquely, trial 1 was always the same for all participants, even though the remainder of trials were presented randomly. For these reasons, this first trial was removed from the data prior to analyses. Consequently, the following analyses are not based on 544 but on 488 decisions (255 of the no pressure group and 233 of the time pressure group).

Time Pressure Manipulation Check

We found that the experimental groups did not self-report changes in their worry (z = 1.8, p = 0.08), distress (z = −0.9, p = 0.40), or engagement (z = 0.7, p = 0.49) as a result of the time pressure manipulation (see Figure 5).

FIGURE 5

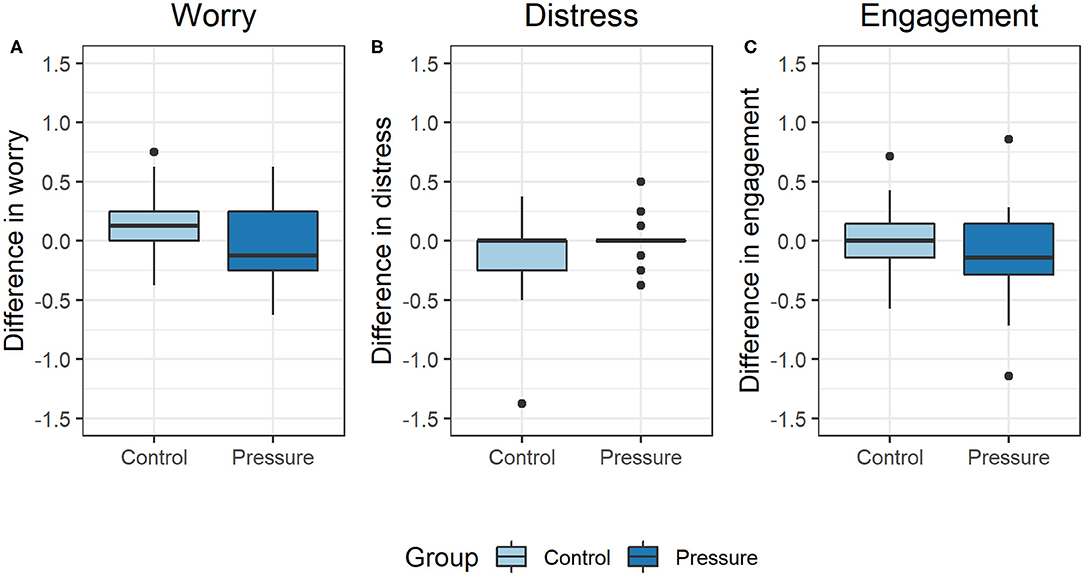
Figure 5. Pre-post experiment difference in self-reported worry [(A), left], distress [(B), center], and engagement [(C), right]. No significant differences were observed in any of these emotional factors due to time pressure.

Decision-Making Results

Decision accuracy and strategy

We found that neither uncertainty (Odds ratio = 0.8, p = 0.46, 95% CI = 0.43, 1.46) or time pressure (Odds ratio = 0.8, p = 0.63, 95% CI = 0.30, 2.07) affected participants' decision accuracy (see Figure 6A). Further, we found that the effect of uncertainty on accuracy did not interact with time pressure condition (Odds ratio = 0.7, p = 0.63, 95% CI = 0.20, 2.32).

FIGURE 6

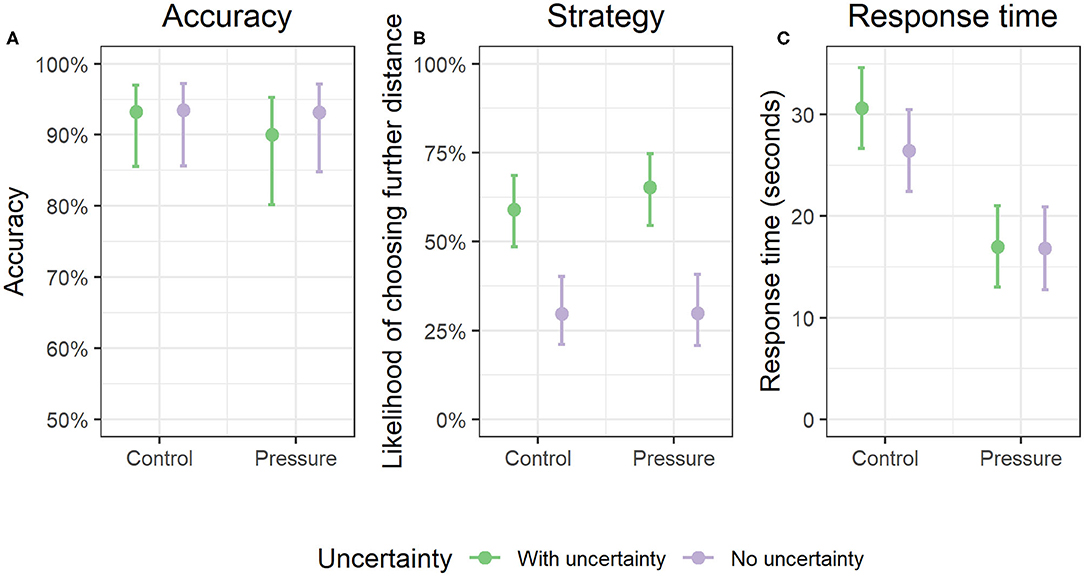
Figure 6. Decision-making results. (A) (left) depicts decision accuracy, (B) (center) depicts decision strategy for correct answers, and (C) (right) depicts decision response time. Error bars indicate bootstrapped 95% confidence intervals from multilevel model estimated marginal effects.

Though there were no accuracy differences based on uncertainty or time pressure, we noticed that the majority of participants answers were either Category 7 or 8 (89.3% of answers), as can be noted by the relatively high mean accuracies for all participants (M accuracy = 89.3%, SD = 30.8). However, not all correct answers are based on the same information. For Category 7 landing sites, the slope inclinations are “ideal” and for Category 8 landing sites, slope inclinations are only “acceptable.” At the same time, Category 7 landing sites are further away from the target than Category 8 landing sites (see Table 1). This is particularly important considering that uncertainty information affected slope but not distance information in the maps. Therefore, we completed a follow-up analysis that analyzed whether time pressure and uncertainty affected the likelihood of choosing a landing site that was further away, but had better slope conditions (choosing landing site 7 over landing site 8).

A follow-up multilevel model showed that uncertainty significantly increased the likelihood of choosing a landing site that was further away, but had better slope conditions (see Figure 6B; Odds ratio = 3.9, p < 0.001, 95% CI = 2.56, 5.86). This effect was consistent regardless of time pressure, as there was no significant interaction with time pressure (Odds ratio=1.3, p = 0.52, 95% CI=0.58, 2.95). Further, time pressure did not affect the likelihood of choosing a landing site that was further away (Odds ratio = 1.15, p = 0.59, 95% CI = 0.70, 1.88), suggesting a unique effect of uncertainty.

Decision response time

We found that both uncertainty (B = 2.19, SE = 0.84, p = 0.01, 95% CI = 0.54, 3.83) and time pressure (B = −11.61, SE = 2.78, p < 0.001, 95% CI = 0.54, 3.83) significantly affected participants' response times. Uncertainty trials resulted in 2.19 s more to respond on average compared to trials without uncertainty. The control group took 11.6 more s on average to respond across all trials compared to the time pressure group. However, this effect was driven by the control group taking longer to respond when presented with uncertainty, as we observed a significant interaction between uncertainty and time pressure such that the effect of uncertainty changed based on the time pressure group (B = −4.01, SE = 1.68, p = 0.02, 95% CI = −7.31, −0.73). Post-hoc simple slopes analyses (available in Supplementary Materials) revealed that this interaction was driven by individuals in the control group taking more time to answer for uncertainty trials than individuals in the time pressure group (see Figure 6C).

Decision confidence

We found that uncertainty (B = −0.23, SE = 0.08, p = 0.003, 95% CI = −0.38, −0.08) resulted in lesser self-reported decision confidence overall than decisions made without uncertainty. The effect was small overall, however, and was only approximately one-quarter of one confidence category on our scale (e.g., certain to neutral; see Figure 7). Time pressure did not affect decision confidence (B = −0.21, SE = 0.23, p = 0.36, 95% CI = −0.67, 0.25), and there was no interaction between uncertainty and time pressure on decision confidence (B = 0.16, SE = 0.15, p = 0.29, 95% CI = −0.14, 0.46). On average, participants reported being between neutral and certain about their decisions.

FIGURE 7

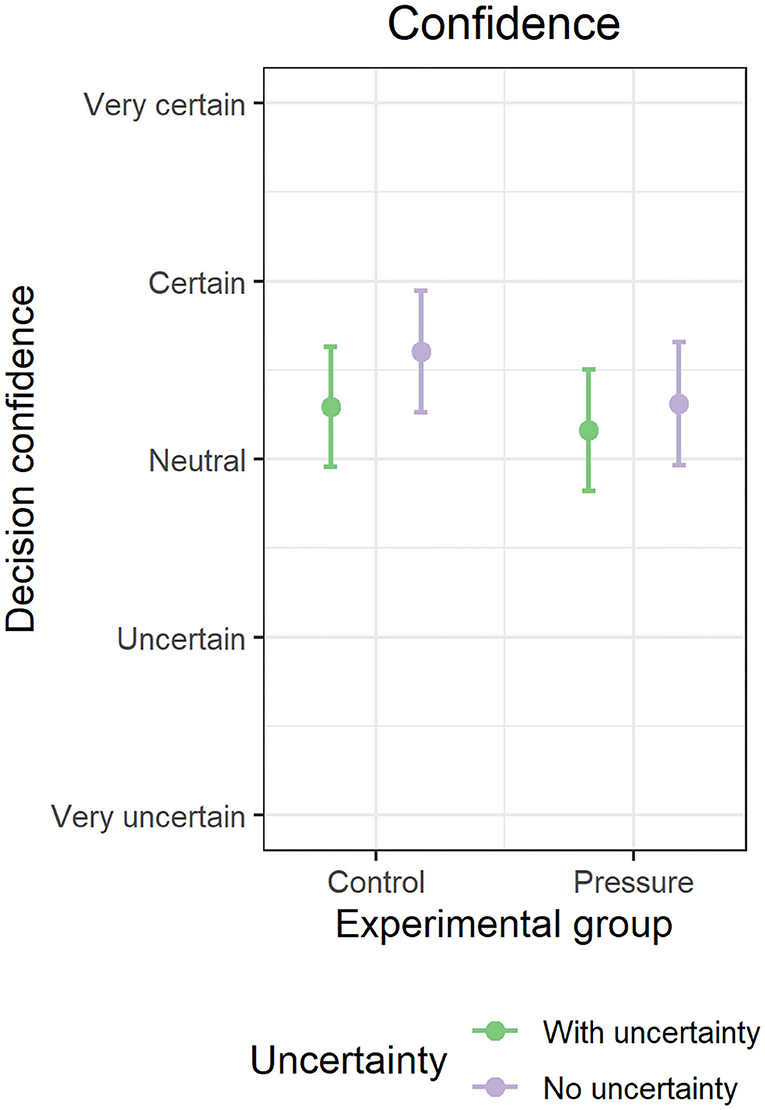
Figure 7. Effect of uncertainty on decision confidence. Error bars indicate bootstrapped 95% confidence intervals from multilevel model estimated marginal effects.

Eye-Tracking Results

Eye-tracking measures were intended to provide qualitative strategy insights to supplement behavioral measures. Using the rmcorr package in R to calculate a bootstrapped (nrep = 5,000) repeated measures correlation coefficient (Bakdash and Marusich, 2017), we found that visit duration and visit count were extremely highly correlated (r = 0.92, p < 0.001, 95% CI = 0.90, 0.93), and thus measured very similar attentional processes. Because of this, we solely focused on analyzing visit duration. We examined how long participants looked at different AOIs on the display during the task (areas shown in Figure 4). We conducted multilevel models for each AOI to determine if time spent looking at each area differed based on uncertainty, time pressure, and their interaction (full model results available in Supplementary Materials). Results are presented in Figure 8 and summarized in Table 3.

FIGURE 8

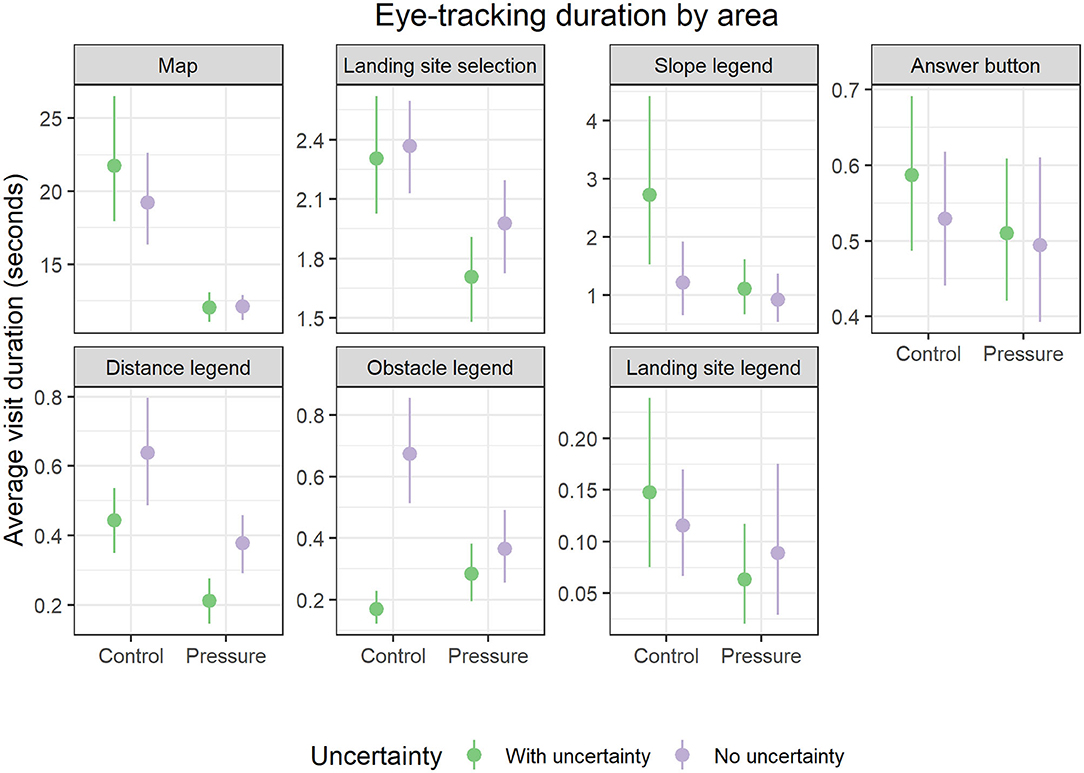
Figure 8. Effect of uncertainty and time pressure on eye gaze duration across display AOIs. Note that y-axis scales differ to show varying mean levels of attention given to each area of interest. Each panel is ordered by mean visit duration in seconds from top left to bottom right. Error bars indicate bootstrapped 95% confidence intervals from raw data.

TABLE 3

Table 3. Effects of uncertainty and time pressure on visit duration by area of interest.

Summary of Results and Descriptive Statistics

Overall, we found limited effects of time pressure on accuracy and decision strategy. Individuals with time pressure spent less time overall on the decision task, which is not surprising considering time constraints. Eye tracking revealed that specifically individuals under time pressure spent less time looking at the map, the landing site decision selection, the slope legend, and the distance legend than individuals in the control group. We found much stronger effects of uncertainty overall on decision strategy, but not accuracy, irrespective of time pressure. Interestingly, we found that individuals without time pressure spent much more time looking at maps that contained uncertainty, but with no benefit to their task accuracy or meaningful change in decision strategy. Descriptive statistics summarizing results can be found in Table 4.

TABLE 4

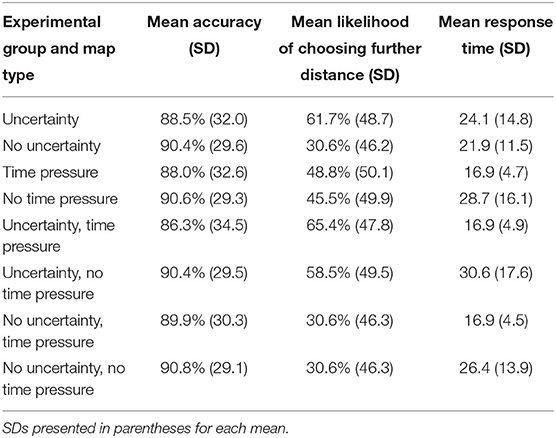
Table 4. Descriptive statistics for key measurements of decision-making (accuracy, strategy, and response time) by experimental group and map type.

Discussion

Do our results offer support of our hypotheses? We briefly revisit each in turn below.

We found extremely limited support for H1a: Uncertainty visualizations will influence map-based decisions regardless of time pressure. Since uncertainty affected decision strategy rather than accuracy, this suggests a potential shift in participants decision-making process more than in “objective” decision outcomes, such as accuracy. While decision confidence was lower with uncertainty than without uncertainty, the effect was fairly small, and participants reported neutral to confident responses on average across all trials. We found no support for H1b, that time pressure systematically changes the effect of uncertainty on decisions. While individuals without time pressure took longer to view uncertainty visualizations, this did not change decision strategy or accuracy.

We found partial support for H2: Uncertainty visualizations influence the decision processes that precede decisions regardless of time pressure. We found that uncertainty reliably and largely affected decision strategy, as participants made decisions that weighted distance information as more important than slope information faced with two equally correct landing sites. We interpret this result consistent with loss aversion (see section Decision Accuracy and Strategy: Loss Aversion as a Strategy With Uncertain Data for more).

Further, we found that individuals changed how they allocated their visual attention when presented with uncertainty, spending more time looking at the map and slope legend with uncertainty, but less time looking at the distance and obstacle legends. Often, however, the effect of uncertainty depended on the time pressure condition, contrary to our hypothesis. Specifically, when viewing uncertainty visualizations without time pressure, individuals allocated more attention to the map and the slope legend, but less time to the obstacle legend. This suggests that individuals utilized extra time to gather more information about the nature of uncertainty and its surrounding map context.

We found very limited support for H3: Decisions made with time pressure will be faster, but less accurate, compared to decisions made without time pressure. Time pressure did not alter decision accuracy or strategy. Though time pressure did alter response time, this is not surprising, as we imposed this task constraint on participants in our experimental design. It is telling, though, that individuals without time pressure did not seem to benefit from the additional time spent on each decision, at least measured in terms of decision accuracy. Therefore, time pressure resulted in individuals coming to equally accurate conclusions much faster than the control group. Time pressure did alter how participants chose to spend their more limited time looking at the display, as time pressure resulted in less time looking at the map, selecting a landing site, looking at the slope legend, and looking at the distance legend.

Decision Accuracy and Strategy: Loss Aversion as a Strategy With Uncertain Data

Without depiction of slope uncertainty, participants selected landing spots that were closer to the person to be rescued, but not necessarily at locations with ideal slope conditions. For decisions supported by visualized slope uncertainty, participants opted for the safer landing location, but further away as necessary from the person to be rescued. Safer in this case means that participants who were not under time constraints chose to land the helicopter at a location, which they knew with more certainty would be suitable for landing.

From a theoretical point of view, the choice of Category 8 landing sites was not a bad decision even with uncertainty. Since uncertainties meant that the slope gradients could be in the previous or next class, participants had to assume that the slope gradients would be or remain unchanged in the previous or next class with a probability of 33.3%. For the Category 8 landing sites, this means that the slope inclinations with uncertainties of 33.3% each are “bad,” “acceptable,” or “ideal.” The probability that the slope inclination of a Category 8 landing site is suitable for landing despite uncertainties is therefore 66.6%, which is greater than the probability that the landing site is unsuitable. Since site 8 is closer to the target person than the landing sites of Category 7, it would be a marginally equal choice to the landing site of Category 7, which had a probability of 100%, depending on how participants weighted information. Nevertheless, the participants more often chose the landing sites of Category 7 for decisions when uncertainty was present in the maps.

We argue that this decision strategy can be explained by the phenomenon of loss aversion. This decision strategy originated from a study by Kahneman and Tversky (1979), which shows that in a bet with the same chance of loss and profit, the participants suffer more from loss than rejoice over the profit, which is why they reject the bet. Since we observed this strategy when participants were confronted with uncertainty regardless of time pressure, it could be that uncertainty leads to loss aversion decisions more broadly and could be a defining feature of decisions made with uncertainty. Is there other evidence that uncertainty provokes these kinds of decisions?

Loss aversion was observed by Hope and Hunter (2007b), in which the participants had to decide on a new airport location based on a soil suitability map. In this study, participants tended to avoid choosing areas with greater uncertainty, since they viewed potentially low land suitability as a greater loss than the potential gain of high land suitability. Therefore, uncertain locations were viewed as risky and avoided more frequency. In addition to Hope and Hunter (2007b), Cheong et al. (2016) also noted that loss aversion probably played a role in forest fire evacuation decisions. Kübler (2016) shows, however, that loss aversion does not play a role in all decisions with uncertainty visualizations. In her study, the participants more frequently chose houses in insecure regions and thus, according to Kübler (2016), estimated the possible profit of a house in a zone with uncertainties higher than the possible loss, contrary to the concept of loss aversion.

Why might loss aversion play a role in some decisions with uncertainty visualizations, but not others? It is conceivable that the risk attitude of the participants may have an influence on whether they estimate possible gains from uncertainties to be less than possible losses. It is also possible that the decision scenario and the nature of the risks will determine whether decision-makers overestimate the potential losses due to uncertainties. Minimizing losses of life (evacuation) and maximizing profits (real estate) are two very different contexts with different stakes. More work should be done determining which specific data domain contexts this effect occurs (such as evacuation, real estate, population, epidemiology, etc.; see section Limitations and Future Directions for more).

Uncertainty Led to Longer Decision Times, but Not Accuracy. Why?

Since uncertainty visualizations affect decisions without time pressure, we expected uncertainty to affect decision accuracy irrespective of time pressure (Deitrick and Edsall, 2006; Riveiro et al., 2014; Kinkeldey et al., 2015a). Still, we considered the alternative hypothesis that decisions with uncertainty might change dependent on time pressure (Padilla et al., 2018). We found that the uncertainty visualizations led to the participants of the control group taking significantly longer to reach a decision, even though it did not benefit their accuracy. This result could be due to the high accuracy overall across all experimental conditions (89%) suggesting that the task may have not required the cognitive effort necessary to provoke type II decision-making, even if decisions were made more slowly (Padilla et al., 2018). Future work could further investigate this effect by introducing a dual-task—such as remembering a sequence of numbers or words—which more directly manipulates cognitive workload (Padilla et al., 2019). This result could also be due to the fact that time pressure did not seem to result in additional stress (see section Limitations and Future Directions for more).

This finding is not necessarily supported by past literature—in many cases uncertainty visualizations do not influence decision time (Leitner and Buttenfield, 2000; Riveiro et al., 2014; Kübler, 2016). In one case, uncertainty visualizations even led to shorter decision times (Andre and Cutler, 1998). In the current study, the participants had to solve multi-criteria decision tasks, similar to Riveiro et al. (2014) and Kübler (2016). The discrepancy between the results here and those from the literature thus likely have a different reason than the complexity of the decision-making tasks.

Hope and Hunter (2007a) noted that uncertainty visualization techniques can have an extremely significant influence on decisions. Kübler (2016) was also able to demonstrate that different uncertainty visualization techniques can lead to significantly different decision-making times. It is therefore conceivable that the discrepancy to the existing literature is due to the uncertainty visualization technique applied here, because none of the authors mentioned used only a texture as uncertainty visualization, as it was done in this study. Kübler (2016) used three different techniques, one of which was texture based. In this study, however, blurring led to longer decision times, but not texture. As explained in the research context, Cheong et al. (2016) compared the influence of six different uncertainty visualization techniques on decisions. One of these techniques was a point-based texture (Johannsen et al., 2018). They found that participants with the texture and two other techniques took slightly longer to reach a decision than with the other three visualization techniques. In the existing literature, there is therefore no clear evidence that mainly texture-based uncertainty visualizations lead to longer decision times, which is why the extended decision time in this study is not clearly attributable to the uncertainty visualization technique used. We still hope future work assesses similar decision tasks using alternative encodings of uncertainty (see section Limitations and Future Directions for more).

Our eye-tracking results provide some insight into how participants utilize extra time during decision-making with uncertainty. Specifically, participants tend to look at the map and decision-relevant map legend more often. It appears that slope classifications were looked at more often during decisions with uncertainty and especially when there was no time pressure. This took away from time to lookup legend information that was decision-relevant, but certain, such as the distance and obstacle information. Since eye tracking has hardly been applied in research on spatial uncertainty visualizations as in research on general information visualization (e.g., Goldberg and Helfman, 2010, 2011; Toker et al., 2017), it is difficult to place these results into a larger context. To our knowledge, Brus et al. (2012) are among the very few who also used the eye-tracking method to investigate how participants make decisions with uncertainty maps. They found that the legend of uncertainty visualizations in particular attracted the attention of the participants, which is why they came to the conclusion that it is particularly important to depict the uncertainties in a legend. This phenomenon was also observed in our study. But since the additional gaze time with these areas during uncertainty was not associated with greater decision accuracy (individuals with time pressure performed equally well), participants may have gained the information necessary to make an informed decision by a certain timepoint. Another interpretation is that individuals became more efficient with their visual search behavior under time pressure, or perhaps implemented strategies to make faster decisions by memorizing the map legends in advance of the task. Additional research is necessary to further disentangle how changes in attentional processes affect visualization decision outcomes.

Limitations and Future Directions

As shown in section Time Pressure Manipulation Check, the SSSQ did not reveal any significant changes in self-assessed worry, stress, or engagement during the decision task. This can imply two things. On the one hand, this result could mean that the time limit used did not result in stress; on the other hand, it could be that the participants felt very well-stressed and under time pressure, but the SSSQ was not the appropriate means to measure this stress. Since time pressure only exists when a time limit triggers a feeling of stress (Ordóñez and Benson, 1997), it is important that our study induced stress in participants. Several studies have shown that the SSSQ is a sensitive indicator of changes in personal sensation and responds sensitively to a wide range of stressors (such as the time limit in the current study) and changes in task complexity (Helton, 2004; Helton and Näswall, 2015). Given that time pressure resulted in equal accuracy and decision strategies and did not affect SSSQ scores, we believe it is likely that participants simply did not feel stressed as a result of the manipulation, or that the task was too easy given a possible ceiling effect of accuracy. We suggest future work that constrains time limits further and implements converging measures of emotional response, such as skin conductance and pupillometry (Bradley et al., 2008). Another approach to make the scenario more realistic or stressful could include providing explicit feedback to participants or “gamifying” the task, which affect engagement, arousal, and performance (Hamari et al., 2014; FeldmanHall et al., 2016; Wichary et al., 2016). This is especially important to address since stress can change risk and reward salience (Mather and Lighthall, 2012). Further work should explore adding explicit feedback to uncertainty visualization decisions under stress.

Further, while our study sought to make claims about uncertainty visualization generally, we only studied one type of uncertainty visualization (texture), which was overlaid on slope data binned according to color hue. There is an entire line of research devoted to color choice and the benefits and pitfalls of binning color hue, saturation, and contrast in visualizations (Iliinsky and Steele, 2011; Padilla et al., 2016; Bujack et al., 2017; Szafir, 2017). For example, some have argued for utilizing value-suppressing methods of depicting uncertainty, where uncertainty constraints both color hue and saturation, as opposed to a separately overlaid texture or bivariate color map (Correll et al., 2018). Therefore, we cannot necessarily generalize our results to other non-texture, non-color-based methods of data and uncertainty visualization, or methods of uncertainty that are depicted using gradients, rather than a binary yes/no classification. We hope that future research explores how the effects of uncertainty on decision-making differ in scenarios where uncertainty is depicted with color only, texture only, and other combinations of visual encoding channels (e.g., where hue encodes data value and saturation encodes uncertainty around that value).

We did not test our display with experts familiar with our display, such as helicopter pilots, who likely utilize existing knowledge to inform their decisions and may have completed the task differently from non-experts. In addition, to make the task manageable, we did not include all possible variables that may have affected pilot decisions, such as visibility. Future work should assess these displays with experts and include all relevant decision variables to determine if these results are generalizable to actual use contexts.

Similarly, our study was limited to a cartographic display in order to simulate a stressful decision-making scenario with geographic data. However, work shows that contextual variables, such as narrative framings and data domain, can affect visualization interpretation (Hullman and Diakopoulos, 2011; Correll and Gleicher, 2014; Hullman et al., 2018). These contexts have also been shown to affect behavior and decision-making under conditions of risk and uncertainty (Kübler et al., 2019). Further, the effectiveness of visualizations can differ based on the task, such as simple value extraction, value comparison, or comparison based on multiple data sources with uncertainty, as was the case in our study (Padilla et al., 2016; Kim and Heer, 2018; Dimara et al., 2020). We therefore implore researchers to further examine decision-making with geographic uncertainty data, including studies that directly compare the same underlying map data with different task framings.

Last, uncertainty can have many meanings and we only provided brief training with uncertainty to non-experts, which may have limited individuals understanding of uncertainty. Different types of uncertainty result in differing interpretations and misinterpretations (Hullman, 2016). For example, inferential uncertainty from statistical models depicted with confidence intervals can lead to overestimations of effects compared to outcome uncertainty depicted with prediction intervals (Hofman et al., 2020). One potential solution to minimizing uncertainty misinterpretations in 2D data is by presenting hypothetical outcome plots, which explicitly depict uncertainty in a frequency framework (Kale et al., 2019). Others have argued that raising user awareness of uncertainty can reduce trust in the data, especially if the source of uncertainty is unclear. Reduced trust may also explain the loss aversion strategy (Sacha et al., 2015). Future work should utilize different definitions, types, and framings of uncertainty to further assess the generalizability of our results, and determine whether shifts in awareness or trust change how users utilize uncertainty information.

Conclusions and Implications

Overall, our study found that texture-based uncertainty affects decision-making with geographic data, but not in the way we expected. Even when users took additional time to view uncertainty visualizations in the control condition, this did not benefit accuracy, suggesting a potential accuracy ceiling effect in our task. However, one unexpected result was that uncertainty systematically altered decision strategy and changed how participants weighed uncertainty vs. more certain Supplementary Data, which were also essential to inform decision-making. When presented with two equally correct potential answers with an uncertainty visualization, participants tended to choose an answer that was less risky, but clearly involved a trade-off where other decision-relevant data were deprioritized. In our case, a search-and-rescue task, individuals chose to land a helicopter at a further distance away at a steeper, more certain slope, rather than closer with an uncertain slope. This effect was quite large (30% shift in strategy with uncertainty vs. without), and thus of practical significance. Importantly, this shift in strategy held with uncertainty irrespective of time pressure, showing that the strategy was not based on a singular use context.

Further, our study adds additional evidence that uncertainty visualization evaluations should include multiple converging measurements of decision-making and decision-relevant attentional processes, similar to other researchers who have called for multiple measurements (Hullman et al., 2018; Padilla et al., 2020). If we had not assessed decision strategy, it may have appeared that uncertainty had no effect on decision-making. This suggests that accuracy and performance are not sufficient to gain complete insights into decision-making with visualizations, though we still believe they are necessary and important.

The primary take-home message of our study is that loss aversion plays a role in decisions made with uncertainty visualizations when there is additional information available that also has to be considered as part of a complex, multicriteria decision with many data sources. In these cases, participants may attempt to minimize losses by putting less weight on uncertain information and more weight on certain information. Therefore, visualization practitioners should take extra care when visualizing uncertainty where multiple data sources inform the decision-making process, especially when there is spatial variability in uncertainty. Future research should further assess when decision strategy shifts occur with uncertainty visualizations across a variety of visualization types and decision contexts.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://osf.io/yz2s6/.

Ethics Statement

The studies involving human participants were reviewed and approved by University of Zurich Faculty of Science. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

MK contributed to study concept, experimental design, data collection, stimuli development, data cleaning, and writing. IR contributed to data cleaning, data analyses, data repository maintenance, writing, and editing. SF contributed to study concept, provided funding, advising, and editing. All authors contributed to the article and approved the submitted version.

Funding

Thank you to the European Research Council (ERC), who funded this work under the GeoViSense Project, Grant number 740426.

Conflict of Interest

MK was employed by the company Skyguide, Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Thank you to the University of Zurich for supporting this research. Specifically, thank you to Prof. Dr. Ross Purves, who provided code for terrain-based uncertainty models.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2020.00032/full#supplementary-material

Footnote

1. ^https://www.onlineumfragen.com/

References

Ahituv, N., Igbaria, M., and Sella, A. V. (1998). The effects of time pressure and completeness of information on decision making. J. Manag. Inf. Syst. 15, 153–172. doi: 10.1080/07421222.1998.11518212