A priori physical information to aid generalization capabilities of neural networks for hydraulic modeling

The application of Neural Networks to river hydraulics and flood mapping is fledgling, despite the field suffering from data scarcity, a challenge for machine learning techniques. Consequently, many purely data-driven Neural Networks have shown limited capabilities when tasked with predicting new scenarios. In this work, we propose introducing physical information into the training phase in the form of a regularization term. Whereas this idea is formally borrowed from Physics-Informed Neural Networks, the proposed methodology does not necessarily resort to PDEs, making it suitable for scenarios with significant epistemic uncertainties, such as river hydraulics. The method enriches the information content of the dataset and appears highly versatile. It shows improved predictive capabilities for a highly controllable, synthetic hydraulic problem, even when extrapolating beyond the boundaries of the training dataset and in data-scarce scenarios. Therefore, our study lays the groundwork for future employment on real datasets from complex applications.

1 Introduction

The ongoing demand for reliable flood maps of ungauged basins is increasingly pressing (Cole et al., 2006; Blöschl, 2013; Hrachowitz et al., 2013), the latter ranging from small catchments to scarcely populated large regions in developing countries. In addition, mapping vast flood-prone areas by means of physically based models requires a considerable computational burden, even assuming drastic conceptual simplifications (Prestininzi et al., 2011). Classical modeling approaches (Kumar et al., 2023) may thus become unfeasible in such cases, and resorting to the exploitation of similarities with other basins has been envisaged. Indeed, data-driven modeling has been proposed (Dasgupta et al., 2024) as a fruitful way to overcome the above problems, with Neural Networks (NNs) specifically employed in the context of environmental hydraulics (Kratzert et al., 2019). A comprehensive review has been developed by Bentivoglio et al. (2022).

However, if classical hydraulic models already face challenges due to the lack of high quality and/or sparse measurements, which do not allow for proper calibration of numerical models, data-driven models are even more affected (Guo et al., 2021). Initial attempts in the field of flood simulations indicate that Machine Learning (ML) applications and NNs struggle with substantial difficulties in generalizing effectively (do Lago et al., 2023), meaning they struggle to provide reasonable predictions for scenarios that differ from the training data (Nguyen et al., 2023), such as different catchments (Guo et al., 2022). This problem stems primarily from the lack of sufficiently large and informative training datasets (Cache et al., 2024), resulting in overfitted models. An effect closely related to overfitting and, as such, attributable to the scarcity of calibration data, is the frequent violation of conservation laws (Berkhahn et al., 2019), leading to marked non-physical results. Compounding this challenge, river flood mapping necessitates models able to explore scenarios not comprised within the training boundaries, i.e., featuring predictive/generalization capabilities. Any ML endeavor aimed at constructing a predictive tool for river flood mapping needs to address such requirement. For instance, Löwe et al. (2021) demonstrated promising accuracy in predicting water depth on raster samples of the same city not used in the training data, but the model struggled to predict flooding outside depressions. Predicting water levels in unseen terrain remains a challenge (do Lago et al., 2023) and the inability to generalize often necessitates retraining the model for new areas or boundary conditions. Recent research has been increasingly focused on developing deep learning models for flood prediction that can generalize effectively to unseen case studies (Bentivoglio et al., 2023).

A recent paradigm shift is represented by Physics-Informed Machine Learning (PIML) (Karniadakis et al., 2021). PIML enhances existing models by introducing physically-based constraints, theoretically reducing learning time, increasing generalization capabilities (Jamali et al., 2021), and trying to satisfy conservation equations (Jagtap et al., 2020). An early and influential example of PIML is Physics-Informed Neural Networks (PINNs), introduced by Raissi et al. (2019), which serve as neural solvers for differential problems (Hao et al., 2022). These networks are specifically designed to find solutions to forward and inverse problems governed by partial differential equations (PDEs), modifying the loss function with a PDE residual term computed via Automatic Differentiation (Baydin et al., 2018) and optional additional terms for initial and boundary conditions (Lu et al., 2021). PINNs have been applied to benchmark problems in fluid mechanics, particularly for Navier-Stokes equations (Jin et al., 2021). They have demonstrated potential advantages over classical techniques by integrating empirical data and handling ill-posed problems (Cai et al., 2021; Cuomo et al., 2022). Additionally, PINNs enable tackling problems of extremely high dimensionality, where traditional solvers would face prohibitive computational costs. In river hydraulics, PINNs have been applied for spatial and temporal forecasting in one-dimensional channels (Mahesh et al., 2022; Xu et al., 2024), for downscaling Large-Scale River Models by assimilating available observations (Feng et al., 2023), and for approximating solutions to the Shallow Water Equations (SWEs) during flood events in a specific river reach, achieving prediction accuracies comparable to Finite-Volume solvers while significantly reducing computational costs (Qi et al., 2024).

However, epistemic uncertainties, such as the incomplete and/or imprecise comprehension of physical processes, plague the field of hydrology, so that the computation of PDE residuals can encounter challenges similar to those faced by classical numerical methods. In this work, we propose to incorporate a priori physical information, i.e., relying on user expertise, into data-driven models in the form of regularization terms. The novelty of our approach lies in deriving physical knowledge from both the inputs and outputs, without relying on the residual of a differential equation. This feature can be a significant advantage in applications where the conceptual model of the phenomenon is partially or entirely unknown (Qian et al., 2019), thus bypassing the limitations and difficulties associated with epistemic uncertainty. Indeed, it is well known that the classical employed models, i.e., numerical solutions of SWEs, are often used in an equifinality framework, meaning that an effective parameterization compensates for the absence of explicit modeling of specific phenomena (Beven, 2006). Neural solvers are prone to suffer the same limitations within the context of river hydraulics. Furthermore, it is widely reported in the literature that the inclusion of physical information into ML models is beneficial, especially in conditions of small data regimes (Zhu et al., 2019; Karniadakis et al., 2021; Eichelsdörfer et al., 2021).

The aim of this work is to demonstrate that a novel way of incorporating physical concepts into existing data-driven (DD) models, unrelated to PDEs, can be beneficial. Our strategy is targeted at scenarios where the underlying mathematical formulation is not fully known, but expert knowledge allows the introduction of physics into the loss function. The present method does not aim to either replace numerical solvers or serve as an alternative numerical model. We investigate how physically-trained NNs can generalize better compared to purely DD ones in a controlled experiment in environmental hydraulics. Analogous to what has been done in Cedillo et al. (2022), we employ a simple yet non-trivial physical problem—namely, the reconstruction of a steady-state, one-dimensional water surface profile in a rectangular channel—to isolate the effects of the physically-aided training. The highly informative content of the analyzed problem comes mainly from the hidden complexity of the underlying physics, associated to the possible occurrence of a hydraulic jump, which is not a solution of the differential equation used to determine the water profile (i.e., specific energy equation) (Cengel and Cimbala, 2013). The simulations encompass a wide range of input variations, testing the efficacy of physical training strategies even in data scarce scenarios. As seldom done in ML applications, we tested the new approaches even in extrapolation, paralleling challenges often encountered in flood mapping applications. Although not proposing here a new ML flood model, the method allows for promising improvements of existing ML flood models, underscoring its potential value for tackling future complex applications.

The paper is structured as follows: section 2 outlines the overall approach adopted in this work; section 3 describes how the methodology is employed in the physical problem; then results are discussed in section 4; in section 5 conclusions are then drawn and perspectives are advanced.

2 Methods

2.1 Data-driven and physics-informed neural networks

Neural Networks aim to approximate complex mappings between inputs $\mathbf{x}$ and outputs $\widehat{\mathbf{y}}$, described by an unknown non-linear function $G^{*}$

$G^{*}\left(\mathbf{x}\right)=\widehat{\mathbf{y}}.(1)$

By tuning the values of the parameter vector $\mathit{\theta }$, the NN learns to mimic $G^{*}$ through the approximate function $G$

$G\left(\mathbf{x};\mathit{\theta }\right)=\mathbf{y}(2)$

where $\mathbf{y}$ are the predicted values.

Neural Networks were inspired by the architecture of biological nerve cells. A single element of the network, called neuron, receives a series of $I$ inputs $a_i$, calculates a weighted sum of these inputs (which may include a bias value $c$), and then applies an activation function $\sigma$ to produce the neuron’s output $z$

$z=\sigma \left({\displaystyle \sum _{i=1}^I}{w}_i{a}_i+c\right).(3)$

Among the most commonly used activation functions are the Sigmoid, Hyperbolic Tangent, Rectified Linear Unit (ReLU), and Leaky ReLU (Apicella et al., 2021). The choice of the activation function affects the model outcome. Neurons are organized into layers, and stacking multiple layers forms a deep neural network.

NNs discover intricate patterns in large data sets LeCun et al. (2015) using the Backpropagation algorithm Rumelhart et al. (1986). The NN parameters $\mathit{\theta }$ are learned from data by leveraging information derived from the training set, namely, the couples $(\mathbf{x},\widehat{\mathbf{y}})$. In a purely DD training process, the network calibrates its parameters by minimizing a loss function $\mathcal{L}$ between $\mathbf{y}$ and $\widehat{\mathbf{y}}$

$argmi{n}_{\mathit{\theta }}\mathcal{L}\left(\mathbf{y},\widehat{\mathbf{y}}\right).(4)$

A common choice for the loss function in a DD model for a regression problem (the output variables are real unbounded numbers) is the Mean Squared Error (MSE)

$MSE=\frac{{\displaystyle \sum _{i=1}^N}{\left(y_i-\widehat{y_i}\right)}^2}{N}(5)$

but other metrics can be used depending on the nature of the data and the goals of the model.

Feed-Forward Neural Networks (FFNN) are among the simplest NN architectures, consisting of an input layer, a series of $H$ hidden layers, and an output layer. All networks employed in this work are FFNNs. The function $G$ represented by a FFNN can then be seen as the composition of several functions $f$, each corresponding to a hidden layer:

$G=f_H◦f_{H-1}◦\dots ◦f_1.(6)$

A FFNN with sufficient layers and neurons can theoretically approximate any continuous or even discontinuous function to arbitrary precision.

PINNs are a new paradigm of ML models that combine principles from physics-based modeling with the flexibility of NNs. They have been used as neural solvers for physical systems governed by a known set of Partial Differential Equations (PDEs), addressing both forward problems (solving the equation) and inverse problems (determining unknown parameters).

The key strategy pursued by PINNs lies in building the loss function as follows:

$\mathcal{L}=\lambda \cdot {\mathcal{L}}_{DD}\left(\mathbf{y},\widehat{\mathbf{y}}\right)+\left(1-\lambda \right)\cdot {\mathcal{L}}_{\mathit{PDE}}\left[G\left(\mathbf{x};\mathit{\theta }\right)\right](7)$

where ${\mathcal{L}}_{DD}$ is a metric which measures the distance between predicted $\mathbf{y}$ and observed data $\widehat{\mathbf{y}}$ [e.g., MSE (5)]. ${\mathcal{L}}_{\mathit{PDE}}$ is the PDE residual, calculated using residual points, also known as Collocation Points, in the spatio-temporal domain of the PDE. The PDE residual becomes an additional term in the loss function, weighted by an hyper-parameter $\lambda$, which balances the data and physical contributions, ranging between 0 and 1. The term $G(\mathbf{x};\mathit{\theta })$ is the function approximating $G^{*}$, as described in Equation 2. Further terms can be included to address initial and boundary conditions (Raissi et al., 2019).

2.2 Proposed methodology

Physical information integration is here accomplished by including an additional term in the guise of a regularization term in the loss function, only formally analogue to that used in PINNs as in Equation 7

$\mathcal{L}=\lambda \cdot {\mathcal{L}}_{DD}\left(\mathbf{y},\widehat{\mathbf{y}}\right)+\left(1-\lambda \right)\cdot {\mathcal{L}}_P\left(\mathbf{x},\mathbf{y},\widehat{\mathbf{y}}\right).(8)$

In ML, the regularization technique limits the growth of weights during the training phase, thus mitigating possible overfitting effects (Ng, 2004). Whereas the term ${\mathcal{L}}_{DD}$ still depends solely on the predicted outputs $\mathbf{y}$ and the true outputs $\widehat{\mathbf{y}}$, the physical term ${\mathcal{L}}_P$ is now a metric that can also involve physical inputs $\mathbf{x}$. Various physical principles can be thus encoded into this term, enabling the model to capture a broader spectrum of physical behaviors and relationships hidden in the data.

Moreover, in a broader context, the methodology shares similarities with data augmentation techniques (Shorten and Khoshgoftaar, 2019; Maharana et al., 2022; Dhanushree et al., 2023; Baydaroğlu and Demir, 2024). Data augmentation involves artificially expanding the training dataset by applying various transformations to the input data. The objective is to improve the model’s performance by exposing it to a more diverse set of examples, thereby enhancing generalization and robustness. Analogously, our approach allows for an enrichment of the informational content of the dataset by combining both input data $\mathbf{x}$ and the predicted outputs $\mathbf{y}$ to formulate new physically-based quantities. From this perspective, this approach can be considered as a kind of physically-based data augmentation and it allows for enriching the informational capacity of the data.

2.3 Synthetic case definition

We construct a specific synthetic case study to test and show the proposed methodology. The problem at hand deals with the reconstruction of the water surface profile along a 1D channel induced by the presence of a weir placed at the outlet cross section. Such problem mimics a commonly occurring scenario of determining the area affected by the presence of a dam in a river. Additionally, if a supercritical flow regime develops in the upstream part of the channel, a hydraulic jump occurs (Figure 1). A comprehensive description of the problem is reported in Cengel and Cimbala (2013) and briefly recalled in Appendix A for the reader’s convenience.

Figure 1

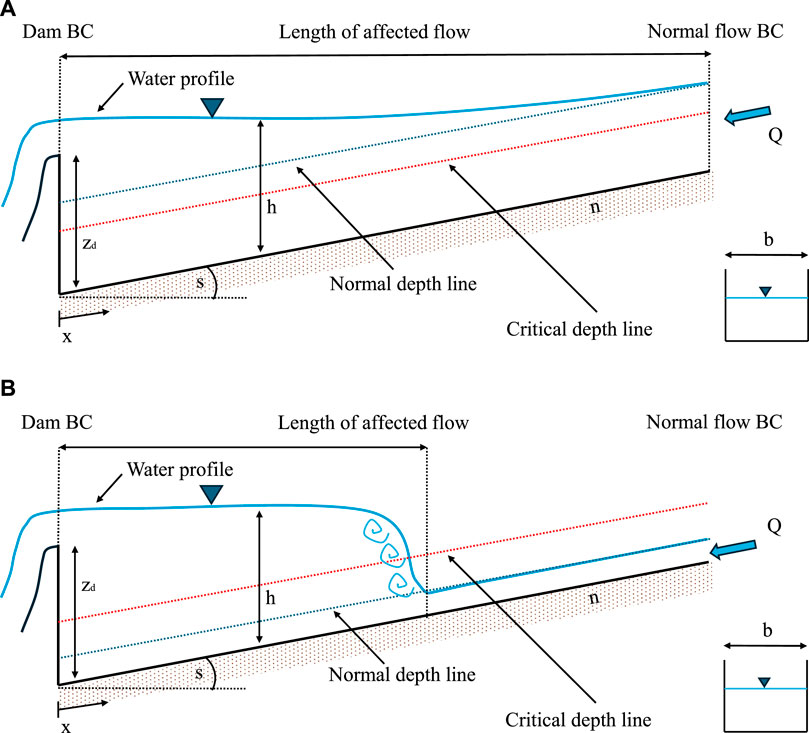
Figure 1. Sketch of the analyzed physical problem, i.e., the steady state water profile in a rectangular prismatic channel. (A) describes the subcritical case; (B) depicts the mixed regime case. For the meaning of the symbols, the reader is referred to the text.

The solution of the physical problem, assuming a prismatic rectangular channel and steady flow conditions, is a function $F^{*}$:

$\widehat{h}=F^{*}\left(x;s,b,n,z_d,Q\right)(9)$

with $\widehat{h}$ representing the true flow depth; $x$, the distance from the dam; $s$, the channel slope; $b$, the channel width; $n$, the Manning coefficient (related to the channel’s roughness); $z_d$, the height of the dam; and $Q$, the water discharge.

The differential Equation A1 generating the gradually-varied water profile is not valid at the location of the hydraulic jump. Indeed, the hydraulic jump represents an internal boundary whose location (and strength of the local discontinuity) needs to be solved for through additional information (see Appendix A).

3 Simulations setup

3.1 Generation of the dataset

A synthetic dataset of water profiles was generated by uniformly varying $s$, $b$, $n$, $z_d$, and $Q$, spanning broad ranges of input variations (e.g., 100% for inputs $n$ and $z_d$, 400% for $Q$, 500% for $b$, and 900% for $s$) using a Finite-Difference scheme (see Appendix A for details). The profiles are sampled with a fixed spatial discretization of $\mathrm{\Delta }x$ set to 10 m, covering a total length of 5,000 m resulting in profiles of $N=501$ points. This generation method results in a uniform sampling of the 6-dimensional domain of the $F^{*}$ function in Equation 9. (see Figure 2).

Figure 2

Figure 2. The plot shows water surface profiles from two subsets of the whole synthetic dataset. The simultaneous effects of dam height ($z_d$, red pillars) and channel slope $(s)$ are illustrated in the upper and lower panel respectively, whereas fixing the remaining parameters to the values reported in the boxes. In both panels, the water surface height $(H)$ is plotted against the distance from the dam $(x)$; grey lines represent the bottom of the channel. Subcritical (Froude number $Fr<1$) and supercritical $(Fr>1)$ flow regimes are depicted in cyan and blue markers, respectively. The discontinuous transitions between the two flow regimes represent hydraulic jumps.

The obtained profiles were randomly divided, with 70% allocated to the training set and the remaining 30% split between the validation and test sets. As is common in the ML framework, model generalization is analyzed by evaluating performance on the test set.

The input data to the various models are always normalized using the Standard Scaler, which is a commonly used data pre-processing technique to scale the features to have a mean of zero and a standard deviation of one. This is necessary to prevent troublesome problems during training due to differences in the numerical values of the features (Ali et al., 2014).

3.2 Employed neural network architectures

To show the versatility of the approach, three FFNN architectures were examined, referred to as the Single-Point (SP), the INTegrator (INT), and the Vector-To-Sequence (VTS). It is here important to state that the aim of this work is not to select the best architecture for solving the problem at hand, but to evaluate the effects of the proposed methodology. Hence, there might exist more effective deep learning approaches for solving the problem.

A sketch of the operating principles of SP, INT, and VTS architectures is illustrated in Figure 3 and the corresponding network topologies are depicted in Figure 4. Further details are in order.

Figure 3

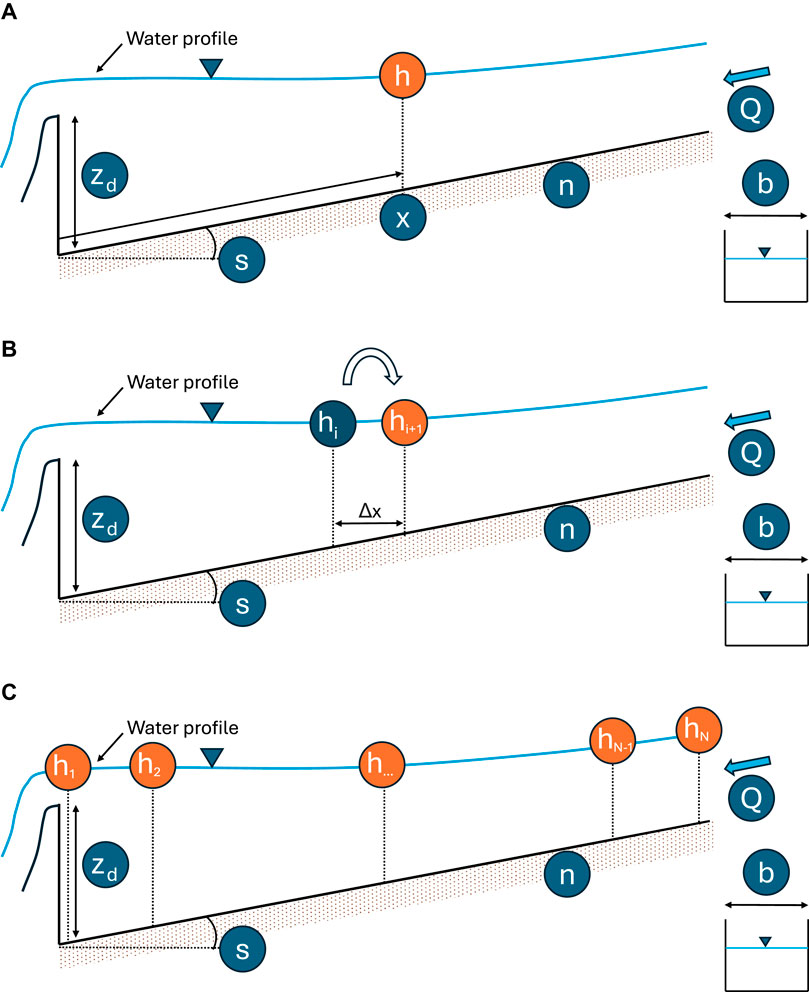
Figure 3. Profile reconstruction using the three different approaches; inputs and outputs are depicted as blue and orange circles, respectively; Single-Point (A) outputs the flow depth at a specific stationing; Integrator (B) requires the neighboring downstream value, regardless of the stationing; Vector-To-Sequence (C) outputs the entire vector of flow depth (i.e., the whole water profile) at once.

Figure 4

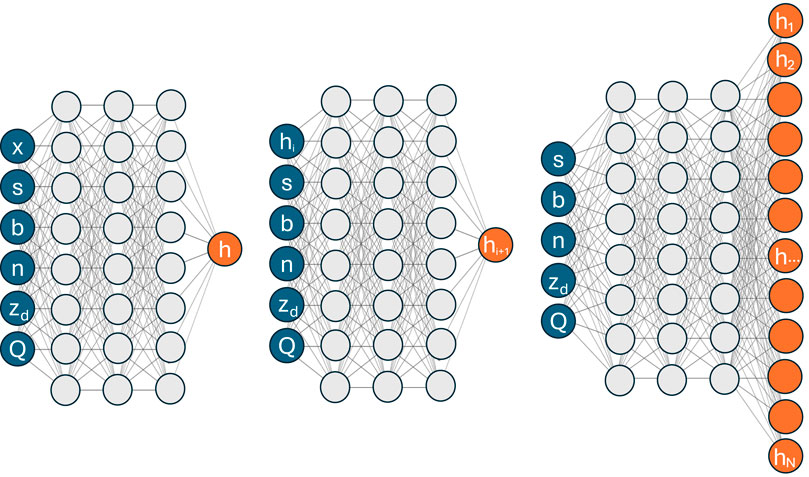
Figure 4. The employed FFNN architectures. Left to right: Single-Point, Integrator, Vector-To-Sequence.

3.2.1 Single-Point

A verbatim translation of the problem formulated in Equation 9 is to employ the NN to approximate the function $F^{*}$ with $SP$

$h=SP\left(x,s,b,n,z_d,Q;\mathit{\theta }\right).(10)$

In this approach, the FFNN takes the six quantities governing the phenomenon as inputs and predicts a single value for the water depth $h$ at the stationing $x$ as an output.

To reconstruct the whole profile $\mathbf{h}$, a SP model needs to be run with all the desired stationing values.

3.2.2 Integrator

In this method, a NN is utilized in the guise of a numerical integrator, that is aimed at determining the local water depth based on its value at the adjacent stationing. An eigenanalysis of the differential problem underpinning a steady-state 1D free surface flow like the one chosen in this study, would require to adopt either a downstream or upstream oriented solution direction based on the local flow regime, namely, super or subcritical, respectively. However, in the context of surrogate models like the one based on ML, due to the lack of any physical support, such requirement can be overlooked. In the following, an upstream moving algorithm has been chosen. This methodology requires a rearrangement of the dataset into the pairs $\left([{\widehat{h}}_i,s,b,n,z_d,Q],{\widehat{h}}_{i+1}\right)$, where ${\widehat{h}}_i$ and ${\widehat{h}}_{i+1}$ must be uniformly spaced by $\mathrm{\Delta }x$ and $i$ spans all stationing points of all profiles.

Due to the above structure, the INT approach misses any information regarding the distance from the dam. As a result, unlike the SP, it cannot predict the height at any distance from the dam but only at multiples of the fixed $\mathrm{\Delta }x$ set by the dataset

$h_{i+1}=INT\left(h_i,s,b,n,z_d,Q;\mathit{\theta }\right).(11)$

Starting from a known downstream boundary condition $(h_1)$, the integrator $INT$ can be applied recursively. At each stationing, the output from the downstream one serves as input, eventually leading to the reconstruction of the whole profile

$h_i=INT\left(h_{i-1},\dots \right)◦\dots ◦INT\left(h_1,s,b,n,z_d,Q;\mathit{\theta }\right).(12)$

It is essential to note that any classical numerical integrator would require a repeated check for the occurrence of a hydraulic jump, as well as an ad hoc procedure for its solution. Instead, this model can be applied flawlessly across such discontinuity.

Two further specific features of the Integrator approach are in order. Firstly, at each location, due to its recursive application, INT outputs a depth value whose error depends on the accuracy of the previous applications. As a consequence, the model’s accuracy is expected to decrease in the marching direction of the algorithm. A side advantage of such upstream marching algorithm lies in the possibility to incorporate physical conservation balances between the current and previous location. Secondly, the recursive application of INT introduces a subtle advantage over the other purely DD approaches: indeed its initialization (occurring at the most downstream stationing in our case) represents an implicit imposition of a physical constraint.

3.2.3 Vector-to-sequence

The Vector-To-Sequence employs a FFNN that receives as input the five parameters determining the profile solution and predicts as output the entire vector $\mathbf{h}$

$\mathbf{h}=VTS\left(s,b,n,z_d,Q;\mathit{\theta }\right).(13)$

The dataset must be rearranged in pairs $\left([s,b,n,z_d,Q],\widehat{\mathbf{h}}\right)$. Just like for the INT approach, the input does not include stationing data, thus implying that the spacing of the output matches the one of the training dataset.

An advantage of this architecture is that it allows for the implementation of physical loss terms whose formulation requires the knowledge of the whole profile, e.g., the volume of water of the profile. Recurrent Neural Networks (Hochreiter and Schmidhuber, 1997; Chung et al., 2014) are a natural evolution of this architecture, but they are outside the scope of this work.

3.3 Physical training strategies

Each of the three NN architectures has undergone both purely DD and physical training strategies, the latter consisting in exploiting the local values of the:

$•$ Specific energy, as in Equation A2, EN strategy in the following;

$•$ Froude number, as in Equation A5, FR strategy in the following.

Utilizing both the specific energy and the Froude number as conveyors of physical information exemplifies expert, a priori knowledge inputs in the training procedure.

The loss function for the purely DD training strategy is formulated in terms of MSE between real and predicted water depth. For the physics-informed training strategies, this function is augmented with an additional loss term, as shown in Equation 8.

The physical loss terms adopted for SP and INT read

${\mathcal{L}}_P^{EN}=\frac{1}{K}{\displaystyle \sum _{k=1}^K}{\left(E\left(h_k,Q_k,b_k\right)-E\left({\widehat{h}}_k,Q_k,b_k\right)\right)}^2(14)$

${\mathcal{L}}_P^{FR}=\frac{1}{K}{\displaystyle \sum _{k=1}^K}{\left(Fr\left(h_k,Q_k,b_k\right)-Fr\left({\widehat{h}}_k,Q_k,b_k\right)\right)}^2(15)$

where $K$ is the batch size, that is the number of training samples utilized at each training iteration (Abadi et al., 2015). The specific energy value, $E$, and the Froude number value, $Fr$, depend on both the output $h$ and the inputs $Q$ and $b$, as in Equations A2, A5.

The loss function for the VTS, the latter outputting the $N$-length profile, needs to be averaged over space as well, that is

${\mathcal{L}}_P^{EN}=\frac{1}{K}{\displaystyle \sum _{k=1}^K}{\left[\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(E\left(h_i,Q_i,b_i\right)-E({\widehat{h}}_i,Q_i,b_i)\right)}^2\right]}_k(16)$

${\mathcal{L}}_P^{FR}=\frac{1}{K}{\displaystyle \sum _{k=1}^K}{\left[\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(Fr\left(h_i,Q_i,b_i\right)-Fr\left(\right.({\widehat{h}}_i,Q_i,b_i)\right)}^2\right]}_k.(17)$

Since the VTS approach outputs the entire profile at once, it is also possible to test two additional training strategies using:

$•$ The volume of water flowing in the river (namely, the area under the water profile), VOL strategy in the following;

$•$ The downstream boundary condition, BC strategy in the following;

The corresponding loss terms read

${\mathcal{L}}_P^{\mathit{V\; OL}}=\frac{1}{KN}{\displaystyle \sum _{k=1}^K}{\left({\displaystyle \sum _{i=1}^N}{h}_i-{\displaystyle \sum _{i=1}^N}{\widehat{h}}_i\right)}_k(18)$

${\mathcal{L}}_P^{BC}=\frac{1}{K}{\displaystyle \sum _{k=1}^K}{\left(h_1-{\widehat{h}}_1\right)}_k^2.(19)$

Whereas the rationale behind the $VOL$ condition stems an integral equivalence between predicted and true profiles, the $BC$ condition leverages on the physical dependence of the backwater subcritical profile on the weir height.

As introduced in Section 2.2, it is now clear from their formulations why the ${\mathcal{L}}_P$ terms act as regularization terms, and the physical training strategies can be also interpreted as a form of physical data augmentation.

Hereinafter, the term “model” refers to the combination of an architecture and a training strategy.

3.4 Hyperparameters

Hyperparameters are values to be set before the training process and not updated during the training phase. They encompass crucial features such as the number of hidden layers and neurons, the optimization algorithm along with its learning rate, and parameters related to early stopping (Chollet et al., 2015). Despite the study not aiming to compare the three employed architectures, the implemented network topologies reflect the output complexities (e.g., local depth versus whole profile): indeed, for both SP and INT we assumed 3 layers with 30 neurons each, whereas for the VTS, we opted for 3 layers with 40 neurons each.

The ReLU activation function (Nair and Hinton, 2010) is here employed, which is defined as

$\text{ReLU}\left(t\right)=max\left(0,t\right).(20)$

ReLU has been chosen for its simplicity and widespread utilization in deep learning applications; however, its selection is not expected to impact the broader objectives of this study, and other activation functions could also be used. The number of layers is fixed for all NNs, and the analysis of its influence is beyond the scope of this work.

The weights optimization phase (training) of NNs exploits a gradient descent optimizer, such as the Adam algorithm (Kingma and Ba, 2014), to iteratively find the minimum of the loss function. The learning rate is another hyperparameter, which determines the step size taken during each iteration of the optimization process and plays a crucial role to ensure convergence.

We employ a learning rate reduction technique, specifically ReduceLROnPlateau, within the Adam (Kingma and Ba, 2014) optimization algorithm. The initial learning rate is set to 0.001 and is progressively reduced when approaching a minimum of the loss function. We also employ an early stopping criterion during the training phase, based on the MSE calculated on the validation set.

The focus of this work is not to evaluate the best model to solve the problem at hand, but rather to assess the effects of the a priori physical information.

The hyperparameter $\lambda$ in Equation 7, which weighs the contribution of the physical information, has been chosen individually for each model as the one yielding the best performance in a discrete set of values comprised in the interval [0,1], so to not introduce any biases in the results.

All the above hyperparameters were fixed within each model to achieve consistent results.

We implemented all neural networks using TensorFlow (Abadi et al., 2015) and Keras (Chollet et al., 2015).

4 Discussion of results

In this section we show the results obtained from the application of the three different FFNN architectures, both in the purely DD and in the physics-informed training strategies.

Solely to familiarize the reader with the physical problem being discussed, Figure 5 depicts a typical water level profile encompassing a hydraulic jump, as predicted by the SP, the latter having been trained with and without the inclusion of physical information. The reference solution, namely, the profile resulting from the Finite Difference integration, is depicted as well.

Figure 5

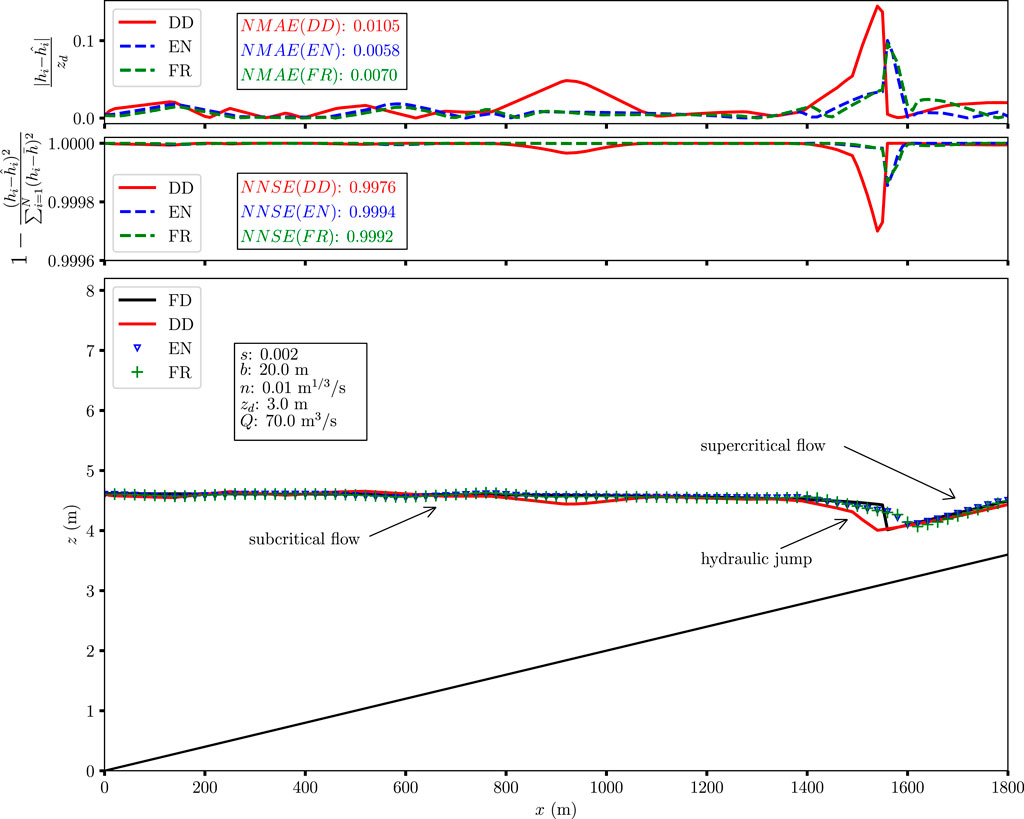
Figure 5. Typical outcome of the comparison between the employed models (DD, EN, and FR), and the reference solution (FD). The lower panel depicts the water surface profile, as predicted by the models, and the reference solution, highlighting the hydraulic jump separating subcritical and supercritical flow regimes. The two upper panels illustrate the spatial distribution of the Normalized Absolute Error and the Nash–Sutcliffe Efficiency along the channel. The values of the corresponding aggregated metrics for the entire profile (NMAE and NNSE, as in Equations 21, 22) and for each model are reported in the insets. Only the case of the SP architecture is shown for the sake of clarity.

In paragraph 4.1, NNs are trained on the complete dataset whereas in paragraph 4.2 several stress tests are carried out by: applying models for extrapolation, i.e., seeking predictions beyond the range of values covered during training, a scenario common to technical applications; exploring both overfitting and underfitting conditions by varying either the training dataset size or the NN complexity.

In all the above tests, the effects of the physics-informed training strategy are evaluated.

We employed two key metrics to evaluate the performance in reconstructing water profiles, namely, the Normalized Mean Absolute Error (NMAE) and the Normalized Nash-Sutcliffe Efficiency (NNSE). The NMAE, assuming the dam’s height as a representative length scale for the flow depth, is defined as

$NMAE=\frac{{\displaystyle \sum _{i=1}^N}|h_i-\widehat{h_i}|}{N{z}_d}.(21)$

The NNSE is formulated as

$NNSE=\frac{1}{\left(2-NSE\right)}(22)$

where

$NSE=1-\frac{{\displaystyle \sum _{i=1}^N}{\left(h_i-{\widehat{h}}_i\right)}^2}{{\displaystyle \sum _{i=1}^N}{\left(h_i-\bar{h}\right)}^2}(23)$

and $\bar{h}$ is the average depth of the profile. The rationale behind the scaling in Equation 22 is to bound the NSE value between 0 and 1, thus avoiding asymptotic tendency towards negative infinite values. A better-performing model is characterized by a lower NMAE and a higher NNSE.

NNSE weighs large and small errors differently, as clearly depicted in the middle panel of Figure 5, and thus provides a more significant measure of the model performance. In our case, the NNSE is employed in addition to the NMAE due to its ability to amplify errors made close to the location of the hydraulic jump. Indeed, NNSE penalizes errors in areas where the flow depth is close to the mean value, and the hydraulic jump is bounded by the two conjugate depths (see Appendix A) which are the closest to the mean value within each profile.

4.1 Complete training dataset

The cumulative frequency distributions of NMAE and NNSE are here employed to provide a comprehensive picture of the model performance over the whole test set. In Figure 6 and in Figure 7, we employ a boxplot representation to depict the cumulative frequency distribution of NMAE and NNSE for each model over the test set.

Figure 6

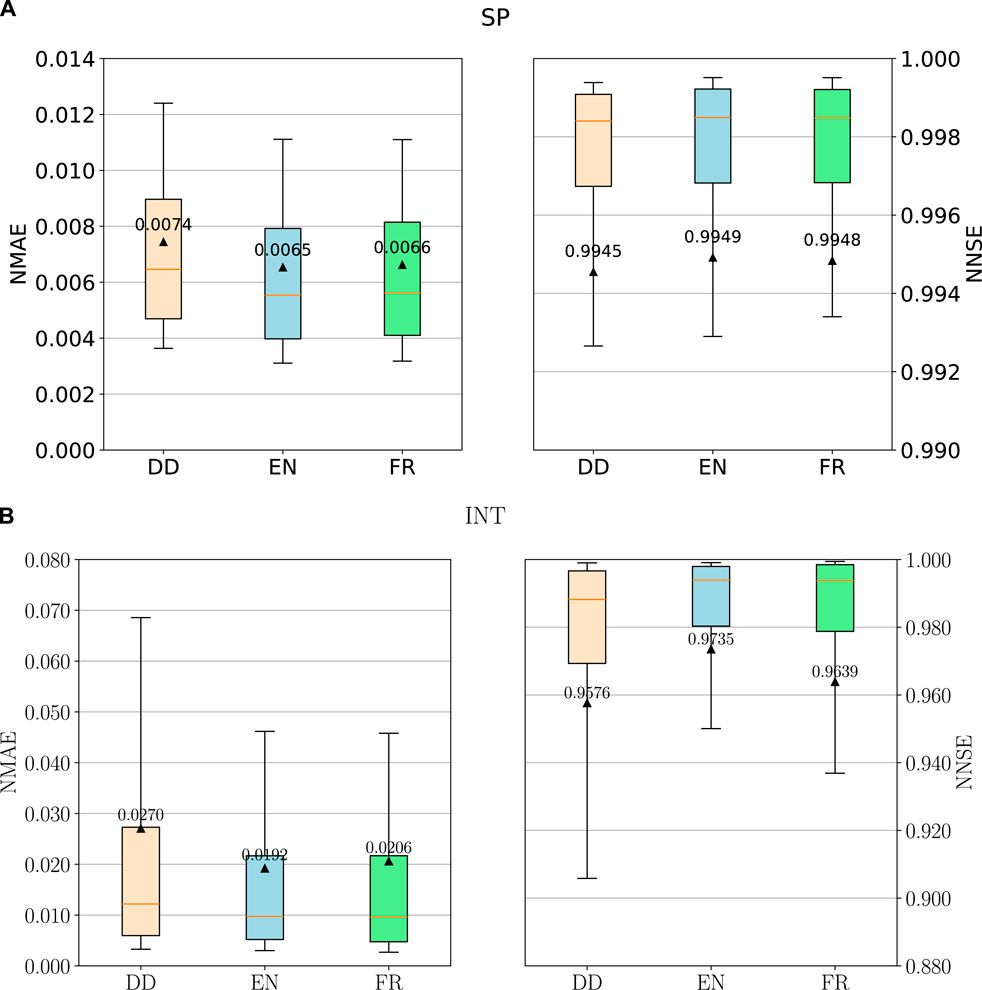
Figure 6. Complete training dataset: box plot of the NMAE and NNSE distributions for SP (A) and INT (B) architectures; boxes extend from the 25th to 75th percentile; whiskers are placed at 10th and 90th percentiles; mean values and median values are respectively shown as triangles (with the respective numerical value) and orange segments. An overall improvement of predictive capabilities is detectable for both architecture employing physical training strategies.

Figure 7

Figure 7. Complete training dataset: box plot of the NMAE and NNSE distributions for the VTS architecture. Box plot features are the same as in Figure 6. VTS also yields better predictions when trained with all types of the proposed physical constraints, but the volume (VOL) one.

The introduction of the physical information for all architectures improves their predictive performance. Looking at the results, the performance obtained by embedding the Froude number training strategy looks very similar to the one given by the energy training strategy. The similarity of results stems from the fact that both the Froude number and the energy depend on the same variables, namely, local depth and velocity. In the context of VTS, all but the VOL training strategies induce a similar improvement in the model’s performance (Figure 7). Constraining the volume of the water profile seems to consistently provide a misleading information content which detrimentally impacts the model’s performance. The reason is that the same volume is shared by a large number of possible output profiles. This example unveils that, despite apparently providing additional and physically sound information (i.e., the volume of water in the channel), the training phase may be diverted towards non-physical solutions.

4.2 Stress tests: extrapolation, training dataset size, and model complexity

As seldom carried out in ML frameworks, we also explore the extrapolation abilities of the models, which we deem crucial to ensure applicability to flood mapping. New water profiles were generated by considering at least one of the values of the five inputs $s,b,n,z_d,Q$ extending by 10% above or below the range covered by the training set. A set of profiles of the same size as the interpolation test set was randomly selected, resulting in a modified test set (referred to as EX).

The curves of average values of the cumulative frequency distributions, for both interpolation and extrapolation (EX) sets in small data regimes (decreasing the size of the training set by up to two orders of magnitude), are illustrated in Figure 8. Whereas, as expected, the performances progressively worsen by reducing the training set, the physical training strategy can almost always achieve better predictions (e.g., the improvement in NMAE is typically between 10% and 15%), thereby effectively enhancing generalization capabilities. In some isolated cases for the INT architecture, performance was not improved with the physical training strategy, most likely due to a particularly unfavorable initialization of the weights. The consistent drop in overall performance for extrapolation cases, compared to interpolation cases, is expected. This performance deterioration is more pronounced with the full dataset and less significant under small data regime conditions. However, models trained with physical information still show improved performance in extrapolation scenarios, with the NMAE improvement ranging in most cases from 5% to 20%.

Figure 8

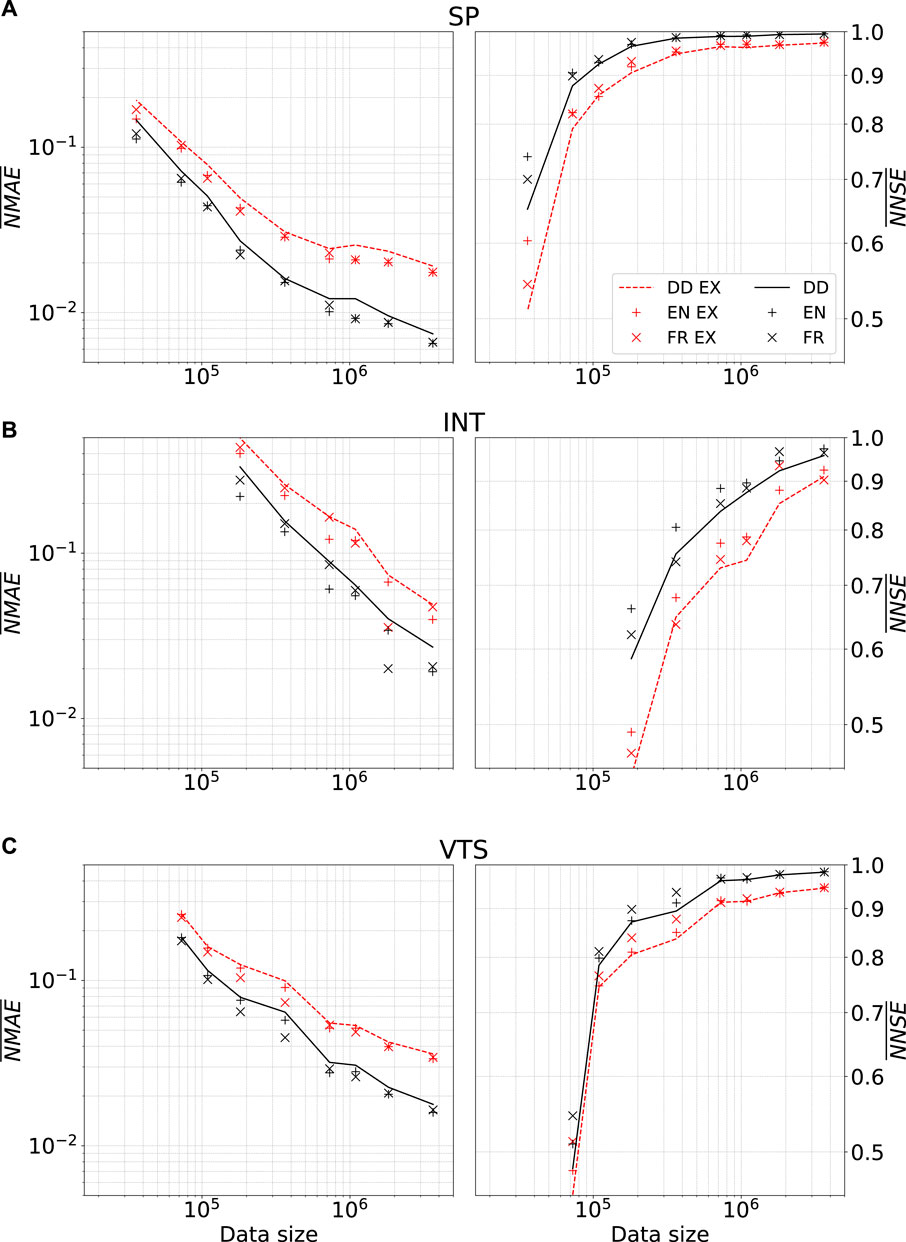
Figure 8. Stress tests: mean values of NMAE and NNSE on the test set against the size of the training dataset for each architecture. Black traces and markers represent models’ results on the test dataset fully contained in the range of the training one; red ones regard the test dataset containing values out of the range of the training dataset (extrapolation, EX series). Although performance is lower for extrapolated scenarios, the beneficial effect of physical information remains evident.

These results are of crucial importance for the perspective application to flood mapping. Indeed, in such field, predictions are often sought not only for scenarios falling within the quantitative range of available observations, though previously unexplored, but also for cases featuring values of the observed quantities falling out of the range of the recorded series.

We also investigated whether the complexity of the model impacts our suggested training approach. The total number of trainable parameters was varied while preserving the three, equally sized layer architecture, and in both a data-rich (complete dataset) and a data-scarce ($5\%$ of the complete dataset) regime. Results are summarized in Figure 9.

Figure 9

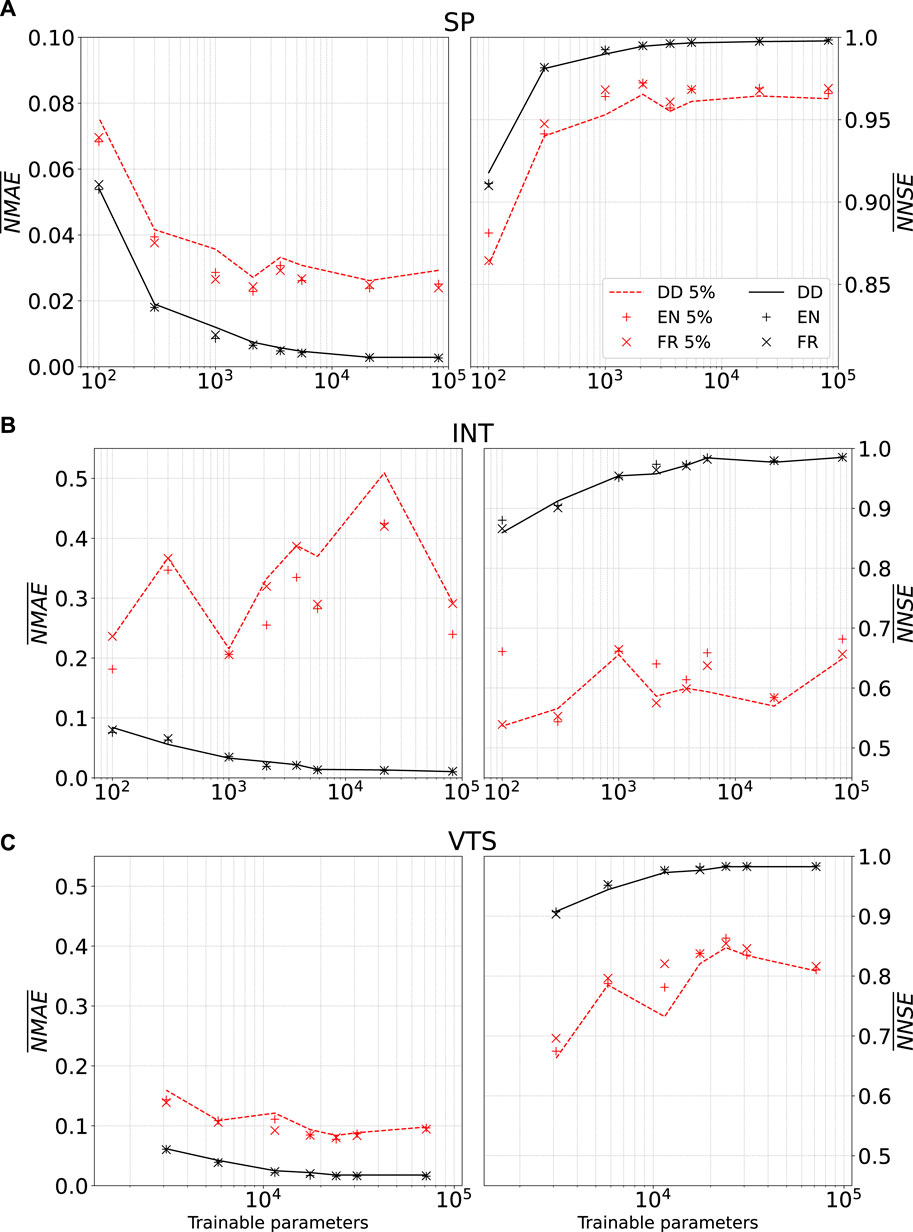
Figure 9. Stress tests: mean values of NMAE and NNSE on the test set against the number of trainable parameters. Black traces and markers represent models’ results after training on the complete dataset; red ones show models’ results after training on a reduced dataset (referred to as 5% in the legend). Physically aided training provides clear improvements only for simpler models and data rich scenario.

When dealing with the complete training dataset, an expected trend emerges as the number of trainable parameters decreases: performance consistently deteriorates across all three architectures. This discernible pattern clearly unveils the occurrence of underfitting. Oppositely to overfitting, underfitting occurs when the model lacks complexity compared to the information-rich training data. The lower complexity architectures now strive to capture the variability spanned by the complete dataset. In such underfitting regime, it is noteworthy that the introduction of a physical training strategy does not yield a consistent improvement in generalization results. This behavior is the consequence of the requirement for the low-complexity model, which is already struggling to discern patterns in the data, to fulfill additional constraints, such as the physical ones.

In the context of a small data regime, however, different behaviors emerge. Model performance can loose dependence on the number of parameters (as for INT) and, in some cases, it even deteriorates as the complexity of the models increases (as for VTS). Even in this clear overfitting scenario, models enhanced with the physical training strategy consistently ensure an improvement in performance. Indeed the physical term, involving both input and output data, akin to a form of data augmentation, provides the model with further insights into the nature of the system to be interpreted.

5 Conclusion

In this work, we propose to incorporate PDE-unrelated physical information into the training strategy of data driven neural networks to improve their generalization capabilities, outside the context of the neural solvers framework. We develop a synthetic case study in the field of environmental hydraulics to implement, apply and evaluate the proposed methodology. Specifically, we test the enhancements in the predictive capabilities of three neural network architectures when recreating the water mixed-regime profile along a rectangular channel, whereas modifying the parameters that define the solution. This physical system often develops a discontinuity, represented by the hydraulic jump, whose solution challenges the employed models.

The independence of our method from the knowledge of the governing PDEs and their parameters (e.g., as exploited by the strategy underlying the PINNs approach) presents a significant advantage in dealing with large epistemic uncertainty, as occurs in river hydraulics.

The NNs predictions are evaluated also for scenarios falling beyond the range of the training data (extrapolation), an aspect which is often overlooked in ML applications. This kind of assessment is of great relevance to the possible applications of NNs to flood mapping, where cases featuring values of the observed quantities falling out of the range of the recorded series need to be predicted. Even in this context, our analysis unveils that the physical information allows for a clear gain in performance.

Better predictive skills are also obtained in presence of overfitting, whereas underfitting cannot be mitigated by the added physical information.

As a complementary finding our analysis unveils the possible occurrence of a detrimental effect of an apparently informative physical constraint, namely, the volume. In this sense, our work calls for the development of a systematic framework to measure the informational content of physical constraints.

The proposed approach, involving only the loss function, is compatible with all NN architectures. Furthermore, it could be applicable to a wide range of physical systems where the underlying governing PDE is not entirely known, but either other physical principles hold true or a priori expert knowledge can be exploited. To adapt this methodology to other problems or applications, further exploration is necessary to integrate the relevant physical insights. Finally, the use of synthetic datasets does not restrict in any case the validity of our conclusions, though the implementation of the proposed technique to real world problem will be the object of future works.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

GG: Conceptualization, Investigation, Methodology, Software, Writing–original draft. AM: Funding acquisition, Writing–review and editing. J-MT: Methodology, Writing–review and editing. MR: Writing–review and editing. PP: Funding acquisition, Supervision, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The GG doctoral scholarship is granted under the National Recovery and Resilience Plan (PNRR, NextGenerationEU). J-MT thanks the FRQNT “Fonds de recherche du Québec–Nature et technologies (FRQNT)” for financial support (Research Scholarship No. 314328).

Acknowledgments

We sincerely thank Andrea Gemma for his valuable support in setting up the initial version of the code.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2015). TensorFlow: large-scale machine learning on heterogeneous systems Software.

Google Scholar

Ali, P. J. M., Faraj, R. H., Koya, E., Ali, P. J. M., and Faraj, R. H. (2014). Data normalization and standardization: a technical report. Mach. Learn Tech. Rep. 1, 1–6.

Google Scholar

Apicella, A., Donnarumma, F., Isgrò, F., and Prevete, R. (2021). A survey on modern trainable activation functions. Neural Netw. 138, 14–32. doi:10.1016/j.neunet.2021.01.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Baydaroğlu, Ö., and Demir, I. (2024). Temporal and spatial satellite data augmentation for deep learning-based rainfall nowcasting. J. Hydroinformatics 26, 589–607. doi:10.2166/hydro.2024.235

CrossRef Full Text | Google Scholar

Baydin, A. G., Pearlmutter, B. A., Radul, A. A., and Siskind, J. M. (2018). Automatic differentiation in machine learning: a survey. J. Marchine Learn. Res. 18, 1–43.

Google Scholar

Bentivoglio, R., Isufi, E., Jonkman, S. N., and Taormina, R. (2022). Deep learning methods for flood mapping: a review of existing applications and future research directions. Hydrology Earth Syst. Sci. 26, 4345–4378. doi:10.5194/hess-26-4345-2022

CrossRef Full Text | Google Scholar

Bentivoglio, R., Isufi, E., Jonkman, S. N., and Taormina, R. (2023). Rapid spatio-temporal flood modelling via hydraulics-based graph neural networks. Hydrology Earth Syst. Sci. 27, 4227–4246. doi:10.5194/hess-27-4227-2023

CrossRef Full Text | Google Scholar

Berkhahn, S., Fuchs, L., and Neuweiler, I. (2019). An ensemble neural network model for real-time prediction of urban floods. J. Hydrology 575, 743–754. doi:10.1016/j.jhydrol.2019.05.066

CrossRef Full Text | Google Scholar

Beven, K. (2006). A manifesto for the equifinality thesis. J. hydrology 320, 18–36. doi:10.1016/j.jhydrol.2005.07.007

CrossRef Full Text | Google Scholar

Blöschl, G. (2013). Runoff prediction in ungauged basins: synthesis across processes, places and scales. Cambridge University Press.

Google Scholar

Cache, T., Gomez, M. S., Beucler, T., Blagojevic, J., Leitao, J. P., and Peleg, N. (2024). Enhancing generalizability of data-driven urban flood models by incorporating contextual information. Hydrology Earth Syst. Sci. Discuss. 2024, 1–23.

CrossRef Full Text | Google Scholar

Cai, S., Mao, Z., Wang, Z., Yin, M., and Karniadakis, G. E. (2021). Physics-informed neural networks (pinns) for fluid mechanics: a review. Acta Mech. Sin. 37, 1727–1738. doi:10.1007/s10409-021-01148-1

CrossRef Full Text | Google Scholar

Cedillo, S., Núñez, A.-G., Sánchez-Cordero, E., Timbe, L., Samaniego, E., and Alvarado, A. (2022). Physics-informed neural network water surface predictability for 1d steady-state open channel cases with different flow types and complex bed profile shapes. Adv. Model. Simul. Eng. Sci. 9, 10–23. doi:10.1186/s40323-022-00226-8

CrossRef Full Text | Google Scholar

Cengel, Y., and Cimbala, J. (2013). Ebook: Fluid mechanics fundamentals and applications (si units). New York, NY: McGraw Hill.

Google Scholar

Chollet, F., et al. (2015). Keras.

Google Scholar

Chung, J., Gulcehre, C., Cho, K., and Bengio, Y. (2014). Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint arXiv:1412.3555.

Google Scholar

Dhanushree, M., Chitrakala, S., and Bhatt, C.M. (2023). Robust human detection system in flood related images with data augmentation. Multimedia Tools Appl. 82, 10661–10679. doi:10.1007/s11042-022-13760-9

CrossRef Full Text | Google Scholar

Cole, S., Moore, R., Bell, V., and Jones, D. (2006). Issues in flood forecasting: ungauged basins, extreme floods and uncertainty in Frontiers in flood forecasting, 8th kovacs colloquium (Paris: UNESCO), 305, 103–122.

Google Scholar

Cuomo, S., Di Cola, V. S., Giampaolo, F., Rozza, G., Raissi, M., and Piccialli, F. (2022). Scientific machine learning through physics–informed neural networks: where we are and what’s next. J. Sci. Comput. 92, 88. doi:10.1007/s10915-022-01939-z

CrossRef Full Text | Google Scholar

Dasgupta, R., Das, S., Banerjee, G., and Mazumdar, A. (2024). Revisit hydrological modeling in ungauged catchments comparing regionalization, satellite observations, and machine learning approaches. HydroResearch 7, 15–31. doi:10.1016/j.hydres.2023.11.001

CrossRef Full Text | Google Scholar

do Lago, C. A., Giacomoni, M. H., Bentivoglio, R., Taormina, R., Gomes, M. N., and Mendiondo, E. M. (2023). Generalizing rapid flood predictions to unseen urban catchments with conditional generative adversarial networks. J. Hydrology 618, 129276. doi:10.1016/j.jhydrol.2023.129276

CrossRef Full Text | Google Scholar

Eichelsdörfer, J., Kaltenbach, S., and Koutsourelakis, P.-S. (2021). Physics-enhanced neural networks in the small data regime. arXiv preprint arXiv:2111, 10329.

Google Scholar

Feng, D., Tan, Z., and He, Q. (2023). Physics-informed neural networks of the saint-venant equations for downscaling a large-scale river model. Water Resour. Res. 59, e2022WR033168. doi:10.1029/2022wr033168

CrossRef Full Text | Google Scholar

Guo, Z., Leitao, J. P., Simões, N. E., and Moosavi, V. (2021). Data-driven flood emulation: speeding up urban flood predictions by deep convolutional neural networks. J. Flood Risk Manag. 14, e12684. doi:10.1111/jfr3.12684

CrossRef Full Text | Google Scholar

Guo, Z., Moosavi, V., and Leitão, J. P. (2022). Data-driven rapid flood prediction mapping with catchment generalizability. J. Hydrology 609, 127726. doi:10.1016/j.jhydrol.2022.127726

CrossRef Full Text | Google Scholar

Hao, Z., Liu, S., Zhang, Y., Ying, C., Feng, Y., Su, H., et al. (2022). Physics-informed machine learning: a survey on problems, methods and applications. arXiv Prepr. arXiv:2211.08064.

Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Hrachowitz, M., Savenije, H., Blöschl, G., McDonnell, J. J., Sivapalan, M., Pomeroy, J., et al. (2013). A decade of predictions in ungauged basins (pub)—a review. Hydrological Sci. J. 58, 1198–1255. doi:10.1080/02626667.2013.803183

CrossRef Full Text | Google Scholar

Jagtap, A. D., Kharazmi, E., and Karniadakis, G. E. (2020). Conservative physics-informed neural networks on discrete domains for conservation laws: applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 365, 113028. doi:10.1016/j.cma.2020.113028

CrossRef Full Text | Google Scholar

Jamali, B., Haghighat, E., Ignjatovic, A., Leitão, J. P., and Deletic, A. (2021). Machine learning for accelerating 2d flood models: potential and challenges. Hydrol. Process. 35, e14064. doi:10.1002/hyp.14064

CrossRef Full Text | Google Scholar

Jin, X., Cai, S., Li, H., and Karniadakis, G. E. (2021). Nsfnets (Navier-Stokes flow nets): physics-informed neural networks for the incompressible Navier-Stokes equations. J. Comput. Phys. 426, 109951. doi:10.1016/j.jcp.2020.109951

CrossRef Full Text | Google Scholar

Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris, P., Wang, S., and Yang, L. (2021). Physics-informed machine learning. Nat. Rev. Phys. 3, 422–440. doi:10.1038/s42254-021-00314-5

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. (2014). Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980.

Google Scholar

Kratzert, F., Klotz, D., Herrnegger, M., Sampson, A. K., Hochreiter, S., and Nearing, G. S. (2019). Toward improved predictions in ungauged basins: exploiting the power of machine learning. Water Resour. Res. 55, 11344–11354. doi:10.1029/2019wr026065

CrossRef Full Text | Google Scholar

Kumar, V., Sharma, K. V., Caloiero, T., Mehta, D. J., and Singh, K. (2023). Comprehensive overview of flood modeling approaches: a review of recent advances. Hydrology 10, 141. doi:10.3390/hydrology10070141

CrossRef Full Text | Google Scholar

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521, 436–444. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Löwe, R., Böhm, J., Jensen, D. G., Leandro, J., and Rasmussen, S. H. (2021). U-flood–topographic deep learning for predicting urban pluvial flood water depth. J. Hydrology 603, 126898. doi:10.1016/j.jhydrol.2021.126898

CrossRef Full Text | Google Scholar

Lu, L., Meng, X., Mao, Z., and Karniadakis, G. E. (2021). Deepxde: a deep learning library for solving differential equations. SIAM Rev. 63, 208–228. doi:10.1137/19m1274067

CrossRef Full Text | Google Scholar

Maharana, K., Mondal, S., and Nemade, B. (2022). A review: data pre-processing and data augmentation techniques. Glob. Transitions Proc. 3, 91–99. doi:10.1016/j.gltp.2022.04.020

CrossRef Full Text | Google Scholar

Mahesh, R. B., Leandro, J., and Lin, Q. (2022). Physics informed neural network for spatial-temporal flood forecasting in Climate change and water security: select proceedings of VCDRR 2021 (Springer), 77–91.

Google Scholar

Nair, V., and Hinton, G. E. (2010). Rectified linear units improve restricted Boltzmann machines in Proceedings of the 27th international conference on machine learning (Haifa, Israel: ICML-10), 807–814.

Google Scholar

Ng, A. Y. (2004) Feature selection, l 1 vs. l 2 regularization, and rotational invariance in Proceedings of the twenty-first international conference on Machine learning, 78, 78. doi:10.1145/1015330.1015435

CrossRef Full Text | Google Scholar

Nguyen, H. D., Dang, D. K., Nguyen, Y. N., Pham Van, C., Van Nguyen, T. T., Nguyen, Q.-H., et al. (2023). Integration of machine learning and hydrodynamic modeling to solve the extrapolation problem in flood depth estimation. J. Water Clim. Change, jwc2023573.

Google Scholar

Prestininzi, P., Di Baldassarre, G., Schumann, G., and Bates, P. (2011). Selecting the appropriate hydraulic model structure using low-resolution satellite imagery. Adv. Water Resour. 34, 38–46. doi:10.1016/j.advwatres.2010.09.016

CrossRef Full Text | Google Scholar

Qi, X., de Almeida, G. A., and Maldonado, S. (2024). Physics-informed neural networks for solving flow problems modeled by the 2d shallow water equations without labeled data. J. Hydrology 636, 131263. doi:10.1016/j.jhydrol.2024.131263

CrossRef Full Text | Google Scholar

Qian, K., Mohamed, A., and Claudel, C. (2019). Physics informed data driven model for flood prediction: application of deep learning in prediction of urban flood development. arXiv preprint arXiv:1908, 10312.

Google Scholar

Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2019). Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707. doi:10.1016/j.jcp.2018.10.045

CrossRef Full Text | Google Scholar

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning representations by back-propagating errors. Nature 323, 533–536. doi:10.1038/323533a0

CrossRef Full Text | Google Scholar

Shorten, C., and Khoshgoftaar, T. M. (2019). A survey on image data augmentation for deep learning. J. Big Data 6, 60–48. doi:10.1186/s40537-019-0197-0

CrossRef Full Text | Google Scholar

Xu, Z., Liu, Z., and Peng, Y. (2024). Performance comparison of prediction of hydraulic jump length under multiple neural network models. IEEE Access 12, 122888–122901. doi:10.1109/access.2024.3430075

CrossRef Full Text | Google Scholar

Zhu, Y., Zabaras, N., Koutsourelakis, P.-S., and Perdikaris, P. (2019). Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 394, 56–81. doi:10.1016/j.jcp.2019.05.024

CrossRef Full Text | Google Scholar

Appendix A: Dataset generation

The dataset was generated by solving the specific energy equation, expressed as [Cengel and Cimbala, 2013]

$\frac{dE}{dx}=s-J.(\mathrm{A1})$

Here, $E$ represents the specific energy relative to the channel bottom, which, for a rectangular channel, can be calculated as

$E=h+\frac{Q^2}{2g{b}^2{h}^2}(\mathrm{A2})$

where $g$ is the gravity, $b$ is the channel width, $h$ is the flow depth; $s$ is the channel slope, whereas $J$ is the energy grade slope, calculated using the Chezy relation

$J=\frac{n^2{Q}^2}{{\mathrm{\Omega }}^2{R}^{4/3}}(\mathrm{A3})$

$n$ is the Manning coefficient, $\mathrm{\Omega }=bh$ is the cross-sectional flow area and $R=\mathrm{\Omega }/(b+2h)$ is the hydraulic radius. The downstream boundary condition is represented by the broad-crested weir equation

$h=z_d+{\left(\frac{3\sqrt{3}Q}{2\sqrt{2g}b}\right)}^{2/3}(\mathrm{A4})$

where $z_d$ is the weir height.

The possible transition from supercritical $(Fr>1)$ to subcritical $(Fr<1)$ flow occurs through a hydraulic jump, where

$Fr=\frac{Q}{\mathrm{\Omega }\sqrt{gh}}.(\mathrm{A5})$

Examining the conservation of momentum within the fluid volume encompassing the hydraulic jump, two cross-sections denoted as 1 (upstream, supercritical flow) and 2 (downstream, subcritical flow) as in Figure A1 can be defined [Cengel and Cimbala, 2013]. The conservation of momentum can be expressed as

${\mathrm{\Pi }}_{p1}+M_1={\mathrm{\Pi }}_{p2}+M_2.(\mathrm{A6})$

FIGURE A1

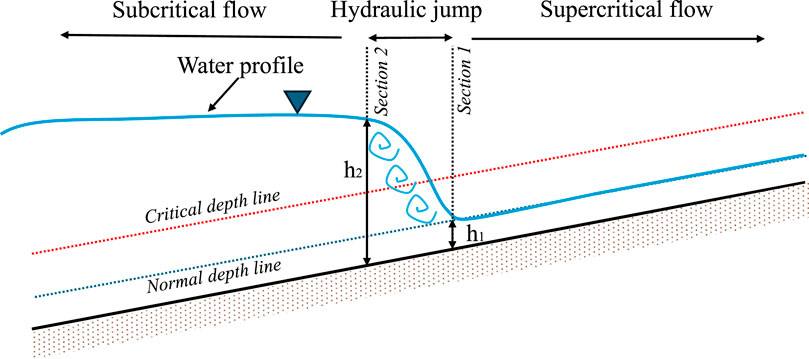
FIGURE A1. Schematic of a hydraulic jump, showing the two control sections (section 1, upstream, and section 2, downstream) with their conjugate depths h1 and h2.

Here, ${\mathrm{\Pi }}_{p1}$ and ${\mathrm{\Pi }}_{p2}$ represent the upstream and downstream values of the hydrostatic force, whereas $M_1$ and $M_2$ denote the upstream and downstream values of the momentum flux, respectively. For a rectangular prismatic channel, (Equation A6) becomes

$\frac{h_1^2}{2}+\frac{Q^2}{g{b}^2{h}_1}=\frac{h_2^2}{2}+\frac{Q^2}{g{b}^2{h}_2}(\mathrm{A7})$

which can be arranged in the following expression, establishing a mathematical relation between $h_1$ and $h_2$, that are called conjugate depths

$h_1=\frac{h_2}{2}\left(-1+\sqrt{1+8F{r}_2^2}\right)(\mathrm{A8})$

$F{r}_2$ is the Froude number (Equation A5) at the cross-Section 2.

The water profile is obtained by solving (Equation A1) using a first order FD scheme, with a constant spatial discretization $\mathrm{\Delta }x$. An upstream marching algorithm is employed, encompassing the solution of the hydraulic jump if necessary.