A three-state language competition model including language learning and attrition

We develop a three-state agent-based language competition model that takes into account the fact that language learning and attrition are not instantaneous but occur over a finite time interval; i.e., we introduce memory in the system. We show that memory effects significantly impact the dynamics of language competition. Furthermore, we find that including heterogeneity in the linguistic skills of the agents affects the results substantially. We also explore the role of other factors, such as different levels of language learning difficulty, initial population fractions, and daily interaction rates.

1 Introduction

The past two decades have witnessed a significant growth of research interest in mathematical modeling of language dynamics. This has been mainly driven by the consideration that according to UNESCO, about 43% of the approximately 6,000 languages currently spoken in the world are at risk of extinction by as early as 2050 (Austin, 2008; Moseley, 2010). In fact, starting from the seminal work by Abrams and Strogatz (2003), the study and modeling of language competition have become one of the key research topics in complex systems theory.

While the Abrams–Strogatz model, based on Lotka–Volterra-type equations, is a two-state model that takes into account monolingual groups only, other models, including the first language competition models by Baggs and Freedman (Baggs et al., 1990; Baggs and Freedman, 1990; Baggs and Freedman, 1993), also incorporate bilingual communities. The various models introduced so far leverage a range of approaches derived not only from population–ecology models but also from statistical physics, game theory, and agent-based modeling (Castellano et al., 2009; Baronchelli, 2016; Marchetti et al., 2020b; Marchetti et al., 2020a; Patriarca et al., 2020; Marchetti et al., 2021; Minett and Wang, 2008; Vazquez et al., 2010; Ya-ping et al., 2015). The inclusion of bilingualism has led to models that demonstrate that under certain conditions, the survival of both competing languages, coexisting within a stable bilingual community, can be achieved (Castellano et al., 2009; Heinsalu et al., 2014; Marchetti et al., 2021).

A feature common to many language dynamics models, encompassing bilingualism or not, is the assumption that the key driving force for adopting one language versus another is its relative prestige or perceived status (Abrams and Strogatz, 2003). This makes sense as it seems plausible that perceived language status played a role, for instance, in the decline of Welsh and Scottish Gaelic in favor of English, or in the progressive disappearance of Quechua, still spoken in some areas of Peru, in favor of Spanish. However, there are other relevant factors that can lead to a language shift (Patriarca et al., 2020). For example, based on Indian census data, De Silva et al. pointed out that the competition between Hindi and English over two decades from 1991 to 2011 has resulted in the saturation of the bilingual community and a steady growth of Hindi monolinguals, in spite of English being a higher status language (De Silva et al., 2021). This is related to the Indian political background and educational infrastructures. Anyway, the main parameters of such language competition models are the transition rates, which reflect the influence of different factors, such as language prestige, the underlying socioeconomic and political situation, and language similarity.

It is to be noted that three-state language dynamics models, in which one of the states corresponds to bilinguals, are formally similar to three-state opinion dynamics models, where one of the states can represent undecided individuals (Castellano et al., 2009). Importantly, in opinion dynamics, in addition to other factors and mechanisms, the role of memory and how it influences even a simple choice, has been recognized and studied (Dall’Asta and Castellano, 2007). For example, some voter models incorporate memory effects in agent-based simulations or through fractional derivatives at the analytical level (Baron et al., 2022), mimicking an opinion change happening only after several interactions have taken place.

Memory effects are expected to play a relevant role whenever the constituent units themselves are complex and can exchange, record, and process information. Taking memory into account is even more relevant when considering the complex processes that underlie language learning and attrition. In fact, a closer analysis of the learning process reveals that even the acquisition of a single word is based on the memory association between the phoneme associated to the word and, e.g., the image corresponding to a real object (Odgen and Richards, 1923) and, thus, should be more properly treated at a cognitive modeling level (Marchetti et al., 2020b; Marchetti et al., 2020a; Marchetti et al., 2021; and references therein). Thus, the acquisition of a new language, as well as its retention, is a time-consuming process that depends on multiple interactions over a finite time interval. Cognitive processes and, in particular, memory-related effects, individual language learning aptitudes, and different degrees of difficulty of learning and retaining a language, from both a grammatical and a phonetic viewpoint, may play a crucial role in determining the outcome of language competition.

Most models of language dynamics describe language acquisition and shift as simple instantaneous transitions between different linguistic states driven by the current state of the system. Instead, in the present paper, we study the role of memory in language competition at a phenomenological level, focusing on the accompanying processes of language learning and attrition (Liivand, 2018). The impact of memory on language adoption is studied as a function of the frequency of interactions with other speakers, taking into account both the difficulty of learning and retaining a foreign language and the possibility of abandoning one’s mother tongue after becoming bilingual. The combination of these effects determines in our model the conditions that may lead to language extinction or survival or to the attainment of an equilibrium involving different linguistic communities.

Research on second language acquisition has shown that, in addition to different language usage frequencies among individuals, there exist additional relevant individual factors, including age, personal skills, aptitude, personality, learning style, motivation, and external (cultural and socioeconomical) environment (Ellis et al., 1994; Griffiths and Soruç, 2020), which shape the observed heterogeneous learning abilities of individuals. However, people also differ vastly in how fast they forget a language (Schmid and Köpke, 2019) for mother tongue attrition and (Mickan et al., 2020) for foreign language attrition. Without trying to model the detailed origin of individual differences but still willing to incorporate some degree of heterogeneity in individuals, we assigned diversified values to the parameters related to language learning and retaining. The inclusion of heterogeneity in the present study is motivated by the research in language acquisition, but the importance of heterogeneity and quenched disorder in complex processes, from economic stability to network synchronization (Bouchaud, 2009; Lafuerza and Toral, 2013; Zhang et al., 2021), is now well recognized.

This paper is organized as follows. Section 2 introduces a three-state agent-based language competition model that takes into account memory effects and the heterogeneity of speakers. We also provide the numerical algorithm to simulate the model. Section 3 presents the results for both homogeneous and heterogeneous populations with identical or diversified linguistic capabilities, respectively. We study the time evolutions and phase portraits of the systems and analyze how the language competition outcome depends on the interaction frequency, level of heterogeneity, initial fractions of the monolingual populations, and the asymmetry between language learning difficulties. Section 4 outlines the conclusions.

2 Model

2.1 Overall description

In order to investigate the impact of memory on language competition, we develop an agent-based model of a population of N speakers, of whom a fraction N_X speak language X, a fraction N_Y speak language Y, and a fraction N_Z are bilinguals speaking both languages X and Y; N_X + N_Y + N_Z = 1. In the following, the symbols X and Y also represent the language state of X- and Y-monolinguals, respectively, while Z represents the state of bilingual agents. It is assumed that initially, there are no bilinguals, i.e., N_Z (t = 0) = 0.

During the time evolution of the system, agents communicate pair-wise. Each time step in the simulations corresponds to 1 day, and an agent is assumed to communicate every day on average with other N_int agents. Thus, there are daily N_int × N/2 interactions in the system.

For the choice of the language used in a communication, we apply the following rules.

• In the encounter between two monolinguals of different languages, since there is no common language to be used, it is assumed that either speaker will try to use their own language, which the other speaker will make an effort to understand so that eventually, either agent will learn something of the other agent’s language.

• The language employed in an interaction between a monolingual and a bilingual agent is that of the monolingual agent.

• In the case of an encounter between two bilinguals, both languages could be used in principle. The choice of the language employed takes into account the cost of language switching (Meuter and Allport, 1999; Jackson et al., 2001; Abutalebi and Green, 2007; Moritz-Gasser and Duffau, 2009; Iriberri and Uriarte, 2012); i.e., it depends on the native language and/or the number of previous communications in one or the other language (see Section 2.3 for details).

In the learning process, memory is taken into account, assuming that a monolingual agent can acquire the other language and become bilingual only through repeated interactions with monolingual speakers of the other language. In the model, we assume that in order to learn a new language and become bilingual, a monolingual agent has to use the new language at least K times within a time interval T^K. If the monolingual agent has used the new language less than K times, as time interval T^K elapses, the agent’s memory is reset. Importantly, the model will use, in general, two different parameters K^X and K^Y for the two languages X and Y, respectively, reflecting the possible different difficulties of learning; i.e., K^X (K^Y) expresses the difficulty of learning language X (Y) and, therefore, will be used to determine if a monolingual agent speaking language Y (X) meets the criterion to become bilingual or not.

Memory effects also influence language maintenance. In the model, we assume that a bilingual has to use both languages X and Y at least M times within a time interval T^M in order to maintain them (for simplicity, we assume the same M and T^M for both the first and second languages). If this condition is not fulfilled for one of the languages, that language will be forgotten.

The model variables are discussed in Section 2.2, and the dynamical rules of time evolution are listed in Section 2.3.

2.2 Microscopic variables

The state of agent i (i = 1, 2, … , N) at time step t is specified by the following set of individual variables:

• Language variables (all agents): The linguistic state of agent i is recorded by the variable $L_i^{[1]}$, representing the (main) language ($L_i^{[1]}=X$ or Y), and, if the agent is bilingual, also by the variable $L_i^{[2]}$, recording the second language ($L_i^{[2]}=Y$ or X, respectively). For a monolingual agent, $L_i^{[2]}=0$.

• Learning variables (monolinguals): For a monolingual agent i $(L_i^{[2]}=0)$, the learning process of a new language at time t is tracked by the time counter ${\tau }_i^k(t)$, recording the time elapsed since the first interaction with a monolingual of the other language, and the language usage counter k_i(t), counting how many times the speaker has used the other language.

• Maintenance variables (bilinguals): For a bilingual agent i $(L_i^{[2]}\ne 0)$, language use at time t is tracked by the time counter ${\tau }_i^m(t)$, measuring the time elapsed since becoming bilingual, and by the usage counters $m_i^{[1]}$, $m_i^{[2]}$ of the two languages. It should be noted that it is assumed that monolinguals do not forget their language, and therefore, $m_i^{[1]}$ is not tracked for them.

2.3 Numerical algorithm

The algorithm employed in the numerical simulations can be summarized as follows:

0. At time t = 0, the population contains only a fraction N_X (0) of X-monolinguals and a fraction N_Y(0) of Y-monolinguals, i.e., N_X (0) + N_Y(0) = 1 and N_Z (0) = 0. Counters ${\tau }_i^k$ and k_i are initialized to zero.

1. A set of N_int × N/2 couples of agents are randomly selected from the population.

2. Agents i and j of each extracted couple interact, and their language use is tracked (Table 1; Table 2).

• If both agents i and j are monolinguals of the same language $(L_i^{[1]}=L_j^{[1]})$, nothing happens.

• If agents i and j are monolinguals with different languages $(L_i^{[1]}\ne L_j^{[1]})$, either of them learns something about the other agent’s language, and their language use counters are updated: k_i → k_i + 1 and k_j → k_j + 1.

• If agent i is bilingual and agent j is monolingual, it is assumed that they communicate in the language of the monolingual agent j. In this case, only the usage counter of the bilingual agent i is updated: $m_i^{[1]}\to m_i^{[1]}+1$ if agent i used the main language or $m_i^{[2]}\to m_i^{[2]}+1$ if the second language was used. Agent j does not learn; consequently, there is no update for agent j. An analogous update is carried out if agent i is monolingual and agent j is bilingual.

• If agents i and j are both bilinguals and have the same main language, this will be used in the communication, and therefore, $m_i^{[1]}\to m_i^{[1]}+1$ and $m_j^{[1]}\to m_j^{[1]}+1$.

• If agents i and j are both bilinguals but their main languages are different, they will make a decision based on their memory information stored in the counters $m_i^{[1]},m_i^{[2]},m_j^{[1]},m_j^{[2]}$ (see Table 2). If both agents have used one of the two languages more frequently, that language will be used. Instead, if the two agents have comparable language use, but for different languages, then the choice will be made randomly. Depending on the language used, the corresponding counters of agents i and j are updated.

TABLE 1

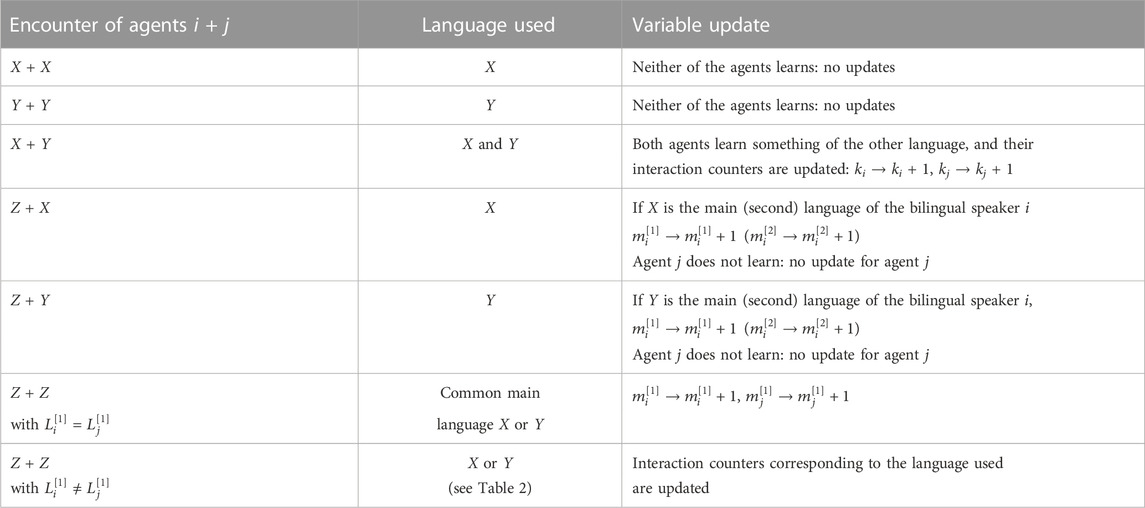
TABLE 1. Possible encounters between agents i and j, the language used, and corresponding updates of their variables (time counters are always updated; see text for details). Here, X, Y, and Z denote the linguistic state of the speaker.

TABLE 2

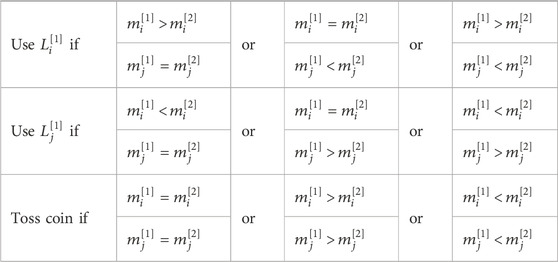
TABLE 2. Language selection and corresponding criteria in an encounter between two bilinguals with different main languages.

3. After the N_int × N/2 couples of agents extracted have interacted, the time variables are updated for each agent i: if agent i is monolingual, time counter ${\tau }_i^k$ is updated, ${\tau }_i^k\to {\tau }_i^k+1$; if agent i is bilingual, time counter ${\tau }_i^m$ is updated, ${\tau }_i^m\to {\tau }_i^m+1$. Furthermore, the system time t is updated, t → t + 1.

4. Language use counters, time counters, and possible transitions between the monolingual and bilingual state are checked for each agent i (see Table 3).

• If agent i is monolingual, the counters k_i and ${\tau }_i^k$ are checked at each time step. If k_i < K and ${\tau }_i^k<T^K$, the learning process continues. If, instead, k_i < K and ${\tau }_i^k=T^K$, the counters are reset, k_i → 0 and ${\tau }_i^k\to 0$, and the learning process starts over. If k_i ≥ K and ${\tau }_i^k\le T^K$, agent i becomes bilingual, and the maintenance variables, ${\tau }_i^m$, $m_i^{[1]}$, and $m_i^{[2]}$, are initialized to zero.

• If agent i is bilingual, the counter ${\tau }_i^m$ is checked at each time step. If ${\tau }_i^m=T^{\mathrm{M}}$, the language usage counters $m_i^{[1]}$ and $m_i^{[2]}$ will be checked. If $m_i^{[1]}\ge M$ but $m_i^{[2]}<M$, the second language is forgotten and agent i becomes monolingual $(L_i^{[2]}\to 0)$. If $m_i^{[1]}<M$ but $m_i^{[2]}\ge M$, the first language is forgotten and the second language is promoted to main language ($L_i^{[1]}\to L_i^{[2]}$ and $L_i^{[2]}\to 0$). In both cases, the learning variables of the now monolingual speaker are reset, k_i → 0 and ${\tau }_i^k\to 0$. If, instead, both $m_i^{[1]}\ge M$ and $m_i^{[2]}\ge M$, the agent remains bilingual and all the maintenance variables are reset. If both $m_i^{[1]}<M$ and $m_i^{[2]}<M$, then the second language is forgotten.

TABLE 3

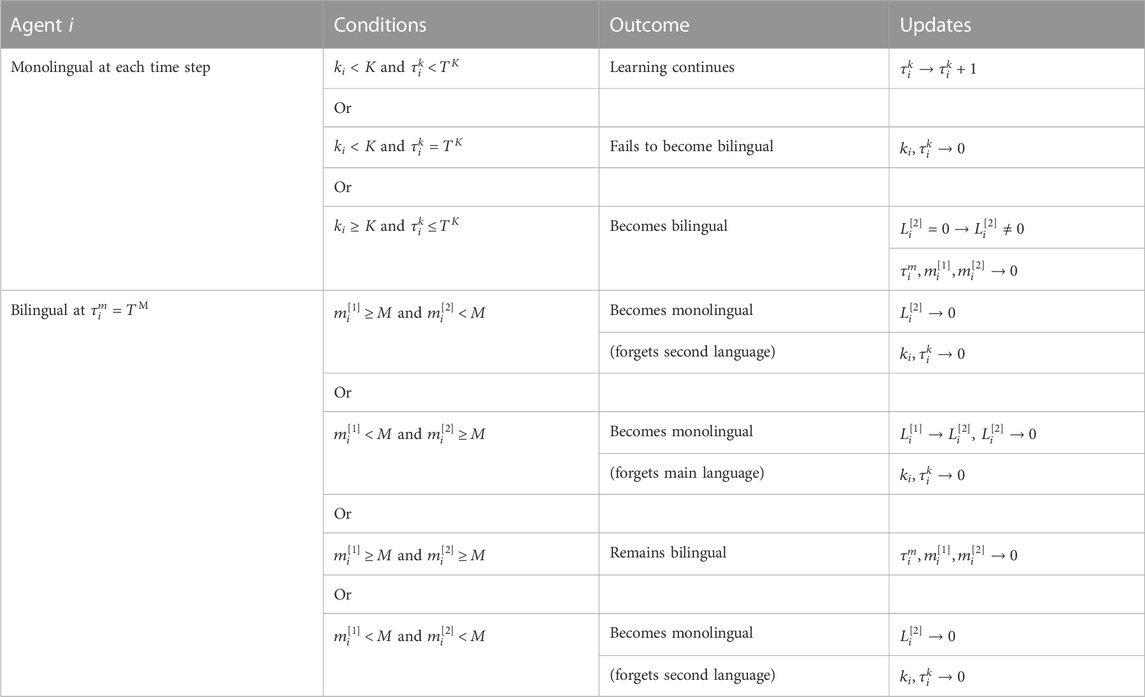
TABLE 3. Checks made on each agent i (i =1,… , N). If for individual i, the conditions are fulfilled, the change described in the column “outcome” takes place and variables are updated as described in column “Updates.”

5. The algorithm is reiterated from step 1 until the final simulation time t = t_fin is reached or until all speakers become monolinguals of the same language.

It should be noted that instead of using an algorithm where the time and language use counters are reset, as explained previously, one could use an alternative more realistic algorithm based on a moving temporal window, i.e., checking at each time step the language use during the reference time intervals T^K or T^M. For computational convenience, we used the aforementioned algorithm, but we checked that within the parameter range used, the two methods provide equivalent results.

2.4 Including heterogeneity

As discussed in Introduction, in a language dynamics model that aims to scrutinize the impact of memory and learning processes, it is relevant to take into account that individual linguistic skills to learn or retain a language are different. This heterogeneity may depend on many factors. In our model, the effect of these factors is described in terms of a heterogeneous distribution of the parameters regulating the learning and maintenance of a language, i.e., the associated time intervals and language usage frequencies.

As far as the learning process is concerned, the global language usage thresholds K^X and K^Y for learning language X and Y by monolingual speakers of language Y and X, respectively, are replaced by a heterogeneous set of parameters $K_i^{\mathrm{X}}$ and $K_i^{\mathrm{Y}}$, respectively, assigned to each agent i. Analogously, to include heterogeneity in language retention, in place of a single value T^M, we extract a different value $T_i^{\mathrm{M}}$ for each agent i. Thus, the time period after which a speaker forgets a language is an individual characteristic.

In the following equation, we limit ourselves to considering a specific case with a simple correlation between the threshold values of language usage and attrition times of generic agent i.

$K_i^{\mathrm{X}}=K^{\mathrm{X}}\left(1+S_i{\sigma }^{\mathrm{X}}\right),(1)$

$K_i^{\mathrm{Y}}=K^{\mathrm{Y}}\left(1+S_i{\sigma }^{\mathrm{Y}}\right),(2)$

$T_i^{\mathrm{M}}=T^{\mathrm{M}}\left(1-S_i{\sigma }^{\mathrm{M}}\right).(3)$

In the aforementioned three equations, S_i is the same random number extracted from a standard normal distribution, the values K^X, K^Y, and T^M represent the means, and σ^X, σ^Y, and σ^M represent the relative standard deviations of the respective distributions. Thus, the standard deviations express the degree of heterogeneity of the agents. Equations 1, 2 describe the learning, and Eq. 3 describes the language maintenance features of individual i. The Gaussian distribution is the most natural one to describe the heterogeneity of the linguistic skills in a population. A value S_i > 0 in Eq. 1 or 2 describes a speaker who needs for learning to practice language X or Y more times than on average; instead, S_i < 0 corresponds to the opposite case. The negative sign in Eq. 3 reflects the fact that, in general, the individuals who learn more slowly are, at the same time, the ones who forget more quickly, and vice versa. For the sake of simplicity, we assume that σ^X = σ^Y = σ^M ≡ σ.

It should be noted that since in Eqs 1–3 S_i is extracted from a standard normal distribution, $K_i^{\mathrm{X}}$, $K_i^{\mathrm{Y}}$,and $T_i^{\mathrm{M}}$ can take also negative values. As long as σ is small enough, this happens only for a small fraction of the extracted values of S_i. In fact, in the following section, we limit ourselves to studying the parameter range σ ∈ (0, 0.5]. For σ = 0.5, agents corresponding to the upper end of the range defined by ± one standard deviation from the mean learn three times faster (and forget three times more slowly) than agents positioned at the opposite end. Larger values of σ would lead to unrealistic differences between the individuals. For a given value of σ, in the case an S_i value leads to a negative parameter $K_i^{\mathrm{X}}$, $K_i^{\mathrm{Y}}$, or $T_i^{\mathrm{M}}$, that parameter is set to zero.

3 Results and discussion

3.1 Simulation parameters

We simulate the model for a population comprising at least N = 10³ agents, unless specified differently. We checked that this is a sufficient population size and the results remain unchanged when increasing the number of speakers even up to N = 10⁴. The simulation time is N_t = 4 × 10⁴ days $\approx 110$ years. We assume that each time step in the simulations corresponds to 1 day and each agent has an average number N_int of daily interactions with other agents. Based on psycho-sociological and epidemiological studies (Valle et al., 2007; Zhaoyang et al., 2018) about social interactions, we explore a range of N_int ∈ [8, 24]. We allow for monolinguals of language Y (X) a time T^K = 730 days = 2 years to acquire language X (Y), during which they should use the language at least K^X (K^Y) times. When exploring the symmetrical case of an equal level of difficulty of language learning, we set K^X = K^Y = 5,110 (i.e., on average, seven practicing events per day to learn a new language). In the asymmetrical case, K^Y is maintained at 5,110 and K^X is varied. The ability of bilinguals to retain the native or acquired language is assessed over the time period T^M = 7,300 days = 20 years, during which the speakers, to remain bilinguals, should use both languages at least M = 43,800 times (on average, six times per day). Unless specified differently, we set σ = 0.5 when diversifying K^X, K^Y, and T^M in order to add heterogeneity to the aforementioned model.

It should be noted that the choice of the minimum number of learning interactions needed to acquire a new language, determined by the thresholds K^X, K^Y, and T^K, as well as of the minimum number of practicing events required to retain a language, determined by M and T^M, is arbitrary. However, studying the dependence of simulation results on the number of daily interactions N_int per agent is equivalent to varying the aforementioned thresholds while keeping N_int constant. This is because the competition outcome is mainly determined by the interplay between the daily interaction frequency and model thresholds.

3.2 Homogeneous population

We begin our study of the effects of memory on language competition dynamics by examining first the case of a homogeneous population.

As long as no bilinguals are present in the system (beginning of the time evolution), a speaker interacts daily, on average, N_X(0)N_int times with X-monolinguals and N_Y(0)N_int times with Y-monolinguals. As discussed in Section 2.3, a monolingual → bilingual transformation, X → Z (or Y → Z), takes place only if an X (or Y)-monolingual has used the other language at least K^Y (or K^X) times within the maximum allowed learning time T^K. This implies the following conditions for the transition times t_X and t_Y:

$t_X\equiv K^X/N_{\mathrm{i}\mathrm{n}\mathrm{t}}{N}_X\left(0\right)\le T^K\mathrm{f}\mathrm{o}\mathrm{r}Y\to Z,(4)$

$t_Y\equiv K^Y/N_{\mathrm{i}\mathrm{n}\mathrm{t}}{N}_Y\left(0\right)\le T^K\mathrm{f}\mathrm{o}\mathrm{r}X\to Z.(5)$

If both conditions are fulfilled, then which of the two possible transformations, Y → Z or X → Z, will take place, i.e., which monolingual community will form the bilingual population, depends on which of the two transition times, t_X ≤ T^K or t_Y ≤ T^K, is smaller. For given values of N_int and T^K, this depends on K^X, K^Y, and the initial fractions N_X (0) and N_Y(0). In the symmetrical case, when K^X = K^Y ≡ K, the transition type is determined only by the values of N_X (0) and N_Y(0); if N_X (0) = N_Y(0), both monolingual populations turn into bilinguals; otherwise, it is the population of the minority language that becomes bilingual. In the asymmetrical case, when K^X ≠ K^Y, for equal initial population fractions, N_X (0) = N_Y(0), the transition type is determined by the values of K^X and K^Y: for K^X > K^Y, the bilingual community will be formed by X-monolinguals and for K^Y > K^X by Y-monolinguals, i.e., by the monolinguals of the language that is more difficult to learn. If neither condition is fulfilled, no bilingual community will appear.

In order to illustrate the beginning of the system time evolution, let us consider the example of a population of 100 identical speakers (we use in this example only 100 individuals for the clarity of visualization) with initial population fractions N_X (0) = 0.6 and N_Y(0) = 0.4. The daily interaction rate is N_int = 16, K^X = K^Y = 5,110, and the transition times for the given parameters are t_X = 532 and t_Y = 798, respectively. In this case, since t_X < T^K < t_Y, all the Y-monolinguals will become bilinguals around time t = t_X. Accordingly, in Figure 1A, the lines depicting the usage counters k_i of the Y-monolinguals stop, while the lines corresponding to the bilinguals’ language usage counters $m_i^{[1]}$ and $m_i^{[2]}$ appear; because N_X(t) > N_Y(t) + N_Z(t) = N_Y(0), the lines corresponding to $m_i^{[2]}(t)$ measuring the usage of the acquired language X have larger slopes than the lines corresponding to $m_i^{[1]}(t)$ measuring the usage of the bilinguals’ first language Y. Instead, because after time t_X, the monolinguals of language X will use only language X, both in the communication among themselves and with the bilinguals, their language usage counters k_i will remain constant until t = T^K, when they are reset to zero.

FIGURE 1

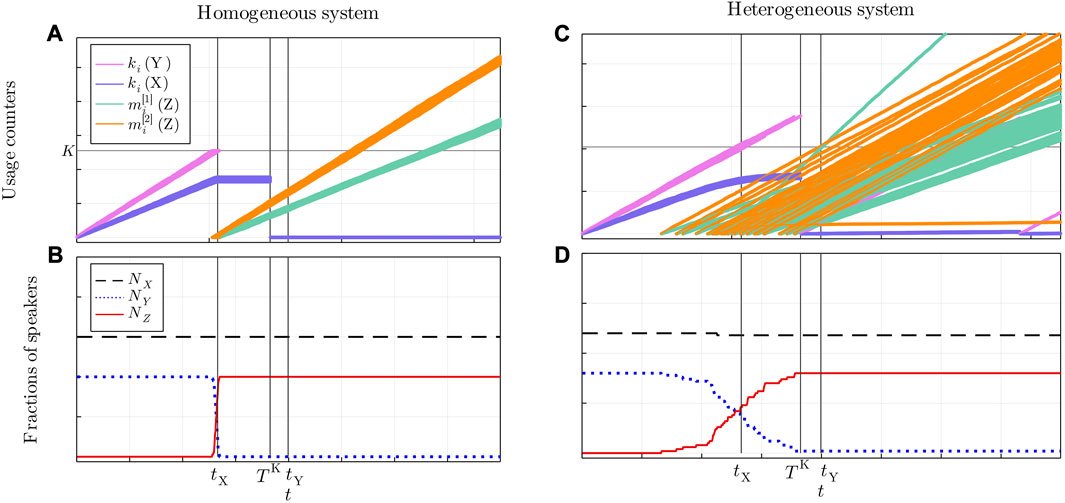
FIGURE 1. (Symmetrical case). Time evolutions in a homogeneous system [(A) and (B)] and in a heterogeneous system with σ = 0.2 [(C) and (D)]. (A), (C) Language usage counters k_i, $m_i^{[1]}$, and $m_i^{[2]}$ versus time. (B,D) Fractions of speakers versus time. The results are obtained using N = 100 agents; N_X (0)/N_Y(0) = 60/40, and N_int = 16. For comparison, the transition times t_X and t_Y for homogeneous populations and threshold time T^K are marked by vertical lines for both systems.

Figure 1B shows the corresponding time evolution of the population fractions: at time t_X, there is the transition Y → Z, i.e., all monolinguals of language Y learn language X and become bilinguals; instead, N_X(t) = N_X (0).

Now, if the parameters are such that one of the monolingual populations becomes bilingual, whether this state is stable or not, it depends on the parameters regulating the attrition process. It will be stable if bilinguals practice both languages at least M times during a time interval T^M. Because in the current example in the communication between bilinguals, only their first language is used (all bilinguals have the same first language), then N_Z(t) = N_Y(0) (as in our example depicted in Figure 1) or N_Z(t) = N_X (0); the second language is used by bilinguals only in the communication with monolinguals, whose population is equal to the initial one. Consequently, the conditions for the bilingual population to maintain languages X and Y are, respectively,

$T^{\mathrm{M}}{N}_{\mathrm{i}\mathrm{n}\mathrm{t}}{N}_X\left(0\right)\ge M\left(\text{to\hspace{0.17em}maintain\hspace{0.17em}language\hspace{0.17em}X}\right),(6)$

$T^{\mathrm{M}}{N}_{\mathrm{i}\mathrm{n}\mathrm{t}}{N}_Y\left(0\right)\ge M\left(\text{to\hspace{0.17em}maintain\hspace{0.17em}language\hspace{0.17em}Y}\right).(7)$

The bilingual community remains bilingual only if both conditions are satisfied. If one of the conditions is not fulfilled, the respective language is forgotten and the bilinguals become monolinguals of the language for which the condition is satisfied. If none of the conditions is fulfilled, the bilinguals become monolinguals of their original language. In the aforementioned example (Figures 1A, B), the bilinguals maintain both languages and the state reached is stable.

The behavior of the system under different initial conditions is illustrated by the phase portraits in Figure 2A for K^X = K^Y (symmetrical language learning difficulty) and Figure 2B for K^X ≠ K^Y (asymmetrical language learning difficulty). Possible initial conditions are represented by the points on the line N_X (0) + N_Y(0) = 1, where N_Z (0) = 0. In this example, we chose N_int = 10, allowing us to observe different regimes: some trajectories evolve toward a final state, where, in addition to bilingual speakers, there are also monolinguals of language X (or Y)—as shown by the dots on the N_X-axis (N_Y-axis); for the rest of the initial conditions, the representative point remains in the initial state. This behavior can be understood by expressing conditions (4)–(5) in terms of the initial fractions N_X (0) and N_Y(0).

$N_X\left(0\right)\ge K^X/N_{\mathrm{i}\mathrm{n}\mathrm{t}}{T}^K\equiv N_X^{*}\mathrm{f}\mathrm{o}\mathrm{r}Y\to Z,(8)$

$N_Y\left(0\right)\ge K^Y/N_{\mathrm{i}\mathrm{n}\mathrm{t}}{T}^K\equiv N_Y^{*}\mathrm{f}\mathrm{o}\mathrm{r}X\to Z,(9)$

which define implicitly the critical initial fractions $N_X^{*}$ and $N_Y^{*}$, above which a transition to bilingualism takes place. In the symmetrical case, when K^X = K^Y = 5,110, the values of the critical initial fractions are $N_X^{*}=N_Y^{*}=0.7$. For the asymmetrical case with K^X = 5,840 and K^Y = 4380 depicted in Figure 2B, $N_X^{*}=0.8$ and $N_Y^{*}=0.6$. No transition to bilinguals takes place if the trajectory starts from an initial condition for which neither inequality is satisfied, i.e., when $N_X(0)<N_X^{*}$ and $N_Y(0)<N_Y^{*}$, corresponding to the interval $1-N_Y^{*}<N_X(0)<N_X^{*}$ (see Figures 2A, B). In this case, the two monolingual communities remain isolated and coexist together so that N_X(t) = N_X (0) and N_Y(t) = N_Y(0). If the parameters are such that $1-N_Y^{*}>N_X^{*}$, such an interval does not exist; for example, for the K^X, K^Y, and T^K values used in Figure 2, it disappears in both symmetrical and asymmetrical cases, if N_int ≥ 14.

FIGURE 2

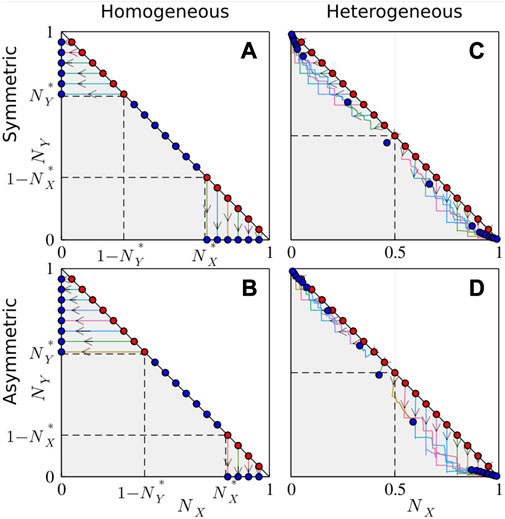
FIGURE 2. Phase portraits of homogeneous [σ = 0—(A) and (B)] and heterogeneous [σ = 0.2—(C) and (D)] systems with symmetrical [K^X = K^Y = 5,110—(A) and (C)] and asymmetrical [K^X = 5,840, K^Y = 4380—(B) and (D)] language learning difficulties. The gray triangle represents the area accessible to the system. The initial conditions are represented by the red dots, and the final positions are represented by the blue dots (overlapping the red ones on the diagonal). The results are obtained using N = 100 agents and N_int = 10. For the homogeneous system, the critical initial densities $N_X^{*}$ and $N_Y^{*}$ are marked by the dashed lines. Trajectories are averaged over 100 runs.

Now, from the last remark, as well as from conditions (4)–(5) and (6)–(7), it is also clear that the number of daily interactions, N_int, is a very important quantity in determining the dynamics and outcome of the language competition. In Figure 3, the final population composition is plotted as a function of N_int, dashed lines, for the homogeneous system. This figure shows clearly how the final outcome of the language competition is determined by the interplay of the learning and attrition processes. Let us determine the conditions for the learning and maintenance of languages X and Y for the example with K^X = K^Y = 5,110 and N_X (0)/N_Y(0) = 60/40. From Eqs (4) and (5), one obtains the conditions on the interaction rate: N_int ≥ K^X/N_X (0)T^K = 11.6 and N_int ≥ K^Y/N_Y(0)T^K = 17.5, for X- and Y-monolinguals, respectively. Therefore, nothing happens until the value N_int = 11.6 is reached (it should be noted that in Figure 3, N_int assumes only integer values), and the two populations speaking languages X and Y remain isolated and do not generate any bilingual community. At N_int ≥ 11.6, Y-monolinguals learn language X and become bilingual. However, in order to remain as such, they have to maintain both languages. According to Eqs (6) and (7), the condition for a bilingual to maintain language X is N_int > M/N_X (0)T^M = 10, whereas for maintaining language Y, the interaction frequency has to satisfy the condition N_int > M/N_Y(0)T^M = 15. Thus, in the interval 11.6 ≤ N_int ≤ 15, bilinguals who appeared in the system during the time evolution will turn into X-monolinguals so that there are only X-monolinguals in the final state of the system. Instead, for N_int > 15, the bilinguals can maintain both languages, and the final population consists of X-monolinguals and bilinguals. Thus, depending on the value of the interaction frequency, one can observe three regimes (see the dashed lines in Figure 3): 1) coexistence of the two monolingual populations (with N_X(t) = N_X (0) and N_Y(t) = N_Y(0)); 2) only the majority language surviving; and 3) coexistence of monolingual speakers of majority language and bilinguals whose first language is the minority language.

FIGURE 3

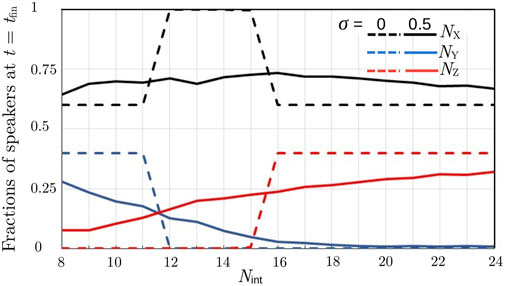
FIGURE 3. (Symmetrical case). Comparison of the final speakers’ compositions versus N_int for homogeneous (σ = 0) and heterogeneous (σ = 0.5) populations; N_X (0)/N_Y(0) = 60/40.

Not taking the memory effects into account, i.e., assuming a time unit much larger than the time scales T^K and T^M, the homogeneous version of the proposed model, discussed in the this section, reduces to the Minett–Wang model that is local in time. The Minett–Wang model with neutral volatility has only two stable equilibrium points: one of the two competing languages surviving and the other one disappearing; which of the two languages survives depends on the model parameters. Instead, introducing the time-consuming language learning and retention processes, for a wide range of parameters, both languages can survive due to two opposing mechanisms: 1) not learning the other language (coexistence of the two isolated languages) or 2) frequent language contact between the minority language speakers, who eventually become bilinguals, and monolinguals of the majority language.

3.3 Heterogeneous population

In the example illustrating the time evolution in a homogeneous population—Figures 1A, B—all monolinguals of language Y become bilinguals around time t_X. The population time evolution is characterized by a simple behavior and sharp transitions because agents are identical to each other in their features and they behave in the same way. The only source of randomness in the homogeneous system is related to the random choice of the interacting agents.

In the corresponding example of a heterogeneous population—Figures 1C, D—because in conditions (4)–(5), K^X and K^Y are replaced by $K_i^{\mathrm{X}}$ and $K_i^{\mathrm{Y}}$, respectively, for each individual i, the transition Y → Z takes place at a different time, resulting in a bundle of parallel lines, as shown in Figure 1C, instead of the overlapping ones, as in (A).

As a consequence, the step-like curves describing the transitions N_Y → 0 and N_Z → 0.4 are replaced by smoother sigmoids. Depending on the value of σ, it can also happen that not all monolinguals of language Y become bilingual at some time t ≤ T^K, whereas some X-monolinguals may do so. Similar considerations are valid for the attrition. In fact, in Figure 1C, one can notice that there is a line $m_i^{[1]}(t)$ which has a slope much larger than that of the other lines, and a line $m_i^{[2]}(t)$ with slope equal to zero. These lines correspond to a bilingual that used to be an X-monolingual and not Y-monolingual as the other bilinguals in this figure.

Such diversity in the behavior of individuals induces significant differences in the dynamics and final competition outcome between the homogeneous and heterogeneous systems. To understand how this happens, let us have a look at the time evolution of the speakers’ fractions N_X, N_Y, and N_Z on a longer time scale, depicted in Figure 4, for a heterogeneous population with σ = 0.5, initial ratio N_X (0)/N_Y(0) = 60/40, K^X = K^Y = 5,110, and three different values of N_int corresponding to low (N_int = 8), medium (N_int = 16), and high (N_int = 24) daily interaction rates.

FIGURE 4

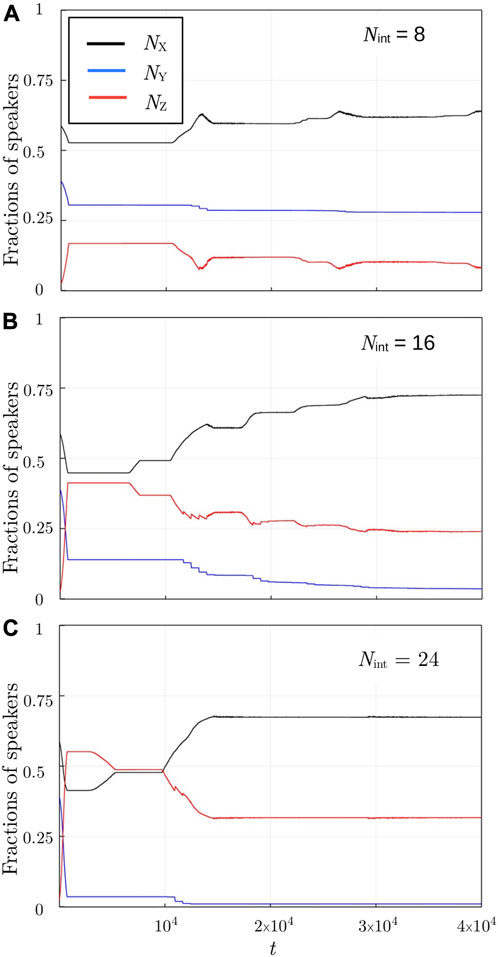
FIGURE 4. (Symmetrical case, heterogeneous population). Time evolution of speakers’ fractions evolving from N_X (0)/N_Y(0) = 60/40 for different daily interaction rates: (A) N_int = 8, (B) N_int = 16, (C) N_int = 24.

In the example of the homogeneous system (Figures 1A, B), only the speakers of minority language Y contributed to the formation of the bilingual community. Instead, in the heterogeneous system, as shown already in Figure 1C, the speakers of majority language X also contribute (see the initial decrease in N_X in all panels of Figure 4), but their contribution is smaller than that of Y-monolinguals. It should be noted that the larger the interaction rate, the larger the contribution of Y-monolinguals (compare the three panels in Figure 4). In the following, the formed bilingual community decreases in time due to the attrition process, leading to a corresponding growth of N_X. The decrease in N_Z and the corresponding increase in N_X become larger for higher values of N_int.

The appearance of a maximum in the bilingual population size is also observed in the Minett–Wang model (Minett and Wang, 2008; Heinsalu et al., 2014), in which, however, finally only one of the languages survives, as mentioned previously.

Before proceeding with the discussion, we analyze the presence of the small zigzagged segments in the time evolution curves shown in Figure 4. They are related to attrition processes taking place at times close to each other due to diversity and initial conditions. We verified that they tend to disappear for t → ∞ and their amplitudes decrease with the system size, as N → ∞. We also checked that they do not significantly influence the final results.

Figures 4A, B show that in a heterogeneous system, it is possible for the two monolingual and bilingual populations to coexist in the final state. The same becomes evident from the phase portraits in Figures 2C, D and from the curves shown in Figure 3 for the heterogeneous system. Although in Figure 3, the dashed curves for the homogeneous system and the solid ones for the heterogeneous system might seem to be qualitatively similar, the fraction of Y-monolinguals decreases and the fraction of bilinguals increases with N_int, and the fraction of X-monolinguals passes through a maximum, and even the phase portraits for heterogeneous and homogeneous populations in Figure 2 might seem to be not so different, the systems are actually fundamentally different. That is, it appears that adding heterogeneity to the population can, for a wide range of parameters, lead to the coexistence of the three linguistic groups, which is not possible in a corresponding homogeneous system. Therefore, we conclude that diversity in linguistic abilities is one of the key factors leading to the possibility of the coexistence of all linguistic groups in a three-state system, and this is the most important difference between the homogeneous and heterogeneous systems.

The reason behind the smoothing of the curves shown in Figure 3 when adding heterogeneity in the population is similar to why the step-like transitions shown in Figures 1B are replaced by smoother curves shown in Figures 1D. That is, the replacement of K^X, K^Y, and T^M by $K_i^{\mathrm{X}}$, $K_i^{\mathrm{Y}}$, and $T_i^{\mathrm{M}}$ consequently satisfies conditions (4)–(5) and (6)–(7) for each individual i at a different value of N_int, instead of a global fixed N_int value, as in the case of a homogeneous population.

In order to evaluate how the degree of heterogeneity, expressed as the relative standard deviation σ, influences the results, we ran simulations for the same system with N_X (0)/N_Y(0) = 60/40 and K^X = K^Y = 5,110 studied previously, varying σ between 0 and 0.5. The results are depicted in Figure 5 for three different values of N_int. Furthermore, the figure shows that adding a certain level of heterogeneity to the system can result in a situation where, in the final state, all three linguistic groups are present in the system: see the lowest group of lines appearing as σ increases. For fixed parameter values and initial composition of the total population, the value of σ leading to such a final state increases slightly when N_int is increased. Furthermore, the diversity of individuals increases the competition advantage of the majority language, with respect to the homogeneous system, for all values of N_int (c.f. also Figure 3), and the effect of varying σ is the largest at intermediate values of N_int.

FIGURE 5

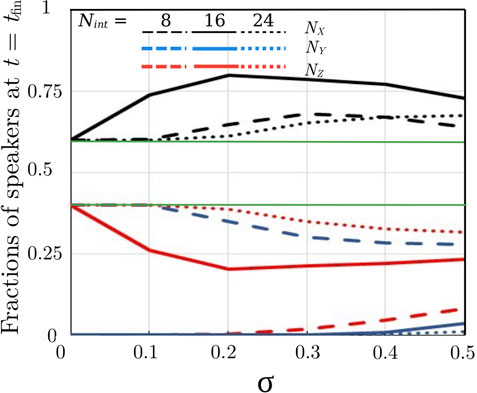
FIGURE 5. (Symmetrical case). Final population composition versus σ for three values of N_int; N_X (0)/N_Y(0) = 60/40. The thin green horizontal lines are a guide to the eye corresponding to the case σ = 0.

From the discussion in Section 3.2, it became clear that the initial conditions play a relevant role in determining the final outcome of the language competition in the homogeneous system. This is also true in the case of heterogeneous populations, as observed from Figures 2C, D and from Figure 6. In the case of equal initial population sizes, N_X (0) = N_Y(0) = 0.5, equal fractions of X- and Y-monolinguals become bilingual. If the interaction frequency is low, e.g., N_int = 8, at equilibrium, relatively large X- and Y-monolingual populations coexist with a small bilingual community. The size of the formed bilingual population increases as the interaction frequency N_int increases; Figure 6 shows the results for N_X (0)/N_Y(0) = 50/50 for three different values of N_int. If the ratio N_X (0)/N_Y(0) is increased, i.e., X becomes the majority language and Y becomes the minority language, the final population composition tends to be more and more dominated by majority language X, as shown in Figure 6. For N_X (0)/N_Y(0) ≳ 80/20, minority language Y becomes extinct, unless the interaction frequency is very low (N_int = 8). In the low interaction limit, the two language populations remain practically isolated from one another and can, in this way, coexist.

FIGURE 6

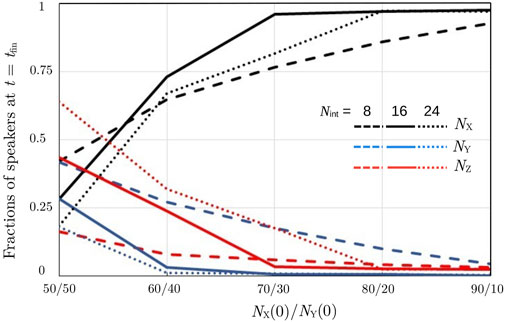
FIGURE 6. (Symmetrical case, heterogeneous population). Final speakers’ compositions as a function of N_X (0)/N_Y(0) for different values of N_int.

3.4 Asymmetrical learning difficulty

So far, we mostly concentrated on the symmetrical case K^X = K^Y ≡ K. Next, we examine in detail the asymmetrical case when K^X ≠ K^Y, i.e., the two competing languages have different degrees of learning difficulty.

From conditions (8)–(9) for the homogeneous population, it is clear that the asymmetry between the parameters K^X and K^Y induces asymmetry also in the critical fractions $N_X^{*}$, $N_Y^{*}$, e.g., for K^X > K^Y, also $N_X^{*}>N_Y^{*}$ (c.f. Figures 2A, B). Therefore, the asymmetry in the language learning difficulty implies that in order to preserve a monolingual community of the language that is more difficult to learn and to induce, at the same time, the transition of the other (minority) language speakers into bilinguals, its minimal initial population fraction has to be larger with respect to the symmetrical case. Similar trends are also present for the heterogeneous systems (c.f. Figures 2C, D). In practice, this means that the more difficult a language is for the learners, the harder it is to integrate the foreign language community members, e.g., immigrants, and the smaller should their proportion in the population be, or/and some measures should be taken to favor the learning of the local language in order to avoid the formation of linguistically isolated communities.

Figure 7 presents the results for a heterogeneous system characterized by the parameter values summarized in Section 3.1 and with N_X (0) = N_Y(0) = 0.5. In this figure, the value of K^X is increased from K^X = K^Y (corresponding to the symmetrical case) up to K^X = 6K^Y in order to observe how the asymmetry in the language learning difficulty influences the language competition outcome. As observed already in Figure 6, for N_X (0) = N_Y(0) and K^X = K^Y, in the final state, N_X = N_Y and the fraction of bilinguals increases with increasing values of N_int. Now, when K^X > K^Y (see Figure 7), the final fractions of X-monolinguals and bilinguals are decreased with respect to the symmetrical case, while N_Y(t_fin) is increased; the larger the N_int is, the larger the influence of asymmetry. However, increasing the asymmetry between the language learning difficulties beyond K^X/K^Y ≈ 3 does not substantially influence the results. For K^X/K^Y = 3, in order to become bilingual within the time interval T^K, a speaker of language Y should practice language X, on average, 21 times per day. Comparing this with the number of average daily interactions (N_int ∈ [8, 24]), it is obvious that the task is very hard for any agent. Therefore, the monolinguals of language Y will remain monolinguals of their mother tongue and N_Y(t_fin) ≈ N_Y(0) = 0.5 for all studied values of N_int. Instead, the monolinguals of language X will become bilingual, the final fraction of bilinguals being larger for larger N_int values. In fact, for N_int = 24, almost all monolinguals of language X will turn into bilinguals, leaving only a very small fraction of X-monolinguals in the system.

FIGURE 7

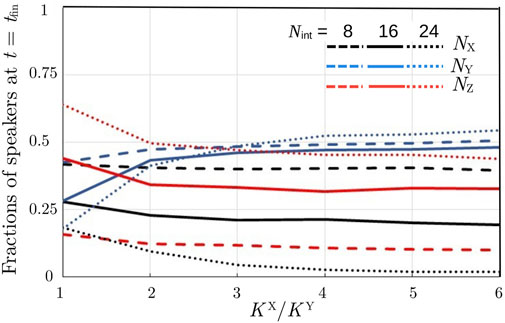
FIGURE 7. (Heterogeneous system). Final population composition versus K^X/K^Y (K^Y = 5110) for three values of N_int; N_X(0)/N_Y(0) = 50/50.

Figure 8 illustrates the case where the initial populations have different sizes and set N_X (0)/N_Y(0) = 60/40. However, we now vary the value of K^X so that the ratio K^X/K^Y goes from 1/7 to 4 (i.e., we go from the case where minority language Y is seven times more difficult to learn for monolinguals of language X than majority language X for monolinguals of Y, to the symmetrical case corresponding to K^X/K^Y = 1, up to the case where majority language X is three times more difficult to learn for monolinguals of Y than minority language Y for monolinguals of X). Figure 8 shows that for all studied values of N_int, an increase in K^X/K^Y, i.e., the learning difficulty of language X, leads to a decrease in N_X, as expected, and an increase in N_Y and N_Z. It should be noted that while in the case N_X (0)/N_Y(0) = 50/50, an increase of K^X/K^Y leads to a decrease in bilinguals (see Figure 7), in the case N_X (0)/N_Y(0) = 60/40, the fraction of bilinguals, instead, increases.

FIGURE 8

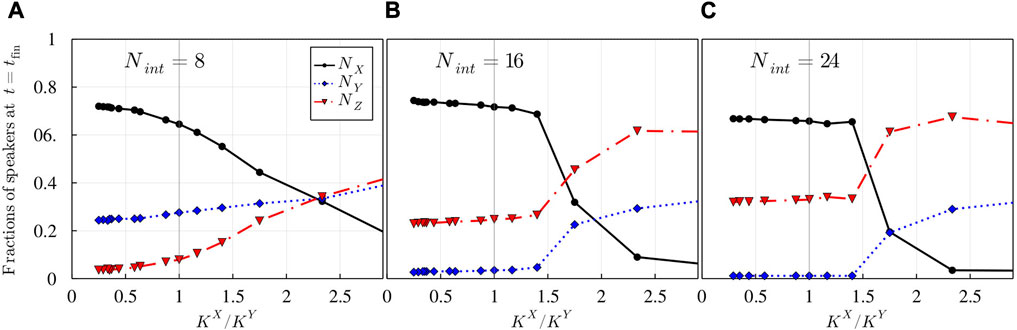
FIGURE 8. (Heterogeneous system). Final population composition versus K^X/K^Y (K^Y = 5110) for different values of N_int; N_X(0)/N_Y(0) = 60/40.

4 Conclusion

In this paper, we developed an agent-based three-state language competition model that incorporates elements mimicking language learning and retention and the underlying memory processes.

We showed that upon including memory in a Minett–Wang-type model with a population of speakers having homogeneous linguistic skills, the final outcome of the language competition can be 1) the extinction of one of the competing languages; 2) the coexistence of two isolated language communities; and 3) a state where the minority language survives due to the bilingual speakers. Which of the three possible scenarios is realized depends on the initial population composition, the parameters that determine learning/attrition (among which is the asymmetry between the language learning difficulties), and the interaction frequency between individuals.

The results of our study suggest that while language prestige is certainly crucial for language shift and in determining the outcome of language competition, memory effects may also play a critical role, and their relative importance versus prestige may depend on the specific features of the system under consideration.

Another relevant issue addressed in the present work concerns the impact of heterogeneity on language dynamics models. We showed that the outcome of language competition depends, in addition to other parameters, on the level of population diversity in terms of language learning and retention skills. In fact, adding heterogeneity to the model significantly changes the time evolution of population fractions and the final population composition. Diversity also allows us to observe, differently from the corresponding homogeneous system, a final equilibrium state where all three linguistic groups—the two monolingual and the bilingual groups—are present. Therefore, we conclude that, in addition to the learning and retention processes, the impact of heterogeneity on language dynamics deserves a broader investigation.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

SS: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, and writing—original draft and review and editing. JK-L: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, and writing—original draft and review and editing. MP: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, and writing—original draft and review and editing. EH: conceptualization, funding acquisition, visualization, investigation, methodology, project administration, supervision, and writing—original draft and review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. The authors acknowledge support from the Estonian Research Council through Grant PRG1059.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

SS, MP and EH declared that they were editorial board members of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abrams, D. M., and Strogatz, S. H. (2003). Modelling the dynamics of language death. Nature 424, 900. doi:10.1038/424900a

PubMed Abstract | CrossRef Full Text | Google Scholar

Abutalebi, J., and Green, D. (2007). Bilingual language production: the neurocognition of language representation and control. J. neurolinguistics 20, 242–275. doi:10.1016/j.jneuroling.2006.10.003

CrossRef Full Text | Google Scholar

Austin, P. K. (2008). 1000 languages: The worldwide history of living and lost tongues. London: Thames and Hudson Ltd.

Google Scholar

Baggs, I., and Freedman, H. (1990). A mathematical model for the dynamics of interactions between a unilingual and a bilingual population: persistence versus extinction. J. Math. Sociol. 16, 51–75. doi:10.1080/0022250x.1990.9990078

CrossRef Full Text | Google Scholar

Baggs, I., Freedman, H., and Aiello, W. (1990). “Equilibrium characteristics in models of unilingual-bilingual population interactions,” in Ocean waves mechanics, computational fluid dynamics, and mathematical modelling: Proceedings of the 11th international annual conference of the Canadian applied mathematics society. Editor M. Rahman (Southampton: Computational Mechanics Publications Ltd), 879.

Google Scholar

Baggs, I., and Freedman, H. (1993). Can the speakers of a dominated language survive as unilinguals — A mathematical-model of bilingualism. Math. Comput. Model. 18, 9–18. doi:10.1016/0895-7177(93)90122-f

CrossRef Full Text | Google Scholar

Baron, J. W., Peralta, A. F., Galla, T., and Toral, R. (2022). Analytical and numerical treatment of continuous ageing in the voter model. Entropy 24, 1331. doi:10.3390/e24101331

PubMed Abstract | CrossRef Full Text | Google Scholar

Baronchelli, A. (2016). A gentle introduction to the minimal naming game. Comput. Constr. Gramm. Constr. Change 30, 171–192. doi:10.1075/bjl.30.08bar

CrossRef Full Text | Google Scholar

Bouchaud, J.-P. (2009). The (unfortunate) complexity of the economy. Phys. World 22, 28–32. doi:10.1088/2058-7058/22/04/39

CrossRef Full Text | Google Scholar

Castellano, C., Fortunato, S., and Loreto, V. (2009). Statistical physics of social dynamics. Rev. Mod. Phys. 81, 591–646. doi:10.1103/RevModPhys.81.591

CrossRef Full Text | Google Scholar

Dall’Asta, L., and Castellano, C. (2007). Effective surface-tension in the noise-reduced voter model. Europhys. Lett. (EPL) 77, 60005. doi:10.1209/0295-5075/77/60005

CrossRef Full Text | Google Scholar

De Silva, K., Basheer, A., Antwi-Fordjour, K., Beauregard, M. A., Chand, V., and Parshad, R. (2021). The “higher” status language does not always win: the fall of English in India and the rise of Hindi. Adv. Complex Syst. 23, 2050021. doi:10.1142/s0219525920500216

CrossRef Full Text | Google Scholar

Del Valle, S., Hyman, J. M., Hethcote, H. W., and Eubank, S. G. (2007). Mixing patterns between age groups in social networks. Soc. Netw. 29, 539–554. doi:10.1016/j.socnet.2007.04.005

CrossRef Full Text | Google Scholar

Ellis, R., Ellis, P., and Ellis, R. (1994). The study of second language acquisition. Oxford, UK: Oxford University Press.

Google Scholar

Griffiths, C., and Soruç, A. (2020). Individual differences in language learning: A complex systems theory perspective. Springer International Publishing.

Google Scholar

Heinsalu, E., Patriarca, M., and Léonard, J. L. (2014). The role of bilinguals in language competition. Adv. Complex Syst. 17, 1450003. doi:10.1142/S0219525914500039

CrossRef Full Text | Google Scholar

Iriberri, N., and Uriarte, J.-R. (2012). Minority language and the stability of bilingual equilibria. Ration. Soc. 24, 442–462. doi:10.1177/1043463112453556

CrossRef Full Text | Google Scholar

Jackson, G. M., Swainson, R., Cunnington, R., and Jackson, S. R. (2001). Erp correlates of executive control during repeated language switching. Biling. Lang. Cognition 4, 169–178. doi:10.1017/S1366728901000268

CrossRef Full Text | Google Scholar

Lafuerza, L., and Toral, R. (2013). On the effect of heterogeneity in stochastic interacting-particle systems. Sci. Rep. 3, 1189. doi:10.1038/srep01189

PubMed Abstract | CrossRef Full Text | Google Scholar

Liivand, J. K. (2018). Memory effects in language acquisition and attrition processes. Master’s thesis. Tartu: University of Tartu.

Google Scholar

Marchetti, G., Patriarca, M., and Heinsalu, E. (2020a). A Bayesian approach to the naming game model. Front. Phys. 8, 10. doi:10.3389/fphy.2020.00010

CrossRef Full Text | Google Scholar

Marchetti, G., Patriarca, M., and Heinsalu, E. (2020b). A bird’s-eye view of naming game dynamics: from trait competition to Bayesian inference. Chaos (Woodbury, N.Y.) 30, 063119. doi:10.1063/5.0009569

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchetti, G., Patriarca, M., and Heinsalu, E. (2021). The role of bilinguals in the Bayesian naming game. Phys. D. Nonlinear Phenom. 428, 133062. doi:10.1016/j.physd.2021.133062

CrossRef Full Text | Google Scholar

Meuter, R. F., and Allport, A. (1999). Bilingual language switching in naming: Asymmetrical costs of language selection. J. Mem. Lang. 40, 25–40. doi:10.1006/jmla.1998.2602

CrossRef Full Text | Google Scholar

Mickan, A., McQueen, J. M., and Lemhöfer, K. (2020). Between-language competition as a driving force in foreign language attrition. Cognition 198, 104218. doi:10.1016/j.cognition.2020.104218

PubMed Abstract | CrossRef Full Text | Google Scholar

Minett, J. W., and Wang, W. S.-Y. (2008). Modelling endangered languages: the effects of bilingualism and social structure. Lingua 118, 19–45. doi:10.1016/j.lingua.2007.04.001

CrossRef Full Text | Google Scholar

Moritz-Gasser, S., and Duffau, H. (2009). Cognitive processes and neural basis of language switching: Proposal of a new model. Neuroreport 20, 1577–1580. doi:10.1097/wnr.0b013e328333907e

PubMed Abstract | CrossRef Full Text | Google Scholar

Moseley, C. (2010). Atlas of the world’s languages in danger. Paris: UNESCO Publishing.

Google Scholar

Odgen, C. K., and Richards, I. A. (1923). The Meaning of Meaning. A study of the influence of thought and of the science of symbolism. New York: Harcourt, Brace and World, Inc.

Google Scholar

Patriarca, M., Heinsalu, E., and Leonard, J. L. (2020). “Languages in space and time: models and methods from complex systems theory,” in Physics of society: Econophysics and sociophysics (Cambridge University Press). doi:10.1017/9781108480659

CrossRef Full Text | Google Scholar

Schmid, M., and Köpke, B. (2019). The Oxford handbook of language attrition. Oxford Handbooks: OUP Oxford.

Google Scholar

Vazquez, F., Castelló, X., and San Miguel, M. (2010). Agent based models of language competition: macroscopic descriptions and order–disorder transitions. J. Stat. Mech. Theory Exp. 2010, P04007. doi:10.1088/1742-5468/2010/04/p04007

CrossRef Full Text | Google Scholar

Ya-ping, Q., Ya, L., Gui-hong, B., Kai-feng, Z., and Chao, W. (2015). “Complex agent network model for the competition among three languages,” in The 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23-25 May 2015 (IEEE), 5910–5917. doi:10.1109/CCDC.2015.7161868

CrossRef Full Text | Google Scholar

Zhang, Y., Ocampo-Espindola, J. L., Kiss, I. Z., and Motter, A. E. (2021). Random heterogeneity outperforms design in network synchronization. Proc. Natl. Acad. Sci. U. S. A. 118, e2024299118. doi:10.1073/pnas.2024299118

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhaoyang, R., Sliwinski, M. J., Martire, L. M., and Smyth, J. M. (2018). Age differences in adults’ daily social interactions: an ecological momentary assessment study. Psychol. Aging 33, 607–618. doi:10.1037/pag0000242

PubMed Abstract | CrossRef Full Text | Google Scholar