Projecting future migration with Bayesian hierarchical gravity models of migration: an application to Africa

In this paper, I present and discuss a novel approach to parameterize a gravity model of migration using Bayesian hierarchical models with random intercepts that are free to vary by country of origin, destination, and directed origin-destination country pairs. I then utilize this model to project transboundary migration flows between African countries to the horizon 2050. To do so, I use data on projected future crop yields and water availability from the ISIMIP2b scenarios in combination with projections on future economic and demographic trends from the Shared Socio-Economic Pathways (SSPs). The results indicate that over the period 2010–2050 between 8 to 17 millions people are projected to migrate internationally on the African continent. Yet, only a small portion of these migrants will be induced to move because of climate change. To the contrary, comparisons between SSPs scenarios suggests that economic development will have a far larger impact on projected level of international migration on the continent than climate change.

1 Introduction

In light of the expected global warming over the course of the 21th century, it is becoming urgent to model and, crucially, project future trans-boundary migration in order to understand how climate change will impact the network of internal migration over the coming decades and support policy development. Of specific interest is to model these flows for sub-Saharan Africa, an area of the world, which has historically received less scholarly attention when it comes to migration flows between countries on the continent. Unlike migration from the Global South to the North which have drawn most of the interest from the scholarly literature (Cattaneo and Peri, 2016; Cai et al., 2016; Missirian and Schlenker, 2017; Hoffmann et al., 2020; Cottier and Salehyan, 2021; Schutte et al., 2021; Rikani and Schewe, 2023; Rikani et al., 2023), international migration across the global south has indeed been historically understudied. Yet, migration between developing countries represents an important component of international migration flows. Demographic projections suggest that the population of the African continent will double by 2100 (KC and Lutz, 2017). It is thus important to examine how migration is susceptible to develop in the future over the Africa continent in light of the expected future demographic change.

In this article, I present and discuss a novel approach to parameterize a gravity model of migration using a Bayesian hierarchical specification (for a similar approach but with a different specification, see Xiao et al., 2022). I then leverage this model to incrementally project transboundary migration flows over the African continent to 2050 at 5-year intervals under different combinations of climate change and socio-economic scenarios. This approach was used to generate projections of future international migration flows between African countries, that were released as part of the African Shifts report under the African Climate Mobility Initiative (see Amakrane et al., 2023).

To calibrate the projection model, I use 5-year interval bilateral migration data provided by Abel and Cohen (2019) computed on the basis of UN migration stock data for the period extending from 1990 to 2010 (United Nations, 2020). The Bayesian hierarchical specification used for the calibration stage relies on the classical gravity model of migration (Beine and Parsons, 2015; Bergstrand, 1985). I model migration as a function of population, GDP per capita at origin, the ratio between GDP per capita at origin and destination, the size of the diaspora at destination, the intensity of political violence at origin and the distance between origin and destination countries, as well as two climate predictors: water availability and crop yields. In addition, the preferred specification—used for projections of future migration flows—incorporates origin, destination, and origin-destination country-pairs random intercepts to model unobserved heterogeneity in migration between countries of origin, destination and migration corridors. Because hierarchical models leverage partial pooling, such an approach makes it possible to obtain finer and more reliable projections of future migration (Gelman et al., 2013). I compare the posterior predictive performance of the preferred model using out-of-sample validations against two simpler versions of the model either omitting the hierarchical structure of the data or incorporating only the random intercepts but omitting the predictors, as well as a more flexible specification letting the climate impacts on migration vary by country of origin (Gelman et al., 2013; Vehtari et al., 2017). The results suggests that the preferred model, which include the predictors and random intercepts, as well as the more flexible specification with random slopes for the climatic predictors, demonstrate a substantial improvement in predictive accuracy, though these two models still struggle to capture temporal variability within migration corridors, reflecting existing concerns about the ability of gravity models to accurately model migration dynamics (Beyer et al., 2022).

Using the parameter estimates of the preferred model, I then incrementally project future migration over the period 2010/15 to 2045/2050 at five year intervals. To do so, I draw on the Shared Socio-Economic Pathways (SSPs) projections for population and GDP (Riahi et al., 2017; KC and Lutz, 2017; Cuaresma, 2017), updating at each time step population figures, as well as estimates of foreign-born populations disaggregated by origin based on the projected number of net migrants both at the country and migration corridor levels. Future trends for crop yields and water availability that drive the model projections are obtained from the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2b) scenarios (Lange and Büchner, 2017).

The results of these projections suggest that by 2050 between 8 (lower bound) to 17 (upper bound) millions will have cumulatively moved internationally within the African continent. Yet, among these, no more than a maximum 1.2 millions are projected to leave because of climate change. In other words, at best <5% of the projected cumulative number of migrants might be associated with the impact of climate change. As opposed to the dominant discourse on the link between poverty and migration, the results indicate that higher levels of economic prosperity is set to increase future migration on the African continent. Thus, the model indicates that for the foreseeable future economic development will remain a more important driver of migration compared to climate change. These results are in line with the findings from the calibration stage, where crop yields at origin are positively associated with out-migration. Arguably, this conclusion is suggestive of ongoing financial barriers to international migration on the African continent and is line with Dustmann and Okatenko (2014), who demonstrate that for low-income countries economic development is likely to cause an increase in migration by enabling more people to overcome barriers to international migration.

In the ensuing text, I first introduce the calibration model in Section 2. Section 3 then presents the data used for the calibration stage. Section 4 discusses the results of the calibration model. The forecasting framework and the projections of international migration are introduced in Section 5. Section 6 examines the performance of the calibration model using posterior predictive checks and out-of-sample validations of the model predictive accuracy. Section 7 concludes.

2 Calibration model

To project future migrations flows across the African continent, reasonable estimates of the parameters reflecting the influence of the migration drivers are necessary, as well as measures of their uncertainty. To do so, I calibrate the model against historical data for the period 1990/5–2005/10 at 5-year intervals. The calibration model is inspired by earlier work by Jones (2020) on modeling international migration out of Mexico and Central America (see also Lustgarten, 2020). In his work, Jones (2020) models international migration flows as a function of population, economic conditions, corruption, political violence and environmental conditions at origin. ¹

While I generally take inspiration from this earlier model reflecting the fact that it was developed as a follow-up to the Groundswell project to which the African Shifts report is also related (Rigaud et al., 2018; Amakrane et al., 2023), I depart from this earlier work in three ways. First, I use a Bayesian hierarchical specification to model unobserved heterogeneity in migration rates between origin, destination and origin-destination country pairs (Gelman et al., 2013). Hierarchical statistical models are useful when the unit of analysis is itself nested within larger data structures (e.g. countries, administrative units), which can be expected to influence the dependent variable. In other words, I account for unobserved heterogeneities from three sources: specific to the country of origin, specific to the country of destination, in addition to heterogeneity that is peculiar to each directed individual migration corridor (origin → destination). There is a potential long list of factors to which these sources of heterogeneities might be tied with and which may assist or hinder international migration. Examples of these sources of heterogeneities are cultural or ethnic ties between countries, historical legacies (e.g. colonization), as well as visa policies, which might make it easier for some nationalities to enter a destination country and integrate in the labor market at destination. Likewise, cultural affinities with migration in certain ethnic groups, the form of political regimes and educational opportunities offered at origin or destination may also cause differing rates of migration between different pairs of origin-destination countries.

Hierarchical models are particularly well suited to account for unobserved heterogeneities as they leverage partial pooling, in effect weighting the information contained in each hierarchical grouping with information from the entire sample, shrinking the parameter toward the latter.² Explicitly modeling these hierarchies generates more accurate country-level projections by accounting for the fact that some countries send/receive an unusually large or small amount of migrants given the model and predictors, and likewise for individual migration corridors. At the same time, partial pooling acts as a guard against bias in parameters estimated on a limited number of noisy data points (Gelman et al., 2013, p. 96). This latter aspect is important in this application as each directed pair of origin-destination countries contains only four observation at 5-year intervals, the means of each panel may thus easily be influenced by an outlier.³

Second, instead of assuming a Poisson distribution on the dependent variable conditional on the estimated model, I use a log-linear specification. This is approach is motivated by the fact that a Poisson distribution assumes that the variance is equal to the conditional mean: Var(λ) = E(λ|X) (Greene, 2012, p. 888). Assuming a log-linear regression framework is more flexible in this context because the variance parameter is estimated separately.⁴ Third, I specifically model the effects of diasporas in countries of destination, as well as cross-sectional temporal patterns. Accounting for diasporas at destination is important as the size of the foreign-born population is known to strongly influence future migration flows (Beine et al., 2011). Similarly, “common shocks” affecting multiple countries in a given time period, such as the 2015 Refugee Crisis in Europe, may correlate with some of the predictors in the estimated model and thereby should be controlled for.

The calibration model, used in this paper, is inspired from the well-known gravity model of migration, which sees—in its most simplistic form—migration as proportional to the product of population at origin and destination and the inverse of the distance between the two, or $Mig{r}_{i,j}=G\frac{Po{p}_i^{{\beta }_1}\times Po{p}_j^{{\beta }_2}}{Dis{t}_{i,j}^{{\beta }_3}}$ (Beine and Parsons, 2015; Bergstrand, 1985 see also Ravenstein, 1889). As is well-known, this model can be linearized and estimated by taking logs on both sides of the equation, ln(Migr_i,j) = α + β₁ × ln(Pop_i) + β₂ × ln(Pop_j) − β₃ × ln(Dist_i,j). The Bayesian hierarchical specification implemented in this paper is equivalent to modeling separate intercepts for the set of origin countries, destination and directed pairs of origin-destination countries. This aspect, as well as a more flexible approach that lets the impact of predictors vary by grouping structure, is important as gravity models of migration have been criticized in the literature due to their rigid framework that ignores significant variations in observed migration between sources and destination countries and thereby results in problematic inferences (Beyer et al., 2022). In formal terms, I thus seek to estimate the following log-linearized gravity equation with a Bayesian hierarchical linear regression:

$\begin{array}{l}\begin{array}{l}{y}_{i,j,t}~\mathcal{N}({\mu }_{i,j,t}+{\varphi }_i+{\gamma }_j+{\theta }_{i\to j},\sigma )\\ {\mu }_{i,j,t}=\alpha +W\beta +X\delta +1(t)\zeta \\ {\varphi }_i~\mathcal{N}(0,{\tau }_{orig})\\ {\gamma }_i~\mathcal{N}(0,{\tau }_{dest})\\ {\theta }_{i\to j}~\mathcal{N}(0,{\tau }_{orig\to dest})\end{array}\end{array}$

In the context of the present application, which seeks to apply this model to international flows between African countries, the indices i and j represent the countries of origin, and destination, respectively, while t represents time periods of five year interval. y denotes the dependent variable, ln(migration + 1).⁵ The matrix W denotes the climate variables (crop yields, water availability), while the matrix X refers to the other predictors (population, economic variables, diasporas, distance, and conflict). 1(t) is a matrix of t − 1 times dummies, one for each 5-year period. ϕ, γ and θ are vectors of random intercepts for origin, destination and directed origin-destination pairs, respectively. α, β, δ and ζ are vectors of population-level parameters to be estimated. σ is a variance parameter for the dependent variable.

In addition, the model is parameterized with weakly informative priors on the population fixed effects. Weakly informative priors help constraining the domain of a parameter to a realistic range (i.e. they provide regularization), thereby helping with the convergence of Markov Chain Monte-Carlo (MCMC) chains, without unduly influencing the values of the parameter estimates (Gelman et al., 2008).⁶ For the β, δ and intercept α, I use a t distribution with 3 degree of freedom, instead of a normal distribution. This specification is an apt choice as the tails of the t distribution are thicker and therefore better accommodate unusually large, but still plausible, estimates of the parameters of interest (Ibid.: 1364):

$\begin{array}{l}{\beta }_k~t(0,2.5\times \frac{sd(y)}{sd(w_k)},3)\\ {\delta }_m~t(0,2.5\times \frac{sd(y)}{sd(x_k)},3)\\ \alpha ~t(ȳ,2.5\times sd(y),3)\end{array}$

For the auxiliary variance parameter, sigma, and the scale parameters of the random intercepts, τ_orig, τ_dest, τ_{orig → dest}, I use half-t distributions with scale parameter set to 2.5 and three degrees of freedom:^7,8

$\begin{array}{l}\sigma ,{\tau }_{orig}{\tau }_{dest},{\tau }_{orig\to dest}~t^{+}(0,2.5,3)\end{array}$

3 Calibration data

In this section, I present the sources of data used for the calibration stage. I start by discussing the dependent variable, trans-boundary migration flows at 5-year intervals, before turning to the predictors included in the regression.

3.1 Migration, y

The dependent variable is a bilateral measure of the number of permanent migrants over a 5-year interval between country_i (origin) and country_j (destination) on the African continent. Due to data sparsity in the region, the source are 5-year migration estimates provided by Abel and Cohen (2019).⁹ This dataset is imputed from United Nations foreign-born population tables disaggregated by country of origin and residence (United Nations, 2020). On this basis, the authors provide estimates of 5-year migration flows using different methods to compute flows from stock data on migration. I use here the “stock differences, reverse negative” approach. This choice is motivated by concerns about error propagation in demographic accounting estimation methods (for a discussion of this issue, see Cottier et al., 2022). One particular issue with these migration estimates is that they include a large number of refugees, which by definition are unlikely to have migrated due to the immediate impact of climate change on social systems. I thus subtract the number of refugees from the estimates of migrants for each directed pair of directed origin-destination country dyads using estimates on the number of refugees provided by the United Nations and adjusted for missingness by Marbach (2018a) (see also Marbach, 2018b; UNHCR, 2022). The dependent variable is included in the empirical model after adding unity and taking logs.¹⁰

3.2 Climatic variables, W

I measure climatic variability using two distinct indexes one for water availability, specifically river discharge, and the other for crop yields. The primary motivation for the choice of climatic variables is the need to coherently reflect the modeling of internal migration flows on the African continent undertaken as part of the African Shifts report (Amakrane et al., 2023, see also Rigaud et al., 2018). Both water availability and crop yields can be arguably tied to long-term climatic trends and are crucial to a continent in which agriculture, fishing and animal husbandry remain the primary economic sector.^11,12 The source of the data is the Inter-Sectoral Impact Model Intercomparison Project 2A (ISIMIP2A) WaterGAP2 (Princeton) simulations for river discharge, and GEPIC simulations for crop yields (summed across four types of widely-used staple crops: maize, wheat, soybean and rice) (Lange and Büchner, 2017; Müller Schmied et al., 2016; Arneth et al., 2017). Both of these global gridded dataset are driven by reanalysis models based on historical climatic and socio-economic conditions and are available annually at a resolution of 0°30^′′ or ~55 km at the equator over the period 1971–2010.¹³

In a first step, I average the annual cell-level data over intervals of 5-years (1971..75, 1976..1980, ..., 2006..2010). The gridded values are then aggregated to the country level by taking the mean cell value across a country's territory.¹⁴ After averaging the variable over the country level, I compute an index of climatic variability as follows:

$\begin{array}{l}{D}_x(t)=\frac{x(t)-x(t_0)}{x(t_0)}\end{array}$

With x(t) corresponding to the average over five year on the original variable scale, and x(t₀) corresponding to average for the baseline period (1971–2010).¹⁵ The resulting D_x(t) is a dimensionless scalar, which varies over the interval [−1;+∞], with 0 denoting 5-year averaged climatic conditions identical to the baseline period. The baseline period was set specifically in view of measuring how the climate might change in the future compared to historical conditions.

3.3 Additional predictors, X

In addition to the climatic variability indexes, I add predictor variables for economic, social and political drivers of migration. First, I include a variable for the demographic size of the origin country. The source of the data is the United Nations World Population Prospects (United Nations, 2022). The Population variable is log-transformed before inclusion.

Second, I include two predictors measuring (a) the level of economic development in the sending country and (b) the difference between the level of economic development in the sending and host countries. The first variable, the level of economic development in the origin country, is a measure of the ability of individuals and households to overcome the financial costs of international migration, which are typically substantially higher than local or internal migration (Angelucci, 2015, see also Dustmann and Okatenko, 2014). In a comparatively richer country, resident should thus have a higher capacity to support the cost involved with international migration, than in a poorer country. The second variable proxies the economic attractiveness of the potential destination as a function of the ratio of the level of economic development between the two countries.¹⁶ As implied from classical economic theory on migration (Todaro, 1969), the desire to migrate should be proportional to expected wage differentials between the origin and destination country. Thus, the larger the gap, the stronger the desire to migrate.

Overall, the joint effect of these two variables should give rise to the well-known “migration hump” function, whereby people in low-income countries may have a strong desire to leave, but may be constrained in their ability to do so by the financial costs of migration, while people in high-income countries may face lower financial barriers, but may experience a lower desire to migrate (as a result of limited expected economic gains of migration). Under this hypothesis, migration can be expected to peak in middle-income countries, where the desire to migrate, albeit lower than in poor countries, remains strong, while the relative costs of migration are not overwhelming.¹⁷ The existence of this hump function has been historically formulated in the context of south-north migration flows (Dustmann and Okatenko, 2014). Yet, it is not unreasonable to expect that it may potentially shape the structure of the migration network in Africa. Both variables are measured using GDP per capita data provided by the Penn World Tables 7.0 (Heston et al., 2011) and included in the empirical model after takings logs.

Next, I add a count of the number of foreign-born population originating from country_i and residing in country_j at the start of each 5-year interval period. This Diaspora variable measures the strength of migrant networks between the sending and hosting states. Including such a variable is important as migrants rely on ethnic kins and/or co-nationals to learn about economic opportunities abroad, secure visa via family reunification, bear the costs of migration, as well as obtain information about potential smugglers' networks if traveling irregularly. Diasporas are also important in helping migrants integrating at destination (Beine et al., 2011). Thus, diasporas are generally considered one of the primary engines of migration (Massey et al., 1993). Moreover, from a projection standpoint, accounting for change in the size of a diaspora is crucial if the goal is to generate incremental projections of migration flows over time, such as is the case here. The source of the data is the United Nations foreign-born population tables (United Nations, 2020). As for the other variables, the data is included in the model after adding unity and takings logs.

The model also contains a predictor for the presence of political violence in the origin country. The inclusion of this variable is motivated by the need to adjust the calibration process for any residual displacement processes linked to armed conflicts, which might not have been corrected by the subtraction of refugees flow from migration data (Moore and Shellman, 2006). The source of the data is the UCDP GED dataset v20.1 (Sundberg and Melander, 2013). The variable, conflict intensity, is the log-transformed count of the number of fatalities caused by armed conflicts over a period of 5-year.¹⁸

Finally, the model includes a population-weighted measure of distance between the sending and hosting country as a proxy for migration costs faced by individuals and households. Data on population is provided by the Gridded Population of the World (GPW) v4.11 dataset at a resolution of 0°15^′′ or ~28 km at the equator (Center for International Earth Science Information Network (CIESIN), Columbia University, 2018). Using a population-weighted measure of distance is important as a number of African countries, in particular those located along the Sahel, demonstrate particularly strong variations in population densities, with large sections of these countries only sparsely inhabited (e.g. Algeria, Mali, Niger).¹⁹ In Supplementary Table A.2, I show the results of a specification that includes as well predictors for common language between dyads, common colonizer prior to 1945 and contiguity between two countries, using data provided by CEPII (Conte et al., 2022).

4 Results and discussion

In total, the regression frame includes 8,190 observations spanning 46 African countries over the period 1990–2010 at 5-year intervals.^20,21 The unit of analysis is the country of origin—country of destination—time period. Supplementary Table A.1 provides summary statistics for the regression frame. The parameters of each empirical models are estimated by Markov Chains Monte Carlo (MCMC) using the Stan Modeling Language framework within R brms package environment (Stan Development Team, 2022; Bürkner, 2017). Each model is estimated with four chains of 4,000 iterations each (incl. 2,000 warmup iterations) for a total of 8,000 post-warm up draws.

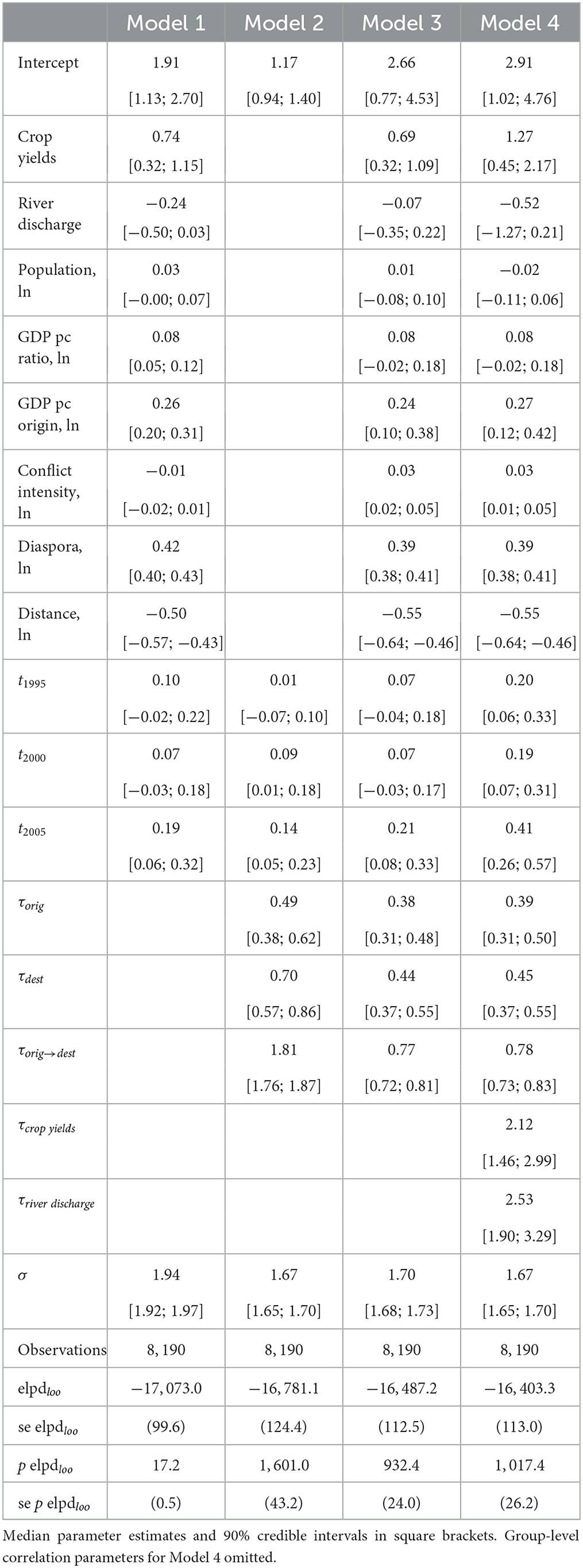
Table 1 presents the results of the Bayesian hierarchical calibration model. Model 1 is a baseline specification including all the population-level predictors, but none of the random intercepts. Model 2 is the reverse specification. It excludes all the population-level predictors, but includes the three sets of random intercepts that capture time-invariant heterogeneities per country of origin, destination and directed origin-destination country pairs. Model 3 includes both population-level predictors and random intercepts. Finally, Model 4 is a more flexible specification, which let the effects of the two climate predictors vary per country of origin.

Table 1

Table 1. Results of the calibration models.

For reasons of scope and model performance, I focus the discussion here on Model 3, the preferred specification and the one used to generate projections of future migration flows.²² In general, the results indicate that the level of crop yields at origin correlate positively with international migration. By contrast, I find little evidence that water availability, as measured by river discharge in the origin country, is associated with migration. At face value, these results thus indicate that, over the period 1990-2010, higher-than-usual crop yields may have correlated with more people leaving their country of residence, and conversely for lower-than-usual crop yields. I note that these findings are consistent with literature arguing that adverse climate shocks may dampen migration, when financial barriers to migration are high (Cattaneo and Peri, 2016; Cottier and Salehyan, 2021, see also Hoffmann et al., 2020). In these circumstances, higher agricultural yields could reasonably increase the income of rural households and ease the financial constraints they face. Thus, these results suggest that adverse climatic conditions caused by climate change could potentially create immobile populations.

Turning to the other predictors included in the calibration model, population during the calibration period does not appear to correlate with out-migration. This result is somewhat unexpected, but is likely related to the fact that there are little clear temporal trends in migration across the set of origin countries, as opposed to a clear increasing linear trend in population.²³ By contrast, the level of economic development is associated with out-migration. In line with the results reported above for crop yields, these results indicate that financial barriers to out-migration may exert a constraint on individuals and households ability to resort to migration. Yet, while the median parameter estimate for the variable measuring the economic attractiveness of migration (i.e. the ratio of economic development between destination and origin) is consistent with theoretical expectation (i.e. positive), the width of the credible interval calls for caution about its interpretation.²⁴

On the other hand, the intensity of armed conflict is positively associated with out-migration, indicating that UNHCR data on refugee flows may be incomplete and do not capture all forms of conflict-induced displacement. Unsurprisingly the variables measuring the size of the diaspora from country_i residing in country_j correlates strongly with international migration, indicating that migrants tend to prefer to travel to countries hosting large populations of co-nationals. As expected, the distance between the sending and the host countries is negatively associated with the size of international migration flows on the African continent.

Finally, the standard deviation estimates for the random intercept parameters suggests that Models 3 and Model 4 capture a significant amount of unobserved heterogeneities, even after accounting for the effects of the population predictors included in the regression. This insight is validated by an out-of-sample examination of the predictive accuracy of the model discussed in Section 6.

5 Projecting future international migration on the African continent

5.1 Projection algorithm

To generate probabilistic projections of future migration flows, I leverage the parameters estimates from the calibration stage to simulate future international migration flows within the African Continent under varying climate and SSPs scenarios up to the horizon 2050. In doing so, I account for both the systematic uncertainty due to imprecise parameter estimates, as well as fundamental stochastic uncertainty that reflect randomness and chance in the data generation process (see King et al., 2000). The strength of this approach lies in enabling researchers and policy-makers to more reliably identify the degree to which different climatic, social and economic trajectories differ from each other.

As a side note, it is important to state here that the objective is not to predict future migration flows per se, rather the goal is to examine the implications of future climate, social and economic scenarios for migration. In doing so, I draw specific attention to differences in projected numbers of migrants between scenarios, instead of focusing on overall migration numbers. Indeed, as de Bruin et al. (2022, p. 2) state “[t]he goal of future scenario assessment is not to gain knowledge on what is likely to happen in the ‘foreseeable' future with a high level of accuracy [...] but rather to trigger deliberations about possible futures and, in turn, to provide a starting point for interventions and adaptive policy options with the long-term perspective in mind.” In that regards, I note that future migration flows are deeply contingent on the migration system and its evolution, as illustrated by recent exogenous shocks on the international migration system caused by the 2008 Great Financial Crisis or recent armed conflicts in West Africa and Eastern Africa. Thus, it is inherently difficult to project even over a limited timescales of the order of a few decades and any projections should be interpreted cautiously.

The approach used to incrementally project future international migration flows under different combinations of climate and socio-economic scenarios can be summarized as follows. Starting from the initial 5-year time period t₀ (2010/2015), I generate new international migration projections by interacting the parameters estimated during the calibration stage, including the random intercepts, with a new set of predictors data, that is composed of both future projections of the drivers (climate, economic and demographic variables), and from assumptions about other predictors (conflict, distance, and temporal effects). Next, I compute net-migration flows and update each country's population, as well as the stock of foreign-born population in each country disaggregated by origin. Using the new sets of estimate I then proceed incrementally one temporal step at a time until reaching the final projection period t_n (2045/50). The process is then repeated for different combinations of climate and socio-economic scenarios. Formally, the projection algorithm is as follows:

For each m in M combinations of [climate, socio-economic] scenarios:

For each time period t (t₀...t_n):

1. Compute matrix M_n×s by linearly combining the calibration matrices of population level parameters [α, β, δ, ζ]_k×s with the projection data matrix ${\left[\tilde{W},\tilde{X};\tilde{1}(t)\right]}_{n\times k}$ and adding the matrix of combined random parameters [ϕ, γ, θ]_n×s, with s, k and n indices for parameters estimates, predictor variables, and directed origin-destination country pairs.

2. Draw matrix $ln({Ỹ}_{n\times s})~\mathcal{N}(M_{n\times s},{\sigma }_{1\times s})$.

3. Use the inverse log operation to obtain Ỹ and round values to the nearest integer.

4. Update projected Diaspora_{i,j,t+1, s} = Diaspora_i,j,t,s + ỹ_j,i,t,s.

5. Update projected $Populatio{n}_{i,t+1,s}=Populatio{n}_{i,t+1,s}+\sum _{j\ne i}^J({ỹ}_{j,i,t,s}-{ỹ}_{i,j,t,s})$.

6. Setting seed number to c(t), permute indices s of matrices of calibration population parameters [α, β, δ, ζ]_k×s and random parameters [_{ϕi, γj, θi → j]n×s}.

I use this algorithm to project future migration from 2010/15 to 2045/50 at intervals of 5-years and for a set of six different combinations of climate and socio-economic scenarios. To speed-up the projection process, I randomly sampled 1,000 sets of parameters draws from the 8,000 sets of parameters estimates obtained in the calibration stage. The same set of 1,000 parameters was used for each scenario.²⁵ The permutation process outlined in step 6 of the algorithm aims at preventing a process whereby projections become increasingly large the farther in time as a result of systematically using the same sets of extreme parameters.²⁶ After each time-step, the entire set of probabilistic projections is stored. In total, for each scenario, I generate 14.39 × 10⁶ individual forecasts distributed over seven time steps.²⁷ Using the percentiles of the predictive distribution, it is then straightforward to generate probabilistic projections of future migration for a desired confidence level.

5.2 Projection data

Data on future climatic trends come from the ISIMIP2b projections. For crop yields, I use the GEPIC experiment, while for river discharge I use the WATERGAP2 experiment.²⁸ These two experiments are driven by the Coupled Model Intercomparison Project (CMIP5) GFDL-ESM2M climate simulations from the NOAA Geophysical Fluid Dynamics Laboratory (Taylor et al., 2012; Lange and Büchner, 2017; Müller Schmied et al., 2016; Arneth et al., 2017). In line with the African Shifts report (Amakrane et al., 2023), I focus on two Representative Concentration Pathways (RCPs): 2.6 and 6.0. The first represents a world in which CO₂ emissions are quickly dropping and global temperature increasing moderately over the course of the 21th century and reaching about 2°C in 2100. By contrast, the second is a more pessimistic scenario that sees CO₂ remaining high for much of the century and temperature increase reaching 3–4°C by the end of the century. In addition, I set a counterfactual scenario, which keeps the climate conditions constant to its average over the period 1990–2010 (i.e. I use the average value of the two climate variables in the calibration dataset).

To project future demographic and economic trends, I draw on the Socio-Economic Pathways (SSPs) and use the IIASA datset (Riahi et al., 2017; KC and Lutz, 2017; Cuaresma, 2017).²⁹ Specifically, I use the SSP1 (“Sustainability”) and SSP3 (“Regional Rivalry”) scenarios. SSP1 is a more optimistic scenario, in which countries experience high levels of economic growth and decreasing rates of fertility, while SSP3 is a more pessimistic scenario, in which economic growth remains low and fertility decreases more slowly. Because the original SSPs demographic projections are generated based on assumptions about how migration might evolve in the future, I use a revised sets of demographic projections, which assume no migration.³⁰ Furthermore, I ensure that economic and demographic projections are in line with the calibration data by rescaling the data such that the SSP projections for GDP and population in the initial period 2010/15 match the observed data for 2010. This is done to prevent projections from being inadvertently influenced by a gap in the initial set of projections compared to the data used for the calibration data.

The size of the foreign-born population (diaspora) is initialized at its 2010 observed values based on the UN Migration stock dataset (United Nations, 2020). In addition, I set the predictor for armed conflict intensity to the average of the entire calibration sample for the period 1990–2010 and set the times dummies to 1 for the 2005 dummy and 0 for the other two temporal dummies.³¹

5.3 Projection results

Future migration are projected under six different combinations of climate scenarios (historical climate held constant, RCP 2.6, and RCP 6.0) and SSPs scenarios (SSP1 and SSP3). I obtain projections of climate-induced migration by subtracting the number of projected migrants in the scenarios that held climatic conditions to the historical average from the migration projections under the RCPs 2.6 and 6.0 scenarios (keeping the SSPs scenarios constant). Figure 1 depicts the total cumulative projected number of international migrants by 2045/50 across the Africa. This 2 × 2 plot is produced by summing across the seven time steps of 5-year intervals. The left-hand side panel A depicts the total cumulative number of international migrants projected by 2045/50 and the right-hand side panel B shows the projected magnitude of climate-related migration. For its part, the top row presents the projections under the more optimistic SSP1 scenario, while the bottom row depicts the same projections under the more pessimistic SSP3 scenario.

Figure 1

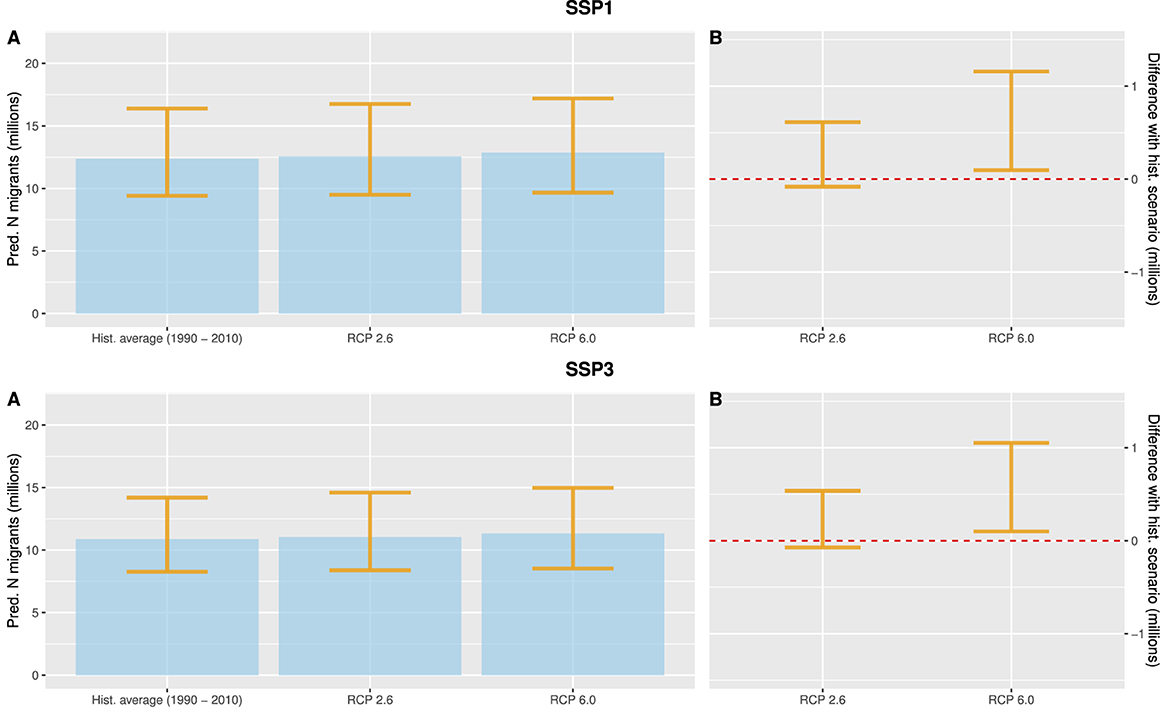
Figure 1. Total cumulative projections of international migration flows for 2045–50. The error bars represent the 90% predictive intervals of the projections. Panels (A) Depict total cumulative projected migration, while Panels (B) depict total cumulative climate-induced migration.

Considering the projections of all the six rounds of projections, the results suggest that between 8.4 million people (lower 90% bound; SSP3 RCP 2.6) and 17.2 million (upper 90% bound; SSP1 RCP 6.0) will have permanently settled in another country on the African continent by 2050. It is worth noting that the SSP1 scenario (top row, Figure 1) systematically projects a significantly higher number of international migrants on the African continent compared to the SSP3 scenarios (bottom row) by about 2 millions. This result, arguably, reflects the link between economic development and migration discussed earlier. As income is projected to increase at a higher pace under the SSP1 scenario, more people are thus able to overcome the financial barriers to international migration on the continent. By contrast, the model projects a lower level of international migration under the more pessimistic SSP3 development scenario.

Turning to the impact of climate change on migration, the differences in projected migration between the three climate scenarios are relatively small and hard to discern as they lay firmly within the margins of errors in the left-hand side of Figure 1A. The right-hand side of Figure 1B thus sheds more light on the projected magnitude of climate-induced migration. These two panels explicitly compare each RCP scenario to the number of international migrants projected under the assumption that future climatic conditions would reflect average conditions over the period 1990–2010. Overall, the results indicate that climate change will likely increase migration, independent of the combination of RCPs and SSPs scenarios. Yet, and unlike in the case of internal migration (Amakrane et al., 2023), the total impact of the climate will remain limited over the period extending to 2050. Indeed, even under the more climate pessimistic, and arguably realistic, RCP 6.0 scenario, the number of additional migrants is projected to increase on the continent by between 100, 000 (lower 90% bound; SSP1 RCP 6.0) and 1, 200, 000 (upper 90% bound; SSP1 RCP 6.0). Taken together, the projections suggest that only about 4% of projected international migrants within the African continent will have been induced to leave as a result of climate change by 2050. By contrast, the more optimistic CO₂ emissions scenario, RCP 2.6 scenario projects a number of additional migrants twice as small, and not fully distinct from zero at the 90% prediction interval. Figure 2 depicts how the projected cumulative number of climate-induced migrants is susceptible to change over time. As revealed by the graph, a slight acceleration in the number of international migrants induced to leave because of climate change can be observed after 2030 in all four scenarios.

Figure 2

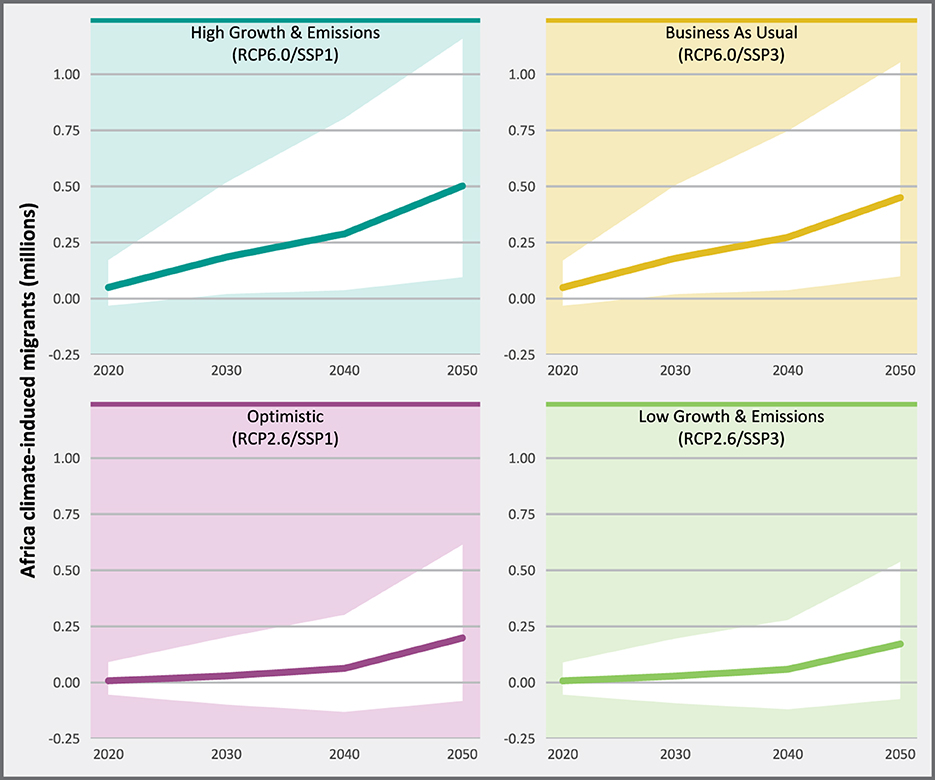
Figure 2. Temporal trends for cumulative projections of international migration flows. The error bars represent the 90% predictive intervals of the projections.

6 Model validation

In general, the MCMC sampling exhibited good convergence for all four sets of calibration models. All the parameters had $\widehat{R}<1.01$ for the reported parameters with large number of Bulk Effective Sample Size (Bulk-ESS) and Tail Effective Sample Size (Tail-ESS). $\widehat{R}$ provides information on the degree to which MCMC chains have mixed and are stationary by evaluating the scale at which the resulting parameter distribution may be reduced if the chains would have run longer (i.e. for more iterations). As MCMC proceeds iteratively, draws are naturally auto-correlated, Bulk-ESS and Tail-ESS measures the number of draws, which can be effectively considered independent (for details see, Gelman et al., 2013). In effects, it is a measure of efficiency of the sampling process. Supplementary Figures A.5–A.8 depict the trace of the MCMC chains for the population parameters of Model 3, Table 1.

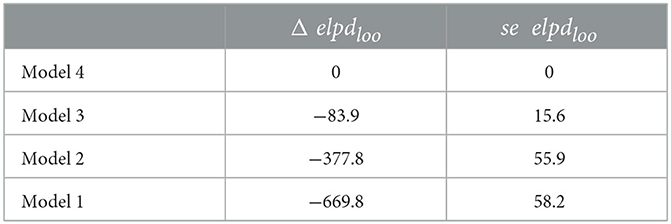
In addition, I examined the out-of-sample performance of the estimated models using the expected log pointwise density (elpd_loo) for a new data point (Gelman et al., 2013; Vehtari et al., 2017). I do so by using the R package loo (Vehtari et al., 2015), which relies on leave-one-out Pareto-smooth importance sampling (PSIS) to approximate leave-one-out cross-validation (Paananen et al., 2021). Table 2 presents the results of a comparisons of each model predictive performance ranked from best to worst. In the first column, I report the difference in model performance summed across all individual observations of the dependent variable, while in the second column I report the standard error of the difference.³² The best performing model is the more flexible specification of Model 4, which includes random slopes on the crop yields and river discharge variables, followed by the preferred model, Model 3. Both of these models perform substantially better than Models 1–2. In effect, Model 3 and Model 4 result in an improvement of the model out-of-sample performance by about 3.4%, respectively 3.8%. In all the four models, the Pareto shape parameters k, that provides information on the reliability of the Pareto-smooth importance sampling (PSIS) approximation, were all below the 0.7 threshold value (for each observation in the calibration dataset). Supplementary Figure A.9 depicts the distribution of the Pareto k values for Model 3.

Table 2

Table 2. Out-of-sample evaluation of model predictive accuracy.

Furthermore, I also conducted a number of posterior predictive checks for Model 3. Unsurprisingly, replicated datasets on the basis of the estimated parameters are able to capture well the mean of the calibration sample, as well as the standard deviation and maxima. However, due to its inability to model the number of zeroes in the data, The log-linear model is unable to effectively model the median (zero) observation in the original data. For this reason, the model performance should be cautiously approached and not overstated. Supplementary Figures A.1a–c visually summarize posterior predictive checks for the mean, standard deviation and maximum, comparing the distribution of the test statistics for replicated datasets to the original dataset. In addition, Supplementary Figure A.1d depicts the posterior predictive density of 25 replicated dataset compared with the original sample.³³

Finally, I also inspected the within-corridor predictive performance of the models for the 12 largest directed migration corridors.³⁴ The results, shown in Supplementary Figure A.3, suggest that, while the model accurately capture the spatial differences in the magnitude of migration flows, it struggles to capture temporal variations within migration corridors. While Models 3 and 4 are able to reproduce some of the temporal variability observed in the data, the magnitude of the period-to-period change in migration is nowhere near the variability observed in the data. This conclusion is further reinforced when examining the share of non-zero corridors with partial $R_{i,j}^2$ above zero. With the possible exception of Model 4, the vast majority of the partial $R_{i,j}^2$ are below zero, in other words they perform worse than the sample average (see Supplementary Figure A.4). Overall, this analysis, arguably, reinforces the critique by Beyer et al. (2022) that gravity migration models are unable to appropriately accurate capture temporal dynamics. It also invites important caution in interpreting the projections presented in the previous section, as they are likely to miss significant aspects of within-corridor migration dynamics.

7 Conclusion

In this paper, I propose an original approach to estimating gravity model of migration using Bayesian hierarchical models with random intercepts for country of origin, country of destination and directed pairs of origin-destination countries. I show that such a framework substantially improves the predictive ability of the gravity model, as compared to a model that only includes population-level predictors.

The model parameters are then used to project future international migration flows on the African continent at 5-year intervals to 2050 based on the ISIMIP2b projections for crop yields and river discharge, as well as the Shared Socio-Economic Pathways. The results indicate that economic development is likely to exert a strong influence on the magnitude of future international migration. As revealed by the calibration models, financial barriers to migration appears to limit international migration flows between African countries. By contrast, climate change is projected to have a much smaller impact on international migration. In addition, close inspection of the projections indicate that the increase in migration flows as a result of climate change will be driven primarily by better expected crop yields over Southern Africa (see Amakrane et al., 2023).

Nevertheless, the present approach suffers from a number of limitations, which future research should strive to address. For reasons of scope, I focus here on four key aspects. First, the calibration model currently uses a log-linear specification. While the hierarchical specification improves the predictive ability of the model substantially, it remains unable to account for some of the key aspects of the calibration data as revealed by the predictive checks, namely the excess number of dyads with zero migration. Thus, future research should strive to use more flexible functional forms, that specifically address this limitations (i.e.Poisson-log normal or zero-inflated negative binomial) in conjunction with a hierarchical structure. These specifications are, however, more demanding of the data when estimated using MCMC. Additionally, gravity model as implemented in the literature have been shown to suffer from a lack of reliability to project future migration flows due to their inability to model dynamics taking place within migration corridors, as opposed to between countries (see Beyer et al., 2022). As revealed in Section 6, the models implemented in this paper are no exception and the projections presented here should thus be interpreted cautiously. Yet, the better performance of Model 4 suggests that more flexible specifications that let the effects of the predictors vary by origin or destination, albeit computationally demanding, may offer an avenue to overcome some the limitations of gravity models in the future.

Second, the quality of migration and foreign-born population data remains problematic on the African continent (United Nations, 2017). To the extent that censuses are infrequent or of problematic quality, this is susceptible to adversely impact the parameter estimates of the calibration model, and thereby the reliability of the projections.³⁵ This is illustrated by the lack of clear correlation between population in the country of origin and migration in Models 3–4. In addition, because the migration data used for the calibration model is computed based on 5-year estimates of foreign-born populations, it is likely to exclude significant number of migrants that may have traveled over shorter intervals ranging from a few months to a few years.

Third, projections generated based on the methodology presented in this paper used only one set of ISIMIP2b experiments for crop yields and river discharge. Future research should aim to use a larger set of climate projections models to generate an ensemble forecast. In addition to being less sensitive to the choice of the projection model, such an approach would also provide a more reliable probabilistic range of the magnitude of future international migration flows.

Fourth, the projections presented here assume that the impact of climate change affects migration through a channel distinct from the economic channel, as represented by the SSP projections for GDP per capita. This is a significant limitation as it has been shown elsewhere that climate change does affect economic activity (e.g. Carleton and Hsiang, 2016). Future projections should strive to better capture how climate change is susceptible to influence economic cycle and thus migration. In this regard, research has since emerged in the literature that attempts to account for the endogenous linkage between climate change and economic activity in projecting future migration patterns (see Rikani et al., 2022).

Author's note

The work presented here was initially undertaken as part of the African Climate Mobility Initiative (ACMI), a joint initiative from the African Union, the World Bank and the United Nations, which aims at projecting how climate change will affect internal and international migration on the African continent (see https://africa.climatemobility.org/, Amakrane et al., 2023). The author of the present paper was responsible for the modeling of international migration flows for the report. I am grateful to Alex de Sherbinin, Jacob Schewe, Kamal Amakrane, Brian Jones, Hélène Benveniste, Samir KC, Sarah Rosengaertner, Richard Seager, Nina von Uexkull and Greg Yetman, as well as members of the ACMI Technical Advisory Group, participants to the 2022 Scenarios Forum in Vienna, Austria and two anonymous reviewers for helpful comments. The projections presented here can be found at https://doi.org/10.7927/4jb8-e177 and replication material for the present paper is available at https://github.com/cottierf/ACMI_frontiers_replication. I acknowledge funding from the African Climate Mobility Initiative.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://figshare.com/articles/dataset/Bilateral_international_migration_flow_estimates_for_200_countries_1990-1995_to_2010-2015_/7731233/5, https://secure.iiasa.ac.at/web-apps/ene/SspDb/dsd?Action=htmlpage&page=about\#v2, and https://www.isimip.org/outputdata/.

Author contributions

FC: Data curation, Methodology, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Funding was received from the African Climate Mobility Initiative and from the Socioeconomic Data and Application Center (SEDAC) as a Distributed Active Archive Center (DAAC) under NASA Grant 80GSFC23CA001.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2024.1384295/full#supplementary-material

Footnotes

1. ^The modeling of international migrations flows presented here differs from the parallel model of internal migration flows in the African Shifts report in that the latter uses a spatial-explicit population gravity model that projects future climate-induced migration from the differences in population projections comparing a scenario accounting for climate change to a scenario that keep the climate conditions to their historical average (with a ~7.5^′′ degree minutes gridded resolution) (For more details, see Amakrane et al., 2023). By contrast, the international migration model presented here relies on a gravity model of migration.

2. ^The amount of shrinkage is a function of the information in each hierarchical structure (i.e. the number of observations and the distribution of the data).

3. ^In addition to adding random intercept, I also experimented with setting random slopes on the two climatic variables, crop yields and river discharge, see Model 4 in Table 1.

4. ^I initially examined an alternative specification relaxing the Poisson assumption of constant variance by using a negative binomial regression, but the performance of the model proved problematic when using it to project future migration flows resulting in implausibly large forecasts. Interested readers may consult Model 2 of Supplementary Table A.2, which presents the result of a negative binomial specification of Model 3, Table 1. Yet, as revealed by Supplementary Figures A.2a–d, such a model suffers from misspecifications that results in projections of the largest migration flows in the calibration dataset that are too large by orders of magnitude.

5. ^I add unity to the migration value to avoid taking the log of zero: ln(0) = −∞.

6. ^In that regard, I also note that the large number of observation means that likelihood equation will dominate the prior for the population fixed-effects parameters (β, δ, α).

7. ^For additional information on prior specifications (see https://mc-stan.org/rstanarm/articles/priors.html) (accessed on January 25th, 2024) and (https://rdrr.io/cran/brms/man/set_prior.html) (accessed on January 25th, 2024).

8. ^For the model letting the climate effects vary by country of origin, I use a LKJ(η) prior with η = 0 for the correlation of the group-level origin intercepts, crop yields and river discharge parameters.

9. ^I use the 5th revision of the data released in 2021. See here https://figshare.com/articles/dataset/Bilateral_international_migration_flow_estimates_for_200_countries_1990-1995_to_2010-2015_/7731233/5.

10. ^It should be noted that owing to the large distance between African countries in the sample and the limitations of the underlying foreign-born population tables due to problematic or infrequent censuses, about 77% of the observations in the sample record zero migrants.

11. ^According to available statistics, agriculture, fishing and forestry amounted to about half of total employment in sub-Saharan Africa in 2020 (International Labour Organization, 2024).

12. ^It is important to note that while crop yields and water availability are important measures of climate change, these are not the only environmental factors influenced by climate change of relevance in Africa. Other environmental variables of relevance, albeit not included in the model here, are flooding (including flash floods), heatwaves, sea level rise or tropical cyclones.

13. ^I am grateful to Jacob Schewe at the Postdam Institute for Climate Impact Research (PIK) for preparing the ISIMIP2a data in the required gridded format.

14. ^The crop yields and river discharge averages were not weighted by population, as the impact of the climate variables is assumed to be primarily over the agricultural channel (Falco et al., 2019; Tuholske et al., 2024).

15. ^The scale of the original variables for river discharge is m³·s⁻¹, and for crop yields is t·ha⁻¹ per growing season for maize, wheat, soy and rice

16. ^formally: $GDPpcrati{o}_{i,j}=\frac{GDPp{c}_i}{GDPp{c}_j}$.

17. ^It should be noted that the model implemented here does not entirely do justice to the “migration hump” hypothesis. This is because the addition of these two variables, GDP per capita at origin and GDP ratio, may technically only approximate a non-linear monotonically increasing or decreasing function, but not model an inverse U-shaped function. In other words, this specification implies that an incremental increase in per capita income results in an increasingly smaller increase in migration as the level of income rises, but would never result in a decrease in migration flows. Nevertheless, because Africa is predominantly composed of low or middle-income countries, this is a limited concern for the present application. For recent advances that attempts to capture non-linearities in the association between economic development and migration, see Rikani and Schewe (2023).

18. ^I add unity to avoid taking the log of zero.

19. ^The GPW population data is set to the year 2000 to avoid generating a time-varying distance measure.

20. ^The panel is balanced, except for Eritrea, which is missing in the first time period from 1990 to 1995.

21. ^Due to a lack of projection data, the following seven countries were excluded from the calibration analysis: Cape Verde, Comoros, Djibouti, Equatorial Guinea, Mauritius, São Tomé and Príncipe and the Seychelles. In addition, Sudan and South Sudan were merged together because of limited data availability prior to South Sudan's independence in 2011.

22. ^In total, Model 3 requires estimating 2,178 parameters, including 12 population fixed effects, one regression variance parameter, three random intercepts standard deviation parameters, and 2,162 separate random intercepts (46 random intercepts each by country of origin and destination, and 2,070 random intercepts for the directed migration corridors).

23. ^In fact, if one examines the correlation between population and out-migration at the country-level, only about 60% of the correlation estimates are positive. Thus, once differences in population magnitude across countries are accounted for, there is little information remaining to precisely estimate the population parameter. This is what probably explains the difference in the size of the credible intervals for the population variable between Models 1 and Models 3–4.

24. ^I note that sizeable uncertainty in the variable measuring the GDP per capita ratio between origin and destination could be, at least in part, be the product of the large negative correlation between the two economic variables included in the model (ρ = −0.71).

25. ^All the parameters were sampled jointly from the same set to maintain correlations between parameters.

26. ^Importantly, each round of projections used the same set of seed number referred on step (6) of the algorithm to ensure that the projections are comparable across scenarios.

27. ^1,000 samples × 2,070 directed migration corridors × seven time steps.

28. ^The two variables are generated in the same manner as outlined in Section 3.1.

29. ^GDP per capita projections for Angola are missing from the IIASA dataset, I thus complement this dataset with the OECD GDP projections for Angola (Dellink et al., 2017)

30. ^These demographic SSPs projections excluding migration were graciously shared by Samir KC and Hélène Benveniste.

31. ^While I could have extrapolated the values for the temporal dummies in the future using linear extrapolation to reflect that fact that migration may become more prevalent in the future, I chose a more conservative approach to guard against over-predicting future migration flows. This is because it is unclear to what extent current migration levels are the results of incidental dynamics (i.e. conflict) as opposed to long-term temporal trends.

32. ^Readers interested in the original elpd_loo values can refer to the last four rows of Table 1. These also show the estimate of effective number of parameters based on the elpd_loo computation.

33. ^As a reminder, I also examined a negative binomial specification with and without random intercepts, but when using these models for projections I obtained implausibly large projections of international migration.

34. ^I am thankful to an anonymous reviewer for the suggestion.

35. ^The estimate for the population parameter in the calibration model likely suffered from this problem.

References

Abel, G. J., and Cohen, J. E. (2019). Bilateral international migration flow estimates for 200 countries. Sci. Data 6, 1–13. doi: 10.1038/s41597-019-0089-3

PubMed Abstract | Crossref Full Text | Google Scholar

Amakrane, K., Rosengaertner, S., Simpson, N., de Sherbinin, A., Linekar, J., Horwood, B., et al. (2023). African shifts: The Africa climate mobility report, addressing climate-forced migration & displacement. New York, NY: Africa Climate Mobility INITIATIVE and Global Centre for Climate Mobility.

Google Scholar

Angelucci, M. (2015). Migration and financial constraints: evidence from Mexico. Rev. Econ. Stat. 97, 224–228. doi: 10.1162/REST_a_00487

Crossref Full Text | Google Scholar

Arneth, A., Balkovic, J., Ciais, P., De Wit, A., Deryng, D., Elliott, J., et al. (2017). ISIMIP2a Simulation Data from Agricultural Sector. GFZ Data Services. doi: 10.5880/PIK.2017.006

Crossref Full Text | Google Scholar

Beine, M., Docquier, F., and Özden, Ç. (2011). Diasporas. J. Dev. Econ. 95, 30–41. doi: 10.1016/j.jdeveco.2009.11.004

Crossref Full Text | Google Scholar

Beine, M., and Parsons, C. (2015). Climatic factors as determinants of international migration. Scand. J. Econ. 117, 723–767. doi: 10.1111/sjoe.12098

Crossref Full Text | Google Scholar

Bergstrand, J. H. (1985). The gravity equation in international trade: Some microeconomic foundations and empirical evidence. Rev. Econ. Stat. 67, 474–481. doi: 10.2307/1925976

Crossref Full Text | Google Scholar

Beyer, R. M., Schewe, J., and Lotze-Campen, H. (2022). Gravity models do not explain, and cannot predict, international migration dynamics. Hum. Soc. Sci. Commun. 9, 1–10. doi: 10.1057/s41599-022-01067-x

Crossref Full Text | Google Scholar

Bürkner, P.-C. (2017). BRMS: an r package for Bayesian multilevel models using Stan. J. Stat. Softw. 80. doi: 10.18637/jss.v080.i01

Crossref Full Text | Google Scholar

Cai, R., Feng, S., Oppenheimer, M., and Pytlikova, M. (2016). Climate variability and international migration: The importance of the agricultural linkage. J. Environ. Econ. Manag. 79, 135–151. doi: 10.1016/j.jeem.2016.06.005

Crossref Full Text | Google Scholar

Carleton, T. A., and Hsiang, S. M. (2016). Social and economic impacts of climate. Science 353:aad9837. doi: 10.1126/science.aad9837

PubMed Abstract | Crossref Full Text | Google Scholar

Cattaneo, C., and Peri, G. (2016). The migration response to increasing temperatures. J. Dev. Econ. 122, 127–146. doi: 10.1016/j.jdeveco.2016.05.004

Crossref Full Text | Google Scholar

Center for International Earth Science Information Network (CIESIN), Columbia University. (2018). Documentation for the Gridded Population of the World, Version 4 (GPWv4), Revision 11 Data Sets. Palisades, NY: NASA Socioeconomic Data and Applications Center (SEDAC). doi: 10.7927/H45Q4T5F

PubMed Abstract | Crossref Full Text | Google Scholar

Conte, M., Cotterlaz, P., and Mayer, T. (2022). “The CEPII gravity database,” in CEPII Working Paper N°2022-05, July 2022. Available at: https://www.cepii.fr/CEPII/en/bdd_modele/bdd_modele_item.asp?id=8

Google Scholar

Cottier, F., and Salehyan, I. (2021). Climate variability and irregular migration to the European Union. Glob. Environ. Change 69:102275. doi: 10.1016/j.gloenvcha.2021.102275

Crossref Full Text | Google Scholar

Cottier, F., Schlenker, W., Iboudo-N?bi?, E., Seager, R., McDermid, S., Puma, M. J., et al. (2022). Crop Price Variability, Environmental Change and Intra-regional Migration in Africa. Working papers. Columbia University.

Google Scholar

Cuaresma, J. C. (2017). Income projections for climate change research: a framework based on human capital dynamics. Glob. Environ. Change 42, 226–236. doi: 10.1016/j.gloenvcha.2015.02.012

Crossref Full Text | Google Scholar

de Bruin, S. P., Hoch, J. M., von Uexkull, N., Buhaug, H., Demmers, J., Visser, H., et al. (2022). Projecting long-term armed conflict risk: an underappreciated field of inquiry? Glob. Environ. Change 72:102423. doi: 10.1016/j.gloenvcha.2021.102423

Crossref Full Text | Google Scholar

Dellink, R., Chateau, J., Lanzi, E., and Magné, B. (2017). Long-term economic growth projections in the shared socioeconomic pathways. Glob. Environ. Change 42, 200–214. doi: 10.1016/j.gloenvcha.2015.06.004

Crossref Full Text | Google Scholar

Dustmann, C., and Okatenko, A. (2014). Out-migration, wealth constraints, and the quality of local amenities. J. Dev. Econ. 110, 52–63. doi: 10.1016/j.jdeveco.2014.05.008

Crossref Full Text | Google Scholar

Falco, C., Galeotti, M., and Olper, A. (2019). Climate change and migration: Is agriculture the main channel? Glob. Environ. Change 59:101995. doi: 10.1016/j.gloenvcha.2019.101995

Crossref Full Text | Google Scholar

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., Rubin, D. B., et al. (2013). Bayesian Data Analysis Third Edition (with errors fixed as of 13 February 2020). Boca Raton, FL: CRC press. doi: 10.1201/b16018

PubMed Abstract | Crossref Full Text | Google Scholar

Gelman, A., Jakulin, A., Pittau, M. G., and Su, Y. S. (2008). A weakly informative default prior distribution for logistic and other regression models. Ann. Appl. Stat. 2, 1360–1383. doi: 10.1214/08-AOAS191

Crossref Full Text | Google Scholar

Greene, W. H. (2012). Econometric Analysis, 8th Edn. Harlow: Pearson.

Google Scholar

Heston, A., Summers, R., and Aten, B. (2011). Penn world table version 7.0. Philadelphia, PA: Center for International Comparisons of Production, Income and Prices at the University of Pennsylvania.

Google Scholar

Hoffmann, R., Dimitrova, A., Muttarak, R., Cuaresma, J. C., and Peisker, J. (2020). A meta-analysis of country-level studies on environmental change and migration. Nat. Clim. Change 10, 904–912. doi: 10.1038/s41558-020-0898-6

PubMed Abstract | Crossref Full Text | Google Scholar

International Labour Organization (2024). ILO modelled estimates database. ILOSTAT. Available at: https://ilostat.ilo.org/data/ (accessed February 07, 2024).

Google Scholar

Jones, B. (2020). Technical methods for Mexico and Central America modeling work. Available at: https://www.nytimes.com/interactive/2020/07/23/magazine/climate-migration.html (accessed January 20, 2024).

Google Scholar

KC, S., and Lutz, W. (2017). The human core of the shared socioeconomic pathways: population scenarios by age, sex and level of education for all countries to 2100. Glob. Environ. Change 42, 181–192. doi: 10.1016/j.gloenvcha.2014.06.004

PubMed Abstract | Crossref Full Text | Google Scholar

King, G., Tomz, M., and Wittenberg, J. (2000). Making the most of statistical analyses: Improving interpretation and presentation. Am. J. Polit. Sci. 44, 347–61. doi: 10.2307/2669316

Crossref Full Text | Google Scholar

Lange, S., and Büchner, M. (2017). ISIMIP2b Bias-Adjusted Atmospheric Climate Input Data. ISIMIP Repository. doi: 10.48364/ISIMIP.208515

Crossref Full Text | Google Scholar

Lustgarten, A. (2020). The great climate migration has begun. New York Times, July 23. Available at: https://www.nytimes.com/interactive/2020/07/23/magazine/climate-migration.html (accessed June 10, 2022).

PubMed Abstract | Google Scholar

Marbach, M. (2018a). On imputing UNHCR data. Res. Polit. 5:2053168018803239. doi: 10.1177/2053168018803239

Crossref Full Text | Google Scholar

Marbach, M. (2018b). World refugee dataset, 1989-2015. Version: 1.1.0. Available at: https://github.com/sumtxt/wrd (accessed June 10, 2022).

Google Scholar

Massey, D. S., Arango, J., Hugo, G., Kouaouci, A., Pellegrino, A., Taylor, J. E., et al. (1993). Theories of international migration: a review and appraisal. Popul. Dev. Rev. 19, 431–466. doi: 10.2307/2938462

Crossref Full Text | Google Scholar

Missirian, A., and Schlenker, W. (2017). Asylum applications respond to temperature fluctuations. Science 358, 1610–1614. doi: 10.1126/science.aao0432

PubMed Abstract | Crossref Full Text | Google Scholar

Moore, W. H., and Shellman, S. M. (2006). Refugee or internally displaced person? to where should one flee? Comp. Political Stud. 39, 599–622. doi: 10.1177/0010414005276457

Crossref Full Text | Google Scholar

Müller Schmied, H., Adam, L., Eisner, S., Fink, G., Flörke, M., Kim, H., et al. (2016). Variations of global and continental water balance components as impacted by climate forcing uncertainty and human water use. Hydrol. Earth Syst. Sci. 20, 2877–2898. doi: 10.5194/hess-20-2877-2016

Crossref Full Text | Google Scholar

Paananen, T., Piironen, J., B?rkner, P. C., and Vehtari, A. (2021). Implicitly adaptive importance sampling. Stat. Comput. 31:16. doi: 10.1007/s11222-020-09982-2

Crossref Full Text | Google Scholar

Ravenstein, E. G. (1889). The laws of migration. J. R. Stat. Soc. 52, 241–310. doi: 10.2307/2979333

Crossref Full Text | Google Scholar

Riahi, K., van Vuuren, D. P., Kriegler, E., Edmonds, J., O'Neill, B. C., Fujimori, S., et al. (2017). The shared socioeconomic pathways and their energy, land use, and greenhouse gas emissions implications: an overview. Glob. Environ. Change 42, 153–168. doi: 10.1016/j.gloenvcha.2016.05.009

Crossref Full Text | Google Scholar

Rigaud, K. K., de Sherbinin, A., Jones, B., Bergmann, J., Clement, V., Ober, S., et al. (2018). Groundswell: Preparing for Internal Climate Migration. Washington, DC: World Bank. doi: 10.1596/29461

Crossref Full Text | Google Scholar

Rikani, A., Frieler, K., and Schewe, J. (2022). Climate change and international migration: exploring the macroeconomic channel. PLoS ONE 17:e0276764. doi: 10.1371/journal.pone.0276764

PubMed Abstract | Crossref Full Text | Google Scholar

Rikani, A., Otto, C., Levermann, A., and Schewe, J. (2023). More people too poor to move: divergent effects of climate change on global migration patterns. Environ. Res. Lett. 18:024006. doi: 10.1088/1748-9326/aca6fe

Crossref Full Text | Google Scholar

Rikani, A., and Schewe, J. (2023). Global bilateral migration projections accounting for diasporas, transit and return flows, and poverty constraints. Demographic Res. 45, 87–140. doi: 10.4054/DemRes.2021.45.4

PubMed Abstract | Crossref Full Text | Google Scholar

Schutte, S., Vestby, J., Carling, J., and Buhaug, H. (2021). Climatic conditions are weak predictors of asylum migration. Nat. Commun. 12:2067. doi: 10.1038/s41467-021-22255-4

PubMed Abstract | Crossref Full Text | Google Scholar

Stan Development Team (2022). Stan modeling language users guide and reference manual. Available at: https://mc-stan.org

Google Scholar

Sundberg, R., and Melander, E. (2013). Introducing the UCDP georeferenced event dataset. J. Peace Res. 50, 523–532. doi: 10.1177/0022343313484347

PubMed Abstract | Crossref Full Text | Google Scholar

Taylor, K. E., Stouffer, R. J., and Meehl, G. A. (2012). An overview of cmip5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498. doi: 10.1175/BAMS-D-11-00094.1

PubMed Abstract | Crossref Full Text | Google Scholar

Todaro, M. P. (1969). A model of labor migration and urban unemployment in less developed countries. Am. Econ. Rev. 59, 138–148.

Google Scholar

Tuholske, C., Di Landro, M. A., Anderson, W., van Duijne, R. J., and de Sherbinin, A. (2024). A framework to link climate change, food security, and migration: unpacking the agricultural pathway. Popul. Environ. 46:8. doi: 10.1007/s11111-024-00446-7

Crossref Full Text | Google Scholar

UNHCR (2022). UNHCR refugee population statistics database. Available at: https://www.unhcr.org/refugee-statistics/methodology/

Google Scholar

United Nations (2017). Trends in international migrations stock: The 2017 revision. documentation. New York, NY: Department of Economics and Social Affairs.

Google Scholar

United Nations (2020). Trends in international migrations stock: The 2020 revision. New York, NY: Department of Economics and Social Affairs.

Google Scholar

United Nations (2022). United Nations, department of economic and social affairs (2022). World population prospects 2022: Ten key messages. New York, NY: Department of Economic and Social Affairs, Population Division.

Google Scholar

Vehtari, A., Gabry, J., Magnusson, M., Yao, Y., B?rkner, P. C., Paananen, T., et al. (2015). loo: Efficient Leave-One-Out Cross-Validation and WAIC for Bayesian Models. CRAN: Contributed Packages.

Google Scholar

Vehtari, A., Gelman, A., and Gabry, J. (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat. Comput. 27, 1413–1432. doi: 10.1007/s11222-016-9696-4

Crossref Full Text | Google Scholar

Xiao, T., Oppenheimer, M., He, X., and Mastrorillo, M. (2022). Complex climate and network effects on internal migration in South Africa revealed by a network model. Popul. Environ. 43, 289–318. doi: 10.1007/s11111-021-00392-8

Crossref Full Text | Google Scholar