Computational measures of irregularity molecular descriptors of octahedral and icosahedral networks

Irregularity measures tend to describe the complexity of networks. Chemical graph theory is a branch of mathematical chemistry that has a significant impact on the development of the chemical sciences. The study of irregularity indices has recently become one of the most active research areas in chemical graph theory. Irregularity indices help us to examine many chemical and biological properties of chemical structures under study. In this article, we study the irregularity indices of the octahedral and icosahedral networks. These networks are used in crystallography, where the topology and structural aspects are carrying some important facts to determine the properties of large structures theoretically. Our results play an important role in pharmacy, drug design, and many other applied areas. We also compared our results graphically to conclude the irregularity with a change in the parameter of structures.

Introduction

Network structure and the pattern in networks carry important facts relating to the chemical properties. Because of the long molecular structure, the properties of some of these networks can’t be easily determined. Metallic-organic frameworks are such large networks whose symmetry and topology are incorporated in the bonding pattern and frequency of the atoms, (Jiang et al., 2016), (Zhao Y. et al., 2016) and (Liu et al., 2016). An indirect way of expressing the properties of these networks is through the use of topological index which fundamentally rely on the topological pattern of these networks.

One useful kind of topological index is the irregularity indices, which determine the complexity and degree of irregular patterns in the networks and graphs. These networks or graphs can be representative models of some crystallographic structures or a polymer where lines represent bonding patterns and vertices show atoms. Irregularity indices of fairly large chemical structures, such as metal organic frameworks, are important not only for characterization of structures but also for computing their physico-chemical properties, which have been otherwise rather difficult to compute for such large networks of importance in chemistry. In some of these networks, covalent fibers are weaved into crystals, which why these networks are becoming increasingly interesting in recent years.

Chemical graph theory is a thriving field with rich applications in industry and pharmacy. Graphs are models of physical networks described by two main sets of entities named as edges and vertices. The number of edges incident to each vertex is termed the degree of vertex. According to (Gutman and Polansky, 1986), a network or graph is considered regular if every vertex has the same degree. But until famous mathematician Paul Erdös stressed this in the study of irregular graphs for the first time in history, irregular graphs were unable to draw in the audience (Majcher and Michael, 1997). The greatest size of irregularity in a network, as suggested by Collatz and Sinogowitz (1957), was the subject of an open topic that he presented. Subsequently, irregularity became so widely accepted that a new class of topological indices emerged, which are now called irregularity indices. The disparity of complex systems can be predicted by these metrics. These systems have a number of well-known topological characteristics, including self-similarity, scale-freeness, network motifs, and small-worldness (Albert et al., 2000). In summary, there is a stark difference between the power-law degree distribution of complex networks and the regularity found in random models such as the one put forth by Erdös and Rényi (1960).

An irregularity index is defined as a topological invariant that vanishes for a regular graph but is non-zero for a non-regular graph. Erdös declared, “The determination of extreme size of highly irregular graphs of given order” to be an unresolved subject at the Second Krakow Conference on Graph Theory (1994) (Chartrand et al., 1988). Since then, irregular graphs and their degree of irregularity have emerged as one of graph theory’s most fundamental open problems. A graph is said to be perfect if each vertex has a different degree than the others. The writers of (Behzad and Chartrand, 1947) established that no graph is flawless. The graphs in between are known as quasi-perfect graphs, because all but two vertices have distinct degrees (Majcher and Michael, 1997). Indices are simplified ways of expressing anomalies, (Horoldagva et al., 2016; Liu et al., 2014), conducted unique research on these irregularity indices. The first such irregularity index was established by Collatz and Sinogowitz (1957). Most of these indices utilize the concept of edge imbalance, defined as imball_uv = |d_u–d_v|, (Dorogovtsev and Mendes, 2000; Krapivsky et al., 2000). The Albertson index, AL(G), was introduced by Albertson in (Albertson, 1997) and is defined as AL(G) = ^∑_uv∈E|d_u − d_v|. The irregularity indices IRL(G) and IRLU(G) were introduced by Vukicevic and Gasparov, (Albert et al., 2000), and are defined as $\text{IRL}\left(G\right)={\sum }_{uv\in E}\left|\ln d_u-\ln d_v\right|$, and $\text{IRLU}\left(G\right)={\sum }_{uv\in E}\frac{\left|d_u-d_v\right|}{\min \left(d_u,d_v\right)}$. Recently, (Abdo et al., 2014), introduced a new concept called the “total irregularity measure of a graph G,” defined as $R_t\left(G\right)=\frac{1}{2}{\sum }_{uv\in E}\left|d_u-d_v\right|$, (Erdös and Rényi, 1960; Estrada et al., 1998; Reti et al., 2018). Recently, Gutman et al. introduced the IRF(G) irregularity index of the graph G, defined as IRF⁽G⁾ = ^∑_uv∈E(d_u − d_v)² (Bell, 1992). The Randić index is closely connected to an irregularity measure, defined as $\left(G\right)={\sum }_{uv\in E}{\left(d_u^{-1/2}-d_v^{-1/2}\right)}^2$ , (Albertson, 1997). Further details on similar irregularity indices may be found in (Abdo and Dimitrov, 2014a). These indices are defined as follows: $IRDIF\left(G\right)={\sum }_{uv\in E}\left|\frac{d_u}{d_v}-\frac{d_v}{d_u}\right|$, $IRLF\left(G\right)={\sum }_{uv\in E}\frac{\left|d_u-d_v\right|}{\sqrt{d_u{d}_v}}$, $IR\text{LA}\left(G\right)=2{\sum }_{uv\in E}\frac{\left|d_u-d_v\right|}{\left(d_u+d_v\right)}$, $IRD1\left(G\right)={\sum }_{uv\in E}\ln \left(1+\left|d_u-d_v\right|\right)$, $IRGA\left(G\right)=2{\sum }_{uv\in E}\mathit{ln}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}$, and $IRD\left(G\right)={\sum }_{uv\in E}{\left(d_u^{1/2}-d_v^{1/2}\right)}^2$. More information can be found in (Abdo and Dimitrov, 2014b; Gutman, 2018; Hu et al., 2005; Li and Gutman, 2006). Recently, (Zahid et al., 2019), calculated the irregularity indices for nanotubes. (Gao et al., 2017; Gao et al., 2019). examined irregularity measurements for different dendrimer architectures (Hussain et al., 2019a; Hussain et al., 2019b). Estimated the irregularity indices for benzenoid systems, nanostar dendrimers, and boron nanotubes. Furthermore, (Xie et al., 2019), estimated these indices for fullerenes and polymer dendrimers. Quiet recently, many new topological characterizations of several chemical structures based on topological indices have been presented along with various applications, (Zhang et al., 2024; Prabhu et al., 2023; Prabhu et al., 2024; Govardhan et al., 2023; Saravanan et al., 2022).

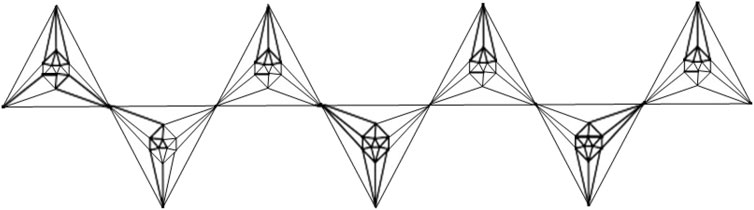
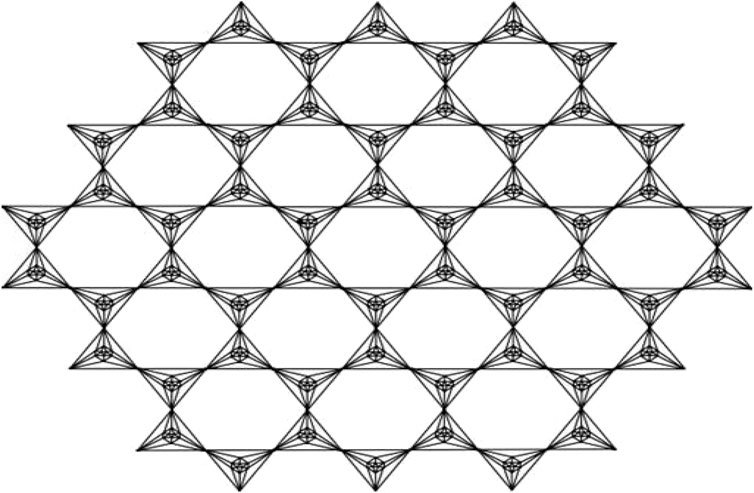
This article examines the irregularity of well-known chemical networks by computing the irregularity indices for octahedral and icosahedral networks. Our goal is to determine which of these networks exhibits greater irregularity. Specifically, we evaluate the degree of irregularity in the octahedral network OTn and the icosahedral network ISn. Figures 1–3 depict the molecular graphs of the octahedral networks, while Figures 4–6 illustrate the molecular graphs of the icosahedral networks. The motivation for this study stems from previous findings that irregularity indices can closely approximate properties such as entropy, standard enthalpy, vaporization, and acentric factors of octane isomers (Abdo et al., 2014). These figures display the molecular patterns and topologies of the two networks under investigation.

Figure 1

Figure 1. Structure of octahedron.

Figure 2

Figure 2. Chain octahedral structure.

Figure 3

Figure 3. Octahedral network.

Figure 4

Figure 4. Structure of icosahedron.

Figure 5

Figure 5. Structure of chain icosahedron.

Figure 6

Figure 6. Icosahedral network.

Octahedral networks OT_n

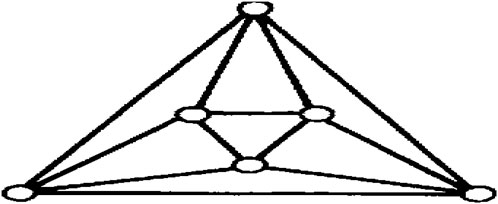
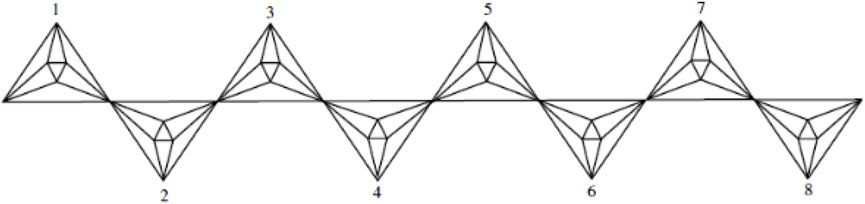
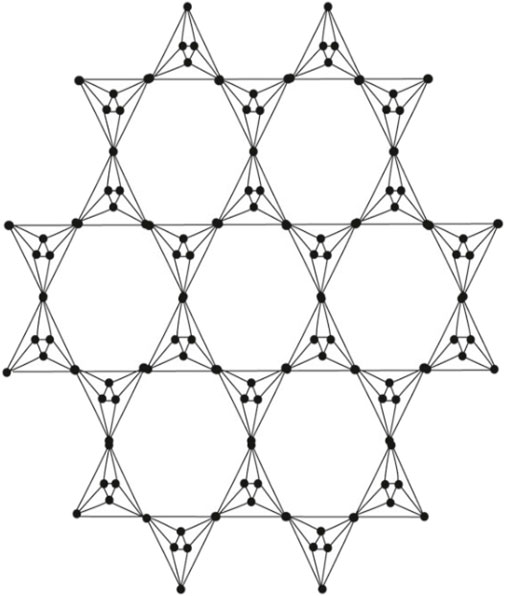
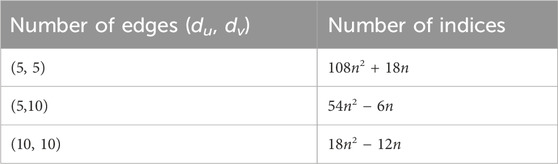
An octahedron graph, shown in Figure 1, is a polyhedral graph corresponding to the skeleton of a platonic solid. This platonic graph consists of 6 vertices and 12 edges. The analogs of this structure play a vital role in the fields of reticular chemistry, which deals with the synthesis and properties of metal-organic frameworks. The different types of octahedral structures arise from the ways these octahedra can be connected. A chain octahedral structure of dimension n denoted as CHO_n is obtained by arranging n octahedra linearly as shown in Figure 2. The number of vertices and edges of CHO_n are 5n + 1 and 12n, respectively. An octahedral sheet-like structure is a ring of octahedral structures that are linked to other rings by sharing corner vertices in a two-dimensional plane. An octahedral network of dimension n is denoted by OT_n, where n is the order of circumscribing, as shown in Figure 3, The number of vertices and edges in OT_n with n ≥ 1 are 27n² + 3n and 72n², respectively.

Icosahedral networks ISn

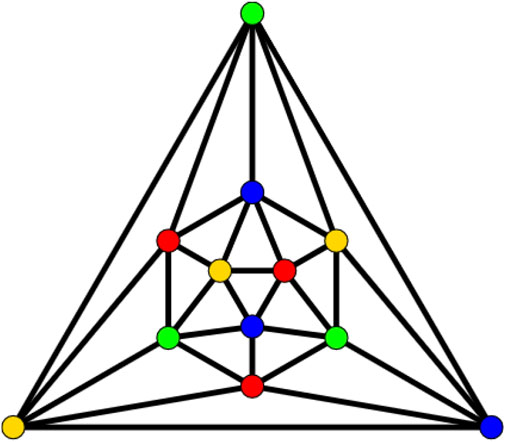
An icosahedron graph is also a platonic graph, having 12 vertices and 30 edges, as shown in Figure 4. The analogs of the frameworks considered here are also the backbones of recent materials of reticular chemistry. The chain icosahedral framework of dimension n is denoted by CHI_n and is shown in Figure 5. It has 11n + 1 number of vertices and 30n number of edges. The icosahedral network is obtained from the octahedral network by replacing all the octahedra with the icosahedra. An n-dimensional icosahedral network is denoted by IS_n is shown in Figure 6. It has 63n² + 3n number of vertices and 180n² number of edges. We discuss the irregularity indices of this network as follows.

Main results

In this section, we present our main theoretical results. Here we denote Γ = OT_n be the octahedral network then.

Theorem 1

Let (Γ, x, y) be the graph of the octahedral networks OT_n, then the irregularity indices of (Γ, x, y) are.

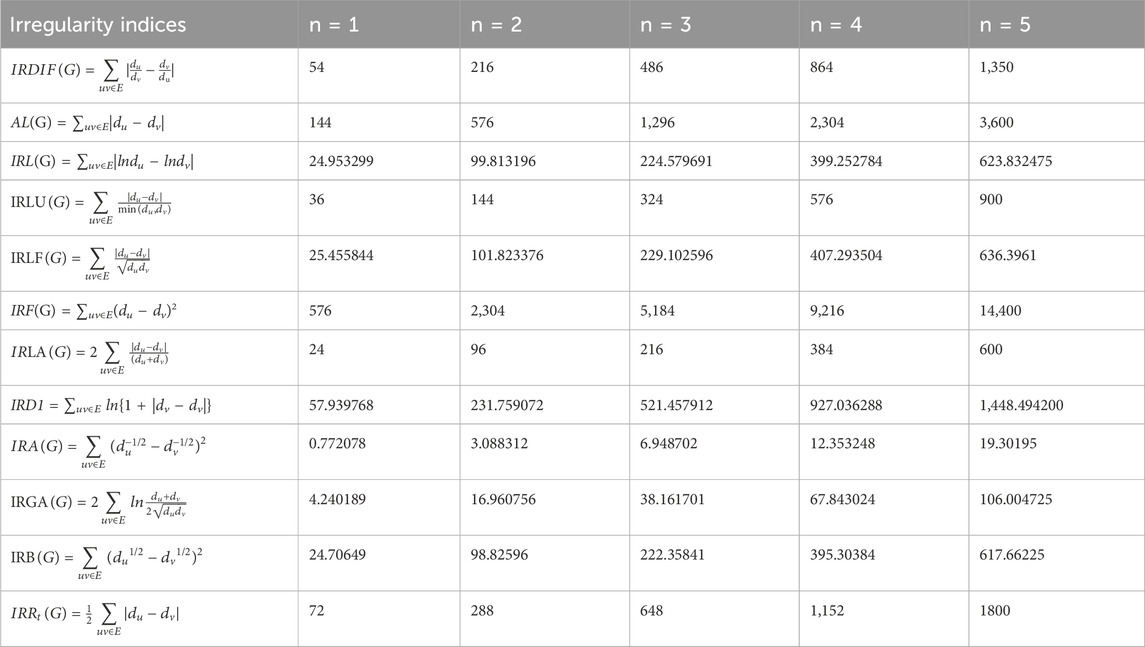
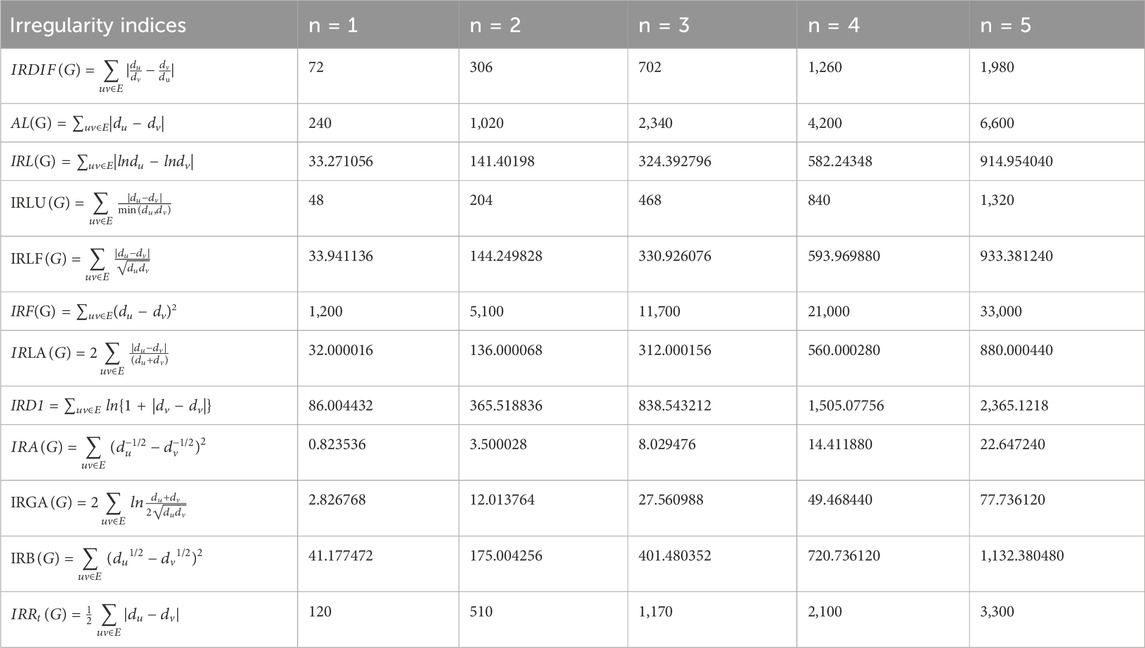
1. IRDI(Γ, x, y) = 54n²

2. A(Γ, x, y) = 144n²

3. IR(Γ, x, y) = 24.953299n²

4. IRL(Γ, x, y) = 36n²

5. IRL(Γ, x, y) = 25.455844n²

6. IR(Γ, x, y) = 576n²

7. IRL(Γ, x, y) = 24n²

8. IRD1 = 57.939768n²

9. IR(Γ, x, y) = 0.772078n²

10. IRG(Γ, x, y) = 4.240189n²

11. IR(Γ, x, y) = 24.70649n²

12. IRR(Γ, x, y) = 72n²

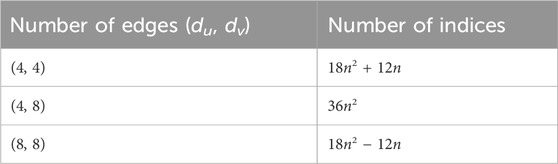
In order to prove the above theorem, we have to consider Figure 3. We can see that the edges of (Γ, x, y) admit the following partition in Table 1.

Table 1

Table 1. Edge partition of Octahedral network OT_n.

Now using Table 1 and the above definitions, we have:

1. $IRDIF\left(G\right)={\displaystyle \sum _{uv\in E}}\left|\frac{d_u}{d_v}-\frac{d_v}{d_{\mathrm{u}}}\right|$

$IRDIF\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(18{\mathrm{n}}^2+12\mathrm{n}\right)\left|\frac{4}{4}-\frac{4}{4}\right|+36{\mathrm{n}}^2\left|\frac{8}{4}-\frac{4}{8}\right|+\left(18{\mathrm{n}}^2-12\mathrm{n}\right)\left|\frac{8}{8}-\frac{8}{8}\right|=54{\mathrm{n}}^2$

2. A(G) = ^∑_uv∈E|d_u − d_v|

$A\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(18n^2+12n\right)\left|4\begin{array}{cc}-& 4\end{array}\right|+36n^2\left|8\begin{array}{cc}-& 4\end{array}\right|+\left(18n^2-12n\right)\left|8\begin{array}{cc}-& 8\end{array}\right|=144n^2.$

3. IR(G) = ^∑_uv∈E|lnd_u − lnd_v|

$\text{IRL}\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(18n^2+12n\right)\left|\mathit{ln}4-\mathit{ln}4\right|+36n^2\left|\mathit{ln}8-\mathit{ln}4\right|+\left(18n^2-12n\right)\left|\mathit{ln}8-\mathit{ln}8\right|=36n^2\mathit{ln}2=24.953299n^2$

4. $\text{IRLU}\left(G\right)={\displaystyle \sum _{uv\in E}}\frac{\left|d_u-d_v\right|}{\min \left(d_u,d_v\right)}$

$\text{IRLU}\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(18{\mathrm{n}}^2+12\mathrm{n}\right)\frac{\left|4-4\right|}{4}+36{\mathrm{n}}^2\frac{\left|8-4\right|}{4}+\left(18{\mathrm{n}}^2-12\mathrm{n}\right)\frac{\left|8-8\right|}{8}=36n^2$

5. $IRLF\left(G\right)={\displaystyle \sum _{uv\in E}}\frac{\left|d_u-d_v\right|}{\sqrt{d_u{d}_v}}$,

$IRLF\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(18{\mathrm{n}}^2+12\mathrm{n}\right)\frac{\left|4-4\right|}{\sqrt{4\times 4}}+36{\mathrm{n}}^2\frac{\left|8-4\right|}{\sqrt{8\times 4}}+\left(18{\mathrm{n}}^2-12\mathrm{n}\right)\frac{\left|8-8\right|}{\sqrt{8\times 8}}=25.455844{\mathrm{n}}^2$

6. IR(G) = ^∑_uv∈E(d_u − d_v)²

$IR\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(18n^2+12n\right){\left(4-4\right)}^2+36n^2{\left(8-4\right)}^2+\left(18n^2-12n\right){\left(8-8\right)}^2=576n^2.$

7. $IR\text{LA}\left(G\right)=2{\displaystyle \sum _{uv\in E}}\frac{\left|d_u-d_v\right|}{\left(d_u+d_v\right)}$

$IR\text{LA}\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=2\left[\left(18{\mathrm{n}}^2+12\mathrm{n}\right)\frac{\left|4-4\right|}{4+4}+36{\mathrm{n}}^2\frac{\left|8-4\right|}{8+4}+\left(18{\mathrm{n}}^2-12\mathrm{n}\right)\frac{\left|8-8\right|}{8+8}\right]=24{\mathrm{n}}^2$

8. $IRD1\left(G\right)={\displaystyle \sum _{uv\in E}}\ln \left(1+\left|d_u-d_v\right|\right)$

$IRD1\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(18n^2+12n\right)\ln \left(1+\left|4-4\right|\right)+36n^2\ln \left(1+\left|8-4\right|\right)+\left(18n^2-12n\right)\ln \left(1+\left|8-8\right|\right)=36{\mathrm{n}}^2\ln 5=57.9397648{\mathrm{n}}^2$

9. $IRA\left(G\right)={\displaystyle \sum _{uv\in E}}{\left(d_u^{-1/2}-d_v^{-1/2}\right)}^2$

$IRA\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(18n^2+12n\right){\left(4^{-0.5}-4^{-0.5}\right)}^2+36n^2{\left(8^{-0.5}-4^{-0.5}\right)}^2+\left(18n^2-12n\right){\left(8^{-0.5}-8^{-0.5}\right)}^2=0.772078n^2$

10. $IRGA\left(G\right)=2{\displaystyle \sum _{uv\in E}}\mathit{ln}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}$

$IRGA\left(\mathrm{\Gamma },x,y\right)=2\left[\left(18n^2+12n\right)\mathit{ln}\frac{4+4}{2\sqrt{4\times 4}}+36n^2\mathit{ln}\frac{8+4}{2\sqrt{8\times 4}}+\left(18n^2-12n\right)\mathit{ln}\frac{8+8}{2\sqrt{8\times 8}}\right]=4.240189n^2$

11. $IRB\left(G\right)={\displaystyle \sum _{uv\in E}}\left({d_u}^{1/2}-{d_v}^{1/2}\right)$²

$IRB\left(\mathrm{\Gamma },x,y\right)=\left(18n^2+12n\right){\left(4^{1/2}-4^{1/2}\right)}^2+36n^2{\left(8^{1/2}-4^{1/2}\right)}^2+\left(18n^2-12n\right){\left(8^{1/2}-8^{1/2}\right)}^2=24.70649n^2$

12. $IR{R}_t\left(G\right)=\frac{1}{2}{\displaystyle \sum _{uv\in E}}\left|d_u-d_v\right|$

$IR{R}_t\left(\mathrm{\Gamma },x,y\right)=\frac{1}{2}\left[\left(18n^2+12n\right)\left|4-4\right|+36n^2\left|8-4\right|+\left(18n^2-12n\right)\left|8-8\right|\right]=72n^2$

Table 2 shows the values of these irregularity indices for some test values of parameter n.

Table 2

Table 2. Irregularity indices for Octahedral network OT_n.

Theorem 2

Let IS_n be the Icosahedral network, which we denote by Γ. The irregularity indices of Γ are as follows:

1. IRDI(Γ, x, y) = 81n² − 9n

2. A(Γ, x, y) = 270n² − 30n

3. IR(Γ, x, y) = 37.429938n² − 4.158883n

4. IRL⁽Γ, x, y⁾ = 54n² − 6n

5. IRL(Γ, x, y) = 38.183778n² − 4.242641n

6. IR(Γ, x, y) = 1350n² − 150n

7. IRL(Γ, x, y) = $36n^2-4n$

8. IRD1 = $96.7550n^2-10.75056\mathrm{n}$

9. IR(Γ, x, y) = $0.926494n^2-0.102944n$

10. IRG(Γ, x, y) = 114.5513 n^2 - 12.72792 n

11. IR(Γ, x, y) = $46.32468n^2-5.14719n$

12. IRR(Γ, x, y) = 135n² − 15n

To prove the above theorem, we must consider Figure 6. As shown, the edges admit the following partition, presented in Table 3.

Table 3

Table 3. Edge partition of Icosahedral network IS_n.

Now using Table 3 and the above definitions, we have:

1. $IRDIF\left(G\right)={\displaystyle \sum _{uv\in E}}\left|\frac{d_u}{d_v}-\frac{d_v}{d_{\mathrm{u}}}\right|$

$IRDIF\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(108{\mathrm{n}}^2+18\mathrm{n}\right)\left|\frac{5}{5}-\frac{5}{5}\right|+\left(54n^2-6n\right)\left|\frac{10}{5}-\frac{5}{10}\right|+\left(18{\mathrm{n}}^2-12\mathrm{n}\right)\left|\frac{10}{10}-\frac{10}{10}\right|=81n^2-9n.$

2. A(G) = ^∑_uv∈E|d_u − d_v|

$A\left(\mathrm{\Gamma },x,y\right)=\left(108{\mathrm{n}}^2+18\mathrm{n}\right)\left|5-5\right|+\left(54n^2-6n\right)\left|10-5\right|+\left(18n^2-12n\right)\left|10-10\right|=270n^2-30n.$

3. $IRL$ (G) = ^∑_uv∈E|lnd_u − lnd_v|

$IRL\left(\mathrm{\Gamma },x,y\right)=\left(108{\mathrm{n}}^2+18\mathrm{n}\right)\left|\mathit{ln}5-\mathit{ln}5\right|+\left(54n^2-6n\right)\left|\mathit{ln}10-\mathit{ln}5\right|+\left(18n^2-12n\right)\left|\mathit{ln}10-\mathit{ln}10\right|=37.429938n^2-4.158883n.$

4. $IRLU\left(G\right)={\displaystyle \sum _{uv\in E}}\frac{\left|d_u-d_v\right|}{\min \left(d_u,d_v\right)}$

$IRLU\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(108{\mathrm{n}}^2+18\mathrm{n}\right)\frac{\left|5-5\right|}{5}+\left(54n^2-6n\right)\frac{\left|10-5\right|}{5}+\left(18{\mathrm{n}}^2-12\mathrm{n}\right)\frac{\left|10-10\right|}{10}=54n^2-6n.$

5. $IRLF\left(G\right)={\displaystyle \sum _{uv\in E}}\frac{\left|d_u-d_v\right|}{\sqrt{d_u{d}_v}}$

$IRLF\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(108{\mathrm{n}}^2+18\mathrm{n}\right)\frac{\left|5-5\right|}{\sqrt{5\times 5}}+\left(\left(54n^2-6\mathrm{n}\right)\right)\frac{\left|10-5\right|}{\sqrt{10\times 5}}+\left(18{\mathrm{n}}^2-12\mathrm{n}\right)\frac{\left|10-10\right|}{\sqrt{10\times 10}}=38.18377n^2-4.242641\mathrm{n}.$

6. IR(G) = ^∑_uv∈E(d_u − d_v)²

$IR\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(108{\mathrm{n}}^2+18n\right){\left(5-5\right)}^2+\left(54n^2-6n\right){\left(10-5\right)}^2+\left(18n^2-12n\right){\left(10-10\right)}^2=1350n^2-150n.$

7. $IR\text{LA}\left(G\right)=2{\displaystyle \sum _{uv\in E}}\frac{\left|d_u-d_v\right|}{\left(d_u+d_v\right)}$

$IR\text{LA}\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=2\left[\left(108{\mathrm{n}}^2+18n\right)\frac{\left|5-5\right|}{5+5}+\left(54n^2-6n\right)\frac{\left|10-5\right|}{10+5}+\left(18n^2-12n\right)\frac{\left|10-10\right|}{10+10}\right]=36{\mathrm{n}}^2-4\mathrm{n}.$

8. $\text{IRD}1\left(G\right)={\displaystyle \sum _{uv\in E}}\mathit{ln}\left(1+\left|d_u-d_v\right|\right)$

$\text{IRD}1\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(108{\mathrm{n}}^2+18n\right)\mathit{ln}\left(1+\left|5-5\right|\right)+\left(54n^2-6n\right)\mathit{ln}\left(1+\left|10-5\right|\right)+\left(18n^2-12n\right)\mathit{ln}\left(1+\left|10-10\right|\right)=\left(54n^2-6n\right)\ln 6=96.7550n^2-10.75056\mathrm{n}.$

9. $IRA\left(G\right)={\displaystyle \sum _{uv\in E}}{\left(d_u^{-1/2}-d_v^{-1/2}\right)}^2$

$IRA\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=\left(108{\mathrm{n}}^2+18n\right){\left(5^{-0.5}-5\right)}^2+\left(54n^2-6n\right){\left({10}^{-0.5}-5^{-0.5}\right)}^2+\left(18n^2-12n\right){\left({10}^{-0.5}-{10}^{-0.5}\right)}^2=0.926494n^2-0.102944n.$

10. $\text{IRGA}\left(G\right)=2{\displaystyle \sum _{uv\in E}}\mathit{ln}\frac{d_u+d_v}{2\sqrt{d_u{d}_v}}$

$\text{IRGA}\left(\mathrm{\Gamma },\mathrm{x},\mathrm{y}\right)=2\left[\left(108{\mathrm{n}}^2+18n\right)\mathit{ln}\left(\frac{5+5}{2\sqrt{5\times 5}}\right)+\left(54n^2-6n\right)\mathit{ln}\left(\frac{10+5}{2\sqrt{10\times 5}}\right)+\left(18n^2-12n\right)\mathit{ln}\left(\frac{10+10}{2\sqrt{10\times 10}}\right)\right]=4.240189n^2.$

11. $\text{IRB}\left(G\right)={\displaystyle \sum _{uv\in E}}{\left({d_u}^{1/2}-{d_v}^{1/2}\right)}^2$

$\text{IRB}\left(\mathrm{\Gamma },x,y\right)=\left(108{\mathrm{n}}^2+18n\right){\left(5^{1/2}-5^{1/2}\right)}^2+\left(54n^2-6n\right){\left({10}^{1/2}-5^{1/2}\right)}^2+\left(18n^2-12n\right){\left({10}^{1/2}-{10}^{1/2}\right)}^2=46.32468n^2-5.14719n.$

12. $IR{R}_t\left(G\right)=\frac{1}{2}{\displaystyle \sum _{uv\in E}}\left|d_u-d_v\right|$

$IR{R}_t\left(\mathrm{\Gamma },x,y\right)=\frac{1}{2}\left[\left(108{\mathrm{n}}^2+18n\right)\left|5-5\right|+\left(54n^2-6n\right)\left|10-5\right|+\left(18n^2-12n\right)\left|10-10\right|\right]=135n^2-15n.$

Table 4 shows the values of these irregularity indices for some test values of parameter n.

Table 4

Table 4. Irregularity indices for Isosahedral network IS_n.

Graphical analysis, discussions and conclusion

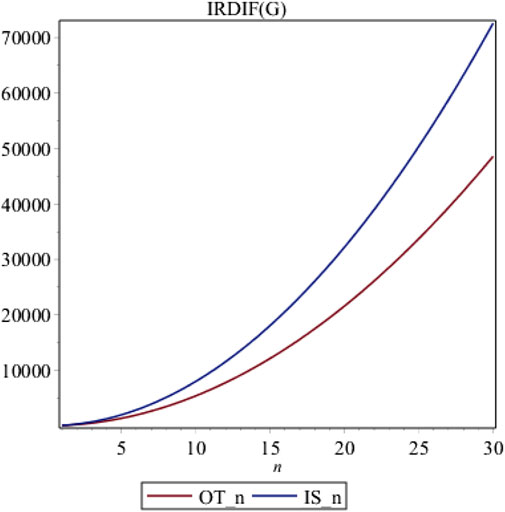
In this part, we conclude our findings of the irregularity indices for these three structures. We use red and blue colors for OT_n and IS_n, respectively. From Figure 7, it is evident that IS_n. is highly irregular than OT_n.

Figure 7

Figure 7. Graphs of irregularity Index IRDIF.

Here we have analyzed the irregularity on the basis of IRDIF. Choosing different irregularity measure, results can vary. However, their graphs can be constructed by any software and results can be analyzed with ease. It is clear from the theorem 1 that all irregularity measures are quadratic so they increase rather quickly. Similarly, the same quadratics are obtained so we conclude that the behavior of all irregularity indices behave similarly so we have only plotted a single irregularity measure.

In this article, we investigated the irregularity measures of various octahedral structures, computing closed forms for many of these indices. The structural dependencies of these measures were analyzed through the provided graphs. These insights can be utilized to control and predict the physical and chemical properties of these networks. Additionally, the results offer a foundation for the development of new, complex networks and structure.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XZ: Conceptualization, Writing–review and editing. HR: Writing–review and editing. MM: Methodology, Writing–original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

We are thankful to the comments of referees for valuable suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdo, H., Brandt, S., and Dimitrov, D. (2014). The total irregularity of a graph. Discr. Math. Theor. Comput. Sci. 16, 201–206. doi:10.46298/dmtcs.126

CrossRef Full Text | Google Scholar

Abdo, H., and Dimitrov, D. (2014a). The irregularity of graphs under graph operations. Discuss. Math. Graph. Theory 34, 263–278. doi:10.7151/dmgt.1733

CrossRef Full Text | Google Scholar

Abdo, H., and Dimitrov, D. (2014b). The total irregularity of graphs under graph operations. Miskolc Math. Notes 15, 3–17. doi:10.18514/mmn.2014.593

CrossRef Full Text | Google Scholar

Albert, R., Jeong, H., and Barabasi, A. L. (2000). Error and attack tolerance of complex networks. Nature 406, 378–382. doi:10.1038/35019019

PubMed Abstract | CrossRef Full Text | Google Scholar

Albertson, M. (1997). The irregularity of a graph. Ars Comb. 46, 219–225.

Google Scholar

Behzad, M., and Chartrand, G. (1947). No graph is perfect. Am. Math. Mon. 74, 962–963. doi:10.2307/2315277

CrossRef Full Text | Google Scholar

Bell, F. K. (1992). A note on the irregularity of graphs. Linear Algebra Appl. 161, 45–54. doi:10.1016/0024-3795(92)90004-t

CrossRef Full Text | Google Scholar

Chartrand, G., Erdos, P., and Oellermann, O. (1988). How to define an irregular graph. Coll. Math. J. 19, 36–42. doi:10.2307/2686701

CrossRef Full Text | Google Scholar

Collatz, L., and Sinogowitz, U. (1957). Spektren endlicher graphen. Abh. Math. Sem. Univ. Hambg. 21, 63–77.

Google Scholar

Dorogovtsev, S. N., and Mendes, J. F. F. (2000). Evolution of networks with aging of sites. Phys. Rev. E 62, 1842–1845. doi:10.1103/physreve.62.1842

PubMed Abstract | CrossRef Full Text | Google Scholar

Erdös, P., and Rényi, A. (1960). on the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5, 17–61.

Google Scholar

Estrada, E., Torres, L., Rodríguez, L., and Gutman, I. (1998). An atom–bond connectivity index: modeling the enthalpy of formation of alkanes. Indian. J. Chem. 37, 849–855.

Google Scholar

Gao, W., Aamir, M., Iqbal, Z., Ishaq, M., and Aslam, A. (2019). On irregularity measures of some dendrimers structures. Mathematics 7, 271. doi:10.3390/math7030271

CrossRef Full Text | Google Scholar

Gao, W., Abdo, H., and Dimitrov, D. (2017). On the irregularity of some molecular structures. Can. J. Chem. 95, 174–183. doi:10.1139/cjc-2016-0539

CrossRef Full Text | Google Scholar

Govardhan, S., Roy, S., Balasubramanian, K., and Prabhu, S. (2023). Topological indices and entropies of triangular and rhomboidal tessellations of kekulenes with applications to NMR and ESR spectroscopies. J. Math. Chem. 61, 1477–1490. doi:10.1007/s10910-023-01465-9

CrossRef Full Text | Google Scholar

Gutman, I. (2018). Topological indices and irregularity measures. J. Bull. 8, 469–475. doi:10.7251/BIMVI1803469G

CrossRef Full Text | Google Scholar

Gutman, I., and Polansky, O. E. (1986). Mathematical concepts in organic chemistry. New York, NY, USA: Springer.

Google Scholar

Horoldagva, B., Buyantogtokh, L., Dorjsembe, S., and Gutman, I. (2016). Maximum size of maximally irregular graphs. Match Commun. Math. Comput. Chem. 76, 81–98.

Google Scholar

Hu, Y., Li, X., Shi, Y., Xu, T., and Gutman, I. (2005). On molecular graphs with smallest and greatest zeroth-Corder general randic index. MATCH Commun. Math. Comput. Chem. 54, 425–434.

Google Scholar

Hussain, Z., Munir, M., Rafique, S., Hussnain, T., Ahmad, H., Chel Kwun, Y., et al. (2019a). Imbalance-based irregularity molecular descriptors of nanostar dendrimers. Processes 7, 517. doi:10.3390/pr7080517

CrossRef Full Text | Google Scholar

Hussain, Z., Rafique, S., Munir, M., Athar, M., Chaudhary, M., Ahmad, H., et al. (2019b). Irregularity molecular descriptors of hourglass, jagged-rectangle, and triangular benzenoid systems. Processes 7, 413. doi:10.3390/pr7070413

CrossRef Full Text | Google Scholar

Jiang, J., Zhao, Y., and Yaghi, O. M. (2016). Covalent chemistry beyond molecules. J.Am. Chem. Soc. 138 (10), 3255–3265. doi:10.1021/jacs.5b10666

PubMed Abstract | CrossRef Full Text | Google Scholar

Krapivsky, P. L., Redner, S., and Leyvraz, F. (2000). Connectivity of growing random networks. Phys. Rev. Lett. 85, 4629–4632. doi:10.1103/physrevlett.85.4629

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., and Gutman, I. (2006). Mathematical aspects of Randic, Type molecular structure descriptors. Math. Chem. Monogr. Univ. Kragujevac Fac. Sci. Kragujevac Kragujevac, Serbia.

Google Scholar

Liu, F., Zhang, Z., and Meng, J. (2014). The size of maximally irregular graphs and maximally irregular triangle–free graphs. Graphs Comb. 30, 699–705. doi:10.1007/s00373-013-1304-1

CrossRef Full Text | Google Scholar

Liu, Y., Ma, Y., Zhao, Y., Sun, X., Gándara, F., Furukawa, H., et al. (2016). Weaving of organic threads into a crystalline covalent organic framework. Adv. Colloid Interface Sci. 351, 365–369. doi:10.1126/science.aad4011

PubMed Abstract | CrossRef Full Text | Google Scholar

Majcher, Z., and Michael, J. (1997). Highly irregular graphs with extreme numbers of edges. Discr. Math. 164, 237–242. doi:10.1016/s0012-365x(96)00056-8

CrossRef Full Text | Google Scholar

Prabhu, S., Arulperumjothi, M., Ghani, M. U., Imran, M., Salu, S., and Jose, B. K. (2023). Computational analysis of some more rectangular tessellations of kekulenes and their molecular characterizations. Molecules 28 (18), 6625. doi:10.3390/molecules28186625

PubMed Abstract | CrossRef Full Text | Google Scholar

Prabhu, S., Arulperumjothi, M., Manimozhi, V., and Balasubramanian, K. (2024). Topological characterizations on hexagonal and rectangular tessellations of antikekulenes and its computed spectral, nuclear magnetic resonance and electron spin resonance characterizations. Int. J. Quantum Chem. 124 (7), e27365. doi:10.1002/qua.27365

CrossRef Full Text | Google Scholar

Reti, T., Sharfdini, R., Dregelyi-Kiss, A., and Hagobin, H. (2018). Graph irregularity indices Used as molecular discriptors in QSPR studies. MATCH Commun. Math. Comput. Chem. 79, 509–524.

Google Scholar

Saravanan, B., Prabhu, S., Arulperumjothi, M., Julietraja, K., and Siddiqui, M. K. (2022). Molecular structural characterization of supercorenene and triangle-shaped discotic graphene. Polycycl. Aromat. Compd. 43 (3), 2080–2103. doi:10.1080/10406638.2022.2039224

CrossRef Full Text | Google Scholar

Xie, Q., Wang, Z., Munir, M., and Ahmad, H. (2019). Molecular irregularity indices of nanostar, fullerene and polymer dendrimers, to appear. J. Chem.

Google Scholar

Zahid, I., Aslam, A., Ishaq, M., and Aamir, M. (2019). Characteristic study of irregularity measures of some Nanotubes. Can. J. Phys. 97, 1125–1132. doi:10.1139/cjp-2018-0619

CrossRef Full Text | Google Scholar

Zhang, X., Prabhu, S., Arulperumjothi, M., Arockiaraj, M., and Manimozhi, V. (2024). Distance based topological characterization, graph energy prediction, and NMR patterns of benzene ring embedded in P-type surface in 2D network. Sci. Rep. 14, 23766. doi:10.1038/s41598-024-75193-8

PubMed Abstract | CrossRef Full Text | Google Scholar