Efficient implementation of analytical gradients for periodic hybrid functional calculations within fitted numerical atomic orbitals from NAO2GTO

The NAO2GTO scheme provides an efficient way to evaluate the electron repulsion integrals (ERIs) over numerical atomic orbitals (NAOs) with auxiliary Gaussian-type orbitals (GTOs). However, the NAO2GTO fitting will significantly impact the accuracy and convergence of hybrid functional calculations. To address this issue, here we propose to use the fitted orbitals as a new numerical basis to properly handle the mismatch between NAOs and fitted GTOs. We present an efficient and linear-scaling implementation of analytical gradients of Hartree-Fock exchange (HFX) energy for periodic HSE06 calculations with fitted NAOs in the HONPAS package. In our implementation, the ERIs and their derivatives for HFX matrix and forces are evaluated analytically with the auxiliary GTOs, while other terms are calculated using numerically discretized GTOs. Several integral screening techniques are employed to reduce the number of required ERI derivatives. We benchmark the accuracy and efficiency of our implementation and demonstrate that our results of lattice constants, bulk moduli, and band gaps of several typical semiconductors are in good agreement with the experimental values. We also show that the calculation of HFX forces based on a master-worker dynamic parallel scheme has a very high efficiency and scales linearly with respect to system size. Finally, we study the geometry optimization and polaron formation due to an excess electron in rutile TiO₂ by means of HSE06 calculations to further validate the applicability of our implementation.

1 Introduction

The Kohn-Sham density-functional theory (KS-DFT) (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) has become the most popular method for predicting the structural and electronic properties of molecular and condensed-matter systems. The success of DFT is attributed to the fact that the local-density approximation (LDA) (Kohn and Sham, 1965) and semilocal generalized-gradient approximation (GGA) (Perdew, 1985; Perdew et al., 1996) for exchange-correlation energy functional can provide reasonable accuracy at a low computational cost. However, local or semilocal functionals severely underestimate band gaps of semiconductors due to their intrinsic self-interaction error (Mori-Sánchez et al., 2008). Dramatic improvements can be achieved by incorporating a certain fraction of non-local orbital-dependent Hartree-Fock exchange (HFX) into the local or semilocal exchange, producing so-called hybrid functionals (Stephens et al., 1994; Adamo and Barone, 1999; Ernzerhof and Scuseria, 1999; Heyd et al., 2003, 2006; Krukau et al., 2006). In particular, the Heyd–Scuseria–Ernzerhof (HSE) screened hybrid functional (HSE03 (Heyd et al., 2003) or HSE06 (Heyd et al., 2006; Krukau et al., 2006)) is the most successful one in solid-state physics, which employs only a short-range HFX to avoid the problematic effects of long-range one in solids (Janesko et al., 2009). It has been shown that HSE can yield improved results of structural, thermochemical, and electronic properties for both molecules and solids (Paier et al., 2006b,a; Marsman et al., 2008; Henderson et al., 2011). Nevertheless, the evaluation of exact exchange is significantly more expensive than the local or semilocal approximations, which formally has a quartic scaling $\mathcal{O}(N^4)$ with system size N and hinders the wide applications of hybrid functionals. As a result, it is of great importance to develop and implement efficient and linear-scaling approaches for large-scale hybrid functional calculations.

The success of hybrid functionals has also prompted the development of efficient numerical techniques for reducing the computational cost and scaling of HFX calculations in the past two decades. Currently, hybrid functional calculations for periodic systems are available in a range of DFT packages with plane-wave (PW) (Marsman et al., 2008; Spencer and Alavi, 2008; Broqvist et al., 2009; Hu et al., 2017b), Gaussian-type orbital (GTO) (Heyd et al., 2003; Guidon et al., 2008; Lee et al., 2022), and numerical atomic orbital (NAO) (Shang et al., 2011; Levchenko et al., 2015; Qin et al., 2015; Lin et al., 2020) basis sets. For PW basis sets, a low-rank approximation called adaptively compressed exchange (ACE) (Lin, 2016; Hu et al., 2017a) operator has been proposed, resulting in significant acceleration of hybrid functional calculations. When combined with the interpolative separable density fitting (ISDF) algorithm (Lu and Ying, 2015; Hu et al., 2017b), the overall computational scaling can be further reduced to $\mathcal{O}(N^3)$. However, linear-scaling hybrid functional calculations within PWs cannot be achieved unless extended KS orbitals are converted to maximally localized Wannier functions (Wu et al., 2009; Ko et al., 2020). To enable linear-scaling hybrid functional calculations, one has to exploit the sparsity of HFX matrix represented with real-space localized basis functions. In this context, GTOs exhibit a natural advantage since they are analytical and decay exponentially in real space. Within GTOs, four-center electron repulsion integrals (ERIs) for constructing the HFX matrix can be evaluated analytically (Reine et al., 2012) and a number of linear-scaling approaches (Burant et al., 1996; Schwegler and Challacombe, 1996; Schwegler et al., 1997; Ochsenfeld et al., 1998) existed in the quantum chemistry community can be used as valuable references. Because of this, GTO-based electronic structure packages such as CP2K(Kühne et al., 2020), CRYSTAL (Dovesi et al., 2020), Q-Chem (Lee et al., 2022), and Pyscf (Sun et al., 2020) have made great progress in periodic HFX calculations.

In fact, current linear-scaling electronic structure packages, such as SIESTA (Soler et al., 2002), CONQUEST (Torralba et al., 2008), OPENMX (Ozaki and Kino, 2005), FHI-aims (Blum et al., 2009), HONPAS(Qin et al., 2015; 2020a) and ABACUS(Li et al., 2016), prefer to adopt NAO basis sets. Compared to exponentially decayed GTOs, NAOs are strictly localized in real space, which provides greater convenience for linear-scaling calculations. However, hybrid functional calculations with NAOs are more challenging since the numerical evaluation of ERIs is much more time-consuming. To reduce the computational cost, three possible routes can be taken. The first route is to expand the products of NAOs in terms of PWs (Chen et al., 2018; Lin et al., 2020), and the computational cost of HFX can be asymptotically quadratic due to the locality of NAOs. The second route is to introduce low-rank approximations, such as the resolution-of-the-identity (RI) approach (Ren et al., 2012; Levchenko et al., 2015; Lin et al., 2020, 2021) and the ISDF decomposition (Qin et al., 2020b,c), which can significantly reduce the computational cost by avoiding four-center integrals. Furthermore, linear-scaling HFX calculation can be implemented by using the localized RI (LRI) approximation (Levchenko et al., 2015; Lin et al., 2020). The third route is to fit the NAOs with a linear combination of several GTOs so that the ERIs can also be calculated analytically with fitted GTOs. We have previously proposed this scheme called NAO2GTO (Shang et al., 2011) to take full advantages of both NAOs and GTOs. In conjunction with several integral screening techniques, HFX calculations based on the NAO2GTO scheme can be very efficient and scale linearly (Shang et al., 2011; Qin et al., 2015). In practice, however, the NAOs cannot be fitted accurately with a small number (e.g., 3–6) of GTOs, which will seriously affects the accuracy and even the convergence of a hybrid functional calculation. We can improve the results by increasing the number of GTOs, but too many GTOs will significantly increase the computational cost of ERIs. To effectively utilize the NAO2GTO scheme for NAO-based hybrid functional calculations, it is crucial to address the mismatch between NAOs and fitted GTOs.

On the other hand, there have been few reports on analytical energy gradients (atomic forces) for periodic hybrid functional calculations with NAOs to date. Atomic forces are defined as analytical gradients of total energy to atomic positions, which are required for geometry optimization and ab initio molecular dynamics simulations. In the PW method, the two-electron HFX term has no contribution to atomic forces according to the Hellmann–Feynman theorem (Feynman, 1939) since the PW basis set is orthogonal and independent of the atomic positions. However, the situation becomes more complicated for NAOs, where the atomic forces also include Pulay corrections (Pulay, 1969) due to changes in the basis functions with respect to atomic positions. For the HFX forces, it is necessary to compute the first derivatives of ERIs in order to obtain analytical gradients of the HFX energy. The NAO2GTO scheme combined with integral screening also provides an efficient way to analytically evaluate the ERI derivatives over NAOs. Therefore, the implementation of HFX forces with NAOs is relatively straightforward.

In this work, we aim to extend the linear-scaling approach for the HFX force calculations of periodic systems based on the NAO2GTO scheme in the HONPAS package. In our approach, the original NAOs are replaced by fitted GTOs, so as to eliminate the errors introduced by the NAO2GTO fitting as much as possible. The ERI derivatives are analytically evaluated with the NAO2GTO scheme, and the computational cost is reduced by using integral screening techniques, enabling linear-scaling HFX force calculations. A master-worker dynamic parallel strategy is also adopted to achieve high parallel efficiency. We benchmark the accuracy and efficiency of our implementation by performing HSE06 calculations for periodic systems and apply it to investigate the small polaronic behavior of excess electrons in rutile TiO₂. The rest of the paper is organized as follows. Section 2 reviews the theoretical framework. Section 3 provides a detailed description of our approach and implementation. Section 4 validates the performance of our implementation. A summary is given in Section 5.

2 Theory

2.1 Hybrid functional for periodic systems

Hybrid functionals currently used in the generalized KS framework contain a fraction of non-local, exact HFX term. In the PBE0 hybrid functional (also known as PBEh or PBE1PBE) (Adamo and Barone, 1999; Ernzerhof and Scuseria, 1999), the exchange-correlation energy is written as

$E_{\text{xc}}^{\text{PBE0}}=\frac{1}{4}{E}_{\mathrm{x}}^{\text{HF}}+\frac{3}{4}{E}_{\mathrm{x}}^{\text{PBE}}+E_{\mathrm{c}}^{\text{PBE}}(1)$

where 25% HFX $E_{\mathrm{x}}^{\text{HF}}$ is mixed with 75% Perdew-Burke–Ernzerhof (PBE) exchange $E_{\mathrm{x}}^{\text{PBE}}$, and the electronic correlation is still represented by the part of the PBE correlation $E_{\mathrm{c}}^{\text{PBE}}$. The inclusion of the HFX in PBE0 reduces the self-interaction error of the density functional, resulting in a substantial improvement over the parent PBE. However, the full-range (FR) HFX is computationally very demanding and may be problematic in solids. To address this issue, Heyd, Scuseria, and Ernzerhof (Heyd et al., 2003; Heyd et al., 2006) proposed to replace the long-range part of HFX in the PBE0 by a corresponding PBE counterpart. Then, the resulting expression for the HSE exchange–correlation energy is given by

$E_{\text{xc}}^{\text{HSE}}=\frac{1}{4}{E}_{\mathrm{x}}^{\text{SR,HF}}\left(\omega \right)+\frac{3}{4}{E}_{\mathrm{x}}^{\text{SR,PBE}}\left(\omega \right)+E_{\mathrm{x}}^{\text{LR,PBE}}\left(\omega \right)+E_{\mathrm{c}}^{\text{PBE}}(2)$

where $E_{\mathrm{x}}^{\text{SR,HF}}$ and $E_{\mathrm{x}}^{\text{LR,PBE}}(\omega )$ is the short-range (SR) HFX and long-range (LR) PBE exchange energies, and $E_{\mathrm{x}}^{\text{SR,PBE}}(\omega )$ is the SR exchange energy. ω is an adjustable screening parameter that defines the range separation, and ω is set to 0.11 Bohr⁻¹ for HSE06 (Heyd et al., 2006). Such a treatment not only improves the computational convenience but also avoids the problematic effects of LR HFX in metals and semiconductors with narrow band gaps.

For periodic systems, the HFX energy per unit cell can be written as

$E_{\mathrm{x}}^{\text{HF}}=-\frac{1}{2}{\displaystyle \sum _{\sigma =\left\{\alpha ,\beta \right\}}}{\displaystyle \sum _{\mathbf{k},\mathbf{q}}^{\text{BZ}}}\times {\displaystyle \sum _{i,j}^{\text{occ}}}{\int }_{\mathrm{\Omega }}\int {\psi }_{i\mathbf{k}}^{\sigma *}\left(\mathbf{r}\right){\psi }_{j\mathbf{q}}^{\sigma }\left(\mathbf{r}\right)\widehat{v}\left(\mathbf{r},{\mathbf{r}}^{\prime }\right){\psi }_{j\mathbf{q}}^{\sigma *}\left({\mathbf{r}}^{\prime }\right){\psi }_{i\mathbf{k}}^{\sigma }\left({\mathbf{r}}^{\prime }\right)\mathrm{d}{\mathbf{r}}^{\prime }\mathrm{d}\mathbf{r}(3)$

where ${\psi }_{i\mathbf{k}}^{\sigma }(\mathbf{r})$ denote the i-th occupied (occ) crystalline spin-orbitals with spin σ for k point sampling in the Brillouin zone (BZ), Ω is the unit cell volume. $E_{\mathrm{x}}^{\text{HF}}$ is used to represent the FR or SR HFX energy, and $\widehat{v}(\mathbf{r},{\mathbf{r}}^{\prime })$ is either the Coulomb operator $\widehat{v}(\mathbf{r},{\mathbf{r}}^{\prime })=1/|\mathbf{r}-{\mathbf{r}}^{\prime }|$ in PBE0 or the screened Coulomb operator $\widehat{v}(\mathbf{r},{\mathbf{r}}^{\prime })=\mathbf{e}\mathbf{r}\mathbf{f}\mathbf{c}(\omega |\mathbf{r}-{\mathbf{r}}^{\prime }|)/|\mathbf{r}-{\mathbf{r}}^{\prime }|$ in HSE. Hereafter, we will formulate only the collinear spin-polarized case with σ = {α, β}.

In the linear combination of atomic orbitals (LCAO) method, the spin-orbitals are expanded in terms of a linear combination of Bloch basis functions

${\psi }_{i\mathbf{k}}^{\sigma }\left(\mathbf{r}\right)=\frac{1}{\sqrt{N}}{\displaystyle \sum _n^N}{\mathbf{e}}^{\mathrm{i}\mathbf{k}\mathbf{R}}{\displaystyle \sum _{\mu }^{N_{\mathrm{b}}}}{c}_{\mu }^{\sigma }\left(\mathbf{k}\right){\varphi }_{\mu }\left(\mathbf{r}-{\mathbf{r}}_{\mu }-\mathbf{R}\right)(4)$

where ϕ_μ(r − r_μ − R) denotes the μ-th NAO centering at r_μ within a lattice translation vector R, $c_{\mu }^{\sigma }(\mathbf{k})$ is the expansion coefficient, and N is the number of primitive unit cells under the Born-von Kármán (BvK) periodic boundary conditions. Within NAOs, the HFX matrix for the self-consistent field (SCF) calculations can be written as

${\left[H_{\mathrm{x}}^{\sigma ,\mathrm{H}\mathrm{F}}\right]}_{\mu \kappa }^{\mathbf{G}}=-{\displaystyle \sum _{\nu \lambda }}{\displaystyle \sum _{\mathbf{N},\mathbf{H}}}{P}_{\nu \lambda }^{\sigma ,\mathbf{H}-\mathbf{N}}\left({\mu }^0{\nu }^{\mathbf{N}}|{\kappa }^{\mathbf{G}}{\lambda }^{\mathbf{H}}\right)(5)$

and the corresponding HFX energy can be obtained by

$E_{\mathrm{x}}^{\text{HF}}=-\frac{1}{2}\sum _{\sigma }\sum _{\mu \nu \kappa \lambda }\sum _{\mathbf{G},\mathbf{N},\mathbf{H}}{P}_{\mu \kappa }^{\sigma ,\mathbf{G}}{P}_{\nu \lambda }^{\sigma ,\mathbf{H}-\mathbf{N}}\left({\mu }^{\mathbf{0}}{\nu }^{\mathbf{N}}|{\kappa }^{\mathbf{G}}{\lambda }^{\mathbf{H}}\right)(6)$

where the subscripts of Greek letters {μ, ν, κ, λ} label NAOs, the superscript 0 represents the reference primitive unit cell, while G, N, and H represent extended unit cells in the BvK supercells. The $P_{\mu \kappa }^{\sigma ,\mathbf{G}}$ is the spin density matrix element, which can be obtained by an integration of the expanded coefficients in the BZ

$P_{\mu \kappa }^{\sigma ,\mathbf{G}}={\displaystyle \sum _j}{\int }_{\text{BZ}}{c}_{\mu ,j}^{\sigma \ast }\left(\mathbf{k}\right)c_{\kappa ,j}^{\sigma }\left(\mathbf{k}\right)\theta \left({ϵ}_{\mathrm{F}}-{ϵ}_j^{\sigma }\left(\mathbf{k}\right)\right)e^{i\mathbf{k}\mathbf{G}}\mathrm{d}\mathbf{k}(7)$

where θ represent the step function, ϵ_F is the fermi energy and ${ϵ}_j^{\sigma }(\mathbf{k})$ is the j-th eigenvalue at k. For hybrid functional calculations with NAOs, the main bottleneck is the evaluation of ERIs

$\begin{array}{c}\hfill \left({\mu }^{\mathbf{0}}{\nu }^{\mathbf{N}}|{\kappa }^{\mathbf{G}}{\lambda }^{\mathbf{H}}\right)=\iint {\varphi }_{\mu }^{\mathbf{0}}\left(\mathbf{r}\right){\varphi }_{\nu }^{\mathbf{N}}\left(\mathbf{r}\right)\widehat{v}\left(\mathbf{r},{\mathbf{r}}^{\prime }\right){\varphi }_{\kappa }^{\mathbf{G}}\left({\mathbf{r}}^{\prime }\right){\varphi }_{\lambda }^{\mathbf{H}}\left({\mathbf{r}}^{\prime }\right)\mathrm{d}\mathbf{r}\mathrm{d}{\mathbf{r}}^{\prime }\end{array}(8)$

2.2 Analytical gradients of HFX energy

Since the NAOs are dependent of atomic positions, in hybrid functional calculations we must additionally calculate the HFX contribution to atomic forces. TheHFX forces acting on the I-th atom can be directly obtained from the negative gradients of the HFX energy with respect to atomic position R_I

$\begin{array}{cc}\hfill F_I^{\text{HF}}& =-\frac{\partial E_{\mathrm{x}}^{\text{HF}}}{\partial {\mathbf{R}}_I}\hfill \\ \hfill & ={\displaystyle \sum _{\sigma }}{\displaystyle \sum _{\mu \kappa }}\frac{\partial P_{\mu \kappa }^{\sigma ,\mathbf{G}}}{\partial {\mathbf{R}}_I}{\displaystyle \sum _{\nu \lambda }}{\displaystyle \sum _{\mathbf{N},\mathbf{H}}}{P}_{\nu \lambda }^{\sigma ,\mathbf{H}-\mathbf{N}}\left({\mu }^{\mathbf{0}}{\nu }^{\mathbf{N}}|{\kappa }^{\mathbf{G}}{\lambda }^{\mathbf{H}}\right)\hfill \\ \hfill & +\frac{1}{2}{\displaystyle \sum _{\sigma }}{\displaystyle \sum _{\mu \nu \kappa \lambda }}{\displaystyle \sum _{\mathbf{G},\mathbf{N},\mathbf{H}}}{P}_{\mu \kappa }^{\sigma ,\mathbf{G}}{P}_{\nu \lambda }^{\sigma ,\mathbf{H}-\mathbf{N}}\frac{\partial \left({\mu }^{\mathbf{0}}{\nu }^{\mathbf{N}}|{\kappa }^{\mathbf{G}}{\lambda }^{\mathbf{H}}\right)}{\partial {\mathbf{R}}_I}\hfill \end{array}(9)$

Note that the first term in Eq. 9 can be rewritten as

${\displaystyle \sum _{\mu \kappa }}\frac{\partial P_{\mu \kappa }^{\sigma ,\mathbf{G}}}{\partial {\mathbf{R}}_I}{\displaystyle \sum _{\nu \lambda }}{\displaystyle \sum _{\mathbf{N},\mathbf{H}}}{P}_{\nu \lambda }^{\sigma ,\mathbf{H}-\mathbf{N}}\left({\mu }^{\mathbf{0}}{\nu }^{\mathbf{N}}|{\kappa }^{\mathbf{G}}{\lambda }^{\mathbf{H}}\right)=-{\displaystyle \sum _{\mu \kappa }}{\left[H_{\mathrm{x}}^{\sigma ,\mathrm{H}\mathrm{F}}\right]}_{\mu \kappa }^{\mathbf{G}}\frac{\partial P_{\mu \kappa }^{\sigma ,\mathbf{G}}}{\partial {\mathbf{R}}_I}(10)$

which is automatically included in the orthogonalization force due to the non-orthonormality of the NAO basis set (Soler et al., 2002; Li et al., 2016). For periodic systems, the orthogonalization force is given by

$F_I^{\text{orth}}=-{\displaystyle \sum _{\sigma }}{\displaystyle \sum _{\mu \kappa }}{H}_{\mu \kappa }^{\sigma ,\mathbf{G}}\frac{\partial P_{\mu \kappa }^{\sigma ,\mathbf{G}}}{\partial {\mathbf{R}}_I}={\displaystyle \sum _{\sigma }}{\displaystyle \sum _{\mu \kappa }}{E}_{\mu \kappa }^{\sigma ,\mathbf{G}}\frac{\partial S_{\mu \kappa }^{\mathbf{G}}}{\partial {\mathbf{R}}_I}.(11)$

where $S_{\mu \lambda }^{\mathbf{G}}=⟨{\varphi }_{\mu }^{\mathbf{0}}|{\varphi }_{\lambda }^{\mathbf{G}}⟩$ is the overlap matrix element, and $E_{\mu \lambda }^{\sigma ,\mathbf{G}}$ is the energy-density matrix element given by

$E_{\mu \kappa }^{\sigma ,\mathbf{G}}={\displaystyle \sum _j}{\int }_{\text{BZ}}{c}_{\mu ,j}^{\sigma *}\left(\mathbf{k}\right)c_{\kappa ,j}^{\sigma }\left(\mathbf{k}\right){ϵ}_j^{\sigma }\left(\mathbf{k}\right)e^{\mathrm{i}\mathbf{k}\mathbf{G}}\mathrm{d}\mathbf{k}(12)$

where ${ϵ}_j^{\sigma }(\mathbf{k})$ is the eigenstate energy.

Thus, we only need to deal with the second term

$\begin{array}{cc}\hfill & \frac{1}{2}{\displaystyle \sum _{\sigma }}{\displaystyle \sum _{\mu \nu \kappa \lambda }}{\displaystyle \sum _{\mathbf{G},\mathbf{N},\mathbf{H}}}{P}_{\mu \kappa }^{\sigma ,\mathbf{G}}{P}_{\nu \lambda }^{\sigma ,\mathbf{H}-\mathbf{N}}\frac{\partial \left({\mu }^{\mathbf{0}}{\nu }^{\mathbf{N}}|{\kappa }^{\mathbf{G}}{\lambda }^{\mathbf{H}}\right)}{\partial {\mathbf{R}}_I}\hfill \\ \hfill & =\frac{1}{2}{\displaystyle \sum _{\sigma }}{\displaystyle \sum _{\mu \nu \kappa \lambda }}{\displaystyle \sum _{\mathbf{G},\mathbf{N},\mathbf{H}}}{P}_{\mu \kappa }^{\sigma ,\mathbf{G}}{P}_{\nu \lambda }^{\sigma ,\mathbf{H}-\mathbf{N}}\hfill \\ \hfill & \times \left(\frac{\partial {\varphi }_{\mu }^{\mathbf{0}}}{\partial {\mathbf{R}}_I}{\varphi }_{\nu }^{\mathbf{N}}|{\varphi }_{\kappa }^{\mathbf{G}}{\varphi }_{\lambda }^{\mathbf{H}}\right)+\left({\varphi }_{\mu }^{\mathbf{0}}\frac{\partial {\varphi }_{\nu }^{\mathbf{N}}}{\partial {\mathbf{R}}_I}|{\varphi }_{\kappa }^{\mathbf{G}}{\varphi }_{\lambda }^{\mathbf{H}}\right)+\left({\varphi }_{\mu }^{\mathbf{0}}{\varphi }_{\nu }^{\mathbf{N}}|\frac{\partial {\varphi }_{\kappa }^{\mathbf{G}}}{\partial {\mathbf{R}}_I}{\varphi }_{\lambda }^{\mathbf{H}}\right)+\left({\varphi }_{\mu }^{\mathbf{0}}{\varphi }_{\nu }^{\mathbf{N}}|{\varphi }_{\kappa }^{\mathbf{G}}\frac{\partial {\varphi }_{\lambda }^{\mathbf{H}}}{\partial {\mathbf{R}}_I}\right)\hfill \end{array}(13)$

in which the ERI derivatives have to be evaluated properly. Since each ERI may have four different centers, a maximum of 12 differentials is required. Therefore, the calculation of HFX forces is formally more troublesome than that of HFX matrix, and a poor implementation will decrease the overall performance.

3 Methodology

3.1 NAO2GTO scheme

A normalized NAO for atom I located at R_I is defined as the product of a numerical radial function and a real regular solid harmonic (Soler et al., 2002)

${\varphi }_{\mathit{Ilm\zeta }}^{\text{NAO}}\left(\mathbf{r}\right)={\varphi }_{Il\zeta }^{\text{NAO}}\left(r_I\right)\left[r_I^l{Y}_{lm}\left(\theta ,\phi \right)\right](14)$

where r_I = r − R_I, r_I = |r_I|, l and m label the angular and magnetic momentum quantum numbers, respectively. In multiple-ζ bases, ζ labels different basis with the same quantum numbers (l, m) but different radial shapes. For simplicity, we will omit the index ζ later. The numerical radial function involves a normalization factor N (l, α) and is numerically tabulated in a linear radial mesh. $[r_I^l{Y}_{lm}(\theta ,\phi )]$ also includes its individual normalization factor. NAOs are strictly localized in real space, which provides greater convenience for linear-scaling DFT calculations. However, the evaluation of ERIs over NAOs in real space is computationally expensive, which will introduce a big prefactor in linear-scaling HFX calculations (Shang et al., 2010).

In the LCAO framework, GTOs are by far the most commonly used basis functions to represent the molecular orbitals. This preference is mainly due to the analytical properties of GTOs, which allow efficient evaluation of ERIs for (post-)Hartree-Fock calculations. A normalized primitive spherical harmonic GTO is defined as

${\varphi }_{\mathit{Ilm\alpha }}^{\text{GTO}}\left(\mathbf{r}\right)=N\left(l,\alpha \right)\exp \left(-\alpha r_I^2\right)\left[r_I^l{Y}_{lm}\left(\theta ,\phi \right)\right](15)$

where α is the orbital exponent, and N (l, α) is the normalization factor over the radial coordinates

$N\left(l,\alpha \right)={\left[\frac{2^{2l+3}\left(l+1\right)!{\alpha }^{l+3/2}}{\left(2l+2\right)!{\pi }^{1/2}}\right]}^{1/2}(16)$

It is worth noting that most efficient algorithms for the evaluation of ERIs are based on Cartesian primitive GTOs

$G_{l\alpha }\left(\mathbf{r}\right)=N\left(l_x,l_y,l_z,\alpha \right){\left(x-R_x\right)}^{l_x}{\left(x-R_y\right)}^{l_y}{\left(z-R_z\right)}^{l_z}\exp \left[-\alpha {\left(\mathbf{r}-{\mathbf{R}}_I\right)}^2\right](17)$

where l = l_x + l_y + l_z labels the angular-momentum quantum number, R_I = (R_x, R_y, R_z) is the orbital center, and N (l_x, l_y, l_z, α) is the normalization factor

$N\left(l_x,l_y,l_z,\alpha \right)=\left[{\left(\frac{2}{\pi }\right)}^{3/4}\frac{2^l{\alpha }^{\left(2l+3\right)/4}}{{\left[\left(2l_x-1\right)‼\left(2l_y-1\right)‼\left(2l_z-1\right)‼\right]}^{1/2}}\right](18)$

For a shell of angular momentum l, there will be 2l + 1 spherical GTOs, but (l + 1) (l + 2)/2 Cartesian GTOs. The transformation between normalized spherical and Cartesian GTOs is required with a transformation matrix c (l, m, l_x, l_y, l_z) given by Schlegel and Frisch (Schlegel and Frisch, 1995).

In order to obtain ERIs efficiently, we can represent the NAOs in terms of a linear combination of spherical primitive GTOs, and then calculate the ERIs analytically by calling available libraries for GTO-based integrals (e.g. LIBINT (Valeev and Fermann, 2014)). This scheme is called NAO2GTO, which in principle is quite similar to the minimal STO-nG basis set used in the quantum chemistry community. In the NAO2GTO scheme, the numerical radial function of each NAO is fitted as a linear combination of different Gaussians,

${\varphi }_l^{\text{NAO}}\left(r\right)\simeq {\varphi }_l^{\text{CGTO}}\left(r\right)={\displaystyle \sum _{i=1}^M}{D}_i\exp \left(-{\alpha }_i{r}^2\right)(19)$

where M is the number of Gaussians, α_i and D_i are the contraction coefficient and exponent, respectively, similar to contracted GTOs (CGTOs).

3.2 Replace NAOs with discretized CGTOs

If the NAO2GTO fitting is strictly accurate, the fitted orbitals will be automatically normalized because of the normalization of NAOs. Once there is a non-negligible fitting error, the fitted orbitals will not be normalized. Since normalization factors between NAOs and CGTOs are different, the following approximation will no longer hold

${\varphi }_{lm}^{\text{NAO}}\left(\mathbf{r}\right)\ne {\varphi }_{lm}^{\text{CGTO}}=N\left(l,\alpha ,\mathbf{D}\right){\displaystyle \sum _{i=1}^M}{D}_i\exp \left(-{\alpha }_i{r}^2\right)r^l{Y}_{lm}\left(\theta ,\phi \right)(20)$

with a normalization factor

$N\left(l,\alpha ,\mathbf{D}\right)={\left[\frac{\left(2l+2\right)!{\pi }^{1/2}}{2^{2l+3}\left(l+1\right)!}{\displaystyle \sum _{i,j=1}^M}\frac{D_i{D}_j}{{\left({\alpha }_i+{\alpha }_j\right)}^{l+3/2}}\right]}^{-1/2}(21)$

where α = {α_i} and D = {D_i}. In practice, it is difficult to achieve an exact NAO2GTO fitting with a small number of GTOs, such as M = 3–6. Then, the NAO2GTO fitting will inevitably introduce the ERI errors between original NAOs and fitted CGTOs. In some cases, such errors can even invalidate the final results. In our previous work, we employed the fitted CGTOs to approximately evaluate the ERIs for the HFX term while retaining original NAOs for pure DFT parts. For most systems, we have found that a self-consistent convergence problem often arises in hybrid functional calculations even with high-precision fitting.

To eliminate the fitting errors properly, here we replace original NAOs with the fitted and discretized CGTOs, which is done as the following steps:

• Perform a less rigorous NAO2GTO fitting for each NAO to obtain a set of CGTOs according to Eq. 19;

• Calculate the normalization constant N (l, α, D) for each CGTO;

• Calculate the cutoff radius for each CGTO;

• Numerically tabulate the radial function of each CGTO multiplied by N (l, α, D).

Note that the fitted CGTOs will give larger cutoff radii compared to the original NAOs. Therefore, we need to feed the values inside a new cutoff radius back to the radial function, beyond which all values are equal to 0.

3.3 Evaluate ERIs and their derivatives with CGTOs

With the auxiliary CGTOs, one shell set of contracted ERIs (ab|cd) can be calculated by

$\left(ab|cd\right)={\displaystyle \sum _k^K}{\displaystyle \sum _l^L}{\displaystyle \sum _m^M}{\displaystyle \sum _n^N}{C}_{ak}{C}_{bl}{C}_{cm}{C}_{dn}\left[a_k{b}_l|c_m{d}_n\right](22)$

with

$C_{ak}=D_{ak}c\left(a,m,a_x,a_y,a_z\right)(23)$

where a denotes the shell orbital with angular momentum a = a_x + a_y + a_z, k is the index of K GTOs, and [a_kb_l|c_md_n] represents a set of primitive ERIs over primitive Cartesian GTOs, in which (2a + 1) (2b + 1) (2c + 1) (2d + 1) primitive and contacted ERIs are calculated at once.

Since a primitive ERI contain four centers of A, B, C, and D, its first-order derivatives should have the following 12 terms

$\frac{\partial \left[ab|cd\right]}{\partial A_i},\frac{\partial \left[ab|cd\right]}{\partial B_i},\frac{\partial \left[ab|cd\right]}{\partial C_i},\frac{\partial \left[ab|cd\right]}{\partial D_i}i\in \left\{x,y,z\right\}.(24)$

but only 9 derivatives are required because of the translational invariance

$\frac{\partial \left[ab|cd\right]}{\partial A_i}+\frac{\partial \left[ab|cd\right]}{\partial B_i}+\frac{\partial \left[ab|cd\right]}{\partial C_i}+\frac{\partial \left[ab|cd\right]}{\partial D_i}=0(25)$

Analogously, the first-order derivatives of contracted ERIs can also be evaluated from the primitive ones, which are actually a linear combination of higher and lower angular momentum ERIs

$\frac{\partial }{\partial A_i}\left[ab|cd\right]=2\alpha \left[\left(a+1_i\right)b|cd\right]-a_i\left[\left(a-1_i\right)b|cd\right](26)$

We obtain the primitive ERIs and their derivatives from the LIBINT library, (Valeev and Fermann, 2014) which implements efficient recursive schemes based on the Obara-Saika method (Obara and Saika, 1986) together with the Head-Gordon-Pople (Head-Gordon and Pople, 1988) and Hamilton-Lindh (Hamilton and Schaefer, 1991; Lindh et al., 1991) variations. We also consider the eight-fold permutational symmetry of ERIs with NAOs, which for periodic systems is given by

$\begin{array}{cc}\hfill & \left({\mu }^{\mathbf{0}}{\nu }^{\mathbf{N}}|{\kappa }^{\mathbf{G}}{\lambda }^{\mathbf{H}}\right)=\left({\mu }^{\mathbf{0}}{\nu }^{\mathbf{N}}|{\lambda }^{\mathbf{H}}{\kappa }^{\mathbf{G}}\right)=\left({\nu }^{\mathbf{0}}{\mu }^{-\mathbf{N}}|{\kappa }^{\mathbf{G}-\mathbf{N}}{\lambda }^{\mathbf{H}-\mathbf{N}}\right)=\left({\nu }^{\mathbf{0}}{\mu }^{-\mathbf{N}}|{\lambda }^{\mathbf{H}-\mathbf{N}}{\kappa }^{\mathbf{G}-\mathbf{N}}\right)\hfill \\ \hfill & =\left({\kappa }^{\mathbf{0}}{\lambda }^{\mathbf{N}-\mathbf{G}}|{\mu }^{-\mathbf{G}}{\nu }^{\mathbf{N}-\mathbf{G}}\right)=\left({\kappa }^{\mathbf{0}}{\lambda }^{\mathbf{N}-\mathbf{G}}|{\nu }^{\mathbf{N}-\mathbf{G}}{\mu }^{-\mathbf{G}}\right)=\left({\lambda }^{\mathbf{0}}{\kappa }^{\mathbf{G}-\mathbf{H}}|{\mu }^{-\mathbf{H}}{\nu }^{\mathbf{N}-\mathbf{H}}\right)=\left({\lambda }^{\mathbf{0}}{\kappa }^{\mathbf{G}-\mathbf{H}}|{\nu }^{\mathbf{N}-\mathbf{H}}{\mu }^{-\mathbf{H}}\right)\hfill \end{array}(27)$

In this way, we only need to handle about 1/8 of ERIs and their derivatives. Furthermore, the translational invariance also gives $\frac{\partial (\mu \mu |\mu \mu )}{\partial {\mathbf{R}}_{\mu }}=0$, which means that we can ignore the ERI derivatives if four orbitals have the same center.

3.4 Integral screening

In practice calculations, most of the ERIs and their derivatives have no significant contributions to the HFX matrix and forces, which can be omitted by using integral screening techniques. Thus, integral screening is essential for reducing the computational cost, which should be able to provide an easy-to-estimate upper bound for ERIs. We have previously employed several ERI screening techniques to obtain an efficient and linear-scaling HFX calculation (Shang et al., 2011; Qin et al., 2015). For the calculation of HFX forces, however, integral screening based on the upper bound of ERI derivatives is not a good choice. The reason is that, according to the Schwarz inequality (Häser and Ahlrichs, 1989), the upper bound of $(\frac{\partial \mu }{\partial {\mathbf{R}}_I}\nu |\lambda \sigma )$ requires a relatively expensive calculation of $(\frac{\partial \mu }{\partial {\mathbf{R}}_I}\nu |\frac{\partial \mu }{\partial {\mathbf{R}}_I}\nu )$(Horn et al., 1991), which does not appear in the ERI derivatives. Alternatively, we can use the same screening techniques based on the upper bound of ERIs as done in the construction of the HFX matrix. That is, if an ERI is skipped during the calculation of the HFX energy, its derivatives should also be neglected for the calculation of HFX forces. Here, we describe all the screening techniques we have employed to compute the HFX forces. For simplicity, we omit the superscripts of 0, G, N, and H later, and the indices {μ, ν, κ, λ} label shell orbitals in the following.

3.4.1 Schwarz screening with prametrized screening functions

The first integral screening is based on Cauthy-Schwarz inequality

$|\left(\mu \nu |\kappa \lambda \right)|\le |\left(\mu \nu |\mu \nu \right){|}^{1/2}|\left(\kappa \lambda |\kappa \lambda \right){|}^{1/2}(28)$

which gives a rigorous upper bound for an ERI or a set of ERIs. The Schwarz screening actually takes advantage of the exponential decay of the orbital-pair charge distributions Ω_μν(r − P) = χ_μ(r − R_μ)χ_ν(r − R_ν) to decrease the total number of ERIs to be considered from $\mathcal{O}(N^4)$ to $\mathcal{O}(N^2)$. To establish a straightforward Schwarz-screening procedure, we need to calculate and store two-center integrals as the screening matrix in the four-index (μ, ν, κ and λ) loop. However, this treatment is not efficient for large systems in which a large screening matrix is needed. Furthermore, it is inconvenient to employ the Schwarz screening for primitive ERIs since each shell quartet also requires calculating and storing its own screening matrix. In fact, it has been observed by Guidon et al. (2009) that the logarithm of a two-center ERI can be approximated as a quadratic function at a relatively large two-center distance R_μν between orbitals μ and ν

$\log |\left(\mu \nu |\mu \nu \right)|\left(R_{\mu \nu }\right)|\approx t_2{R}_{\mu \nu }^2+t_0.(29)$

These quadratic functions only depend on the two-center distance R_μν but have different parameters t₀ and t₂ for different types of orbitals. Thus, we can use a set of quadratic functions (screening functions) instead of the screening matrix to estimate the upper bounds of both primitive and contracted ERIs. We obtain the fitting parameters t₀ and t₂ by minimizing an asymmetric penalty function (Guidon et al., 2009),

$\sum _{i}k\left({\mathrm{\Delta }}_i\right){\mathrm{\Delta }}_i^2.(30)$

at a radial grid of $R_{\mu \nu }^i$ with the maximum distance $R_{\mu \nu }=R_c^{\mu }+R_c^{\nu }$, and the error is defined as

${\mathrm{\Delta }}_i=\log |\left(\mu \nu |\mu \nu \right)\left(R_{\mu \nu }\right)|-\left(t_2{R}_{\mu \nu }^2+t_0\right)(31)$

and

$k\left({\mathrm{\Delta }}_i\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{i}\mathrm{f}{\mathrm{\Delta }}_i<0;\hfill \\ 10^4\hfill & \mathrm{i}\mathrm{f}{\mathrm{\Delta }}_i\ge 0.\hfill \end{array}\right.(32)$

where the choice of k (Δ_i) ensures the fitted value at $R_{\mu \nu }^i$ is always not less than the true one. In Figure 1, we plot the fitting results for both primitive and contracted two-center integrals. It can be seen that the fitted value for each two-center distance is never less than the true one, indicating that the screening function can be approximately used as an upper bound in the Schwarz screening. As a result, we only need to fit the screening functions and store the fitting parameters for each type of shell pairs in advance, as shown in Algorithm 1 (Step 1).

FIGURE 1

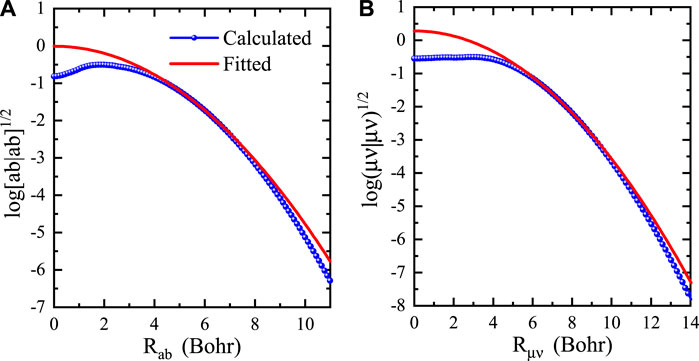
FIGURE 1. Logarithm of two-center integrals (blue solids) and fitting functions (red lines) as a function of the two-center distance for (A) primitive and (B) contracted integrals of p-type and d-type Si orbitals.

Algorithm 1. Flowchat of density matrix weighted Schwarz screening for HFX forces.

1: Step 1: Fit screening functions ⊳ For different types of shell orbitals

2: for is and js ∈ N_species do ⊳ Atomic species N_species

3: for μ ∈ is, ν ∈ js do

4: for a ∈ μ, b ∈ ν do

5: R_ab = R_a + R_b

6: Interpolate R_i and calculate[ab|ab](R_i)

7: Fit $\log |{[ab|ab]}^{1/2}(R_{ab})|\approx t_2^{ab}{R}_{ab}^2+t_0^{ab}$.

8: end for

9: R_μν = max{R_μν, R_ab}

10: Interpolate R_i and calculate (μν|μν)(R_i)

11: Fit $\log |{(\mu \nu |\mu \nu )}^{1/2}(R_{\mu \nu })|\approx t_2^{\mu \nu }{R}_{\mu \nu }^2+t_0^{\mu \nu }$

12: end for

13: end for

14: Step 2: Build shell-pair lists ⊳ For all shell orbitals

15: for μ = 1, N_b do

16: for ν = 1, μ do

17:  $t_2^{\text{max}}=\max \{t_2^{\text{max}},t_2^{\mu \nu }\}$

18:  $t_0^{\text{max}}=\max \{t_0^{\text{max}},t_0^{\mu \nu }\}$

19:  if $R_{\mu \nu }\le R_c^{\mu }+R_c^{\nu }$ and $(t_2^{\mu \nu }{R}_{\mu \nu }+t_0^{\mu \nu })+(t_2^{\text{max}}{R}_{\mu \nu }+t_0^{\text{max}})>\log {ϵ}_{\text{Schwarz}}$ then

20:  Add μ, ν to shell-pair list_μν

21:  end if

22:  end for

23:  end for

24:  Step3: Compute HFX forces

25:  for (μ, ν) ∈ list_μν do

26:  for (κ, λ) ∈ list_κλ do

27:  $P_{\text{max}}=2\times \max \{|P_{\mu \kappa }^{\sigma }|\times |P_{\nu \lambda }^{\sigma }|,|P_{\mu \lambda }^{\sigma }|\times |P_{\nu \kappa }^{\sigma }|\}$

28:  if $\log P_{\text{max}}+t_2^{\mu \nu }{R}_{\mu \nu }+t_0^{\mu \nu }+t_2^{\kappa \lambda }{R}_{\kappa \lambda }+t_0^{\kappa \lambda }>\log {ϵ}_{\text{Schwarz}}$ then

29:   for (k, l, m, n) ∈ (K, L, M, N) do

30:   $C_{\text{max}}=\max \{C_{\text{max}},C_{a_k}{C}_{b_l}{C}_{c_m}{C}_{d_n}\}$

31:   if $\log P_{\text{max}}+\log C_{\text{max}}+(t_2^{ab}{R}_{ab}+t_0^{ab})+(t_2^{cd}{R}_{cd}+t_0^{cd})>\log {ϵ}_{\text{Schwarz}}$ then

32:    if Far-field SR ERIs and P_max × C_max × [ab|cd]_SR > ϵ_Far-filed then

33:     Call LIBINT to calculate primitive ERI derivatives

34:    end if

35:   end if

36:   Calculate contracted ERI derivatives

37:  end for

38:   Calculate HFX forces according to Eq. 13

39:  end if

40: end for

41: end for

3.4.2 Far-field distance screening

The distance screening proposed by Izmaylov et al. (Izmaylov et al., 2006) further takes into account the decay of SR ERIs with respect to the distance R_PQ between two charge distribution centers P and Q. According to the multipole expansion, the primitive ERIs can be divided into near-field and far-field parts by (Burant et al., 1996)

$R_{\text{PQ}}\ge {\tilde{R}}_{\mathrm{P}}+{\tilde{R}}_{\mathrm{Q}},\tilde{R}=\mathrm{i}\mathrm{n}\mathrm{t}\left[{\left(2\alpha \right)}^{-1/2}{\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}}^{-1}\left(ϵ\right)\right]+1,(33)$

where ϵ is a threshold that defines the spatial range of a distribution $\tilde{R}$. The far-field SR ERIs have the following approximation

${\left[ab|cd\right]}_{\text{SR}}\approx K_{ab}{K}_{cd}\frac{\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left({\theta }_{\omega }^{1/2}{R}_{\text{PQ}}\right)}{R_{\text{PQ}}}(34)$

with

$K_{ab}=\frac{\sqrt{2}{\pi }^{5/4}}{\alpha +\beta }\exp \left[-\frac{\alpha \beta }{\alpha +\beta }{\left(\mathbf{A}-\mathbf{B}\right)}^2\right](35)$

Thus, in HSE calculations we can employ the distance screening based on Eq. 34 to screen out far-field primitive ERIs.

3.4.3 NAO screening

The NAOs are strictly localized in real space, so the ERIs over NAOs will be strictly zero and negligible if two shell orbitals μ and ν (or κ and λ) do not overlap with $R_{\mu \nu }>R_{\mathrm{c}}^{\mu }+R_{\mathrm{c}}^{\nu }$. To reduce the number of four-index loops, as shown in Algorithm 1 (Step 2), we first construct two shell-pair lists (list_μν and list_κλ) by taking into account the locality of NAOs, which is done prior to entering the calculation of HFX forces.

On the other hand, both the Hamiltonian and density matrices in pure DFT calculations exhibit a sparse pattern determined by the locality of NAOs. The matrix element H_μκ is non-zero only when the orbitals μ and κ directly overlap each other or indirectly overlap through a non-local pseudopotential projector. For hybrid functional calculations, the HFX matrix can also be stored in the same sparse format as that of pure DFT. According to Eq. 5, the NAO screening can screen out the ERIs for all shell pairs (μ, κ), (μ, λ), (ν, κ), and (ν, λ) do not overlap when considering the full ERI symmetry.

3.4.4 Density matrix screening

Our initial implementation of hybrid functionals is based on a non-direct SCF scheme, in which the ERIs are precalculated and stored in memory or disk with the above integral screening approaches (Shang et al., 2011). However, this scheme has a storage bottleneck and is not efficient for large systems since it does not exploit the sparse density matrix for integral screening. In fact, the ERIs are coupling with the density matrix in Eq. 5 and Eq. 6, which means that a large ERI (μν|κλ) may also be negligible if the density matrix elements P_μκ and P_νλ are fairly small. The integral screening techniques to achieve linear scaling HFX calculations are linked closely to the sparse density matrix, such as the ONX (Burant et al., 1996; Schwegler and Challacombe, 1996) and LinK (Schwegler et al., 1997) algorithms. It should be pointed out that the NAO screening partially takes into account the sparsity of the density matrix, so it can also lead to a linear scaling HFX calculation (Shang et al., 2011).

In order to improve the screening efficiency, we employ the density-matrix- based screening approach combined with a direct SCF scheme to calculate ERIs on-the-fly at each SCF iteration, which avoids the usage of memory for ERIs. The density matrix screening is to introduce the density matrix in the Schwarz and distance screening procedures. Considering the full ERI symmetry, the density matrix weighted Schwarz screening for building the HFX matrix is given by

$\max \left\{|P_{\mu \kappa }^{\sigma }|,|P_{\mu \lambda }^{\sigma }|,|P_{\nu \kappa }^{\sigma }|,|P_{\nu \lambda }^{\sigma }|\right\}\times |\left(\mu \nu |\mu \nu \right){|}^{1/2}|\left(\kappa \lambda |\kappa \lambda \right){|}^{1/2}\le {ϵ}_{\text{Schwarz}}(36)$

where the initial density matrix can be obtained from a post-PBE calculation for the first SCF step. The HFX forces are calculated by direct differentiation of the HFX energy after the SCF convergence, thus the ERI derivatives can be screened out if the corresponding ERIs have a negligible contribution to the HFX energy. Following Guidon et al. (Guidon et al., 2008), we adopt the following screening criterion for the calculation of HFX forces

$2\times \max \left\{|P_{\mu \kappa }^{\sigma }|\times |P_{\nu \lambda }^{\sigma }|,|P_{\mu \lambda }^{\sigma }|\times |P_{\nu \kappa }^{\sigma }|\right\}\times |\left(\mu \nu |\mu \nu \right){|}^{1/2}|\left(\kappa \lambda |\kappa \lambda \right){|}^{1/2}\le {ϵ}_{\text{Schwarz}}.(37)$

where the factor 2 is derived from the double contributions of ERIs to the first term of HFX forces in Eq. 9. Our density matrix weighted Schwarz screening for the calculation of HFX forces is shown in Algorithm 1 (Step 3). Since the products of converged density matrix elements are used, the calculation of the HFX forces will be more faster than the construction of the HFX matrix at each SCF step.

3.5 Parallelization strategy

With the rapid development of computer clusters and supercomputers, high-performance computing (HPC) is now essential for program design. In the parallel implementation of HFX forces, the key is to distribute the calculation of ERI derivatives across different central processing unit (CPU) cores. Of course, a straightforward way is to evenly distribute all shell quartets on each processor. However, the total amount of shell quartets is unknown until the integral screening is finished. Furthermore, the computational cost for different types of shell quartets may be very different. For instance, (dd|dd) with higher order angular momentum may be hundreds of times more expensive than (ss|ss), which also may cause serious load imbalance. On the other hand, the distribution of the density matrix may also introduce additional communication when considering the full ERI symmetry. Therefore, load balancing and minimizing communication overhead are essential considerations in the parallel design of HFX force calculation.

For massively parallel computing, a better choice is to employ the master-worker dynamic parallel scheme, which can yield very high load balance and parallel efficiency. We have established a master-worker parallel scheme for the calculation of HFX forces as that for the construction of HFX matrix based on the dynamic parallel distribution algorithm (Shang et al., 2020). In this scheme, one message passing interface (MPI) process is designated as the master to manage the distribution of the shell quartets, while the remaining processes act as the workers responsible for integral evaluation. The computational task corresponding to the total amount of shell quartets is obtained by multiplying the size of shell-pair lists. Then, the shell quartets are assigned by the master to the worker processes in batches by request at a time. Each worker process requests individual and batched shell quartets from the master, and computes the ERI derivatives and HFX forces with integral screening. Once the current tasks are completed, the worker process continues to request new shell quartets until there are no tasks left. In order to further reduce the data communication for the density matrix, we replicate the global density matrix on each individual MPI process. Unlike the HFX matrix construction, the calculation of HFX forces does not require a MPI_ALLREDUCE operation, thus global communication can be avoided.

In recent years, heterogeneous architectures with dedicated accelerators have become increasingly available in modern HPC systems. As one of the most widely used accelerators, graphics processing unit (GPU) is designed specifically for handling massive parallelism and performing multiple computational tasks simultaneously. Nowadays, numerous quantum chemistry software packages have been equipped with GPU support, in particular, to accelerate the evaluation of ERIs and their subsequent contraction for constructing the HFX matrix (Ufimtsev and Martinez, 2008, 2009; Barca et al., 2020). The GPU acceleration can be accomplished by mapping ERIs onto GPU threads, using either a one-block-one-contracted-integral algorithm or a one-thread-one-contracted-integral algorithm (Ufimtsev and Martinez, 2008). Regarding the master-worker parallel distribution, we can set an appropriate batch size and map the batched ERIs of a request across the GPU blocks or threads, which depends on the available resources on the GPU associated with each worker process. Therefore, our parallelization strategy presented above could also be extended to CPU-GPU heterogeneous parallelism, even though such an extension is not covered in the present work.

4 Results and discussion

In this section, we focus on demonstrating the numerical accuracy and efficiency of our implementation for HFX force calculations of periodic systems in the HONPAS package (Qin et al., 2015; Qin et al., 2020a). The norm-conserving PBE pseudopotentials of the Troullier-Martins type (Troullier and Martins, 1991) are used to represent the core-valence interaction. The pseudopotential for Ti includes semicore states (3s and 3p) in the valence. The NAOs are generated using default parameters or are optimized using the simplex utility in SIESTA, and the double-ζ plus polarization (DZP) basis set is employed. 5, 4, and 3 GTOs, namely 543, are used for s-, p-, and d-type NAOs of B, C, O, Si, and P, while a 544 fitting is used for Ti. The real-space mesh cutoff for all systems is set to 250 Ry. The tolerance of density matrix for the SCF convergence and the force tolerance in coordinate optimization are set to the values of 10^–4 and 0.01 eV/Å, respectively. After k-point convergence tests, the 8 × 8 × 8 Monkhorst-Pack k-point sampling in the BZ is chosen for bulk systems (Diamond, Si, SiC, BN, and BP).

4.1 Numerical accuracy and efficiency

4.1.1 Fitted orbitals for NAOs

In this work, we first use a linear combination of several Gaussians to fit the tabulated radial function of NAOs based on the NAO2GTO scheme and take the renormalized CGTOs as the new numerical basis functions with a cutoff radius R_c. Since the CGTOs decay exponentially in real space, we need to truncate them with a cutoff threshold defined as ϕ^CGTO (R_c) < ϵ_cut. As illustrated in Table 1, a smaller threshold will result in a larger cutoff radius for each CGTO. When ϵ_cut is set to 10^–3, the radius of a CGTO is slightly larger than that of its original NAO. However, a smaller value of ϵ_cut = 10^–7 will yield 1.5–2 times larger cutoff radii. In practice, the cutoff radius also depends on the minimum fitting exponent α_min, which is selected to be 0.15 in order to prevent the generation of too diffuse GTOs.

TABLE 1

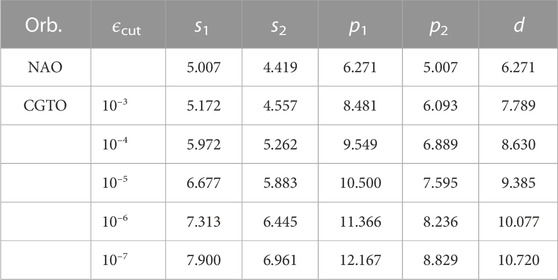
TABLE 1. The cutoff radii (in Bohr) of orbitals at a given threshold (ϵ_cut) for silicon atom with the DZP basis set. s₁ and s₂ label the 1st-ζ and 2nd-ζ s-type orbitals, p₁ and p₂ label the 1st-ζ and 2nd-ζ p-type orbitals, and d denotes the polarized d-type orbital.

We determine the cutoff radii by examining the ERI errors resulting from the truncation of CGTOs. We compare the ERIs for fitted CGTOs with different cutoff thresholds by using numerical and analytical integrations, respectively. As listed in Table 2, the maximum absolute error (ΔE_max) of ERIs can be as less as 2.4 × 10^–6 eV (1.76 × 10^–7 Ry) if ϵ_cut = 10^–5 is given. Therefore, we decide to choose ϵ_cut = 10^–5 as the default cutoff threshold for all hybrid functional calculations. From Table 2, we can also observe that the calculated ERIs over original NAO and fitted CGTO differ by a maximum of 0.533 eV. Such a significant difference may render the hybrid functional calculation invalid if we use the fitted CGTOs for the HFX term while still relying on the original NAOs for other terms. To ensure the accuracy and reliability of the NAO2GTO scheme, we decide to apply the fitted CGTOs consistently across all components of the hybrid functional calculations. Specifically, we employ the analytical CGTOs for the HFX calculation while the numerically discretized CGTOs for other pure DFT calculations.

TABLE 2

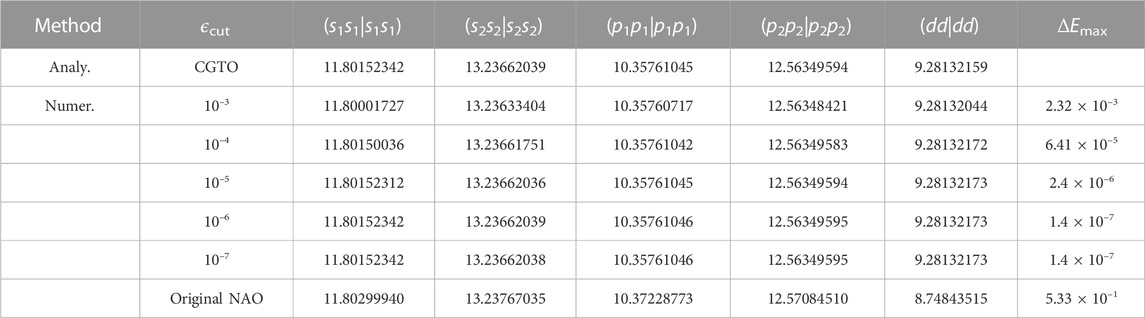
TABLE 2. Analytical (Analy.) and Numerical (Numer.) ERIs (in eV) at a given cutoff threshold (ϵ_cut). The tested system is the silicon atom with the DZP basis set. s₁ and s₂ label the 1st-ζ and 2nd-ζ s-type orbitals, p₁ and p₂ label the 1st-ζ and 2nd-ζ p-type orbitals with m = −1, d label the polarized d-type orbitals with m = −2, ΔE_max is the maximum absolute error between numerical and analytical ERIs.

4.1.2 Integral screening

We then benchmark the numerical accuracy and efficiency of different screening methods for the Si crystal with HSE06 calculations. The lattice constant is chosen to be 5.43 Å, and the primitive unit cell containing two Si atoms is used. The Cartesian coordinates of two atoms are set to non-equilibrium positions of (0, 0, 0) and (1.3175, 1.3575, 1.3575), respectively, so that a relatively large value of atomic force in the x direction can be obtained. Table 3 shows the absolute errors (total energy, band gap, and atomic force) and the wall time for the calculation of HFX matrix and forces under different screening methods and thresholds. The reference values in the table are obtained using Schwarz-screening only with a threshold of ϵ_Schwarz = 10^–10 (in Ry), in which the HFX time is taken from the last SCF step.

TABLE 3

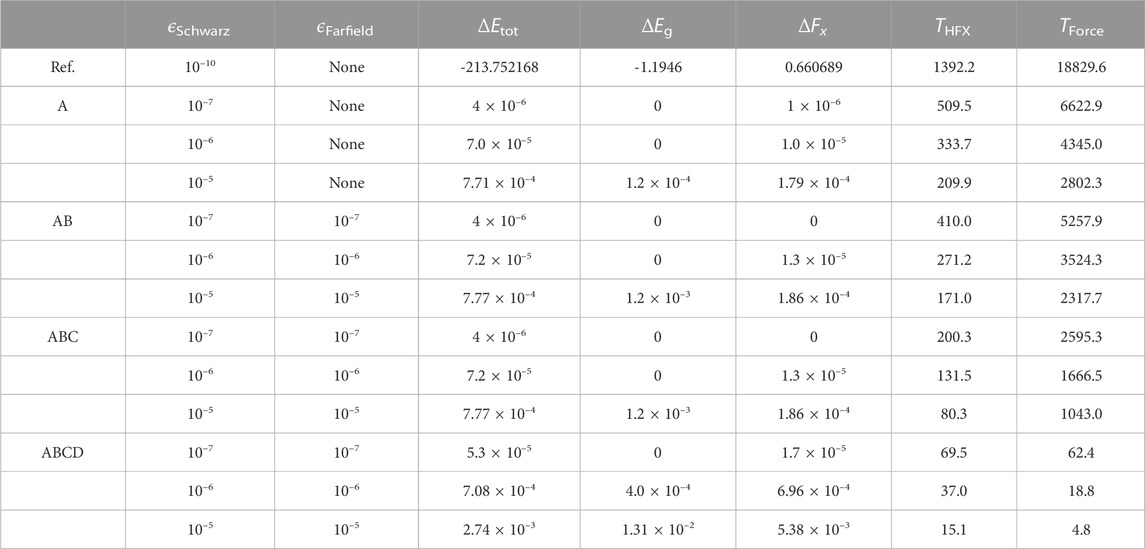
TABLE 3. Absolute errors (total energy ΔE_tot and band gap ΔE_g in eV, while atomic force ΔF_x in eV/Å) and wall time (in seconds) of different integral screening techniques for the Si crystal. All calculations are performed on 24 CPU cores.

As can be seen from Table 3, both the numerical accuracy and computational cost can efficiently be controlled by the thresholds. The screening methods of Schwarz (A), far-field (B), and NAO (C) show almost the same errors in energy and force at given thresholds, while the density matrix screening (D) yields relatively larger errors. All absolute errors lie within the range of 10⁻⁵–10⁻⁴ (eV or eV/Å) when the thresholds are set to be 10^–6 (Ry), which is then chosen as the global default threshold. For building the HFX matrix, we find that applying more screening methods of A, B, and C only leads to 1-2 speed-up, which can be improved by further including D. The calculation of HFX forces requires to evaluate the first-order derivatives of ERIs, which contain 12 components. Therefore, we can also see that the computational time of HFX forces under the same screening methods without the density matrix is about 12 times higher than that of HFX matrix. However, if the density matrix screening is involved, the computational cost of HFX forces can be reduced by nearly 2-3 orders of magnitude. In particular, the HFX force calculation can eventually be faster than the HFX matrix construction with the thresholds larger than 10^–7. This dramatic improvement in efficiency can be attributed to two aspects: (1) the fully converged density matrix after the SCF iteration is more sparse; (2) the product of the sparse density matrix yields a smaller upper bound to filter out much more shell quartets.

We also compare the analytical and numerical gradients of total energy for the Si crystal. The numerical gradients are obtained by using the finite difference method, in which the first atom Si₁ is fixed at the origin and the other atom Si₂ located at (x, 1.3575, 1.3575) is moved along x direction. We perform a series of HSE06 calculations by varying the x coordinate of Si₂ from 1.3075 to 1.4075 Å. As shown in Figure 2, the x component of analytical forces acting on Si₂ are in very good agreement with the numerical differentiations of total energies. The maximum discrepancy between the analytical and numerical forces is less than 1.5 × 10^–3 eV/Å, which also indicates that our implementation is correct.

FIGURE 2

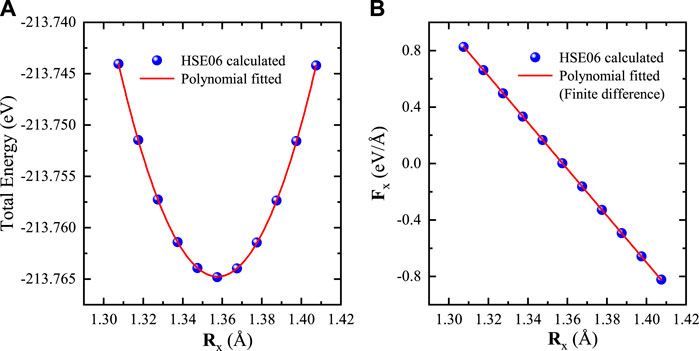
FIGURE 2. (A) Total energy and (B) atomic force as a function of Si coordinates. One atom is fixed at the origin, whereas the other atom is moved along the x direction. The curve shows a polynomial fitting of total energy, and its partial differential (the slope) is the numerical force F_x = ∂E_tot/∂R_x with the finite difference method.

4.1.3 Lattice constant, bulk modulus, and band gap

Furthermore, we verify the reliability of our improved NAO2GTO scheme that replaces the NAOs with numerically discretized CGTOs. We calculate the equilibrium lattice constants a₀, bulk moduli B₀, and band gaps E_g for several typical semiconductors with HSE06, and compare them with experimental (Heyd and Scuseria, 2004) and other theoretical (Paier et al., 2006a; Levchenko et al., 2015) results. The equilibrium lattice constants and bulk moduli are determined by fitting energy-volume (E-V) data with the third-order Birch-Murnaghan equation of state (Birch, 1947). The band gaps are obtained using single-point calculations at the optimized lattice constant. A 543 NAO2GTO fitting and cutoff threshold of ϵ_Schwarz = 10^–5 are chosen. All screening methods with the default thresholds (ϵ_Schwarz = ϵ_Farfield = 10^–6) are applied.

As summarized in Table 4, our HSE06 results agree satisfactorily with the experimental values. It can also be seen that our results differ slightly from other theoretical values with a difference of 0.01–0.025 Å for a₀, 4–10 GPa for B₀, and 0.02–0.18 eV for E_g, respectively. Actually, such a discrepancy can also be found in other codes (Levchenko et al., 2015; Lin et al., 2020), which can be attributed to the use of different pseudopotentials and basis sets. In the NAO framework, it has been shown that the radial range and shape can influence the final results of DFT calculations (Junquera et al., 2001; Anglada et al., 2002). We use the NAO2GTO fitting to generate new numerical radial functions with a large cutoff radius, which will result in deviations in the HSE06 calculations due to the changes in the radial range and shape of NAOs. As a result, we decide to use 3-6 GTOs with the exponents larger than 0.15 to fit NAOs so that the basis functions do not change significantly. It is important to stress that, we have not observed numerical instability when using truncated CGTOs for HSE06 calculations, but more detailed tests for different systems are still necessary.

TABLE 4

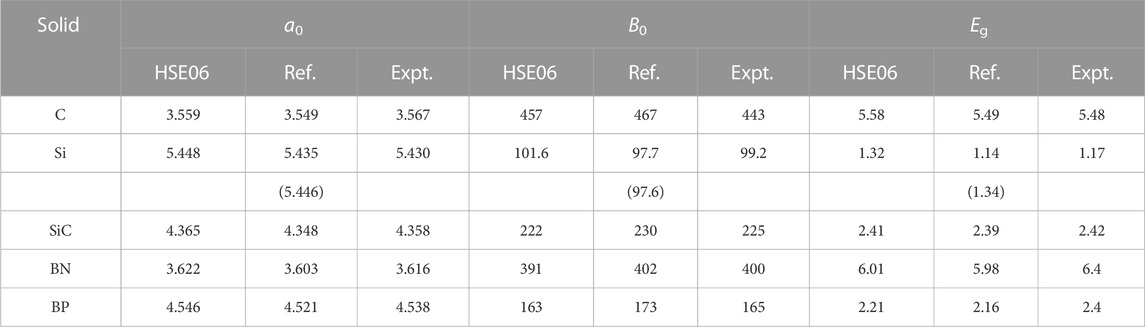
TABLE 4. Lattice constants a₀ (Å), bulk moduli B₀ (GPa), and band gaps E_g (eV) for C, Si, SiC, BN, and BP with the cubic diamond structure. Experimental (Expt.) results are taken from in the literature (Heyd and Scuseria, 2004). Theoretical values are from Ref. (Paier et al., 2006a) with plane-wave basis sets, whereas values in parentheses are NAO-based results (Levchenko et al., 2015).

4.2 Parallel efficiency and computational scaling

In order to illustrate the parallel scalability of our implementation, we perform Γ-only HSE06 calculations for the Si crystal with a supercell containing 512 atoms by using different CPU cores. The default parameters are used for NAO2GTO fitting and integral screening. Our calculations are performed on Intel(R) Xeon(R) CPUs (6258R CPU@2.70GHz). The wall time for building the HFX matrix in the last SCF step is recorded, while the reported wall time for computing the HFX forces only includes the second term in Eq. 13

Figure 3A shows the change of wall times with respect to the number of CPU cores ranging from 48 to 768. The calculation of HFX forces takes 222.1 and 99.2 s for 48 and 768 CPU cores, respectively, which is 1.4–2.2 times faster than the HFX matrix construction (2142.9 and 1521.9 s). In the master-worker dynamic parallelization of HFX force calculation, the load balance can be effectively achieved, and only point-to-point communication of shell quartet indices is needed between the master and worker processes. Thus, the HFX force calculation scales nearly perfectly up to 768 CPU cores with a very high parallel efficiency of 95.9% as expected. However, the parallel efficiency for the construction of HFX matrix is significantly reduced to 57.8%. This reduction can be attributed to all-to-all communications required for building the global HFX matrix, which has been demonstrated in our previous work (Shang et al., 2020).

FIGURE 3

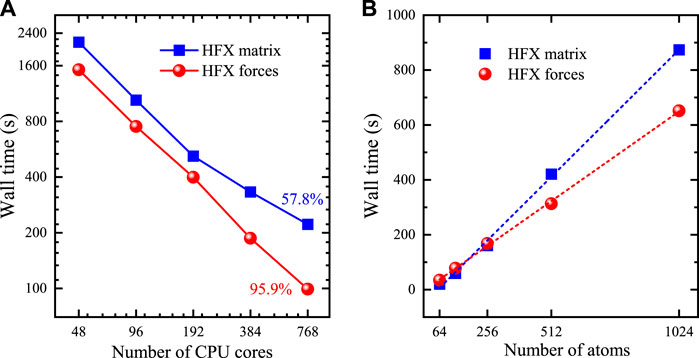
FIGURE 3. (A) The change of wall clock time for HFX matrix and forces with respect to the number of CPU cores for the Si supercell containing 512 atoms. (B) The change time of wall clock time for HFX matrix and forces with respect to system size for Si supercells containing from 64 to 1024 atoms running on 240 CPU cores. The dashed lines correspond to a linear fit for the data. All calculations are performed on Intel(R) Xeon(R) CPUs (6258R CPU@2.70GHz).

With such a good parallel scalability, we demonstrate the linear-scaling behavior of our implementation with respect to system size in parallel. We perform a series of Γ-only HSE06 calculations for the Si crystal with different supercells containing from 64 up to 1024 atoms on 240 CPU cores, in which the HFX matrix construction still maintains high parallel efficiency. As shown in Figure 3B, the wall time of both HFX matrix and force computations scale linearly with respect to system size. In particular, the linear-scaling calculation of HFX forces has a smaller prefactor than that of HFX matrix.

4.3 Small electron polaron in rutile TiO₂

As a prototypical photocatalyst, TiO₂ is one of the most intensively studied materials, and polarons often play a decisive role in its applications (De Lile et al., 2022). For bulk rutile TiO₂, excess electrons can self-trap to form small polarons associated with local lattice distortion (Setvin et al., 2014). It has shown that hybrid functionals are sufficiently accurate to describe the formation and properties of small polarons in rutile TiO₂(Janotti et al., 2013; Elmaslmane et al., 2018; De Lile et al., 2022). Herein, we apply our code to investigate the small polaron due to the excess electron in bulk rutile TiO₂ with HSE06. In all our calculations, the experimental lattice constants of a = 4.594 Å and c = 2.959 Å are used. The calculated band gap for rutile TiO₂ is 3.28 eV, slightly higher than the experimental value of 3.03 eV (Amtout and Leonelli, 1995) but lower than the reported HSE06 value of 3.39 eV (Landmann et al., 2012). To simulate the formation of small polaron, a 3 × 3 × 4 supercell containing 216 atoms and −1|e| net charge is used for spin-polarized HSE06 calculations. The k-point meshes of 2 × 2 × 2 and 4 × 4 × 4 are chosen for structural relaxation and electronic structure calculations, respectively. One Ti atom is specified an initial displacement ($\sim 0.18$ Å) for localization of the polaron, and all atomic coordinates are relaxed until the forces acting on each atom are less than 0.04 eV/Å.

After full structural optimization, we observe a local lattice distortion around one Ti ion in the electron-doped rutile TiO₂. Compared to the pristine structure, the two Ti-O bonds perpendicular to the c-axis relax outward, increasing from 1.981 to 1.991 Å in length. In particular, the other four bonds with an initial length of 1.948 Å undergo two distinct changes: two of them increase to 2.011 Å, while the remaining two decrease to 1.891 Å. Figure 4A shows the band structure, where we can find a localized spin-electron state located at roughly 0.88 eV below the conduction band minimum (CBM). We also plot the spin density for this localized state in Figure 4B. As expected, the spin density is localized on the single Ti ion with a local lattice distortion, indicating the formation of a small electron polaron. Our results are in good agreement with the reported HSE06 results, in which an electron polaron state at 0.77 eV below the CBM was predicted by using VASP (Janotti et al., 2013).

FIGURE 4

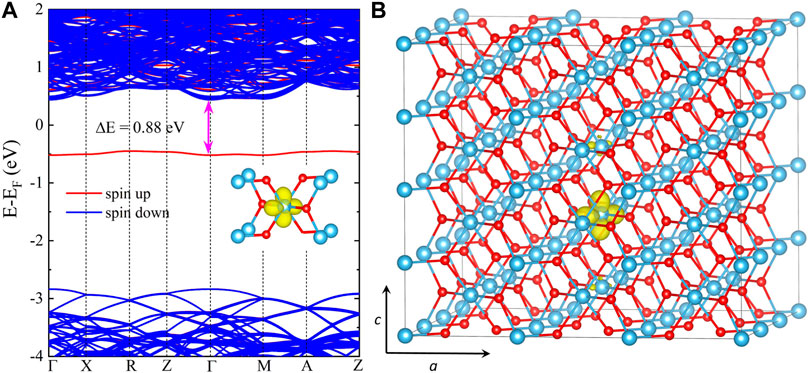
FIGURE 4. (A) HSE06 band structure and (B) spin density of the self-trapped electron for the supercell of rutile TiO₂ with an excess electron. The isosurface is set to be 10% of the maximum charge density, and a 3 × 3 × 4 supercell containing 216 atoms is used.

5 Conclusion

In summary, we have presented an efficient and linear-scaling implementation of analytical gradients of HFX energy for periodic HSE06 calculations within NAOs based on the NAO2GTO scheme. To minimize the errors caused by the NAO2GTO fitting, the original NAOs are replaced by the numerically discretized CGTOs. The ERIs and their derivatives for the HFX term are analytically evaluated with CGTOs, whereas other terms are obtained using discretized CGTOs. Several integral screening methods are utilized to reduce the computational cost of HFX forces, among which the density matrix screening can lead to a linear-scaling calculation of HFX forces with a smaller prefactor compared to the HFX matrix construction. We have demonstrated our implementation can yield accurate results of lattice constants, bulk moduli, and band gaps for several semiconductors. In addition, a master-worker dynamic parallel strategy is employed for computing the HFX forces, which can lead to very high parallel efficiency. We have also studied the small polaronic behavior of excess electrons in rutile TiO₂, validating the capability of our code for predicting the polarons.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

JY designed and directed the project. HS developed the theoretical formulas and techniques. XQ carried out the implementation and performed the numerical simulations. All authors contributed to the article and approved the submitted version.

Funding

This work is partly supported by the National Natural Science Foundation of China (Grant Nos. 22003061, 22003073, T2222026, 22288201, and 22273092), by the Innovation Program for Quantum Science and Technology (Grant No. 2021ZD0303306), by the National Key Research and Development Program of China (Grant No. 2021YFB0300600), by the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB0450101), and by the Anhui Initiative in Quantum Information Technologies (Grant No. AHY090400).

Acknowledgments

The authors acknowledge Prof. Javier Junquera (Departamento CITIMAC, Facultad de Ciencias, Universidad de Cantabria) and Dr. Yann Pouillon (Departamento CITIMAC, Facultad de Ciencias, Universidad de Cantabria) for helpful discussions. The authors thank the Supercomputing Center of Chinese Academy of Sciences, the Supercomputing Center of USTC, and the National Supercomputing Center in Jinan, Tianjin, and Guangzhou Supercomputing Centers for the computational resources.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adamo, C., and Barone, V. (1999). Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 110, 6158–6170. doi:10.1063/1.478522

CrossRef Full Text | Google Scholar

Amtout, A., and Leonelli, R. (1995). Optical properties of rutile near its fundamental band gap. Phys. Rev. B 51, 6842–6851. doi:10.1103/PhysRevB.51.6842

CrossRef Full Text | Google Scholar

Anglada, E., Soler, M., Junquera, J., and Artacho, E. (2002). Systematic generation of finite-range atomic basis sets for linear-scaling calculations. Phys. Rev. B 66, 205101. doi:10.1103/PhysRevB.66.205101

CrossRef Full Text | Google Scholar

Barca, G. M. J., Galvez-Vallejo, J. L., Poole, D. L., Rendell, A. P., and Gordon, M. S. (2020). High-performance, graphics processing unit-accelerated fock build algorithm. J. Chem. Theory Comput. 16, 7232–7238. doi:10.1021/acs.jctc.0c00768

PubMed Abstract | CrossRef Full Text | Google Scholar

Birch, F. (1947). Finite elastic strain of cubic crystals. Phys. Rev. 71, 809–824. doi:10.1103/PhysRev.71.809

CrossRef Full Text | Google Scholar

Blum, V., Gehrke, R., Hanke, F., Havu, P., Havu, V., Ren, X., et al. (2009). Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 180, 2175–2196. doi:10.1016/j.cpc.2009.06.022

CrossRef Full Text | Google Scholar

Broqvist, P., Alkauskas, A., and Pasquarello, A. (2009). Hybrid-functional calculations with plane-wave basis sets: Effect of singularity correction on total energies, energy eigenvalues, and defect energy levels. Phys. Rev. B 80, 085114. doi:10.1103/PhysRevB.80.085114

CrossRef Full Text | Google Scholar

Burant, J. C., Scuseria, G. E., and Frisch, M. J. (1996). A linear scaling method for Hartree–Fock exchange calculations of large molecules. J. Chem. Phys. 105, 8969–8972. doi:10.1063/1.472627

CrossRef Full Text | Google Scholar

Chen, Y.-C., Chen, J.-Z., Michaud-Rioux, V., Shi, Q., and Guo, H. (2018). Efficient evaluation of nonlocal operators in density functional theory. Phys. Rev. B 97, 075139. doi:10.1103/PhysRevB.97.075139

CrossRef Full Text | Google Scholar

De Lile, J. R., Bahadoran, A., Zhou, S., and Zhang, J. (2022). Polaron in TiO₂ from first-principles: A review. Adv. Theory Simul. 5, 2100244. doi:10.1002/adts.202100244

CrossRef Full Text | Google Scholar

Dovesi, R., Pascale, F., Civalleri, B., Doll, K., Harrison, N. M., Bush, I., et al. (2020). The CRYSTAL code, 1976–2020 and beyond, a long story. J. Chem. Phys. 152, 204111. doi:10.1063/5.0004892

PubMed Abstract | CrossRef Full Text | Google Scholar

Elmaslmane, A. R., Watkins, M. B., and McKenna, K. P. (2018). First-principles modeling of polaron formation in TiO₂ polymorphs. J. Chem. Theory Comput. 14, 3740–3751. doi:10.1021/acs.jctc.8b00199

PubMed Abstract | CrossRef Full Text | Google Scholar

Ernzerhof, M., and Scuseria, G. E. (1999). Assessment of the Perdew-Burke-Ernzerhof exchange-correlation functional. J. Chem. Phys. 110, 5029–5036. doi:10.1063/1.478401

CrossRef Full Text | Google Scholar

Feynman, R. P. (1939). Forces in molecules. Phys. Rev. 56, 340–343. doi:10.1103/PhysRev.56.340

CrossRef Full Text | Google Scholar

Guidon, M., Hutter, J., and VandeVondele, J. (2009). Robust periodic Hartree-Fock exchange for large-scale simulations using Gaussian basis sets. J. Chem. Theory Comput. 5, 3010–3021. doi:10.1021/ct900494g

PubMed Abstract | CrossRef Full Text | Google Scholar

Guidon, M., Schiffmann, F., Hutter, J., and VandeVondele, J. (2008). Ab initio molecular dynamics using hybrid density functionals. J. Chem. Phys. 128, 214104. doi:10.1063/1.2931945

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamilton, T. P., and Schaefer, H. F. (1991). New variations in two-electron integral evaluation in the context of direct SCF procedures. Chem. Phys. 150, 163–171. doi:10.1016/0301-0104(91)80126-3

CrossRef Full Text | Google Scholar

Häser, M., and Ahlrichs, R. (1989). Improvements on the direct SCF method. J. Comput. Chem. 10, 104–111. doi:10.1002/jcc.540100111

CrossRef Full Text | Google Scholar

Head-Gordon, M., and Pople, J. A. (1988). A method for two-electron Gaussian integral and integral derivative evaluation using recurrence relations. J. Chem. Phys. 89, 5777–5786. doi:10.1063/1.455553

CrossRef Full Text | Google Scholar

Henderson, T. M., Paier, J., and Scuseria, G. E. (2011). Accurate treatment of solids with the HSE screened hybrid. Phys. Status Solidi B 248, 767–774. doi:10.1002/pssb.201046303

CrossRef Full Text | Google Scholar

Heyd, J., and Scuseria, G. E. (2004). Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 121, 1187–1192. doi:10.1063/1.1760074

PubMed Abstract | CrossRef Full Text | Google Scholar

Heyd, J., Scuseria, G. E., and Ernzerhof, M. (2006). Erratum: “Hybrid functionals based on a screened Coulomb potential” [J chem phys 118, 8207 (2003)]. J. Chem. Phys. 124, 219906. doi:10.1063/1.2204597

CrossRef Full Text | Google Scholar

Heyd, J., Scuseria, G. E., and Ernzerhof, M. (2003). Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215. doi:10.1063/1.1564060

CrossRef Full Text | Google Scholar

Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136, B864–B871. doi:10.1103/physrev.136.b864

CrossRef Full Text | Google Scholar

Horn, H., Weiß, H., Háser, M., Ehrig, M., and Ahlrichs, R. (1991). Prescreening of two-electron integral derivatives in SCF gradient and Hessian calculations. J. Comput. Chem. 12, 1058–1064. doi:10.1002/jcc.540120903

CrossRef Full Text | Google Scholar

Hu, W., Lin, L., Banerjee, A. S., Vecharynski, E., and Yang, C. (2017a). Adaptively compressed exchange operator for large-scale hybrid density functional calculations with applications to the adsorption of water on silicene. J. Chem. Theory Comput. 13, 1188–1198. doi:10.1021/acs.jctc.6b01184

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, W., Lin, L., and Yang, C. (2017b). Interpolative separable density fitting decomposition for accelerating hybrid density functional calculations with applications to defects in silicon. J. Chem. Theory Comput. 13, 5420–5431. doi:10.1021/acs.jctc.7b00807

PubMed Abstract | CrossRef Full Text | Google Scholar

Izmaylov, A. F., Scuseria, G. E., and Frisch, M. J. (2006). Efficient evaluation of short-range Hartree-Fock exchange in large molecules and periodic systems. J. Chem. Phys. 125, 104103. doi:10.1063/1.2347713

PubMed Abstract | CrossRef Full Text | Google Scholar

Janesko, B. G., Henderson, T. M., and Scuseria, G. E. (2009). Screened hybrid density functionals for solid-state chemistry and physics. Phys. Chem. Chem. Phys. 11, 443–454. doi:10.1039/B812838C

PubMed Abstract | CrossRef Full Text | Google Scholar

Janotti, A., Franchini, C., Varley, J. B., Kresse, G., and Van de Walle, C. G. (2013). Dual behavior of excess electrons in rutile TiO₂. Phys. Status Solidi RRL 7, 199–203. doi:10.1002/pssr.201206464

CrossRef Full Text | Google Scholar

Junquera, J., Paz, O., Sánchez-Portal, D., and Artacho, E. (2001). Numerical atomic orbitals for linear-scaling calculations. Phys. Rev. B 64, 235111. doi:10.1103/PhysRevB.64.235111

CrossRef Full Text | Google Scholar

Ko, H.-Y., Jia, J., Santra, B., Wu, X., Car, R., and DiStasio, R. A. (2020). Enabling large-scale condensed-phase hybrid density functional theory based ab initio molecular dynamics. 1. theory, algorithm, and performance. J. Chem. Theory Comput. 16, 3757–3785. doi:10.1021/acs.jctc.9b01167

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138. doi:10.1103/physrev.140.a1133

CrossRef Full Text | Google Scholar

Krukau, A. V., Vydrov, O. A., Izmaylov, A. F., and Scuseria, G. E. (2006). Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125, 224106. doi:10.1063/1.2404663

PubMed Abstract | CrossRef Full Text | Google Scholar

Kühne, T. D., Iannuzzi, M., Del Ben, M., Rybkin, V. V., Seewald, P., Stein, F., et al. (2020). CP2K: An electronic structure and molecular dynamics software package-Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 152, 194103. doi:10.1063/5.0007045

PubMed Abstract | CrossRef Full Text | Google Scholar

Landmann, M., Rauls, E., and Schmidt, W. G. (2012). The electronic structure and optical response of rutile, anatase and brookite tio2. J. Phys. Condens. Matter 24, 195503. doi:10.1088/0953-8984/24/19/195503

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J., Rettig, A., Feng, X., Epifanovsky, E., and Head-Gordon, M. (2022). Faster exact exchange for solids via occ-ri-k: Application to combinatorially optimized range-separated hybrid functionals for simple solids with pseudopotentials near the basis set limit. J. Chem. Theory Comput. 18, 7336–7349. doi:10.1021/acs.jctc.2c00742

PubMed Abstract | CrossRef Full Text | Google Scholar

Levchenko, S. V., Ren, X., Wieferink, J., Johanni, R., Rinke, P., Blum, V., et al. (2015). Hybrid functionals for large periodic systems in an all-electron, numeric atom-centered basis framework. Comput. Phys. Commun. 192, 60–69. doi:10.1016/j.cpc.2015.02.021

CrossRef Full Text | Google Scholar

Li, P., Liu, X., Chen, M., Lin, P., Ren, X., Lin, L., et al. (2016). Large-scale ab initio simulations based on systematically improvable atomic basis. Comput. Mat. Sci. 112, 503–517. doi:10.1016/j.commatsci.2015.07.004

CrossRef Full Text | Google Scholar

Lin, L. (2016). Adaptively compressed exchange operator. J. Chem. Theory Comput. 12, 2242–2249. doi:10.1021/acs.jctc.6b00092

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, P., Ren, X., and He, L. (2020). Accuracy of localized resolution of the identity in periodic hybrid functional calculations with numerical atomic orbitals. J. Phys. Chem. Lett. 11, 3082–3088. doi:10.1021/acs.jpclett.0c00481

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, P., Ren, X., and He, L. (2021). Efficient hybrid density functional calculations for large periodic systems using numerical atomic orbitals. J. Chem. Theory Comput. 17, 222–239. doi:10.1021/acs.jctc.0c00960

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindh, R., Ryu, U., and Liu, B. (1991). The reduced multiplication scheme of the rys quadrature and new recurrence relations for auxiliary function based two-electron integral evaluation. J. Chem. Phys. 95, 5889–5897. doi:10.1063/1.461610

CrossRef Full Text | Google Scholar

Lu, J., and Ying, L. (2015). Compression of the electron repulsion integral tensor in tensor hypercontraction format with cubic scaling cost. J. Comput. Phys. 302, 329–335. doi:10.1016/j.jcp.2015.09.014

CrossRef Full Text | Google Scholar

Marsman, M., Paier, J., Stroppa, A., and Kresse, G. (2008). Hybrid functionals applied to extended systems. J. Phys. Condens. Matter 20, 064201. doi:10.1088/0953-8984/20/6/064201

PubMed Abstract | CrossRef Full Text | Google Scholar

Mori-Sánchez, P., Cohen, A. J., and Yang, W. (2008). Localization and delocalization errors in density functional theory and implications for band-gap prediction. Phys. Rev. Lett. 100, 146401. doi:10.1103/PhysRevLett.100.146401

PubMed Abstract | CrossRef Full Text | Google Scholar

Obara, S., and Saika, A. (1986). Efficient recursive computation of molecular integrals over Cartesian Gaussian functions. J. Chem. Phys. 84, 3963–3974. doi:10.1063/1.450106

CrossRef Full Text | Google Scholar

Ochsenfeld, C., White, C. A., and Head-Gordon, M. (1998). Linear and sublinear scaling formation of Hartree-Fock-type exchange matrices. J. Chem. Phys. 109, 1663–1669. doi:10.1063/1.476741

CrossRef Full Text | Google Scholar

Ozaki, T., and Kino, H. (2005). Efficient projector expansion for the ab initio LCAO method. Phys. Rev. B 72, 045121. doi:10.1103/PhysRevB.72.045121

CrossRef Full Text | Google Scholar

Paier, J., Marsman, M., Hummer, K., Kresse, G., Gerber, I. C., and Ángyán, J. G. (2006a). Erratum: “Screened hybrid density functionals applied to solids” [J chem phys 124, 154709 (2006)]. J. Chem. Phys. 125. doi:10.1063/1.2187006

CrossRef Full Text | Google Scholar

Paier, J., Marsman, M., Hummer, K., Kresse, G., Gerber, I. C., and Ángyán, J. G. (2006b). Screened hybrid density functionals applied to solids. J. Chem. Phys. 124, 154709. doi:10.1063/1.2187006

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P. (1985). Accurate density functional for the energy: Real-space cutoff of the gradient expansion for the exchange hole. Phys. Rev. Lett. 55, 1665–1668. doi:10.1103/physrevlett.55.1665

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Pulay, P. (1969). Ab initio calculation of force constants and equilibrium geometries in polyatomic molecules. Mol. Phys. 17, 197–204. doi:10.1080/00268976900100941

CrossRef Full Text | Google Scholar

Qin, X., Hu, W., Yang, J., Shang, H., and Xiang, H. (2020a). The HONPAS software webpage. Available at: http://honpas.ustc.edu.cn.Version.1.0.

Google Scholar

Qin, X., Li, J., Hu, W., and Yang, J. (2020b). Machine learning K-Means clustering algorithm for interpolative separable density fitting to accelerate hybrid functional calculations with numerical atomic orbitals. J. Phys. Chem. A 124, 10066–10074. doi:10.1021/acs.jpca.0c06019

PubMed Abstract | CrossRef Full Text | Google Scholar

Qin, X., Liu, J., Hu, W., and Yang, J. (2020c). Interpolative separable density fitting decomposition for accelerating Hartree–Fock exchange calculations within numerical atomic orbitals. J. Phys. Chem. A 124, 5664–5674. doi:10.1021/acs.jpca.0c02826

PubMed Abstract | CrossRef Full Text | Google Scholar

Qin, X., Shang, H., Xiang, H., Li, Z., and Yang, J. (2015). HONPAS: A linear scaling open-source solution for large system simulations. Int. J. Quantum Chem. 115, 647–655. doi:10.1002/qua.24837

CrossRef Full Text | Google Scholar

Reine, S., Helgaker, T., and Lindh, R. (2012). Multi-electron integrals. WIREs Comput. Mol. Sci. 2, 290–303. doi:10.1002/wcms.78

CrossRef Full Text | Google Scholar

Ren, X., Rinke, P., Blum, V., Wieferink, J., Tkatchenko, A., Sanfilippo, A., et al. (2012). Resolution-of-identity approach to Hartree-Fock, hybrid density functionals, RPA, MP2 and GW with numeric atom-centered orbital basis functions. New J. Phys. 14, 053020. doi:10.1088/1367-2630/14/5/053020

CrossRef Full Text | Google Scholar

Schlegel, H. B., and Frisch, M. J. (1995). Transformation between Cartesian and pure spherical harmonic Gaussians. Int. J. Quantum Chem. 54, 83–87. doi:10.1002/qua.560540202

CrossRef Full Text | Google Scholar

Schwegler, E., Challacombe, M., and Head-Gordon, M. (1997). Linear scaling computation of the Fock matrix. II. rigorous bounds on exchange integrals and incremental Fock build. J. Chem. Phys. 106, 9708–9717. doi:10.1063/1.473833

CrossRef Full Text | Google Scholar

Schwegler, E., and Challacombe, M. (1996). Linear scaling computation of the Hartree-Fock exchange matrix. J. Chem. Phys. 105, 2726–2734. doi:10.1063/1.472135

CrossRef Full Text | Google Scholar

Setvin, M., Franchini, C., Hao, X., Schmid, M., Janotti, A., Kaltak, M., et al. (2014). Direct view at excess electrons in TiO₂ rutile and anatase. Phys. Rev. Lett. 113, 086402. doi:10.1103/PhysRevLett.113.086402

PubMed Abstract | CrossRef Full Text | Google Scholar

Shang, H., Li, Z., and Yang, J. (2010). Implementation of exact exchange with numerical atomic orbitals. J. Phys. Chem. A 114, 1039–1043. doi:10.1021/jp908836z

PubMed Abstract | CrossRef Full Text | Google Scholar

Shang, H., Li, Z., and Yang, J. (2011). Implementation of screened hybrid density functional for periodic systems with numerical atomic orbitals: Basis function fitting and integral screening. J. Chem. Phys. 135, 034110. doi:10.1063/1.3610379

PubMed Abstract | CrossRef Full Text | Google Scholar

Shang, H., Xu, L., Wu, B., Qin, X., Zhang, Y., and Yang, J. (2020). The dynamic parallel distribution algorithm for hybrid density-functional calculations in HONPAS package. Comput. Phys. Commun. 254, 107204. doi:10.1016/j.cpc.2020.107204

CrossRef Full Text | Google Scholar

Soler, J. M., Artacho, E., Gale, J. D., García, A., Junquera, J., Ordejón, P., et al. (2002). The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 14, 2745–2779. doi:10.1088/0953-8984/14/11/302

CrossRef Full Text | Google Scholar

Spencer, J., and Alavi, A. (2008). Efficient calculation of the exact exchange energy in periodic systems using a truncated Coulomb potential. Phys. Rev. B 77, 193110. doi:10.1103/PhysRevB.77.193110

CrossRef Full Text | Google Scholar

Stephens, P. J., Devlin, F. J., Chabalowski, C. F., and Frisch, M. J. (1994). Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 98, 11623–11627. doi:10.1021/j100096a001

CrossRef Full Text | Google Scholar

Sun, Q., Zhang, X., Banerjee, S., Bao, P., Barbry, M., Blunt, N. S., et al. (2020). Recent developments in the PySCF program package. J. Chem. Phys. 153, 024109. doi:10.1063/5.0006074

PubMed Abstract | CrossRef Full Text | Google Scholar

Torralba, A. S., Todorović, M., Brázdová, V., Choudhury, R., Miyazaki, T., Gillan, M. J., et al. (2008). Pseudo-atomic orbitals as basis sets for the O(N) DFT code CONQUEST. J. Phys. Condens. Matter 20, 294206. doi:10.1088/0953-8984/20/29/294206

CrossRef Full Text | Google Scholar

Troullier, N., and Martins, J. L. (1991). Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 43, 1993–2006. doi:10.1103/PhysRevB.43.1993

CrossRef Full Text | Google Scholar

Ufimtsev, I. S., and Martinez, T. J. (2008). Quantum chemistry on graphical processing units. 1. strategies for two-electron integral evaluation. J. Chem. Theory Comput. 4, 222–231. doi:10.1021/ct700268q

PubMed Abstract | CrossRef Full Text | Google Scholar

Ufimtsev, I. S., and Martinez, T. J. (2009). Quantum chemistry on graphical processing units. 2. direct self-consistent-field implementation. J. Chem. Theory Comput. 5, 1004–1015. doi:10.1021/ct800526s

PubMed Abstract | CrossRef Full Text | Google Scholar

Valeev, E. F., and Fermann, J. T. (2014). Libint: A library for the evaluation of molecular integrals of many-body operators over Gaussian functions. Available at: http://libint.valeyev.net.Version.1.1.5.

Google Scholar

Wu, X., Selloni, A., and Car, R. (2009). Order-N implementation of exact exchange in extended insulating systems. Phys. Rev. B 79, 085102. doi:10.1103/PhysRevB.79.085102

CrossRef Full Text | Google Scholar