- Chemistry Department, Duke University, Durham, NC, United States
The quantitative description of the supramolecular interaction occurring at the adhesion surfaces of different polymers has enabled elaborate dissections of contributions to cohesive and surface energies. An alternative analysis is proposed here based on solubility parameters and binding constants that traditionally describe the weakest and relatively larger association energies in polymer blends. The article emphasizes a feature of supramolecular polymers that has not received adequate consideration: The dynamic bond scrambling that allows a most efficient molecular recognition over significant areas of synthetic and biological surfaces.
Introduction
Adhesion is the ability of two phases, usually two solid surfaces of similar or dissimilar substances, to bind (cling together) by virtue of supramolecular interaction or mechanical interlocking. Wetting is the term used in the case of a solid-liquid interface Awaja et al., (2009). Typical practical examples involving polymers include coating and painting (Zheng, 2020), wetting as in the printing ink industry (Cern et al., 2021), cases in which adhesion is enhanced by promoters (i.e., chemicals that act at the interface between an organic polymer and an inorganic substrate) (Peter, 2011). Relevant are also cases of self-healing (when two fractured surfaces of the same polymer will seal again if brought in close contact) (Ciferri, 2013). Among biological materials, the enzyme-substrate complex shows a remarkable association mechanism, extending to the most complex cases of cell adhesion associated with a variety of function (Buckley et al., 1998; Ciferri, 2021).
There is not a general molecular theory for chemical adhesion. However, several studies have highlighted the need of dissecting the supramolecular components of cohesive and surface energies that control solubility, surface wettability and the strength of the interfacial association (Hansen, 2007; Abdullah et al., 2015; Nanoscience Instruments; Ciferri, 2021). The present note includes a review of cohesive and surface energies and suggests the application of the classical parameters that control the interactions of supramolecular polymers, emphasizing their bond scrambling features.
Cohesive energy
The cohesive energy (ωcoh) of a substance in the bulk phase is defined by the internal energy per mole that results from the balance of all its supramolecular interactions (Flory, 1953; Hildebrand et al., 1970; Burke, 1984). Cohesive energy densities can be rigorously determined using ab initio calculations (Abdullah et al., 2015). For low molecular weight substances, the cohesive energy is the energy required to evaporate the material, assessed from the heat of vaporization in calories per cubic centimeter. For materials that decompose before evaporating, cohesive energies are often evaluated from known group contributions (Marsano et al., 1984).
Cohesive energy is also related to solubility parameters. The Hildebrand solubility parameter (δ) is defined by the square root of the cohesive energy density (Hildebrand et al., 1970):
where ΔH is the measurable enthalpy of vaporization and V the molar volume. The Hildebrand solubility parameter is related to the Flory-Huggins solubility parameter χ (Flory, 1953):
where z is the coordination number and Δω expresses the energy change upon rupture of contacts between each of the two components of a mixture with formation of new contacts between these components (Flory, 1953):
The concept of solubility is relevant to the description of cohesive energy since it involves the rupture and the association of two compounds. The relationship between the Hildebrand and the Flory-Huggins solubility parameters is:
where
The Flory-Huggins free energy of mixing real solutions (Flory, 1953) includes different contributions, in particular one expressing the ideal mixing entropy, another expressing weak interactions through the diluent parameter χ (Flory, 1953), and another expressing stronger attractive interactions through binding constant kj (Orofino et al., 1967). A relevant expression for the melting temperature depression of a polymer in a binary diluent is (Orofino et al., 1967):
On the right-hand side (RHS), χ12 and Kj equal zero for an ideal solution, p is the number of binding sites and cj represents the activity of a binding agent. Different solvents and different binding agents (i.e., water, salts….) can be evaluated with the latter equation. Corresponding Kj could be evaluated from enrichment data (Orofino et al., 1967). We discuss separately the cases of weak and relatively stronger interactions.
Weak supramolecular interactions
In terms of current polymer solution theory (Flory, 1953) any weak favorable attraction between the components (good solvents) is characterized by negative values of χ12, whereas repulsive interactions, including excluded volume effects, are characterized by positive values of χ12.
The work of Blanks and Prausnitz stands above the earliest investigations of polymer solutions (Blanks and Prausnitz, 1984). They demonstrated that the validity or self-consistency of the above relationships is restricted to systems with low polarity, primarily due to van der Waals interactions.
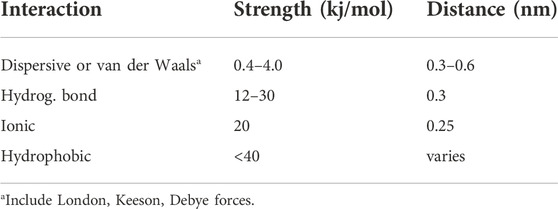
They analyzed different solvents and model substances that included three components, namely dispersive (London) interactions (induced by transient dipoles even in non-polar molecules), polar (Debye) interactions between permanent dipoles, and Keeson interactions between permanent and induced dipoles (Hiemenz and Rajagopalan, 1997). Table 1 reveals that the global van der Waals interactions are the weakest supramolecular interactions, having association strength below 1 kcal/mol and active separation distances smaller than about 0.5 nm. Corresponding χ12 values evaluated by Blanks and Prausnitz are in the range −0.1 to + 0.516.
Table 2 evidences a more detailed evaluation of the separate contributions to van der Waals interaction. The results are based on a sophisticated approach, primarily the temperature and enthalpies of evaporation (Hiemenz and Rajagopalan, 1997). Included are representative data for molecules chosen as to have comparable values of dipolar moment and polarizability (the latter is a measure of the easiness of electrons to move around the molecule in response to an external electric field or a neighboring dipole) (Hiemenz and Rajagopalan, 1997). The data show that dispersive London interactions are generally prevailing. Nevertheless, the dipolar moment and the molecular polarizability also have a role, complicating the assignment of the various contributions. Additional difficulties have been more recently reported, suggesting that solvents may mitigate the intensity of the components evaluated from vaporization enthalpies (Young et al., 2013). In fact, cohesive solvent-solvent interactions (cf., Eq. 3) were found to be the major driving force for apolar association in solution (Young et al., 2013).
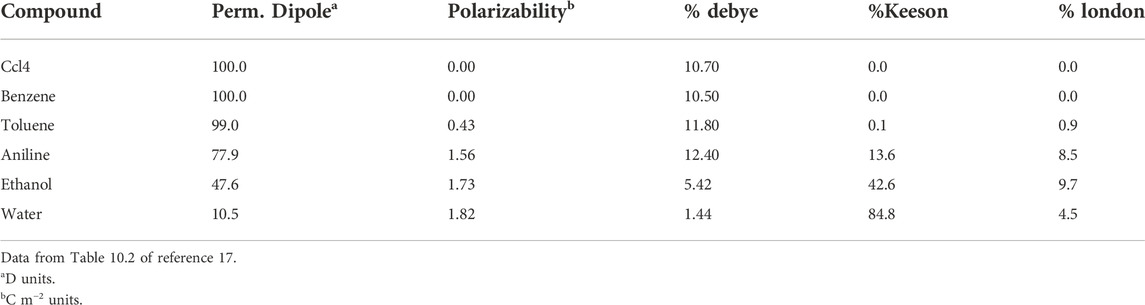
TABLE 2. Percentage of the Debye (permanent-permanent), Keeson (permanent-induced) and London (induced-induced) contributions to van der Waals dipolar interactions, as related to the permanent dipole and polarizability of typical compounds.
Stronger supramolecular interactions
Stronger specific interactions occurring between polymeric solutes may be described by a binding constant (Orofino et al., 1967). An example is the electrostatic attraction between a proton in one molecule and an electronegative atom in another one forming the intermolecular hydrogen bond having dissociation constants in the range 10–30 kcal/mol (Steiner, 2002), see Table 1. Other strong interactions include ϖ-ϖ (Ma et al., 2021), hydrophobic and ion binding interactions (see Table 1). Ion binding typical of salting-in ions in the Hofmeister series (i.e., calcium ions) can also induce intra or intermolecular bridges (Ciferri et al., 2012).
An approach allowing a quantitative assessment of weak van der Waals and stronger bonding contributions is afforded by the generalized Flory-Huggins Eq. 5. The χ12 parameters and equilibrium constants for ionic interactions were evaluated from viscosity analysis and enrichment data for gelatin-water solutions in the presence of salts of the Hofmeister series (Ciferri et al., 2012). The analysis provided definite evidence that the solubility of proteins is controlled by van der Waals interactions in the case of typical salting-out agents (i.e., KCl) and by specific binding in the case of typical salting-in agents (i.e., CaCl2) (Ciferri et al., 2012). No values for Kw relevant to H-bonding were reported.
An alternative thermodynamic approach to describe the simultaneous occurrence of weak and specific supramolecular interactions was elaborated by Hanson (Hansen, 2007). He suggested that the global interaction could be dissected into three additive components characterizing, respectively, the dispersive (London), polar (Debye) and hydrogen bonding contributions.
Various analytical approaches were elaborated to dissect the three components from raw solubility data. A complex approach based on inverse gas chromatography is detailed by Adamska and Voelkel (2006). The solubility behavior relevant to a variety of technological processes was reasonably well described by the Hansen parameters (Hansen, 2007). These parameters were also used to assess the compatibility between a dispersed and a continuous phase (Bapat et al., 2021).
Specific selections of the relevant components of the cohesive energy may be relevant to special formulations for industry (Abdullah et al., 2015; Haixia et al., 2021).
Surface energy
Within a bulk phase, the interaction forces on an atom/molecule are mutually equilibrated whereas unbalanced interactions prevail at the surface. Such an unbalanced energy is referred to as the surface “energy” in the case of attractive interactions between two solid substances. Surface “tension” is instead when liquids are involved. The surface energy/tension increases with number of bulk interactions. A high surface energy refers to a strong molecular attraction, whereas a low surface energy refers to a weak molecular attraction or low compatibility (cph Deutschland Chemie GmbH, 2020; Brighton Science, 2021).
Whereas adhesion is the term preferentially uses for association of two solid surfaces, wetting is used when a liquid spreads over a solid. In contrast to wetting, an incompatible liquid will form a drop characterized by a contact angle. The boundary between solid-solid or solid-liquid systems is referred to as the interface (cph Deutschland Chemie GmbH, 2020; Brighton Science, 2021).
Surface energy is often assessed using contact angle data obtained for solid-liquid systems. The Yung equation allows a quantitative relationship between the surface energies of solid and liquids (σs and σl), the interfacial tension between liquid and solid
Several methods for the evaluation of the surface tension of solids and liquids are described in the literature. Contact angles of test liquids may be used (Cheng et al., 1990). In the case of incompatible liquids, determination of contact angles with an optical goniometer may be facilitated by drop shape analysis (Bouge et al., 1986).
There is some evidence that surface energy is affected by chain conformation (Flory, Statistical, 1969; Chalykh, 2020; Dataphysics, 2021). The bulk conformation of flexible polymers is often described as that prevailing under theta conditions when excluded volume effects are balanced by supramolecular attraction. More rigid polymers are characterized by parallel orientation of the macromolecular chains in the surface layer (Dataphysics, 2021). The latter effect has recently been shown to correspond to an enhancement of surface energy.
A model for the adhesion mechanism proposed by Data Physics (Dataphysics) is based on only two types of surface energy, one involving transient dipoles (included in dispersive interactions, cf. Table 1) and the other polar (Debye and H-bond) interactions.
These interactions were schematized on a simple figure in which the adhesion of two surfaces was promoted by the recognition of the two types of bonds (Figure 1A) (Dataphysics). The model based on our Eq. 5 is also based on just two types of interactions: one based on the χ12 parameter (representing all weak interactions of the van der Waals type, the other all strong interactions described by an equilibrium constant K). Thus, we include in Figure 1B a schematization of how two surfaces should bind, consistently with general principles of supramolecular polymers (Ciferri, 2016; Ciferri, 2020).
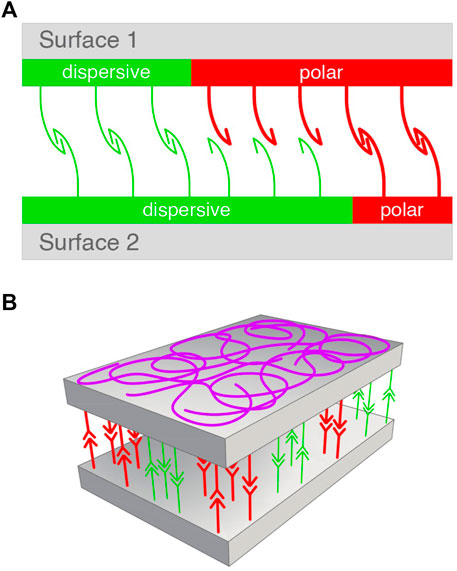
FIGURE 1. Models for surface association. (A) Data-Physics model based on dispersive (green) and polar interactions (red) balanced between two surfaces (Eq. 8). Adapted from Dataphysics. (B) Presently suggested model based on balanced and randomly oriented weak interactions represented by the Flory’Huggins parameter (green), and a stromger binding constant (red) (Eq. 5). All supramolecular bonds undergo dynamic scrambling (exchanging partners) under equilibrium conditions. Designer: Luca Galbusera, 2022.
Bond scrambling
Bond scrambling is a fundamental motion occurring in processes such as reversible chemical reactions and supramlecular associations, both characterized by small equilibrium constants. In these processes, an active terminal group continues to associate and dissociate various complementary groups. The motion greatly assists the recognition of binding partners even in the absence of mechanical sliding or main chains reorganization. A dynamic equilibrium will be reached when the rates of association and dissociation with adjacent oligomers are equal. Under equilibrium, alteration of the composition of the reactants (i.e., the degree of polymerization, DP) is not allowed and a direct relationship between DP and the binding constant is predicted and experimentally verified (i.e., DP ∼ K1/2) (Ciferri, 2016). Nevertheless, bond scrambling motion can affect some labile structurization.
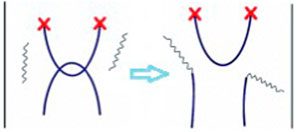
As first suggested by J. M. Lehn, bond scrambling allows the elimination of steric constraints in supramolecular networks (i.e., entanglements, see schematization in Figure 2) (CiferriBond and Network Elasticity, 2009). These networks have indeed been described as dynamic materials having adaptive features (Cordier et al., 2008). Similar features have been documented even for hydrogels (Sinawang et al., 2020). Moreover, scrambling has also been shown to induce the randomization of ordered sequences (Bleiholder et al., 2008). The role of scrambling in promoting a chain size distributions has also been documented (Matula et al., 1964; Moedritzer, 1964).
Particularly relevant to surface recognition is the self-healing of freshly fractured surfaces of a given polymer (Cordier et al., 2008; CiferriBond and Network Elasticity, 2009). In this case, it could be argued that the detailed location and orientation of proton donors and acceptors of the H-bonds, severed during fracture, might have been only slightly altered, thus aiding the recognition process.
A more complex mismatch between the position and orientation of the H-bond components is instead expected when two different surfaces of a non-fractured polymer are adhering. Complex rearrangement of the chains connecting the various components has been frequently suggested. However, bond scrambling could enhance the recognition of different surfaces.
A related feature of surface recognition is exhibited by biological systems. In the case of the enzyme-substrate association, new material is synthesized to fill empty cavities occurring between two adhering surfaces (Figure 3) (Ciferri, 2021).
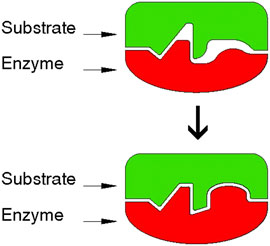
FIGURE 3. The induced fit in the enzyme–substrate model. Preliminary binding in a limited area is followed by induced synthesis to insure better fit between the surfaces of the enzyme and the substrate, also generating micro interlocking. Adapted from Ciferri 2021. Designer: Luca Galbusera, 2021.
Concluding remarks
A recent article focuses on theories and simulations related to adhesion, emphasizing problems associated with molecular models and experimental methods for assessing forces and characterizing interfaces at the molecular level (Raos and Zappone, 2021). The quantitative evaluation of van der Waals supramolecular interactions is particularly complicated by the low values of some of the energies involved.
Various authors have therefore avoided direct measurements of the weakest components of the surface energy (cf. Eqs 6, 8). The approach suggested here, based on Eq. 5, likewise avoids a detailed evaluation of the van der Waals energy components, but has the advantage of extending to adhesion process concepts and parameters proper to supramolecular chemistry. Wettability might indeed be regarded as the first step in the dissolution of a solvophilic particle in excess solvent. The uncompensated bonds on the external boundary of the particle are saturated by bond exchange with solvent molecules. Dispersive interactions do not prevent the dissolution of the first polymer layer, and the above binding-dissolution sequence is transferred to successive layers on the particle.
It is to be noticed that here is not a clear-cut boundary between the energies represented by χ12 and very small binding constants. The identification might be regarded as an operational one, depending upon how small K can be measured.
The present emphasis on the scrambling features of supramolecular polymers highlights a new mechanism that amplifies the local recognition process. Intense motions of chain segments connecting supramolecular groups, or mechanical sliding motions of the surfaces need no longer be postulated. Awaja et al., 2009; Data Physics Instruments, 2021.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
AC pointed out the relevance of the bond scrambling motion to the molecular recognition of adhering surfaces. He also suggested that solubility parameters and supramolecular binding constants be used to appreciate the strength of cohesive energy.
Acknowledgments
The author expresses his appreciation to Guido Raos (Raos and Zappone, 2021) for reading the ms and relevant advice. Great appreciation is also expressed to the Chemistry Department at Duke University for a long-range, constructive affiliation.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdullah, B. J., Omar, M. S., Saadi, N. S., and Jiang, Q. (2015). First-principles calculations on cohesive energy of bulk and Nano Si. Int. J. Sci. Eng. Res. 6, 842’846.
Adamska, K., and Voelkel, A. (2006). Hansen solubility parameters for polyethylene glycols by inverse gas chromatography. J. Chromatogr. A 1132, 260–267. doi:10.1016/j.chroma.2006.07.066
Awaja, F., Gilbert, M., Kelly, G., Fox, B., and Pigram, P. J. (2009). Adhesion of polymers. Prog. Polym. Sci. 84, 948–968. doi:10.1016/j.progpolymsci.2009.04.007
Bapat, S., Kilian, S. O., Wiggers, H., and Segets, D. (2021). Towards a framework for evaluating and reporting hansen solubility parameters: Applications to particle dispersions. Nanoscale Adv. 3, 4400–4410. doi:10.1039/d1na00405k
Blanks, R. F., and Prausnitz, J. M. (1984). Thermodynamics of polymer solubility in polar and nonpolar systems. Ind. Eng. Chem. Fund. 3, 1–8. doi:10.1021/i160009a001
Bleiholder, C., Osburn, S., Williams, T. D., Suhai, S., Van Stipdonk, M., Harrison, A. G., et al. (2008). Sequence-scrambling fragmentation pathways of protonated peptides pathways of protonated peptides. J. Am. Chem. Soc. 130, 17774–17789. doi:10.1021/ja805074d
Bouge, R., Gamet, D., and Schreiber, H. P. (1986). Chain conformation and surface characteristics of polymers. J. Adhes. 23, 15–28. doi:10.1080/00218468608073237
Brighton Science. (2021). What is the difference between surface tension and surface energy. March 2021. Blog. Available from: https://www.brighton-science.com/blog/what-is-the-difference-between-surface-tension-and-surface-energy-1.
Buckley, C., Rainger, G. E., Bradfield, P. F., Nash, G. B., and Simmons, D. L. (1998). Cell adhesion: More than just glue (review). Mol. Membr. Biol. 15, 167–176. doi:10.3109/09687689709044318
Burke, J. (1984). Solubility parameters: Theory and application. Washington, United States: The American Institute for Conservation. https://cool.culturalheritage.org/coolaic/sg/bpg/annual/v03/bp03-04.html.
Cern, A., Altay, B. N., and Akyol, M. (2021). Surface analysis of polymer films for wettability and ink adhesion. Color Res. Appl. 46, 489–499. doi:10.1002/col.22579
Chalykh, A. E. (2020). Adhesion and surface characteristics of rigid polymers. Polymers (Basel) 12 (12), 2956. doi:10.3390/polym12122956
Cheng, P., Li, D., Boruvka, L., Rotenberg, Y., and Neumann, A. (1990). Automation of axisymmetric drop shape analysis for measurements of interfacial tensions and contact angles. Colloids Surfaces 43, 151–167. doi:10.1016/0166-6622(90)80286-D
Ciferri, A. (2021). Critical issues in molecular recognition: The enzyme-substrate association. Soft Matter (RCS) 17, 8585–8589. doi:10.1039/d1sm00470k
Ciferri, A. (2013). Healing and self-healing polymers: Composite networks revisited. Polym. Chem. 4, 4980–4986. doi:10.1039/C3PY21156H
Ciferri, A. (2012). “Ionic mixed interactions and the Hofmeister effect,” in Ioni interactions in natural and synthetic macromolecules. Editors A. Ciferri, and A. Perico (New York, United States: Wiley).
Ciferri, A. (2020). Molecular recognition mechanisms directing the self-assembly of biological structures biological structures. Soft Matter 16, 8985–8995. doi:10.1039/D0SM01301C
Ciferri, A. (2016). Translation of molecular order to the macroscopic level. Chem. Rev. 116, 1353–1374. doi:10.1021/acs.chemrev.5b00143
CiferriBond, A. S., and Network Elasticity, (2009). Bond scrambling and network elasticity. Chem. Eur. J. 15, 6920–6925. doi:10.1002/chem.200802746
Cordier, P., Tournilhac, F., Soulie´-Ziakovic, C., and Leibler, L. (2008). Self-healing and thermoreversible rubber from supramolecular assembly assembly, 2008 assembly. Nature 451, 977–980. doi:10.1038/nature06669
cph Deutschland Chemie GmbH., (2020). Surface energy and the young equation. Available at: http://www.cph-group.com/wp-content/uploads/2020/12/TT-06-Surface-Energy-and-the-Young-Equation-eng-2020.pdf.
Data Physics Instruments. Optical contact angle measuring and contour analysis systems. Available at: https://www.dataphysics-instruments.com/products/oca/.
DataPhysics Instruments, (2021). Dispersive & polar parts of the surface energy and surface tension. Available at: https://www.dataphysics-instruments.com/knowledge/understanding-interfaces/dispersive-polar-parts/.
Flory, Statistical, P. J. (1969). Mechanics of chain molecules. Interscience. Munich, Germany: Hanser.
Haixia, H., Wan, Y., Jiang, G., Sun, R., Sha, J., Li, Y., et al. (2021). Solubility determination, model evaluation, Hansen solubility parameter and thermodynamic properties of N-hydroxyphthalimide in eleven neat solvents. J. Mol. Liq. 325, 114677. doi:10.1016/j.molliq.2020.114677
Hansen, C. M. (2007). Hansen solubility parameters. A User’s Handbook. Second Edition. Boca Raton FLA: CRC Press Taylor & Francis Group.
Hiemenz, P. C., and Rajagopalan, R. (1997). Principles of colloid and surface Chemistry. 3th edition. Florida, United States: CRC Press.
Hildebrand, J. H., Prausnitz, J. M., and Scott, R. L. (1970). Regulated and related solutions. New York, United States: Van Nostrand Reinhold Co.
Ma, S., Zhao, W., Zhou, J., Wang, J., Chu, S., Liu, Z., et al. (2021). A new type of noncovalent surface–π stacking interaction occurring on peroxide-modified titania nanosheets driven by vertical π-state polarization. Chem. Sci. 12, 4411–4417. doi:10.1039/D0SC06601J
Marsano, E., Bianchi, E., and Ciferri, A. (1984). Mesophase formation and polymer compatibility. 2. Cellulose acetate/(hydroxypropyl)cellulose/diluent system. Macromolecules 1712, 2886–2889. doi:10.1021/ma00142a075
Matula, D. W., Groenweghe, L. C. D., and Van Wazer, J. R. (1964). Molecular distributions at equilibrium. I. Theory of equilibria in scrambling reactions and interpretation of NMR spectra. J. Chem. Phys. 41, 3105–3121. doi:10.1063/1.1725683
Moedritzer, K. (1964). J. R. Van WazerExchange of parts between molecules at equilibrium. I. Α, ω-disubstituted PolydimethylsiloxanesExchange of parts between molecules at equilibrium. I. Α, ω-disubstituted polydimethylsiloxanes. J. Am. Chem. Soc. 86 (5), 802–807. doi:10.1021/ja01059a011
Nanoscience Instruments. Surface tension, surface free energy, and wettability. Available at: https://www.nanoscience.com/techniques/tensiometry/surface-tension-surface-free-energy-and-wettability/.
Orofino, T. A., Ciferri, A., and Hermans, J. J. (1967). Effect of binding on melting transitions in polymer-diluent systems. Biopolymers 5, 773–783. doi:10.1002/bip.1967.360050810
Peter, G. (2011). Adhesion Promoters: Chemicals that contain double functionality. Handb. Adhesive Surf. Prep.
Raos, G., and Zappone, B. (2021). Polymer adhesion. Searching new solutions for an old problem. Macromolecules 54, 10617–10644.
Sinawang, M., Osaki, M., Takashima, Y., Yamaguchi, H., and Harada, A. (2020). Biofunctional hydrogels based on host–guest interactions. Polym. J. 52, 839–859. doi:10.1038/s41428-020-0352-7
Steiner, T. (2002). The hydrogen bond in the solid state. Angew. Chem. Int. Ed. 76, 48–76. doi:10.1002/1521-3773(20020104)41:1<48:aid-anie48>3.0.co;2-u
Young, L., Adam, C., Nichol, G. S., and Cockroft, S. L. (2013). How much do van der Waals dispersion forces contribute to molecular recognition in solution? Nat. Chem. 5, 1006–1010. doi:10.1038/nchem.1779
Keywords: cohesive energy, surface energy, solubility parameters, binding constants, adhesion, wetting, molecular recognition, bond scrambling
Citation: Ciferri A (2022) Molecular recognition at interfaces. Adhesion, wetting and bond scrambling. Front. Chem. 10:1088613. doi: 10.3389/fchem.2022.1088613
Received: 03 November 2022; Accepted: 21 November 2022;
Published: 09 December 2022.
Edited by:
Da-Hui Qu, East China University of Science and Technology, ChinaReviewed by:
Zonglin Chu, Hunan University, ChinaCopyright © 2022 Ciferri. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alberto Ciferri, YWxiZXJ0by5jaWZlcnJpQGR1a2UuZWR1
 Alberto Ciferri
Alberto Ciferri