Navigating industry 4.0 and 5.0: the role of hybrid modelling in (bio)chemical engineering’s digital transition

This work investigates the potential of hybrid modelling in the digitalization of the chemical and biochemical industries. Hybrid modelling combines first-principles with data-driven models and is a vital enabler for the knowledge-informed transition to Industry 4.0 and, ultimately, 5.0. By integrating data with mechanistic know-how, hybrid modelling facilitates the implementation of “smart manufacturing”. Although there have been many innovations in the field of machine learning, AI, and cloud computing, the industry is still some distance away from becoming truly digital; this is particularly true in the case of the biochemical industry, which in many ways still is in the industry 3.0 stages. This gap hinders the full realization and benefits of the digital transition, such as easier process optimization, better cost-efficiency balance, and overall improved competitiveness and sustainability. This research delves into documented examples of hybrid modeling in chemical and biochemical engineering research and industries. It aims to illustrate current motivations, implementation challenges, and practical issues that hybrid modeling can address. The goal is to derive the path towards fully implementing hybrid modeling as an effective tool and key enabler for creating true digital twins and successful digitalization.

1 Introduction

The chemical and biochemical industries face numerous challenges and opportunities due to the ever-changing technological landscape. The rise of Industry 4.0 and Industry 5.0, as presented in Figure 1, has brought about digitalization and automation, offering the potential for significant efficiency and productivity improvements. As presented in Figure 2, companies can improve operations and transition to Industry 4.0 and 5.0 by employing advanced technologies such as Digital Twins (DTs), Internet of Things (IoT), Artificial Intelligence (AI), and big data analytics, among others (Udugama et al., 2021; Gargalo et al., 2021; Pandey et al., 2024; Isoko et al., 2024). Indeed, Industry 4.0 is the embodiment of digital transformation through the development of high-fidelity digital copies of the processing plant operations (Gargalo et al., 2021; Isoko et al., 2024). Although Industries 4.0 and 5.0 both leverage advanced technologies (see Figure 2), the former is focused mainly on automation and digital transformation towards smart manufacturing, whereas the latter targets improving the collaboration between humans and machines towards a more “human-centric” approach (Aheleroff et al., 2022; Maddikunta et al., 2022; Nahavandi, 2019). Moreover, while Industry 4.0 paves the way for a sustainable (bio)economy, Industry 5.0 emphasizes and implements the concept of circularity (Pandey et al., 2024). Adopting circular (bio)economy leads companies to reduce, reuse, and recycle by leveraging technologies like IoT sensors for continuous energy monitoring, AI-powered analytics, and additive manufacturing. This paradigm targets to reconcile technological advancements with human values (“human-centric”), sustainability and environmental-conscious decision-making (aiming to reduce the environmental impact in place since the rise of Industry 2.0), and workforce well-being, promoting agile and robust production systems (Aheleroff et al., 2022; Bazel et al., 2024; He and Chand, 2024; Maddikunta et al., 2022).

Figure 1

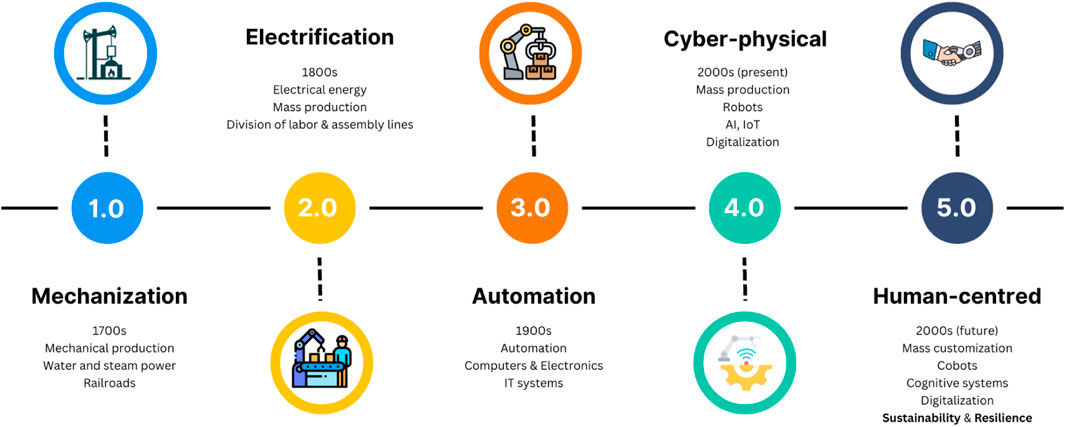
Figure 1. Illustration of the Industrial Revolution stages. Diagram created in Canva.com, icons obtained from Flaticon.

Figure 2

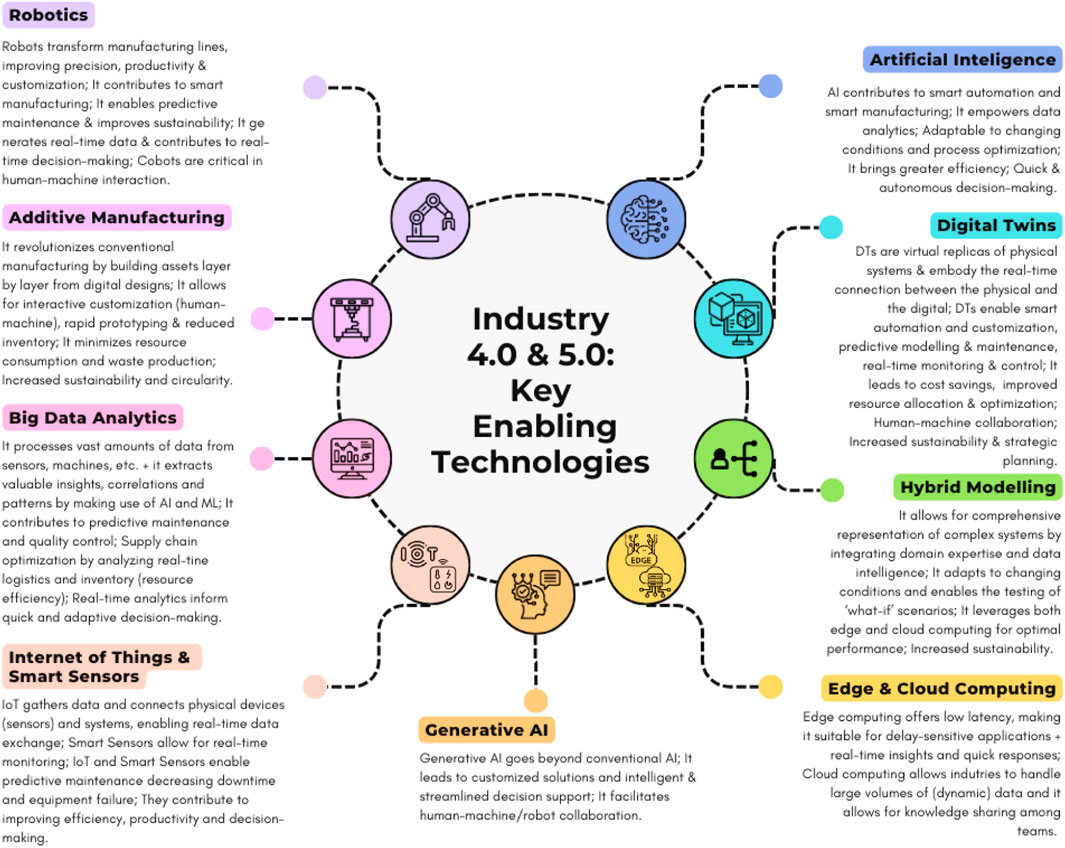
Figure 2. Key enabling technologies of Industry 4.0 and 5.0. Diagram created in Canva.com, icons obtained from Flaticon.

Yet, the journey towards successful implementation of Industry 4.0 in (bio)chemical processing plants is not simple and/or straightforward (Pandey et al., 2024; Isoko et al., 2024; Udugama et al., 2021). It implies not only technological advancements but also workforce training, organizational changes, and regulatory backing (Pandey et al., 2024; Isoko et al., 2024; Udugama et al., 2021; Gargalo et al., 2021). In particular, the biochemical industry, including sectors such as enzyme production and biopharma, seems to be falling behind, with many companies still operating within the limitations of Industry 3.0 (Arden et al., 2021). This gap can be due to various reasons, including the intrinsic complexity of biological systems (difficult to optimize and scale), regulatory guidelines, scalability, data security, and the high expenses linked with upgrading current infrastructure (e.g., sensors, cloud computing, cybersecurity) (Isoko et al., 2024; Gargalo et al., 2021; Arden et al., 2021; Maddikunta et al., 2022). Another significant barrier to the digitalization of the (bio) industry is the shortage of skilled workforce - digital literacy is now a mandatory set of skills (Caccavale et al., 2024). Thus, the adoption of Education 4.0 in educational institutions is under discussion, with some Universities taking the lead in training students towards this goal (Caccavale et al., 2024).

Despite these and other challenges companies face in implementing Industry 4.0 principles in the chemical and biochemical industries, several technologies have emerged that could facilitate the implementation of these strategies. Hybrid modelling is a promising approach that combines first-principles models with the flexibility of data-driven techniques to make more accurate predictions, improving process control and optimization, and increasing efficiency and flexibility (Narayanan et al., 2023; Sokolov et al., 2021; Narayanan et al., 2020; Albino et al., 2024). Hybrid models work on counteracting the advantages/disadvantages of both mechanistic and data-driven approaches. This synergy not only improves the predictive accuracy of models but also provides deeper insights into process dynamics, enabling better control and optimization (Narayanan et al., 2020; Narayanan et al., 2023). This approach is especially applicable and beneficial for industries where data generation is highly resource intensive, and the fundamental processes are not 100% understood (e.g., biochemical processes, transport and reaction mechanisms) (Narayanan et al., 2023; Yu et al., 2022). This is due to the fact that hybrid modelling identifies a compromise between the governing relationships among the variables while permitting the flexibility to discover possible interactions between these variables (Narayanan et al., 2023). Therefore, in essence, one substitutes excessively intricate processes that cannot be physically modelled with simplified dynamic, machine learning (ML) processes, or time series modelling. This enables the direct acquisition of new parameterizations from observations and/or high-resolution model simulations using machine ML methods (Kasilingam et al., 2024). Even before coining the term of hybrid modelling in 1992 (Psichogios and Ungar, 1992), numerous works on grey box modeling have demonstrated their successful implementation in representing complex systems, such as, for example, kinetic modelling (e.g., Monod), mass transfer between liquid and gas phases, among others. In summary, the shift toward Industry 4.0 and 5.0 brings both challenges and opportunities for the chemical and biochemical industries. Although the journey ahead may be challenging, the potential benefits in terms of efficiency, improved sustainability, and competitiveness are too significant to overlook. We believe that this article will shed light on these challenges and motivate further research and discussion.

The remaining manuscript is organized as follows. Section 2 delves deeper into concepts and principles behind the successful implementation of hybrid modelling, and discusses the advantages over conventional modelling approaches in the context of Industries 4.0 and 5.0. Section 3 presents a pragmatic review of works detailing the implementation of hybrid modelling and discusses the lessons learned. Section 4 presents perspectives on the use of hybrid modelling for resource optimization and the pursuit of sustainability. Lastly, Section 5 summarizes the main findings and provides insights for future advancements in this field.

2 Hybrid modelling in the digital era: concepts and principles

As previously mentioned, we distinguish between two distinct modelling approaches: i) knowledge-driven, and ii) data-driven. Combining these two results in a third approach, a hybrid modelling approach. Each approach will be elaborated on in this section so as to provide the rationale for the emergence of hybrid modelling.

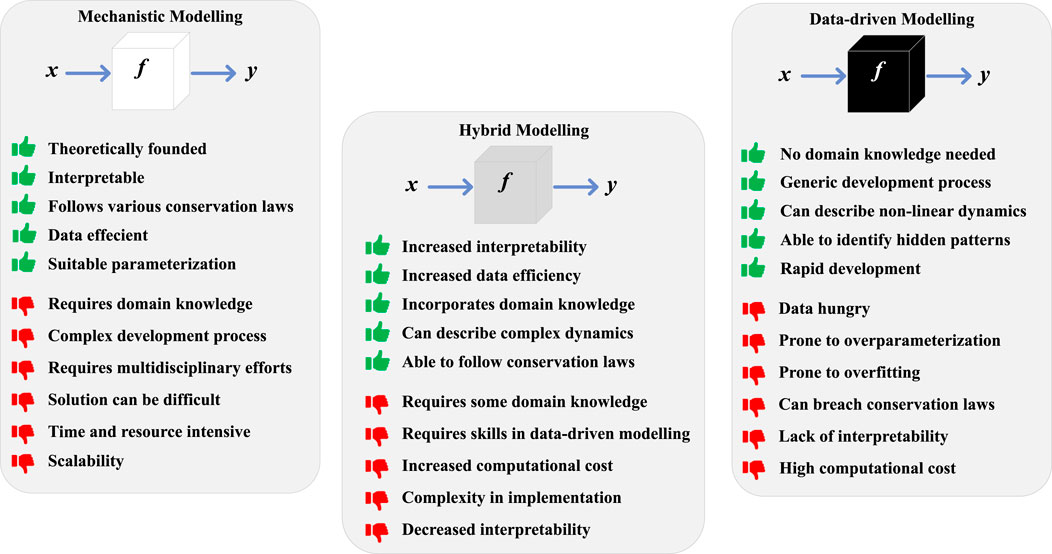
Knowledge-based modelling is also referred to as mechanistic modelling, first-principles modelling, white-box modelling, parametric modelling, or physics/science-based modelling. Despite the wide range of terminologies used, the concurring fact is that such an approach is based on a first-principles understanding of the phenomena occurring in the system, where the parameters in the model have a physical meaning. Such models include physical laws and constraints resulting from combining observations, theoretical analysis, hypothesis construction, and experimental validation (Rudolph et al., 2024). These laws usually result in mass, energy, and momentum conservation laws. First principle models conventionally take the form of either algebraic equations, systems of ordinary differential equations (ODEs), or systems of partial differential equations (PDEs).

Many studies have focused on the mechanistic modelling of various processes relating to the upstream and downstream of chemical and biochemical industries. Some examples are: Saccharomyces cerevisiae fermentation process (Sonnleitner and Käppeli, 1986), lactic acid bacteria fermentation (Spann et al., 2018), filamentous fungal fermentation (Mears et al., 2017), membrane filtration (Rischawy et al., 2023), pectin extraction (Andersen et al., 2017), ion exchange chromatography (Rischawy et al., 2022; Meyer et al., 2023) and distillation processes (Bisgaard et al., 2017).

Mechanistic models are usually data-efficient (in contrast to data-hungry) and are capable of providing a causal explanation of the generated output. As such, they are reliable as long as the underlying assumptions and the domain of applicability are valid. One major drawback of this modelling approach is that it requires expert domain knowledge to derive the underlying dynamics. Considering the multiscale nature of many of the phenomena occurring in a chemical process and the wide range of expertise required (metabolism, metagenomics, fluid dynamics, etc.), this could pose a serious challenge. This a challenge many have sought to solve using data-driven modelling.

Data-driven modelling is also referred to as black-box modelling and non-parametric modelling. The concept of nonparametric reflects the fact that the parameters in these models do not carry any physically meaningful sense. These models are data-centric and use the data to deduce the underlying patterns between a set of inputs and outputs. This pattern recognition is used to approximate the underlying mechanism, which is especially important when the true dynamics are too complex for to derive first-principles models. Data-driven modelling is usually based either on statistical modelling or more recently on ML principles. Statistical modelling has been used for many years, e.g., the use of autoregressive and moving average models for time series, linear multivariate models (partial least square model), as well as non-linear multivariable models (polynomial functions). The major distinction between ML-based models and statistical or classical first-principles models is that the relationship between the input and output is not explicitly programmed or encoded in the program. ML covers a wide range of modelling techniques that can be classified based on the model structure, the learning process, or the intended application. Model structures include deep neural networks, Gaussian processes, graph neural networks, support vector machines, random forests, k-nearest neighbors, etc. Intended applications include regression (predicting numerical values), classification (predicting classes), or clustering (group data based on similarity). The learning process covers supervised (data used are labeled) and unsupervised learning (data used are not labeled).

The strength of data-driven models is that they do not “require” expert domain knowledge and are capable of extracting highly non-linear relationships between the input and output. This is especially the case for deep neural networks, which, in theory, are capable of approximating any non-linear function (hence the universal approximation nature). However, data-driven models are data inefficient (data “hungry”) as the data demand scales exponentially with the feature dimensions (Schweidtmann et al., 2023). This results in over-parameterized models (with many weights), which ultimately results in overfitting, especially if the number of parameters exceeds that of the data used for model training. Furthermore, the nonparametric models lack an aspect of explainability, meaning that despite the ability to capture the intricate relationships between input and output, they cannot explain the underlying mechanism of a given system, thus the black-box notation. A model’s ability to extrapolate is of great interest regardless of the underlying modelling approach. Mechanistic models are well suited for extrapolation (as long as the assumptions hold) and the limits of the models can be subjected to analysis. Meanwhile, some data-driven techniques such as deep neural networks are subject to the universal approximation principle and can in theory replicate any non-linear continuous trend. However, the validity of these models when subjected to extreme values is not well described but can be inferred through simulation.

Efforts to alleviate the weaknesses of both modelling approaches while leveraging their individual strengths gave birth to the concept of hybrid modelling. As such, a hybrid model is any model that combines first-principles and data-centric approaches. These models are also referred to as semi-parametric, as only a subset of its parameters carries any physical meaning. Hybrid models can potentially provide high accuracies while maintaining a certain degree of interpretability. The work by Psichogios and Ungar (1992) as highlighted by Schweidtmann et al. (2023) reported an improved model performance through better extrapolation, a reduced need for data, and an increased interpretability of the models. However, hybrid modelling could also pose a new challenge as such approaches require both expertise and knowledge in first-principles modelling and data-driven modelling to ensure efficient integration Rudolph et al. (2024). Such an added layer of complexity can arise in determining the level of detail of each compartment and a suitable configuration to combine the two approaches.

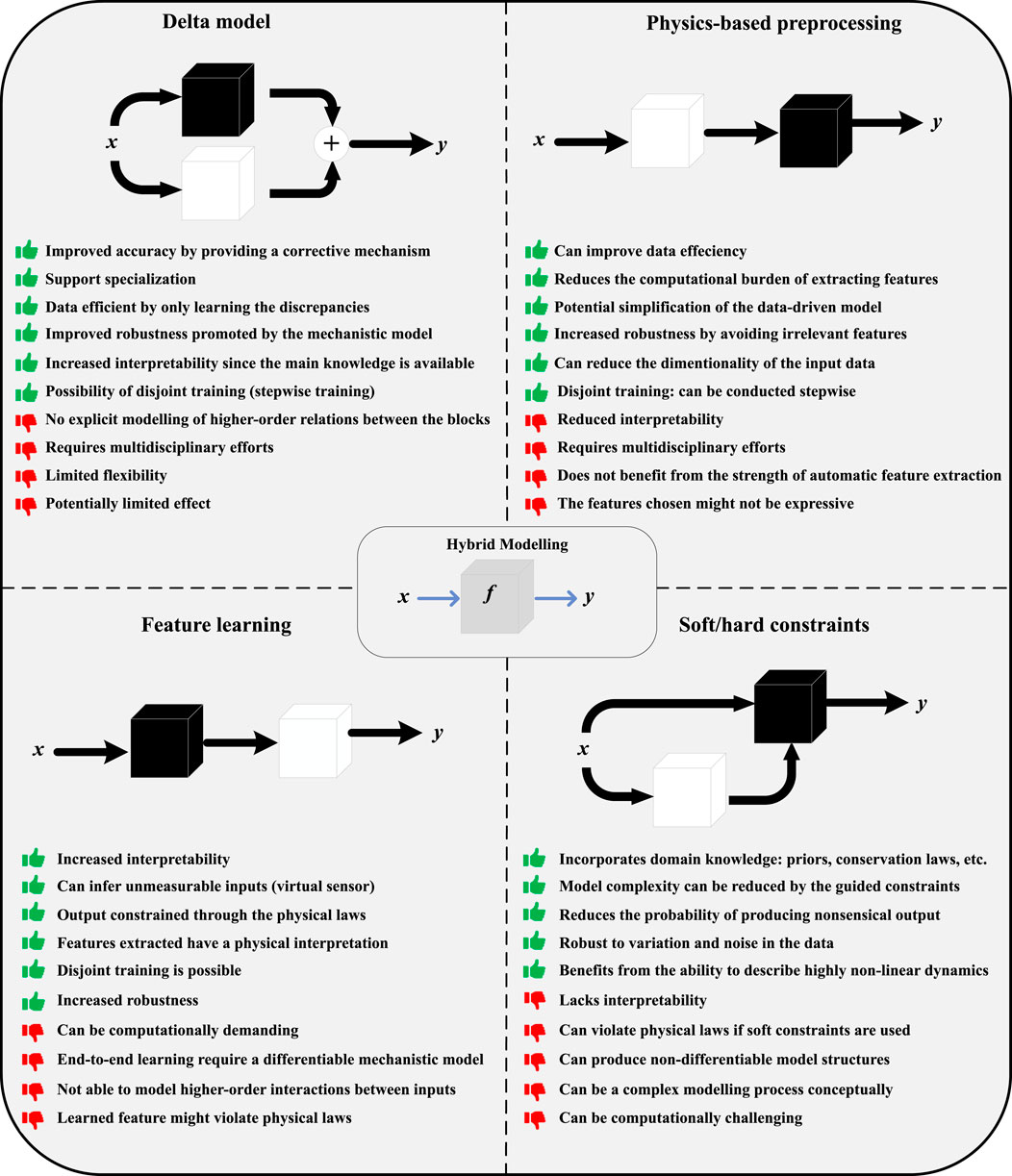
Rudolph et al. (2024) provide an extensive overview of hybrid models design patterns. These design patterns are generalized to unify and formalize the various modelling approaches across domains and applications. These design patterns are introduced in the following and exemplified by a few selected relevant studies from the literature. A more extensive list can be found in Section 3 (dissection and analysis of case studies). Rudolph et al. (2024) defined two types of hybrid modelling design patterns based on how the parametric and the non-parametric models interact into base patterns and composition patterns. The base patterns cover basic elemental units and take two computational models (one parametric and one non-parametric). These base patterns cover the delta model, physics-based preprocessing, feature learning, and physical constraints (soft and hard constraints). The delta model is identical to what Psichogios and Ungar (1992) and von Stosch et al. (2014) refer to as the parallel structure. This design pattern aims to use the same input for both models and combine their output into the final target through, e.g., summation. This is especially useful when the mechanistic model is not entirely understood nor capable of capturing the entire dynamics exhibited by the system. Therefore, the data-driven part compensates for this lack of details in the mechanistic model, yielding higher accuracy and robustness. An example could be that the mechanistic part describes an ideal system with a set of associated assumptions, while the data-driven model provides corrective action to overcome these assumptions. Bradley et al. (2022) also refer to this as “mechanism correction”. As such, an important distinction of this configuration is that the two models are, in principle, “independent” of each other, and the sole functionality of the data-driven model is to “improve” and “correct” the performance of the mechanistic model. An advantage of the delta model configuration is that it is less data dependent, as modelling residuals of the mechanistic model is easier than modelling the complete dynamics of the system and thus will require less data than a complete data-driven model. From a conceptual point of view, this configuration supports “specialization”. The delta model is capable of overcoming cases where it is infeasible for data to be obtained abundantly over the entire input space (expensive, safety, or time-consuming). For data beyond the training domain (aka the test set), the mechanistic model allows for safe extrapolation, while for data already considered in the training domain, the data-driven model is already “specialized” as it offers accurate and reliable predictions. One disadvantage of this approach is that it does not allow for higher-order interactions between the two blocks, as their output is only added together. Besides the parallel combination of the two modelling approaches, combining these sequentially (serial model structure) is also possible. For this, Rudolph et al. (2024) distinguishes between two types of serial combinations based on their purpose: “physics-based preprocessing” or “feature learning”, depending on the relative positions of the mechanistic and data-driven model.

If the data-driven approach processes the data-driven model, it is called “feature learning”. This pattern is used when the mechanistic model requires input that might be either difficult or infeasible to measure directly, and thus, the need for the data-driven model to infer these from auxiliary measurements or inputs. Within this pattern, we further distinguish between two “learning paradigms”: sequential and end-to-end learning. In sequential learning, the training of the two models is decoupled. This can be used when the desired feature or input to the mechanistic model is available but at much less frequency or size than the other measurements. Then, a data-driven model can be trained using a set of inputs to predict this correctly. The output of this can then be used in the mechanistic model. In end-to-end learning, the training of the models is combined, and the two models are jointly optimized using, e.g., backpropagation of the errors and gradient-based algorithms. This, however, requires both models to be differentiable, which is always the case for the data-driven model, but in some cases, the derivative of the mechanistic model can be non-tractable. In both cases, the main advantage is that the output of the hybrid model is still physically constrained by the mechanistic part, increasing its reliability. State estimators for control systems are a perfect example of this approach.

In the “physics-based preprocessing” design pattern, domain knowledge is used to perform a set of transformations to produce a set of inputs that can support and enhance the performance of the data-driven model. This reduces the resources allocated by the data-driven model for feature extraction, making it easier to relate the input to the output. This is especially true as the risk of learning irrelevant features is avoided. This also potentially reduces the need for complex architecture and long training time. This inductive bias reduces the input data dimensionality and can enhance accuracy and interpretability. However, it is important to note that in some cases and due to the “representation learning capabilities” of data-driven models, they might be capable of extracting better underlying features than humans. This renders the mechanistic part an obstacle rather than an advantage.

The final base pattern defined by Rudolph et al. (2024) is the physically constrained hybrid approach. These constraints can affect the parameters, structure, or output of the hybrid model. As such, two types of constraints are introduced: soft and hard constraints. The mechanistic part of this pattern is not necessarily a model but can also be domain knowledge. The difference is that hard constraints cannot be violated, while soft constraints exhibit some elasticity that occasionally allows them to be breached. The previously described feature learning pattern is comparable to a hard constraint design pattern but ultimately differs in the aim and purpose, while the physics-informed neural network is an example of a soft constraint design pattern. An example of a hard constraint could be the addition of a ReLU layer at the end of a neural network to ensure that the output is non-negative to model concentrations and pressure or using a softmax layer to ensure output is between zero and one for molar fractions (Aouichaoui et al., 2023). An important prerequisite for the hard constraint modelling approach is that the data used are in fact in line with said constraint. This corrective action is also known as data reconciliation. A major challenge with introducing hard constraints is that it might result in non-differentiable models making it harder to use gradient-based optimization (Rudolph et al., 2024).

In soft-constrained design, the mechanistic insight is incorporated into the loss function as a penalty to guide the data-driven model toward fulfilling the domain knowledge during training. The aim is that this constraint is somehow retained at inference time, and therefore, at inference, the model is purely data-driven, where knowledge is implicitly encoded. An example of such an approach includes physics-informed neural networks (PINNs). These models have been heavily used in problems that include differential and partial differential equations. These models introduce an additional term to the loss function of the neural network that reflects the dynamics that occur in the system. This term usually reflects the “initial and boundary conditions along the space-time domins as well as the residuals of the (partial) differential equation system” (Cuomo et al., 2022). It is important to note that this adds an additional challenge to the modelling process as the objective function now becomes multi-objective, which will then require calibration in order to balance the two target objectives. Another potential issue arises, such models might not be able to catch complex dynamics that present multi-scale behaviours (Cuomo et al., 2022).

Finally, these base design patterns can be combined in many ways to create composition patterns. Two patterns are defined: recurrent composition and hierarchical composition. The recurrent composition involves models that are updated using an internal state. This update can either be in the form of a data-driven model or a mechanistic model. The recurrent pattern is similar to recurrent neural networks and numerical integration for differential equations. The advantage of this composite pattern is that it enables pattern recognition across time and parameter sharing (the same parameters are used for all time steps). This parameter sharing will then result in a model with a reduced number of parameters and resulting in a model with a global understanding of the dynamics of the system. The hierarchical pattern composition consists of combining two or more distinct hybrid modelling patterns. This allows modelling for more complex problems. An example would be to apply a delta pattern to two distinct hybrid models, each trained with soft constraints in the form of domain knowledge in the loss function. Figure 3 revisits the advantages of white-, gray- (hybrid modelling), and black-box modelling, while Figure 4 presents an overview of the various base design patterns along with their advantages and disadvantages.

Figure 3

Figure 3. Advantages and disadvantages of mechanistic, data-driven, and hybrid modelling.

Figure 4

Figure 4. Overview of various hybrid modelling pattens.

3 Case studies and lessons learned: a pragmatic review

As previously mentioned, hybrid modelling has gained increased interest from the modelling and digitalization communities within the biochemical industry, combining the strengths of mechanistic and data-driven modelling paradigms to address the complexities inherent in various biological processes. This review examines 50 case studies published between 2020 and 2024, providing a comprehensive analysis of the principles, challenges, and lessons learned from the application of hybrid modelling across a range of biochemical processes. This comprehensive review is presented in Supplementary Table S1. Of the 50 case studies reviewed, a significant proportion (28) dealt with fermentation and bioprocesses, 12 on downstream processes, eight on upstream chemical processes, and two on the holistic chemical processes. A schematic overview of the analyzed case studies is presented in Supplementary Figure S1. In this figure, the case studies are categorized and examined based on the year of publication, citation count, the process investigated, and the hybrid model pattern used.

3.1 Fermentation and bioprocesses

3.1.1 Addressing nonlinearities and time-varying parameters

One of the primary challenges across biochemical processes, particularly those relating to fermentation, revolves around their complex and nonlinear dynamics, making them difficult to model and predict accurately. These complexities arise from incomplete mechanistic knowledge, as well as the variability that comes with biological processes. For instance, Lee et al. (2020) worked on modelling intracellular signaling pathways, where conventional models struggled to capture all necessary dynamics, resulting in significant discrepancies between predictions and actual measurements. By combining mechanistic models with artificial neural networks, the authors were able to improve the accuracy of predictions for TNF$\alpha$ and I$\kappa$B$\alpha$ dynamics. Similarly, Vega-Ramon et al. (2021) focused on optimizing astaxanthin production, where they combined kinetic models with probabilistic methods, represented by Gaussian processes, to better handle batch–to–batch variability and improve robustness under uncertain conditions. Bangi et al. (2022) also addressed the challenges posed by nonlinear and time-dependent parameters using similar hybrid modelling approaches. Specifically, the authors focused on modelling the production of beta-carotene using S. cerevisiae in batch fermentation. They employed a hybrid modelling approach using universal differential equations (UDEs), which combined traditional kinetic models with neural networks to capture the complex, unknown dynamics of the process. This approach significantly improved the prediction of critical parameters, such as biomass, acetic acid, and $\beta$-carotene concentrations, in the fermentation production of beta-carotene using S. cerevisiae. Similarly, Da Silva Pereira et al. (2021) aimed to optimize ethanol production from cashew apple juice. This was achieved by using a hybrid neural model (HNM) combined with particle swarm optimization (PSO) which resulted in high accuracy in predicting the dynamic behavior of the fermentation process, with a low residual standard deviation for the model predictions. Cui et al. (2024) addressed the challenge of modelling CHO cell bioreactor dynamics, where incomplete knowledge of metabolic processes complicates simulation and control. They employed a gray-box hybrid modelling approach, combining mechanistic models with physics-informed neural networks (PINNs). This approach allowed the model to learn and predict partially unknown kinetic expressions, resulting in a robust model capable of adapting to changes in operating conditions without extensive re-parameterization.

3.1.2 Model integration and reduction

Integrating mechanistic models with data-driven approaches is challenging, particularly when incorporating complex dynamics and nonlinear behaviors. Pinto et al. (2023) exemplified this by developing a general hybrid modelling framework for systems biology applications. The study focused on integrating deep neural networks (DNNs) with mechanistic models encoded in the Systems Biology Markup Language (SBML). They addressed the complexity of training such hybrid models by using the SBML2HYB tool, which facilitates the conversion of existing models into hybrid formats. The use of the ADAM optimizer and stochastic regularization were used in managing the training complexity and ensuring the models could capture complex dynamics, such as yeast glycolytic oscillations, that the original mechanistic models were not able to achieve. Similarly, Rogers et al. (2023a) explored the application of physics-informed neural networks (PINNs) in hybrid modelling for bioprocesses. Their study focused on constructing models for $\gamma$-linolenic acid (GLA) production, where one of the main challenges was the complex model structure identification. The PINN framework allowed for the simultaneous determination of model structure and parameter trajectories, improving the accuracy and efficiency of hybrid model construction. However, challenges remain in achieving global optima and accurately identifying parameters in highly nonlinear systems. Bae et al. (2020) emphasized the importance of defining and maintaining a valid domain of applicability for hybrid models to ensure accurate predictions, particularly in dynamic optimization scenarios. By carefully constructing and updating the valid domain, the study was able to maintain prediction reliability while optimizing fed-batch bioreactor operations, leading to improvements in production yields. This is known as domain shift, where the current data domain differs from the one the model was originally trained on. Zhang et al. (2020) focused on balancing the complexity of kinetic models with data-driven components to avoid overfitting while maintaining accuracy. In their study on photo-production in microalgae, they combined a simplified kinetic model with a polynomial regression-based data-driven model. This approach not only improved predictive accuracy but also simplified the model structure, making it easier to manage and less prone to overfitting. The use of sparse identification of nonlinear dynamics (SINDy) further optimized the model, demonstrating the effectiveness of hybrid models in scenarios with limited data availability. Maton et al. (2022) developed a minimal bioreaction model by integrating elementary flux modes (EFMs) with multilayer perceptrons (MLPs). The study addressed the challenge of reducing the initial large set of EFMs to a biologically meaningful subset while the MLPs captured complex kinetic behaviors. This approach successfully reduced the model’s complexity without compromising predictive accuracy, making it a valuable tool for process monitoring and control. In another study, Xu et al. (2022) combined a mechanistic model (ASM3) with a recurrent neural network (RNN) to predict the enrichment of polyhydroxyalkanoates (PHA) accumulating bacteria. The integration allowed for accurate long-term predictions, demonstrating the effectiveness of hybrid models in optimizing microbial enrichment processes under dynamic conditions. Rogers et al. (2023b) focused on the challenge of balancing the amount of kinetic information incorporated into hybrid models. In this study, the authors developed three hybrid models with varying degrees of kinetic information combined with Gaussian Processes (GPs) to simulate unknown kinetics during the fermentation process of the fungus C. echinulata. The study found that a moderate amount of kinetic information provided the best balance between accuracy and uncertainty, demonstrating that there is an optimal degree of “grayness” in hybrid modelling. Cheng et al. (2021) introduced a novel approach for bioelectrochemical systems by integrating mechanistic models with Bayesian networks to enhance prediction robustness and interpretability. This hybrid model effectively linked microbial population dynamics with microbial kinetics, addressing the challenge of parameter identifiability and improving prediction accuracy.

3.1.3 Model transferability and scalability

A critical challenge in fermentation processes is ensuring the transferability of hybrid modelling across different scales. Bayer et al. (2021) and Hutter et al. (2021) addressed this by developing models that could effectively predict process behavior across scales, reducing the experimental burden. Bayer et al. (2021), for instance, addressed this issue in their study on CHO cell culture processes. They developed a hybrid model that predicted viable cell concentration (VCC) and product titer across different scales, from shake flasks to 15 L bioreactors. This was achieved by combining mechanistic models with artificial neural networks, along with an intensified design of experiments (iDoE) approach. The model demonstrated good transferability with minimal recalibration. Hutter et al. (2021) further explored this by using a hybrid Gaussian process model, which successfully transferred knowledge across different cell lines, reducing the need for extensive experimental work.

The majority of these studies were conducted at the theoretical or laboratory scale, with only a few advancing to pilot or industrial-scale applications. Bayer et al. (2021) and Okamura et al. (2022) successfully scaled up their models from lab to pilot scale, showing the potential of these approaches in larger operations. In particular, Okamura et al. (2022) addressed scale transferability in their study on CHO cells, where they developed a three-module hybrid model to predict cell growth, metabolism, and impurity generation under varying cultivation conditions. The inclusion of a data-driven module allowed the model to dynamically update parameters and improve prediction accuracy, particularly for metabolites like lactate, which exhibit fluctuations that are difficult to capture with the kinetic model alone. Building on top of that, Shah et al. (2022) applied their models to a full industrial-scale fermentation process with a volume of over 100,000 gallons. In particular, the authors provided a comprehensive case study on the large-scale production of various biochemical products by developing a hybrid model that combined modified kinetic models with deep neural networks (DNNs). The hybrid model showed improved performance across various conditions, except for predicting an intermediate component where it was comparable to the kinetic model alone. This indicates that while the hybrid approach offers substantial improvements, there is still room for further refinement, particularly in complex multi-step processes. The study is a prime example of how hybrid modelling can be applied to large-scale industrial processes, addressing the challenges of scalability and real-world application. Future work suggested by the authors includes addressing potential issues like overfitting and exploring the effectiveness of simpler ANN models compared to more complex DNNs.

3.1.4 Overcoming limited and noisy data

A significant challenge in hybrid modelling for biochemical processes is managing data quality and availability. This issue is particularly important in processes where data are noisy, sparse, or limited. Several studies have addressed these challenges using various strategies. For instance, Faure et al. (2023) addressed the issue of sparse data in genome-scale metabolic models (GEMs) by integrating neural networks with flux balance analysis (FBA). They developed an artificial metabolic network (AMN) that preprocesses input data and refines predictions through mechanistic solvers, reducing the need for extensive datasets and improving prediction accuracy in metabolic flux distributions. Similarly, Lopez et al. (2021) addressed the problem of noisy data in lignocellulosic ethanol fermentation processes. They combined a kinetic model with a data-driven model using a continuous-discrete extended Kalman filter (CD-EKF) to reconcile noisy spectroscopic data with mechanistic predictions. This hybrid model significantly improved the robustness of real-time estimates, outperforming standalone models in handling process disturbances and measurement noise. Kay et al. (2023) approached the challenge of limited and sparse data by using transfer learning within a hybrid modelling framework. Their study on lutein production in microalgal strains demonstrated how knowledge from well-understood systems could be transferred to new, less-studied domains, overcoming the limitations of data scarcity. The concept of transfer learning is well established in the field of AI/ML where an initial model is trained on a related application with abundant data potentially with lower quality. By then using this as the starting point for the application of interest, the prior knowledge is refined and adjusted to the new data/application. This method not only improved model accuracy but also provided robust predictions with uncertainty estimates, even in data-poor scenarios. Lagergren et al. (2020) focused on modelling biological systems with sparse and noisy data by introducing biologically-informed neural networks (BINNs). This method allowed the learning of nonlinear terms directly from data within a mechanistic framework, significantly enhancing the model’s ability to capture complex dynamics in cell migration studies. Narayanan et al. (2022), on the other hand, emphasized balancing model accuracy with interpretability while dealing with noisy and limited data. Their functional-hybrid model used symbolic regression to integrate domain-specific knowledge into the model structure, improving both accuracy and interpretability and performing well even with limited experimental data. Cruz-Bournazou et al. (2022) addressed these challenges in their work on fed-batch bioprocesses for monoclonal antibody production. By integrating Gaussian process state space models (GPSSMs) with polynomial regression, they addressed the issues of noise sensitivity and multi-rate data handling. Their approach provided smooth and accurate predictions of system dynamics, demonstrating the utility of hybrid models in optimizing fed-batch processes despite the inherent challenges of data quality. Morabito et al. (2021) addressed batch-to-batch variability and uncertainty in early-stage bioprocesses by incorporating Bayesian inference and Gaussian processes within a hybrid model. This approach allowed the quantification of model uncertainty and the integration of risk measures into process optimization, ensuring robust performance even with limited data.

3.1.5 Reducing computational cost

A critical aspect of hybrid modelling in biochemical processes is computational cost, particularly in the context of training complex models. Kotidis and Kontoravdi (2020) addressed the computational burden in predicting protein glycosylation by developing a hybrid model that integrates kinetic models with artificial neural networks (ANNs). Their approach reduced the need for extensive parameterization and training time while also improving prediction accuracy. However, Pinto et al. (2022) demonstrated that by using a deep hybrid model framework, the CPU time was reduced by 43.4% with respect to using shallow hybrid models. Several studies highlighted the importance of balancing model complexity with the need for accurate predictions while minimizing computational costs. Mowbray et al. (2023) introduced a hybrid framework combining kinetic modelling with reinforcement learning (RL) to tackle the challenges of over-parameterization and overfitting in models dealing with time-varying and history-dependent kinetics. Their RL-based approach effectively identified correct model structures and provided accurate parameter estimates, even in the presence of noise and sparse data. This framework proved robust in navigating the trade-off between model complexity and prediction accuracy, avoiding over-parameterization. In contrast, Ramos et al. (2024) investigated the application of long short-term memory (LSTM) networks within hybrid models for HEK293 cell culture dynamics. While LSTM models offered superior predictive power and robustness compared to classical feedforward neural networks (FFNNs), the study highlighted the significant computational costs associated with training these models. The complexity of the LSTM models, though advantageous in handling time-series data, resulted in higher computational demands, which could be a limiting factor in their broader application. Conclusively, the computational cost reduction is highly dependent on the hybrid configuration used and the underlying mechanistic and data-driven compartments chosen.

3.2 Chemical processes

3.2.1 Challenges addressed by hybrid modelling in the chemical industry

The case studies by Chakraborty et al. (2021), Polak et al. (2023), Huster et al. (2020), and Bui et al. (2022) address similar issues in hybrid modelling of chemical processes as the ones encountered in fermentation processes, such as managing noise, handling sparse data, accounting for process variability, and incorporating complex dynamics into models. In particular, Chakraborty et al. (2021) addressed the issue of noise and sparse data in nonlinear parametric systems by developing the AI-DARWIN approach, which combines genetic algorithms with nonlinear regression for parameter estimation. This hybrid approach was effective in identifying accurate and interpretable models, even with limited and noisy data, showing the potential of genetic algorithms to improve the reliability of hybrid models. Polak et al. (2023) focused on the impact of raw material variations and process parameter changes in continuous manufacturing processes. Their hybrid model, which combined mechanistic models with artificial neural networks (ANNs), was able to capture the influence of these variations on product quality. However, the study also highlighted challenges in extrapolating model performance to unseen process conditions and the need for robust training datasets that integrate a wide range of operational scenarios. Huster et al. (2020) addressed the challenge of incorporating accurate thermodynamic models into the optimization of a transcritical organic Rankine cycle (ORC) for geothermal power generation. By integrating data-driven surrogate models with mechanistic models, they were able to optimize the ORC system more effectively than traditional methods. This study emphasized the importance of accurate thermodynamic modelling in achieving optimal performance in energy systems. Bui et al. (2022) dealt with process variability and unplanned events in an industrial-scale catalytic process. Their hybrid model, which combined a fundamental reactor model with an empirical partial least-squares (PLS) model, predicted catalyst lifetime and allowed for real-time monitoring and adaptive recalibration (Ryu et al., 2023). utilized PINNs as a surrogate model to replace the computational fluid dynamics (CFD) calculation. This was done through including a physics loss that describes the loss w.r.t. the governing equations (continuity, momentum and species transport). The model has demonstrated the impact of operating conditions and various design variables on the performance of a polymerization reaction. The results obtained suggest that while intrapolation loss might be comparable to that of purely data-driven model, the loss when extrapolating is almost a third of that of a data-driven approach. These findings are in accordance with the theoretical motivation of building such models.

3.2.2 Model predictive control (MPC)

The studies by Wu et al. (2020), Alhajeri et al. (2022), and Bangi and Kwon (2023) all emphasize the application of hybrid models in improving model predictive control (MPC) frameworks in continuous stirred tank reactors (CSTRs). These studies address the challenges of predicting the dynamic behavior in chemical processes while minimizing computational costs. Wu et al. (2020) introduced partially connected and weight-constrained RNNs, integrating first-principles models to improve both accuracy and computational efficiency. Similarly, Alhajeri et al. (2022) explored fully-connected versus partially-connected RNNs, with the latter showing improved performance in terms of reduced computational time and process stability. Bangi and Kwon (2023) took this a step further by incorporating NNs into first-principles models, creating a deep hybrid model (DHM) within a control Lyapunov-Barrier function-based MPC framework. This approach ensured system stability and accurate predictions, even under complex dynamic conditions. Despite being applied at a theoretical scale, these studies demonstrate that integrating process knowledge into neural network architectures improves the performance of MPC, making it a promising approach for real-time control in chemical processes.

3.2.3 Comparison of hybrid modelling approaches

The studies by Jul-Rasmussen et al. (2023) and Peterson et al. (2024) focused on comparing different hybrid modelling approaches. Jul-Rasmussen et al. (2023) compared stochastic gray-box modelling and serial semi-parametric hybrid modelling for a CSTR. The stochastic gray-box model, which incorporated system knowledge through stochastic differential equations, was more robust to noisy data and varying measurement frequencies than the semi-parametric approach. The effectiveness of hybrid models in real-world applications often depends on their ability to outperform purely data-driven models, as demonstrated by Peterson et al. (2024) in their study on CO₂ methanation in a CSTR. The study compared purely data-driven models with hybrid models incorporating mechanistic elements. The findings revealed that while the hybrid models generally outperformed data-driven models in terms of accuracy and reliability, the complexity of the hybrid models required careful calibration and could lead to increased computational costs. Bikmukhametov and Jäschke (2020) explored various methods of combining machine learning with first-principles models for estimating multiphase flow rates in a petroleum production system. Their findings showed that hybrid models, which incorporated physically meaningful features from first-principles models, improved the accuracy and interpretability of predictions compared to purely data-driven models. These findings demonstrate the importance of carefully selecting hybrid modelling approaches based on the specific requirements of accuracy, robustness, and data availability.

3.3 Downstream processes

3.3.1 Challenges addressed by hybrid modelling in downstream processing

The case studies by Di Caprio et al. (2023), Narayanan et al. (2021), Krippl et al. (2020), Jul-Rasmussen et al. (2024), and Schäfer et al. (2020) address various challenges in hybrid modelling of downstream processes, including data quality, model integration, and scalability. Di Caprio et al. (2023) addressed the issue of poor data quality in the constant volume solvent switch (CSS) process, a critical downstream operation in active pharmaceutical ingredients (API) production. By combining first-principles models with multivariate rational functions and polynomial functions, they developed a hybrid model that outperformed traditional models in both accuracy and robustness. The study showed the importance of model configuration and optimization techniques in achieving reliable predictions, even with low-quality data. Narayanan et al. (2021) addressed the challenge of modelling chromatographic processes, which require accurate knowledge of adsorption isotherms and mass transfer kinetics. Their model integrated the mechanistic framework of the lumped kinetic model (LKM) with a neural network that learns the adsorption dynamics of the protein. This approach bypassed the need for detailed mechanistic assumptions. This approach proved flexible and accurate, particularly in scenarios involving unknown adsorption isotherms or conditions outside the training data. Krippl et al. (2020) explored the application of hybrid modelling in cross-flow ultrafiltration (UF) processes, focusing on predicting flux evolution and process duration. Their hybrid model, which integrated mechanistic models with artificial neural networks, showed high accuracy and adaptability across different UF modes and feed characteristics. The study highlighted the potential of hybrid models to reduce experimental workload and improve process control. Jul-Rasmussen et al. (2024) focused on improving the prediction accuracy and robustness of models for aeration in bubble columns. Their study compared different hybrid AI modelling techniques, finding that AI-Darwin symbolic regression-inspired techniques provided a valuable alternative to traditional neural networks, particularly in scenarios requiring model interpretability and better generalization. Schäfer et al. (2020) addressed the complexity of dynamic modelling for distillation columns, a challenging task due to their nonlinear thermodynamic behaviour. By integrating artificial neural networks with existing model reduction approaches, they developed a hybrid model that achieved a good balance between computational efficiency and accuracy. This study proves the potential of hybrid models in real-time control applications, particularly in complex dynamic systems.

3.3.2 Application of hybrid modelling in particle processes

Several studies have focused on the application of hybrid models to particle processes, such as crystallization, flocculation, and sieve tray extraction. The works of Nielsen et al. (2020), Nazemzadeh et al. (2021), Sitapure and Kwon (2023), Lima et al. (2023), and Palmtag et al. (2024) exemplifies the diverse approaches and innovations in this area. Nielsen et al. (2020) explored the control and modelling of crystallization processes, which are notoriously difficult due to their complex dynamics and limited solubility information. The hybrid model developed integrated deep neural networks (DNNs) with mechanistic population balance models. This allows for better prediction of particle properties and process dynamics, being particularly successful in pharmaceutical crystallization. Similarly, Nazemzadeh et al. (2021) focused on flocculation processes, where the aggregation and breakage phenomena present significant modelling challenges. The study compared three models with different degrees of “grayness” of first principle and kinetic information showing that a simple first principles model had limited accuracy, while the hybrid model integrating PBM and DNN improved accuracy. However, some challenges were also reported in the form of increased sensitivity to the initialization of the neural network. The hybrid model incorporating additional kinetic information showed the best performance. The integration of kinetic expressions into the deep learning framework also reduced the model’s sensitivity to initialization, a common issue in purely data-driven approaches. In another study, Sitapure and Kwon (2023) developed hybrid models using time-series-transformers (TST) for batch crystallization processes. They compared series and parallel configurations, finding that the series model provided more accurate predictions, especially over long-term process dynamics. Lima et al. (2023) introduced a novel approach by integrating population balance models with universal differential equations (UDEs). Their UDE-based hybrid model reduced the need for extensive experimental data while maintaining high prediction accuracy. This approach is particularly valuable in crystallization processes where data availability is often a limiting factor. Finally, Palmtag et al. (2024) addressed the challenges in modelling pulsed sieve tray extraction columns, focusing on drop breakage and coalescence phenomena. By integrating data-driven parameter estimator models with physical models, they developed a hybrid model that reduced the need for re-parameterization. This model demonstrated high accuracy and robustness, making it a promising tool for industrial applications.

3.3.3 Hybrid modelling in water treatment applications

Water treatment processes present a unique set of challenges due to their inherent complexity and fuzziness. This is largely due to the mixture of microbial entities present in the sludge. The studies by Quaghebeur et al. (2022) and Cheng et al. (2023) illustrate the application of hybrid models in this domain, particularly in wastewater treatment and water resource recovery. Quaghebeur et al. (2022) developed a hybrid model by integrating neural differential models into existing mechanistic models. The hybrid model outperformed purely mechanistic or data-driven models, demonstrated robustness and accuracy in both dry and rainy weather scenarios. Cheng et al. (2023) focused on a fuzzy wastewater treatment process, using a hybrid model that integrated an activated sludge model (ASM) with a convolutional neural network (CNN) and long short-term memory (LSTM) network. This hybrid approach showed better predictive performance compared to traditional models and robustness in handling the fuzziness inherent in wastewater treatment processes. Asrav and Aydin (2023) proposed two approaches to integrate physics into recurrent neural networks and applied it on synthetic data generated from benchmark simulation models (BSM1). The first approach consisted of augmenting the loss function with a discretized form of the dynamic mass balance of the soluble nitrogen-containing species. The second includes repurposing the recurrent cell to include the Euler discretization of the dynamic balance of nitrogen-containing species. Their results showed that the physics-informed approaches provided were better at extrapolating to unseen data (the test set). The same approach was later applied to an industrial case study of wastewater treatment, obtaining test errors that were 82% lower than that of a purely data-driven approach.

3.4 Discussion and outlook

The case studies analyzed showed hybrid modelling to be particularly successful in capturing complex dynamics that are difficult to model using purely mechanistic or data-driven approaches, such as, for example, in MPC applications. In processes involving time-varying or non-linear kinetics, several studies have demonstrated the successful application of hybrid models across different scales, from laboratory to industrial scale. This scalability is important in the biochemical industry, where processes often need to be transferred from small-scale experiments to large-scale production, reducing in this way the need for extensive experimental data. Furthermore, a great promise has been seen in situations with limited or sparse data. Techniques such as transfer learning, where knowledge from well-studied processes is applied to less-understood ones, have been effective in overcoming data scarcity. This approach allows for accurate predictions even when experimental data is scarce, as at the beginning of a process. In water treatment processes, the integration of mechanistic and data-driven models was successful in handling the fuzziness and complexity inherent in these systems. However, the model performance is largely dependent on the quality of the training data, highlighting the need for rigorous data preprocessing and quality control. An important challenge in these processes is the presence of gradients and that target variables are measured locally and might not capture gradients. A critical lesson is the trade-off between model accuracy and interpretability. Particularly in complex systems like distillation columns or protein purification processes, achieving high accuracy often comes at the cost of model interpretability. For example, while ANNs incorporated into hybrid models provide high accuracy in predicting system behaviors, they often lack transparency, which can be problematic for understanding and validating the model’s predictions in industrial applications. This might also hinder their wider applicability and adoption in the process industry. The development of symbolic regression techniques, such as AI-DARWIN, presents a promising approach to balancing these competing needs. Despite their advantages, hybrid models also present challenges, particularly in terms of computational cost and the risk of overfitting. The integration of deep learning components, for example, can lead to high computational demands. Moreover, ensuring that these models generalize well to new data while avoiding overfitting remains a significant challenge. Strategies such as regularization, cross-validation, and careful selection of model architecture have been used to address these issues, but they require careful consideration during model development.

Looking forward, several areas of research and development could further improve the effectiveness of hybrid modelling in the biochemical industry. For example, focus should be put on optimizing the architecture of hybrid models to balance accuracy and computational efficiency. This includes exploring new machine learning algorithms, improving neural network training techniques, and refining hybrid frameworks to reduce the computational cost while maintaining high predictive accuracy. The integration of hybrid models with real-time monitoring systems presents a significant opportunity for improving process control and optimization. By combining real-time data with predictive models, it may be possible to develop adaptive control strategies that can respond dynamically to process changes, leading to more efficient and robust processes. Another important direction is the development of hybrid modelling frameworks that are more interpretable and user-friendly. As industries increasingly adopt digital twins and predictive control systems, there will be a growing demand for models that not only provide accurate predictions but also offer insights into the underlying process dynamics. This could involve further exploration of techniques like symbolic regression or the integration of explainable AI methods within hybrid models. Moreover, there is a need to explore the application of hybrid models to a broader range of processes and scales. While current research has demonstrated the effectiveness of hybrid models in specific applications like fermentation and catalytic processes, expanding these approaches to other areas, such as continuous manufacturing or additional biochemical systems, could unlock new opportunities for process optimization and control. This expansion will require not only the refinement of existing models but also the development of new hybrid frameworks that can handle the unique challenges of these processes. In conclusion, while hybrid modelling has demonstrated significant potential in improving process understanding, control, and predictability in the biochemical industry, its successful implementation requires careful consideration of data quality, model interpretability, and scalability. Addressing these challenges through ongoing research and innovation will be key to realizing the full benefits of hybrid models in industrial applications. An important aspect going forward is to introduce these concepts to future practitioners through an updated curriculum for various STEM educations.

4 Perspectives on digital transition, hybrid modelling, and sustainability

Industries are under increasing pressure to adapt, innovate, and strike a balance between environmental accountability and economic prosperity (highlighted by the Green Deal (European Commission, 2019)). The digital transformation is a paramount element in achieving the goals set by the Green Deal (Garske et al., 2024; Bauer et al., 2021; European Commission, 2020), and of note is that the sustainability and sustainable and digital transition are intertwined in a myriad of ways (Garske et al., 2024; Ekardt, 2022).

The digital transition paradigm aims at streamlining and improving accessibility by converting analog information into digital platforms. The changing landscape, marked by evolving regulations, customer demands, and environmental considerations, is currently challenging conventional processes and standards. The drive towards implementing Industry 4.0, and even 5.0, offers an excellent opportunity (and challenges) to address these concerns and ensure positive steps towards increased sustainability in all regards; thus, it plans for social welfare, economic growth, and positive environmental impact (three pillars of sustainability). This section, as illustrated in Figure 5, explores the interplay/relationships between digitalization, hybrid modelling, and sustainability and the opportunities they hold for the future of manufacturing.

Figure 5

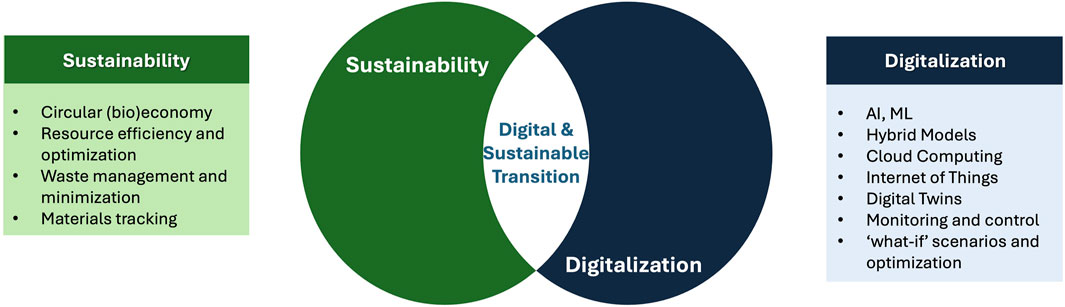
Figure 5. Digital and Sustainable Transition: the intersection of digitalization and sustainability.

Several concepts have arisen as key drivers of efficiency and sustainability in this fast-evolving technological paradigm. A crucial example is, as previously mentioned, the concept of digital twins (DTs), virtual copies of entire running physical production plants, processes and/or supply chains. DTs allow for real-time monitoring and control, predictive analytics and scenario simulation, optimization, and predictive maintenance, among others. DTs enable organizations to pinpoint inefficiencies, decrease waste production, and optimize processes and systems (Gargalo et al., 2021; Udugama et al., 2021).

DTs are built on a complex setup of coupled-up high-level technologies (hybrid modelling, IoT, Cloud computing, smart sensors, etc.). Smart technologies such as smart sensors are integral and critical parts of DTs. They are integrated to enable predictive maintenance and enhance performance. By combining data-driven techniques with conventional first principles-based models, hybrid modelling improves the predictive ability of digital twins by providing a more holistic way to predict and understand complex system behaviors. Thus, it leads to more accurate simulations and better management of resources and optimization due to having a more detailed and comprehensive understanding of the system and system dynamics (Boschert and Rosen, 2016; Tzachor et al., 2022; Sansana et al., 2021). DTs can monitor the real-time dynamic behavior of the physical running plant and experiment/simulate different conditions (‘what if’ scenarios) and resource allocation, thus optimizing resource consumption and allocation from supply to final production steps (Tzachor et al., 2022; Garske et al., 2024; Bauer et al., 2021). Of note is that hybrid modelling is especially useful in handling the multifaceted nature of sustainability, where there are multiple interacting elements and preexisting correlations (Bennett et al., 2005). For example, depicting the relationship between technical and economic factors and variables allows one to strategize to improve environmental impact while maintaining economic growth and prosperity and thus obtaining sustainable business models. Furthermore, in order to achieve the mentioned goals, DTs should enable decision-makers, policymakers, and scientists to evaluate environmental impact and human influence to make decisions that will indeed support sustainable development, as well as production and consumption, all safely within planetary boundaries (Garske et al., 2024; Li et al., 2023; Rockström et al., 2023).

By relying on digital transformation, hybrid modelling, and other enabling technologies, a symbiotic relationship is achieved between these concepts and DTs. Together, they drive optimization, resource efficiency, and sustainability - by leveraging these concepts and technologies, industries can positively contribute to sustainable development, where societal wellbeing aligns with environmental demands and economic growth (as pointed out by the 17 Sustainable Development Goals (Nations, 2024)).

5 Conclusion and the road ahead

Hybrid modelling integrates human expertise, in the form of domain-specific process knowledge, with data-driven information and machine learning techniques. In this work, to pinpoint essential concepts and critical insights regarding successful implementation, we have performed a pragmatic literature review of works exploring the use of hybrid modelling. It is noteworthy that hybrid modelling is paramount in the digital transformation of (bio)chemical industries (where intrinsically complex processes prevail) into Industry 4.0 and beyond. Some key takeaways are as follows.

$•$ Holistic understanding and insights. The synergy obtained by applying hybrid modelling and thus integrating different sources of information can help with resource-intensive challenges (e.g., biopharma, enzyme production) and provide a more comprehensive understanding and overview of complex processes.

$•$ Real-time decision-making and predictive power. Digital twins, enabled by hybrid modelling and other technologies, simulate the behavior of the physical plant, allowing for monitoring, predictive analytics, process optimization, fault detection, real-time decision-making, and predictive maintenance, avoiding costly downtime. Hybrid models perform well in dynamic conditions, adjusting predictions based on incoming data/information. Hence, as pointed out by the works reviewed in Section 3, it is essential to have this tool in the (bio)chemical engineer toolkit due to the innate dynamic nature of these processes.

$•$ Sustainability and resource optimization. As discussed in Section 4, hybrid models, coupled with digital twins, can potentially lead industries to significantly reduce resource consumption and minimize waste production and emissions by increasing overall and process-specific efficiency. This is highly significant when aiming at reaching environmental targets and leads to improved cost-effectiveness circularity.

$•$ Skilled workforce. Successful digitalization and use of hybrid models (and other technologies) require skilled professionals who are fluent in both the technical aspects of implementation and also have domain-specific knowledge. As pointed out in Section 1, more institutions (universities and companies) are increasingly embracing this and focusing on educating students/workforce on key topics and these technologies.

Furthermore, regarding the technical aspects of the successful development and implementation of hybrid models, the literature review has demonstrated that the main lessons are the effectiveness of hybrid models in providing robust predictions even with noise or sparse data, reducing the need for extensive datasets, the need to balance model accuracy with computational efficiency to ensure practicality in industrial applications, and the challenge of maintaining model interpretability, particularly in complex systems, to facilitate wider adoption and effective process control.

In summary, the transition towards digitalized operations can help the industry become resilient and attain remarkable levels of efficiency and sustainability. Thus, it is highly desirable and is on the agenda of most (bio) chemical industries. Since hybrid modelling plays a key role in this, it must be embraced and taken on as part of our toolset. Therefore, continuous efforts should be allocated to exploring different opportunities and implementation techniques and deep diving into developing and (when possible) sharing models for the digitalization of downstream and upstream processing steps at different scales.

Author contributions

CG: Writing–review and editing, Writing–original draft, Visualization, Validation, Supervision, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal Analysis, Data curation, Conceptualization. AM: Writing–review and editing, Writing–original draft, Visualization, Investigation, Formal Analysis, Data curation, Conceptualization. AA: Writing–review and editing, Writing–original draft, Methodology, Investigation, Formal Analysis, Data curation, Conceptualization. JH: Writing–review and editing, Validation, Supervision. KG: Writing–review and editing, Validation, Supervision, Resources, Funding acquisition.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the (i) Novo Nordisk Foundation-funded Sustain4.0: Real-time sustainability analysis for Industry 4.0 (NNF0080136); and (ii) Novo Nordisk Foundation-funded “Accelerated Innovation in Manufacturing Biologics” (AIMBio) project (NNF19SA0035474).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2024.1494244/full#supplementary-material

References

Aheleroff, S., Huang, H., Xu, X., and Zhong, R. Y. (2022). Toward sustainability and resilience with industry 4.0 and industry 5.0. Front. Manuf. Technol. 2. doi:10.3389/fmtec.2022.951643

CrossRef Full Text | Google Scholar

Albino, M., Gargalo, C. L., Nadal-Rey, G., Albaek, M. O., Krühne, U., and Gernaey, K. V. (2024). Hybrid modeling for on-line fermentation optimization and scale-up: a review. Processes 12, 1635. doi:10.3390/pr12081635

CrossRef Full Text | Google Scholar

Alhajeri, M. S., Luo, J., Wu, Z., Albalawi, F., and Christofides, P. D. (2022). Process structure-based recurrent neural network modeling for predictive control: a comparative study. Chem. Eng. Res. Des. 179, 77–89. doi:10.1016/j.cherd.2021.12.046

CrossRef Full Text | Google Scholar

Andersen, N., Cognet, T., Santacoloma, P., Larsen, J., Armagan, I., Larsen, F., et al. (2017). Dynamic modelling of pectin extraction describing yield and functional characteristics. J. Food Eng. 192, 61–71. doi:10.1016/j.jfoodeng.2016.08.006

CrossRef Full Text | Google Scholar

Aouichaoui, A. R., Fan, F., Abildskov, J., and Sin, G. (2023). Application of interpretable group-embedded graph neural networks for pure compound properties. Comput. and Chem. Eng. 176, 108291. doi:10.1016/j.compchemeng.2023.108291

CrossRef Full Text | Google Scholar

Arden, N. S., Fisher, A. C., Tyner, K., Yu, L. X., Lee, S. L., and Kopcha, M. (2021). Industry 4.0 for pharmaceutical manufacturing: preparing for the smart factories of the future. Int. J. Pharm. 602, 120554. doi:10.1016/j.ijpharm.2021.120554

PubMed Abstract | CrossRef Full Text | Google Scholar

Asrav, T., and Aydin, E. (2023). Physics-informed recurrent neural networks and hyper-parameter optimization for dynamic process systems. Comput. and Chem. Eng. 173, 108195. doi:10.1016/j.compchemeng.2023.108195

CrossRef Full Text | Google Scholar

Bae, J. J., Lee, H. J., Jeong, D. H., and Lee, J. M. (2020). Construction of a valid domain for a hybrid model and its application to dynamic optimization with controlled exploration. Industrial Eng. Chem. Res. 59, 16380–16395. doi:10.1021/acs.iecr.0c02720

CrossRef Full Text | Google Scholar

Bangi, M. S. F., Kao, K., and Kwon, J. S.-I. (2022). Physics-informed neural networks for hybrid modeling of lab-scale batch fermentation for β-carotene production using Saccharomyces cerevisiae. Chem. Eng. Res. Des. 179, 415–423. doi:10.1016/j.cherd.2022.01.041

CrossRef Full Text | Google Scholar

Bangi, M. S. F., and Kwon, J. S.-I. (2023). Deep hybrid model-based predictive control with guarantees on domain of applicability. AIChE J. 69. doi:10.1002/aic.18012

CrossRef Full Text | Google Scholar

Bauer, P., Stevens, B., and Hazeleger, W. (2021). A digital twin of earth for the green transition. Nat. Clim. Change 11, 80–83. doi:10.1038/s41558-021-00986-y

CrossRef Full Text | Google Scholar

Bayer, B., Duerkop, M., Striedner, G., and Sissolak, B. (2021). Model transferability and reduced experimental burden in cell culture process development facilitated by hybrid modeling and intensified design of experiments. Front. Bioeng. Biotechnol. 9, 740215. doi:10.3389/fbioe.2021.740215

PubMed Abstract | CrossRef Full Text | Google Scholar

Bazel, M. A., Mohammed, F., Baarimah, A. O., Alawi, G., Al-Mekhlafi, A. B. A., and Almuhaya, B. (2024). The era of industry 5.0: an overview of technologies, applications, and challenges. Lect. Notes Data Eng. Commun. Technol. 211, 274–284. doi:10.1007/978-3-031-59707-7_24

CrossRef Full Text | Google Scholar

Bennett, E. M., Cumming, G. S., and Peterson, G. D. (2005). A systems model approach to determining resilience surrogates for case studies. Ecosystems 8, 945–957. doi:10.1007/s10021-005-0141-3

CrossRef Full Text | Google Scholar

Bikmukhametov, T., and Jäschke, J. (2020). Combining machine learning and process engineering physics towards enhanced accuracy and explainability of data-driven models. Comput. Chem. Eng. 138, 106834. doi:10.1016/j.compchemeng.2020.106834

CrossRef Full Text | Google Scholar

Bisgaard, T., Mauricio-Iglesias, M., Huusom, J. K., Gernaey, K. V., Dohrup, J., Petersen, M. A., et al. (2017). Adding value to bioethanol through a purification process revamp. Industrial and Eng. Chem. Res. 56, 5692–5704. doi:10.1021/acs.iecr.7b00442

CrossRef Full Text | Google Scholar

Boschert, S., and Rosen, R. (2016). Digital twin-the simulation aspect. Mechatron. Futur. Challenges Solutions Mechatron. Syst. Their Des., 59–74. doi:10.1007/978-3-319-32156-1_5

CrossRef Full Text | Google Scholar

Bradley, W., Kim, J., Kilwein, Z., Blakely, L., Eydenberg, M., Jalvin, J., et al. (2022). Perspectives on the integration between first-principles and data-driven modeling. Comput. Chem. Eng. 166, 107898. doi:10.1016/j.compchemeng.2022.107898

CrossRef Full Text | Google Scholar

Bui, L., Joswiak, M., Castillo, I., Phillips, A., Yang, J., and Hickman, D. (2022). A hybrid modeling approach for catalyst monitoring and lifetime prediction. ACS Eng. Au 2, 17–26. doi:10.1021/acsengineeringau.1c00015

CrossRef Full Text | Google Scholar

Caccavale, F., Gargalo, C. L., Gernaey, K. V., and Krühne, U. (2024). Towards education 4.0: the role of large language models as virtual tutors in chemical engineering. Educ. Chem. Eng. 49, 1–11. doi:10.1016/j.ece.2024.07.002

CrossRef Full Text | Google Scholar

Chakraborty, A., Sivaram, A., and Venkatasubramanian, V. (2021). Ai-Darwin: a first principles-based model discovery engine using machine learning. Comput. Chem. Eng. 154, 107470. doi:10.1016/j.compchemeng.2021.107470

CrossRef Full Text | Google Scholar

Cheng, X., Guo, Z., Shen, Y., Yu, K., and Gao, X. (2023). Knowledge and data-driven hybrid system for modeling fuzzy wastewater treatment process. Neural Comput. Appl. 35, 7185–7206. doi:10.1007/s00521-021-06499-1

CrossRef Full Text | Google Scholar

Cheng, Z., Yao, S., and Yuan, H. (2021). Linking population dynamics to microbial kinetics for hybrid modeling of bioelectrochemical systems. Water Res. 202, 117418. doi:10.1016/j.watres.2021.117418

PubMed Abstract | CrossRef Full Text | Google Scholar

Cruz-Bournazou, M. N., Narayanan, H., Fagnani, A., and Butté, A. (2022). Hybrid Gaussian process models for continuous time series in bolus fed-batch cultures. IFAC-PapersOnLine 55, 204–209. doi:10.1016/j.ifacol.2022.07.445

CrossRef Full Text | Google Scholar

Cui, T., Bertalan, T. S., Ndahiro, N., Khare, P., Betenbaugh, M., Maranas, C., et al. (2024). Data-driven and physics informed modelling of Chinese Hamster Ovary cell bioreactors. Comput. Chem. Eng. 183, 108594. doi:10.1016/j.compchemeng.2024.108594

CrossRef Full Text | Google Scholar

Cuomo, S., Di Cola, V. S., Giampaolo, F., Rozza, G., Raissi, M., and Piccialli, F. (2022). Scientific machine learning through physics–informed neural networks: where we are and what’s next. J. Sci. Comput. 92, 88. doi:10.1007/s10915-022-01939-z

CrossRef Full Text | Google Scholar

Da Silva Pereira, A., Pinheiro, Á. D. T., Rocha, M. V. P., Gonçalves, L. R. B., and Cartaxo, S. J. M. (2021). Hybrid neural network modeling and particle swarm optimization for improved ethanol production from cashew apple juice. Bioprocess Biosyst. Eng. 44, 329–342. doi:10.1007/s00449-020-02445-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Caprio, U., Wu, M., Elmaz, F., Wouters, Y., Vandervoort, N., Anwar, A., et al. (2023). Hybrid modelling of a batch separation process. Comput. Chem. Eng. 177, 108319. doi:10.1016/j.compchemeng.2023.108319

CrossRef Full Text | Google Scholar

Ekardt, F. (2022). Für eine integrierte nachhaltige und digitale, sozial (rechtlich) flankierte transformation. Z. für neues Energier. 26, 433–436.

Google Scholar

European Commission (2019). Communication from the commission to the European parliament, the European council, the council, the European economic and social committee and the committee of the regions: the European green deal. Tech. Rep.

Google Scholar

European Commission (2020). Communication from the commission to the European parliament, the council, the European economic and social committee and the committee of the regions: a European strategy for data. Tech. Rep.

Google Scholar

Faure, L., Mollet, B., Liebermeister, W., and Faulon, J.-L. (2023). A neural-mechanistic hybrid approach improving the predictive power of genome-scale metabolic models. Nat. Commun. 14, 4669. doi:10.1038/s41467-023-40380-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Gargalo, C., Caño de Las Heras, S., Jones, M. N., Udugama, I., Mansouri, S. S., Krühne, U., et al. (2021). Towards the development of digital twins for the bio-manufacturing industry. Adv. Biochem. Engineering/biotechnology 176, 1–35. doi:10.1007/10_2020_142

CrossRef Full Text | Google Scholar

Garske, B., Holz, W., and Ekardt, F. (2024). Digital twins in sustainable transition: exploring the role of eu data governance. Front. Res. Metrics Anal. 9, 1303024. doi:10.3389/frma.2024.1303024

CrossRef Full Text | Google Scholar

He, M., and Chand, B.-u.-n. (2024). Industry 5.0, future of workforce beyond efficiency and productivity. Innovation, Sustain. Technol. Megatrends Face Uncertainties, 23–40. doi:10.1007/978-3-031-46189-7_2

CrossRef Full Text | Google Scholar

Huster, W. R., Schweidtmann, A. M., and Mitsos, A. (2020). Hybrid mechanistic data-driven modeling for the deterministic global optimization of a transcritical organic rankine cycle. Comput. Aided Chem. Eng. 48, 1765–1770. doi:10.1016/B978-0-12-823377-1.50295-0

CrossRef Full Text | Google Scholar

Hutter, C., von Stosch, M., Cruz Bournazou, M. N., and Butté, A. (2021). Knowledge transfer across cell lines using hybrid Gaussian process models with entity embedding vectors. Biotechnol. Bioeng. 118, 4389–4401. doi:10.1002/bit.27907

PubMed Abstract | CrossRef Full Text | Google Scholar

Isoko, K., Cordiner, J. L., Kis, Z., and Moghadam, P. Z. (2024). Bioprocessing 4.0: a pragmatic review and future perspectives. Digit. Discov. 3, 1662–1681. doi:10.1039/D4DD00127C

CrossRef Full Text | Google Scholar

Jul-Rasmussen, P., Chakraborty, A., Venkatasubramanian, V., Liang, X., and Huusom, J. K. (2024). Hybrid ai modeling techniques for pilot scale bubble column aeration: a comparative study. Comput. Chem. Eng. 185, 108655. doi:10.1016/j.compchemeng.2024.108655

CrossRef Full Text | Google Scholar

Jul-Rasmussen, P., Liang, X., Zhang, X., and Huusom, J. K. (2023). Developing robust hybrid-models. Comput. Aided Chem. Eng. 52, 361–366. doi:10.1016/B978-0-443-15274-0.50058-5

CrossRef Full Text | Google Scholar

Kasilingam, S., Yang, R., Singh, S. K., Farahani, M. A., Rai, R., and Wuest, T. (2024). Physics-based and data-driven hybrid modeling in manufacturing: a review. Prod. Manuf. Res. 12, 2305358. doi:10.1080/21693277.2024.2305358

CrossRef Full Text | Google Scholar

Kay, S., Kay, H., Rogers, A. W., and Zhang, D. (2023). Integrating hybrid modelling and transfer learning for new bioprocess predictive modelling. Comput. Aided Chem. Eng. 52, 2595–2600. doi:10.1016/B978-0-443-15274-0.50412-1

CrossRef Full Text | Google Scholar

Kotidis, P., and Kontoravdi, C. (2020). Harnessing the potential of artificial neural networks for predicting protein glycosylation. Metab. Eng. Commun. 10, e00131. doi:10.1016/j.mec.2020.e00131

PubMed Abstract | CrossRef Full Text | Google Scholar

Krippl, M., Dürauer, A., and Duerkop, M. (2020). Hybrid modeling of cross-flow filtration: predicting the flux evolution and duration of ultrafiltration processes. Sep. Purif. Technol. 248, 117064. doi:10.1016/j.seppur.2020.117064

CrossRef Full Text | Google Scholar

Lagergren, J. H., Nardini, J. T., Baker, R. E., Simpson, M. J., and Flores, K. B. (2020). Biologically-informed neural networks guide mechanistic modeling from sparse experimental data. PLoS Comput. Biol. 16, e1008462. doi:10.1371/journal.pcbi.1008462

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, D., Jayaraman, A., and Kwon, J. S. (2020). Development of a hybrid model for a partially known intracellular signaling pathway through correction term estimation and neural network modeling. PLoS Comput. Biol. 16, e1008472. doi:10.1371/journal.pcbi.1008472

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Feng, M., Ran, Y., Su, Y., Liu, F., Huang, C., et al. (2023). Big data in earth system science and progress towards a digital twin. Nat. Rev. Earth and Environ. 4, 319–332. doi:10.1038/s43017-023-00409-w

CrossRef Full Text | Google Scholar

Lima, F. A. R. D., Rebello, C. M., Costa, E. A., Santana, V. V., de Moares, M. G. F., Barreto, A. G., et al. (2023). Improved modeling of crystallization processes by universal differential equations. Chem. Eng. Res. Des. 200, 538–549. doi:10.1016/j.cherd.2023.11.032

CrossRef Full Text | Google Scholar

Lopez, P. C., Udugama, I. A., Thomsen, S. T., Roslander, C., Junicke, H., Iglesias, M. M., et al. (2021). Transforming data to information: a parallel hybrid model for real-time state estimation in lignocellulosic ethanol fermentation. Biotechnol. Bioeng. 118, 579–591. doi:10.1002/bit.27586

PubMed Abstract | CrossRef Full Text | Google Scholar

Maddikunta, P. K. R., Pham, Q. V., B, P., Deepa, N., Dev, K., Gadekallu, T. R., et al. (2022). Industry 5.0: a survey on enabling technologies and potential applications. J. Industrial Inf. Integration 26, 100257. doi:10.1016/j.jii.2021.100257

CrossRef Full Text | Google Scholar

Maton, M., Bogaerts, P., and Vande Wouwer, A. (2022). Hybrid dynamic models of bioprocesses based on elementary flux modes and multilayer perceptrons. Processes 10, 2084. doi:10.3390/pr10102084

CrossRef Full Text | Google Scholar

Mears, L., Stocks, S. M., Albaek, M. O., Sin, G., and Gernaey, K. V. (2017). Application of a mechanistic model as a tool for on-line monitoring of pilot scale filamentous fungal fermentation processes—the importance of evaporation effects. Biotechnol. Bioeng. 114, 589–599. doi:10.1002/bit.26187

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer, K., Ibsen, M. S., Vetter-Joss, L., Hansen, E. B., and Abildskov, J. (2023). Industrial ion-exchange chromatography development using discontinuous galerkin methods coupled with forward sensitivity analysis. J. Chromatogr. A 1689, 463741. doi:10.1016/j.chroma.2022.463741

PubMed Abstract | CrossRef Full Text | Google Scholar

Morabito, B., Pohlodek, J., Matschek, J., Savchenko, A., Carius, L., and Findeisen, R. (2021). Towards risk-aware machine learning supported model predictive control and open-loop optimization for repetitive processes. IFAC-PapersOnLine 54, 321–328. doi:10.1016/j.ifacol.2021.08.564

CrossRef Full Text | Google Scholar

Mowbray, M. R., Wu, C., Rogers, A. W., Rio-Chanona, E. A. D., and Zhang, D. (2023). A reinforcement learning-based hybrid modeling framework for bioprocess kinetics identification. Biotechnol. Bioeng. 120, 154–168. doi:10.1002/bit.28262

PubMed Abstract | CrossRef Full Text | Google Scholar

Nahavandi, S. (2019). Industry 5.0-a human-centric solution. Sustain. Switz. 11, 4371. doi:10.3390/su11164371

CrossRef Full Text | Google Scholar

Narayanan, H., Behle, L., Luna, M. F., Sokolov, M., Guillén-Gosálbez, G., Morbidelli, M., et al. (2020). Hybrid-ekf: hybrid model coupled with extended kalman filter for real-time monitoring and control of mammalian cell culture. Biotechnol. Bioeng. 117, 2703–2714. doi:10.1002/bit.27437

PubMed Abstract | CrossRef Full Text | Google Scholar

Narayanan, H., Cruz Bournazou, M. N., Guillén Gosálbez, G., and Butté, A. (2022). Functional-hybrid modeling through automated adaptive symbolic regression for interpretable mathematical expressions. Chem. Eng. J. 430, 133032. doi:10.1016/j.cej.2021.133032

CrossRef Full Text | Google Scholar

Narayanan, H., Seidler, T., Luna, M. F., Sokolov, M., Morbidelli, M., and Butté, A. (2021). Hybrid models for the simulation and prediction of chromatographic processes for protein capture. J. Chromatogr. A 1650, 462248. doi:10.1016/j.chroma.2021.462248

PubMed Abstract | CrossRef Full Text | Google Scholar

Narayanan, H., von Stosch, M., Feidl, F., Sokolov, M., Morbidelli, M., and Butté, A. (2023). Hybrid modeling for biopharmaceutical processes: advantages, opportunities, and implementation. Front. Chem. Eng. 5, 1157889. doi:10.3389/fceng.2023.1157889

CrossRef Full Text | Google Scholar

Nations, U. (2024). Sustainable development goals.

Google Scholar

Nazemzadeh, N., Malanca, A. A., Nielsen, R. F., Gernaey, K. V., Andersson, M. P., and Mansouri, S. S. (2021). Integration of first-principle models and machine learning in a modeling framework: an application to flocculation. Chem. Eng. Sci. 245. doi:10.1016/j.ces.2021.116864

CrossRef Full Text | Google Scholar

Nielsen, R. F., Nazemzadeh, N., Sillesen, L. W., Andersson, M. P., Gernaey, K. V., and Mansouri, S. S. (2020). Hybrid machine learning assisted modelling framework for particle processes. Comput. Chem. Eng. 140, 106916. doi:10.1016/j.compchemeng.2020.106916

CrossRef Full Text | Google Scholar

Okamura, K., Badr, S., Murakami, S., and Sugiyama, H. (2022). Hybrid modeling of cho cell cultivation in monoclonal antibody production with an impurity generation module. Industrial Eng. Chem. Res. 61, 14898–14909. doi:10.1021/acs.iecr.2c00736

CrossRef Full Text | Google Scholar

Palmtag, A., Rousselli, J., Dohmen, J., and Jupke, A. (2024). Hybrid modeling of liquid-liquid pulsed sieve tray extraction columns. Chem. Eng. Sci. 287, 119755. doi:10.1016/j.ces.2024.119755

CrossRef Full Text | Google Scholar

Pandey, K., Pandey, M., Kumar, V., Aggarwal, U., and Singhal, B. (2024). Bioprocessing 4.0 in biomanufacturing: paving the way for sustainable bioeconomy. Syst. Microbiol. Biomanufacturing 4, 407–424. doi:10.1007/s43393-023-00206-y

CrossRef Full Text | Google Scholar

Peterson, L., Bremer, J., and Sundmacher, K. (2024). Challenges in data-based reactor modeling: a critical analysis of purely data-driven and hybrid models for a cstr case study. Comput. Chem. Eng. 184, 108643. doi:10.1016/j.compchemeng.2024.108643

CrossRef Full Text | Google Scholar

Pinto, J., Mestre, M., Ramos, J., Costa, R. S., Striedner, G., and Oliveira, R. (2022). A general deep hybrid model for bioreactor systems: combining first principles with deep neural networks. Comput. Chem. Eng. 165, 107952. doi:10.1016/j.compchemeng.2022.107952

CrossRef Full Text | Google Scholar

Pinto, J., Ramos, J. R. C., Costa, R. S., and Oliveira, R. (2023). A general hybrid modeling framework for systems biology applications: combining mechanistic knowledge with deep neural networks under the sbml standard. AI Switz. 4, 303–318. doi:10.3390/ai4010014

CrossRef Full Text | Google Scholar

Polak, J., von Stosch, M., Sokolov, M., Piccioni, L., Streit, A., Schenkel, B., et al. (2023). Hybrid modeling supported development of an industrial small-molecule flow chemistry process. Comput. Chem. Eng. 170, 108127. doi:10.1016/j.compchemeng.2022.108127

CrossRef Full Text | Google Scholar

Psichogios, D., and Ungar, L. (1992). A hybrid neural network-first principles approach to process modeling. Aiche J. 38, 1499–1511. doi:10.1002/aic.690381003

CrossRef Full Text | Google Scholar

Quaghebeur, W., Torfs, E., De Baets, B., and Nopens, I. (2022). Hybrid differential equations: integrating mechanistic and data-driven techniques for modelling of water systems. Water Res. 213, 118166. doi:10.1016/j.watres.2022.118166

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramos, J. R. C., Pinto, J., Poiares-Oliveira, G., Peeters, L., Dumas, P., and Oliveira, R. (2024). Deep hybrid modeling of a hek293 process: combining long short-term memory networks with first principles equations. Biotechnol. Bioeng. 121, 1554–1568. doi:10.1002/bit.28668

PubMed Abstract | CrossRef Full Text | Google Scholar

Rischawy, F., Briskot, T., Hopf, N., Saleh, D., Wang, G., Kluters, S., et al. (2023). Connected mechanistic process modeling to predict a commercial biopharmaceutical downstream process. Comput. and Chem. Eng. 176, 108292. doi:10.1016/j.compchemeng.2023.108292

CrossRef Full Text | Google Scholar

Rischawy, F., Briskot, T., Schimek, A., Wang, G., Saleh, D., Kluters, S., et al. (2022). Integrated process model for the prediction of biopharmaceutical manufacturing chromatography and adjustment steps. J. Chromatogr. A 1681, 463421. doi:10.1016/j.chroma.2022.463421

PubMed Abstract | CrossRef Full Text | Google Scholar

Rockström, J., Gupta, J., Qin, D., Lade, S. J., Abrams, J. F., Andersen, L. S., et al. (2023). Safe and just earth system boundaries. Nature 33, 102–111. doi:10.1038/s41586-023-06083-8

CrossRef Full Text | Google Scholar

Rogers, A. W., Cardenas, I. O. S., Del Rio-Chanona, E. A., and Zhang, D. (2023a). Investigating physics-informed neural networks for bioprocess hybrid model construction. Comput. Aided Chem. Eng. 52, 83–88. doi:10.1016/B978-0-443-15274-0.50014-7

CrossRef Full Text | Google Scholar

Rogers, A. W., Song, Z., Ramon, F. V., Jing, K., and Zhang, D. (2023b). Investigating ‘greyness’ of hybrid model for bioprocess predictive modelling. Biochem. Eng. J. 190, 108761. doi:10.1016/j.bej.2022.108761

CrossRef Full Text | Google Scholar

Rudolph, M., Kurz, S., and Rakitsch, B. (2024). Hybrid modeling design patterns. J. Math. Industry 14 (3), 3. doi:10.1186/s13362-024-00141-0

CrossRef Full Text | Google Scholar

Ryu, Y., Shin, S., Liu, J. J., Lee, W., and Na, J. (2023). Physics-informed neural networks for optimization of polymer reactor design. Comput. Aided Chem. Eng., 493–498. doi:10.1016/B978-0-443-15274-0.50079-2

CrossRef Full Text | Google Scholar

Sansana, J., Joswiak, M. N., Castillo, I., Wang, Z., Rendall, R., Chiang, L. H., et al. (2021). Recent trends on hybrid modeling for industry 4.0. Comput. Chem. Eng. 151, 107365. doi:10.1016/j.compchemeng.2021.107365

CrossRef Full Text | Google Scholar

Schäfer, P., Caspari, A., Schweidtmann, A. M., Vaupel, Y., Mhamdi, A., and Mitsos, A. (2020). The potential of hybrid mechanistic/data-driven approaches for reduced dynamic modeling: application to distillation columns. Chemie-Ingenieur-Technik 92, 1910–1920. doi:10.1002/cite.202000048

CrossRef Full Text | Google Scholar

Schweidtmann, A. M., Zhang, D., and von Stosch, M. (2023). A review and perspective on hybrid modeling methodologies. Digit. Chem. Eng. 10, 100136. doi:10.1016/j.dche.2023.100136

CrossRef Full Text | Google Scholar

Shah, P., Sheriff, M. Z., Bangi, M. S. F., Kravaris, C., Kwon, J. S.-I., Botre, C., et al. (2022). Deep neural network-based hybrid modeling and experimental validation for an industry-scale fermentation process: identification of time-varying dependencies among parameters. Chem. Eng. J. 441, 135643. doi:10.1016/j.cej.2022.135643

CrossRef Full Text | Google Scholar

Sitapure, N., and Kwon, J. S.-I. (2023). Introducing hybrid modeling with time-series-transformers: a comparative study of series and parallel approach in batch crystallization. Industrial Eng. Chem. Res. 62, 21278–21291. doi:10.1021/acs.iecr.3c02624

CrossRef Full Text | Google Scholar

Sokolov, M., von Stosch, M., Narayanan, H., Feidl, F., and Butté, A. (2021). Hybrid modeling — a key enabler towards realizing digital twins in biopharma? Curr. Opin. Chem. Eng. 34, 100715. doi:10.1016/j.coche.2021.100715

CrossRef Full Text | Google Scholar

Sonnleitner, B., and Käppeli, O. (1986). Growth of saccharomyces cerevisiae is controlled by its limited respiratory capacity: formulation and verification of a hypothesis. Biotechnol. Bioeng. 28, 927–937. doi:10.1002/bit.260280620

PubMed Abstract | CrossRef Full Text | Google Scholar

Spann, R., Lantz, A. E., Roca, C., Gernaey, K. V., and Sin, G. (2018). Model-based process development for a continuous lactic acid bacteria fermentation. Comput. Aided Chem. Eng. (Elsevier) 43, 1601–1606. doi:10.1016/b978-0-444-64235-6.50279-5

CrossRef Full Text | Google Scholar

Tzachor, A., Sabri, S., Richards, C. E., Rajabifard, A., and Acuto, M. (2022). Potential and limitations of digital twins to achieve the sustainable development goals. Nat. Sustain. 5, 822–829. doi:10.1038/s41893-022-00923-7

CrossRef Full Text | Google Scholar

Udugama, I., Öner, M., Lopez, P. C., Beenfeldt, C., Bayer, C., Huusom, J. K., et al. (2021). Towards digitalization in bio-manufacturing operations: a survey on application of big data and digital twin concepts in Denmark. Front. Chem. Eng. 3, 727152. doi:10.3389/fceng.2021.727152

CrossRef Full Text | Google Scholar

Udugama, I. A., Lopez, P. C., Gargalo, C. L., Li, X., Bayer, C., and Gernaey, K. V. (2021). Digital twin in biomanufacturing: challenges and opportunities towards its implementation. Syst. Microbiol. Biomanufacturing 1, 257–274. doi:10.1007/s43393-021-00024-0

CrossRef Full Text | Google Scholar

Vega-Ramon, F., Zhu, X., Savage, T. R., Petsagkourakis, P., Jing, K., and Zhang, D. (2021). Kinetic and hybrid modeling for yeast astaxanthin production under uncertainty. Biotechnol. Bioeng. 118, 4854–4866. doi:10.1002/bit.27950

PubMed Abstract | CrossRef Full Text | Google Scholar

von Stosch, M., Oliveira, R., Peres, J., and Feyo de Azevedo, S. (2014). Hybrid semi-parametric modeling in process systems engineering: past, present and future. Comput. Chem. Eng. 60, 86–101. doi:10.1016/j.compchemeng.2013.08.008

CrossRef Full Text | Google Scholar

Wu, Z., Rincon, D., and Christofides, P. D. (2020). Process structure-based recurrent neural network modeling for model predictive control of nonlinear processes. J. Process Control 89, 74–84. doi:10.1016/j.jprocont.2020.03.013

CrossRef Full Text | Google Scholar

Xu, R.-Z., Cao, J.-S., Luo, J.-Y., Feng, Q., Ni, B.-J., and Fang, F. (2022). Integrating mechanistic and deep learning models for accurately predicting the enrichment of polyhydroxyalkanoates accumulating bacteria in mixed microbial cultures. Bioresour. Technol. 344, 126276. doi:10.1016/j.biortech.2021.126276

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, J., Shan, D., Song, H., and Yang, M. (2022). A novel hybrid machine learning model for predicting rate constants of the reactions between alkane and ch3 radical. Fuel 322, 124150. doi:10.1016/j.fuel.2022.124150

CrossRef Full Text | Google Scholar

Zhang, D., Savage, T. R., and Cho, B. A. (2020). Combining model structure identification and hybrid modelling for photo-production process predictive simulation and optimisation. Biotechnol. Bioeng. 117, 3356–3367. doi:10.1002/bit.27512

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomenclature

ML Machine Learning

DT Digital Twin

AI Artificial Intelligence

IoT Internet of Things

PDE Partial Differential Equations

ODE Ordinary Differential Equations

ANN Artificial Neural Networks

RL Reinforcement Learning

LSTM Long Short-Term Memory

FFNN Feedforward Neural Networks

DNN Deep Neural Networks

SBML Systems Biology Markup Language

GPSSM Gaussian Process State Space Models

CHO Chinese Hamster Ovary (in reference to cell lines)

STEM Science, Technology, Engineering, and Mathematics

PINN Physics-Informed Neural Networks

HNM Hybrid Neural Models

PSO Particle Swarm Optimization

UDE Universal Differential Equations

EFM Elementary Flux Modes

RNN Recurrent Neural Network

BINN Biologically-Informed Neural Networks

CD-EKF Continuous-Discrete Extended Kalman Filter

iDoE Intensified Design of Experiments

ASM Activated Sludge Model

GLA $\gamma$-Linolenic Acid

PHA Polyhydroxyalkanoates

MPC Model Predictive Control

CSTR Continuous Stirred Tank Reactor

DHM Deep Hybrid Model

PLS Partial Least Squares

ORC Organic Rankine Cycle

CSS Constant Volume Solvent Switch

API Active Pharmaceutical Ingredients

TST Time-Series-Transformers