Bioprocess feeding optimization through in silico dynamic experiments and hybrid digital models—a proof of concept

The development of cell cultures to produce monoclonal antibodies is a multi-step, time-consuming, and labor-intensive procedure which usually lasts several years and requires heavy investment by biopharmaceutical companies. One key aspect of process optimization is improving the feeding strategy. This step is typically performed though design of experiments (DoE) during process development, in such a way as to identify the optimal combinations of factors which maximize the productivity of the cell cultures. However, DoE is not suitable for time-varying factor profiles because it requires a large number of experimental runs which can last several weeks and cost tens of thousands of dollars. We here suggest a methodology to optimize the feeding schedule of mammalian cell cultures by virtualizing part of the experimental campaign on a hybrid digital model of the process to accelerate experimentation and reduce experimental burden. The proposed methodology couples design of dynamic experiments (DoDE) with a hybrid semi-parametric digital model. In particular, DoDE is used to design optimal experiments with time-varying factor profiles, whose experimental data are then utilized to train the hybrid model. This will identify the optimal time profiles of glucose and glutamine for maximizing the antibody titer in the culture despite the limited number of experiments performed on the process. As a proof-of-concept, the proposed methodology is applied on a simulated process to produce monoclonal antibodies at a 1-L shake flask scale, and the results are compared with an experimental campaign based on DoDE and response surface modeling. The hybrid digital model requires an extremely limited number of experiments (nine) to be accurately trained, resulting in a promising solution for performing in silico experimental campaigns. The proposed optimization strategy provides a 34.9% increase in the antibody titer with respect to the training data and a 2.8% higher antibody titer than the optimal results of two DoDE-based experimental campaigns comprising different numbers of experiments (i.e., 9 and 31), achieving a high antibody titer (3,222.8 mg/L) —very close to the real process optimum (3,228.8 mg/L).

1 Introduction

Monoclonal antibodies (mAbs) are biological drugs which have attracted attention for the treatment of autoimmune, oncological, and infectious diseases (Castelli et al., 2019). In 2018, they represented 53% of overall biopharmaceutics approvals by regulatory agencies and 65.6% of entire biopharmaceutical sales (Walsh, 2018). At the industrial scale, mAbs are produced in fed-batch cultures of mammalian cells which are appositely generated to secrete the desired product (O’Flaherty et al., 2020; Wurm, 2004).

The development of mAbs is a multi-step process which requires a lot of resources, both of time and capital investment, because it usually lasts several years and costs billions of dollars (Epifa, 2021; Farid et al., 2020). The upstream development of mAbs starts with cell line generation, screening and selection, and process characterization. At these stages, a large pool of cell lines is generated and tested at different process scales (Barberi et al., 2022; Facco et al., 2020) to identify those that meet the desired performance in terms of growth, productivity, and product quality (Gronemeyer et al., 2014; Tripathi and Shrivastava, 2019). Furthermore, the relationship between critical process parameters (CPP) and critical quality attributes (CQA) is studied for regulatory compliance and for process optimization. During process optimization, bioreactor operating parameters—such as temperature, pH, agitation, and dissolved oxygen—are adapted to the specific host system to enhance cell growth and specific productivity (Gronemeyer et al., 2014; Li et al., 2010; Tripathi and Shrivastava, 2019). Similarly, an appropriate optimization of the medium and feeding strategy is required to balance cell growth, productivity, and product quality (Kim and Lee, 2009; Ling et al., 2015; Tripathi and Shrivastava, 2019).

High-throughput scaled-down equipment and statistical design of experiments (DoE) are the most common methodologies for systematically optimizing media and feeding strategy (Li et al., 2010; Mora et al., 2019; Zhou et al., 1997). Typically, cell cultures are fed with frequent boluses of glucose and glutamine to maintain a low concentration and minimize the production of by-products such as lactate and ammonia (Li et al., 2010). Hence, the optimization of the feeding strategy requires determining the best way of providing feed boluses over time. However, DoE only deals with “static” factors. To deal with the batch process dynamics, DoE can be exploited by assigning a different DoE factor to the feeding action at each day (Mora et al., 2019); however, this results in a design with too many factors that requires several dozen experiments. An appropriate solution to this issue is the adoption of design of dynamic experiments (DoDE), which guarantees the optimization of time-varying factors while minimizing the number of experimental runs (Georgakis, 2013). In fact, DoDE utilizes dynamic subfactors to code the profiles of the time-varying factors and then build a response surface model (RSM) to correlate the factors’ dynamic profile to the CQA. Research on DoDE applied to the bioprocessing field is still ongoing, with few examples of application. Specifically, DoDE has been used to optimize process conditions in 200 L bioreactors for producing monoclonal antibodies (Luo et al., 2023) and on simulated fermentation processes (Klebanov and Georgakis, 2016) and mammalian cell cultures (Wang and Georgakis, 2017).

However, despite being designed to maximize the content of information obtained by experiments while minimizing the number experimental runs, the number of experiments designed by DoDE rapidly increases with the number of dynamic variables and the complexity of their dynamic profiles, leading to high numbers of required experimental runs. Since each experimental run lasts several weeks and costs tens of thousands of dollars, the duration and cost of large experimental campaigns limits the applicability of DoDE in the biopharmaceutical industry. Accordingly, strategies to limit the allocation of resources for experimental campaigns are of paramount importance.

First-principles models are extremely effective tools for digitally representing biological systems since they incorporate fundamental physical and biological phenomena. However, first-principles model identification requires a long trial-and-error procedure, which can be supported by model-based optimal experiment design (Abt et al., 2018; Huang et al., 2020). Furthermore, both the model complexity and the requirement of training data strongly increase when representing complex dynamics, as in the case of mAbs cultures. This leads to model over-parametrization, difficult estimation of model parameters, and thus to the inability to correctly simulate the system under study (Mahanty, 2023).

Hybrid semi-parametric digital models, instead, represent an innovative solution to reducing experimental requirements and development timelines while improving robustness and extrapolation. Such models combine first principles models, embedding the mechanistic knowledge of the system under investigation with data-driven methods which learn complex and possibly unknown relationships among the system variables from experimental data (Sansana et al., 2021; von Stosch et al., 2014; Yang et al., 2020). The data-driven aspect often limits the applicability of the model-based optimal DoE in hybrid modeling. In fact, these methodologies are extremely sensitive to uncertainty in model parameters (Galvanin et al., 2013), which is typical of certain data-driven methods (e.g., artificial neural networks—ANN).

Hybrid semi-parametric models have been widely applied to the bioprocess development of tasks such as prediction, process understanding, and process and quality monitoring. For example, an improved understanding of the relationship between biomass and productivity with the process parameters in microbial cell culture was achieved through hybrid semi-parametric models (von Stosch et al., 2016), while good prediction accuracy was attained by hybrid models trained on intensified DoE data (von Stosch and Willis, 2017), allowing the acceleration of upstream process characterization (Bayer et al., 2020). In mammalian cell cultures, the prediction performance of hybrid models was tested in interpolation and extrapolation scenarios (Narayanan et al., 2021), while, compared to purely multivariate techniques, the prediction of the main culture variables through hybrid models resulted in greater accuracy (Narayanan et al., 2019). In the same context, hybrid semi-parametric models coupled with the extended Kalman filter were used to monitor glucose concentration in bioreactors, suggesting the appropriate timing of feeding action to avoid cell starvation (Narayanan et al., 2020).

Hybrid semi-parametric models were also used for bioprocess optimization. For example, the optimal processing conditions (Ferreira et al., 2014) and glucose feeding strategy (Teixeira et al., 2006) for microbial cell cultures were identified through an iterative batch-to-batch strategy based on hybrid models: the optimal condition identified by the hybrid model at each step was used to retrain the model for further optimizations. A similar strategy identified static process parameters to improve product yield in E. Coli cultures by means of nine experimental runs, with only five from the initial exploratory campaign and four suggested in the batch-to-batch optimization (Bayer et al., 2021). Furthermore, the feeding schedule of mammalian cell culture was optimized by means of hybrid semi-parametric models (Teixeira et al., 2005; 2007), showing the applicability of these methodologies in optimizing mammalian cell culture. In many cases, dynamic feeding optimization is performed by a direct parametrization of the control vector (Banga et al., 2005), where the feeding strategy over the entire culture duration is discretized in several segments using a predefined basis function (e.g., piecewise constant parametrization). For example, such direct dynamic optimization was conducted to optimize the feeding strategy in mAbs production using a fully mechanistic model setup (Kaysfeld et al., 2023). However, in this approach, the number of optimization variables rapidly increases together with the complexity of the optimization problem because one control variable is required for each nutrient and control interval. Instead, conducting optimization in the DoDE framework, where dynamic profiles are represented using specific polynomials controlled by a reduced set of subfactors, can reduce the overall number of optimization variables and the complexity of the problem (Rodrigues and Bonvin, 2020).

Furthermore, although hybrid models have been applied for bioprocess optimization and their added value for the optimization of mammalian feeding schedule has been proven, the advantages of using hybrid semi-parametric models in feeding schedule optimization during bioprocess development is underexplored, and research is still needed to allow a consistent applicability of hybrid models in bioprocess optimization.

This study compares an in silico experimental campaign for the optimization of the feeding schedule in mammalian cell cultures through hybrid digital models with an experimental campaign on the process to evaluate whether the in silico experiments can accelerate experimentation and reduce the experimental burden in the process development. In particular, we use a hybrid semi-parametric model calibrated on the experiments designed through DoDEs in such a way as to identify the time profiles of fed glucose and glutamine, which maximize the antibody titer. The proposed methodology is tested on a well-established simulated process for the production of mAbs at a shake flask scale (Kontoravdi et al., 2010).

2 Materials and methods

2.1 Proposed methodology

In this work, an in silico experimental campaign (strategy #1) for optimizing the feeding schedule of mammalian cell cultures is proposed (Figure 1A). The adopted procedure comprises five steps.

1. DoDE planning: initially, experiments are planned according to a DoDE (Section 2.1.1) on two dynamic factors: the time profiles of glucose and glutamine concentrations; and as response, the antibody titer at harvest.

2. Experiment execution: planned experiments are executed on the process under study, which in this study is a simulated process for producing monoclonal antibodies at 1-L shake flask scale (Kontoravdi et al., 2010; Section 2.2). This study used a simulated process because it allows: i) knowing the exact relationship between nutrients and antibody titer which can be exploited to identify the optimal feeding schedule to use as reference for the performance of the proposed optimization strategy; ii) following in real-time the entire time evolution of the culture variables, whose measurements are available only at a much lower frequency (every few hours) in real processes.

3. Training the hybrid model: a hybrid semi-parametric model (Section 2.1.2) is trained on the data collected from the experiments executed at step 2.

4. Optimization: a genetic algorithm (Section 2.1.3) is used to identify the feeding schedule that maximizes the antibody titer at harvest. This algorithm exploits the hybrid model to simulate in silico experiments and predict the resulting antibody titer, given the profiles of both glucose and glutamine.

5. Execution of the confirmatory experiment at the optimal conditions: once the optimal nutrient profiles (i.e., feeding schedule) are identified, they are executed in the process to assess the antibody titer that the process can achieve and the reliability of the predicted values.

Figure 1

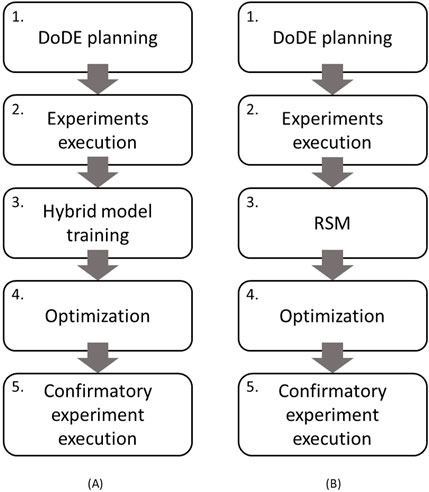
Figure 1. Proposed methodology: (A) optimization strategy #1 (in silico) and (B) optimization strategy #2 (experimental).

Optimization strategy #1 is compared with a standard experimental campaign for optimizing the feeding schedule carried out directly on the process (strategy #2, Figure 1B). Although steps 1, 2, and 5 are the same as those of strategy #1, steps 3 and 4 are as follows.

3. Response surface modeling: RSM is built with the data collected from the experiments executed at step 2 according to the DoDE theory. The model is used to predict the antibody titer at harvest from the DoDE dynamic subfactors after being updated by excluding those effects with low influence on the response (Section 2.1.1.2);

4. Optimization: in this case, the genetic algorithm exploits the RSM to predict the antibody titer given the profiles of glucose and glutamine.

The confirmatory experiments performed at step 5 of both optimization strategies are then compared with the process optimum, which is known in this study because the process is simulated. In the next sections, details on the DoDE, the process, the hybrid model, and the techniques used for experimentation and optimization are presented.

2.1.1 Design of dynamic experiments

Design of dynamic experiments (DeDE) (Georgakis, 2013) is used in this study to plan the experimental campaign for optimizing the glucose and glutamine profiles in the cell culture.

2.1.1.1 Design of dynamic experiment fundamentals and applications

In DoDE, the time-varying factors (i.e., manipulated variables) are expressed as normalized dynamic variables $z\left(\tau \right)$, which vary between −1 and 1. Normalized dynamic variables are the sum of orthogonal time-varying profiles weighted by dynamic subfactors $x_i$, which are equivalent to the design of experiment factors. The normalized dynamic variables (Equation 1) are defined as follows:

$z\left(\tau \right)={\displaystyle \sum _{i=1}^I}{x}_i{P}_{i-1}\left(\tau \right),(1)$

where $P_{i-1}\left(\tau \right)$ is a shifted Legendre polynomial of degree $i-1$ and $\tau =t/t_b$ is the dimensionless culture time (i.e., the fraction of experimental batch completion) being $t_b$, the culture duration. Details on the expression of the Legendre polynomials can be found in Georgakis (2013). The number of subfactors defines the maximum degree of the $z\left(\tau \right)$ profile. In our study, to have independent profiles for each nutrient with second degree curvature and avoid an excessive number of factors, $I=3$ dynamic subfactors are used for each nutrient, summing up to a total of $K=6$ dynamic subfactors; subfactors $x_1^{glc},x_2^{glc},x_3^{glc}$ refer to the glucose profile and $x_1^{gln},x_2^{gln},x_3^{gln}$ to the glutamine one. Independently of the specific nutrient, subfactor $x_1$ (Figure 2A) controls the initial value of the profile (e.g., 1 corresponds to the top of the interval while −1 to the bottom), $x_2$ (Figure 2B) controls the overall increasing or decreasing tendency of the profile (e.g., 1 corresponds to fully increasing profiles while −1 to fully decreasing), and $x_3$ (Figure 2C) controls the concavity of the profile (e.g., 1 upward and −1 downward).

Figure 2

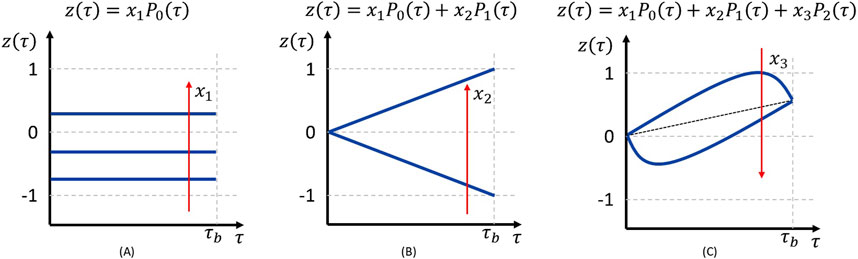
Figure 2. Effect of dynamic subfactors on the normalized dynamic variable $z\left(\tau \right)$ for a three-subfactor design: (A) $x_1$, (B) $x_2$, and (C) $x_3$. The red arrows indicate the direction of increasing subfactors.

To ensure that $-1\le z\left(\tau \right)\le 1$, the dynamic subfactors must satisfy the following constraints:

$-1\le x_1^{glc}\pm x_2^{glc}\pm x_3^{glc}\le 1,(2)$

$-1\le x_1^{gln}\pm x_2^{gln}\pm x_3^{gln}\le 1,(3)$

and the value of each subfactor must also be bounded:

$-1\le x_i\le 1.(4)$

The glucose and glutamine concentration profiles $u_j\left(\tau \right)$ (Equation 5) planned through the DoDE can be determined from the respective $z\left(\tau \right)$ according to the relation:

$u_j\left(\tau \right)=u_{j,0}+z_j\left(\tau \right)∆u_j\text{\hspace{0.17em}with\hspace{0.17em}}j=\text{glc\hspace{0.17em}or\hspace{0.17em}gln},(5)$

where

$u_{j,0}=\frac{u_{j,\mathit{max}}+u_{j,\mathit{min}}}{2},\text{and}$

$∆u_j=\frac{u_{j,\mathit{max}}-u_{j,\mathit{min}}}{2},$

being $u_{j,\mathit{max}}$ and $u_{j,\mathit{min}}$—the maximum and minimum values in which the profile of each nutrient $j$ is allowed to vary. We here assume glucose and glutamine to vary in the ranges $\left[20,50\right]$ mM and $\left[2,10\right]$ mM, respectively. These values are selected to remain in proximity to the concentration at which the process operates (Kontoravdi et al., 2010).

Since the nutrients are both manipulated and observed, their concentrations vary because of both cell consumption and feeding. Here, we simulate off-line measurements because advanced monitoring strategies, such as on-line monitoring and control systems, are not yet standard in industrial mammalian cell cultures, especially in the small scales for the early stages of product development. Furthermore, the measurements and feeding actions are performed in boluses once every 24 h. Consequently, the nutrient profile cannot precisely follow that proposed by the DoDE. To deal with this issue, we introduce a specific procedure to replicate as precisely as possible the profiles indicated by the DoDE during the experiments, which is schematically represented in Figure 3. The proposed procedure consists of:

• defining a 10% band around the DoDE profile which is used to control the feeding actions (Figure 3A, black dashed lines);

• performing the feeding action only if the nutrient concentration in the culture at the sampling time is $<90\%$ of the concentration defined by the designed experiment (Figure 3A, lower black dashed line);

• performing the feeding of a predefined amount (i.e., constant) of fresh medium with a nutrient concentration calculated to achieve 110% of the concentration defined by the designed experiment (Figure 3A, upper black dashed line).

Figure 3

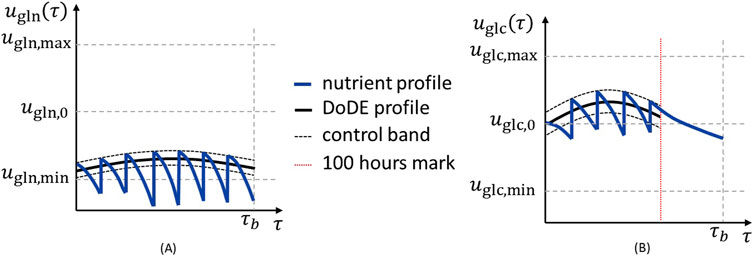
Figure 3. Schematic representation of (A) glutamine and (B) glucose profiles (blue lines), with the profile determined by DoDE (black line), the 110/90% control band (black dashed lines), and the 100-h limit for glucose feeding (red dotted line).

The feeding actions are visible in the nutrient profiles (Figure 3A) as the vertical jumps in the blue line where the nutrient concentration is brought to 110% of that defined by the designed experiment. Furthermore, since the glucose consumption is slow and hardly decreases in the final part of the batch, the glucose cannot follow sharply decreasing profiles; hence it is controlled (and, accordingly, feeding performed) only in the first 100 h of the batch (Figure 3B, red dotted line). After this point, the glucose is fed only to compensate for any dilution effect due to glutamine addition. This is shown in Figure 3B, where after 100 h (red dotted line) the feeding is not performed and nutrient concentration decreases because of cell consumption. Accordingly, the glucose profile after 100 h has no controllable effect on the antibody titer and is not considered in the analysis.

2.1.1.2 Design of dynamic experiments response surface modeling

In this study, the DoDE nutrient profiles are designed by means of a D-optimal DoE (de Aguiar et al., 1995) applied to the $K=6$ subfactors. Once the experiments are executed on the process, an RSM (Montgomery, 2007) is fitted to the experimental data obtained from the designed experimental campaign through multiple linear regression. A second-order RSM (typically used for optimization) is built to predict the antibody titer at harvest $y$ from the dynamic subfactors:

$\widehat{y}={\beta }_0+\left[\begin{array}{ccc}{\beta }_1& {\beta }_2& \begin{array}{cc}\cdots & {\beta }_K\end{array}\end{array}\right]\mathbf{x}+{\mathbf{x}}^{\mathrm{T}}\left[\begin{array}{ccc}{∆}_{1,1}& {∆}_{1,2}& \begin{array}{cc}\cdots & {∆}_{1,K}\end{array}\\ 0& {∆}_{2,2}& \begin{array}{cc}\cdots & {∆}_{2,K}\end{array}\\ \begin{array}{c}⋮\\ 0\end{array}& \begin{array}{c}⋮\\ 0\end{array}& \begin{array}{cc}\begin{array}{c}\ddots \\ \cdots \end{array}& \begin{array}{c}⋮\\ {∆}_{K,K}\end{array}\end{array}\end{array}\right]\mathbf{x},(6)$

where $\widehat{y}$ is the predicted antibody titer, $\mathbf{x}=\left[\begin{array}{ccc}{x}_1^{glc}& x_2^{glc}& \begin{array}{cc}{x}_3^{glc}& \begin{array}{cc}{x}_1^{gln}& \begin{array}{cc}{x}_2^{gln}& x_3^{gln}\end{array}\end{array}\end{array}\end{array}\right]$ is the column vector of the dynamic subfactors for a single experiment, and ${\beta }_k$ and ${∆}_{k,k}$ are the first and higher order parameters of the RSM, respectively. The model parameters are estimated by minimizing the residual error in a least-square manner.

The RSM is affected by uncertainty. The uncertainty of the estimated parameter ${\widehat{\beta }}_e$ (i.e., ${\widehat{\beta }}_k$ or ${\widehat{∆}}_{k,k}$) for each term $e$ of Equation 6 is determined through the parameter confidence intervals:

${\widehat{\beta }}_e\pm t_{1-\alpha 2,N-E}\sqrt{\frac{\frac{1}{N-E}{\displaystyle \sum _{n=}^N}{\left(y_n-{\widehat{y}}_n\right)}^2}{{\displaystyle \sum _{n=1}^N}{\left(x_{n,e}-{\overline{\mathbf{x}}}_e\right)}^2}},(7)$

where $y_n$ is the measured response of the $n$^th experiment, ${\widehat{y}}_n$ is the response of the $n$^th experiment predicted by Equation 6, $x_{n,e}$ is the value of the $e$^th term for the $n$^th experiment, ${\overline{x}}_e$ is the average value of the $e$^th term, $N$ is the total number of experiments, $E$ is the total number of terms of Equation 6, and $t_{1-\alpha 2,N-E}$ is the critical value of Student’s $t$ distribution with $N-E$ degrees of freedom calculated at the confidence level $\alpha =0.05$. The effects with an uncertainty not different from zero from the statistical point of view (namely, where the parameter confidence interval comprises the 0) are removed from the model because they are considered not significant with a confidence of 95%.

The uncertainty on the parameter propagates in the uncertainty of the predictions, which, for a validatory experiment with subfactors ${\mathbf{x}}_{\text{NEW}}$, is assessed through the 95% prediction interval (Wang and Georgakis, 2019):

$PI=t_{1-\alpha 2,N-E}\sqrt{s^2\left(1+{\mathbf{x}}_{\text{NEW}}^{\mathrm{T}}{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{x}}_{\text{NEW}}\right)},(8)$

where $s^2=SSE/\left(N-E\right)$, $SSE$ being the sum squared error of the model, $\mathbf{X}$ is the matrix containing the subfactors vectors for all the $N$ designed DoDE experiments placed along the rows, and $t_{1-\alpha 2,N-E}$ is the critical value of Student’s $t$ distribution with $N-E$ degrees of freedom calculated at the confidence level $\alpha =0.05$. The real response $y$ of a confirmatory experiment is expected to lie within the interval $\widehat{y}-PI\le y\le \widehat{y}+PI$ with a confidence of 95%.

To assess the extent of process improvement that can be achieved when planning a different number of experiments, DoDE is adopted to design the alternative experimental campaigns A and B. Experimental campaign A is a complete campaign for process optimization and is used to assess the process improvement that can be achieved with an extended experimental campaign. A second-order with pairwise interaction RSM (as Equation 6) is fitted with data from 31 experiments planned by assigning the values of the dynamic subfactors through a D-optimal DoE (Supplementary Table S1). Among the 31 experiments, 28 are required to fit the RSM for the six dynamic subfactors, while the three remaining experiments are used to estimate the model’s lack-of-fit (Georgakis, 2013). Experimental campaign B is used to assess the process improvement that can be achieved through a small number of experiments. Data from nine experiments planned by assigning the values of the dynamic subfactors through a D-optimal DoE (Supplementary Table S2) are used to fit a first-order RSM:

$\widehat{y}={\beta }_0+\left[\begin{array}{ccc}{\beta }_1& {\beta }_2& \begin{array}{cc}\cdots & {\beta }_K\end{array}\end{array}\right]\mathbf{x}.(9)$

Among the nine experimental runs, seven are used to fit the RSM for the six dynamic subfactors while the two remaining experiments are used to estimate the model’s lack-of-fit (Georgakis, 2013).

2.1.2 Hybrid model

A serial hybrid semi-parametric model is used (Oliveira, 2004; Teixeira et al., 2005; von Stosch et al., 2014) to capture the behavior of mammalian cell cultures producing mAbs (Figure 4). This digital model combines a mechanistic model, which embeds the knowledge of the system, and an ANN, which accounts for the unknown dependencies in the system under study.

Figure 4

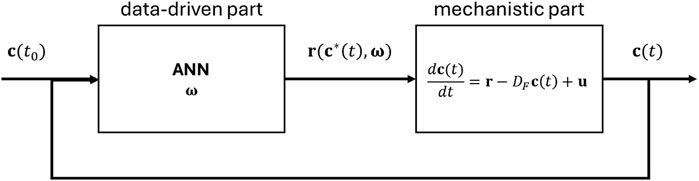
Figure 4. Schematic representation of the serial hybrid model structure, which comprises the culture material balances and the data-driven part (i.e., an artificial neural network—ANN), capturing the complex and unknown relationship between the concentrations and reaction rates.

The mechanistic knowledge of the cell culture is described by the concentration balances of the main culture variables (Equation 10), organized in the column vector $\mathbf{c}=\left[\begin{array}{ccc}{X}_v& c_{glc}& \begin{array}{ccc}{c}_{gln}& c_{lac}& \begin{array}{cc}{c}_{amm}& c_{mAb}\end{array}\end{array}\end{array}\right]$:

$\frac{\mathrm{d}\mathbf{c}\left(t\right)}{\text{d}t}=\mathbf{r}\left({\mathbf{c}}^{*}\left(t\right),\mathbf{\omega }\right)-D_F\mathbf{c}\left(\mathrm{t}\right)+\mathbf{u},(10)$

where $\mathbf{r}\left({\mathbf{c}}^{*}\left(t\right),\mathbf{\omega }\right)\left[V\times 1\right]=\left[6\times 1\right]$ is the vector of volumetric reaction rates for the $V$ culture variables, ${\mathbf{c}}^{*}=\left[\begin{array}{ccc}{X}_{\mathrm{v}}& c_{glc}& \begin{array}{ccc}{c}_{gln}& c_{lac}& c_{amm}\end{array}\end{array}\right]$ is the column vector of culture variables with the exclusion of the antibody titer, $\mathbf{\omega }$ is the vector of the ANN parameters (weights and biases), $D_F$ is the dilution factor, and $\mathbf{u}\left[6\times 1\right]$ is the vector of controlled inputs. The volumetric reaction rates can be expressed as a combination of the specific production/consumption rates and the viable cell concentration $X_{\mathrm{v}}$:

$\mathbf{r}\left({\mathbf{c}}^{*}\left(t\right),\mathbf{\omega }\right)=\mathbf{S}{X}_{\mathrm{v}}\mathbf{\mu }\left({\mathbf{c}}^{*}\left(t\right),\mathbf{\omega }\right),(11)$

where $\mathbf{S}$ is the stoichiometric matrix with −1 and 1 on the diagonal for consumed and produced components, respectively, and $\mathbf{\mu }\left({\mathbf{c}}^{*}\left(t\right),\mathbf{\omega }\right)\left[6\times 1\right]$ is the vector of the specific production/consumption rates. In Equation 11, we assume that the production/consumption rates do not depend on antibody titer because it is expected to have no impact on other culture variables (Narayanan et al., 2021). The stoichiometric matrix $\mathbf{S}$ embeds the mechanistic knowledge of the system, indicating whether a component is consumed or produced by the cells.

The relationship between specific production/consumption rates and culture variables, $\mathbf{\mu }=f\left({\mathbf{c}}^{*}\left(t\right)\right)$, is very complex, and accurate mechanistic expressions are not typically available. This lack of knowledge is compensated by a data-driven model which captures the relationship between specific production/consumption rates and culture variables learnt from experimental data. A single hidden-layer ANN with five neurons and a hyperbolic tangent activation function (Equation 12) is used to capture the nonlinear relationship between culture variables and volumetric production/consumption rates:

$\mathbf{\mu }\left({\mathbf{c}}^{*}\left(t\right),\mathbf{\omega }\right)={\mathbf{\mu }}_{\max }○{\mathbf{\omega }}^{\left(2,1\right)}\tanh \left({\mathbf{\omega }}^{\left(1,1\right)}{\mathbf{c}}^{*}\left(t\right)+{\mathbf{\omega }}^{\left(1,2\right)}\right)+{\mathbf{\omega }}^{\left(2,2\right)},(12)$

where ${\mathbf{\omega }}^{\left(1,1\right)}$ and ${\mathbf{\omega }}^{\left(2,1\right)}$ are the weights, ${\mathbf{\omega }}^{\left(1,2\right)}$ and ${\mathbf{\omega }}^{\left(2,2\right)}$ are the biases of the hidden and output layer, respectively, ${\mathbf{\mu }}_{\max }\left[6\times 1\right]$ is the vector of the maximum production/consumption rates, and $○$ represents the Hadamard product. The vector of maximum production/consumption rates, ${\mathbf{\mu }}_{\max }$, is used to scale the output of the ANN at different magnitudes (Teixeira et al., 2007) and is heuristically determined in preliminary tests. The number of hidden neurons was selected as that maximizing the Bayesian information criterion (Schwarz, 1978; von Stosch and Willis, 2017).

The hybrid model is trained with the nine experiments of experimental campaign B (Section 2.1.1.2) with a stepwise decreasing learning rate (from 0.005 to 0.0001). The model parameters $\mathbf{\omega }$ are estimated through the Adam optimization algorithm (Kingma and Ba, 2015). Additional detail on hybrid model training is reported in the Supplementary Material.

The hybrid model is used to perform an in silico experimental campaign. It receives as input both the initial viable cell concentration and the culture volume, which are required to simulate the entire experimental run. Feeding is simulated by adjusting the appropriate value of the controlled input vector $\mathbf{u}$. Like the process, feeding is performed once daily by adding 20 mL of fresh medium in 10 min if the nutrient concentration is found to be outside the control band (as performed in optimization strategy #2; Section 2.1.1).

2.1.3 Feeding optimization

The optimal profile for glucose and glutamine is determined as that which maximizes the antibody titer at harvest through an optimization problem. Since the shape of the nutrient profiles is defined by the value of the dynamic subfactors according to Equation 1, the optimization problem is formulated considering the DoDE dynamic subfactors $x_i$ as

$\underset{x_i}{\max }\widehat{y}\left(x_i\right)(13)$

subject to the constraints of Equations 2–4. These constraints on the subfactor values $x_i$ ensure that the optimization algorithm remains within the experimental space spanned in experimental campaigns A and B, thus limiting the extrapolation of the models that predict $\widehat{y}\left(x_i\right)$.

The antibody titer at harvest $\widehat{y}\left(x_i\right)$ is predicted either by the RSM in optimization strategy #2 or directly by the hybrid model in optimization strategy #1. The optimization problem of Equation 13 is solved through a genetic algorithm (Sivanandam and Deepa, 2008) with a starting population of 200 individuals.

All the simulations described in this work are performed in Matlab^® 2020b through the optimization toolbox and in-house developed routines.

2.2 Case study: simulated process for the production of monoclonal antibodies at 1-L shake flask scale

A simulated process for producing monoclonal antibodies at 1-L shake flask scale (Kontoravdi et al., 2010) is considered in this study; we will refer to it as “the process” for the reminder of the manuscript. It models the dynamic behavior of the viable cell density (VCD, $X_v$) and the concentration of the main nutrients and by-products such as glucose ($c_{glc}$), glutamine ($c_{gln}$), lactate ($c_{lac}$), and ammonia ($c_{amm}$). Additionally, RNA and light and heavy chain balances in the cytosol and Golgi apparatus are considered to simulate protein synthesis and model the dynamic behavior of antibody titer ($c_{mAb}$). Details of the model and the respective parameters can be found in Kontoravdi et al. (2010).

The total duration of a batch is set to $t_b=168$ hours, with an initial volume of 200 mL and inoculation cell density of $0.2\cdot {10}^6$ cell/mL (Kontoravdi et al., 2010). Measurement sampling is performed every 24 h through the withdrawal of 2.5 mL from the culture. Feed of glucose and/or glutamine is performed after the sampling by adding 20 mL of concentrated medium in 10 min—a bolus addition which does not cause a severe concentration change. Constant feeding volume is used to easily maintain the culture volume within specified ranges and without the addition of any constraint, simulated overflow, or control loop; however, the same result can be achieved using variable feeding volumes of media with constant concentration. To simplify the modeling of the cell culture system and the demonstration of the proposed approach, offline measurements of culture variables (i.e., glucose, glutamine, lactate) are assumed to be available immediately after sampling, and the measurement delay is not accounted for because the total batch duration ($t_b$) is much longer than the time required for analytical measurements. The concentration of glucose and glutamine is determined at any feeding addition in such a way as to reach the nutrient concentration profiles planned by DoDE. The model is integrated between each sampling time instant through a variable-step–variable-order solver, with a maximum order of 5. A 6% white noise added as measurement error.

3 Results

The results of optimization strategy #2 for experimental campaigns A and B followed by optimization strategy #1 are presented here. These results are then compared with the process optimum.

3.1 Nutrient profile optimization through full experimental campaign on the process

This section aims to identify the optimal nutrient profile that maximizes the antibody titer at harvest by performing an extended experimental campaign on the process through DoDE.

To this purpose, experimental campaign A with 31 experiments planned through DoDE is performed on the process. The values of the dynamic subfactors $x_1^{glc},x_2^{glc},x_3^{glc}$ and $x_1^{gln},x_2^{gln},x_3^{gln}$ for glucose and glutamine, respectively, and the antibody titer at harvest obtained by experimental campaign A are used to fit a second-order RSM. The values of the dynamic subfactors affect the DoDE nutrient profiles as explained in Section 2.1.1.

The RSM shows a very high coefficient of determination $R^2=0.999$ (with an adjusted coefficient of determination $R_{adj}^2=0.999$), indicating the that the model provides an optimal fitting of the data. Supplementary Figure S1A shows the RSM regression coefficient with their 95% confidence interval for all the dynamic subfactors $x_{i^{\prime }}^j$, their interactions $x_{i^{\prime }}^j{x}_{i^{″}}^j$, and second-order terms $x_{i^{\prime }}^j{x}_{i^{\prime }}^j$, where $i^{\prime }$ and $i^{″}$ are the factor number and $j=glc,gln$ is the nutrient. The terms showing high uncertainty (Equation 7)—those whose error bars in the figure cross 0 in Supplementary Figure S1—are considered not statistically significant for the model and are excluded from the updated RSM. The latter (Supplementary Figure S1B) shows optimal fitting of the data with $R^2=0.997$ ($R_{adj}^2=0.997$).

Recalling that the subfactors define the shape of the nutrient profile and, specifically, that $x_1$ defines the initial value, $x_2$ defines the increasing or decreasing tendency of the profile and $x_3$ defines the concavity of the profile. The glutamine profile has a large and strongly nonlinear effect on the antibody titer at harvest, since all glutamine first- and second-order terms are significant for the model. Specifically, $x_1^{gln}$ and $x_3^{gln}$ show negative parameter values, while $x_2^{gln}$ and all second-order terms show positive parameter values. Accordingly, antibody titer is expected to be higher when the glutamine profile has a small initial value and shows an increasing tendency with a downward (negative) concavity. However, the initial glutamine value and shape of the profile are not independent and must be carefully tuned, since the effects of the interaction terms $x_1^{gln}{x}_2^{gln}$ and $x_1^{gln}{x}_3^{gln}$ are significant for the model. The negative effect of the interaction $x_1^{gln}{x}_2^{gln}$ means that the low initial value of the glutamine should be associated with a profile with an increasing tendency to induce an increased antibody titer at harvest, while the positive effect of the interaction $x_1^{gln}{x}_3^{gln}$ means that the low initial value of the glutamine should be associated with a negative (downward) concavity to increase the antibody titer. The glucose profile, instead, has a limited influence on the antibody concentration at harvest. In fact, the effects of all first- and second-order glucose terms are negligible and are not included in the updated RSM (Supplementary Figure S1B). Furthermore, the profile of the two nutrients does not present any interaction, with all interaction terms $x_{i^{\prime }}^{glc}{x}_{i^{″}}^{gln}$ non-significant.

According to these results, the antibody titer will not change much in response to different glucose profiles when set within the factor ranges. Instead, the glutamine profile is extremely important for achieving high antibody titer and must be carefully optimized.

The RSM is then used for process optimization through a genetic algorithm (Section 2.1.1.2) to determine the nutrient profile that provides the highest possible antibody titer at harvest. The optimal nutrient profiles (black line) and the confirmatory experiment at the optimal conditions executed on the process (red points—process measurements) are shown in Figure 5. There, the continuous measurement (blue line) of the nutrient profile is also reported. Considering that, at shake flask scale, this profile is typically not available, in this case it is because the process is simulated. In general: i) the optimal glucose profile (Figure 5A) starts at around half (33.6 mM) of the range of possible values and follows a decreasing profile with a very small downward concavity; ii) the optimal glutamine profile (Figure 5B) starts at the minimum value (2 mM) of its possible range and follows an almost constant profile for the entire culture. The optimal values of the glucose and glutamine subfactors are ${\mathbf{x}}_{\mathrm{A}}^{\text{opt}}=\left[\begin{array}{ccc}-0.439& -0.385& \begin{array}{ccc}-0.04& -0.999& \begin{array}{cc}-0.0006& -0.0002\end{array}\end{array}\end{array}\right]$. As expected, the continuous measured profiles of glucose and glutamine (blue lines) cannot perfectly adhere to the respective optimal profiles because nutrients are continuously consumed by cells, while nutrients are fed in boluses once daily. Since the nutrients are fed only when the measured value (the red dot) falls below the control band (black dashed line), a sawtooth time profile of the variables is found. This behavior is common to all experimental runs, which show natural experimental variability. Furthermore, the lack of feeding in the final part of the batch does not produce negative effects on antibody titer because in this phase the viable cell concentration decreases and the available glucose, which is usually high, is sufficient to avoid cell starvation.

Figure 5

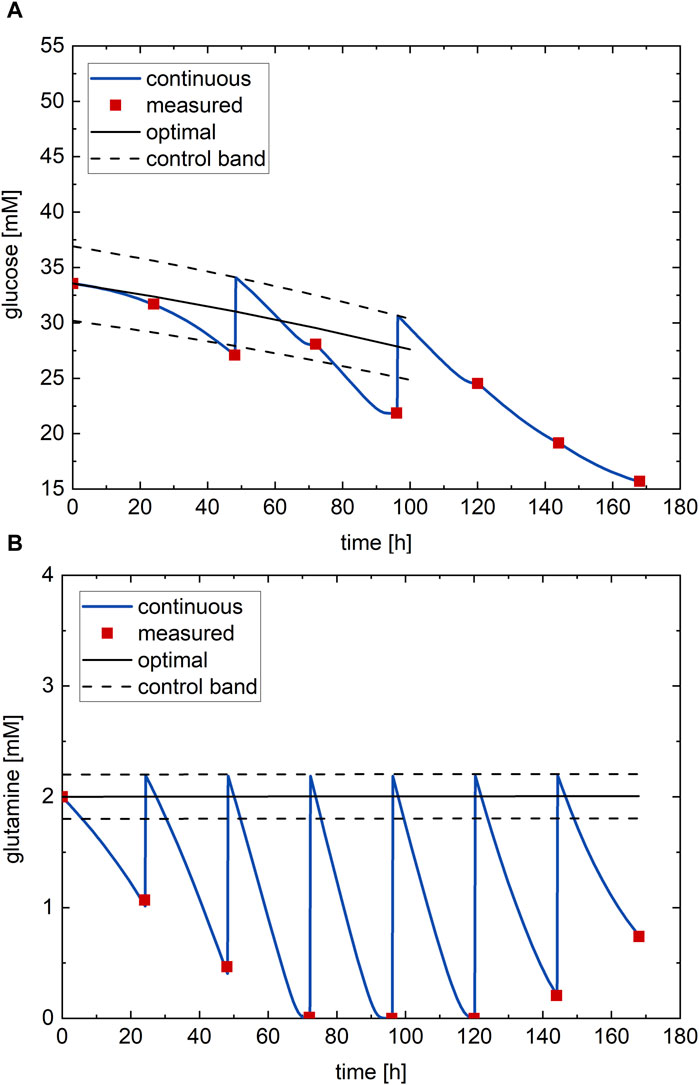
Figure 5. Optimal nutrient profile, determined from DoDE experimental campaign A with 31 experiments, performed on the process: (A) glucose and (B) glutamine. Red dots—process measurements; black line—optimal nutrient profile; black dashed line—control band; blue line–continuous measurement.

The optimal antibody titer at harvest predicted by the RSM with the optimal nutrient profiles is ${\widehat{y}}_{\mathrm{A}}=3530.0\pm 54.6$ mg/L, while the confirmatory experiment at the optimal conditions executed on the process results in an antibody titer at harvest of $y_{\mathrm{A}}=3118.2$ mg/L. The experimental antibody titer is outside the prediction interval (Equation 8), and the RSM in this case is affected by an error of 13.2%. Accordingly, the RSM from an extended experimental campaign on the process has limited predictive accuracy, despite effectively describing the calibration data ($R^2=0.997$). This is due to the highly nonlinear nature of the relationship between the subfactor values (i.e., the shape of the nutrient profiles) and the product titer at harvest, which cannot be properly captured by the second-order model.

3.2 Nutrient profile optimization through reduced experimental campaign on the process

This section aims to identify the optimal nutrient profile that maximizes the antibody titer at harvest using a limited set of experiments planned through the DoDE. This is intended to describe how the optimal nutrient profiles identified through DoDE change when the number of performed experimental runs is low.

Therefore, experimental campaign B with nine experiments planned through the DoDE is used. The values of the dynamic subfactors $x_1^{glc},x_2^{glc},x_3^{glc}$ and $x_1^{gln},x_2^{gln},x_3^{gln}$ for glucose and glutamine, respectively, and the antibody titer at harvest are then used to fit a first-order RSM (Equation 9).

The RSM fitted onto the process data shows a coefficient of determination of $R^2=0.999$ ($R_{adj}^2=0.998$), indicating that calibration data are well captured by the model. Similarly, the updated RSM describes the calibration data very well, with $R^2=0.996$ ($R_{adj}^2=0.994$). The model coefficients are similar to the linear terms shown in Supplementary Figure S1A, and hence they are not shown for brevity. In this case, the initial glucose value results have a small positive impact, indicating that only the initial glucose concentration slightly influences antibody titer, while the shape of the profile has no significant effect. Glutamine instead shows a strong effect, having negative $x_1^{gln}$ and $x_3^{gln}$ and positive $x_2^{gln}$. Accordingly, as previously observed, the antibody titer increases with the glutamine profile, having a low initial value and an increasing profile with downward (negative) concavity.

The RSM is then used for process optimization to determine the nutrient profile that achieves the highest possible antibody titer at harvest by means of a genetic algorithm.

The resulting optimal nutrient profiles (black lines) and the confirmatory experiment executed on the process (red points–process measurements) are shown in Figure 6 with the continuous measurement (blue lines). The optimal glucose profile (Figure 6A) starts at around half its possible range and follows a linearly increasing profile with almost no concavity. The optimal glutamine profile (Figure 6B) instead shows a constant profile along the culture at the minimum value of its possible range. The optimal values of the glucose and glutamine subfactors are ${\mathbf{x}}_{\mathrm{B}}^{\text{opt}}=\left[\begin{array}{ccc}0.476& 0.433& \begin{array}{ccc}-0.002& -0.978& \begin{array}{cc}0.015& 0.002\end{array}\end{array}\end{array}\right]$.

Figure 6

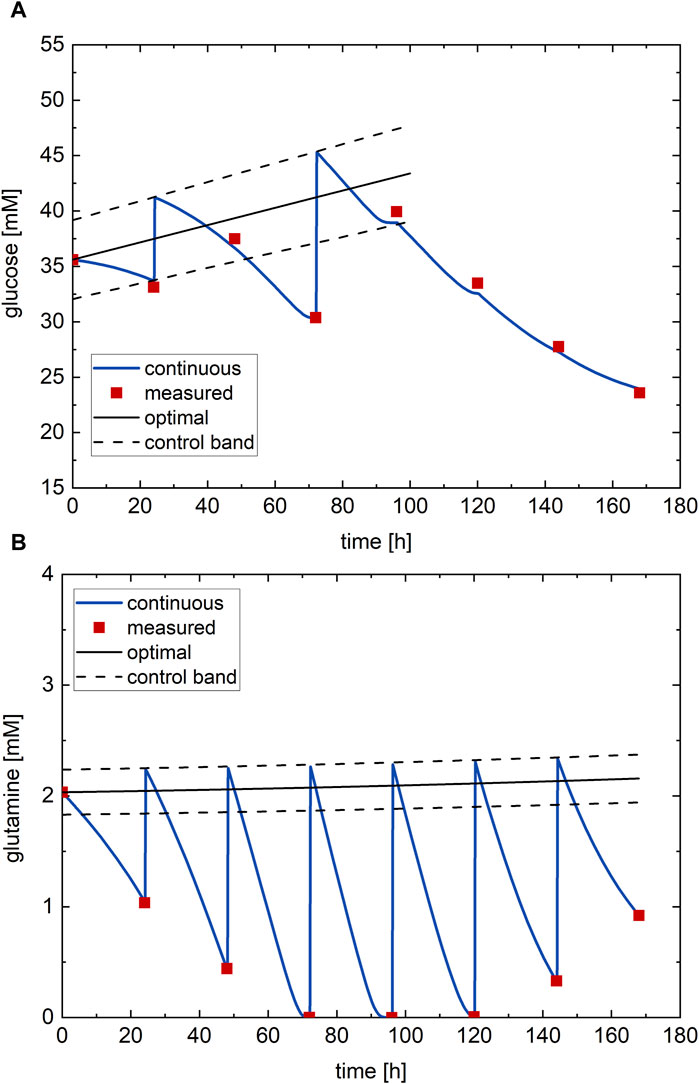
Figure 6. Optimal nutrient profile, determined from DoDE experimental campaign B with nine experiments, tested on the process: (A) glucose and (B) glutamine. Red dots—process measurements; black line—optimal nutrient profile; black dashed line—control band; blue line–continuous measurement.

The RSM predicts with the optimal nutrient profiles an antibody titer at harvest of ${\widehat{y}}_{\mathrm{B}}=3021.8\pm 112.6$ mg/L, which is lower that the value predicted by the second-order RSM built in experimental campaign A in 31 experiments. The confirmatory experiment with the optimal feeding strategy executed on the process shows an antibody titer at harvest of $y_{\mathrm{B}}=3136.3$ mg/L. The experimental antibody is slightly outside the prediction interval, and the RSM shows an error of 3.8%. In this case, the error between predicted and experimental value is lower than in the case of the second-order RSM (Section 3.1) built on a large number of experiments, indicating that the second-order model slightly overfits the calibration data, providing worse prediction than the first-order, demonstrating better generalization capability. Despite the better prediction performance, the predicted value is still outside the prediction intervals, probably due to the highly nonlinear relationship between nutrient profiles and antibody titer, which cannot be captured by a first-order model.

3.3 Nutrient profile optimization through an in silico experimental campaign on the hybrid model

This section shows the optimization of the nutrient profiles by performing an in silico experimental campaign through a hybrid model. This will serve as proof of concept to understand the applicability and advantage of conducting virtual experimental campaigns for optimizing cell culture quality attributes through hybrid models.

Consequently, a hybrid model (Section 2.1.2) is trained on the data collected during experimental campaign B planned through the DoDE (Section 3.2), comprising nine experiments. The hybrid model is exploited to perform an in silico experimental campaign, where a genetic algorithm guides the experiments by suggesting the values of the dynamic subfactors defining the nutrient profiles.

The optimal nutrient profiles (black lines), those simulated though the hybrid model (green dashed lines), and the profiles at the optimal conditions executed on the process (blue lines) are shown in Figure 7. The initial value of the optimal glucose profile (Figure 7A) is close to the upper bound of the glucose range (47.7 mM) and follows a monotonically decreasing profile with slight downward concavity, while the initial value of the optimal glutamine profile (Figure 7B) starts at the lower bound of its span range and follows an increasing profile with a small slope and almost no concavity. The optimal values of the glucose and glutamine subfactors are ${\mathbf{x}}_{\text{HM}}^{\text{opt}}=\left[\begin{array}{ccc}0.146& -0.772& \begin{array}{ccc}-0.074& -0.880& \begin{array}{cc}0.118& 0.001\end{array}\end{array}\end{array}\right]$. The glucose predicted by the hybrid model (Figure 7A, green dashed line) matches the simulated process profile before the first feeding action; it overestimates the process profile in the final part of the batch. This suggests that the addition of the glucose bolo drives the culture state to a region only partially explored by the training samples, resulting in the underestimation of the glucose consumption rate and a reduction in the prediction performance. Instead, the overall glutamine profile (Figure 7B) is better predicted throughout the entire culture, although showing a slight underestimation of the glutamine consumption.

Figure 7

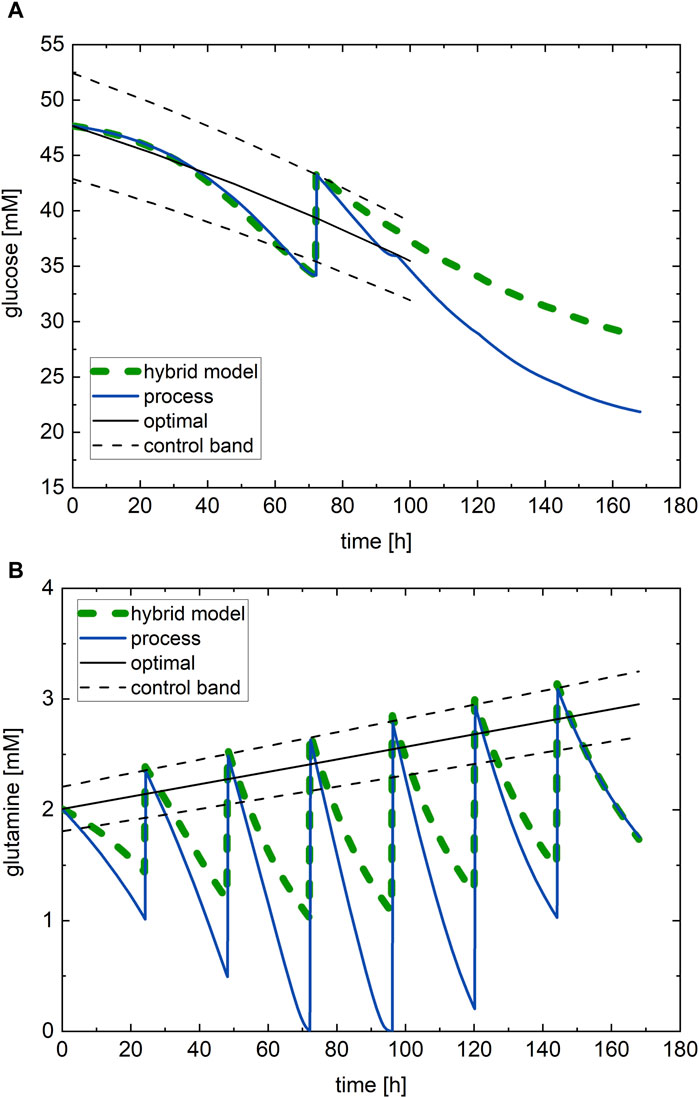
Figure 7. Optimal nutrient profile, determined from the in silico experimental campaign through the hybrid model trained on the nine experiments of experimental campaign B: (A) glucose and (B) glutamine. Green dashed line—hybrid model simulation; black line—optimal nutrient profile; black dashed line—control band; blue line—process continuous measurement.

The hybrid model predicts with the optimal nutrient profiles an antibody titer at harvest of ${\widehat{y}}_1=2624.6$ mg/L, while the confirmatory experimental run at the optimal conditions performed on the process provided an antibody titer at harvest of $y_1=3222.8$ mg/L. Accordingly, the hybrid model underpredicts the antibody titer by 18.6%, confirming that the hybrid model does not accurately predict the correct numerical value of the antibody titer. The high error of hybrid model prediction is due to the low extrapolation capabilities of the hybrid models, which cannot accurately predict values far from those observed in the training data. Despite this large error, the antibody titer predicted by the hybrid model is much higher than those observed in the training data (experimental campaign B), indicating that the model correctly captures the relationship between nutrients and antibody titer and identifies the region of experimental domain with the highest antibody titer.

3.4 Optimal nutrient profile

This section presents the real optimum of the process to understand how well the investigated methodologies can identify the optimal feeding schedule for the cell cultures. The optimum of the process is known because a simulated process is considered; this information would not be available in a real scenario. The genetic algorithm presented in Section 2.1.3 is applied to the process to determine the optimal feeding conditions.

The optimal values of the glucose and glutamine subfactors are ${\mathbf{x}}_{\mathrm{P}}^{\text{opt}}=\left[\begin{array}{ccc}0.078& 0.405& \begin{array}{ccc}-0.174& -0.882& \begin{array}{cc}0.074& -0.042\end{array}\end{array}\end{array}\right]$. The optimal nutrient profiles of the process are shown in Figure 8 (black lines–target profile; blue line–continuous process measurement; red dots–measurements). The initial value of the glucose profile is in the middle of its possible range and monotonically grows with an upward concavity (Figure 8A). The initial value of the glutamine profile (Figure 8B) is at the lower bound of its range and it follows a slightly increasing profile with a small downward concavity.

Figure 8

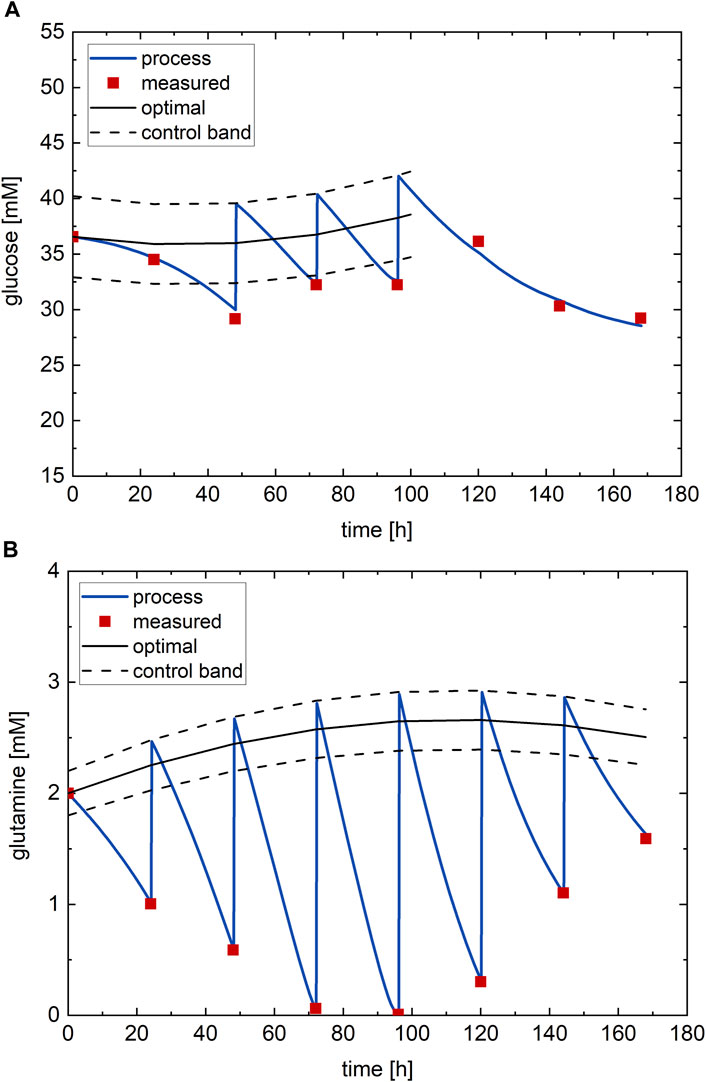
Figure 8. Optimal nutrient profile of the process: (A) glucose and (B) glutamine. Blue line—continuous process measurement; red dots—process measurements; black line—optimal profile; black dashed line—control band.

The optimal nutrient profiles allow the process to achieve an antibody titer $y_{\mathrm{P}}=3228.8$ mg/L.

4 Discussion

This section compares the optimal feeding schedule of the process with those obtained through optimization strategies #1 and #2. At its end, the antibody titer in the confirmatory experiment at the optimal conditions is used to identify the best optimization strategy.

4.1 Optimal feeding schedule

The optimal feeding schedule of the process (Section 3.4) is characterized by an initial glucose concentration at approximately the average value in the range of possible concentrations, which allows sustained cell growth in the initial part of the culture, and an increasing profile, which maintains high cell growth even at high viable cell concentration. The low initial glutamine concentration provides enough nutrient for sustained growth and at the same time determines reduced ammonia formation, which is detrimental because it limits cell growth and favors cell death. Furthermore, the downward concavity of the glutamine profile is coherent with the necessity of providing more glutamine when the viable cell concentration is higher (i.e., in the central part of the culture) while also limiting ammonia formation. These results are coherent with previous studies (Teixeira et al., 2005), which recommended limiting the availability of glutamine in the initial growth phase and increasing it later in the culture. Unlike here, previous studies have recommended a low concentration of glucose along the entire culture, possibly decreasing it later in the culture (Teixeira et al., 2007). Even if low glucose concentration is reasonable for limiting lactate production, feeding enough glucose (as in our case) is of paramount importance for avoiding cell starvation, which negatively affects cell growth, productivity, and product quality (Narayanan et al., 2020; Sen et al., 2015).

4.2 Comparison among optimal feeding schedules

In optimization strategy #2 (experimental campaign planned through DoDE), the optimal low level of glutamine throughout the entire duration of the culture is identified in both experimental campaigns A and B. However, the increased amount required in the central part of the culture to compensate for the increased viable cell concentration is not identified in both approaches (that is, experimental campaign A, with 31 experiments, and B, with nine experiments). Regarding glucose, a profile similar to the process optimum is identified only in experimental campaign B (with nine experiments). However, in experimental campaign A, the identified glucose profile with high initial concentration and a decreasing profile leads to a more sustained production of lactate, especially in the initial part of the culture.

In optimization strategy #1 (in silico experimental campaign), correct behavior of the glutamine concentration, which starts at a low level and increases along the culture, is identified. The optimal glucose profile instead has a high initial concentration and decreases along the culture, showing some similarity with experimental campaign A of optimization strategy #2.

These differences in the optimal glucose profiles are due to the small influence that glucose has on the antibody titer in the process. In fact, if glucose is not limited, the growth rate (which also determines the productivity) is only controlled by the glutamine level and by the ammonia produced, leading to a reduced effect of glucose on antibody productivity. For this reason, both modeling strategies effectively capture the glucose behavior. In particular, the second-order RSM is not affected by glucose and does not capture the relationship between glucose, lactate, and a lower cell growth, while the hybrid model underestimates the impact that lactate has on cell growth. This leads both modeling strategies to suggest high levels of glucose at the beginning of the culture.

The predicted antibody titer by the two optimization strategies is compared to that achieved in the process (Section 3.4), with results summarized in Table 1.

Table 1

Table 1. Optimal nutrient profiles obtained with different strategies: subfactor value, simulated experimental antibody titer, predicted antibody titer, and 95% confidence interval of the predicted antibody titer.

DoDE is thus demonstrated to be applicable in mammalian cell cultures to optimize the feeding schedule, providing a simple and robust science-based strategy to improve antibody yield. In fact, in optimization strategy #2, experimental campaigns A (3,118.2 mg/L) and B (3,136.3 mg/L) both achieved an improved yield of antibodies in the confirmatory experiments at the optimal conditions. In particular, experimental campaign B achieved with only nine experiments a higher yield than experimental campaign A with 31 experiments. However, optimization strategy #2 achieved antibody titer consistently lower than the real process optimum $y_P$ (3,228.8 mg/L). Despite the high yield achieved, the predictions of the antibody titer performed by the two RSMs of optimization strategy #2 are inaccurate. The second-order RSM fitted on the 31 experiments from experimental campaign A shows a 13.2% prediction error, which is much greater than the 3.8% error shown by the first-order RSM trained on the nine experiments of campaign B. These results suggest that the RSM does not completely capture the complex relationship between nutrients and product titer independently of model complexity. Furthermore, the performance of the first-order RSM of experimental campaign B, which is better than that of experimental campaign A, indicates that a large number of samples is not beneficial for optimization when the selected modeling strategy cannot handle the complexity of the relationship under study. For this reason, the planning of a large number of experimental runs must be coupled with a model of adequate complexity. Hence, the generalizability of the developed models should be carefully tested though validation experiments in order to avoid overfitting.

Hybrid semi-parametric models are promising tools which allow performing of in silico experimental campaigns since they provide a very good representation of the system even when built on a reduced number of runs. In fact, the confirmatory experiment with the optimal feeding schedule identified by optimization strategy #1 achieved a very high antibody titer (3,222.8 mg/L), with results very close to the real process optimum $y_P$ (3,228.8 mg/L). Optimization strategy #1 improved the antibody titer by 34.9% with respect to the training data and provided a 2.8% increase in antibody titer with respect to the optimal antibody obtained through experimental campaign B of optimization strategy #2 (3,222.8 mg/L vs. 3,136.3 mg/L). However, the antibody titer $y_1$ predicted in optimization strategy #1 (2,624.6 mg/L) is the lowest predicted value, showing the largest prediction error (18.6%). Despite that, the hybrid model captures a relationship between subfactors and antibody titer which is closer to the real one than the RSM. This can be observed in Figure 9, where the values of the optimal subfactors are reported. Concerning glutamine—the most important factor—the hybrid model identifies profile initial value ($x_1^{gln}$) and slope ($x_2^{gln}$), which are closer to the process optimum than the RSM, while similar values of the concavity ($x_3^{gln}$) are identified by both hybrid model and RSM on experimental campaign B. Concerning glucose, the hybrid model identifies profile initial value ($x_1^{glc}$) and concavity ($x_3^{glc}$), which are more similar to the process optimum than the RSM; the slope of glucose profile ($x_2^{glc}$) is accurately captured only by the RSM. However, the difference in the slope of the glucose profile is only partially significant because all glucose profiles, provided that they do not cause cell starvation, have a similar effect on antibody titer due to the low influence of glucose in the range selected for this study. The identification of subfactor values similar to the process optimum, especially for the subfactors with the largest influence on the response (i.e., glutamine), indicates that the hybrid model describes the correct functional relationship between nutrient profiles and antibody titer, thus successfully identifying the experiment region with the highest antibody titer. However, since training data does not explore regions with very high antibody titer values, the hybrid model is not able to correctly extrapolate an accurate value of antibody titer, leading to biased predictions. This result indicates that hybrid models are promising methods for capturing complex relationships thanks to their underlying mechanistic knowledge. However, predicted numerical values are not always accurate, especially when extrapolating; this is a well-known drawback of data-driven models. Prediction accuracy can be improved by introducing new experimental runs into the hybrid model training data close to the optimal region. In fact, adding only one experiment in the optimal region to hybrid model training data leads to a lower error in predicting the optimal antibody titer (8.7%).

Figure 9

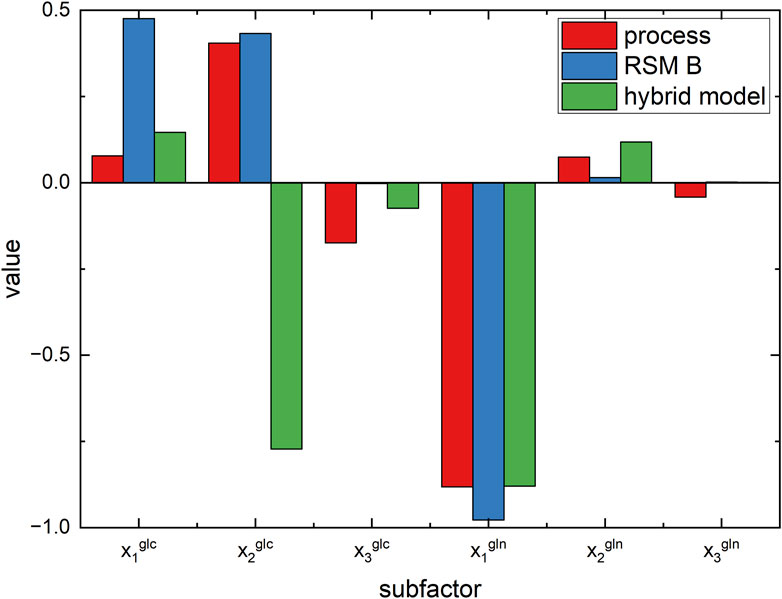
Figure 9. Comparison of values of the optimal subfactors for process, RSM of experimental campaign B, and hybrid model.

It is extremely important to point out that in optimization strategy #1, an antibody titer so close to the real optimal value is identified by only nine experiments (i.e., used to train the hybrid model) on the process. Accordingly, the hybrid model correctly learns and generalizes the relationship between nutrients and antibody titer and captures the cross-correlation between them, even if it is trained from a limited number of experiments. This is somehow expected because hybrid models combine the knowledge of the biological phenomena involved in cell cultures with the capability of learning the complex relationships of data-driven models.

It is also notable that the selected hybrid model structure is the best in terms of the number of samples required for training and extrapolation with a different feeding schedule (Narayanan et al., 2021). In fact, the improvement of the model structure by introducing additional mechanistic knowledge improves the description of the system but requires a larger number of training samples to achieve comparable prediction performance. Accordingly, a trade-off is required between model effectiveness and complexity (which requires a higher number of training samples).

5 Conclusion

This study has compared different strategies of experimentation to optimize the feeding schedule of a mammalian cell culture. In particular, in silico experimentation was compared with an experimental campaign on the process to assess if in silico experimentation can accelerate process development and reduce experimental burden. To conduct in silico experiments, we used a combination of design of dynamics experiments (DoDE) and a hybrid semi-parametric model to virtually identify the optimal shape of glucose and glutamine profile. The optimal nutrient profiles were compared with those obtained through two experimental campaigns planned with DoDE: an extended campaign with 31 experiments (experimental campaign A) and a more parsimonious campaign with nine experiments (experimental campaign B).

Experimental campaign B reached an improved antibody titer of 3,136.3 mg/L, while experimental campaign A provided a smaller antibody titer than experimental campaign B had achieved with nine experiments. Despite being able to improve the antibody titer, the experimental campaigns planned with DoDE could not achieve titer values similar to the real process optimum.

The in silico campaign, which required only nine experimental runs to train the hybrid digital model, provided a 34.9% overall improvement in the antibody titer with respect to training data and a 2.8% improvement with respect to experimental campaigns A and B, reaching a titer very close to the process optimum. The hybrid model accurately captures the relationship between nutrient profiles and antibody titer but underpredicts the numerical value of the antibody titer. Accordingly, hybrid semi-parametric models are promising tools and can be used to conduct in silico experimental campaigns, providing very high performance and reducing the experimental burden and time required to perform feeding schedule optimization in the real world.

A simulated process to produce monoclonal antibodies at 1-L shake flask scale was considered as a case study. In future research, the proposed framework will be checked on a real process to confirm our findings. Furthermore, a thorough comparison of the proposed framework with dynamic optimization methods will be conducted in future studies.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

GB: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Supervision, Visualization, Writing–original draft, Writing–review and editing. CG: Data curation, Formal Analysis, Software, Writing–review and editing. PF: Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Writing–original draft, Writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. Open Access funding was provided by University of Padova, Open Science Committee.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2024.1456402/full#supplementary-material

References

Abt, V., Barz, T., Cruz-Bournazou, M. N., Herwig, C., Kroll, P., Möller, J., et al. (2018). Model-based tools for optimal experiments in bioprocess engineering. Curr. Opin. Chem. Eng. 22, 244–252. doi:10.1016/j.coche.2018.11.007

CrossRef Full Text | Google Scholar

Banga, J. R., Balsa-Canto, E., Moles, C. G., and Alonso, A. A. (2005). Dynamic optimization of bioprocesses: efficient and robust numerical strategies. J. Biotechnol. 117, 407–419. doi:10.1016/j.jbiotec.2005.02.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Barberi, G., Benedetti, A., Diaz-Fernandez, P., Sévin, D. C., Vappiani, J., Finka, G., et al. (2022). Integrating metabolome dynamics and process data to guide cell line selection in biopharmaceutical process development. Metab. Eng. 72, 353–364. doi:10.1016/j.ymben.2022.03.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Bayer, B., Diaz, R. D., Melcher, M., Striedner, G., and Duerkop, M. (2021). Digital twin application for model-based doe to rapidly identify ideal process conditions for space-time yield optimization. Processes 9, 1109. doi:10.3390/pr9071109

CrossRef Full Text | Google Scholar

Bayer, B., Striedner, G., and Duerkop, M. (2020). Hybrid modeling and intensified DoE: an approach to accelerate upstream process characterization. Biotechnol. J. 15, 2000121. doi:10.1002/biot.202000121

PubMed Abstract | CrossRef Full Text | Google Scholar

Castelli, M. S., McGonigle, P., and Hornby, P. J. (2019). The pharmacology and therapeutic applications of monoclonal antibodies. Pharmacol. Res and Perspec 7, e00535. doi:10.1002/prp2.535

PubMed Abstract | CrossRef Full Text | Google Scholar

de Aguiar, P. F., Bourguignon, B., Khots, M. S., Massart, D. L., and Phan-Than-Luu, R. (1995). D-optimal designs. Chemom. Intelligent Laboratory Syst. 30, 199–210. doi:10.1016/0169-7439(94)00076-X

CrossRef Full Text | Google Scholar

Epifa, (2021). The pharmaceutical industry in figures: key data 2021.

Google Scholar

Facco, P., Zomer, S., Rowland-jones, R. C., Marsh, D., Diaz-fernandez, P., Finka, G., et al. (2020). Using data analytics to accelerate biopharmaceutical process scale-up. Biochem. Eng. J. 164, 107791. doi:10.1016/j.bej.2020.107791

CrossRef Full Text | Google Scholar

Farid, S. S., Baron, M., Stamatis, C., Nie, W., and Coffman, J. (2020). Benchmarking biopharmaceutical process development and manufacturing cost contributions to R&D. mAbs 12, 1754999. doi:10.1080/19420862.2020.1754999

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferreira, A. R., Dias, J. M. L., Von Stosch, M., Clemente, J., Cunha, A. E., and Oliveira, R. (2014). Fast development of Pichia pastoris GS115 Mut+ cultures employing batch-to-batch control and hybrid semi-parametric modeling. Bioprocess Biosyst. Eng. 37, 629–639. doi:10.1007/s00449-013-1029-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Galvanin, F., Ballan, C. C., Barolo, M., and Bezzo, F. (2013). A general model-based design of experiments approach to achieve practical identifiability of pharmacokinetic and pharmacodynamic models. J. Pharmacokinet. Pharmacodyn. 40, 451–467. doi:10.1007/s10928-013-9321-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Georgakis, C. (2013). Design of dynamic experiments: a data-driven methodology for the optimization of time-varying processes. Industrial Eng. Chem. Res. 52, 12369–12382. doi:10.1021/ie3035114

CrossRef Full Text | Google Scholar

Gronemeyer, P., Ditz, R., and Strube, J. (2014). Trends in upstream and downstream process development for antibody manufacturing. Bioeng. (Basel). 1, 188–212. doi:10.3390/bioengineering1040188

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Y., Gilmour, S. G., Mylona, K., and Goos, P. (2020). Optimal design of experiments for hybrid nonlinear models, with applications to extended michaelis–menten kinetics. JABES 25, 601–616. doi:10.1007/s13253-020-00405-3

CrossRef Full Text | Google Scholar

Kaysfeld, M. W., Kumar, D., Nielsen, M. K., and Jørgensen, J. B. (2023). Dynamic optimization for monoclonal antibody production. IFAC-PapersOnLine 56, 6229–6234. doi:10.1016/j.ifacol.2023.10.747

CrossRef Full Text | Google Scholar

Kim, S. H., and Lee, G. M. (2009). Development of serum-free medium supplemented with hydrolysates for the production of therapeutic antibodies in CHO cell cultures using design of experiments. Appl. Microbiol. Biotechnol. 83, 639–648. doi:10.1007/s00253-009-1903-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. L. (2015). ADAM: a method for stochastic optimization. arXiv. doi:10.48550/arXiv.1412.6980

CrossRef Full Text | Google Scholar

Klebanov, N., and Georgakis, C. (2016). Dynamic response surface models: a data-driven approach for the analysis of time-varying process outputs. Industrial Eng. Chem. Res. 55, 4022–4034. doi:10.1021/acs.iecr.5b03572

CrossRef Full Text | Google Scholar

Kontoravdi, C., Pistikopoulos, E. N., and Mantalaris, A. (2010). Systematic development of predictive mathematical models for animal cell cultures. Comput. Chem. Eng. 34, 1192–1198. doi:10.1016/j.compchemeng.2010.03.012

CrossRef Full Text | Google Scholar

Li, F., Vijayasankaran, N., Shen, A., Kiss, R., and Amanullah, A. (2010). Cell culture processes for monoclonal antibody production. mAbs 2, 466–479. doi:10.4161/mabs.2.5.12720

PubMed Abstract | CrossRef Full Text | Google Scholar

Ling, W. L. W., Bai, Y., Cheng, C., Padawer, I., and Wu, C. (2015). Development and manufacturability assessment of chemically-defined medium for the production of protein therapeutics in CHO cells. Biotechnol. Prog. 31, 1163–1171. doi:10.1002/btpr.2108

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, Y., Stanton, D. A., Sharp, R. C., Parrillo, A. J., Morgan, K. T., Ritz, D. B., et al. (2023). Efficient optimization of time-varying inputs in a fed-batch cell culture process using design of dynamic experiments. Biotechnol. Prog. 39, e3380. doi:10.1002/btpr.3380

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahanty, B. (2023). Hybrid modeling in bioprocess dynamics: structural variabilities, implementation strategies, and practical challenges. Biotech and Bioeng. 120, 2072–2091. doi:10.1002/bit.28503

CrossRef Full Text | Google Scholar

Montgomery, D. C. (2007). Design and analysis of experiments. Fifth Ed. New York (USA): John Wiley and Sons, Inc.

Google Scholar

Mora, A., Nabiswa, B., Duan, Y., Zhang, S., Carson, G., and Yoon, S. (2019). Early integration of Design of Experiment (DOE) and multivariate statistics identifies feeding regimens suitable for CHO cell line development and screening. Cytotechnology 71, 1137–1153. doi:10.1007/s10616-019-00350-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Narayanan, H., Behle, L., Luna, M. F., Sokolov, M., Guillén-Gosálbez, G., Morbidelli, M., et al. (2020). Hybrid-EKF: hybrid model coupled with extended Kalman filter for real-time monitoring and control of mammalian cell culture. Biotechnol. Bioeng. 117, 2703–2714. doi:10.1002/bit.27437

PubMed Abstract | CrossRef Full Text | Google Scholar

Narayanan, H., Luna, M., Sokolov, M., Arosio, P., Butté, A., and Morbidelli, M. (2021). Hybrid models based on machine learning and an increasing degree of process knowledge: application to capture chromatographic step. Industrial and Eng. Chem. Res. 60, 10466–10478. doi:10.1021/acs.iecr.1c01317

CrossRef Full Text | Google Scholar

Narayanan, H., Sokolov, M., Morbidelli, M., and Butté, A. (2019). A new generation of predictive models: the added value of hybrid models for manufacturing processes of therapeutic proteins. Biotechnol. Bioeng. 116, 2540–2549. doi:10.1002/bit.27097

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Flaherty, R., Bergin, A., Flampouri, E., Mota, L. M., Obaidi, I., Quigley, A., et al. (2020). Mammalian cell culture for production of recombinant proteins: a review of the critical steps in their biomanufacturing. Biotechnol. Adv. 43, 107552. doi:10.1016/j.biotechadv.2020.107552

PubMed Abstract | CrossRef Full Text | Google Scholar

Oliveira, R. (2004). Combining first principles modelling and artificial neural networks: a general framework. Comput. Chem. Eng. 28, 755–766. doi:10.1016/j.compchemeng.2004.02.014

CrossRef Full Text | Google Scholar

Rodrigues, D., and Bonvin, D. (2020). On reducing the number of decision variables for dynamic optimization. Optim. Control Appl. Methods 41, 292–311. doi:10.1002/oca.2543

CrossRef Full Text | Google Scholar

Sansana, J., Joswiak, M. N., Castillo, I., Wang, Z., Rendall, R., Chiang, L. H., et al. (2021). Recent trends on hybrid modeling for Industry 4.0. Comput. Chem. Eng. 151, 107365. doi:10.1016/j.compchemeng.2021.107365

CrossRef Full Text | Google Scholar

Schwarz, G. (1978). Estimating the dimension of a model. Ann. Statistics 6, 461–464. doi:10.1214/aos/1176344136

CrossRef Full Text | Google Scholar

Sen, J. W., Fan, Y., Jimenez, I., Val, D., Mu, C., Rasmussen, S. K., et al. (2015) Amino acid and glucose metabolism in fed-batch CHO cell culture affects antibody production and glycosylation, 112, 521–535. doi:10.1002/bit.25450

CrossRef Full Text | Google Scholar

Sivanandam, S. N., and Deepa, S. N. (2008). Introduction to genetic algorithms. Springer Berlin Heidelberg.

Google Scholar

Teixeira, A., Cunha, A. E., Clemente, J. J., Moreira, J. L., Cruz, H. J., Alves, P. M., et al. (2005). Modelling and optimization of a recombinant BHK-21 cultivation process using hybrid grey-box systems. J. Biotechnol. 118, 290–303. doi:10.1016/j.jbiotec.2005.04.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Teixeira, A. P., Alves, C., Alves, P. M., Carrondo, M. J. T., and Oliveira, R. (2007). Hybrid elementary flux analysis/nonparametric modeling: application for bioprocess control. BMC Bioinforma. 8, 30–15. doi:10.1186/1471-2105-8-30

PubMed Abstract | CrossRef Full Text | Google Scholar

Teixeira, A. P., Clemente, J. J., Cunha, A. E., Carrondo, M. J. T., and Oliveira, R. (2006). Bioprocess iterative batch-to-batch optimization based on hybrid parametric/nonparametric models. Biotechnol. Prog. 22, 247–258. doi:10.1021/bp0502328

PubMed Abstract | CrossRef Full Text | Google Scholar

Tripathi, N. K., and Shrivastava, A. (2019). Recent developments in bioprocessing of recombinant proteins: expression hosts and process development, Front. Bioeng. Biotechnol. 7. 420. doi:10.3389/fbioe.2019.00420

PubMed Abstract | CrossRef Full Text | Google Scholar

von Stosch, M., Hamelink, J. M., and Oliveira, R. (2016). Hybrid modeling as a QbD/PAT tool in process development: an industrial E. coli case study. Bioprocess Biosyst. Eng. 39, 773–784. doi:10.1007/s00449-016-1557-1

PubMed Abstract | CrossRef Full Text | Google Scholar

von Stosch, M., Oliveira, R., Peres, J., and Feyo de Azevedo, S. (2014). Hybrid semi-parametric modeling in process systems engineering: past, present and future. Comput. Chem. Eng. 60, 86–101. doi:10.1016/j.compchemeng.2013.08.008

CrossRef Full Text | Google Scholar

von Stosch, M., and Willis, M. J. (2017). Intensified design of experiments for upstream bioreactors. Eng. Life Sci. 17, 1173–1184. doi:10.1002/elsc.201600037

PubMed Abstract | CrossRef Full Text | Google Scholar

Walsh, G. (2018). Biopharmaceutical benchmarks 2018. Nat. Biotechnol. 36, 1136–1145. doi:10.1038/nbt.4305

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., and Georgakis, C. (2017). An in silico evaluation of data-driven optimization of biopharmaceutical processes. AIChE J. 63, 2796–2805. doi:10.1002/aic.15659

CrossRef Full Text | Google Scholar

Wang, Z., and Georgakis, C. (2019). A dynamic response surface model for polymer grade transitions in industrial plants. Industrial Eng. Chem. Res. 58, 11187–11198. doi:10.1021/acs.iecr.8b04491

CrossRef Full Text | Google Scholar

Wurm, F. M. (2004). Production of recombinant protein therapeutics in cultivated mammalian cells. Nat. Biotechnol. 22, 1393–1398. doi:10.1038/nbt1026

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, S., Navarathna, P., Ghosh, S., and Bequette, B. W. (2020). Hybrid modeling in the era of smart manufacturing. Comput. Chem. Eng. 140, 106874. doi:10.1016/j.compchemeng.2020.106874

CrossRef Full Text | Google Scholar

Zhou, W., Rehm, J., Europa, A., and Hu, W. (1997). Alteration of mammalian cell metabolism by dynamic nutrient feeding. Cytotechnology 24, 99–108. doi:10.1023/a:1007945826228

PubMed Abstract | CrossRef Full Text | Google Scholar