Circular economy-based multi-objective decentralized controller for activated sludge wastewater treatment plant

Introduction: Water scarcity and water pollution are two major issues in India. Circular economy-based wastewater treatment technology provides the most sustainable solutions for solving these issues. In this paper, a novel multi-objective decentralized controller (MODC) is proposed for benchmarking a multi-input multi-output (MIMO) activated sludge wastewater treatment plant (WWTP) to achieve maximum effluent quality with minimum cost. WWTPs with conventional control schemes consume more energy to achieve the desired effluent quality.

Methods: In this study, a MIMO model is developed for the activated sludge process (ASP) from a physics-based model, and relative gain array (RGA) analysis are carried out to determine the interaction between the loops to identify a suitable control scheme for the MIMO process. In addition, a multi-objective decentralized control problem is formulated to achieve the conflicting multiple objectives of improving effluent quality and minimizing operational costs by efficient usage of energy.

Results and discussion: The desired quality and cost reduction are verified by comparing the integral square error (ISE) and control effort (CE) values of a closed-loop WWTP. A multi-objective evolutionary algorithm (MOEA), namely, the non-dominated sorting genetic algorithm (NSGA)-II, successfully solves the multi-objective control problem. NSGA-II provides several optimal solutions in the Pareto front. In order to demonstrate the feasibility of the proposed controller, three optimal solutions are selected from the Pareto-optimal front, and their closed-loop performances are evaluated qualitatively and quantitatively for both servo and regulatory operations. Improving the quality of effluent enhances active sludge production, which in turn increases the methane production in the anaerobic digester.

1 Introduction

Wastewater treatment plays a major role in developing countries like India due to water scarcity and environmental pollution. The population rise in major cities leads to more water consumption and wastewater discharge into natural water bodies. According to the Central Ground Water Authority, Government of India report, an average individual utilizes 150–200 L of water per day. Only 10 L is consumed for cooking and drinking; 40 L per day is spent on washing dishes, washing clothes, and floor cleaning; and the remaining 85 L is utilized for toilet flushing and bathing. In general, the 80 L of wastewater used for washing and bathing could be reused for gardening, toilet flushing, and other useful applications with proper treatment. Many cities in India have centralized wastewater treatment plants (WWTPs) with conventional treatment techniques. However, most of them are less effective because they require underground pipe lining, pumping stations, and extensive maintenance. In contrast, a WWTP with advanced technologies would improve the quality of water and reduce maintenance costs (Grobelak et al., 2019). These technologies could lead to the design of decentralized WWTPs that deploy sophisticated techniques closer to the water generation point to enable more effective reuse of water. Two types of treatment plants, namely, sewage treatment plants (STPs) and effluent treatment plants (ETPs), are used to treat sewage and industrial wastewater, respectively (Negi et al., 2022). In a WWTP, wastewater undergoes three stages: primary treatment, secondary treatment, and tertiary treatment.

Generally, untreated sewage has biological oxygen demand (BOD) and total solid substrate (TSS) values in the range of 250–350 mg/L and 150–200 mg/L, respectively. The characteristics of the effluent are predominantly influenced by its levels of BOD and TSS. A considerable proportion of sewage treatment plants (STPs) yield effluent containing BOD concentrations lower than 20 mg/L and TSS concentrations lower than 10 mg/L. In order to improve the quality of effluent, ETP requires conventional biological wastewater treatment techniques like the activated sludge process (ASP) to control dissolved oxygen concentration and substrate concentration in the effluent. The ASP is an effective secondary treatment process that uses an aeration tank and a sludge-settling tank. Organic matter in the sewage is digested by aerobic bacteria in the aeration tank. Aerobic bacteria within the aeration tank facilitate the digestion of organic substances present in sewage. Ensuring the growth of these aerobic bacteria necessitates an effective control system. According to Malaysia (2011), there’s a notable need for advanced control strategies to enhance or uphold the effluent quality of wastewater treatment plants (WWTPs). As a result, the processes of modeling, control variable selection, and designing control structures assume crucial importance in the pursuit of optimizing control objectives.

Hodasz et al. (2016) developed a linear model to estimate the unmeasured process parameters of an activated sludge model (ASM1). They also suggested that good control of a WWTP leads to better water quality and an efficient use of energy. Castro-Amoedo et al. (2022) presented an overview of energy potentials present in a WWTP and demonstrated the concepts for local energy supply based on integrated perspectives. The control of dissolved oxygen levels in WWTPs has considerably reduced the energy required for aeration purposes in aerobic-activated sludge plants. de Araujo et al. (2013) discussed the application of sensitivity analysis for the selection of economic controlled variables for the optimal operation of a WWTP. Samuelsson et al. (2005) analyzed the cross coupling between loops in a bioreactor model using the relative gain array (RGA) and Hankel interaction index array (HIIA) methods. In addition, they compared the performances of a decentralized control scheme and a multivariable control scheme. Vilanova and Alfaro (2009) proposed a multi-loop decentralized control strategy for the control of a WWTP based on an ASP. Vinayak and Narayanan (2017) attempted a centralized nonlinear state feedback proportional integral (PI) controller for an ASP and compared its performance with a centralized linear state feedback controller. Nor’Azlan et al. (2017) developed a centralized controller for a linear system using the Davison, Penttinen–Koivo, and Maciejowski methods. They have also tuned the centralized controller parameters using single objective optimization techniques, such as a genetic algorithm (GA), particle swarm optimization (PSO), and the bat algorithm. Holenda et al. (2007, 2008) applied a model predictive controller for an activated sludge wastewater treatment process to control the dissolved oxygen level in the reactor and optimize the effluent quality and aeration energy cost against the number of aeration cycles required per day using a GA. Sweetapple et al. (2014) demonstrated the potential of multi-objective optimization of WWTP control strategies for the reduction of greenhouse gas emissions. Chen et al. (2014) optimized benchmark simulation model 1 (BSM1) parameters to achieve the percentage of effluent violation (PEV), overall cost index (OCI), total volume (TV), and total solid substrate (TSS) using a non-dominated sorting genetic algorithm (NSGA)-II.

A multi-objective optimization is a valuable tool in control engineering for controller design and process optimization. Hu et al. (2014) proposed a multi-objective nonlinear PID controller parameter for greenhouse systems to minimize cost and maximize performance using NSGA-II. Tian et al. (2023) recently proposed that the installation position parameters of a submersible mixer can be optimized using multi-input multi-output (MIMO) for improved performance.

Compromising the performance and cost becomes a critical issue in WWTP. In recent years, applications of multi-objective optimization have played a major role in WWTP for control and process optimization. Reynoso-Meza and Carreño-Alvarado (2019) designed a multi-objective controller for a multivariable active sludge process with nitrification and denitrification. Qiao and Zhang (2018) developed a multi-objective control scheme for the Benchmark Simulation Model 1 (BSM1) MIMO process. Ghimire et al. (2021) reviewed two routes for developing more sustainable and circular economy-based wastewater treatment systems and challenges in those approaches. Kaur (2023) applied multi-objective optimization to improve the quality of WWTP effluent based on a data-driven model. The ASP utilizes suspended growth microorganisms to effectively remove organic matter and nutrients from wastewater, but it demands substantial energy and land resources and generates sludge. Trickling filters, in contrast, employ attached growth microorganisms and offer simpler operations with lower energy requirements but may not efficiently remove nutrients and face potential media clogging issues. Membrane bioreactors (MBRs) combine biological treatment with membrane filtration, producing high-quality effluent with reduced sludge, yet they come with higher capital and operational costs and are susceptible to membrane fouling. Sequential batch reactors (SBRs) feature flexible operation and good nutrient removal but may cause variations due to intermittent operation and require longer treatment time. Constructed wetlands provide an eco-friendly and aesthetically pleasing approach with low operating costs but necessitate larger land areas and may not be suitable for high-strength industrial wastewater. Advanced oxidation processes (AOPs) utilize chemical reactions to effectively remove recalcitrant pollutants without producing sludge, but their high cost and potential secondary waste generation remain drawbacks. Ultimately, the choice of the wastewater treatment model depends on the specific characteristics of the wastewater, treatment goals, available resources, and environmental considerations. Often, a combination of different treatment processes is adopted to optimize efficiency and achieve the desired effluent quality.

Much literature has been reported on circular-economy-based wastewater treatments (Neczaj and Grosser, 2018; Spreafico, 2022; Zhang and Liu, 2022). These studies have reported on circular economics in WWTPs and challenges, barriers that prevent the implementation of circular economics, and analysis and design for circular economics.

To our knowledge, using a multi-objective decentralized controller (MODC) for WWTP with ASM1 to control effluent substrate concentration and DO concentration by maximizing effluent quality and minimizing production cost has not yet been explored. MIMO systems allow for better control performance by considering multiple variables simultaneously. They can take into account cross-coupling effects between inputs and outputs, which often exist in interconnected processes. By controlling multiple variables concurrently, MIMO models can achieve tighter control and improved overall system stability. The main aim of this paper is to design a multi-objective decentralized PI controller for an ASP to achieve the conflicting multi-objectives of maximizing the performance of effluent quality and minimizing the production cost.

The main contributions of the proposed work are i) identifying inputs and outputs and developing an ASM1 model for a WWTP, ii) identification of a suitable controller (centralized/decentralized) for a MIMO process, iii) multi-objective control problem formulation for a decentralized controller, and iv) design of a circular economy-based MODC for WWTP using NSGA-II.

The paper is organized as follows: the modeling of benchmark ASP is described in Section 2. RGA analysis and multi-objective problem formulation are elucidated in Section 3. The design of the proposed MODC is discussed in Section 4. Section 5 presents closed-loop simulation studies of ASP. The concluding remarks are presented at the end.

2 Modeling of activated sludge process

2.1 Benchmark ASP

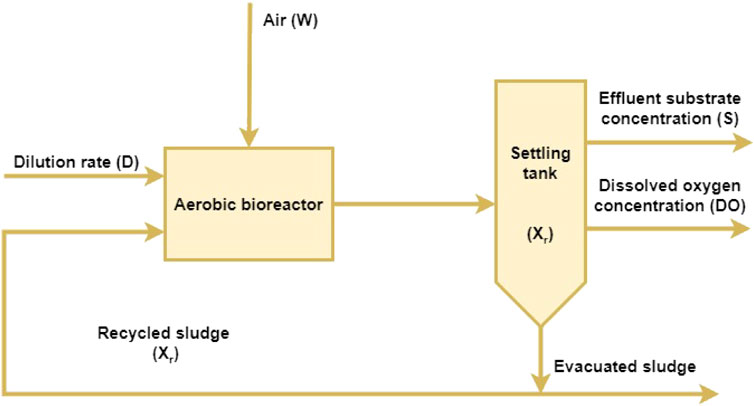
Secondary treatment plays a major role in treating wastewater in STPs. Secondary treatment consists of an aerobic bioreactor for aeration purposes and a settling tank, which is used to settle the sludge at the bottom while effluent is collected at the top of the tank. The schematic diagram of the ASP is given in Figure 1.

FIGURE 1

FIGURE 1. Schematic diagram of activated sludge process.

The aerator is taken to be a well-stirred tank for complete mixing in which microorganisms start reacting with organic pollutants in the wastewater. Six major groups of microorganisms, namely, bacteria, protozoa, metazoa, filamentous bacteria, algae, and fungi, are generally found in the aeration basin of the ASP. Microorganisms take the organic pollutants as food material and start growing; they collide to form sludge. Then, the suspended microorganisms are given to the settling tank (gravitational settling tank). In order to maintain the microorganism level in the tank, a part of the concentrated biomass is recycled back to the bioreactor, and the remaining material is removed from the settling tank. This study assumes that there is no microorganism growth in the settling tank.

2.2 Modeling of ASP

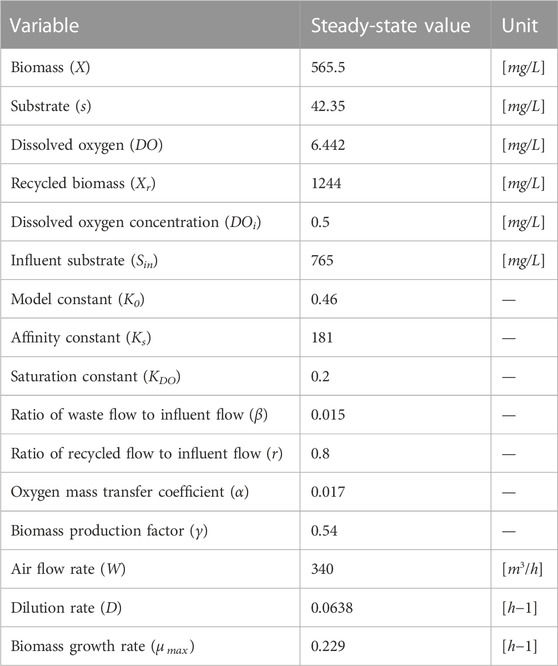
Modeling and control of an ASP is more complex due to biological reactions and variations in the influent characteristics. The ASM1 model is developed from the real-time ASP under the following assumptions: i) complete mixing takes place in the aeration tank, ii) the substrate concentration of influent wastewater is constant, iii) all reactions take place only in the aeration basin, and iv) no reaction takes place in the settling tank. Hence, the concentration of substrate in the aerobic bioreactor is the same as the concentration of substrate in the settling tank. Hodasz et al. (2016) reported the dynamic model of the ASP, which is given in Eqs 1–5.

Mass balance equation of biomass in aeration tank:

$\frac{dX\left(t\right)}{dt}=\mu \left(t\right)-D\left(t\right)\left(1+r\left(t\right)\right)X\left(t\right)+r\left(t\right)D\left(t\right)X_r\left(t\right)-bX\left(t\right).(1)$

Mass balance equation of substrate present in aeration tank:

$\frac{dS\left(t\right)}{dt}=-\frac{\mu \left(t\right)}{Y}X\left(t\right)-D\left(t\right)(1+r\left(t\right)S\left(t\right)+D\left(t\right)S_{in}\left(t\right).(2)$

Mass balance equation of dissolved oxygen concentration:

$\frac{dDO\left(t\right)}{dt}=-K_0\frac{\mu \left(t\right)}{Y}X\left(t\right)-D\left(t\right)\left(1+r\left(t\right)\right)DO\left(t\right)+D\left(t\right){DO}_i+\alpha W\left(t\right)\left[{DO}_{\mathit{max}}-DO\left(t\right)\right].(3)$

Mass balance equation in the activated sludge in the settling tank:

$\frac{d{X}_r\left(t\right)}{dt}=D\left(t\right)\left(1+r\left(t\right)\right)X\left(t\right)-D\left(t\right)\left(\beta +r\left(t\right)\right)X_r\left(t\right).(4)$

Biomass growth rate in aeration tank:

$\mu ={\mu }_{\mathit{max}}\frac{S\left(t\right)}{K_s+S\left(t\right)}\frac{DO\left(t\right)}{K_{DO}+DO\left(t\right)},(5)$

where $X\left(t\right),S\left(t\right),DO\left(t\right),X_r\left(t\right)$ are the state variables. In the ASP, the dilution rate $\left(D\right)$ and the air flow rate $W\left(t\right)$ are taken as manipulated variables to control the substrate $\left(S\right)$ and dissolved oxygen $\left(DO\right)$, and the biomass production factor $\left(Y\right)$ is taken to be the disturbance variable.

The transfer function plays a pivotal role in wastewater treatment plant and significantly impacts its performance. It represents the relationship between input variables, such as influent characteristics or control actions, and the corresponding output variables, usually effluent quality or process variables. Understanding the transfer function allows process engineers and operators to gain insight into the dynamic behavior of the WWTP and its response to changes in influent conditions or operational parameters. With this knowledge, they can design effective control strategies, optimize process conditions, and enhance treatment efficiency. Additionally, transfer functions are vital for process modeling and simulation, aiding in predicting system behavior under different scenarios and facilitating process optimization. They also play a crucial role in control system design and performance evaluation, enabling the WWTP to achieve stable operation, comply with regulatory standards, and consistently deliver high-quality effluent while minimizing environmental impact.

The transfer function model for MIMO is developed by linearizing the dynamic equations given in Eq. 1–4 around the steady-state operating points tabulated in Table 1 (Hodasz et al., 2016). The transfer function model is presented in Eq. 6:

$\left[S\left(s\right);DO\left(s\right)\right]=\left[G_{11}{G}_{12};G_{21}{G}_{22}\right]\left[D\left(s\right);W\left(s\right)\right],(6)$

where

$G_{11}\left(s\right)=\frac{S\left(s\right)}{D\left(s\right)}=\frac{688.8s^3+4261s^2+680.9s+0.4246}{s^4+7.651s^3+7.277s^2+1.136s+0.01056},$

$G_{12}\left(s\right)=\frac{S\left(s\right)}{W\left(s\right)}=\frac{-0.01268s^2-0.002405s-2.457*{10}^{-5}}{s^4+7.651s^3+7.277s^2+1.136s+0.01056},$

$G_{21}\left(s\right)=\frac{DO\left(s\right)}{D\left(s\right)}=\frac{-11.1s^3-278.7s^2-52.54s-0.5329}{s^4+7.651s^3+7.277s^2+1.136s+0.01056},$

$G_{22}\left(s\right)=\frac{DO\left(s\right)}{W\left(s\right)}=\frac{-0.06151s^3+0.06734s^2+0.01078s+0.0001004}{s^4+7.651s^3+7.277s^2+1.136s+0.01056}.$

TABLE 1

TABLE 1. Steady-state operating points.

The aforementioned transfer function model is used for RGA analysis to identify a suitable control scheme for the ASP in the subsequent section.

3 Identification of control strategy and multi-objective control problem formulation

In this section, RGA analysis is applied to the WWTP transfer function model, and the multi-objective control problem formulation is discussed.

3.1 RGA analysis

RGA is used to determine the best input (u)–output (y) pairing for multivariable systems. It quantifies the change in steady-state gain between an input–output pair that occurs when other control loops are closed. It provides a measure of steady-state interactions from gain. The relative gain between input j and output i is given by Eq. 7:

${\lambda }_{ij}=\frac{{\left(\mathit{\partial }{y}_i/\mathit{\partial }{u}_j\right)}_u}{{\left(\mathit{\partial }{y}_i/\mathit{\partial }{u}_j\right)}_y},(7)$

where${\left(\mathit{\partial }{y}_i/\mathit{\partial }{u}_j\right)}_u$ is the open-loop gain with all other control loops open, and${\left(\mathit{\partial }{y}_i/\mathit{\partial }{u}_j\right)}_y$ is the closed-loop gain with all other control loops closed.

The ASP is a 2 × 2 system; its RGA structure is presented in Eq. 8:

$\wedge =\left[{\lambda }_{11}{\lambda }_{12};{\lambda }_{21}{\lambda }_{22}\right]=\left[\frac{1}{1-\frac{K_{12}{K}_{21}}{K_{22}{K}_{11}}}\frac{1}{1-\frac{K_{11}{K}_{22}}{K_{12}{K}_{21}}};\frac{1}{1-\frac{K_{11}{K}_{22}}{K_{12}{K}_{21}}}\frac{1}{1-\frac{K_{12}{K}_{21}}{K_{22}{K}_{11}}}\right].(8)$

The steady-state gain matrix of the ASP is computed from Eq. 6 given in Eq. 9:

$\left[K_{11}{K}_{12};K_{21}{K}_{22}\right]=\left[40.20833-0.00232670;-50.46400.0095075\right].(9)$

Using the gain matrix given in Eq. 9, the RGA matrix is developed using Eq. 10:

$\left[{\lambda }_{11}{\lambda }_{12};{\lambda }_{21}{\lambda }_{22}\right]=\left[1.443293-0.443293;-0.4432931.443293\right].(10)$

From the obtained RGA matrix, it is recommended that $u_1$ be paired with $y_1$ and $u_2$ be paired with $y_2$. The obtained RGA matrix shows that there is a minimum interaction between the process loops. Hence, a decentralized control scheme is preferred for an ASP. Muntean et al. (2015) also carried out RGA analysis for the WWTP process with recycled sludge flow to influent flow and aeration rate from the bioreactor as manipulated variables and used the substrate and dissolved oxygen as controlled variables and reported that a decentralized control scheme is more suitable for the WWTP process with the identified model due to fewer interactions between the loops.

3.2 Decentralized PI controller

As stated earlier, the interaction between inputs and outputs is weak; hence, a decentralized control architecture with a PI controller is proposed. The decentralized control is given in Eq. 11:

$G_c\left(s\right)=\left[\begin{array}{cc}{G}_{c11}\left(s\right)& 0\\ 0& G_{c22}\left(s\right)\end{array}\right],(11)$

where $G_{c11}\left(s\right)=K_{c1}+\frac{K_{i1}}{s}$ and

$G_{c22}\left(s\right)=K_{c2}+\frac{K_{i2}}{s}.$

To tune the PI controller parameters, a multi-objective control problem is formulated in the next subsection.

3.3 Multi-objective problem formulation (MOO)

The multi-objective control problem is formulated by identifying the PI control structure to improve the quality of effluent by minimizing the integral square error (ISE) and reducing production costs by minimizing control effort (CE). The conflicting objective functions of the multi-objective control problem are given in Equations (12) and (13):

$\min f_1\left(ISE\right)={\displaystyle {\int }_0^{\infty }}{\left({\alpha }_1{e}_1\right.}^2+{\alpha }_2{e_2}^2)dt=f\left(K_{C1},K_{i1}{,K_{C2},K_{i2},\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2\right),(12)$

$\min f_2\left(CE\right)={\displaystyle {\int }_0^{\infty }}{\left({\beta }_1{c}_1\right.}^2+{\beta }_2{c_2}^2)dt=f\left(K_{C1},K_{i1}{,K_{C2},K_{i2},\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2\right).(13)$

The aforementioned two objective functions are optimized using eight decision variables. $K_{C1}$ and $K_{i1}$ are proportional gain and integral gain of the substrate (loop 1), respectively.$K_{C2}$ and $K_{i2}$ are proportional gain and integral gain of dissolved oxygen (loop 2), respectively.${\alpha }_1$ and ${\alpha }_2$ are weighting factors for loop 1 and loop 2, respectively.${\beta }_1$ and ${\beta }_2$ are weighting factors for loop 1 and loop 2, respectively.$e_1$ and $e_2$ are errors in loop 1 and loop 2, respectively.$c_1$ and $c_2$ are control efforts of loop 1 and loop 2, respectively.

4 Design of a multi-objective decentralized controller

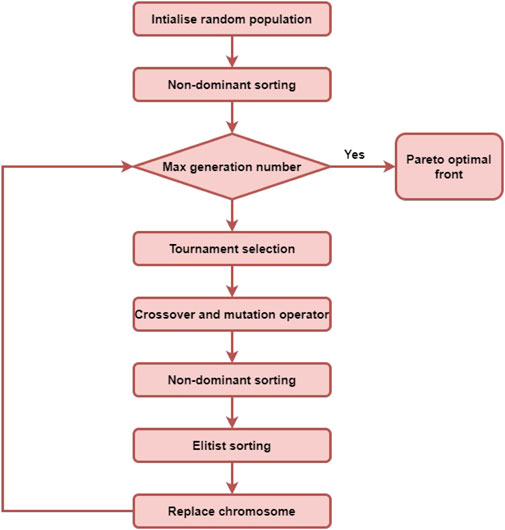
Multi-objective optimization involves more than one objective function, and the functions must be optimized simultaneously. The multi-objective control problem is commonly solved by evolutionary algorithms (EAs). The primary reason for using EAs is their ability to find multiple Pareto-optimal solutions in one single simulation run. Deb et al. (2002) reported the performance comparisons of various multi-objective evolutionary algorithms (MOEAs) such as a niched Pareto genetic algorithm (NPGA), a Pareto-archived evolution strategy (PAES), a strength Pareto evolutionary algorithm (SPEA) and a non-dominant sort genetic algorithm-II (NSGA-II) for different test problems. Most EAs have been successfully applied for design optimization and controller optimization over the past two decades. However, NSGA-II outperforms other EAs for most multi-objective problems. It can provide a better spread of solutions and better convergence near the true Pareto-optimal front. In this paper, NSGA-II is selected to solve the multi-objective control problem of ASP.

4.1 Non-dominant sort genetic algorithm-II

Deb et al. (2002) proposed NSGA-II, which alleviates the difficulty of NSGA. The important features of NSGA-II are as follows:

• NSGA-II is based upon a GA.

• It is an extended version of NSGA.

• It overcomes the difficulties faced in NSGA, which are complexity, lack of elitism, and choosing the optimal parameter for the sharing parameter.

• The main aim of NSGA-II is to preserve elitism and diversity.

• NSGA-II gives a Pareto-optimal front, which consists of a set of optimal solutions for conflicting objective functions.

The algorithm and detailed implementation procedure of NSGA-II are found in Kalyanmoy Deb (2002). The flowchart of NSGA-II is shown in Figure 2.

FIGURE 2

FIGURE 2. Flow chart of NSGA-II.

4.2 Implementation of NSGA-II

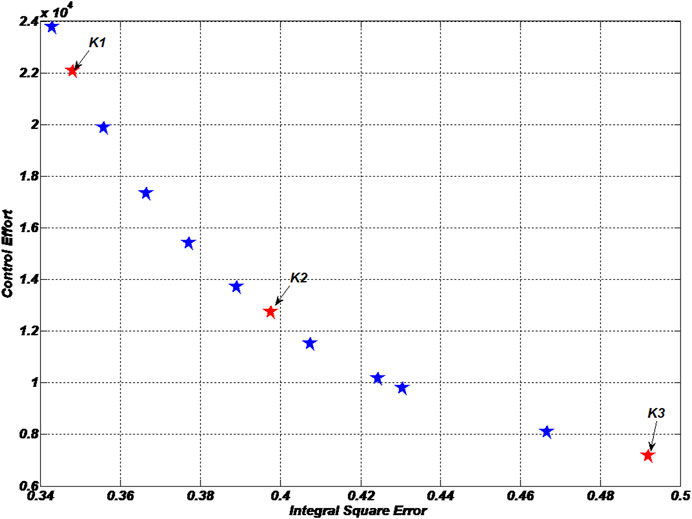
The parameters of NSGA-II used for execution are given in Table 2. The Pareto-optimal front provides the optimal solutions for the conflicting objective functions, and it is shown in Figure 3.

TABLE 2

TABLE 2. Parameters of NSGA-II.

FIGURE 3

FIGURE 3. Pareto optimal front of NSGA-II.

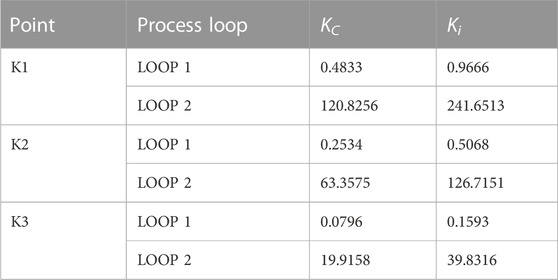
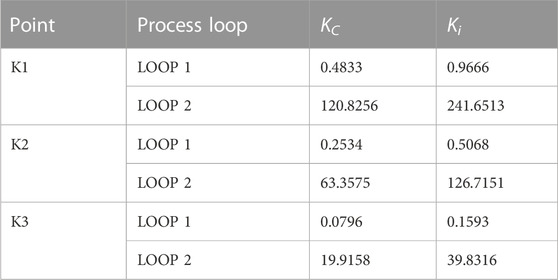
To study the trade-off between the performance and cost of production, three controller parameters at points K1, K2, and K3 are selected from the Pareto-optimal front and are tabulated in Table 3.

TABLE 3

TABLE 3. Controller parameters for the selected three points.

5 Closed-loop simulation studies of ASP

5.1 Servo response

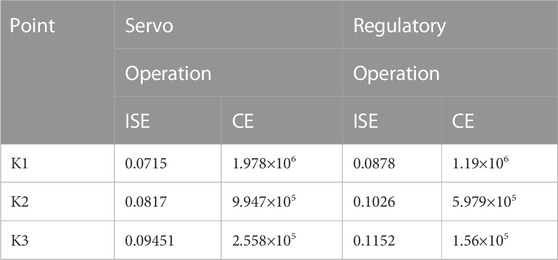
The ASP is simulated using the set of differential equations given in the modeling section. Then, the closed-loop servo responses are obtained for the selected controllers and qualitatively compared in Figure 4, and associated manipulated variables are shown in Figure 5. For quantitative comparison, the performance measures are given in Table 4.

FIGURE 4

FIGURE 4. Servo response of Activated Sludge Process (A) Substrate (B) Dissolved oxygen.

FIGURE 5

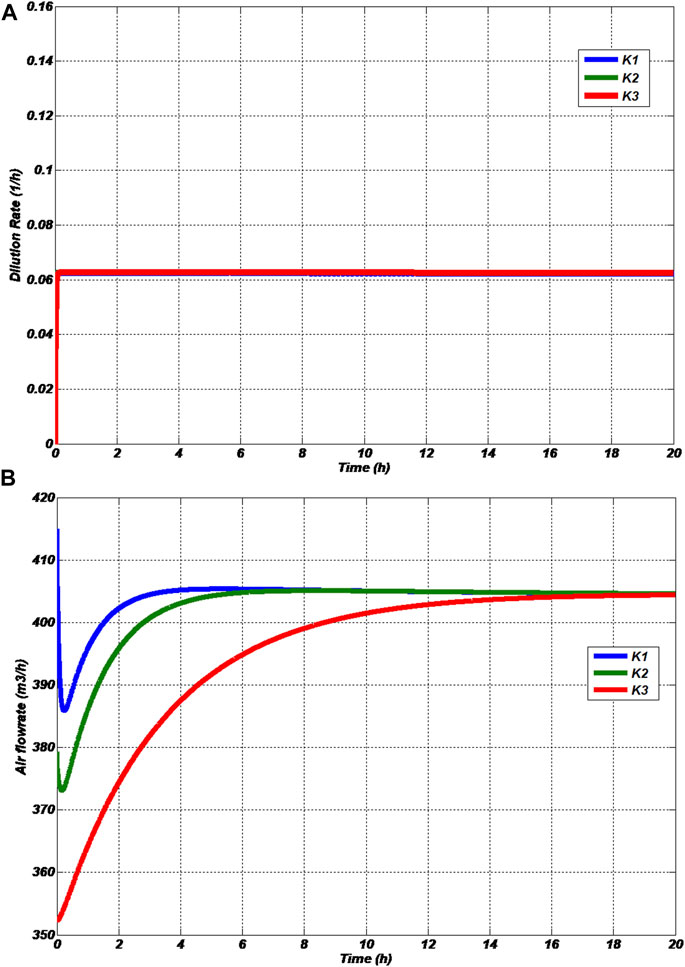
FIGURE 5. Variations in manipulated variables under servo operation (A) Dilution rate (B) Airflow rate.

TABLE 4

TABLE 4. Performance measures of MODC.

The servo responses with controller gains at the K₁ point do not provide significant variation in the substrate concentration. However, the responses show the variation in the dissolved oxygen concentration in the effluent. From Figures 4B,5B, it is observed that the process with controller gains at the K₁ point takes less retention time and settles very quickly at the steady-state value due to large CE (refer Table 4). It is observed from Table 4 that controller gains at the K₁ point give a much smaller integral square error. Hence, in order to improve the performance, the closed-loop system must compromise on CE.

The process with controller gains at the K₂ point gives the trade-off between the performance and CE (refer Table 4). The retention time of the process with controller gains at the K₂ point shown in Figures 4B, 5B is larger than the controller gains at the K₁ point; meanwhile, it takes a smaller CE than a process with controller gains at the K₁ point.

The closed-loop servo response with controller gains at K₃ shown in Figures 4B, 5B exhibited a longer retention time than other controllers. The controller gains at the K₃ point have less CE (refer Table 4). At the same time, it should compromise on the performance of the system.

5.2 Regulatory response

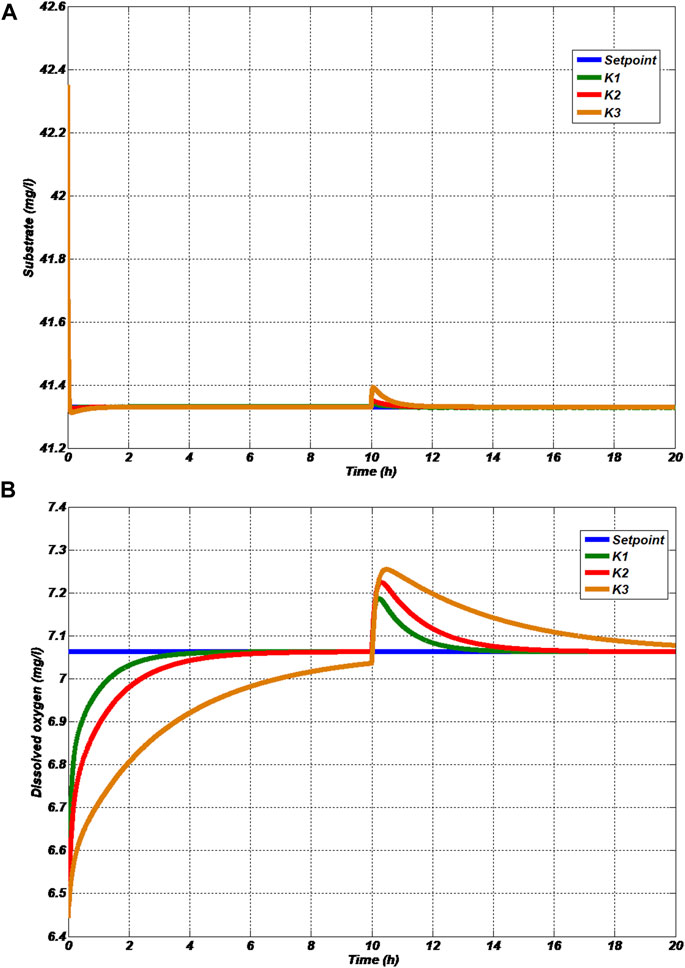
To study the regulatory operation of the ASP, biomass production factor (Y) is selected as a disturbance and is changed from 0.54 to 0.594 at the tenth hour. The simulated regulatory responses of loop 1 and loop 2 are shown in Figure 6, and the corresponding manipulated variables are shown in Figure 7. The quantitative comparison of the regulatory operation with various controllers is tabulated in Table 4.

FIGURE 6

FIGURE 6. Regulatory response of activated sludge process (A) Substrate (B) Dissolved oxygen.

FIGURE 7

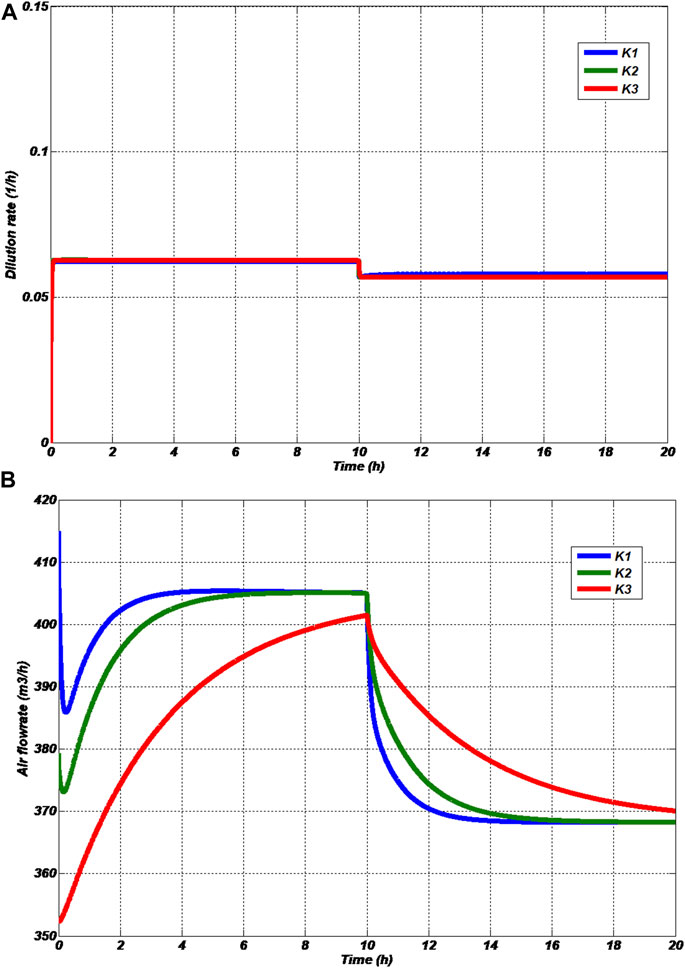
FIGURE 7. Variations in manipulated variables under regulatory operation (A) Dilution rate (B) Airflow rate.

It is found from Figures 6A, B that the effect of disturbance on substrate concentration and dilution rate is less than the effect on dissolved oxygen concentration and air flow rate. In quantitative comparison, it is noted that the CE required for regulatory operation is less than the CE required by the servo operation. However, the ISEs provided by the regulatory operation are larger than those of the servo operation. Hence, minimization of CE will affect the performance of the process. Meanwhile, minimization of CE reduces the production cost of freshwater.

The circular economy in wastewater treatment leads to freshwater, nutrient, and energy recovery from wastewater. Improvement in effluent water quality leads to the reuse of water for domestic applications, which will reduce water stress. Furthermore, nutrients recovered from active sludge can be used as fertilizers. Energy recovery can also be done by producing biogas from active sludge.

6 Conclusion

In this work, a novel circular economy-based MODC design is proposed for the MIMO ASP. The transfer function model is developed from nonlinear differential equations to select an appropriate control scheme to control dissolved oxygen concentration and substrate concentration in the effluent of the ASP. Then, RGA analysis is performed to determine the interactions between the loops. From the interaction analysis, it is concluded that a decentralized controller is the best control scheme for the ASP due to less interaction between the loops. A multi-objective control problem is formulated to improve effluent quality and reduce costs. The multi-objective control problem is successfully solved by the MOEA NSGA-II. Some of the conventional wastewater treatment techniques are simple and have low production costs; however, they require a long treatment time and result in poor effluent quality. Whereas sophisticated treatment techniques are more expensive due to high production costs but can provide good-quality effluent. The advantage of the proposed multi-objective controller is that it can provide a number of optimal solutions in the Pareto-optimal front. The users can select their own solutions according to the applications from the Pareto-optimal front. The feasibility of the proposed controller is demonstrated by selecting three controller parameters from the Pareto-optimal front, and their closed-loop servo and regulatory performances are compared qualitatively as well as quantitatively. The proposed circular economy-based multi-objective controller will be very useful for the reuse of wastewater, nutrients, and energy.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

SS: writing—original draft, conceptualization, methodology, and software. CM: writing—review, editing, conceptualization, methodology, and software. PN: writing and conceptualization. All authors contributed to the article and approved the submitted version.

Acknowledgments

The authors gratefully acknowledge the Department of Instrumentation, Madras Institute of Technology, for their support with conducting the experiments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Castro-Amoedo, R., Morisod, N., Granacher, J., and Maréchal, F. (2021). The role of biowaste: A multi-objective optimization platform for combined heat, power and fuel. Front. Energy Res. 9, 718310. doi:10.3389/fenrg.2021.718310

CrossRef Full Text | Google Scholar

Chen, W., Yao, C., and Lu, X. (2014). Optimal design activated sludge process by means of multi-objective optimization: case study in benchmark simulation model 1 (BSM1). Water Sci. Technol. 69 (10), 2052–2058. doi:10.2166/wst.2014.119

PubMed Abstract | CrossRef Full Text | Google Scholar

de Araujo, A. C., Gallani, S., Mulas, M., and Skogestad, S. (2013). Sensitivity analysis of optimal operation of an activated sludge process model for economic controlled variable selection. Industrial Eng. Chem. Res. 52 (29), 9908–9921. doi:10.1021/ie4006673

CrossRef Full Text | Google Scholar

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. A. M. T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6 (2), 182–197. doi:10.1109/4235.996017

CrossRef Full Text | Google Scholar

Ghimire, U., Sarpong, G., and Gude, V. G. (2021). Transitioning wastewater treatment plants toward circular economy and energy sustainability. ACS omega 6 (18), 11794–11803. doi:10.1021/acsomega.0c05827

PubMed Abstract | CrossRef Full Text | Google Scholar

Grobelak, A., Grosser, A., Kacprzak, M., and Kamizela, T. (2019). Sewage sludge processing and management in small and medium-sized municipal wastewater treatment plant-new technical solution. J. Environ. Manag. 234, 90–96. doi:10.1016/j.jenvman.2018.12.111

PubMed Abstract | CrossRef Full Text | Google Scholar

Hodasz, N. I., Brădilă, V. I., Nascu, I., and Lendek, Z. “Modeling and parameter estimation for an activated sludge wastewater treatment process,” in Proceedings of the 2016 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 2016, May, 1–6.

Google Scholar

Holenda, B., Domokos, E., Rédey, A., and Fazakas, J. (2007). Aeration optimization of a wastewater treatment plant using genetic algorithm. Optim. control Appl. methods 28 (3), 191–208. doi:10.1002/oca.796

CrossRef Full Text | Google Scholar

Holenda, B., Domokos, E., Redey, A., and Fazakas, J. (2008). Dissolved oxygen control of the activated sludge wastewater treatment process using model predictive control. Comput. Chem. Eng. 32 (6), 1270–1278. doi:10.1016/j.compchemeng.2007.06.008

CrossRef Full Text | Google Scholar

Hu, H., Xu, L., Goodman, E. D., and Zeng, S. (2014). NSGA-II-based nonlinear PID controller tuning of greenhouse climate for reducing costs and improving performances. Neural Comput. Appl. 24, 927–936. doi:10.1007/s00521-012-1312-8

CrossRef Full Text | Google Scholar

Kaur, N. (2023). “Modeling and multi-objective optimization of wastewater treatment process,”. Doctoral dissertation (Canada: The University of Western Ontario).

Google Scholar

Malaysia, M. (2011). Control strategies of wastewater treatment plants. Aust. J. Basic Appl. Sci. 5 (8), 446–455.

Google Scholar

Muntean, I., Both, R., Crisan, R., and Nascu, I. “RGA analysis and decentralized control for a wastewater treatment plant,” in Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, March 2015.

Google Scholar

Neczaj, E., and Grosser, A. (2018). Circular economy in wastewater treatment plant–challenges and barriers. Proceedings 2 (11), 614. doi:10.3390/proceedings2110614

CrossRef Full Text | Google Scholar

Negi, P., Verma, H., Singh, S. P., Mahapatra, B. S., and Jatav, H. S. (2022). “Global scenario of sewage-sludge management,” in Sustainable management and utilization of sewage sludge (Berlin, Germany: Springer), 383–401.

CrossRef Full Text | Google Scholar

Nor’Azlan, N. A., Selamat, N. A., and Yahya, N. M. (2018). Multivariable PID controller design tuning using bat algorithm for activated sludge process IOP Conference Series: materials science and engineering. IOP Conf. Ser. Mater. Sci. Eng. 342 (1), 012030. doi:10.1088/1757-899x/342/1/012030

CrossRef Full Text | Google Scholar

Qiao, J., and Zhang, W. (2018). Dynamic multi-objective optimization control for wastewater treatment process. Neural Comput. Appl. 29, 1261–1271. doi:10.1007/s00521-016-2642-8

CrossRef Full Text | Google Scholar

Reynoso-Meza, G., and Carreño-Alvarado, E. P. (2019). November). PI tuning of a multivariable activated sludge process with nitrification and denitrification with multi-objective optimization. Proceedings 48 (1), 4. doi:10.3390/ECWS-4-06434

CrossRef Full Text | Google Scholar

Samuelsson, P., Halvarsson, B., and Carlsson, B. (2005). Interaction analysis and control structure selection in a wastewater treatment plant model. IEEE Trans. Control Syst. Technol. 13 (6), 955–964. doi:10.1109/tcst.2005.854322

CrossRef Full Text | Google Scholar

Spreafico, C. (2022). An analysis of design strategies for circular economy through life cycle assessment. Environ. Monit. Assess. 194 (3), 180. doi:10.1007/s10661-022-09803-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Sweetapple, C., Fu, G., and Butler, D. (2014). Multi-objective optimisation of wastewater treatment plant control to reduce greenhouse gas emissions. Water Res. 55, 52–62. doi:10.1016/j.watres.2014.02.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, F., Yang, C., Zhang, E., Sun, D., Shi, W., and Chen, Y. (2023). A study on the multi-objective optimization method and characteristic analysis of installation locations of submersible mixer for sewage. Front. Energy Res. 11, 1180607. doi:10.3389/fenrg.2023.1180607

CrossRef Full Text | Google Scholar

Vilanova, R., and Alfaro, V. “Multi-loop PI-based control strategies for the activated sludge process,” in Proceedings of the 2009 IEEE Conference on Emerging Technologies & Factory Automation, Palma de Mallorca, Spain, 2009, September, 1–8.

Google Scholar

Vinayak, J. R., and Narayanan, S. “Nonlinear PI with state feedback control for activated sludge process,” in Proceedings of the 2017 International Conference on Information, Communication, Instrumentation and Control (ICICIC), Indore, India, 2017, August, 1–7.

Google Scholar

Zhang, X., and Liu, Y. (2022). Circular economy is game-changing municipal wastewater treatment technology towards energy and carbon neutrality. Chem. Eng. J. 429, 132114. doi:10.1016/j.cej.2021.132114

CrossRef Full Text | Google Scholar